Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
| Справочник по математике | Геометрия (Планиметрия) | Треугольники |
| Серединный перпендикуляр к отрезку |
| Окружность описанная около треугольника |
| Свойства описанной около треугольника окружности. Теорема синусов |
| Доказательства теорем о свойствах описанной около треугольника окружности |
Серединный перпендикуляр к отрезку
Определение 1. Серединным перпендикуляром к отрезку называют, прямую, перпендикулярную к этому отрезку и проходящую через его середину (рис. 1).
Рис.1
Теорема 1. Каждая точка серединного перпендикуляра к отрезку находится на одном и том же расстоянии от концов этого отрезка.
Доказательство. Рассмотрим произвольную точку D, лежащую на серединном перпендикуляре к отрезку AB (рис.2), и докажем, что треугольники ADC и BDC равны.
Рис.2
Действительно, эти треугольники являются прямоугольными треугольниками, у которых катеты AC и BC равны, а катет DC является общим. Из равенства треугольников ADC и BDC вытекает равенство отрезков AD и DB. Теорема 1 доказана.
Теорема 2 (Обратная к теореме 1). Если точка находится на одном и том же расстоянии от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.
Доказательство. Докажем теорему 2 методом «от противного». С этой целью предположим, что некоторая точка E находится на одном и том же расстоянии от концов отрезка, но не лежит на серединном перпендикуляре к этому отрезку. Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точки E и A лежат по разные стороны от серединного перпендикуляра (рис.3). В этом случае отрезок EA пересекает серединный перпендикуляр в некоторой точке, которую мы обозначим буквой D.
Рассмотрим сначала случай, когда точки E и A лежат по разные стороны от серединного перпендикуляра (рис.3). В этом случае отрезок EA пересекает серединный перпендикуляр в некоторой точке, которую мы обозначим буквой D.
Рис.3
Докажем, что отрезок AE длиннее отрезка EB. Действительно,
Таким образом, в случае, когда точки E и A лежат по разные стороны от серединного перпендикуляра, мы получили противоречие.
Рис.4
Теперь рассмотрим случай, когда точки E и A лежат по одну сторону от серединного перпендикуляра (рис.4). Докажем, что отрезок EB длиннее отрезка AE. Действительно,
Полученное противоречие и завершает доказательство теоремы 2
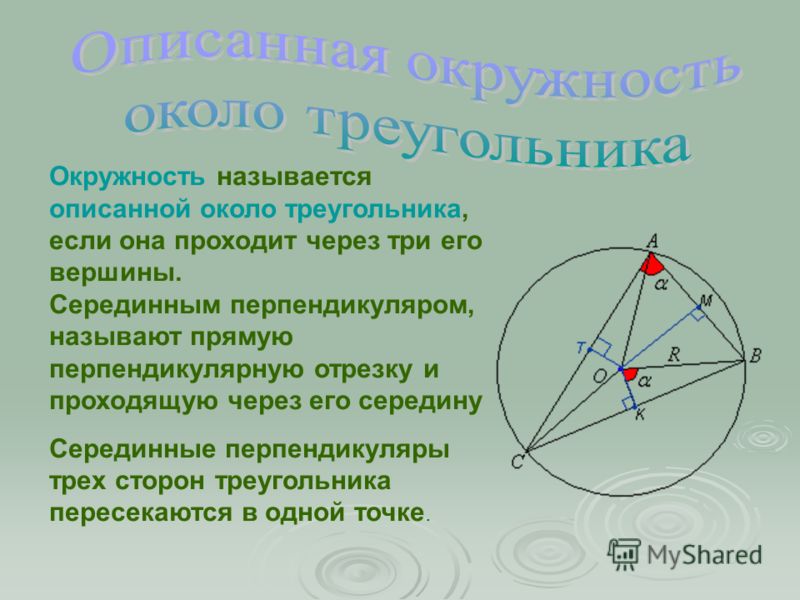
Окружность, описанная около треугольника
Определение 2. Окружностью, описанной около треугольника, называют окружность, проходящую через все три вершины треугольника (рис.5). В этом случае треугольник называют треугольником, вписанным в окружность, или вписанным треугольником.
Окружностью, описанной около треугольника, называют окружность, проходящую через все три вершины треугольника (рис.5). В этом случае треугольник называют треугольником, вписанным в окружность, или вписанным треугольником.
Рис.5
Свойства описанной около треугольника окружности. Теорема синусов
| Фигура | Рисунок | Свойство |
| Серединные перпендикуляры к сторонам треугольника | Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. Посмотреть доказательство | |
| Окружность, описанная около треугольника | Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. Посмотреть доказательство | |
| Центр описанной около остроугольного треугольника окружности | Центр описанной около остроугольного треугольника окружности лежит внутри треугольника. | |
| Центр описанной около прямоугольного треугольника окружности | Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. Посмотреть доказательство | |
| Центр описанной около тупоугольного треугольника окружности | Центр описанной около тупоугольного треугольника окружности лежит вне треугольника. | |
| Теорема синусов | Для любого треугольника справедливы равенства (теорема синусов): , где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности. Посмотреть доказательство | |
| Площадь треугольника | Для любого треугольника справедливо равенство: S = 2R2 sin A sin B sin C , где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности. Посмотреть доказательство | |
| Радиус описанной окружности | Для любого треугольника справедливо равенство: где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности. Посмотреть доказательство |
| Серединные перпендикуляры к сторонам треугольника |
Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. Посмотреть доказательство |
| Окружность, описанная около треугольника |
Около любого треугольника можно описать окружность. Посмотреть доказательство |
| Центр описанной около остроугольного треугольника окружности |
Центр описанной около остроугольного треугольника окружности лежит внутри треугольника. |
| Центр описанной около прямоугольного треугольника окружности |
Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. Посмотреть доказательство |
| Центр описанной около тупоугольного треугольника окружности |
Центр описанной около тупоугольного треугольника окружности лежит вне треугольника. |
| Теорема синусов |
Для любого треугольника справедливы равенства (теорема синусов): , где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности. Посмотреть доказательство |
| Площадь треугольника |
Для любого треугольника справедливо равенство: S = 2R2 sin A sin B sin C , где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности. Посмотреть доказательство |
| Радиус описанной окружности |
Для любого треугольника справедливо равенство: где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности. Посмотреть доказательство |
Доказательства теорем о свойствах описанной около треугольника окружности
Теорема 3. Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.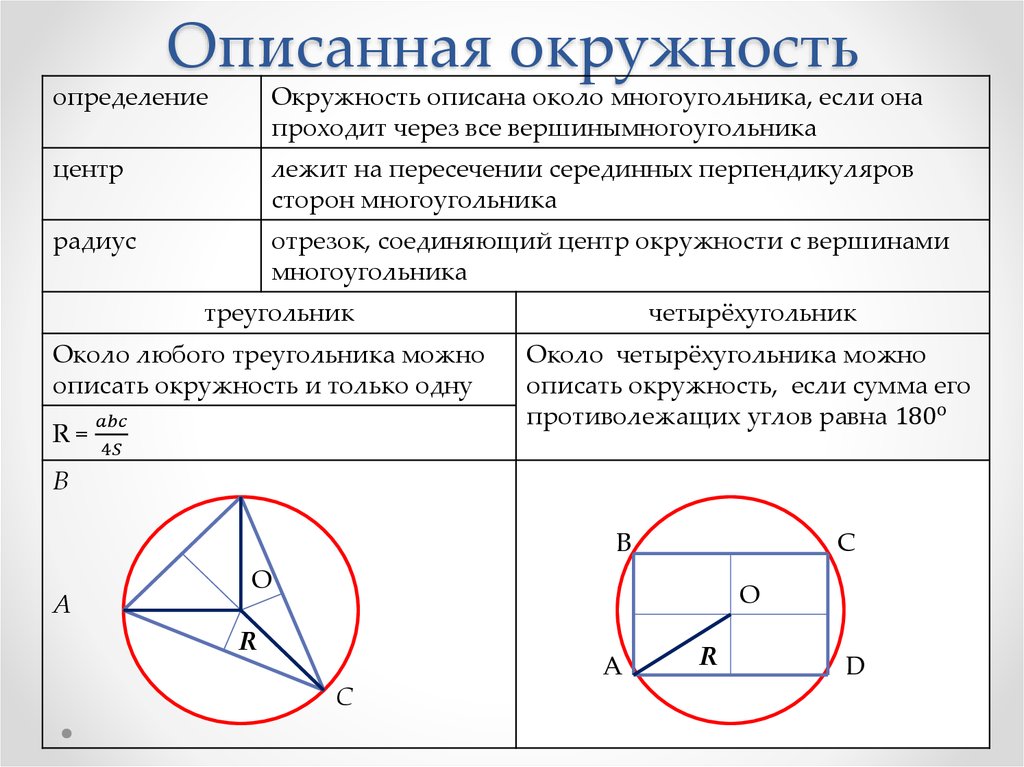
Доказательство. Рассмотрим два серединных перпендикуляра, проведённых к сторонам AC и AB треугольника ABC, и обозначим точку их пересечения буквой O (рис. 6).
Рис.6
Поскольку точка O лежит на серединном перпендикуляре к отрезку AC, то в силу теоремы 1 справедливо равенство:
CO = AO .
Поскольку точка O лежит на серединном перпендикуляре к отрезку AB, то в силу теоремы 1 справедливо равенство:
AO = BO .
Следовательно, справедливо равенство:
CO = BO ,
откуда с помощью теоремы 2 заключаем, что точка O лежит на серединном перпендикуляре к отрезку BC. Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.
Следствие. Около любого треугольника можно описать окружность.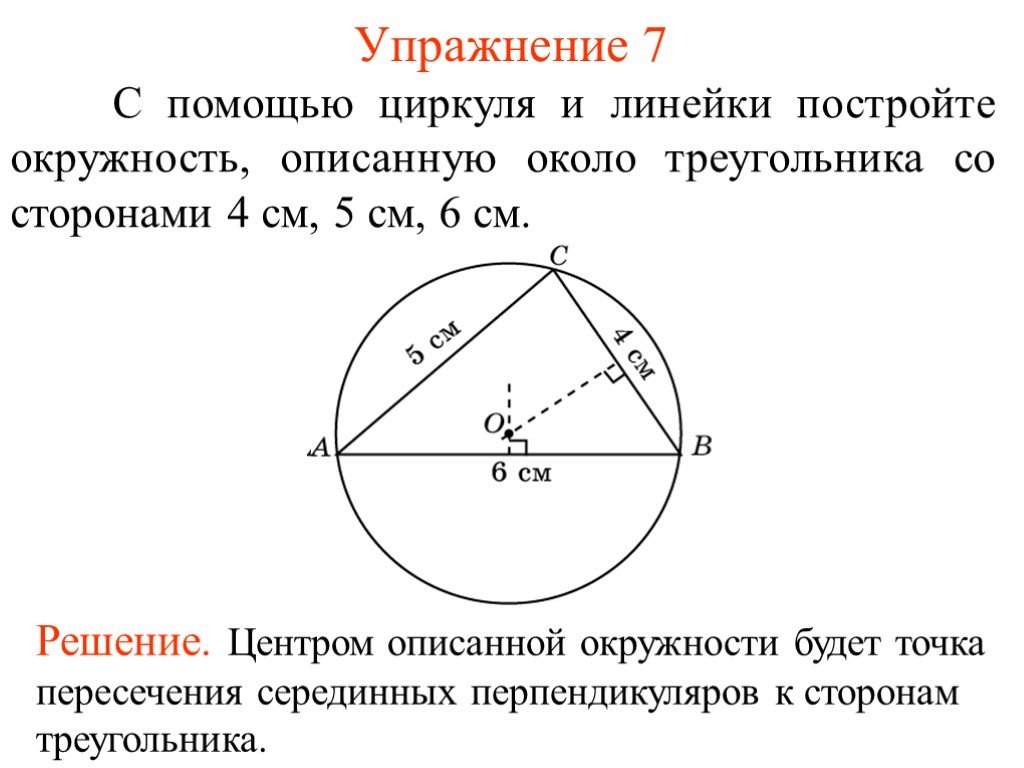 Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.
Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.
Доказательство. Рассмотрим точку O, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника ABC (рис. 6).
При доказательстве теоремы 3 было получено равенство:
AO = OB = OC ,
из которого вытекает, что окружность с центром в точке O и радиусами OA, OB, OC проходит через все три вершины треугольника ABC, что и требовалось доказать.
Теорема 4 (теорема синусов). Для любого треугольника (рис. 7)
Рис.7
справедливы равенства:
.
Доказательство. Докажем сначала, что длина хорды окружности радиуса R хорды окружности радиуса R, на которую опирается вписанный угол величины φ , вычисляется по формуле:
l = 2Rsin φ . | (1) |
Рассмотрим сначала случай, когда одна из сторон вписанного угла является диаметром окружности (рис.8).
Рис.8
Угол MPN, как угол,опирающийся на диаметр, является прямым угломугол,опирающийся на диаметр, является прямым углом, и равенство (1) вытекает из определения синуса угла прямоугольного треугольника.
Поскольку все вписанные углы, опирающиеся на одну и ту же дугу, равны, то для произвольного вписанного угла всегда найдется равный ему вписанный угол, у которого одна из сторон является диаметром окружности.
Формула (1) доказана.
Из формулы (1) для вписанного треугольника ABC получаем (рис.7):
Теорема синусов доказана.
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Геометрические утверждения — Математика — Экзамены, ЕГЭ, ОГЭ
Зачетная работа по теме «Геометрические утверждения»
Примечание
Выполните задание, выбрав нужные утверждения
1.Какое из следующих утверждений верно?
1) В прямоугольном треугольнике гипотенуза равна сумме катетов.
2) Всегда один из двух смежных углов острый, а другой тупой.
3) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
2.Какое из следующих утверждений верно?
1) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
2) В параллелограмме есть два равных угла.
3) Площадь прямоугольного треугольника равна произведению длин его катетов.
3.Какие из следующих утверждений верны?
1) Все высоты равностороннего треугольника равны.
2) Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу.
3) В любой ромб можно вписать окружность.
4. Какое из следующих утверждений верно?
1) Диагонали ромба точкой пересечения делятся пополам.
2) В тупоугольном треугольнике все углы тупые.
3) Каждая из биссектрис равнобедренного треугольника является его высотой.
5. Какие из следующих утверждений верны?
1) Существуют три прямые, которые проходят через одну точку.
2) Боковые стороны любой трапеции равны.
3) Сумма углов равнобедренного треугольника равна 180 градусам.
6.Какое из следующих утверждений верно?
1) Диагональ трапеции делит её на два равных треугольника.
2) Косинус острого угла прямоугольного треугольника равен отношению гипотенузы к прилежащему к этому углу катету.
3) Расстояние от точки, лежащей на окружности, до центра окружности равно радиусу.
7. Какое из следующих утверждений верно?
1) Все углы ромба равны.
2) Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.
3) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
8.Какое из следующих утверждений верно?
1) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.
2) Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.
3) Смежные углы равны.
9. Какие из следующих утверждений верны?
1) Треугольника со сторонами 1, 2, 4 не существует.
2) Смежные углы равны.
3) Все диаметры окружности равны между собой.
10.Какие из следующих утверждений верны?
1) Треугольника со сторонами 1, 2, 4 не существует.
2) Сумма углов любого треугольника равна 360 градусам.
3) Серединные перпендикуляры к сторонам треугольника пересекаются в центре его описанной окружности.
11. Какие из следующих утверждений верны?
1) Один из углов треугольника всегда не превышает 60 градусов.
2) Диагонали трапеции пересекаются и делятся точкой пересечения пополам.
3) Все диаметры окружности равны между собой.
12.Какое из следующих утверждений верно?
1) Точка касания двух окружностей равноудалена от центров этих окружностей.
2) В параллелограмме есть два равных угла.
3) Площадь прямоугольного треугольника равна произведению длин его катетов.
13.Какие из следующих утверждений верны?
1) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
2) Средняя линия трапеции параллельна её основаниям.
3) Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
14.Какие из следующих утверждений верны?
1) Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
2) В тупоугольном треугольнике все углы тупые.
3) Средняя линия трапеции равна полусумме её оснований.
15.Какое из следующих утверждений верно?
1) Диагонали параллелограмма равны.
2) Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.
3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
16. Укажите номера неверных утверждений.
1) При пересечении двух параллельных прямых третьей прямой сумма накрест лежащих углов равна 180°.
2) Диагонали ромба перпендикулярны.
3) Центром окружности, описанной около треугольника, является точка пересечения его биссектрис.
17.Укажите номера верных утверждений.
1) Любые три прямые имеют не более одной общей точки.
2) Если угол равен 120°, то смежный с ним равен 120°.
3) Если расстояние от точки до прямой больше 3, то и длина любой наклонной, проведённой из данной точки к прямой, больше 3.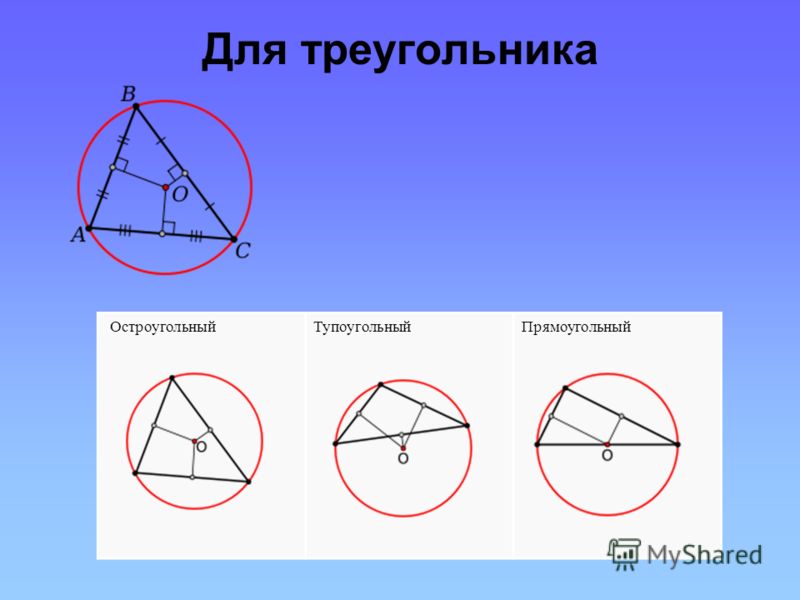
18.Укажите номера верных утверждений.
1) Если угол равен 47°, то смежный с ним равен 153°.
2) Если две прямые перпендикулярны третьей прямой, то эти две прямые параллельны.
3) Через любую точку проходит ровно одна прямая.
19.Укажите номера верных утверждений.
1) Смежные углы равны.
2) Любые две прямые имеют ровно одну общую точку.
3) Если угол равен 108°, то вертикальный с ним равен 108°.
20.Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.
2) Диагональ трапеции делит её на два равных треугольника.
3) Если в ромбе один из углов равен 90° , то такой ромб — квадрат.
21.Какие из данных утверждений верны? Запишите их номера.
1) Каждая из биссектрис равнобедренного треугольника является его медианой.
2) Диагонали прямоугольника равны.
3) У любой трапеции боковые стороны равны.
22.Какие из данных утверждений верны? Запишите их номера.
1) Вокруг любого треугольника можно описать окружность.
2) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.
3) Площадь трапеции равна произведению средней линии на высоту.
23.Укажите номера верных утверждений.
1) В любую равнобедренную трапецию можно вписать окружность.
2) Диагональ параллелограмма делит его углы пополам.
3) Площадь прямоугольного треугольника равна половине произведения его катетов.
24.Укажите номера верных утверждений.
1) Площадь трапеции равна половине высоты, умноженной на разность оснований.
2) Через любые две точки можно провести прямую.
3) Через точку, не лежащую на данной прямой, можно провести единственную прямую, перпендикулярную данной прямой.
25.Укажите номера верных утверждений.
1) Если при пересечении двух прямых третьей прямой соответственные углы равны 37°, то эти две прямые параллельны.
2) Через любые три точки проходит не более одной прямой.
3) Сумма вертикальных углов равна 180°.
26.Укажите номера верных утверждений.
1) Через любую точку проходит не менее одной прямой.
2) Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.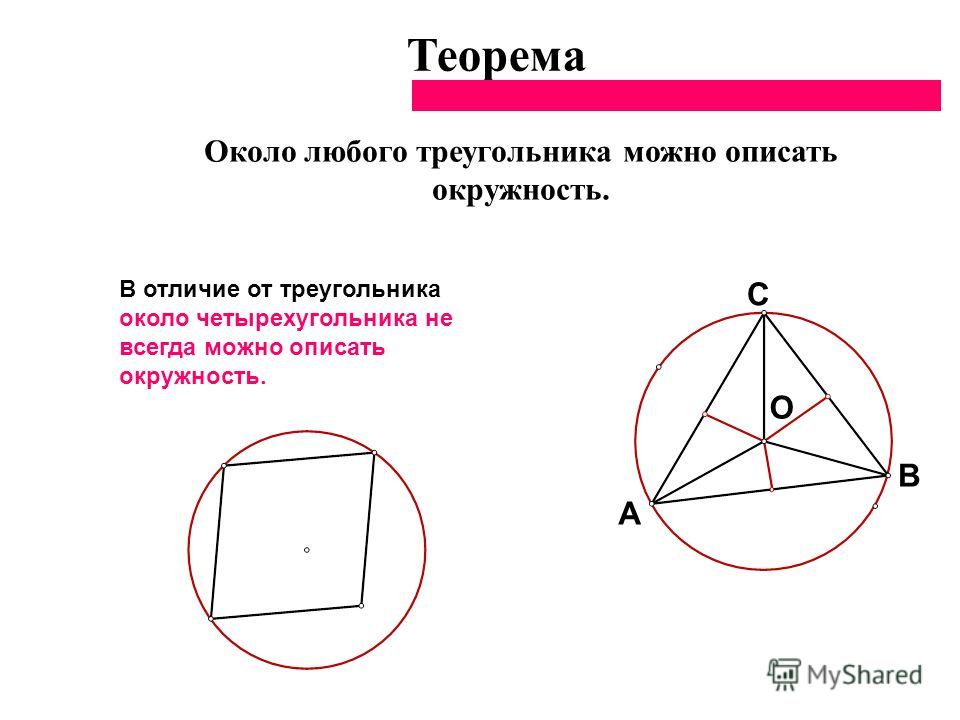
3) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.
27. Укажите номера верных утверждений.
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Треугольник со сторонами 1, 2, 4 существует.
3) Если в ромбе один из углов равен 90°, то такой ромб — квадрат.
4) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
28. Какие из следующих утверждений верны?
1) Площадь многоугольника, описанного около окружности, равна произведению его периметра на радиус вписанной окружности.
2) Если диагонали ромба равна 3 и 4, то его площадь равна 6.
3) Площадь трапеции меньше произведения суммы оснований на высоту.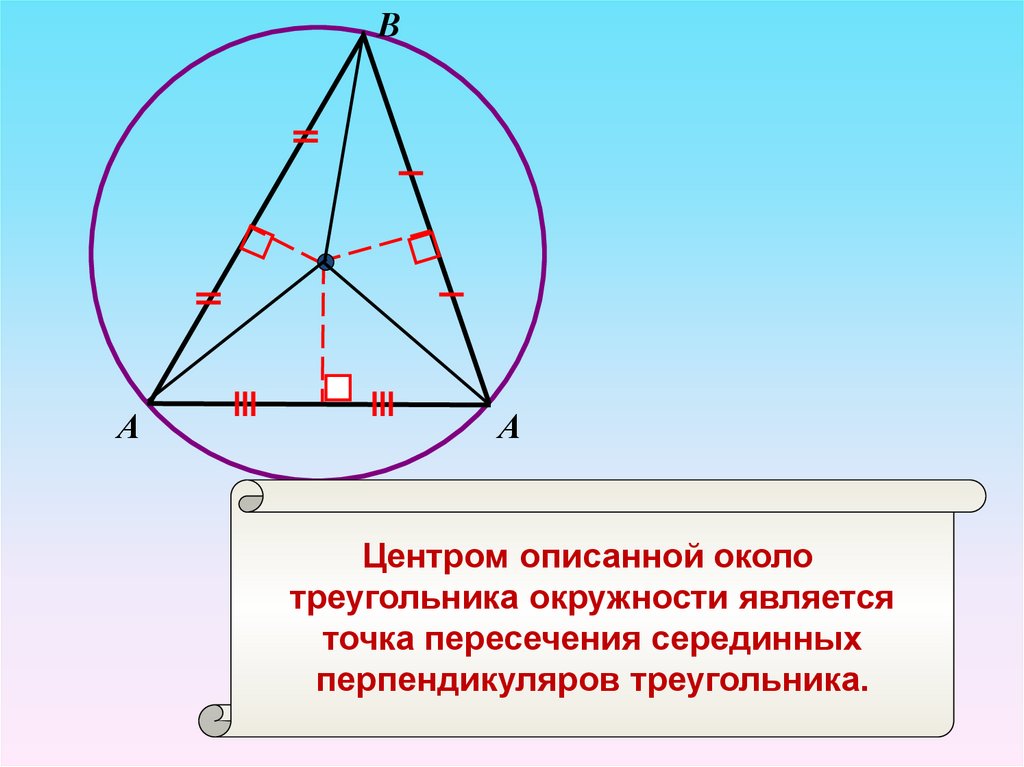
4) Площадь прямоугольного треугольника меньше произведения его катетов.
29.Какие из следующих утверждений верны?
1) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на синус угла между ними.
2) Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.
3) Треугольник ABC, у которого AB = 5, BC = 6, AC = 7, является остроугольным.
4) В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета.
30.Какие из следующих утверждений верны?
1) Любые два прямоугольных треугольника подобны.
2) Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.
3) Стороны треугольника пропорциональны косинусам противолежащих углов.
4) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
31.Какие из следующих утверждений верны?
1) Правильный шестиугольник имеет шесть осей симметрии.
2) Прямая не имеет осей симметрии.
3) Центром симметрии ромба является точка пересечения его диагоналей.
4) Равнобедренный треугольник имеет три оси симметрии.
32.Укажите номера верных утверждений.
1) Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то треугольники подобны.
2) Сумма смежных углов равна 180°.
3) Любая высота равнобедренного треугольника является его биссектрисой.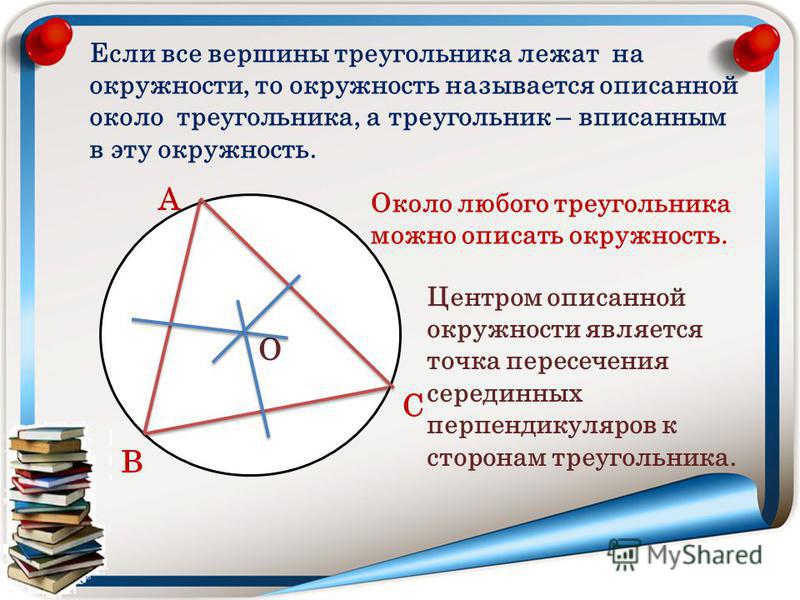
33. Укажите номера верных утверждений.
1) Если угол острый, то смежный с ним угол также является острым.
2) Диагонали квадрата взаимно перпендикулярны.
3) В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности.
34.Укажите номера верных утверждений.
1) Центры вписанной и описанной окружностей равностороннего треугольника совпадают.
2) Существует квадрат, который не является ромбом.
3) Сумма углов любого треугольника равна 180° .
Описанные и вписанные окружности треугольников — Криста Кинг Математика
Описанные и вписанные окружности нарисованы вокруг центра описанной окружности и центра вписанной окружности
В этом уроке мы рассмотрим описанные и вписанные окружности и особые отношения, которые формируются из этих геометрических идей.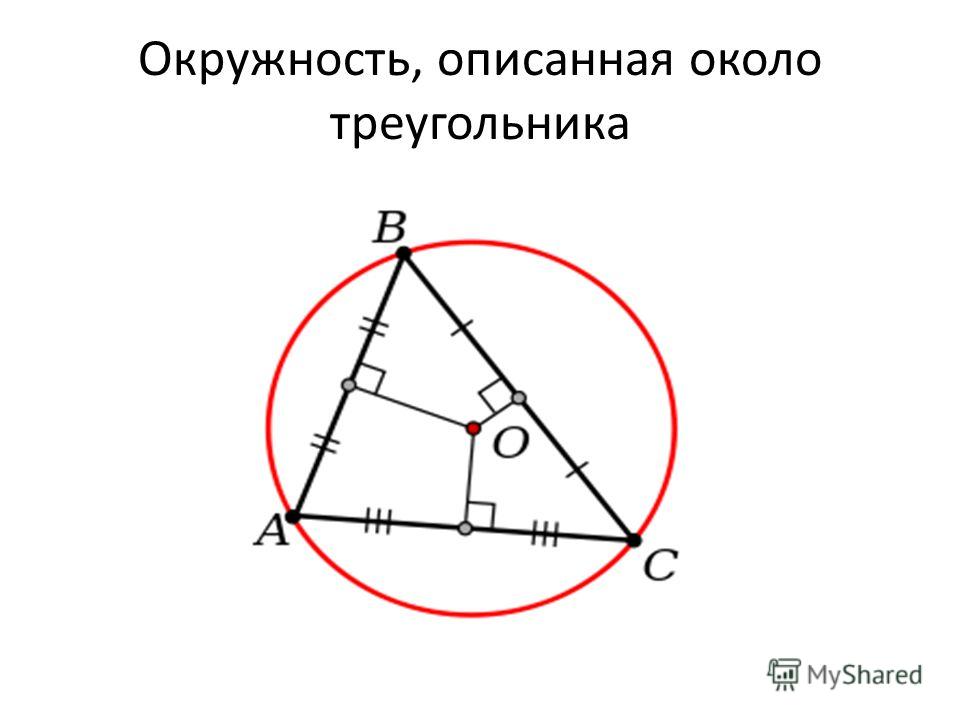
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Описанные окружности
Когда окружность описывает треугольник, треугольник находится внутри круга, и треугольник касается окружности каждой вершиной.
Вы используете серединные перпендикуляры каждой стороны треугольника, чтобы найти центр окружности, которая будет описана вокруг треугольника. Так, например, учитывая ???\треугольник GHI???,
найти середину каждой стороны.
Точка пересечения серединных перпендикуляров является центром окружности.
Центр описанной окружности называется « центром окружности ».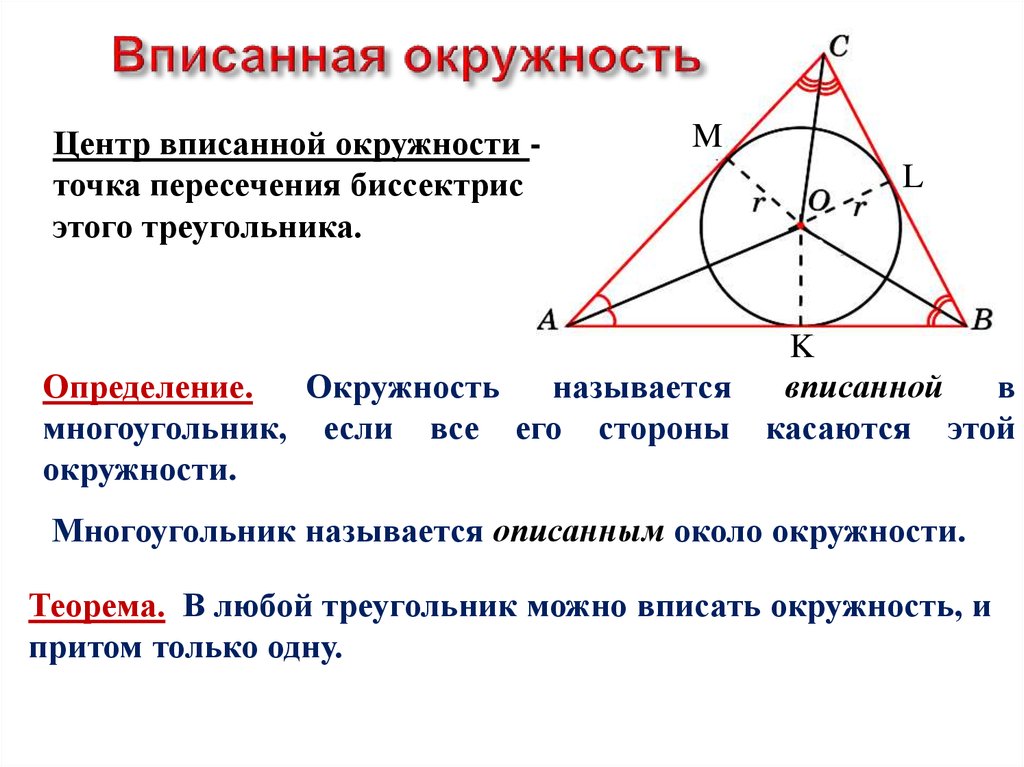
Для остроугольного треугольника центр описанной окружности находится внутри треугольника.
В прямоугольном треугольнике центр описанной окружности находится на стороне, противоположной прямому углу.
В тупоугольном треугольнике центр описанной окружности находится вне треугольника.
Вписанные окружности
Когда окружность вписана в треугольник, треугольник находится вне круга, а окружность касается сторон треугольника в одной точке с каждой стороны. Стороны треугольника касаются окружности.
Чтобы нарисовать вписанную окружность внутри равнобедренного треугольника, используйте биссектрисы каждой стороны, чтобы найти центр окружности, вписанной в треугольник. Например, учитывая ???\треугольник PQR???,
Пересечение биссектрисы угла является центром вписанной окружности.
Помните, что каждая сторона треугольника касается окружности, поэтому, если вы проведете радиус от центра окружности до точки, где окружность касается края треугольника, радиус образует прямой угол с краем треугольника. треугольник.
Центральная точка вписанного круга называется « incenter ». Центр всегда будет внутри треугольника.
Давайте используем то, что мы знаем об этих конструкциях, для решения нескольких задач.
Нахождение и зарисовка описанных и вписанных окружностей
Пройти курс
Хотите узнать больше о геометрии? У меня есть пошаговый курс для этого. 🙂
Узнать больше
Нахождение радиуса окружности, описывающей треугольник
Пример
???\overline{GP}???, ???\overline{EP}???, и ???\overline{ ФП}??? являются серединными перпендикулярами треугольника ???\vartriangle ABC???, и ???AC=24??? единицы измерения. Чему равен радиус окружности, описанной вокруг ???\треугольника ABC????
Чему равен радиус окружности, описанной вокруг ???\треугольника ABC????
Мы также знаем, что ???AC=24??? единиц, а так как ???\overline{EP}??? является серединным перпендикуляром к ???\overline{AC}???, точка ???E??? является средней точкой. Следовательно,
???EC=\frac{1}{2}AC=\frac{1}{2}(24)=12??? 9{2}}???
???ПК=13???
Давайте попробуем другую задачу.
Вы используете серединные перпендикуляры каждой стороны треугольника, чтобы найти центр окружности, которая будет описана вокруг треугольника.
Пример
Если ???CQ=2x-7??? и ???CR=x+5???, какова мера ???CS???, учитывая, что ???\overline{XC}???, ???\overline{YC}?? ? и ???\overline{ZC}??? являются биссектрисами треугольника ???\треугольника XYZ???.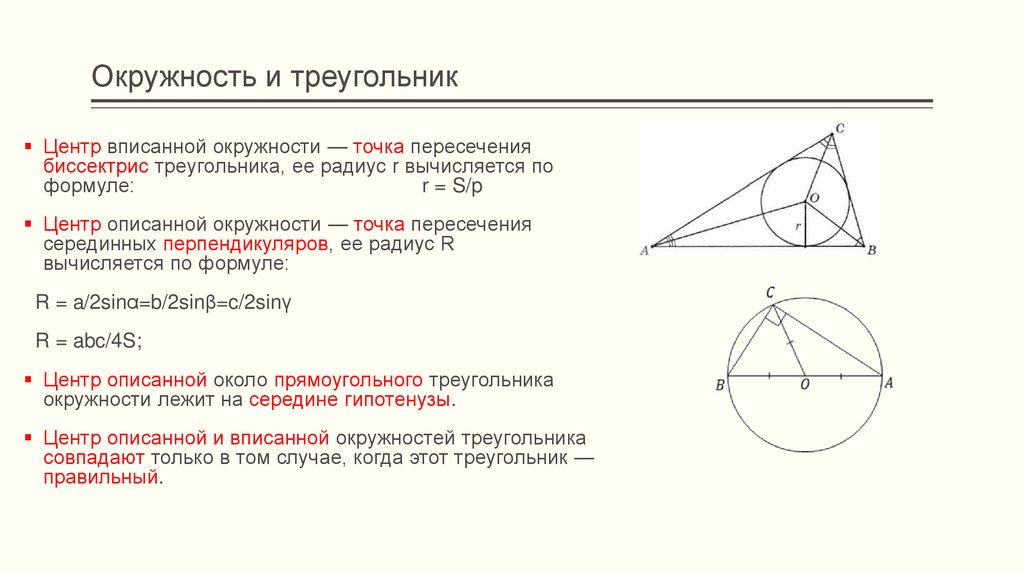
Потому что ???\overline{XC}???, ???\overline{YC}??? и ???\overline{ZC}??? являются биссектрисами треугольника ???\треугольника XYZ???, ???C??? является центром треугольника. Окружность с центром ???C??? будет касаться каждой стороны треугольника в точке пересечения.
???\overline{CQ}???, ???\overline{CR}??? и ???\overline{CS}??? все радиусы окружности ???C???, поэтому все они равны по длине.
???CQ=CR=CS???
Нам нужно найти длину радиуса. Мы знаем???CQ=2x-7??? и ???CR=x+5???, поэтому
???CQ=CR???
???2x-7=x+5???
???х=12???
Следовательно,
???CQ=CR=CS=x+5=12+5=17???
Получить доступ к полному курсу геометрии
Начать
Изучение математикиКриста Кинг математика, изучение онлайн, онлайн-курс, онлайн-математика, описанные окружности, вписанные окружности, треугольники, геометрия, описанная окружность треугольника, вписанная окружность треугольника, центр описанной окружности, центр вписанной окружности, перпендикулярные биссектрисы стороны треугольника, биссектрисы угла треугольника, описанная окружность вне треугольника, вписанная окружность внутри треугольника
Points of Concurrency by Lisa Hastings-Smith
1 of 25
Slide Notes
Download Go Live
Share
Copy
Download
0
0
Published on Nov 18, 2015
Описание отсутствует
Посмотреть схему
ДРУГИЕ КОЛОДЫ ДЛЯ ИЗУЧЕНИЯ ПЛАН ПРЕЗЕНТАЦИИ 1.
Специальные сегменты в треугольниках
Фото Джо Шлаботника
2.
Интерактивные рисунки для использования
3.
Perpendicular Bisecter ОКРУЖНОЙ ЦЕНТР.
4.
В остроугольном треугольнике ЦЕНТР ОКРУЖНОСТИ лежит ВНУТРИ треугольника.
5.
В ПРЯМОУГОЛЬНОМ треугольнике ЦЕНТР ОКРУЖНОСТИ лежит НА треугольнике в середине гипотенузы.
6.
Обратите внимание, что гипотенуза BC прямоугольного треугольника является ДИАМЕТРОМ описанной окружности.

7.
В ТУПИЧНОМ треугольнике ЦЕНТР ОКРУЖНОСТИ лежит ВНЕ треугольника.
8.
Обратите внимание, что тупоугольный треугольник «вписывается» менее чем в половину круга.
9.
Биссектрисы угла в треугольниках
- Напомним, что биссектрисы угла пересекаются в точке, называемой ВКЛ.
- Центр вписанной окружности — это центр окружности, которую можно вписать внутрь треугольника.
- Вписанный центр равноудален от сторон треугольника.
- Расстояние от центра треугольника до каждой из сторон равно радиусу вписанной окружности.
- Центр вписанной окружности всегда лежит внутри треугольника, потому что вписанная окружность полностью лежит внутри треугольника.
10.
ИНЦЕНТР лежит внутри остроугольного треугольника.

11.
ICENTER лежит внутри прямоугольного треугольника.
12.
ICENTER лежит внутри прямоугольного треугольника.
13.
Высоты в треугольниках
- Высота — это отрезок от вершины, перпендикулярный противоположной стороне (или содержащей ее линии).
- Высота — это то же самое, что и высота треугольника.
- Вспомним, что высоты совпадают в точке, которая называется ОРТОЦЕНТР.
- Ортоцентр может лежать внутри, на или вне треугольника. (См. следующие слайды)
14.
ОРТОЦЕНТР ОСТРОГО треугольника лежит ВНУТРИ треугольника.
15.
ОРТОЦЕНТР ПРЯМОУГОЛЬНОГО треугольника лежит НА треугольнике.
16.
Обратите внимание, что ОРТОЦЕНТР ПРЯМОУГОЛЬНОГО треугольника лежит НА треугольнике в ВЕРШИНЕ прямого угла, точка C.

18.
Обратите внимание, что стороны, образующие тупой угол, должны быть расширены, чтобы получить эти две высоты.
19.
Обратите внимание, что ортоцентр будет лежать «позади» точки C и будет сформирован там, где пересекаются продолжения высот.
20.
Медианы в треугольниках
- Медиана — это отрезок, концами которого являются вершина треугольника и середина противоположной стороны.
- Напомним, что медианы совпадают в точке, называемой ЦЕНТРОИДОМ.
- Центроид — это «точка равновесия» или центр масс треугольника.
- Продолжение на следующем слайде…
21.
Медианы в треугольниках
- Центроид делит каждую медиану в соотношении 2:1. (Он ближе к средней точке, чем к противоположной вершине.


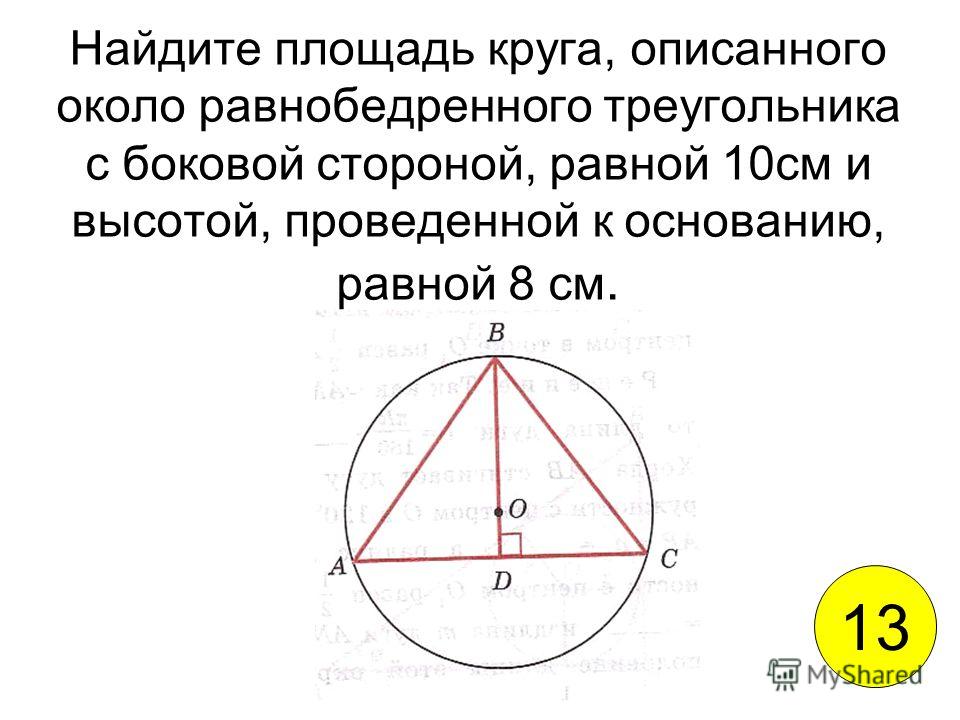
 Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.
Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.
Leave A Comment