Информатика формулы для решения задач: Все формулы по информатике

Решение задач на определение информационного объема текста

Просмотр содержимого документа
«Решение задач на определение информационного объема текста»

Задачи на определение информационного объема текста

Проверяется умение оценивать количественные параметры информационных объектов.

Теоретический материал:

N = 2ⁱ, где N – мощность алфавита (количество символов в используемом
алфавите),

i – информационный объем одного символа (информационный
вес символа), бит

I = K*i, где I – информационный объем текстового документа (файла),

K – количество символов в тексте

Задача 1.

Считаем количество символов в заданном тексте (перед и после тире – пробел, после знаков препинания, кроме последнего – пробел, пробел – это тоже символ). В результате получаем – 52 символа в тексте.

Дано:

i = 16 бит

K = 52

I — ?

Решение:

I = K*i

I = 52*16бит = 832бит (такой ответ есть — 2)

Ответ: 2

Задача 2.

Дано:

K = 16*35*64 – количество символов в статье

i = 8 бит

I — ?

Решение: Чтобы перевести ответ в Кбайты нужно разделить результат на 8 и на 1024 (8=2³, 1024=2¹⁰)

I=16*35*64*8 бит==35Кбайт Ответ: 4

Задача 3.

Пусть x – это количество строк на каждой странице, тогда K=10*x*64 – количество символов в тексте рассказа.

Дано:

I = 15 Кбайт

K =10*x*64

i = 2 байта

x — ?

Решение:

Переведем информационный объем текста из Кбайт в байты.

I = 15 Кбайт = 15*1024 байт (не перемножаем)

Подставим все данные в формулу для измерения количества информации в тексте.

I = K*i

15*1024 = 10*x*64*2

Выразим из полученного выражения x

x = – количество строк на каждой странице – 4

Ответ: 4

Задачи для самостоятельного решения:

Задача 1.

Задача 2.

Задача 3.

Задача 4.

Задача 5.

Задача 6.

Задача 7.

Задачи взяты с сайта fipi.ru из открытого банка заданий (с.1-7)

Задача №27. Написание сложной программы

Автор статьи — репетитор-профессионал Лада Борисовна Есакова.

Поговорим о задаче 27 (С4) на ЕГЭ по информатике. Она оценивается следующим образом:

— 4 балла, если написанная программа работает верно, она эффективна и содержит до трех синтаксических ошибок;
— 3 балла, если написанная программа работает верно, она не эффективна по памяти (но эффективна по времени), содержит не более пяти синтаксических ошибок и не более одной смысловой ошибки;
— 2 балла, если написанная программа работает верно, но она неэффективна, содержит не более семи синтаксических ошибок и не более двух смысловых ошибок;
— 1 балл, если программа не написана или работает неверно, однако алгоритм решения описан правильно.

Про синтаксические и смысловые ошибки мы сейчас говорить не будем. Наша задача научиться их не делать. Правда, профессиональные программисты до сих пор не могут понять, как можно без ошибок написать работающую эффективную программу без компьютера, при помощи только бумаги и ручки. Будем считать, что программировать мы умеем хорошо и в написании операторов не путаемся.

Давайте выделим основные моменты в решении этой самой сложной задачи.

1. Правильный алгоритм

До того, как начать программировать, мы должны хорошо понять, что собственно мы собираемся запрограммировать. Причем продумать алгоритм нужно до мелочей, учесть все возможные варианты поведения программы. После этого обязательно подробно и понятно записать алгоритм на простом языке, в виде блок-схемы или в виде таблицы. Кому как удобнее. Это описание будет нашей путеводной нитью при разработке программы. А заодно мы заработаем 1 балл.

Я настойчиво рекомендую подробно описывать алгоритм, даже если Вы уверены в абсолютной правильности программы.

Во-первых, Вы облегчаете себе дальнейшее выполнение задания.. Программировать, имея перед глазами продуманную схему, гораздо легче.
Во-вторых, Вы гарантируете себе 1 балл (пусть будет, запас карман не тянет).
В-третьих, Вы облегчаете работу проверяющего, вызываете его позитивный настрой, ведь способов решения задачи очень много, возможно, Ваш самый изящный, но уловить и оценить идею решения по голому программному тексту не так-то просто.

2. Эффективность.

В постановке задачи требуется не просто написать программу, а написать эффективную программу. Давайте разберемся, что же такое эффективность.

Эффективность в данном смысле – это умение экономно расходовать основные ресурсы: память компьютера и время.

Зачастую практического смысла такая экономия при современном развитии компьютерной техники не имеет. Выигрыш во времени у эффективной программы по сравнению с неэффективной может составить доли секунды, а уж оперативная память при решении задач такого объема и сложности давно не является дефицитом у современных компьютеров. Смысл задачи – проверить умение распоряжаться ограниченными ресурсами.

2.1. Эффективность по времени.

Наиболее ценным ресурсом в этой задаче считается время. Эффективность по времени расценивается «дороже», чем эффективность по памяти.

Как же написать эффективную по времени программу?

Обозначим время выполнения программы T. Допустим, нам нужно последовательно просмотреть в цикле N элементов массива. Тогда время выполнения программы будет прямо пропорционально количеству элементов (T~N).

Если же для каждого из N элементов нам нужно заново просмотреть весь массив (цикл в цикле), то время будет пропорционально квадрату количества элементов.

Эта программа менее эффективна, чем первая.
Очевидно, что третий вложенный цикл даст нам уменьшение эффективности еще в N раз.

Таким образом, нужно стараться избегать вложенных циклов. Это не всегда возможно. Любая сортировка (например, метод пузырька) обязывает нас использовать цикл в цикле.

2.2. Эффективность по памяти.

Все, что выполняет наша программа, происходит в памяти компьютера.
Объявляя переменные, мы резервируем ячейки памяти (переменная типа Integer занимает в классическом Паскале 2 байта, переменная типа Real – 6 байт).
Записывая введенные данные в массив или переменные, мы используем память.

Поэтому основные приемы экономии памяти:
— Правильно выбирать тип переменной;
— При возможности не сохранять вводимые данные в массив или переменные, а анализировать сразу при вводе;

— Экономно использовать переменные (если возможно, использовать одну переменную для разных целей).
И опять же, позаботьтесь о проверяющем. После написания программы сделайте анализ эффективности. Объясните, почему вы выбрали такие типы переменных. Укажите, где вы экономно использовали одну и ту же переменную в разных целях. Возможно, Вы сознательно уменьшили эффективность по памяти для увеличения эффективности по времени.

3. Культура оформления программного кода.

Вы не представляете, какой это кошмар – проверять сухой программный код, никак не описанный, нигде не прокомментированный, использующий безликие переменные a1, a2 и тому подобные.

Способы решения задачи могут быть самые разные, и проверяющему предстоит понять, что же именно делает ваша программа.

Настоятельно рекомендую выполнять следующие правила, которые не добавят Вам лишний балл, но позитивно настроят проверяющего и застрахуют от возможной недооценки вашей работы:
— Используйте имена переменных, указывающие на их назначение. Например, для обозначения переменной, хранящей максимальную сумму можно использовать наименование maxsum, для массива с номерами школ – schoolnum. Только не переусердствуйте! Под счетчики достаточно ввести переменные i, j…

— Форматируйте текст отступами, обозначая начало-конец программных блоков. Такое форматирование избавит Вас от потери закрывающих скобок и упростит чтение текста;

— Используйте комментарии, коротко описывающие основной смысл происходящего.

Ты нашел то, что искал? Поделись с друзьями!

Выполнив эти несложные требования, Вы гарантированно получите высший балл за самую сложную задачу ЕГЭ по информатике!

ЕГЭ по информатике 2021 — Задание 18 (Таблица чисел)

Привет! Мы добрались до 18 задания из ЕГЭ по информатике 2021.

Это задание снова решается с помощью компьютера.

Восемнадцатое задание направлено на обработку вещественных чисел с помощью таблиц. Мы с вами будет использовать программу Excel от компании Microsoft.

Перейдём к к тренировке решения 18 задания из ЕГЭ по информатике 2021.

Задача (Стандартная)

Квадрат разлинован на N×N клеток (1

Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой нижней клетки в правую верхнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную.

Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.

Пример входных данных:

Для указанных входных данных ответом должна быть пара чисел 35 и 15.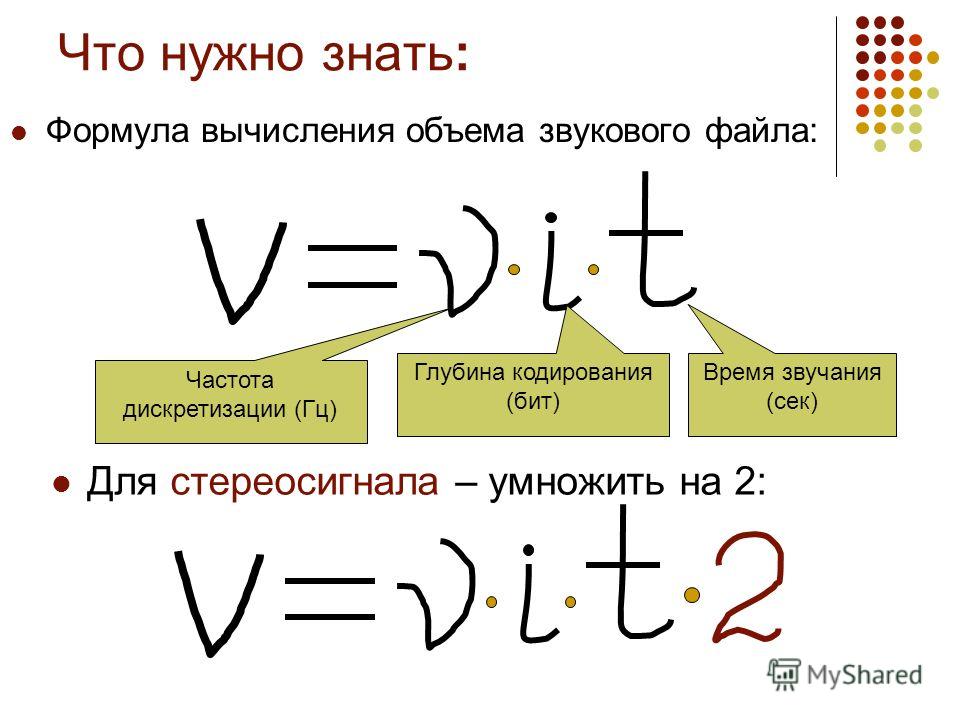

Решение:

Открываем файл к данной задачке.

В начале найдём максимальную сумму.

Выделяем область всех ячеек, где написаны числа, вырезаем её и вставляем на столбец правее. Это нужно для того, чтобы при составлении формулы решения не было ошибок.

Обозначим мысленно ту область, где мы будем составлять наше решение, пропустив одну или две строчки снизу. По размеру область будет такая же.

В каждой ячейке этой области будет лежать максимальная cумма, которую может собрать Робот, дойдя до этой клетки. Т.к. Робот идёт в верхнюю правую клетку, то, соответственно, в ячейке K12 будет находится нужный нам ответ.

Наш Робот идёт из левой нижней клетки. Поэтому формулу, решающую эту задачу, составим сначала для ячейки B21.

Кликаем на ячейку B21 и пишем формулу:

=МАКС(A21;B22)+B10

Примечание: Чтобы в ячейке начать писать формулу, нужно поставить знак «=».

В любую ячейку нашей области можно попасть либо слева, либо снизу (Т.к. составляем формулу для любой ячейки, то не играет роли, что в данная ячейка угловая). Поэтому для ячейки B21 мы берём предыдущий результат — либо из левой ячейки, либо из правой ячейки, в зависимости от того, где собранная сумма больше.

Эту роль исполняет функция МАКС(). Она помогает выбрать откуда нужно идти, чтобы сумма всегда была максимальна.

Плюс, мы должны добавить сумму для данной ячейки к максимальной сумме предыдущей клетки. Поэтому в формулу дописываем ячейку B10

После того, как составили формулу для одной ячейки B21, можно распространить формулу на всю область.

Подносим мышку к правому нижнему углу. Как только появился чёрный крестик, кликаем левую кнопку мыши, и тянем вверх на 10 строчек вверх.

После того, как столбец готов, выделяем этот столбец, и аналогично, распространяем его на всё пространство.

В итоге получается такая картина:

Видим, что в ячейке K12 значение 1298.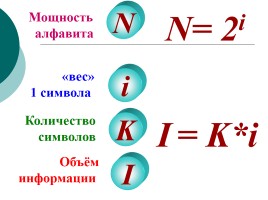 Это значение нам и нужно.

Аналогичным образом ищется минимальное значение, только в формуле вместо функции МАКС будет использоваться функция МИН.

Минимальное значение получилось 589.

Ответ: 1298589

Посмотрим ещё одну интересную задачу из примерны задач ЕГЭ по информатике нового образца 2021.

Задача (Два Робота)

Квадрат разлинован на N×N клеток (2

Два исполнителя – ВЕРХ и НИЗ – существуют на одинаковых полях. Первый имеет две команды – вверх и вправо, второй – вниз и вправо, которые, соответственно, перемещают исполнитель на одну клетку вверх, вниз или вправо. Исполнитель ВЕРХ начинает движение в левой нижней ячейке, исполнитель НИЗ – в левой верхней.

Откройте файл. Какой из исполнителей соберет большее количество монет в результате своей работы, если известно, что каждый из них запрограммирован собрать максимальное количество монет?

Пример:

1	8	8	4	10
10	1	1	3	2
1	3	12	2	8
2	3	5	6	11
3	19	14	11	5

Для указанных входных данных ответом является комбинация из названия исполнителя и количества собранных монет

ВЕРХ84

Решение:

Перенесём таблицу чисел на один столбец вправо.

Найдём, сколько соберёт монет исполнитель ВЕРХ.

Исполнитель «ВЕРХ» начинает идти с левой нижней клетки. Поэтому первую формулу мы зададим для клетки B27. Эта ячейка является нижней левой клеткой для области, где мы будем составлять решение.

Напишем в ячейке B27:

=МАКС(A27;B28)+B13

Распространим формулу на всё пространство.

Когда исполнитель пройдёт всё поле, в ячейке N15 будет находится ответ. Максимальное количество монет, которое может собрать исполнитель ВЕРХ будет 1743.

Теперь найдём максимальное количество монет, которое может собрать исполнитель НИЗ.

Решать будем аналогичным образом, удалив все следы от предыдущего исполнителя.

Т.к. исполнитель НИЗ стартует с левой верхней клетки, то мы сначала составим формулу для ячейки B15. Эта клетка олицетворяет левую верхнюю ячейку для области, где будет происходить решение.

=МАКС(B14;A15)+B1

В любую ячейку мы можем попасть либо сверху, либо слева. Это не относится к боковым и угловым ячейкам, но формула будет работать и для них.

При составлении максимальной суммы для любой ячейки, мы выбираем максимальное значение суммы из двух предыдущих ячеек + добавляем значение для этой ячейки.

Распространим формулу на всё пространство.

В ячейке N27 будет максимальное значение для исполнителя НИЗ. Получилось 1686.

Видим, что у исполнителя ВЕРХ получилось собрать больше монет.

Ответ: ВЕРХ1743

Решим ещё одну задачу из примерных вариантов ЕГЭ по информатике 2021.

Задача (Роботы встречаются в одной из клеток)

Квадрат разлинован на N×N клеток (2

Два исполнителя – ПРАВО и ЛЕВО – существуют в рамках одного поля. Первый имеет две команды – вверх и вправо, второй – вверх и влево, которые, соответственно, перемещают исполнитель на одну клетку вверх, вправо или влево. Исполнитель ПРАВО начинает движение в левой нижней ячейке, исполнитель ЛЕВО – в правой нижней.

Исполнители обязательно встречают в одной из клеток, находящихся в среднем столбце. При этом движение вверх по данному столбцу запрещено. Например, при работе в квадрате 5х5 исполнители встречаются в одной из клеток третьего столбца.

Какую максимальную сумму монет могут собрать исполнители.

Пример входных данных:

1	4	3	1	2
10	1	1	3	2
1	3	13	10	8
2	3	5	6	11
3	19	14	11	5

Для указанных входных данных ответом является число 75 (3+19+3+3, 5+11+8+10, 13)

Решение:

Перенесём таблицу чисел на один столбец вправо.

Роботы должны встретится в среднем столбце.

Один робот перемещается в левой части таблицы, другой в правой.

Найдём максимальное значение суммы количества монет для каждой ячейки левой и правой области (Исключая средний столбец).

Составим формулу для исполнителя ПРАВО в ячейке B27:

=МАКС(A27;B28)+B13

Распространим данную формулу на левую часть рабочей области.

Теперь составим формулу для исполнителя ЛЕВО в ячейке N27:

=МАКС(N28;O27)+N13

Распространим эту формулу для правой части.

Получается следующая картина:

Теперь нужно заполнить средний столбец и определить, где сумма получится наибольшая.

Пишем в ячейку h25:

=G15+h2+I15

Распространяем данную формулу на весь столбец H внутри рабочей области.

Видим, что максимальное значение в среднем столбце будет 22884. Это и будет ответ.

Ответ: 22884

Измерение информации. Часть 3. Не равновероятные события. Решение задач.

В «Измерение информации. Часть 2» мы разбирали решение задач, в которых рассматривались равновероятные события (например: орел или решка — вероятность выпадения 50\50). Сегодня мы рассмотрим несколько задач на тему «Измерение количества информации при не равновероятностном подходе».

Задача 1.

В корзине лежат 8 черных шаров и 24 белых. Сколько информации несет сообщение о том, что достали черный шар?

Задача 2.

В коробке лежат 64 цветных карандаша. Сообщение о том, что достали белый карандаш, несет 4 бита информации. Сколько белых карандашей было в корзине?

Задача 3.

За четверть ученик получил 100 оценок. Сообщение о том, что он получил пятерку несет 2 бита информации. Сколько пятерок ученик получил за четверть?

Задача 4.

Для ремонта школы использовали красную, зеленую и коричневую краски. Израсходовали одинаковое количество банок красной, зеленой и коричневой краски. Сообщение о том, что закончилась банка красной краски несет 2 бита информации. Зеленой краски израсходовали 8 банок. Сколько банок коричневой краски израсходовали на ремонт школы?

Задача 5.

В коробке лежат белые и черные шары. Среди них 18 черных шаров. Сообщение о том, что из корзины достали белый шар, несет 2 бита информации. Сколько всего в корзине шаров?

Решение задач, в условии которых события не равновероятны

Формулы, которые необходимы для решения таких задач можно посмотреть на «Измерение информации. Часть 1»

Мы имеем 2 формулы:

Формулы вероятности и формула Шеннона

Если применим преобразования и подставим переменную p из первой формулы во вторую, получим новую формулу, которая значительно упростит нам жизнь:

Новая формула

Решение задачи №1.

K_ч = 8
К_б = 24

i_б— ?

(индексы «б» и «ч» указывают на то, к каким шарика, белым или черным, относится данная переменная)

Воспользуемся выведенной формулой:

Формула

В данной формуле неизвестна переменная N — это общее число событий (или шариков). N=K_б + К_ч = 8 +24 = 32 (шарика)

Получим, что i_б = 2 (бита). (т.к. 2² = 4) (при решении можно использовать логарифм, если с ним знакомы).

Ответ: сообщение о том, что достали белый шарик, несет 2 бита информации.

Решение задачи №2

N = 64 карандаша
i_б = 4 бита

К_б — ?

Воспользуемся той же выведенной формулой:

Формула

Подставив в нее известные величины, получим:

Решение задачи №2

Ответ: количество белых карандашей равно 4.

Решение задачи №3

N = 100
i₅ = 2 бита

K₅ — ?

Аналогично предыдущей задаче:

Решение задачи №3

Ответ: ученик получил 25 пятерок.

Решение задачи №4

K_к = К_з = К_кор
i_к = 2 бита
К_з = 8 банок

К_кор — ?

Т.к. K_к = К_з = К_кор следует, что: количество красной краски равно 8 банок, количество зеленой краски — 8 банок и количество коричневой краски — 8 банок.

Зная, что К_к = 8, можем воспользоваться нашей выведенной формулой:

Решение задачи №4

Нашли общее число банок.

Чтобы найти количество коричневой краски необходимо из общего числа вычесть количество красной и зеленой краски.

Решение задачи №4

Ответ: количество коричневой краски — 16 банок

Решение задачи №5

К_ч = 18
i_б = 2 бита

N — ?

Пожалуйста, зарегистрируйтесь, чтобы увидеть скрытый текст

на Ваш сайт.

15 приложений по физике, математике и информатике, которые позволят забыть про учебники

Искать формулы или рисовать прямой угол куда проще в телефоне, чем в бесконечных конспектах и учебниках. Накануне всероссийской контрольной «Выходи решать!» мы собрали самые удачные приложения по математике, физике и информатике, которые не только помогут подготовиться к тестам и ЕГЭ, но и выучить язык программирования или понять, как работает теория относительности.

Первый класс. Рассылка

Ценные советы и бесценная поддержка для родителей первоклассников

Математика

1. «Алгебра»

Справочное приложение, в котором можно быстро найти все необходимые для школьной математики формулы с краткими пояснениями. Искать, конечно, удобнее, чем в тетради. Можно использовать как шпаргалку, но не рекомендуем. Если подглядывать в приложение во время домашнего задания, получается эффективнее.

Скачать приложение

2. «Пифагория»

Самые увлекательные и наглядные игры, основанные на математических законах, получаются, конечно, из геометрических задач. В приложении «Пифагория» нужно строить фигуры и находить расстояния на координатной сетке. Сначала кажется, что это очень просто, но затем в ход идут довольно непростые построения, а расстояния и углы приходится вычислять на бумажке. Игра поможет по-другому взглянуть на обычный тетрадный листок в клеточку и увидеть новые фигуры и закономерности в сочетании точек.

Скачать приложение

3. Euclidea

Ещё одна игра про геометрические построения, но теперь уже на белом листе, с помощью циркуля и линейки. Решая задачки, чувствуешь себя древним греком и пытаешься додуматься, как построить серединный перпендикуляр, вписать окружность в треугольник или квадрат в окружность. Дополнительная сложность в том, что это нужно сделать за минимальное число элементарных построений. Игра быстро становится сложной, но зато в ней есть подсказки, которые могут сообщить последовательность ходов или полезный для решения факт из геометрии.

Скачать приложение

4. Geogebra Classic

Приложение для построений. Если нужно нарисовать картинку к геометрической задаче, то можно сделать это на телефоне. К тому же в приложении проще нарисовать ровный прямой угол и заметить все равные углы и стороны, чем на чертеже от руки в тетради. Отличное приложение в помощь к школьным и более сложным задачам.

Скачать приложение

Приложения, которые решают задачи

Среди приложений по математике помимо обучающих программ много таких, которые помогают решить задачи. При этом многие из них очень полезные, интересные и помогают посмотреть на задачи под новым углом, так что молчать о них не хочется. Итак, приложения для тех, кто привык выводить решение из ответа.

5. Geogebra Graphing Calculator

Строит графики функций, умеет определять нули функций (то есть корни уравнений, умеет находить точки пересечения графиков (то есть решения систем уравнений), умеет находить максимумы и минимумы функций. В целом это просто полезное приложение для построения графиков с большим набором инструментов и простым интерфейсом, но из-за большого «читерского» потенциала в основной список приложений по математике его ставить не хочется.

Скачать приложение

6. Photomath

Приложение, которое по фотографии умеет решать уравнения, сокращать выражения, находить область определения, строить график функции и многое другое. В общем, это калькулятор, в который не нужно напряжённо и скрупулёзно вписывать выражения. Для тех, кто действительно хочет чему-нибудь научиться, есть пошаговый разбор решения задачи и дополнительные факты. Лучше сканировать задачи прямо из учебника — написанное от руки программа воспринимает не всегда хорошо.

Скачать приложение

7. Geometryx

Умеет определять параметры геометрических фигур. Достаточно вписать всю известную информацию, и если её хватит, приложение выдаст длины всех высот и диагоналей, углы и другие полезные факты о вашей фигуре. Здесь тоже есть полезный раздел со всеми использованными формулами, в который можно заглянуть, чтобы всё-таки разобраться и в следующий раз решить задачу самостоятельно.

Скачать приложение

Физика

8. Snapshots of the universe

Приложений по физике в магазинах Apple и Android очень мало, но тем не менее одна занимательная вещь всё же нашлась. Snapshots of the universe в виде интерактивных экспериментов поясняет работу законов, применяемых в астрофизике. Например, законы Кеплера, по которым вращаются планеты вокруг Солнца, теорию относительности и многое другое. Отлично подходит для того, чтобы проиллюстрировать формулы из учебников. Приложение на английском языке и платное, но стоит недорого. Если вас это не пугает, рекомендуем ознакомиться.

Скачать приложение

9. «Бетафизикс»

«Читерское» приложение есть и по физике. По фотографии задачи оно даёт её решение или по ключевым словам находит основные формулы по теме и табличные значения справочных величин. Идеально, когда не хочется копаться в конспекте, чтобы вспомнить одну маленькую формулу. Пока есть не все темы задач из курса, но основные направления охвачены, а новые задачи должны появиться в следующих обновлениях.

Скачать приложение

10. Slower Light (бонус)

Игра для персональных компьютеров, которая поясняет, как выглядит мир, если двигаться со скоростью, близкой к скорости света. Её разработали учёные из Массачусетского технологического института, так что с научной точки зрения она сделана точно. После прохождения игры все эффекты, которые вы увидите, объяснят доступным языком. Она помогает уложить в голове непонятные концепции теории относительности, такие как замедление времени и сокращение длины. Только на английском языке.

Скачать приложение

Уже в эту субботу, 17 ноября, состоится всероссийская физико-техническая контрольная «Выходи решать!». Чтобы проверить свои знания по физике, математике и информатике за 8 класс вместе с другими участниками, нужно только зарегистрироваться на сайте. Писать контрольную можно как онлайн, так и на одной из очных площадок.

Информатика

11. Sololearn

Очень крутое приложение для обучения программированию. Можно выбрать язык и пройти по нему вводный курс с решением задач и теорией. Кроме того, можно писать тесты по терминологии и командам для лучшего запоминания и соревноваться с другими пользователями. Для начального уровня очень удобно и полезно.

Скачать приложение

12. Learn programming

Хороший текстовый учебник по программированию. К сожалению, только по нему программирование не выучишь, но в дополнение к задачам из других источников он работает как отличный справочный материал. Содержит примеры кода и поддерживает огромное количество языков программирования. Приложение доступно только на английском.

Скачать приложение

13. Tynker

Целое семейство игровых приложений для IOS. Цель игры заключается в том, чтобы с помощью кода персонаж на экране выполнил определённую задачу. Такая механика позволяет наглядно и просто объяснить, как работает программирование и строятся алгоритмы. Визуально игра яркая и красочная, поэтому отлично подходит для детей. Она есть только на английском, но текста немного и большинство слов интуитивно понятны при прохождении.

Скачать приложение

Для всех предметов

14. «Супершкольник»

Приложение для подготовки к тестовой части ЕГЭ по математике, физике, химии, биологии, русскому и английскому языкам, истории, обществознанию и литературе. Для теста по каждой теме есть теоретический раздел, где можно повторить основные правила и законы. Кроме того, в приложении есть поисковик по названию формул для математики и физики, что может быть полезно при решении задач. Отличная функция — режим репетитора, который при каждой разблокировке телефона предлагает ответить на вопрос из теста.

Скачать приложение

15. «Фоксфорд.Учебник»

Приложение-учебник по математике, физике, информатике, химии, биологии, русскому языку, истории и обществознанию. Всё разбито по темам и разобрано подробно, с примерами и картинками. Отлично работает для повторения теории перед решением задач и для того, чтобы быстро разобраться в неизвестной теме.

Скачать приложение

НОУ ИНТУИТ | Решение олимпиадных задач по информатике

Форма обучения:

дистанционная

Стоимость самостоятельного обучения:

бесплатно

Доступ:

свободный

Документ об окончании:

Уровень:

Для всех

Длительность:

6:48:00

Выпускников:

167

Качество курса:

4. 44 | 4.19

Авторская программа предпрофильной подготовки учеников 6 или 7 классов. Главной целью программы является развитие творческого потенциала школьников, их способностей к плодотворной умственной деятельности.

Важнейшей ролью математических кружков является индивидуальная работа с одаренными школьниками, направленная на развитие их мыслительных способностей, настойчивости в выполнении заданий, творческого подхода и навыков в решении нестандартных задач. Необходимо расширить кругозор школьников, для этого в программу работы математического кружка включаются темы, которые не входят в базовую программу или не получают там должного внимания. Эти темы, с одной стороны, должны быть доступны обучаемым, с другой стороны, позволять им успешно выступать на олимпиадах. Человеку нужна мотивация его деятельности, участие в различных конкурсах и олимпиадах, и особенно победа в них побуждает учащихся продолжать изучение данного предмета, дух соревнования поддерживает интерес. С другой стороны, отсутствие «наказания» в виде оценок позволяет ребенку чувствовать себя свободнее, чем на традиционных уроках, формирует умение высказывать гипотезы, опровергать или доказывать их, искать ошибки и неточности в рассуждениях. Необходимо также заметить, что участие в работе кружка математики создает необходимую базу для успешного изучения других предметов естественнонаучного цикла, таких как информатика, физика, химия, астрономия. Поэтому часто занятия математикой, несмотря на отсутствие видимых достижений в математических соревнованиях, приводят к успехам в других дисциплинах. Содержание курса разбито на 5 модулей, каждый из которых содержит изучение теории и применение ее при решении задач.

Теги: BGI, SHL, алгоритмы, базы данных, бином Ньютона, директива компилятора, драйверы, побочная диагональ, поиск, процедуры, размещения без повторений, решето эратосфена, сортировка, треугольник паскаля, цвета, элемент цикла, элементы

2 часа 30 минут

—

Базовые формулы (зависимости) и задачи, решаемые с их помощью

Цель лекции: научиться применять некоторые формулы и зависимости (зависимость уменьшающегося значения переменной в теле цикла от увеличивающегося значения счетчика цикла, формулу для определения кратности двух чисел, формулу для нахождения длины отрезка по заданным координатам его концов) в решении классических задач.

—

Типовые алгоритмы и задачи, решаемые с их помощью

Используя типовые алгоритмы можно решить любую задачу. В лекции очерчен круг НЕОБХОДИМЫХ ТИПОВЫХ АЛГОРИТМОВ (для обработки одномерных массивов и обработки строк), рассмотрены некоторые олимпиадные задачи, которые решаются с использованием этих алгоритмов. Цель лекции: научиться применять изученные типовые алгоритмы при решении классических задач.

—

Задачи «Операции со сверхбольшими числами»

Часто на олимпиадах предлагаются задачи, в которых необходимо вычислить результат арифметических операций над сверхбольшими числами. При решении этих задач мы будем опираться на рассмотренные в предыдущей лекции типовые алгоритмы обработки одномерных массивови строк. Цель лекции: научиться производить операции со «сверхбольшими» числами при решении классических задач.

—

Типовые алгоритмы обработки одномерных массивов. Сортировка методом «Пузырька»

В лекции продолжено знакомство с типовыми алгоритмами обработки одномерных массивов — рассмотрен типовой алгоритм сортировки элементов массива и разобраны некоторые олимпиадные задачи, которые решаются с использованием сортировки. Цель лекции: научиться применять изученный типовой алгоритм при решении классических задач.

—

Типовые алгоритмы обработки двумерных массивов

В лекции рассматриваются типовые алгоритмы обработки двумерных массивов. рассмотрены некоторые олимпиадные задачи, которые решаются с использованием этих алгоритмов.

Цель лекции: научиться применять изученные типовые алгоритмы при решении классических задач.

—

Задачи, сгруппированные по методам решения. Использование дополнительного массива «флажков»

Что еще, кроме подбора типовых алгоритмов поможет в подготовке к олимпиадам? Огромную помощь может оказать группировка задач — не по темам (задачи на строки, задачи из теории чисел и др.), а по методам решения этих задач. Рассмотрим некоторые методы решения часто встречающихся в практике программирования задач. В данной лекции будет рассмотрен прием «Использование флажков», отработаны типовые алгоритмы обработки одномерных массивов. Цель лекции: научиться применять изученный метод при решении классических задач.

—

Задачи, сгруппированные по методам решения. Использование дополнительного массива «флажков» (три задачи — один алгоритм)

Продолжаем отрабатывать пройденный прием (использование дополнительного массива «флажков») в ситуациях, когда необходимо отметить наступление и окончание какого-то события (открытие-закрытие скобок, приход-уход сторожа, начало-конец отрезка). При наступлении события «флажок» примет значение «1», при окончании — «-1». Материалы лекции базируются на типовых алгоритмах обработки одномерных массивов и строк. Цель лекции: научиться применять изученный метод при решении классических задач.

—

Задачи, сгруппированные по методам решения. Метод вложенных матриц

Направление (порядок) обхода элементов двумерного массива может пригодиться в решениях некоторых задач повышенной сложности, например, в решениях таких задач, как «Магический квадрат» и «Скатерть Улама».

{17} \) = 131072

Ответ: 131072 символов в сообщении.

Вычисление по формулам

Эта глава взята из книги Х. П. Лангтангена A Primer on Scientific Programming with Python, 5-е издание, Springer, 2016.

О решении упражнений

Есть только один способ научиться программированию: вы должны программировать себя. Это значит, что вам нужно сделать много, упражнений! Читая эту книгу необходимо изучить синтаксис Python и изучить примеры необходимо понимать, как думать о программировании и решении проблемы.Но главное усилие в процессе обучения — это ваша работа. с упражнениями или собственными программными проектами.

Решение упражнения — это трехэтапная процедура. Во-первых, вы должны внимательно изучите текст в упражнении, чтобы понять, что проблема вот в чём. Упражнения по программированию, особенно в этой книге, о постановке проблемы, которую необходимо полностью понять перед этим имеет смысл понять конкретные вопросы в упражнении. В Второй этап — написание программы.Чем больше усилий ты вкладываешь на первом этапе, тем легче будет найти правильные утверждения и напишите код. Третий и заключительный этап — тестирование программы. и удалить ошибки (известные как отладка и проверка из раздела Глоссарий по информатике). Это, безусловно, самая большая проблема для новички. Очень часто, особенно новичкам в программировании, все сводится к записи результата каждое утверждение и внимательно проверяя эти результаты, играя компьютер с ручкой и бумагой.

Новички часто недооценивают объем работы, необходимой на первом этапе. и третий этап и вместо этого попробуйте выполнить второй этап (т. е. напишите программу) как можно быстрее. Чем больше работы вы вложите в первый этап, тем легче будет найти пример в этой книге или в другом месте, которое похоже на упражнение и может помочь вам получить началось. И чем больше работы вы вкладываете в третий этап, построив тестовый пример, тем лучше вы понимаете будет и тем меньше ошибок вы совершите. Опыт докажет, что все эти утверждения верны!

Большинство упражнений связаны с именем файла, например, myexer . Если ответом на упражнение является программа Python, вам следует сохранить программа в файле myexer.py . Если ответ может быть объяснением, вы можете сохранить его в текстовом файле myexer.txt или записать текст в текстовый редактор и создайте файл PDF ( myexer.pdf ).

Когда вы передаете упражнения помощникам учителя, это часто бывает требование, чтобы пробный запуск программы был вставлен в конец кода.Это означает, что вы запускаете какое-то дело с известным результатом, направить вывод в файл результат ,

 Терминал> python myprogram.py> результат

и скопируйте содержимое result в строку с тройными кавычками с соответствующие комментарии после заявлений программы. Вот пример программы с пробным запуском:

 F = 69,8 # градусов Фаренгейта
C = (5.0 / 9) * (F - 32) # Соответствующие градусы Цельсия
печать C

'' '
Пробный запуск (правильный результат 21):
питон f2c.ру
21,0
'' '

Пробный запуск показывает, что программа работает и дает правильные результаты. в тестовом случае.

Упражнение 1: Вычисление 1 + 1

Первое упражнение касается самой базовой математики и программирование: присвоить результат 1 + 1 переменной и распечатать значение этой переменной. Имя файла: 1plus1 .

Упражнение 2. Напишите программу Hello World

Почти все книги по языкам программирования начинаются с очень простого программа, которая печатает текст Hello, World! на экран.9 \)) секунды? Напишите программу на Python для выполнения арифметических операций, чтобы ответить на вопрос. Имя файла: секунд2 года .

Упражнение 4. Преобразование метров в британские единицы длины

Создайте программу, в которой вы задаете длину в метрах, а затем вычисляете и запишите соответствующую длину в дюймах, футах, дюймах. 2 \ right]}, \ tag {7} \ end {уравнение} $$ является одной из наиболее широко используемых функций в науке и технике.Параметры \ (m \) и \ (s> 0 \) являются заданными действительными числами. Делать программа для вычисления этой функции, когда \ (m = 0 \), \ (s = 2 \) и \ (х = 1 \). Проверьте результат программы, сравнив с ручными вычислениями на калькуляторе. Имя файла: gaussian1 .

Примечания

Функция (7) названа в честь Карл Фридрих Гаусс, 1777-1855 гг., Который был немецкий математик и ученый, теперь считается одним из величайших ученых всех времен. Он внес вклад во многие области, включая теорию чисел, статистику, математический анализ, дифференциальная геометрия, геодезия, электростатика, астрономия и оптика.{2} \)). Также распечатайте соотношение силы сопротивления и силы тяжести. Определите \ (C_D \), \ (\ varrho \), \ (A \), \ (V \), \ (m \), \ (g \), \ (F_d \) и \ (F_g \) в качестве переменных и добавьте комментарий с соответствующим блоком. Воспользуйтесь программой для расчета сил по мячу для сильного удара \ (V = 120 \ hbox {km} / \ hbox {h} \) и для мягкий удар, \ (V = 30 \ hbox {km} / \ hbox {h} \) (легко смешать несовместимые единиц, поэтому убедитесь, что вы выполняете вычисления с \ (V \), выраженным в м / с). Имя файла: kick .

Упражнение 12: Как приготовить идеальное яйцо

Во время приготовления яйца белки сначала денатурируют, а затем коагулируют. Когда температура превышает критическую точку, реакции начинаются и продолжаются быстрее при повышении температуры. В яичном белке белки начинают коагулировать при температуре выше 63 C, при этом в желтке белки начинают коагулировать при температуре выше 70 С. Для мягкого вареное яйцо, белок должен быть нагрет достаточно долго, чтобы коагулируют при температуре выше 63 С, но желток не должен нагревается выше 70 С.{-1} \). Кроме того, \ (T_w \) — температура (в градусах Цельсия) кипения. вода, а \ (T_o \) — исходная температура (в градусах Цельсия) яйца перед тем, как положить в воду. Реализуйте формулу в программе, установить \ (T_w = 100 \) C и \ (T_y = 70 \) C, и вычислить \ (t \) для взятого большого яйца от холодильника (\ (T_o = 4 \) C) и от комнатной температуры (\ (T_o = 20 \) C). Имя файла: egg .

Упражнение 13: Вывести траекторию полета мяча

Цель этого упражнения — объяснить, как уравнение (6) для траектории мяча возникает из фундаментальной физики.В этом упражнении нет программирования, просто физика и математика.

Движение мяча регулируется вторым законом Ньютона: $$ \ begin {align} F_x & = ma_x \ tag {10} \\ F_y & = ma_y \ tag {11} \ end {align} $$ где \ (F_x \) и \ (F_y \) — сумма сил в \ (x \) и \ (y \) направлениях соответственно, \ (a_x \) и \ (a_y \) — ускорения шар в направлениях \ (x \) и \ (y \), а \ (m \) — масса шара. Пусть \ ((x (t), y (t)) \) — положение шара, i.2} \ tp \ tag {13} \ end {align} $$ Если предположить, что гравитация — единственная важная сила, действующая на мяч, \ (F_x = 0 \) и \ (F_y = -mg \).

Дважды проинтегрируйте два компонента второго закона Ньютона. Использовать начальные условия по скорости и положению, $$ \ begin {align} {d \ over dt} x (0) & = v_0 \ cos \ theta, \ tag {14} \\ {d \ over dt} y (0) & = v_0 \ sin \ theta, \ tag {15} \\ х (0) & = 0, \ tag {16} \\ у (0) & = y_0, \ tag {17} \ end {align} $$ для определения четырех постоянных интегрирования. Напишите финал выражения для \ (x (t) \) и \ (y (t) \).Покажите, что если \ (\ theta = \ pi / 2 \), т.е. движение чисто вертикальное, получаем формулу (1) для позиции \ (y \). Также покажите, что если мы исключить \ (t \), получим соотношение (6) между координатами \ (x \) и \ (y \) мяча. Вы можете узнать больше об этом типе движения в физике. книга, например, [6]. Имя файла: траектория .

Упражнение 14: Найдите ошибки в кодировании формул

Некоторые версии нашей программы для расчета формулы (3) перечислены ниже.Найдите версии это не будет работать правильно и объяснить, почему в каждом конкретном случае. 2 -4ac} \ over 2a} \ tp \ tag {18} \ end {уравнение} $$ Какие проблемы со следующей программой?

 а = 2; b = 1; с = 2
из математического импорта sqrt
д = б * б - 4 * а * в
q_sr = sqrt (д)
x1 = (-b + q_sr) / 2 * а
x2 = (-b - q_sr) / 2 * а
печать x1, x2

Исправьте программу так, чтобы она решала данное уравнение.Имя файла: find_errors_roots .

Упражнение 18: Найдите ошибки в программе

В чем проблема в следующей программе?

 из math import pi, tan
загар = загар (пи / 4)
tan2 = tan (пи / 3)
печать загар, загар2

Имя файла: find_errors_tan .

Х. П. Лангтанген . Как получить доступ к Python для выполнения научных вычислений, \ emphhttp: //hplgit.github.io/primer.html/doc/pub/accesspy, http: // hplgit.github.io/primer.html/doc/pub/accesspy.
Х. П. Лангтанген . Различные способы запуска программ Python, \ emphhttp: //hplgit.github.io/primer.html/doc/pub/runpy, http://hplgit.github.io/primer.html/doc/pub/runpy.
Д. Э. Кнут . Теория и практика, EATCS Bull. , г. 27, стр. 14-21, 1985.
Х. П. Лангтанген . Циклы и списки, \ emphhttp: //hplgit.github.io/primer.html/doc/pub/looplist, http: // hplgit.github.io/primer.html/doc/pub/looplist.
Х. П. Лангтанген . Функции и ветвление, \ emphhttp: //hplgit.github.io/primer.html/doc/pub/funcif, http://hplgit.github.io/primer.html/doc/pub/funcif.
Л. С. Лернер . Физика для ученых и инженеров , Джонс и Барлетт, 1996.

Как это решить: математический подход к программированию

Каждый день мы решаем задачи более сложные, чем те, которые мы решали ранее.В этом сообщении в блоге я хотел бы расширить концепции, ранее обсуждавшиеся в моем предыдущем сообщении, — решение проблем с помощью математического подхода.

Каждый день мы решаем проблемы более сложные, чем те, которые мы решали ранее. В этом сообщении в блоге я хотел бы расширить концепции, ранее обсуждавшиеся в моем сообщении, о секретах успешного юниорства. Изучая математику, я прочитал книгу «Как ее решить», посвященную упрощению сложных задач. Речь шла об эвристике — очень прямых (хотя и не обязательно наиболее эффективных) способах поиска решений.

В этом сообщении блога представлены некоторые эвристики, обсужденные Джорджем Полиа, великим венгерским математиком. Мы поговорим о некоторых успешных подходах к поиску решений. Полиа полностью изменил мой подход к решению проблем. Не только математические — его идеи могут быть успешно применены в других областях, в том числе в информатике. Я собираюсь объяснить, как мы можем использовать эти эвристики в программировании, и приведу примеры, показывающие, как они работают в реальном коде. Я приглашаю вас прочитать Полю и попытаться найти свои собственные решения.Пример кода написан на Ruby, не забывайте об этом!

Ниже я представляю основные шаги из книги Поли с короткими комментариями. Я считаю эти мелочи чрезвычайно полезными при поиске решений:

1. Разобраться в проблеме

Внимательно прочтите задание, постарайтесь понять его и глубоко подумайте. Подумайте, что у вас есть и что вы хотите найти. Сформулируйте задачу своими словами.

2. Сформировать алгоритм

Найдите связь между предоставленной информацией и тем, что вы хотите найти.В одних и тех же случаях будет намного проще решить немного другую проблему, если вы не сможете найти решение напрямую. В конце работы вы должны были составить алгоритм решения проблемы. Представьте себе функцию в виде черного ящика , в который вы вводите некоторую информацию, а затем возвращаете ее в некоторой измененной форме.

Подумайте о подобной проблеме. Возможно, вы решили нечто похожее и можете повторно использовать решение немного по-другому, с немного другим подходом. Как можно преобразовать данные? Какая структура данных вам нужна? Какие параметры нужно передавать через функции? Подумайте о структуре данных, которая у вас есть, возможно, она имеет особую структуру, которая позволяет вам использовать подходящие алгоритмы.

3. Просто составьте алгоритм!

Двигайтесь шаг за шагом и посмотрите, сможете ли вы доказать каждый шаг. Сделайте что-нибудь разумное. Не повторяйте бездумно. Хороший алгоритм защищает себя. Теперь вы можете написать программу для ее решения.

4. Посмотрите на свое решение

Второй взгляд позволяет найти более эффективные решения. После того, как найдете ответ — подумайте, можно ли лучше . Иногда улучшения незначительны и неопределенны, обычно они позволяют писать более эффективные программы и заботиться о большей временной сложности. Обратная связь дает вам как положительную, так и отрицательную информацию. Это позволяет вам увидеть свои сильные и слабые стороны, чтобы вы могли знать, в каких областях вам нужно работать, чтобы улучшить свои навыки.В следующий раз, когда вы столкнетесь с проблемой, вы сможете решить ее быстрее и лучше.

Давайте напишем программу, которая вычисляет n-е число Фибоначчи, а затем для двух соседних таких чисел найдет способ вычислить их наибольший общий делитель, gcd (F (n), F (n + 1)) =? .

Понять

Что вам нужно? Наибольший общий делитель двух чисел Фибоначчи.

Как вы его получили? Напишите универсальную функцию для вычисления чисел Фибоначчи для заданной переменной.

Какой тип переменной нам нужен? Это должно быть целое число

Нам еще что-нибудь нужно? Да, функция наибольшего общего делителя.

Составьте план

Мой план довольно короткий:

Я собираюсь написать функцию Фибоначчи — мне нужна для нее формула, и это будет функция повторения. Затем я напишу функцию, которая находит наибольший общий делитель (НОД) двух чисел. Наконец, подставьте первое во второе, и я получу наибольший общий делитель двух чисел Фибоначчи.

Я представляю функцию, основанную на формуле, и она довольно проста. Первое и второе числа в последовательности равны единице, а каждый следующий элемент — это сумма двух предыдущих элементов в последовательности. Подробнее см. Число Фибоначчи (в Википедии).

Теперь функция gcd

Выполнить

Для данного n

Например, n = 32

Вы можете использовать отладчик для пошагового перехода и проверки работы этой функции — это полезно, когда что-то идет не так.

Оглянуться назад

Что я могу сделать лучше? Я считаю, что функция Фибоначчи недостаточно эффективна. Я могу вычислить массив, а затем выбрать соседние записи.

Эта функция возвращает n чисел Фибоначчи в массиве:

, а следующая функция возвращает массив из двух соседних чисел

, то я могу соединить эти две функции и использовать оператор splat для передачи параметров функции gcd .

Он должен вернуть «1», если числа не имеют общего делителя.Это более быстрое решение, чем предыдущее, с повторением и не требует стольких вычислений.

Я возвращаюсь к его книгам, потому что с каждым новым чтением всегда нахожу что-то новое. В 20 веке впервые заговорили о герменевтическом круге. Он описывает простое наблюдение: каждый раз, когда мы читаем текст, предыдущее чтение меняет текущее. В результате мы лучше и глубже понимаем идею текста. Когда мы применяем это к эвристике Поли, мы получаем мощное и полезное оборудование, которое мы можем использовать в нашей работе.Кроме того, в его книге есть словарь эвристики, думаю, любопытный читатель найдет в нем много полезных тактик и средств взлома блокировок.

В завершение — вы должны проверить, равен ли наибольший общий делитель всех соседних чисел Фибоначчи 1. Я оставлю вам цитату другого замечательного математика, Пола Халмоса, которая показывает удивительную важность вопросов и является хорошим резюме. это сообщение:

Не просто читайте; борись с этим! Задавайте собственные вопросы, ищите собственные примеры, находите собственные доказательства.Нужна ли гипотеза? Верно ли обратное? Что происходит в классическом частном случае? А как насчет вырожденных случаев? Где доказательство использует гипотезу?

5 типов математики, используемых в информатике

Различные виды математики, используемые в компьютерных науках

Двоичная математика
Алгебра колледжа
Статистика
Исчисление
Дискретная математика

В качестве сложной области существуют различные виды математики в информатике.Информатика изучает принципы и использование компьютеров при обработке информации, разработке аппаратного и программного обеспечения и использовании приложений. Обладание основательными математическими знаниями жизненно важно для понимания того, как работают компьютеры. Математика — это фундаментальный научный инструмент в области вычислений.

Ресурс по теме: 50 лучших бакалавров в области компьютерных наук

1. Двоичная математика

Двоичная математика — это сердце работы компьютера и один из наиболее важных видов математики, используемых в информатике.Двоичный формат используется для обозначения каждого числа в компьютере. Двоичная система счисления является альтернативой десятичной системе счисления. Использование этой системы упрощает компьютерный дизайн. Чтение и простые математические операции жизненно важны для аппаратного программирования низкого уровня. Знание того, как работать с шестнадцатеричной системой счисления, необходимо для различных функций программирования, включая установку цвета элемента. Стандартная арифметика используется во многих функциях компьютерного программирования. Практически в каждой написанной программе используются области сложения, вычитания, умножения и деления.

2. Алгебра колледжа

Алгебра колледжа охватывает различные концепции, включая линейные уравнения, операции, разложение на множители, показатели, полиномы, квадратные уравнения, рациональные выражения, радикалы, отношения, пропорции и прямоугольные координаты. Он фокусируется на алгебраических связях, графиках и функциях, и студенты учатся решать одну или две неизвестные переменные в различных сложных уравнениях. Студенты также узнают, как графически отображать алгебраические функции. Алгебра используется в информатике при разработке алгоритмов и программного обеспечения для работы с математическими объектами.Он также используется для разработки формул, которые используются в числовых программах и для полных научных вычислений.

3. Статистика

Статистика — это форма математики, используемая в информатике, которая использует количественные модели, представления и резюме для предоставленного набора экспериментальных данных или реальных исследований. Методики полевых исследований для получения, анализа, оценки и формирования выводов на основе данных. Некоторые статистические показатели включают среднее значение, асимметрию, регрессионный анализ, дисперсию, дисперсионный анализ и эксцесс.Статистика играет фундаментальную роль в информатике, поскольку она используется для интеллектуального анализа данных, распознавания речи, зрения и анализа изображений, сжатия данных, моделирования трафика и даже искусственного интеллекта, как и в Medium. Он также используется для моделирования. Для понимания алгоритмов и статистических свойств информатики необходим опыт в области статистики.

4. Исчисление

Исчисление — это исследование непрерывного изменения и скорости изменения. Он обрабатывает нахождение и свойства интегралов и производных функций.Существует два типа исчисления: дифференциальное исчисление и интегральное исчисление. Дифференциальное исчисление имеет дело со скоростью изменения количества. Интегральное исчисление определяет величину, для которой известна скорость изменения. Исчисление используется во множестве областей компьютерных наук, включая создание графиков или визуальных элементов, моделирование, приложения для решения проблем, кодирование в приложениях, создание статистических решателей, а также разработку и анализ алгоритмов.

5. Дискретная математика

Дискретная математика исследует объекты, которые должны быть представлены конечным образом.Он включает в себя множество тем, на которые можно ответить на различные вопросы. Он включает в себя несколько концепций, включая логику, теорию чисел, счет, вероятность, теорию графов и повторения. Дискретная математика обеспечивает важную основу для всех областей информатики. Дискретная математика используется в различных областях, включая компьютерную архитектуру, алгоритмы, компьютерные системы, базы данных, функциональное программирование, распределенные системы, машинное обучение, операционные системы, компьютерную безопасность и сети.Методы решения задач, которым обучают в дискретной математике, необходимы для составления сложного программного обеспечения.

Студенты, которые любят компьютеры и обладают сильными навыками решения проблем, найдут карьеру в области информатики прибыльной и полезной, поскольку Бюро статистики труда предоставит ключевые данные в этой области. Завершение курсов по двоичной математике, алгебре колледжей, статистике, исчислению и дискретной математике — идеальный способ получить прочную основу в различных типах математики, используемых в информатике.

(PDF) Решение текстовых задач с помощью компьютерного программирования

Мы предлагаем в номинации использовать аналогичные венгерские обозначения, которые Чарльз

Симони представил для компьютерного программирования на языке C [22].

4. Блочно. Редактор визуального программирования

Теперь мы представляем Blockly, бесплатный, открытый, графический, веб-интерактивный инструмент для разработки, предназначенный для

молодых людей и непрофессионалов для изучения компьютерного программирования. Blockly — один из проектов Google

Inc; он начался в августе 2012 года под руководством команды инженеров Нила Фрейзера

[10].Давайте посмотрим его основные характеристики.

— Это бесплатно: никакие расходы не перегружают семьи и бюджет нашей школы, если мы

хотим использовать это в наших уроках математики.

— Открытый: им может пользоваться кто угодно без регистрации.

— Графический: нам не нужно набирать программный код, мы просто «загадываем» код

— Веб-ориентированный и интерактивный: Большинство интерактивных веб-инструментов — это всего лишь

интерактивная Flash-анимация, ничего больше.Blockly — это не инструмент на основе Flash.

Blockly действительно основан на сети, он работает в вычислительном облаке. Таким образом, это бесплатно для устройств,

, и нам не нужно устанавливать ничего особенного на наше вычислительное устройство

(смартфон, компьютер, планшет, интерактивная доска и т. Д.), Нам просто нужен веб-браузер

. По правде говоря, он оптимизирован для браузера Chrome, но у него

стали одним из самых популярных браузеров за последние два года. Когда мы заканчиваем

нашей программы, мы получаем ссылку на наш проект, который хранится в облаке Google, а

мы можем ссылаться и оглядываться на нашу работу каждый раз, когда мы открываем эту ссылку.

Наша встреча с Blockly состоялась, когда — как обычно — Google переводил «аутсорс»,

натурализовал и тестировал их бета-версию программного продукта. Один из авторов провел

это тестирование и перевел на венгерский язык как хобби. Сделал собственные заявки как скважина

. Позже мы решили обучить этому простому инструменту программирования детей в венгерских начальных и средних школах

5. О блочных языках

Blockly — один из новейших представителей большого семейства блочных языков.Есть еще

других проектов (например, Scratch [20], MIT App Inventor [17], Code.org [6]), которые очень интересны и мотивируют для изучения компьютерного программирования, и, конечно же, есть длинная

история языков этого типа и идея «демократизации» компьютерного программирования.

В 1970-х годах, когда персональные компьютеры стали более популярными, считалось, что

детей с раннего возраста должны будут познакомиться с компьютерами и компьютерным

программированием [18].И не только детям, но и всем нужны некоторые знания о компьютерном программировании

, потому что в нашей повседневной жизни мы можем понять, что компьютеры могут помочь

в нашей работе, если мы можем их контролировать, но они могут озлобить, если мы не можем. Некоторые из

(PDF) Среды решения проблем для вычислительной науки

ИЮЛЬ – СЕНТЯБРЬ 1997 21

энтузиастам необходимо написать значительный настраиваемый код, который имеет мало шансов на повторное использование

Другой целью проектирования PSE является способность sym-

болически генерировать исполняемый код из высокоуровневой спецификации

проблемы вместе с особенностями алгоритма решения

. Это важная цель, особенно

для трехмерных задач, где сложность геометрии

значительно возрастает. Задача здесь состоит в том, чтобы объединить

геометрических характеристик проблемной области с соответствующими

функциями решения.В «SciNapse: Проблема —

, решающая среда для уравнений с частными производными»,

Роберт Акерс, Элейн Кант, Кертис Рэндалл, Стэнли Стейн-

берг и Роберт Янг рассматривают некоторые аспекты генерации символического кода

для начального краевые задачи на основе

систем уравнений в частных производных, определенных на простых геометриях.

Разработка специфичных для предметной области PSE, которые объединяют

библиотек и «связанных» программных систем на нескольких уровнях

(представление, данные и выполнение) на нескольких вычислительных платформах, была определена как необходимость в em-

сила практиков и разработчиков новых алгоритмов

микрофонных решений.

Интернет и, в частности, Интернет имеют

помог ученым представить себе это программное обеспечение в среде ЧПУ. Это видение

обещает доступность мощных PSE и коммерческих серверов

в любое время и в любом месте без чрезмерных затрат на

голов и затрат, связанных с установкой, обслуживанием и обновлением программных и аппаратных ресурсов

. В статье

«Научные вычисления через Интернет: сервер Net Pellpack PSE

» Шахани Маркус, Санджива Вираварана, Элиас

Хустис и Джон Райс описывают доменно-ориентированную PSE для

PDE и демонстрируют проблемы, связанные с PDE. выполнимость сценария

NC в контексте вычислений PDE.

Прогнозируемый рост вычислительной мощности и

рабочей полосы пропускания предполагает, что вычислительное моделирование

и эксперименты перейдут от текущего моделирования физических или биологических систем

к моделированию

нескольких физических или биологических систем, взаимодействующих с

друг друга через большое количество параметров. Роберт

Нокс, Вирджиния Калб, Дэвид Кендиг и Элисса Левин

разработали PSE для связывания моделей экосистем

и выполнения связанных симуляций.О конструкции этого PSE

сообщается в их статье «Инструментальная среда

для решения проблем для интерактивного моделирования экосистем».

Каждый из этих вычислительных и инфраструктурных усовершенствований

имеет фундаментальное значение для многих других человеческих усилий, чем наука и инженерия. PSE, однако, занимают

центральную роль в CSE. Их проектирование и строительство требует сотрудничества между учеными и инженерами, и

, таким образом, представляет собой тип междисциплинарной деятельности, характерной для данной области

.Как один из нас ранее утверждал,

PSE являются продуктом поля, которое мы называем CSE.

♦

Список литературы

1. Э. Галлопулос, Э. Хустис и Дж. Р. Райс, «Компьютер как

Мыслитель / Деятель: Среда решения проблем для вычислительной науки», IEEE Computational Science & Eng., Vol. 1,

No. 2, Summer 1994, pp. 11-23.

2. Дж. Р. Райс и Р. Ф. Бойсверт, «От научных библиотек программного обеспечения

к средам для решения проблем», IEEE Computational Sci-

ence & Eng., Vol. 3, No. 3, Fall 1996, pp. 44-53.

3. G.J. Каллер и Б.Д. Фрид, «Он-лайн вычислительный центр

для научных задач», Proc. 1963 г., Тихоокеанская компьютерная конференция,

IEEE, Пискатауэй, штат Нью-Джерси, 1963 г., стр. 221-242.

4. Э. Галлопулос и А. Самех, «CSE: контент и продукт»,

IEEE Computational Science & Eng., Vol. 4, No. 2, April-June

1997, pp. 39-43.

5. Домашняя страница OpenMath: http://www.openmath.org (текущая

аренда 11 сен.1997).

Элиас Н. Хустис является профессором информатики и директором программы «Вычислительные науки и инженерия» в

Университете Пердью. Его исследовательские интересы включают PSE; компьютерные

финансовые финансы; параллельные, нейронные и мобильные вычисления; оценка и моделирование пер-

; экспертные системы для научных вычислений

; числовой анализ; и распределенное обучение. Он повторно получил

докторскую степень по математике в Университете Пердью и степень бакалавра математики

в Афинском университете.WWW, http: //

www.cs.purdue.edu/people/enh.

Рэндалл Брэмли — адъюнкт-профессор информатики в

Индианском университете, директор IU Scienti ‑ Computing Pro-

грамм и директор проекта SCAAMP, финансируемого NSF. Его re-

поисковые интересы включают параллельные вычисления, методы для больших

линейных систем, визуализацию, среду решения проблем,

и приложения для CFD. Он также является редактором «Новости технологий

и обзоры» IEEE CS&E.Электронная почта: [email protected].

Эфстратиос Галлопулос — профессор компьютерной инженерии и

информатики Университета Патры, Греция. Он получил докторскую степень

в области информатики в Университете Иллинойса в Урбане,

Шампейн и степень бакалавра наук (с отличием первого класса) в Имперском колледже,

, Лондон. Он участвовал в разработке и практическом применении

мультипроцессора Cedar в Центре исследований и разработок Supercom

, а также в Goodyear MPP в

NASA Goddard Space Flight Center.Его исследовательские интересы включают

алгоритмов и сред для крупномасштабных научных вычислений, а также образование в области CSE. Он является редактором IEEE CS&E и членом

IEEE и SIAM. Электронная почта, [email protected].

Джон Р. Райс — профессор компьютерных наук в У. Брукс Форчун,

университета Пердью. Он является автором нескольких книг по теории приближений

, численному анализу, информатике,

и научному программному обеспечению.Он основал ACM’s Transactions on Math-

ematical Software в 1975 году и был ее главным редактором до 1993 года.

Он также является редактором области программного обеспечения IEEE CS&E. Райс получил степень доктора философии

в Калифорнийском технологическом институте и степень бакалавра и магистра в Университете штата Оклахома

, все по математике. Он является членом Национальной инженерной академии

, компьютерного общества IEEE, ACM, IMACS и

SIAM. WWW, http://www.cs.purdue.edu/people/jrr.

Решена сложнейшая математическая задача | Ответы на диофантово уравнение

Были найдены еще два ответа на сложную математическую задачу.
Задача, называемая «суммированием трех кубов», состоит в том, чтобы найти x, y и z.
На поиск решения потребовалось более миллиона вычислительных часов.

На протяжении десятилетий математическая головоломка ставила в тупик самых умных математиков в мире. x ³ + y ³ + z ³ = k , , где k — все числа от одного до 100, является диофантовым уравнением, которое иногда называют «суммированием трех кубов».

Когда есть два или более неизвестных, как здесь, исследуются только целые числа.Уловка состоит в том, чтобы найти целые числа, которые работают для всех уравнений, или числа для x, y и z, которые все будут равны k. За прошедшие годы ученые решили почти все целые числа от 0 до 100. Последние два оставшихся числа — 33 и 42.

Вот видео Numberphile, объясняющее, почему эта задача оказалась такой сложной:

Этот контент импортирован с YouTube. Вы можете найти тот же контент в другом формате или найти дополнительную информацию на их веб-сайте.

Ранее в этом году Эндрю Букер из Бристольского университета провел недели с суперкомпьютером, чтобы наконец найти решение для 33. Но 42, которое по совпадению является хорошо известным числом в поп-культуре, оказалось намного сложнее.

Итак, Букер обратился к профессору математики Массачусетского технологического института Эндрю Сазерленду, а Сазерленд, в свою очередь, обратился за помощью к Charity Engine, которая использует простаивающие, неиспользованные вычислительные мощности более 500 000 домашних ПК для создания краудсорсингового и экологически безопасного суперкомпьютера.

На вычисление ответов ушло более миллиона часов. Без лишних слов они следующие:

X = -80538738812075974, Y = 80435758145817515 и Z = 12602123297335631.

Ну, , очевидно, .

«Я чувствую облегчение», — говорит Букер о решении головоломки 65-летней давности, впервые заданной в Кембридже, в заявлении для прессы. «В этой игре невозможно быть уверенным, что ты что-то найдешь. Это немного похоже на попытку предсказывать землетрясения, поскольку у нас есть только приблизительные вероятности.Итак, мы можем найти то, что ищем, через несколько месяцев поиска, или может оказаться, что решение не будет найдено в течение следующего столетия ».

Этот контент создается и поддерживается третьей стороной и импортируется на эту страницу, чтобы помочь пользователям указать свои адреса электронной почты. Вы можете найти больше информации об этом и подобном контенте на сайте piano.io.

Как алгоритмы решают все наши проблемы. . . и Create More: Dormehl, Luke: 9780399170546: Amazon.com: Книги

Благодарности

Написание книги — это почти всегда уединенное занятие, но мне посчастливилось быть в окружении группы людей, любовь и / или поддержка которых сделали The Formula удовольствием для работы. Прежде всего, спасибо Кларе, Тиму и Селии Лант, а также членам моей семьи. Я не смог бы завершить этот проект без неоценимой помощи Эда Фолкнера, в то время как он никогда бы не прошел, если бы не мой агент Мэгги Хэнбери, Генри де Ружмонт, Саймон Гарфилд и Джейк Лингвуд.Большое спасибо Мариан Лиззи, моему редактору в США. Благодарные кивки также направляются всем тем, кто провел бесчисленные часы, разговаривая со мной в рамках моего исследования (полный список их имен напечатан на странице 243), в дополнение к моему редактору FastCo.Labs Крису Даннену, Леандер Кэни из Mac , превосходная Николь Мартинелли, Карл Френч, гуру технических коммуникаций Алиса Бонасио-Аткинсон, Тим Мэттс, Алекс Миллингтон, Майкл Гротхаус, Том Аткинсон, Саймон Кэллоу и мои братья-от-матери, Андре и Натан Трантраал.Все так или иначе помогли этой книге. Все, что я могу отдать должное, — это (надеюсь, несколько) ошибок.

Объяснение названия и прочее Cyberbole

По своей сути алгоритмы представляют собой не что иное, как серию пошаговых инструкций, обычно выполняемых компьютером. Однако, если их описание прямолинейно, их внутренняя работа и влияние на нашу жизнь совсем не так.

Алгоритмы сортируют, фильтруют и выбирают информацию, которая предоставляется нам ежедневно.Они несут ответственность за результаты поиска, показываемые нам Google, информацию о наших друзьях, которую выделяет Facebook, и типы продуктов, которые, по прогнозам Amazon, мы с большей вероятностью купим. Во все большей степени они также будут нести ответственность за то, как выглядят фильмы, музыка и другие развлечения, с какими людьми мы сотрудничаем в рамках прогнозных отношений и даже за то, как применяются законы и действует полиция. Алгоритм может сканировать ваши метаданные и порекомендовать, что вы, вероятно, станете трудолюбивым сотрудником, так же, как вас могут обвинить в преступлении или определить, что вы неспособны водить машину.В процессе алгоритмы коренным образом меняют наш взгляд (по словам Дугласа Адамса) на жизнь, вселенную и все остальное.

Одно из моих любимых наблюдений о технологиях — это то, которое часто приписывают теоретику культуры Полю Вирилио: «Изобретение корабля было также изобретением кораблекрушения». Можно, конечно, перевернуть это и сказать, что изобретатель кораблекрушения был также человеком, который изобрел корабль. Алгоритмы имели свою долю кораблекрушений (о которых я буду говорить в ходе этой книги), но они также выполняют невероятно полезные функции: позволяют нам перемещаться по 2.5 квинтиллионов байт данных, которые генерируются каждый день (в миллион раз больше информации, чем способен вместить человеческий мозг), и на их основе делаются практические выводы.

Как и в старой пословице о том, как вырезать статую слона (вы отрубаете все, что не является слоном), я начну с объяснения того, чем не является эта книга. Во-первых, это не учебник по информатике, посвященный алгоритмам. Есть книги гораздо лучше (и, действительно, гораздо более квалифицированные писатели) для решения этой задачи.

Это не история алгоритма как концепции. Хотя я подумывал о такой попытке, меня оттолкнул как сам масштаб проекта, так и тот факт, что его конечный результат — хотя, без сомнения, захватывающий под руководством правильного автора — не будет полностью отличаться от учебника, который я также уклонялся от. Под этим я не имею в виду, что книга по истории и учебник обязательно одно и то же, а скорее, что история некогда нишевой математической концепции, вероятно, понравится только тем математикам или компьютерным специалистам, которые уже знакомы с ней.

Вместо этого я хочу рассказать о бесчисленных способах (некоторые тонкие, другие менее), которыми алгоритмы влияют на всю нашу жизнь: от развлечений, которые нам нравятся, до того, как мы думаем о человеческих отношениях. Что общего между забиванием горячих свиданий, стрельбой по голливудским индюшатам, сбором какашек и сокращением гонораров юристам? Это книга об алгоритмизации жизни, какой мы ее знаем.

В моей повседневной работе, когда я пишу о сфере, известной как «цифровые гуманитарные науки» для Fast Company , я постоянно рассматриваю последствия «алгоритмической» культуры и идеи (не всегда ошибочной), что несмотря ни на что проблема, ее можно решить с помощью правильного алгоритма.

Типичную иллюстрацию того, что я имею в виду, можно увидеть в книге Билла Тансера (2009 г.) Click: What We Do Online and Why It Matters . Тансер, которого по крайней мере в одном месте называют «выдающимся мировым экспертом по [поведению] в Интернете», начинает свою книгу с описания радиоинтервью, которое он однажды прослушал в машине. На собеседовании был британский психолог, который сослался на математическую формулу, которую он разработал для определения наиболее объективно депрессивной недели в году. После долгой работы он обнаружил, что это была третья неделя января, подвиг, вызванный слиянием невыполненных новогодних решений, задолженностей по кредитным картам, накопленных за праздничный сезон, и обычных мрачных погодных условий.Тансер отмечает, что его это не убедило: эта точка зрения была подтверждена позже, когда формула была подвергнута резкой критике за отсутствие научной строгости. Однако его неуверенность не имеет ничего общего с предположением о том, что редукционная формула могла бы дать ответы на такую сложную и многогранную тему, как депрессия, а скорее потому, что он считает, что он придумал лучшую формулу.1

In Другими словами, его проблема заключалась не в существовании суммы, а скорее в ее работе.

Эта книга возникла в результате многолетних наблюдений за подобными наблюдениями, в которых утверждается, что не существует проблемы, которую технология не может свести к ее наиболее шаблонному уровню и тем самым дать объективные ответы на них. Это мышление является причиной того, что «Формула» написана прописными буквами, а не просто существует как обобщение для различных технических процессов, которые я описываю. Это подразумевает идеологический элемент, и эта идеология подтверждается более широким взглядом, который я беру на алгоритмы и связанный с ними технологический аппарат: их понимание как воплощение особой формы техно-рациональности, симптоматическое для типа социального порядка, построенного вокруг обещание объективности.Таким образом, я использую Формулу во многом так же, как покойный американский политолог и теоретик коммуникаций Гарольд Лассуэлл использовал слово «техника»: имея в виду, по словам Лассуэлла, «совокупность практик, с помощью которых человек использует доступные ресурсы для достижения ценностей». Речь идет как о применении, так и о сфере применения, а также о существовании объективных истин, скрывающихся под поверхностью, которые необходимо выявить с помощью правильных инструментов интеллектуального анализа данных.

Писатели, пишущие о технологиях, обычно, за некоторыми заметными исключениями, в подавляющем большинстве своем утопичны в своих взглядах.Для них любой прогресс положительный. В результате, среди авторов, пишущих о технологиях, существует тенденция называть каждое новое изобретение тотемным образцом своей собственной «эпохи» — что привело к пренебрежительному термину «кибербола». Хотя эта книга вполне может присоединиться к тому количеству томов об алгоритмах и больших данных, которые уже выстроились на полках, то, что меня интересует, уходит корнями гораздо дальше, чем просто рождение Интернета или век персональных компьютеров.

Французский социолог (и христианский анархист!) Жак Эллул, писавший в первой половине 1960-х годов, описал существо, известное как Технический человек, человека, «очарованного результатами, непосредственными последствиями запуска стандартизированных устройств в действие.. . привержены нескончаемому поиску «единственного наилучшего способа» достижения поставленной цели ». Достижение этой цели иногда могло быть омрачено (или ускорено) из-за наивного энтузиазма по поводу средств достижения цели: не из-за чего-то столь не поддающегося количественной оценке, как этические соображения, а, скорее, из-за энтузиазма по поводу изобретательности, элегантности и «впечатляющей эффективности» человеческих способностей. придумывать решения.

Как показывает наблюдение Эллула, такой подход не нов, и основатели Google и руководители различных высокотехнологичных компаний, о которых я говорю, не первые люди, демонстрирующие то, что покойный американский социолог Льюис Мамфорд назвал « воля к порядку », что означает желание разобраться в мире по шаблонам.В 1930-х годах, задолго до рождения современного компьютера, Мамфорд отмечал, что автоматизация одновременно предназначена для «увеличения механических или сенсорных возможностей человеческого тела» и «для уменьшения до измеримого порядка и регулярности жизненных процессов». «Чтобы понять общую картину, мы ее уменьшаем», — предложил он. Чтобы взять абстрактное понятие, такое как человеческий интеллект, и превратить его в нечто поддающееся количественной оценке, мы абстрагируем его дальше, убирая сложность и присваивая ему, казалось бы, произвольное число, которое становится IQ человека.

Новым является масштаб, на котором сейчас воплощается эта идея, до такой степени, что трудно представить себе сферу работы или отдыха, которая не подлежит алгоритмизации и Формуле. Эта книга о том, как мы достигли этой точки, и как возраст алгоритма влияет и формирует такие разные предметы, как человеческое творчество, человеческие отношения (и, более конкретно, романтические отношения), представления о личности и вопросы права.

Алгоритмы очень хорошо дают нам ответы во всех этих случаях.

Реальный вопрос в том, дают ли они ответы, которые мы хотим.

ГЛАВА 1

Количественное определение «Я»

Ларри Смарр весил около 200 фунтов, когда он прибыл в Ла-Хойю, Калифорния, в 2000 году. На фотографии из его водительских прав в то время изображен полноватый 51-летний мужчина с мягким телом. , круглое лицо и мясистая рябь на двойном подбородке. Хотя он регулярно проверял свой ум как ведущий физик и эксперт в области суперкомпьютеров, Смарр годами не тренировал свое тело должным образом.Он регулярно пил кока-колу и наслаждался прожаренными во фритюре пирожными с сахарной глазурью1. Переехав на Западное побережье, чтобы открыть новый институт при Калифорнийском университете под названием Калифорнийский институт телекоммуникаций и информационных технологий, он внезапно столкнулся с проблемой чувство, которое он не испытывал годами: чувство глубокой неполноценности. «Я огляделся и увидел всех этих худых, подтянутых людей», — вспоминает он. «Они бегали, ехали на велосипеде, выглядели красиво. Я понял, насколько я был другим.

Следующий вопрос Смарра разделяли как ученые, так и философы: почему? Он посетил местный книжный магазин и купил «около миллиона» диетических книг. Ни один из них не считался удовлетворительным для человека, чей мозг мог справиться с запутанными деталями сверхновых звезд и сложных звездных образований, но для которого здоровое питание и регулярные упражнения казались, как ни странно, сложной астрофизикой. «Все они казались такими произвольными», — говорит он. Только когда он обнаружил книгу под названием Зона , написанную биохимиком Барри Сирсом, Смарр нашел то, что искал.Сирс рассматривал тело как связанную нелинейную систему, в которой механизмы обратной связи, такие как глюкозно-инсулиновая и иммунная системы, взаимодействуют друг с другом. Это был подход, который мог понять Смарр. Вдохновленный, он начал измерять свой вес, каждый день забираясь голым на весы и записывая число, которое появлялось перед ним. Затем он нанял личного тренера и начал ежедневно отслеживать количество упражнений, в которых он участвовал. После этого он сел на диету — разбив пищу на «элементарные единицы» из белков, жиров, углеводов, клетчатки, сахара и соли, и изменил свой рацион, чтобы удалить те входы, которые оказывались пагубными для благополучия.«Думайте об этом, как о инженере, который реконструирует подсистемы автомобиля», — говорит Смарр. «Из этого вы можете сделать вывод, что вам нужен определенный уровень бензина для того, чтобы работать, и что, если вы залите воду в свой бензобак, вы разнесете машину на части. Мы не думаем так о своем теле, но мы должны думать так ».

Прошло совсем немного времени, и Смарр обратился к более сложным технологиям, которые помогли ему похудеть. Он купил и начал носить браслеты для измерения пульса Polar WearLink, FitBits, BodyMedia и другие носимые устройства, которые используют алгоритмы для преобразования показателей тела в данные.Желая проверить свои успехи, Смарр начал платить за анализы крови в частной лаборатории, а затем — в поисках еще большего количества цифр, которые можно было бы изучить — начал FedEx отказываться от своего стула для регулярных анализов. «У меня не было биологического или медицинского образования, поэтому мне пришлось учиться самому», — говорит Смарр о своем процессе.

Одно из чисел, на котором он остановился, связано со сложными реактивными белками, которые действуют как прямая мера воспаления в организме. В нормальном человеческом теле это число должно быть меньше единицы.В случае Смарра их было пять. Со временем оно выросло до 10, а затем до 15. Как ученый он открыл парадокс. «Как получилось, что я сократил все факторы, которые обычно вызывают воспаление, с точки зрения моих запасов пищи, но их количество росло и росло вместе с этим хроническим воспалением?» он размышляет. «В этом не было никакого смысла».

В этот момент Смарр решил посетить своего врача, чтобы представить результаты. Встреча прошла не так, как планировалось.

«У вас есть симптомы?» — спросил доктор.

«Нет», — ответил Смарр. «Я хорошо себя чувствую.»

«Ну, тогда зачем ты меня беспокоишь?»

«Что ж, у меня есть отличные графики моих личных данных».

«Зачем вы это делаете?» пришел ответ.

Врач сказал Смарру, что его данные слишком «академические» и не пригодны для клинической практики. «Возвращайтесь, когда с вами что-то действительно не так, а не просто аномалии в ваших графиках», — сказал доктор.

Несколько недель спустя Смарр почувствовал сильную боль в левой части живота.Он вернулся к врачу, и ему поставили диагноз дивертикулит — заболевание, вызванное острым воспалением. Это была прекрасная иллюстрация проблемы Смарра: врачи будут заниматься только клиническими симптомами, не желая углубляться в данные, которые могут оказаться профилактическими. Усвоив важный урок, Смарр решил взять на себя отслеживание своего здоровья.

«Людям промыли мозги, заставив думать, что они не несут ответственности за состояние своего тела», — говорит он. «Я подсчитал соотношение двух 20-минутных посещений врача в год по сравнению с общим количеством минут в году, и оказалось, что это один на 10 000.Если вы думаете, что кто-то сможет сказать вам, что с вами не так, и решить проблему за одну десятитысячную времени, которое у вас есть, чтобы сделать то же самое, я бы сказал, что это определение безумия. В этом нет никакого смысла ».

После визита к врачу Смарр начал одержимо отслеживать все симптомы, которые он заметил, и связывать каждый из них с колебаниями данных своего тела. Он также увеличил объем информации, на которую смотрел, и начал использовать сложные алгоритмы интеллектуального анализа данных, чтобы просеивать ее в поисках нарушений.Еще одно большое число, на которое он обратил внимание, касается лактоферрина, антибактериального агента, выделяемого лейкоцитами, когда они находятся в режиме атаки, что немного похоже на баллончик слезоточивого газа, распыляемый в толпе людей. Это число должно было быть меньше семи. Когда Смарр впервые проверил его, его было 200, а к маю 2011 года оно выросло до 900. Изучая научную литературу, Смарр поставил себе диагноз хронического аутоиммунного заболевания, которое позже он сузил до того, что называется болезнью Крона.«Меня полностью привели туда биомаркеры», — отмечает он.

В этом смысле Smarr — воплощение алгоритмической жизни. Он постоянно отслеживает 150 переменных, проходит 7000 шагов каждый день и имеет доступ к миллионам отдельных точек данных о себе. Таким образом, и его тело, и его повседневная жизнь разделены, математизированы и систематизированы таким образом, чтобы он мог следить за тем, что происходит внутри него, с точки зрения чистых чисел. «По мере того, как наша технологическая способность« считывать »состояние основных подсистем нашего тела улучшается, отслеживание изменений наших ключевых биохимических маркеров с течением времени станет рутиной, а отклонения от нормы будут легче выявлять ранние сигналы развития болезни», Смарр утверждает в эссе, озаглавленном «На пути к цифровой геномной медицине: 10-летняя детективная история количественной оценки моего тела.2

Используя свой доступ к суперкомпьютерам Калифорнийского университета, Смарр в настоящее время работает над созданием распределенного планетарного компьютера, состоящего из миллиарда процессоров, который, как он утверждает, в течение десяти лет, позволит ученым создавать рабочие алгоритмические модели человеческого тела. Что же, в конце концов, представляет собой тело, как не сложная система, которую можно настраивать и модифицировать?

Как заметил журналист Марк Боуден в статье 2012 года для Atlantic : «Если бы мыслители прошлого сильно полагались на паровой двигатель как на универсальную аналогию, то e.g., содержание под давлением взорвется (вспомните идеи Маркса о революции или Фрейда о подавленных желаниях) — сегодня мы предпочитаем, чтобы наши метафоры были электронными ».

А когда дело доходит до символических представлений, многие люди (включая Смарра) предпочитают формулы метафорам.3

Самопознание через числа

Подбирая исследование « n = 1», в котором участвует только один человек, История Ларри Смарра исключительна. Не все являются экспертами в области суперкомпьютеров, и не у всех есть возможности или ресурсы (его режим стоит от 5000 до 10000 долларов в год) для сбора огромных объемов личных данных или понимания их смысла в случае, если они это сделают.

Но Смарр не одинок. Как наркоман данных, он является ценным членом так называемого движения Quantified Self: постоянно расширяющейся группы подобных людей, которые с энтузиазмом принимают участие в форме самоконтроля, соматического наблюдения. Движение Quantified Self, основанное редакторами журнала Wired Гэри Вольфом и Кевином Келли в середине 2000-х, выражает свои устремления в смелых философских терминах, обещая преданным «самопознание через числа». 4 Принимая позитивистский взгляд на верификацию и эмпиризм, и, комбинируя это с либеральной дозой технологического детерминизма, движение Quantified Self поднимает экзистенциальный вопрос о том, какой тип «я» может существовать, если его нельзя вычислить с помощью правильных алгоритмов?

Если Сократ пришел к выводу, что неизученная жизнь не стоит того, чтобы жить, то обновление 21-го века могло бы предложить то же самое относительно неизученной жизни.Как и в известном высказывании Рене Декарта: cogito ergo sum («Я мыслю, следовательно, существую») — я измеряю, следовательно, существую.

В некотором смысле «селферы» выводят идеи Декарта о себе на еще более детальный уровень. Декарт воображал, что сознание не может быть разделено на части, как тело, поскольку оно не имеет телесной формы. Селферс считает, что человека можно эффективно резюмировать, если используется правильная технология и собираются правильные данные.Входными факторами могут быть потребляемая пища или качество окружающего воздуха, в то время как состояние можно измерять по настроению, возбуждению и уровню кислорода в крови, а также по производительности с точки зрения психического и физического благополучия.

«Мне нравится идея, что кто-то где-то собирает все эти данные», — говорит Кевин Конбой, создатель количественного секс-приложения Bedpost, к которому я вернусь позже в этой книге. «У меня есть такая философская надежда, что эти числа где-то существуют, и что, возможно, когда я умру, я увижу их.Идея о том, что компьютерный код может дать вам представление о вашей реальной жизни, очень сильна ».

Типичным самооцененным преданным (если таковой существует) является «Майкл». Каждую ночь Майкл ложится спать с датчиком на голове. Он делает это раньше, потому что именно тогда датчик сообщает ему, что его циклы сна, вероятно, будут наиболее глубокими и восстановительными. Когда Майкл просыпается, он смотрит на данные, чтобы узнать, насколько хорошо он спал. Затем он встает, отжимается и некоторое время медитирует, а затем включает компьютер и загружает письменное упражнение под названием «750 слов», в котором ему предлагается записать первые 750 слов, которые приходят на ум.5 Когда он это делает, алгоритмы текстового анализа просматривают запись и выявляют статистические данные о настроении, образе мышления и текущих заботах Майкла, о некоторых из которых он, возможно, даже не осознает, о чем беспокоится. После этого он, наконец, готов двигаться (конечно, используя FitBit для отслеживания своих шагов). Если он не выполнит эти шаги, он говорит: «Я ухожу на остаток дня». 6

Робо-цитируй мир

В то время как опора QS на передовые технологии, социальные сети и свободу — Сквозное наблюдение может показаться типично современным — во многом созданием Америки после 11 сентября — корни того, что можно описать как «бодибилдинг», уходят на несколько лет назад.80-е годы привели к появлению «роботизированных» спортсменов, которые использовали Nautilus, Stairmaster и другие высокотехнологичные тренажеры для моделирования и доводки своего тела до физического совершенства. В то же десятилетие появилась портативная технология, известная как Sony Walkman (зарождающееся видение будущего Google Glass), которая превратила общественные места в управляемый частный опыт.7 Основываясь на этой парадигме, 1990-е годы были домом для Wearable Computing Массачусетского технологического института. Group, которые оспорили то, что они считали преждевременным использованием термина «персональный компьютер», и настаивали на том, что:

Человек должен носить компьютер так же, как очки или одежду, и взаимодействовать с пользователем на основе контекст ситуации.Благодаря проекционным дисплеям, ненавязчивым устройствам ввода, персональным беспроводным локальным сетям и множеству других средств определения контекста и связи, носимый компьютер может действовать как интеллектуальный помощник, будь то через агента воспоминаний, дополненную реальность или интеллектуальные функции. коллективы.8

Кажется, есть несколько ограничений для того, что могут измерить сегодняшние количественные селферы. Красота механизма (если можно назвать его такими эстетическими терминами) заключается в том, что он делает возможной массовую настройку.Количественно оценивая себя, человек может найти явно строгие ответы на такие широкие или конкретные вопросы, как, сколько минут сна теряется каждую ночь на единицу потребляемого алкоголя, насколько последовательны его удары в гольф и следует ли им оставаться в привычном состоянии. текущая работа. Рассмотрим, например, историю молодой женщины, участницы движения «Количественное определение Я», которую называют просто «Анжелой».

Анджела работала на том, что она считала работой своей мечты, когда она загрузила приложение, которое «пинговало» ее несколько раз каждый день, прося ее каждый раз оценивать свое настроение.Когда в данных начали выявляться закономерности, Анжела поняла, что ее «оценка настроения» показывает, что она, в конце концов, не очень счастлива на работе. Когда она обнаружила это, она подала уведомление и ушла.

«Единственное, что я вижу среди людей, участвующих в движении« Количественная оценка себя », — это то, что у них есть вопросы, на которые могут дать ответы только данные, — говорит 43-летний Селфер Винсент Дин Бойс. «Поначалу эти вопросы могут быть очень упрощенными, но они очень быстро становятся более сложными. Человеку может быть интересно узнать, сколько миль он пробежал.Благодаря технологиям это сделать очень легко. Однако более сложный вопрос будет заключаться не только в том, сколько миль пробежал человек, но и сколько других людей пробежали такое же количество? Вот где нужны данные и алгоритмы. Речь идет о поисках знаний, поисках более глубокого понимания не только самих себя, но и мира, в котором мы живем ».

Бойс всегда интересовался количественной оценкой. Будучи студентом Нью-Йоркского университета, участвовавшим в программе интерактивных телекоммуникаций, он однажды прикрепил несколько датчиков, микроконтроллеров и акселерометр к модели ракеты и запустил ее с земли.«Что было интересно, — говорит он, — так это то, что я смог создать автономный компонент, который можно было куда-то отправить, который мог бы собирать информацию, а затем я мог бы извлечь и узнать что-то о нем». Проанализировав данные ракеты, Бойс получил свое «Эврика!» момент. Скейтбордист и серфер на протяжении всей жизни, он решил прикрепить аналогичные датчики к своему верному скейтборду и доске для серфинга, чтобы измерять механические движения каждого из них. Он также разбил окружающую среду на сотни поддающихся количественной оценке переменных, от погоды и времени суток до (в случае серфинга) приливных изменений и высоты волн.«С точки зрения количественной самооценки, — отмечает Бойс, — я могу. . . подумайте о том, где я занимался серфингом из геопространственного каркаса, или какое оборудование я использовал, каковы были условия. . . [Он] представляет, что я делаю что-то в пространстве и времени ».

Таким образом, Селферс возвращается к романтическому образу суровых индивидуалистов американской границы: образу, который регулярно используют промышленники Кремниевой долины и их последователи. Человек, который отслеживает свои данные, ничем не отличается от человека, который вырезает свой собственный участок земли для жизни, который черпает свою воду, генерирует свою собственную энергию и выращивает себе пищу.В мире, где пользовательские данные и личная информация собираются и передаются в беспрецедентных количествах, самоконтроль представляет собой попытку вернуть некоторую степень контроля. Подобно Google Maps, он снова помещает человека в центр его или ее вселенной. «Я верю, что однажды это станет нормой», — говорит Бойс о Количественном Я. «Он станет товаром со своим собственным чувством социальной валюты».

Покупки создают

Одна из глав в дебютном романе Дугласа Купленда « Generation X », написанном в начале века сетевых компьютеров, называется «Покупки не создают.9 Это удивительно содержательное наблюдение об активизме 1960-х, продаваемом как коммерциализм 1990-х, от автора, чьи художественные книги Microserfs и JPod прекрасно высмеивают технооптимизм на рубеже тысячелетий. Это тоже уже не так. Каждый раз, когда человек делает покупки в Интернете (или в супермаркете с помощью карты лояльности), его личность немного изменяется, создается и курируется таким образом, что почти незаметно.

Конечно, это не ограничивается только покупками.То же самое происходит всякий раз, когда вы открываете новое окно просмотра веб-страниц и выходите в Интернет. Где-то далеко в базе данных ваши передвижения были идентифицированы и зарегистрированы. Ваш IP-адрес записывается, и на вашем компьютере устанавливаются файлы cookie, что позволяет более эффективно ориентироваться на вас с помощью персонализированной рекламы и предложений. Регулярно ищите новости об определенном виде спорта, и вы начнете замечать рекламу, связанную с ним, куда бы вы ни посмотрели — например, убийцу, которого играет Роберт Уокер в фильме Хичкока « Незнакомцы в поезде », который постоянно видит напоминания о женщине, которую он убил.Упомяните, например, слова «Кейптаун» в электронном письме и посмотрите, как поток сообщений «Дешевые полеты в Южную Африку» хлынет.

Это был американский философ и психолог Уильям Джеймс, который заметил в первом томе книги его текст 1890 года Принципы психологии , что «Я человека — это совокупность всего того, что он [может] назвать своим, не только своим телом и своими психическими способностями, но и его одеждой и своим домом, его женой и детьми, его предки и друзья, его репутация и работа, его земли, яхта и банковский счет.10 Это имеет значение вдвое в эпоху алгоритмов и формул. На основе местоположения человека, сайтов, которые он посещает и проводит время, а также ключевых слов, которые он использует для поиска, на постоянной основе делаются статистические выводы о поле, расе, социальном классе, интересах и располагаемом доходе. Посещение Perez Hilton предполагает совсем другое, чем Gizmodo , в то время как покупка авиабилетов говорит о другом, чем покупка видеоигр. Во всех смыслах и целях, когда они объединены, они становятся алгоритмической самостью: идентичность и идентификация перешли в полностью цифровую (и, следовательно, измеримую) плоскость.

Ваше удовольствие — это наш бизнес

Идентификация — это большой бизнес в эпоху Формулы. Возможность отслеживать перемещения пользователей по разным веб-сайтам и серверам привела к появлению огромной индустрии фирм, занимающихся веб-аналитикой. Эти компании ставят перед собой задачу не только собирать большие объемы информации о людях, но и использовать собственные алгоритмы для анализа этих данных.

Одна из крупнейших компаний, работающих в этой области, называется Quantcast.Штаб-квартира компании находится в центре Сан-Франциско, но с дополнительными офисами в Нью-Йорке, Дублине, Лондоне, Детройте, Атланте, Чикаго и Лос-Анджелесе. Quantcast входит в пятерку крупнейших мировых компаний по оценке аудитории, собрав более 53,2 миллиона долларов. в венчурном финансировании с момента своего основания в 2006 году. Его бизнес вращается вокруг поиска формулы, которая лучше всего описывает конкретных пользователей, а затем консультирует компании о том, как извлечь из этого максимальную выгоду. «Вы уходите от человеческой гипотезы рекламы, — объясняет соучредитель Конрад Фельдман, — когда кто-то теоретизирует, какой будет идеальная аудитория для продукта и где вы могли бы найти этих людей, — к фактическому измерению кампании рекламодателя, глядя на что на самом деле работает, а затем обратное проектирование характеристик аудитории путем анализа огромных объемов данных.

Перед тем, как начать работу с Quantcast, выпускник Лондонского университетского колледжа английского происхождения Фельдман основал еще один бизнес, в котором он использовал алгоритмы для обнаружения отмывания денег для некоторых ведущих банков мира. «Мы просматривали миллиарды транзакций, с которыми эти банки проводят ежемесячно, чтобы найти подозрительную активность», — говорит он. Именно изучение мошенничества позволило Фельдману осознать мощь способности алгоритмов сортировать массивы данных в поисках шаблонов, по которым можно было бы действовать. «Он может представлять все, что интересует людей», — взволнованно говорит он.«Финансы были интересными данными, но они касались только того, на что люди тратят деньги. С другой стороны, в Интернете есть информация об интересах и изменениях в тенденциях на макро- и микроуровне, и все это в едином формате данных ». Он был завербован.

«Исторически измерения производились ретроспективно, на агрегированном уровне», — говорит Фельдман о рекламной индустрии. «Это то, что люди понимали: совокупные характеристики аудитории». Когда Фельдман впервые переехал в Соединенные Штаты, он был сбит с толку количеством рекламы на телевидении, которое часто составляло 20 минут в час.Это был подход, похожий на ружье, похожее на распыление пулеметных пуль в реку в надежде поразить отдельную рыбу. Все, что было поймано, было сделано более или менее удачно. Конечно, телеканал не может изменить его для каждого зрителя, — объясняет Фельдман. Интернет, однако, был другим. Подобно индивидуальным рекомендациям для пользователей на Amazon, алгоритмически генерируемые идеи Quantcast означали, что владельцы интернет-магазинов могли обновлять фасад магазина для каждого нового покупателя. Таким образом, аудитории могут быть разделены на демографические, психографические, интересы, образы жизни и другие детализированные категории.«Да, мы почти экстрасенсы, когда дело доходит до чтения моделей поведения и интерпретации данных», — хвастаются рекламные материалы Quantcast. «Мы знаем раньше, чем они. Мы знаем раньше вас. Мы можем сказать вам не только, куда идут ваши клиенты, но и как они собираются туда попасть, чтобы мы действительно могли повлиять на их пути ».

Образ мышления Quantcast быстро становится нормой как в Интернете, так и вне его. Стартап Facedeals из Нэшвилла обещает магазинам возможность оснастить себя камерами с функцией распознавания лиц.После установки эти камеры позволяют розничным продавцам сканировать клиентов и связывать их со своими профилями в Facebook, а затем нацеливать их на персонализированные предложения и услуги, основанные на «лайках», которые они высказали в Интернете. В конце 2013 года британский гигант супермаркетов Tesco объявил о аналогичных планах по установке видеоэкранов на своих кассах по всей стране, используя встроенные камеры, оснащенные специальными алгоритмами для определения возраста и пола отдельных покупателей. Подобно картам лояльности на стероидах, они позволят клиентам показывать индивидуализированную рекламу, которая может изменяться с течением времени, в зависимости от даты и времени дня, а также любые дополнительные сведения, полученные в результате отслеживания покупок.«Пришло время для кардинальных изменений в рекламе», — сказал Саймон Шугар, исполнительный директор Amscreen, который разработал технологию OptimEyes, скрывающуюся за экранами. «Бренды заслуживают знать не только оценку того, сколько глазных яблок просматривают их рекламу, но и то, кем они являются». 11

The Wave Theory

Это понятие привлечения пользователей на основе их индивидуальных привычек просмотра — достаточно иронично — в так называемую волновую теорию футуриста Элвина Тоффлера12. В своей книге « Третья волна » 1980 года Тоффлер описал волнообразное развитие технологий, каждая последующая волна сметает более старые общества и культуры.13 По словам Тоффлера, на сегодняшний день было три таких волны. Первая была сельскохозяйственной по своей природе, пришла на смену культурам охотников-собирателей и сосредоточилась на человеческом труде. Второй появился с промышленной революцией, был построен на крупномасштабном оборудовании и принес с собой различные «массы», которые с тех пор размножались: массовое производство, массовое распространение, массовое потребление, массовое образование, средства массовой информации, массовый отдых и т. Д. массовые развлечения и оружие массового поражения. Третья волна, таким образом, была информационным веком, открывшим славную эру «демассификации», при которой индивидуальные свободы наконец могли быть реализованы вне жестких ограничений массового общества.Демассификация, как утверждал Тоффлер, была бы «самым глубоким социальным потрясением и творческой реструктуризацией всех времен», ответственной за «построение [] замечательной новой цивилизации с нуля». И все это было построено на персонализации.

Пожалуйста, подождите, чтобы подключиться к нашему алгоритму

Хорошо известно, что не каждый агент call-центра способен обрабатывать все типы входящих звонков. Чем крупнее компания, тем меньше вероятность того, что кто-то один иметь возможность обрабатывать каждый запрос, поэтому клиенты обычно направляются в разные отделы, где агенты обучаются различным навыкам и базам знаний.Простым примером может служить глобальная компания, в колл-центры которой регулярно поступают звонки на нескольких разных языках. И вызывающие абоненты, и операторы могут говорить на одном или нескольких из нескольких возможных языков, но не обязательно на всех. Когда франкоговорящий клиент перезвонит, ему могут посоветовать нажать «1» на клавиатуре, в то время как англоговорящий клиент может быть проинструктирован нажать «2». Затем они перенаправляются к человеку, который лучше всего подходит для обработки их звонка.

Но что, если — вместо простого перенаправления клиентов к разным агентам колл-центра на основе языка или специальных знаний — можно было бы использовать алгоритм для определения конкретных качеств звонящего: на основе речевых шаблонов, конкретных слов, которые они использовали, и даже такие, казалось бы, тривиальные детали, как сказали они «э-э» или «ошиблись» — а затем использовать эти идеи, чтобы передать их агенту, наиболее подходящему для решения их эмоциональных потребностей?

Чикагская корпорация Mattersight делает именно это.Mattersight, основанный на пользовательских алгоритмах, называет свой бизнес «прогнозирующей поведенческой маршрутизацией». Разделив как вызывающих абонентов, так и агентов на разные типы личности, он может сделать бизнес быстрее и более удовлетворительным для всех участников. «У каждого отдельного клиента разные ожидания и поведение», — отмечает Mattersight в рекламных материалах. «Точно так же у каждого отдельного сотрудника есть свои сильные и слабые стороны при обработке разных типов звонков. В результате успех взаимодействия с конкретным клиентом часто определяется тем, какой сотрудник управляет этим взаимодействием и насколько хорошо его компетенции и поведенческие характеристики соответствуют потребностям каждого конкретного клиента.

Автором поведенческих моделей Mattersight является клинический психолог по имени доктор Тайби Калер. Калер является создателем типа психологического поведенческого профилирования, который называется «коммуникация процесса». Еще в начале 1970-х Калер проходил практику в частной психиатрической больнице. Находясь там, он создал нечто, называемое «Минискрипт», на основе своих наблюдений за пациентами, находящимися в бедственном положении. Эта работа принесла ему в 1977 году научную премию памяти Эрика Берна. Калер заметил, что определенные предсказуемые признаки предшествуют конкретным случаям бедствия и что эти признаки бедствия связаны с определенными речевыми моделями.Это, в свою очередь, привело к тому, что он разработал профили шести различных типов личности, которые он видел повторяющимися. Типы личности следующие:

Хотя каждый человек в большей или меньшей степени обладает всеми шестью типами личности, люди лучше всего реагируют на людей, которые отражают их собственный основной тип личности. Если потребности людей в общении не удовлетворяются путем получения положительной «обратной связи», в которой они нуждаются (например, человека, ориентированного на чувства, спрашивают холодные неопровержимые факты), они впадают в беду, которая может быть устранена только в том случае, если человек на другом конец разговора способен адекватно улавливать предупреждающие сигналы и соответствующим образом реагировать.

Согласно Mattersight, в среде call-центра эти знания приводят к необычайным качественным изменениям. Человек, подключенный к человеку со схожим типом личности, будет иметь среднюю продолжительность разговора в пять минут с 92-процентным уровнем разрешения проблем. С другой стороны, у вызывающего абонента, связанного с конфликтующим типом личности, продолжительность разговора удвоится до десяти минут, а уровень разрешения проблем упадет до 47 процентов.

Process Communication, однако, используется не только Mattersight.В прошлом Калер помогал НАСА разрабатывать алгоритмы, помогающие выбирать астронавтов, поскольку его модель может точно предсказать типы личности, которые не сломаются в атмосфере высокого давления во время космических путешествий. («Настойчивые» — которые стремятся к совершенству и поощряют других к достижению максимальной производительности — оказываются наиболее подходящими личностями.) Компания Калера, Kahler Communications, также имеет ряд текущих проектов, направленных на то, чтобы помочь организациям придумать основанные на данных и алгоритмические решения вопросов, связанных с личностью.

«С нашей точки зрения, это ключ к разнообразию», — говорит Роберт Верт, бывший поверенный, который работал главным операционным директором Kahler Communications, когда у меня была возможность поговорить с ним. «Если все культуры состоят из одних и тех же строительных блоков, и все они имеют один и тот же тип взаимодействий, как положительных, так и отрицательных, тогда реальное разнообразие заключается в типах личности. Дело не в этнической принадлежности, не в поле и не в чем-то еще. Я вижу в этом отличный эквалайзер. Если вы можете войти в комнату и сразу же начать говорить с кем-то другого, чем вы, и вы можете определить в нем те же черты, с которыми вы имели дело всю оставшуюся жизнь, этот человек больше не Другой .”

Стратегия Lake Wobegon

Основанная в 2011 году, Gild — кадровая компания, обслуживающая некоторых из крупнейших и наиболее известных игроков технологической индустрии. В настоящее время основное внимание уделяется автоматизации поиска талантливых программистов. Миссия Гильда состоит в том, чтобы применить Формулу к заведомо ненадежному процессу найма. Для этого компания использует алгоритмы для анализа людей по десяткам тысяч (а вскоре и по сотням тысяч) различных показателей и точек данных, извлекая их для понимания того, что Гилд называет «широким прогнозным моделированием».”

Истории успеха компании впечатляют. Типичный пример повествует о 26-летней бросившей колледж Джейд Домингес, которая жила на растущие долги по кредитной карте в Южной Пасадене, штат Калифорния, когда училась программированию14. работает программистом в компании, которая его нашла.

Информатика формулы для решения задач: Все формулы по информатике | Gadget-apple.ru

Решение задач на определение информационного объема текста

Задача №27. Написание сложной программы

1. Правильный алгоритм

2. Эффективность.

2.1. Эффективность по времени.

2.2. Эффективность по памяти.

3. Культура оформления программного кода.

ЕГЭ по информатике 2021 — Задание 18 (Таблица чисел)

Измерение информации. Часть 3. Не равновероятные события. Решение задач.

Решение задач, в условии которых события не равновероятны

15 приложений по физике, математике и информатике, которые позволят забыть про учебники

Математика

1. «Алгебра»

2. «Пифагория»

3. Euclidea

4. Geogebra Classic

Приложения, которые решают задачи

5. Geogebra Graphing Calculator

6. Photomath

7. Geometryx

Физика

8. Snapshots of the universe

9. «Бетафизикс»

10. Slower Light (бонус)

Информатика

Для всех предметов

НОУ ИНТУИТ | Решение олимпиадных задач по информатике

Базовые формулы (зависимости) и задачи, решаемые с их помощью

Типовые алгоритмы и задачи, решаемые с их помощью

Задачи «Операции со сверхбольшими числами»

Типовые алгоритмы обработки одномерных массивов. Сортировка методом «Пузырька»

Типовые алгоритмы обработки двумерных массивов

Задачи, сгруппированные по методам решения. Использование дополнительного массива «флажков»

Задачи, сгруппированные по методам решения. Использование дополнительного массива «флажков» (три задачи — один алгоритм)

Задачи, сгруппированные по методам решения. Метод вложенных матриц

Вычисление по формулам

О решении упражнений

Упражнение 1: Вычисление 1 + 1

Упражнение 2. Напишите программу Hello World

Упражнение 4. Преобразование метров в британские единицы длины

Примечания

Упражнение 12: Как приготовить идеальное яйцо

Упражнение 13: Вывести траекторию полета мяча

Упражнение 14: Найдите ошибки в кодировании формул

Упражнение 18: Найдите ошибки в программе

Как это решить: математический подход к программированию

1. Разобраться в проблеме

2. Сформировать алгоритм

3. Просто составьте алгоритм!

4. Посмотрите на свое решение

Понять

Составьте план

Выполнить

Оглянуться назад

5 типов математики, используемых в информатике

Различные виды математики, используемые в компьютерных науках

1. Двоичная математика

2. Алгебра колледжа

3. Статистика

4. Исчисление

5. Дискретная математика

(PDF) Решение текстовых задач с помощью компьютерного программирования

(PDF) Среды решения проблем для вычислительной науки

Решена сложнейшая математическая задача | Ответы на диофантово уравнение

Как алгоритмы решают все наши проблемы. . . и Create More: Dormehl, Luke: 9780399170546: Amazon.com: Книги

Share This Story, Choose Your Platform!

Related Posts

Приставки рос рас роз рас рос: Ошибка 403 — доступ запрещён

2 х 5 9: решите уравнение 2(x-5)=9 — Школьные Знания.com

Какие свойства человека относят к биологическим: 1. Какие свойства человека относят к биологическим? 2. Что, по вашему мнению, произошло бы с

Высшим исполнительным органом рф является: Статья 32. Высший исполнительный орган субъекта Российской Федерации \ КонсультантПлюс

Leave A Comment Отменить ответ