В треугольнике абс аб бс 10 ас 12 найдите син а: В равнобедренном треугольнике ABC AB BC = =10, AC =12. Найдите синус угла B.

В треугольнике ABC , известно что AB=10. BC=12, sin угла ABC=8/15. Най… — Учеба и наука

Ответы

24. 12.21

Михаил Александров Читать ответы

Андрей Андреевич Читать ответы

Eleonora Gabrielyan Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

Осевое сечение цилиндра –квадрат, диагональ которого равна 4 см. 3-54 на отрезке [-4;-1]

Пользуйтесь нашим приложением

Теорема косинусов и синусов треугольника. Формулы и примеры

Поможем понять и полюбить математику

Начать учиться

222.5K

9 класс — насыщенное новыми знаниями время. Чтобы не запутаться в теории по геометрии, рекомендуем сделать карточки с информацией по каждой теме. В этой статье вы найдете самое важное про теорему косинусов.

Формулировка и доказательство теоремы косинусов

Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Формула Теоремы Пифагора:

a²> + b²> = c²>, где a, b — катеты, с — гипотенуза.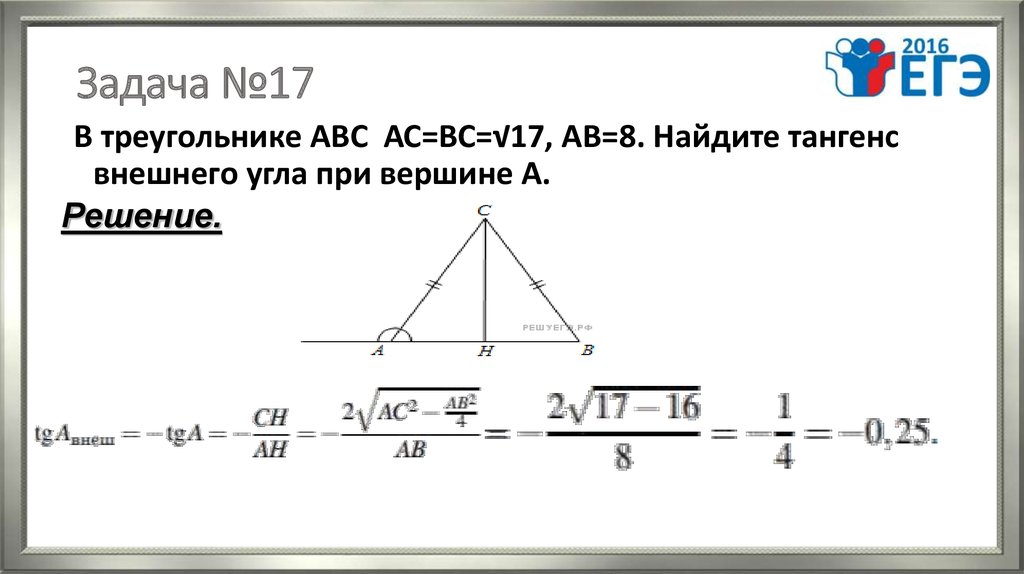

Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними. Формула теоремы косинусов: a2 = b2 + c2 — 2bc cos α

В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:

BC² = (x₂ — x₁)² + (y₂ — y₁)²

В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).

Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).

cos²α + sin²α = 1 — основное тригонометрическое тождество.

BC² = a² = (b cos α — c)² + b²sin²α = b²cos²α + b²sin²α — 2bc cos α + c² = b²(cos²α + sin²α) — 2bc cos α + c²

Что и требовалось доказать.

Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-курсы по математике для детей и подростков.

С помощью теоремы косинусов можно найти косинус угла треугольника:

 

• Когда b² + c² — a² > 0, угол α будет острым.
• Когда b² + c² — a² = 0, угол α будет прямым.
• Когда b² + c² — a² < 0, угол α будет тупым.

Запоминаем

Когда угол α прямой, то теорема косинусов превращаеся в теорему Пифагора.

Сформулируем еще одно

доказательство теоремы косинусов.

Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:

• AD = b × cos α,
• DB = c – b × cos α.

Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:

• h² = b² — (b × cos α)²
• h² = a² — (c – b × cos α)²

Приравниваем правые части уравнений:

• b² — (b × cos α)² = a² — (c — b × cos α)²

либо

• a² = b² + c² — 2bc × cos α

Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.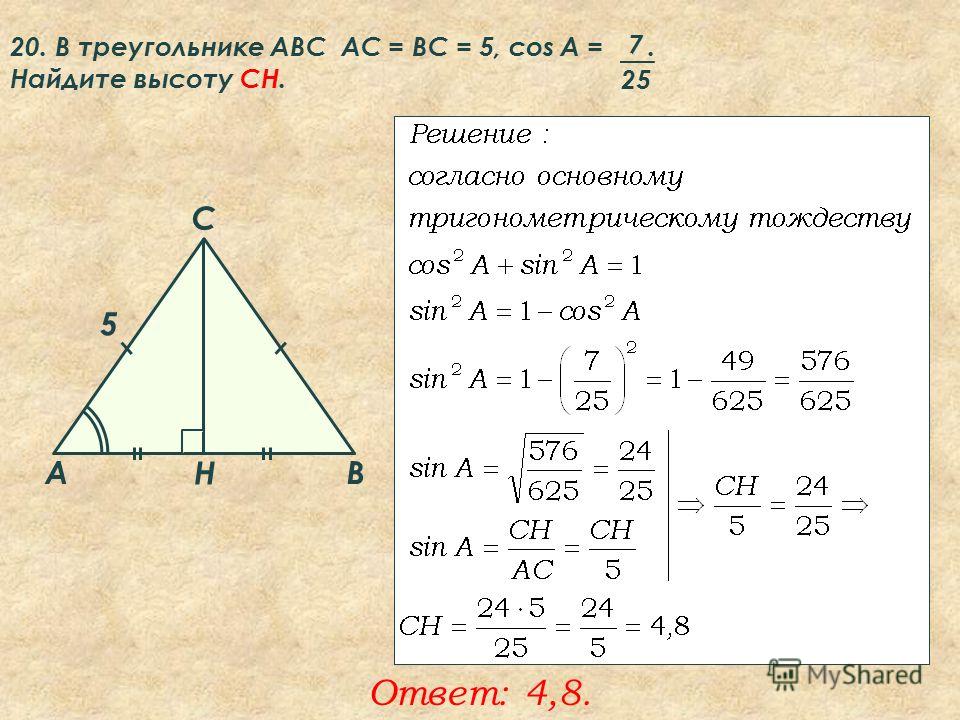

Определим стороны b и c:

• b² = a² + c² — 2ac × cos β;
• c² = a² + b² — 2ab × cos γ.

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Формулировка теоремы для каждой из сторон треугольника

Теорема косинусов справедлива для всех сторон треугольника, то есть:

a² = b² + c² — 2bc cos α

b² = c² + a² — 2ca cos β

c² = a² + b² — 2ab cos γ

Теорема косинусов может быть использована для любого вида треугольника.

Косинусы углов треугольника

Теорема косинусов позволяет найти как косинус, так и угол треугольника.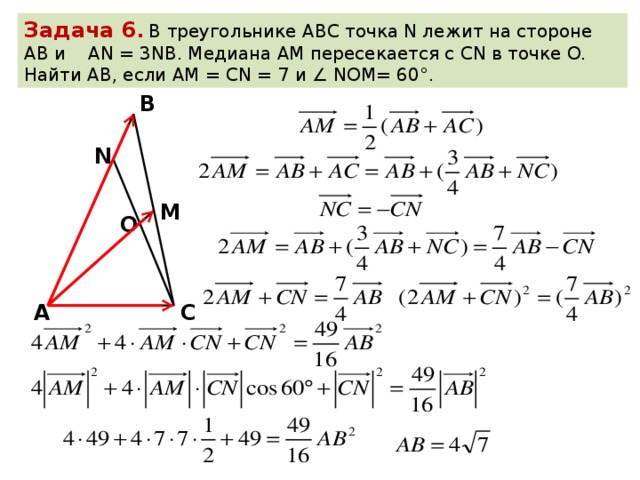 Найдём косинусы углов:

Аналогично:

Определение угла с помощью косинуса

А теперь обратим внимание на углы.

Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).

Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.

Рассмотрение пределов изменения cos α и sin α

Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.

Предел изменения косинуса: -1 < cos α < 1.

Предел изменения синуса: 0 < sin α ≤ 1.

• Если cos α > 0, то α ∈ (0°;90°)
• Если cos α < 0, то α ∈ (90°;180°)
• Если cos α = 0, то α = 90°

Примеры решения задач

При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.

Пример 1. Дан треугольник АВС. Найти длину СМ.

∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.

Как решаем:

 

1. Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
   Из треугольника АВС найдем cos B:



2. Из треугольника СМВ по теореме косинусов найдём СМ:
   

Ответ: СМ = .

Пример 2. Дан треугольник АВС, в котором a2  + b2 < c2. Доказать, что ∠C — тупой угол.

Как доказываем:

1. Для доказательства нужно вспомнить теорему косинусов для угла ∠C: 
   


2. Так как a²  + b² < c², то cos C < 0, следовательно, ∠C — тупой.

Что и требовалось доказать.

Эта задача нам показала, что с помощью теоремы косинусов можно определить тупой угол или острый.

• Если c² = a² + b², то ∠C = 90°.

• Если c² < a² + b², то ∠C — острый.

Больше объяснений по этой и другим темам вы найдете в справочнике по математике — с формулами, чертежами и примерами решения задач.

 

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Лидия Казанцева

Автор Skysmart

К предыдущей статье

Теоремы, которые точно пригодятся на ЕГЭ

К следующей статье

148.1K

Векторное произведение векторов

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

ABC равнобедренный треугольник с AB AC 12 см и BC 8 см.

Найдите высоту на BC и отсюда вычислите…

Перейти к

• Теорема Пифагора. Упражнение 12.

• Рациональные и иррациональные числа
• Сложные проценты
• Расширения
• Факторизация
• Одновременные линейные уравнения
• Задачи на одновременные линейные уравнения
• Квадратные уравнения
• Индексы
• Логарифмы
• Треугольники
• Теорема о средней точке
• Теорема Пифагора
• Прямолинейные фигуры
• Теоремы о площади
• Круг
• Измерение
• Тригонометрические отношения
• Тригонометрические отношения и стандартные углы
• Координатная геометрия
• Статистика

Главная > ML Aggarwal Solutions Класс 9 Математика > Глава 12.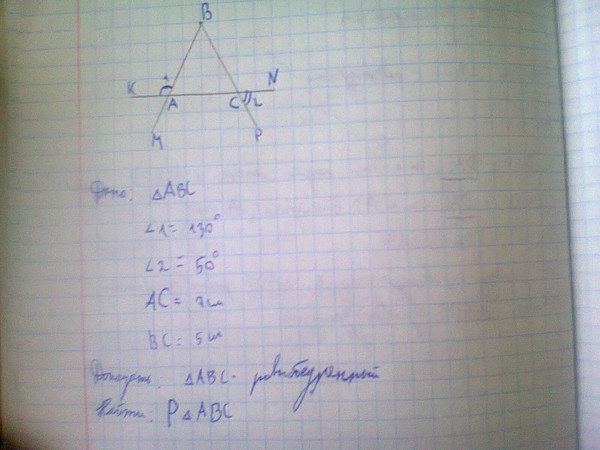 Теорема Пифагора > Теорема Пифагора. Упражнение 12. > Вопрос 5

Вопрос 5 Теорема Пифагора Упражнение 12

ABC — равнобедренный треугольник, в котором AB = AC = 12 см и BC = 8 см. Найдите высоту на BC и, следовательно,

рассчитайте его площадь.

Ответ:

Пусть AD будет высотой ABC.

Дано AB = AC = 12 см

BC = 8 см

Высота основания равнобедренного треугольника делит его основание пополам.

Так BD = DC

BD = 8/2 = 4 см

DC = 4 см

9{2} \текст { . } \end{выровнено}

Связанные вопросы

Ниже приведены длины сторон треугольников. Определите, какие из них прямоугольные. В случае …

Ножка лестницы длиной 10 м, прислоненной к вертикальному колодцу, находится на расстоянии 6 м от основания стены. Фи…

В прямоугольном треугольнике, если гипотенуза равна 20 см, а отношение двух других сторон равно 4:3, найти. ..

Для поездки в город B из города A существует маршрут через город C такой, что AC ⊥ CB, AC = 2x км и CB =…

(a) На рисунке (i), приведенном ниже, AB = 12 см, AC = 13 см, CE = 10 см и DE = 6 см. Вычислить длину…

(a) На приведенном ниже рисунке (i) BC = 5 см, ∠B = 90°, AB = 5AE, CD = 2AE и AC = ED. Рассчитать длину…

Фейсбук WhatsApp

Копировать ссылку

Было ли это полезно?

Упражнения

Теорема Пифагора Упражнение 12

Главы

Рациональные и иррациональные числа

Сложные проценты

Расширения

Factorization

Simultaneous Linear Equations

Problems on Simultaneous Linear Equations

Quadratic Equations

Indices

Logarithms

Triangles

Mid Point Theorem

Pythagoras Theorem

Rectilinear Figures

Theorems on Area

Circle

Измерение

Тригонометрические отношения

Тригонометрические отношения и стандартные углы

Координатная геометрия

Статистика

Курсы

Быстрые ссылки

Условия и политика

Условия и политика

2022 © Quality Tutorials Pvt Ltd Все права защищены

Прямоугольный треугольник ABC имеет AB=6, BC=8 и AC является гипотенузой.

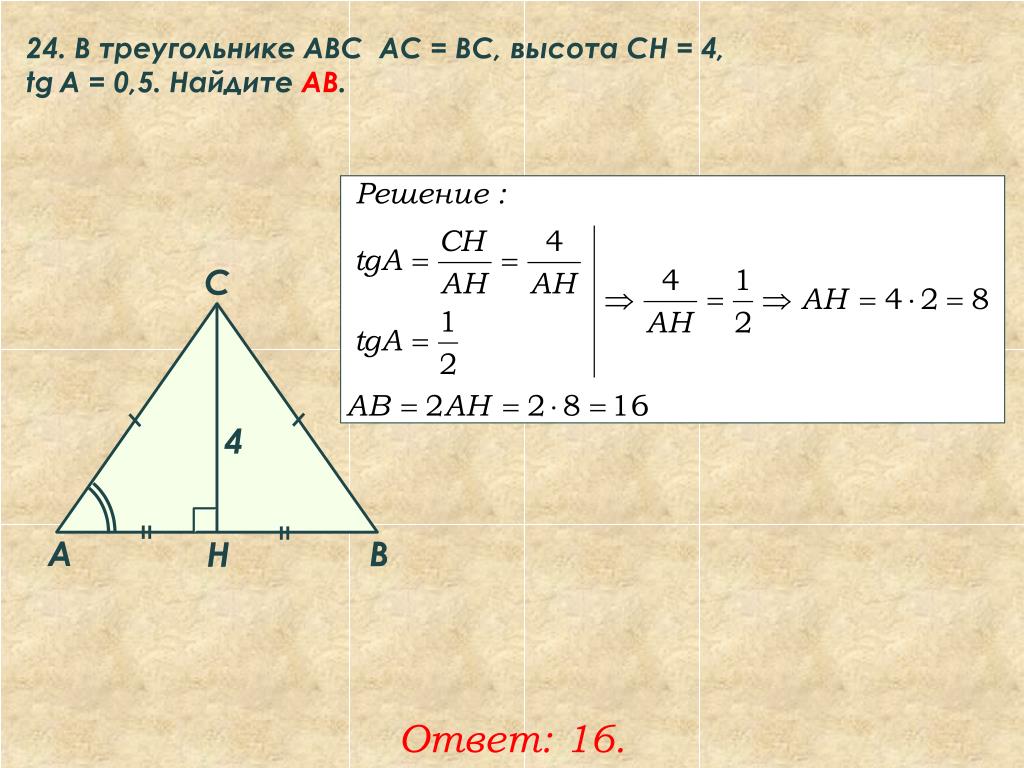Найдите sinA, cosA и tanA. Цитата страницы Начать эссе значок-вопрос Спросите репетитора

Начать бесплатную пробную версию

Скачать PDF PDF Цитата страницы Цитировать Поделиться ссылкой Делиться

Укажите эту страницу следующим образом:

«В прямоугольном треугольнике ABC AB=6, BC=8, а AC — гипотенуза. Найдите sinA, cosA и tanA». Редакционная статья eNotes , 5 января 2011 г., https://www.enotes.com/homework-help/right-angle-triangle-abc-ab-6-bc-8-ac-hypotenuse-233871. По состоянию на 6 марта 2023 г.

Ответы экспертов

92

=> AC = sqrt [ 36 + 64]

=> AC = sqrt 100

=> AC = 10

Теперь sin A = 8/10 = 4/5

cos A = /10 = 3/5

и загар A = 8/6 = 4/3

Утверждено редакцией eNotes

Дан прямоугольный треугольник ABC, гипотенуза которого равна AC.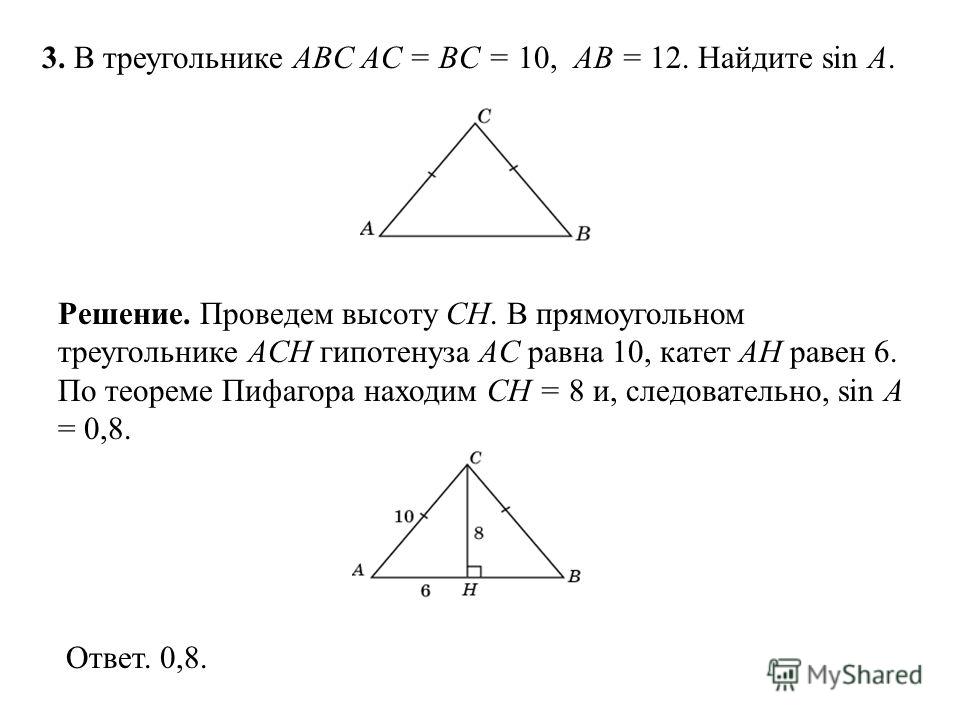

Тогда прямой угол равен В. 92 = 36+64 = 100

==> AC = 10

Теперь нам нужно найти следующее:

sinA = противоположность/гипотенуза.

Мы знаем, что сторона, противолежащая углу A, равна BC

==> sinA = BC/AC = 8/10 = 4/5

==> cosA = прилежащая/гипотенуза

                 = AB/AC = 6/10 = 3/5

==> tanA = sinA/cosA = 4/3

==> sinA = 0,8

==>cosA = 0,6

==> tanA = 4/3

 

См. eNotes без рекламы

Начните 48-часовую бесплатную пробную версию , чтобы получить доступ к более чем 30 000 дополнительных руководств и более чем 350 000 вопросов помощи при выполнении домашних заданий, на которые ответили наши эксперты.

Получите 48 часов бесплатного доступа

Уже зарегистрирован? Войдите здесь.

Утверждено редакцией eNotes

Математика

Последний ответ опубликован 07 сентября 2010 г.