Числовые иррациональные выражения — Математика
Преобразование числовых иррациональных выражений
0 вариант
1. Найдите значение выражения .
2. Найдите значение выражения .
3. Найдите значение выражения .
4. Найдите значение выражения .
5. Найдите значение выражения .
6. Найдите значение выражения .
7. Найдите значение выражения .
8. Найдите значение выражения .
9. Найдите значение выражения .
10. Найдите значение выражения .
11. Найдите значение выражения .
Преобразование числовых иррациональных выражений
1 вариант
Найдите значение выражения:
Найдите значение выражения .
Найдите значение выражения .
Найдите значение выражения
Найдите значение выражения .
Найдите значение выражения .
Найдите значение выражения .
Найдите значение выражения .
Найдите значение выражения .
Найдите значение выражения .
Преобразование числовых иррациональных выражений
2 вариант
Найдите значение выражения:
Найдите значение выражения .
Найдите значение выражения
Найдите значение выражения .
Найдите значение выражения .
Найдите значение выражения .
Найдите значение выражения .
Найдите значение выражения .
Найдите значение выражения .
Найдите значение выражения .
Найдите значение выражения
Преобразование числовых иррациональных выражений
3 вариант
Найдите значение выражения:
Найдите значение выражения .
Найдите значение выражения
Найдите значение выражения .
Найдите значение выражения
Найдите значение выражения .
Найдите значение выражения .
Найдите значение выражения .
Найдите значение выражения .
Найдите значение выражения .
Найдите значение выражения .
Преобразование числовых иррациональных выражений
4 вариант
Найдите значение выражения:
Найдите значение выражения .
Найдите значение выражения
Найдите значение выражения .
Найдите значение выражения .
Найдите значение выражения
Найдите значение выражения .
Найдите значение выражения .
Найдите значение выражения .
Найдите значение выражения .
Найдите значение выражения .
Преобразование числовых иррациональных выражений
5 вариант
Найдите значение выражения:
Найдите значение выражения .
Найдите значение выражения
Найдите значение выражения .
Найдите значение выражения
Найдите значение выражения
Найдите значение выражения .
Найдите значение выражения .
Найдите значение выражения .
Найдите значение выражения .
Найдите значение выражения .
ОТВЕТЫ к теме «Преобразование числовых иррациональных выражений»
0 вариант | 1 вариант | 2 вариант | 3 вариант | 4 вариант | 5 вариант | ||||||||
1 | 33 | 1 | 414 | 1 | 352 | 1 | 96 | 1 | 280 | 1 | 14 | ||
2 | 2 | 2 | 2,4 | 2 | 24 | 2 | 3,6 | 2 | 0,96 | 2 | 3 | ||
3 | 6 | 3 | -24 | 3 | -2 | 3 | -16 | 3 | 6 | 3 | 17 | ||
4 | 7 | 4 | 3 | 4 | 7 | 4 | 3 | 4 | 2 | 4 | 7 | ||
5 | 2 | 5 | -2 | 5 | -15 | 5 | -2 | 5 | 2 | 5 | -5 | ||
6 | 1 | 6 | 1 | 6 | 1 | 6 | 1 | 6 | 1 | 6 | 5 | ||
7 | 2 | 7 | 3 | 7 | 2 | 7 | 5 | 7 | 3 | 7 | 3 | ||
8 | 2 | 8 | 6 | 8 | 2 | 8 | 6 | 8 | 2 | 8 | 2 | ||
9 | 15 | 9 | 27 | 9 | 15 | 9 | 24 | 9 | 72 | 9 | 24 | ||
10 | 7 | 10 | 2 | 10 | 3 | 10 | 6 | 10 | 3 | 10 | 2 | ||
11 | -15 | 11 | -3 | 11 | -20 | 11 | -14 | 11 | 3 | 11 | -12 | ||
Иррациональные выражения (выражения с корнями) и их преобразование
Статья раскрывает смысл иррациональных выражений и преобразования с ними.
Что такое иррациональные выражения?
При знакомстве с корнем в школе мы изучаем понятие иррациональных выражений. Такие выражения тесно связаны с корнями.
Определение 1Иррациональные выражения – это выражения, которые имеют корень. То есть это выражения, имеющие радикалы.
Основываясь на данном определении, мы имеем, что x-1, 83·36-12·3, 7-4·3·(2+3), 4·a2d5:d92·a35 — это все выражения иррационального типа.
При рассмотрении выражения x·x-7·x+7x+32·x-83 получаем, что выражение является рациональным. К рациональным выражениям относят многочлены и алгебраические дроби. Иррациональные включают в себя работу с логарифмическими выражениями или подкоренными выражениями.
Основные виды преобразований иррациональных выражений
При вычислении таких выражений необходимо обратить внимание на ОДЗ. Часто они требуют дополнительных преобразований в виде раскрытия скобок, приведения подобных членов, группировок и так далее. Основа таких преобразований – действия с числами. Преобразования иррациональных выражений придерживаются строгого порядка.
Пример 1Преобразовать выражение 9+33-2+4·33+1-2·33.
Решение
Необходимо выполнить замену числа 9 на выражение, содержащее корень. Тогда получаем, что
81+33-2+4·33+1-2·33==9+33-2+4·33+1-2·33
Полученное выражение имеет подобные слагаемые, поэтому выполним приведение и группировку. Получим
9+33-2+4·33+1-2·33==9-2+1+33+4·33-2·33==8+3·33
Ответ: 9+33-2+4·33+1-2·33=8+3·33
Представить выражение x+352-2·x+35+1-9 в виде произведения двух иррациональных с использованием формул сокращенного умножения.
Решения
x+352-2·x+35+1-9==x+35-12-9
Представляем 9 в виде 32, причем применим формулу разности квадратов:
x+35-12-9=x+35-12-32==x+35-1-3·x+35-1+3==x+35-4·x+35+2
Результат тождественных преобразований привел к произведению двух рациональных выражений, которые необходимо было найти.
Ответ:
x+352-2·x+35+1-9==x+35-4·x+35+2
Можно выполнять ряд других преобразований, которые относятся к иррациональным выражениям.
Преобразование подкоренного выражения
Важно то, что выражение, находящееся под знаком корня, можно заменить на тождественно равное ему. Данное утверждение дает возможность работать с подкоренным выражением. К примеру, 1+6 можно заменить на 7 или 2·a54-6 на 2·a4·a4-6. Они тождественно равные, поэтому замена имеет смысл.
Когда не существует а1, отличное от a, где справедливо неравенство вида an=a1n, тогда такое равенство возможно только при а=а1. Значения таких выражений равны с любыми значениями переменных.
Использование свойств корней
Свойства корней применяют для упрощения выражений. Чтобы применить свойство a·b=a·b, где a≥0, b≥0, тогда из иррационального вида 1+3·12 можно стать тождественно равным 1+3·12. Свойство …ankn2n1=an1·n2·,…,·nk , где a≥0 говорит о том, что x2+443 можно записать в форме x2+424.
Имеются некоторые нюансы при преобразовании подкоренных выражений. Если имеется выражение, то -7-814=-74-814 записать не можем, так как формула abn=anbn служит только для неотрицательного a и положительного b. Если свойство применить правильно, тогда получится выражение вида 74814.
Для правильного преобразования используют преобразования иррациональных выражений с использованием свойств корней.
Внесение множителя под знак корня
Определение 3Внести под знак корня – значит заменить выражение B·Cn, а B и C являются некоторыми числами или выражениями, где n – натуральное число, которое больше 1, равным выражением, которое имеет вид Bn·Cn или -Bn·Cn.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеЕсли упростить выражение вида 2·x3, то после внесения под корень, получаем, что 23·x3. Такие преобразования возможны только после подробного изучения правил внесения множителя под знак корня.
Вынесение множителя из-под знака корня
Если имеется выражение вида Bn·Cn, тогда его приводят к виду B·Cn, где имеется нечетные n, которые принимают вид B·Cn с четными n, В и C являются некоторыми числами и выражениями.
То есть, если брать иррациональное выражение вида 23·x3, вынести множитель из-под корня, тогда получим выражение 2·x3. Или x+12·7 даст в результате выражение вида x+1·7, которое имеет еще одну запись в виде x+1·7.
Вынесение множителя из-под корня необходимо для упрощения выражения и его быстрого преобразования.
Преобразование дробей, содержащих корни
Иррациональное выражение может быть как натуральным числом, так и в виде дроби. Для преобразования дробных выражений большое внимание обращают на его знаменатель. Если взять дробь вида (2+3)·x4x2+53, то числитель примет вид 5·x4, а, использовав свойства корней, получим, что знаменатель станет x2+56. Исходную дробь можно будет записать в виде 5·x4x2+56.
Необходимо обратить внимание на то, что необходимо изменять знак только числителя или только знаменателя. Получим, что
-x+2·x-3·x2+74=x+2·x-(-3·x2+74)=x+2·x3·x2-74
Сокращение дроби чаще всего используется при упрощении. Получаем, что
3·x+43-1·xx+43-13 сокращаем на x+43-1. Получим выражение 3·xx+43-12.
Перед сокращением необходимо выполнять преобразования, которые упрощают выражение и дают возможность разложить на множители сложное выражение. Чаще всего применяют формулы сокращенного умножения.
Если взять дробь вида 2·x-yx+y, то необходимо вводить новые переменные u=x и v=x, тогда заданное выражение поменяет вид и станет 2·u2-v2u+v. Числитель следует разложить на многочлены по формуле, тогда получим, что
2·u2-v2u+v=2·(u-v)·u+vu+v=2·u-v. После выполнения обратной замены придем к виду 2·x-y, которое равно исходному.
Допускается приведение к новому знаменателю, тогда необходимо числитель умножать на дополнительный множитель. Если взять дробь вида x3-10,5·x, тогда приведем к знаменателю x. для этого нужно умножить числитель и знаменатель на выражение 2·x, тогда получаем выражение x3-10,5·x=2·x·x3-10,5·x·2·x=2·x·x3-1x.
для этого нужно умножить числитель и знаменатель на выражение 2·x, тогда получаем выражение x3-10,5·x=2·x·x3-10,5·x·2·x=2·x·x3-1x.
Сокращение дробей или приведение подобных необходимо только на ОДЗ указанной дроби. При умножении числителя и знаменателя на иррациональное выражение получаем, что мы избавляемся от иррациональности в знаменателе.
Избавление от иррациональности в знаменателе
Когда выражение избавляется от корня в знаменателе путем преобразования, то это называется избавлением от иррациональности. Рассмотрим на примере дроби вида x33. После избавления от иррациональности получаем новую дробь вида 93·x3.
Переход от корней к степеням
Переходы от корней к степеням необходимы для быстрого преобразования иррациональных выражений. Если рассмотреть равенство amn=amn, то видно, что его использование возможно, когда a является положительным числом, m –целым числом, а n – натуральным. Если рассматривать выражение 5-23, то иначе имеем право записать его как 5-23. Эти выражения равнозначны.
Когда под корнем имеется отрицательное число или число с переменными, тогда формула amn=amn не всегда применима. Если нужно заменить такие корни (-8)35 и (-16)24 степенями, тогда получаем, что -835 и -1624 по формуле amn=amn не работаем с отрицательными а. для того, чтобы подробно разобрать тему подкоренных выражений и их упрощений, необходимо изучать статью о переходе от корней к степеням и обратно. Следует помнить о том, что формула amn=amn применима не для всех выражений такого вида. Избавление от иррациональности способствует дальнейшему упрощению выражения, его преобразованию и решению.
Иррациональные выражения
Иррациональные выражения, решение примеров. В прошлой статье мы рассмотрели несколько примеров на преобразование числовых рациональных и иррациональных выражений. Здесь представлены ещё несколько буквенных иррациональных выражений. Если совсем позабыли как выполнять данные операции, то сделаю основные акценты:
Если совсем позабыли как выполнять данные операции, то сделаю основные акценты:
1. Если дан (имеется в выражении) корень следующего вида:
то это означает, что
Просто обычно в примерах двойка не пишется.
*Поэтому такой корень и называют квадратным (корень второй степени).
2. Если под корнем имеется ещё корень, то можем преобразовать:
И ещё одно очень важное свойство:
Оно легко доказывается. Мы знаем, что:
Как следствие:
То есть, если мы имеем корень какой-то степени и под корнем выражение с такой же степенью, то в результате получится это самое выражение.
Конечно, есть и другие, но они часто используются вами при решении заданий с обычным квадратным корнем:
26833. Найдите значение выражения
Второй способ:
*Использовали свойство степени.
Ответ: 9
26837. Найдите значение выражения
Ответ: 0,25
26842. Найдите значение выражения
Ответ: 4
26838. Найдите значение выражения
Посмотреть другое решение
77388. Найдите значение выражения:
При х = 3 получится 7+3∙3–4=12
Ответ: 12
26824. Найдите значение выражения
Посмотреть решение
26825. Найдите значение выражения
Посмотреть решение
26829. Найдите значение выражения
Посмотреть решение
26830. Найдите значение выражения
Посмотреть решение
26840. Найдите
Посмотреть решение
Надеюсь данные решения изложены подробно и вам все действия понятны.
На этом всё. Успеха Вам!
С уважением, Александр
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Преобразования иррациональных выражений | О математике понятно
Иррациональные выражения и их преобразования
В прошлый раз мы вспомнили (или узнали — кому как), что же такое корень n-й степени, научились извлекать такие корни, разобрали по винтикам основные свойства корней и решали несложные примеры с корнями.
Этот урок будет продолжением предыдущего и будет посвящён преобразованиям самых разных выражений, содержащих всевозможные корни. Такие выражения называются иррациональными. Здесь появятся и выражения с буквами, и дополнительные условия, и избавление от иррациональности в дробях, и некоторые продвинутые приёмы в работе с корнями. Те приёмы, которые будут рассматриваться в данном уроке, станут хорошей базой для решения задач ЕГЭ (и не только) практически любого уровня сложности. Итак, давайте приступим.
Прежде всего я продублирую здесь основные формулы и свойства корней. Чтобы не скакать из темы в тему. Вот они:
при
Формулы эти надо обязательно знать и уметь применять. Причём в обе стороны — как слева направо, так и справа налево. Именно на них и основывается решение большинства заданий с корнями любой степени сложности. Начнём пока с самого простого — с прямого применения формул или их комбинаций.
Простое применение формул
В этой части будут рассматриваться простые и безобидные примеры — без букв, дополнительных условий и прочих хитростей. Однако даже в них, как правило, имеются варианты. И чем навороченнее пример, тем больше таких вариантов. И у неопытного ученика возникает главная проблема — с чего начинать? Ответ здесь простой — не знаешь, что нужно — делай что можно. Лишь бы ваши действия шли в мире и согласии с правилами математики и не противоречили им.) Например, такое задание:
Вычислить:
Даже в таком простеньком примере возможны несколько путей к ответу.
Первый — просто перемножить корни по первому свойству и извлечь корень из результата:
Второй вариант такой: не трогаем, работаем с . Выносим множитель из-под знака корня, а дальше — по первому свойству. Вот так:
Решать можно как больше нравится. В любом из вариантов ответ получается один — восьмёрка. Мне, например, проще перемножить 4 и 128 и получить 512, а из этого числа отлично извлекается кубический корень. Если кто-то не помнит, что 512 — это 8 в кубе, то не беда: можно записать 512 как 29 (первые 10 степеней двойки, я надеюсь, помните?) и по формуле корня из степени:
В любом из вариантов ответ получается один — восьмёрка. Мне, например, проще перемножить 4 и 128 и получить 512, а из этого числа отлично извлекается кубический корень. Если кто-то не помнит, что 512 — это 8 в кубе, то не беда: можно записать 512 как 29 (первые 10 степеней двойки, я надеюсь, помните?) и по формуле корня из степени:
Другой пример.
Вычислить: .
Если работать по первому свойству (всё загнать под один корень), то получится здоровенное число, из которого корень потом извлекать — тоже не сахар. Да и не факт, что он извлечётся ровно.) Поэтому здесь полезно в числе вынести множители из-под корня. Причём вынести по максимуму:
И теперь всё наладилось:
Осталось восьмёрку и двойку записать под одним корнем (по первому свойству) и — готово дело. 🙂
Добавим теперь немного дробей.
Вычислить:
Пример совсем примитивный, однако и в нём имеются варианты. Можно с помощью вынесения множителя преобразовать числитель и сократить со знаменателем:
А можно сразу воспользоваться формулой деления корней:
Как видим, и так, и сяк — всяко правильно.) Если не споткнуться на полпути и не ошибиться. Хотя где тут ошибаться-то…
Разберём теперь самый последний пример из домашнего задания прошлого урока:
Упростить:
Совершенно немыслимый набор корней, да ещё и вложенных. Как быть? Главное — не бояться! Здесь мы первым делом замечаем под корнями числа 2, 4 и 32 — степени двойки. Первое что нужно сделать — привести все числа к двойкам: всё-таки чем больше одинаковых чисел в примере и меньше разных, тем проще.) Начнём отдельно с первого множителя:
Число можно упростить, сократив двойку под корнем с четвёркой в показателе корня:
Теперь, согласно корню из произведения:
.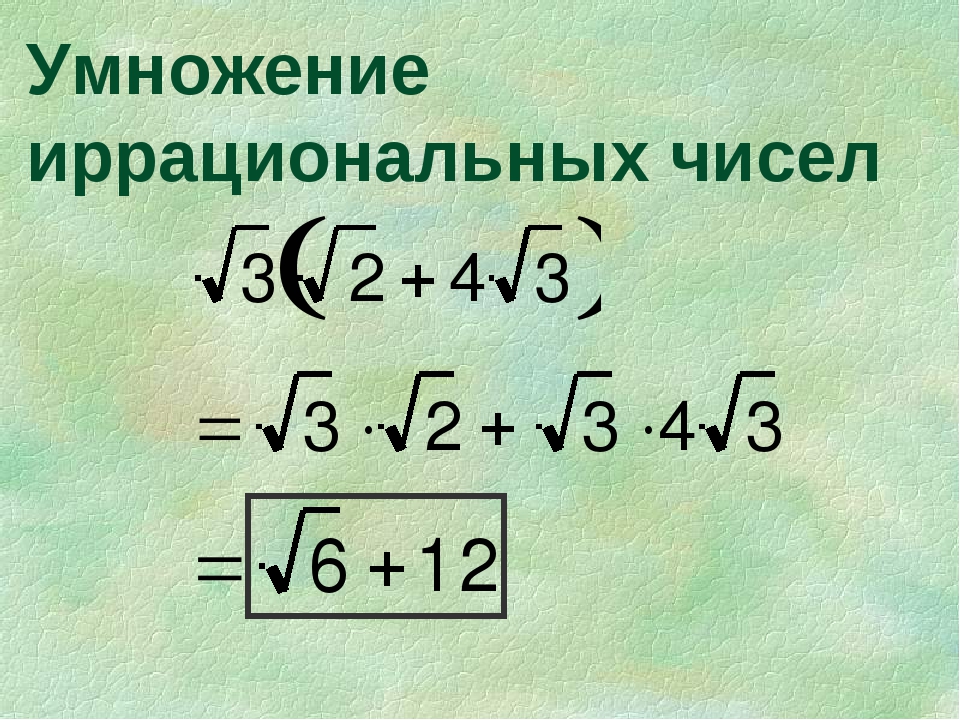
В числе выносим двойку за знак корня:
А с выражением расправляемся по формуле корня из корня:
Значит, первый множитель запишется вот так:
.
Вложенные корни исчезли, числа стали поменьше, что уже радует. Вот только корни разные, но пока так и оставим. Надо будет — преобразуем к одинаковым. Берёмся за второй множитель.)
Второй множитель преобразовываем аналогично, по формуле корня из произведения и корня из корня. Где надо — сокращаем показатели по пятой формуле:
Вставляем всё в исходный пример и получаем:
Получили произведение целой кучи совершенно разных корней. Неплохо было бы привести их все к одному показателю, а там — видно будет. Что ж, это вполне возможно. Наибольший из показателей корней равен 12, а все остальные — 2, 3, 4, 6 — делители числа 12. Поэтому будем приводить все корни по пятому свойству к одному показателю — к 12:
Считаем и получаем:
Красивого числа не получили, ну и ладно. Нас просили упростить выражение, а не посчитать. Упростили? Конечно! А вид ответа (целое число или нет) здесь уже не играет никакой роли.
Немного сложения / вычитания и формул сокращённого умножения
К сожалению, общих формул для сложения и вычитания корней в математике нету. Однако, в заданиях сплошь и рядом встречаются эти действия с корнями. Здесь необходимо понимать, что любые корни — это точно такие же математические значки, как и буквы в алгебре.) И к корням применимы те же самые приёмы и правила, что и к буквам — раскрытие скобок, приведение подобных, формулы сокращённого умножения и т.п.
Например, каждому ясно, что . Точно так же одинаковые корни можно совершенно спокойно между собой складывать/вычитать:
Если корни разные, то ищем способ сделать их одинаковыми — внесением/вынесением множителя или же по пятому свойству. Если ну никак не упрощается, то, возможно, преобразования более хитрые.
Если ну никак не упрощается, то, возможно, преобразования более хитрые.
Смотрим первый пример.
Найти значение выражения: .
Все три корня хоть и кубические, но из разных чисел. Чисто не извлекаются и между собой складываются/вычитаются. Стало быть, применение общих формул здесь не катит. Как быть? А вынесем-ка множители в каждом корне. Хуже в любом случае не будет.) Тем более что других вариантов, собственно, и нету:
Стало быть, .
Вот и всё решение. Здесь мы от разных корней перешли к одинаковым с помощью вынесения множителя из-под корня. А затем просто привели подобные.) Решаем дальше.
Найти значение выражения:
С корнем из семнадцати точно ничего не поделаешь. Работаем по первому свойству — делаем из произведения двух корней один корень:
А теперь присмотримся повнимательнее. Что у нас под большим кубическим корнем? Разность ква.. Ну, конечно! Разность квадратов:
Теперь осталось только извлечь корень: .
Дальше очень похожий пример, но посложнее.
Вычислить:
Здесь придётся проявить математическую смекалку.) Мыслим примерно следующим образом: «Так, в примере произведение корней. Под одним корнем разность, а под другим — сумма. Очень похоже на формулу разности квадратов. Но… Корни — разные! Первый квадратный, а второй — четвёртой степени… Хорошо бы сделать их одинаковыми. По пятому свойству можно легко из квадратного корня сделать корень четвёртой степени. Для этого достаточно подкоренное выражение возвести в квадрат.»
Если вы мыслили примерно так же, то вы — на полпути к успеху. Совершенно верно! Превратим первый множитель в корень четвёртой степени. Вот так:
Теперь, ничего не поделать, но придётся вспомнить формулу квадрата разности. Только в применении к корням. Ну и что? Чем корни хуже других чисел или выражений?! Возводим:
Ну и что? Чем корни хуже других чисел или выражений?! Возводим:
«Хм, ну возвели и что? Хрен редьки не слаще. Стоп! А если вынести четвёрку под корнем? Тогда выплывет то же самое выражение, что и под вторым корнем, только с минусом, а ведь именно этого мы и добиваемся!»
Верно! Выносим четвёрку:
.
А теперь — дело техники:
.
Вот так распутываются сложные примеры. ) Теперь пора потренироваться с дробями.
Вычислить:
Ясно, что надо преобразовывать числитель. Как? По формуле квадрата суммы, разумеется. У нас есть ещё варианты разве? 🙂 Возводим в квадрат, выносим множители, сокращаем показатели (где надо):
Во как! Получили в точности знаменатель нашей дроби. ) Значит, вся дробь, очевидно, равна единице:
Ещё пример. Только теперь на другую формулу сокращённого умножения.)
Вычислить:
Понятно, что квадрат разности надо в дело применять. Выписываем знаменатель отдельно и — поехали!
Выносим множители из-под корней:
Следовательно,
.
Теперь всё нехорошее великолепно сокращается и получается:
Что ж, поднимаемся на следующий уровень. 🙂
Буквы и дополнительные условия
Буквенные выражения с корнями — штука более хитрая, чем числовые выражения, и является неиссякаемым источником досадных и очень грубых ошибок. Перекроем этот источник.) Ошибки всплывают из-за того, что частенько таких заданиях фигурируют отрицательные числа и выражения. Они либо даны нам прямо в задании, либо спрятаны в буквах и дополнительных условиях. А нам в процессе работы с корнями постоянно надо помнить, что в корнях чётной степени как под самим корнем, так и в результате извлечения корня должно быть неотрицательное выражение. Ключевой формулой в задачах этого пункта будет четвёртая формула:
Ключевой формулой в задачах этого пункта будет четвёртая формула:
С корнями нечётной степени вопросов никаких — там всегда всё извлекается что с плюсом, что с минусом. И минус, если что, выносится вперёд. Будем сразу разбираться с корнями чётных степеней.) Например, такое коротенькое задание.
Упростить: , если .
Казалось бы, всё просто. Получится просто икс. ) Но зачем же тогда дополнительное условие ? В таких случаях полезно прикинуть на числах. Чисто для себя.) Если , то икс — заведомо отрицательное число. Минус три, например. Или минус сорок. Пусть . Можно минус три возвести в четвёртую степень? Конечно! Получится 81. Можно из 81 извлечь корень четвёртой степени? А почему нет? Можно! Получится тройка. Теперь проанализируем всю нашу цепочку:
Что мы видим? На входе было отрицательное число, а на выходе — уже положительное. Было минус три, стало плюс три.) Возвращаемся к буквам. Вне всяких сомнений, по модулю это будет точно икс, но только сам икс у нас с минусом (по условию!), а результат извлечения (в силу арифметического корня!) должен быть с плюсом. Как получить плюс? Очень просто! Для этого достаточно перед заведомо отрицательным числом поставить минус.) И правильное решение выглядит так:
Кстати сказать, если бы мы воспользовались формулой , то, вспомнив определение модуля, сразу получили бы верный ответ. Поскольку
|x| = -x при x<0.
Дальше тренируемся.)
Вынести множитель за знак корня: , где .
Первый взгляд — на подкоренное выражение. Тут всё ОК. При любом раскладе оно будет неотрицательным. Начинаем извлекать. По формуле корня из произведения, извлекаем корень из каждого множителя:
Откуда взялись модули, объяснять, думаю, уже не надо.) А теперь анализируем каждый из модулей.
Множитель |a| так и оставляем без изменений: у нас нету никакого условия на букву a. Мы не знаем, положительное она или отрицательная. Следующий модуль |b2| можно смело опустить: в любом случае выражение b2 неотрицательно. А вот насчёт |c3| — тут уже задачка.) Если , то и c3<0. Стало быть, модуль надо раскрыть с минусом: |c3| = —c3. Итого верное решение будет такое:
Мы не знаем, положительное она или отрицательная. Следующий модуль |b2| можно смело опустить: в любом случае выражение b2 неотрицательно. А вот насчёт |c3| — тут уже задачка.) Если , то и c3<0. Стало быть, модуль надо раскрыть с минусом: |c3| = —c3. Итого верное решение будет такое:
А теперь — обратная задача. Не самая простая, сразу предупреждаю!
Внести множитель под знак корня: .
Если вы сразу запишете решение вот так
,
то вы попали в ловушку. Это неверное решение! В чём же дело?
Давайте вглядимся в выражение под корнем . Под корнем четвёртой степени, как мы знаем, должно находиться неотрицательное выражение. Иначе корень смысла не имеет.) Поэтому А это, в свою очередь, значит, что и, следовательно, само также неположительно: .
И ошибка здесь состоит в том, что мы вносим под корень неположительное число : четвёртая степень превращает его в неотрицательное и получается неверный результат — слева заведомый минус, а справа уже плюс. А вносить под корень чётной степени мы имеем право только неотрицательные числа или выражения. А минус, если есть, оставлять перед корнем.) Как же нам выделить неотрицательный множитель в числе , зная, что оно само стопудово отрицательное? Да точно так же! Поставить минус.) А чтобы ничего не поменялось, скомпенсировать его ещё одним минусом. Вот так:
И теперь уже неотрицательное число (-b) спокойно вносим под корень по всем правилам:
Этот пример наглядно показывает, что, в отличие от других разделов математики, в корнях правильный ответ далеко не всегда вытекает автоматически из формул. Необходимо подумать и лично принять верное решение.) Особенно следует быть внимательнее со знаками в иррациональных уравнениях и неравенствах.
Разбираемся со следующим важным приёмом в работе с корнями — избавлением от иррациональности.
Избавление от иррациональности в дробях
Если в выражении присутствуют корни, то, напомню, такое выражение называется выражением с иррациональностью. В некоторых случаях бывает полезно от этой самой иррациональности (т.е. корней) избавиться. Как можно ликвидировать корень? Корень у нас пропадает при… возведении в степень. С показателем либо равным показателю корня, либо кратным ему. Но, если мы возведём корень в степень (т.е. помножим корень сам на себя нужное число раз), то выражение от этого поменяется. Нехорошо.) Однако в математике бывают темы, где умножение вполне себе безболезненно. В дробях, к примеру. Согласно основному свойству дроби, если числитель и знаменатель умножить (разделить) на одно и то же число, то значение дроби не изменится.
Допустим, нам дана вот такая дробь:
Можно ли избавиться от корня в знаменателе? Можно! Для этого корень надо возвести в куб. Чего нам не хватает в знаменателе для полного куба? Нам не хватает множителя , т.е. . Вот и домножаем числитель и знаменатель дроби на
Корень в знаменателе исчез. Но… он появился в числителе. Ничего не поделать, такова судьба.) Нам это уже не важно: нас просили знаменатель от корней освободить. Освободили? Безусловно.)
Кстати, те, кто уже в ладах с тригонометрией, возможно, обращали внимание на то, что в некоторых учебниках и таблицах, к примеру, обозначают по-разному: где-то , а где-то . Вопрос — что правильно? Ответ: всё правильно! ) Если догадаться, что – это просто результат освобождения от иррациональности в знаменателе дроби . 🙂
Зачем нам освобождаться от иррациональности в дробях? Какая разница — в числителе корень сидит или в знаменателе? Калькулятор всё равно всё посчитает.) Ну, для тех, кто не расстаётся с калькулятором, разницы действительно практически никакой… Но, даже считая на калькуляторе, можно обратить внимание на то, что делить на целое число всегда удобнее и быстрее, чем на иррациональное. А уж про деление в столбик вообще умолчу.)
А уж про деление в столбик вообще умолчу.)
Следующий пример только подтвердит мои слова.
Освободиться от иррациональности в знаменателе дроби:
Как здесь ликвидировать квадратный корень в знаменателе? Если числитель и знаменатель помножить на выражение , то в знаменателе получится квадрат суммы. Сумма квадратов первого и второго чисел дадут нам просто числа безо всяких корней, что очень радует. Однако… всплывёт удвоенное произведение первого числа на второе, где корень из трёх всё равно останется. Не канает. Как быть? Вспомнить другую замечательную формулу сокращённого умножения! Где никаких удвоенных произведений, а только квадраты:
Такое выражение, которое при домножении какой-то суммы (или разности) выводит на разность квадратов, ещё называют сопряжённым выражением. В нашем примере сопряжённым выражением будет служить разность . Вот и домножаем на эту разность числитель и знаменатель:
Что тут можно сказать? В результате наших манипуляций не то что корень из знаменателя исчез — вообще дробь исчезла! 🙂 Даже с калькулятором отнять корень из трёх от тройки проще, чем считать дробь с корнем в знаменателе. Ещё пример.
Освободиться от иррациональности в знаменателе дроби:
Как здесь выкручиваться? Формулы сокращённого умножения с квадратами сразу не катят — не получится полной ликвидации корней из-за того, что корень у нас в этот раз не квадратный, а кубический. Надо, чтобы корень как-то возвёлся в куб. Стало быть, применять надо какую-то из формул с кубами. Какую? Давайте подумаем. В знаменателе — сумма . Как нам добиться возведения корня в куб? Домножить на неполный квадрат разности! Значит, применять будем формулу суммы кубов. Вот эту:
В качестве a у нас тройка, а в качестве b — корень кубический из пяти:
И снова дробь исчезла. ) Такие ситуации, когда при освобождении от иррациональности в знаменателе дроби у нас вместе с корнями полностью исчезает сама дробь, встречаются очень часто. Как вам вот такой примерчик!
) Такие ситуации, когда при освобождении от иррациональности в знаменателе дроби у нас вместе с корнями полностью исчезает сама дробь, встречаются очень часто. Как вам вот такой примерчик!
Вычислить:
Попробуйте просто сложить эти три дроби! Без ошибок! 🙂 Один общий знаменатель чего стоит. А что, если попробовать освободиться от иррациональности в знаменателе каждой дроби? Что ж, пробуем:
Ух ты, как интересно! Все дроби пропали! Напрочь. И теперь пример решается в два счёта:
Просто и элегантно. И без долгих и утомительных вычислений. 🙂
Именно поэтому операцию освобождения от иррациональности в дробях надо уметь делать. В подобных навороченных примерах только она и спасает, да.) Разумеется, внимательность никто не отменял. Бывают задания, где просят избавиться от иррациональности в числителе. Эти задания ничем от рассмотренных не отличаются, только от корней очищается числитель.)
Более сложные примеры
Осталось рассмотреть некоторые специальные приёмы в работе с корнями и потренироваться распутывать не самые простые примеры. И тогда полученной информации уже будет достаточно для решения заданий с корнями любого уровня сложности. Итак — вперёд.) Для начала разберёмся, что делать со вложенными корнями, когда формула корня из корня не работает. Например, вот такой примерчик.
Вычислить:
Корень под корнем… К тому же под корнями сумма или разность. Стало быть, формула корня из корня (с перемножением показателей) здесь не действует. Значит, надо что-то делать с подкоренными выражениями: у нас просто нету других вариантов. В таких примерах чаще всего под большим корнем зашифрован полный квадрат какой-нибудь суммы. Или разности. А корень из квадрата уже отлично извлекается! И теперь наша задача — его расшифровать.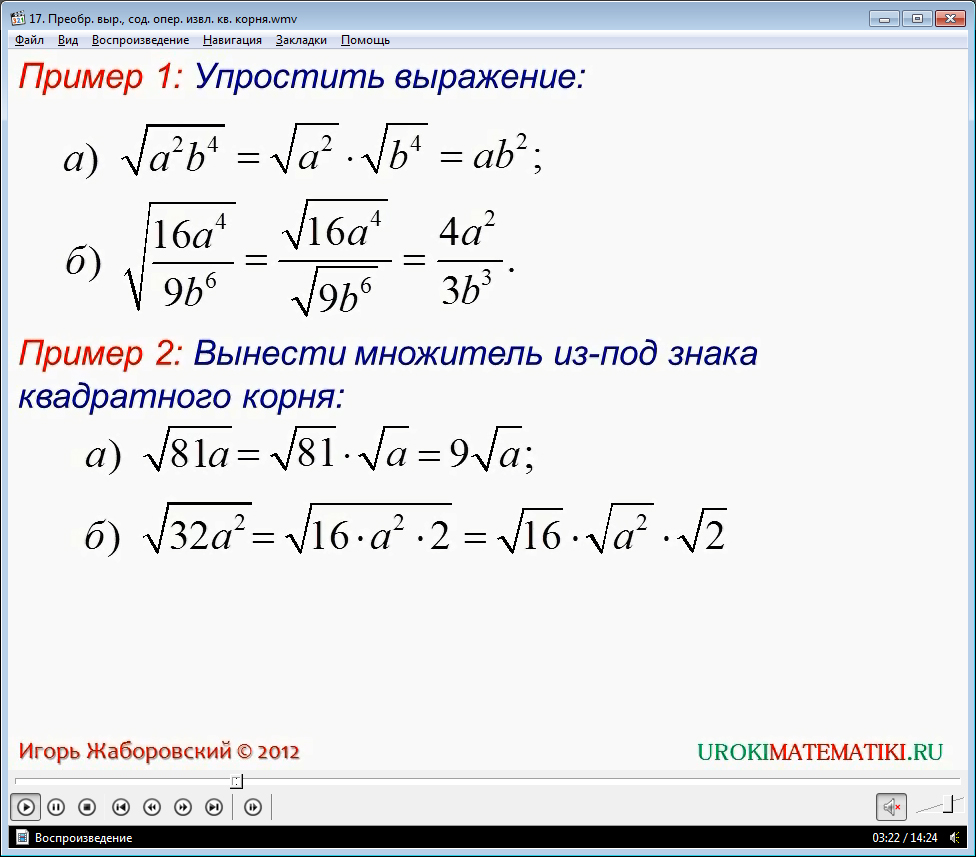 ) Такая расшифровка красиво делается через систему уравнений. Сейчас всё сами увидите.)
) Такая расшифровка красиво делается через систему уравнений. Сейчас всё сами увидите.)
Итак, под первым корнем у нас вот такое выражение:
А вдруг, не угадали? Проверим! Возводим в квадрат по формуле квадрата суммы:
Всё верно.) Но… Откуда я взял это выражение ? С неба?
Нет.) Мы его чуть ниже получим честно. Просто по данному выражению я показываю, как именно составители заданий шифруют такие квадраты. 🙂 Что такое 54? Это сумма квадратов первого и второго чисел. Причём, обратите внимание, уже без корней! А корень остаётся в удвоенном произведении, которое в нашем случае равно . Поэтому распутывание подобных примеров начинается с поиска удвоенного произведения. Если распутывать обычным подбором. И, кстати, о знаках. Тут всё просто. Если перед удвоенным плюс, то квадрат суммы. Если минус, то разности.) У нас плюс — значит, квадрат суммы.) А теперь — обещанный аналитический способ расшифровки. Через систему.)
Итак, у нас под корнем явно тусуется выражение (a+b)2, и наша задача — найти a и b. В нашем случае сумма квадратов даёт 54. Вот и пишем:
Теперь удвоенное произведение. Оно у нас . Так и записываем:
Получили вот такую системку:
Решаем обычным методом подстановки. Выражаем из второго уравнения, например, и подставляем в первое:
Решим первое уравнение:
Получили биквадратное уравнение относительно a. Считаем дискриминант:
Значит,
Получили аж четыре возможных значения a. Не пугаемся. Сейчас мы всё лишнее отсеем.) Если мы сейчас для каждого из четырёх найденных значений посчитаем соответствующие значения , то получим четыре решения нашей системы. Вот они:
И тут вопрос — а какое из решений нам подходит? Давайте подумаем. Отрицательные решения можно сразу отбросить: при возведении в квадрат минусы «сгорят», и всё подкоренное выражение в целом не изменится.) Остаются первые два варианта. Выбрать их можно совершенно произвольно: от перестановки слагаемых сумма всё равно не меняется.) Пусть, например, , а .
Отрицательные решения можно сразу отбросить: при возведении в квадрат минусы «сгорят», и всё подкоренное выражение в целом не изменится.) Остаются первые два варианта. Выбрать их можно совершенно произвольно: от перестановки слагаемых сумма всё равно не меняется.) Пусть, например, , а .
Итого получили под корнем квадрат вот такой суммы:
Всё чётко.)
Я не зря так детально описываю ход решения. Чтобы было понятно, как происходит расшифровка.) Но есть одна проблемка. Аналитический способ расшифровки хоть и надёжный, но весьма длинный и громоздкий: приходится решать биквадратное уравнение, получать четыре решения системы и потом ещё думать, какие из них выбрать… Хлопотно? Согласен, хлопотно. Этот способ безотказно работает в большинстве подобных примеров. Однако очень часто можно здорово сократить себе работу и найти оба числа творчески. Подбором.) Да-да! Сейчас, на примере второго слагаемого (второго корня), я покажу более лёгкий и быстрый способ выделения полного квадрата под корнем.
Итак, теперь у нас вот такой корень: .
Размышляем так: «Под корнем — скорее всего, зашифрованный полный квадрат. Раз перед удвоенным минус — значит, квадрат разности. Сумма квадратов первого и второго чисел даёт нам число 54. Но какие это квадраты? 1 и 53? 49 и 5? Слишком много вариантов… Нет, лучше начать распутывать с удвоенного произведения. Наши можно расписать как . Раз произведение удвоенное, то двойку сразу отметаем. Тогда кандидатами на роль a и b остаются 7 и . А вдруг, это 14 и /2? Не исключено. Но начинаем-то всегда с простого!» Итак, пусть , а . Проверим их на сумму квадратов:
Получилось! Значит, наше подкоренное выражение — это на самом деле квадрат разности:
Вот такой вот способ-лайт, чтобы не связываться с системой. Не всегда работает, но во многих таких примерах его вполне достаточно. Итак, под корнями — полные квадраты. Осталось только правильно извлечь корни, да досчитать пример:
А теперь разберём ещё более нестандартное задание на корни. )
)
Докажите, что число A – целое, если .
Впрямую ничего не извлекается, корни вложенные, да ещё и разных степеней… Кошмар! Однако, задание имеет смысл.) Стало быть, ключ к его решению имеется.) А ключ здесь такой. Рассмотрим наше равенство
как уравнение относительно A. Да-да! Хорошо бы избавиться от корней. Корни у нас кубические, поэтому возведём-ка обе части равенства в куб. По формуле куба суммы:
Кубы и корни кубические друг друга компенсируют, а под каждым большим корнем забираем одну скобку у квадрата и сворачиваем произведение разности и суммы в разность квадратов:
Отдельно сосчитаем разность квадратов под корнями:
Отлично! Значит, всё наше равенство ещё сильнее упростится:
А теперь делаем финт ушами — заменяем сумму корней в скобках на A (согласно условию примера!).
Получаем кубическое уравнение или .
Здесь как раз тот случай, когда один из корней легко угадывается — это . Значит, наш многочлен можно разложить как
Как разложить? Либо по схеме Горнера, либо делением «уголком» на скобку (A-4), либо даже группировкой (если представить -3A как -16A+13A). Объяснять подробно деление уголком или схему Горнера в теме про корни — уже совсем отклоняться от курса.) Кто в теме — и так поймёт.
А теперь легко заметить, что квадратный трёхчлен во вторых скобках имеет отрицательный дискриминант, а значит, наше уравнение имеет единственный действительный корень . И поэтому наша страшная сумма корней в действительности равна просто 4. То есть, явно целому числу. Что и требовалось доказать.)
А теперь — поупрощаем некоторые дробные выражения с корнями. От простого — к сложному. Здесь всё точно так же, как и с многочленами. Только в применении к корням.) Я же говорил, что действия с корнями ничем не отличаются от таковых с буквами. И к корням с таким же успехом применима вся алгебра седьмого класса — формулы сокращённого умножения, разложение на множители, приведение подобных и т.п.
Только в применении к корням.) Я же говорил, что действия с корнями ничем не отличаются от таковых с буквами. И к корням с таким же успехом применима вся алгебра седьмого класса — формулы сокращённого умножения, разложение на множители, приведение подобных и т.п.
Например, такое задание.
Сократить дробь:
Пример явно намекает на применение формулы разности квадратов:
Спрашивается, а где же здесь квадраты? Сплошные корни… Сейчас покажу. 🙂
Берём числитель нашей дробушки: .
Что такое ? По свойству корня из степени, мы можем вынести квадрат наружу. Вот так:
Хорошо, а из как квадрат сделать? Не вопрос! По пятому свойству, домножаем на двойку показатели корня и подкоренного выражения:
По такой технологии, между прочим, можно совершенно любой корень превратить в совершенно любую степень. Какую хотим. 🙂 Как, например, представить в виде 4-й степени? Нет проблем:
Хотим из степеней корни делаем, хотим — наоборот, степени из корней. Что хотим, то и творим. Математика, однако! 🙂
Итак, весь наш числитель можно представить как разность квадратов:
А дальше никаких проблем — раскладываем числитель на множители и сокращаем:
Следующий пример.
Упростить:
Действуем аналогично. Раскладываем на множители и сокращаем. 🙂 В числителе применяем группировку. Например, вот такую:
А в знаменателе просто выносим общий множитель :
Подставляем всё в нашу дробь и сокращаем:
Как видим, разложение на множители очень популярно в теме с корнями. Очень! И особенно — формула разности квадратов. Именно поэтому формулы сокращённого умножения так важно знать и уметь применять. 🙂
Ну и на десерт распутаем что-нибудь навороченное. )
)
Упростить:
Чтобы не запутаться и не наляпать ошибок, будем действовать по порядку. При взгляде на любой пример всегда задаём сами себе вопрос: «Что в примере мне больше всего не нравится?» В данном примере большинство скажет: «Числитель первой дроби!» Верно! Вот и упростим его отдельно: остальная часть примера от этого никак не пострадает.) Итак,
Вместо знака деления удобно использовать черту дроби. Вот так:
Сначала упростим дробь. Как? Попробуем сократить.) Для этого, ясное дело, надо разложить на множители числитель и знаменатель, да… Берём отдельно числитель . Можно его разложить на множители? Можно! Для этого из a надо сделать корень. Вот так:
Если теперь подставить вместо a выражение , то всплывёт общий множитель. 🙂
Со знаменателем полная аналогия:
Таким образом,
Теперь от упрощённой дроби отнимаем единичку. Как? Делаем из единички дробь и — вперёд!
Следующим пунктом идёт деление полученной дроби на выражение . Это означает, что оно пойдёт у нас в знаменатель:
Уфф… Дальше… Отнимаем от полученного выражения дробь :
И, наконец, последнее усилие. Возводим результат в куб:
Ну как, всё понятно? Тогда — вперёд, набиваем руку и делаем примеры!
Вычислить:
Вынести множители за знак корня: , , где .
Внести множители под знак корня: , .
Освободиться от иррациональности в знаменателе дробей:
, .
Вычислить:
Доказать, что A – целое число, если .
Упростить:
Ответы (пока) давать не буду — иначе неинтересно. 🙂 До встречи и успехов!
🙂 До встречи и успехов!
Глава 2 преобразование иррациональных выражений
Содержание
Введение……………………………………………………………………………2
Глава 1. История возникновения иррациональных чисел………………………………………………………………………………..4
Глава 2. Преобразование иррациональных выражений
2.1 Квадратный корень из числа……………………………………………
82. 2 Вычисление квадратных корней……………………………………….
92.3 Основные тождества для квадратных уравнений……………………
112. 4 Извлечение квадратного корня из произведения, дроби и степени…………………………………………………………………………….12
2.5 Преобразование выражений……………………………………………13
2.6 Правила извлечения квадратного корня из натурального числа…………………………………………………………………………………14
2.7 Сравнение корней…………………………………………………………..17
Глава 3. Практика решения уравнений, содержащих переменную под знаком корня.
3.1 Решение иррациональных равнений………………………………………..19 3.2 Преобразование графика функции в график функции …………………………………………………………………………..20
3.3 Два способа решения иррациональных уравнений: аналитический и графический……………………………………………………………………..22
Выводы………………………………………………………………………….28
Список использованной литературы…………………………………………..29
Введение
Совокупность цифр – это бескрайняя азбука весьма выразительного языка математики – вот уже тысячелетиями поражает воображение человечества.
Традиция интереса к очень крупным числам восходит, по крайней мере, к Архимеду, который, решив определить, сколько песчинок может поместиться во Вселенной, разработал систему классов и порядков арифметических величин. Он даже предложил принципы, с помощью которых можно «придумывать» названия сколько угодно больших чисел.
Математика – наука, изучающая соотношения между числами, между пространственными конфигурациями и абстрактными структурами. Понимание самостоятельного положения математики как особой науки возникло в Древней Греции в VI -V в.в. до н. э. Математика объединяет комплекс дисциплин: арифметика, алгебра, геометрия, теория вероятности, математический анализ.
Понимание самостоятельного положения математики как особой науки возникло в Древней Греции в VI -V в.в. до н. э. Математика объединяет комплекс дисциплин: арифметика, алгебра, геометрия, теория вероятности, математический анализ.
В каждой из этих дисциплин есть ключевые понятия. В алгебре одним из
важнейших понятий является корень. Введение квадратных корней – не прихоть математиков, а объективная необходимость: в реальной жизни встречаются ситуации, математические модели которых содержат операцию извлечения квадратного корня. Однако интерес к квадратному корню из двух, видимо, возник ещё раньше. Учёные по-разному предлагают решать квадратные уравнения. Возникает спор о надобности использования формул квадратного уравнения с использованием . В этом мы видим актуальность нашей темы.
Объект исследования: теория числовых множеств.
Предмет исследования: решение проблемы иррациональности в алгебре.
Цель работы: провести анализ введения и использования иррациональных чисел.
Задачи:
Рассмотреть историю возникновения иррациональных чисел.
Сопоставить определение корня разными учеными.
Проанализировать и описать способы извлечения корня.
Исследовать применение иррациональных выражений при решении иррациональных уравнений.
Исследовать решение иррациональных уравнений графическим методом с использованием дробно-линейной функции.
Методы исследования: описательный, сопоставительный, анализ литературы, поисковый.
Структура работы: работа состоит из введения, трех глав, выводов, списка использованной литературы, приложений.
Глава 1. История возникновения иррациональных чисел.
Потребность в действиях возведения в степень и извлечения корня была вызвана, как и другие четыре арифметических действия, практической жизнью. Так, наряду с задачей вычисления площади квадрата, сторона которого а известна, с давних пор встречалась обратная задача: «Какую длину должна иметь сторона квадрата, чтобы его площадь равнялась в?»
В собрании Вавилонских исторических ценностей, хранящемся в Йельском университете, есть круглая глиняная табличка, относящаяся к 1750 г. до н.э. На ней изображён рассечённый диагоналями квадрат и чёткими клинописными знаками выписаны три цифры. Когда их прочли, стало ясно. Что без малого 4000 тысячи лет назад в Вавилоне умели определять диагональ квадрата по его стороне, умножая, его длину на квадратный корень из двух.
Невольно хочется повторить: это подсчитано в 18 веке до н.э.!
За пять столетий до нашей эры школа Пифагора сделала одно из величайших математических открытий. Пифагорейцы пытались доказать, что любое число может быть выведено путём сложения, вычитания, умножения и деления положительных целых чисел. А корень квадратный из двух – число иррациональное и конечным числом таких операций не получается. Это и было обнаружено последователями Пифагора. Однако они любили всяческую секретность и «законспирировали» своё открытие на многие годы.
Его доказательство впервые появилось в «Началах» Евклида около 300 г. до н.э. А затем примерно в 140 г. н. э. Теону из Смирны удалось разработать интереснейший алгоритм вычисления корня из двух. Этот алгоритм стал истоком всей методики использования непрерывных дробей. В 19 в. Математик Бурман довёл вычисление квадратного корня из двух до 486-ог десятичного знака. Его победа, добытая «голыми руками», омрачается тем, что в 316-ом знаке Бурман допустил ошибку. И далее его вычисления неверны.
В последнее время интерес к подобным операциям стал не только данью традиции. «Неупорядоченные» величины, вроде корня квадратного из двух могут служить для моделирования случайно происходящих массовых явлений. Всё это входит в круг математической теории с прозаическим названием «теория массового обслуживания».
Математикам необходимо знать, появляются ли где-либо в этой величине такие последовательности, как, например, 7,7,7,7,7 или 1,2,3,4,5,6,7,8,9. подобные события теория пока предсказать не в силах, так что приходится добиваться ответа эмпирически, путем приближения и приближения к истине. Поэтому с момента появления скоростных
электронных вычислительных машин математики не жалели сил и довели вычисление до стотысячного знака. Недавним достижением была титаническая работа сотрудника Отдела математических методов в инженерном деле при Колумбийском университете профессора Жака Дутки (Нью-Йорк). Он специально разработал совершенно новый алгоритм и подсчитал величину названного корня до миллион восемьдесят второго десятичного знака! Это наиболее длинная из всех вычислительных величин за всю историю математики.
Хотя алгоритм профессора Дутки и рассчитан на эффективное и быстрое вычисление, мощная ЭВМ «ИБМ 360 – 91» потратила на эту работу сорок семь с половиной часов машинного времени. А ведь обычно решение даже сравнительно сложных задач отнимает у современной ЭВМ если не секунды, то лишь минуту. К этому нужно добавить сотни часов, ушедших у группы специалистов, составлявших программу для вычислений. В напечатанном виде результат работы Дутки занимает книгу в 201 страницу сжатого текста – 5000 десятичных знаков на каждой странице.
Теперь Дутка и его сотрудники намерены заняться числами π- отношением длины окружности к диаметру – и е— основанием натурального логарифма. Эти «орешки» будут ещё труднее, чем корень квадратный из двух, но к π математики испытывают прямо-таки «историческую нежность», а е – одна из важнейших констант во всей системе исчисления, во всей высшей математике.
Ныне применяемый знак корня произошел от обозначения, которое применяли немецкие математики 15-16 в.в., называвшие алгебру «Косс», а алгебраистами «косстистами». Неизвестные числа с 17 века стали обозначать последними буквами латинского алфавита x, y, z. Однако долго ещё неизвестное в уравнении писали буквой R (от «Radix» — « корень»), а квадрат его – буквой q (« quadratus»). Это объяснение не является общепринятым. В самых старых рукописях перед числом, из которого нужно извлечь корень, ставилась точка, а позднее точка или узкий ромбик с черточкой, направленной вправо и вверх. Так образовался знак .
«Источником алгебраических иррациональностей является двузначность или многозначность задачи; ибо было бы невозможно выразить одним и тем же вычислением многие значения, удовлетворяющие одной и той же задаче, иначе, чем при помощи корней…; они же разве только в частных случаях могут быть сведены к рациональностям» — Лейбниц Г.
Одной из конкретных причин появления математических теорий явилось открытие иррациональностей. Вначале это произошло в пределах геометрических изысканий в виде установления факта несоизмеримости двух отрезков прямой. Значение этого открытия в математике трудно переоценить.
Математики Индии, Ближнего и Среднего Востока, развивая алгебру, тригонометрию и астрономию, не могли обойтись без иррациональных
величин, которые, однако, длительное время не признавали за числа. Греки называли иррациональную величину, например, корень из квадратного числа, «алогос»- невыразимое словами. Позже европейские переводчики с арабского языка на латынь перевели это слово латинским словом surdus- глухой. В Европе этот термин впервые появился в середине 12в. У Геродота Кремонского, известного переводчика математических произведений с арабского на латынь, вплоть до 18в. Позже, математик Симон Стевин считали понятие иррационального числа равноправным с рациональным.
В математику, едва ли не впервые, вошла сложная теоретическая абстракция, не имеющая аналога в донаучном общечеловеческом опыте. Вероятно, самой иррациональностью, открытой древнегреческими математиками, было число.
Можно с определённой уверенностью считать, что исходным пунктом этого открытия были попытки найти общую меру с помощью алгоритма попеременного вычитания, известного сейчас как алгоритм Евклида.
Глава 2. Преобразование иррациональных выражений
2.1 Квадратный корень из числа
Зная время , можно найти путь при свободном падении по формуле: Решим обратную задачу.
Задача. Сколько секунд будет падать камень, сброшенный с высоты 122,5 м?
Решение: Чтобы найти ответ, нужно решить уравнение Из него находим, что Теперь осталось найти такое положительное число t, что его квадрат равняется 25. Этим числом является 5, так как Значит, камень будет падать 5 с.
Искать положительное число по его квадрату приходится и при решении других задач, например при отыскании длины стороны квадрата по его площади. Введем следующее определение:
Определение. Неотрицательное число, квадрат которого равен неотрицательному числу а, называется квадратным корнем из а.
Это число обозначают . Таким образом
Пример. Так как
Из отрицательных чисел нельзя извлекать квадратные корни, так как квадрат любого числа или положителен, или равен нулю. Например, выражение не имеет числового значения.
В записи знак называют знаком радикала (от латинского «;радикс»; — корень), а число а — подкоренным числом. Например, в записи подкоренное число равно 25. Так как Это означает, что квадратный корень из числа, записанного единицей и 2n нулями, равен числу, записываемому единицей и n нулями: .
Аналогично доказывается, что
Например,
2. 2 Вычисление квадратных корней
Мы знаем, что не существует рационального числа, квадрат которого равен 2. Это означает, что не может быть рациональным числом. Он является иррациональным числом, т.е. записывается в виде непериодической бесконечной десятичной дроби, причем первые десятичные знаки этой дроби имеют вид 1,414… Чтобы найти следующий десятичный знак, надо взять число 1.414х, где х может принимать значения 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, возвести по порядку эти числа в квадрат и найти такое значение х, при котором квадрат меньше, чем 2, но следующий за ним квадрат больше, чем 2. Таким значением является х=2. Далее повторяем то же самое с числами вида 1,4142х. Продолжая этот процесс, получаем одну за другой цифры бесконечной десятичной дроби, равной .
Аналогично доказывается существование квадратного корня из любого положительного действительного числа. Разумеется, последовательное возведение в квадрат весьма трудоемкое занятие, и потому существуют способы быстрее находить десятичные знаки квадратного корня. С помощью микрокалькулятора можно найти значение с восемью верными цифрами. Для этого достаточно ввести в микрокалькулятор число а>0 и нажать клавишу — на экране высветится 8 цифр значения . В некоторых случаях приходится использовать свойства квадратных корней, которые мы укажем ниже.
Если точность, даваемая микрокалькулятором, недостаточна, можно воспользоваться способом уточнения значения корня, даваемым следующей теоремой:
Теорема. Если а — положительное число и — приближенное значение для по избытку, то — приближенное значение для по недостатку.
Доказательство:
По условию x1>и потому х12 >a, 2 = = a. Т.к. aI>a. Значит, а и — приближенное значение для по недостатку.
Аналогично доказывается, что если — приближенное значение для по недостатку, то — приближенное значение по избытку.
Поскольку и являются приближенными значениями для по избытку и по недостатку, то в качестве лучшего приближения для
естественно выбрать среднее арифметическое этих чисел, т. е. число
х2 = . А чтобы получить еще более точное значение для , надо взять среднее арифметическое чисел , т. е. число
х3 = . Так вычисляются одно за другим все лучшие и лучшие приближенные значения для . Приближения ведут до тех пор, пока два полученных значения не совпадут в пределах заданной точности. Можно доказать, что каждое приближение примерно удваивает число верных десятичных знаков.
Пример 1. Уточним по формуле = приближение
= 1,414 для .
В нашем случае а=2. Поэтому
= (1,414 + 1,4144271) + 1,4142135…
Выполнив еще одно приближение, мы убедимся, что все выписанные знаки полученного ответа верны, т. е. число верных знаков удвоилось.
Пример 2. Найдем приближенное значение для с точностью до 0,0001.
Выберем за первое приближение для число 2. Тогда второе приближение вычисляется так: = = 2,25
Далее имеем == 2,2361, ==2,2361.
Значит, с точностью до 0,0001 имеем =2,2361.
2.3 Основные тождества для квадратных корней
Из определения квадратного корня вытекает, что равенство, где , верно в том и только в том случае, когда, причем . Заменяя в равенстве переменную на , получаем тождество
, (1)
верное для всех . Заменяя в равенстве = переменную на , получаем тождества, которое верно для всех
= , (2) .
Например,2 = 25;2 = 8; 2 = 0,11; = 6; =0,24.
Формулы и показывают, что длянеотрицательных чисел операции возведения в квадрат и извлечения квадратного корня взаимообратным.
Т.е. если выполнить над каким-нибудь неотрицательным числом сначала одну из этих операций, а потом другую, то число не изменится.
Если а – отрицательное число, то равенство неверно, так как не имеет числового значения. При отрицательных значениях х неверно и равенство . Например,2 ==5, а не –5. Так как х2 =2, а при х х> 0, то при х/I> 0 верно равенство =2 = — х (3)
Итак, Но мы знаем, что
Поэтому для всех чисел х верно равенство
= . (4)
Например,==8, 2 = = 12.
Пример 1. Упростим выражение +2 + — 2.
Так как 2 = 3, 2 = 2, то +2 + — 2 =2 +
2· + 2 +2 – 2∙ + 2 =2· 2 + 2 · 2 = 2 · 3 + 2 · 2 = =10.
Пример 2. Найдем значения выражения , при а = 2,1; b = 3,6 .
При любом значении х выполняется равенство
= . Поэтому = . Но == 1,5. Значит, при а = 2,1; b =3,6 имеем =1,5.
2.4 Извлечение квадратного корня из произведения, дроби и степени
Выражения · и имеют одно и то же значение 6. В самом деле, = 3, = 2, = 6, поэтому ·= 3 · 2 = 6 и = == 6. Равенство ·= — частный случай общего утверждения:
Теорема. Квадратный корень из произведения двух неотрицательных чисел равен произведению квадратных корней из этих чисел, т.е. при а 0, b 0 имеем= · (1)
Доказательство:
Пусть число а и b неотрицательны. Тогда по правилу возведения в степень имеем · 2 = · = а ·b.
Кроме того, · — неотрицательное число как произведение двух неотрицательных чисел и . Поэтому · =
Пример 1. Найдем значения выраженияМы имеем = 25, = 16, = 0,01,
и потому = 25·16·0,01= 4.
Аналогично доказывается, что = (2)
2.5 Преобразование выражений
При преобразовании выражении, содержащих квадратные корни, оказывается полезной следующая формула
= ,
где А2 В (в обеих частях равенства одновременно берутся знаки “ плюс “ и “ минус “). Чтобы доказать это равенство, заметим, во-первых, что и левая, и правая его части являются при А 0, В 0, А2 – В 0 неотрицательными числами. Возведем теперь обе части равенства в квадрат. В левой части имеем А , в правой части по формуле квадрата суммы или разности получаем
2 + =
= А 2 = А 2 =
= А 2 = А 2 = А .
Таким образом, квадраты обеих частей равенства оказались одинаковыми, а поскольку эти части – неотрицательные числа, то равенство доказано.
Пример 1. Упростим выражение .
1-й способ. В одном случае имеем А = 5, В = 21, А2 – В =
= 52 – 21 = 4, и поэтому по формуле
= — = — .
2-й способ. Приведем подкоренное выражение к полному квадрату:
5 — = = = = =
= . Поэтому = = .
Пример 2. Упростим выражение
1-й способ:
= + = + = .
2-й способ: = =
===
Поэтому = .
Пример 3. Доказать, что = 10.
= 28 – 10= 25 – 10+3 = 52 – 10= .
Поэтому 2 = 5 – .
= 28 + 10= 25 + 10 + 3 = .
Поэтому = 5 + =
= 5 – = 5 + 5 = 10.
2.6 Правила извлечения квадратного корня из натурального числа
Пусть нужно извлечь квадратный корень из натурального числа m. Чтобы найти результат можно воспользоваться следующим правилом:
Разобьем число mна грани (справа налево, начиная с последней цифры), включив в каждую грань по две рядом стоящие цифры. При этом следует учесть, что если mсостоит из четного числа цифр, то в первой грани (слева) будет две цифры; если же число m состоит из нечетного числа цифр, то первая грань состоит из одной цифры. Количество граней показывает количество цифр результата.
Подбираем наибольшую цифру, такую, что ее квадрат не превосходит числа, находящегося в первой грани; эта цифра – первая цифра результата.
Возведем первую цифру результата в квадрат, вычтем полученное число из первой грани, припишем к найденной разности справа вторую грань. Получится некоторое число A. Удвоив имеющуюся часть результата, получим число a. Теперь подберем такую наибольшую цифру x, чтобы произведение числа ax на x не превосходило числаA. Цифра x – вторая цифра результата.
Произведение числа ax на xвычтем из числа A, припишем к данной разности справа третью грань, получится некоторое число В.84 – их три, значит, в результате должно получиться трехзначное число. Первая цифра результата 3, так как 322>13. Вычтя 9 из 13, получим 4. Приписав к 4 следующую грань, получим A =483. Удвоив имеющуюся часть результата, то есть число 3, получим a=6. Подберем теперь такую цифру х, чтобы произведение двузначного числа ax на x было меньше числа 483. Такой цифрой будет 7, так как — это меньше 483, тогда как — это больше 483. Итак, вторая цифра результата 7. Вычтя 469 из 483, получим 14. Приписав к этому числу справа последнюю грань, получим В = 1484. Удвоив имеющуюся часть результата, то есть число 37, получим b=74. Подберем теперь такую наибольшую цифру у, чтобы произведение трехзначного числа bу на у не превосходило 1484. Такой цифрой будет 2, так как . Цифра 2 – последняя цифра результата. В ответе получили 372.
=372
32=9
*67 —483
7 469
*742 —1484
2 1484
0
Пример 2. Вычислить .
=543
52=25
*104 —448
4 416
*1083 —3249
3 3249
0
Пример 3. Вычислить .
=123
12=1
*22 —51
2 44
* 243—729
3 729
0
Пример 4. Вычислить .
=1264
12=1
*22 —59
2 44
*246 —1576
6 1476
*2524 —10096
4 10096
0
Пример 5. Вычислить .
=3530
32=9
*65 —346
5 325
* 703 —2109
3 2109
0
Если корень не извлекается, то после последней цифры заданного числа ставят запятую и образуют дальнейшие грани, каждая из которых имеет вид 00. В этом случае процесс извлечения корня бесконечен; он прекращается, когда достигается требуемая точность
Пример 1. Вычислить с точностью до 0,01.
=2,645
4
*46 —300
6 276
*524 —2400
4 2096
*5285 —30400
5 26425
3975
. . . . .
2.7 Сравнение корней
Для того чтобы сравнить квадратный корень из иррационального числа с квадратным корнем из другого числа или любым другим числом (рациональным, иррациональным, целым или натуральным), необходимо найти его приблизительное значение.
Пример 1. Сравнить и .
Выберем за первое приближение для число 2. Тогда следующие приближения вычисляется так:
= = 2,5 = = 2,45 = = 2,4494
Итак
Выберем за первое приближение для число 3. Тогда следующие приближения вычисляется так:
= = 3,1666 = = 3,1622. Итак
Окончательно
Выберем за первое приближение для число 2. Тогда второе приближение вычисляется так: = = 2,25.
Далее имеем == 2,2361. Итак
Выберем за первое приближение для число 3. Тогда второе приближение вычисляется так: = = 3,33.
Далее имеем == 3,316. Итак
Окончательно
Ответ =
Пример 2. Сравнить и 0.
Решение: 1) 2)
3) Итак >0
Пример 3. Сравнить и
Решение: 1) 2) 3) 4)
5)
6)
>
Глава 3. Практика решения уравнений содержащих переменную под знаком корня
3.1 Решение иррациональных уравнений
Иррациональным называется уравнение, в котором переменная содержится под знаком корня.
Рассмотрим два метода решения иррациональных уравнений: метод возведения обеих частей уравнения в одну и ту же степень и метод введения новых переменных.
Метод возведения обеих частей уравнения в одну и ту же степень состоит в следующем:
а) преобразуют заданное иррациональное уравнение к виду ;
б) возводят обе части полученного уравнения в n-ю степень:
;
в) учитывая, что , получают уравнениеf(х) = g(х);
г) решают уравнение и делают проверку, так как возведение обеих частей уравнения в одну и ту же четную степень может привести к появлению посторонних корней. Эта проверка чаще всего осуществляется с помощью подстановки найденных значений переменной в исходное уравнение.
Пример 1.
Решение. Данное уравнение содержит всего один радикал; оставим его в левой части, а все остальные члены уравнения перенесём в правую часть, получим
=2х-1; возведем обе части в квадрат: х²+5х+1=(2х-1)²,
х²+5х+1=4х²-4х+1; после переноса всех членов в левую часть и приведения подобных членов имеем х(х-3)=0 х1=0 или х2=3.
Проверка. Если х1=0, то + 1 — 2∙0≠0. Следовательно, первый корень х=0 не удовлетворяет уравнению. Второй корень х=3 удовлетворяет данному уравнению. Ответ: 3.
Пример 2. =
Решение. Возведём обе части в квадрат и получим 2х-3=х-2, откуда х=1. Проверка показывает, что этот корень посторонний (при х=1 обе части уравнения не имеют смысла). Заметим, что проверку можно выполнить так: областью определения уравнения служит луч [2;+∞), и так как 1 не
= принадлежит данному лучу, то х=1 – посторонний корень.
Ответ: нет корней.
Метод введения новой переменной объясним на примере.
Пример 3. .
Решение.1) Введем новую переменную , тогда уравнение примет вид:
. Умножим обе части уравнения на , получим .
Возведем обе части уравнения в квадрат: . Помножив, обе части уравнения на 4 получим квадратное уравнение: у1 = 4; у2= .
2) Так как , то получаем два уравнения: и
корни уравнений и.
3) Выполним проверку: пусть и
. Пусть ( посторонний корень)
Ответ: 3.
3.2 Преобразование графика функции в график функции
Пример 1. Построить график функции , зная .
1) 2)
Составим таблицу значений: Составим таблицу значений:
Х
1
4
16
25
0,01
0,0001
У
1
0,5
0,25
0,2
10
100
Сравнивая таблицы значений, видим, что при нахождении соответствующих координат для построения второго графика функции увеличивая значения координаты х значения координаты у уменьшаются, а, уменьшая значения координаты х значения координаты у увеличиваются. Таким образом, ветвь параболы преобразуется в ветвь гиперболы.Пример 2. Построить график функции , зная график функции
Пример 3. Построить график функции , зная график функции
3.3 Два способа решения иррациональных уравнений: аналитический и графический
Пример 1.
а)
Первый способ.
1) Возведем обе части уравнения в квадрат: . Получим квадратное уравнение:
2) Выполним проверку: пусть ( посторонний корень)
Пусть
Ответ: .
Второй способ.
Ответ: .
б) Составим дробно-рациональное уравнение:
Первый способ.
Возведем обе части в квадрат: . Приведем дроби к общему знаменателю:
и
Ответ:
Второй способ.
Ответ:
Пример 2.
а)
1) Возведем обе части уравнения в квадрат:
D уравнение не имеет корней.
Ответ: нет корней.
Второй способ.
Ответ: нет корней.
б) Составим дробно-рациональное уравнение:
.
Первый способ.
Возведем обе части уравнения в квадрат: Приведем дроби к общему знаменателю и получим: .
D уравнение не имеет корней
Ответ: нет корней.
Второй способ.
Ответ: нет корней.
Пример 3.
а) .
Первый способ.
1) Возведем обе части уравнения в квадрат: Приведем дроби к общему знаменателю и получим:
Ответ:
Второй способ.
Ответ:
б) Составим дробно-рациональное уравнение:
Первый способ.
Возведем обе части уравнения в квадрат: Приведем дроби к общему знаменателю и получим:
Ответ:
Второй способ.
Ответ:
Пример 4.
а)
Первый способ.
1) Возведем обе части уравнения в квадрат: Получим квадратное уравнение:
2) Выполним проверку: пусть 1 = 1.
Ответ:.
Второй способ.
Ответ:.
б) Составим дробно-рациональное уравнение:
Первый способ.
Возведем обе части уравнения в квадрат: Приведем дроби к общему знаменателю и получим:
Ответ:.
Второй способ.
Ответ:.
Выводы
Настоящая работа посвящена проблеме иррациональности в алгебре. Сопоставлено определение корня разными учеными. Рассмотрены и проанализированы способы извлечения квадратного корня; способы преобразования выражений, содержащих квадратные корни. В работе приведены примеры действий с квадратными корнями и преобразования выражений с ними. Проведено исследование применения иррациональных выражений при решении иррациональных уравнений.
Практическая значимость результатов исследования состоит в том, что подобран алгоритм для извлечения квадратного корня из натуральных чисел и из иррациональных чисел.
Новизна данной работы состоит в том, что исследован графический метод решения иррациональных уравнений с использованием дробно-линейной функции.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
Глейзер Г.И. История математики в школе. – М., 1982.
Депман И.А. Рассказы о математике. – Л., 1954.
Кордемский Б.А. Великие жизни в математике. – М., 1995.
Колягин Ю.М. Русская школа и математическое образование. – М., 2001.
Леокум А. Скажи мне почему?- М.,1994.
Мордкович А.Г. Алгебра.8 класс.- М., 2002.
Пичурин Л.Ф. За страницами алгебры. – М., 1999.
Перельман Я.И. Занимательная алгебра. – М., 1976.
Рыбников К.А. Возникновение и развитие математической науки. – М.,1987.
Силкин Б.И. С корнем квадратным сквозь историю. – М., 1971.
Энциклопедия книжного клуба XXI век. – М., 2002.
Муниципальное общеобразовательное учреждение лицей №8 «Олимпия» Дзержинского района г. Волгограда
Иррациональная алгебра
Выполнили: ученики 8 «Б» класса
Донника Данил
Ровенко Дарья
Сеимова Оксана
Руководитель: учитель математики
Солодовникова И.В.
Волгоград 2007 г.
Иррациональные выражения. Преобразование иррациональных выражений
Выражения, содержащие корень, который нельзя извлечь, называются иррациональными или радикальными.
Примеры:
— иррациональные выражения.
Сложение и вычитание корней
При сложении или вычитании иррациональных выражений их пишут одно за другим с сохранением их знаков.
Примеры:
В некоторых случаях с помощью преобразования можно сделать иррациональные выражения подобными, то есть, имеющими одинаковые показатели корней и подкоренные числа (или выражения), а затем сделать приведение.
Примеры:
Умножение и деление корней
При умножении иррациональных выражений с одинаковыми показателями корней перемножаются их подкоренные числа или выражения:
При делении иррациональных выражений с одинаковыми показателями корней подкоренное число или выражение делимого делится на подкоренное число или выражение делителя:
Примеры:
Возведение корня в степень
Чтобы возвести в степень иррациональное выражение, следует возвести в степень подкоренное число или выражение:
Примеры:
При возведении в n-ю степень знак корня отбрасывается, так как возведение числа (или выражения) в n-ю степень и извлечение из него корня n-ой степени — это взаимно сокращающиеся действия:
Извлечение корня
Чтобы извлечь корень из иррационального выражения, следует показатели корней перемножить:
, так как
Пример.
С помощью таких преобразований можно упростить извлечение корней 4-й, 6-й, 8-й, 9-й и т. п. степеней из чисел.
Примеры:
Сокращение корней
Величина иррационального выражения не изменится, если показатель корня и подкоренного выражения умножить или разделить на одно и то же число:
так как извлечение корня и возведение в степень — это взаимно сокращающиеся действия, если их показатели равны.
На этом свойстве основано сокращение корней и приведение их к общему показателю.
Сокращение корней — это деление показателей корня и подкоренного числа (или выражения) на одно и то же число, если оно является общим множителем для всех показателей.
Примеры:
Приведение корней к общему показателю
Приведение корней к общему показателю имеет большое сходство с приведением дробей к общему знаменателю. Рассмотрим два способа:
- Показатели корней не имеют общих множителей. В этом случае показатель каждого корня и его подкоренное число (или выражение) умножают на произведение остальных корней.
Рассмотрим три выражения:
,
Так как у данных показателей нет общего множителя, то просто перемножаем все показатели между собой. Полученный результат и станет общим показателем. После приведения к общему показателю выражения будут иметь следующий вид:
- Показатели корней имеют общий множитель. В этом случае надо найти НОК показателей и умножить показатель каждого корня на недостающий множитель.
Рассмотрим два выражения:
,
НОК (4, 6) = 12, значит, для первого выражения дополнительным множителем будет 3, а для второго 2. После приведения к общему показателю выражения будут иметь следующий вид:
При умножении и делении иррациональных выражений с разными показателями их приводят к общему показателю, а затем уже умножают или делят их подкоренные числа или выражения.
Примеры:
Урок 47. преобразование выражений — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №47. Преобразование выражений.
Перечень вопросов, рассматриваемых в теме:
- Преобразование рациональных выражений;
- Преобразование иррациональных выражений;
- Преобразование логарифмических выражений.
Глоссарий по теме
Алгебраическая сумма — это запись, состоящая из нескольких алгебраических выражений, соединенных знаком «+» или «-».
Одночлен – это произведение числовых и буквенных множителей, являющихся степенями с натуральными показателями.
Многочлен – это алгебраическая сумма нескольких одночленов.
Алгебраическая дробь – это дробь, числитель и знаменатель которой являются алгебраическими выражениями.
Степень с натуральным и целым показателем. Степень числа a с натуральным показателем n, большим 1, — это произведение n множителей, равных a , , где a — основание степени, n — показатель степени, – степень.
Если и n — натуральное число, то ,
если . то .
Арифметический корень. Арифметическим корнем натуральной степени из неотрицательного числа a называется неотрицательное число, n-я степень которого равна a. Обозначается , где a — подкоренное выражение.
Степень с рациональным показателем. Если n — натуральное число, m — целое число и частное является целым числом, то при справедливо равенство
Логарифмом положительного числа в по основанию а, где a > 0, a ≠ 1, называется показатель степени, в которую надо возвести а, чтобы получить в.
Основная литература:
Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. Под ред. А.Б. Жижченко. Алгебра и начала математического анализа. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. Уровни. – 2-е изд. – М.: Просвещение, 2010. – 336 с.: ил. – ISBN 978-5-09-025401-4
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.
Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.
Теоретический материал для самостоятельного изучения
- Выделение полного квадрата или куба. под знаком корня. Например, необходимо упростить выражение:
Предположим, что под корнем стоит полный квадрат.
Тогда
Так как сумма квадратов не может равняться иррациональному числу, то в нашем случае сумма квадратов равна четырнадцати, а удвоенное произведение равно шесть корней из пяти.
Мы получили систему, которую можно решить методом подстановки
Решая первое уравнение как биквадратное, получим
Так как в формуле квадрат суммы переменные a и b равноправны, получаем
Аналогично
Итак, заданное выражение
Аналогично можно выделять полный куб под корнем.
- В некоторых случаях выделить полный куб не представляется возможным, тогда можно поступить следующим образом:
Обозначим указанное выражение буквой А и получим равенство
возведем обе части равенства в куб.
Учитывая, что сумму кубических корней равна А, получим
A = 3
Таким образом, найдено значение выражения
Примеры и разбор решения заданий тренировочного модуля
Пример 1.
Упростить выражение и найти его значение при заданном значении переменной:
при
Варианты ответа: 0,2; 4; 0,4; 0,04;
Решение.
Обозначим , тогда наше выражение будет иметь вид:
Вернемся к первоначальной переменной
Вычислим при заданном значении переменной
Пример 2. Упростите и вычислите: при a = 125.
Варианты ответов: 125; 3,2; 6,4; 32; 62,5;
Решение.
Найдем значение при заданном значении переменной
Рациональные и иррациональные числа | Алгебраические выражения
1.3 Рациональные и иррациональные числа (EMA4)
- Рациональное число
Рациональное число (\ (\ mathbb {Q} \)) — это любое число, которое можно записать как:
\ [\ frac {a} {b} \], где \ (a \) и \ (b \) — целые числа, а \ (b \ ne 0 \).
Все следующие числа являются рациональными числами:
\ [\ frac {10} {1} \; ; \; \ frac {21} {7} \; ; \; \ frac {-1} {- 3} \; ; \; \ frac {10} {20} \; ; \; \ frac {-3} {6} \]Мы видим, что все числители и все знаменатели целые.
Это означает, что все целые числа являются рациональными числами, потому что они могут быть записаны со знаменателем \ (\ text {1} \).
- Иррациональные числа
Иррациональные числа (\ (\ mathbb {Q} ‘\)) — это числа, которые нельзя записать в виде дроби с числителем и знаменателем в виде целых чисел.
Примеры иррациональных чисел:
\ [\ sqrt {2} \; ; \; \ sqrt {3} \; ; \; \ sqrt [3] {4} \; ; \; \число Пи \; ; \; \ frac {1 + \ sqrt {5}} {2} \]Это не рациональные числа, потому что числитель или знаменатель не является целым числом.
Десятичные числа (EMA5)
Все целые числа и дроби с целыми числителями и ненулевым целым знаменателем являются рациональными числами. Помните, что когда знаменатель дроби равен нулю, дробь не определена.
Вы можете записать любое рациональное число в виде десятичного числа, но не все десятичные числа являются рациональными числами. Эти типы десятичных чисел являются рациональными числами:
Десятичные числа, которые заканчиваются (или заканчиваются).Например, дробь \ (\ frac {4} {10} \) может быть записана как \ (\ text {0,4} \).
Десятичные числа, состоящие из одной повторяющейся цифры. Например, дробь \ (\ frac {1} {3} \) может быть записана как \ (\ text {0,} \ dot {3} \) или \ (\ text {0,} \ overline {3} \). Обозначения точки и полосы эквивалентны, и оба представляют собой повторяющиеся символы \ (\ text {3} \), то есть \ (\ text {0,} \ dot {3} = \ text {0,} \ overline {3} = \ text {0,333 …} \).
Десятичные числа, повторяющиеся из нескольких цифр.Например, дробь \ (\ frac {2} {11} \) также может быть записана как \ (\ text {0,} \ overline {18} \). Полоса представляет собой повторяющийся узор из \ (\ text {1} \) и \ (\ text {8} \), то есть \ (\ text {0,} \ overline {18} = \ text {0 , 181818 …} \).
Вы можете увидеть точку вместо запятой, используемой для обозначения десятичного числа. Таким образом, число \ (\ text {0,4} \) также можно записать как 0,4
Обозначение: Вы можете использовать точку или черту над повторяющимися цифрами, чтобы указать, что десятичная дробь является повторяющейся десятичной.Если полоса охватывает более одной цифры, то все числа под полосой повторяются.
Если вас попросят определить, является ли число рациональным или иррациональным, сначала запишите число в десятичной форме. Если число заканчивается, то это рационально. Если так будет продолжаться вечно, ищите повторяющийся набор цифр. Если нет повторяющегося рисунка, то цифра иррациональна.
Когда вы записываете иррациональные числа в десятичной форме, вы можете продолжать записывать их для многих-многих десятичных знаков.Однако это неудобно и часто необходимо округлять.
Округление иррационального числа делает его рациональным числом, которое приближается к иррациональному числу.
Рабочий пример 1: Рациональные и иррациональные числа
Какие из следующих чисел не являются рациональными?
\ (\ pi = \ text {3,1415
- 5897462643383279502884197169390 …} \)
\ (\ text {1,4} \)
\ (\ text {1,618033989…} \)
\ (\ text {100} \)
\ (\ text {1,7373737373 …} \)
\ (\ text {0,} \ overline {02} \)
Иррациональная, десятичная дробь не оканчивается и не повторяется
Рациональное, десятичное завершение.
Иррациональная, десятичная дробь не оканчивается и не повторяется
Рационально, все числа рациональны.
Рациональная десятичная дробь имеет повторяющийся образец.
Рациональная десятичная дробь имеет повторяющийся образец.
Преобразование завершающих десятичных знаков в рациональные числа (EMA6)
Десятичное число состоит из целой и дробной части. Например, \ (\ text {10,589} \) имеет целую часть \ (\ text {10} \) и дробную часть \ (\ text {0,589} \), потому что \ (10 + \ text {0,589} = \ текст {10,589} \).
Каждая цифра после десятичной точки представляет собой дробь со знаменателем в возрастающей степени \ (\ text {10} \).
Например:
\ (\ text {0,1} \) равно \ (\ frac {1} {\ text {10}} \)
\ (\ text {0,01} \) равно \ (\ frac {1} {\ text {100}} \)
\ (\ text {0,001} \) равно \ (\ frac {1} {\ text {1 000}} \)
Это означает, что
\ begin {align *} \ text {10,589} & = 10 + \ frac {5} {10} + \ frac {8} {100} + \ frac {9} {\ text {1 000}} \\ & = \ frac {\ text {10 000}} {\ text {1 000}} + \ frac {\ text {500}} {\ text {1 000}} + \ frac {80} {\ text {1 000 }} + \ frac {9} {\ text {1 000}} \\ & = \ frac {\ text {10 589}} {\ text {1 000}} \ end {выровнять *}В следующих двух видеороликах объясняется, как преобразовать десятичные дроби в рациональные числа.
Часть 1
Видео: 2DBJ
Часть 2
Видео: 2DBK
Преобразование повторяющихся десятичных знаков в рациональные числа (EMA7)
Когда десятичная дробь является повторяющейся десятичной дробью, требуется немного больше работы, чтобы записать дробную часть десятичного числа в виде дроби.
Рабочий пример 2: Преобразование десятичных чисел в дроби
Запишите \ (\ text {0,} \ dot {3} \) в форме \ (\ frac {a} {b} \) (где \ (a \) и \ (b \) — целые числа).
Определите уравнение
\ [\ text {Let} x = \ text {0,33333 …} \]Умножить на \ (\ text {10} \) с обеих сторон
\ [10x = \ текст {3,33333 …} \]Вычтите первое уравнение из второго уравнения
\ [9x = 3 \]Упростить
\ [x = \ frac {3} {9} = \ frac {1} {3} \]Рабочий пример 3: Преобразование десятичных чисел в дроби
Запишите \ (\ text {5,} \ dot {4} \ dot {3} \ dot {2} \) в виде рациональной дроби.
Определите уравнение
\ [x = \ текст {5,432432432 …} \]Умножить на \ (\ text {1 000} \) с обеих сторон
\ [\ text {1 000} x = \ text {5 432,432432432 …} \]Вычтите первое уравнение из второго уравнения
\ [\ text {999} x = \ text {5 427} \]Упростить
\ [x = \ frac {\ text {5 427}} {\ text {999}} = \ frac {\ text {201}} {\ text {37}} = \ text {5} \ frac {\ text { 16}} {\ text {37}} \]В первом примере десятичное число умножалось на \ (\ text {10} \), а во втором примере десятичное число умножалось на \ (\ text {1 000} \).Это связано с тем, что в первом примере повторялась только одна цифра (т. Е. \ (\ Text {3} \)), а во втором — три повторяющиеся цифры (т. Е. \ (\ Text {432} \)).
В общем, если у вас повторяется одна цифра, умножьте ее на \ (\ text {10} \). Если у вас повторяются две цифры, умножьте их на \ (\ text {100} \). Если у вас повторяются три цифры, умножьте их на \ (\ text {1 000} \) и так далее.
Не все десятичные числа можно записать как рациональные числа. Почему? Иррациональные десятичные числа, например \ (\ sqrt {2} = \ text {1,4142135…} \) нельзя записать с целым числителем и знаменателем, потому что они не имеют шаблона повторяющихся цифр и не завершаются.
Ты справишься! Позвольте нам помочь вам учиться с умом для достижения ваших целей. Siyavula Practice направит вас в удобном для вас темпе, когда вы задаете вопросы в Интернете.
Зарегистрируйтесь, чтобы улучшить свои оценки Упражнение 1.1Какое место на диаграмме занимает число \ (- \ frac {12} {3} \)?
Сначала упростите дробь: \ (- \ frac {12} {3} = -4 \)
\ (- \ text {4} \) является целым числом, поэтому оно попадает в набор \ (\ mathbb {Z} \).
В следующем списке два ложных утверждения и одно истинное утверждение. Какое из утверждений соответствует действительности ?
- Каждое целое число — натуральное число.
- Каждое натуральное число — это целое число.
- В целых числах нет десятичных знаков.
Тщательно обдумайте каждый вариант:
- Есть целые числа, которые не попадают в натуральные числа (все отрицательные числа), поэтому это неверно.
- Натуральные числа — это \ (\ left \ {1; 2; 3; \ ldots \ right \} \), а целые числа — это \ (\ left \ {0; 1; 2; 3; \ ldots \ right \} \ ) (круг \ (\ mathbb {N} \) находится внутри \ (\ mathbb {N} _ {0} \)), поэтому, если число является натуральным числом, оно должно быть целым числом. Это верно.
- Целые числа \ (\ left \ {0; 1; 2; 3; \ ldots \ right \} \) увеличиваются только с шагом 1, поэтому в целых числах не может быть никаких десятичных чисел, что делает это ложным.
Итак, верно только (ii).
Какое место на диаграмме занимает число \ (- \ frac {1} {2} \)?
\ (- \ frac {1} {2} \) находится в своей простейшей форме, поэтому его нет в \ (\ mathbb {N} \), \ (\ mathbb {N} _0 \) или \ (\ mathbb {Z} \).Он находится в пространстве между прямоугольником и \ (\ mathbb {Z} \).
В следующем списке два ложных утверждения и одно истинное утверждение. Какое из утверждений соответствует действительности ?
- Каждое целое число — натуральное число.
- Каждое целое число является целым числом.
- В целых числах нет десятичных знаков.
Тщательно обдумайте каждый вариант:
- Есть целые числа, которые не попадают в натуральные числа (все отрицательные числа), поэтому это неверно.
- Целые числа \ (\ left \ {\ ldots; -3; -2; -1; 0; 1; 2; 3; \ ldots \ right \} \), а целые числа — \ (\ left \ {0 ; 1; 2; 3; \ ldots \ right \} \) (круг \ (\ mathbb {Z} \) находится внутри \ (\ mathbb {N} _ {0} \)), поэтому, если число является целым это должно быть целое число. Это верно.
- Целые числа \ (\ left \ {0; 1; 2; 3; 4; \ ldots \ right \} \) увеличиваются только с шагом 1, поэтому в целых числах не может быть никаких десятичных чисел, что делает это ложным .
Итак, верно только (ii).
\ (- \ sqrt {3} \)
\ (- \ sqrt {3} \) не имеет знака минус под квадратным корнем (минус находится за пределами корня) и не делится на ноль, поэтому он действительный.
\ (\ dfrac {0} {\ sqrt {2}} \)
\ (\ dfrac {0} {\ sqrt {2}} \) не имеет знака минус под квадратным корнем (минус находится вне корня) и не делится на ноль, поэтому он действительный.
\ (\ sqrt {-9} \)
\ (\ sqrt {-9} \) имеет знак минус под квадратным корнем, поэтому он не является действительным.
\ (\ dfrac {- \ sqrt {7}} {0} \)
\ (\ dfrac {- \ sqrt {7}} {0} \) имеет деление на ноль, поэтому не определено.
\ (- \ sqrt {-16} \)
\ (- \ sqrt {-16} \) имеет отрицательное число под квадратным корнем, поэтому оно не является действительным.
\ (\ sqrt {2} \)
\ (\ sqrt {2} \) не имеет минуса под квадратным корнем (минус находится вне корня), не делится на ноль, поэтому он действительный.
\ (- \ frac {1} {3} \) рационально. Дробь целых чисел — это рациональное число.
\ (\ text {0,651268962154862.7 \) является рациональным, целым, целым и натуральным числом. Его можно записать как целое число.
\ (\ пи + 3 \)
\ (\ pi \) иррационально. \ (\ text {3} \) рационально (это целое число). Любое рациональное число, добавленное к любому иррациональному числу, иррационально.
Следовательно, \ (\ pi + 3 \) иррационально.
\ (\ пи + \ текст {0,858408346} \)
\ (\ pi \) иррационально.\ (\ text {0,858408346} \) является рациональным (это конечная десятичная дробь). Любое рациональное число, добавленное к любому иррациональному числу, иррационально.
Следовательно, \ (\ pi + \ text {0,858408346} \) иррационально.
\ (\ frac {5} {6} \) рационально.
Поскольку \ (a \) — целое число, \ (\ frac {a} {3} \) рационально.
Поскольку \ (b \) — целое число, \ (\ frac {-2} {b} \) рационально.
Обратите внимание, что \ (b \) не может быть \ (\ text {0} \), так как это делает дробь неопределенной.
Поскольку \ (c \) иррационально, \ (\ frac {1} {c} \) иррационально.
\ (\ frac {a} {14} = \ frac {1} {14} \) рационально.
\ (\ frac {a} {14} = \ frac {-10} {14} \) рационально.
\ (\ frac {a} {14} = \ frac {\ sqrt {2}} {14} \) иррационально.
\ (\ frac {a} {14} = \ frac {\ text {2,1}} {14} \) рационально.
Проверить, какое из чисел входит в набор \ (\ left \ {1; 2; 3; 4; \ ldots \ right \} \). Следовательно, \ (\ text {7} \) и \ (\ text {11} \) — натуральные числа.
Помните, что рациональные числа можно записать как \ (\ frac {a} {b} \), где \ (a \) и \ (b \) — целые числа. Также помните, что рациональные числа включают завершающие десятичные числа. Следовательно, \ (- \ sqrt {8} \;; \; \ text {3,3231089 …} \; \; 3+ \ sqrt {2} \;; \; \ pi \) все иррациональны.
Любое число, являющееся квадратным корнем из отрицательного числа, не является действительным.Следовательно, нереально только \ (\ sqrt {-1} \).
Помните, что рациональные числа можно записать как \ (\ frac {a} {b} \), где \ (a \) и \ (b \) — целые числа. Также помните, что рациональные числа включают завершающие десятичные числа. Следовательно, \ (- 3 \;; \; 0 \;; \; -8 \ frac {4} {5} \;; \; \ frac {22} {7} \; \; 7 \;; \; \ text {1,} \ overline {34} \; \; 9 \ frac {7} {10} \;; \; 11 \) — все рациональные числа.
Проверьте, какое из чисел входит в набор \ (\ left \ {\ ldots; -3; -2; -1; 0; 1; 2; 3; \ ldots \ right \} \).Следовательно, \ (- 3 \;; \; 7 \;; \; 11 \) — целые числа.
Любая дробь, разделенная на \ (\ text {0} \), не определена. Следовательно, только \ (\ frac {14} {0} \) не определено.
\ (\ текст {2,121314 …} \)
Номер не заканчивается (это показано \ (\ ldots \)). Также отсутствует указание на повторяющийся узор цифр, поскольку ни над одним из чисел нет точки или полосы. Следующие три цифры могут быть любыми числами.
Обратите внимание, что, хотя кажется, что в цифрах есть шаблон, мы не знаем, продолжается ли этот шаблон.
Иррационально, нет повторяющегося рисунка.
\ (\ текст {1,242244246 …} \)
Номер не заканчивается (это показано \ (\ ldots \)). Также отсутствует указание на повторяющийся узор цифр, поскольку ни над одним из чисел нет точки или полосы. Следующие три цифры могут быть любыми числами.
Обратите внимание, что, хотя кажется, что в цифрах есть шаблон, мы не знаем, продолжается ли этот шаблон.
Иррационально, нет повторяющегося рисунка.
\ (\ текст {3,324354 …} \)
Номер не заканчивается (это показано \ (\ ldots \)). Также отсутствует указание на повторяющийся узор цифр, поскольку ни над одним из чисел нет точки или полосы. Следующие три цифры могут быть любыми числами.
Обратите внимание, что, хотя кажется, что в цифрах есть шаблон, мы не знаем, продолжается ли этот шаблон.
Иррационально, нет повторяющегося рисунка.
\ (\ текст {3,3243} \ dot {5} \ dot {4} \)
\ (\ text {0,1} = \ frac {1} {10} \)
\ begin {align *} \ text {0,12} & = \ frac {1} {10} + \ frac {2} {100} \\ & = \ frac {10} {100} + \ frac {2} {100} \\ & = \ frac {12} {100} \\ & = \ frac {3} {25} \ end {выровнять *}
\ begin {align *} \ text {0,58} & = \ frac {5} {10} + \ frac {8} {100} \\ & = \ frac {50} {100} + \ frac {8} {100} \\ & = \ frac {58} {100} \\ & = \ frac {29} {50} \ end {выровнять *}
\ begin {align *} \ text {0,2589} & = \ frac {2} {10} + \ frac {5} {100} + \ frac {8} {\ text {1 000}} + \ frac {9} {\ text { 10 000}} \\ & = \ frac {\ text {2 000}} {\ text {10 000}} + \ frac {500} {\ text {10 000}} + \ frac {80} {\ text {10 000}} + \ гидроразрыв {9} {\ text {10 000}} \\ & = \ frac {\ text {2 589}} {\ text {10 000}} \ end {выровнять *}
Мы видим, что повторяется только цифра \ (\ text {1} \), поэтому мы можем записать это как \ (\ text {0,} \ dot {1} \).
\ (\ text {0,1212121212 …} \)
Существует повторяющийся образец \ (\ text {12} \), поэтому мы можем записать это число как: \ (\ text {0,} \ overline {12} \)
\ (\ text {0,123123123123 …} \)
Существует повторяющийся шаблон \ (\ text {123} \), поэтому мы можем записать это число как: \ (\ text {0,} \ overline {123} \)
\ (\ text {0,11414541454145 …} \)
Шаблон 4145 повторяется, поэтому мы можем записать это число как: \ (\ text {0,11} \ overline {4145} \).7 \ текст {00}} & = \ текст {2} \ текст {остаток} \ текст {4} \\ \ frac {\ text {7}} {\ text {33}} & = \ text {0,} \ text {2 121} \ ldots \\ & = \ текст {0,} \ точка {\ текст {2}} \ точка {\ текст {1}} \ end {выровнять *}
\ begin {align *} \ frac {2} {3} & = 2 \ left (\ frac {1} {3} \ right) \\ & = 2 (\ text {0,333333 …}) \\ & = \ текст {0,666666 …} \\ & = \ текст {0,} \ точка {6} \ end {выровнять *}
\ begin {align *} 1 \ frac {3} {11} & = 1 + 3 \ left (\ frac {1} {11} \ right) \\ & = 1 + 3 (\ text {0,0
…}) \\
& = 1 + \ текст {0,27272727 …} \\
& = \ текст {1,} \ overline {27}
\ end {выровнять *}- Определить рациональные числа и иррациональные числа
- Классифицируйте различные типы действительных чисел
- ⓐ
- ⓑ
- ⓐ
- ⓑ
- останавливается или повторяется, число рациональное.
- не останавливается и не повторяется, цифра иррациональна.
- ⓐ рациональный
- ⓑ рациональный
- ⓒ иррационально
- ⓐ рациональный
- ⓑ рациональный
- ⓒ иррационально
- ⓐ рациональный
- ⓑ иррационально
- ⓐ иррационально
- ⓑ рациональный
- ⓐ
- ⓑ
- ⓐ
- ⓑ
- ⓐ
- ⓑ
- ⓐ рациональный
- ⓑ иррационально
- ⓐ
- ⓑ
- ⓐ
- ⓑ
- ⓐ иррационально
- ⓑ рациональный
- ⓐ
- ⓑ
- ⓐ 4
- ⓑ Учителей нельзя делить
- ⓒ Это приведет к меньшему количеству.
- Классифицируйте действительное число.
- Выполните вычисления, используя порядок операций.
- Используйте свойства действительных чисел.
- Оценивать и упрощать алгебраические выражения.
- завершающий десятичный разделитель: [латекс] \ frac {15} {8} = 1.875 [/ латекс] или
- повторяющееся десятичное число: [latex] \ frac {4} {11} = 0,36363636 \ dots = 0. \ Overline {36} [/ latex]
- 7
- 0
- –8
- [латекс] 7 = \ dfrac {7} {1} [/ латекс]
- [латекс] 0 = \ dfrac {0} {1} [/ latex]
- [латекс] -8 = — \ dfrac {8} {1} [/ латекс]
- 11
- 3
- –4
- [латекс] \ dfrac {11} {1} [/ латекс]
- [латекс] \ dfrac {3} {1} [/ латекс]
- [латекс] — \ dfrac {4} {1} [/ латекс]
- [латекс] — \ dfrac {5} {7} [/ латекс]
- [латекс] \ dfrac {15} {5} [/ латекс]
- [латекс] \ dfrac {13} {25} [/ латекс]
- [латекс] — \ dfrac {5} {7} = — 0. \ overline {714285} [/ latex], повторяющееся десятичное число
- [latex] \ dfrac {15} {5} = 3 [/ latex] (или 3,0), завершающее десятичное число
- [латекс] \ dfrac {13} {25} = 0,52 [/ латекс], завершающее десятичное число
- [латекс] \ sqrt {25} [/ латекс]
- [латекс] \ dfrac {33} {9} [/ латекс]
- [латекс] \ sqrt {11} [/ латекс]
- [латекс] \ dfrac {17} {34} [/ латекс]
- [латекс] 0.3033033303333 \ точки [/ латекс]
- [латекс] \ sqrt {25}: [/ latex] Это можно упростить как [латекс] \ sqrt {25} = 5 [/ latex]. Следовательно, [latex] \ sqrt {25} [/ latex] рационально.
- [latex] \ dfrac {33} {9}: [/ latex] Поскольку это дробь, [latex] \ dfrac {33} {9} [/ latex] является рациональным числом. Затем упростите и разделите.
[латекс] \ dfrac {33} {9} = \ dfrac {{11} \ cdot {3}} {{3} \ cdot {3}} = \ dfrac {11} {3} = 3. \ Overline { 6} [/ латекс]
Итак, [latex] \ dfrac {33} {9} [/ latex] является рациональным и повторяющимся десятичным числом.
- [latex] \ sqrt {11}: [/ latex] Это нельзя упростить дальше. Следовательно, [latex] \ sqrt {11} [/ latex] — иррациональное число.
- [latex] \ dfrac {17} {34}: [/ latex] Поскольку это дробь, [latex] \ dfrac {17} {34} [/ latex] является рациональным числом. Упростите и разделите.
[латекс] \ dfrac {17} {34} = \ dfrac {1 \ cdot {17}} {2 \ cdot {17}} = \ dfrac {1} {2} = 0,5 [/ латекс]
Итак, [latex] \ dfrac {17} {34} [/ latex] является рациональным и завершающим десятичным числом.
- 0,3033033303333… не является завершающим десятичным числом.Также обратите внимание, что здесь нет повторяющегося шаблона, потому что группа из трех увеличивается каждый раз. Следовательно, это не завершающее и не повторяющееся десятичное число и, следовательно, не рациональное число. Это иррациональное число.
- [латекс] — \ dfrac {10} {3} [/ латекс]
- [латекс] \ sqrt {5} [/ латекс]
- [латекс] — \ sqrt {289} [/ латекс]
- [латекс] -6 \ pi [/ латекс]
- [латекс] 0.{2}} = — 17 [/ latex] — это отрицательно и рационально. Он находится слева от 0.
- [латекс] -6 \ пи [/ латекс] отрицательно и нерационально. Он находится слева от 0.
- [латекс] 0,616161 \ точки [/ латекс] — повторяющееся десятичное число, поэтому оно рационально и положительно. Он находится справа от 0.
- [латекс] 0,13 [/ латекс] является конечным десятичным числом и может быть записано как 13/100. Так что это рационально и позитивно.
- [латекс] \ sqrt {73} [/ латекс]
- [латекс] -11.411411411 \ точки [/ латекс]
- [латекс] \ dfrac {47} {19} [/ латекс]
- [латекс] — \ dfrac {\ sqrt {5}} {2} [/ латекс]
- [латекс] 6.210735 [/ латекс]
- положительный, иррациональный; правый
- отрицательный, рациональный; левый
- положительный, рациональный; правый
- негативный, иррациональный; левый
- положительный, рациональный; правый
- [латекс] \ sqrt {36} [/ латекс]
- [латекс] \ dfrac {8} {3} [/ латекс]
- [латекс] \ sqrt {73} [/ латекс]
- [латекс] -6 [/ латекс]
- [латекс] 3,2121121112 \ точки [/ латекс]
- [латекс] — \ dfrac {35} {7} [/ латекс]
- [латекс] 0 [/ латекс]
- [латекс] \ sqrt {169} [/ латекс]
- [латекс] \ sqrt {24} [/ латекс]
- [латекс] 4,763763763 \ точки [/ латекс]
- [латекс] 3 \ cdot 6 + 3 \ cdot 4 [/ латекс]
- [латекс] \ влево (5 + 8 \ вправо) + \ влево (-8 \ вправо) [/ латекс]
- [латекс] 6- \ левый (15 + 9 \ правый) [/ латекс]
- [латекс] \ dfrac {4} {7} \ cdot \ left (\ frac {2} {3} \ cdot \ dfrac {7} {4} \ right) [/ latex]
- [латекс] 100 \ cdot \ left [0,75+ \ left (-2,38 \ right) \ right] [/ латекс]
- [латекс] \ left (- \ dfrac {23} {5} \ right) \ cdot \ left [11 \ cdot \ left (- \ dfrac {5} {23} \ right) \ right] [/ латекс]
- [латекс] 5 \ cdot \ left (6.2 + 0,4 \ правый) [/ латекс]
- [латекс] 18- \ левый (7-15 \ правый) [/ латекс]
- [латекс] \ dfrac {17} {18} + \ cdot \ left [\ dfrac {4} {9} + \ left (- \ dfrac {17} {18} \ right) \ right] [/ latex]
- [латекс] 6 \ cdot \ left (-3 \ right) +6 \ cdot 3 [/ латекс]
- 11, коммутативное свойство умножения, ассоциативное свойство умножения, обратное свойство умножения, тождественное свойство умножения;
- 33, распределительное имущество;
- 26, распределительное имущество;
- [latex] \ dfrac {4} {9} [/ latex], коммутативное свойство сложения, ассоциативное свойство сложения, обратное свойство сложения, тождественное свойство сложения;
- 0, свойство распределения, свойство, обратное сложению, свойство идентичности добавления
- [латекс] x = 0 [/ латекс]
- [латекс] x = 1 [/ латекс]
- [латекс] x = \ dfrac {1} {2} [/ латекс]
- [латекс] x = -4 [/ латекс]
- Заменить 0 на [латекс] x [/ латекс].
[латекс] \ begin {align} 2x-7 & = 2 \ left (0 \ right) -7 \\ & = 0-7 \\ & = -7 \ end {align} [/ latex]
- Заменить 1 на [латекс] x [/ латекс].
[латекс] \ begin {align} 2x-7 & = 2 \ left (1 \ right) -7 \\ & = 2-7 \\ & = -5 \ end {align} [/ latex]
- Замените [латекс] \ dfrac {1} {2} [/ latex] на [latex] x [/ latex].
[латекс] \ begin {align} 2x-7 & = 2 \ left (\ frac {1} {2} \ right) -7 \\ & = 1-7 \\ & = -6 \ end {align} [ / латекс]
- Заменить [латекс] -4 [/ латекс] на [латекс] х [/ латекс].
[латекс] \ begin {align} 2x-7 & = 2 \ left (-4 \ right) -7 \\ & = -8-7 \\ & = -15 \ end {align} [/ latex]
\ begin {align *} 4 \ frac {5} {6} & = 4 + 5 \ left (\ frac {1} {6} \ right) \\ & = 4+ 5 (\ text {0,1666666 …}) \\ & = 4 + \ текст {0,833333 …} \\ & = \ текст {4,8} \ точка {3} \ end {выровнять *}
\ begin {align *} 2 \ frac {1} {9} & = 2 + \ text {0,1111111 …} \\ & = \ текст {2,} \ точка {1} \ end {выровнять *}
\ begin {align *} х & = \ текст {0,55555…} \ text {и} \\ 10x & = \ text {5,55555 …} \\ 10x — x & = (\ text {5,55555 …}) — (\ text {0,55555 …}) \\ \ text {9} x & = \ text {5} \\ \ поэтому x & = \ frac {5} {9} \ end {выровнять *}
\ begin {align *} 10x & = \ text {6,3333 …} \ text {и} \\ 100x & = \ текст {63,3333 …} \\ 100x — 10x & = (\ text {63,3333 …}) — (\ text {6,3333 …}) \\ \ text {99} x & = \ text {57} \\ \ поэтому x & = \ frac {57} {90} \ end {выровнять *}
\ (\ текст {0,} \ точка {4} \)
\ begin {align *} х & = \ текст {0,4444…} \ text {и} \\ \ text {10} x & = \ text {4,4444 …} \\ 10x — x & = (\ text {4,4444 …}) — (\ text {0,4444 …}) \\ \ text {9} x & = \ text {4} \\ \ поэтому x & = \ frac {\ text {4}} {\ text {9}} \ end {выровнять *}
\ (\ text {5,} \ overline {31} \)
\ begin {align *} х & = \ текст {5,313131 …} \ текст {и} \\ 100x & = \ text {531,313131 …} \\ 100x — x & = (\ text {531,313131…}) — (\ text {5,313131 …}) \\ \ text {99} x & = \ text {526} \\ \ поэтому x & = \ frac {526} {99} \ end {выровнять *}
\ (\ text {4,} \ overline {\ text {93}} \)
\ begin {align *} х & = \ текст {4,939393 …} \ текст {и} \\ 100x & = \ text {493,939393 …} \\ 100x — x & = (\ text {493,939393 …}) — (\ text {4,939393 …}) \\ \ text {99} x & = \ text {489} \\ \ поэтому x & = \ frac {\ text {163}} {\ text {33}} \ end {выровнять *}
\ (\ text {3,} \ overline {\ text {93}} \)
\ begin {align *} х & = \ текст {3,939393…} \ text {и} \\ 100x & = \ text {393,939393 …} \\ 100x — x & = (\ text {393,939393 …}) — (\ text {3,939393 …}) \\ \ text {99} x & = \ text {390} \\ \ поэтому x & = \ frac {\ text {130}} {\ text {33}} \ end {выровнять *}
Что такое рациональные числа? Как преобразовать повторяющуюся десятичную дробь в дробь?
Вы здесь: На главную → Статьи → Рациональные числаРациональные числа — это целых, дробных и десятичных чисел — чисел, которые мы используем в нашей повседневной жизни.Их можно записать как отношения двух целых чисел. Рациональные числа противопоставляются иррациональным числам — числам, таким как Pi, √2, √7, другим корням, синусам, косинусам и логарифмам чисел. В этой статье основное внимание уделяется рациональным числам.
В определении говорится, что число является рациональным, если вы можете записать его в форме a / b , где a и b — целые числа, а b не равно нулю . Очевидно, что все дроби имеют такую форму, поэтому дроби являются рациональными числами.Завершающие десятичные числа также могут быть легко записаны в такой форме: например, 0,67 = 67/100, 3,40938 = 340938/100000 и т. Д.
Мы можем проиллюстрировать положительные рациональные числа в координатной плоскости с помощью прямых , проходящих через начало координат, и другой точки с целочисленными координатами. Например:
Линия y = 5 x проходит через точку (1, 5). | Линия y = (1/3) x проходит через точку (3, 1). | Линия y = (9/2) x проходит через точку (2, 9). |
И так далее. Кроме того, точки, которые я перечислил, являются ПЕРВЫМИ точками с целочисленными координатами, через которые проходят эти линии (после начала координат).
| Потренируйтесь немного: Какую первую точку с целочисленными координатами проходят эти линии? a) y = 9x b) y = 243x c) y = 5 / 6x d) y = 8/3 x e) y = 345/1039 x |
Теперь вы можете представить линию, проходящую через начало координат, которая НЕ касается ЛЮБОЙ из этих точек с координатами целых чисел ????? Это сложно, но такие строки существуют.Они просто не касаются ни одной из точек с целочисленными координатами, а их наклон — это иррациональное число !!! Трудно понять. Конечно, когда вы рисуете линии на бумаге или на компьютере, ваша точность ограничена, и даже линия y = Pi * x, вероятно, пройдет через точку с целочисленными координатами, а именно точку (7,22). Это действительно не пошло бы через это, если бы мы могли рисовать очень точно, это было бы просто близко. Но поскольку он приближается, 22/7 — хорошее приближение к Пи.
Линия y = Pi * x действительно выглядит так, как будто она проходит через точку (7,22), поскольку графическая программа не может рисовать достаточно точно.
Непрерывные повторяющиеся десятичные дроби являются рациональными
Мы говорили о том, что завершающие десятичные числа, очевидно, являются рациональными числами. Как насчет бесконечных десятичных чисел? Возможно, вы никогда не слышали о них, хотя я надеюсь, что слышали. Их тоже много. Возьмите, например, 1/9 и преобразуйте его в десятичное число с помощью алгоритма длинного деления.Что вы получаете? Как насчет 2/9? 3/9? 1/11? 2/13? 15/7? Сможете ли вы найти больше дробей, которые превращаются в непрерывные десятичные числа?
Поскольку 0,11111 … = 1/9, то десятичное число 0,11111 … является рациональным числом . Фактически, каждое бесконечное десятичное число, которое ПОВТОРЯЕТ определенный образец цифр , является рациональным числом. Например, давайте составим десятичное число 0,135135135135135 … которое никогда не заканчивается. Вы верите, что мы МОЖЕМ записать это дробью в форме a / b? Звучит так, будто это чистая догадка, но нет, есть метод, на мой взгляд, хороший и умный.Как преобразовать повторяющееся десятичное число в дробь
Давайте назовем наше число a = 0,135135135 … и умножим его на степень 10, затем вычтем исходное a и новое число, чтобы повторяющиеся десятичные части уравняли друг друга при вычитании.
| a | = | 0. | 135135135 … |
| 10 a | = | 1. | 35135135135 … |
| 100 a | = | 13. | 5135135135 … |
| 1000 a | =4 | 135 … |
Хорошо, с 1000 и будут работать, десятичные дроби выровняются! Итак, теперь мы вычитаем 1000 и :
| 1000 | = | 135. | 135135135 … | |
| — и | = | 0. | 135135135 … | |
| 9993 | 904 904 904 904 904 904 904 904, | |||
, из которых a = 135/999.
Другой пример записи повторяющейся десятичной дроби в виде дроби
Иногда первая пара десятичных цифр не является частью повторяющегося шаблона.Например, b = 5,65787878787 … такое число. Однако работает тот же трюк: мы умножаем b на такую степень десяти, что повторяющиеся части уравновешивают друг друга при вычитании.
| b | = | 5. | 65787878787 … | 10 b | = | 56. | 578787878 … |
| 100 b | = | 565. | 7878787 … |
Как видите, десятичные части b и 100 b идентичны! Итак, мы можем вычесть их:
| 100 b | = | 565. | 78787878 … | |||
| — b | = | — 5. | 6578787316 | 99 b= | 560. | 13 |
, откуда b = 560.13/99 = 56013/9900.
| Потренируйтесь немного: Можете ли вы преобразовать эти десятичные дроби в дроби, используя ту же идею? а) 0,186186186186 … б) 4,1515151515 … в) 0,139999999 …. г) 4,50398989898 … д) 0,30458304583045830458 …. |
Иррациональные числа
Мы обсуждали завершение десятичных чисел и повторение десятичных чисел.Угадай, что? НЕПОВТОРИМЫЕ и НЕЗАКОНЧИВАЮЩИЕСЯ десятичные числа — это ИРРАЦИОННЫЕ ЧИСЛА .
См. Также:
Рациональные числа исчисляемы
О рациональных числах
Вы можете объяснить мне «рациональные числа»? Как вы их выражаете?
Преобразование повторяющихся десятичных знаков в дроби
Я знаю .333333333333 — это 1/3, но в чем тут фокус?
Рациональные и иррациональные числа — Предалгебра
Цели обучения
К концу этого раздела вы сможете:
Определите рациональные числа и иррациональные числа
Поздравляем! Вы прочитали первые шесть глав этой книги! Пришло время подвести итоги того, что вы уже сделали в этом курсе, и подумать о том, что вас ждет впереди.Вы научились складывать, вычитать, умножать и делить целые числа, дроби, целые числа и десятичные дроби. Вы познакомились с языком и символами алгебры, а также упростили и оценили алгебраические выражения. Вы решили много разных типов приложений. Вы заложили хорошую прочную основу, необходимую для достижения успеха в алгебре.
В этой главе мы позаботимся о том, чтобы ваши навыки твердо закрепились. Мы еще раз взглянем на типы чисел, с которыми работали во всех предыдущих главах.Мы будем работать со свойствами чисел, которые помогут вам улучшить ваше чувство числа. И мы будем практиковаться в их использовании, как при решении уравнений и выполнении других процедур в алгебре.
Мы уже описали числа как счетные числа, целые числа и целые числа. Вы помните, в чем разница между этими типами чисел?
| счетные числа | |
| целые числа | |
| целые числа |
Рациональные числа
Какой тип чисел вы получите, если начнете со всех целых чисел, а затем включите все дроби? Числа, которые у вас получились бы, составили набор рациональных чисел.Рациональное число — это число, которое можно записать как отношение двух целых чисел.
Рациональные числа
Рациональное число — это число, которое можно записать в виде где и являются целыми числами, а
Все дроби, как положительные, так и отрицательные, являются рациональными числами. Несколько примеров:
Каждый числитель и каждый знаменатель — целое число.
Нам нужно посмотреть на все числа, которые мы использовали до сих пор, и убедиться, что они рациональны. Определение рациональных чисел говорит нам, что все дроби рациональны.Теперь мы посмотрим на счетные числа, целые числа, целые числа и десятичные дроби, чтобы убедиться, что они рациональны.
Целые числа — рациональные числа? Чтобы решить, является ли целое число рациональным числом, мы пытаемся записать его как отношение двух целых чисел. Легкий способ сделать это — записать дробь со знаминателем один.
Поскольку любое целое число можно записать как отношение двух целых чисел, все целые числа являются рациональными числами. Помните, что все счетные числа и все целые числа также являются целыми числами, а значит, они тоже рациональны.
А как насчет десятичных знаков? Они рациональны? Давайте посмотрим на несколько, чтобы увидеть, можем ли мы записать каждое из них как отношение двух целых чисел. Мы уже видели, что целые числа — это рациональные числа. Целое число может быть записано как десятичное. Итак, очевидно, что некоторые десятичные дроби рациональны.
Подумайте о десятичном. Можем ли мы записать его как отношение двух целых чисел? Потому что означает, что мы можем записать это как неправильную дробь, Так — это отношение целых чисел, а это рациональное число.
Обычно любое десятичное число, которое заканчивается рядом цифр (например, или является рациональным числом.Мы можем использовать разряд последней цифры в качестве знаменателя при записи десятичной дроби в виде дроби.
Запишите каждое как отношение двух целых чисел:
ⓐⓑⓒ.Запишите каждое как отношение двух целых чисел:
ⓐⓑ.Запишите каждое как отношение двух целых чисел:
ⓐⓑ.Давайте посмотрим на десятичную форму рациональных чисел. Мы видели, что каждое целое число является рациональным числом, поскольку для любого целого числа мы также можем преобразовать любое целое число в десятичное, добавив десятичную точку и ноль.
Мы также видели, что каждая дробь является рациональным числом. Посмотрите на десятичную форму только что рассмотренных дробей.
Что вам говорят эти примеры? Каждое рациональное число можно записать как в виде отношения целых чисел, так и в виде десятичной дроби, которая либо останавливается, либо повторяется. В таблице ниже показаны числа, которые мы рассматривали, выраженные как отношение целых чисел и десятичной дроби.
Иррациональные числа
Есть ли десятичные дроби, которые не останавливаются и не повторяются? да.Число (греческая буква пи, произносится как «пирог»), которое очень важно при описании кругов, имеет десятичную форму, которая не останавливается и не повторяется.
Точно так же десятичные представления квадратных корней чисел, не являющихся точными квадратами, никогда не прекращаются и никогда не повторяются. Например,
Десятичная дробь, которая не останавливается и не повторяется, не может быть записана как отношение целых чисел. Мы называем такое число иррациональным числом.
Иррациональное число
Иррациональное число — это число, которое нельзя записать как отношение двух целых чисел.Его десятичная форма не останавливается и не повторяется.
Давайте резюмируем метод, который мы можем использовать, чтобы определить, является ли число рациональным или иррациональным.
Если десятичная форма числа
Определите каждое из следующего как рациональное или иррациональное:
ⓐ
ⓑ
ⓒ
Определите каждое из следующего как рациональное или иррациональное:
ⓐⓑⓒ
Определите каждое из следующего как рациональное или иррациональное:
ⓐⓑⓒ
Давайте теперь подумаем о квадратных корнях.Квадратные корни из полных квадратов всегда целые числа, поэтому они рациональны. Но десятичные формы квадратных корней чисел, которые не являются точными квадратами, никогда не прекращаются и никогда не повторяются, поэтому эти квадратные корни иррациональны.
Определите каждое из следующего как рациональное или иррациональное:
ⓐ
ⓑ
Определите каждое из следующего как рациональное или иррациональное:
ⓐ
ⓑ
Определите каждое из следующего как рациональное или иррациональное:
ⓐ
ⓑ
Классифицируйте действительные числа
Мы видели, что все счетные числа являются целыми числами, все целые числа являются целыми числами и все целые числа являются рациональными числами.Иррациональные числа — отдельная категория. Когда мы соединяем рациональные числа и иррациональные числа, мы получаем набор действительных чисел.
(рисунок) показывает, как связаны наборы чисел.
Эта диаграмма иллюстрирует отношения между различными типами действительных чисел.
Вещественные числа
Вещественные числа — это числа, которые могут быть рациональными или иррациональными.
Вам не кажется странным термин «действительные числа»? Существуют ли какие-либо числа, которые не являются «настоящими», и если да, то какими они могут быть? На протяжении веков люди знали только цифры, которые мы сейчас называем настоящими числами.Затем математики открыли набор из мнимых чисел. В этом курсе вы не встретите мнимые числа, но вы встретитесь позже при изучении алгебры.
Определите, является ли каждое из чисел в следующем списке ⓐ целым числом, ⓑ целым числом, рациональным числом, ⓓ иррациональным числом и действительным числом.
Сведем результаты в таблицу.
Определите, является ли каждое число ⓐ целым числом, ⓑ целым числом, рациональным числом, ⓓ иррациональным числом и действительным числом:
Определите, является ли каждое число ⓐ целым числом, ⓑ целым числом, рациональным числом, ⓓ иррациональным числом и действительным числом:
Практика ведет к совершенству
Рациональные числа
В следующих упражнениях запишите как отношение двух целых чисел.
В следующих упражнениях определите, какие из приведенных чисел рациональны, а какие иррациональны.
Рациональный:. Иррациональный:
Рациональный:,. Иррациональный:
,
В следующих упражнениях определите, является ли каждое число рациональным или иррациональным.
Классификация вещественных чисел
В следующих упражнениях определите, является ли каждое число целым, целым, рациональным, иррациональным и действительным.
Повседневная математика
Экскурсия Все ученики начальной школы Линкольна отправятся на экскурсию в музей науки. Считая всех детей, учителей и сопровождающих, найдутся люди. Каждый автобус вмещает людей.
ⓐ Сколько потребуется автобусов?
ⓑ Почему ответ должен быть целым числом?
ⓒ Почему бы вам не округлить ответ обычным способом?
Присмотр за детьми Серена хочет открыть лицензированный детский сад.Ее состояние требует, чтобы на каждого учителя приходилось не более детей. Она хотела бы, чтобы ее детский сад обслуживал детей.
ⓐ Сколько потребуется учителей?
ⓑ Почему ответ должен быть целым числом?
ⓒ Почему бы вам не округлить ответ обычным способом?
Письменные упражнения
Объясните своими словами разницу между рациональным числом и иррациональным числом.
Объясните, как наборы чисел (счетные, целые, целые, рациональные, иррациональные, действительные) связаны друг с другом.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Если большая часть ваших чеков была:
… уверенно. Поздравляю! Вы достигли целей в этом разделе. Поразмышляйте над своими учебными навыками, чтобы вы могли продолжать их использовать.Что вы сделали, чтобы убедиться в своей способности делать эти вещи? Быть конкретной.
… с некоторой помощью. Эту проблему нужно решать быстро, потому что темы, которые вы не освоили, становятся ухабами на вашем пути к успеху. В математике каждая тема основывается на предыдущей работе. Прежде чем двигаться дальше, важно убедиться, что у вас есть прочный фундамент. К кому обратиться за помощью? Ваши одноклассники и инструктор — хорошие ресурсы. Есть ли в кампусе место, где доступны репетиторы по математике? Можно ли улучшить свои учебные навыки?
… нет, я не понимаю! Это предупреждающий знак, игнорировать его нельзя.Вам следует немедленно обратиться за помощью, иначе вы быстро не справитесь. Как можно скорее обратитесь к своему инструктору, чтобы обсудить вашу ситуацию. Вместе вы сможете составить план оказания вам необходимой помощи.
вещественных чисел | Колледж алгебры
Результаты обучения
Из-за эволюции системы счисления теперь мы можем выполнять сложные вычисления, используя несколько категорий действительных чисел. В этом разделе мы исследуем наборы чисел, выполним вычисления с различными типами чисел и начнем узнавать об использовании чисел в алгебраических выражениях.
Классифицируйте реальное число
Числа, которые мы используем для подсчета или перечисления элементов, — это натуральные числа : 1, 2, 3, 4, 5 и так далее. Мы описываем их в обозначениях множества как {1, 2, 3,…}, где многоточие (…) указывает, что числа продолжаются до бесконечности.Натуральные числа, конечно же, также называются счетными числами . Каждый раз, когда мы перечисляем членов команды, считаем монеты в коллекции или подсчитываем деревья в роще, мы используем набор натуральных чисел. Набор целых чисел — это набор натуральных чисел плюс ноль: {0, 1, 2, 3,…}.
Набор целых чисел добавляет противоположности натуральных чисел к набору целых чисел: {…, -3, -2, -1, 0, 1, 2, 3,…}. Полезно отметить, что набор целых чисел состоит из трех различных подмножеств: отрицательных целых чисел, нуля и положительных целых чисел.В этом смысле положительные целые числа — это просто натуральные числа. Другой способ думать об этом — это то, что натуральные числа являются подмножеством целых чисел.
[латекс] \ begin {align} & {\ text {отрицательные целые числа}} && {\ text {zero}} && {\ text {положительные целые числа}} \\ & {\ dots, -3, -2, -1 ,} && {0,} && {1,2,3, \ dots} \\ \ text {} \ end {align} [/ latex]
Набор рациональных чисел записывается как [latex] \ left \ {\ frac {m} {n} | m \ text {и} {n} \ text {являются целыми числами и} {n} \ ne {0 } \ right \} [/ латекс].Обратите внимание на определение, что рациональные числа — это дроби (или частные), содержащие целые числа как в числителе, так и в знаменателе, а знаменатель никогда не равен 0. Мы также можем видеть, что каждое натуральное число, целое число и целое число является рациональным числом с знаменатель 1.
Поскольку это дроби, любое рациональное число также может быть выражено в десятичной форме. Любое рациональное число может быть представлено как:
Мы используем линию, проведенную над повторяющимся блоком чисел, вместо того, чтобы писать группу несколько раз.
Пример: запись целых чисел в виде рациональных чисел
Запишите каждое из следующих чисел в виде рациональных чисел.
Запишите дробь с целым числом в числителе и единицей в знаменателе.
Попробуйте
Запишите каждое из следующих чисел в виде рациональных чисел.
Пример: определение рациональных чисел
Запишите каждое из следующих рациональных чисел как завершающее или повторяющееся десятичное число.
Запишите каждую дробь в виде десятичной дроби, разделив числитель на знаменатель.
Иррациональные числа
В какой-то момент в древнем прошлом кто-то обнаружил, что не все числа являются рациональными числами.Строитель, например, мог обнаружить, что диагональ квадрата с единичными сторонами не равна 2 и даже не [латекс] \ frac {3} {2} [/ latex], а что-то другое. Или производитель одежды мог заметить, что отношение длины окружности к диаметру рулона ткани было немного больше 3, но все же не рациональное число. Такие числа называются иррациональными , потому что они не могут быть записаны в виде дробей. Эти числа составляют набор из иррациональных чисел . Иррациональные числа нельзя выразить дробью двух целых чисел.Невозможно описать этот набор чисел одним правилом, кроме как сказать, что число иррационально, если оно нерационально. Итак, мы пишем это, как показано.
{ч | h не рациональное число}
Пример: различение рациональных и иррациональных чисел
Определите, является ли каждое из следующих чисел рациональным или иррациональным. Если это рационально, определите, является ли это завершающей или повторяющейся десятичной дробью.
Реальные числа
Для любого числа n мы знаем, что n либо рационально, либо иррационально. Не может быть и того, и другого. Наборы рациональных и иррациональных чисел вместе составляют набор из действительных чисел . Как мы видели с целыми числами, действительные числа можно разделить на три подмножества: отрицательные действительные числа, ноль и положительные действительные числа.Каждое подмножество включает дроби, десятичные дроби и иррациональные числа в соответствии с их алгебраическим знаком (+ или -). Ноль не считается ни положительным, ни отрицательным.
Действительные числа можно визуализировать на горизонтальной числовой строке с произвольной точкой, выбранной как 0, с отрицательными числами слева от 0 и положительными числами справа от 0. Затем используется фиксированное единичное расстояние, чтобы отметить каждое целое число ( или другое базовое значение) по обе стороны от 0. Любое действительное число соответствует уникальной позиции в числовой строке.Верно и обратное: каждое место в числовой строке соответствует ровно одному действительному числу. Это называется взаимно-однозначным соответствием. Мы называем это строкой действительного числа .
Строка вещественных чисел
Пример: классификация действительных чисел
Классифицируйте каждое число как положительное или отрицательное, а также как рациональное или иррациональное. Число находится слева или справа от 0 на числовой прямой?
Попробуйте
Классифицируйте каждое число как положительное или отрицательное, а также как рациональное или иррациональное.Число находится слева или справа от 0 на числовой прямой?
Наборы чисел как подмножества
Начиная с натуральных чисел, мы расширили каждый набор, чтобы сформировать более крупный набор, что означает, что между наборами чисел, с которыми мы столкнулись до сих пор, существует связь подмножества.Эти отношения становятся более очевидными, если рассматривать их в виде диаграммы.
Наборы цифр. N : набор натуральных чисел W : набор целых чисел I : набор целых чисел Q : набор рациональных чисел Q´ : набор иррациональных чисел
Общее примечание: наборы чисел
Набор натуральных чисел включает числа, используемые для подсчета: [латекс] \ {1,2,3, \ точки \} [/ латекс].
Набор целых чисел — это набор натуральных чисел плюс ноль: [latex] \ {0,1,2,3, \ dots \} [/ latex].
Набор целых чисел добавляет отрицательные натуральные числа к набору целых чисел: [latex] \ {\ dots, -3, -2, -1,0,1,2,3, \ dots \} [/ латекс].
Набор рациональных чисел включает дроби, записанные как [латекс] \ {\ frac {m} {n} | m \ text {и} n \ text {целые числа и} n \ ne 0 \} [/ latex] .
Набор иррациональных чисел — это набор чисел, которые не являются рациональными, неповторяющимися и неповторяющимися: [latex] \ {h | h \ text {не является рациональным числом} \} [/ latex].
Пример: дифференцирование наборов чисел
Классифицируйте каждое число как натуральное число, целое число, целое число, рациональное число и / или иррациональное число.
| натуральное число | целое число | целое число | рациональное число | иррациональное число | |
| [латекс] \ sqrt {36} = 6 [/ латекс] | да | да | да | да | № |
| [латекс] \ dfrac {8} {3} = 2.\ overline {6} [/ latex] | № | № | № | да | № |
| [латекс] \ sqrt {73} [/ латекс] | № | № | № | № | да |
| [латекс] –6 [/ латекс] | № | № | да | да | № |
| [латекс] 3,2121121112 \ точки [/ латекс] | № | № | № | № | да |
Попробуйте
Классифицируйте каждое число как натуральное число ( N ), целое число ( W ), целое число ( I ), рациональное число ( Q ) и / или иррациональное число ( Q ’).
| натуральное число | целое число | целое число | рациональное число | иррациональное число | |||||||||||||||
| [латекс] — \ dfrac {35} {7} [/ латекс] | да | да | да | да | № | ||||||||||||||
| [латекс] 0 [/ латекс] | № | да | да | да | № | ||||||||||||||
| [латекс] \ sqrt {169} [/ латекс] | да | да | да | да | № | ||||||||||||||
| [латекс] \ sqrt {24} [/ латекс] | № | № | № | № | да | ||||||||||||||
| [латекс] 4.{2} [/ latex] — математическое выражение. Чтобы вычислить математическое выражение, мы выполняем различные операции. Однако мы не выполняем их в произвольном порядке. Мы используем порядок операций . Это последовательность правил для вычисления таких выражений. Напомним, что в математике мы используем круглые скобки (), квадратные скобки [] и фигурные скобки {} для группировки чисел и выражений, так что все, что появляется в символах, рассматривается как единое целое. Кроме того, столбцы дробей, радикалов и абсолютных значений обрабатываются как символы группировки.{2} = 12 [/ латекс]. Для некоторых сложных выражений потребуется несколько проходов по порядку операций. Например, внутри круглых скобок может быть радикальное выражение, которое необходимо упростить перед вычислением скобок. Соблюдение порядка операций гарантирует, что любой, кто упрощает одно и то же математическое выражение, получит тот же результат. A Общее примечание: порядок работыОперации в математических выражениях должны оцениваться в систематическом порядке, который можно упростить, используя аббревиатуру PEMDAS : . {2} \ right] +1 [/ латекс] Показать решение1.{2} -4} {7} -3 && \ text {Упрощение радикала} \\ & = \ frac {25-4} {7} -3 && \ text {Степень упрощения} \\ & = \ frac {21} {7} -3 && \ text {Упростить вычитание в числителе} \\ & = 3-3 && \ text {Упростить деление} \\ & = 0 && \ text {Упростить вычитание} \ end {align} [/ latex] Обратите внимание, что на первом шаге радикал рассматривается как символ группировки, например круглые скобки. Кроме того, на третьем этапе полоса дроби считается символом группировки, поэтому числитель считается сгруппированным.{2}] + 1 && \ text {Упростить в круглых скобках} \\ & 7 \ left (15 \ right) -2 \ left (3-16 \ right) +1 && \ text {Упростить показатель степени} \\ & = 7 \ left (15 \ right) -2 \ left (-13 \ right) +1 && \ text {Subtract} \\ & = 105 + 26 + 1 && \ text {Умножение} \\ & = 132 && \ text {Добавить } \ end {align} [/ latex] Посмотрите следующее видео, чтобы увидеть больше примеров использования порядка операций для упрощения выражения.
Использование свойств действительных чиселДля некоторых действий, которые мы выполняем, порядок некоторых операций не имеет значения, но порядок других операций имеет значение.Например, не имеет значения, надеваем ли мы правую обувь перед левой или наоборот. Однако не имеет значения, наденем ли мы сначала туфли или носки. То же самое и с математическими операциями. Коммутативные свойстваКоммутативное свойство сложения гласит, что числа можно складывать в любом порядке, не влияя на сумму. [латекс] a + b = b + a [/ латекс] Мы можем лучше увидеть эту взаимосвязь при использовании действительных чисел. [латекс] \ left (-2 \ right) + 7 = 5 \ text {и} 7+ \ left (-2 \ right) = 5 [/ latex] Точно так же коммутативное свойство умножения гласит, что числа можно умножать в любом порядке, не влияя на произведение. [латекс] a \ cdot b = b \ cdot a [/ латекс] Снова рассмотрим пример с действительными числами. [латекс] \ left (-11 \ right) \ cdot \ left (-4 \ right) = 44 \ text {и} \ left (-4 \ right) \ cdot \ left (-11 \ right) = 44 [ / латекс] Важно отметить, что ни вычитание, ни деление не коммутативны.Например, [латекс] 17-5 [/ латекс] не то же самое, что [латекс] 5-17 [/ латекс]. Аналогично [латекс] 20 \ div 5 \ ne 5 \ div 20 [/ латекс]. Ассоциативные свойстваАссоциативное свойство умножения говорит нам, что не имеет значения, как мы группируем числа при умножении. Мы можем перемещать символы группировки, чтобы упростить расчет, при этом продукт остается прежним. [латекс] a \ left (bc \ right) = \ left (ab \ right) c [/ латекс] Рассмотрим этот пример. [латекс] \ left (3 \ cdot4 \ right) \ cdot5 = 60 \ text {и} 3 \ cdot \ left (4 \ cdot5 \ right) = 60 [/ латекс] Ассоциативное свойство сложения говорит нам, что числа могут быть сгруппированы по-разному, не влияя на сумму. [латекс] a + \ left (b + c \ right) = \ left (a + b \ right) + c [/ латекс] Это свойство может быть особенно полезно при работе с отрицательными целыми числами. Рассмотрим этот пример. [латекс] [15+ \ left (-9 \ right)] + 23 = 29 \ text {и} 15 + [\ left (-9 \ right) +23] = 29 [/ латекс] Ассоциативны ли вычитание и деление? Просмотрите эти примеры. [латекс] \ begin {align} 8- \ left (3-15 \ right) & \ stackrel {?} {=} \ Left (8-3 \ right) -15 \\ 8- \ left (-12 \ справа) & \ stackrel {?} = 5-15 \\ 20 & \ neq 20-10 \\ \ text {} \ end {align} [/ latex] [латекс] \ begin {align} 64 \ div \ left (8 \ div4 \ right) & \ stackrel {?} {=} \ Left (64 \ div8 \ right) \ div4 \\ 64 \ div2 & \ stackrel { ?} {=} 8 \ div4 \\ 32 & \ neq 2 \\ \ text {} \ end {align} [/ latex] Как видим, ни вычитание, ни деление не ассоциативны. Распределительная собственностьРаспределительное свойство утверждает, что произведение множителя на сумму является суммой множителя, умноженного на каждый член в сумме. [латекс] a \ cdot \ left (b + c \ right) = a \ cdot b + a \ cdot c [/ латекс] Это свойство сочетает в себе как сложение, так и умножение (и это единственное свойство). Рассмотрим пример. Обратите внимание, что 4 находится за пределами символов группировки, поэтому мы распределяем 4, умножая его на 12, умножая на –7 и складывая произведения. Чтобы быть более точным, описывая это свойство, мы говорим, что умножение распределяется по сложению. Обратное неверно, как мы видим в этом примере. [латекс] \ begin {align} 6+ \ left (3 \ cdot 5 \ right) и \ stackrel {?} {=} \ Left (6 + 3 \ right) \ cdot \ left (6 + 5 \ right) \\ 6+ \ left (15 \ right) & \ stackrel {?} {=} \ Left (9 \ right) \ cdot \ left (11 \ right) \\ 21 & \ ne 99 \ end {align} [/ latex ] Умножение не распределяет по вычитанию, а деление не распределяет ни по сложению, ни по вычитанию. Особый случай свойства распределения возникает при вычитании суммы членов. [латекс] a-b = a + \ left (-b \ right) [/ латекс] Например, рассмотрим разницу [латекс] 12- \ влево (5 + 3 \ вправо) [/ латекс].Мы можем переписать разницу между двумя терминами 12 и [латекс] \ left (5 + 3 \ right) [/ latex], превратив выражение вычитания в сложение противоположного. Поэтому вместо вычитания [латекс] \ влево (5 + 3 \ вправо) [/ латекс] мы добавляем противоположное. [латекс] 12+ \ влево (-1 \ вправо) \ cdot \ left (5 + 3 \ вправо) [/ латекс] Теперь распределите [latex] -1 [/ latex] и упростите результат. [латекс] \ begin {align} 12+ \ left (-1 \ right) \ cdot \ left (5 + 3 \ right) & = 12 + [\ left (-1 \ right) \ cdot5 + \ left (-1 \ right) \ cdot3] \\ & = 12 + (- 5-3) \\ & = 12+ \ left (-8 \ right) \\ & = 4 \ end {align} [/ latex] Это кажется большой проблемой для простой суммы, но это иллюстрирует мощный результат, который будет полезен, когда мы введем алгебраические термины.Чтобы вычесть сумму членов, измените знак каждого члена и сложите результаты. Имея это в виду, мы можем переписать последний пример. [латекс] \ begin {align} 12- \ left (5 + 3 \ right) & = 12 + \ left (-5-3 \ right) \\ & = 12 + \ left (-8 \ right) \\ & = 4 \ end {align} [/ latex] Свойства идентичностиСвойство идентификатора дополнения утверждает, что существует уникальный номер, называемый аддитивным идентификатором (0), который при добавлении к номеру дает исходный номер. [латекс] a + 0 = a [/ латекс] Свойство идентичности умножения утверждает, что существует уникальный номер, называемый мультипликативным идентификатором (1), который при умножении на число дает исходное число. [латекс] a \ cdot 1 = a [/ латекс] Например, у нас есть [латекс] \ left (-6 \ right) + 0 = -6 [/ latex] и [latex] 23 \ cdot 1 = 23 [/ latex]. Для этих свойств нет исключений; они работают для всех действительных чисел, включая 0 и 1. Обратные свойстваСвойство , обратное сложению , утверждает, что для каждого действительного числа a существует уникальное число, называемое аддитивным обратным (или противоположным), обозначаемое — a , которое при добавлении к исходному числу дает в аддитивном тождестве 0. [латекс] a + \ left (-a \ right) = 0 [/ латекс] Например, если [latex] a = -8 [/ latex], аддитивная инверсия равна 8, поскольку [latex] \ left (-8 \ right) + 8 = 0 [/ latex]. Свойство, обратное умножению , сохраняется для всех действительных чисел, кроме 0, поскольку величина, обратная 0, не определена. Свойство заявляет, что для каждого действительного числа a существует уникальное число, называемое обратным мультипликативным (или обратным), обозначаемое [latex] \ frac {1} {a} [/ latex], которое при умножении на исходное число, приводит к мультипликативному тождеству, 1. [латекс] a \ cdot \ dfrac {1} {a} = 1 [/ латекс] Например, если [latex] a = — \ frac {2} {3} [/ latex], обратная величина, обозначенная [latex] \ frac {1} {a} [/ latex], будет [latex] — \ гидроразрыв {3} {2} [/ latex], потому что [латекс] a \ cdot \ dfrac {1} {a} = \ left (- \ dfrac {2} {3} \ right) \ cdot \ left (- \ dfrac {3} {2} \ right) = 1 [/ латекс] Общее примечание: свойства действительных чиселСледующие свойства имеют место для действительных чисел a , b и c .
Пример: использование свойств действительных чиселИспользуйте свойства действительных чисел, чтобы переписать и упростить каждое выражение.Укажите, какие свойства применимы. 1. [латекс] \ begin {align} 3 \ cdot6 + 3 \ cdot4 & = 3 \ cdot \ left (6 + 4 \ right) && \ text {Распределительное свойство} \\ & = 3 \ cdot10 && \ text {Simplify} \\ & = 30 && \ text {Simplify} \ end {align} [/ latex] 2. [латекс] \ begin {align} \ left (5 + 8 \ right) + \ left (-8 \ right) & = 5 + \ left [8+ \ left (-8 \ right) \ right] && \ text {Ассоциативное свойство сложения} \\ & = 5 + 0 && \ text {Обратное свойство сложения} \\ & = 5 && \ text {Идентификационное свойство сложения} \ end {align} [/ latex] 3. [латекс] \ begin {align} 6- \ left (15 + 9 \ right) & = 6 + (- 15-9) && \ text {Распределительное свойство} \\ & = 6 + \ left (-24 \ right ) && \ text {Simplify} \\ & = -18 && \ text {Simplify} \ end {align} [/ latex] 4. [латекс] \ begin {align} \ frac {4} {7} \ cdot \ left (\ frac {2} {3} \ cdot \ frac {7} {4} \ right) & = \ frac {4} {7} \ cdot \ left (\ frac {7} {4} \ cdot \ frac {2} {3} \ right) && \ text {Коммутативное свойство умножения} \\ & = \ left (\ frac {4} {7} \ cdot \ frac {7} {4} \ right) \ cdot \ frac {2} {3} && \ text {Ассоциативное свойство умножения} \\ & = 1 \ cdot \ frac {2} {3} && \ text {Обратное свойство умножения} \\ & = \ frac {2} {3} && \ text {Идентификационное свойство умножения} \ end {align} [/ latex] 5. [латекс] \ begin {align} 100 \ cdot [0,75+ \ left (-2,38 \ right)] & = 100 \ cdot0.75 + 100 \ cdot \ left (-2,38 \ right) && \ text {Распределительное свойство} \\ & = 75 + \ left (-238 \ right) && \ text {Simplify} \\ & = -163 && \ text {Simplify} \ end {align} [/ latex] ПопробуйтеИспользуйте свойства действительных чисел, чтобы переписать и упростить каждое выражение. Укажите, какие свойства применимы. Вычисление и упрощение алгебраических выраженийДо сих пор в математических выражениях, которые мы видели, использовались только действительные числа.{2}} [/ латекс]. В выражении [latex] x + 5,5 [/ latex] называется константой , потому что она не меняется, а x называется переменной , потому что это так. (При именовании переменной игнорируйте любые экспоненты или радикалы, содержащие переменную.) Алгебраическое выражение — это набор констант и переменных, объединенных вместе алгебраическими операциями сложения, вычитания, умножения и деления. Мы уже видели несколько реальных числовых примеров экспоненциальной записи, сокращенного метода записи продуктов того же множителя.{3} = \ left (yz \ right) \ cdot \ left (yz \ right) \ cdot \ left (yz \ right) \\ \ text {} \ end {align} [/ latex] В каждом случае показатель степени говорит нам, сколько факторов базы использовать, независимо от того, состоит ли база из констант или переменных. Любая переменная в алгебраическом выражении может принимать или иметь разные значения. Когда это происходит, значение алгебраического выражения меняется. Вычислить алгебраическое выражение означает определить значение выражения для данного значения каждой переменной в выражении.{2}} [/ латекс] | 2 | [латекс] м, н [/ латекс] |
Пример: вычисление алгебраического выражения при различных значениях
Вычислите выражение [латекс] 2x — 7 [/ latex] для каждого значения x.
Пример: вычисление алгебраических выражений
Оцените каждое выражение для заданных значений.{2}} [/ latex] для [латекса] m = 2, n = 3 [/ latex]
- Заменить [латекс] -5 [/ латекс] на [латекс] x [/ латекс].
[латекс] \ begin {align} x + 5 & = \ left (-5 \ right) +5 \\ & = 0 \ end {align} [/ latex]
- Заменитель 10 на [латекс] т [/ латекс].
[латекс] \ begin {align} \ frac {t} {2t-1} & = \ frac {\ left (10 \ right)} {2 \ left (10 \ right) -1} \\ & = \ frac {10} {20-1} \\ & = \ frac {10} {19} \ end {align} [/ latex]
- Заменитель 5 на [латекс] r [/ латекс]. {3} \\ & = \ frac {4} {3} \ pi \ left (125 \ right) \\ & = \ frac {500} {3} \ pi \ end {align} [/ latex]
- Замените 11 вместо [латекс] a [/ латекс] и –8 вместо [латекс] b [/ латекс].{2}} \\ & = \ sqrt {2 \ left (8 \ right) \ left (9 \ right)} \\ & = \ sqrt {144} \\ & = 12 \ end {align} [/ latex]
В следующем видео мы представляем больше примеров того, как вычислить выражение для заданного значения.
Формулы
Уравнение — это математическое утверждение, указывающее, что два выражения равны. Выражения могут быть числовыми или алгебраическими. Уравнение не является истинным или ложным по своей сути, а всего лишь предположением.Значения, которые делают уравнение истинным, решения находятся с использованием свойств действительных чисел и других результатов. Например, уравнение [латекс] 2x + 1 = 7 [/ latex] имеет единственное решение [latex] x = 3 [/ latex], потому что, когда мы заменяем 3 [latex] x [/ latex] в уравнении, мы получить истинное утверждение [латекс] 2 \ left (3 \ right) + 1 = 7 [/ latex].
Формула — это уравнение, выражающее связь между постоянными и переменными величинами. Очень часто уравнение является средством нахождения значения одной величины (часто одной переменной) с точки зрения другой или других величин.{2} [/ латекс].
Пример: использование формулы
Правый круговой цилиндр радиусом [латекс] r [/ латекс] и высотой [латекс] h [/ латекс] имеет площадь поверхности [латекс] S [/ латекс] (в квадратных единицах), определяемую формулой [латекс] S = 2 \ pi r \ left (r + h \ right) [/ латекс]. Найдите площадь поверхности цилиндра радиусом 6 дюймов и высотой 9 дюймов. Оставьте ответ в виде [латекс] \ pi [/ латекс].
Цилиндр круговой правый
Показать решениеВычислите выражение [латекс] 2 \ pi r \ left (r + h \ right) [/ latex] для [latex] r = 6 [/ latex] и [latex] h = 9 [/ latex].
[латекс] \ begin {align} S & = 2 \ pi r \ left (r + h \ right) \\ & = 2 \ pi \ left (6 \ right) [\ left (6 \ right) + \ left ( 9 \ right)] \\ & = 2 \ pi \ left (6 \ right) \ left (15 \ right) \\ & = 180 \ pi \ end {align} [/ latex]
Площадь поверхности [латекс] 180 квадратных дюймов [/ латекс].
Попробуйте
Рисунок 4
Фотография длиной L и шириной W размещается на мате шириной 8 сантиметров (см). Площадь матового покрытия (в квадратных сантиметрах или см 2 ) оказалась [латексной] A = \ left (L + 16 \ right) \ left (W + 16 \ right) -L \ cdot W [/ латекс].Найдите площадь матовой фотографии для фотографии длиной 32 см и шириной 24 см.
Упростите алгебраические выражения
Иногда мы можем упростить алгебраическое выражение, чтобы его было легче вычислить или использовать каким-либо другим способом. Для этого мы используем свойства действительных чисел. Мы можем использовать те же свойства в формулах, потому что они содержат алгебраические выражения.
Пример: упрощение алгебраических выражений
Упростите каждое алгебраическое выражение.
- [латекс] 3x — 2y + x — 3y — 7 [/ латекс]
- [латекс] 2р — 5 \ влево (3-р \ вправо) +4 [/ латекс]
- [латекс] \ left (4t- \ dfrac {5} {4} s \ right) — \ left (\ dfrac {2} {3} t + 2s \ right) [/ latex]
- [латекс] 2–5 мес. + 3 мин. + N [/ латекс]
- [латекс] \ begin {align} 3x-2y + x-3y-7 & = 3x + x-2y-3y-7 && \ text {Коммутативное свойство сложения} \\ & = 4x-5y-7 && \ text {Simplify} \\ \ text {} \ end {align} [/ latex]
- [латекс] \ begin {align} 2r-5 \ left (3-r \ right) +4 & = 2r-15 + 5r + 4 && \ text {Распределительное свойство} \\ & = 2r + 5r-15 + 4 && \ text {Коммутативное свойство сложения} \\ & = 7r-11 && \ text {Simplify} \\ \ text {} \ end {align} [/ latex]
- [латекс] \ begin {align} 4t- \ frac {5} {4} s — \ left (\ frac {2} {3} t + 2s \ right) & = 4t- \ frac {5} {4} s- \ frac {2} {3} t-2s && \ text {Распределительное свойство} \\ & = 4t- \ frac {2} {3} t- \ frac {5} {4} s-2s && \ text {Коммутативное свойство сложения} \\ & = \ frac {12} {3} t- \ frac {2} {3} t- \ frac {5} {4} s- \ frac {8} {4} s && \ text {Общие знаменатели} \\ & = \ frac {10} {3} t- \ frac {13} {4} s && \ text {Simplify} \\ \ text {} \ end {align} [/ latex]
- [латекс] \ begin {align} mn-5m + 3mn + n & = 2mn + 3mn-5m + n && \ text {Коммутативное свойство сложения} \\ & = 5mn-5m + n && \ text {Simplify} \ конец {align} [/ latex]
Пример: упрощение формулы
Прямоугольник длиной [латекс] L [/ латекс] и шириной [латекс] W [/ латекс] имеет периметр [латекс] P [/ латекс], задаваемый формулой [латекс] P = L + W + L + W [/ латекс].Упростите это выражение.
Показать решение[латекс] \ begin {align} & P = L + W + L + W \\ & P = L + L + W + W && \ text {Коммутативное свойство сложения} \\ & P = 2L + 2W && \ text {Упростить } \\ & P = 2 \ left (L + W \ right) && \ text {Распределительное свойство} \ end {align} [/ latex]
Попробуйте
Если сумма [латекс] P [/ латекс] депонируется на счет, на который выплачиваются простые проценты [латекс] r [/ латекс] за время [латекс] t [/ латекс], общая стоимость депозита [латекс] A [ / latex] определяется как [latex] A = P + Prt [/ latex].Упростите выражение. (Эта формула будет рассмотрена более подробно позже в курсе.)
Показать решение[латекс] A = P \ left (1 + rt \ right) [/ latex]
Ключевые концепции
- Рациональные числа могут быть записаны как дроби, завершающие или повторяющиеся десятичные дроби.
- Определите, является ли число рациональным или иррациональным, записав его в виде десятичной дроби.
- Рациональные числа и иррациональные числа составляют множество действительных чисел. Число можно разделить на натуральное, целое, целое, рациональное или иррациональное.
- Порядок операций используется для оценки выражений.
- Действительные числа при операциях сложения и умножения подчиняются основным правилам, известным как свойства действительных чисел. Это коммутативные свойства, ассоциативные свойства, распределительное свойство, свойства идентичности и обратные свойства.
- Алгебраические выражения состоят из констант и переменных, которые объединяются с помощью сложения, вычитания, умножения и деления.Они принимают числовое значение при оценке путем замены переменных константами.
- Формулы — это уравнения, в которых одна величина представлена через другие величины. Их можно упростить или оценить как любое математическое выражение.
Глоссарий
алгебраическое выражение константы и переменные, объединенные с помощью сложения, вычитания, умножения и деления
ассоциативное свойство сложения сумма трех чисел может быть сгруппирована по-разному, не влияя на результат; в символах, [латекс] a + \ left (b + c \ right) = \ left (a + b \ right) + c [/ latex]
ассоциативное свойство умножения произведение трех чисел может быть сгруппировано по-разному, не влияя на результат; в символах, [латекс] a \ cdot \ left (b \ cdot c \ right) = \ left (a \ cdot b \ right) \ cdot c [/ latex]
основание в экспоненциальной записи, выражение, которое умножается
свойство коммутативности сложения два числа могут быть добавлены в любом порядке, не влияя на результат; в символах, [латекс] a + b = b + a [/ latex]
свойство коммутативности умножения два числа можно перемножать в любом порядке, не влияя на результат; в символах, [латекс] a \ cdot b = b \ cdot a [/ latex]
константа величина, не меняющая значения
распределительное свойство произведение множителя на сумму является суммой множителя, умноженного на каждый член в сумме; в символах, [латекс] a \ cdot \ left (b + c \ right) = a \ cdot b + a \ cdot c [/ latex]
уравнение математическое утверждение, указывающее, что два выражения равны
показатель степени в экспоненциальном представлении, увеличенное число или переменная, указывающая, сколько раз умножается основание
экспоненциальная запись сокращенный метод записи произведений того же множителя
формула уравнение, выражающее связь между постоянными и переменными величинами
свойство идентичности добавления существует уникальный номер, называемый аддитивным идентификатором, 0, который при добавлении к номеру дает исходный номер; в символах, [латекс] a + 0 = a [/ latex]
свойство идентичности умножения существует уникальный номер, называемый мультипликативным идентификатором, 1, который при умножении на число дает исходное число; в символах, [латекс] a \ cdot 1 = a [/ latex]
целых чисел набор, состоящий из натуральных чисел, их противоположностей и 0: [latex] \ {\ dots, -3, -2, -1,0,1,2,3, \ dots \} [/ latex ]
свойство обратного сложения для каждого действительного числа [латекс] a [/ latex] существует уникальный номер, называемый аддитивным обратным (или противоположным), обозначаемый [latex] -a [/ latex], который при добавлении к исходному номеру, приводит к аддитивной идентичности, 0; в символах, [латекс] a + \ left (-a \ right) = 0 [/ latex]
свойство обратного умножения для каждого ненулевого действительного числа [latex] a [/ latex] существует уникальное число, называемое мультипликативным обратным (или обратным), обозначаемое [latex] \ dfrac {1} {a} [/ latex], которое при умножении на исходное число дает мультипликативную идентичность, 1; в символах [латекс] a \ cdot \ dfrac {1} {a} = 1 [/ latex]
иррациональных чисел совокупность всех нерациональных чисел; они не могут быть записаны как завершающие или повторяющиеся десятичные дроби; они не могут быть выражены дробью двух целых чисел
натуральные числа набор счетных чисел: [латекс] \ {1,2,3, \ точки \} [/ латекс]
порядок операций набор правил, определяющих, как математические выражения должны оцениваться, назначая приоритеты операциям
рациональные числа набор всех чисел вида [латекс] \ dfrac {m} {n} [/ latex], где [latex] m [/ latex] и [latex] n [/ latex] — целые числа и [латекс] n \ ne 0 [/ латекс].Любое рациональное число может быть записано в виде дроби, завершающей или повторяющейся десятичной дроби.
линия вещественных чисел горизонтальная линия, используемая для представления действительных чисел. Для представления 0 выбирается произвольная фиксированная точка; положительные числа лежат справа от 0, а отрицательные числа слева.
вещественных чисел совокупность рациональных и иррациональных чисел
переменная величина, которая может изменять значение
целые числа набор, состоящий из 0 и натуральных чисел: [latex] \ {0,1,2,3, \ dots \} [/ latex]
1.5. Десятичные знаки — математика LibreTexts
Цели обучения
К концу этого раздела вы сможете:
- Круглые десятичные дроби
- Сложение и вычитание десятичных знаков
- Умножение и деление десятичных знаков
- Преобразование десятичных дробей, дробей и процентов
- Упростить выражения квадратными корнями
- Определить целые, рациональные, иррациональные и действительные числа
- Найдите дробные и десятичные знаки в числовой строке
Более подробное введение в темы, затронутые в этом разделе, можно найти в главе Элементарная алгебра Основы.
Круглые десятичные знаки
Десятичные дроби — это еще один способ записать дроби, знаменатели которых являются степенями десяти.
\ [\ begin {array} {rcll} 0.1 & = & \ dfrac {1} {10} & \ text {«одна десятая»} \\ 0.01 & = & \ dfrac {1} {100} & \ text {составляет «сотую»} \\ 0,001 & = & \ dfrac {1} {1000} & \ text {составляет «одну тысячную»} \\ 0,0001 & = & \ dfrac {1} {10,000} & \ text {равно «Одна десятитысячная»} \ end {array} \]
Как и в случае с целыми числами, каждая цифра десятичной дроби соответствует разряду, основанному на степенях десяти.На рисунке показаны названия разрядов слева и справа от десятичной точки.
Рисунок 1.Когда мы работаем с десятичными знаками, часто бывает необходимо округлить число до ближайшего требуемого разряда. Мы резюмируем шаги для округления десятичной дроби.
КРУГЛЫЙ ДЕСЯТИЛЕТ.
- Найдите указанное значение разряда и отметьте его стрелкой.
- Подчеркните цифру справа от числового значения.
- Подчеркнутая цифра больше или равна 5?
- Да: прибавить 1 к цифре в заданном разряде.
- Нет: не изменить цифру в данном разряде значение
- Перепишите число, удалив все цифры справа от цифры округления.
ПРИМЕР \ (\ PageIndex {1} \)
Округлите \ (18,379 \) до ближайшего целого числа сотых ⓑ десятых.
- Ответ
Круглый \ (18.379. \)
ⓐ с точностью до сотых
ⓑ с точностью до десятой
ⓒ до ближайшего целого числа
ПРИМЕР \ (\ PageIndex {2} \)
Круглый \ (6.582 \) с точностью до сотых ⓑ десятых ⓒ целого числа.
- Ответ
ⓐ \ (6.58 \) ⓑ \ (6.6 \) ⓒ \ (7 \)
ПРИМЕР \ (\ PageIndex {3} \)
Круглый \ (15,2175 \) до ближайших ⓐ тысячных ⓑ сотых ⓒ десятых.
- Ответ
ⓐ \ (15,218 \) ⓑ \ (15,22 \)
ⓒ \ (15,2 \)
Сложение и вычитание десятичных знаков
Чтобы добавить или вычесть десятичные дроби, мы выстраиваем десятичные точки.Выстраивая таким образом десятичные точки, мы можем складывать или вычитать соответствующие значения разряда. Затем мы складываем или вычитаем числа, как если бы они были целыми числами, а затем помещаем десятичную точку в сумму.
ДОБАВИТЬ ИЛИ ВЫЧИТАТЬ ДЕСЯТИЧНЫЕ ЧИСЛА.
- Определите знак суммы или разницы.
- Напишите числа так, чтобы десятичные точки располагались вертикально.
- При необходимости используйте нули в качестве заполнителей.
- Сложите или вычтите числа, как если бы они были целыми числами.Затем поместите десятичную точку
в ответ под десятичными точками в данных числах. - Напишите сумму или разницу соответствующим знаком.
ПРИМЕР \ (\ PageIndex {4} \)
Сложить или вычесть: ⓐ \ (- 23,5−41,38 \) ⓑ \ (14,65−20. \)
- Ответ
ⓐ
\ (\ begin {array} {ll} \ text {} & −23.5-41.38 \\ \\ \\ {\ text {Разница будет отрицательной. Чтобы вычесть, мы добавляем числа} \\ \ text {.Напишите числа так, чтобы десятичная точка была строчкой} \\ \ text {вертикально вверх.}} & {\; \; 23.5 \\ \ underline {+41.38}} \\ \\ \\ {\ text {Поместите 0 в качестве заполнителя после 5 в 23,5.} \\ \ text {Помните,} \ frac {5} {10} = \ frac {50} {100} \ text {so} 0,5 = 0,50.} & {\; \; 23.50 \\ \ underline {+41.38}} \\ \\ \\ {\ text {Сложите числа, как если бы они были целыми числами.} \\ \ text {Затем поместите десятичную точку в сумму.}} & {\ ; \; 23,50 \\ \ underline {+41,38} \\ \; \; 64.88} \\ \\ \\ \ text {Напишите результат с правильным знаком.} & 64.88−23.5−41.38 = −64.88 \ end {array} \)
ⓑ
\ (\ begin {array} {ll} \ text {} & 14.65−20 \\ \\ \\ {\ text {Разница будет отрицательной. Чтобы вычесть, мы} \\ \ text {вычтем 14,65 из 20. }} \\ \\ \\ {\ text {Напишите числа так, чтобы десятичные точки выровнялись} \\ \ text {вертикально.}} & {\; \; 20 \\ \ underline {−14.65}} \\ \ \ \\ {\ text {Помните, что 20 — это целое число, поэтому поместите десятичную точку} \\ \ text {после 0.}} \\ \\ \\ \ text {Поместите нули справа в качестве заполнителей.} & {\; \; 20.00 \\ \ underline {−14.65}} \\ \\ \\ \ text {Вычтите и поместите десятичную точку в ответ.} & {\ Begin {array} {lcccc} {} & 9 & {} & 9 & {} \\ 1 & \ cancel {10} & {} & \ cancel {10} & 10 \\ 2 & 0 &. & 0 & 0 \\ −1 & 4 &. & 6 & 5 \ end {array} \\ \ text {______________________} \\ \ begin {array} {lcccc} {\; \; \; \; \; \; \; \; \; } & 5 &. & 3 & 5 \ end {array}} \\ \\ \\ \ text {Запишите результат с правильным знаком.} & 14.65−20 = −5.35 \ end {array} \)
ПРИМЕР \ (\ PageIndex {5} \)
Сложите или вычтите: ⓐ \ (- 4.8−11.69 \) ⓑ \ (9.58−10 \).
- Ответ
ⓐ \ (- 16,49 \) ⓑ \ (- 0,42 \)
ПРИМЕР \ (\ PageIndex {6} \)
Сложите или вычтите: \ (- 5.123−18.47 \) ⓑ \ (37.42−50 \).
- Ответ
ⓐ \ (- 23,593 \) ⓑ \ (- 12,58 \)
Умножение и деление десятичных знаков
Когда мы умножаем десятичные дроби со знаком, сначала мы определяем знак произведения, а затем умножаем, как если бы оба числа были положительными.Мы умножаем числа, временно игнорируя десятичную точку, а затем подсчитываем количество десятичных знаков в множителях, и эта сумма сообщает нам количество десятичных знаков в произведении. Напоследок пишем товар соответствующим знаком.
НЕСКОЛЬКО ДЕСЯТЕЙ ЧАСТИ.
- Определите знак товара.
- Пишите в вертикальном формате, выравнивая числа справа. Умножайте числа, как если бы они были целыми числами, временно игнорируя десятичные точки.
- Поставьте десятичную точку. Количество десятичных знаков в произведении представляет собой сумму
десятичных знаков в множителях. - Напишите продукт соответствующим знаком.
Умножить: \ ((- 3.9) (4.075) \).
- Ответ
\ ((- 3,9) (4,075) \) Знаки разные. Произведение
будет отрицательным.Товар будет отрицательным. Пишите в вертикальном формате, выравнивая числа
справа.Умножить. Сложите количество десятичных знаков в
множителях (1 + 3). Разместите десятичную точку на 4 разряда справа.Знаки разные, значит, товар отрицательный. \ ((- 3,9) (4,075) = — 15,8925 \)
Умножить: \ (- 4.5 (6.107) \).
- Ответ
\ (- 27,4815 \)
ПРИМЕР \ (\ PageIndex {9} \)
Умножить: \ (- 10,79 (8,12) \).
- Ответ
\ (- 87,6148 \)
Часто, особенно в естественных науках, вы умножаете десятичные дроби на 10 (10, 100, 1000 и т. Д.).Если вы умножите несколько продуктов на бумаге, вы можете заметить закономерность, связывающую количество нулей в степени 10 с количеством десятичных разрядов. Мы перемещаем десятичную точку вправо, чтобы получить продукт.
УМНОЖИТЬ ДЕСЯТИЧНОСТЬ НА СТЕПЕНЬ ДЕСЯТИ.
- Переместите десятичную запятую вправо на то же количество разрядов, что и количество нулей
в степени 10. - При необходимости добавьте нули в конце числа.
ПРИМЕР \ (\ PageIndex {11} \)
Умножить 2.58 по ⓐ 10 ⓑ 100 ⓒ 1000.
- Ответ
25,8 258 2,580
ПРИМЕР \ (\ PageIndex {12} \)
Умножить 14,2 на ⓐ 10 ⓑ 100 ⓒ 1000.
- Ответ
ⓐ 142 ⓑ 1,420 ⓒ 14 200
Как и в случае с умножением, деление десятичных знаков со знаком очень похоже на деление целых чисел. Нам просто нужно выяснить, где нужно поставить десятичную запятую и знак частного.При делении десятичных знаков со знаком сначала определите знак частного, а затем разделите, как если бы оба числа были положительными. Наконец, запишите частное соответствующим знаком.
Пересматриваем обозначения и лексику для деления:
Мы напишем шаги, которые необходимо предпринять при делении десятичных дробей, для удобства.
РАЗДЕЛИТЬ ДЕСЯТИЧНЫЕ ЧИСЛА.
- Определите знак частного.
- Сделайте делитель целого числа, «сдвинув» десятичную запятую до упора вправо.«Переместите» десятичную точку в делимом на такое же количество разрядов, добавляя нули по мере необходимости.
- Разделить. Поместите десятичную точку в частном над десятичной точкой в делимом.
- Запишите частное с соответствующим знаком.
ПРИМЕР \ (\ PageIndex {13} \)
Деление: \ (- 25,65 ÷ (-0,06) \).
- Ответ
Помните, что вы можете «перемещать» десятичные дроби в делителе и делимом благодаря свойству эквивалентных дробей.
Знаки такие же. Частное положительное. Сделайте делитель целым числом, «сдвинув» десятичную запятую до упора вправо. «Переместите» десятичную запятую в делимое на такое же количество разрядов. Разделить.Поместите десятичную точку в частном над десятичной точкой в делимом. Запишите частное с соответствующим знаком.
ПРИМЕР \ (\ PageIndex {14} \)
Деление: \ (- 23,492 ÷ (-0,04) \).
- Ответ
\ (587,3 \)
ПРИМЕР \ (\ PageIndex {15} \)
Разделить: \ (- 4.11 ÷ (-0,12) \).
- Ответ
\ (34,25 \)
Преобразование десятичных дробей, дробей и процентов
В нашей работе часто бывает необходимо изменить форму числа. Возможно, нам придется заменить дроби на десятичные или десятичные на проценты.
Мы преобразуем десятичные дроби в дроби, определяя разряд последней (самой правой) цифры. В десятичной дроби 0,03. 3 находится в сотых долях, поэтому 100 — знаменатель дроби, эквивалентной 0.03.
\ [0,03 = \ dfrac {3} {100} \]
Шаги, которые необходимо предпринять для преобразования десятичной дроби в дробь, приведены в блоке процедуры.
ПРЕОБРАЗОВАТЬ ДЕСЯТИЧНУЮ ЧАСТЬ В ПРАВИЛЬНУЮ ФРАКЦИЮ И ДЕСЯТУЮ ЧАСТЬ В ДЕСЯТУЮ
- Чтобы преобразовать десятичную дробь в правильную дробь, определите разряд последней цифры.
- Напишите дробь.
- числитель — «числа» справа от десятичной точки Знаменатель
- — разрядное значение, соответствующее последней цифре .
- Чтобы преобразовать дробь в десятичную, разделите числитель дроби на знаменатель дроби.
ПРИМЕР \ (\ PageIndex {16} \)
Запишите: ⓐ \ (0,374 \) в виде дроби ⓑ \ (- \ frac {5} {8} \) в виде десятичной дроби.
- Ответ
ⓐ
ⓑ Поскольку черта дроби означает деление, мы начнем с записи дроби \ (\ frac {5} {8} \) как \ (8 \ sqrt {5} \). Теперь разделите.
ПРИМЕР \ (\ PageIndex {17} \)
Запишите: ⓐ \ (0,234 \) в виде дроби ⓑ \ (- \ frac {7} {8} \) в виде десятичной дроби.
- Ответ
ⓐ \ (\ frac {117} {500} \) ⓑ \ (- 0,875 \)
ПРИМЕР \ (\ PageIndex {18} \)
Запишите: ⓐ \ (0,024 \) в виде дроби ⓑ \ (- \ frac {3} {8} \) в виде десятичной дроби.
- Ответ
ⓐ \ (\ frac {3} {125} \) ⓑ \ (- 0,375 \)
процентов — это отношение, знаменатель которого равен 100. Процент означает на сотню. Мы используем символ процента,%, чтобы показать процент.Поскольку процент — это соотношение, его легко выразить дробью. Процент означает 100, поэтому знаменатель дроби равен 100. Затем мы меняем дробь на десятичную, разделив числитель на знаменатель. Сделав это много раз, вы можете увидеть узор.
Чтобы преобразовать процентное число в десятичное, мы перемещаем десятичную точку на два разряда влево.
Чтобы преобразовать десятичную дробь в процент, помните, что процент означает сотню.Если мы изменим десятичную дробь на дробь, знаменатель которой равен 100, эту дробь легко заменить на процент. После многих преобразований вы можете распознать закономерность.
Чтобы преобразовать десятичную дробь в процент, мы перемещаем десятичную запятую на два разряда вправо, а затем добавляем знак процента.
ПРЕОБРАЗОВАТЬ ПРОЦЕНТ В ДЕСЯТИЧНУЮ И ДЕСЯТИЧНУЮ ЧАСТЬ В ПРОЦЕНТ.
- Чтобы преобразовать процент в десятичное, переместите десятичную запятую на два разряда влево после удаления знака процента.
- Чтобы преобразовать десятичную дробь в процент, переместите десятичную запятую на два разряда вправо и затем добавьте знак процента.
ПРИМЕР \ (\ PageIndex {19} \)
Преобразовать каждый:
ⓐ процентов до десятичной дроби: 62%, 135% и 13,7%.
ⓑ от десятичной дроби до процентов: 0,51, 1,25 и 0,093.
- Ответ
ⓐ

Leave A Comment