Сила, действующая на проводник с током в магнитном поле. Закон Ампера
Сила, действующая на проводник с током в магнитном поле, называется силой Ампера.
Экспериментальное изучение магнитного взаимодействия показывает, что модуль силы Ампера пропорционален длине проводника с током, силе тока и зависит от ориентации проводника в магнитном поле.
Опыт показывает, что магнитное поле, вектор индукции которого направлен вдоль проводника с током, не оказывает влияния на ток. Поэтому модуль силы зависит лишь от модуля составляющей вектора магнитной индукции, перпендикулярной проводнику.
Закон Ампера заключается в следующем. Сила Ампера равна произведению магнитной индукции поля на силу тока, длину участка проводника и на синус угла между магнитной индукцией и участком проводника:
Направление
силы ампера определяется по правилу
левой руки: если левую руку расположить
так, чтобы перпендикулярная составляющая
магнитной индукции входила в ладонь, а
четыре вытянутых пальца были направлены
по направлению тока, то отогнутый на 90
большой палец покажет направление силы,
действующей на отрезок проводника.
Магнитное взаимодействие проводников с током используется в Международной системе для определения единицы сила тока –ампера.
Ампер –сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии 1 м друг от друга в вакууме, вызывал бы между этими проводниками силу магнитного взаимодействия, равную Н на каждый метр длины.
Действие магнитного поля на движущийся заряд. Сила Лоренца
Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца.
Модуль силы Лоренца равен отношению модуля силы Ампера, действующей на участок проводника, к числу заряженных частиц в этом участке проводника:
Сила
Ампера равна ,
сила тока равна (см.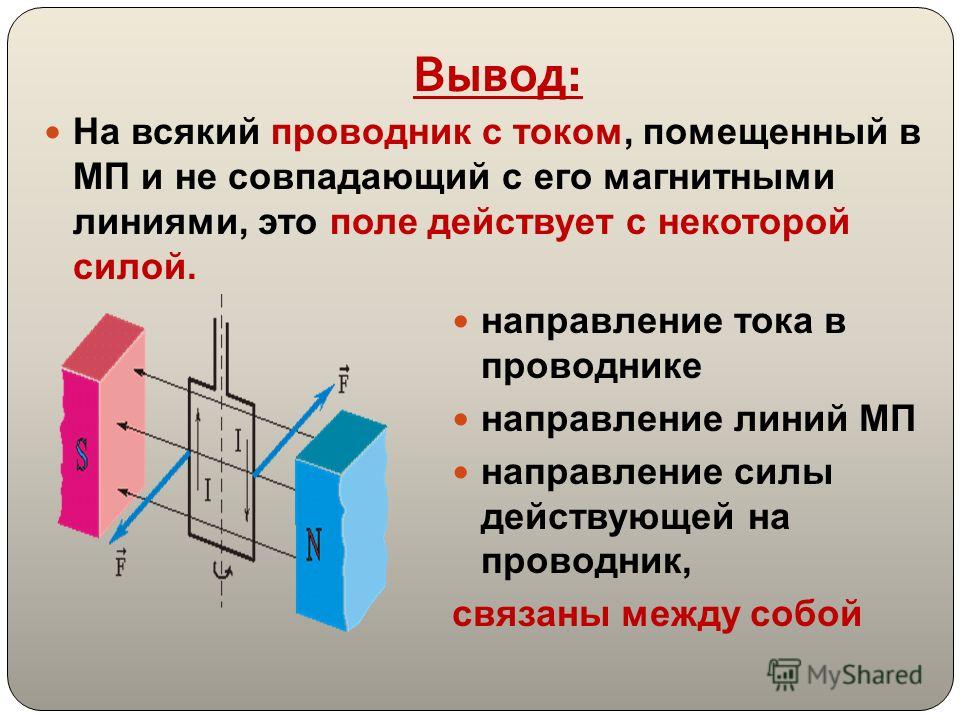 стр. 12). Подставив эти выражения в
формулу для силы Лоренца, получим:
стр. 12). Подставив эти выражения в
формулу для силы Лоренца, получим:
где — угол между векторами скорости и магнитной индукции.
Направление силы Лоренца определяют для положительного заряда по правилу левой руки. (Для отрицательного заряда сила Лоренца будет направлена в противоположную сторону).
Так как сила Лоренца перпендикулярна скорости частицы, то она не совершает работу. А, согласно теореме о кинетической энергии, это означает, что сила Лоренца не меняет кинетическую энергию частицы и, следовательно модуль ее скорости. Под действием силы Лоренца меняется лишь направление скорости частицы.
Магнитные свойства вещества
Все вещества, помещенные в магнитное поле, намагничиваются, т. е. сами создают магнитное поле. Поэтому индукция магнитного поля в однородной среде отличается от индукции поля в вакууме.
Физическая величина, показывающая, во сколько раз индукция магнитного поля в однородной среде отличается по модулю от индукции магнитного поля в вакууме, называется магнитной проницаемостью:
Все
вещества в зависимости от их магнитной
проницаемости разделяют на ферромагнетики,
парамагнетики и диамагнетики.
К ферромагнетикам относятся железо, никель, кобальт и некоторые соединения этих металлов с другими элементами. У них значения магнитной проницаемости достигают тысяч единиц. Поэтому при внесении железного сердечника в катушку с током, индукция магнитного поля увеличивается во много раз.
К парамагнетикам относятся вещества, магнитная проницаемость которых немного больше единицы. (Платина, жидкий кислород)
К диамагнетикам можно отнести вещества с малой магнитной проницаемостью. Они ослабляют магнитное поле. (Серебро, свинец, кварц, висмут).
Ферромагнетизм
объясняется магнитными свойствами
электронов. Электрон эквивалентен
круговому току или вращающемуся
заряженному телу и поэтому обладает
собственным магнитным полем. В большинстве
кристаллов магнитные поля электронов
взаимно компенсируются благодаря
попарной антипараллельной ориентации
магнитных полей электронов. Лишь в
некоторых кристаллах, например в
кристалле железа, возникают условия
для параллельной ориентации собственных
магнитных полей электронов.
С увеличением магнитной индукции внешнего поля возрастает степень упорядоченности ориентации отдельных доменов – магнитная индукция возрастает. При некотором значении индукции внешнего поля наступает полное упорядочение ориентации доменов, возрастание магнитной индукции прекращается. Это явление называется магнитным насыщением.
При вынесении ферромагнитного образца из внешнего магнитного поля значительная часть доменов сохраняет упорядоченную ориентацию – образец становится постоянным магнитом.
Упорядоченность
ориентации доменов в ферромагнетике
нарушается тепловыми колебаниями атомов
в кристалле.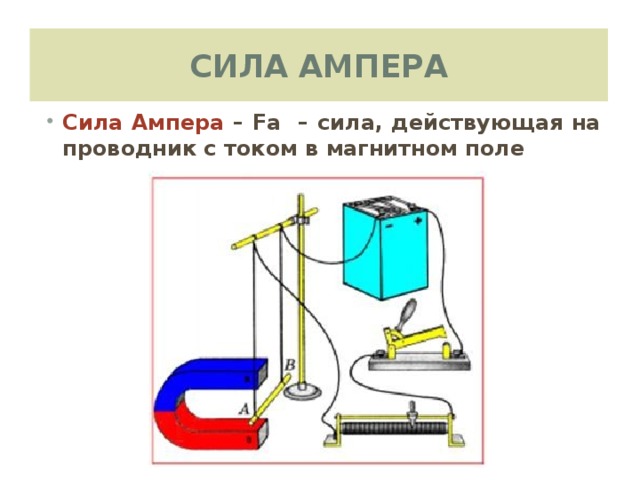 Чем выше температура
кристалла, тем быстрее разрушается
порядок в ориентации доменов, вследствие
чего образец размагничивается.
Температура, выше которой вещество
перестает быть ферромагнетиком,
называется температурой Кюри.
Чем выше температура
кристалла, тем быстрее разрушается
порядок в ориентации доменов, вследствие
чего образец размагничивается.
Температура, выше которой вещество
перестает быть ферромагнетиком,
называется температурой Кюри.
Электричество и магнетизм
Теперь мы готовы к обсуждению взаимодействия тока с магнитным полем.
Ампер установил наличие силового взаимодействия между двумя проводниками, по которым текут электрические токи. Пусть имеются два длинных параллельных проводника (рис. 5.25-1).
Рис. 5.25. Опыт Ампера по исследованию взаимодействия параллельных токов:
1 — схема установки; 2 — отталкивание антипараллельных токов; 3 — притяжение параллельных токов
Если по ним пропускать токи, текущие в противоположных направлениях, то проводники будут отталкиваться друг от друга (см. рис. 5.25-2). Если же токи будут течь в одном направлении, то они будут притягиваться (см. рис. 5.25-3).
Видео 5.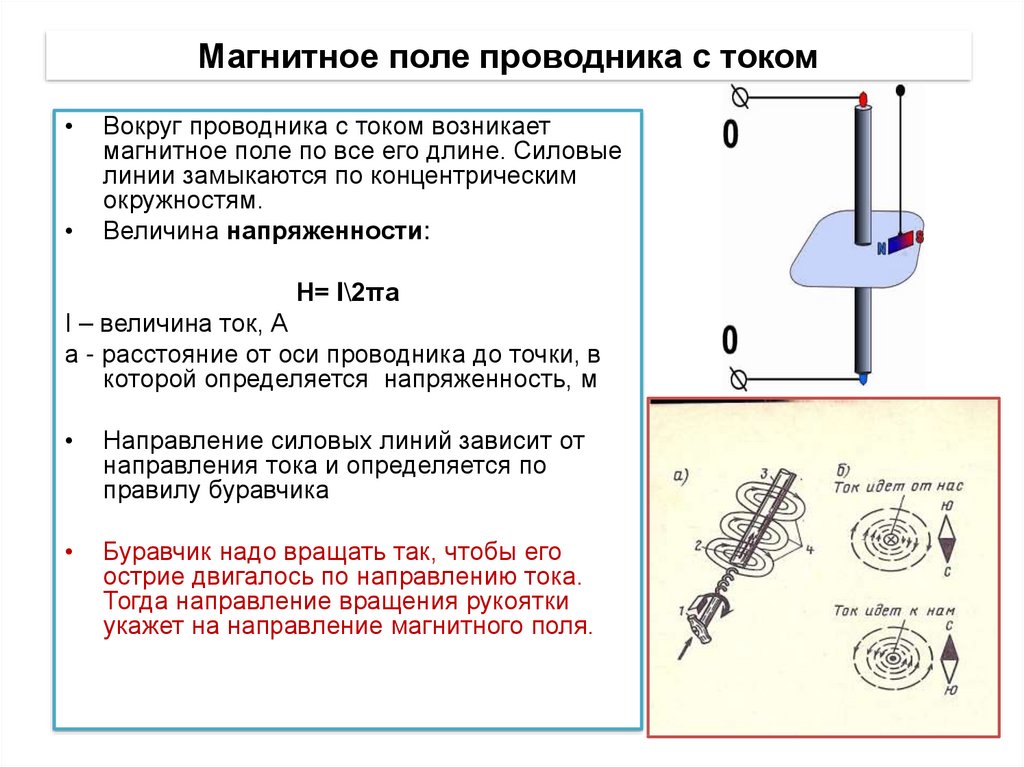 4. Взаимодействие параллельных токов.
4. Взаимодействие параллельных токов.
Эксперименты, проведенные Ампером, показали, что на проводник с током, помещенный в магнитное поле, действует сила. Откуда же она берется? Обсуждая эффект Холла, мы видели, что сила электрического поля EХ уравновешивает силу Лоренца, действующую на электроны. Но холловское поле EХ действует также и на кристаллическую ионную решетку вещества. На рис. 5.23 поле EХ направлено вверх, ортогонально току и магнитной индукции. Туда же будет направлена и сила, действующая на проводник. Найдем ее величину. Если поперечное сечение проводника равно S, а его длина (в направлении тока) — dl, то в данном объеме dV
 Используя формулу (5.28), находим суммарную силу, действующую на остов кристаллической решетки рассматриваемой части проводника
Используя формулу (5.28), находим суммарную силу, действующую на остов кристаллической решетки рассматриваемой части проводника|
|
|
где мы выразили плотность тока через его силу
Обращаем внимание, что в эту формулу не вошли характеристики конкретных носителей заряда, но лишь полный ток через проводник.
У нас внешнее магнитное поле было ортогонально току. В общем случае направление тока будем характеризовать вектором dl, имеющем длину dl и направленным вдоль течения тока. В холловскую напряженность электрического поля дает вклад только компонента магнитного поля, ортогональная вектору dl. Эта компонента равна по величине
где есть угол между векторами B Тогда для величины силы имеем
Тогда для величины силы имеем
|
|
(5.31) |
Учитывая направление этой силы (правило винта), можем записать ее в векторной форме
|
|
(5.32) |
Выражение (5.32) носит название закона Ампера, а сила называется силой Ампера (рис. 5.26).
Рис. 5.26. Сила Ампера, действующая на провод с током в поле постоянного магнита
Видео 5.5. Сила Ампера: выпрыгивание провода из магнита.
Мы получили выражение для силы, действующей на элемент проводника dl. Для определения полной силы, действующей на проводник, надо проинтегрировать (5. 32) вдоль его длины, учитывая зависимость магнитного поля от положения элемента. Такое интегрирование становится тривиальным для прямолинейного проводника в однородном магнитном поле
32) вдоль его длины, учитывая зависимость магнитного поля от положения элемента. Такое интегрирование становится тривиальным для прямолинейного проводника в однородном магнитном поле
|
|
(5.33) |
Направление силы Ампера определяется по правилу левой руки (рис. 5.27):
|
Если левую руку расположить таким образом, чтобы линии магнитной индукции входили в ладонь, а вытянутые пальцы были направлены в направлении тока, то отогнутый большой палец покажет направление действия силы Ампера, действующей на проводник. |
Рис. 5.27. Определение направления силы Ампера
Видео 5.6. Сила Ампера: тележка Эйхенвальда.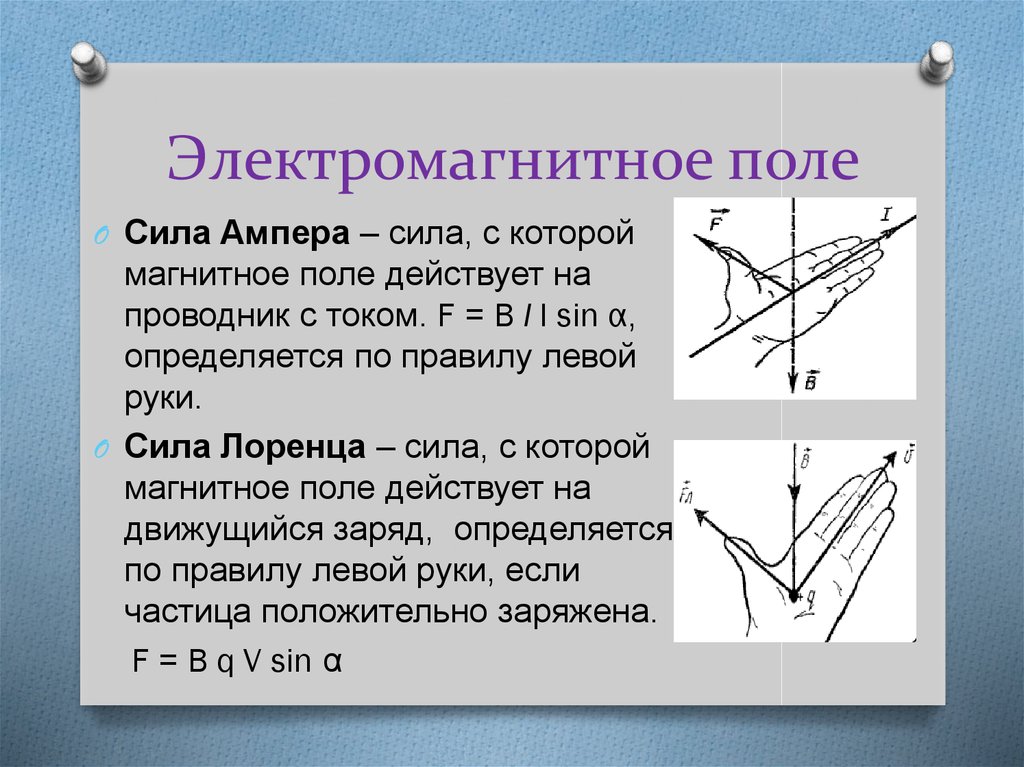
Действие силы Ампера на проводник с током демонстрируется в опыте, показанном на рис. 5.28. На торце вертикальной цилиндрической катушки положены горизонтальные проводящие рельсы, по которым может катиться алюминиевая трубка. После включения тока через катушку к рельсам прикладывается постоянное напряжение, и по трубке начинает течь ток. Под действием силы Ампера трубка катится по рельсам. При изменении направления тока в трубке она катится в противоположную сторону.
Рис. 5.28. Экспериментальное изучение силы Ампера
В общем случае произвольного проводника и магнитного поля силы, действующие на различные элементы проводника, различаются как величиной, так и направлением (рис. 5.29).
Рис. 5.29. В общем случае силы, действующие на различные элементы проводника,
различаются как величиной, так и направлением
С помощью формулы (5.31) можно определить величину магнитной индукции по максимальной силе Ампера dFA (в этом случае ), действующей на элемент dl проводника с током I
То есть величина магнитной индукции численно равна максимальной силе, действующей на единичный элемент тока.
22.7 Магнитное воздействие на проводник с током – Колледж физики: OpenStax
Глава 22 Магнетизм
Резюме
- Описать действие магнитной силы на проводник с током.
- Рассчитайте магнитную силу, действующую на проводник с током.
Поскольку обычно заряды не могут покинуть проводник, магнитная сила, действующая на заряды, движущиеся в проводнике, передается самому проводнику.
Рис. 1. Магнитное поле действует на проводник с током в направлении, определяемом правилом правой руки 1 (то же направление, что и на отдельные движущиеся заряды). Эта сила легко может быть достаточно большой, чтобы сдвинуть провод, поскольку типичные токи состоят из очень большого количества движущихся зарядов. Мы можем получить выражение для магнитной силы, действующей на ток, взяв сумму магнитных сил, действующих на отдельные заряды. (Силы складываются, потому что они имеют одинаковое направление. ) Сила, действующая на отдельный заряд, движущийся со скоростью дрейфа vdvd, определяется как [латекс]\boldsymbol{F = qv_dB \;\textbf{sin} \;\theta}[ /латекс]. Принимая [латекс]\boldsymbol{B}[/латекс] равномерным по всей длине провода [латекс]\boldsymbol{l}[/латекс] и равным нулю в других местах, тогда общая магнитная сила на проводе равна [латекс]\ boldsymbol{F = (qv_dB \;\textbf{sin} \;\theta)(N)}[/latex], где [latex]\boldsymbol{N}[/latex] – количество носителей заряда в сечении проволока длиной [латекс]\boldsymbol{l}[/латекс]. Теперь [латекс]\boldsymbol{N=nV}[/latex], где [латекс]\boldsymbol{n}[/латекс] — количество носителей заряда в единице объема, а [латекс]\boldsymbol{V}[/ латекс] — объем проволоки в поле. Отметив, что [латекс]\boldsymbol{V=Al}[/латекс], где [латекс]\жирный символ{А}[/латекс] — площадь поперечного сечения проволоки, сила, действующая на проволоку, равна [латекс] \boldsymbol{F=(qv_dB \;\textbf{sin} \;\theta)(nAl)}[/latex]. Условия сбора,
) Сила, действующая на отдельный заряд, движущийся со скоростью дрейфа vdvd, определяется как [латекс]\boldsymbol{F = qv_dB \;\textbf{sin} \;\theta}[ /латекс]. Принимая [латекс]\boldsymbol{B}[/латекс] равномерным по всей длине провода [латекс]\boldsymbol{l}[/латекс] и равным нулю в других местах, тогда общая магнитная сила на проводе равна [латекс]\ boldsymbol{F = (qv_dB \;\textbf{sin} \;\theta)(N)}[/latex], где [latex]\boldsymbol{N}[/latex] – количество носителей заряда в сечении проволока длиной [латекс]\boldsymbol{l}[/латекс]. Теперь [латекс]\boldsymbol{N=nV}[/latex], где [латекс]\boldsymbol{n}[/латекс] — количество носителей заряда в единице объема, а [латекс]\boldsymbol{V}[/ латекс] — объем проволоки в поле. Отметив, что [латекс]\boldsymbol{V=Al}[/латекс], где [латекс]\жирный символ{А}[/латекс] — площадь поперечного сечения проволоки, сила, действующая на проволоку, равна [латекс] \boldsymbol{F=(qv_dB \;\textbf{sin} \;\theta)(nAl)}[/latex]. Условия сбора,
[латекс]\boldsymbol{F=(nqAv_d)lB \;\textbf{sin} \;\theta}. [/latex]
[/latex]
Поскольку [латекс]\boldsymbol{nqAv_d = I}[/латекс] (см. Главу 20.1 Текущая версия),
[латекс]\boldsymbol{F = IlB \;\textbf{sin} \;\theta}[/latex]
представляет собой уравнение для магнитной силы, действующей на отрезок [латекс]\boldsymbol{l}[/латекс] провода, по которому течет ток [латекс]\boldsymbol{I}[/латекс] в однородном магнитном поле [латекс]\boldsymbol {B}[/latex] , как показано на рисунке 2. Если мы разделим обе части этого выражения на [latex]\boldsymbol{l}[/latex], мы обнаружим, что магнитная сила на единицу длины провода в однородное поле равно [латекс]\boldsymbol{\frac{F}{l} = IB \;\textbf{sin} \;\theta}[/latex]. Направление этой силы задается RHR-1, с большим пальцем в направлении текущего [латекс]\boldsymbol{I}[/латекс]. Затем, с пальцами в направлении [латекс]\boldsymbol{B}[/латекс], перпендикуляр к ладони указывает в направлении [латекс]\жирныйсимвол{F}[/латекс], как на рисунке 2.
Рис. 2. Сила, действующая на проводник с током в магнитном поле, равна F = IlB sin θ . Его направление задает RHR-1.
Его направление задает RHR-1.Расчет магнитной силы на проводе с током: сильное магнитное поле
Рассчитайте силу, действующую на провод, показанную на рис. 1, при [латексе]\boldsymbol{B = 1,50 \;\textbf{T}}[/latex] , [латекс]\boldsymbol{l = 5,00 \;\textbf{см}}[/латекс] и [латекс]\boldsymbol{I = 20,0 \;\textbf{A}}[/латекс].
9{\circ}}[/latex], так что [латекс]\boldsymbol{\textbf{sin} \;\theta = 1}[/latex].Решение
Ввод заданных значений в [латекс]\boldsymbol{F = IlB \;\textbf{sin} \theta}[/latex] дает
[латекс]\boldsymbol{F = IlB \;\ textbf{sin} \theta = (20.0 \;\textbf{A}) \; (0,0500 \;\textbf{м}) \; (1.50 \;\textbf{T}) \; (1)}.[/latex]
Единицы тесла: [латекс]\boldsymbol{1 \;\textbf{T} = \frac{\textbf{N}}{\textbf{A} \cdot \; \textbf{м}}}[/латекс]; таким образом,
[латекс]\boldsymbol{F = 1,50 \;\textbf{N}}.[/latex]
Обсуждение
Это большое магнитное поле создает значительную силу на проводе небольшой длины.
Магнитная сила на проводниках с током используется для преобразования электрической энергии в работу. (Ярким примером являются двигатели — в них используются петли из проволоки, и они рассматриваются в следующем разделе.) Магнитогидродинамика (МГД) — это техническое название, данное умному приложению, в котором магнитная сила перекачивает жидкости без движущихся механических частей. (См. рис. 3.)
Рис. 3. Магнитогидродинамика. Магнитная сила тока, проходящего через эту жидкость, может быть использована в качестве немеханического насоса. Сильное магнитное поле прикладывается к трубке, и ток проходит через жидкость под прямым углом к полю, в результате чего на жидкость действует сила, параллельная оси трубки, как показано на рисунке. Отсутствие движущихся частей делает его привлекательным для перемещения горячего химически активного вещества, такого как жидкий натрий, используемый в некоторых ядерных реакторах. Экспериментальные искусственные сердца тестируются с использованием этой техники для перекачивания крови, возможно, для обхода неблагоприятных последствий механических насосов. (Однако на клеточные мембраны влияют большие поля, необходимые для МГД, что задерживает его практическое применение у людей.) Был предложен двигатель МГД для атомных подводных лодок, потому что он может быть значительно тише, чем обычные гребные двигатели. Сдерживающая ценность атомных подводных лодок основана на их способности скрыться и пережить первый или второй ядерный удар. По мере того, как мы постепенно разбираем наши арсеналы ядерного оружия, подводная ветвь будет выведена из эксплуатации последней из-за этой способности (см. рис. 4). Существующие МГД-приводы тяжелые и неэффективные — требуется много доработок.
(Однако на клеточные мембраны влияют большие поля, необходимые для МГД, что задерживает его практическое применение у людей.) Был предложен двигатель МГД для атомных подводных лодок, потому что он может быть значительно тише, чем обычные гребные двигатели. Сдерживающая ценность атомных подводных лодок основана на их способности скрыться и пережить первый или второй ядерный удар. По мере того, как мы постепенно разбираем наши арсеналы ядерного оружия, подводная ветвь будет выведена из эксплуатации последней из-за этой способности (см. рис. 4). Существующие МГД-приводы тяжелые и неэффективные — требуется много доработок.
- Магнитная сила, действующая на проводники с током, определяется выражением
[латекс]\boldsymbol{F = IlB \;\textbf{sin} \;\theta},[/latex]
, где [латекс]\boldsymbol{I}[/латекс] – сила тока, [латекс]\boldsymbol{l}[/латекс] – длина прямого проводника в однородном магнитном поле [латекс]\boldsymbol{B} [/latex], а [latex]\boldsymbol{\theta}[/latex] — это угол между [latex]\boldsymbol{I}[/latex] и [latex]\boldsymbol{B}[/latex].
 Сила следует за RHR-1 большим пальцем в направлении [латекс]\boldsymbol{I}[/латекс].
Сила следует за RHR-1 большим пальцем в направлении [латекс]\boldsymbol{I}[/латекс].
Задачи и упражнения
1: Каково направление действия магнитной силы на ток в каждом из шести случаев на рис. 5?
Рисунок 5.2: Каково направление тока, на который действует магнитная сила, показанная в каждом из трех случаев на рисунке 6, если предположить, что ток течет перпендикулярно [латексу]\boldsymbol{B}[/ латекс]?
Рисунок 63: Каково направление магнитного поля, которое создает магнитную силу, показанную на токах в каждом из трех случаев на рисунке 7, при условии, что [latex]\boldsymbol{B}[/latex] перпендикулярно [латексу]\boldsymbol{I}[/латекс]? 9{-5}- \textbf{T}}[/latex]. Какая сила действует на отрезке этой линии длиной 100 м? (b) Обсудите практические проблемы, которые это вызывает, если таковые имеются.
6: Какая сила действует на воду в МГД-приводе с трубкой диаметром 25,0 см, если через трубку, перпендикулярную магнитному полю напряженностью 2,00 Т, пропускают ток силой 100 А? (Относительно небольшой размер этой силы указывает на необходимость очень больших токов и магнитных полей для практических МГД-приводов. )
)
7:9{\circ}}[/latex] с полем?
10: Сила, действующая на прямоугольную проволочную петлю в магнитном поле на рисунке 8, может использоваться для измерения напряженности поля. Поле однородно, и плоскость петли перпендикулярна полю. а) Как направлена магнитная сила, действующая на петлю? Обоснуйте утверждение, что силы на сторонах петли равны и противоположны, независимо от того, какая часть петли находится в поле, и не влияют на результирующую силу, действующую на петлю. (b) Если используется ток 5,00 А, какова сила на тесла на петле шириной 20,0 см?
Рисунок 8.11.5: Магнитное воздействие на проводник с током
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4417
- OpenStax
- ОпенСтакс
Цели обучения
К концу этого раздела вы сможете:
- Определять направление, в котором на провод с током действует сила во внешнем магнитном поле
- Расчет силы, действующей на проводник с током во внешнем магнитном поле
На движущиеся заряды действует сила магнитного поля. Если эти движущиеся заряды находятся в проводе, то есть если по проводу течет ток, на провод также должна действовать сила. Однако, прежде чем мы обсудим силу, действующую на ток со стороны магнитного поля, мы сначала исследуем магнитное поле, создаваемое электрическим током. Здесь мы изучаем два отдельных эффекта, которые тесно взаимодействуют друг с другом: проводник с током создает магнитное поле, и магнитное поле воздействует на проводник с током.
Если эти движущиеся заряды находятся в проводе, то есть если по проводу течет ток, на провод также должна действовать сила. Однако, прежде чем мы обсудим силу, действующую на ток со стороны магнитного поля, мы сначала исследуем магнитное поле, создаваемое электрическим током. Здесь мы изучаем два отдельных эффекта, которые тесно взаимодействуют друг с другом: проводник с током создает магнитное поле, и магнитное поле воздействует на проводник с током.
Магнитные поля, создаваемые электрическими токами
Обсуждая исторические открытия в области магнетизма, мы упомянули открытие Эрстеда о том, что провод, по которому течет электрический ток, заставляет ближайший компас отклоняться. Была установлена связь, что электрические токи создают магнитные поля. (Эта связь между электричеством и магнетизмом обсуждается более подробно в разделе «Источники магнитных полей».)
На стрелку компаса, расположенную рядом с проводом, действует сила, которая выравнивает стрелку по касательной к окружности вокруг провода. Следовательно, провод с током создает круговые петли магнитного поля. Чтобы определить направление магнитного поля, создаваемого проводом, мы используем второе правило правой руки. В RHR-2 большой палец указывает в направлении тока, а пальцы обхватывают провод, указывая в направлении создаваемого магнитного поля (рис. \(\PageIndex{1}\)). Если магнитное поле исходило от вас или исходило от страницы, мы обозначаем это точкой. Если бы магнитное поле попадало на страницу, мы обозначаем это знаком ×.
Следовательно, провод с током создает круговые петли магнитного поля. Чтобы определить направление магнитного поля, создаваемого проводом, мы используем второе правило правой руки. В RHR-2 большой палец указывает в направлении тока, а пальцы обхватывают провод, указывая в направлении создаваемого магнитного поля (рис. \(\PageIndex{1}\)). Если магнитное поле исходило от вас или исходило от страницы, мы обозначаем это точкой. Если бы магнитное поле попадало на страницу, мы обозначаем это знаком ×.
Эти символы возникли при рассмотрении векторной стрелки: стрелка, направленная к вам, с вашей точки зрения выглядела бы как точка или кончик стрелки. Стрелка, направленная от вас, с вашей точки зрения выглядела бы как крестик или ×. Составной эскиз магнитных кругов показан на рисунке \(\PageIndex{1}\), где показано, что напряженность поля уменьшается по мере удаления от провода за счет петель, которые находятся дальше друг от друга.
Рисунок \(\PageIndex{1}\): (a) Когда провод находится в плоскости бумаги, поле перпендикулярно бумаге.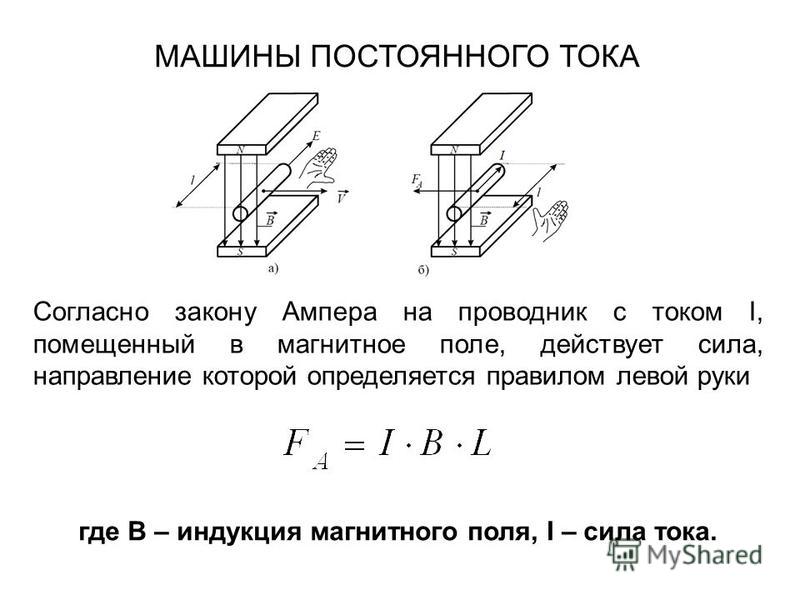 Обратите внимание на символы, используемые для поля, указывающего внутрь (например, хвост стрелы), и поля, указывающего наружу (например, кончик стрелки). (b) Длинный и прямой провод создает поле с силовыми линиями магнитного поля, образующими круглые петли.
Обратите внимание на символы, используемые для поля, указывающего внутрь (например, хвост стрелы), и поля, указывающего наружу (например, кончик стрелки). (b) Длинный и прямой провод создает поле с силовыми линиями магнитного поля, образующими круглые петли.Расчет магнитной силы
Электрический ток представляет собой упорядоченное движение заряда. Следовательно, проводник с током в магнитном поле должен испытывать силу, обусловленную полем. Чтобы исследовать эту силу, давайте рассмотрим бесконечно малый отрезок проволоки, как показано на рисунке \(\PageIndex{3}\). Длина и площадь поперечного сечения сечения равны дл и А соответственно, поэтому его объем равен \(V = A \cdot дл\). Проволока изготовлена из материала, содержащего n носителей заряда в единице объема, поэтому число носителей заряда в сечении равно \(nA \cdot dl\). Если носители заряда движутся со скоростью дрейфа \(\vec{v}_d\), то ток I в проводе равен (из тока и сопротивления)
\[I = neAv_d.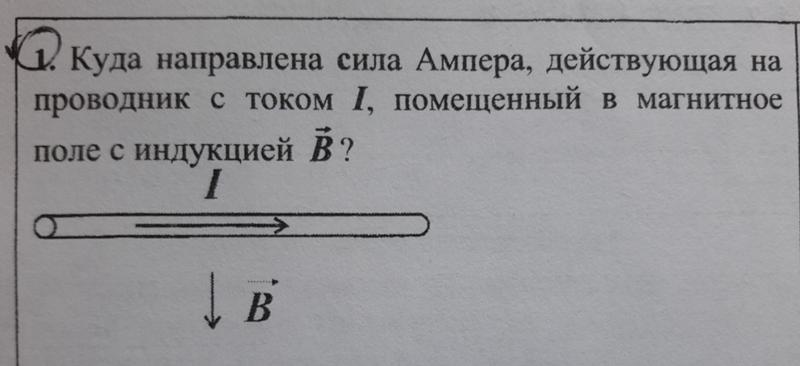 \]
\]
Магнитная сила на любой один носитель заряда равен \(e\vec{v}_d \times \vec{B}\), поэтому полная магнитная сила \(d\vec{F}\) на \(nA\cdot dl\) носителей заряда в сечении провода
\[d\vec{F} = (nA \cdot dl)e\vec{v}_d \times \vec{B}.\]
Мы можем определить dl как вектор длины dl , указывающий вдоль \(\vec{v}_d\), что позволяет нам переписать это уравнение как
\[d\vec{F} = neAv_dd \vec{l} \times \vec{B},\] или
\[d\vec{F} = Id\vec{l} \times \vec{B}. \label{11.12}\]
Это сила магнитного поля, действующая на сечение провода. Обратите внимание, что на самом деле это чистая сила, действующая со стороны поля на сами носители заряда. Направление этой силы задается RHR-1, где вы указываете пальцами в направлении тока и скручиваете их в сторону поля. Затем ваш большой палец указывает направление силы.
Рисунок \(\PageIndex{2}\): Бесконечно малый участок провода с током в магнитном поле. Чтобы определить магнитную силу \(\vec{F}\) на проводе произвольной длины и формы, мы должны проинтегрировать уравнение \ref{11.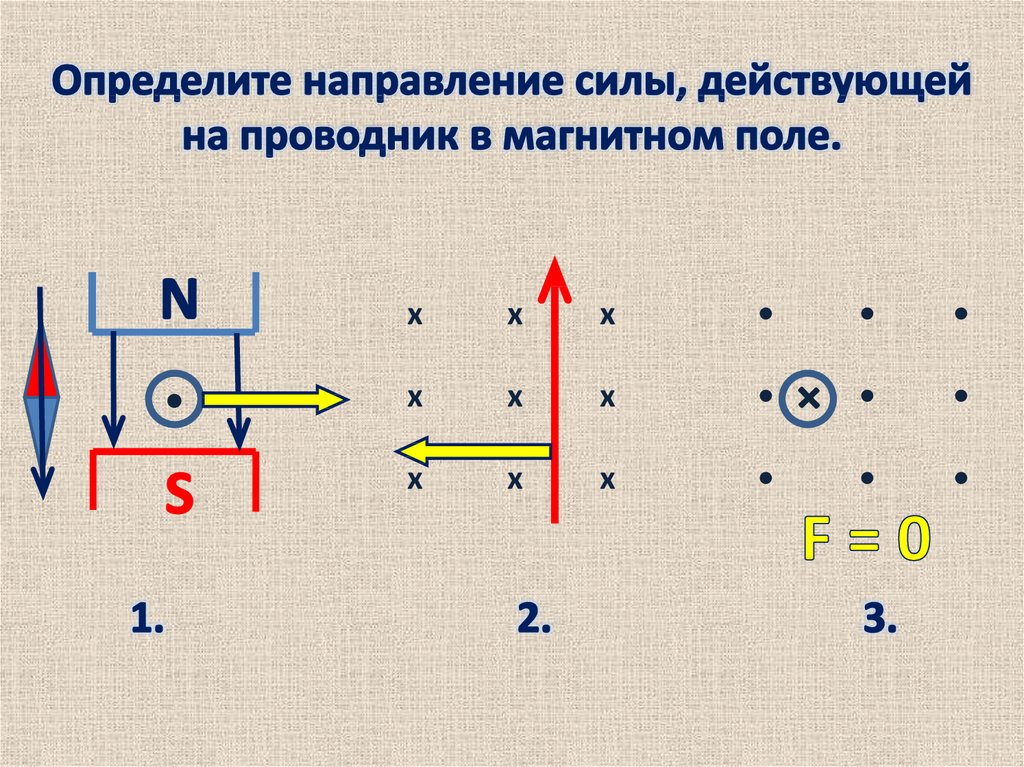 12} по всему проводу. Если сечение провода прямое, а B однородное, дифференциалы уравнения становятся абсолютными величинами, что дает нам
12} по всему проводу. Если сечение провода прямое, а B однородное, дифференциалы уравнения становятся абсолютными величинами, что дает нам
\[\vec{F} = I\vec{l} \times \vec{B}.\]
Это сила, действующая на прямой провод с током в однородном магнитном поле.
Пример \(\PageIndex{1}\): Уравновешивание гравитационных и магнитных сил на проводе с током
Провод длиной 50 см и массой 10 г подвешен в горизонтальной плоскости на паре гибких проводов ( Рисунок \(\PageIndex{3}\)). Затем провод подвергается воздействию постоянного магнитного поля величиной 0,50 Тл, которое направлено, как показано на рисунке. Каковы величина и направление тока в проводе, необходимые для снятия напряжения в опорных выводах?
Рисунок \(\PageIndex{3}\): (a) Провод, подвешенный в магнитном поле. (b) Диаграмма свободного тела для провода.Стратегия
Судя по диаграмме свободного тела на рисунке, натяжение в опорных проводах становится равным нулю, когда гравитационные и магнитные силы уравновешивают друг друга.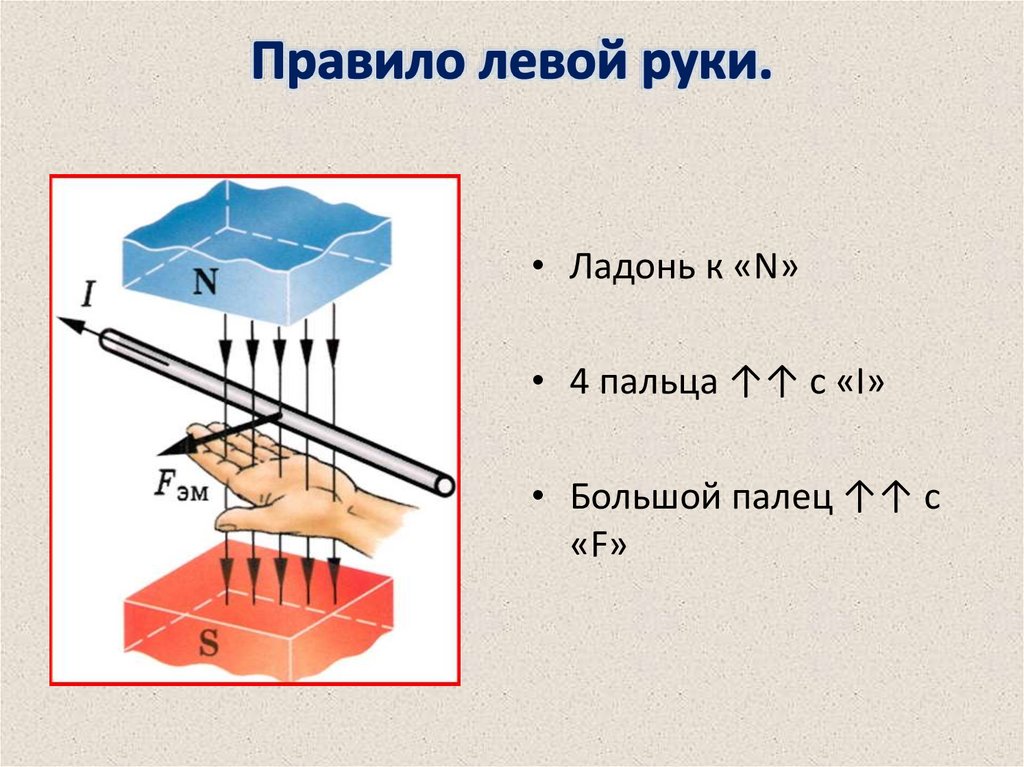 Используя RHR-1, мы обнаруживаем, что магнитная сила направлена вверх. Затем мы можем определить ток I , приравняв две силы.
Используя RHR-1, мы обнаруживаем, что магнитная сила направлена вверх. Затем мы можем определить ток I , приравняв две силы.
Решение
Приравняем две силы веса и магнитной силы, действующие на провод:
\[mg = IlB.\] Таким образом,
\[I = \frac{mg}{lB} = \frac{ (0,010 \, кг}{92)}{(0,50 \, м)(0,50 \, T)} = 0,39 \, А.\]
Значение
Это большое магнитное поле создает значительную силу на длине провода, чтобы противодействовать весу провод.
Пример \(\PageIndex{2}\): Расчет силы магнитного поля на проводе с током
Длинный жесткий провод, проложенный вдоль оси y , несет ток силой 5,0 А, текущий в положительном направлении y -направление. а) Если постоянное магнитное поле величиной 0,30 Тл направлено вдоль положительного x -ось, какова магнитная сила на единицу длины провода? б) Если постоянное магнитное поле с напряженностью 0,30 Тл направлено под углом 30 градусов от оси + x к оси + y , какова магнитная сила на единицу длины провода?
Стратегия
Магнитная сила, действующая на провод с током в магнитном поле, определяется выражением \(\vec{F} = I\vec{l} \times \vec{B}\). Для части а, поскольку в этой задаче ток и магнитное поле перпендикулярны, мы можем упростить формулу, чтобы получить величину и найти направление через RHR-1. Угол θ равно 90 градусам, что означает \(sin\, \theta = 1.\). Кроме того, длину можно разделить на левую часть, чтобы найти силу на единицу длины. Для части b текущая длина записывается в виде единичного вектора, а также магнитное поле. После взятия перекрестного произведения направленность очевидна по результирующему единичному вектору.
Для части а, поскольку в этой задаче ток и магнитное поле перпендикулярны, мы можем упростить формулу, чтобы получить величину и найти направление через RHR-1. Угол θ равно 90 градусам, что означает \(sin\, \theta = 1.\). Кроме того, длину можно разделить на левую часть, чтобы найти силу на единицу длины. Для части b текущая длина записывается в виде единичного вектора, а также магнитное поле. После взятия перекрестного произведения направленность очевидна по результирующему единичному вектору.
Решение
- Начнем с общей формулы для магнитной силы, действующей на провод. Мы ищем силу на единицу длины, поэтому мы делим на длину, чтобы вывести ее в левую часть. Мы также устанавливаем \(sin\,\theta\). Таким образом, решение: {l} = 1,5 \, Н/м.\] Направленность: Укажите пальцами на положительную 9о)\шат{i}\] \[\vec{F}/l = -1,30 \шат{к} \, Н/м.\]
Значение
Это большое магнитное поле создает значительную силу на проводе небольшой длины. По мере того, как угол магнитного поля становится ближе к току в проводе, на него действует меньшая сила, как видно из сравнения частей а и б.
По мере того, как угол магнитного поля становится ближе к току в проводе, на него действует меньшая сила, как видно из сравнения частей а и б.
Упражнение \(\PageIndex{1}\)
Прямая гибкая медная проволока погружена в магнитное поле, направленное на страницу. а) Если ток в проводе течет по + x -направление, в какую сторону будет изгибаться провод? б) В какую сторону изгибается провод, если ток течет в направлении – x ?
Раствор
а. наклоняется вверх; б. изгибается вниз
Пример \(\PageIndex{3}\): Сила, действующая на круговой провод
Круговая петля с током радиуса R , по которой течет ток I , расположена в плоскости xy . Постоянное однородное магнитное поле прорезает петлю параллельно оси y (рис. \(\PageIndex{4}\)). Найдите магнитную силу, действующую на верхнюю половину петли, нижнюю половину петли и полную силу, действующую на петлю.
Стратегия
Магнитная сила на верхней петле должна быть выражена через дифференциальную силу, действующую на каждый сегмент петли. Если мы проинтегрируем по каждой дифференциальной части, мы найдем общую силу на этом участке петли. Аналогично находится сила на нижней петле, а полная сила есть сложение этих двух сил.
Решение
Дифференциальная сила, действующая на произвольный отрезок проволоки, расположенный на верхнем кольце: направление магнитного поля (+ y ) и отрезок провода. Дифференциальный сегмент расположен на том же радиусе, поэтому, используя формулу длины дуги, мы имеем:
\[dl = Rd\theta\]
\[dF = IBR \, sin \, \theta \, d\ theta.\]
Чтобы найти силу, действующую на сегмент, мы интегрируем по верхней половине круга от 0 до \(\pi\). В результате получается: 90 sin \, \theta \, d\theta = IBR(-cos 0 + cos \pi) = -2 IBR. \]
\]
Чистая сила представляет собой сумму этих сил, которая равна нулю.
Значение
Суммарная сила, действующая на любой замкнутый контур в однородном магнитном поле, равна нулю. Несмотря на то, что на каждую часть петли действует сила, результирующая сила, действующая на систему, равна нулю. (Обратите внимание, что в петле есть чистый крутящий момент, который мы рассмотрим в следующем разделе.)
Эта страница под названием 11.5: Магнитное воздействие на проводник с током распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts. ; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать оглавление
- нет
- Метки
- Магнитная сила
- источник@https://openstax.


 Сила следует за RHR-1 большим пальцем в направлении [латекс]\boldsymbol{I}[/латекс].
Сила следует за RHR-1 большим пальцем в направлении [латекс]\boldsymbol{I}[/латекс].
Leave A Comment