Из двух городов одновременно навстречу друг другу выехали автомобиль и мотоцикл и встретились через: Из двух городов одновременно навстречу друг другу выехали автомобиль и мотоцикл и...

Урок 39. задачи на встречное движение — Математика — 4 класс

Математика, 4 класс

Урок №39. Задачи на встречное движение

Перечень вопросов, рассматриваемых в теме:

— какие бывают направления движения?

— что такое скорость сближения?

— как узнать скорость сближения?

Глоссарий по теме:

Скорость сближения – расстояние, на которое сближаются движущиеся предметы в единицу времени.

Встречное движение – движение навстречу друг другу.

Основная и дополнительная литература по теме урока:

1. Моро М.И.,Бантова М.А. и др. Математика 4 класс. Учебник для общеобразовательных организаций. Ч.2 — М.; Просвещение, 2017. – с.6-8.

2. Моро М. И., Волкова С. И. Математика. Рабочая тетрадь 4 класс. Часть 2. М.; Просвещение, 2016. – с.15.

3. Волкова С. И. Математика. Проверочные работы 4 класс. М.; Просвещение, 2017. – с.54.

Теоретический материал для самостоятельного изучения

Рассмотрим новый вид задач, задачи на встречное движение.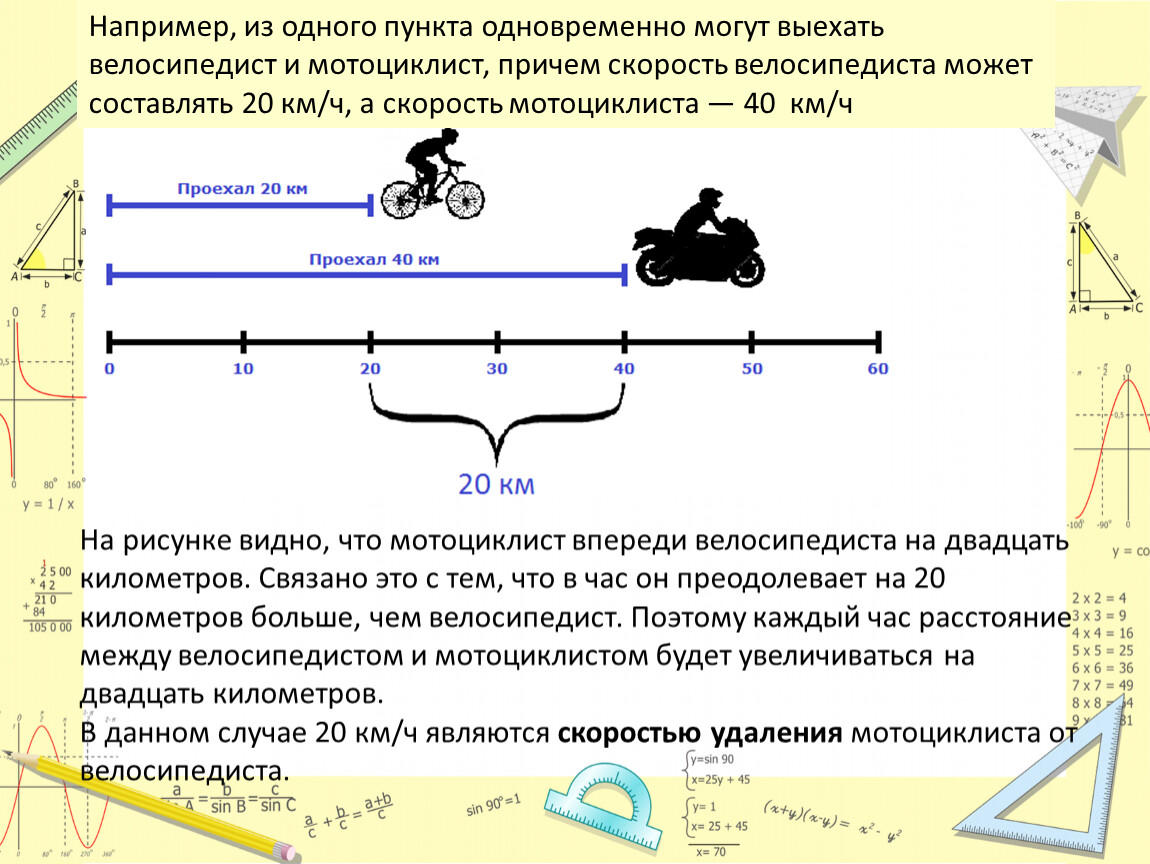

Автобус и автомобиль выехали одновременно навстречу друг другу из двух городов и встретились через 3 ч. Автобус ехал со скоростью 60 км/ч, а автомобиль – 90 км/ч.

Найдите расстояние между городами. Это задача на встречное движение, потому что в ней речь идёт о двух транспортных средствах, которые движутся навстречу друг другу. При этом расстояние между ними сокращается.

После встречи автобус и автомобиль движутся в противоположных направлениях, удаляются друг от друга. Это уже другой вид движения и другой тип задач. Таким образом, существует встречное движение (навстречу друг другу) и движение в противоположных направлениях.

Сделаем чертёж к нашей задаче. На чертеже отрезком обозначают расстояние между городами. Его нужно найти. Записываем под отрезком вопросительный знак. Автобус и автомобиль движутся навстречу друг другу. Покажем это на чертеже стрелками.

В условии задачи даны скорости движения машин. Запишем их на чертеже. Место встречи машин отмечено флажком. Обрати внимание, что автомобиль двигался быстрее автобуса. Он проехал большее расстояние, чем автобус. Поэтому флажок на чертеже располагается ближе к тому месту, откуда выехал автобус. Время в пути автобуса и автомобиля одинаковое, 3 часа. Поэтому отрезки, обозначающие расстояние, пройденное до встречи каждым транспортным средством, поделим на три равные части. Каждая такая часть будет означать расстояние, пройденное за один час. Заметьте, части слева и справа от флажка получились разными, т.к. разными были скорости движения. Каждая часть слева от флажка обозначает 60 км в час. А каждая часть справа от флажка обозначает 90 км, которые проезжает за один час автомобиль.

Теперь приступим к решению задачи. Общее расстояние между городами складывается из расстояния, которое проехал автобус и расстояния, которое проехал автомобиль до их встречи. Каждое из этих расстояний находится умножением скорости на время. После этого полученные величины надо сложить. Мы ответили на вопрос задачи.

Запишем ответ.

1) 60 ∙ 3 = 180 (км) – расстояние, которое проехал автобус.

2) 90 ∙ 3 = 270 (км) — расстояние, которое проехал автомобиль.

3) 180 + 270 = 450 (км) – расстояние между городами.

Ответ: расстояние между городами 450 км.

Эту задачу можно решить другим способом. Автобус и автомобиль начали движение одновременно. После первого часа пути автобус проехал 60 км, а автомобиль 90 км. Значит, за один час они сблизились на 150 км. По другому можно сказать, что скорость сближения машин равна 150 км в час. За следующий час пути автобус и автомобиль сблизились ещё на 150 км. За третий час они сблизились ещё на 150 км. И так, до встречи машины сближались три раза по 150 км, т.к. были в пути 3 часа. Значит, чтобы узнать расстояние между ними в самом начале пути, надо 150 умножить на 3. То есть, скорость сближения умножить на время движения до встречи.

1) 60 + 90 = 150 (км/ч) – скорость сближения.

2) 150 ∙ 3 = 450 (км)

Ответ: расстояние между городами 450 км.

Это второй способ решения задачи.

Расстояние, на которое сближаются движущиеся предметы в единицу времени, называют скоростью сближения.

Задания тренировочного модуля:

1. Вставьте в таблицу пропущенные данные.

Два лыжника вышли одновременно навстречу друг другу из двух посёлков и встретились через 3 часа. Первый лыжник шёл со скоростью 12 км/ч, второй – 14 км/ч. Найдите расстояние между посёлками.

	Скорость	Время	Расстояние
Первый лыжник			?
Второй лыжник			?

Правильный ответ:

	Скорость	Время	Расстояние
Первый лыжник	12 км/ч	3 ч	?
Второй лыжник	14 км/ч	3 ч	?

2. Распределите решения задач по группам.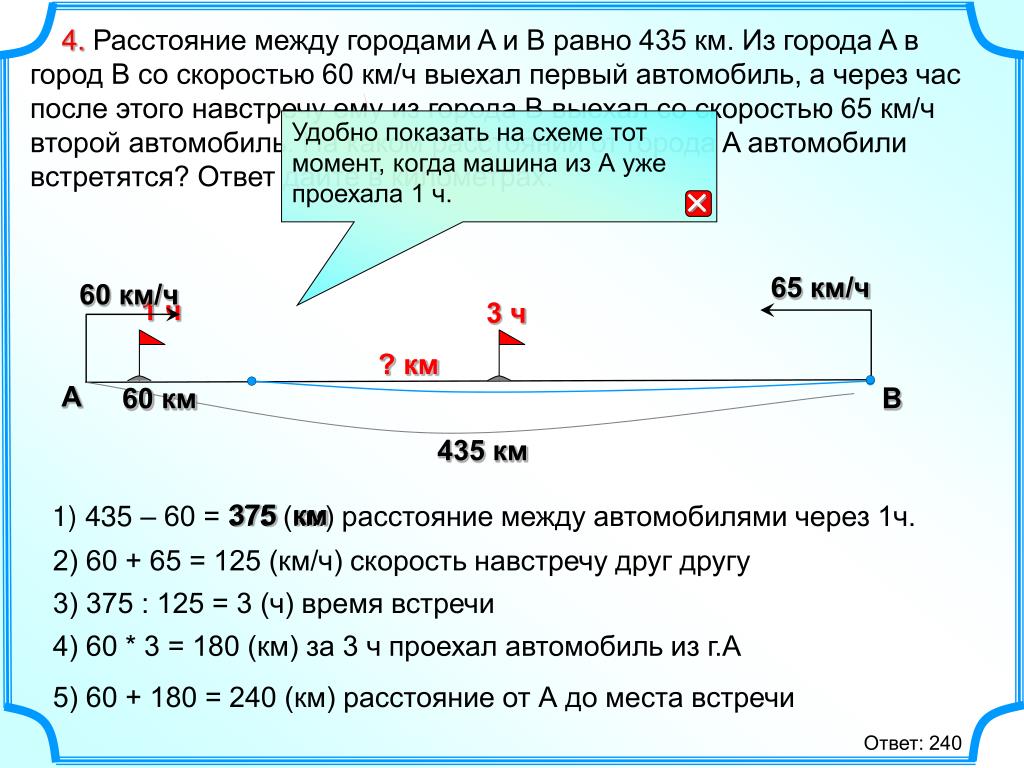 Перенесите их в соответствующие столбики.

Из двух посёлков, расстояние между которыми 78 км, вышли одновременно навстречу друг другу два лыжника. Первый из них шёл со скоростью 12 км/ч, второй – 14 км/ч. Через сколько часов лыжники встретились?	Из двух посёлков, находящихся на расстоянии 78 км, вышли одновременно навстречу друг другу два лыжника и встретились через 3 ч. Первый лыжник шёл со скоростью 12 км/ч. С какой скоростью шёл второй лыжник?

Варианты ответа:

(78 – 12 ∙ 3) : 3

78 : (12 + 14)

Правильный вариант:

Из двух посёлков, расстояние между которыми 78 км, вышли одновременно навстречу друг другу два лыжника. Первый из них шёл со скоростью 12 км/ч, второй – 14 км/ч. Через сколько часов лыжники встретились?	Из двух посёлков, находящихся на расстоянии 78 км, вышли одновременно навстречу друг другу два лыжника и встретились через 3 ч. Первый лыжник шёл со скоростью 12 км/ч. С какой скоростью шёл второй лыжник?
78 : (12 + 14)	(78 – 12· 3) : 3

3. Расположите величины по возрастанию.

От порта к бухте отправился катер. В то же время навстречу ему от бухты поплыла вёсельная лодка. Через 20 минут они одновременно проплыли мимо одного и того же пляжа.

Варианты ответа: Скорость катера; Скорость сближения катера и лодки; Скорость лодки.

Правильный вариант: Скорость лодки; Скорость катера; Скорость сближения катера и лодки.

Движение навстречу друг другу | Математика

Задачи на движение навстречу друг другу (встречное движение) — один из трех основных видов задач на движение.

Если два объекта движутся навстречу друг другу, то они сближаются:

Чтобы найти скорость сближения двух объектов, движущихся навстречу друг другу, надо сложить их скорости:

Скорость сближения больше, чем скорость каждого из них.

Скорость, время и расстояние связаны между собой формулой пути:

Рассмотрим некоторые задачи на встречное движение.

Задача 1

Два велосипедиста выехали навстречу друг другу. Скорость одного из низ 12 км/ч, а другого — 10 км/ч. Через 3 часа они встретились. Какое расстояние было между ними в начале пути?

Решение:

Условие задач на движение удобно оформлять в виде таблицы:

	v, км/ч	t, ч	s, км
I велосипедист	12	3	?
II велосипедист	10	3	?

1) 12+10=22 (км/ч) скорость сближения велосипедистов

2) 22∙3=66 (км) было между велосипедистами в начале пути.

Ответ: 66 км.

Задача 2

Два поезда идут навстречу друг другу. Скорость одного из них 50 км/ч, скорость другого — 60 км/ч. Сейчас между ними 440 км. Через сколько часов они встретятся?

Решение:

v, км/ч

t, ч

s, км

I поезд

II поезд

1) 60+50=110 (км/ч) скорость сближения поездов

2) 440:110=4 (ч) время, через которое поезда встретятся.

Ответ: через 4 ч.

Задача 3.

Два пешехода находились на расстоянии 20 км друг от друга. Они вышли одновременно навстречу друг другу и встретились через 2 часа. Скорость одного пешехода 6 км/ч. Найти скорость другого пешехода.

	v, км/ч	t, ч	s, км
I пешеход	6	2	?
II пешеход	?	2	?

1) 20:2=10 (км/ч) скорость сближения пешеходов

2) 10-6=4 (км/ч) скорость другого пешехода.

Ответ: 4 км/ч.

«Задачи на движение 4 класс»

Самостоятельная работа

Вариант 1.

1.Из двух городов, расстояние между которыми 484 км, вышли одновременно навстречу друг другу два поезда. Скорость одного поезда 45 км/ч. Определите скорость другого поезда, если они встретились через 4 часа.

2.Велосипедист и мотоциклист выехали одновременно из двух поселков навстречу друг другу. Велосипедист ехал со скоростью 15 км/ч, а мотоциклист — со скоростью 57 км/ч. Через сколько часов они встретятся, если расстояние между поселками 288 км?

3.Из двух деревень одновременно навстречу друг другу выехали мотоциклист и автомобилист и встретились через 4 часа. Скорость мотоциклиста 32 км/ч, скорость автомобилиста в 3 раза больше. Найдите расстояние между деревнями.

4*.Из двух городов, расстояние между которыми 780 км, одновременно навстречу друг другу вышли два поезда со скоростью 70 км/ч и 60 км/ч.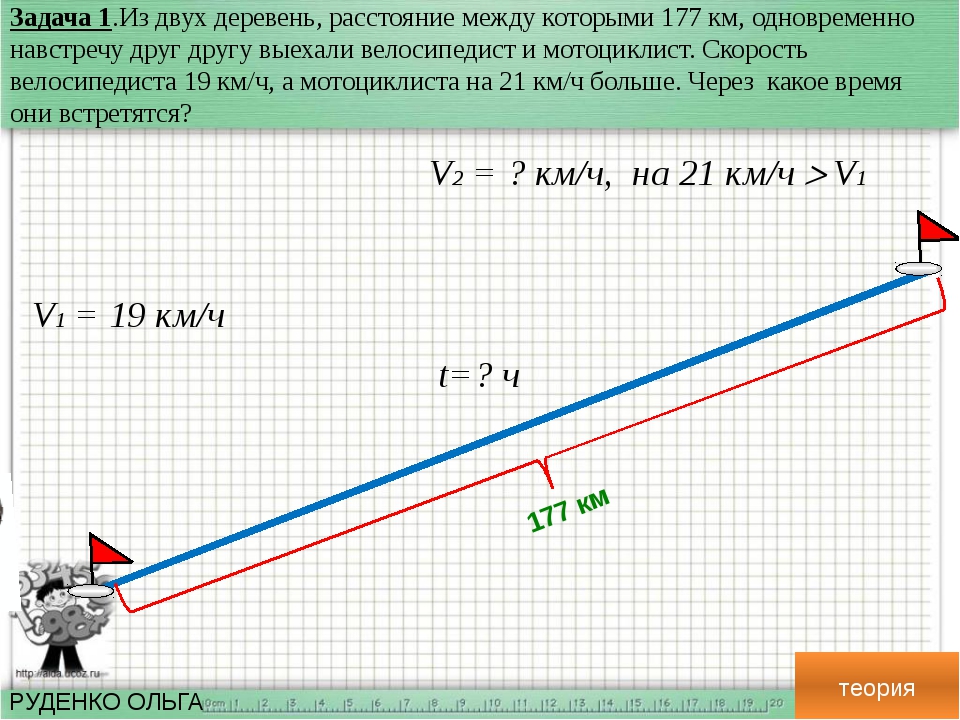 Какой путь до встречи прошел каждый поезд?

__________________________________________________________________

Вариант 2.

1.Из двух городов, расстояние между которыми 600 км, выехали одновременно навстречу друг другу два автобуса и встретились через 5 часов. Скорость первого автобуса 65 км/ч. Найдите скорость второго автобуса.

2.Автомобиль и автобус выехали одновременно из двух городов навстречу друг другу. Скорость автомобиля 90 км/ч, автобуса 70 км/ч. Через сколько часов они встретятся, если расстояние между городами 1600 км?

3.0т двух пристаней отошли одновременно навстречу друг другу катер и лодка и встретились через 3 часа. Скорость лодки 15 км/ч, скорость катера в 4 раза больше. Найдите расстояние между пристанями.

4*.Из двух пунктов, находящихся на расстоянии 500 км, одновременно навстречу друг другу выехали два автобуса, скорость которых 54 км/ч и 46 км/ч. Какой путь до встречи прошел каждый автобус?

Административная контрольная работа по математике за 3 четверть 4 класса

АДМИНИСТРАТИВНАЯ Контрольная работа

ПО МАТЕМАТИКЕ

4 класс

III четверть

Цели:

проверить умения: алгоритмы письменного умножения и деления на числа, оканчивающиеся нулями, алгоритмы письменного умножения на двузначные числа; решать текстовые задачи на движение;

совершенствовать вычислительные умения и навыки, навыки самостоятельной работы;

прививать аккуратность, интерес к изучению математики.

1 в а р и а н т

1. Решите задачу.

Из двух городов, расстояние между которыми 390 км, одновременно навстречу друг другу выехали два мотоциклиста и встретились через 3 ч. Один мотоциклист ехал со скоростью 60 км/ч. Найдите скорость другого мотоциклиста.

2. Решите задачу.

Автомобиль и мотоцикл выехали одновременно в противоположных направлениях из одного города. Скорость автомобиля 60 км/ч, мотоцикла – 70 км/ч. Какое расстояние будет между ними через 3 часа?

3. Решите примеры.

72 090 · 768 240 : 40 68 · 47

2 160 · 400238 800 : 600 259 · 72

4. Решите уравнение.

Х · 100= 15800-1600

2 в а р и а н т

1. Решите задачу.

Из двух городов, расстояние между которыми 600 км, одновременно выехали навстречу друг другу два автомобиля, которые встретились через 4 ч. Один автомобиль ехал со скоростью 70 км/ч. Какова скорость второго автомобиля?

2. Решите задачу.

Из гаража одновременно в противоположных направлениях вышли две автомашины. Одна шла со скоростью 50 км/ч, другая – со скоростью 70 км/ч. Какое расстояние будет между ними через 4 часа?

3. Решите примеры.

93 650 · 675 270 : 30 76 · 54

78 240 · 900205 100 : 700 349 · 62

4.Решите уравнение.

Х:10=1360 — 760

Адрес публикации: https://www.prodlenka.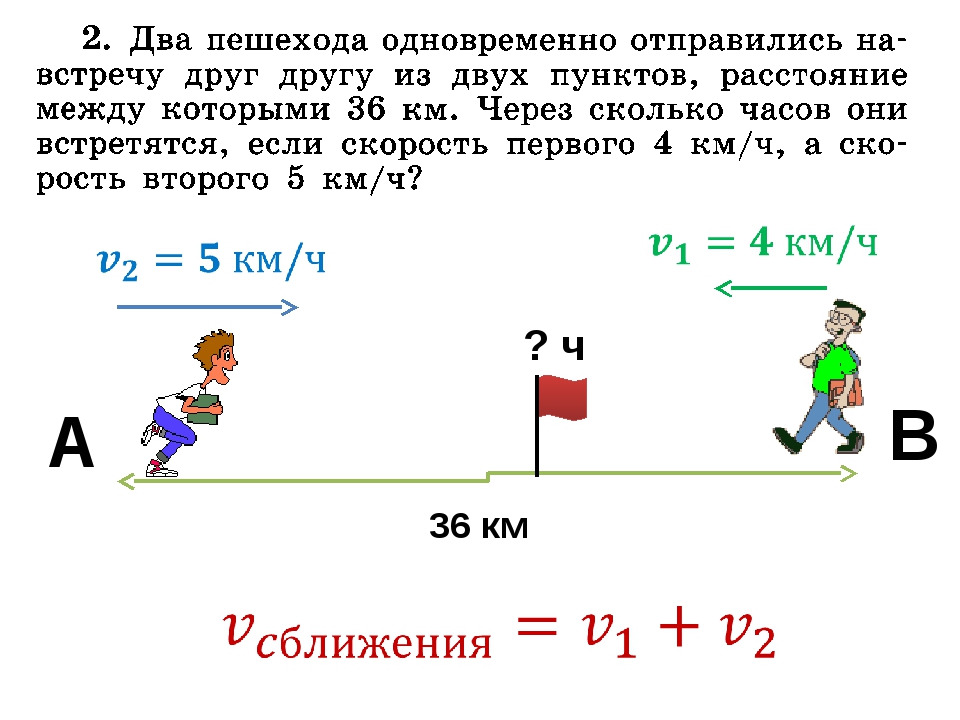 org/metodicheskie-razrabotki/192609-administrativnaja-kontrolnaja-rabota-po-matem

Система задач на движение .

Задачи на движение .

1. Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 24 км/ч, а вторую половину пути – со скоростью, на 16 км/ч большей скорости первого, в результате чего прибыл в пункт B одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч.

2. Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 13 км/ч, а вторую половину пути – со скоростью 78 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилем.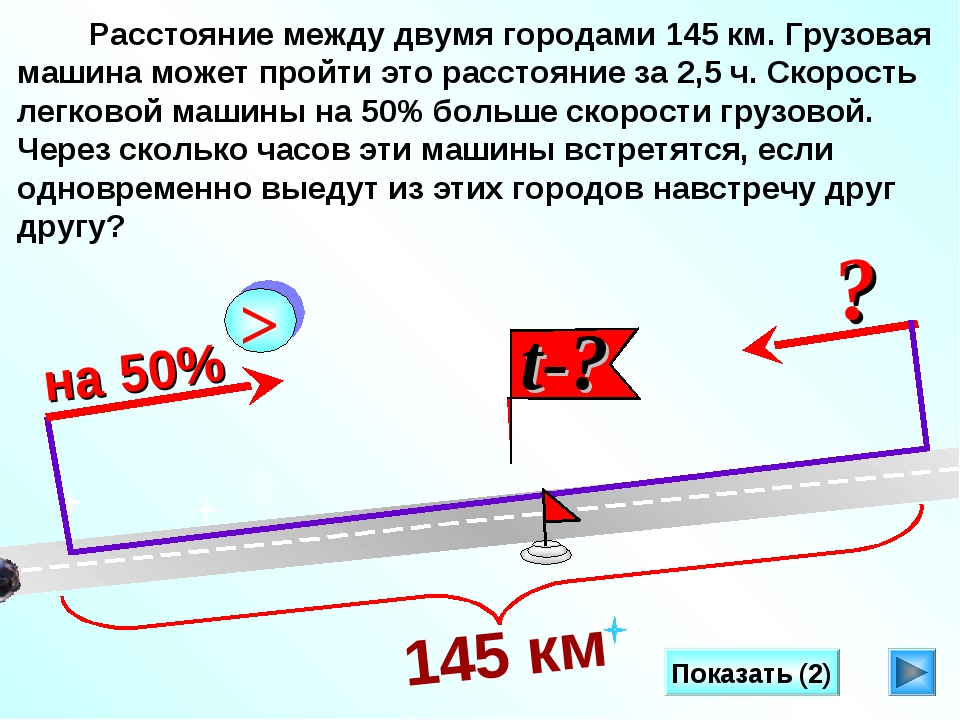 Найдите скорость первого автомобиля, если известно, что она больше 48 км/ч. Ответ дайте в км/ч.

3. Из пункта A в пункт B, расстояние между которыми 75 км, одновременно выехали автомобилист и велосипедист. Известно, что за час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт B на 6 часов позже автомобилиста. Ответ дайте в км/ч.

4. Велосипедист выехал с постоянной скоростью из города A в город B, расстояние между которыми равно 70 км. На следующий день он отправился обратно в A со скоростью на 3 км/ч больше прежней. По дороге он сделал остановку на 3 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость велосипедиста на пути из B в A. Ответ дайте в км/ч.

5. Велосипедист выехал с постоянной скоростью из города A в город B, расстояние между которыми равно 98 км. На следующий день он отправился обратно со скоростью на 7 км/ч больше прежней. По дороге он сделал остановку на 7 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость велосипедиста на пути из A в B. Ответ дайте в км/ч.

6. Два велосипедиста одновременно отправились в 240-километровый пробег. Первый ехал со скоростью, на 1 км/ч большей, чем скорость второго, и прибыл к финишу на 1 час раньше второго. Найти скорость велосипедиста, пришедшего к финишу первым. Ответ дайте в км/ч.

7. Два велосипедиста одновременно отправились в 88–километровый пробег. Первый ехал со скоростью, на 3 км/ч большей, чем скорость второго, и прибыл к финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.

8. Из двух городов, расстояние между которыми равно 560 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 65 км/ч и 75 км/ч?

9. Из городов и , расстояние между которыми равно 330 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 3 часа на расстоянии 180 км от города Найдите скорость автомобиля, выехавшего из города Ответ дайте в км/ч.

10. Расстояние между городами и равно 435 км. Из города в город со скоростью 60 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города выехал со скоростью 65 км/ч второй автомобиль. На каком расстоянии от города автомобили встретятся? Ответ дайте в километрах.

11. Расстояние между городами и равно 470 км. Из города в город выехал первый автомобиль, а через 3 часа после этого навстречу ему из города выехал со скоростью 60 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 350 км от города Ответ дайте в км/ч.

12. Из городов A и B навстречу друг другу выехали мотоциклист и велосипедист. Мотоциклист приехал в B на 3 часа раньше, чем велосипедист приехал в A, а встретились они через 48 минут после выезда. Сколько часов затратил на путь из B в A велосипедист?

13. Товарный поезд каждую минуту проезжает на 750 метров меньше, чем скорый, и на путь в 180 км тратит времени на 2 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.

14. Расстояние между городами и равно 150 км. Из города в город выехал автомобиль, а через 30 минут следом за ним со скоростью 90 км/ч выехал мотоциклист, догнал автомобиль в городе и повернул обратно. Когда он вернулся в , автомобиль прибыл в Найдите расстояние от до Ответ дайте в километрах.

15. Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 300 метрам?

16. Первый велосипедист выехал из поселка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 10 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого – третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч.

17. Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени – со скоростью 66 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

18. Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую треть – со скоростью 120 км/ч, а последнюю – со скоростью 110 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

19. Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий час – со скоростью 100 км/ч, а затем два часа – со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

20. Первые 190 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км — со скоростью 90 км/ч, а затем 170 км — со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

21. Поезд, двигаясь равномерно со скоростью 80 км/ч, проезжает мимо придорожного столба за 36 секунд. Найдите длину поезда в метрах.

22. Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо лесополосы, длина которой равна 400 метрам, за 1 минуту. Найдите длину поезда в метрах.

23. По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 90 км/ч и 30 км/ч. Длина товарного поезда равна 600 метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно 1 минуте. Ответ дайте в метрах.

24. По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах.

25. Два человека отправляются из одного дома на прогулку до опушки леса, находящейся в 4,4 км от дома. Один идёт со скоростью 2,5 км/ч, а другой — со скоростью 3 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от дома произойдёт их встреча? Ответ дайте в километрах.

26. Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 8 км. Путь из А в В занял у туриста 5 часов, из которых 1 час ушёл на спуск. Найдите скорость туриста на спуске, если она больше скорости на подъёме на 3 км/ч. Ответ дайте в км/ч.

27. Автомобиль выехал с постоянной скоростью 75 км/ч из города А в город В, расстояние между которыми равно 275 км. Одновременно с ним из города С в город В, расстояние между которыми равно 255 км, с постоянной скоростью выехал мотоциклист. По дороге он сделал остановку на 50 минут. В результате автомобиль и мотоцикл прибыли в город В одновременно. Найдите скорость мотоциклиста. Ответ дайте в км/ч.

28. Иван и Алексей договорились встретиться в Н-ске. Они едут к Н-ску разными дорогами. Иван звонит Алексею и узнаёт, что тот находится в 168 км от Н-ска и едет с постоянной скоростью 72 км/ч. Иван в момент звонка находится в 165 км от Н-ска и ещё должен по дороге сделать 30-минутную остановку. С какой скоростью должен ехать Иван, чтобы прибыть в Н-ск одновременно с Алексеем?

29. Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 8 км. Пешеход прошёл путь из А в В за 2 часа 45 минут. Время его движения на спуске составило 1 час 15 минут.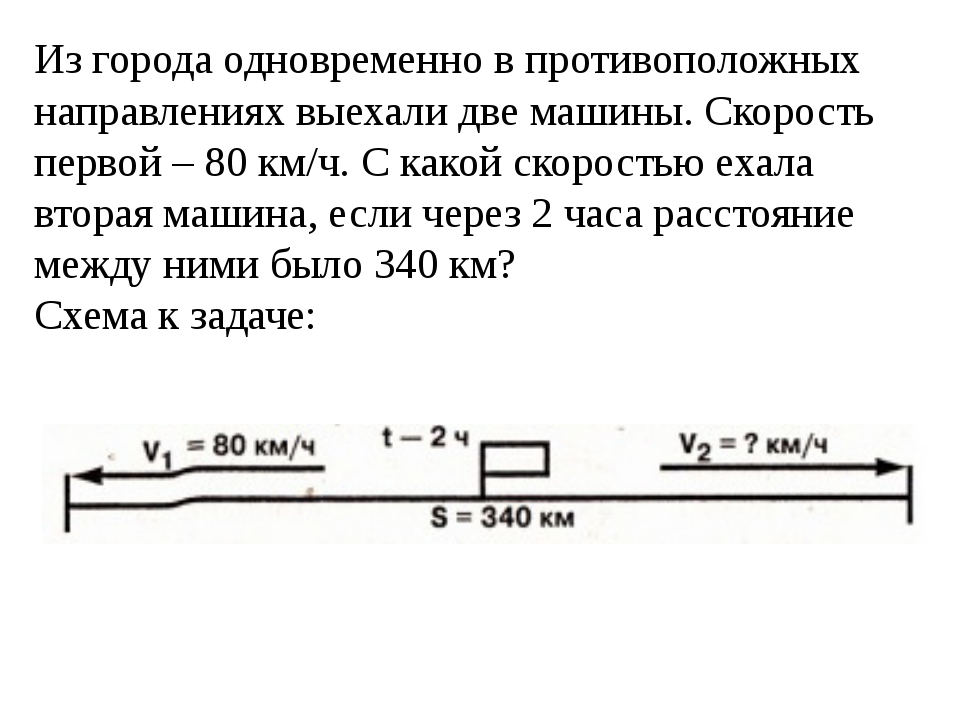 С какой скоростью пешеход шёл на спуске, если скорость его движения на подъёме меньше скорости движения на спуске на 2 км/ч? Ответ выразите в км/ч.

30. Автомобиль, движущийся с постоянной скоростью 70 км/ч по прямому шоссе, обгоняет другой автомобиль, движущийся в ту же сторону с постоянной скоростью 40 км/ч. Каким будет расстояние (в километрах) между этими

автомобилями через 15 минут после обгона?

Решения и ответы

Решение.

Пусть км/ч — скорость первого автомобиля, тогда скорость второго автомобиля на второй половине пути равна км/ч. Примем расстояние между пунктами за 1. Автомобили были в пути одно и то же время, отсюда имеем:

Таким образом, скорость первого автомобиля была равна 32 км/ч.

Ответ: 32.

Решение.

Пусть км/ч – скорость первого автомобиля, тогда скорость второго автомобиля на первой половине пути равна км/ч. Примем расстояние между пунктами за 2. Автомобили были в пути одно и то же время, отсюда имеем:

Таким образом, скорость первого автомобиля была равна 52 км/ч.

Ответ: 52.

Решение.

Пусть км/ч – скорость велосипедиста, тогда скорость автомобилиста равна км/ч. Велосипедист был в пути на 6 часов больше, отсюда имеем:

Таким образом, скорость велосипедиста была равна 10 км/ч.

Ответ: 10.

Решение.

Пусть км/ч – скорость велосипедиста на пути из B в A, тогда скорость велосипедиста на пути из A в B равна км/ч. Сделав на обратном пути остановку на 3 часа, велосипедист затратил на обратный путь столько же времени, сколько на путь из A в B, отсюда имеем:

Таким образом, скорость велосипедиста была равна 10 км/ч.

Ответ: 10.

Решение.

Пусть км/ч – скорость велосипедиста на пути из A в B, тогда скорость велосипедиста на пути из B в A – км/ч. Сделав на обратном пути остановку на 7 часов, велосипедист затратил на обратный путь столько же времени, сколько на путь из A в B, отсюда имеем:

Таким образом, скорость велосипедиста была равно 7 км/ч.

Ответ: 7.

Решение.

Пусть км/ч — скорость велосипедиста, пришедшего к финишу первым, тогда скорость второго велосипедиста — км/ч, Первый велосипедист прибыл к финишу на 1 час раньше второго, отсюда имеем:

Значит, первым финишировал велосипедист, двигавшийся со скоростью 16 км/ч.

Ответ: 16.

Решение.

Пусть км/ч – скорость велосипедиста, пришедшего к финишу вторым, тогда скорость первого велосипедиста равна км/ч. Первый велосипедист прибыл к финишу на 3 часа раньше второго, отсюда имеем:

Таким образом, скорость велосипедиста, пришедшего к финишу вторым, равна 8 км/ч.

Ответ: 8.

Решение.

Пусть t ч – время движения автомобилей до встречи. Первый автомобиль пройдет расстояние 65t км, а второй – 75t км. Тогда имеем:

Таким образом, автомобили встретятся через 4 часа.

Ответ: 4.

Решение.

Автомобиль, выехавший из города , преодолел расстояние (330 – 180) км = 150 км за 3 часа. Пусть км/ч – скорость данного автомобиля. Таким образом,

км/ч.

Ответ: 50.

Решение.

Пусть автомобили встретятся на расстоянии км от города , тогда второй автомобиль пройдет расстояние км. Второй автомобиль находился в пути на 1 час меньше первого, отсюда имеем:

Ответ: 240.

Решение.

Пусть км/ч – скорость первого автомобиля. Автомобиль, выехавший из города , преодолел расстояние (470 – 350) км = 120 км. Первый автомобиль находился в пути на 3 часа больше, чем второй. Таким образом,

Ответ: 70.

Решение.

Примем расстояние между городами 1. Пусть время движения велосипедиста равно ч, тогда время движения мотоциклиста равно ч, К моменту встречи они находились в пути 48 минут и в сумме преодолели всё расстояние между городами, поэтому

Таким образом, велосипедист находился в пути 4 часа.

Ответ: 4.

Решение.

Скорость товарного поезда меньше, чем скорого на 750 м/мин или на

Пусть км/ч — скорость товарного поезда, тогда скорость скорого поезда км/ч. На путь в 180 км товарный поезд тратит времени на 2 часа больше, чем скорый, отсюда имеем:

Ответ: 45.

Решение.

Обозначим км – расстояние от A до C, км/ч – скорость автомобиля, ч – время движения мотоциклиста от A до C. Тогда и Решим систему полученных уравнений:

Тогда км.

Ответ: 90.

Приведём другой способ решения.

Обозначим км — скорость автомобиля. В момент выезда мотоциклиста между автомобилем и мотоциклом было 0,5v км, и мотоциклист догонит автомобиль в городе C за ч. За это же время мотоцикл вернётся в A, а автомобиль доедет до B.

Всего автомобиль затратит времени За это время он со скоростью v проедет 150 км. Получим уравнение:

Положительный корень уравнения Тогда мотоцикл затратит на дорогу до C час, а поскольку его скорость равна 90, то расстояние до C равно 90 км.

Ответ: 90.

Решение.

Пусть км/ч – скорость второго пешехода, тогда скорость первого – км/ч. Пусть через часов расстояние между пешеходами станет равным 0,3 километра. Таким образом,

часа или минут.

Ответ: 12.

Решение.

Пусть км/ч – скорость третьего велосипедиста, а ч – время, которое понадобилось ему, чтобы догнать второго велосипедиста. Таким образом,

А через 2 часа 20 минут после этого догнал первого. Таким образом,

Таким образом,

Ответ: 25.

Решение.

Чтобы найти среднюю скорость на протяжении пути, нужно весь путь разделить на все время движения. Пусть автомобиль находился в пути часов, тогда его средняя скорость равна:

км/ч.

Ответ: 70.

Решение.

Чтобы найти среднюю скорость на протяжении пути, нужно весь путь разделить на все время движения. Пусть км – весь путь автомобиля, тогда средняя скорость равна:

км/ч.

Ответ: 88.

Решение.

Чтобы найти среднюю скорость на протяжении пути, нужно весь путь разделить на все время движения. Средняя скорость равна:

км/ч.

Ответ: 70.

Решение.

Чтобы найти среднюю скорость на протяжении пути, нужно весь путь разделить на все время движения. Средняя скорость автомобиля равна

км/ч.

Ответ: 72.

Решение.

Скорость поезда равна За 36 секунд поезд проходит мимо придорожного столба расстояние, равное своей длине:

Ответ: 800.

Решение.

Скорость поезда равна 60 км в час, значит, за 1 минуту поезд проезжает 1 км. За это время поезд проезжает мимо лесополосы, то есть проходит расстояние, равное сумме длин лесополосы и самого поезда. Поэтому длина поезда равна метров.

Ответ: 600.

Решение.

Скорость сближения поездов равна 60 км/ч или 1 км/мин. Следовательно, за 1 минуту пассажирский поезд сместится относительно товарного на 1 км. При этом он преодолеет расстояние, равное сумме длин поездов. Поэтому длина пассажирского поезда равна 1000 − 600 = 400 м.

Приведём другое решение.

Скорость сближения поездов равна

Пусть длина пассажирского поезда равна х метров. За 60 секунд один поезд проходит мимо другого, то есть преодолевает расстояние х + 600. Тогда:

Поэтому длина пассажирского поезда 400 м.

Ответ: 400.

Решение.

Относительная скорость поездов равна

За 36 секунд один поезд проходит мимо другого, то есть вместе поезда преодолевают расстояние, равное сумме их длин:

м,

поэтому длина скорого поезда

Ответ: 300.

Решение.

Пусть х км — искомое расстояние, его проходит путник, движущийся медленнее, за часов. Другой путник вначале проходит 4,4 км до опушки, а затем возвращается на км назад, то есть всего он проходит км за часа. Времена движения путников равны, тогда:

Тем самым, искомое расстояние равно 4 км.

Ответ: 4.

Приведем другое решение.

Пусть x км — расстояние, которое не дошел до опушки первый путник, оно равно расстоянию, которое прошел от опушки до места встречи второй путник. Путники затратили одно и то же время, поэтому

Не дойдя 0,4 км до опушки, первый путник оказался на расстоянии 4,4 − 0,4 = 4 км от дома. Это и есть искомое расстояние.

Приведем другое решение.

Пусть x ч — время, прошедшее от начала движения до момента встречи пешеходов. Тогда к моменту их встречи тот, кто шёл медленнее, прошёл 2,5x км, а тот, кто шёл быстрее, прошёл 3x км, из которых 4,4 км до опушки, а 3х − 4,4 в обратном направлении. Пешеходы встретились на одном и том же расстоянии от опушки, поэтому расстояние, которое ещё осталось пройти до опушки более медленному из них, равно расстоянию, на которое более быстрый от неё уже удалился. Следовательно, 4,4 − 2,5х = 3х − 4,4, откуда х = 1,6 ч, а искомое расстояние равно 2,5 · 1,6 = 4 км.

Комментарий. Уравнение можно было бы составить несколько по-другому. По каждому участку либо прошли оба пешехода, либо один пешеход дважды, поэтому общий пройденный путь равен удвоенному расстоянию от дома до опушки: 3х + 2,5х = 8,8.

Приведем другое решение.

Тот, кто идет быстрее, дойдет до опушки за 4,4 : 3 = 22/15 часа. За это время тот, кто идет медленнее, пройдет 2,5 · 22/15 = 11/3 км и окажется на расстоянии 4,4 − 11/3 = 11/15 км от опушки. Далее они пойдут на встречу друг другу со скоростью сближения 5,5 км/час и преодолеют разделяющее их расстояние за (11/15) : 5,5 = 2/15 часа. За это время медленно идущий пешеход пройдет еще 2,5 · 2/15 = 1/3 км и окажется на расстоянии 11/3 + 1/3 = 4 км от точки отправления.

Приведем ещё одно решение.

Условие задачи равносильно тому, что два человека, каждый из которых находится на расстоянии 4,4 км от опушки, идут навстречу друг другу. Скорость их сближения равна 5,5 км/час. Встреча произойдёт через 8,8 : 5,5 = 1,6 часа на расстоянии 2,5 · 1,6 = 4 км от дома.

Решение.

Пусть скорость, с которой турист спускался, равна х км/час, тогда его скорость на подъёме равна х − 3 км/ч, длина спуска равна х км, длина подъёма равна 4(х − 3) км. Поскольку весь путь равен 8 км, имеем: х + 4(х − 3) = 8, откуда х = 4 км/ч.

Ответ: 4.

Решение.

Время, необходимое, чтобы доехать до города, равно 275 : 75 = 11/3 часа или 3 часа 40 минут. Поскольку мотоциклист должен сделать 50-минутную остановку, у него остаётся 2 часа 50 минут или 17/6 часа на движение. За это время он должен проехать 255 км, поэтому его скорость должна быть равной 255 : (17/6) = 90 км/час.

Ответ: 90.

Решение.

Алексей приедет в Н-ск через

Обозначим скорость Ивана за Поскольку время его движения с учётом получасовой остановки равно времени движения Алексея, получаем уравнение:

Ответ: 90.

Решение.

Заметим, что время подъема составило 1 час 30 минут или 1,5 часа, а время спуска 1,25 часа. Пусть x км/ч — скорость движения пешехода на спуске, тогда х − 2 км/ч — скорость движения пешехода на подъеме, 1,25х км — длина пути на спуске, 1,5(х − 2) км — длина пути на подъеме. Всего было пройдено 8 км, откуда имеем:

Тем самым, скорость пешехода на спуске была равна 4 км/ч.

Ответ: 4.

автомобилями через 15 минут после обгона?

Решение.

Скорость удаления автомобилей друг от друга составляет: 70 − 40 = 30 км/ч.

Переведем минуты в часы: 15 минут составляют часа.

Таким образом, через 15 минут после обгона расстояние составит: км.

Ответ: 7,5.

Как найти встречное время

Рассмотрим задачи, в которых речь идёт о встречном движении. В таких задачах два каких-нибудь объекта движутся на встречу друг другу. Задачи на встречное движение можно решать двумя способами.

Задача 1. Два автомобиля выехали одновременно из двух населённых пунктов и встретились через 4 часа. Первый автомобиль ехал со скоростью 100 км/ч, а второй – со скоростью 70 км/ч. На каком расстоянии друг от друга находятся населённые пункты?

Решение: Из условия задачи известны скорость каждого автомобиля и время, которое автомобили были в пути. Значит, можно найти расстояние, которое проехал каждый автомобиль до встречи. Для этого нужно скорость умножить на время:

1) 100 · 4 = 400 (км) – проехал первый автомобиль

2) 70 · 4 = 280 (км) – проехал второй автомобиль

Найдя сумму полученных результатов, узнаем расстояние между населёнными пунктами:

400 + 280 = 680 (км)

Данную задачу можно решить и другим способом. Каждый час расстояние между автомобилями сокращалось на 170 километров (100 + 70), 170 км/ч – это скорость сближения автомобилей. За 4 часа они проехали расстояние:

Таким образом, задачу на встречное движение можно решить двумя способами:

1-й способ:	2-й способ:
1) 100 · 4 = 400 (км)	1) 100 + 70 = 170 (км/ч)
2) 70 · 4 = 280 (км)	2) 170 · 4 = 680 (км)
3) 400 + 280 = 680 (км)

Ответ: Населённые пункты находятся на расстоянии 680 км.

Задача 2. Из двух посёлков навстречу друг другу вышли одновременно два пешехода. Скорость первого пешехода 4 км/ч, а скорость второго пешехода 5 км/ч. Какое расстояние будет между пешеходами через 5 часов после выхода, если расстояние между посёлками 70 км?

Решение: Сначала можно определить сколько километров прошёл каждый из пешеходов за 5 часов, для этого скорость пешеходов умножим на 5:

1) 4 · 5 = 20 (км) – прошёл первый пешеход

2) 5 · 5 = 25 (км) – прошёл второй пешеход

Затем можно найти общий путь, пройденный двумя пешеходами за 5 часов:

Теперь можно найти расстояние между пешеходами, отняв от общего расстояния между посёлками 45 уже пройденных километров:

У данной задачи есть и второй вариант решения. Можно сначала найти скорость сближения пешеходов:

Затем найти пройденное расстояние, умножив скорость сближения (9 км/ч) на время движения пешеходов (5 ч):

А теперь, для нахождения расстояния между пешеходами, вычесть пройденное расстояние (45 км) из общего:

Таким образом, данная задача имеет два варианта решения:

1-й способ:	2-й способ:
1) 4 · 5 = 20 (км)	1) 4 + 5 = 9 (км/ч)
2) 5 · 5 = 25 (км)	2) 9 · 5 = 45 (км)
3) 20 + 25 = 45 (км)	3) 70 – 45 = 25 (км)
3) 70 – 45 = 25 (км)

Ответ: Через 5 часов расстояние между пешеходами будет 25 км.

Главная > Памятка

Информация о документе
Дата добавления:
Размер:
Доступные форматы для скачивания:

Памятка «Учимся решать задач на движение»

В задачах на движение рассматриваются три взаимосвязанные величины:

S – расстояние (пройденный путь),

t – время движения и

V – скорость – расстояние, пройденное за единицу времени.

Расстояние – это произведение скорости на время движения

Скорость – это частное от деления расстояния на время движения

Время – это частное от деления расстояния на скорость движения

Задачи на встречное движение

Если два тела одновременно движутся навстречу друг другу, то расстояние между ними постоянно изменяется на одно и то же число, равное сумме расстояний, которые проходят тела за единицу времени.

Скорость сближения – это сумма скоростей, движущихся навстречу друг другу тел. V сближ. = 1V + 2V

Пример 1. Два велосипедиста одновременно выехали навстречу друг другу из двух посёлков и встретились через 3 часа. Первый велосипедист ехал со скоростью 12 км/ч, а второй – 14 км/ч. На каком расстоянии находятся посёлки?

V сближ. = 1V + 2V

1) 12 • 3 = 36 (км) – проехал первый велосипедист до встречи

2) 14 • 3 = 42 (км) – проехал второй велосипедист до встречи

3) 36 + 42 = 78 (км)

1) 12 + 14 = 26 (км/ч) – скорость сближения

Ответ : расстояние между посёлками 78 км.

Пример 2. Из двух городов навстречу друг другу выехали две машины. Скорость первой – 80 км/ч, скорость второй – 60 км/ч. Через, сколько часов машины встретятся, если расстояние между городами 280 км?

V сближ. = 1V + 2V

1) 80 + 60 = 140 (км/ч) – скорость сближения

2) 280 : 140 = 2 (ч)

Ответ : машины встретятся через 2 часа.

Пример 3. Из двух городов, расстояние между которыми 340 км, выехали одновременно навстречу друг другу две машины. Скорость первой – 80 км/ч. С какой скоростью ехала вторая машина, если встретились они через 2 часа?

2V = V сближ. – 1V

1) 340 : 2 = 170 (км/ч) – скорость сближения

2) 170 – 80 = 90 (км/ч)

Ответ : 90 км/ч. скорость второй машины

Задачи на движение в противоположных направлениях

Если два тела одновременно движутся в противоположных направлениях, то расстояние между ними постепенно увеличивается.

Скорость удаления – это расстояние, которое проходят тела за 1 ч при движении в противоположных направлениях. V удал. = 1V + 2V

Пример 1. Два лыжника одновременно вышли из пункта А в противоположных направлениях. Первый лыжник шёл со скоростью 12 км/ч, а второй – 14 км/ч. На каком расстоянии друг от друга они будут через 3 ч?

1)12 • 3 = 36 (км) – расстояние, которое прошёл первый лыжник за 3 ч

2)14 • 3 = 42 (км) – расстояние, которое прошёл второй лыжник за 3 ч

1)12 + 14 = 26 (км/ч) – скорость удаления

Ответ: через 3 ч они будут друг от друга на расстоянии 78 км.

Пример 2. Из города в противоположных направлениях выехали две машины. Скорость первой – 80 км/ч, скорость второй – 60 км/ч. Через сколько часов расстояние между машинами будет 280 км?

1) 80 + 60 = 140 (км/ч) – скорость удаления

2) 280 : 140 = 2 (ч)

Ответ: через 2 часа расстояние между машинами будет 280 км

Пример 3. Из города одновременно в противоположных направлениях выехали две машины. Скорость первой – 80 км/ч. С какой скоростью ехала вторая машина, если через 2 часа расстояние между ними было 340 км?

1) 340 : 2 = 170 (км/ч) – скорость удаления машин

2) 170 – 80 = 90 (км/ч)

Ответ: скорость второй машины 90 км/ч.

Задачи на движение в одном направлении

Пример 1. Автомобиль за 2 ч проехал 192 км. Следующие 3 ч он двигался со скоростью на 6 км/ч меньше. Сколько всего километров проехал автомобиль?

1)192 : 2 = 96 (км/ч) – первая скорость

2)96 – 6 = 90 (км/ч) – вторая скорость

3)90 • 3 = 270 (км) – второе расстояние

4)192 + 270 = 462 (км)

Пример 2. Из двух пунктов, расстояние между которыми 24 км, одновременно вышел спортсмен и выехал велосипедист. Скорость спортсмена 6 км/ч., а скорость велосипедиста 18 км/ч..

1).Через сколько часов велосипедист догонит спортсмена?

2).На каком расстоянии от пункта В велосипедист догонит спортсмена?

3). На сколько километров путь велосипедиста больше пути спортсмена?

18 км/ч 6 км/ч ?

V приближ. = 2V -1V , где 2V ֺ > 1V

1). 18 – 6 = 12 (км /ч.) – скорость приближения велосипедиста и спортсмена

2). 24 : 12 = 2 (ч.) – время, через которое велосипедист догонит спортсмена.

3). 6 ●2 = 12 (км) – расстоянии, на котором велосипедист догонит спортсмена.

Ответ: через 2 часа; 12 км.

Пример 3. За какое время мотоцикл догонит грузовой автомобиль, если расстояние между ними 45 км, а скорость мотоцикла больше скорости грузовика на 15 км/ч?

Цель: закрепить умение решать задачи на встречное движение.

Карточки можно использовать и для индивидуальной, и для парной работы.

Скачать:

Вложение	Размер
zadachi_na_vstrechnoe_dvizhenie_4_klass.docx	14.58 КБ

Предварительный просмотр:

1. Из двух деревень одновременно вышли навстречу друг другу две группы туристов. Одна группа шла со скоростью 3 км/ч, а другая 4 км/ч. Встретились они через 2 ч. Чему равно расстояние между деревнями?

2. С двух полярных станций одновременно навстречу друг другу выехали две собачьи упряжки. Одна упряжка двигалась со скоростью 14 км/ч, а скорость другой 12 км/ч. Через сколько часов упряжки встретятся, если расстояние между полярными станциями 52 км?

3. Два лыжника вышли одновременно навстречу друг другу из двух разных пунктов, расстояние между которыми

66 км. Скорость первого 12 км/ч. С какой скоростью ехал второй лыжник, если они встретились через 3 часа?

1. Из двух городов одновременно вылетели навстречу друг другу два голубя. Они встретились через 5 ч. Скорость одного голубя 62 км/ч, а второго 68 км/ч. Узнай расстояние между городами.

2. Два пешехода вышли одновременно из двух деревень навстречу друг другу. Один шёл со скоростью 5 км/ч, скорость другого 4 км/ч. Через сколько часов они встретятся, если расстояние между деревнями 36 км?

3. Два пловца поплыли одновременно навстречу друг другу с двух разных концов бассейна, длина которого 100 метров. Первый плыл со скоростью 20 м/мин. С какой скоростью плыл второй пловец, если они встретились через 2 минуты?

1.Из двух посёлков одновременно выехали навстречу друг другу велосипедист и мотоциклист. Они встретились через 4 ч. Скорость велосипедиста 15 км/ч, а мотоциклиста 57 км/ч. Узнай расстояние между посёлками.

2. Две многоножки ползли навстречу друг другу. Скорость одной 2 дм/мин, а скорость второй 3 дм/мин. Через сколько минут они встретятся, если первоначальное расстояние между ними было 15 дм?

3. Две ласточки одновременно вылетели навстречу друг другу. Одна летит со скоростью 23 м/с. С какой скоростью летит вторая ласточка, если первоначальное расстояние между ними 920 м и встретились они через 20 секунд?

1.От двух пристаней одновременно навстречу друг другу отошли катер и лодка. Они встретились через 6 ч. Скорость лодки 8 км/ч, а скорость катера 35 км/ч. Узнай расстояние между пристанями.

2.Дв пчелы вылетели из ульев одновременно навстречу друг другу. Одна пчела летела со скоростью 8 м/с, скорость другой 7 м/с. Через сколько секунд пчёлы встретятся, если расстояние между ульями 135 м?

3. Автомобиль и автобус выехали одновременно из двух городов навстречу друг другу. Скорость автомобиля 90 км/ч. Расстояние между городами 1600 км. С какой скоростью шёл автобус, если они встретились через 10 часов?

1. Две водомерки отправились одновременно с противоположных концов пруда навстречу друг другу. Они встретились через 3 минуты. Одна водомерка плыла со скоростью 48 м/мин, а другая со скоростью 40 м/мин. Узнай расстояние между берегами пруда.

2. С двух станций, расстояние между которыми равно 320 км, вышли одновременно два товарных поезда. Один поезд проходил 29 км, а другой 35 км. Через сколько часов эти поезда встретятся?

3. Расстояние между сёлами 48 км. Из них вышли одновременно навстречу друг другу два пешехода. Скорость одного пешехода 3 км/ч. С какой скоростью шёл второй пешеход, если они встретились через 6 часов?

1. От двух городов одновременно отошли навстречу друг другу товарный и пассажирский поезда. Товарный поезд шёл со скоростью 56 км/ч, а пассажирский со скоростью 74 км/ч. Каково расстояние между городами, если поезда встретились через 4 ч?

2.От двух раковин два рака ползут навстречу друг другу. Скорость первого 18 м/мин, а скорость второго 20 м/мин. Через сколько минут раки встретятся, если расстояние между раковинами равно 114 м?

3. От двух причалов, расстояние между которыми 90 км, одновременно вышли навстречу друг другу две лодки. Первая шла со скоростью 8 км/ч. С какой скоростью шла вторая лодка, если они встретились через 5 часов?

1. Две группы туристов вышли одновременно навстречу друг другу из двух сёл. Расстояние между сёлами 27 км. Одна группа шла со скоростью 4 км/ч. С какой скоростью шла вторая группа, если они встретились через 3 часа?

2. Теплоход и катер отошли от двух пристаней одновременно навстречу друг другу. Скорость теплохода 30 км/ч, скорость катера 25 км/ч. Через сколько часов суда встретятся, если расстояние между пристанями равно 330 км?

3. Две гремучие змеи выползли одновременно из своих укрытий навстречу друг другу и встретились через 5 минут. Скорость одной змеи 48 м/мин, а скорость другой 53 м/мин. Каково расстояние между укрытиями змей?

1.Два мотоциклиста выехали одновременно навстречу друг другу из двух городов. Расстояние между городами 465 км. Первый мотоциклист ехал со скоростью 80 км/ч. С какой скоростью ехал второй мотоциклист, если они встретились через 3 часа?

2. Две медузы плыли навстречу друг другу. Скорость одной 50 м/мин, а скорость другой 55 м/мин. Через сколько минут они встретятся, если первоначальное расстояние между ними было 315 метров?

3. Две девочки вышли одновременно навстречу друг другу из своих домов. Они встретились через 8 минут. Одна шла со скоростью 60 м/мин, а другая со скоростью 70 м/мин. Какое расстояние между домами девочек?

Ответы к задаче Ответы к задачам 4 класс по математике (Часть 1)

Задача №5048

Ответы в самом низу встроенного документа

4 класс
ПРОСТЫЕ ЗАДАЧИ НА ДВИЖЕНИЕ
1789)   Лыжник прошёл дистанцию 24 км за 3 ч. С какой скоростью он шёл?
1790)   Мотоциклист ехал 4 ч со скоростью 80 км/ч. Какое расстояние он проехал?
1791)   Лодка проплыла 28 км со скоростью 7 км/ч. Какое время она была в пути?
1792)   бегая от кота, пробежала 12 м до своей норки за 4 с. С какой скоростью она бежала?
1793)   За какое время пешеход пройдёт 15 км, идя со скоростью 5 км/ч?
1794)   С какой скоростью должен ехать вело-сипедист, чтобы за 3 ч проехать 33 км?
1795)   Самолёт летел 4 ч со скоростью 600 км/ч. Какое расстояние он пролетел?
1796)   За какое время прошёл турист 28 км, если он шёл со скоростью 4 км/ч?
1797)   Гепард пробежал 6000 м за 4 мин. С какой скоростью он бежал?
1798)   Спасаясь от собаки, кошка вскарабкалась на дерево со скоростью 2 м/с за 3 с. На какую высоту забралась кошка?
1799)   Бамбук за 24 ч вырос на 72 см. С какой скоростью рос бамбук?
1800)   Какое расстояние проплывёт катер за 4 ч, если он движется со скоростью 32 км/ч?
1801)   Почтовый голубь летел 3 ч со скоростью 90 км/ч. Какое расстояние он пролетел?
1802)   Скорость звука в воздухе 330 м/с. Через какое время мы услышим звук выстрела, произведенного на расстоянии 990 м?
1803)   За 3 ч поезд прошёл 210 км. Чему равна скорость поезда?
1804)   Расстояние до школы 1200 м мальчик прошёл за 20 мин. С какой скоростью он шёл в школу?
1805)   Плот проплыл по течению реки 18 км за 6 ч. Какова скорость течения реки?
1806)   Скорость грузового поезда 35 км/ч. Поезд был в пути 2 ч. Какое расстояние он прошёл?
1807)   Велосипедист проехал 36 км за 2 ч. С какой скоростью он двигался?
1808)   Охотник верхом на лошади проехал 28 км со скоростью 14 км/ч. Сколько времени он потратил на дорогу?
1809)   Расстояние от города до посёлка 30 км. Сколько времени потребуется пешеходу, чтобы пройти это расстояние со скоростью 6 км/ч?
1810)   Мальчик пробежал 20 м за 10 с. С какой скоростью бежал мальчик?
1811)   Крейсер проплыл 80 км со скоростью 40 км/ч. Сколько времени он затратил?
1812)   Муха летела 15 с со скоростью 5 м/с. Какое расстояние она пролетела?
1813)   Грач пролетел 100 м со скоростью 10 м/с. Сколько времени он был в пути?
1814)   За 3 с сокол пролетел 78 м. Какова скорость сокола?
1815)   Орёл летел 6 с со скоростью 30 м/c. Сколько метров пролетел орёл?
1816)   Расстояние в 450 км скорый поезд проехал за 5 ч. С какой скоростью ехал поезд?
1817)   Лыжник прошёл с одинаковой скоростью 70 км за 5 ч. Какова скорость лыжника?
1818)   Туристы плыли 5 ч на лодке со скоростью 12 км/ч. Какое расстояние они проплыли?
1819)   Расстояние в 240 км мотоциклист проехал со скоростью 40 км/ч. За сколько часов мотоциклист проехал это расстояние?
1820)   толёт пролетел 600 км. С какой скоростью летел вертолёт?
1821)   За 3 дня верблюд прошёл 240 км. С какой скоростью шёл верблюд?
ЗАДАЧИ НА ВСТРЕЧНОЕ ДВИЖЕНИЕ
1822)   Два пешехода вышли одновременно из двух деревень навстречу друг другу. Один шёл со скоростью 5 км/ч, другой — 4 км/ч. Встретились они через 3 ч. Каково расстояние между деревнями?
1823)   Два лыжника вышли одновременно на-встречу друг другу из двух пунктов, расстояние между которыми 66 км. Скорость первого 12 км/ч, второго — 10 км/ч. Через какое время они встретятся?
1824)   Два поезда вышли одновременно навстречу друг другу из двух городов, расстояние между которыми 650 км, и встретились через 5 ч. Чему равна скорость второго поезда, если скорость первого равна 62 км/ч?
1825)   Велосипедист и мотоциклист выехали одновременно из двух посёлков навстречу друг другу. Велосипедист ехал со скоростью 15 км/ч, а мотоциклист — со скоростью 57 км/ч. Через сколько часов они встретятся, если расстояние между посёлками 288 км?
1826)   Товарный и пассажирский поезда вышли одновременно навстречу друг другу из двух городов, расстояние между которыми 520 км. Товарный поезд шёл со скоростью 56 км/ч и прошёл до встречи 224 км. Какова скорость пассажирского поезда?
1827)   От двух пристаней одновременно от-правились два теплохода навстречу друг другу. Они встретились через 6 ч. Какой путь прошёл каждый теплоход, если скорость первого 42 км/ч, а расстояние между пристанями 474 км?
1828)   Два самолёта вылетели из двух городов одновременно навстречу друг другу и встретились через 3 ч. Скорость первого 320 км/ч, второго — 450 км/ч. Каково расстояние между городами?
1829)   Две девочки вышли одновременно из своих домов навстречу друг другу. Первая девочка шла со скоростью 60 м/мин и прошла до встречи 420 м. Вторая девочка шла со скоростью 70 м/мин. Какое расстояние до встречи прошла вторая девочка?
1830)   Два автомобиля выехали одновременно навстречу друг другу из двух городов, расстояние между которыми 450 км. Скорость первого авто-мобиля 70 км/ч. Какова скорость второго автомобиля, если они встретились через 3 ч?
1831)   Два мальчика поплыли одновременно навстречу друг другу с двух концов бассейна, длина которого 100 м. Первый плыл со скоростью 20 м/мин, второй — со скоростью 30 м/мин. Какое расстояние до встречи проплыл каждый?
1832)   От двух пристаней, расстояние между ко-торыми 90 км, одновременно направились навстречу друг другу два теплохода. Первый теплоход шёл со скоростью 20 км/ч, второй — со скоростью 25 км/ч. Через сколько часов они встретились?
1833)   Из посёлка и города выехали одновременно навстречу друг другу велосипедист и мотоциклист. Велосипедист ехал со скоростью 16 км/ч, а мотоциклист — со скоростью 54 км/ч. Велосипедист проехал до встречи 48 км. Какое расстояние до встречи проехал мотоциклист?
1834)   Две ласточки летят со скоростью 23 м/с. Через сколько секунд они встретятся, если расстояние между ними 920 м?
1835)   Два поезда вышли из двух городов од-новременно навстречу друг другу. Один поезд шёл со скоростью 63 км/ч. С какой скоростью шёл второй поезд, если расстояние между городами 564 км? Встретились поезда через 4 ч.
1836)   От двух причалов, расстояние между которыми 90 км, одновременно вышли навстречу друг другу две лодки. Первая шла со скоростью 8 км/ч, вторая — со скоростью 10 км/ч. Через сколько часов лодки встретились?
1837)   Два мальчика одновременно побежали навстречу друг другу по спортивной дорожке, длина которой 200 м. Они встретились через 20 с. Первый бежал со скоростью 5 м/с. С какой скоростью бежал второй мальчик?
1838)   От двух станций отошли одновременно два грузовых поезда. Встретились они через 5 ч. Один поезд проходил в час 29 км, а другой — 35 км. Каково расстояние между этими станциями?
1839)   Из двух городов одновременно навстречу друг другу выехали два автобуса. Скорость первого автобуса 25 км/ч, скорость второго — 50 км/ч. Первый автобус прошёл до встречи 100 км. Сколько километров прошёл до встречи второй автобус?
1840)   * Расстояние между двумя городами 81 км. Из них одновременно навстречу друг другу выехали два велосипедиста. Один велосипедист проезжает в час на 3 км больше другого. На каком расстоянии от городов они встретились, если встреча произошла через 3 ч после выезда?
1841)   Два всадника поскакали одновременно навстречу друг другу из двух пунктов, расстояние между которыми 100 км. Всадники встретились через 4 ч. Найдите скорость первого всадника, если скорость второго — 13 км/ч.
1842)   От двух пристаней одновременно навстречу друг другу отошли катер и лодка. До встречи катер прошёл 48 км, а лодка — 24 км. Скорость лодки 8 км/ч. Найдите скорость катера.
1843)   От двух пристаней одновременно отошли навстречу друг другу два катера, которые встретились через 3 ч. Скорость первого катера 15 км/ч, скорость второго — 18 км/ч. Найдите расстояние между пристанями.
1844)   Из двух городов выехали одновременно навстречу друг другу два мотоциклиста. Один двигался со скоростью 80 км/ч. Он проехал до встречи 320 км. Какое расстояние до встречи проехал второй мотоциклист, если он двигался со скоростью 65 км/ч?
1845)   От двух пристаней отошли одновременно навстречу друг другу катер и лодка. Встретились они через 3 ч. Скорость лодки 15 км/ч, скорость катера — в 4 раза больше. Найдите расстояние между пристанями.
1846)   С двух аэродромов одновременно вылетели навстречу друг другу два самолёта и встретились через 3 ч. Скорость первого самолёта 600 км/ч, а второго — 900 км/ч. Найдите расстояние между аэродромами.
1847)   Из двух городов, расстояние между ко-торыми 840 км, вышли одновременно навстречу друг другу два поезда. Скорость первого поезда 100 км/ч, второго — на 10 км/ч больше. Через сколько часов поезда встретятся?
1848)   От двух пристаней отошли одновременно навстречу друг другу катер и лодка. Они встретились через 5 ч. Скорость лодки 12 км/ч, скорость катера — в 5 раз больше. Найдите расстояние между пристанями.
1849)   * От одной пристани отплыл в 11 ч ночи теплоход, проходивший по 25 км/ч, а от другой при-стани навстречу ему в 3 ч следующего утра вышёл другой теплоход, проходивший по 27 км/ч. Через сколько часов после отплытия второго теплохода они встретятся, если между пристанями 360 км?
1850)   *Два туриста, расстояние между которыми 140 км, выехали навстречу друг другу один после другого через 3 ч. Через сколько часов после отъезда первого они встретятся, если скорость первого туриста 10 км/ч, а второго 12 км/ч?
1851)   От двух пристаней навстречу друг другу одновременно отошли теплоход и катер. Теплоход шёл со скоростью 33 км/ч, а катер — 25 км/ч. Через 3 ч они встретились. Чему равно расстояние между пристанями?
1852)   Из двух деревень одновременно навстречу друг другу вышли девочка, которая двигалась со скоростью 3 км/ч, и мальчик, который двигался в 2 раза быстрее девочки. Встреча произошла через 4 ч. Каково расстояние между деревнями?
1853)   *Два поезда идут навстречу друг другу с двух станций, расстояние между которыми 385 км. Первый вышёл раньше на 2 ч и движется со скоростью 53 км/ч. Через 3 ч после выхода второго поезда они встретились. Какова скорость второго поезда?
1854)   Из двух городов, расстояние между ко-торыми 484 км, вышли одновременно навстречу друг другу два поезда. Скорость одного поезда 45 км/ч. Определите скорость другого поезда, если поезда встретились через 4 ч.
1855)   Из двух городов одновременно навстречу друг другу отправились пассажирский и товарный поезда. Они встретились через 12 ч. Каково расстояние между городами, если известно, что скорость пассажирского поезда 75 км/ч, а товарного — 35 км/ч?
1856)   Из двух городов одновременно навстречу друг другу вышли два поезда. Один шёл со скоростью 42 км/ч, а другой — 52 км/ч. Через 6 ч поезда встретились. Найдите расстояние между городами.
1857)   Расстояние по реке между двумя при-станями 275 км. От них одновременно навстречу друг другу отошли пароход и баржа. Пароход шёл со скоростью 28 км/ч. Найдите скорость баржи, если известно, что её встреча с пароходом произошла через 5 ч после выхода.
1858)   Из двух городов, расстояние между ко-торыми 1380 км, вышли одновременно навстречу друг другу два поезда и встретились через 10 ч. Скорость одного из них 75 км/ч. Найдите скорость другого поезда.
1859)   Расстояние между сёлами 48 км. Через сколько часов встретятся два пешехода, которые вышли одновременно навстречу друг другу, если скорость одного 3 км/ч, а другого — 5 км/ч?
1860)   * От деревни до города 300 км. Из деревни в город выехал мотоциклист со скоростью 42 км/ч. Спустя 2 ч навстречу ему выехал велосипедист со скоростью 12 км/ч. Через сколько часов они встретятся?
1861)   Из двух городов одновременно навстречу друг другу выехали два мотоциклиста и встретились через 10 мин. Скорость одного из них 920 м/мин, другого — 970 м/мин. Найдите расстояние между городами.
1862)   Из одного города в другой одновременно навстречу друг другу вышли два поезда. Они встретились через 9 ч. Скорость одного поезда 48 км/ч, а скорость другого — на 5 км/ч больше. Найдите расстояние между городами.
Зачёт 9
Вариант 1
1863)   Скорость пешехода 60 м/мин. Какой путь он пройдёт за 30 мин?
1864)   Расстояние между городами 366 км поезд прошёл за 6 ч. Чему равна скорость поезда?
1865)   За какое время самолёт пролетит 1200 км, если его скорость 300 км/ч?
1866)   Два поезда вышли из двух городов одно-временно навстречу друг другу и встретились через 4 ч.

Скорость первого поезда 68 км/ч, второго — 72 км/ч. Чему равно расстояние между городами?
1867)   Автомобиль и автобус выехали одно-временно из двух пунктов навстречу друг другу. Скорость автомобиля 90 км/ч, автобуса — 70 км/ч. Через сколько часов они встретятся, если расстояние между пунктами 1600 км?
1868)   Из двух городов, расстояние между которыми 600 км, выехали одновременно навстречу друг другу два автобуса и встретились через 5 ч. Скорость первого автобуса 65 км/ч. Найдите скорость второго автобуса.
1869)   От двух причалов одновременно навстречу друг другу отошли две лодки. Скорость первой лодки 6 км/ч, и она прошла до встречи 18 км. Скорость второй лодки 9 км/ч. Какой путь до встречи прошла вторая лодка?
1870)   От двух пристаней одновременно навстречу друг другу отошли два теплохода. Скорость первого 24 км/ч и он прошёл до встречи 96 км. Второй теплоход прошёл до встречи 120 км. Какова его скорость?
1871)   Два пешехода вышли одновременно навстречу друг другу из двух сёл. Первый прошёл до встречи 12 км со скоростью 4 км/ч. Второй шёл со скоростью 5 км/ч. Чему равно расстояние между сёлами?
1872)   Из двух городов, расстояние между кото-рыми 780 км, одновременно навстречу друг другу вышли два поезда со скоростью 70 км/ч и 60 км/ч. Какой путь до встречи прошёл каждый поезд?
Вариант 2
1873)   Автомобиль ехал от города до посёлка 3 ч со скоростью 55 км/ч. Каково расстояние от города до посёлка?
1874)   Велосипедист проехал 30 км за 3 ч. Какова его скорость?
1875)   Турист прошёл 20 км со скоростью 4 км/ч. Сколько времени он был в пути?
1876)   Теплоход и катер отошли от двух пристаней одновременно навстречу друг другу. Скорость теплохода 30 км/ч, катера — 25 км/ч. Чему равно расстояние между пристанями, если суда встретились через 6 ч?
1877)   Девочка и мальчик побежали с двух концов беговой дорожки одновременно навстречу друг другу и встретились через 30 с. Длина беговой дорожки 300 м. Скорость девочки 4 м/с. Какова скорость мальчика?
1878)   Из двух городов одновременно навстречу друг другу вышли два поезда. Скорость первого поезда 65 км/ч, скорость второго — 70 км/ч, он прошёл до встречи 350 км. Какой путь до встречи прошёл первый поезд?
1879)   С двух станций одновременно навстречу друг другу вышли два поезда. Первый поезд прошёл до встречи 360 км со скоростью 60 км/ч, второй поезд прошёл до встречи 384 км. Какова его скорость?
1880)   Два мотоциклиста выехали одновременно навстречу друг другу из двух городов. Первый проехал до встречи 240 км со скоростью 80 км/ч. Скорость второго — 75 км/ч. Чему равно расстояние между городами?
1881)   Из двух пунктов, находящихся на рассто-янии 500 км, одновременно навстречу друг другу выехали два автобуса, скорость которых 54 км/ч и 46 км/ч. Какой путь до встречи прошёл каждый автобус?
Вариант 3
1882)   Из двух деревень одновременно навстречу друг другу выехали два велосипедиста. Скорость первого а км/ч, второго — b км/ч. Чему равно расстояние между деревнями, если велосипедисты встретились через d ч?
1883)   Катер плыл а ч со скоростью d км/ч. Чему равен путь катера?
1884)   Пловец проплыл p м за m с. Чему равна его скорость?
1885)   Скорость поезда b км/ч. За какое время он проедет n км?
1886)   Два пешехода вышли одновременно навстречу друг другу из двух сёл, расстояние между которыми f км. Скорость первого пешехода b км/ч, второго — d км/ч. Через какое время они встретятся?
1887)   Расстояние между двумя городами q км. Из них одновременно навстречу друг другу выехали два велосипедиста и встретились через n ч. Скорость первого велосипедиста p км/ч. Найдите скорость второго велосипедиста.
1888)   Два лыжника вышли одновременно на-встречу друг другу с двух лыжных баз. Первый лыжник прошёл до встречи а км со скоростью m км/ч. Скорость второго лыжника b км/ч. Какой путь до встречи прошёл второй лыжник?
1889)   Два мальчика вышли из своих домов одновременно навстречу друг другу. Первый мальчик прошёл до встречи z м со скоростью к м/мин. С какой скоростью шёл второй мальчик, если он прошёл до встречи x м.
1890)   Из двух аэропортов одновременно на-встречу друг другу вылетели два самолёта. Один пролетел до встречи m км со скоростью z км/ч. Скорость второго — и км/ч. Каково расстояние между аэропортами?
1891)   Два пешехода вышли из двух пунктов одновременно навстречу друг другу со скоростью w км/ч и g км/ч. Какой путь до встречи прошёл каждый, если расстояние между пунктами n км?
Вариант 4
1892)   Какое расстояние проедет мотоцикл, движущийся со скоростью b км/ч, за n ч?
1893)   Плот проплыл по течению реки r км за f ч. Чему равна скорость течения реки?
1894)   Мотоциклист проехал d км со скоростью к км/ч. Какое время он был в пути?
1895)   Два мальчика одновременно навстречу друг другу отплыли от двух концов бассейна и встретились через n мин. Скорость первого мальчика p м/мин, а второго — q м/мин. Чему равна длина бассейна?
1896)   Два велосипедиста выехали одновременно навстречу друг другу из двух сёл, расстояние между которыми а км. Скорость первого x км/ч, а второго — m км/ч. Через какое время они встретятся?
1897)   Расстояние между посёлком и деревней c км. Из них одновременно навстречу друг другу выехали мотоциклист и велосипедист. Скорость велосипедиста j км/ч. Найдите скорость мотоциклиста, если они встретились через m ч.
1898)   Два конькобежца побежали с двух концов ледяной дорожки одновременно навстречу друг другу. Скорость первого конькобежца w м/с, а второго — z м/с. Какой путь до встречи пробежал первый конькобежец, если путь второго равен q м?
1899)   Два поезда вышли одновременно навстречу друг другу с двух станций. Первый шёл со скоростью m км/ч и прошёл до встречи f км. Второй поезд прошёл до встречи p км. Какова скорость второго поезда?
1900)   Из двух хозяйств одновременно навстречу друг другу выехали два трактора со скоростью p км/ч и q км/ч. Первый проехал до встречи f км. Найдите расстояние между хозяйствами.
1901)   Из двух сёл, расстояние между которыми z км, одновременно навстречу друг другу вышли два туриста со скоростью n км/ч и m км/ч. Какой путь до встречи прошёл каждый?
ЗАДАЧИ НА ДВИЖЕНИЕ В ОДНОМ
НАПРАВЛЕНИИ
1902)   От города до поселка автобус ехал 2 ч со скоростью 75 км/ч. Сколько времени понадобится велосипедисту, чтобы проехать этот путь со скоростью 15 км/ч?
1903)   В первый день туристы прошли 30 км, а во второй — 24 км, затратив на весь путь 9 ч. Сколько часов они были в пути каждый день, если двигались с одинаковой скоростью?
1904)   Автомобилист проехал за два дня 770 км. В первый день он ехал 4 ч со скоростью 80 км/ч, во второй день он ехал со скоростью 90 км/ч. Сколько часов был в пути автомобилист во второй день?
1905)   Первую часть пути поезд шёл со скоростью 50 км/ч, вторую часть пути — 5 ч — со скоростью 70 км/ч. За какое время поезд прошёл весь путь, равный 900 км?
1906)   Велосипедист ехал по просёлочной дороге 3 ч со скоростью 7 км/ч, затем по шоссе со скоростью 10 км/ч. На весь путь он затратил 5 ч. Какое расстояние он проехал?
1907)   Автобус, скорость которого 54 км/ч, прошёл путь между двумя пунктами за 8 ч. За какое время проедет этот путь автомобиль, скорость которого 72 км/ч?
1908)   До привала велосипедисты ехали 5 ч, после привала, отдохнув, ещё 3 ч и проехали с той же скоростью, что и до привала, на 22 км меньше. Какой путь проехали велосипедисты за весь день?
1909)   Санки съехали с горки за 10 с со скоростью 2 м/с, а потом по ровной дороге проделали путь в 2 раза больший. Сколько всего метров проехали санки?
1910)   Часть пути до школы школьник шёл со скоростью 50 м/мин в течение 4 мин. Остальную часть пути он шёл со скоростью 80 м/мин. На весь путь до школы он затратил 10 минут. Чему равно расстояние до школы?
1911)   От дома до леса лыжник шёл 2 ч со скоростью 8 км/ч. По лесу он шёл со скоростью 7 км/ч. Сколько времени он шёл по лесу, если всего прошёл 37 км?
1912)   Автобус проехал 180 км за 4 ч. За какое время проедет это расстояние автомобиль, скорость которого в 2 раза больше?
1913)   Велосипедист за 3 ч проехал 24 км, а пешеход за 4 ч прошёл 16 км. Во сколько раз скорость велосипедиста больше скорости пешехода?
1914)   В первый день автомобилист ехал 5 ч со скоростью 72 км/ч, во второй день он проехал такое же расстояние за 4 ч. С какой скоростью ехал автомобилист во второй день?
1915)   Самолет за 3 ч пролетел 960 км, а ав-томобиль за 5 ч проехал 400 км. Во сколько скорость самолета больше скорости автомобиля?
1916)   Мотоциклист ехал 2 ч со скоростью 80 км/ч и 3 ч со скоростью 70 км/ч. Какой путь проехал автомобилист?
1917)   Мотоциклист проехал до места назначения 420 км, сделав в пути одну остановку. До остановки он был в пути 4 ч и ехал со скоростью 80 км/ч. Остальной путь он проехал за 2 ч. С какой скоростью ехал мотоциклист после остановки?
1918)   Автотуристы в первый день проехали 600 км, во второй день — 200 км. На весь этот путь они затратили 8 ч. Сколько часов были в пути туристы каждый день, если они ехали с одинаковой скоростью?
1919)   Моторная лодка, двигаясь со скоростью 17 км/ч, прошла путь между пристанями за 5 ч. Сколько потребуется времени, чтобы пройти этот же путь на байдарке, если она движется со скоростью 5 км/ч?
1920)   Турист прошёл 45 км. Первые 3 ч он шёл со скоростью 5 км/ч. Остальную часть пути он прошёл за 5 ч. С какой скоростью шёл турист остальную часть пути?
1921)   Лыжник шёл со скоростью 18 км/ч и был в пути 3 ч. Сколько времени потребуется пешеходу, чтобы пройти такое же расстояние, если его скорость 9 км/ч?
1922)   Отряд прошёл 39 км. Первые 3 ч он шёл со скоростью 5 км/ч. Остальную часть пути отряд прошёл за 6 ч. С какой скоростью отряд прошёл остальную часть пути?
1923)   Ворона летела 3 ч со скоростью 50 км/ч. Скворец такое же расстояние пролетит за 2 ч. С какой скоростью летит скворец?
1924)   Туристы в первый день были в пути 7 ч, а во второй день — 4 ч, двигаясь с одинаковой скоростью. В первый день туристы прошли на 15 км больше, чем во второй день. Сколько километров проходили туристы в каждый день?
1925)   Лыжник шёл со скоростью 12 км/ч и был в пути 3 ч. Сколько времени понадобится, чтобы пройти такое же расстояние пешеходу, скорость которого 6 км/ч?
1926)   Теплоход в течение двух дней был в пути 15 ч. В первый день он прошёл 200 км, а во второй — 175 км. Сколько часов теплоход был в пути каждый день, если он всё время шёл с одинаковой скоростью?
1927)   От первого города до второго 37 км, а от второго до третьего — 83 км. За сколько часов можно проехать от первого города до третьего на мотоцикле, если каждый час проезжать 40 км?
1928)   За 3 мин самолёт пролетел 30 км. Какое расстояние он пролетит за 40 мин, если его скорость увеличится на 5 км/мин?
1929)   За два дня самолёт пролетел с одинаковой скоростью 10240 км. В первый день в полёте он был 10 ч, а во второй — 6 ч. Сколько километров пролетал самолёт каждый день?
1930)   Машина в первый день за 9 ч прошла 522 км. Во второй день машина была в пути 7 ч и шла с прежней скоростью. Сколько всего километров прошла машина за эти дни?
1931)   Самолёт пролетает 960 км за 2 ч. За сколько часов пролетит то же расстояние другой самолёт, скорость которого в 2 раза больше?
1932)   Автомобиль за 4 ч прошёл 240 км. Сколько километров он пройдёт за 7 ч, если его скорость увеличится на 6 км/ч?
1933)   Поезд, скорость которого 30 км/ч, проходит путь от одного города до другого за 6 ч. За сколько часов проедет автомобиль половину этого пути, если будет ехать по 45 км/ч?
1934)   Туристы за два дня похода прошли 84 км, двигаясь с одинаковой скоростью. В первый день они были в пути 7 ч, а во второй — 5 ч. Какое расстояние прошли туристы в каждый из этих дней?
1935)   Какое время туристы затратили на весь путь, если 90 км они проехали на катере со скоростью 30 км/ч и 12 км прошли пешком со скоростью 4 км/ч?
1936)   Пешеход шёл со скоростью 9 км/ч в течение 2 ч. После этого ему осталось пройти в 3 раза больше того, что он прошёл. Сколько всего километров должен пройти пешеход?
1937)   Спортсмены бежали 3 забега по 500 м, а потом ещё 1000 м. Сколько метров им осталось пробежать, если весь путь равен 6000 м?
1938)   За 6 ч теплоход прошёл 300 км, а поезд за 6 ч прошёл 450 км. На сколько скорость поезда больше скорости теплохода?
1939)   Туристы сделали 3 перехода по 4 км, а по-том прошли ещё 9 км. Сколько километров им оста-лось пройти, если весь путь составляет 32 км?
1940)   За 5 ч грузовая машина прошла 195 км, а легковая машина за 3 ч прошла 360 км. На сколько скорость легковой машины больше скорости грузовой?
1941)   Экскурсанты ехали на пароходе 7 ч со скоростью 32 км/ч и на автобусе 3 ч со скоростью 70 км/ч. Сколько всего километров проехали экскурсанты?
1942)   Студенты ехали по железной дороге 12 ч и на автобусе 8 ч. На сколько больше они проехали по железной дороге, если скорость поезда 65 км/ч, а автобуса — 40 км/ч?
1943)   Гоночный автомобиль за 6 ч прошёл 720 км, а легковой автомобиль за 4 ч — 240 км. Во сколько раз больше скорость гоночного автомобиля?
1944)   Туристы в первый день ехали 5 ч со скоростью 18 км/ч. Во второй день они проехали такое же расстояние за 10 ч. С какой скоростью ехали туристы во второй день?
1945)   Какое расстояние прошли туристы, если в первый день они шли 6 ч со скоростью 4 км/ч, а во второй день столько же времени в 2 раза быстрее?
1946)   Поезд прошёл 352 км. 3 ч он шёл со ско-ростью 48 км/ч. Остальную часть пути прошёл за
4   ч. С какой скоростью шёл поезд остальной путь?
1947)   Черепаха проползла 12 м со скоростью 6 м/мин. За это же время улитка проползла 30 см. С какой скоростью двигалась улитка?
Зачёт 10
Вариант 1
1948)   Туристы шли до привала 4 ч со скоростью
5   км/ч. Отдохнув, они шли ещё 3 ч. Какова была их скорость после привала, если весь путь равен 32 км?
1949)   Путь между двумя деревнями мальчик проезжает на велосипеде за 2 ч со скоростью 10 км/ч. За какое время он пройдет этот путь пешком со скоростью 4 км/ч?
1950)   Расстояние от деревни до посёлка 40 км, а от посёлка до города — 200 км. За какое время можно доехать от деревни до города со скоростью 60 км/ч?
1951)   Автомобиль проехал 210 км со скоростью 70 км/ч и еще 240 км со скоростью 60 км/ч. Какое время он затратил на всю дорогу?
1952)   В первый день туристы за 6 ч прошли 30 км. Во второй день они шли с прежней скоростью и были в пути 7 ч. Какой путь прошли туристы за два дня?
1953)   Катер прошёл 96 км за 3 ч. За какое время он пройдёт тот же путь, если его скорость уменьшится на 8 км/ч?
1954)   Самолет пролетел 1260 км за 3 ч. Какой путь он пролетит за 4 ч, если увеличит свою скорость на 60 км/ч?
1955)   Велосипедист ехал 2 ч со скоростью 10 км/ч. После этого ему осталось проехать в 2 раза больше того, что он проехал. Сколько всего кило-метров он должен проехать?
1956)   Лыжник за 3 ч прошёл 36 км, пешеход за 4 ч прошёл 16 км. Во сколько раз скорость лыжника больше скорости пешехода?
1957)   Туристы ехали на автобусе 3 ч со скоростью 60 км/ч и шли пешком 5 ч со скоростью 6 км/ч. На сколько больше их путь на автобусе, чем пешком?
1958)   Поезд прошёл 250 км со скоростью 50 км/ч. За то же время автомобиль проехал 300 км. Какова скорость автомобиля?
1959)   От дома до школы девочка прошла
2   квартала по 300 м и еще 200 м. Сколько ей осталось пройти, если расстояние до школы 1200 м?

Вариант 2
1960)   Расстояние между городами 260 км. Часть пути автобус проехал за 3 ч со скоростью 32 км/ч, остальной путь он проехал за 4 ч. Какова скорость автобуса на второй части пути?
1961)   Путь между двумя городами можно проехать на поезде за 12 ч со скоростью 80 км/ч. За какое время пролетит этот путь самолёт со скоростью 320 км/ч?
1962)   Путь от посёлка до реки лесом 1500 м и ещё полем 1700 м. За какое время можно дойти от посёлка до реки со скоростью 80 м/мин?
1963)   Самолёт пролетел до посадки 960 км за
3   ч. После заправки он летел с той же скоростью еще 4 ч. Сколько всего пролетел самолёт?
1964)   До станции поезд шёл со скоростью 60 км/ч и прошёл 180 км. До следующей остановки он шёл со скоростью 70 км/ч ещё 280 км. За какое время он прошёл весь путь?
1965)   Автобус проехал 240 км за 4 ч. За какое время проедет этот путь автомобиль, скорость которого на 20 км/ч больше?
1966)   Автобус проезжает 180 км за 4 ч. Какое расстояние он проедет за 3 ч, если увеличит свою скорость на 10 км/ч?
1967)   В первый день туристы шли 6 ч со ско-ростью 5 км/ч. После этого им осталось пройти в 3 раза больше того, что они прошли. Чему равен весь путь туристов?
1968)   Самолет за 4 ч пролетел 1280 км, а авто-мобиль за 5 ч проехал 400 км. Во сколько раз скорость автомобиля меньше скорости самолета?
1969)   Теплоход шёл по озеру 2 ч со скоростью 42 км/ч, затем 3 ч вверх по реке со скоростью 40 км/ч. Какой путь прошёл теплоход?
1970)   Велосипедист проехал 30 км со скоростью 10 км/ч. За это же время пешеход прошёл 12 км. С какой скоростью шёл пешеход?
1971)   Бегун пробежал 2 круга по 600 м, потом ещё 500 м. Сколько ему осталось пробежать, если вся дистанция равна 2 км?
Вариант 3
1972)   От дома до школы а м. Часть пути до по-ворота ученик прошёл за b мин со скоростью d м/мин. Остальной путь он прошёл за n мин. Какова его скорость на пути после поворота?
1973)   Пешеход шёл р ч со скоростью к км/ч. За какое время он сможет пройти этот путь на лыжах со скоростью n км/ч?
1974)   Расстояние между первым и вторым городами b км, между вторым и третим — d км. За какое время поезд со скоростью f км/ч пройдет расстояние между первым и третьим городами?
1975)   Расстояние между пристанями m км катер проплывает за b ч. До следующей пристани он плыл d ч с той же скоростью. Чему равен весь путь, пройденный катером?
1976)   Половину пути до города, равную d км, автобус ехал со скоростью m км/ч. Вторую поло-вину пути он ехал со скоростью n км/ч. За какое время автобус проехал весь путь?
1977)   Велосипедист проехал b км за m ч. За какое время проедет этот путь мотоцикл, ско-рость которого на n км/ч больше?
1978)   Пешеход проходит а км за b ч. Какое расстояние он проедет на велосипеде за к ч, если его скорость увеличится на d км/ч?
1979)   Плот проплыл по течению реки b км за m ч, а лодка проплыла d км за n ч. Во сколько раз скорость лодки больше, чем скорость плота?
1980)   Мальчик шёл до школы а мин со скоростью а м/мин, потом бежал бегом b мин со скоростью q м/мин. Каков путь до школы?
1981)   Автомобиль проехал m км со скорос-тью b км/ч. За это же время мотоцикл проехал n км. Какова скорость мотоцикла?
1982)   Автомобиль проехал первую часть пути за s ч со скоростью b км/ч. Вторая часть пути в n раз длиннее. Сколько всего километров должен проехать автомобиль?
1983)   Туристы проходили за s дней по b км в день, потом еще q км. Сколько им осталось пройти, если весь путь d км?
Вариант 4
1984)   Длина лыжной дистанции f км. Часть пути лыжник прошёл за m ч со скоростью a км/ч, остальной путь он прошёл за b ч. Какова его скорость на второй части пути?
1985)   Лодка плыла f ч со скоростью q км/ч. За какое время пройдет этот путь катер со скоростью j км/ч?
1986)   От города до поселка h км, а от поселка до турбазы g км. За какое время туристы дойдут от города до турбазы, если их скорость r км/ч?
1987)   Пешеход прошёл от деревни до леса и км за l ч, затем по лесу он шёл еще d ч с той же скоростью. Каков общий путь пешехода?
1988)   Путь w км от города до поселка мото-циклист ехал со скоростью p км/ч, а d км от поселка до второго города он ехал со скоростью q км/ч. За какое время он доехал от первого города до второго?
1989)   Автомобиль проехал за t ч w км. За какое время проедет этот путь автобус, скорость которого на к км/ч меньше?
1990)   Пассажирский поезд проехал m км за и ч. Скорость товарного поезда на t км/ч меньше. Какой путь проедет товарный поезд за к ч?
1991)   Когда лодка проплыла от одной пристани до другой f ч со скоростью d км/ч, ей осталось проплыть в s раз меньше того, что она проплыла. Какое расстояние должна проплыть лодка?
1992)   Грузовик за d ч прошёл m км, а автобус прошёл за кч n км. На сколько скорость грузовика меньше скорости автобуса?
1993)   Лыжник шёл в гору n ч со скоростью j км/ч, потом с горы m ч со скоростью h км/ч. Каков весь путь, пройденный лыжником?
1994)   Автобус проехал f км со скоростью w км/ч. За это же время велосипедист проехал к км. Чему равна скорость велосипедиста?
1995)   Катер сделал g рейсов по p км и еще проплыл b км. Сколько ему осталось плыть, если весь путь составляет а км?
ЗАДАЧИ НА ПРОТИВОПОЛОЖНОЕ
ДВИЖЕНИЕ И ДВИЖЕНИЕ
В ОБРАТНОМ НАПРАВЛЕНИИ
1996)   Из одного пункта одновременно в про-тивоположных направлениях вышли два лыжника. Через 3 ч расстояние между ними было 60 км. Чему равна скорость второго лыжника, если скорость первого 11 км/ч?
1997)   Расстояние между двумя городами машина проехала за 6 ч со скоростью 80 км/ч. Обратный путь она проехала за 8 ч. На сколько уменьшилась её скорость?
1998)   Из одного города одновременно в про-тивоположных направлениях выехали автобус и мотоцикл. Скорость автобуса 40 км/ч, мотоцикла — в 2 раза больше. Какое расстояние будет между ними через 3 ч?
1999)   Расстояние между пристанями 150 км теплоход прошёл за 6 ч. На обратном пути его скорость увеличилась на 5 км/ч. За какое время теплоход пройдёт весь путь туда и обратно?
2000)   От пристани одновременно в противо-положных направлениях отошли два катера. Скорость первого 32 км/ч, второго — на 4 км/ч меньше. Через какое время расстояние между ними будет 180 км?
2001)   Расстояние до стадиона 1200 м мальчик прошёл за 15 мин. На обратный путь он потратил на 5 мин больше. С какой скоростью мальчик шёл обратно?
2002)   Из посёлка одновременно в противопо-ложных направлениях вышел пешеход и выехал велосипедист. Когда велосипедист проехал 22 км со скоростью 11 км/ч, расстояние между ними стало 30 км. С какой скоростью шёл пешеход?
2003)   Расстояние между посёлками 30 км лыжник прошёл за 3 ч. На обратном пути он уменьшил скорость на 4 км/ч. Сколько времени он потратил на путь туда и обратно?
2004)   От одной станции одновременно в про-тивоположных направлениях вышли два поезда, один из которых шёл со скоростью 62 км/ч. Через 5 ч расстояние между ними было 630 км. Чему равна скорость второго поезда?
2005)   С одного аэродрома одновременно в противоположных направлениях вылетели два самолёта. Один летел со скоростью 420 км/ч, скорость другого на — 80 км/ч меньше. Какое расстояние будет между ними через 3 ч?
2006)   Автомобиль и мотоцикл выехали одно-временно в противоположных направлениях из одного города. Скорость автомобиля 60 км/ч, мотоцикла — 70 км/ч. Какое расстояние будет между ними через 3 ч.
2007)   Машина шла до остановки 5 ч со скоростью 72 км/ч. После этого ей осталось проехать вдвое меньший путь, на который она потратила 3 ч. С какой скоростью ехала машина вторую часть пути?
2008)   Велосипедист проехал 24 км со скоростью 8 км/ч. Пешеход потратил на этот путь на 1 ч больше. С какой скоростью шёл пешеход?
2009)   Мальчик проплыл 100 м со скоростью 25 м/мин. Девочка потратила на эту дистанцию на 1 мин больше. С какой скоростью плыла девочка?
2010)   От одной станции одновременно в про-тивоположных направлениях отошли товарный и пассажирский поезда. Скорость товарного 42 км/ч, а пассажирского — в 2 раза больше. Через какое время расстояние между ними будет 504 км?
2011)   *Как двум мальчикам, используя один велосипед, одновременно и в кратчайшее время добраться до станции, расстояние до которой 2400 м, если скорость каждого пешком 60 м/мин, а на велосипеде — 120 м/мин?
2012)   Два электропоезда одновременно отошли от одной станции в противоположных направлениях. Скорость первого поезда 90 км/ч, скорость второго — на 30 км/ч меньше. Какое расстояние будет между поездами через 4 ч?
2013)   От автостанции одновременно отошли в противоположных направлениях грузовая и легковая автомашины. Когда грузовик прошёл 70 км, легковая машина прошла 140 км. Скорость грузовой машины — 35 км/ч. Найдите скорость легковой машины.
2014)   С автостанции одновременно отошли в противоположных направлениях автобус и такси. Скорость такси 60 км/ч, а скорость автобуса — в 2 раза меньше. Через сколько часов расстояние между ними составит 360 км?
2015)   Из гаража одновременно в противопо-ложных направлениях вышли две автомашины. Одна шла со скоростью 50 км/ч, другая — со скоростью 70 км/ч. На каком расстоянии друг от друга будут эти машины через 4 ч?
2016)   Из турбазы вышли одновременно и пошли в противоположных направлениях два человека. Один шёл со скоростью 5 км/ч, а другой — со скоростью 4 км/ч. На каком расстоянии друг от друга будут эти люди через 5 ч после выхода?
2017)   С аэродрома вылетели в одно и то же время в противоположных направлениях два самолёта. Через 3 ч расстояние между ними было 3630 км. Один из них летел со скоростью 640 км/ч. С какой скоростью летел другой самолёт?
2018)   Из одного посёлка вышли в одно и то же время в противоположных направлениях два пешехода. Скорость одного 5 км/ч, скорость другого — 6 км/ч. Через сколько часов расстояние между ними будет равно 33 км?
2019)   Из одной деревни в одно и то же время в противоположных направлениях вышли два крестьянина. Скорость одного из них 6 км/ч, другого — 3 км/ч. На каком расстоянии друг от друга будут пешеходы через 5 ч?
2020)   Со станции одновременно в противо-положных направлениях отошли автобус и машина. Скорость машины 70 км/ч, а скорость автобуса — в 2 раза меньше. Через сколько часов расстояние между ними составит 525 км?
2021)   Велосипедист от города до дачи ехал 3 ч со скоростью 12 км/ч, а на обратный путь он затратил 4 ч. На сколько велосипедист изменил свою скорость?
2022)   Пароход прошёл путь между пристанями за 8 ч со скоростью 30 км/ч. На обратном пути то же расстояние теплоход прошёл за 6 ч. С какой скоростью шёл теплоход на обратном пути?
2023)   Из двух пунктов в одно и то же время в противоположных направлениях выехали два мотоциклиста. Скорость первого мотоциклиста
60   км/ч, скорость второго — на 15 км/ч больше. Найдите расстояние между пунктами, если известно, что они ехали 6 ч.
2024)   Поезд проехал 400 км со скоростью 50 км/ч, а на обратном пути это расстояние он проехал в 2 раза быстрее. За сколько часов проехал это расстояние поезд на обратном пути?
2025)   Баржа проплыла против течения расстояние в 100 км за 10 ч, а на обратном пути её скорость увеличилась на 10 км/ч. За сколько часов проплыла баржа обратный путь по течению?
2026)   Машина прошла расстояние между го-родами за 5 ч, идя со скоростью 48 км/ч. Обратный путь она прошла за 6 ч. На сколько скорость машины на обратном пути была меньше?
2027)   От пристани одновременно в противо-положных направлениях отошли два теплохода. Через 6 ч расстояние между ними было 360 км. Один из них шёл со скоростью 28 км/ч. С какой скоростью шёл другой теплоход?
2028)   Со станции в одно и то же время в про-тивоположных направлениях вышли два поезда. Скорость одного из них 74 км/ч, а другого —
61   км/ч. Через сколько часов поезда будут нахо-диться на расстоянии 540 км друг от друга?
2029)   Расстояние между двумя пристанями 864 км. Теплоход прошёл это расстояние по течению со скоростью 27 км/ч, а обратный путь против течения — со скоростью 24 км/ч. За сколько часов прошёл весь путь теплоход туда и обратно?
2030)   Расстояние между городами 432 км. Сколько времени потребуется машине на проезд туда и обратно, если её скорость в одном направлении 54 км/ч, а в другом — на 6 км/ч меньше?
2031)   Мальчики прошли до деревни 20 км, двигаясь со скоростью 5 км/ч, а обратно они ехали на велосипеде в 2 раза быстрее. За сколько часов они проедут это расстояние?
2032)   Одновременно в противоположных на-правлениях отправились катер со скоростью 60 км/ч и байдарка, скорость которой в 4 раза меньше. Через сколько часов расстояние между ними будет 375 км?
2033)   Два лыжника вышли из посёлка в одно и то же время в противоположных направлениях. Один шёл со скоростью 14 км/ч, а другой — 10 км/ч. Через сколько часов расстояние между ними будет 96 км?
Зачёт 11
Вариант 1
2034)   Из одного города одновременно в про-тивоположных направлениях выехали два вело-сипедиста. Через 3 ч расстояние между ними стало 57 км. Скорость первого велосипедиста 10 км/ч. Найдите скорость второго велосипедиста.
2035)   Из одного города одновременно в про-тивоположных направлениях выехали два автобуса. Скорость первого 36 км/ч, второго — 45 км/ч. Какое расстояние будет между ними через 3 ч?
2036)   Из одного пункта одновременно в про-тивоположных направлениях вышли два туриста со скоростью 4 км/ч и 5 км/ч. Через сколько часов расстояние между ними будет 36 км?
2037)   От одной пристани одновременно в про-тивоположных направлениях отошли два теплохода со скоростью 37 км/ч и 43 км/ч. Какой путь прошёл каждый теплоход, когда расстояние между ними стало 240 км?
2038)   Из одной деревни одновременно в противоположных направлениях вышли два пешехода со скоростью 6 км/ч и 5 км/ч. Какое расстояние было между ними, когда первый пешеход прошёл 18 км?
2039)   Из одного поселка одновременно в про-тивоположных направлениях выехали велосипедист и мотоциклист. Скорость велосипедиста 12 км/ч, мотоциклиста — в 4 раза больше. Через какое время расстояние между ними будет 180 км?
2040)   Мотоциклист доехал до города за 3 ч со скоростью 72 км/ч, а на обратный путь он потратил 4 ч. На сколько мотоциклист уменьшил свою скорость?
2041)   Расстояние от дома до школы 1200 м ученик прошёл за 20 мин, а на обратном пути его скорость была на 20 м/мин больше. За какое время он дошёл обратно?
2042)   Путь до станции 3600 м мальчик прошёл со скоростью 100 м/мин, а обратно он шёл со скоростью 90 м/мин. Какое время он потратил на весь путь?
Вариант 2
2043)   Из одного пункта одновременно в про-тивоположных направлениях вышли два лыжника, скорость которых 6 км/ч и 10 км/ч. Какое расстояние будет между ними через 2 ч?
2044)   Из одного села одновременно в проти-воположных направлениях выехали два велосипе-диста со скоростью 12 км/ч и 8 км/ч. Через какое время расстояние между ними будет 60 км?
2045)   От одной станции одновременно в про-тивоположных направлениях вышли два поезда. Через 6 ч расстояние между ними стало 840 км.
Найти скорость второго поезда, если скорость первого 75 км/ч.
2046)   Из одного посёлка одновременно в про-тивоположных направлениях выехали мотоцикл и автобус. Скорость мотоцикла 76 км/ч, автобуса — 44 км/ч. Какой путь проделал каждый, когда расстояние между ними стало 600 км?
2047)   Из одного посёлка одновременно в про-тивоположных направлениях вышли два туриста со скоростью 4 км/ч и 5 км/ч. Какое расстояние будет между ними, когда первый турист пройдет 8 км?

2048)   Из одного города одновременно в про-тивоположных направлениях выехали два автомобиля. Скорость первого 82 км/ч, второго — на 14 км/ч меньше. Через какое время расстояние между ними будет 600 км?
2049)   Теплоход шёл по течению 6 ч со скоростью 48 км/ч. Обратный путь он прошёл за 8 ч. На сколько изменилась скорость теплохода?
2050)   Автомобиль проехал 420 км между двумя городами со скоростью 70 км/ч. А его скорость на обратном пути была 60 км/ч. Сколько часов автомобиль потратил на весь путь туда и обратно?
2051)   Расстояние между двумя поселками 180 км автобус проехал за 4 ч. На обратном пути его скорость увеличилась на 15 км/ч. Какое время автобус потратил на весь путь туда и обратно?
Вариант 3
2052)   От одной пристани одновременно в противоположных направлениях отошли два катера со скоростью d км/ч и b км/ч. Какое расстояние будет между ними через а ч?
2053)   Из одного города одновременно в про-тивоположных направлениях выехали два поезда со скоростью n км/ч и m км/ч. Через какое время расстояние между ними будет p км?
2054)   С одного аэродрома одновременно в противоположных направлениях вылетели самолёт и вертолёт. Скорость вертолёта f км/ч. Через p ч расстояние между ними стало d км. Найдите скорость самолёта.
2055)   Из одного посёлка одновременно в противоположных направлениях выехали два автомобиля со скоростью а км/ч и b км/ч. Какой путь проехал каждый, когда расстояние между ними стало m км?
2056)   Из одного города одновременно в проти-воположных направлениях выехали два автобуса со скоростью и км/ч и z км/ч. Какое расстояние будет между ними, когда первый автобус проедет r км?
2057)   Путь от посёлка до города автомобиль проехал за f ч со скоростью p км/ч. Обратный путь он проехал за d ч. На сколько автомобиль изменил свою скорость?
2058)   От одной станции одновременно в про-тивоположных направлениях отошли два поезда. Скорость первого d км/ч, второго — на к км/ч больше. Через какое время расстояние между ними будет m км?
2059)   Расстояние а км между двумя пристанями лодка прошла со скоростью m км/ч, на обратном пути её скорость уменьшилась на n км/ч. За сколько часов лодка прошла обратный путь?
2060)   Расстояние m км между двумя аэродро-мами самолёт пролетел со скоростью b км/ч. На обратном пути его скорость была d км/ч. Какое время затратил самолёт на путь туда и обратно?
Вариант 4
2061)   С одного аэродрома одновременно в противоположных направлениях вылетели два самолёта со скоростью с км/ч и d км/ч. Какое расстояние будет между ними через n ч?
2062)   Из одного города одновременно в проти-воположных направлениях выехали два мотоциклиста со скоростью b км/ч и c км/ч. Через сколько времени расстояние между ними будет d км?
2063)   Из одного посёлка одновременно в про-тивоположных направлениях выехали автомобиль и автобус. Через m ч расстояние между ними стало p км. Найдите скорость автомобиля, если скорость автобуса b км/ч.
2064)   От одной станции одновременно в про-тивоположных направлениях отошли два поезда со скоростью m км/ч и n км/ч. Какой путь прошёл каждый поезд, когда расстояние между ними стало p км?
2065)   Из одного города одновременно в про-тивоположных направлениях выехали два вело-сипедиста со скоростью c км/ч и d км/ч. Какое расстояние будет между ними, когда первый ве-лосипедист проедет f км?
2066)   Из одного города одновременно в про-тивоположных направлениях выехал велосипедист и вышел пешеход. Скорость пешехода d км/ч, ве-лосипедиста — в n раз больше. Через какое время расстояние между ними будет к км?
2067)   Расстояние между двумя пунктами лыжник прошёл со скоростью p км/ч за c ч. Обратно этот путь он прошёл за b ч. Как лыжник изменил свою скорость?
2068)   Путь от города до поселка, равный m км, велосипедист проехал за f ч. На обратном пути он увеличил скорость на к км/ч. За какое время велосипедист проехал обратный путь?
2069)   Девочка проплыла p м в бассейне со скоростью m м/мин, обратно она плыла со скоростью n м/мин. Сколько времени занял весь заплыв?
ЗАДАЧИ
НА ПРОПОРЦИОНАЛЬНОЕ ДЕЛЕНИЕ
2070)   Две бригады изготовили за смену 128 де-талей. Сколько деталей изготовила каждая бригада, если в одной из них 7 человек, а в другой 9 человек?
2071)   Разложили в коробки 96 цветных и простых карандашей: по 6 цветных и по 2 простых карандаша в каждую. Сколько было всего цветных карандашей? Сколько было всего простых карандашей?
2072)   В соревнованиях участвовало 140 детей. В каждой команде было по 8 мальчиков и 6 девочек. Сколько было всего мальчиков? Сколько было всего девочек?
2073)   За 2 дня наладчик обслужил 56 станков. В первый день он работал 8 ч, а во второй — 6 ч. Сколько станков он настраивал в каждый день?
2074)   Для детского сада купили 120 кукол и машин. Каждая группа получила по 7 кукол и 5 машин. Сколько всего было кукол и сколько машин?
2075)   Портниха пришила к платьям 48 пуговиц: по 3 больших и по 5 маленьких на каждое платье. Сколько всего было больших и сколько маленьких пуговиц?
2076)   Девочка сделала несколько букетов из ромашек и васильков. В каждом букете было 15 ромашек и 10 васильков. Сколько всего у неё ромашек и сколько васильков, если общее количество цветов 125?
2077)   В первых классах школы учится всего 75 детей. В каждом классе по 13 девочек и 12 мальчиков. Сколько всего девочек и сколько мальчиков в первых классах?
2078)   В 2 книгах 312 страниц. Первую книгу мальчик читал 8 дней, а вторую — 5 дней, прочитывая каждый день одинаковое количество страниц. Сколько страниц в каждой книге?
2079)   Хозяйка сварила варенье из 12 кг клубники и 4 кг вишни, расходуя на каждую банку одинаковую массу ягод. Всего у неё получилось 8 банок. Сколько банок каждого варенья она сварила?
2080)   В 9 клетках 20 серых и 25 белых кроликов. Сколько клеток с серыми и сколько клеток с белыми кроликами?
2081)   В нескольких дворах установили 30 ска-меек: по 2 зелёные и 4 коричневые в каждом дворе. Сколько всего было зелёных и сколько коричневых скамеек?
2082)   Для участия в зимней олимпиаде от не-скольких школ выделили по 42 лыжника и 24 конь-кобежца. Всего было 396 участников. Сколько всего было лыжников и сколько конькобежцев?
2083)   Двое рабочих заработали 900 р. Один работал 2 недели, а другой — 8 недель. Сколько денег заработал каждый?
2084)   Двое рабочих получили 800 р. Как они разделят свой заработок, если один работал 6 недель, а другой — 4 недели?
2085)   25 м проволоки весят 700 г. В одном куске 30 м проволоки, а в другом — на 15 м больше. Сколько весит каждый кусок?
2086)   Для приготовления торфоперегнойных горшочков берут на 7 частей земли 2 части торфа. Сколько нужно взять земли на 200 кг торфа?
2087)   Две школы выписали на 96 р. клубничной рассады. Одна школа взяла 3 ящика, а другая — 5 ящиков. Сколько должна заплатить каждая школа за рассаду?
2088)   Два   ювезли 77 т груза, сделав одинаковое число рейсов. Сколько тонн груза перевёз каждый грузовик, если один грузовик за рейс перевозил 3 т, а другой — 4 т?
2089)   Двое рабочих выписали из питомника 26 яблонь. Как они должны разделить яблони, если один дал на покупку 50 р., а другой — 80 р.?
2090)   Сколько граммов резинового клея по-лучится из 50 г каучука, если для приготовления клея берут на 1 часть каучука 9 частей очищенного бензина?
2091)   Двое рабочих заработали 840 р. Первый работал 5 недель, а второй — 7 недель. Сколько денег заработал каждый рабочий?
2092)   Две бригады работали одинаковое время и заработали вместе 810 р. Как они должны разделить этот заработок, если в одной бригаде было 4 человека, а в другой — 5?
2093)   Клуб купил одинаковое число лыж и конь-ков. Пара коньков стоит 6 долларов, а пара лыж — 9 долларов. Сколько стоят отдельно коньки и лыжи, если за всю покупку заплатили 900 долларов?
2094)   Для приготовления жидкого столярного клея берут 15 одинаковых по весу частей плиточного клея и 17 таких же частей воды. Сколько нужно взять граммов плиточного клея для изготовления 640 г жидкого столярного клея?
2095)   На 118 евро купили одинаковое число пальто для мальчиков и девочек. Сколько куплено тех и других, если каждое пальто для мальчиков стоило 31 евро, а для девочек — 28 евро?
2096)   Колхоз привёз одинаковое количество ящиков яблок и груш. Каждый ящик груш весил 50 кг, а ящик яблок — 40 кг. Все фрукты вместе весили 810 кг. Сколько килограммов тех и других фруктов отдельно привезли?
2097)   В двух кусках 24 м сукна. Один кусок стоит 240 долларов, а другой — 480 долларов. Сколько метров сукна в каждом куске?
2098)   «Москвич» на 100 км пути расходует 9 л бензина, «Волга» — 13 л. Обеим машинам отпущено 66 л бензина на 300 км пути. Сколько литров бензина отпущено каждой машине?

Скорость, расстояние и время — промежуточная алгебра

Глава 8: Рациональные выражения

Задачи о расстоянии, скорости и времени являются стандартным приложением линейных уравнений. При решении этих задач используйте соотношение : скорость (скорость или скорость) умножить на , время равно , расстояние .

Например, предположим, что человек должен был проехать 30 км / ч за 4 часа. Чтобы найти общее расстояние, умножьте скорость на время или (30 км / ч) (4 ч) = 120 км.

Задачи, которые будут решены здесь, будут состоять на несколько шагов больше, чем описано выше. Поэтому, чтобы систематизировать информацию о проблеме, используйте таблицу. Пример базовой структуры таблицы ниже:

Пример графика расстояния, скорости и времени
Кто или что	Оценить	Время	Расстояние

Третий столбец, расстояние, всегда заполняется путем умножения столбцов скорости и времени вместе.Если дано общее расстояние обоих людей или поездок, поместите эту информацию в столбец расстояния. Теперь используйте эту таблицу для настройки и решения следующих примеров.

Джои и Наташа начинают с одной и той же точки и идут в противоположных направлениях. Джои идет на 2 км / ч быстрее Наташи. Через 3 часа их разделяет 30 километров. Как быстро каждый шагал?

Расстояние, пройденное обоими — 30 км. Следовательно, решаемое уравнение:

Это означает, что Наташа ходит со скоростью 4 км / ч, а Джоуи ходит со скоростью 6 км / ч.

Ник и Хлоя покинули лагерь на каноэ и поплыли вниз по течению со средней скоростью 12 км / ч. Они развернулись и поплыли вверх по течению со средней скоростью 4 км / ч. Общая поездка заняла 1 час. Через сколько времени туристы повернули вниз по течению?

Расстояние, пройденное вниз по течению, равно расстоянию, пройденному ими вверх по течению. Следовательно, решаемое уравнение:

Это означает, что туристы плыли вниз по течению 0,25 часа и потратили 0.Гребля назад 75 ч.

Терри выезжает из дома на велосипеде со скоростью 20 км / ч. Салли уезжает через 6 часов на скутере, чтобы догнать его, едущего со скоростью 80 км / ч. Сколько времени ей понадобится, чтобы его догнать?

Расстояние, пройденное обоими, одинаково. Следовательно, решаемое уравнение:

Это означает, что Терри путешествует 8 часов, а Салли нужно всего 2 часа, чтобы его догнать.

Во время 130-километровой поездки автомобиль двигался со средней скоростью 55 км / ч, а затем снизил скорость до 40 км / ч на оставшуюся часть пути.Поездка заняла 2,5 часа. Как долго машина двигалась со скоростью 40 км / ч?

Расстояние, пройденное обоими — 30 км. Следовательно, решаемое уравнение:

Это означает, что время, потраченное на поездку со скоростью 40 км / ч, составило 0,5 часа.

Задачи расстояния, времени и скорости имеют несколько вариаций, в которых смешиваются неизвестные значения между расстоянием, скоростью и временем. Обычно они включают решение проблемы, в которой суммарное пройденное расстояние равно некоторому расстоянию, или задачи, в которой расстояния, пройденные обеими сторонами, одинаковы.К этим задачам расстояния, скорости и времени мы вернемся позже в этом учебнике, где для их решения потребуются квадратичные решения.

Для вопросов с 1 по 8 найдите уравнения, необходимые для решения проблем. Не решай.

A находится в 60 километрах от B. Автомобиль в точке A стартует в направлении B со скоростью 20 км / ч, в то время как автомобиль в точке B стартует в направлении A со скоростью 25 км / ч. Сколько времени осталось до встречи автомобилей?
Два автомобиля находятся на расстоянии 276 километров друг от друга и одновременно начинают движение навстречу друг другу.Они едут со скоростью, различающейся на 5 км / ч. Если они встречаются через 6 часов, узнайте скорость каждого из них.
Два поезда, отправляющиеся на одной станции, идут в противоположных направлениях. Они едут со скоростью 25 и 40 км / ч соответственно. Если они начнутся одновременно, как скоро они разделятся на 195 километров?
Два велосипедных посыльных, Джерри и Сьюзен, едут в противоположных направлениях. Если Джерри едет со скоростью 20 км / ч, с какой скоростью должна ехать Сьюзен, если они разделяют 150 километров за 5 часов?
Пассажирский и грузовой поезд одновременно отправляются навстречу друг другу из двух пунктов, разнесенных на 300 километров.Если скорость пассажирского поезда превышает скорость грузового поезда на 15 км / ч, и они встречаются через 4 часа, какой должна быть скорость каждого?
Два автомобиля одновременно начали движение в противоположных направлениях из одной и той же точки. Их скорость составляла 25 и 35 км / ч соответственно. Через сколько часов их разделяло 180 километров?
Человек, имеющий в своем распоряжении десять часов, совершил экскурсию на велосипеде, выехав со скоростью 10 км / ч и вернувшись пешком со скоростью 3 км / ч.Найдите расстояние, которое он проехал.
Человек идет со скоростью 4 км / ч. Как далеко он может дойти до деревни и вернуться обратно на тележке, которая движется со скоростью 20 км / ч, если ему нужно вернуться домой через 3 часа после того, как он отправился в путь?

Решите вопросы с 9 по 22.

Мальчик уезжает из дома на автомобиле со скоростью 28 км / ч и ходит обратно со скоростью 4 км / ч. Дорога туда и обратно занимает 2 часа. Как далеко он едет?
Моторная лодка покидает гавань и движется со средней скоростью 15 км / ч к острову.Средняя скорость на обратном пути составила 10 км / ч. Как далеко находился остров от гавани, если поездка длилась в общей сложности 5 часов?
Семья ехала на курорт со средней скоростью 30 км / ч, а затем возвращалась по той же дороге со средней скоростью 50 км / ч. Найдите расстояние до курорта, если общее время в пути составило 8 часов.
В рамках своей летной подготовки пилот-студент должен был вылететь в аэропорт, а затем вернуться. Средняя скорость до аэропорта составляла 90 км / ч, а средняя скорость возврата — 120 км / ч.Найдите расстояние между двумя аэропортами, если общее время полета составило 7 часов.
Сэм начинает движение со скоростью 4 км / ч от кемпинга на 2 часа раньше Сью, которая движется со скоростью 6 км / ч в том же направлении. Сколько часов потребуется Сью, чтобы догнать Сэма?
Человек едет 5 км / ч. После 6 часов путешествия другой человек стартует с того же места, что и первый, двигаясь со скоростью 8 км / ч. Когда второй догонит первого?
Моторная лодка покидает гавань и движется со средней скоростью 8 км / ч к небольшому острову.Два часа спустя круизный лайнер покидает ту же гавань и движется со средней скоростью 16 км / ч к тому же острову. Через сколько часов после отбытия круизера с каютами он будет рядом с моторной лодкой?
Бегун на длинные дистанции начал дистанцию со средней скоростью 6 км / ч. Через час второй бегун начал тот же курс со средней скоростью 8 км / ч. Через какое время после старта второго бегуна они догонят первого?
Двое мужчин едут в противоположных направлениях со скоростью 20 и 30 км / ч одновременно и из одного места.Через сколько часов они будут в 300 км друг от друга?
Два поезда одновременно отправляются из одного и того же места и едут в противоположных направлениях. Если скорость одного из них на 6 км / ч больше, чем у другого, и по прошествии 4 часов расстояние между ними составляет 168 километров, какова скорость каждого из них?
Два велосипедиста стартуют с одной и той же точки и едут в противоположных направлениях. Один велосипедист едет вдвое быстрее другого. Через три часа их разделяет 72 километра. Найдите рейтинг каждого велосипедиста.
Два маленьких самолета стартуют из одной точки и летят в противоположных направлениях. Первый самолет летит на 25 км / ч медленнее второго. За два часа самолеты разделяют 430 километров. Найдите скорость каждого самолета.
Во время 130-километровой поездки автомобиль двигался со средней скоростью 55 км / ч, а затем снизил скорость до 40 км / ч на оставшуюся часть пути. Поездка заняла 2,5 часа. Как долго машина двигалась со скоростью 40 км / ч?
Бегая со средней скоростью 8 м / с, спринтер пробежал до конца трассы, а затем вернулся к исходной точке со средней скоростью 3 м / с.Спринтеру потребовалось 55 секунд, чтобы пробежать до конца трассы и вернуться обратно. Найдите длину дорожки.

Ключ ответа 8.8

Темы по алгебре: Задачи с дистанционным словом

	расстояние	ставка	время
в городе		30
межгосударственный		70

Мы заполнили ставки, но как насчет расстояния и время ? Если вы посмотрите на проблему, то увидите, что это , всего цифр, что означает, что они включают время в городе и на межштатной автомагистрали.Таким образом, общее расстояние равно 225. Это означает, что это правда:

Межгосударственное расстояние + расстояние до города = Общее расстояние

Вместе, расстояние между штатами и расстояние между городами равны , всего . Видеть?

В любом случае, мы пытаемся выяснить, как далеко проехал Билл на шоссе между штатами , поэтому представим это число как d . Если расстояние между штатами составляет d , это означает, что расстояние между городом — это число, равное итоговому значению 225, когда прибавляет к d .Другими словами, это 225 — d .

Мы можем заполнить нашу диаграмму так:

	расстояние	скорость	время
в городе	225 — d	30
межгосударственный	d	70

9000 тех же2 заполнить графу раз . Общее время 3,5 часов . Если мы говорим, что время на межштатной автомагистрали составляет t , то оставшееся время в городе равно 3.5 — т . Мы можем заполнить остальную часть нашей диаграммы.

7 9456

0 Теперь мы можем работать над решением проблемы. Основное различие между задачами на первой странице и этой задачей состоит в том, что эта задача включает

двух уравнений.Вот тот, на проезд по городу :

225 — d = 30 ⋅ (3,5 — т)

А вот тот для межгосударственного проезда :

d = 70 т

Если вы попытались решить любую из этих задач самостоятельно, вы могли бы найти это невозможным: поскольку каждое уравнение содержит две неизвестные переменные, они не могут быть решены сами по себе. Попробуйте сами. Если вы работаете с любым уравнением отдельно, вы не сможете найти числовое значение для d . Чтобы найти значение d , нам также необходимо знать значение t .

Мы можем найти значение т в обеих задачах, объединив их. Давайте еще раз посмотрим на наше уравнение путешествия между штатами.

Хотя нам неизвестно числовое значение d , это уравнение говорит нам, что d равно 70 t .

d = 70 т

Поскольку 70 t и d равны , равны , мы можем заменить d на 70 t .Подстановка 70 t вместо d в нашем уравнении для межштатных путешествий не поможет нам найти значение t — все это говорит нам о том, что 70 t равно самому себе, что мы уже знали.

70т = 70т

А как насчет нашего другого уравнения, уравнения для путешествий по городу?

225 — d = 30 ⋅ (3,5 — т)

Когда мы заменяем d в этом уравнении на 70 t , решение уравнения внезапно становится намного проще.

225 — 70 т = 30 ⋅ (3,5 — т)

Наше новое уравнение может показаться более сложным, но на самом деле мы можем его решить. Это потому, что у него только одна переменная: t . Найдя t , мы можем использовать его для вычисления значения d — и найти ответ на нашу проблему.

Чтобы упростить это уравнение и найти значение t , нам нужно получить только t на одной стороне знака равенства. Нам также нужно будет максимально упростить правую часть .

225 — 70 т = 30 ⋅ (3,5 — т)

Начнем с правой стороны: 30 раз (3,5 — т ) это 105-30 т .

225 — 70 т = 105 — 30 т

Затем давайте сократим 225 рядом с 70 t . Для этого вычтем 225 с обеих сторон. Справа это означает вычитание 225 из 105. 105 — 225 равно -120.

— 70 т = -120 — 30 т

Наш следующий шаг — объединить в группу подобных терминов — помните, наша конечная цель — иметь t слева от знака равенства и число справа .Мы сократим -30 t с правой стороны на , добавив 30 t с обеих сторон. С правой стороны мы добавим его к -70 t . -70 т + 30 т составляет -40 т .

— 40 т = -120

Наконец, чтобы получить t отдельно, мы разделим каждую сторону на ее коэффициент: -40. -120 / — 40 составляет 3.

т = 3

Таким образом, t равно 3. Другими словами, время, в течение которого Билл проехал по межгосударственной магистрали, равно 3 часам .Помните, мы в конечном итоге пытаемся найти distanc e Bill, который путешествовал по автомагистрали между штатами. Давайте еще раз посмотрим на строку между штатами нашего графика и посмотрим, достаточно ли у нас информации, чтобы выяснить это.

	расстояние	скорость	время
в городе	225 — d	30	3,5 — t
межгосударственный	d	70

	расстояние	скорость	время
межгосударственный	d	70	3

Похоже, что мы. Теперь, когда нам не хватает только одной переменной, мы сможем довольно быстро найти ее значение.

Чтобы найти расстояние, воспользуемся формулой перемещения расстояние = скорость ⋅ время .

d = rt

Теперь мы знаем, что Билл ехал по межгосударственной автомагистрали 3 часа со скоростью 70 миль в час, поэтому мы можем заполнить эту информацию.

d = 3 ⋅ 70

Наконец, мы закончили упрощать правую часть уравнения. 3 ⋅ 70 это 210.

д = 210

Итак, d = 210. У нас есть ответ на нашу проблему! Расстояние 210.Другими словами, Билл проехал 210 миль по шоссе.

Решение задачи туда и обратно

Может показаться, что решение первой проблемы заняло много времени. Чем больше вы будете практиковаться в решении этих задач, тем быстрее они решатся. Попробуем аналогичную задачу. Эта задача называется проблемой туда и обратно , потому что она описывает поездку туда и обратно — поездку, которая включает в себя обратный путь. Несмотря на то, что поездка, описанная в этой задаче, немного отличается от поездки в нашей первой задаче, вы сможете решить ее таким же образом.Давайте посмотрим:

Ева ехала на работу со средней скоростью 36 миль в час. По дороге домой она попала в пробку и проехала в среднем 27 миль в час. Ее общее время в машине составило 1 час 45 минут, или 1,75 часа. Как далеко Ева живет от работы?

Если у вас возникли проблемы с пониманием этой проблемы, вы можете представить себе дорогу Евы на работу следующим образом:

Как всегда, начнем с заполнения таблицы с важной информацией. Сделаем ряд с информацией о ее поездке на работу и с работы .

1,75 — т для описания поездки с работы. (Помните, общее время в пути составляет 1,75 часа , поэтому время с до работы и из должно равняться 1,75.)

Из нашей таблицы мы можем написать два уравнения:

Поездку на работу можно представить как d = 36 t .
Поездку с работы можно представить как d = 27 (1.75 — т ).

В обоих уравнениях d представляет собой общее расстояние. Из диаграммы вы можете видеть, что эти два уравнения равны друг другу — в конце концов, Ева проезжает на одинаковое расстояние до и от работы .

Как и в случае с предыдущей задачей, которую мы решили, мы можем решить эту, объединив двух уравнений.

Начнем с нашего уравнения для поездки из работы .

d = 27 (1.75 — т)

Затем мы подставим значение d из нашего для работы уравнения , d = 36 t . Поскольку значение d равно 36 t , мы можем заменить любое вхождение d на 36 t .

36т = 27 (1,75 — т)

Теперь давайте упростим правую часть. 27 ⋅ (1,75 — т ) составляет 47,25.

36 т = 47,25 — 27 т

Затем мы сократим -27 t на , добавив 27 t к обеим сторонам уравнения. 36 т + 27 т это 63 т .

63т = 47,25

Наконец, мы можем получить t отдельно, разделив обе части на его коэффициент: 63. 47,25 / 63 равно 0,75.

т = 0,75

т равно 0,75. Другими словами, время , которое потребовалось Еве, чтобы ехать на работу, составляет ,75 часа . Теперь, когда мы знаем значение t , мы сможем найти расстояние до работы Евы.

Если вы догадались, что мы снова будем использовать уравнение перемещения , вы были правы. Теперь мы знаем значение двух из трех переменных, что означает, что мы знаем достаточно, чтобы решить нашу проблему.

d = rt

Во-первых, давайте введем известные нам значения. Будем работать с номерами для поездки на работу . Мы уже знали коэффициент : 36. И мы только что узнали время : 0,75.

d = 36 ⋅ 0,75

Теперь все, что нам нужно сделать, это упростить уравнение: 36 ⋅.75 = 27,

д = 27

d равно 27. Другими словами, расстояние до места работы Евы составляет 27 миль . Наша проблема решена.

Проблемы с пересекающимися расстояниями

Проблема с расстоянием пересечения — это проблема, при которой две вещи движутся навстречу друг другу. Вот типичная проблема:

Пауни и Спрингфилд находятся в 420 милях друг от друга. Поезд покидает Пауни, направляясь в Спрингфилд, в то время как поезд покидает Спрингфилд, направляясь в Пауни.Один поезд движется со скоростью 45 миль в час, а другой — 60 миль в час. Как долго они будут путешествовать до встречи?

Эта задача просит вас рассчитать, сколько времени потребуется этим двум поездам, движущимся навстречу друг другу, чтобы пересечь пути. Поначалу это может показаться запутанным. Несмотря на то, что это реальная ситуация, может быть сложно абстрактно представить расстояние и движение. Эта диаграмма может помочь вам понять, как выглядит эта ситуация:

Если вы все еще не уверены, не волнуйтесь! Вы можете решить эту проблему так же, как вы решили две задачи на предыдущей странице.Вам просто понадобится диаграмма и формула перемещения .

Пауни и Спрингфилд находятся на расстоянии 420 миль друг от друга, км. Поезд покидает Пауни, направляясь в Спрингфилд, в то время как поезд покидает Спрингфилд, направляясь в Пауни. Один поезд движется со скоростью 45 миль в час , а другой 60 миль в час . Как долго они будут путешествовать до встречи?

Начнем с заполнения нашей диаграммы. Это снова проблема, на этот раз с подчеркнутой важной информацией.Начнем с заполнения самой очевидной информации: рейтинг . Проблема дает нам скорость каждого поезда. Мы обозначим их , быстрый поезд и медленный поезд , . Скоростной поезд идет со скоростью 60 миль в час . Медленный поезд идет всего 45 миль в час .

Мы также можем поместить эту информацию в таблицу:

	расстояние	скорость	время
быстрый поезд		60
медленный поезд		45

Мы не знаем расстояние, на которое едет каждый поезд. встретить другого еще — мы просто знаем общее расстояние .Чтобы встретиться, поезда преодолеют общее расстояние , равное общему расстоянию. Как вы можете видеть на этой диаграмме, это верно независимо от того, как далеко едет каждый поезд.

Это означает, что, как и в прошлый раз, мы представим расстояние одного из них как d , а расстояние до другого — как минус d. Таким образом, расстояние для быстрого поезда будет d , а для медленного поезда — 420 — d .

	расстояние	скорость	время
быстрый поезд	d	60
медленный поезд	420 — d	45

Потому что мы ищем для времени оба поезда едут до встречи, время будет одинаковым для обоих поездов. Мы можем представить это с т .

3 45 9457 9004 900 таблица дает нам два уравнения: d = 60 t и 420 — d = 45 t .Точно так же, как мы сделали с задачей , состоящей из двух частей, , мы можем объединить эти два уравнения.
Уравнение для быстрого поезда не может быть решено само по себе, но оно говорит нам, что d равно 60 t .
d = 60 т
Другое уравнение, описывающее медленный поезд , тоже не может быть решено в одиночку. Однако мы можем заменить d его значением из первого уравнения.
420 — d = 45 т
Поскольку мы знаем, что d равно 60 t , мы можем заменить d в этом уравнении на 60 t .Теперь у нас есть уравнение, которое мы можем решить.
420 — 60 т = 45 т
Чтобы решить это уравнение, нам нужно получить t и его коэффициенты с одной стороны от знака равенства и любые другие числа с другой. Мы можем начать с отмены -60 t слева на , добавив 60 t с обеих сторон. 45 т + 60 т — 105 т .
420 = 105 т
Теперь нам просто нужно избавиться от коэффициента, следующего за t .Мы можем сделать это, разделив обе стороны на 105. 420/105 равно 4.
4 = т
t = 4. Другими словами, время , необходимое поездам для встречи, равно 4 часа . Наша проблема решена!
Если вы хотите быть уверены в своем ответе, вы можете проверить его , используя уравнение расстояния с t , равным 4. Для нашего скоростного поезда уравнение будет иметь вид d = 60 ⋅ 4. 60 ⋅ 4 равно 240, поэтому расстояние, которое проехал наш быстрый поезд , составит 240 миль. Для нашего медленного поезда уравнение будет d = 45 ⋅ 4. 45 ⋅ 4 равно 180, поэтому расстояние, пройденное медленным поездом , составляет 180 миль .
Помните, как мы сказали, что расстояние, на которое едет медленный поезд и быстрый поезд, должно равняться общему расстоянию ? 240 миль + 180 миль равно 420 миль, что является полным расстоянием от нашей задачи. Наш ответ правильный.
Практическая задача 1
Вот еще одна проблема с расстоянием пересечения.Он похож на тот, который мы только что решили. Посмотрим, сможете ли вы решить эту проблему самостоятельно. Когда вы закончите, прокрутите вниз, чтобы увидеть ответ и объяснение.
Джон и Дэни живут в 270 милях друг от друга. Однажды они решили ехать навстречу друг другу и тусоваться везде, где встречались. Джон ехал в среднем 65 миль в час, а Дэни ехал в среднем 70 миль в час. Как долго они ехали, прежде чем встретились?
Задача 1 ответ
Вот практическая задача 1:
Джон и Дэни живут в 270 милях друг от друга.Однажды они решили ехать навстречу друг другу и тусоваться везде, где встречались. Джон проехал в среднем 65 миль в час, а Дэни — 70 миль в час. Как долго они ехали, прежде чем встретились?
Ответ: 2 часа .
Давайте решим эту задачу так же, как и другие. Сначала попробуйте составить диаграмму. Должно получиться так:

	расстояние	скорость	время
быстрый поезд	d	60	t
медленный поезд	420 — d

t 9 в графике заполнено:
Расстояние: Вместе, Дэни и Джон преодолеют общего расстояния между ними к тому времени, когда они встретятся.Это 270. Расстояние Джона представлено как d , поэтому расстояние Дани составляет 270 — d .
Оценка: Проблема сообщает нам скорости Дэни и Джона. Дэни едет со скоростью 65 миль в час , а Джон — со скоростью 70 миль в час .
Время: Поскольку Джон и Дэни проезжают одинаковое количество времени до встречи, их время в пути равно t .
Теперь у нас есть два уравнения. Уравнение для перемещения Джона: d = 65 t .Уравнение путешествия Дэни: 270 — d = 70 t . Чтобы решить эту проблему, нам нужно объединить их.
Уравнение для Джона говорит нам, что d равно 65 t . Это означает, что мы можем объединить два уравнения, заменив d в уравнении Дэни на 65 t .
270 — 65 т = 70 т
Давайте получим t с одной стороны уравнения и число с другой. Первый шаг к этому — избавиться от -65 t с левой стороны.Мы отменим его на , добавив 65 t в обе стороны: 70 t + 65 t это 135 t .
270 = 135 т
Все, что осталось сделать, это избавиться от 135 рядом с t . Мы можем сделать это, разделив обе стороны на 135: 270/135 равно 2.
2 = т
Вот и все. t равно 2. У нас есть ответ на нашу проблему: Дэни и Джон проехали 2 часа до встречи.
Проблемы с дистанцией обгона
Последний тип проблемы расстояния, который мы обсудим в этом уроке, — это задача, в которой один движущийся объект обгоняет — или проходит — другой. Вот типичная проблема обгона:
Семья Хилл и семья Платтеров отправляются в путешествие. Холмы уехали за 3 часа до Platters, но Platters едут в среднем на 15 миль в час быстрее. Если семье Платтер требуется 13 часов, чтобы догнать семью Хилл, насколько быстро едут Хиллз?
Вы можете представить себе момент, когда семья Платтеров отправилась в путешествие, примерно так:
Задача говорит нам, что семья Платтера догонит семью Хилл через 13 часов, и просит нас использовать эту информацию, чтобы найти для семьи Хилл рейтинг .Как и в случае с некоторыми другими проблемами, которые мы решили в этом уроке, может показаться, что у нас недостаточно информации для решения этой проблемы, но у нас есть. Приступим к составлению нашей диаграммы. Расстояние может быть d как для Холмов, так и для Платтеров — когда Платтеры догонят Холмы, обе семьи пройдут точно такое же расстояние.

	расстояние	скорость	время
Jon	d	65	t
Dani	270 — d	70

	расстояние	скорость	время
Холмы	d
Пластины	d

Время заполнения и требуется еще немного подумать.Мы не знаем ставки для каждой семьи — помните, это то, что мы пытаемся выяснить. Однако мы знаем, что Platters ехали на на 15 миль в час быстрее, чем на , чем на Hills. Это означает, что если рейтинг семьи Хилл составляет рублей , то ставка семьи Платтеров будет рублей + 15.

0

все осталось

	расстояние	скорость	время
холмы	d	r
пластины	d	r + 15

Урок 39. задачи на встречное движение — Математика — 4 класс

Движение навстречу друг другу | Математика

«Задачи на движение 4 класс»

Административная контрольная работа по математике за 3 четверть 4 класса

Система задач на движение .

Как найти встречное время

Главная > Памятка

Задачи на движение в одном направлении

Скачать:

Предварительный просмотр:

Ответы к задаче Ответы к задачам 4 класс по математике (Часть 1)

Скорость, расстояние и время — промежуточная алгебра

0 Теперь мы можем работать над решением проблемы. Основное различие между задачами на первой странице и этой задачей состоит в том, что эта задача включает

Решение задачи туда и обратно

Проблемы с пересекающимися расстояниями

Практическая задача 1

Задача 1 ответ

Проблемы с дистанцией обгона

0

Наши диаграмма дает нам два уравнения.Поездку семьи Хилл можно описать следующим образом:

Практическая задача 2

Ответ на задачу 2

Задачи о дистанции, времени и скорости | GMAT GRE Maths

Решенные вопросы по поездам

Вопросы по лодкам / самолетам

Больше решенных примеров по скорости, расстоянию и времени

Практические вопросы, которые вам нужно решить

Советы по безопасному вождению и предотвращению дорожно-транспортных происшествий

Проблема с велосипедом, которая чуть не сломала математику

Два колеса в хорошем состоянии

Подготовка

Катастрофа

Вернуться к байку

Как добраться до Германии — вождение в Германии

Получение немецких водительских прав

Регистрация, проверка и налоги автотранспортных средств

Автострахование

Правила дорожного движения

Немецкие автомобильные клубы

Еще кое-что, что вы должны знать

Немецкие дорожные знаки

Немецкие правила дорожного движения

Что делать, если за вами следят

Почему кто-то последует за вами?

Унция профилактики стоит фунта лечения: как стать менее заметным

Как узнать, что кто-то следит за вами?

В машине

Пешком

Что делать, если кто-то преследует вас

В машине

Пешком

Но что, если я в бегах, в стиле Джейсона Борна?

Related Posts

Leave A Comment Отменить ответ