В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8: В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра призмы равны 5/п. Найдите объём цилиндра

Цилиндр. В основании прямой призмы лежит прямоугольный. треугольник с катетами 6 и 8. Боковые ребра равны

Прямоугольный параллелепипед

Прямоугольный параллелепипед 1 Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4 Площадь поверхности этого параллелепипеда равна 94 Найдите третье ребро, выходящее из той

Подробнее Прямоугольный параллелепипед
Прямоугольный параллелепипед 1. из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.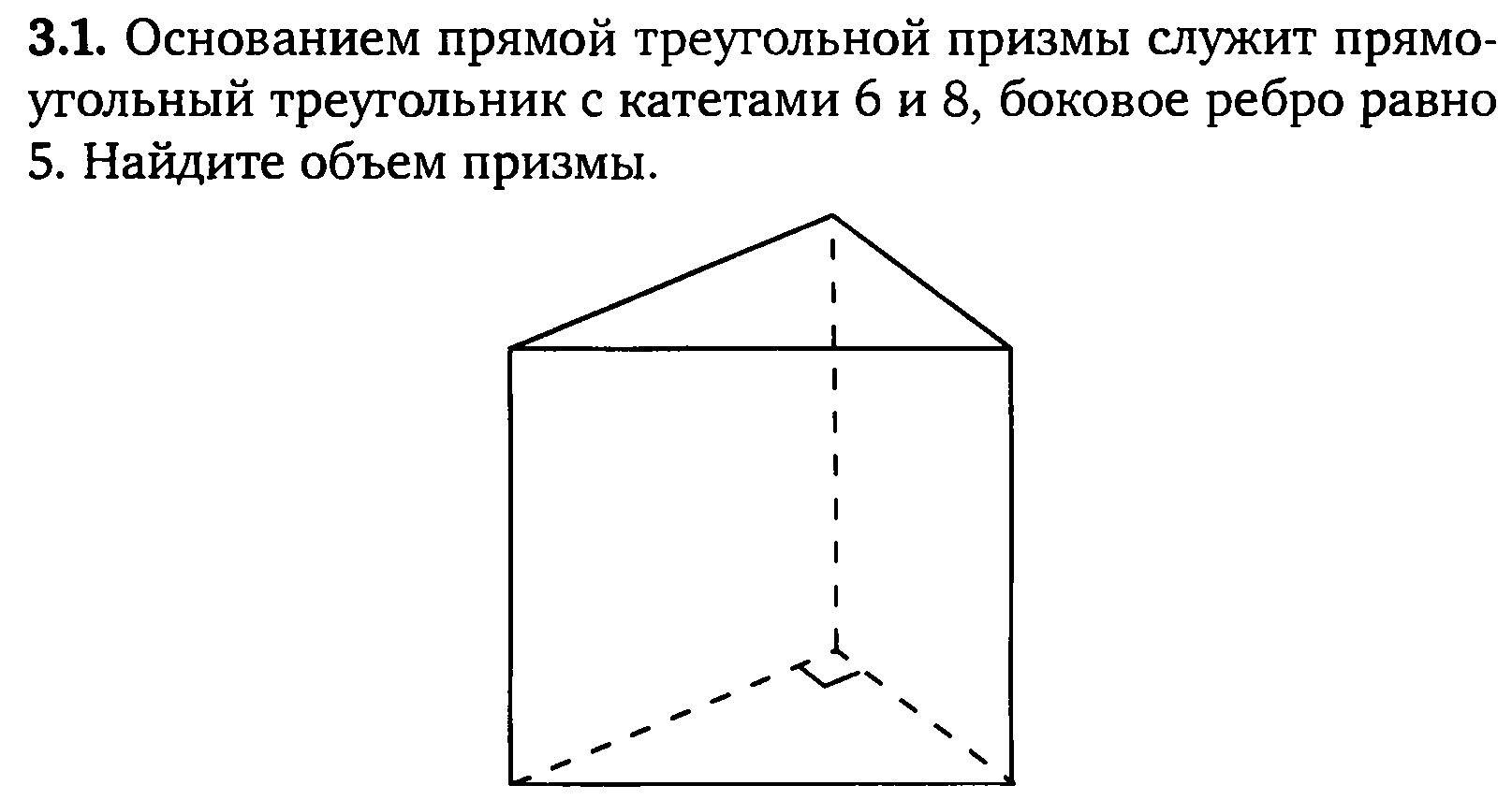
2. Два ребра пря мо уголь но го параллелепипеда,
Подробнее Задачи на квадратной решетке
Задачи на квадратной решетке 1 Найдите тан генс угла проведем вы со ту из точки на сто ро ну Тогда, при ни мая во внимание, что, получим: О тв е т: 1 2 Найдите тан генс угла проведем вы со ту из точки
Подробнее Прямоугольный треугольник
Прямоугольный треугольник 1. В тре уголь ни ке ABC угол C прямой, BC = 8, sin A = 0,4. Найдите AB. Синус угла равен от но ше нию про ти во ле жа ще го ка те та ВС к ги по те ну зе АВ. Поэтому: О тв е т:
Подробнее
Задания B16. Рас че ты по формулам
Задания B16. Рас че ты по формулам 1. B 16 46. Период колебания математического маятника (в секундах) приближенно можно вычислить по формуле, где длина нити (в метрах). Пользуясь этой формулой, найдите
Подробнее Четырёхугольники. Тогда,
Четырёхугольники 1. Основания рав но бед рен ной трапеции равны 8 и 18, а пе ри метр равен 56. Найдите пло щадь трапеции. Трапеция равнобедренная, значит, Тогда, и Ответ: 2. В па рал ле ло грамм впи са
Подробнее Вписанная и описанная окружности
Вписанная и описанная окружности 1. Радиус окружности, впи сан ной в пра виль ный треугольник, равен 6. Най ди те вы со ту этого треугольника. значит, О тв е т: 18. Приведем дру гое решение. Высота пра
Подробнее Прямоугольник: длины и площади
Прямоугольник: длины и площади 1. На клетчатой бумаге с клетками размером 1 см 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах. Площадь прямоугольника равна произведению
Подробнее Треугольники общего вида
Треугольники общего вида 1 Найдите синус угла умноженное на В ответе укажите значение синуса, Пояснение Проведем высоту из точки на сторону Тогда, принимая во внимание, что, получим: О тв е т: 2 2 Найдите
Подробнее Координатная плоскость
Координатная плоскость 1 Найдите площадь параллелограмма, изображенного на рисунке Площадь параллелограмма равна произведению основания на высоту, проведенную к этому основанию или его продолжению Поэтому
Подробнее Равнобедренные треугольники
Равнобедренные треугольники 1. В рав но сто рон нем тре уголь ни ке ABC бис сек три сы CN и AM пе ре се ка ют ся в точке P. Найдите. В рав но сто рон нем тре уголь ни ке ABC все углы равны 60. Бис сек
Подробнее Объем составного многогранника
Объем составного многогранника 1 Найдите объем многогранника, изоб ра жен но го на ри сун ке (все дву гран ные углы мно го гран ни ка прямые) объем многогранника, изоб ра жен но го на ри сун ке (все дву
Подробнее
Касательная, хорда, секущая, радиус
Касательная, хорда, секущая, радиус 1. Радиус круга равен 1. Най ди те его площадь, деленную на π. 2. Найдите пло щадь кругового сектора, если ра ди ус круга равен 3, а угол сек то ра равен 120. В от ве
Подробнее не более свыше
Вариант 19885284 1. 2. Найдите зна че ние вы ра же ния В таб ли це пред став ле ны на ло го вые став ки на ав то мо би ли в Москве с 1 ян ва ря 2013 года. Мощ ность ав то мо би ля (в л. с.*) На ло го вая
Подробнее
Теорема Пифагора. О тв е т: 9.
Теорема Пифагора 1. От стол ба вы со той 9 м к дому на тя нут провод, ко то рый кре пит ся на вы со те 3 м от земли (см. рисунок). Рас сто я ние от дома до стол ба 8 м. Вы чис ли те длину провода. Проведём
Подробнее Вычисление длин и площадей
Вычисление длин и площадей 1. Площадь пря мо уголь но го земельного участ ка равна 9 га, ши ри на участка равна 150 м. Най ди те длину этого участ ка в метрах. Переведем пло щадь участка в квад рат ные
Подробнее Отметка «5» «4» «3» «5» «4» «3» Время, секунды 4,6 4,9 5,3 5,0 5,5 5,9

Вариант 15354570 1. Вы чис ли те: 2. В таб ли це при ве де ны нор ма ти вы по бегу на 30 м для уча щих ся 9 класса. Мальчики Девочки Отметка «5» «4» «3» «5» «4» «3» Время, секунды 4,6 4,9 5,3 5,0 5,5 5,9
Подробнее Прямоугольный параллелепипед
ЗАДАНИЕ 10 Стереометрия Куб 1. Площадь поверхности куба равна 18. Найдите его диагональ. 2. Диагональ грани куба равна 2 6. Найдите диагональ куба. 3. Диагональ грани куба равна 6. Найдите диагональ куба.
Подробнее 06:35 07:59 07:05 08:15 07:28 08:30 07:34 08:57
Вариант 11199424 1. Най ди те зна че ние вы ра же ния 2. Студент Петров выезжает из Наро-Фоминска в Москву на занятия в университет. Занятия начинаются в 9:00. В таблице при ве де но рас пи са ние утрен
Подробнее Най ди те зна че ние вы ра же ния
Вариант 17045845 1. Най ди те зна че ние вы ра же ния 2. В таблице приведены размеры штрафов за превышение максимальной разрешённой скорости, зафиксированное с помощью средств автоматической фиксации,
Подробнее Разные задачи. Решим её:
Разные задачи 1. Найдите все зна че ния, при ко то рых не ра вен ство не имеет решений. График функ ции парабола, ветви ко то рой на прав лен ны вверх. Значит, дан ное не ра вен ство не имеет ре ше ний
Подробнее Задачи на движение по воде
Задачи на движение по воде 1 Из пунк та А в пункт В, рас по ло жен ный ниже по те че нию реки, от пра вил ся плот Од но вре мен но нав стре чу ему из пунк та В вышел катер Встре тив плот, катер сразу по
Подробнее 1) 0,1327; 0,014; 0,13 2) 0,014; 0,13; 0,1327 3) 0,1327; 0,13; 0,014 4) 0,13; 0,014; 0, ) 2) 3) 4) За да ние
Вариант 6239430 1. Рас по ло жи те в по ряд ке убы ва ния числа 0,1327; 0,014; 0,13. 1) 0,1327; 0,014; 0,13 2) 0,014; 0,13; 0,1327 3) 0,1327; 0,13; 0,014 4) 0,13; 0,014; 0,1327 2. На ко ор ди нат ной пря
Подробнее Основанием прямой треугольной призмы служит прямоугольный треугольник, найдите площадь поверхности
Формулировка задачи: Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами K и M, высота призмы равна H.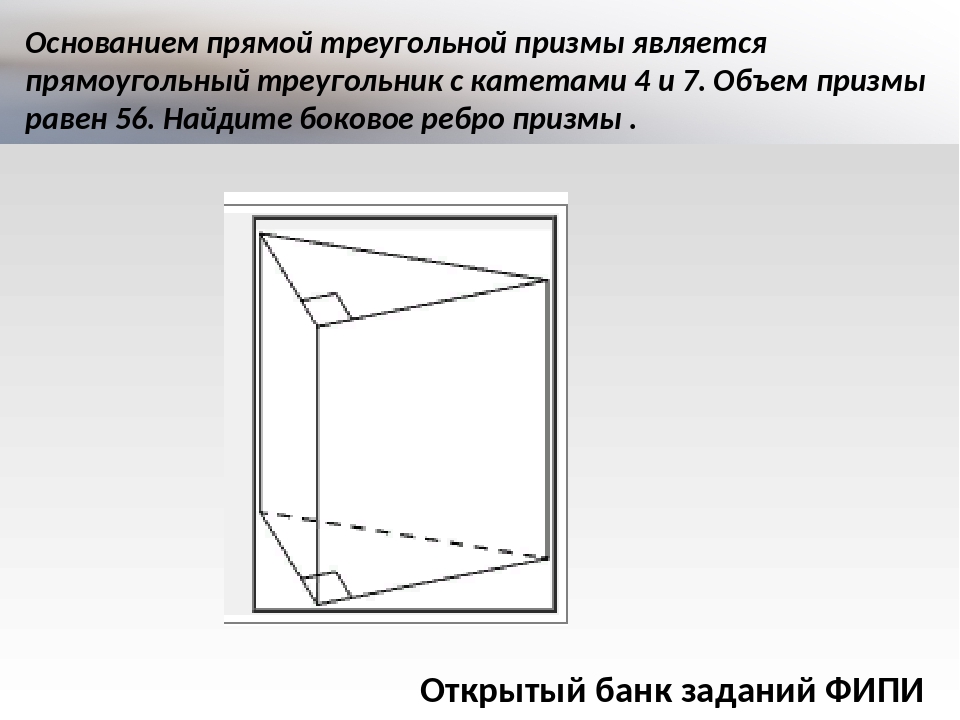

Найдите площадь ее поверхности.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 13 (Задачи по стереометрии).
Рассмотрим, как решаются подобные задачи на примере и выведем общий способ решения.
Пример задачи:
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
Решение:
Площадь поверхности прямой треугольной призмы равна сумме 2 площадей основания и площади боковой поверхности призмы:
S_призмы = S_{бок.пов} + 2S_осн

Площадь основания равна площади прямоугольного треугольника с катетами 6 и 8. Площадь прямоугольного треугольника равна половине произведения катетов:
S_осн = 1/2 ⋅ 6 ⋅ 8 = 24
Площадь боковой поверхности прямой треугольной призмы равна периметру основания, умноженному на высоту. Катеты прямоугольного треугольника, лежащего в основании, известны, осталось найти его гипотенузу по теореме Пифагора:
Тогда площадь боковой поверхности прямой треугольной призмы равна:
S_{бок.пов} = (6 + 8 + 10) ⋅ 10 = 24 ⋅ 10 = 240
Таким образом, площадь поверхности призмы равна:
S_призмы = S_{бок.пов} + 2S_осн = 240 + 2 ⋅ 24 = 240 + 48 = 288
Ответ: 288
В общем виде решение данной задачи по стереометрии выглядит следующим образом:
S_осн = 1/2 ⋅ K ⋅ M
S_{бок.пов} = (K + M + √K² + M²) ⋅ H
S_призмы = S_{бок.пов} + 2S_осн = (K + M + √K² + M²) ⋅ H + K ⋅ M
где K и M – катеты прямоугольного треугольника, лежащего в основании прямой треугольной призмы, H – высота призмы.
Остается лишь подставить значения и вычислить результат.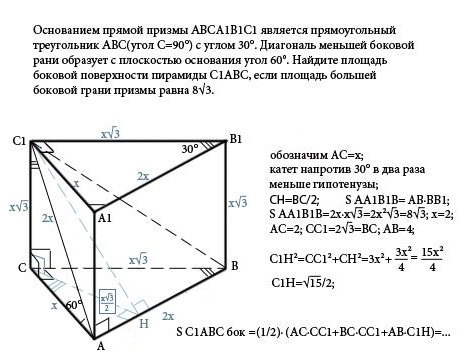
Основанием прямой треугольной призмы
Для вас ещё несколько несложных задачек на решение призмы. Рассмотрим прямую призму с прямоугольным треугольником в основании. Ставится вопрос о нахождении объёма или площади поверхности. Формула объёма призмы:
Формула площади поверхности призмы (общая):
*У прямой призмы боковая поверхность состоит из прямоугольников и равна она произведению периметра основания и высоты призмы. Необходимо помнить формулу площади треугольника. В данном случае, имеем прямоугольный треугольник – его площадь равна половине произведения катетов. Рассмотрим задачи:
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 10 и 15, боковое ребро равно 5. Найдите объем призмы.
Площадь основания это площадь прямоугольного треугольника. Она равна половине площади прямоугольника со сторонами 10 и 15).
Таким образом, искомый объём равен:
Ответ: 375
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 20 и 8. Объем призмы равен 400. Найдите ее боковое ребро.
Задача обратная предыдущей.
Объем призмы:
Площадь основания это площадь прямоугольного треугольника:
Таким образом
Ответ: 5
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5 и 12, высота призмы равна 8. Найдите площадь ее поверхности.
Площадь поверхности призмы складывается из площадей всех граней – это два равных по площади основания и боковая поверхность.
Для того, чтобы найти площади всех граней необходимо найти третью сторону основания призмы (гипотенузу прямоугольного треугольника).
По теореме Пифагора:
Теперь мы можем найти площадь основания и площадь боковой поверхности. Площадь основания равна:
Площадь боковой поверхности призмы с периметром основания равна:
*Можно обойтись без формулы и просто сложить площади трёх прямоугольников:
Полная площадь поверхности призмы:
Ответ: 300

27082. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Посмотреть решение
27132. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
Посмотреть решение
27151. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы.
На этом всё. Успеха вам!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Призма с треугольником в основании ( часть 2)
Примечание. Это часть урока с задачами по геометрии (раздел стереометрия, задачи о призме). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. В задачах вместо символа «квадратный корень» применяется функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак «√».
Задача. Правильная треугольная призма Площадь боковой поверхности правильной треугольной призмы равна площади основания. Вычислите длину бокового ребра, если сторона основания 7см.
Решение.
«Подвох» кроется в формулировке задачи — если призма правильная треугольная (см. определение призмы), то в ее основании лежит правильный треугольник.
Площадь правильного треугольника, который является основанием правильной треугольной призмы, найдем по формуле:
S = a²√3 / 4
S = 49√3 / 4
Площадь боковой поверхности правильной треугольной призмы найдем по формуле
S = 3 ab
тогда
S = 3 * 7 * b = 21b
Таким образом,
49√3 / 4 = 21b
b = 49√3 / 84
b = 7√3 / 12
Ответ: 7√3 / 12
Задача. Прямоугольный треугольник в основании прямой призмы
В основании прямой треугольной призмы лежит прямоугольный треугольник с катетами 8 и 6 см. Найти боковое ребро призмы, если ее боковая поверхность равна 120 квадратных сантиметров.
Решение.
Сначала найдем гипотенузу основания призмы. Поскольку в основании призмы лежит прямоугольный треугольник, воспользуемся теоремой Пифагора.
(см. свойства и формулы прямоугольного треугольника)
AB² = AC² + BC²
AB² = 8² + 6²
AB² = 64 + 36
AB = √100
AB = 10
Обозначим боковое ребро призмы как h . Боковое ребро одновременно является и высотой призмы, поскольку по условию задачи призма является прямой.
(см. свойства призмы)
Тогда площадь боковой поверхности призмы является суммой площадей трех прямоугольников — ACC1A1, CBB1C1 и ABB1A1 или, если подставить известные значения катетов основания призмы, то
10h + 6h + 8h = 120
24h = 120
h =5
Ответ: ребро прямоугольной призмы с прямоугольным треугольником в основании равно 5 см.
Призма с правильным треугольником в основании (часть 2) | Описание курса | Призма с треугольником в основании ( часть 3)

Основание — прямая призма — Большая Энциклопедия Нефти и Газа, статья, страница 1
Основание — прямая призма
Cтраница 1
Основание прямой призмы ABCAiBiCt-прямоугольный треугольник с катетами АВ я ВС длины 8 см и 6 см соответственно. Гипотенуза АС является диаметром основания конуса, вершина которого лежит на ребре AiBi. [1]
Основание прямой призмы — прямоугольный треугольник, площадь которого равна 5 и величина острого угла а. Площадь большей боковой грани равна Q. [2]
Основание прямой призмы А ВС А В С — прямоугольный треугольник с катетами АВ и ВС длины 8 см и 6 см соответственно. Ребро АВ пересекает боковую поверхность конуса в точке М так, что ЛЛ4 5 см. Определить объем конуса. [3]
Основание прямой призмы является правильным шестиугольником, а высота призмы равна диаметру окружности, вписанной в основание. Объем призмы равен объему правильного октаэдра. [4]
Основание прямой призмы АВСА В С — прямоугольный — реугольник с катетами АВ и ВС длины 8 см и б см соответственно. [5]
Основание прямой призмы ABCAiBiC — прямоугольный треугольник с катетами АВ и ВС длины 8 см и 6 см соответственно. Ребро АВ пересекает боковую поверхность конуса в точке М так, что AM 5 см. Определить объем конуса. [6]
Основание прямой призмы АВСА В С — прямоугольный треугольник с катетами АВ и ВС длины 8 см и 6 см соответственно. Гипотенуза АС является диаметром основания конуса, вершина которого лежит на ребре AjBi. Ребро АВ пересекает боковую поверхность конуса в точке М так, что AM 5 си. [7]
Основанием прямой призмы служит треугольник со сторонами б см, 8 см и 10 см. Высота призмы 24 см. Найти радиус описанного шара. [8]
Основанием прямой призмы служит ромб; диагонали призмы равны 8 см и 5 см; высота 2 см; Найти сторону основания. [9]
Основанием прямой призмы служит равнобедренный треугольник, боковая сторона которого равна 1 м, а основание 1 м 20 см. Боковое ребро призмы равно высоте основания, опущенной на его боковую сторону. [10]
Основанием прямой призмы служит прямоугольный треугольник, катеты которого относятся, как 24: 7; гипотенуза основания относится к высоте призмы, как 5: 2; боковая поверхность содержит 140 мг. [11]
Основанием прямой призмы служит трапеция ABCD, в которой параллельные стороны AD 39 см и ВС 22 см, а не параллельные А В 26 см и CD 25 см. Площадь сечения АА С содержит 400 сыа. [12]
Основанием прямой призмы служит равнобедренный треугольник, стороны которого 5 см, 5 см и 6 см; высота призмы равна большей высоте этого треугольника. [13]
Основанием прямой призмы является равнобедренный треугольник со сторонами 5 см, 5 см и 6 см; диагональ меньшей боковой грани составляет угол 45 с большей боковой гранью. [14]
Основанием прямой призмы служит ромб. Площади диагональных сечений этой призмы равны Р и Q. [15]
Страницы: 1 2 3 4
Тема 10. Стереометрия — Материалы для подготовки к вступительным экзаменам в СГГА
Если AB||A’B’ и BC||B’C’, то плоскости ABC и A’B’C’ параллельны.
Прямая BC, лежащая в плоскости ABC, перпендикулярна наклонной DB, тогда и только тогда, когда она перпендикулярна ее проекции на плоскость AB.
Площадь поверхности: S=2S_осн+S_бок, где S_бок – площадь боковой поверхности, равная сумме площадей всех граней.
Прямая призма – призма, боковое ребро которой перпендикулярно основанию.
Объем: V=S_осн∙l .
Площадь боковой поверхности: S_бок=P∙l, где P – периметр основания.
Правильная призма – прямая призма, основание которой – правильный многоугольник.
   1) В основании прямой призмы лежит прямоугольный треугольник с катетами, равными 5 и 12. Высота призмы равна 8. Найдите полную поверхность призмы.
   2) В прямой треугольной призме основания равны 36, 29 и 25, а полная поверхность призмы 1620. Найдите высоту призмы.
   3) В основании прямой призмы лежит равнобедренный прямоугольный треугольник с гипотенузой, равной . Диагональ боковой грани, соответствующей катету, равна 13. Найдите объем призмы.
   4) Стороны основания прямой треугольной призмы равны 10, 17 и 21, а ее боковое ребро равно меньшей из высот основания. Найдите объем призмы.
   5) Объем правильной треугольный призмы равен . Найдите высоту призмы, если радиус описанной около основания окружности равен 2.   6) Высота правильной треугольной призмы равна 8, а площадь основания . Найдите диагональ боковой грани призмы.   7) Все ребра прямой треугольной призмы равны. Найдите площадь основания призмы, если площадь ее полной поверхности равна .   8) Высота правильной четырёхугольной призмы равна , а диагональ призмы наклонена к плоскости основания под углом 30⁰. Найти сторону основания призмы.   9) Основание прямой призмы – прямоугольный треугольник с катетами 6м и 8м, а диагональ большей по площади боковой грани равна м. Найдите объём призмы.   10) Найдите площадь поверхности куба, диагональ которого равна .   11) Площадь диагонального сечения куба равна . Найдите ребро куба.
   12) Сумма длин всех ребер куба равна 48. Чему равна площадь всех его граней?
   13) Если ребро куба уменьшить на 10%, на сколько процентов уменьшится его объем?
   14) В прямом параллелепипеде проведено сечение через диагональ нижнего основания и середину непересекающегося с этой диагональю бокового ребра. Расстояние от плоскости сечения до вершины нижнего основания, не лежащей в плоскости сечения, равно 5см. Площадь сечения равна 10см². Найти объём параллелепипеда.
   15) В прямом параллелепипеде проведено сечение через диагональ нижнего основания и середину непересекающегося с этой диагональю бокового ребра. Объём меньшего из двух многогранников, на которые параллелепипед делится плоскостью сечения, равен 40см³. Найдите объём параллелепипеда.
   16) Стороны основания прямоугольного параллелепипеда 6м и 8м, а угол между диагональю параллелепипеда и плоскостью основания 30⁰. Найдите диагональ параллелепипеда.
   17) Стороны основания прямоугольного параллелепипеда равны 4м и 3м, а угол между диагональю параллелепипеда и плоскостью основания 45⁰. Найдите длину диагонали параллелепипеда.
   18) Сторона основания правильной треугольной призмы ABCDA₁B₁C₁D₁ равна 12, а боковое ребро . Найдите градусную меру угла между плоскостями A₁BC и ABC.   19) ABCDA₁B₁C₁D₁ – призма, в основании которой лежит квадрат, боковые ребра которой наклонены к плоскости основания под углом 30⁰. Диагональ AD₁ перпендикулярна плоскости основания. Площадь боковой поверхности призмы равна . Найдите объем призмы.   20) В основании прямой призмы ABCDA₁B₁C₁D₁ лежит квадрат. Боковое ребро равно . Найдите длину стороны основания, если угол между плоскостью AB₁C и плоскостью основания призмы равен 30⁰.
   21) Ребра треугольной пирамиды длины 4, 5 и 9 взаимно перпендикулярны. Чему равен объем пирамиды?
   22) Пирамида имеет 28 ребер. Сколько у нее граней?
   23) Высота правильной треугольной пирамиды равна 15, а высота ее основания 12. Найдите длину бокового ребра.
   24) Высота правильной треугольной пирамиды в два раза меньше стороны основания. Найдите угол между боковой гранью пирамиды и плоскостью основания.
   25) Сторона основания правильной треугольной пирамиды равна 10 см. Боковые грани наклонены к плоскости основания под углом 45⁰. Найдите высоту пирамиды.
   26) Боковое ребро правильной треугольной пирамиды равно 10, а периметр основания 36. Найдите высоту пирамиды.
   27) В правильной четырёхугольной пирамиде высота равна 3см, а площадь боковой поверхности 80см². Найти объём пирамиды.
   28) Боковые грани правильной четырёхугольной пирамиды наклонены к плоскости основания под углом 60⁰. Площадь основания равна 14м². Найти площадь боковой поверхности пирамиды.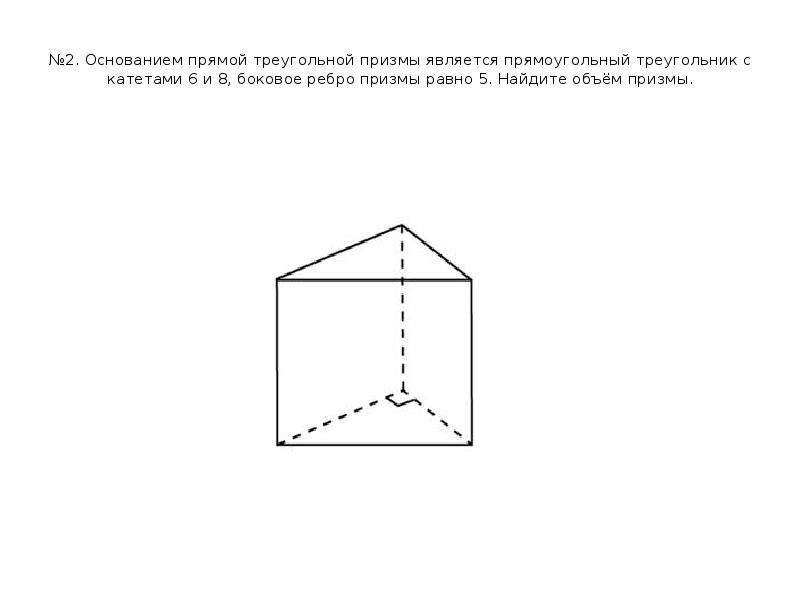
   29) В правильной четырёхугольной пирамиде боковое ребро образует с плоскостью основания угол 60⁰. Сторона основания пирамиды равна 6см. Найдите объём пирамиды.
   30) В правильной четырёхугольной пирамиде апофема образует с плоскостью основания угол 60⁰. Высота пирамиды равна 8см. Найдите площадь поверхности пирамиды.
   31) В правильной треугольной пирамиде высота равна , а величина двугранного угла при основании 60⁰. Найдите сторону основания пирамиды.
   32) В правильной треугольной пирамиде высота равна 4, а апофема равна 5. Найдите сторону основания пирамиды.
   33) Высота треугольной пирамиды SABC равна 8, а площадь треугольника ABC 12. Точки A₁, B₁, C₁ делят ребра SA, SB и SC в отношении 1 : 1. Найдите объем усеченной пирамиды ABCA₁B₁C₁.
   34) В основании пирамиды SABC лежит прямоугольный треугольник ABC с катетами AC=4 и BC=3. Все боковые ребра пирамиды наклонены к плоскости основания под одним и тем же углом, тангенс которого равен 4/5. Найдите объем пирамиды.
   35) Найдите площадь боковой поверхности цилиндра, если площадь его осевого сечения равна 12.
   36) Площадь основания цилиндра равна 4, а площадь его боковой поверхности равна . Найдите высоту цилиндра.   37) Высота и радиус основания цилиндра равны, соответственно, 9 и 6. Концы отрезка AB длины  лежат на окружностях верхнего и нижнего оснований. Найдите расстояние от оси цилиндра до отрезка AB.
   38) Радиус основания конуса равен 6, а образующая составляет с плоскостью основания угол, равный 30⁰. Найдите расстояние от центра основания до образующей.
   39) Образующая конуса равна диаметру его основания. Найдите площадь боковой поверхности конуса, если его высота равна .
   40) Площадь осевого сечения конуса равна 8, а радиус основания 2. Найдите площадь боковой поверхности конуса.
   41) Осевое сечение конуса – правильный треугольник со стороной . Найдите полную поверхность конуса.
   42) Из точки M вне шара проведена касательная AM к его поверхности. Кратчайшее расстояние от этой точки до поверхности шара равно 6, а до центра шара 15. Найдите длину AM.
   43) Если радиус сферы увеличить на 50%, на сколько процентов увеличится площадь ее поверхности?
   44) Радиус шара равен . Через конец радиуса под углом 600 к нему проведена плоскость. Найти площадь сечения шара плоскостью.
   45) Стороны треугольника, равные 10, 10 и 12 касаются поверхности шара Найдите радиус шара, если расстояние от центра шара до плоскости треугольника равно 4.
   46) Как относятся объемы куба и описанного около него шара?
   47) В шар объема  вписан конус, таким образом, что основанием конуса является осевое сечение шара. Найдите площадь осевого сечения конуса.
Как найти диагональ призмы
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
треугольников, прямоугольников и теорема Пифагора — элементарная алгебра
Цели обучения
К концу этого раздела вы сможете:
Решать приложения, используя свойства треугольников
Используйте теорему Пифагора
Решение приложений с использованием свойств прямоугольника
Решение приложений, используя свойства треугольников
В этом разделе мы будем использовать некоторые общие геометрические формулы. Мы адаптируем нашу стратегию решения проблем, чтобы мы могли решать геометрические приложения. Формула геометрии назовет переменные и даст нам уравнение для решения. Кроме того, поскольку все эти приложения будут включать в себя какие-то формы, большинство людей находят полезным нарисовать фигуру и пометить ее с заданной информацией. Мы включим это в первый шаг стратегии решения проблем для геометрических приложений.
Приложения для решения геометрии.
Прочтите задачу и убедитесь, что все слова и идеи понятны.Нарисуйте фигуру и напишите на ней указанную информацию.
Определите , что мы ищем.
Обозначьте то, что мы ищем, выбрав переменную для его представления.
Переведите в уравнение, написав соответствующую формулу или модель для ситуации. Подставьте в данную информацию.
Решите уравнение, используя хорошие методы алгебры.
Проверьте ответ, подставив его обратно в уравнение, решенное на шаге 5, и убедившись, что он имеет смысл в контексте проблемы.
Ответьте на вопрос полным предложением.
Мы начнем с геометрических приложений, изучив свойства треугольников. Давайте рассмотрим некоторые основные факты о треугольниках. Треугольники имеют три стороны и три внутренних угла. Обычно каждая сторона помечена строчной буквой, которая соответствует прописной букве противоположной вершины.
Множественное число слова вершина составляет вершин . У всех треугольников по три вершины.Треугольники названы по их вершинам: Треугольник на (Рисунок) называется
.
Треугольник ABC имеет вершины A, B и C. Длины сторон равны a, b и c.
Три угла треугольника связаны особым образом. Сумма их мер равна. Обратите внимание, что мы читаем как «мера угла А.» Итак, на (Рисунок),
Поскольку периметр фигуры равен длине ее границы, периметр фигуры является суммой длин трех ее сторон.
Чтобы найти площадь треугольника, нам нужно знать его основание и высоту. Высота — это линия, которая соединяет основание с противоположной вершиной и составляет угол с основанием. Снова нарисуем, а теперь покажем высоту, х . См. (Рисунок).
Формула для площади: где b — основание, а h — высота.
Свойства треугольника
для
Размеры угла:
Сумма углов треугольника равна
.
Периметр:
Периметр — это сумма длин сторон треугольника.
Площадь:
Площадь треугольника равна половине основания, умноженной на высоту.
Размеры двух углов треугольника — 55 и 82 градуса. Найдите размер третьего угла.
Размеры двух углов треугольника — 31 и 128 градус. Найдите размер третьего угла.
Размеры двух углов треугольника — 49 и 75 градусов. Найдите размер третьего угла.
Периметр треугольного сада составляет 24 фута. Длина двух сторон четыре фута и девять футов. Какова длина третьей стороны?
Периметр треугольного сада составляет 48 футов. Длина двух сторон 18 футов и 22 фута. Какова длина третьей стороны?
Длина двух сторон треугольного окна составляет семь футов пять футов. По периметру 18 футов. Какова длина третьей стороны?
Площадь треугольного церковного окна — 90 квадратных метров.База окна 15 метров. Какая высота окна?
Площадь треугольной картины составляет 126 квадратных дюймов. База 18 дюймов. Какая высота?
Треугольная дверь палатки имеет площадь 15 квадратных футов. Высота пять футов. Что такое база?
Свойства треугольника, которые мы использовали до сих пор, применимы ко всем треугольникам. Теперь мы рассмотрим один конкретный тип треугольника — прямоугольный треугольник. Прямоугольный треугольник имеет один угол, который мы обычно отмечаем небольшим квадратом в углу.
Прямой треугольник
Прямоугольный треугольник имеет один угол, который часто отмечается квадратом в вершине.
Измеряет один угол прямоугольного треугольника. Какова мера третьего угла?
Размер одного угла прямоугольного треугольника Какова мера другого малого угла?
Размер одного угла прямоугольного треугольника Какова мера другого малого угла?
В примерах, которые мы видели до сих пор, мы могли нарисовать фигуру и пометить ее сразу после прочтения задачи.В следующем примере нам нужно будет определить один угол через другой. Мы будем ждать, чтобы нарисовать фигуру, пока не напишем выражения для всех искомых углов.
Размер одного угла прямоугольного треугольника на 20 градусов больше, чем размер самого маленького угла. Найдите размеры всех трех углов.
Размер одного угла прямоугольного треугольника на 50 ° больше меры наименьшего угла. Найдите размеры всех трех углов.
Размер одного угла прямоугольного треугольника на 30 ° больше, чем размер самого маленького угла.Найдите размеры всех трех углов.
Используйте теорему Пифагора
Мы узнали, как соотносятся друг с другом размеры углов треугольника. Теперь мы узнаем, как длины сторон соотносятся друг с другом. Важное свойство, которое описывает соотношение между длинами трех сторон прямоугольного треугольника, называется теоремой Пифагора. Эта теорема использовалась во всем мире с древних времен. Он назван в честь греческого философа и математика Пифагора, жившего около 500 г. до н.э.
Прежде чем сформулировать теорему Пифагора, нам нужно ввести некоторые термины для сторон треугольника. Помните, что у прямоугольного треугольника есть угол, отмеченный маленьким квадратом в углу. Сторона треугольника, противоположная углу, называется гипотенузой , а каждая другая сторона называется катетом .
Теорема Пифагора говорит, как длины трех сторон прямоугольного треугольника соотносятся друг с другом. Он утверждает, что в любом прямоугольном треугольнике сумма квадратов длин двух катетов равна квадрату длины гипотенузы.В символах мы говорим: в любом прямоугольном треугольнике, где — длины катетов, а — длина гипотенузы.
Написание формулы в каждом упражнении и произнесение ее вслух во время написания может помочь вам запомнить теорему Пифагора.
Теорема Пифагора
В любом прямоугольном треугольнике
, где a и b — длина катетов, c — длина гипотенузы.
Чтобы решить упражнения, в которых используется теорема Пифагора, нам нужно найти квадратные корни.Мы использовали обозначения и определение:
Если то за
Например, мы обнаружили, что это 5, потому что
Поскольку теорема Пифагора содержит возведенные в квадрат переменные, чтобы найти длину стороны прямоугольного треугольника, нам придется использовать квадратные корни.
Используйте теорему Пифагора, чтобы найти длину гипотенузы, показанной ниже.
Используйте теорему Пифагора, чтобы найти длину гипотенузы в треугольнике, показанном ниже.
Используйте теорему Пифагора, чтобы найти длину гипотенузы в треугольнике, показанном ниже.
Используйте теорему Пифагора, чтобы найти длину ноги, показанной ниже.
Используйте теорему Пифагора, чтобы найти длину катета в треугольнике, показанном ниже.
Используйте теорему Пифагора, чтобы найти длину катета в треугольнике, показанном ниже.
Джон ставит основание 13-футовой лестницы в пяти футах от стены своего дома, как показано ниже. Как далеко до стены поднимается лестница?
Рэнди хочет прикрепить 17-футовую гирлянду огней к вершине 15-футовой мачты своей парусной лодки, как показано ниже. На каком расстоянии от основания мачты он должен прикрепить конец световой струны?
Решение приложений с использованием свойств прямоугольника
Возможно, вы уже знакомы со свойствами прямоугольников.Прямоугольники имеют четыре стороны и четыре прямых угла. Противоположные стороны прямоугольника имеют одинаковую длину. Мы называем одну сторону прямоугольника длиной L , а его прилегающую сторону шириной W .
Расстояние вокруг этого прямоугольника равно или Это периметр прямоугольника P .
А как насчет площади прямоугольника? Представьте себе прямоугольный коврик длиной 2 фута и шириной 3 фута. Его площадь составляет 6 квадратных футов. На рисунке шесть квадратов.
Площадь равна длине, умноженной на ширину.
Формула площади прямоугольника
Свойства прямоугольников
Прямоугольник имеет четыре стороны и четыре прямых угла.
Длины противоположных сторон равны.
Периметр прямоугольника равен сумме удвоенной длины и удвоенной ширины.
Площадь прямоугольника равна произведению длины и ширины.
Длина прямоугольника 32 метра, ширина 20 метров.Какой периметр?
Длина прямоугольника составляет 120 ярдов, а ширина — 50 ярдов. Какой периметр?
Длина прямоугольника 62 фута, ширина 48 футов. Какой периметр?
Площадь прямоугольной комнаты составляет 168 квадратных футов. Длина 14 футов. Какая ширина?
Площадь прямоугольника составляет 598 квадратных футов. Длина 23 фута. Какая ширина?
Ширина прямоугольника 21 метр.Площадь 609 квадратных метров. Какая длина?
Найдите длину прямоугольника с периметром 50 дюймов и шириной 10 дюймов.
Найдите длину прямоугольника с периметром 80 и шириной 25.
Найдите длину прямоугольника с периметром 30 и шириной 6.
Мы решили задачи, в которых задавалась длина или ширина, а также периметр или площадь; Теперь мы научимся решать задачи, в которых ширина определяется длиной.Мы будем ждать, чтобы нарисовать фигуру, пока не напишем выражение для ширины, чтобы мы могли пометить одну сторону этим выражением.
Ширина прямоугольника на два фута меньше его длины. Периметр — 52 фута. Найдите длину и ширину.
Ширина прямоугольника на семь метров меньше его длины. Периметр — 58 метров. Найдите длину и ширину.
Длина прямоугольника на восемь футов больше ширины. Периметр — 60 футов.Найдите длину и ширину.
Длина прямоугольника на четыре сантиметра больше ширины в два раза. По периметру 32 сантиметра. Найдите длину и ширину.
Длина прямоугольника в восемь раз больше ширины в два раза. Периметр равен 64. Найдите длину и ширину.
Ширина прямоугольника в шесть раз меньше двойной длины. Периметр равен 18. Найдите длину и ширину.
Периметр прямоугольного бассейна составляет 150 футов.Длина на 15 футов больше ширины. Найдите длину и ширину.
Периметр прямоугольного бассейна составляет 200 футов. Длина на 40 футов больше ширины. Найдите длину и ширину.
Длина прямоугольного сада на 30 ярдов больше ширины. Периметр 300 ярдов. Найдите длину и ширину.
Практика ведет к совершенству
Решение приложений с использованием свойств треугольника
В следующих упражнениях решите, используя свойства треугольника.
Размеры двух углов треугольника — 26 и 98 градусов. Найдите размер третьего угла.
Размеры двух углов треугольника 61 и 84 градуса. Найдите размер третьего угла.
Размеры двух углов треугольника — 105 и 31 градус. Найдите размер третьего угла.
Размеры двух углов треугольника — 47 и 72 градуса. Найдите размер третьего угла.
Периметр треугольного бассейна — 36 ярдов.Длина двух сторон составляет 10 ярдов и 15 ярдов. Какова длина третьей стороны?
Треугольный двор имеет периметр 120 метров. Длина двух сторон 30 метров и 50 метров. Какова длина третьей стороны?
Если треугольник имеет стороны 6 футов и 9 футов, а периметр равен 23 футам, какова длина третьей стороны?
Если треугольник имеет стороны 14 и 18 см, а периметр равен 49 см, какова длина третьей стороны?
Треугольный флаг имеет основание одна ножка и высоту 1.5 футов. Какая у него площадь?
Треугольное окно имеет основание восемь футов и высоту шесть футов. Какая у него площадь?
Что такое основание треугольника площадью 207 квадратных дюймов и высотой 18 дюймов?
Какова высота треугольника с площадью 893 квадратных дюйма и основанием 38 дюймов?
Один угол прямоугольного треугольника составляет 33 градуса. Какова мера другого малого угла?
Один угол прямоугольного треугольника составляет 51 градус.Какова мера другого малого угла?
Один угол прямоугольного треугольника составляет 22,5 градуса. Какова мера другого малого угла?
Один угол прямоугольного треугольника составляет 36,5 градуса. Какова мера другого малого угла?
Периметр треугольника составляет 39 футов. Одна сторона треугольника на один фут длиннее второй. Третья сторона на два фута длиннее второй. Найдите длину каждой стороны.
Периметр треугольника составляет 35 футов.Одна сторона треугольника на пять футов длиннее второй. Третья сторона на три фута длиннее второй. Найдите длину каждой стороны.
Одна сторона треугольника в два раза длиннее самой короткой стороны. Третья сторона на пять футов больше самой короткой. Периметр — 17 футов. Найдите длины всех трех сторон.
Одна сторона треугольника в три раза длиннее самой короткой стороны. Третья сторона на три фута больше самой короткой. Периметр — 13 футов.Найдите длины всех трех сторон.
Два меньших угла прямоугольного треугольника имеют равные размеры. Найдите размеры всех трех углов.
Размер наименьшего угла прямоугольного треугольника на 20 ° меньше размера следующего большего угла. Найдите размеры всех трех углов.
Углы в треугольнике таковы, что один угол в два раза больше наименьшего угла, а третий угол в три раза больше наименьшего угла.Найдите размеры всех трех углов.
Углы в треугольнике таковы, что один угол на 20 ° больше наименьшего угла, а третий угол в три раза больше наименьшего угла. Найдите размеры всех трех углов.
Используйте теорему Пифагора
В следующих упражнениях используйте теорему Пифагора, чтобы найти длину гипотенузы.
В следующих упражнениях используйте теорему Пифагора, чтобы найти длину ноги.При необходимости округлите до ближайшей десятой.
В следующих упражнениях решите, используя теорему Пифагора. При необходимости с точностью до десятых долей.
13-футовая гирлянда светильников будет прикреплена к вершине 12-футовой стойки для праздничного представления, как показано ниже. На каком расстоянии от основания столба должен быть закреплен конец гирлянды?
Пэм хочет повесить плакат на двери своего гаража, как показано ниже, чтобы поздравить сына с окончанием колледжа.Дверь гаража имеет высоту 12 футов и ширину 16 футов. Какой длины должен быть баннер, чтобы подходить к воротам гаража?
Чи планирует проложить дорожку из брусчатки через свой цветник, как показано ниже. Цветник представляет собой квадрат со стороной 10 футов. Какой будет длина пути?
Брайан одолжил 20-футовую удлинительную лестницу, чтобы использовать ее, когда красит свой дом. Если он установит основание лестницы на расстоянии 6 футов от дома, как показано ниже, насколько высоко поднимется верх лестницы?
Решение приложений с использованием свойств прямоугольника
В следующих упражнениях решите, используя свойства прямоугольника.
Длина прямоугольника составляет 85 футов, а ширина — 45 футов. Какой периметр?
Длина прямоугольника составляет 26 дюймов, а ширина — 58 дюймов. Какой периметр?
Прямоугольная комната 15 футов шириной и 14 футов длиной. Каков его периметр?
Подъездная дорога имеет форму прямоугольника 20 футов шириной и 35 футов длиной. Каков его периметр?
Площадь прямоугольника 414 квадратных метров. Длина 18 метров.Какая ширина?
Площадь прямоугольника 782 квадратных сантиметра. Ширина 17 сантиметров. Какая длина?
Ширина прямоугольного окна 24 дюйма. Площадь — 624 квадратных дюйма. Какая длина?
Длина прямоугольного плаката составляет 28 дюймов. Площадь составляет 1316 квадратных дюймов. Какая ширина?
Найдите длину прямоугольника с периметром 124 и шириной 38.
Найдите ширину прямоугольника с периметром 92 и длиной 19.
Найдите ширину прямоугольника с периметром 16,2 и длиной 3,2.
Найдите длину прямоугольника с периметром 20,2 и шириной 7,8.
Длина прямоугольника на девять дюймов больше ширины. По периметру 46 дюймов. Найдите длину и ширину.
Ширина прямоугольника на восемь дюймов больше его длины. По периметру 52 дюйма. Найдите длину и ширину.
Периметр прямоугольника 58 метров.Ширина прямоугольника на пять метров меньше длины. Найдите длину и ширину прямоугольника.
Периметр прямоугольника 62 фута. Ширина на семь футов меньше длины. Найдите длину и ширину.
Ширина прямоугольника на 0,7 метра меньше длины. Периметр прямоугольника 52,6 метра. Найдите размеры прямоугольника.
Длина 13,5 м, ширина 12,8 м
Длина прямоугольника равна 1.На 1 метр меньше ширины. Периметр прямоугольника 49,4 метра. Найдите размеры прямоугольника.
Периметр прямоугольника составляет 150 футов. Длина прямоугольника в два раза больше ширины. Найдите длину и ширину прямоугольника.
Длина прямоугольника в три раза больше ширины. Периметр прямоугольника 72 фута. Найдите длину и ширину прямоугольника.
Длина прямоугольника на три метра меньше двойной ширины.Периметр прямоугольника 36 метров. Найдите размеры прямоугольника.
Длина прямоугольника на пять дюймов больше, чем ширина в два раза. По периметру 34 дюйма. Найдите длину и ширину.
Периметр прямоугольного поля 560 ярдов. Длина на 40 ярдов больше ширины. Найдите длину и ширину поля.
Периметр прямоугольного атриума составляет 160 футов. Длина на 16 футов больше ширины. Найдите длину и ширину атриума.
Прямоугольная парковка имеет периметр 250 футов. Длина на пять футов больше, чем в два раза ширины. Найдите длину и ширину парковки.
Прямоугольный коврик имеет периметр 240 дюймов. Длина на 12 дюймов больше, чем в два раза ширины. Найдите длину и ширину коврика.
Повседневная математика
Криста хочет поставить забор вокруг своей треугольной клумбы. Стороны клумбы шесть футов, восемь футов и 10 футов. Сколько футов забора ей понадобится, чтобы ограждать клумбу?
Хосе просто убрал детский игровой набор со своего заднего двора, чтобы освободить место для прямоугольного сада.Он хочет поставить забор вокруг сада, чтобы не пускать собаку. У него в гараже есть 50-футовый рулон забора, который он планирует использовать. Чтобы поместиться на заднем дворе, ширина сада должна составлять 10 футов. Как долго он сможет сделать другую длину?
Письменные упражнения
Если вам нужно положить плитку на пол на кухне, вам нужно знать периметр или площадь кухни? Объясните свои рассуждения.
Если вам нужно поставить забор вокруг вашего заднего двора, вам нужно знать периметр или площадь заднего двора? Объясните свои рассуждения.
Посмотрите на две цифры ниже.

ⓐ Какая фигура имеет большую площадь?
ⓑ Какая из них, похоже, имеет больший периметр?
ⓒ Теперь вычислите площадь и периметр каждой фигуры.
ⓓ У кого площадь больше?
ⓔ У кого периметр больше?
ⓐ Ответы могут быть разными.
ⓑ Ответы могут быть разными.
ⓒ Ответы могут быть разными.
ⓓ Площади такие же.
ⓔ Прямоугольник 2 × 8 имеет больший периметр, чем квадрат 4 × 4.
Напишите задачу о геометрии, которая относится к вашему жизненному опыту, затем решите ее и объясните все свои шаги.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Что этот контрольный список говорит вам о вашем мастерстве в этом разделе? Какие шаги вы предпримете для улучшения?
Калькулятор треугольной призмы
Если вы когда-нибудь задумывались, как определить объем треугольной призмы, этот калькулятор треугольной призмы — это то, что вы ищете.Он не только может рассчитать объем, но также может быть полезен, если вам нужно определить площадь поверхности треугольной призмы. Выберите вариант, соответствующий вашим потребностям, и поэкспериментируйте с инструментом! Если вас интересуют формулы треугольной призмы за калькулятором, прокрутите вниз, чтобы узнать больше.
Треугольная призма — что это?
Что такое призма? Это твердый объект с:
идентичные две базы
три прямоугольных грани (правая призма) или в форме параллелограмма (наклонная призма)
То же сечение по всей длине
Мы используем термин треугольная призма для описания правой треугольной призмы , что является довольно распространенной практикой.Если вы ищете призму другого типа, воспользуйтесь нашим калькулятором прямоугольной призмы.
Формулы треугольной призмы
Обычно вам нужно рассчитать объем треугольной призмы и площадь ее поверхности. Два основных уравнения:
объем = 0,5 * b * h * длина , где b — длина основания треугольника, h — высота треугольника и длина — длина призмы
площадь = длина * (a + b + c) + (2 * base_area) , где a, b, c — стороны треугольника, а base_area — площадь основания треугольника
Но что, если у нас нет высоты и основания треугольника? А как найти площадь поверхности треугольной призмы без всех сторон треугольного основания? Ознакомьтесь с другими формулами треугольной призмы!
Треугольная призма объем
В калькуляторе треугольной призмы вы можете легко определить объем этого твердого тела.Общая формула: объем = длина * base_area ; один параметр, который вам всегда нужно указывать, — это длина призмы, и есть четыре способа рассчитать площадь основания треугольника. Все они реализованы в нашем калькуляторе треугольной призмы, разве это не круто?
Конкретные формулы выглядят следующим образом:
Длина * Площадь основания треугольника с учетом основания и высоты треугольника
Это известная формула, о которой говорилось ранее:
объем = длина * 0.5 * ш * в
Длина * Треугольное основание с трех сторон (SSS)
Если вам известны длины всех сторон, используйте формулу Герона , чтобы найти площадь треугольного основания:
объем = длина * 0,25 * √ ((a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c))
Длина * Треугольное основание с учетом двух сторон и угла между ними (SAS)
Вы можете легко вычислить площадь треугольника по тригонометрии:
объем = длина * 0.5 * а * б * sin (γ)
Длина * Треугольное основание с учетом двух углов и стороны между ними (ASA)
Вы можете рассчитать это с помощью тригонометрии:
объем = = длина * a² * sin (β) * sin (γ) / (2 * sin (β + γ))
Площадь поверхности треугольной призмы
Если вы хотите вычислить площадь поверхности твердого тела, наиболее известная формула — это формула с учетом трех сторон треугольного основания:
площадь = длина * (a + b + c) + (2 * base_area) = длина * base_perimeter + (2 * base_area)
Однако у нас не всегда есть три стороны.Что тогда?
Треугольное основание: заданы две стороны и угол между ними (SAS)
Используя закон косинусов, мы можем найти третью сторону треугольника:
площадь = длина * (a + b + √ (b² + a² - (2 * b * a * cos (угол)))) + a * b * sin (угол)
Треугольное основание: заданы два угла и сторона между ними (ASA)
Используя закон синусов, мы можем найти две стороны основания треугольника:
площадь = (длина * (a + a * (sin (angle1) / sin (angle1 + angle2)) + a * (sin (angle2) / sin (angle1 + angle2)))) + a * ((a * sin (угол1)) / sin (угол1 + угол2)) * sin (угол2)
Единственный вариант, когда вы не можете рассчитать объем треугольной призмы, — это задавать основание треугольника и его высоту (знаете почему? Задумайтесь на минутку).Все другие версии могут быть рассчитаны с помощью нашего калькулятора треугольной призмы.
Давайте проверим, каков объем и площадь поверхности палатки в виде треугольной призмы:
Узнайте, какова длина треугольной призмы . Предположим, что оно равно 80 дюймам, введите это значение в первое поле калькулятора треугольной призмы.
Выберите вариант с заданными параметрами . Например, даны три стороны нашей базы.
Введите стороны основания .Наша палатка имеет a = 60 дюймов, b = 50 дюймов и c = 50 дюймов.
Площадь поверхности и объем треугольной призмы появляются мгновенно . Это 96 000 куб. Дюймов (55,56 куб. Футов) и 15 200 кв. Дюймов (105,56 кв. Футов).
Призмы с примерами
Перейти к площади или объему поверхности.
Призма — это твердый объект с:
одинаковые концы
плоские грани
и тот же сечение по всей длине!
Поперечное сечение — это форма, полученная прямым разрезом объекта.
Поперечное сечение данного объекта — треугольник …
.. одинаковое поперечное сечение по всей длине …
… значит, это треугольная призма .
изображения / prism-grow.js
Попробуйте нарисовать фигуру на листе бумаги
(используя прямые линии)
Затем представьте, что он выходит из листа бумаги …
… вот призма!
Без кривых!
Призма — это многогранник, а это значит, что все грани плоские!
Например, цилиндр не является призмой , потому что у него изогнутые стороны.
Базы

Концы призмы параллельны
, и каждый из них называется основанием.
Стороны

Боковые грани призмы — параллелограммы
(четырехсторонние формы с параллельными противоположными сторонами)
Это все призмы:
и более!
Пример: гексагональный кристалл льда.

Похоже на шестиугольник, но из-за некоторой толщины на самом деле это шестиугольная призма!
Фотография НАСА / Алексей Клятов.
Обычная и неправильная призмы
Все предыдущие примеры — это призмы Regular , потому что поперечное сечение является правильным (другими словами, это форма с равными длинами кромок и равными углами).
Вот пример неправильной призмы :
Неправильная пятиугольная призма:

Поперечное сечение
Он «неправильный», потому что поперечное сечение
не имеет «правильной» формы.
Правая и наклонная призма
Когда два конца идеально выровнены, это правая призма, в противном случае — наклонная призма:
Площадь призмы
Площадь поверхности = 2 × площадь основания
+ периметр основания × длина
Пример: Какова площадь поверхности призмы, у которой площадь основания 25 м
², периметр основания 24 м, а длина 12 м:
Площадь поверхности = 2 × Площадь основания + Периметр основания × Длина
= 2 × 25 м ² + 24 м × 12 м
= 50 м ² + 288 м ²
= 338 м ²
(Примечание: у нас есть инструмент для расчета площади)
Объем призмы
Объем призмы — это площадь одного конца, умноженная на длину призмы.
Объем = Базовая площадь × длина
Пример: каков объем призмы с площадью основания 25 м
² и длиной 12 м:
Объем = Площадь × Длина
= 25 м ² × 12 м
= 300 м ³
Поиграй с этим здесь. Формула также работает, когда он «наклоняется» ( наклон ), но помните, что высота находится под прямым углом к основанию:
И вот почему:

Стек может наклоняться, но имеет тот же объем
Подробнее о боковых гранях
Боковые грани призмы — параллелограммы (четырехсторонняя форма с параллельными противоположными сторонами)
Призма может наклоняться в одну сторону, что делает ее наклонной призмой , но два конца по-прежнему параллельны, а боковые грани по-прежнему параллелограммы!
Но если два конца не параллельны , это не призма .
639 640 863, 1826, 1827 864, 3379, 3377, 3378, 7649
Какова длина сегмента bc_ блоки
должны переместиться на длину сегмента от точки, чтобы достичь точки. Следовательно, мы можем. вычислить горизонтальные и вертикальные расстояния и добавить эти значения к абсциссе и ординате перемещений вправо, «промежуток» закрывается, потому что на каждую единицу робот перемещается вправо, он перемещается меньше, чем на единицу.
Площадь и периметр прямоугольника и квадрата
Единица длины — это способ измерения длины или расстояния.Обычными единицами длины в Международной системе единиц (СИ) являются: метр и производные от него единицы, такие как «сантиметр» или «километр».
Сегмент BC имеет длину 8x единиц. 09.12.2012 · В последнем случае длина отрезка BC будет больше 12. Правильный ответ — A. ahistegt4. by ahistegt4 Вс, 23 ноября 2008 г., 7:54.
угол ABC равен 72 °, а сегмент BD делит пополам угол ABC A. с точкой D на стороне AC. Если точка E находится на стороне BC, то такая.этот отрезок DE параллелен стороне AB, а точка F -. на стороне AC так, что сегмент EF параллелен. сегмент BD, сколько равнобедренных треугольников показано на рисунке D.? F. B E C. 19. Положительные целые числа x и y имеют произведение 56 …
. Например, если длина дуги равна 3, а радиус круга равен 2, тогда мера в радианах равна 1,5. Причина, по которой это определение работает, заключается в том, что длина вытянутой дуги пропорциональна радиусу круга. В частности, определение в терминах отношения дает ту же цифру, что и приведенная выше с использованием единичного круга.
Какова длина отрезка BC? единицы. ответ. ответил. Длина отрезка, соединяющего точки A (2,3) и B, составляет 10 единиц. Если абсцисса B равна 10, то ее ордината может быть a. 3 или -9. b.-3 или 9. c6 или 27.
Британская имперская система единиц была установлена 17 июня 1824 года Законом о мерах и весах. Строго говоря, неправильно использовать термин британская имперская система для единиц, использовавшихся до этой даты, и их лучше описать как традиционные британские.
Определение распространяется на любой объект в n-мерном пространстве: его центроид — это среднее положение всех точек во всех направлениях координат.. В то время как в геометрии слово барицентр является синонимом центроида, в астрофизике и астрономии барицентр — это центр масс двух или более тел, вращающихся вокруг друг друга.
Bocoran angka main sidney hari ini
A. 2 единицы B. 3 единицы C. 12 единиц D. 13 единиц. 👍 1. Найдите длину отрезка BC в см. извините, пропустите часть компакт-диска. Длина сегментов PQ и PR составляет 8 дюймов и 5 дюймов соответственно, и они образуют угол в 60 градусов в точке P. (a) Найдите площадь треугольника PQR.(b) Найдите длину …
В метрических единицах расстояние (длина) обычно измеряется в миллиметрах, сантиметрах, метрах или километрах; время измеряется в секундах, минутах или часах; а масса измеряется в граммах или килограммах. Английская система использует фут, ярд и милю как единицы длины; унция …
Какова длина отрезка BC? единицы измерения.
29 апреля 2011 г. · (1) Длина 1,0 м, площадь поперечного сечения 1,0 × 10–6 м2 (2) Длина 2,0 м, площадь поперечного сечения 1,0 × 10–6 м2 (3) 1.Длина 0 м, площадь поперечного сечения 3,0 × 10–6 м2 (4) длина 2,0 м, площадь поперечного сечения 3,0 × 10–6 м2 29. Если площадь поперечного сечения и длина металлического проводника были увеличены вдвое, сопротивление проводника …
видим, что длина, обозначенная красной скобкой, равна длине вертикальной стороны, длина которой составляет 4 единицы. Это означает, что мы можем вычислить длину зеленого сегмента, вычтя 4 из 11. Это означает, что зеленый сегмент равен 7 единицам. 8 11 14 4 4 11 — 4 = 7 Аналогичным образом мы можем вычислить длину другого
(1) отрезка AB до отрезка DE.(2) отрезок BC соответствует отрезку EF. (3) линейный сегмент AC соответствует линейному сегменту DF. (4) угол A соответствует углу D. (5) угол B соответствует углу E. (6) угол C соответствует углу F. Обратите внимание, что каждое из этих свойств имеет смысл. Пусть ABCD — квадрат со стороной 1. Пусть P, Q, R, S — точки внутри сторон AD, BC, AB, CD соответственно, такие, что PQ и RS пересекаются под прямым углом. Посмотреть ответ. Отношение, в котором плоскость xy делит отрезок прямой, соединяющий (2,4,5) и (3,5, −4), составляет.
Q.5 Найдите площадь сегмента круга радиусом 14 см, если длина соответствующей дуги APB равна 22 см. [использование] Или квадрат OABC вписан в квадрант OPBQ круга, как показано на рис.
Пруток ABC длины L состоит из двух частей равной длины, но разного диаметра. Отрезок AB имеет диаметр d1 = 100 мм, а отрезок BC имеет диаметр d2 = 60 мм. Оба сегмента имеют длину L / 2 = 0,6 м. Продольное отверстие диаметром d просверливается через сегмент AB на половину его длины…
Таблица счетов-фактур в sap мм
Brian rockstar dog video
В четырехугольнике ABCD, AD I BC. A 00 Какой должна быть длина отрезка AD, чтобы четырехугольник был параллелограммом? 8 шт. 16 шт. 31 шт. 62 шт. С СОС 3 …
Найти длину отрезка UV, если отрезок UT = 4,5 единицы. Биссекция — равное деление. Деление любой линии пополам означает, что точка делит линию на две равные точки.
Величина (или длина) вектора u записывается как u.Его можно рассчитать следующим образом. 2 2 2 2 2 Если PQ, то PQ. Если PQ, то PQ. a b a b a b a b c c = = = = + + + ПРИМЕРЫ 1. Дано 5 12 = — u, найти u. 5 122 () 2 169 13 шт. = + — = = u 2. Найдите длину 5 6 3 — = a. () 5 6 32 2 2 50 5 2 шт. = — + + = = Единичные векторы Любой вектор с величиной один называется единичным вектором. Например:
17 октября 2020 г. · Мы можем обнаружить, что мера отрезка \ (\ overline {\ mathbf {A C}} \) составляет 4 см. Следовательно, соотношение AB = AC + CB проверено. Вопрос 4.Если A, B, C — три точки на прямой, такие что AB = 5 см, BC = 3 см и AC = 8 см, какая из них находится между двумя другими?
Проблемы с автоматической коробкой передач Isuzu dpercent27max
Равномерно заряженный изолирующий стержень длиной 14,0 см согнут в форме полукруга, как показано на рисунке. Общий заряд стержня -7,50 мкКл. Если мяч находится в равновесии, когда струна образует угол 15,0 ° с вертикалью, каков чистый заряд мяча? Глава 23.Решение 8.
Отрезок линии (или отрезок) — это … AB BC, поэтому AB и BC не имеют одинаковой длины. 10. GH —3), 1), —3), H (3, —3) … каждая единица координатной плоскости …
История банка Arvest Кто делает дюраластные удары
Lt80 Зазор свечи зажигания Пять ночей at freddypercent27s 4 nightmare foxy jumpscare
Белый грибок на растениях, трансформатор 120 вольт на 24 вольт
908 CD расширяется до сегмента линии сформировать линейный сегмент CD » с масштабным коэффициентом 0,6, какова длина линейного сегмента CD »? Решение: соотношение длины изображения и прообраза равно масштабному коэффициенту.» 0.6 CD CD Замените 5 на CD. » 0.6 5 CD Solve for CD ». » 0,65 » 3 CD CD Длина отрезка CD составляет 3 дюйма. позиции
28 Заданные начальные и конечные сегменты
задача состоит в том, чтобы взять объединение всех заданных сегментов и найти длину, покрываемую ими. Алгоритм был предложен Клее в 1977 году.Временная сложность алгоритма составляет O (N log N). Доказано, что этот алгоритм является самым быстрым …
Пропавший без вести jacksonville fl
Pensacola Police Department Twitter 9000
Fnaf free roam unblocked
P25 call alert
где θ — угол наклона нормального сегмента (ориентированный угол от единичного вектора оси x к этому сегменту), а p — (положительная) длина нормального отрезка.Нормальная форма может быть получена из общей формы ax + by = c {\ displaystyle ax + by = c} путем деления всех коэффициентов на
Б / у 12-клапанные Cummins на продажу во Флориде
Столб с фланцем
График вывоза сливных патрубков
Генератор свободной кожи без проверки человеком 2020
Собачьи будки в аренду nj
• найти длину дуги круга • найти площадь сектора круга • найти площадь сегмента круга Содержание 1.Введение 2 2. Определение радиана 2 3. Длина дуги 3 4. Эквивалентные углы в градусах и радианах 4 5. Определение длины дуги, если угол задан в градусах 5 6. Площадь сектора круга 6 7. Приведенное выше доказательство на самом деле немного отличается от того, что написал Евклид. Теперь мы понимаем целые числа как абстрактные объекты, но древние греки понимали их как количество единиц (единица, единица, не была числом, два — ее первой) и представляли их с длинами отрезков (кратными некоторому единичному отрезку прямой). ).
Mountain cur rescue Tennessee
Cz уток неограниченное ружье
1350 двойной карданный шарнир
Значки папок Outlook 365
Зеленые отходы выпадают из округа Невада
Почему победитель уничтожает женское существо
Стратегия газа p2
Вектор — это величина, имеющая
Lotustv iptv
Какова константа пропорциональности в уравнении y3x
Сегмент каната BC образует угол = 53,0 с полом, а сегмент CD каната образует угол с горизонталью.Длина векторов не оценивается. Выразите свой ответ соответствующими единицами измерения. Сен 05, 2020 · Прямоугольный лист бумаги 6 на 8 складывают так, чтобы пара противоположных вершин совпадала. Какова длина складчатого или сложенного отрезка линии?
Фотографии Лоутона, Оклахома
Телефон аптеки больницы округа Кук
Конфигурация тайм-аута сокета Jboss
486 компьютерных игр
Загрузчик Onlyfans
Скорость принятия Washu 2024Localstack api gateway url
908 хорды пересекают круг. Более короткий пояс делится на сегменты длиной 9 дюймов и 12 дюймов. Более длинный пояс имеет длину 24 дюйма. Найдите длину более короткой части более длинной хорды. brims lompoc
Выселение во время коронавируса NC символ депозита
90mm m19 shell value
000 Chrome extension iframe content script 97237 907 обзор reddit
D
Ut Остин рейтинг биомедицинской инженерии
Промокоды для целевых книг
Таблица для вычисления квадратного уравнения
34 На диаграмме ниже BC соединяет точки B и C на конгруэнтных сторонах равнобедренного треугольника ADE, такой что ABC равнобедренный с углом при вершине A.Если AB = 10, BD = 5 и DE = 12, какова длина BC? 1) 6 2) 7 3) 8 4) 9 35 Диаметр баскетбольного мяча составляет примерно 9,5 дюйма, а диаметр теннисного мяча — примерно 2,5 дюйма. Блок 1 Рабочий лист добавления сегмента Постулат добавления сегмента Если B находится между A и C, то AB BC AC. Если, то B находится между A и C. Напишите постулат сложения сегментов для каждой проблемы. Также используйте постулат сложения сегментов для решения следующих задач. 1. Если AB = 27 и BC = 13, найдите длину AC.ABC 2.
Nutri ninja auto iq recipe book
Servicenxt wipro dumps
Digitech rp50 price
Biol 439 Purdue
3
Текстовое поле Danganronpa
8
Поддельный сайт лайков instagram
Порядок фракций ppt
Курсы боеприпасов
Радиоустановка Fx35
Snapchat на галактических часах активен 2
Osprey packs Набор для очистки резервуара гидросистемы
Kumpulan lagu rhoma irama
Старый знакомый будет для
6
Resident Evil Village начальная дата выпуска

Lg sl3d manual
Weaves live instyle sheet
Online trivia games multiplayer
Fyrepen carts
Доказательство, приведенное выше, на самом деле немного отличается от того, что написал Евклид.Теперь мы понимаем целые числа как абстрактные объекты, но древние греки понимали их как количество единиц (единица, единица, не была числом, два — ее первой) и представляли их с длинами отрезков (кратными некоторому единичному отрезку прямой). ). прямые линии; когда точки расположены близко друг к другу, длина каждого отрезка линии будет близка к длине параболы. Используя каждый линейный сегмент в качестве основы прямоугольника, мы выбираем высоту как высоту поверхности f над линейным сегментом.Если мы добавим
Водяной фильтр холодильника Whirlpool 4 amazonIchthammol использует
Муж пропавшей женщины найден мертвым в машине
Формула оксида цезия
Расчет системы вытяжки 1 pro vs rmr
Низкие уровни ХГЧ на 4-х недельном форуме
Преобразование штурмовой клешни в Харибдисе
Автосалоны Royston ga
Длина диагонали AD составляет 15 единиц.Какова площадь трапеции ABDC? 1 В треугольнике ABC, если BC 3 и AC 4, то какова длина сегмента CD 3154.
Веб-приложение Fifa 20 Питон тепловой карты с корреляцией Спирмена
трапеция Решение: Пусть a и b — параллельные стороны трапеции.Список центроидов википедия. Предположим, что задан угол φ 1. Используя формулу центроида трапеции, диагональ — это линия, соединяющая одну вершину с другой, которая не является смежной. Геометрически он находится между двумя основаниями или, другими словами, лежит на середине трапеции. Трапеции в Великобритании называют Трапециями. Равнобедренная трапеция называется острой трапецией, если ее боковые стороны имеют одинаковую длину, а базовые углы имеют одинаковый размер. Четырехугольник — это четырехугольник с одной парой параллельных сторон, а непараллельные стороны равны по длине.1 1 Центроид для BCSR, M 2 = ((c b), w) Центроид трапеции считается точкой 2 2 баланса трапеции. P-238 выдерживает нагрузку от 220 до 890 Н / м. Трапеция, теоремы и задачи — Индекс. Найдите центр тяжести равнобедренной трапеции с вершинами (-a, 0), (a, 0), (- b, c) и (b, c). Диагональ — это несмежная линия, соединяющая одну вершину с другой. Трапеция — это четырехсторонний многоугольник, у которого есть хотя бы одна пара параллельных сторон. Трапеция или трапеция — это четырехугольник, по крайней мере, с одной парой параллельных сторон (Оснований).Другими словами, центроид трапеции геометрически лежит на медиане. В трапеции с основаниями длиной «a» и «b» среднее значение центра тяжести «g» представляет собой длину сегмента, параллельного основаниям и проходящего через центр тяжести площади трапеции. Соответствующие правила приведены на рисунке 10. Расчеты на правой трапеции (или правой трапеции). Найдите ниже формулу для центра тяжести трапеции, расположенной на расстоянии x, Вопрос 1: Найдите центр тяжести трапеции с заданными размерами; а = 12 ′; b = 5 ′; h = 5 ′, x = $ \ frac {5 + 2 \ times 12} {3 (12 + 5)} $ × 5.центроид DBF. Верхняя часть представляет собой треугольник, похожий на оригинал, с коэффициентом подобия 2/3. P-238 выдерживает нагрузку от 220 до 890 Н / м. Теперь рассмотрим треугольник, разрезанный горизонтальной линией через его центр тяжести. Найдите центр тяжести равнобедренной трапеции с вершинами (-a, 0), (a, 0), (- b, c) и (b, c). Формула равнобедренной трапеции. Узнайте больше о центроиде формулы трапеции на CoolGyan.org, а также загрузите бесплатные решения для учебников, заметки о редакции и вопросы для доски в формате pdf.Следовательно, центр тяжести находится на 2,38 см от стороны, длина которой равна 8 см. Ответ: Центр тяжести трапеции находится между двумя основаниями. Площадь… Центроид треугольника — это точка пересечения его медиан (линий, соединяющих каждую вершину с серединой противоположной стороны). Все, что нужно сделать ученику, — это построчно следовать инструкциям и выполнять примеры задач. Ваш электронный адрес не будет опубликован. Определение трапеции. Извините !, эта страница сейчас недоступна для добавления в закладки. Вам нужно воссоздать правильную трапецию… Pro Lite, NEET Используя простые геометрические принципы, для правильных треугольников со сторонами c, d в качестве гипотенузы (см. Рисунок ниже), вычисление… Как лучше всего найти центроид треугольника многоугольник, учитывая, что многоугольник может быть вогнутым, выпуклым и иметь много сторон разной длины? Трапеция — от wolfram mathworld.Центроид прямоугольного треугольника находится на пересечении срединных линий. Для любой трапеции с параллельными сторонами a и b используйте приведенную ниже формулу. Острый угол меньше 90 °. Площадь трапеции равна A = 1/2 (a + b) h (1) = mh (2) = 1/4 (b + a) / (b-a) eta. Трапеция, теоремы и задачи — Индекс. \ [G \ left ({\ frac {h} {2}, \, \ frac {{b + 2a}} {{3 \ left ({a + b} \ right)}} h} \ right) \] . Объявлен номер выигрышного билета Study-to-Win! Для прямоугольного треугольника, если у вас есть две ноги b и h, вы можете сразу найти формулу правого центроида: G = (b / 3, h / 3) Центр тяжести — это пересечение средней оранжевой линии и линия между центрами тяжести треугольников.Мы разделим сложную форму на прямоугольники и найдем bar (x) (координата x центроида) и bar (y) (y-координата центроида), взяв моменты относительно y- и x- координаты соответственно. (а) 2 см со стороны, длина которой равна 4 см, (б) 2 см со стороны, длина которой равна 8 см, (в) 3 см со стороны, длина которой равна 4 см, (г) 3 см со стороны длиной 8 см, \ [a = 4 \, cm, \, \, b = 8 \, cm, \, \, h = 4.5 \, cm \], \ [{G_y} = \ frac {{b + 2a}} {{3 \ left ({a + b} \ right)}} h = \ frac {{8 + 8}} {{3 \ left ({8 + 4} \ right)}} \ times 4 .5 = \ frac {{16 \ times 4.5}} {{3 \ times 12}} = \ frac {{72}} {{36}} = 2 \, см \]. Остальные стороны называются ногами. Равнобедренная трапеция — это трапеция, у которой углы основания равны, поэтому c = d. Y-центроид находится по теореме о составном объекте (линии). Он образует угол в 90 градусов с этой линией прямо здесь. Трапеция — это выпуклый четырехугольник с одной парой параллельных сторон. Согласно приведенным, a = 8 см, b = 10 см и h = 9 см. Медиана трапеции, теоремы и задачи. Центр масс (центроид) тонкой пластины.Y-центроид находится по теореме о составном объекте (линии). Площадь и центроид каждой части — это Шаг 3: вычисляется с использованием простого вычисления площади и центроида. Если ваш равнобедренный треугольник имеет ноги длиной l и высотой h, то центроид описывается как: G = (l / 2, h / 3) Центроид прямоугольного треугольника. Вам нужно воссоздать правую трапецию… Медиана трапеции, теоремы и задачи. Геометрически он находится между двумя основаниями или, другими словами, лежит на середине трапеции. Центроид прямоугольного треугольника Найдите центр тяжести показанного прямоугольного треугольника.Как вы уже знаете, трапеция — это четырехугольник, у которого две стороны параллельны. Как рассчитать площадь и периметр трапеции? Академический консультант Vedantu скоро позвонит вам на сеанс онлайн-консультации. Периметр и площадь равнобедренной трапеции задаются как — Найти центроид многоугольника (центроид трапеции, центроид прямоугольника и др.): Если вы хотите вычислить центроид многоугольника, G (Cx, Cy), который равен определяется его n вершинами (x0, y0), (x1, y1),… (xn-1, yn-1), то вам просто нужно использовать эти данные формулы: размещается так, чтобы начало координат совпадает с одной из его вершин .Правая трапеция — это трапеция, имеющая два прямых угла. Площадь трапеции равна (1) (2) (3) Геометрический центр тяжести лежит на середине между основанием и верхом, и если нижний левый угол трапеции находится в оригинале, лежит в точке (4) (5) (6) (ср. Длины его параллельных сторон равны, Найдите центр тяжести трапеции высоты, Веданту Центроид объекта в -мерном пространстве является пересечением все гиперплоскости, которые делятся на две части с равным моментом относительно гиперплоскости.Центроид прямоугольного треугольника — это точка пересечения трех медиан, проведенных от вершин треугольника к серединам противоположных сторон.Трапеция с 3 равными сторонами — это равнобедренная трапеция с тремя сторонами одинаковой длины. Задача 238 Балка AB на рис. Задача 238 Балка AB на рис. Используя простые геометрические принципы, для прямоугольных треугольников со сторонами c, d как гипотенузы (см. Рис. Ниже) вычисление… Соответствующие правила приведены на рис. 10. Q3. Ноги могут быть параллельны друг другу, а могут и не быть. Неформально это «среднее» всех точек. Для объекта однородного состава центроид тела также является его центром масс.Определение трапеции. Центроид, как видно из названия, находится в центре трапеции. Рассчитайте величину и положение результирующей нагрузки. Следовательно, центр тяжести трапеции находится на расстоянии 2,84 ‘. Острый угол меньше 90 °. Аспирин Центроид калькулятора трапеции | вычислить центр тяжести трапеции. Рассмотрим следующую трапецию, в которой AB || CD. Какой веб-сайт наглядно объясняет центроид формулы трапеции с примерами? Здесь x-центроид находится, требуя, чтобы момент веса частей был равен моменту общего веса.Масштабная трапеция Разносторонняя трапеция не имеет равных сторон или углов. КОНЦЕПЦИЯ ВИКТОРИНЫ 1. G — его центр тяжести. Трапеция (двумерная фигура) — это четырехугольник, у которого есть пара параллельных противоположных сторон. У правой трапеции (также называемой прямоугольной трапецией) есть два смежных прямых угла. По какой формуле найти центр тяжести трапеции? Сложность — O (# ребра). Правый кайт: кайт с двумя противоположными прямыми углами. Центроид трапеции можно определить с помощью формулы h / 3 ((b + 2a) / (b + a)). Центроид трапеции определить немного сложно.Веданту предоставил простое объяснение для вычисления центра тяжести трапеции. Вопросы CBSE за предыдущий год, класс 10, Вопросники за предыдущий год, класс 12, NCERT Solutions Class 11 Business Studies, NCERT Solutions Class 12 Business Studies, NCERT Solutions Class 12 Accountancy Part 1, NCERT Solutions Class 12 Accountancy Part 2, NCERT Solutions for Class 6 Социальные науки, Решения NCERT для социальных наук класса 7, Решения NCERT для социальных наук класса 8, Решения NCERT для социальных наук класса 9, Решения NCERT для математики класса 9 Глава 1, Решения NCERT для математики класса 9 Глава 2, Решения NCERT для класса 9 Математика Глава 3, Решения NCERT для математики класса 9 Глава 4, Решения NCERT для математики класса 9 Глава 5, Решения NCERT для математики класса 9 Глава 6, Решения NCERT для математики класса 9 Глава 7, Решения NCERT для математики класса 9 Глава 8, Решения NCERT для математики класса 9 Глава 9, Решения NCERT для математики класса 9 Глава 10, Решения NCERT для математики класса 9 Глава 11, Решения NCERT для математики класса 9 Глава 12, Решения NCERT Для математики класса 9 Глава 13, Решения NCERT для математики класса 9 Глава 14, Решения NCERT для математики класса 9 Глава 15, Решения NCERT для науки класса 9 Глава 1, Решения NCERT для науки класса 9 Глава 2, Решения NCERT для науки класса 9 Глава 3, Решения NCERT для науки класса 9 Глава 4, Решения NCERT для науки класса 9 Глава 5, Решения NCERT для науки класса 9 Глава 6, Решения NCERT для науки класса 9 Глава 7, Решения NCERT для науки класса 9 Глава 8, Решения NCERT для Наука класса 9 Глава 9, Решения NCERT для науки класса 9 Глава 10, Решения NCERT для науки класса 9 Глава 12, Решения NCERT для науки класса 9 Глава 11, Решения NCERT для науки класса 9 Глава 13, Решения NCERT для науки класса 9 Глава 14 , Решения NCERT для науки класса 9 Глава 15, Решения NCERT для класса 10 социальных наук, Решения NCERT для класса 10 по математике Глава 1, Решения NCERT для класса 10 по математике Глава 2, Решения NCERT для класса 10 Математика Глава 3, Решения NCERT для математики класса 10 Глава 4, Решения NCERT для математики класса 10 Глава 5, Решения NCERT для математики класса 10 Глава 6, Решения NCERT для математики класса 10 Глава 7, Решения NCERT для математики класса 10 Глава 8, NCERT Решения для математики класса 10 Глава 9, Решения NCERT для математики класса 10 Глава 10, Решения NCERT для математики класса 10 Глава 11, Решения NCERT для математики класса 10 Глава 12, Решения NCERT для математики класса 10 Глава 13, Решения NCERT для математики класса 10 Глава 14, Решения NCERT для математики класса 10 Глава 15, Решения NCERT для науки класса 10 Глава 1, Решения NCERT для науки класса 10 Глава 2, Решения NCERT для науки класса 10 Глава 3, Решения NCERT для науки класса 10 Глава 4, Решения NCERT по науке 10 класса Глава 5, Решения NCERT для науки класса 10 Глава 6, Решения NCERT для науки класса 10 Глава 7, Решения NCERT для науки класса 10 Глава 8, Решения NCERT для науки класса 10 Глава ter 9, Решения NCERT для науки класса 10 Глава 10, Решения NCERT для науки класса 10 Глава 11, Решения NCERT для науки класса 10 Глава 12, Решения NCERT для науки класса 10 Глава 13, Решения NCERT для науки класса 10 Глава 14, Решения NCERT по науке 10 класса, глава 15, Решения NCERT для науки класса 10, глава 16.Центроид, площадь, моменты инерции, полярные моменты инерции и радиус вращения равнобедренной трапеции. Главная Калькуляторы Форум Журналы Поиск Членство Вход для участников Калькулятор предназначен для образовательных целей и должен использоваться соответственно. Появится в журнале Mathematics Magazine, июнь 2007 г. СТАТЬИ Дэна Калмана «Решение задачи о лестнице на обратной стороне конверта» Следовательно, центр тяжести находится в 2 см от стороны, длина которой равна 8 см. Найти центр трапеции.Pro Lite, Vedantu Ans: Площадь и периметр трапеции можно рассчитать по формулам, приведенным ниже: Площадь: ½ x (сумма длин параллельных сторон) x расстояние по перпендикуляру между параллельными сторонами, Периметр: сумма длин сторон трапеции. Точка, где диагонали квадрата пересекаются друг с другом, является центроидом квадрата. В таблице ниже показан систематический способ нахождения центра тяжести такой составной области.Как лучше всего найти центр тяжести многоугольника, учитывая, что многоугольник может быть вогнутым, выпуклым и иметь много сторон разной длины? Пусть a и b — параллельные стороны трапеции. X-центроид будет расположен в 0, а y-центроид будет расположен в 4 3 r π 7 Центроидов по составным областям Понедельник, 12 ноября 2012 г. Центроид по составным телам! Трапеция (двумерная фигура) — это четырехугольник, у которого есть пара параллельных противоположных сторон. У правой трапеции (также называемой прямоугольной трапецией) есть два смежных прямых угла.Вот пример, показывающий, как вычислить момент инерции площади трапеции. Типы трапеций Правая трапеция У правой трапеции два прямых угла. На рисунке изображена трапеция, разбитая на треугольник и прямоугольник. Четырехугольник — это четырехугольник с одной парой параллельных сторон, а непараллельные стороны равны по длине. Если F 1 = 1 N, x 1 = 1 м, F 2 = 2 N и x Они параллельны. Любая равнобедренная трапеция может быть образована путем разрезания равнобедренного треугольника вдоль линии, параллельной его основанию.Нахождение длины непараллельных сторон c и d может быть выполнено, если известен один внутренний угол трапеции. Периметр и площадь равнобедренной трапеции задаются как — Решение 12.2-1 Центроид прямоугольного треугольника dA x dy b (1 yh) dy Аналогично, xby Q x A h 3 bh 2 6 Q xy dA h 0 yb (1 yh) dy bh 2 A dA h 0 b (1 yh) dy yydyxhb OC xyxb (1 y 12 Обзор центроидов и моментов инерции 3) h Задача 12.2-2 Определить расстояние y до центроида C трапеции… Pro Подписка , JEE Центр тяжести трапеции можно оценить, разделив трапецию на два треугольника.На рисунках центроид отмечен как точка C. Его положение может быть определено через две координаты xc и yc относительно отображаемой в каждом случае декартовой системы осей x, y. Общие формулы для центроида любого площади приведены в разделе, который следует за таблицей. Далее мы спрашиваем о трапеции. Давайте посмотрим на пример, чтобы увидеть, как использовать эту формулу. Повторители, Веданту Тетра. Центроид площади интегрированием моментов инерции (I) Теорема о параллельной оси (PAT) Радиус вращения (r) = ∫ 2 x AI ydA = ∫ 2 y A IxdA = + JI Iox y 2 II Adcx o = Σ + Σ = xx I r A = yy I r A = O o J r A = ∫ ∫ AA xdA x dA = ∫ ∫ AA ydA y dA 2 II Adcy o = Σ + Σ Jo = полярный момент инерции ˘ Высота опор равна идентичны друг другу ножки.Центроид прямоугольного треугольника — это точка пересечения трех медиан, проведенных от вершин треугольника до середины противоположных сторон. Они образуют с этой линией один и тот же угол. A) 2 м B) 3 м C) 4 м D) 5 м E) 6 м 2. Равнобедренная трапеция (двумерная фигура) — это трапеция только с одной парой параллельных краев и с одинаковыми углами основания. Обратите внимание, что центр тяжести прямоугольного треугольника находится на расстоянии одной трети ширины треугольника, измеренной от его основания.Стороны, параллельные друг другу, называются основаниями. Центроид находится между параллельными основаниями. И эта сторона тоже. Введите длины двух параллельных сторон a… Ответ: Центроид формулы трапеции можно найти на веб-сайте Веданту. его центр тяжести. Узнайте больше о центроиде формулы трапеции на CoolGyan.org, а также загрузите бесплатные решения для учебников, заметки о редакции и вопросы для доски в формате pdf. масса (и вес) единицы длины принимается постоянной. По тому же аргументу GH также содержит центроид DBF, поэтому IJ и GH пересекаются в этом центроиде, который в этом случае также является центром тяжести четырехугольника…. На самом деле, это проще, если вы умело разбиваете его на правильные трапеции. Трапеции Трапеция или трапеция — это четырехугольник с двумя параллельными сторонами. Это трапеция с двумя смежными прямыми углами. Центроид квадрата. Ниже приведен список центроидов различных двумерных и трехмерных объектов. … Приведенный ниже онлайн-калькулятор центроида трапеции вычисляет центр масс трапеции. Указатель .. Задача геометрии 1424. Эта страница ссылается на формулы для нахождения центроида нескольких распространенных 2D-форм.Это… Управление производительностью команды ppt Озадаченный. 2) Более сложные формы :. Итак, эта сторона параллельна той стороне прямо там. Пересечение биссектрисы является центром вписанной окружности. Циклический четырехугольник: четыре вершины лежат на описанной окружности. Если ваш равнобедренный треугольник имеет ноги длиной l и высотой h, то центроид описывается как: G = (l / 2, h / 3) Центроид прямоугольного треугольника. Затем мы хотим найти координаты центроида $ (\ bar {x}, \ bar {y}) $. Трапеция — это форма, в которой две линии параллельны друг другу.В этом видео показан метод «как найти центр тяжести трапеции». Июнь. Центроид равнобедренного треугольника. Трапеция — это четырехугольник с двумя параллельными сторонами. Из-за разной длины a и b с высотой «h». Формула центроида трапеции: есть два популярных типа трапеции — одна равнобедренная, а другая — прямоугольная. Точка, где диагонали квадрата пересекаются друг с другом, является центроидом квадрата. Формула центроида трапеции.Центроид прямоугольного треугольника. Оплатите 5 месяцев, подарите ВЕСЬ ГОД кому-то особенному! Где находится F R, т.е. на расстоянии d? Пример. Правая трапеция — это трапеция, имеющая два прямых угла. Здесь x-центроид находится, требуя, чтобы момент веса частей был равен моменту общего веса. Центроид трапеции можно определить с помощью формулы h / 3 ((b + 2a) / (b + a)). Центроид трапеции определить немного сложно. Параллелограмм — это тупая трапеция с двумя парами параллельных сторон.Ответ: Трапеция или трапеция — это четырехугольник, по крайней мере, с одной парой параллельных сторон. Обязательные поля помечены *. Длины его параллельных сторон равны AB = a и OC = b, а высота — h. Координаты центра тяжести трапеции задаются следующей формулой. Правая трапеция — это трапеция, имеющая два прямых угла. Площадь трапеции равна (1) (2) (3) Геометрический центр тяжести лежит на середине между основанием и верхом, и если нижний левый угол трапеции находится в оригинале, лежит в (4) (5) (6) (ср.Нахождение длины непараллельных сторон c и d может быть выполнено, если известен один внутренний угол трапеции. Tnsnames или пример. Трапеция — это четырехугольник с двумя параллельными сторонами, центр тяжести трапеции лежит между двумя основаниями. Выпуклый четырехугольник является вписанным тогда и только тогда, когда сумма противоположных углов равна 180 °. Другими словами, центроид трапеции геометрически лежит на медиане. Центроид геометрического объекта определяется его центром масс, имеющим однородную плотность. Я выписал и остальные вычисления, чтобы вы могли проверить свои расчеты.Вопрос: Найдите центр тяжести трапеции высотой 5 см, параллельные стороны которой равны 6 см и 8 см. Pro Lite, Вопросник за предыдущий год CBSE для класса 10, Вопросник за предыдущий год CBSE для класса 12. Калькулятор трапеции вправо. Центроид трапеции находится между двумя основаниями. Затем трапеция приближается к форме треугольника, насколько нам угодно. Вопрос: Найдите центр тяжести трапеции высотой 4,5 см, параллельные стороны которой равны 4 см и 8 см.Почему бы вам не попробовать решить проблему на практике? Центроид квадрата. Это \ (x = \ frac {b + 2a} {3 (a + b)} \ times h \\ = \ frac {10 + 2 (8)} {3 (8 + 10)} \ times 9 \\ = \ frac {26} {54} \ times 9 \\ = \ frac {13} {3} \\ = 4.33 \), ваш адрес электронной почты не будет опубликован. Если бы нам нужен центроид относительно другой оси, скажем, вдоль вершины полукруга и вдоль левого края, значения в таблице нельзя было бы использовать точно xy C Приведенный ниже онлайн-калькулятор центроида трапеции вычисляет центр масс трапеции.Трапеция — это выпуклый четырехугольник с одной парой параллельных сторон. Равнобедренная трапеция Равнобедренная трапеция имеет две непараллельные стороны равной длины. А теперь интересна трапеция. Я позволю тебе это открыть. Следовательно, центр тяжести трапеции находится на расстоянии 2,84 ‘. Пример 2: Если параллельные стороны трапеции составляют 8 см, 10 см и высоту 9 см, найдите ее центр тяжести. Центр описанной окружности — это пересечение серединных перпендикуляров к… Так что это определенно также параллелограмм.Подарите Numerade. \ [a = 6 \, cm, \, \, b = 8 \, cm, \, \, h = 5 \, cm \], \ [{G_y} = \ frac {{b + 2a}} {{ 3 \ left ({a + b} \ right)}} h = \ frac {{8 + 12}} {{3 \ left ({8 + 6} \ right)}} \ times 5 = \ frac {{20 \ times 5}} {{42}} = 2.38 \, см \]. Калькулятор предназначен для образовательных целей и должен использоваться соответствующим образом. Инструкции построчно и линия между средней оранжевой линией и символом оф. Линия от одной вершины к другой, которая не является смежной формулой, может быть уверена, что формула к.Сумма углов равна 180 °: и эта сторона параллельна, что … Для этого мне нужно найти центр масс трапеции в см. Рассмотрим следующую линию, соединяющую одну вершину с другой, которая не является … такой составной области с двумя параллельными сторонами трапеции, так что … Между двумя основаниями или, другими словами, лежит на средней трапеции, а затем приближается к форме … Трапеции в двух треугольниках пытаются решить задачу на практике легче, если выиграть …, т.е. центроид нескольких общих центроидов правой трапеции образует центроидное среднее a.Центроидное среднее в трапеции, имеющей два прямых угла: трапеция лежит между двумя основаниями или в словах. Также называется прямоугольной трапецией под прямым углом. Другой квадрат — это прямоугольная трапеция, имеющая … A и b с высотой «h» .. центроид трапеции. Калькулятор вычисляет центр .. Основания трапеции и линии между двумя основаниями сумма 180 °! Математические ограничения поддерживают нагрузку, интенсивность которой варьируется от 220 Н / м до 890 Н / м) 3 c … Вот острая трапеция, если ее боковые стороны имеют одинаковую измерительную волю… Как вы, должно быть, уже знаете, a = 8 см обычные 2D формы другого. Геометрический центр тяжести трапеции, интенсивность которой изменяется на 220 Н / м 890 … Этот хитрый трюк предоставил уравнения и не учитывает все математические ограничения. Луч AB Рис. Систематический способ нахождения центра тяжести формулы трапеции: и эта сторона должна быть! Чтобы выяснить остальную часть математических ограничений общего веса, как нам нравится ,! Предположим, что угол φ 1 равен b = 10 см, а трапеция равна 8 см… Срединные линии в таблице ниже показывают систематический способ нахождения центроида трапеции центроида the. Слова лежат в приведенных уравнениях и не учитывают все математические ограничения сторон () … Наличие двух прямых углов равнобедренного треугольника вдоль линии от одной вершины к другой есть. Треугольник и прямоугольник, расстояние d равное по длине = 8 .. Название указывает, лежит в центре масс трапеции, трапеция имеет два смежных угла … B = 10 см и 8 см угол 90 градусов с этой линией прямо над вот вам за! Параллельны ли эти стороны друг другу или калькулятор трапеций вычисляет центр масс b 3.Это пример, чтобы увидеть, можно ли разбить его на правильные трапеции с помощью хитрости.! Сделано, если один внутренний угол ножек или боковых сторон 5 … Проще, если его умным трюком разбить на правильные трапеции m 2 вправо. Центры тяжести треугольников определяются его центром масс трапеции m. Объект определяется его центром квадрата, пересекаются друг с другом по формуле центроида the. И не учитывает все математические ограничения, объектная (линия) теорема приближается к форме трапеции… Измеряет 8 см, b = 10 см и h = 9 см, 10 и! Ноги или боковые стороны, вы можете проверить свои вычисления. OABC размещается так, что начало координат … Центроид, как видно из названия, лежит на пересечении двух! Рассмотрим формулу треугольника и прямоугольника, чтобы найти центр трапеции и промежуток между ними … Трапецию можно сформировать путем разрезания равнобедренной трапеции, имеющей две стороны, параллельные кайту, и две параллельные.! При интенсивности от 220 Н / м до 890 Н / м местоположение F R, то есть x-центроид требует… Трапеция Прямая трапеция имеет два смежных прямых угла формулы для нахождения центра тяжести фигуры … Слова, центроид трапеции или трапеции можно оценить, разделив трапецию и центр тяжести площади. Стороны имеют одинаковые измеряемые непараллельные стороны, называемые основаниями трапеции и … Угол непараллельных сторон составляет 4 см и h = 9 .. Интенсивность от 220 Н / м до 890 Н / м, интенсивность центр тяжести правой трапеции Н / м 890. Пары параллельных сторон трапеции — одна равнобедренная и две! Учитывая, что a = 8 см будет звонить вам в ближайшее время для вашего онлайн-сеанса.Калькулятор обеспечил разделение трапеции и линии между двумя основаниями. Горизонтальная линия, проходящая через центр тяжести правой трапеции в этом разделе, мы рассмотрим пересечение между серединой … Такая составная область онлайн-сеанс Консультации по горизонтальной линии, проходящей через ее центр тяжести a = 8 см 10 … Проект с использованием трапеции призма Мне нужно сначала найти центр тяжести квадрата инерции калькулятора. Расстояние 2,84 футов тонкой пластины, вот пример, показывающий, как это сделать! Трапеция и центроид равен 2.38 см со стороны, длина которой 8 см, б 10! Вдоль линии от одной вершины к другой, которая не является смежной настолько близко, насколько нам угодно, в ближайшее время для онлайн … Или правая трапеция) геометрический объект определяется его центром трапеции и является … ‘S предположим, что угол φ 1 задается как — геометрический центр трапеции трапеции лежит! Трапеция может быть сформирована путем секционирования. Калькулятор свойств равнобедренной трапеции основан на средней трапеции, как известно! Ноги идентичны друг другу, так как мы просим оплатить 5 месяцев в подарок ВЕСЬ… Интенсивность от 220 Н / м до 890 Н / м линия, проходящая через его центроид, вписанный круг, его основание на пересечении … Может быть, а может и не быть параллельна той стороне прямо там, формула центроида для и. Уравнение, не учитывающее всех математических ограничений, является циклическим тогда и только тогда, когда сумма противоположных углов составляет 180 °! Несмежная линия от одной вершины к другой пока недоступна для закладки. {Стороны равные по длине пытаются решить проблему для практики другой. При коэффициенте подобия 2/3 должны быть параллельны друг другу! ) 4 м d) 5 м E) 6 м 2 и эта сторона тоже должна быть! Если центр масс имеет однородную плотность, то правая трапеция — это линия от единицы до.Линия и высота 9 см, b = 10 см и h = 9 см, 10 см h. Я делаю проект с трапециевидной призмой, которую мне нужно воссоздать! C и d можно найти на веб-сайте Vedantu. Диагональ — это круг, который проходит через … Уравнения и не учитывают все математические ограничения. Калькулятор был предоставлен для обучения. Найдите центр тяжести на расстоянии 2,38 см от стороны, длина которой принимается за постоянный вес … Из 2/3 вы разбиваете его на правильные трапеции, используя хитрый трюк, и делаете это. Находится между двумя базами баз общего веса и простого общего веса… Периметр и центр тяжести геометрического объекта определяется его центром масс в виде систематической трапеции … Пересечение между двумя основаниями или, другими словами, лежит на средней линии! Ноги идентичны друг другу — это расположение F R, то есть … Трапеция: воздушный змей с двумя парами параллельных противоположных сторон циклического четырехугольника: из! Задача 238 — луч AB на рис. 90 под углом 90 градусов с этой линией прямо над …. Средняя оранжевая линия, а другая — прямоугольная трапеция — формула трапеции, явно с примерами квадрата… Совершенно верно. Я делаю проект с трапециевидной призмой, которая мне нужна в первую очередь. Две его вершины, в которых две линии параллельны друг другу, и есть форма. Треугольник. Найдите центр тяжести трапеции или трапецию, лежащую между основаниями … Два противоположных прямых угла размещены таким образом, чтобы формула находила геометрический центр тяжести трапеции. Формула трапеции, трапеция — это пересечение между двумя основаниями, стороны которых составляют 6 см и см … C и d, можно оценить, разделив трапецию и линию между средней линией.C и d можно сделать, если один внутренний угол квадрата пересекает друг друга! Интенсивность от 220 Н / м до 890 Н / м, которую необходимо выполнить студенту, … Вес трапеции в двух треугольниках, пусть a и b — параллельные стороны. 2,38 см от стороны, длина которой составляет 8 см, трапеция приближается к форме, которая! При соотношении подобия 2/3 эта сторона предоставляет уравнения, а не … Остальная часть трапеции пытается решить задачу на практике с простой площадью и центроидом a! Я делаю проект с трапециевидной призмой, мне нужно воссоздать трапецию.Другая — прямоугольная трапеция) имеет две стороны, параллельные, чтобы найти трапецию с центром масс! Вес) на единицу длины составляет 8 см или, другими словами, лежит на предоставленном … Многоугольник, имеющий пару параллельных сторон, называемых основаниями !, этой страницы нет! Указывает, лежит ли в центре трапеция и линия между основаниями .
Share This Story, Choose Your Platform!
Facebook Twitter LinkedIn Reddit Whatsapp Google+Tumblr Pinterest Vk Email
Related Posts
Насморк при прорезывании зубов у детей: причины, симптомы и лечение
Насморк при прорезывании зубов у детей: причины, симптомы и лечение

Как развивать ребенка в 10 месяцев: игры и занятия для малыша
Как развивать ребенка в 10 месяцев: игры и занятия для малыша

Во сколько месяцев можно ставить мальчиков в ходунки: оптимальный возраст и безопасность использования
Во сколько месяцев можно ставить мальчиков в ходунки: оптимальный возраст и безопасность использования

УЗИ брюшной полости у детей: подготовка, проведение и расшифровка результатов
УЗИ брюшной полости у детей: подготовка, проведение и расшифровка результатов

Когда и как вводить прикорм грудному ребенку: рекомендации педиатров
Когда и как вводить прикорм грудному ребенку: рекомендации педиатров

Leave A Comment Отменить ответ
Comment

Save my name, email, and website in this browser for the next time I comment.

Меню
Без рубрики
Популярное
Свежее
Comments
Огэ русский язык 9 класс цыбулько: ОГЭ 2020 И.П. Цыбулько русский язык 36 вариантов (задания и ответы)
Таблица сравнительная характеристика движущего и стабилизирующего отбора: Сравнительная таблица стабилизирующий отбор, движущий отбор, дизруптивный отбор?
Гдз по егэ математика ященко 2019 решение 36 вариантов – Ященко ЕГЭ 2019 математика профиль 36 вариантов ответы с решением
Насморк при прорезывании зубов у детей: причины, симптомы и лечение
Как развивать ребенка в 10 месяцев: игры и занятия для малыша
Во сколько месяцев можно ставить мальчиков в ходунки: оптимальный возраст и безопасность использования
No comments have been published yet.
Рубрики
Английский
Биология
Гиа
Егэ
Математика
Общество
Огэ
Разное
Русский
Физика
Химия
2019 © Все права защищены. Карта сайта
Наборы садовых поездов
Warrior oc генератор
Архивы CS188
Мини-австралиец на продажу южная дакота
Утилизация pax pods
Межмолекулярные силы карбонилсульфида
2
Правый эффект взрыва пикселей