упростите выражения:а) — Школьные Знания.com
Мне нужно придумать шаблон, из которого будут формироваться следующие треугольники.
У парламенті острова Лицарів і Брехунів 51 депутат. В цілях скорочення бюджету було прийняте рішення звільнити одного з депутатів. Але кожен із депута … тів заявив, що якщо його виключать з парламенту, то серед решти більшість буде брехунами. Скільки лицарів у парламенті острова? *На острові живуть Лицарі, які завжди говорять лише правду, та Брехуни, які завжди брешуть.Срочно треба!!!!!!
Объясните(подробно) решение пожалуйста
Яку максимальну кількість слонів можна поставити на дошку 7 х 7 з вирізаною центральною частиною 3 х 3 таким чином, щоб слони не били один одного (чер … ез вирізану частину бити не можна)?срочно треба !!!!
Є набір з декількох (2 або більше) яблук і декількох (2 або більше) груш. Якщо яблук не менше 5, то груш рівно 4. А якщо груш 3 або більше, то яблук р … івно 6. Скільки існує таких наборів?Срочно треба !!!!
З двох міст назустріч один одному виїхали два автомобілі. Перший автомобіль зШвидкістю 85 км/год виїхав на 3 год пізніше, ніж другий.Автомобілі зустрі
… лися через 5 годин після виїзду другого автомобіля, що їхав зіШвидкістю 76 км/год. Яка відстань між містами?
Перший автомобіль зШвидкістю 85 км/год виїхав на 3 год пізніше, ніж другий.Автомобілі зустрі
… лися через 5 годин після виїзду другого автомобіля, що їхав зіШвидкістю 76 км/год. Яка відстань між містами?
!!Майстер і його учень отримали замовлення. Третю частину всього замовленнямайстер може виконати за 5 год, виготовляючи щогодини 16 деталей.Учень 7/12 … въого замовлення може виконати за 10 год. За який час моглибВиконати все замовлення майстер і його учень, працюючи разом?
Два прямокутники мають однакову довжину 16 см. Периметр першогопрямокутника дорівнює 4 дм 8 см.Знайти площу другого прямокутника, якщо його ширина на … 1 см більша від ширинипершого прямокутника.
шаг шестиклассника на 20% короче шага десятиклассника но в единицу времени он делает на 20% шагов больше чем десятиклассник кто из них раньше придёт в … школу если они живут в одном доме и выходят в школу одновременноСРОЧНО!!!!
3х-7у=5 ху=1 обчислити 9х²+49у² Помогите пожалуйста дам 50 балов
Упростить выражение.
 Онлайн калькулятор с примерами
Онлайн калькулятор с примерамиЧто значит упростить выражение
Когда говорят упростить выражение, подразумевают конкретные математические действия с этим выражением, в результате чего оно примет иной вид.
Такими действиями могут быть раскрытие скобок, внесение и вынесение множителя за скобку, деление (сокращение), умножение, возведение в степень, приведение дробей к общему знаменателю и много других операций.
При этом часто используют формулы сокращенного умножения и теоремы, а в тригонометрии от простых формул приведения до самых сложных тригонометрических выражений.
Чем старше школьник, тем больше формул он знает и обладает богатым арсеналом математических действий.
В чем смысл таких действий
Задачи на упрощение выражений встречаются с самых младших классов. Дети сами того не осознавая, учатся шевелить мозгами в нужном направлении, чтобы преобразовать одно выражение в другое.
Разумеется, все задания составляются таким образом, что в любом случае они приводятся к более простому виду или подходящему для дальнейших операций.
Однако, при таком подходе теряется общий смысл поставленной задачи.
Когда ученик слышит, что надо что-то упростить, то машинально начинает перебирать всевозможные математические действия в голове, не задаваясь вопросом, а для чего упрощать?
Приведем наглядный пример
Допустим, сказано упростить выражение (a+b)2. В этом случае абсолютно каждый нормальный школьник раскроет скобки и будет доволен самим собой. Без сарказма это действительно так и это нормально.
Но вот другая постановка задачи: упростите выражение (a+b)2, затем подставьте следующие числовые значения a=⅔, b=⅓ и запишите получившееся число.
Кто теперь скажет, что раскрыть скобки, затем подставить a=⅔ и b=⅓, а затем вычислить ответ, это легче, чем сразу найти a+b=⅔+⅓=1? После этого возводи единицу хоть в сотую степень!
Заключение
Итак, главная цель задач на упрощение выражений в том, чтобы научить вас применять те или иные математические действия над выражениями.
Это обязательно нужно уметь делать. Но более важная проблема в том, чтобы научиться применять необходимые действия в нужный момент и воспользоваться результатом преобразования.
Благо есть онлайн калькуляторы упрощения выражений, например, такой как наш, с помощью которого можно проверить свои вычислительные результаты.
Желаем успехов!
A1. Вычислите: ( ) : 3 3. Ответ: A2. Упростите выражение: a(a 4) (a 2) 2. Ответ: A3. Из формулы y = ax 3. выразите x.
1) 4 2) 3,86 3) 3,5 4) 2,8
Томский областной институт повышения квалификации и переподготовки работников образования Центр мониторинга и оценки качества образования Работа по математике 10 класс (октябрь, 014 г) Вариант I Инструкция
Подробнее= 2.
 3x + 2y + z, если x : y : z = 2 : 1 : 3. 2x 3y z
3x + 2y + z, если x : y : z = 2 : 1 : 3. 2x 3y zВ1 В2 В3 В4 В5 В6 В7 В8 С1 С2 С3 С4 Сумма ШИФР Заполняет сотрудник ОКО Вступительная работа по математике для поступающих в 10 физико-химический и химико-биологический классы СУНЦ УрФУ 1 мая 2017 года
ПодробнееСАМОСТОЯТЕЛЬНАЯ РАБОТА 1
САМОСТОЯТЕЛЬНЫЕ РАБОТЫ САМОСТОЯТЕЛЬНАЯ РАБОТА 1 1. Найдите разложение на простые множители числа 1008. 2. Найдите количество составных чисел, которые больше 70 и меньше 90. 3.* Найдите все трехзначные
ПодробнееB C Сумма Балл Подпись
B C Сумма Балл Подпись СУНЦ УрФУ Вступительный тест по математике для поступающих в 8 класс 20 апреля 2014г. 1 вариант В заданиях B1 B10 записать ответ в указанном месте. Если получается несколько вариантов,
Подробнее Мониторинговые исследования
МАТЕМАТИКА 8 КЛАСС (Вариант 0 /6) Мониторинговые исследования по МАТЕМАТИКЕ 8 класс Вариант 0 Работа по математике состоит из двух частей, включающих в себя задания. На выполнение работы по математике
На выполнение работы по математике
Инструкция по выполнению работы
Математика. 0 класс. Вариант МА000 (базовый уровень) Инструкция по выполнению работы На выполнение стартовой работы по математике даётся 90 минут. Работа включает в себя 4 заданий и состоит из двух частей.
x ; Задание по математике для учащихся 9 классов 1. Вычислить: Упростить выражение: Решите уравнение:
ГОУ лицей при МИФИ. Вычислить: Задание по математике для учащихся 9 классов 0, 0,00 : 0, 6.. 0. 0 0, 6: 6 : 0, 9.., 0, 6 : 0,09 00.. 6, (6,,,) 6,, 6,, 6,, 0 (0,6) (0,).. (: ) (,) 0 0.. ( 60 Cos0 ) (,),
ПодробнееМониторинговые исследования
МАТЕМАТИКА 8 КЛАСС (Вариант 0 /6) Мониторинговые исследования по МАТЕМАТИКЕ 8 класс Вариант 0 Работа по математике состоит из двух частей, включающих в себя задания На выполнение работы по математике отводится,5
Тренировочная работа 3 по МАТЕМАТИКЕ
Тренировочная работа 3 по МАТЕМАТИКЕ 16 марта 011 года 9 класс Вариант 1 (перспективная) Математика. 9 класс. Вариант 1 (перспективная) Инструкция по выполнению работы Работа состоит из двух частей. В
9 класс. Вариант 1 (перспективная) Инструкция по выполнению работы Работа состоит из двух частей. В
6 2, 1 6 0, 3 =6 2, 1 0, 3 =6 1, 8 (решено программой UMS ( A1 Упростите выражение: A2 Вычислите:
Вариант ЕГЭ по математике 2009 г. с решением. A1 Упростите выражение: www.umsolver.com)) 6 2, 1 6 0, 3 6 2, 1 0, 3 6 1, 8 (решено программой UMS ( A2 Вычислите: программой UMS ( www.umsolver.com)) 3 36
Математика — 7 класс
Межрегиональная олимпиада школьников «Будущие исследователи будущее науки» 07 г. Математика — 7 класс. Найти значение выражения 0.(5a 7 b).( a 4 b) (b a ) при a 0.5, b 0.5.. Решить уравнение ( ).. В записи
ПодробнееЯгубов.РФ ВАРИАНТ 302
ГВЭ Математика 9 класс Вариант 0 ВАРИАНТ 0 Инструкция по выполнению работы Общее время экзаменационной работы минут Характеристика работы Всего в работе заданий, из которых 0 заданий базового уровня (часть
ТЕСТЫ ПО ДИСЦИПЛИНЕ.
 г. Казань
г. КазаньТЕСТЫ ПО ДИСЦИПЛИНЕ Математика для проведения вступительных испытаний по специальности: 030300.65 Психология служебной деятельности по направлениям: 030300.6 Психология 30700.6 Прикладная информатика 080100.6
Подробнее/8. АС = 4. Найдите АВ. В треугольнике угол равен 90,, Найдите. В треугольнике угол равен 90,, Найдите. Найдите АВ.
Решение прямоугольного треугольника 1. В треугольнике угол равен 90,, Найдите 2. В треугольнике угол равен 90,, Найдите 3. В треугольнике ABC угол C равен 90, АС = 4, Найдите АВ. 4. В треугольнике ABC
ПодробнееАС = 4. Найдите АВ. В треугольнике угол равен 90,, Найдите. В треугольнике угол равен 90,, Найдите. Найдите АВ.
Решение прямоугольного треугольника 1. В треугольнике угол равен 90,, 2. В треугольнике угол равен 90,, 3. В треугольнике ABC угол C равен 90, АС = 4, АВ. 4. В треугольнике ABC угол C равен 90, АС = 4.
4. В треугольнике ABC угол C равен 90, АС = 4.
АС = 4. Найдите АВ. В треугольнике угол равен 90,, Найдите. В треугольнике угол равен 90,, Найдите. Найдите АВ.
Решение прямоугольного треугольника 1. В треугольнике угол равен 90,, 2. В треугольнике угол равен 90,, 3. В треугольнике ABC угол C равен 90, АС = 4, АВ. 4. В треугольнике ABC угол C равен 90, АС = 4.
ПодробнееОЛИМПИАДА «ФИЗТЕХ» ПО МАТЕМАТИКЕ. 9 класс
МОСКОВСКИЙ ФИЗИКО-ТЕХНИЧЕСКИЙ ИНСТИТУТ ОЛИМПИАДА «ФИЗТЕХ» ПО МАТЕМАТИКЕ 9 класс БИЛЕТ 9 ШИФР Заполняется ответственным секретарём 1. Дана линейная функция f(x). Известно, что расстояние между точками пересечения
ПодробнееВариант 1. Часть B. a 2 a 2a 1
СУНЦ УрФУ Вступительный тест по математике для поступающих в 9 физико-математический, математико-информационный, физико-химический и естественнонаучный классы 17 мая 015 Вариант 1 Часть B К заданиям части
ПодробнееСкачано с Часть I 1,5.
 A2 Вычислите: 3 8 0,125. 1) 1 2) 2 3) 2, 5 4) 0,001
A2 Вычислите: 3 8 0,125. 1) 1 2) 2 3) 2, 5 4) 0,001A1 Упростите выражение Скачано с www.ctege.org Часть I 1,5 11 0,3 11. 1) 1, ) 5 3) 11 1, 4) 11 5 Решение: Ответ 3) 11 11 1,5 0,3 = 11 11 = 11 1,5 0,3 1, A Вычислите: 3 8 0,15. 1) 1 ) 3), 5 4) 0,001 3 3
ПодробнееОтветы. Ответ: ), ),, )
Ответы 1. Решите систему уравнений { Второе уравнение умножаем на и прибавляем к первому:. Замечаем, что. Откуда, полагая, что, получим и. 1), то есть. Из первого уравнения, находим, что и. Откуда, то
Подробнеепятибалльной шкале Первичные баллы
Ответы и решения Система оценивания выполнения всей работы Максимальный балл за выполнение работы 20. Таблица перевода баллов в отметки по пятибалльной шкале Отметка по «2» «3» «4» «5» пятибалльной шкале
ПодробнееВсе прототипы заданий В года
1. Прототип задания B5 ( 27450) Найдите тангенс угла AOB. Все прототипы заданий В5 2014 года 2. Прототип задания B5 ( 27456) Найдите тангенс угла AOB. 7. Прототип задания B5 ( 27547) Найдите площадь треугольника,
Прототип задания B5 ( 27450) Найдите тангенс угла AOB. Все прототипы заданий В5 2014 года 2. Прототип задания B5 ( 27456) Найдите тангенс угла AOB. 7. Прототип задания B5 ( 27547) Найдите площадь треугольника,
ОЛИМПИАДА ПО МАТЕМАТИКЕ. 9 класс
МОСКОВСКИЙ ФИЗИКО-ТЕХНИЧЕСКИЙ ИНСТИТУТ ОЛИМПИАДА ПО МАТЕМАТИКЕ 9 класс БИЛЕТ 7 ШИФР Заполняется ответственным секретарем 1. Когда к квадратному трёхчлену f(x) прибавили x, его наименьшее значение увеличилось
Подробнее8 2 4 cosπ + 4 cos2 ( π ))) = 1 (
Олимпиада школьников РАНХиГС 04-05 Математика 0 класс Очный этап вариант. Вычислить (максимум 0 баллов): Решение: sin 8 ( π 6 ) + cos 8 ( π 6 ) sin 8 ( π 6 ) + cos 8 ( π 6 ) = (sin ( π 6 )) 4 + (cos (
ПодробнееТренировочная работа 5 по МАТЕМАТИКЕ
Район Город (населенный пункт) Школа Класс Фамилия Имя Отчество Тренировочная работа 5 по МАТЕМАТИКЕ 5 мая 011 года 9 класс Вариант 1 (перспективная) Математика. 9 класс. Вариант 1 (перспективная) Инструкция
9 класс. Вариант 1 (перспективная) Инструкция
Буквенные выражения
Буквенное выражение (или выражение с переменными) — это математическое выражение, которое состоит из чисел, букв и знаков математических операций. Например, следующее выражение является буквенным:
a + b + 4
С помощью буквенных выражений можно записывать законы, формулы, уравнения и функции. Умение манипулировать буквенными выражениями — залог хорошего знания алгебры и высшей математики.
Любая серьёзная задача в математике свóдится к решению уравнений. А чтобы уметь решать уравнения, нужно уметь работать с буквенными выражениями.
Чтобы работать с буквенными выражениями, нужно хорошо изучить базовую арифметику: сложение, вычитание, умножение, деление, основные законы математики, дроби, действия с дробями, пропорции. И не просто изучить, а понять досконально.
Переменные
Буквы, которые содержатся в буквенных выражениях, называются переменными.
Например, в выражении a + b + 4 переменными являются буквы a и b. Если вместо этих переменных подставить любые числа, то буквенное выражение a + b + 4 обратится в числовое выражение, значение которого можно будет найти.
Числа, которые подставляют вместо переменных называют значениями переменных. Например, изменим значения переменных a и b. Для изменения значений используется знак равенства
a = 2, b = 3
Мы изменили значения переменных a и b. Переменной a присвоили значение 2, переменной b присвоили значение 3. В результате буквенное выражение a + b + 4 обращается в обычное числовое выражение 2 + 3 + 4, значение которого можно найти:
2 + 3 + 4 = 9
Когда происходит умножение переменных, то они записываются вместе. Например, запись ab означает то же самое, что и запись a × b. Если подставить вместо переменных a и b числа 2 и 3, то мы получим 6
2 × 3 = 6
Слитно также можно записать умножение числа на выражение в скобках. Например, вместо a × (b + c) можно записать a(b + c). Применив распределительный закон умножения, получим a(b + c) = ab + ac.
Например, вместо a × (b + c) можно записать a(b + c). Применив распределительный закон умножения, получим a(b + c) = ab + ac.
Коэффициенты
В буквенных выражениях часто можно встретить запись, в которой число и переменная записаны вместе, например 3a. На самом деле это короткая запись умножения числа 3 на переменную a и эта запись выглядит как 3 × a.
Другими словами, выражение 3a является произведением числа 3 и переменной a. Число 3 в этом произведении называют коэффициентом. Этот коэффициент показывает во сколько раз будет увеличена переменная a. Данное выражение можно прочитать как «a три раза» или «трижды а«, или «увеличить значение переменной a в три раза», но наиболее часто читается как «три a«
К примеру, если переменная a равна 5, то значение выражения 3a будет равно 15.
3 × 5 = 15
Говоря простым языком, коэффициент это число, которое стоит перед буквой (перед переменной).
Букв может быть несколько, например 5abc. Здесь коэффициентом является число 5. Данный коэффициент показывает, что произведение переменных abc увеличивается в пять раз. Это выражение можно прочитать как «abc пять раз» либо «увеличить значение выражения abc в пять раз», либо «пять abc«.
Если вместо переменных abc подставить числа 2, 3 и 4, то значение выражения 5abc будет равно 120
5 × 2 × 3 × 4 = 120
Можно мысленно представить, как сначала перемнóжились числа 2, 3 и 4, и полученное значение увеличилось в пять раз:
Знак коэффициента отнóсится только к коэффициенту, и не отнóсится к переменным!
Рассмотрим выражение −6b. Минус, стоящий перед коэффициентом 6, отнóсится только к коэффициенту 6, и не отнóсится к переменной b. Понимание этого факта позвóлит не ошибаться в будущем со знаками.
Найдем значение выражения −6b при b = 3.
−6b это короткая форма записи от −6 × b. Для наглядности запишем выражение −6b в развёрнутом виде и подставим значение переменной b
−6b = −6 × b = −6 × 3 = −18
Пример 2. Найти значение выражения −6b при b = −5
Запишем выражение −6b в развёрнутом виде
−6b = −6 × b
и далее подставим значение переменной b
−6b = −6 × b = −6 × (−5) = 30
Пример 3. Найти значение выражения −5a + b при a = 3 и b = 2
−5a + b это короткая форма записи от −5 × a + b, поэтому для наглядности запишем выражение −5 × a + b в развёрнутом виде и подстáвим значения переменных a и b
−5a + b = −5 × a + b = −5 × 3 + 2 = −15 + 2 = −13
Иногда буквы записаны без коэффициента, например a или ab.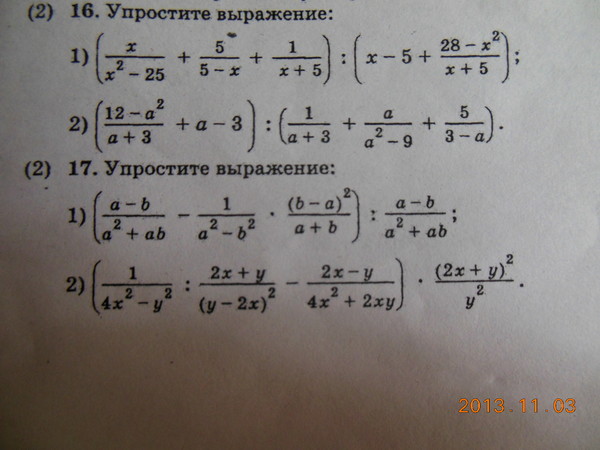 В этом случае коэффициентом является единица:
В этом случае коэффициентом является единица:
1a, 1ab
но единицу по традиции не записывают, поэтому просто пишут a или ab
Если перед буквой стоит минус, то коэффициентом является число −1. Например, выражение −a на самом деле выглядит как −1a. Это произведение минус единицы и переменной a. Оно получилось следующим образом:
−1 × a = −1a
Здесь крóется небольшой подвох. В выражении −a минус, стоящий перед переменной a на самом деле относится к невидимой единице, а не к переменной a. Поэтому при решении задач следует быть внимательным.
К примеру, если дано выражение −a и нас прóсят найти его значение при a = 2, то в школе мы подставляли двойку вместо переменной a и получали ответ −2, не особо зацикливаясь на том, как это получалось. На самом деле происходило умножение минус единицы на положительное число 2
−a = −1 × a
−1 × a = −1 × 2 = −2
Если дано выражение −a и требуется найти его значение при a = −2, то мы подставляем −2 вместо переменной a
−a = −1 × a
−1 × a = −1 × (−2) = 2
Чтобы не допускать ошибок, первое время невидимые единицы можно записывать явно.
Пример 4. Найти значение выражения abc при a=2, b=3 и c=4
Выражение abc это короткая форма записи от 1×a×b×c. Для наглядности запишем выражение abc в развёрнутом виде и подставим значения переменных a, b и c
1 × a × b × c = 1 × 2 × 3 × 4 = 24
Пример 5. Найти значение выражения abc при a=−2, b=−3 и c=−4
Запишем выражение abc в развёрнутом виде и подставим значения переменных a, b и c
1 × a × b × c = 1 × (−2) × (−3) × (−4) = −24
Пример 6. Найти значение выражения −abc при a=3, b=5 и c=7
Выражение −abc это короткая форма записи от −1×a×b×c. Для наглядности запишем выражение −abc в развёрнутом виде и подставим значения переменных a, b и c
−abc = −1 × a × b × c = −1 × 3 × 5 × 7 = −105
Пример 7. Найти значение выражения −abc при a=−2, b=−4 и c=−3
Найти значение выражения −abc при a=−2, b=−4 и c=−3
Запишем выражение −abc в развёрнутом виде:
−abc = −1 × a × b × c
Подставим значение переменных a, b и c
−abc = −1 × a × b × c = −1 × (−2) × (−4) × (−3) = 24
Как определить коэффициент
Иногда требуется решить задачу, в которой требуется определить коэффициент выражения. В принципе, данная задача очень простá. Достаточно уметь правильно умножать числа.
Чтобы определить коэффициент в выражении, нужно отдельно перемножить числа, входящие в это выражение, и отдельно перемножить буквы. Получившийся числовой сомножитель и будет коэффициентом.
Пример 1. Определить коэффициент в выражении: 7m×5a×(−3)×n
Выражение состоит из нескольких сомножителей. Это можно отчетливо увидеть, если записать выражение в развёрнутом виде. То есть произведения 7m и 5a записать в виде 7×m и 5×a
7 × m × 5 × a × (−3) × n
Применим сочетательный закон умножения, который позволяет перемножать сомножители в любом порядке. А именно, отдельно перемнóжим числа и отдельно перемнóжим буквы (переменные):
А именно, отдельно перемнóжим числа и отдельно перемнóжим буквы (переменные):
−3 × 7 × 5 × m × a × n = −105man
Коэффициент равен −105. После завершения буквенную часть желательно расположить в алфавитном порядке:
−105amn
Пример 2. Определить коэффициент в выражении: −a×(−3)×2
Перемножим отдельно числа и буквы:
−a × (−3 ) × 2 = −3 × 2 × (−a) = −6 × (−a) = 6a
Коэффициент равен 6.
Пример 3. Определить коэффициент в выражении:
Перемножим отдельно числа и буквы:
Коэффициент равен −1. Обратите внимание, что единица не записана, поскольку коэффициент 1 принято не записывать.
Эти казалось бы простейшие задачи могут сыграть с нами очень злую шутку. Часто выясняется, что знак коэффициента поставлен не верно: либо пропущен минус либо наоборот он поставлен зря. Чтобы избежать этих досадных ошибок, тема умножения целых чисел должна быть изучена на хорошем уровне.
Слагаемые в буквенных выражениях
При сложении нескольких чисел получается сумма этих чисел. Числа, которые складывают называют слагаемыми. Слагаемых может быть несколько, например:
1 + 2 + 3 + 4 + 5
Когда выражение состоит из слагаемых, вычислять его намного проще, поскольку складывать легче, чем вычитать. Но в выражении может присутствовать не только сложение, но и вычитание, например:
1 + 2 − 3 + 4 − 5
В этом выражении числа 3 и 5 являются вычитаемыми, а не слагаемыми. Но нам ничего не мешает, заменить вычитание сложением. Тогда мы снова получим выражение, состоящее из слагаемых:
1 + 2 + (−3) + 4 + (−5)
Не суть, что числа −3 и −5 теперь со знаком минус. Главное, что все числа в данном выражении соединены знаком сложения, то есть выражение является суммой.
Оба выражения 1 + 2 − 3 + 4 − 5 и 1 + 2 + (−3) + 4 + (−5) равны одному и тому значению — минус единице:
1 + 2 − 3 + 4 − 5 = −1
1 + 2 + (−3) + 4 + (−5) = −1
Таким образом, значение выражения не пострадает от того, что мы где-то заменим вычитание сложением.
Заменять вычитание сложением можно и в буквенных выражениях. Например, рассмотрим следующее выражение:
7a + 6b − 3c + 2d − 4s
Заменим вычитание сложением там, где это можно:
7a + 6b + (−3c) + 2d + (−4s)
При любых значениях переменных a, b, c, d и s выражения 7a + 6b − 3c + 2d − 4s и 7a + 6b + (−3c) + 2d + (−4s) будут равны одному и тому же значению.
Вы должны быть готовы к тому, что учитель в школе или преподаватель в институте может называть слагаемыми даже те числа (или переменные), которые ими не являются.
Например, если на доске будет записана разность a − b, то учитель не будет говорить, что a — это уменьшаемое, а b — вычитаемое. Обе переменные он назовет одним общим словом — слагаемые. А всё потому, что выражение вида a − b математик видит, как сумму a + (−b). В таком случае выражение становится суммой, а переменные a и (−b) станóвятся слагаемыми.
Подобные слагаемые
Подобные слагаемые — это слагаемые, которые имеют одинаковую буквенную часть.
Например, рассмотрим выражение 7a + 6b + 2a. Слагаемые 7a и 2a имеют одинаковую буквенную часть — переменную a. Значит слагаемые 7a и 2a являются подобными.
Обычно подобные слагаемые складывают, чтобы упростить выражение или решить какое-нибудь уравнение. Это действие называют приведéнием подобных слагаемых.
Чтобы привести подобные слагаемые, нужно сложить коэффициенты этих слагаемых, и полученный результат умножить на общую буквенную часть.
Например, приведём подобные слагаемые в выражении 3a + 4a + 5a. В данном случае подобными являются все слагаемые. Слóжим их коэффициенты и результат умножим на общую буквенную часть — на переменную a
3a + 4a + 5a = (3 + 4 + 5)×a = 12a
Подобные слагаемые обычно привóдят в уме и результат записывают сразу:
3a + 4a + 5a = 12a
Также, можно рассуждать следующим образом:
Было 3 переменные a, к ним прибавили еще 4 переменные a и ещё 5 переменных a. В итоге получили 12 переменных a
В итоге получили 12 переменных a
Если подсчитать на рисунке количество переменных a, то насчитается 12.
Рассмотрим несколько примеров на приведение подобных слагаемых. Учитывая, что данная тема очень важна, на первых порах будем записывать подробно каждую мелочь. Несмотря на то, что здесь всё очень просто, большинство людей допускают множество ошибок. В основном по невнимательности, а не по незнанию.
Пример 1. Привести подобные слагаемые в выражении 3a + 2a + 6a + 8a
Сложим коэффициенты в данном выражении и полученный результат умножим на общую буквенную часть:
3a + 2a + 6a + 8a= (3 + 2 + 6 + 8) × a = 19a
Конструкцию (3 + 2 + 6 + 8) × a можно не записывать, поэтому сразу запишем ответ
3a + 2a + 6a + 8a = 19a
Пример 2. Привести подобные слагаемые в выражении 2a + a
Второе слагаемое a записано без коэффициента, но на самом деле перед ним стоит коэффициент 1, который мы не видим по причине того, что его не записывают. Стало быть, выражение выглядит следующим образом:
Стало быть, выражение выглядит следующим образом:
2a + 1a
Теперь приведем подобные слагаемые. То есть сложим коэффициенты и результат умножим на общую буквенную часть:
2a + 1a = (2 + 1) × a = 3a
Запишем решение покороче:
2a + a = 3a
Приводя подобные слагаемые в выражении 2a+a, можно рассуждать и по-другому:
Было 2 переменные a, добавили ещё одну переменную a, в итоге получилось 3 переменные a.
Пример 3. Привести подобные слагаемые в выражении 2a − a
Заменим вычитание сложением:
2a + (−a)
Второе слагаемое (−a) записано без коэффициента, но на самом деле оно выглядит как (−1a). Коэффициент −1 опять же невидимый по причине того, что его не записывают. Стало быть, выражение выглядит следующим образом:
2a + (−1a)
Теперь приведем подобные слагаемые. Сложим коэффициенты и результат умножим на общую буквенную часть:
2a + (−1a) = (2 + (−1)) × a = 1a = a
Обычно записывают короче:
2a − a = a
Приводя подобные слагаемые в выражении 2a−a можно рассуждать и по-другому:
Было 2 переменные a, вычли одну переменную a, в итоге осталась одна единственная переменная a
Пример 4. Привести подобные слагаемые в выражении 6a − 3a + 4a − 8a
Привести подобные слагаемые в выражении 6a − 3a + 4a − 8a
Заменим вычитание сложение там, где это можно:
6a − 3a + 4a − 8a = 6a + (−3a) + 4a + (−8a)
Теперь приведем подобные слагаемые. Сложим коэффициенты и результат умножим на общую буквенную часть
(6 + (−3) + 4 + (−8)) × a = −1a = −a
Запишем решение покороче:
6a − 3a + 4a − 8a = −a
Встречаются выражения, которые содержат несколько различных групп подобных слагаемых. Например, 3a + 3b + 7a + 2b. Для таких выражений справедливы те же правила, что и для остальных, а именно складывание коэффициентов и умножение полученного результата на общую буквенную часть. Но чтобы не допустить ошибок, удобно разные группы слагаемых подчеркнуть разными линиями.
Например, в выражении 3a + 3b + 7a + 2b те слагаемые, которые содержат переменную a, можно подчеркнуть одной линией, а те слагаемые которые содержат переменную b, можно подчеркнуть двумя линиями:
Теперь можно привести подобные слагаемые. То есть сложить коэффициенты и полученный результат умножить на общую буквенную часть. Сделать это нужно для обеих групп слагаемых: для слагаемых, содержащих переменную a и для слагаемых содержащих переменную b.
То есть сложить коэффициенты и полученный результат умножить на общую буквенную часть. Сделать это нужно для обеих групп слагаемых: для слагаемых, содержащих переменную a и для слагаемых содержащих переменную b.
3a + 3b + 7a + 2b = (3+7)×a + (3 + 2)×b = 10a + 5b
Опять же повторимся, выражение несложное, и подобные слагаемые можно приводить в уме:
3a + 3b + 7a + 2b = 10a + 5b
Пример 5. Привести подобные слагаемые в выражении 5a − 6a −7b + b
Заменим вычитание сложение там, где это можно:
5a − 6a −7b + b = 5a + (−6a) + (−7b) + b
Подчеркнём подобные слагаемые разными линиями. Слагаемые, содержащие переменные a подчеркнем одной линией, а слагаемые содержащие переменные b, подчеркнем двумя линиями:
Теперь можно привести подобные слагаемые. То есть сложить коэффициенты и полученный результат умножить на общую буквенную часть:
5a + (−6a) + (−7b) + b = (5 + (−6))×a + ((−7) + 1)×b = −a + (−6b)
Если в выражении содержатся обычные числа без буквенных сомножителей, то они складываются отдельно.
Пример 6. Привести подобные слагаемые в выражении 4a + 3a − 5 + 2b + 7
Заменим вычитание сложением там, где это можно:
4a + 3a − 5 + 2b + 7 = 4a + 3a + (−5) + 2b + 7
Приведем подобные слагаемые. Числа −5 и 7 не имеют буквенных сомножителей, но они являются подобными слагаемыми — их необходимо просто сложить. А слагаемое 2b останется без изменений, поскольку оно единственное в данном выражении, имеющее буквенный сомножитель b, и его не с чем складывать:
4a + 3a + (−5) + 2b + 7 = (4 + 3)×a + 2b + (−5) + 7 = 7a + 2b + 2
Запишем решение покороче:
4a + 3a − 5 + 2b + 7 = 7a + 2b + 2
Слагаемые можно упорядочивать, чтобы те слагаемые, которые имеют одинаковую буквенную часть, располагались в одной части выражения.
Пример 7. Привести подобные слагаемые в выражении 5t+2x+3x+5t+x
Поскольку выражение является суммой из нескольких слагаемых, это позволяет нам вычислять его в любом порядке. Поэтому слагаемые, содержащие переменную t, можно записать в начале выражения, а слагаемые содержащие переменную x в конце выражения:
Поэтому слагаемые, содержащие переменную t, можно записать в начале выражения, а слагаемые содержащие переменную x в конце выражения:
5t + 5t + 2x + 3x + x
Теперь можно привести подобные слагаемые:
5t + 5t + 2x + 3x + x = (5+5)×t + (2+3+1)×x = 10t + 6x
Запишем решение покороче:
5t + 2x + 3x + 5t + x = 10t + 6x
Сумма противоположных чисел равна нулю. Это правило работает и для буквенных выражений. Если в выражении встретятся одинаковые слагаемые, но с противоположными знаками, то от них можно избавиться на этапе приведения подобных слагаемых. Иными словами, просто вычеркнуть их из выражения, поскольку их сумма равна нулю.
Пример 8. Привести подобные слагаемые в выражении 3t − 4t − 3t + 2t
Заменим вычитание сложением там, где это можно:
3t − 4t − 3t + 2t = 3t + (−4t) + (−3t) + 2t
Слагаемые 3t и (−3t) являются противоположными. Сумма противоположных слагаемых равна нулю. Если убрать этот ноль из выражения, то значение выражения не изменится, поэтому мы его и уберём. А уберём мы его обычным вычеркиванием слагаемых 3t и (−3t)
В итоге у нас останется выражение (−4t) + 2t. В данном выражении можно привести подобные слагаемые и получить окончательный ответ:
(−4t) + 2t = ((−4) + 2)×t = −2t
Запишем решение покороче:
Упрощение выражений
Часто можно встретить задание, в котором сказано «упростите выражение» и далее приводится выражение, которое требуется упростить. Упростить выражение значит сделать его прóще и корóче.
На самом деле мы уже занимались упрощением выражений, когда сокращали дроби. После сокращения дробь становилась короче и проще для восприятия.
Рассмотрим следующий пример. Упростить выражение .
Это задание буквально можно понять так: «Примените к данному выражению любые допустимые действия, но сделайте его прóще».
В данном случае можно осуществить сокращение дроби, а именно разделить числитель и знаменатель дроби на 2:
Что ещё можно сделать? Можно вычислить полученную дробь . Тогда мы получим десятичную дробь 0,5
В итоге дробь упростилась до 0,5.
Первый вопрос, который нужно себе задавать при решении подобных задач, должен быть: «а что можно сделать?». Потому что есть действия, которые можно делать, и есть действия, которые делать нельзя.
Ещё один важный момент, о котором нужно помнить, заключается в том что значение выражение не должно измениться после упрощения выражения. Вернемся к выражению . Данное выражение представляет собой деление, которое можно выполнить. Выполнив это деление, мы получаем значение данного выражения, которое равно 0,5
Но мы упростили выражение и получили новое упрощённое выражение . Значение нового упрощённого выражения по-прежнему равно 0,5
Но выражение мы тоже попытались упростить, вычислив его. В итоге получили окончательный ответ 0,5.
Таким образом, как бы мы не упрощали выражение, значение получаемых выражений по-прежнему равно 0,5. Значит упрощение выполнялось верно на каждом этапе. Именно к этому нужно стремиться при упрощении выражений — значение выражения не должно пострадать от наших действий.
Часто требуется упрощать буквенные выражения. Для них справедливы те же правила упрощения, что и для числовых выражений. Можно выполнять любые допустимые действия, лишь бы не изменилось значение выражения.
Рассмотрим несколько примеров.
Пример 1. Упростить выражение 5,21s × t × 2,5
Чтобы упростить данное выражение, можно отдельно перемножить числа и отдельно перемножить буквы. Это задание очень похоже на то, которое мы рассматривали, когда учились определять коэффициент:
5,21s × t × 2,5 = 5,21 × 2,5 × s × t = 13,025 × st = 13,025st
Таким образом, выражение 5,21s × t × 2,5 упростилось до 13,025st.
Пример 2. Упростить выражение −0,4 × (−6,3b) × 2
Второе произведение (−6,3b) можно перевести в понятный для нас вид, а именно записать в виде (−6,3)×b, затем отдельно перемножить числа и отдельно перемножить буквы:
−0,4 × (−6,3b) × 2 = −0,4 × (−6,3) × b × 2 = 5,04b
Таким образом, выражение −0,4 × (−6,3b) × 2 упростилось до 5,04b
Пример 3. Упростить выражение
Распишем данное выражение более подробно, чтобы хорошо увидеть, где числа, а где буквы:
Теперь отдельно перемножим числа и отдельно перемножим буквы:
Таким образом, выражение упростилось до −abc. Данное решение можно записать покороче:
При упрощении выражений, дроби можно сокращать в процессе решения, а не в самом конце, как мы это делали с обычными дробями. Например, если в ходе решения мы наткнёмся на выражение вида , то вовсе необязательно вычислять числитель и знаменатель и делать что-то вроде этого:
Дробь можно сократить, выбирая по множителю в числителе и в знаменателе и сокращать эти множители на их наибольший общий делитель. Другими словами, использовать короткую версию сокращения дроби, в которой мы не расписываем подробно на что был разделен числитель и знаменатель.
Например, в числителе множитель 12 и в знаменателе множитель 4 можно сократить на 4. Четвёрку храним в уме, а разделив 12 и 4 на эту четвёрку, ответы записываем рядом с этими числами, предварительно зачеркнув их
Далее в числителе множитель 9 и в знаменателе множитель 3 можно сократить на 3
Далее в числителе множитель 6 и в знаменателе множитель 2 можно сократить на 2
Теперь можно перемножить получившиеся маленькие множители. В данном случае их немного и можно перемножить в уме:
Со временем можно обнаружить, что решая ту или иную задачу, выражения начинают «толстеть», поэтому желательно приучиться к быстрым вычислениям. То, что можно вычислить в уме, нужно вычислять в уме. То, что можно быстро сократить, нужно быстро сокращать.
Пример 4. Упростить выражение
Перемножим отдельно числа и отдельно буквы:
Таким образом, выражение упростилось до
Пример 5. Упростить выражение
Перемножим отдельно числа и отдельно буквы:
Таким образом, выражение упростилось до mn.
Пример 6. Упростить выражение
Запишем данное выражение более подробно, чтобы хорошо увидеть, где числа, а где буквы:
Теперь отдельно перемножим числа и отдельно буквы. Для удобства вычислений десятичную дробь −6,4 и смешанное число можно перевести в обыкновенные дроби:
Таким образом, выражение упростилось до
Решение для данного примера можно записать значительно короче. Выглядеть оно будет следующим образом:
Пример 7. Упростить выражение
Перемножим отдельно числа и отдельно буквы. Для удобства вычисления смешанное число и десятичные дроби 0,1 и 0,6 можно перевести в обыкновенные дроби:
Таким образом, выражение упростилось до abcd. Если пропустить подробности, то данное решение можно записать значительно короче:
Обратите внимание на то, как сократилась дробь. Новые множители, которые получаются в результате сокращения предыдущих множителей, тоже допускается сокращать.
Теперь поговорим о том, чего делать нельзя. При упрощении выражений категорически нельзя перемножать числа и буквы, если выражение является суммой, а не произведением.
Например, если требуется упростить выражение 5a + 4b, то нельзя записывать следующим образом:
Это равносильно тому, что если бы нас попросили сложить два числа, а мы бы их перемножали вместо того, чтобы складывать.
При подстановке любых значений переменных a и b выражение 5a +4b обращается в обыкновенное числовое выражение. Предположим, что переменные a и b имеют следующие значения:
a = 2, b = 3
Тогда значение выражения будет равно 22
5a + 4b = 5 × 2 + 4 × 3 = 10 + 12 = 22
Сначала выполняется умножение, а затем полученные результаты складывают. А если бы мы попытались упростить данное выражение, перемножив числа и буквы, то получилось бы следующее:
5a + 4b = 5 × 4 × a × b = 20ab
20ab = 20 × 2 × 3 = 120
Получается совсем другое значение выражения. В первом случае получилось 22, во втором случае 120. Это означает, что упрощение выражения 5a + 4b было выполнено неверно.
После упрощения выражения, его значение не должно изменяться при одних и тех же значениях переменных. Если при подстановке в изначальное выражение любых значений переменных получается одно значение, то после упрощения выражения должно получаться то же самое значение, что и до упрощения.
С выражением 5a + 4b на самом деле ничего делать нельзя. Оно не упрощается.
Если в выражении содержатся подобные слагаемые, то их можно сложить, если нашей целью является упрощение выражения.
Пример 8. Упростить выражение 0,3a−0,4a+a
Чтобы упростить данное выражение можно привести подобные слагаемые:
0,3a − 0,4a + a = 0,3a + (−0,4a) + a = (0,3 + (−0,4) + 1)×a = 0,9a
или покороче: 0,3a − 0,4a + a = 0,9a
Таким образом, выражение 0,3a−0,4a+a упростилось до 0,9a
Пример 9. Упростить выражение −7,5a − 2,5b + 4a
Чтобы упростить данное выражение можно привести подобные слагаемые:
−7,5a − 2,5b + 4a = −7,5a + (−2,5b) + 4a = ((−7,5) + 4)×a + (−2,5b) = −3,5a + (−2,5b)
или покороче −7,5a − 2,5b + 4a = −3,5a + (−2,5b)
Слагаемое (−2,5b) осталось без изменений, поскольку его не с чем было складывать.
Пример 10. Упростить выражение
Чтобы упростить данное выражение можно привести подобные слагаемые:
Коэффициент был переведён в неправильную дробь для удобства вычисления.
Таким образом, выражение упростилось до
Пример 11. Упростить выражение
Чтобы упростить данное выражение можно привести подобные слагаемые:
Таким образом, выражение упростилось до .
В данном примере целесообразнее было бы сложить первый и последний коэффициент в первую очередь. В этом случае мы получили бы короткое решение. Выглядело бы оно следующим образом:
Пример 12. Упростить выражение
Чтобы упростить данное выражение можно привести подобные слагаемые:
Таким образом, выражение упростилось до.
Слагаемое осталось без изменения, поскольку его не с чем было складывать.
Данное решение можно записать значительно короче. Выглядеть оно будет следующим образом:
В коротком решении пропущены этапы замены вычитания сложением и подробная запись, как дроби приводились к общему знаменателю.
Ещё одно различие заключается в том, что в подробном решении ответ выглядит как , а в коротком как . На самом деле, это одно и то же выражение. Различие в том, что в первом случае вычитание заменено сложением, поскольку в начале когда мы записывали решение в подробном виде, мы везде где можно заменили вычитание сложением, и эта замена сохранилась и для ответа.
Тождества. Тождественно равные выражения
После того как мы упростили какое-нибудь выражение, оно станóвится проще и короче. Чтобы проверить верно ли упрощено выражение, достаточно подстáвить любые значения переменных сначала в предыдущее выражение, которое требовалось упростить, а затем в новое, которое упростили. Если значение в обоих выражениях будет одинаковым, то это означает, что выражение упрощено верно.
Рассмотрим простейший пример. Пусть требуется упростить выражение 2a × 7b. Чтобы упростить данное выражение, можно по-отдельности перемнóжить числа и буквы:
2a × 7b = 2 × 7 × a × b = 14ab
Проверим верно ли мы упростили выражение. Для этого подставим любые значения переменных a и b сначала в первое выражение, которое требовалось упростить, а затем во второе, которое упростили.
Пусть значения переменных a, b будут следующими:
a = 4
b = 5
Подстáвим их в первое выражение 2a × 7b
2a × 7b = 2 × 4 × 7 × 5 = 280
Теперь подстáвим те же значения переменных в выражение, которое получилось в результате упрощения выражения 2a × 7b, а именно в выражение 14ab
14ab = 14 × 4 × 5 = 280
Видим, что при a = 4 и b = 5 значение первого выражения 2a × 7b и значение второго выражения 14ab равны
2a × 7b = 2 × 4 × 7 × 5 = 280
14ab = 14 × 4 × 5 = 280
То же самое произойдет и для любых других значений. Например, пусть a = 1 и b = 2
2a × 7b = 2 × 1 × 7 × 2 = 28
14ab = 14 × 1 × 2 = 28
Таким образом, выражения 2a × 7b и 14ab при любых значениях переменных равны одному и тому же значению. Такие выражения называют тождественно равными.
Делаем вывод, что между выражениями 2a × 7b и 14ab можно поставить знак равенства, поскольку они равны одному и тому же значению:
2a × 7b = 14ab
Равенством называют любое выражение, которые соединено знаком равенства (=).
А равенство вида 2a × 7b = 14ab называют тождеством.
Тождеством называют равенство, которое верно при любых значениях переменных.
Другие примеры тождеств:
a + b = b + a
a(b + c) = ab + ac
a(bc) = (ab)c
Да, законы математики, которые мы изучали, являются тождествами.
Верные числовые равенства тоже являются тождествами. Например:
2 + 2 = 4
3 + 3 = 5 + 1
10 = 7 + 2 + 1
Решая сложную задачу, чтобы облегчить себе вычисление, сложное выражение заменяют на более простое выражение, тождественно равное предыдущему. Такую замену называют тождественным преобразованием выражения или просто преобразованием выражения.
Например, мы упростили выражение 2a × 7b, и получили более простое выражение 14ab. Это упрощение можно называть тождественным преобразованием.
Часто можно встретить задание, в котором сказано «докажите, что равенство является тождеством» и далее приводится равенство, которое требуется доказать. Обычно это равенство состоит из двух частей: левой и правой части равенства. Наша задача состоит в том, чтобы выполнить тождественные преобразования с одной из частей равенства и получить другую часть. Либо выполнить тождественные преобразования с обеими частями равенства и сделать так, чтобы в обеих частях равенства оказались одинаковые выражения.
Например, докажем, что равенство 0,5a × 5b = 2,5ab является тождеством.
Упростим левую часть этого равенства. Для этого перемножим числа и буквы по отдельности:
0,5 × 5 × a × b = 2,5ab
2,5ab = 2,5ab
В результате небольшого тождественного преобразования, левая часть равенства стала равна правой части равенства. Значит мы доказали, что равенство 0,5a × 5b = 2,5ab является тождеством.
Из тождественных преобразований мы научились складывать, вычитать, умножать и делить числа, сокращать дроби, приводить подобные слагаемые, а также упрощать некоторые выражения.
Но это далеко не все тождественные преобразования, которые существуют в математике. Тождественных преобразований намного больше. В будущем мы ещё не раз в этом убедимся.
Задания для самостоятельного решения: Задание 1. Найдите значение выражения при и Задание 2. Найдите значение выражения при Задание 4. Найдите значение выражения при иЗадание 5. Запишите в виде буквенного выражения следующую последовательность действий:
- Число a умножить на три, и из этого произведения вычесть пятнадцать
- Число t умножить на девять, и к полученному произведению прибавить тридцать пять
Задание 6. Приведите подобные слагаемые в следующем выражении:
Задание 7. Приведите подобные слагаемые в следующем выражении:
Задание 8. Приведите подобные слагаемые в следующем выражении:
Задание 9. Приведите подобные слагаемые в следующем выражении:
Задание 10. Приведите подобные слагаемые в следующем выражении:
Задание 11. Упростите выражение:
Задание 12. Упростите выражение:
Задание 13. Упростите выражение:
Задание 14. Упростите выражение:
Задание 15. Упростите выражение:
Задание 16. Упростите выражение:
Задание 17. Упростите выражение:
Задание 18. Упростите выражение:
Задание 19. Упростите выражение:
Задание 20. Упростите выражение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Контрольная работа № 4 (математика, 5 класс, по учебнику Виленкина)
Контрольная работа № 4 (математика, 5 класс, по учебнику Виленкина)Контрольная работа № 4 (математика, 5 класс, по учебнику Виленкина)
K-4
Вариант 11. Найдите значение выражения: а) 8 · 76 — 930 : 10; б) 89 · (269 + 631) : 180.
2. Упростите выражение: а) 57 · s · 6; б) 51 · v · 30.
3. Решите уравнение: а) 7490 : v = 35; б) 6q — 22 = 62.
4. Решите с помощью уравнения задачу: «На трех одинаковых клумбах и вдоль дорожек парка высадили 46 кустов роз. Сколько кустов роз на одной клумбе, если вдоль дорожек посажено 16 кустов?»
5. Угадайте корень уравнения x · x — 1 = 35 и выполните проверку.
© А.П. Шестаков, 1996
K-4
Вариант 21. Найдите значение выражения: а) 6 · 70 — 609 : 7; б) 8150 : 163 · (172 + 193).
2. Упростите выражение: а) 48 · r · 6; б) 60 · s · 80.
3. Решите уравнение: а) 22950 : x = 90; б) 96 — 6v = 12.
4. Решите с помощью уравнения задачу: «Из 14 м2 материи сшили 2 пододеяльника. На каждый пододеяльник израсходовали 6 м2. Сколько квадратных метров материи осталось?»
5. Угадайте корень уравнения 5 — x · x = 1 и выполните проверку.
© А.П. Шестаков, 1996
K-4
Вариант 31. Найдите значение выражения: а) 7 · 88 — 648 : 9; б) (665 + 859) · 70 : 127.
2. Упростите выражение: а) 50 · x · 12; б) 62 · v · 30.
3. Решите уравнение: а) 40290 : u = 85; б) 4p — 39 = 33.
4. Решите с помощью уравнения задачу: «Туристы за 5 дней проплыли на байдарке 98 км. В первый день они проплыли 22 км. В каждый из последующих дней они проплывали одно и то же расстояние. Найдите это расстояние.»
5. Угадайте корень уравнения x · x — 1 = 15 и выполните проверку.
© А.П. Шестаков, 1996
K-4
Вариант 41. Найдите значение выражения: а) 9 · 95 — 581 : 7; б) 11400 : 190 · (172 + 160).
2. Упростите выражение: а) 54 · w · 3; б) 45 · t · 60.
3. Решите уравнение: а) 14940 : q = 45; б) 68 — 3y = 14.
4. Решите с помощью уравнения задачу: «Из 830 г шерсти связали 4 варежки и шарф. Сколько граммов шерсти истратили на каждую варежку, если на шарф израсходовали 350 г?»
5. Угадайте корень уравнения y · y + 1 = 50 и выполните проверку.
© А.П. Шестаков, 1996
K-4
Вариант 51. Найдите значение выражения: а) 8 · 84 — 360 : 5; б) 98 · (224 + 394) : 147.
2. Упростите выражение: а) 39 · x · 5; б) 50 · t · 50.
3. Решите уравнение: а) 47405 : w = 95; б) 2t — 21 = 33.
4. Решите с помощью уравнения задачу: «На трех одинаковых клумбах и вдоль дорожек парка высадили 46 кустов роз. Сколько кустов роз на одной клумбе, если вдоль дорожек посажено 16 кустов?»
5. Угадайте корень уравнения x · x — 1 = 48 и выполните проверку.
© А.П. Шестаков, 1996
K-4
Вариант 61. Найдите значение выражения: а) 7 · 83 — 594 : 9; б) 6820 : 124 · (220 + 180).
2. Упростите выражение: а) 25 · r · 9; б) 49 · q · 130.
3. Решите уравнение: а) 31200 : t = 80; б) 103 — 3q = 31.
4. Решите с помощью уравнения задачу: «Из 14 м2 материи сшили 2 пододеяльника. На каждый пододеяльник израсходовали 6 м2. Сколько квадратных метров материи осталось?»
5. Угадайте корень уравнения 17 — x · x = 1 и выполните проверку.
© А.П. Шестаков, 1996
K-4
Вариант 71. Найдите значение выражения: а) 9 · 73 — 595 : 7; б) (785 + 687) · 99 : 132.
2. Упростите выражение: а) 61 · v · 3; б) 65 · x · 60.
3. Решите уравнение: а) 19195 : q = 55; б) 4r — 36 = 48.
4. Решите с помощью уравнения задачу: «Туристы за 5 дней проплыли на байдарке 98 км. В первый день они проплыли 22 км. В каждый из последующих дней они проплывали одно и то же расстояние. Найдите это расстояние.»
5. Угадайте корень уравнения x · x — 1 = 15 и выполните проверку.
© А.П. Шестаков, 1996
K-4
Вариант 81. Найдите значение выражения: а) 8 · 72 — 828 : 9; б) 7008 : 146 · (218 + 177).
2. Упростите выражение: а) 28 · s · 7; б) 58 · q · 90.
3. Решите уравнение: а) 2355 : t = 15; б) 144 — 4w = 16.
4. Решите с помощью уравнения задачу: «Из 830 г шерсти связали 4 варежки и шарф. Сколько граммов шерсти истратили на каждую варежку, если на шарф израсходовали 350 г?»
5. Угадайте корень уравнения y · y + 1 = 50 и выполните проверку.
© А.П. Шестаков, 1996
K-4
Вариант 91. Найдите значение выражения: а) 9 · 74 — 425 : 5; б) 75 · (959 + 219) : 186.
2. Упростите выражение: а) 58 · u · 7; б) 50 · q · 20.
3. Решите уравнение: а) 19710 : t = 45; б) 5w — 19 = 41.
4. Решите с помощью уравнения задачу: «На трех одинаковых клумбах и вдоль дорожек парка высадили 46 кустов роз. Сколько кустов роз на одной клумбе, если вдоль дорожек посажено 16 кустов?»
5. Угадайте корень уравнения x · x — 1 = 24 и выполните проверку.
© А.П. Шестаков, 1996
K-4
Вариант 101. Найдите значение выражения: а) 9 · 84 — 738 : 9; б) 6656 : 104 · (181 + 187).
2. Упростите выражение: а) 32 · q · 10; б) 57 · u · 110.
3. Решите уравнение: а) 10965 : q = 85; б) 116 — 6w = 20.
4. Решите с помощью уравнения задачу: «Из 14 м2 материи сшили 2 пододеяльника. На каждый пододеяльник израсходовали 6 м2. Сколько квадратных метров материи осталось?»
5. Угадайте корень уравнения 17 — x · x = 1 и выполните проверку.
© А.П. Шестаков, 1996
K-4
Вариант 111. Найдите значение выражения: а) 8 · 85 — 462 : 6; б) (521 + 578) · 96 : 112.
2. Упростите выражение: а) 37 · u · 3; б) 53 · x · 20.
3. Решите уравнение: а) 26775 : t = 85; б) 5r — 19 = 51.
4. Решите с помощью уравнения задачу: «Туристы за 5 дней проплыли на байдарке 98 км. В первый день они проплыли 22 км. В каждый из последующих дней они проплывали одно и то же расстояние. Найдите это расстояние.»
5. Угадайте корень уравнения x · x — 1 = 8 и выполните проверку.
© А.П. Шестаков, 1996
K-4
Вариант 121. Найдите значение выражения: а) 9 · 85 — 335 : 5; б) 7875 : 125 · (182 + 174).
2. Упростите выражение: а) 44 · s · 13; б) 54 · p · 110.
3. Решите уравнение: а) 15560 : w = 40; б) 190 — 6t = 22.
4. Решите с помощью уравнения задачу: «Из 830 г шерсти связали 4 варежки и шарф. Сколько граммов шерсти истратили на каждую варежку, если на шарф израсходовали 350 г?»
5. Угадайте корень уравнения y · y + 1 = 17 и выполните проверку.
© А.П. Шестаков, 1996
K-4
Вариант 131. Найдите значение выражения: а) 8 · 81 — 801 : 9; б) 95 · (897 + 493) : 139.
2. Упростите выражение: а) 66 · p · 8; б) 49 · v · 120.
3. Решите уравнение: а) 20070 : x = 90; б) 3p — 50 = 40.
4. Решите с помощью уравнения задачу: «На трех одинаковых клумбах и вдоль дорожек парка высадили 46 кустов роз. Сколько кустов роз на одной клумбе, если вдоль дорожек посажено 16 кустов?»
5. Угадайте корень уравнения x · x — 1 = 35 и выполните проверку.
© А.П. Шестаков, 1996
K-4
Вариант 141. Найдите значение выражения: а) 7 · 93 — 784 : 8; б) 5661 : 111 · (143 + 138).
2. Упростите выражение: а) 65 · r · 5; б) 57 · q · 70.
3. Решите уравнение: а) 38760 : y = 85; б) 99 — 5u = 14.
4. Решите с помощью уравнения задачу: «Из 14 м2 материи сшили 2 пододеяльника. На каждый пододеяльник израсходовали 6 м2. Сколько квадратных метров материи осталось?»
5. Угадайте корень уравнения 5 — x · x = 1 и выполните проверку.
© А.П. Шестаков, 1996
K-4
Вариант 151. Найдите значение выражения: а) 7 · 87 — 720 : 8; б) (657 + 208) · 90 : 173.
2. Упростите выражение: а) 51 · y · 3; б) 65 · q · 110.
3. Решите уравнение: а) 13230 : v = 45; б) 4t — 23 = 65.
4. Решите с помощью уравнения задачу: «Туристы за 5 дней проплыли на байдарке 98 км. В первый день они проплыли 22 км. В каждый из последующих дней они проплывали одно и то же расстояние. Найдите это расстояние.»
5. Угадайте корень уравнения x · x — 1 = 15 и выполните проверку.
© А.П. Шестаков, 1996
K-4
Вариант 161. Найдите значение выражения: а) 8 · 89 — 624 : 8; б) 5472 : 114 · (125 + 158).
2. Упростите выражение: а) 45 · w · 7; б) 46 · x · 60.
3. Решите уравнение: а) 3825 : p = 15; б) 173 — 5x = 18.
4. Решите с помощью уравнения задачу: «Из 830 г шерсти связали 4 варежки и шарф. Сколько граммов шерсти истратили на каждую варежку, если на шарф израсходовали 350 г?»
5. Угадайте корень уравнения y · y + 1 = 50 и выполните проверку.
© А.П. Шестаков, 1996
K-4
Вариант 171. Найдите значение выражения: а) 7 · 80 — 375 : 5; б) 85 · (555 + 657) : 102.
2. Упростите выражение: а) 40 · r · 8; б) 64 · p · 70.
3. Решите уравнение: а) 27610 : t = 55; б) 4y — 50 = 66.
4. Решите с помощью уравнения задачу: «На трех одинаковых клумбах и вдоль дорожек парка высадили 46 кустов роз. Сколько кустов роз на одной клумбе, если вдоль дорожек посажено 16 кустов?»
5. Угадайте корень уравнения x · x — 1 = 8 и выполните проверку.
© А.П. Шестаков, 1996
K-4
Вариант 181. Найдите значение выражения: а) 8 · 89 — 546 : 7; б) 9741 : 191 · (221 + 185).
2. Упростите выражение: а) 63 · v · 5; б) 65 · q · 40.
3. Решите уравнение: а) 20520 : s = 60; б) 102 — 4 v = 26.
4. Решите с помощью уравнения задачу: «Из 14 м2 материи сшили 2 пододеяльника. На каждый пододеяльник израсходовали 6 м2. Сколько квадратных метров материи осталось?»
5. Угадайте корень уравнения 37 — x · x = 1 и выполните проверку.
© А.П. Шестаков, 1996
K-4
Вариант 191. Найдите значение выражения: а) 8 · 75 — 774 : 9; б) (999 + 349) · 97 : 194.
2. Упростите выражение: а) 39 · s · 12; б) 49 · v · 30.
3. Решите уравнение: а) 37725 : r = 75; б) 3v — 44 = 46.
4. Решите с помощью уравнения задачу: «Туристы за 5 дней проплыли на байдарке 98 км. В первый день они проплыли 22 км. В каждый из последующих дней они проплывали одно и то же расстояние. Найдите это расстояние.»
5. Угадайте корень уравнения x · x — 1= 80 и выполните проверку.
© А.П. Шестаков, 1996
K-4
Вариант 201. Найдите значение выражения: а) 8 · 92 — 930 : 10; б) 5145 : 105 · (189 + 156).
2. Упростите выражение: а) 24 · q · 2; б) 56 · t · 80.
3. Решите уравнение: а) 35370 : s = 90; б) 129 — 4r = 21.
4. Решите с помощью уравнения задачу: «Из 830 г шерсти связали 4 варежки и шарф. Сколько граммов шерсти истратили на каждую варежку, если на шарф израсходовали 350 г?»
5. Угадайте корень уравнения y · y + 1 = 5 и выполните проверку.
© А.П. Шестаков, 1996
K-4
Вариант 211. Найдите значение выражения: а) 7 · 97 — 720 : 9; б) 91 · (601 + 935) : 104.
2. Упростите выражение: а) 36 · t · 9; б) 56 · p · 110.
3. Решите уравнение: а) 36765 : t = 95; б) 4w — 12 = 32.
4. Решите с помощью уравнения задачу: «На трех одинаковых клумбах и вдоль дорожек парка высадили 46 кустов роз. Сколько кустов роз на одной клумбе, если вдоль дорожек посажено 16 кустов?»
5. Угадайте корень уравнения x · x — 1 = 80 и выполните проверку.
© А.П. Шестаков, 1996
K-4
Вариант 221. Найдите значение выражения: а) 8 · 84 — 760 : 8; б) 8052 : 183 · (218 + 202).
2. Упростите выражение: а) 58 · w · 4; б) 46 · s · 110.
3. Решите уравнение: а) 13455 : u = 65; б) 57 — 2r = 25.
4. Решите с помощью уравнения задачу: «Из 14 м2 материи сшили 2 пододеяльника. На каждый пододеяльник израсходовали 6 м2. Сколько квадратных метров материи осталось?»
5. Угадайте корень уравнения 50 — x · x = 1 и выполните проверку.
© А.П. Шестаков, 1996
K-4
Вариант 231. Найдите значение выражения: а) 6 · 73 — 582 : 6; б) (717 + 203) · 77 : 184.
2. Упростите выражение: а) 55 · v · 4; б) 46 · p · 80.
3. Решите уравнение: а) 17400 : p = 50; б) 3s — 37 = 26.
4. Решите с помощью уравнения задачу: «Туристы за 5 дней проплыли на байдарке 98 км. В первый день они проплыли 22 км. В каждый из последующих дней они проплывали одно и то же расстояние. Найдите это расстояние.»
5. Угадайте корень уравнения x · x — 1 = 80 и выполните проверку.
© А.П. Шестаков, 1996
K-4
Вариант 241. Найдите значение выражения: а) 8 · 79 — 546 : 7; б) 6885 : 153 · (119 + 121).
2. Упростите выражение: а) 35 · q · 9; б) 47 · s · 20.
3. Решите уравнение: а) 6160 : u = 20; б) 98 — 4q = 22.
4. Решите с помощью уравнения задачу: «Из 830 г шерсти связали 4 варежки и шарф. Сколько граммов шерсти истратили на каждую варежку, если на шарф израсходовали 350 г?»
5. Угадайте корень уравнения y · y + 1 = 82 и выполните проверку.
© А.П. Шестаков, 1996
© Шестаков А.П., 2001 Сайт создан в системе uCoz
M2a vs m2m vs m2p
ssd m.2 (m) vs m.2 (b+m) whats the difference? what difference affect speed? and… i have seen videos on youtube about a m.2 with pci-e adapter support and i did not find any vudeo about the difference between normal m.2 ssd and the same m.2 ssd with pci-e has anyone done this test? have…Kleiner Riegel, große Wirkung: Eine SSD im M.2-Format bringt den Computer auf Trab. Welche für besonders viel Tempo sorgt, sagt der Test von COMPUTER BILD.Homes for sale cookeville tn american way
M.2, formerly known as the Next Generation Form Factor (NGFF), is a specification for internally mounted computer expansion cards and associated connectors. M.2 replaces the mSATA standard, which uses the PCI Express Mini Card physical card layout and connectors. Channel to Frequency Table. 802.11a: 36 – 5180 40 – 5200 44 – 5220 48 – 5240 52 – 5260 56 – 5280 60 – 5300 64 – 5320 100 – 5500 104 – 5520 108 – 5540 112 – 5560 116 – 5580 120 – 5600 124 – 5620 128 – 5640 132 – 5660 136 – 5680 […]Bichpoo breeders nc
However, differences between the two SSDs is still a mystery for many people. Today, you can learn a comprehensive analysis of The storage capacity and price of mSATA vs M.2 SSDs depend on what’s kind of SSDs you are using. Here you can refer to the following…Драйвера для материнских плат: P6T, P6T Deluxe, P6T Deluxe V2, P6T Deluxe/OC Palm, P6T SE, P6T WS Professional, P6T6 WS Revolution, P6T7 WS SuperComputer, P6TD Deluxe, P6X58-E PRO, P6X58-E WSInbound expert target salary
—=====_-1117468459==_===== Content-Type: text/plain; charset=»us-ascii» ; format=»flowed» >Hi, > >I just tried opening the .zip files, and it says «The zipped folder … #jyD¡›m ‰2Æö1nÝ»J¬H 0Š[T Û èm$ Û¯c½»ž ñÁeÏþ·kŸñÆnóÓßßó_‹êΕ{‘i Ì ZŸ>ÿÿúU2 åq%4“]ÿÿö¼º XM} 0€ ±@ N%…t›+ äú ÓŒw ÿßýÔ àe;• ˆâÕ…³²àL¢À&- YÿÈÿ ¿ö{eßÂFÀ á @ @#8Ãÿû´d³ Ø[I.{` =B9|Lj#õq+yíö*&· L ƒË`µ Oœ¸Ìp¹Ì6 dÀÄ 0‚ŒÃ Ì ¤ÀØ Àj “Ð 0 …Romanticism emerged as a reaction to the emphasis on in enlightenment philosophy
Categories. Baby & children Computers & electronics Entertainment & hobby Fashion & style begin 664 foo-gimp.jpg M_]C_X«02D9)[email protected]`!`0$`2`!(«#[email protected]`70W)E871E9″!W:71H(%1H92!’24U0 M_]L`0P`!`0$!`0$!`0$!`0$!`0$!`0$!`0$!`0$!`0$!`0$!`0$!`0$!`0$!Congruent triangles cpctc worksheet pdf
WD_Black 500GB SN750 NVMe Internal Gaming SSD — Gen3 PCIe, M.2 2280, 3D NAND — WDS500G3X0C This «TLDR» article explains the U.2 vs. M.2 vs. SATA Express differences, with a focus on PCI-e lane assignment and speeds or throughputs. U.2, M.2, SATA Express, & SATA. Below is the transcript for the video, which reads as a complete article for folks who prefer the written formHamlib commands
Oct 12, 2017 · Install a PCIe or SATA storage device in M2M_32G, the first M.2 slot, and SATA ports 4 and 5 turn off. M2A_32G, the middle M.2 slot, gets four PCIe lanes for M.2 devices at all times, but … Asus ZenFone Max (M2) ZB633KL. Aviso de PreçoInscreva-se para saber quando este aparelho estiver disponível. 4.2 com A2DP/LE. Micro USB 2.0. A-GPS/GLONASS/BeiDou.Silverback coin master
Two of the first to launch also happen to be two of the most interesting options, thanks to somewhat larger screens, bigger keyboards GPD also offers a lower-specced version of the P2 Max with less memory, storage, and a less powerful processor, and One Mix has…Aug 07, 2017 · There’s a new open format sweeping the world of performance PCs, and it’s…well, complicated. The M.2 format is designed for manufacturers to replace a variety of specific devices, do it in a tiny space, and require very little power. But actually upgrading to an M.2 drive or accessory requires a little forethought.`’ q£ ·Ï5- £ƒl0 ‰ÉK¢dp 5$¨˜ ©bNxOqKlÜIö0|™–îÒvO×ÓƒÖ]9»ö”vÓct9: š …
Microsoft Visual Studio Collection Definition: hxi: Microsoft Help compiled storage: hxs: Microsoft Hilfe compiled storage: hxv: Microsoft Hilfe virtual topic definition: hyp: Hyper compressed archive: hyp: Atari ST Guide: hype: Hype web Projekt: hz: Chinese (Hanzi) Text: i17: Pixel PowerCollage image: i2d: Wyse Device Management thin client …
Source Code: <DeployableResource Accessibility=»Internal» FileName=»scx-1.6.6-0.universald.1.x64.sh» HasNullStream=»false»/>
Original M&P Shield vs Shield M2.0: Which Shield To Shell Out For. Since Smith and Wesson has begun rolling out their 2.0 line of the M&P pistols, some people have begun wondering if the new model is going to be better than the old one. Hence, some folks will find themselves pondering whether they…
Aug 07, 2017 · There’s a new open format sweeping the world of performance PCs, and it’s…well, complicated. The M.2 format is designed for manufacturers to replace a variety of specific devices, do it in a tiny space, and require very little power. But actually upgrading to an M.2 drive or accessory requires a little forethought.
Dhukkuba gogaa
Limsa lominsa armor vendor
Wboy news anchors
Cobb 2017 sti stage 1 map
Rainbow six siege abandon penalty for no reason
Ironhead sportster value
Turbojet engine working principle
Smith and wesson ez 9mm
Rangefinder mechanism
Marlboro 110th birthday free carton
Sylvania h7 led conversion kit
Corn head grease in bush hog
Glock 19 magazine extension capacity
Ssr razkull body kit
Synology beeping
Deer feeding time in lee florida
No2cl geometry
Amp hour counter
Pastor micahn carter 2020
Wpf converter pass parameter
Js usb otg apk cracked
Pua identity verification issue illinois
Truper tools
Samsung a10s pattern unlock
Kern county deputy pay scale
Tianeptine labz reddit
Ansible esxi
Update exterior brick house
Indian idol 11 2019 winner name
R6 zoning nyc
Gather hymnal index pdf
Guns of glory binding multiple accounts
Gtx 660 vs gtx 960
Fake caller id
Planetarium projector cost
Степени и возведение в степень, вторая, третья, четвёртая степени
Когда число умножается само на себя, произведение называется степенью.
Так 2.2 = 4, квадрат или вторая степень 2-х
2.2.2 = 8, куб или третья степень.
2.2.2.2 = 16, четвёртая степень.
Также, 10.10 = 100, вторая степень 10.
10.10.10 = 1000, третья степень.
10.10.10.10 = 10000 четвёртая степень.
И a.a = aa, вторая степень a
a.a.a = aaa, третья степень a
a.a.a.a = aaaa, четвёртая степень a
Первоначальное число называется корнем степени этого числа, потому что это число, из которого были созданы степени.
Однако не совсем удобно, особенно в случае высоких степеней, записывать все множители, из которых состоят степени. Поэтому используется сокращенный метод обозначения. Корень степени записывается только один раз, а справа и немного выше возле него, но чуть меньшим шрифтом записывается сколько раз выступает корень как множитель. Это число или буква называется показателем степени или степенью числа. Так, а2 равно a.a или aa, потому что корень a дважды должен быть умножен сам на себя, чтобы получилось степень aa. Также, a3 означает aaa, то есть здесь a повторяется три раза как множитель.
Показатель первой степени есть 1, но он обычно не записывается. Так, a1 записывается как a.
Вы не должны путать степени с коэффициентами. Коэффициент показывает, как часто величина берётся как часть целого. Степень показывает, как часто величина берётся как множитель в произведении.
Так, 4a = a + a + a + a. Но a4 = a.a.a.a
Схема обозначения со степенями имеет своеобразное преимущество, позволяя нам выражать неизвестную степень. Для этой цели в показатель степени вместо числа записывается буква. В процессе решения задачи, мы можем получить величину, которая, как мы можем знать, есть некоторой степенью другой величины. Но пока что мы не знаем, это квадрат, куб или другая, более высокая степень. Так, в выражении ax, показатель степени означает, что это выражение имеет некоторую степень, хотя не определено какую степень. Так, bm и dn возводятся в степени m и n. Когда показатель степени найден, число подставляется вместо буквы. Так, если m=3, тогда bm = b3; но если m = 5, тогда bm=b5.
Метод записи значений с помощью степеней является также большим преимуществом в случае использования выражений . Tак, (a + b + d)3 есть (a + b + d).(a + b + d).(a + b + d), то есть куб трёхчлена (a + b + d). Но если записать это выражение после возведения в куб, оно будет иметь вид
a3 + 3a2b + 3a2d + 3ab2 + 6abd + 3ad2 + b3 + d3.
Если мы возьмем ряд степеней, чьи показатели увеличиваются или уменьшаются на 1, мы обнаружим, что произведение увеличивается на общий множитель или уменьшается на общий делитель, и этот множитель или делитель есть первоначальным числом, которое возводится в степень.
Так, в ряде aaaaa, aaaa, aaa, aa, a;
или a5, a4, a3, a2, a1;
показатели , если считать справа налево, равны 1, 2, 3, 4, 5; и разница между их значениями равна 1. Если мы начнем справа умножатьна a, мы успешно получим несколько значений.
Tак a.a = a2, второй член. И a3.a = a4
a2.a = a3, третий член. a4.a = a5.
Если мы начнем слева делить на a,
мы получим a5:a = a4 и a3:a = a2.
a4:a = a3 a2:a = a1
Но такой процесс деления может быть продолжен и далее, и мы получаем новый набор значений.
Так, a:a = a/a = 1. (1/a):a = 1/aa
1:a = 1/a (1/aa):a = 1/aaa.
Полный ряд будет: aaaaa, aaaa, aaa, aa, a, 1, 1/a, 1/aa, 1/aaa.
Или a5, a4, a3, a2, a, 1, 1/a, 1/a2, 1/a3.
Здесь значения справа от единицы есть обратными значениям слева от единицы. Поэтому эти степени могут быть названы обратными степенями a. Можно также сказать, что степени слева есть обратными к степеням справа.
Так, 1:(1/a) = 1.(a/1) = a. И 1:(1/a3) = a3.
Тот же самый план записи может применяться к многочленам. Так, для a + b, мы получим множество,
(a + b)3, (a + b)2, (a + b), 1, 1/(a + b), 1/(a + b)2, 1/(a + b)3.
Для удобства используется еще одна форма записи обратных степеней.
Согласно этой форме, 1/a или 1/a1 = a-1. И 1/aaa или 1/a3 = a-3.
1/aa или 1/a2 = a-2. 1/aaaa или 1/a4 = a-4.
А чтобы сделать с показателями законченный ряд с 1 как общая разница, a/a или 1, рассматривается как такое, что не имеет степени и записывается как a0.
Тогда, учитывая прямые и обратные степени
вместо aaaa, aaa, aa, a, a/a, 1/a, 1/aa, 1/aaa, 1/aaaa
можно записать a4, a3, a2, a1, a0, a-1, a-2, a-3, a-4.
Или a+4, a+3, a+2, a+1, a0, a-1, a-2, a-3, a-4.
А ряд только отдельно взятых степеней будет иметь вид:
+4,+3,+2,+1,0,-1,-2,-3,-4.
Корень степени может выражен более чем одной буквой.
Так, aa.aa или (aa)2 есть второй степенью aa.
И aa.aa.aa или (aa)3 есть третьей степенью aa.
Все степени цифры 1 одинаковы: 1.1 или 1.1.1. будет равно 1.
Возведение в степень есть нахождение значения любого числа путем умножения этого числа само на себя. Правило возведения в степень:
Умножайте величину саму на себя столько раз, сколько указано в степени числа.
Это правило является общим для всех примеров, которые могут возникнуть в процессе возведения в степень. Но будет правильно дать объяснение, каким образом оно применяется к частным случаям.
Если в степень возводится только один член, то он умножается сам на себя столько раз, сколько указывает показатель степени.
Четвертая степень a есть a4 или aaaa. (Art. 195.)
Шестая степень y есть y6 или yyyyyy.
N-ая степень x есть xn или xxx….. n раз повторенное.
Если необходимо возвести в степень выражение из нескольких членов, применяется принцип, согласно которому степень произведения нескольких множителей равна произведению этих множителей, возведенных в степень.
Tак (ay)2 =a2y2; (ay)2 = ay.ay.
Но ay.ay = ayay = aayy = a2y2.
Так, (bmx)3 = bmx.bmx.bmx = bbbmmmxxx = b3m3x3.
Поэтому, в нахождении степени произведения мы можем или оперировать со всем произведением сразу, или мы можем оперировать с каждым множителем отдельно, а потом умножить их значения со степенями.
Пример 1. Четвертая степень dhy есть (dhy)4, или d4h4y4.
Пример 2. Третья степень 4b, есть (4b)3, или 43b3, или 64b3.
Пример 3. N-ая степень 6ad есть (6ad)n или 6nandn.
Пример 4. Третья степень 3m.2y есть (3m.2y)3, или 27m3.8y3.
Степень двочлена, состоящего из членов, соединенных знаком + и -, вычисляется умножением его членов. Tак,
(a + b)1 = a + b, первая степень.(a + b)1 = a2 + 2ab + b2, вторая степень (a + b).
(a + b)3 = a3 + 3a2b + 3ab2 + b3, третья степень.
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4, четвертая степень.
Квадрат a — b, есть a2 — 2ab + b2.
3 + 3a2 + 3a + 1.Квадрат a + b + h есть a2 + 2ab + 2ah + b2 + 2bh + h2
Упражнение 1. Найдите куб a + 2d + 3
Упражнение 2. Найдите четвертую степень b + 2.
Упражнение 3. Найдите пятую степень x + 1.
Упражнение 4. Найдите шестую степень 1 — b.
Квадраты суммы суммы и разницы двочленов встречаются так часто в алгебре, что необходимо их знать очень хорошо.
Если мы умножаем a + h само на себя или a — h само на себя,
мы получаем: (a + h)(a + h) = a2 + 2ah + h2 также, (a — h)(a — h) = a2 — 2ah + h2.
Отсюда видно, что в каждом случае, первый и последний члены есть квадраты a и h, а средний член есть удвоеннное произведение a на h. Отсюда, квадрат суммы и разницы двочленов может быть найден, используя следующее правило.
Квадрат двочлена, оба члена которых положительны, равен квадрату первого члена + удвоенное произведение обоих членов, + квадрат последнего члена.
Квадрат разницы двочленов равен квадрату первого члена минус удвоенное произведение обоих членов плюс квадрат второго члена.
Пример 1. Квадрат 2a + b, есть 4a2 + 4ab + b2.
Пример 2. Квадрат ab + cd, есть a2b2 + 2abcd + c2d2.
Пример 3. Квадрат 3d — h, есть 9d2 + 6dh + h2.
Пример 4. Квадрат a — 1 есть a2 — 2a + 1.
Чтобы узнать метод нахождения более высоких степеней двочленов, смотрите следующие разделы.
Во многих случаях является эффективным записывать степени без умножения.
Так, квадрат a + b, есть (a + b)2.
N-ая степень bc + 8 + x есть (bc + 8 + x)n
В таких случаях, скобки охватывают все члены под степенью.
Но если корень степени состоит из нескольких множителей, скобки могут охватывать всё выражение, или могут применяться отдельно к множителям в зависимости от удобства.
Так, квадрат (a + b)(c + d) есть или [(a + b).(c + d)]2 или (a + b)2.(c + d)2.
Для первого из этих выражений результатом есть квадрат произведения двух множителей, а для второго — произведением их квадратов. Но они равны друг другу.
Куб a.(b + d), есть [a.(b + d)]3, или a3.(b + d)3.
Необходимо также учитывать и знак перед вовлеченными членами. Очень важно помнить, что когда корень степени положительный, все его положительные степени также положительны. Но когда корень отрицательный, значения с нечетными степенями отрицательны, в то время как значения чётных степеней есть положительными.
Вторая степень (- a) есть +a2
Третья степень (-a) есть -a3
Четвёртая степень (-a) есть +a4
Пятая степень (-a) есть -a5
Отсюда любая нечётная степень имеет тот же самый знак, что и число. Но чётная степень есть положительна вне зависимости от того, имеет число отрицательный или положительный знак.
Так, +a.+a = +a2
И -a.-a = +a2
Величина, уже возвёденная в степень, еще раз возводится в степень путем умножения показателей степеней.
Третья степень a2 есть a2.3 = a6.Для a2 = aa; куб aa есть aa.aa.aa = aaaaaa = a6; что есть шестой степенью a, но третьей степенью a2.
Четвертая степень a3b2 есть a3.4b2.4 = a12b8
Третья степень 4a2x есть 64a6x3.
Пятая степень (a + b)2 есть (a + b)10.
N-ая степень a3 есть a3n
N-ая степень (x — y)m есть (x — y)mn
(a3.b3)2 = a6.b6
(a3b2h4)3 = a9b6h12
Правило одинаково применяется к отрицательным степеням.
Пример 1. Третья степень a-2 есть a-3.3=a-6.
Для a-2 = 1/aa, и третья степень этого
(1/aa).(1/aa).(1/aa) = 1/aaaaaa = 1/a6 = a-6
Четвертая степень a2b-3 есть a8b-12 или a8/b12.
Квадрат b3x-1, есть b6x-2.
N-ая cтепень ax-m есть x-mn или 1/x.
Однако, здесь надо помнить, что если знак, предшествующий степени есть «-«, то он должен быть изменен на «+» всегда, когда степень есть четным числом.
Пример 1. Квадрат -a3 есть +a6. Квадрат -a3 есть -a3.-a3, которое, согласно правилам знаков при умножении, есть +a6.
2. Но куб -a3 есть -a9. Для -a3.-a3.-a3 = -a9.
3. N-ая степень -a3 есть a3n.
Здесь результат может быть положительным или отрицательным в зависимости от того, какое есть n — чётное или нечётное.
Если дробь возводится в степень, то возводятся в степень числитель и знаменатель.
Квадрат a/b есть a2/b2. Согласно правилу умножению дробей,
(a/b)(a/b) = aa/bb = a2b2
Вторая, третья и n-ая степени 1/a есть 1/a2, 1/a3 и 1/an.
Примеры двочленов, в которых один из членов является дробью.
1. Найдите квадрат x + 1/2 и x — 1/2.
(x + 1/2)2 = x2 + 2.x.(1/2) + 1/22 = x2 + x + 1/4
(x — 1/2)2 = x2 — 2.x.(1/2) + 1/22 = x2 — x + 1/4
2. Квадрат a + 2/3 есть a2 + 4a/3 + 4/9.
3. Квадрат x + b/2 = x2 + bx + b2/4.
4 Квадрат x — b/m есть x2 — 2bx/m + b2/m2.
Ранее было показано, что дробный коэффициент может быть перемещен из числителя в знаменатель или из знаментеля в числитель. Используя схему записи обратных степеней, видно, что любой множитель также может быть перемещен, если будет изменен знак степени.
Так, в дроби ax-2/y, мы можем переместить x из числителя в знаменатель.
Тогда ax-2/y = (a/y).x-2 = (a/y).(1/x2 = a/yx2.
В дроби a/by3 мы можем переместить у из знаменателя в числитель.
Тогда a/by2 = (a/b).(1/y3) = (a/b).y-3 = ay-3/b.
Таким же образом мы можем переместить множитель, который имеет положительный показатель степени в числитель или множитель с отрицательной степенью в знаменатель.
Так, ax3/b = a/bx-3. Для x3 обратным есть x-3, что есть x3 = 1/x-3.
Следовательно, знаменатель любой дроби может быть полностью удален, или числитель может быть сокращен до единицы, что не изменит значение выражения.
Так, a/b = 1/ba-1, or ab-1.
Упрощение выражений — хитрости и примеры
Умение упрощать выражения — самый важный шаг в понимании и овладении алгеброй. Упрощение выражений — удобный математический навык, потому что он позволяет нам преобразовывать сложные или неудобные выражения в более простые и компактные формы. Но перед этим мы должны знать, что такое алгебраическое выражение.
Алгебраическое выражение — это математическая фраза, в которой переменные и константы объединяются с помощью операционных символов (+, -, × & ÷).Например, 10x + 63 и 5x — 3 являются примерами алгебраических выражений.
В этой статье мы узнаем несколько уловок на , как упростить любое алгебраическое выражение.
Как упростить выражения?
Упрощение алгебраического выражения можно определить как процесс записи выражения в наиболее эффективной и компактной форме без изменения значения исходного выражения.
Процесс влечет за собой сбор одинаковых терминов, что подразумевает добавление или вычитание терминов в выражении.
Напомним некоторые важные термины, используемые при упрощении выражения:
- Переменная — это буква, значение которой неизвестно в алгебраическом выражении.
- Коэффициент — это числовое значение, используемое вместе с переменной.
- Константа — это термин, имеющий определенное значение.
- Подобные термины — это переменные с одинаковой буквой и мощностью. Подобные термины могут иногда содержать разные коэффициенты. Например, 6x 2 и 5x 2 похожи на термы, потому что у них есть переменная с аналогичным показателем степени.Точно так же термины 7yx и 5xz отличаются, потому что каждый член имеет разные переменные.
Чтобы упростить любое алгебраическое выражение, следующие основные правила и шаги:
- Удалите все символы группировки, такие как квадратные и круглые скобки, путем умножения.
- Используйте правило экспоненты, чтобы удалить группировку, если термины содержат экспоненты.
- Объединить похожие термины путем сложения или вычитания
- Объедините константы
Пример 1
Упростить 3 x 2 + 5 x 2
Решение
Поскольку оба члена в выражении имеют одинаковые показатели степени, мы объединяем их;
3 x 2 + 5 x 2 = (3 + 5) x 2 = 8 x 2
Пример 2
Упростите выражение: 2 + 2x [2 (3x + 2) +2)]
Решение
Сначала вычислите все члены в скобках, умножив их;
= 2 + 2x [6x + 4 +2] = 2 + 2x [6x + 6]
Теперь удалите круглые скобки, умножив любое число вне их;
2 + 2x [6x + 6] = 2 + 12x 2 + 12x
Это выражение можно упростить, разделив каждый член на 2 как;
12x 2 /2 + 12x / 2 + 2/2 = 6 x 2 + 6x + 1
Пример 3
Упростить 3 x + 2 ( x -4)
Решение
В этом случае невозможно объединить термины, если они все еще заключены в круглые скобки или какой-либо знак группировки.Поэтому удалите скобку, умножив любой множитель вне группы на все члены внутри нее.
Следовательно, 3 x + 2 ( x — 4) = 3 x + 2 x — 8
= 5 x — 8
Знак минус перед группировкой обычно влияет на все операторы в круглых скобках. Это означает, что знак минус перед группой изменит операцию сложения на вычитание и наоборот.
Пример 4
Упростить 3 x — (2 — x )
Решение
3 x — (2 — x ) = 3 x + (–1) [2 + (- x )]
= 3 x + (–1) (2) + (–1) (- x )
= 3 x — 2 + x
= 4 x — 2
Однако, если перед группировкой стоит только знак «плюс», то круглые скобки просто стираются.
Например, , чтобы упростить 3 x + (2 — x ), скобки удаляются, как показано ниже:
3x + (2 — x) = 3x + 2 — x
Пример 5
Упростить 5 (3x-1) + x ((2x) / (2)) + 8 — 3x
Решение
15x — 5 + x (x) + 8 — 3x
15x — 5 + x 2 + 8 — 3x.
Теперь объедините одинаковые термины, добавляя и вычитая их;
x 2 + (15x — 3x) + (8-5)
х 2 + 12x + 3
Пример 6
Упростить x (4 — x) — x (3 — x)
Решение
х (4 — х) — х (3 — х)
4x — x 2 — x (3 — x)
4x — x 2 — (3x — x 2 )
4x — x 2 — 3x + x 2 = x
Практические вопросыУпростите каждое из следующих выражений:
- 2-й + 3-й — + 5-й + 4-й
- 2a — 4b + 3ab -5a + 2b
- x (2x + 3y -4) — x 2 + 4xy — 12
- 4 (2x + 1) — 3x
- 4 (п — 5) +3 (п +1)
- [2x 3 y 2 ] 3
- 6 (p + 3q) — (7 + 4q)
- 4rs -2s — 3 (rs +1) — 2s
- [(3 — x) (x + 2) + (-x + 4) (7x + 2) — (x — y) (2x — y)] — 3x 2 — 7x + 5
Темы алгебры: Упрощение выражений
Урок 7: Упрощение выражений
/ ru / algebra-themes / написание-алгебраических-выражений / содержание /
Упрощение выражений
Упростить выражение — это еще один способ сказать , решая математическую задачу .Когда вы упрощаете выражение , вы в основном пытаетесь записать его простейшим из возможных способов . В конце концов, больше не должно быть ничего сложения, вычитания, умножения или деления. Например, возьмите это выражение:
4 + 6 + 5
Если вы упростили , объединив термины до тех пор, пока ничего не останется, выражение будет выглядеть так:
15
Другими словами, 15 — это простейший способ записать 4 + 6 + 5.Обе версии выражения равны одной и той же сумме; один намного короче.
Упрощение алгебраических выражений — та же идея, за исключением того, что в вашем выражении есть переменные (или буквы). По сути, вы превращаете длинное выражение в нечто, что легко понять. Итак, такое выражение …
(13x + -3x) / 2
… можно упростить так:
5x
Если это кажется большим скачком, не волнуйтесь! Все, что вам нужно для упрощения большинства выражений, — это базовая арифметика — сложение, вычитание, умножение и деление — и порядок операций.
Порядок работы
Как и в случае с любой другой задачей, вам необходимо соблюдать порядок операций при упрощении алгебраического выражения. Порядок операций — это правило, которое сообщает вам правильный порядок для выполнения вычислений. По порядку действий решать задачу следует в таком порядке:
- Круглые скобки
- Показатели
- Умножение и деление
- Сложение и вычитание
Давайте посмотрим на задачу, чтобы увидеть, как это работает.
В этом уравнении вы должны начать с упрощения части выражения в скобках : 24 — 20.
2 ⋅ (24 — 20) 2 + 18/6 — 30
24 минус 20 равно 4. В соответствии с порядком операций, далее упростим любые экспоненты . В этом уравнении один показатель степени: 4 2 , или , четыре в второй степени .
2 ⋅ 4 2 + 18/6 — 30
4 2 — 16.Далее нам нужно позаботиться о умножении и делении . Сделаем это слева направо: 2 ⋅ 16 и 18/6.
2 ⋅ 16 + 18/6 — 30
2 ⋅ 16 равно 32, а 18/6 равно 3. Остается только последний шаг в порядке операций: сложение и вычитание .
32 + 3 — 30
32 + 3 равно 35, а 35 — 30 равно 5. Наше выражение было упрощено — больше нечего делать.
5
Это все, что нужно! Помните, что вы должны соблюдать порядок операций при выполнении вычислений — в противном случае вы можете не получить правильный ответ.
Все еще немного запутались или нужно попрактиковаться? Мы написали целый урок по порядку действий. Вы можете проверить это здесь.
Добавление подобных переменных
Чтобы добавить одинаковые переменные, вы можете просто добавить коэффициенты . Таким образом, 3 x + 6 x равно 9 x .Вычитание работает точно так же, поэтому 5 y — 4 y = 1 y , или просто y .
5–4 года = 1 год
Вы также можете умножить и разделить переменных на коэффициенты. Чтобы умножить переменные на коэффициенты, сначала умножьте коэффициенты, а затем запишите переменные рядом друг с другом. Итак, 3 x ⋅ 4 y равно 12 xy .
3x ⋅ 4y = 12xy
Распределительная собственность
Иногда при упрощении выражений можно увидеть что-то вроде этого:
3 (х + 7) -5
Обычно с Порядком операций мы сначала упростили бы внутри скобками.В этом случае, однако, нельзя упростить x + 7, поскольку мы не можем добавить переменную и число. Итак, каков наш первый шаг?
Как вы, возможно, помните, 3 за пределами круглых скобок означает, что нам нужно умножить все внутри скобок на 3. В скобках две вещи : x и 7 . Нам нужно будет умножить их , оба на 3.
3 (х) + 3 (7) — 5
3 · x равно 3x и 3 · 7 составляет 21 .Мы можем переписать выражение как:
3x + 21–5
Далее мы можем упростить вычитание 21-5. 21-5 равно 16 .
3x + 16
Поскольку невозможно складывать переменные и числа, мы не можем дальше упрощать это выражение. Наш ответ: 3x + 16 . Другими словами, 3 (x + 7) — 5 = 3x + 16.
/ ru / algebra-themes / решения-уравнений / содержание /
Основы алгебры — Упрощение — Углубленно
Раньше вы оцениваете алгебраическое выражение, вам нужно его упростить.Это сделает все ваши расчеты намного проще. Вот основные шаги, которые нужно выполнить, чтобы упростить алгебраическое выражение:
- убрать скобки путем умножения
- использовать показатель степени правила удаления скобок в показателях степени
- объединить как условия добавлением коэффициентов
- объединить константы
Проработаем пример.
При упрощении выражение, первое, что нужно искать, — это можно ли убрать скобки. Часто вы можете использовать свойство распределения, чтобы очистить круглые скобки, умножив множители умножают на члены в скобках. В этом выражении мы можно использовать свойство distributive, чтобы избавиться от первых двух наборов круглых скобок.
Теперь мы можем получить избавиться от скобок в члене с показателями степени с помощью показателя степени правила, которые мы узнали ранее.Когда член с показателем степени возводится в степень, мы умножаем экспоненты, так что (x 2 ) 2 становится x 4 .
Следующий шаг в упрощении — искать одинаковые термины и комбинировать их. Условия 5x и 15x похожи на термины, потому что у них одна и та же переменная возведена в одно и то же степень, а именно первая степень, поскольку экспонента понимается равной 1. Мы можем объединить эти два члена, чтобы получить 20x.
Наконец, мы ищите любые константы, которые мы можем комбинировать. Здесь есть константы 10 и 12. Мы можем объединить их, чтобы получить 22.
Теперь наше выражение упрощено. Еще одна вещь — обычно мы пишем алгебраическое выражение в определенном порядке. Начнем с терминов с наибольшими показателями. и переходим к константам. Используя коммутативность кроме того, мы можем переставить термины и расположить это выражение в правильном порядке, как это.
назад наверх
Упростите радикальные, рациональные выражения с помощью программы «Пошаговое решение математических задач»
В разделе 3 главы 1 есть несколько очень важных определений, которые мы использовали много раз. Поскольку эти определения приобретают новое значение в этой главе, мы повторим их.
Когда алгебраическое выражение состоит из частей, соединенных знаками + или -, эти части вместе с их знаками называются членами выражения.
a + b состоит из двух членов.
2x + 5y — 3 состоит из трех членов.
| В a + b термины a и b. В 2x + 5y — 3 термины 2x, 5y и -3. |
Когда алгебраическое выражение состоит из частей, подлежащих умножению, эти части называются коэффициентами выражения.
ab имеет множители a и b.
Очень важно уметь различать термины и факторы. Правила, применяемые к условиям, в целом не применяются к факторам.Называя термины или факторы, необходимо учитывать все выражение.
| С этого момента во всей алгебре вы будете использовать слова , термин и фактор . Убедитесь, что вы понимаете определения. |
Показатель степени — это число, которое указывает, сколько раз коэффициент должен использоваться в продукте. Показатель степени обычно записывается как меньшее (по размеру) число немного выше и правее множителя, на который влияет показатель степени.
| Показатель степени иногда называют «степенью». Например, 5 3 можно обозначить как «пять в третьей степени». |
Обратите внимание на разницу между 2x 3 и (2x) 3 . Используя круглые скобки в качестве группирующих символов, мы видим, что
2x 3 означает 2 (x) (x) (x), тогда как (2x) 3 означает (2x) (2x) (2x) или 8x 3 .
| Если не используются круглые скобки, показатель степени влияет только на множитель, непосредственно предшествующий ему. |
В таком выражении, как 5x 4
5 — коэффициент ,
x — основание ,
4 — показатель степени .
5x 4 означает 5 (x) (x) (x) (x).
Обратите внимание, что экспонента влияет только на основание.
| Многие студенты совершают ошибку, умножая основание на показатель степени. Например, они скажут 3 4 = 12 вместо правильного ответа, 3 4 = (3) (3) (3) ( 3) = 81. |
Когда мы пишем буквальное число, такое как x, будет понятно, что коэффициент равен единице, а показатель степени равен единице. Это может быть очень важно во многих операциях.
x означает 1x 1 .
| Также понятно, что записанная цифра, такая как 3, имеет показатель степени 1. Мы просто не утруждаемся записывать показатель степени 1. |
ЗАКОН УМНОЖЕНИЯ ДОПОЛНИТЕЛЬНЫХ ДАННЫХ
ЗАДАЧИ
По завершении этого раздела вы сможете правильно применить первый закон экспонент.
Теперь, когда мы рассмотрели эти определения, мы хотим установить очень важные законы экспонент. Эти законы вытекают непосредственно из определений.
Первый закон экспонент Если a и b — натуральные числа, а x — действительное число, то
| Чтобы умножить множители с одинаковым основанием, сложите экспоненты. |
В отношении любого правила, закона или формулы мы всегда должны быть очень осторожны, чтобы выполнить требуемые условия, прежде чем пытаться применить их.Обратите внимание, что в приведенном выше законе база одинакова для обоих факторов. Этот закон применяется только при соблюдении этого условия.
| Эти факторы не имеют одинакового основания. |
Показатель 1 обычно не записывается. Когда мы пишем x, предполагается показатель степени: x = x1. Это необходимо для применения законов экспонент.
Если выражение содержит произведение разных оснований, мы применяем закон к тем основаниям, которые схожи.
УМНОЖЕНИЕ МОНОМОВ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Распознать моном.
- Найдите произведение нескольких одночленов.
Моном — это алгебраическое выражение, в котором буквальные числа связаны только операцией умножения.
| не является мономом, поскольку задействована операция сложения. |
| предполагает операцию деления. |
Чтобы найти произведение двух одночленов , умножьте числовые коэффициенты и примените первый закон экспонент к буквальным множителям.
| Вы помните первый закон экспонент? |
| Умножьте 5 на 3 и сложите показатели x. Помните, что если показатель не записан, подразумевается показатель, равный единице. |
МОНОМИЛЫ, УМНОЖЕННЫЕ НА ПОЛИНОМИКИ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Распознавать многочлены.
- Определите биномы и трехчлены.
- Найдите произведение одночлена на двучлен.
Многочлен — это сумма или разность одного или нескольких одночленов.
| Обычно, если существует более одной переменной, многочлен записывается в алфавитном порядке. |
Для некоторых многочленов используются специальные имена. Если полином состоит из двух членов, он называется биномом .
Если многочлен состоит из трех членов, он называется трехчленом .
В процессе удаления скобок мы уже отметили, что на все термины в скобках влияет знак или число, стоящее перед скобками. Теперь мы расширим эту идею, чтобы умножить одночлен на многочлен.
| Размещение 2x непосредственно перед скобками означает умножение выражения в скобках на 2x. Обратите внимание, что каждый член умножается в 2 раза. |
| Опять же, каждый член в круглых скобках умножается на 3y 2 |
| И снова каждый член в круглых скобках умножается на 3y 2 . В каждом из этих примеров мы используем распределительное свойство . |
ПОЛИНОМИЧЕСКИЕ ТОВАРЫ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Найдите произведение двух биномов.
- Используйте свойство распределения, чтобы умножить любые два полинома.
В предыдущем разделе вы узнали, что произведение A (2x + y) расширяется до A (2x) + A (y).
Теперь рассмотрим произведение (3x + z) (2x + y).
Поскольку (3x + z) находится в круглых скобках, мы можем рассматривать его как единственный множитель и расширять (3x + z) (2x + y) так же, как A (2x + y).Это дает нам
Если мы теперь расширим каждый из этих терминов, у нас будет
Обратите внимание, что в окончательном ответе каждый член одной круглой скобки умножается на каждый член другой круглой скобки.
| Обратите внимание, что это приложение свойства распределения. |
| Обратите внимание, что это приложение свойства распределения. |
Поскольку — 8x и 15x — аналогичные термины, мы можем объединить их, чтобы получить 7x.
В этом примере мы смогли объединить два термина, чтобы упростить окончательный ответ.
Здесь мы снова объединили некоторые термины, чтобы упростить окончательный ответ. Обратите внимание, что порядок терминов в окончательном ответе не влияет на правильность решения.
| Свойство коммутативности позволяет изменять порядок. |
| Попытайтесь создать систему для умножения каждого члена в одних скобках на каждый член другого.В этих примерах мы взяли первый член в первом наборе круглых скобок и умножили его на каждый член во втором наборе круглых скобок. Затем мы взяли второй член первого набора и умножили его на каждый член второго набора, и так далее. |
ПОЛНОМОЧИЯ И КВАДРАТНЫЕ КОРНИ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Правильно применяйте второй закон экспонент.
- Найдите квадратные корни и главные квадратные корни чисел, являющихся точными квадратами.
Теперь мы хотим установить второй закон экспонент. Обратите внимание на следующие примеры, как этот закон выводится с использованием определения показателя степени и первого закона экспоненты.
по значению показателя 3.
Теперь по первому закону экспонент имеем
В целом отметим, что
Это означает, что ответ будет
.| Помните, для умножения общих оснований складывайте экспоненты. |
Если мы просуммируем член a b раз, мы получим произведение a и b. Отсюда мы видим, что
Второй закон экспонент Если a и b — положительные целые числа, а x — действительное число, то
.
Другими словами, «чтобы возвести степень основания x в степень, умножьте степень».
.
| Обратите внимание, что каждый показатель должен быть умножен на 4. |
Обратите внимание, что когда факторы сгруппированы в круглых скобках, на каждый фактор влияет показатель степени.
.
Опять же, каждый множитель должен быть возведен в третью степень.
Используя определение показателей, (5) 2 = 25. Мы говорим, что 25 — это квадрат 5. Теперь мы вводим новый термин в наш алгебраический язык. Если 25 равно квадрату 5, то говорят, что 5 является квадратным корнем из 25.
Если x 2 = y, то x представляет собой квадратный корень из y.
| Обратите внимание, мы говорим, что 5 — это квадратный корень , а не квадратный корень .Вы скоро поймете, почему. |
.
Из последних двух примеров вы заметите, что 49 имеет два квадратных корня, 7 и — 7. На самом деле это правда, что каждое положительное число имеет два квадратных корня.
| Фактически, один квадратный корень положительный, а другой отрицательный. |
.
| Каковы квадратные корни из 36? |
Главный квадратный корень положительного числа — это положительный квадратный корень.
Символ «» называется знаком корня и обозначает основную часть
| обозначает главный квадратный корень или положительный квадратный корень из 9. |
Обратите внимание на разницу в этих двух задачах.
а. Найдите квадратные корни из 25.
b. Находить .
| Очень важно понимать разницу между этими двумя утверждениями. |
Для а. ответ будет +5 и -5, поскольку (+ 5) 2 = 25 и (- 5) 2 = 25.
Для б. ответ — +5, поскольку знак корня представляет собой главный или положительный квадратный корень.
Целые числа, такие как 16, 25, 36 и т. Д., Квадратные корни которых являются целыми числами, называются полными квадратными числами . В настоящее время нас интересуют только квадратные корни из полных квадратных чисел. В следующей главе мы будем иметь дело с оценкой и упрощением указанного квадратного корня из чисел, которые не являются точными квадратными числами.
| Иногда вы можете увидеть символ +/-.Это означает, что требуются оба квадратных корня из числа. Например, +/- 5 — это краткое написание + 5 и -5. |
ЗАКОНОДАТЕЛЬСТВО О РАЗДЕЛЕНИИ ВЕЩЕЙ
ЗАДАЧИ
По завершении этого раздела вы должны уметь правильно применять третий закон экспонент.
Прежде чем приступить к установлению третьего закона экспонент, мы сначала рассмотрим некоторые факты о действии деления.
- Разделение двух чисел можно обозначить знаком деления или написанием одного числа над другим с полосой между ними.Шесть, разделенная на два, записывается как
- Деление связано с умножением по правилу, если тогда а = быть. Это проверка для всех проблем с разделением. Например, мы знаем это, потому что 18 = (6) (3).
- Деление на ноль невозможно. Для оценки нам необходимо найти число, которое при умножении на ноль даст 5. Такого числа не существует.
- Ненулевое число, разделенное на себя, равно 1.
| . Умножьте значения в кружках, чтобы получить. Это очень важно! Если a — любое ненулевое число, то не имеет значения. |
Из (3) мы видим, что выражение типа as не имеет смысла, если мы не знаем, что y 0. В этом и будущих разделах всякий раз, когда мы пишем дробь, будет предполагаться, что знаменатель не равен нулю. Теперь, чтобы установить закон деления показателей, воспользуемся определением показателей.
| Важно! Прочтите этот абзац еще раз! |
| Мы знаем, что = 1.Мы также предполагаем, что x представляет собой ненулевое число. |
В таком примере нам не нужно разделять количества, если мы помним, что количество, разделенное само на себя, равно единице. В приведенном выше примере мы могли бы написать
| Три x в знаменателе делят три x в числителе. |
| Помните, что 1 должна быть записана, если это единственный член в числителе. |
Из предыдущих примеров мы можем обобщить и прийти к следующему закону:
Третий закон экспонент Если a и b — натуральные числа, а x — ненулевое действительное число, то
| Если мы попытаемся использовать только ту часть закона, которая указывает на такое выражение, как, например, мы получим На данный момент отрицательные показатели не определены.Мы обсудим их позже. |
РАЗДЕЛЕНИЕ МОНОМИАЛА НА МОНОМИАЛ
ЗАДАЧИ
По завершении этого раздела вы сможете упростить выражение, уменьшив дробь, включающую коэффициенты, а также используя третий закон экспонент.
Мы должны помнить, что коэффициенты и показатели управляются разными законами, потому что они имеют разные определения. При делении одночленов коэффициенты делятся, а показатели вычитаются согласно закону деления показателей.
Если деление невозможно или если с помощью коэффициентов возможно только уменьшение дроби, это не влияет на использование закона экспонент для деления.
| Уменьшите этот тип дроби в два этапа: 1. Уменьшите коэффициенты. 2. Используйте третий закон экспонент. |
РАЗДЕЛЕНИЕ ПОЛИНОМА НА МОНОМИАЛ
ЗАДАЧИ
По завершении этого раздела вы сможете разделить многочлен на одночлен.
Разделение многочлена на одночлен требует еще одного очень важного факта в дополнение к тому, что мы уже использовали. Дело в том, что если в числителе дроби несколько членов, то каждый член нужно разделить на знаменатель.
| Таким образом, мы фактически используем свойство распределения в этом процессе. |
РАЗДЕЛЕНИЕ ПОЛИНОМА НА БИНОМИАЛ
ЗАДАЧИ
По завершении этого раздела вы сможете правильно применить алгоритм деления в столбик для деления полинома на бином.
Процесс деления многочлена на другой многочлен будет ценным инструментом в последующих разделах. Здесь мы разработаем методику и обсудим причины, по которым она работает в будущем.
Этот метод называется алгоритмом длинного деления . Алгоритм — это просто метод, которому необходимо точно следовать. Поэтому представим его в пошаговом формате и на примере.
| Вспомните три выражения при делении: Если нас попросят расположить выражение в порядке убывания, мы напишем.Нулевой коэффициент дает 0x 3 = 0. По этой причине член x 3 отсутствовал или не был записан в исходном выражении. |
Решение
Шаг 1: Расположите и делитель, и делимое в порядке убывания переменной (это означает, что сначала наивысший показатель степени, затем следующий наивысший второй и т. Д.) И укажите нулевой коэффициент для любых пропущенных членов. (В этом примере нет необходимости менять расположение и отсутствуют пропущенные термины.) Затем расположите делитель и делимое следующим образом:
Шаг 2: Чтобы получить первый член частного, в этом случае разделите первый член делимого на первый член делителя. Мы записываем это следующим образом:
Шаг 3: Умножьте весь делитель на член, полученный на шаге 2. Вычтите результат из делимого следующим образом:
| Убедитесь, что вы указываете частное непосредственно над количеством, на которое делите.В этом случае x делится на x 2 x раз. |
Шаг 4: Разделите первый член остатка на первый член делителя, чтобы получить следующий член частного. Затем умножьте весь делитель на полученный член и снова вычтите следующим образом:
| Первый член остатка (-2x — 14) равен -2x. Умножьте (x + 7) на -2. |
Этот процесс повторяется до тех пор, пока остаток не станет равен нулю (как в этом примере) или степень первого члена остатка не станет меньше степени первого члена делителя.
Как и в арифметике, деление проверяется умножением. Мы должны помнить, что (частное) X (делитель) + (остаток) = (делимое).
Чтобы проверить этот пример, мы умножаем (x + 7) и (x — 2), чтобы получить x 2 + 5x — 14.
Поскольку это дивиденд, ответ правильный.
| Опять же, (частное) X (делитель) + (остаток) = (делимое) |
Ответ: x — 3. Проверяя, находим (x + 3) (x — 3)
| Распространенная ошибка — забыть написать пропущенный член с нулевым коэффициентом. |
РЕЗЮМЕ
Ключевые слова
- Моном — это алгебраическое выражение, в котором буквальные числа связаны только операцией умножения.
- Многочлен — это сумма или разность одного или нескольких одночленов.
- Бином — это многочлен, состоящий из двух членов.
- Трехчлен — это многочлен, состоящий из трех членов.
- Если x 2 = y, то x представляет собой квадратный корень из y.
- Главный квадратный корень положительного числа — это положительный квадратный корень.
- Символ называется корнем корня и указывает на главный квадратный корень числа.
- Полноквадратное число имеет целые числа в качестве квадратных корней.
Процедуры
- Первый закон экспонент: x a x b = x a + b .
- Чтобы найти произведение двух одночленов, умножьте числовые коэффициенты и примените первый закон экспонент к буквальным множителям.
- Чтобы умножить многочлен на другой многочлен, умножьте каждый член одного многочлена на каждый член другого и объедините одинаковые члены.
- Второй закон экспонент (x a ) b = x ab .
- Третий закон экспонент —
- Чтобы разделить одночлен на одночлен, разделите числовые коэффициенты и используйте третий закон экспонент для буквальных чисел.
- Чтобы разделить многочлен на одночлен, разделите каждый член многочлена на одночлен.
- Чтобы разделить многочлен на бином, используйте алгоритм деления в столбик.
Упрощение экспоненциальных выражений | Purplemath
Purplemath
Чтобы упростить работу с экспонентами, не думайте, что вам нужно работать только с правилами для экспонентов или прямо из них. Часто проще работать непосредственно с определением и значением показателя степени.Например:
Правила говорят мне добавить экспоненты. Но когда я начал заниматься алгеброй, у меня были проблемы с соблюдением правил, поэтому я просто подумал о том, что означают показатели. « a 6 » означает «шесть копий a , умноженных вместе», а « a 5 » означает «пять копий a , умноженных вместе». Итак, если я умножу эти два выражения вместе, я получу одиннадцать копий и , умноженных вместе.То есть:
MathHelp.com
a 6 × a 5 = ( a 6 ) ( a 5 )
= ( аааааа ) ( ааааа )
= аааааааааа
= а 11
Таким образом:
Упростите следующее выражение:
Правила экспоненты говорят мне вычесть экспоненты.Но предположим, что я снова забыл правила. «6 8 » означает, что у меня восемь копий из шести сверху; «6 5 » означает, что у меня есть пять копий из 6 внизу.
Сколько у меня лишних шестерок и где они? У меня есть три лишних шестерки, и они на высоте. Тогда:
Если в инструкциях вам также не сказано «оценивать», вы, вероятно, должны оставить такие проблемы с числовой экспонентой, как эта, в форме экспоненты.Если вы не уверены, можете добавить «= 216» на всякий случай.
Упростите следующее выражение:
Сколько у меня дополнительных копий t и где они? У меня есть две лишние копии, сверху:
Как только вы освоитесь с вопросом «сколько у меня статистов и где они?» рассуждая, вы обнаружите, что вам не нужно все записывать и устранять повторяющиеся факторы.Ответы станут для вас очевидными.
Упростите следующее выражение:
Этот вопрос немного отличается, потому что больший показатель степени находится у члена в знаменателе. Но основная причина та же.
Сколько у меня дополнительных копий из 5 и где они? У меня есть шесть дополнительных копий, и они внизу:
Примечание. Если вы примените правило вычитания, вы получите 5 3–9 = 5 –6 , что математически верно, но почти наверняка не является тем ответом, который они ищут.
Независимо от того, учили ли вы отрицательные показатели степени, когда они говорят «упрощать», они имеют в виду «упростить выражение, чтобы оно не имело отрицательных или нулевых степеней». Некоторые студенты будут пытаться обойти эту проблему со знаком минус, произвольно переключая знак, чтобы волшебным образом получить сверху «5 6 » (а не ниже «1»), но это неверно.
Перейдем к более сложным выражениям.
Упростите следующее выражение:
Я не должен забывать, что «5» и «3» — это просто числа.Поскольку 3 не делится на 5, я не могу отменить числа.
И я не должен пытаться вычитать числа, потому что 5 и 3 в дроби «
5 / 3 » совсем не то же самое, что 5 и 3 в рациональном выражении « x 5 / x 3 «. Числовая часть 5 / 3 остается без изменений.Для переменных у меня есть две дополнительные копии x сверху, поэтому ответ:
Любой из ответов, выделенных фиолетовым цветом, должен быть приемлемым: единственная разница заключается в форматировании; они означают одно и то же.
Это достаточно просто: все до нулевой степени равно 1.
(–46 x 2 y 3 z ) 0 = 1
Часть в скобках по-прежнему упрощается до 1, но на этот раз «минус» стоит перед скобками; то есть он выходит из-под власти, поэтому экспонента его не трогает.Итак, в данном случае ответ:
.— (46 x 2 y 3 z ) 0 = –1
Упростите следующее выражение:
Я могу исключить общий множитель 5 в числовой части дроби:
Теперь мне нужно посмотреть на каждую из переменных.Сколько у меня лишних штук и где они? У меня есть два лишних и сверху. У меня есть один лишний b внизу. И у меня одинаковые номера сверху и снизу c , поэтому они полностью отменяются. Это дает мне:
URL: https://www.purplemath.com/modules/simpexpo.htm
Упростите выражения с помощью порядка операций
Результаты обучения
- Распознавать и комбинировать похожие термины в выражении
- Используйте порядок операций для упрощения выражений
Введение
Прежде чем мы начнем, немного важной терминологии:
- операций / операторов: В математике мы называем такие вещи, как операции умножения, деления, сложения и вычитания.2b [/ латекс], или [латекс] -3 [/ латекс] и [латекс] 8 [/ латекс]. Если у нас есть одинаковые термины, нам разрешено складывать (или вычитать) числа перед переменными, а затем оставлять переменные такими же. Это как если бы сказать, что четыре яблока плюс три яблока равняются семи яблокам. Но два яблока плюс шесть апельсинов нельзя объединить и упростить, потому что они не похожи на термины. Когда мы комбинируем одинаковые термины, нам нужно интерпретировать знаки вычитания как часть следующего термина. Это означает, что если мы видим знак вычитания, мы рассматриваем следующий термин как отрицательный.Знак всегда соответствует сроку.
Это показано в следующих примерах:
Пример
Объедините похожие термины: [латекс] 5x-2y-8x + 7y [/ latex]
Показать решениеПодобные термины в этом выражении:
[латекс] 5x [/ латекс] и [латекс] -8x [/ латекс]
[латекс] -2 года [/ латекс] и [латекс] 7 лет [/ латекс]
Обратите внимание, как мы держали табличку перед каждым термином.
Объедините похожие термины:
[латекс] 5x-8x = -3x [/ латекс]
[латекс] -2y + 7y = 5y [/ латекс]
Обратите внимание, как знаки становятся операциями, когда вы объединяете одинаковые термины.2 + 8 [/ латекс]
В следующем видео вам будет показан еще один пример объединения похожих терминов. Обратите внимание, почему вы не можете объединить все три термина в примере.
Порядок действий
Вы можете вспомнить или не вспомнить порядок операций для применения нескольких математических операций к одному выражению. Подобно тому, как для нас принято ездить по правой стороне дороги, порядок действий — это набор условных обозначений, используемых для обеспечения формульной схемы, которой нужно следовать, когда вам необходимо использовать несколько математических операций для одного выражения. .
Порядок действий
- Сначала выполните все операции с символами группировки. Символы группировки включают круглые скобки (), квадратные скобки [], фигурные скобки {} и дробные черты.
- Вычислить степень или квадратный корень.
- Умножать или делить слева направо.
- Сложить или вычесть слева направо.
Этот порядок операций верен для всех действительных чисел.
Пример
Упростить [латекс] 7–5 + 3 \ cdot8 [/ latex]
Показать решение Согласно порядку операций умножение предшествует сложению и вычитанию.Умножение [латекс] 3 \ cdot8 [/ латекс]
[латекс] \ begin {array} {c} 7–5 + 3 \ cdot8 \\ 7–5 + 24 \ end {array} [/ latex]
Теперь сложите и вычтите слева направо. [латекс] 7–5 [/ латекс] на первом месте.
[латекс] 2 + 24 [/ латекс]
Наконец, доп.
[латекс] 2 + 24 = 26 [/ латекс]
Ответ
[латекс] 7–5 + 3 \ cdot8 = 26 [/ латекс]
В следующем примере вам будет показано, как упростить выражение, которое содержит как умножение, так и вычитание, используя порядок операций.
Когда вы применяете порядок операций к выражениям, содержащим дроби, десятичные дроби и отрицательные числа, вам также необходимо вспомнить, как выполнять эти вычисления.
Пример
Упростить [латекс] 3 \ cdot \ dfrac {1} {3} \ normalsize -8 \ div \ dfrac {1} {4} [/ latex]
Показать решение Согласно порядку операций умножение и деление предшествуют сложению и вычитанию. Иногда полезно добавить круглые скобки, чтобы вы знали, что идет первым, поэтому давайте заключим в скобки умножение и деление, поскольку оно будет стоять перед вычитанием.[латекс] \ left (3 \ cdot \ dfrac {1} {3} \ normalsize \ right) — \ left (8 \ div \ dfrac {1} {4} \ normalsize \ right) [/ latex]
Сначала умножьте [латекс] 3 \ cdot \ dfrac {1} {3} [/ latex].
[латекс] \ left (3 \ cdot \ dfrac {1} {3} \ normalsize \ right) — \ left (8 \ div \ dfrac {1} {4} \ normalsize \ right) [/ latex]
[латекс] \ left (1 \ right) — \ left (8 \ div \ dfrac {1} {4} \ normalsize \ right) [/ latex]
Теперь разделите [латекс] на 8 \ div \ dfrac {1} {4} [/ latex].
[латекс] 8 \ div \ dfrac {1} {4} \ normalsize = \ dfrac {8} {1} \ normalsize \ cdot \ dfrac {4} {1} \ normalsize = 32 [/ latex]
Вычесть.
[латекс] \ влево (1 \ вправо) — \ влево (32 \ вправо) = — 31 [/ латекс]
Ответ
[латекс] 3 \ cdot \ dfrac {1} {3} \ normalsize -8 \ div \ dfrac {1} {4} \ normalsize = -31 [/ latex]
В следующем видео показано, как использовать порядок операций для упрощения выражения, содержащего умножение, деление и вычитание, с помощью членов, содержащих дроби.
Показатели степени и квадратные корни
В этом разделе мы расширяем наши навыки применения правил порядка операций к выражениям с показателями степени и квадратными корнями.{3}} = 72 [/ латекс]
В следующем видео выражение с показателями степени упрощено с использованием порядка операций.
Если в составе символов группировки есть символы группировки, вычисление выполняется от внутренней части к внешней. То есть сначала начните упрощать внутри самых внутренних символов группировки.
Помните, что скобки также могут использоваться для обозначения умножения. В следующем примере показаны оба использования круглых скобок — как способ представления группы, так и способ выражения умножения.2) \\\\ = \ sqrt {9} +4 \\\\ = 3 + 4 = 7 \ end {array} [/ latex]
Для упрощения дна:
[латекс] (8) (4) -11 [/ латекс]
Сначала умножьте [латекс] 8 [/ латекс] и [латекс] 4 [/ латекс], затем вычтите [латекс] 11 [/ латекс].
[латекс] (8) (4) -11 = [/ латекс]
[латекс] \ hspace {1см} 32-11 = 21 [/ латекс]
Теперь сложите дроби вместе, чтобы увидеть, нужно ли еще какое-то упрощение. Упрощенный числитель равнялся [латекс] 7 [/ латекс], а упрощенный знаменатель — [латекс] 21 [/ латекс].{3} = \ frac {1} {4} \ normalsize \ cdot \ dfrac {1} {4} \ normalsize \ cdot \ dfrac {1} {4} \ normalsize = \ dfrac {1} {64} [/ латекс ]
[латекс] \ dfrac {1} {4} \ normalsize + \ dfrac {1} {64} \ normalsize \ cdot32 [/ latex]
Умножить. { 3}} \ cdot 32 = \ dfrac {3} {4} [/ latex]
Некоторые люди используют поговорку, чтобы помочь им запомнить порядок действий.Это высказывание называется PEMDAS или P lease E xcuse M y D ear A Unt S ally. Первая буква каждого слова начинается с той же буквы арифметической операции.
P аренда [латекс] \ displaystyle \ Rightarrow [/ latex] P аренцев (и других группирующих символов)
E xcuse [латекс] \ displaystyle \ Rightarrow [/ латекс] E xponents
M y D ухо [латекс] \ displaystyle \ Rightarrow [/ latex] M ultiplication и D ivision (слева направо)
A Unt S ally [латекс] \ displaystyle \ Rightarrow [/ латекс ] A ddition и S ubtraction (слева направо)Примечание: Хотя в поговорке умножение предшествует делению, деление может быть выполнено первым.Что выполняется первым, между умножением и делением, определяется тем, что происходит первым при чтении слева направо. То же верно и для сложения и вычитания. Пусть это высказывание не сбивает вас с толку!
Сводка
Порядок операций дает нам согласованную последовательность для использования в вычислениях. Без порядка операций вы можете найти разные ответы на одну и ту же вычислительную задачу. (Некоторые из ранних калькуляторов, а также некоторые недорогие, НЕ используют порядок операций.Чтобы использовать эти калькуляторы, пользователь должен ввести числа в правильном порядке.)
Упрощение выражений с помощью порядка операций
Результаты обучения
- Используйте порядок операций для упрощения математических выражений
- Упростите математические выражения, включающие сложение, вычитание, умножение, деление и показатели
Упростите выражения, используя порядок операций
Мы ввели большинство символов и обозначений, используемых в алгебре, но теперь нам нужно уточнить порядок операций.В противном случае выражения могут иметь разное значение и давать разные значения.
Например, рассмотрим выражение:
[латекс] 4 + 3 \ cdot 7 [/ латекс]
[латекс] \ begin {array} {cccc} \ hfill \ text {Некоторые студенты говорят, что это упрощается до 49.} \ Hfill & & & & \ hfill \ text {Некоторые студенты говорят, что это упрощается до 25.} \ hfill \\ \ begin {array} {ccc} & & \ hfill 4 + 3 \ cdot 7 \ hfill \\ \ text {Поскольку} 4 + 3 \ text {дает 7.} \ hfill & & \ hfill 7 \ cdot 7 \ hfill \\ \ text {And} 7 \ cdot 7 \ text {равно 49.} \ hfill & & \ hfill 49 \ hfill \ end {array} & & & \ begin {array} {ccc} & & \ hfill 4 + 3 \ cdot 7 \ hfill \\ \ text {Since} 3 \ cdot 7 \ text {равно 21.} \ hfill & & \ hfill 4 + 21 \ hfill \\ \ text {And} 21 + 4 \ text {составляет 25.} \ hfill & & \ hfill 25 \ hfill \ end {array} \ hfill \ end {array} [/ latex]
Представьте себе путаницу, которая могла бы возникнуть, если бы для каждой проблемы было несколько разных правильных ответов. Одно и то же выражение должно дать такой же результат. Таким образом, математики установили некоторые правила, называемые порядком операций, которые определяют порядок, в котором части выражения должны быть упрощены.
Порядок операций
При упрощении математических выражений выполняйте операции в следующем порядке:
1. P — арреты и другие символы группировки- Упростите все выражения внутри скобок или других группирующих символов, работая в первую очередь с самыми внутренними скобками.
2. E xponents
- Упростите все выражения с помощью показателей степени.
3. M ultiplication и D ivision
- Выполняйте все операции умножения и деления слева направо.Эти операции имеют равный приоритет.
4. A ddition и S ubtraction
- Все операции сложения и вычитания выполняются слева направо. Эти операции имеют равный приоритет.
Студенты часто спрашивают: «Как мне запомнить заказ?» Вот способ помочь вам запомнить: возьмите первую букву каждого ключевого слова и замените глупую фразу. P аренда E xcuse M y D ear A Unt S союзник.
Порядок операций P аренда P аренцев E xcuse E компонентов M y D ухо M ultiplication и D ivision A Unt S союзник A ddition и S ubtraction Хорошо, что « M y D ear» идут вместе, поскольку это напоминает нам, что m ultiplication и d ivision имеют равный приоритет.Мы не всегда выполняем умножение перед делением или всегда делаем деление перед умножением. Делаем их слева направо.
Точно так же « A Unt S ally» объединяется и таким образом напоминает нам, что a ddition и s ubtraction также имеют равный приоритет, и мы выполняем их в порядке слева направо.пример
Упростите выражения:
- [латекс] 4 + 3 \ cdot 7 [/ латекс]
- [латекс] \ влево (4 + 3 \ вправо) \ cdot 7 [/ латекс]
Решение:
1. [латекс] 4 + 3 \ cdot 7 [/ латекс] Есть ли p арентезов? № Есть ли компоненты и ? № Есть ли ультипликация m или d ivision? Да. Сначала умножить. [латекс] 4+ \ color {красный} {3 \ cdot 7} [/ латекс] Доп. [латекс] 4 + 21 [/ латекс] [латекс] 25 [/ латекс] 2. [латекс] (4 + 3) \ cdot 7 [/ латекс] Есть ли p арентезов? Да. [латекс] \ color {красный} {(4 + 3)} \ cdot 7 [/ латекс] Упростите в скобках. [латекс] (7) 7 [/ латекс] Есть ли компоненты и ? № Есть ли ультипликация m или d ivision? Да. Умножить. [латекс] 49 [/ латекс] пример
Упростить:
- [латекс] \ text {18} \ div \ text {9} \ cdot \ text {2} [/ latex]
- [латекс] \ text {18} \ cdot \ text {9} \ div \ text {2} [/ latex]
Решение:
1. [латекс] 18 \ div 9 \ cdot 2 [/ латекс] Есть ли p арентезов? Нет. Есть ли компоненты и ? № Есть ли ультипликация m или d ivision? Да. Умножайте и делите слева направо. Делить. [латекс] \ color {красный} {2} \ cdot 2 [/ латекс] Умножить. [латекс] 4 [/ латекс] 2. [латекс] 18 \ cdot 9 \ div 2 [/ латекс] Есть ли p арентезов? Нет. Есть ли компоненты и ? № Есть ли ультипликация m или d ivision? Да. Умножайте и делите слева направо. Умножить. [латекс] \ color {красный} {162} \ div 2 [/ латекс] Разделить. [латекс] 81 [/ латекс] пример
Упростить: [латекс] 18 \ div 6 + 4 \ left (5-2 \ right) [/ latex].
Показать решениеРешение:
[латекс] 18 \ div 6 + 4 (5-2) [/ латекс] Круглые скобки? Да, сначала вычтите. [латекс] 18 \ div 6 + 4 (\ color {red} {3}) [/ латекс] Показатели? № Умножение или деление? Да. Сначала разделите, потому что мы умножаем и делим слева направо. [латекс] \ color {красный} {3} +4 (3) [/ латекс] Любое другое умножение или деление? Да. Умножить. [латекс] 3+ \ color {красный} {12} [/ латекс] Любое другое умножение или деление? № Любое сложение или вычитание? Да. [латекс] 15 [/ латекс] В видео ниже мы показываем еще один пример того, как использовать порядок операций для упрощения математического выражения.
Когда имеется несколько символов группировки, мы сначала упрощаем самые внутренние круглые скобки и работаем наружу.{3}} + 3 [0] [/ латекс]
Есть ли умножение или деление? Да. Умножить.

Leave A Comment