Точность и погрешность измерений — урок. Физика, 7 класс.
Измерить какую-нибудь величину — это значит сравнить её с однородной величиной, принятой за единицу.
Точность измерений зависит от многих причин:
- расположение наблюдателя относительно измерительного прибора: если на линейку смотреть сбоку, погрешность измерений произойдёт по причине неточного определения полученного значения;
- деформация измерительного прибора: металлические и пластиковые линейки могут изогнуться, сантиметровая лента растягивается со временем;
- несоответствие шкалы прибора эталонным значениям: при множественном копировании эталонов может произойти ошибка, которая будет множиться;
- физический износ шкалы измерений, что приводит к невозможности распознавания значений
Рассмотрим на примере измерения длины бруска линейкой с сантиметровой шкалой.
Внимательно рассмотрим шкалу. Расстояние между двумя соседними метками составляет \(1\) см.
Если этой линейкой измерять брусок, который изображён на рисунке, то правый конец бруска будет находиться между \(9\) и \(10\) метками.
У нас есть два варианта определения длины этого бруска.
\(1\). Если мы заявим, что длина бруска — \(9\) сантиметров, то недостаток длины от истинной составит более половины сантиметра (\(0,5\) см \(= 5\) мм).
\(2\). Если мы заявим, что длина бруска — \(10\) сантиметров, то избыток длины от истинной составит менее половины сантиметра (\(0,5\) см \(= 5\) мм).
Погрешность измерений — это отклонение полученного значения измерения от истинного.
Погрешность измерительного прибора составляет половину цены деления прибора.
Для первой линейки цена деления составляет \(1\) сантиметр. Значит, погрешность этой линейки \(\Delta l = \frac{1 см}{2}=0,5 см\).
Если нам необходимо произвести более точные измерения, то следует поменять линейку на другую, например, с миллиметровыми делениями. В этом случае цена деления будет равна \(1\) мм, а длина бруска — \(9,8\) см.
Если же необходимы еще более точные измерения, то необходимо найти прибор с меньшей ценой деления, например, штангенциркуль. Существуют штангенциркули с ценой деления \(0,1\) мм и \(0,05\) мм.
Из этого примера видно, что точность измерений зависит от цены деления шкалы прибора.
Обрати внимание!
Точность измерения тем больше, чем меньше цена деления шкалы прибора.
Точность измерения зависит и от других факторов. Например, насколько человек, использующий данный инструмент, умеет им пользоваться (как расположен прибор при измерении; как расположены глаза при определении показания прибора).
Считается, что погрешность прибора превосходит по величине погрешность метода вычисления, поэтому за абсолютную погрешность принимают погрешность прибора.
Результаты измерения записывают в виде A=a±Δa, где \(A\) — измеряемая величина, \(a\) — средний результат полученных измерений, Δa — абсолютная погрешность измерений.
Задание №22 ЕГЭ по физике 🐲 СПАДИЛО.РУ
Измерительные приборы
Чтобы успешно справиться с решением задания № 22, требуется ориентироваться в комплексе устройств, используемых для различных физических величин. На основании показаний прибора нужно уметь вычислить цену деления его шкалы. Кроме этого, следует понимать, что представляет собой понятие погрешности. Сведения, необходимые для решения задания, представлены в разделе теории.
Теория к заданию №22 ЕГЭ по физике
Динамометр
Простейшим (пружинным) динамометром является механический измерительный прибор для определения силы (трения, тяжести и пр.) и момента силы. Действие прибора основано на упругих свойствах металлической пружины. Единицей шкалы пружинного динамометра является ньютон (т.е. ед.измерения силы в СИ). На практике – для промышленных и других нужд – используют динамометры с единицей шкалы в кратных и дольных ньютону единицах, например, в МН (меганьютонах), мН (миллиньютонах) и др.
Термометр
Термометром называют измерительный прибор, используемый для определения температур. Его применяют для работ в разных средах. Так, известны термометры для измерения температуры воды, почвы, тела (людей, животных), воздуха. Единицей шкалы термометров в России принято считать градусы Цельсия (оС).
Барометр
Барометр – измерительный прибор, используемый для определения значений атмосферного давления. Традиционно на барометре представлены 2 шкалы, обеспечивающие показания: 1) в мм рт.ст., 2) в паскалях (Па). Как правило, цена деления в паскалях представлена в кратных значениях Па, например, в гектапаскалях (гПа, 1 гПа=105 Па).
Амперметр
Амперметр – устройство для измерения величины силы тока (I). Соответственно, шкала прибора градуируется в амперах (А). Обозначение «А» фиксируется на приборе, указывая на то, что он является именно амперметром.
Кроме цены деления в 1 А, распространено использование дольных и кратных величин этой единицы измерения, принятой в СИ.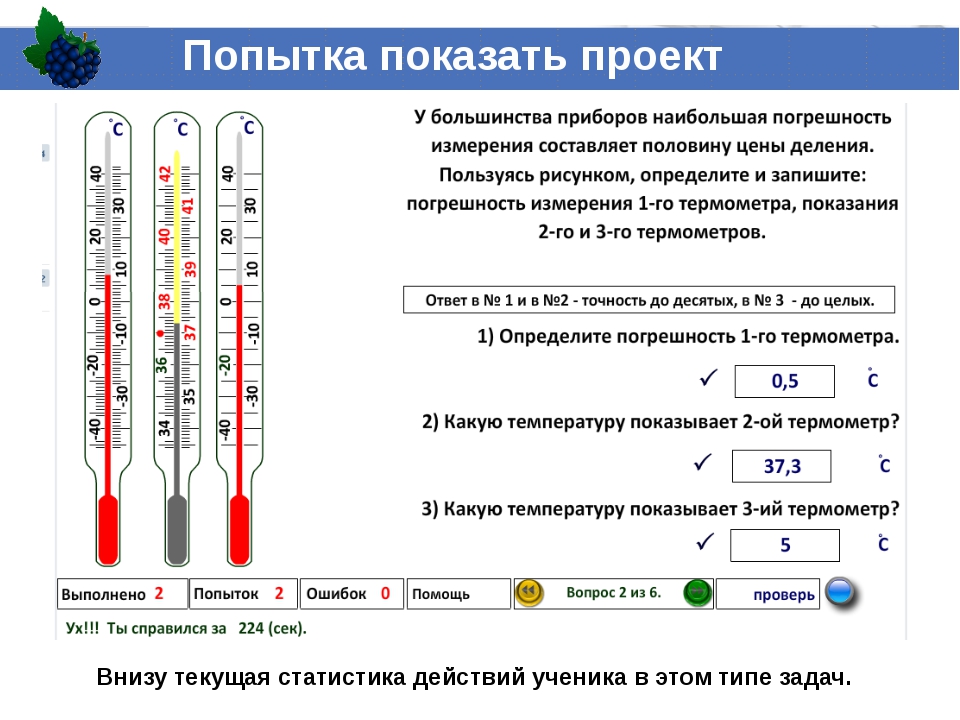
Практикуется шкала в мкА (микроамперах), мА (миллиамперах), кА (килоамперах).
Вольтметр
Вольтметр – прибор, предназначенный для определения значений напряжения (U) и ЭДС в цепях постоянного или переменного эл.тока. Воjльтметр может иметь шкалу, градуированную в вольтах (В), а также в дольных (мВ, мкВ) и в кратных (кВ) единицах, что позволяет повышать точность измерений.Определение цены деления измерительных приборов
Величина цены (промежутка) деления указывается на приборе. Но в некоторых случаях определить ее невозможно – когда соответствующая надпись повреждена, если видна только часть прибора и т.п. В подобных ситуациях ее приходится измерять.
Расчет цены деления осуществляется как разница пары соседних чисел на шкале прибора делится на количество промежутков, поместившихся между ними:
Погрешность
В физике под погрешностью понимают возможную неточность, допускаемую при измерении различных величин. Предельно допустимое ее значение не может превышать величину цены деления конкретного измерительного устройства.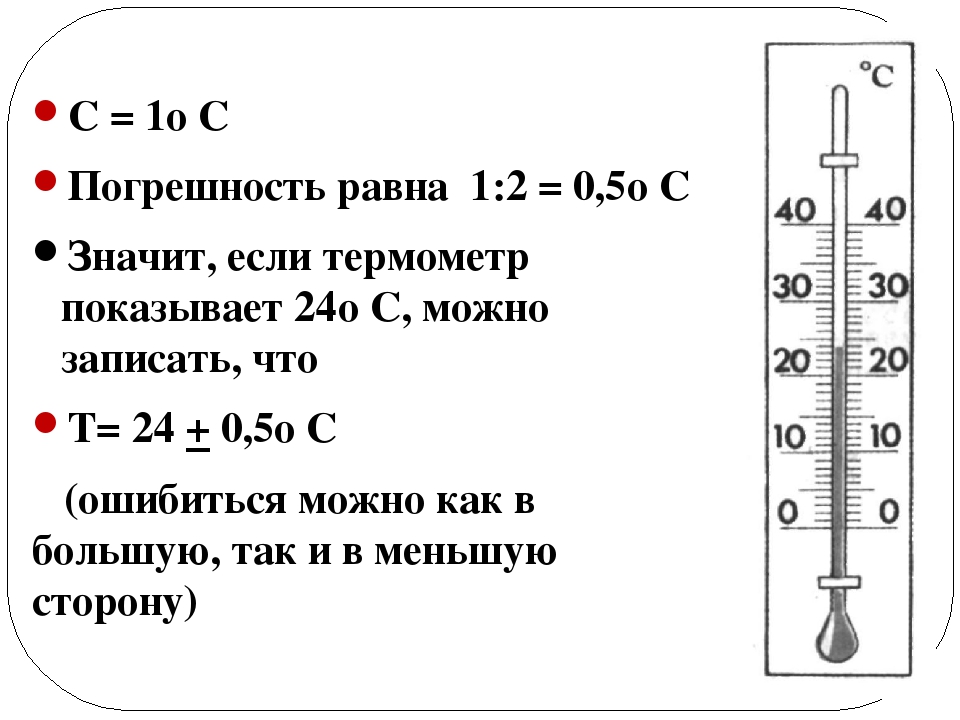
Разбор типовых вариантов заданий №22 ЕГЭ по физике
Демонстрационный вариант 2018
Определите показания амперметра (см. рисунок), если погрешность прямого измерения силы тока равна цене деления амперметра. В ответе запишите значение и погрешность слитно без пробела.
Алгоритм решения:
- Определяем число промежутков между парой соседних (видимых на рисунке) чисел на измерительном устройстве. По этим значениям высчитываем цену деления.
- Определяем величину погрешности. Фиксируем конечное (с погрешностью) показание с амперметра.
- Записываем ответ в соответствующей фирме.
Решение:
- На рисунке видима пара значений шкалы – 0,2А и 0,4А. Число промежутков между 0,2А и 0,4А – 10. Отсюда цена деления: .
- Поскольку погрешность (по условию) соответствует цене деления, то она равна 0,02А. Поэтому стрелка на приборе показывает .
Первый вариант (Демидова, №8)
На производстве измеряли температуру воды.
Показания термометра приведены на фотографии. Погрешность измерения температуры равна цене деления термометра. Чему равна температура воды по результатам этих измерений?
Запишите в ответ показания термометра с учётом погрешности измерений.
Алгоритм решения:
- Определяем цену деления по паре соседних чисел на шкале и количеству делений между ними.
- Находим погрешность. Записываем искомое показание.
- Записываем ответ в требуемой форме.
Решение:
- Берем произвольную пару значений на шкале, например, 20 и 40оС. Подсчет между ними количества делений дает число 10. Отсюда получаем цену деления: (оС).
- Учитывая, что погрешность совпадает с ценой деления (это известно из условия), определяем, что ее значение равно 2оС. Поэтому итоговое показание: (24±2) оС.
Второй вариант (Демидова, №9)
С помощью барометра проводились измерения атмосферного давления.
Верхняя шкала барометра проградуирована в мм рт. ст., а нижняя шкала — в гектопаскалях (гПа). Погрешность измерений давления равна цене деления шкалы барометра. Чему равно атмосферное давление по результатам этих измерений (в кПа)?
Запишите в ответ показания барометра с учётом погрешности измерений.
Алгоритм решения задания:
- Используя нижнюю – внутреннюю – шкалу, определяем цену деления. Переводим ее в кПа.
- Размер погрешности переводим в необходимую кратную величину. Фиксируем показание устройства в этой же кратности. Записываем его с учетом погрешности.
- Записываем результат в требуемой форме.
Решение задания:
- Из увеличенной части рисунка возьмем 2 соседних числа на шкале, скажем, 1020 и 1010. Подсчитаем между ними кол-во промежутков. Оно равно 10. Отсюда рассчитаем цену деления в гПа: . Переведем ее в кПа: 1гПа = 0,1кПа.
- Поскольку по условию принято, что погрешность совпадает с ценой деления, то ее нужно считать равной 0,1кПа.
В соответствии с направлением стрелки фиксируем показание на приборе. Оно составляет 1019гПа. Переведем его в кПа: 1019гПа = 101,9кПа. Отсюда конечный результат: .
В соответствии с направлением стрелки фиксируем показание на приборе. Оно составляет 1019гПа. Переведем его в кПа: 1019гПа = 101,9кПа. Отсюда конечный результат: .Третий вариант (Демидова, №11)
Ученик измерял силу тяжести, действующую на груз. Показания динамометра приведены на фотографии. Погрешность измерения равна цене деления динамометра.
Запишите показания динамометра с учетом погрешности измерений.
Алгоритм решения:
- Вычисляем цену деления, пользуясь рисунком устройства.
- Определяем величину погрешности. Фиксируем итоговое показание.
- Записываем ответ в требуемой форме.
Решение:
- Берем 2 соседних значения шкалы: 1,5Н и 1Н. Подсчитываем кол-во промежутков между ними. Получаем 5 промежутков. Цена деления: .
- Согласно условию задания принято, что погрешность совпадает с ценой деления. Поэтому ее размер – 0,1Н. Отсюда итоговое показание: .
В алюминиевом чайнике массой 300 г нагревают 2 л воды от 16 градусов до кипения.
Какое количество теплоты затрачено на нагревание пожалуйста помогитеОтвет:
Чтобы канат не соскальзывал на столе должно находиться 0,83 от его длины
Объяснение:
Обозначим массу каната через m, а минимальную часть — x. Для того, чтобы канат не соскальзывал необходимо, чтобы вес свисающей части каната P’=(1-x)*m*g , был уравновешен силой трения Fтр=μ*x*m*g, т е
(1-x)*m*g=μ*x*m*g, 1-x=μ*x, x*(1+μ)=1 ⇒ x=1/(1+μ)=1/(1+0,2)≈0,83
Смотря какая нагрузка в цепи.Если лампочка или какой-нибудь другой предмет то будет светится.
Прикрепляю рисунок с решением. Но мне что-то не очень нравится ответ.
Пусть радиусы шариков R1, R2 R1>R2
Потенциалы шариков ф1=k*q/R1 ф2=k*q/R2 У меньшего шарика потенциал больше, значит ток пойдет от него, до тех пор, пока потенциалы не сравняются.
Ответ: т меньшего шарика к большему.
Работа A=F*h; где F — сила тяжести (F=mg), а h — высота на которую поднимают балку (h=20 м.).
g- ускорение свободного падения (g=10 Н./кг.)
Осталось найти массу m, по формуле m=(ро)*V; где (ро) — это плотность железа (не нашёл здесь в редакторе формул греческую букву ро, поэтому написал русскими буквами ро в скобках) ((ро)=7800 кг./м),
а V — это объём железной балки который мы вычислим по формуле: V=l*S; где l — длина балки (l=5 м.), а S — это площадь поперечного сечения балки (S=25 см).
Однако чтобы найти объём V, нам нужно площадь перевести из см в м.
То-есть S=25 см=0.0025 м
Тогда V=l*S=5*0.0025=0.0125 м.
Находим m=(ро)*V=7800*0.0125=97.5 кг.
Находим F=m*g=97.5*10=975 Н.
И в итоге находим работу A=F*h=975*20=19500 Дж.
ошибок измерения
| Ошибка? Нет … вы не измерили неправильно … это примерно точность . |
Измерительные приборы не точны!
Степень точности
Точность зависит от инструмента, которым вы проводите измерения. Но как правило:
Степень точности составляет половинной единицы с каждой стороны единицы измерения
Примеры:
| Когда ваш прибор измеряет за «1», тогда любое значение от 6½ до 7½ измеряется как «7» | |
| Если ваш прибор измеряет за «2» с , тогда любое значение от |
Обратите внимание, что стрелка указывает на одно и то же место, но измеренные значения отличаются!
плюс или минус
| Мы можем показать ошибку с помощью знака «плюс» или «минус»: | ± |
Когда значение может быть между 6½ и 7½ : 7 ± 0. Погрешность ± 0,5 | |
Когда значение может быть между 8 ± 1 Погрешность ± 1 |
5Пример: длина забора составляет 12,5 метра с точностью до 0,1 метра
Точность до 0,1 м означает, что она может быть до 0,05 м в любую сторону:
Длина = 12.5 ± 0,05 м
Таким образом, это действительно может быть от 12,45 м до 12,55 м в длину.
Абсолютная, относительная и процентная ошибка
Абсолютная ошибка — это разница между фактическим и измеренным значением .Но … при измерении мы не знаем действительного значения! Итак, мы используем максимально возможную ошибку.
В приведенном выше примере абсолютная погрешность составляет 0,05 м
Что случилось с ±…? Ну, нам просто нужен размер (абсолютное значение) разницы.
Мы не знаем фактического измерения, поэтому лучшее, что мы можем сделать, это использовать измеренное значение :
Относительная ошибка = Абсолютная ошибка Измеренное значение
Ошибка в процентах — это относительная ошибка, отображаемая в процентах (см. Ошибка в процентах).Рассмотрим их на примере:
Пример: забор (продолжение)
Длина = 12.5 ± 0,05 м
Итак:
Абсолютная ошибка = 0,05 м
А:
Относительная погрешность =
А:
Ошибка в процентах = 0,4%
Другие примеры:
Пример: термометр измеряет с точностью до 2 градусов. Температура составила 38 ° C
Температура может составлять до 1 ° в любую сторону от 38 ° (т. Е. От 37 ° до 39 °).
Температура = 38 ± 1 °
Итак:
Абсолютная ошибка = 1 °
А:
Относительная погрешность = 1 ° 38 ° = 0.
0263 …
А:
Ошибка в процентах = 2,63 …%
Пример: Вы измеряете высоту растения 80 см (с точностью до сантиметра)
Это означает, что вы ошиблись на 0,5 см (высота растения может быть от 79,5 до 80,5 см).
Высота = 80 ± 0,5 см
Итак:
Абсолютная ошибка = 0,5 см
А:
Относительная погрешность = 0,5 см 80 см = 0.00625
А:
Ошибка в процентах = 0,625%
Площадь
При проработке областей вы должны думать как о ширине , так и о длине … они могут быть как наименьшей мерой, так и обеими наибольшими.
Пример: Алекс измерил поле с точностью до метра и получил ширину 6 м и длину 8 м.
Измерение с точностью до метра означает, что истинное значение может быть до полметра меньше или больше.
Ширина (w) может быть от 5,5 м до 6,5 м:
5,5 ≤ ширина <6,5
Длина (l) может быть от 7,5 м до 8,5 м:
7,5 ≤ л <8,5
A = ш × д
Наименьшая возможная площадь: 5,5 м × 7,5 м = 41,25 м 2
Измеренная площадь: 6 м × 8 м = 48 м 2
И максимально возможная площадь: 6,5 м × 8.
5 м = 55,25 м 2
41,25 ≤ A <55,25
Абсолютная, относительная и процентная ошибка
Единственная хитрость здесь … какой является абсолютной ошибкой?
- От 41,25 до 48 = 6,75
- От 48 до 55,25 = 7,25
Ответ: выберите самый большой! Итак:
Абсолютная ошибка = 7,25 м
= 7.25 м 2 48 м 2 = 0,151 …
Ошибка в процентах = 15,1%
(что не очень точно, правда?)
Том
А объем имеет три измерения: ширины, длины и высоты!
Каждое измерение могло быть наименьшим из возможных или наибольшим.
Пример: Сэм измерил коробку с точностью до 2 см и получил 24 см × 24 см × 20 см
Измерение с точностью до 2 см означает, что истинное значение может быть до на 1 см меньше или больше.
Три размера:
- 24 ± 1 см
- 24 ± 1 см
- 20 ± 1 см
Объем: ширина × длина × высота:
В = ш × д × в
Наименьший возможный объем: 23 см × 23 см × 19 см = 10051 см 3
Измеренный объем: 24 см × 24 см × 20 см = 11520 см 3
Максимально возможный объем: 25 см × 25 см × 21 см = 13125 см 3
И так получаем:
10051 ≤ В <13125
Абсолютная, относительная и процентная ошибка
Абсолютная ошибка:
- От 10051 до 11520 = 1469
- от 11520 до 13125 = 1605
Выберите самый большой:
Абсолютная ошибка = 1605 см 3
Относительная погрешность = 1605 см 3 11520 см 3 = 0.
139 …
Ошибка в процентах = 13,9%
Как рассчитать процент ошибки
Ошибка в процентах или ошибка в процентах выражает в процентах разницу между приблизительным или измеренным значением и точным или известным значением. Он используется в науке для сообщения о разнице между измеренным или экспериментальным значением и истинным или точным значением. Вот как вычислить процентную ошибку с примером расчета.
Ключевые моменты: процент ошибки
- Цель вычисления процентной ошибки — определить, насколько близко измеренное значение к истинному значению.
- Ошибка в процентах (ошибка в процентах) — это разница между экспериментальным и теоретическим значением, деленная на теоретическое значение, умноженное на 100 для получения процента.
- В некоторых полях процент ошибки всегда выражается положительным числом. В других случаях правильно иметь либо положительное, либо отрицательное значение. Знак может быть сохранен, чтобы определить, постоянно ли зарегистрированные значения оказываются выше или ниже ожидаемых значений.
- Ошибка в процентах — это один из видов вычисления ошибок.Абсолютная и относительная погрешности — два других общих вычисления. Процент ошибки — это часть всестороннего анализа ошибок.
- Ключи к правильному сообщению процентной ошибки — это знать, следует ли опускать знак (положительный или отрицательный) в вычислении, и сообщать значение с использованием правильного количества значащих цифр.
Формула процентной ошибки
Ошибка в процентах — это разница между измеренным или экспериментальным значением и принятым или известным значением, деленная на известное значение, умноженное на 100%.
Для многих приложений процентная погрешность всегда выражается положительным значением. Абсолютное значение ошибки делится на допустимое значение и выражается в процентах.
| принятое значение — экспериментальное значение | \ допустимое значение x 100%
Для химии и других наук принято оставлять отрицательное значение, если оно произойдет.
Важно, является ли ошибка положительной или отрицательной. Например, вы не ожидаете получить положительную процентную ошибку при сравнении фактического выхода с теоретическим в химической реакции.Если было вычислено положительное значение, это дало бы ключ к разгадке потенциальных проблем с процедурой или неучтенных реакций.
При сохранении знака ошибки расчет представляет собой экспериментальное или измеренное значение за вычетом известного или теоретического значения, деленное на теоретическое значение и умноженное на 100%.
процентная ошибка = [экспериментальное значение — теоретическое значение] / теоретическое значение x 100%
Шаг вычисления процентной ошибки
- Вычтите одно значение из другого.Порядок не имеет значения, если вы опускаете знак (беря абсолютное значение. Вычтите теоретическое значение из экспериментального значения, если вы сохраняете отрицательные знаки. Это значение является вашей «ошибкой».
- Разделите ошибку на точное или идеальное значение (не на экспериментальное или измеренное значение). Это даст десятичное число.
- Преобразуйте десятичное число в процент, умножив его на 100.
- Добавьте символ процента или%, чтобы сообщить значение ошибки в процентах.
Это даст десятичное число.Пример расчета процентной ошибки
В лаборатории вам дают кусок алюминия. Вы измеряете размеры блока и его объем в емкости с водой известного объема. Вы рассчитываете, что плотность алюминиевого блока составляет 2,68 г / см 3 . Вы смотрите на плотность алюминиевого блока при комнатной температуре и обнаруживаете, что она составляет 2,70 г / см 3 . Рассчитайте процентную погрешность вашего измерения.
- Вычтите одно значение из другого:
2.68 — 2,70 = -0,02 - В зависимости от того, что вам нужно, вы можете отбросить любой отрицательный знак (взять абсолютное значение): 0,02
Это ошибка. - Разделите ошибку на истинное значение: 0,02 / 2,70 = 0,0074074
- Умножьте это значение на 100%, чтобы получить процентную ошибку:
0,0074074 x 100% = 0,74% (выражается двумя значащими цифрами).
Значительные цифры важны в науке. Если вы сообщите об ответе, используя слишком много или слишком мало ответов, это может быть сочтено неверным, даже если вы правильно настроили проблему.
Процент ошибки в сравнении с абсолютной и относительной ошибкой
Процентная ошибка связана с абсолютной ошибкой и относительной ошибкой. Разница между экспериментальным и известным значением — это абсолютная ошибка. Когда вы разделите это число на известное значение, вы получите относительную ошибку. Ошибка в процентах — это относительная ошибка, умноженная на 100%. Во всех случаях сообщайте значения, используя соответствующее количество значащих цифр.
Источники
- Беннет, Джеффри; Бриггс, Уильям (2005), Использование и понимание математики: количественный подход к рассуждению (3-е изд.), Бостон: Пирсон.
- Торнквист, Лео; Вартия, Пентти; Вартия, Юрьё (1985), «Как следует измерять относительные изменения?», Американский статистик , 39 (1): 43–46.
IB Physics Notes — 1.2 Измерения и погрешности
В физике выполняется множество различных типов измерений. Чтобы предоставить четкий и сжатый набор данных, во всех науках используется определенная система единиц. Эта система называется Международной системой единиц (СИ от французского «Système International d’unités»).
Система СИ состоит из семи основных единиц:
| Кол-во | Название агрегата | Условное обозначение |
| масса | килограмм | кг |
| время | секунды | с |
| длина | метр | кв.м |
| температура | кельвина | К |
| Электрический ток | ампер | А |
| Количество вещества | моль | моль |
| Сила света | кандела | кд |
Обратите внимание, что последняя единица, кандела, не используется в дипломной программе IB.
Чтобы выразить определенные величины, мы объединяем базовые единицы СИ для образования новых. Например, если мы хотим выразить количество скорости, равное расстоянию / времени, мы пишем м / с (или, точнее, мс -1 ). Для некоторых величин мы объединяем одну и ту же единицу дважды или более, например, для измерения площади, равной длине x ширине, мы пишем m 2 .
Некоторые комбинации или единицы СИ могут быть довольно длинными и трудными для чтения, по этой причине некоторым из этих комбинаций были присвоены новые единицы и символ, чтобы упростить чтение данных.
Например: мощность, которая представляет собой коэффициент использования энергии, записывается как кг м 2 с -3 . Эта комбинация используется так часто, что на ее основе была получена новая единица измерения, которая называется ватт (символ: W).
Ниже приведена таблица, содержащая некоторые производные единицы СИ, с которыми вы часто сталкиваетесь:
| Производная единица СИ | Символ | Базовый блок СИ | Альтернативный блок |
| ньютон | N | кг м с -2 | – |
| джоуль | Дж | кг м 2 с -2 | Н м |
| герц | Гц | с -1 | – |
| ватт | Вт | кг м 2 с -3 | Дж с -1 |
| вольт | В | кг м 2 с -3 A -1 | Вт А -1 |
| Ом | Ом | кг м 2 с -3 A -2 | В А -1 |
| паскаль | Па | кг м -1 с -2 | Н · м -2 |
2.2 — Производные единицы СИ Часто нам нужно конвертировать между разными единицами.
Например, если бы мы пытались рассчитать стоимость нагрева литра воды, нам нужно было бы преобразовать джоули (Дж) в киловатт-часы (кВт-ч), поскольку энергия, необходимая для нагрева воды, выражается в джоулях, а стоимость электричество, используемое для нагрева воды, — это определенная цена за кВт · ч.
Если мы посмотрим на таблицу 1.2.2, то увидим, что один ватт равен джоуля в секунду. Это упрощает преобразование джоулей в ватт-часы: 60 секунд в минутах и 60 минут в час, поэтому 1 Вт · ч = 60 x 60 Дж, а один кВт · ч = 1 Вт · ч / 1000 (k в кВт · ч — это префикс, обозначающий килограммы, равный 1000).
Есть несколько способов записать большинство производных единиц. Например: метры в секунду можно записать как м / с или мс -1 . Важно отметить, что только последний, m s -1 , принимается в качестве допустимого формата. Поэтому вы всегда должны записывать метры в секунду (скорость) как m s -1 и метры в секунду в секунду (ускорение) как m s -2 .
Обратите внимание, что это относится ко всем устройствам, а не только к двум, указанным выше.
При выражении больших или малых количеств мы часто используем префиксы перед единицей.Например, вместо 10000 В мы пишем 10 кВ, где k означает килограммы, то есть 1000. Мы делаем то же самое для небольших величин, таких как 1 мВ, который равен 0,001 В, m означает милли, что означает одну тысячную (1 / 1000).
Выражая единицы измерения словами, а не символами, мы говорим 10 киловатт и 1 милливатт.
Таблица префиксов приведена на странице 2 буклета с физическими данными.
Случайные ошибки
Случайная ошибка — это ошибка, которая влияет на чтение случайным образом.
Источники случайных ошибок:
- Наблюдатель не идеален
- Читаемость оборудования
- Внешнее воздействие на наблюдаемый объект
Систематические ошибки
Систематическая ошибка — это ошибка, которая возникает при каждом чтении.
Источники систематических ошибок включают:
- Наблюдатель не идеален каждый раз одинаково
- Инструмент с ошибкой смещения нуля
- Инструмент, который неправильно откалиброван
Точность
Измерение считается точным, если оно имеет небольшие систематические ошибки.
Точность
Измерение считается точным, если оно имеет небольшие случайные ошибки.
Измерение может быть очень точным, но неточным (например, если используемый инструмент имел ошибку смещения нуля).
Влияние случайных ошибок на набор данных можно уменьшить путем повторения считывания. С другой стороны, поскольку систематические ошибки возникают при каждом чтении, повторение показаний не снижает их влияния на данные.
Количество значащих цифр в результате должно отражать точность входных данных.То есть при делении и умножении количество значащих цифр не должно превышать количество наименее точного значения.
Пример :
Найдите скорость автомобиля, который преодолевает 11,21 метра за 1,23 секунды.
11,21 x 1,13 = 13,7883
Ответ состоит из 6 значащих цифр. Однако, поскольку значение времени (1,23 с) составляет всего 3 с.ф. запишем ответ как 13,7 мс -1 .
Количество значащих цифр в любом ответе должно отражать количество значащих цифр в данных.
Абсолютные погрешности
При обозначении абсолютной погрешности в части данных мы просто добавляем ± 1 от наименьшего значащего числа.
Пример :
13,21 м ± 0,01
0,002 г ± 0,001
1,2 с ± 0,1
12 В ± 1
Дробные неопределенности
Чтобы вычислить дробную неопределенность части данных, мы просто делим неопределенность на значение данных.
Пример :
1.2 с ± 0,1
Дробная погрешность:
0,1 / 1,2 = 0,0625
Погрешности в процентах
Для расчета погрешности в процентах части данных мы просто умножаем дробную погрешность на 100.
Пример :
1,2 с ± 0,1
Погрешность в процентах:
0,1 / 1,2 x 100 = 6,25%
Недостаточно просто отобразить неопределенность данных, мы должны включать ее в любые вычисления, которые мы делаем с данными.
Сложение и вычитание
При выполнении сложения и вычитания нам просто нужно сложить абсолютные погрешности.
Пример :
Сложите значения 1,2 ± 0,1, 12,01 ± 0,01, 7,21 ± 0,01
1,2 + 12,01 + 7,21 = 20,42
0,1 + 0,01 + 0,01 = 0,12
20,42 ± 0,12
Умножение, деление и степени
При выполнении умножений и делений или, имея дело с степенями, мы просто складываем процентные погрешности.
Пример :
Умножить значения 1,2 ± 0,1, 12,01 ± 0,01
1,2 x 12,01 = 14
0,1 / 1,2 x 100 = 8,33%
0,01 / 12,01 X 100 = 0,083%
8,33 + 0,083 = 8,413%
14 ± 8,413%
Другие функции
Для других функций, таких как тригонометрические, мы вычисляем среднее, максимальное и минимальное значение, чтобы определить диапазон неопределенности.
Для этого мы вычисляем результат, используя данные значения как обычно, с добавленной погрешностью и вычтенной погрешностью.Затем мы проверяем разницу между лучшим значением и значениями с добавленной и вычитаемой погрешностью и используем наибольшую разницу в качестве погрешности результата.
Пример :
Вычислить площадь поля, если его длина составляет 12 ± 1 м, а ширина — 7 ± 0,2 м.
Лучшее значение для площади:
12 x 7 = 84 м 2
Наибольшее значение для площади:
13 x 7,2 = 93,6 м 2
Наименьшее значение для площади:
11 x 6,8 = 74.8 м 2
Если округлить значения, мы получим площадь:
84 ± 10 м 2
При представлении данных в виде графика мы представляем неопределенность в точках данных путем добавления полос погрешностей. Мы можем увидеть диапазон неопределенности, проверив длину полос ошибок в каждом направлении. Планки погрешностей можно увидеть на рисунке 1.
2.1 ниже:
Рисунок 1.2.1 — График с планками погрешностей
В физике IB, планки погрешностей необходимо использовать только в том случае, если неопределенность в одной или обеих нанесенных на график величинах значительна.Планки погрешностей не требуются для тригонометрических и логарифмических функций.
Чтобы добавить планки погрешностей к точке на графике, мы просто берем диапазон неопределенности (выраженный в данных как «значение ±») и рисуем линии соответствующего размера выше и ниже или с каждой стороны точки в зависимости от оси. значение соответствует.
Пример :
Нанесите следующие данные на график с учетом неопределенности.
| Время ± 0.2 с | Расстояние ± 2 м |
| 3,4 | 13 |
| 5,1 | 36 |
| 7 | 64 |
Таблица 1.
2.1 — Данные о расстоянии от времени
Рисунок 1.2.2 — График зависимости расстояния от времени с полосами ошибок
На практике построение каждой точки с ее конкретными планками погрешностей может занять много времени, так как нам нужно будет вычислить диапазон неопределенности для каждой точки.Поэтому мы часто пропускаем определенные моменты и добавляем планки ошибок только к определенным. Мы можем использовать приведенный ниже список правил, чтобы сэкономить время:
- Добавляйте полосы погрешностей только к первой и последней точкам
- Добавляйте планки погрешностей только в точку с наихудшей погрешностью
- Добавьте планки ошибок ко всем точкам, но используйте неопределенность наихудшей точки
- Добавляйте только полосы погрешностей к оси с наихудшей погрешностью
Градиент
Чтобы вычислить неопределенность градиента, мы просто добавляем полосы ошибок в первую и последнюю точку, а затем рисуем прямую линию, проходящую через полосу наименьшей ошибки в одной точке и наибольшую в другой, и наоборот.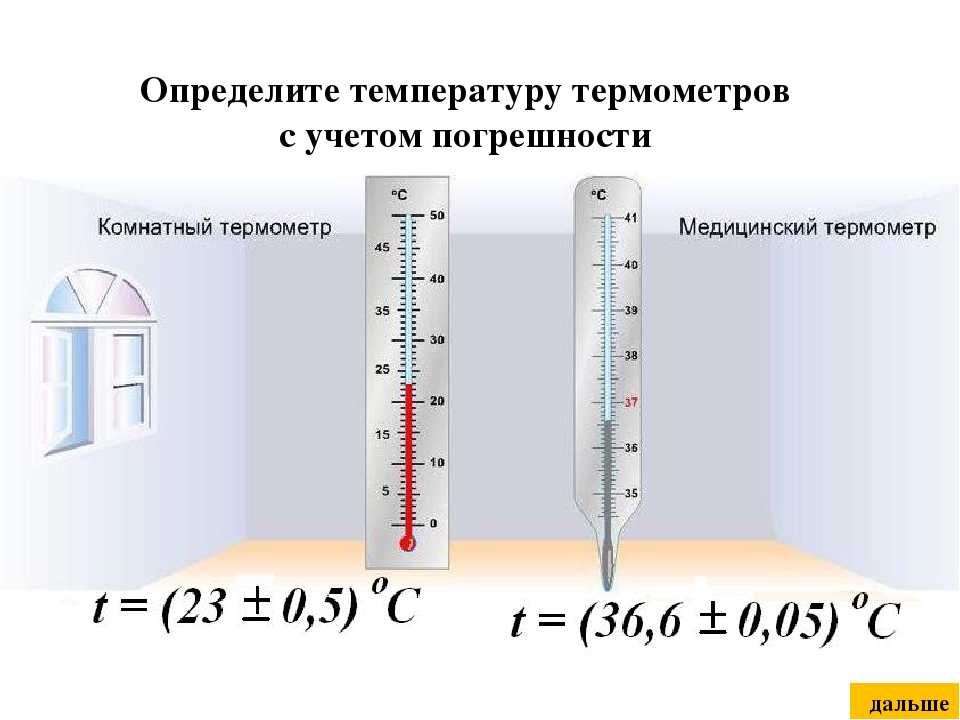
наоборот.Это дает две линии, одну с самым крутым возможным градиентом, а другую с самым мелким, затем мы вычисляем градиент каждой линии и сравниваем его с наилучшим значением. Это показано на рисунке 1.2.3 ниже:
Рисунок 1.2.3 — Неопределенность градиента на графике
Пересечение
Чтобы вычислить неопределенность точки пересечения, мы делаем то же самое, что и при вычислении неопределенности в градиенте. Однако на этот раз мы проверяем наименьшее, наибольшее и наилучшее значение для перехвата.Это показано на рисунке 1.2.4 ниже:
Рисунок 1.2.4 — Погрешность отсечения на графике
Обратите внимание, что на двух рисунках выше планки погрешностей увеличены для улучшения читаемости.
Распространение ошибки — Chemistry LibreTexts
Распространение ошибки (или распространение неопределенности) определяется как влияние на функцию неопределенности переменной.
Это статистический расчет на основе расчетов, предназначенный для объединения неопределенностей от нескольких переменных, чтобы обеспечить точное измерение неопределенности.
Введение
В каждом измерении присутствует некоторая неопределенность, и не все погрешности равны. Поэтому возможность правильно комбинировать неопределенности из разных измерений имеет решающее значение. Неопределенность в измерениях возникает по-разному: изменчивость прибора, разные наблюдатели, различия выборки, время суток и т. Д. Обычно ошибка выражается в стандартном отклонении (\ (\ sigma_x \)) измерения.
Каждый раз, когда вычисление требует для решения более одной переменной, необходимо распространение ошибки для правильного определения неопределенности.Например, допустим, мы используем спектрофотометр UV-Vis для определения молярной поглощающей способности молекулы по закону Бера: A = ε l c. Поскольку по крайней мере две переменные имеют неопределенность, зависящую от используемого оборудования, необходимо применить формулу распространения ошибки для измерения более точной неопределенности молярной поглощающей способности.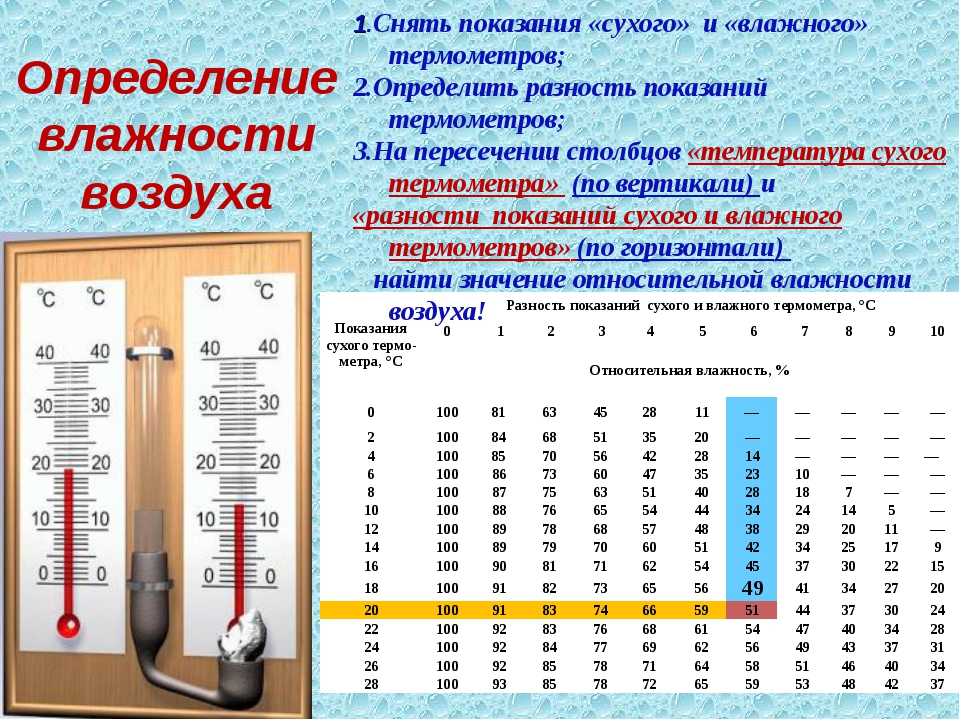
Этот пример будет продолжен ниже после вывода.
Получение точной формулы
Предположим, что для проведения определенного эксперимента требуется несколько инструментов.Каждый из этих инструментов имеет различную вариабельность своих измерений. Результаты для каждого инструмента представлены в виде: a, b, c, d … (для упрощения во всем этом выводе будут использоваться только переменные a, b , и c ) . Желаемый конечный результат — \ (x \), так что \ (x \) зависит от a, b, и c . Можно записать, что \ (x \) является функцией этих переменных:
\ [x = f (a, b, c) \ label {1} \]
Поскольку каждое измерение имеет неопределенность относительно своего среднего значения, можно записать, что неопределенность dx i i -го измерения \ (x \) зависит от неопределенности — -го измерения a, b, и c:
\ [dx_i = f (da_i, db_i, dc_i) \ label {2} \]
Общее отклонение \ (x \) затем получается из частной производной x по каждой из переменных:
\ [dx = \ left (\ dfrac {\ delta {x}} {\ delta {a}} \ right) _ {b, c} da, \; \ left (\ dfrac {\ delta {x}} {\ delta {b}} \ right) _ {a, c} db, \; \ left (\ dfrac {\ delta {x}} {\ delta {c}} \ right) _ {a, b} dc \ label {3} \]
Отношение между стандартными отклонениями x и a, b, c и т.
Д.2 \ label {4} \]
Перекрестные термины:
\ [\ left (\ dfrac {\ delta {x}} {da} \ right) \ left (\ dfrac {\ delta {x}} {db} \ right) da \; db, \; \ left (\ dfrac {\ delta {x}} {da} \ right) \ left (\ dfrac {\ delta {x}} {dc} \ right) da \; dc, \; \ left (\ dfrac {\ delta {x}) } {db} \ right) \ left (\ dfrac {\ delta {x}} {dc} \ right) db \; dc \ label {5} \]
Квадратные члены из-за природы возведения в квадрат всегда положительны и поэтому никогда не исключают друг друга. Напротив, перекрестные термины могут нейтрализовать друг друга из-за возможности того, что каждый член может быть положительным или отрицательным.Если da, db, и dc представляют случайные и независимые неопределенности, примерно половина перекрестных членов будет отрицательной, а половина положительной (это в первую очередь связано с тем, что переменные представляют собой неопределенность относительно среднего значения). Фактически, сумма перекрестных членов должна приближаться к нулю, особенно при увеличении \ (N \).
2} {N -1} \ label {7} \]
На предыдущем шаге была создана ситуация, когда уравнение \ ref {7} может имитировать уравнение стандартного отклонения.2_c \ label {9} \]
Таким образом, конечный результат достигнут. Уравнение \ ref {9} показывает прямую статистическую связь между несколькими переменными и их стандартными отклонениями. В следующем разделе приведены выводы для общих вычислений с примером того, как был получен вывод.
| Тип | Пример | Стандартное отклонение (\ (\ sigma_x \)) |
|---|---|---|
| Сложение или вычитание | \ (х = а + Ь — с \) | \ (\ sigma_x = \ sqrt {{\ sigma_a} ^ 2 + {\ sigma_b} ^ 2 + {\ sigma_c} ^ 2} \ label {10} \) |
| Умножение или деление | \ (x = \ dfrac {a x b} {c} \) | \ (\ dfrac {\ sigma_x} {x} = \ sqrt {\ left (\ dfrac {\ sigma_a} {a} \ right) ^ 2 + \ left (\ dfrac {\ sigma_b} {b} \ right) ^ 2+ \ влево (\ dfrac {\ sigma_c} {c} \ right) ^ 2} \) (11) |
| Экспоненциальная | \ (х = а ^ у \) | \ (\ dfrac {\ sigma_x} {x} = y (\ dfrac {\ sigma_a} {a}) \) (12) |
| Логарифмический | \ (х = \ журнал (а) \) | \ (\ sigma_x = 0.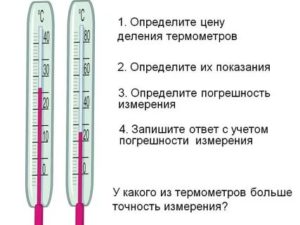 434 (\ dfrac {\ sigma_a} {a}) \) (13) |
| Антилогарифмический | \ (х = антилогарифм (а) \) | \ (\ dfrac {\ sigma_x} {x} = 2.303 ({\ sigma_a}) \) (14) |
Где \ (a \), \ (b \) и \ (c \) — измеряемые переменные из эксперимента, а \ (\ sigma_a \), \ (\ sigma_b \) и \ (\ sigma_c \) — стандартные отклонения этих переменных.
Сложение, вычитание и логарифмические уравнения приводят к абсолютным стандартным отклонениям, тогда как умножение, деление, экспоненциальные и антилогарифмические уравнения приводят к относительным стандартным отклонениям.
Вывод арифметического примера
Точная формула распространения ошибки в уравнении \ (\ ref {9} \) может использоваться для получения арифметических примеров, приведенных в таблице \ (\ PageIndex {1} \).
2}} \ label {11} \]
Пример \ (\ PageIndex {1} \)
Продолжая пример из введения (где мы вычисляем молярную поглощающую способность молекулы), предположим, что у нас есть концентрация 13.2}} \]
\ [\ dfrac {\ sigma _ {\ epsilon}} {\ epsilon} = 0.10237 \]
Как указано в примечании выше, уравнение 11 дает относительное стандартное отклонение или процент от переменной ε . Используя закон Бера, ε = 0,012614 L моль -1 см -1 Следовательно, \ (\ sigma _ {\ epsilon} \) для этого примера будет 10,237% от ε , что составляет 0,001291.
С учетом значащих цифр окончательный ответ будет:
ε = 0.013 ± 0,001 л моль -1 см -1
Пример \ (\ PageIndex {2} \)
Если вам дано уравнение, которое связывает две разные переменные, и учитывая относительную неопределенность одной из переменных, можно определить относительную неопределенность другой переменной с помощью исчисления.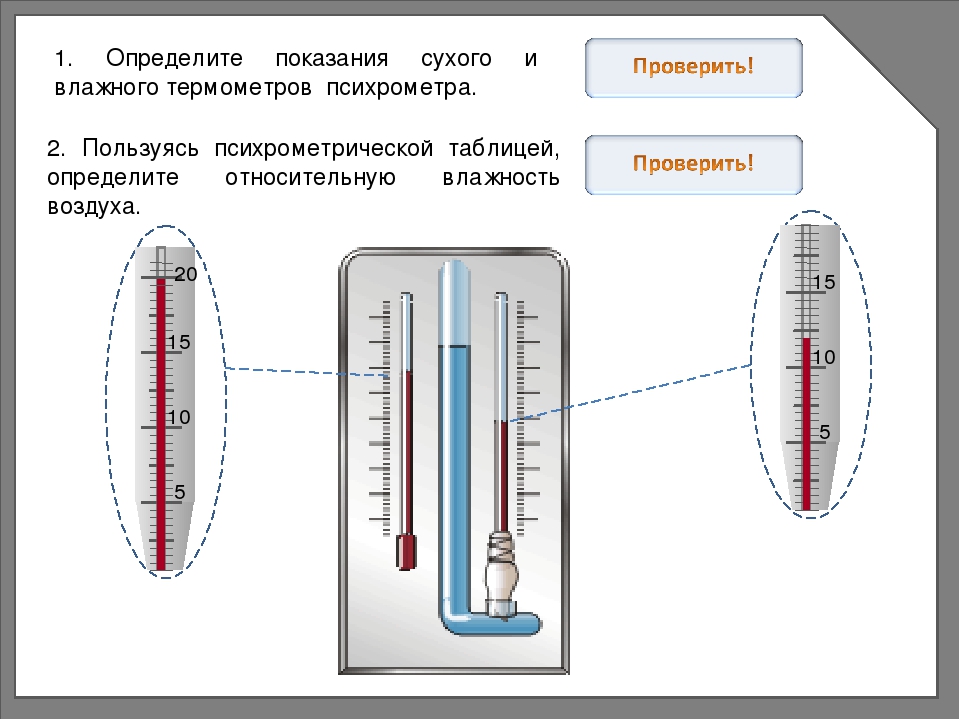
В задачах неопределенность обычно выражается в процентах. Допустим, мы измеряем радиус очень маленького объекта. Проблема может заключаться в том, что погрешность измерения этого радиуса составляет 5%.
Раствор
Чтобы на самом деле использовать этот процент для расчета неизвестных неопределенностей других переменных, мы должны сначала определить, что такое неопределенность. Неопределенность в расчетах определяется как:
(dx / x) = (∆x / x) = неопределенность
Пример \ (\ PageIndex {3} \)
Давайте еще раз посмотрим на пример радиуса объекта. Если мы знаем, что неопределенность радиуса составляет 5%, неопределенность определяется как (dx / x) = (∆x / x) = 5% = 0,05.
Теперь мы готовы использовать исчисление для получения неизвестной неопределенности другой переменной.2) \ nonumber \]
Где c — постоянная величина, r — радиус, а V (r) — объем.
Раствор
Первым шагом к обнаружению неопределенности объема является понимание данной нами информации.
2} \ nonumber \]
Теперь мы можем отменить переменные, которые находятся как в числителе, так и в знаменателе, чтобы получить:
\ [\ dfrac {∆V} {V} = \ dfrac {2∆r} {r} = 2 \ left (\ dfrac {∆r} {r} \ right) \]
Мы сузили уравнение, так что осталось ∆r / r.Нам известно значение погрешности для ∆r / r, равное 5% или 0,05. Подставляя это значение для ∆r / r, получаем:
\ dfrac {∆V} {V} = 2 (0,05) = 0,1 = 10 \% \]
Неопределенность объема 10%. Этот метод можно использовать и в химии, а не только в биологическом примере, показанном выше.
Погрешности измерения температуры термопарами типа K (хромель против алюмеля) из-за краткосрочного заказа хромеля (Технический отчет)
Колли, Т. Г., Карр, К. Р., Хортон, Дж. Л., Херсковиц, М. Б., и Моссман, К. А. Погрешности измерения температуры термопарами типа K (хромель против алюмеля) из-за короткого заказа хромеля . США: Н. П., 1975.
Интернет. DOI: 10,2172 / 4213761.
Колли, Т. Г., Карр, К. Р., Хортон, Дж. Л., Херсковиц, М. Б., и Моссман, К. А. Ошибки измерения температуры с термопарами типа K (хромель против алюмеля) из-за короткого порядка в хромеле .Соединенные Штаты. https://doi.org/10.2172/4213761
Колли, Т. Г., Карр, К. Р., Хортон, Дж. Л., Херсковиц, М. Б., и Моссман, К. А. Сб.
«Ошибки измерения температуры термопарами типа K (хромель против алюмеля) из-за короткого заказа в хромеле». Соединенные Штаты. https://doi.org/10.2172/4213761. https://www.osti.gov/servlets/purl/4213761.
@article {osti_4213761,
title = {Ошибки измерения температуры термопарами типа K (хромель против алюмеля) из-за короткого заказа в хромеле},
author = {Колли, Т.
Г. и Карр, К. Р. и Хортон, Дж. Л. и Херсковиц, М. Б. и Моссман, С. А.},
abstractNote = {},
doi = {10.2172/4213761},
url = {https://www.osti.gov/biblio/4213761},
журнал = {},
номер =,
объем =,
place = {United States},
год = {1975},
месяц = {3}
}
Земной термометр Потенциалы ошибки свободной конвекции
Эмпирическая модель
Для оценки основных вкладов принудительной и свободной конвекции вокруг черного шара были получены корреляции чисел Нуссельта.Число Нуссельта, N u , является безразмерным параметром, который описывает отношение конвективной теплопередачи к кондуктивной теплопередаче, и показано в уравнении. 5. Из N и можно получить коэффициенты конвективной теплопередачи, как показано в уравнении. (5), где h c — коэффициент конвективной теплопередачи [ W м −2 K −1 ], D — гидравлический диаметр [ м ], а k — теплопроводность воздуха [0.
02662 W м -1 K -1 ]. Следовательно, если для земного шара известно N и , коэффициент конвективной теплопередачи можно рассчитать, как в формуле. (6).
$$ Nu = \ frac {{h} _ {c} D} {k} $$
(5)
$$ {h} _ {c} = \ frac {Nu \ cdot k} {D} $$
(6)
Уравнения корреляции чисел Нуссельта получены из литературы.{\ frac {4} {9}}} $$
(7)
В экв. (7) R a — это число Рэлея, а P r — это число Прандтля. Уравнение (7) действительно для R a <10 11 и P r ≥ 0,7. R рассчитывается по формуле. 8 и P r вычисляется по формуле. 9. Фактически, это отношение к D , скрытое в R a для свободной конвекции, которое упускается из виду в литературе и препятствует прямому сравнению между формулой.
{3} $$
(8)
$$ Pr = \ frac {{c} _ {p} \ mu} {k} $$
(9)
В уравнениях. 8 и 9, g — ускорение свободного падения [9,81 м с −2 ], β — коэффициент теплового расширения воздуха [0,0034 K −1 ], ν — кинематическая вязкость [1,48 ⋅ 10 −5 м 2 с −1 ], α — коэффициент температуропроводности воздуха [2.591 ⋅ 10 −5 м 2 с −1 ], c p — удельная теплоемкость воздуха [1005 J k г — ]. 1 K -1 ], а μ — динамическая вязкость воздуха [1,81 ⋅ 10 -5 P a с ]. Для сравнения со случаем свободной конвекции те же отношения принудительной конвекции были получены с использованием корреляции Нуссельта, представленной в формуле.
{0,4} $$
(10)
В уравнении. 10, R e — это число Рейнольдса, данное в уравнении. 11. Используя эти корреляции конвекции, величина каждого режима теплопередачи была оценена для различных скоростей воздуха и температуры земного шара. Уравнение 10 действительно для 3,5 < R e <7,6 ⋅ 10 4 и 0,7 < P r <380, подходящих для этого приложения.
$$ Re = \ frac {{v} _ {a} D} {\ nu} $$
(11)
Часто в конвективных процессах теплопередача обусловлена как принудительной, так и свободной конвекцией, известной как смешанная конвекция.Часто оба фактора вносят значительный вклад, и игнорирования одного или простого суммирования коэффициентов теплопередачи недостаточно. Экспериментальные данные показали, что сочетание N u f r e e и N u f o
918 r d как в формуле.
12 со значениями n = 3 или 4 достаточно для большинства задач 32 .{\ frac {1} {n}} $$(12)
Чтобы повторно параметризовать версию уравнения. 1 для эффектов свободной, принудительной или смешанной конвекции при считывании t g в средах с большими градиентами температуры от поверхности к воздуху, можно просто решить энергетический баланс между конвекцией и излучением с помощью N u , обеспечив коэффициент конвективной теплоотдачи. Уравнение описания устойчивого состояния равновесия шара, показанное как Ур.{4} + \ frac {Nu \ cdot k} {\ epsilon \ sigma D} ({t} _ {g} — {t} _ {a})} $$
(14)
Форма уравнения. 14 полезен, поскольку поправку можно применять для свободной, принудительной и смешанной конвекции, пытаясь получить наилучшее соответствие экспериментальным данным.
Экспериментальная установка
Исходя из предыдущей логики моделирования, было желательно провести эксперименты для наблюдения за потенциалами ошибок, реализованными в созданной среде.
Чтобы максимизировать разницу между температурой воздуха, t a , и средней радиационной температурой, t r , и, следовательно, радиационно форсировать температуру земного шара, t g Вдали от температуры воздуха эксперименты проводились в павильоне лучистого охлаждения Cold Tube.
The Cold Tube — это экспериментальный павильон с лучистым охлаждением на открытом воздухе в Сингапуре, демонстрирующий, как можно достичь комфорта с помощью излучения, без использования кондиционера. В то время как основным техническим механизмом павильона Cold Tube была прозрачная для инфракрасного излучения мембрана, чтобы избежать конденсации на панелях излучающего охлаждения, в которые подается жидкость ниже точки росы на открытом воздухе во влажной среде, этот механизм также служил для обеспечения конвективной изоляции. Поскольку холодная поверхность была конвективно изолирована от воздуха в помещении, температура воздуха часто не опускалась более чем на 2 ° C ниже температуры окружающей среды.
Эта особенность сделала холодную трубку идеальной средой для проверки влияния свободной конвекции на показания земной температуры, поскольку она была разработана для достижения разделения до 10 ° C между t r и t a . Фотография Cold Tube показана на рис. 11.
Панели излучающего охлаждения с мембранной системой избегают конденсации и конвекции, что является идеальной средой для тестирования возможных вкладов в погрешность свободной конвекции.
Охлажденная вода подается на синие капиллярные маты на панелях на рис. 11 при температуре от 3 ° C до t a . Павильон находился снаружи в Сингапуре, где точка росы постоянно оставалась между 23 и 24 ° C. Прозрачная мембрана была прозрачной для 80% теплового излучения, описанного в Teitelbaum et al . 33 .
Мембрана крепилась к панели, изолируя холодные капилляры от теплого и влажного воздуха.
Тепловое излучение могло проходить через мембрану, не охлаждая ее, так что не было механизма для охлаждения воздуха. Возникла кондукция и ограниченная конвекция, но с низкой скоростью по сравнению с излучением. Холодная труба состояла из 10 панелей излучающего охлаждения, 8 вертикальных панелей и 2 горизонтальных наверху.
Четыре глобусные измерительные системы, расположенные на высоте 12,5, 63, 114 и 174 см, были размещены в одном углу холодной трубки, как показано на фотографиях на рис. 12, а размеры показаны на рис.13. Шары были диаметром 100 мм. Каждый черный глобус сопровождался датчиком температуры воздуха, датчиком относительной влажности и датчиком скорости воздуха, включая систему измерения ThermCondSys 5500. Датчики температуры и температуры воздуха — терморезисторы Pt-100 (± 0,1 ° C). Датчик температуры воздуха был защищен от излучения сильноотражающим серебряным конусом. Датчик скорости воздуха представляет собой сферический всенаправленный датчик скорости воздуха и датчик температурной компенсации, покрытый вакуумом с алюминиевым покрытием, которое увеличивает их устойчивость к загрязнению и снижает влияние теплового излучения на точность измерения (± 0.
02 м с -1 ). Датчик относительной влажности имеет точность ± 2%. Для достоверных данных t r измерений, набор из 6 радиометров (Apogee, SL-510-SS; 0,12 мВ на Вт м −2 ; повторяемость измерений 1%; калибровка 5% погрешность; ± ° C) ориентированы ортогонально, измеряя лучистый поток во всех 6 сторонах света. Кубический набор из 6 радиометров считался основным для измерения t r , поскольку чувствительный элемент не чувствителен к конвекции.Эти 6 значений были усреднены и составляют t r в месте измерения. Все датчики были откалиброваны в течение 1 месяца экспериментов. Шесть пиргеометров были размещены на небольшом деревянном кубе (длина стороны = 4,5 см), чтобы минимизировать смещения, которые смещали бы датчики далеко от точки измерения, как в установке, предложенной Торссоном 10 . В небольших помещениях эти смещения могут значительно исказить показания, если их держать ближе к источникам холода в пределах досягаемости рукавов.
Измерение средней лучистой температуры в холодной трубке с помощью 6 пиргеометров, расположенных перпендикулярно деревянному кубу рядом с 4 черными шарами с анемометрами, датчиками температуры и влажности воздуха. В этой статье использовались данные с верхнего глобуса, так как он физически был ближе всего к пиргеометру.
Рис. 13Схемы в разрезе и в плане холодной трубы, показывающие панели излучающего охлаждения и положение контрольно-измерительной установки.
Пиргеометр — разумный выбор наземного прибора из-за его метода измерения.В пиргеометр встроен высокоточный термистор, который непрерывно измеряет температуру устройства, t p y r g . Сам пиргеометр имеет пропорциональное выходное напряжение, которое соответствует лучистому потоку между устройством и поверхностью в поле зрения 150 °. Зная как температуру устройства, так и лучистый поток, Q r a d in W m −2 позволяет уравнение.
{4}) $$
(15)
Измерения были записаны для всех устройств с 2-секундными интервалами, а 10-секундные и 5-минутные средние скорости ветра использовались для расчета t r с использованием формул. 1 и 2. 5-минутные средние значения времени рекомендуются для использования формул. 1 и 2 7 . Рассчитанные средние лучистые температуры сравнивались с измеренными средними лучистыми температурами пиргеометрами.
Пиргеометры измеряют поток излучения в поле зрения 150 °, а также температуру устройства, что позволяет точно рассчитать средние значения поверхностей в поле зрения.Усреднение по всем 6 сторонам света помогает уменьшить зависимость от угла падения излучения между поверхностями и датчиком пиргеометра и устраняет окклюзию. В Cold Tube также был установлен пиранометр для измерения коротковолнового излучения. Павильон был затенен как непрозрачной холщовой тканью, так и стальной конструкцией и панелями, поэтому прямой вид на небо не просматривался.
Коротковолновое излучение измерялось на месте датчика пиргеометра с помощью пиранометра (SP-510; 0,057 мВ на Вт м −2 ; повторяемость измерений 1%), направленного вручную во все 6 сторон света.Поступающее коротковолновое излучение в среднем составляло 6,8 ± 1,1 Вт м −2 и было инвариантным по направлению. Коротковолновое излучение в W м −2 было добавлено к усредненным показаниям пиргеометра также в W м −2 перед преобразованием в значение для t r с использованием уравнения . 16 и S t o t — суммарное измерение коротковолновой и средней длинноволновой радиации в W m −2 .
$$ {t} _ {r} = \ sqrt [4] {\ frac {{S} _ {tot}} {\ sigma}} — 273,15 $$
(16)
Различия между стандартным методом корректировки t g для конвекции для получения t r , как показано в уравнениях.
1 и 2, а также достоверные данные, собранные с помощью пиргеометра, можно сравнить, чтобы продемонстрировать разницу в лучистой теплопередаче, Δ Q r a d [ W m −2 ], обитатель будет ощущать себя в каждой среде.{4}) $$
(17)
Согласно Принципу нуля, «термометр может измерять только свою собственную температуру». По сути, датчик температуры Pt-100 измеряет температуру воздуха внутри черного шара, которая направляется к средней температуре излучения за счет излучения. принцип, лежащий в основе поправок на среднюю излучаемую температуру черного шара. Напротив, пиргеометры представляют собой датчики теплового потока черного тела, которые посредством обратного расчета (показанного в уравнении 15) дают температуру черного тела окружающей среды в точке измерения.Эта процедура описана в стандартах 12 , и результирующее показание температуры будет называться в этом документе «основной истиной», поскольку это желаемое значение, которое должно быть извлечено из измерения черного шара после соответствующей коррекции.
Тип Неопределенность A и типа B: оценка компонентов неопределенности
Введение
Неопределенность типа A и типа B — это два элемента, которые обычно обсуждаются при оценке неопределенности измерения.
Тип неопределенности описан в большинстве руководств по неопределенности измерений и учебных курсов по неопределенности. Аудиторы просматривают бюджеты неопределенностей, чтобы убедиться, что компоненты правильно классифицированы.
Тем не менее, просматривали ли вы большую часть опубликованной информации о неопределенностях типа A и типа B?
Очень минималистично. Никто не освещает тему типа неопределенности так, как ГУМ. Так много информации упущено из других руководств и тренингов.
Это может быть причиной того, что большинство людей оценивают неопределенность типа B только с прямоугольным распределением, когда существует так много более реалистичных вариантов.
Почему не указаны другие параметры?
В этом руководстве я расскажу вам о неопределенностях типа A и типа B, как описано в GUM.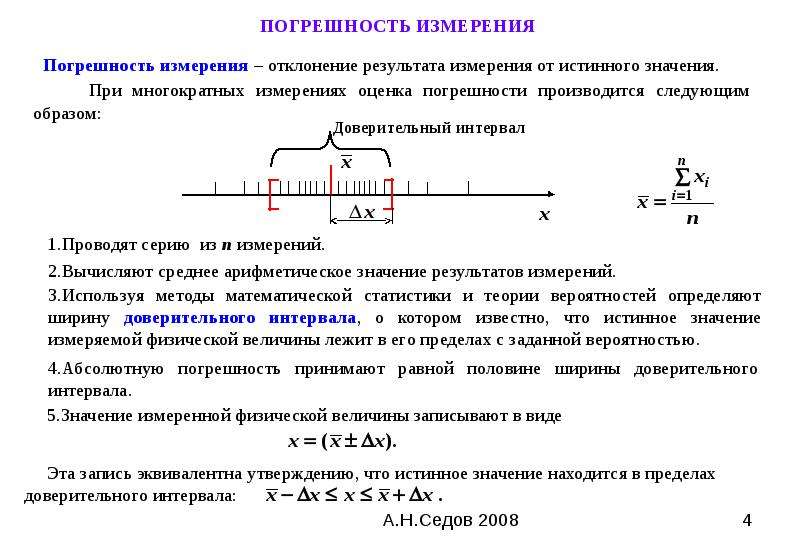
Однако я собираюсь объяснить, не требуя от вас степени доктора философии.
Итак, если вы хотите научиться рассчитывать неопределенность, обязательно прочтите это руководство, чтобы узнать все, что вам нужно знать о неопределенности типа A и типа B.
Фон
Прежде чем вы узнаете о классификациях типов неопределенности, неплохо узнать больше о том, почему они существуют и откуда они взялись.
В 1980 г. в Рекомендации CIPM INC-1 было предложено разделить компоненты неопределенности измерения на две категории; Тип A и тип B.
Ниже приводится отрывок из Словарь по метрологии ;
“ В Рекомендации CIPM INC-1 (1980) по Заявлению о неопределенностях предлагается, чтобы компоненты неопределенности измерения были сгруппированы в две категории, Тип A и Тип B, в зависимости от того, были ли они оценены статистическими методами. или иначе, и чтобы они были объединены для получения дисперсии в соответствии с правилами математической теории вероятностей, также рассматривая компоненты типа B с точки зрения дисперсии.
Результирующее стандартное отклонение является выражением неопределенности измерения. Взгляд на подход неопределенности был подробно описан в Руководстве по выражению неопределенности в измерениях (GUM) (1993, исправлено и переиздано в 1995 году), в котором основное внимание уделялось математической обработке неопределенности измерения с помощью явной модели измерения в предположении, что измеряемая величина можно охарактеризовать по существу уникальным значением. Более того, в GUM, а также в документах IEC представлены рекомендации по подходу неопределенности в случае однократного считывания калиброванного прибора, что обычно встречается в промышленной метрологии. ”- VIM 2012
Как видите, VIM дает отличное объяснение и рекомендует вам прочитать GUM для получения более подробной информации.
Вот отрывок из «Руководство по выражению неопределенности в измерениях» ;
“ 3.3.4 Целью классификации типа A и типа B является указание двух различных способов оценки составляющих неопределенности и только для удобства обсуждения; Классификация не предназначена для указания того, что существует какое-либо различие в природе компонентов, полученных в результате двух типов оценки.
Оба типа оценки основаны на распределении вероятностей (C.2.3), а компоненты неопределенности, возникающие в результате любого типа, количественно оцениваются с помощью дисперсий или стандартных отклонений. ”- JCGM 100
Для получения дополнительной информации о рекомендации CIPM INC-1 (1980) посетите веб-сайт iso.org . Текст на французском языке, но его легко перевести с помощью таких инструментов, как Google Translate .
Теперь, когда вы прочитали VIM и GUM, вы можете понять, что использование типов неопределенности (т.е. A и B) призваны помочь вам быстро определить, как были оценены данные.
Если вы продолжите читать GUM, он научит различать неопределенности типа A и типа B. См. Отрывок ниже.
“ 3.3.5 Расчетная дисперсия u2, характеризующая компонент неопределенности, полученный в результате оценки типа A , вычисляется из серии повторных наблюдений и представляет собой известную статистически оцененную дисперсию s2 (см. 4.2). Расчетное стандартное отклонение (C.2.12, C.2.21, C.3.3) u, положительный квадратный корень из u2, таким образом, u = s и для удобства иногда называется стандартной неопределенностью типа A. Для компонента неопределенности, полученного из оценки типа B, оцененная дисперсия u2 оценивается с использованием имеющихся знаний (см. 4.3), а оцененное стандартное отклонение u иногда называют стандартной неопределенностью типа B. ”- JCGM 100
Из приведенного выше отрывка вы можете определить две вещи;
• Неопределенность типа A рассчитывается на основе серии наблюдений,
• Неопределенность типа B оценивается с использованием доступной информации.
Кроме того, GUM предоставляет вам информацию о распределениях вероятностей для каждого типа неопределенности .
– Таким образом, стандартная неопределенность типа A получается из функции плотности вероятности (C.2.5), полученной из наблюдаемого частотного распределения (C.2.18), в то время как стандартная неопределенность типа B получается из предполагаемой функции плотности вероятности , основанный на степени уверенности в том, что событие произойдет [часто называемая субъективной вероятностью (C.2.1)]. Оба подхода используют признанные интерпретации вероятности. ”- JCGM 100
Неопределенность типа A характеризуется наблюдаемым частотным распределением, что означает, что вы должны смотреть на гистограмму, чтобы найти правильное распределение вероятностей.
Согласно центральной предельной теореме, чем больше выборок вы соберете, тем больше данные будут напоминать нормальное распределение. Вот ссылка на удивительное видео о центральной предельной теореме .Рекомендую посмотреть.
С другой стороны, неопределенность типа B характеризуется использованием предполагаемого распределения вероятностей, основанного на доступной информации. Без исходных данных или гистограммы вам остается определить, как данные характеризуются на основе ваших источников информации.
В большинстве случаев вам не предоставляют много информации. Поэтому люди обычно предполагают прямоугольное распределение.
Однако есть много других способов оценить данные неопределенности типа B, на которые никто никогда не ссылается; нет даже в лучших руководствах по оценке неопределенности.
Сегодня я собираюсь охватить все, что вам нужно знать о неопределенности типа A и типа B. Посмотрите на список ниже, чтобы узнать, что описано в этом руководстве.
1. Что такое неопределенность типа A
2. Оценка неопределенности типа A
3. Примеры оценки неопределенности типа A
4. Что такое неопределенность типа B
5. Оценка неопределенности типа B
6. Примеры оценки неопределенности типа B Неопределенность
7. Разница между неопределенностью типа A и типа B
8.Как выбрать тип A или тип B
Что такое неопределенность типа А
Согласно словарю метрологии (VIM), неопределенность типа A — это «оценка компонента неопределенности измерения путем статистического анализа значений измеренных величин, полученных при определенных условиях измерения».
В Руководстве по выражению неопределенности измерений (GUM) оценка неопределенности типа А определяется как метод оценки неопределенности путем статистического анализа серий наблюдений.
По сути, неопределенность типа А — это данные, собранные в результате серии наблюдений и оцененные с использованием статистических методов, связанных с дисперсионным анализом (ANOVA).
Итак, если вы собираете повторяющиеся выборки схожих результатов измерений и оцениваете их, вычисляя среднее значение, стандартное отклонение и степени свободы, ваш компонент неопределенности будет классифицирован как неопределенность типа А.
Оценка неопределенности типа А
В большинстве случаев лучший способ оценить данные неопределенности типа А — это вычислить;
• Среднее арифметическое,
• Стандартное отклонение и
• Степени свободы
Среднее арифметическое
При выполнении серии повторных измерений вы захотите узнать среднее значение вашего набора образцов.
Здесь уравнение среднего арифметического может помочь вам оценить неопределенность типа А. Вы можете использовать это значение позже, чтобы предсказать ожидаемое значение будущих результатов измерения.
Определение
Центральное число набора чисел, которое вычисляется путем сложения количеств и последующего деления общего количества количеств.
Уравнение
Как рассчитать
1. Сложите все значения вместе.
2. Подсчитайте количество значений.
3. Разделите шаг 1 на шаг 2.
Стандартное отклонение
При выполнении серии повторных измерений вы также захотите узнать среднюю дисперсию вашего набора образцов.
Здесь вам нужно рассчитать стандартное отклонение. Это наиболее распространенная оценка типа А, используемая при анализе неопределенности.
Итак, если бы нужно было изучить только одну функцию, на ней бы вы сосредоточили свое внимание.
Определение
Мера разброса набора данных от его среднего значения (т.е. в среднем).
Уравнение
Как рассчитать
1. Вычтите каждое значение из среднего.
2. Возвести в квадрат каждое значение на шаге 1.
3. Сложить все значения из шага 2.
4. Подсчитать количество значений и вычесть его на 1.
5. Разделить шаг 3 на шаг 4.
6. Вычислить Корень квадратный из шага 5.
степеней свободы
После вычисления среднего и стандартного отклонения вам необходимо определить степени свободы, связанные с вашим набором образцов.
Это важное значение, которое большинство людей пренебрегают вычислением. Даже большинство руководств по неопределенности измерений забывают включать это в свой текст. Однако в ГУМе не забывают об этом упомянуть.
Фактически, в разделе 4.2.6 GUM рекомендует, чтобы вы всегда включали степени свободы при документировании оценок неопределенности типа А.
Согласен.
Я всегда включаю степени свободы при оценке данных типа A и в свои бюджеты неопределенности.
Вы также можете использовать его для оценки доверительных интервалов и коэффициентов охвата.
Определение
Количество значений в окончательном вычислении статистики, которые могут изменяться.
Уравнение
Как рассчитать
1. Подсчитайте количество значений в наборе образцов.
2. Вычтите значение шага 1 на 1.
Пример оценки неопределенности типа А
Чтобы дать вам пример оценки данных неопределенности типа А, я собираюсь показать вам два распространенных сценария, с которыми люди сталкиваются при оценке неопределенности измерения.
• Однократный тест на повторяемость и
• Многократный тест на повторяемость
Тест однократной повторяемости
Представьте, что вы оцениваете неопределенность измерения и вам нужно получить некоторые данные типа А. Итак, вы выполняете тест на повторяемость и собираете серию повторных измерений.
Теперь, когда вы собрали данные, вам нужно их оценить. Таким образом, вы вычисляете среднее значение, стандартное отклонение и степени свободы.
Затем вы добавляете стандартное отклонение и степени свободы в свой бюджет неопределенности для воспроизводимости.
Тесты многократной повторяемости
В этом сценарии представим, что вы оцениваете неопределенность измерения для измерительной системы, которая имеет решающее значение для вашей лаборатории. Попробуйте придумать эталон, который у вас есть.
Это так важно, чтобы вы выполняли тест на повторяемость для этой системы каждый месяц и документировали результаты.
В ваших записях указаны среднее значение, стандартное отклонение и степени свободы для каждого месяца.
При таком большом количестве данных типа A вы, вероятно, задаетесь вопросом: «Какие результаты я должен включить в свой бюджет неопределенности?»
Ответ — все они; или, по крайней мере, последние двенадцать месяцев.
Для оценки ваших данных о неопределенности типа A вам нужно будет использовать метод объединенной дисперсии . Это лучший способ объединить или объединить ваши стандартные отклонения.
После выполнения этого анализа вам потребуется объединенное стандартное отклонение для вашего бюджета неопределенности для воспроизводимости.
Что такое неопределенность типа B
Согласно словарю по метрологии (VIM), неопределенность типа B — это «оценка компонента неопределенности измерения, определяемая другими способами, кроме оценки неопределенности измерения типа A».
В Руководстве по выражению неопределенности измерений (GUM) оценка неопределенности типа B определяется как метод оценки неопределенности средствами, отличными от статистического анализа серий наблюдений.
По сути, неопределенность типа B — это данные, собранные в результате чего-либо, кроме проведенного вами эксперимента.
Даже если вы можете анализировать данные статистически, это не данные типа A, если вы не собрали их из серии наблюдений.
Большая часть данных типа B, которые вы будете использовать для оценки неопределенности, будет взята из;
• Отчеты о калибровке,
• Отчеты о проверке квалификации,
• Руководства производителя,
• Таблицы данных,
• Стандартные методы,
• Процедуры калибровки,
• Журнальные статьи,
• Материалы конференций,
• Официальные документы,
• Отраслевые руководства,
• Учебники и
• Другая доступная информация.
Оценка неопределенности типа B
Поскольку неопределенность типа B может происходить из множества различных источников, существует множество способов ее оценки.
Это означает, что в этом разделе содержится много информации.
В большинстве случаев люди по умолчанию назначают прямоугольное распределение компоненту неопределенности и используют квадратный корень из трех делителей для преобразования величин в стандартную неопределенность.
Если это описывает, как вы оцениваете погрешность измерения, поднимите руку.
Хорошая новость в том, что это сработает для 90% вычислений неопределенности, которые вы будете выполнять в течение своей жизни. Однако есть гораздо более реалистичные варианты, которые вы можете использовать для оценки неопределенности типа B.
Это зависит от того, хотите вы их использовать или нет.
Если вам интересно, продолжайте читать. Я собираюсь рассказать о методах оценки в GUM, которые большинство руководств по неопределенности измерений, как правило, не учитывают.
«Следует признать, что оценка стандартной неопределенности типа B может быть такой же надежной, как оценка типа A»Технические характеристики и отчеты о калибровке
В разделе 4.3.3 ГУМа, руководство дает рекомендации по оценке информации, опубликованной в спецификациях производителя и отчетах о калибровке.
“ 4.3.3 Если оценка x i взята из спецификации производителя, сертификата калибровки, справочника или другого источника и указанная неопределенность указана как конкретное кратное стандартному отклонению, стандартная неопределенность u (xi) — это просто указанное значение, деленное на множитель , а оценочная дисперсия u 2 (xi) — это квадрат этого частного. ”
Кроме того, в разделе 4.3.4 GUM, руководство дает вам дополнительную информацию для оценки технических характеристик производителя.
“ 4.3.4 Указанная неопределенность x i не обязательно должна быть кратной стандартному отклонению, как в 4.3.3. Вместо можно обнаружить, что указанная неопределенность определяет интервал с уровнем достоверности 90, 95 или 99 процентов (см. 6.2.2). Если не указано иное, можно предположить, что нормальное распределение (C.2.14) был использован для расчета указанной неопределенности, и восстановил стандартную неопределенность x i путем деления указанной неопределенности на соответствующий коэффициент для нормального распределения . Факторы, соответствующие трем вышеупомянутым уровням уверенности, равны 1,64; 1,96; и 2,58 (см. также Таблицу G.1 в Приложении G). ”
Если неопределенность сообщается с определенным доверительным интервалом (например, 95%), используйте соответствующий коэффициент охвата для преобразования в стандартную неопределенность.
На изображении ниже — выдержка из таблицы данных Fluke 5700A. Вы должны заметить, что спецификации указаны для доверительных интервалов 95% и 99%.
Чтобы найти стандартную неопределенность, просто разделите опубликованную неопределенность на коэффициент охвата (k), связанный с доверительным интервалом, указанным в спецификациях.
Если уровень достоверности не указан в спецификациях (в большинстве случаев он не предоставляется), лучше всего предположить, что он задан с доверительным интервалом 95%.Только предполагайте 99% доверительный интервал, если он указан.
СОВЕТ ПРОФЕССИОНАЛА : в следующий раз, когда ваш аудитор предложит вам оценить спецификации производителя на точность или неопределенность с помощью прямоугольного распределения, попросите его прочитать разделы 4.3.3 и 4.3.4 GUM.
Вероятность появления 50/50
В разделе 4.3.5 GUM вы узнаете, как оценивать неопределенность типа B, если вы считаете, что вероятность возникновения составляет 50%.В руководстве рекомендуется разделить интервал на 1,48.
Следовательно, вы должны использовать следующее уравнение для преобразования в стандартную неопределенность.
« 4.3.5. Рассмотрим случай, когда на основе доступной информации можно утверждать, что« существует вероятность пятьдесят на пятьдесят, что значение входной величины X i лежит в интервале от до до a + ”(другими словами, вероятность того, что X i лежит в пределах этого интервала, составляет 0,5 или 50 процентов).Если можно предположить, что распределение возможных значений X i является приблизительно нормальным, то наилучшую оценку x i X i можно принять за середину интервала. Далее, если полуширина интервала обозначена как a = (a + — a — ) / 2, можно взять u (xi) = 1,48a, поскольку для нормального распределения с математическим ожиданием μ и стандартное отклонение σ интервал μ ± σ / 1,48 охватывает примерно 50 процентов распределения. ”
Если вы запутались, не волнуйтесь. Это не обычное явление.
Я никогда не сталкивался с ситуацией, когда мне приходилось использовать этот метод для оценки неопределенности типа B. Скорее всего, вы никогда не будете использовать его, если только вы не выполняете измерения, которые могут иметь только два возможных результата.
Вероятность появления 2/3
В разделе 4.3.6 GUM вы узнаете, как оценить неопределенность типа B, если вы считаете, что вероятность ее возникновения составляет примерно 67%.В руководстве рекомендуется разделить интервал на 1, поскольку он близок к интервалу конференции, охватываемому одним стандартным отклонением, 68,3%.
Следовательно, вы должны использовать следующее уравнение для преобразования в стандартную неопределенность.
« 4.3.6 Рассмотрим случай, аналогичный случаю 4.3.5, но где, основываясь на доступной информации, можно утверждать, что« существует примерно два из трех шансов, что значение X i лежит в интервал от до до + ”(другими словами, вероятность того, что X i лежит в пределах этого интервала, составляет около 0,67).Тогда можно разумно принять u (xi) = a, потому что для нормального распределения с математическим ожиданием μ и стандартным отклонением σ интервал μ ± σ охватывает около 68,3 процента распределения. ”
Подобно вероятности возникновения 50/50, это не обычная оценка.
Я никогда не сталкивался с ситуацией, когда мне приходилось использовать этот метод для оценки неопределенности типа B. Скорее всего, вы тоже никогда не воспользуетесь им.
Только верхний и нижний пределы
В разделе 4.3.7 GUM, руководство расскажет вам, как оценивать неопределенность типа B, если вы считаете, что существует 100% вероятность того, что значение будет между верхним и нижним пределом.
« 4.3.7. В других случаях можно оценить только границы (верхний и нижний пределы) для X i , в частности, чтобы указать, что« вероятность того, что значение Xi находится в интервале a — для + для всех практических целей равно единице, и вероятность того, что X i лежит вне этого интервала, по существу равна нулю ”.Если нет конкретных сведений о возможных значениях X i в пределах интервала, можно только предположить, что X i с равной вероятностью находится где-нибудь в пределах этого интервала (равномерное или прямоугольное распределение возможных значений — см. 4.4. .5 и рисунок 2 а). Тогда x i , математическое ожидание или ожидаемое значение X i , является средней точкой интервала, x i = (a — + a + ) / 2, с соответствующей дисперсией… ”
В этом сценарии руководство рекомендует назначить прямоугольное распределение и разделить интервал на квадратный корень из 12 или квадратный корень из 3.
Если ожидается, что значение среднего будет средней точкой интервала, разделите на квадратный корень из 12.
Если разница между пределами интервала эквивалентна 2a, разделите на квадратный корень из 3.
Если вы не знаете, как оценить интервал, используйте второе уравнение и разделите на квадратный корень из 3. Это, скорее всего, правильный метод оценки.
Асимметричные пределы
Время от времени вы можете встретить несимметрично распределенные спецификации или данные.Это означает, что пределы не равны как для верхнего, так и для нижнего пределов.
“ 4.3.8 В 4.3.7, верхняя и нижняя границы + и – для входной величины X i могут не быть симметричными относительно его наилучшей оценки x i ; более конкретно, если нижняя граница записана как — = x i — b — , а верхняя граница — как + = x i — b + , то b — ≠ б + .Поскольку в этом случае x i (предполагается, что это ожидание от X i ) не находится в центре интервала от — до + , распределение вероятностей X i не может быть равномерным на всем протяжении интервал. Однако может быть недостаточно информации для выбора подходящего распределения; разные модели приведут к разным выражениям дисперсии. При отсутствии такой информации простейшее приближение… ”
Например, верхний предел может быть на большем расстоянии от номинала, чем нижний предел.Посмотрите на изображение ниже, чтобы увидеть спецификации Grade 2 для манометрического блока в соответствии со спецификацией GGG.
Если вы заметили, верхний и нижний пределы не равны по величине. Поэтому они асимметричны.
Когда вы сталкиваетесь со сценарием этого типа, GUM рекомендует следующие инструкции для оценки неопределенности типа B;
Если ваши пределы асимметричны, вычтите верхний предел на нижний и разделите результат на квадратный корень из 12.
Равная вероятность
Итак, если вы кое-что знаете о статистике, то вы знаете, что используется прямоугольное распределение, когда все шансы появления равновероятны.
Однако вы, вероятно, не знали, что можно также использовать трапециевидное распределение.
Если да, отлично. Если нет, читайте раздел 4.3.9 ГУМа.
“ 4.3.9 В 4.3.7, поскольку не было конкретных знаний о возможных значениях Xi в пределах его оценочных границ от a– до a +, можно было только предположить, что для X i было равновероятно принимать любое значение в пределах этих границ с нулевой вероятностью выхода за их пределы.Такие разрывы ступенчатой функции в распределении вероятностей часто являются нефизическими. Во многих случаях более реалистично ожидать, что значения около границ менее вероятны, чем значения около середины. Тогда разумно заменить симметричное прямоугольное распределение симметричным трапециевидным распределением с равными наклонными сторонами (равнобедренная трапеция), основанием шириной a + — a — = 2a и вершиной шириной 2aβ, где 0 <β <1. При β → 1 это трапециевидное распределение приближается к прямоугольному распределению 4.3.7, тогда как для β = 0 это треугольное распределение [см. 4.4.6 и рисунок 2 b)]. Предполагая такое трапециевидное распределение для X i , можно найти, что математическое ожидание для X i составляет x i = (a — + a + ) / 2, а соответствующая дисперсия составляет… ”
В ГУМе поясняется, что прямоугольное распределение не всегда реально. Если вы ожидаете, что значения будут ближе к средней точке и менее вероятны на пределе, вам следует использовать трапециевидное распределение.
Кроме того, он даже дает некоторые дополнительные сведения, чтобы рекомендовать использование треугольного распределения.
Я думаю, что эта оценка неопределенности типа B очень интересна. Это реалистично и практично для большинства приложений, где люди обычно используют прямоугольное распределение.
Однако я не вижу, чтобы он использовался очень часто, и не ожидаю, что в ближайшее время многие люди перейдут с прямоугольных распределений.
Для тех, кто это делает, вы можете воспользоваться преимуществами меньшей оценки неопределенности и дополнительных вопросов со стороны ваших аудиторов.Поэтому обязательно обратитесь к этому разделу GUM, чтобы защитить его от использования в своих бюджетах неопределенности.
Еще один хороший ресурс — эта статья Говарда Каструпа . Внизу страницы 15 Ховард дает вам хорошее альтернативное уравнение для трапецеидального распределения.
Неопределенность двойного счета
В анализе неопределенности есть две общие проблемы; отсутствие достаточного количества источников неопределенности в вашем бюджете неопределенности и двойной учет компонентов неопределенности.
Раздел 4.3.10 GUM предупреждает вас о двойном учете неопределенности во избежание завышенных оценок неопределенности измерения.
« 4.3.10 Важно не« пересчитывать »компоненты неопределенности . Если компонент неопределенности, возникающий из-за определенного эффекта, получен в результате оценки типа B, он должен быть включен в качестве независимого компонента неопределенности в расчет комбинированной стандартной неопределенности результата измерения только в той степени, в которой эффект не вносит вклад. наблюдаемой изменчивости наблюдений.Это связано с тем, что неопределенность из-за той части эффекта, которая способствует наблюдаемой изменчивости, уже включена в компонент неопределенности, полученный в результате статистического анализа наблюдений. ”
Я часто вижу компоненты неопределенности с двойным счетом в оценках неопределенности калибровки.
Например, лаборатория рассматривает «идеальное» испытуемое устройство (то есть UUT) для разрешения UUT в своем анализе неопределенности CMC, а затем включает фактическое разрешение UUT при вычислении неопределенности калибровки.
Это двойной счет; и это происходит постоянно.
Даже аудиторы не умеют побуждать лаборатории дважды подсчитывать компоненты неопределенности в том самом сценарии, который приведен в приведенном выше примере.
Фактически, на этой неделе я разговаривал с оценщиком, который хотел знать, почему разрешение UUT не было включено в расчет неопределенности CMC. Мне пришлось с радостью посоветовать ему прочитать раздел 5.4 ILAC P14: 01/2013 .
Другой распространенный пример двойного подсчета — это когда лаборатория включает компоненты неопределенности, которые обычно включаются в компоненты неопределенности типа А; повторяемость и повторяемость.
Плохая новость заключается в том, что может быть трудно определить, учтен ли уже компонент неопределенности в другом компоненте неопределенности. Это означает, что предотвратить неопределенность двойного счета практически невозможно.
Примеры оценки неопределенности типа B
Оценка данных из отчетов о калибровке
Оценить данные из отчетов о калибровке довольно просто, если вы получаете калибровки, аккредитованные по стандарту ISO / IEC 17025.
Большинство аккредитованных калибровок сообщают результат измерения и связанную с ним неопределенность измерения. Кроме того, отчет сообщит вам уровень достоверности оцененной неопределенности; обычно 95%, где k = 2.
Следовательно, все, что вам нужно сделать, это разделить указанную неопределенность на коэффициент расширения (k).
Используя информацию, представленную в отчете о калибровке ниже, и приведенное выше уравнение, вы сможете преобразовать расширенную неопределенность в стандартную неопределенность.
Просто разделите расширенную неопределенность (U) на коэффициент охвата (k). Ваш результат будет стандартной неопределенностью.
Оценка данных из спецификаций производителя
Оценить данные из спецификаций производителя так же просто, как оценить данные из отчетов о калибровке.
Обычно спецификации производителя можно найти в руководствах производителя, технических описаниях, каталогах или других маркетинговых материалах.
Однако не все производители проявляют должную осмотрительность при публикации спецификаций. Итак, вам, возможно, придется сделать некоторые предположения.
Наиболее надежные производители публикуют спецификации с соответствующим доверительным интервалом. На изображении ниже вы увидите, что компания Fluke опубликовала спецификации для доверительных интервалов 95% и 99%.
В этом примере давайте сосредоточимся на спецификации 95%, чтобы оценить сигнал 10 В с использованием диапазона 11 В.
Если посмотреть на спецификацию абсолютной погрешности за 1 год для диапазона 11 вольт, погрешность для 10 вольт составляет приблизительно 38 микровольт.
Используя информацию, приведенную в спецификации производителя, используйте приведенное ниже уравнение для преобразования расширенной неопределенности в стандартную неопределенность.
После этого ваша оценка неопределенности типа B должна быть приблизительно 19,4 мкВ.
Теперь вы, вероятно, думаете: «А что, если в спецификациях производителя не указан доверительный интервал?»
Ответ: предположим, что это указано с доверительным интервалом 95%, и оценим его аналогично приведенному выше примеру.Не стесняйтесь использовать значения 2 или 1,96 для коэффициента охвата k.
Оценка данных из руководств, справочников, статей и статей
При оценке неопределенности типа B не всегда удобно использовать собственные данные.
У большинства лабораторий нет времени или ресурсов, необходимых для проверки всех факторов, влияющих на неопределенность измерения. Поэтому вы собираетесь использовать данные из других лабораторий, которые уже сделали эту работу за вас.
Самая большая проблема — найти данные! Вы должны потратить некоторое время и усилия на проведение исследования. Чтобы облегчить жизнь, я уже составил список из 15 мест, где можно найти источники неопределенности .
Как только вы найдете данные и сочтете их применимыми для вашего процесса измерения, вы можете оценить их для анализа неопределенности.
Теперь вы можете оценивать данные неопределенности типа B разными способами. Однако я сосредоточусь на ситуации, с которой вы будете сталкиваться в 90% случаев.
Как правило, вы найдете информацию в руководстве, статье конференции или журнальной статье, которая дает вам данные без дополнительной информации о них.
Следовательно, вы, скорее всего, характеризуете данные с помощью прямоугольного распределения и используете следующее уравнение для оценки компонента неопределенности.
Например, представьте, что вы оцениваете погрешность измерения напряжения с помощью цифрового мультиметра. Вы проводите исследование и наткнулись на статью, опубликованную Keysight Technologies, в которой содержится действительно хорошая информация, относящаяся к процессу измерения, неопределенность которого вы оцениваете.
Итак, вы решили включить некоторую информацию в свой бюджет неопределенности.
Изображение ниже представляет собой отрывок из статьи «Ошибки системного кабеля» и «Ошибки измерения постоянного напряжения в цифровых мультиметрах» , опубликованной Keysight Technologies. Он содержит информацию об ошибках термо-ЭДС, которые вы хотите включить в свой бюджет неопределенности.
В таблице на изображении есть отличная информация, которая поможет вам количественно оценить ошибки термо-ЭДС, но очень мало информации о происхождении данных.Поэтому было бы лучше предположить, что данные имеют прямоугольное распределение.
Для соединения медь-медь с изменением температуры на 1 ° C погрешность термо-ЭДС должна составлять примерно 0,3 микровольта. Чтобы преобразовать компонент неопределенности в стандартную неопределенность, вы должны разделить компонент неопределенности на квадратный корень из трех.
С другой стороны, вы можете найти данные в руководстве, документе конференции или журнальной статье, которые обычно распространяются или уже преобразованы в стандартную неопределенность.
Не предполагайте, что все данные типа B имеют прямоугольную форму, вы преувеличите свои оценки неопределенности. Ищите подсказки, которые помогут вам найти правильный метод для его оценки.
Например, представьте, что вы проводите исследование и наткнулись на статью, опубликованную в журнале NIST Journal of Research . В найденном вами исследовании содержится информация, относящаяся к процессу измерения, неопределенность которого вы оцениваете.
Итак, вы решили включить некоторую информацию в свой бюджет неопределенности.
Изображение ниже представляет собой отрывок из статьи Теда Дойрона о неопределенности и калибровке размеров , опубликованной в журнале исследований NIST. Он содержит данные об упругой деформации измерительных блоков, откалиброванные путем механического сравнения, которые вы хотите включить в свой бюджет неопределенности.
Обратите внимание, что в документе указано, что данные представлены как стандартная неопределенность, где k = 1.
Предполагая, что данные имеют нормальное распределение и коэффициент охвата, равный единице, используйте приведенное ниже уравнение для оценки неопределенности типа B.
Следовательно, ваша оценка неопределенности типа B должна составлять приблизительно 2 микрометра, поскольку ваш коэффициент охвата (k) равен единице.
Разница между неопределенностью типа A и типа B
Существует много дезинформации о неопределенности типа A и типа B.
Определения VIM являются наиболее точными. Неопределенность типа А оценивается с использованием статистических средств. Неопределенность типа B оценивается не только с помощью статистических средств.
Все оценивается статистическими методами . Следовательно, разница заключается в том, как собираются данные, а не в том, как они оцениваются.
Неопределенность типа A собирается из серии наблюдений. Данные типа B собираются из других источников.
Хотя неопределенность типа B, обнаруженная в публикациях, могла быть получена в результате серии наблюдений, она не была собрана вами или вашим лабораторным персоналом.
Следовательно, вы не уверены, что данные были собраны в результате серии наблюдений.Кроме того, вы не знаете, как проводился эксперимент.
Экспериментальными результатами можно манипулировать, особенно если они выполняются группой, которая извлекает выгоду из результатов (например, производитель, спонсируемое агентство и т. Д.).
За прошедшие годы многие исследователей и лабораторий были уличены в манипулировании экспериментами для достижения результатов, которые приносят пользу им самим или их миссии. Итак, нужно быть осторожным.
Изображение ниже взято с сайта phdcomics.com.Мне это показали в аспирантуре, когда я освещал тему этики в исследованиях. Он изображает реалистичное манипулирование научным методом.
Как выбрать тип A или тип B
Многим людям трудно решить, относятся ли их данные к неопределенности типа A или типа B.
Однако это не должно быть сложным процессом. Фактически, я собираюсь показать вам простой двухэтапный процесс, который поможет вам каждый раз выбирать правильный тип неопределенности.
Все, что вам нужно сделать, это задать себе эти два вопроса;
Вопрос 1 : Собирали ли вы данные самостоятельно, тестируя и экспериментируя?
• Если да, переходите к вопросу 2.
• Если нет, выберите тип B.
Вопрос 2 : Ваши данные старше 1 года?
• Если да, выберите тип B
• Если нет, выберите тип A
Я даже сделал вам удобную блок-схему, которая поможет вам решить, относятся ли ваши данные к неопределенности типа A или типа B.
Подумайте об этом.Если вы сами собрали данные, то оцените их статистически. Следовательно, это данные типа А.
Однако, если вы провели эксперимент с повторяемостью 5 лет назад и все же хотите включить его в свой бюджет неопределенности, то это данные типа B.
Возраст данных важен. Следовательно, причина второго вопроса. Вам необходимо регулярно обновлять данные о неопределенности типа А.
Если он старше года, то, скорее всего, это данные типа B, и вам следует собрать больше данных в ближайшее время.
Есть несколько исключений. На протяжении многих лет я читал некоторые процедуры повторяемости, в которых рекомендовалось, чтобы данные за два года всегда регистрировались.
Однако процедура требовала, чтобы новые данные собирались каждый месяц, что означает, что записи испытаний включали 24 независимых события выборки. Таким образом, новые данные постоянно собирались и добавлялись в записи о повторяемости.
В этом случае я бы назвал это данными неопределенности типа А.
Не беспокойтесь о выборе типа неопределенности, используйте два вопроса, перечисленных выше, и свое здравое суждение. Это поможет вам принять правильное решение.
Заключение
Неопределенность типа A и неопределенность типа B — это две классификации, обычно используемые при анализе неопределенности. Обычно используются только в информационных целях, они позволяют другим узнать, как данные собираются и оцениваются.
Это руководство охватывает все, что вам нужно знать о неопределенностях типа A и B.Он должен помочь вам различать разницу между двумя типами неопределенности, чтобы вы могли выбрать подходящий метод оценки для анализа неопределенности.
Итак, используйте информацию и попробуйте некоторые из этих методов оценки. Они должны помочь вам улучшить вашу способность вычислять неопределенность.
Теперь оставьте комментарий ниже и расскажите, как вы выбираете неопределенность типа A и типа B.
.
Leave A Comment