Урок 13. Страничка для любознательных
№ 1
Условие:
В числе 608 содержится 6 сотен и 8 десятков.
Решение:
Неверно. 6 сотен и 8 единиц.
Советы:
Вспомни классы и разряды.
№ 2
Условие:
В одной тысяче содержится 10 сотен.
Решение:
Верно.
Советы:
Вспомни таблицу разрядов и классов.
№ 3
Условие:
98 : 4 = 23 (ост. 6).
Решение:
Неверно. 98 : 4 = 24 (ост. 2)
Советы:
Остаток всегда меньше делителя.
№ 4
Условие:
В частном чисел 864 и 9 будет две цифры.
Решение:
Верно.
Советы:
Вспомни деление на однозначное число.
№ 5
Условие:
36 • 0 + 638 : 1 = 638.
Решение:
Верно.
Советы:
Важен порядок действий.
№ 6
Условие:
Высказывание “Сумму чисел 45 и 5 увеличить в 3 раза” можно записать так: 45 + 5 • 3.
Решение:
Неверно. (45 + 5) • 3 = 150
Советы:
Сумма — это +.
№ 7
Условие:
Егор сказал: “За 7 тетрадей я заплатил 28 р., а за 3 ластика – 18 р. Значит, тетрадь дороже ластика”.
Решение:
Неверно.
28 : 7 = 4 (р.) – цена 1 тетради
18 : 3 = 6 (р.) – цена 1 ластика
Советы:
Чтобы найти цену, надо стоимость разделить на количество.
№ 8
Условие:
В выражении 70 – 27 : 9 + 9 • 6 порядок действий указан правильно.
Решение:
Верно.
Советы:
Деление, умножение слева направо.
№ 9
Условие:
Задача “Первая серия фильма продолжалась 40 мин, а последняя в 2 раза меньше. Сколько минут продолжалась последняя серия фильма?” решается сложением.
Решение:
Неверно. Делением: 40 : 2 = 20 (мин)
Советы:
Меньше в — :.
№ 10
Условие:
Фигуры
отличаются друг от друга числом углов.
Решение:
Верно.
Советы:
Это четырехугольник и пятиугольник.
№ 11
Условие:
Если периметр прямоугольника равен 24 см, то длина одной из его сторон может быть равна 14 см.
Решение:
Неверно. Если одна из сторон прямоугольника равна 14 см, то его периметр будет больше 28 см, т.к. у прямоугольника 2 стороны длиной 14 см и еще 2 стороны.
Советы:
Периметр — это сумма длин сторон фигуры.
№ 12
Условие:
Площадь прямоугольника со сторонами 18 см и 5 см можно вычитать так: 18 • 5.
Решение:
Верно.
Советы:
Площадь — это произведение смежных сторон.
4 класс. Моро. Учебник №1. Ответы к стр. 20
Числа от 1 до 1000
Странички для любознательных
Ответы к стр. 201. В числе 608 содержится 6 сотен и 8 десятков.
Неверно. 6 сотен и 8 единиц.
2. В одной тысяче содержится 10 сотен.
Верно.
3. 98 : 4 = 23 (ост. 6).
Неверно. 98 : 4 = 24 (ост. 2)
Верно.
5. 36 • 0 + 638 : 1 = 638.
Верно.
6. Высказывание «Сумму чисел 45 и 5 увеличить в 3 раза» можно записать так: 45 + 5 • 3.
Неверно. (45 + 5) • 3
7. Егор сказал: «За 7 тетрадей я заплатил 28 р., а за 3 ластика — 18 р. Значит, тетрадь дороже ластика».
Неверно.
28 : 7 = 4 (р.) — цена 1 тетради
18 : 3 = 6 (р.) — цена 1 ластика
3 1 4 2
8. В выражении 70 — 27 : 9 + 9 • 6 порядок действий указан правильно.
9. Задача «Первая серия фильма продолжалась 40 мин, а последняя в 2 раза меньше. Сколько минут продолжалась последняя серия фильма?» решается сложением.
Неверно. 40 : 2 = 20 (мин)
10. Фигуры отличаются друг от друга числом углов.
Верно.
11. Если периметр прямоугольника равен 24 см, то длина одной из его сторон может быть равна 14 см.
Неверно. Если одна сторона 14 см, а другая хотя бы 1 см, то периметр будет равен: (14 + 1) • 2 = 30 см, а по условию задачи он равен 24 см.
12. Площадь прямоугольника со сторонами 18 см и 5 см можно вычитать так: 18 • 5.
Верно.
ГДЗ по математике. Учебник. 4 класс. Часть 1. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.
Математика. 4 класс
4 класс. Моро. Учебник №1. Ответы к стр. 20
4.2 (83.83%) от 47 голосующихРешение столбиком сложение и вычитание. Как правильно объяснить ребёнку деление в столбик
Деление столбиком или, правильнее сказать, письменный прием деления уголком, школьники проходят уже в третьем классе начальной школы, но зачастую этой теме уделяется так мало внимания, что к 9-11 классу не все ученики могут им свободно пользоваться. Деление столбиком на двузначное число проходят в 4 классе, как и деление на трехзначное число, а далее этот прием используется только как вспомогательный при решении каких-либо уравнений или нахождении значения выражения.
Очевидно, что уделив делению столбиком больше внимания, чем заложено в школьной программе, ребенок облегчит себе выполнение заданий по математике вплоть до 11 класса. А для этого нужно немногое — понять тему и позаниматься, порешать, держа алгоритм в голове, довести навык вычисления до автоматизма.
Алгоритм деления столбиком на двузначное число
Как и при делении на однозначное число, будем последовательно переходить от деления более крупных счетных единиц к делению более мелких единиц.
1. Находим первое неполное делимое . Это число, которое делится на делитель с получением числа больше или равного 1. Это значит, что первое неполное делимое всегда больше делителя. При делении на двузначное число в первом неполном делимом минимум 2 знака.
Примеры 76
8:24. Первое неполное делимое 76
265
:53 26 меньше 53, значит не подходит. Нужно добавить следующую цифру (5). Первое неполное делимое 265.
2. Определяем количество цифр в частном . Для определения числа цифр в частном следует помнить, что неполному делимому соответствует одна цифра частного, а всем остальным цифрам делимого — еще по одной цифре частного.
Примеры 768:24. Первое неполное делимое 76. Ему соответствует 1 цифра частного. После первого неполного делителя есть еще одна цифра. Значит в частном будет всего 2 цифры.
265:53. Первое неполное делимое 265. Оно даст 1 цифру частного. Больше в делимом цифр нет. Значит в частном будет всего 1 цифра.
15344:56. Первое неполное делимое 153, а после него еще 2 цифры. Значит в частном будет всего 3 цифры.
3. Находим цифры в каждом разряде частного . Сначала найдем первую цифру частного. Подбираем такое целое число, чтобы при умножении его на наш делитель получилось число, максимально приближенное к первому неполному делимому. Цифру частного записываем под уголок, а значение произведения вычитаем столбиком из неполного делителя. Записываем остаток. Проверяем, что он меньше делителя.
Затем находим вторую цифру частного. Переписываем в строку с остатком цифру, следующую за первым неполным делителем в делимом. Полученное неполное делимое снова делим на делитель и так находим каждое последующее число частного, пока не закончатся цифры делителя.
4. Находим остаток (если есть).
Если цифры частного закончились и получился остаток 0, то деление выполнено без остатка. В ином случае значение частного записывается с остатком.
Так же выполняется деление на любое многозначное число (трехзначное, четырехзначное и т.
Разбор примеров на деление столбиком на двузначное число
Сначала рассмотрим простые случаи деления, когда в частном получается однозначное число.
Найдем значение частного чисел 265 и 53.
Первое неполное делимое 265. Больше в делимом цифр нет. Значит в частном будет однозначное число.
Чтобы было легче подобрать цифру частного, разделим 265 не на 53, а на близкое круглое число 50. Для этого 265 разделим на 10, будет 26 (остаток 5). И 26 разделим на 5, будет 5 (остаток 1). Цифру 5 нельзя сразу записывать в частном, поскольку это пробная цифра. Сначала нужно проверить, подойдет ли она. Умножим 53*5=265. Мы видим, что цифра 5 подошла. И теперь можем ее записать в частном под уголок. 265-265=0. Деление выполнено без остатка.
Значение частного чисел 265 и 53 равно 5.
Иногда при делении пробная цифра частного не подходит, и тогда ее нужно менять.
Найдем значение частного чисел 184 и 23.
В частном будет однозначное число.
Чтобы было легче подобрать цифру частного, разделим 184 не на 23, а на 20. Для этого разделим 184 на 10, будет 18 (остаток 4). И 18 разделим на 2, будет 9. 9 – это пробная цифра, мы ее сразу писать в частном не будем, а проверим, подойдет ли она. Умножим 23*9=207. 207 больше, чем 184. Мы видим, что цифра 9 не подходит. В частном будет меньше 9. Попробуем, подойдет ли цифра 8. Умножим 23*8=184. Мы видим, что цифра 8 подходит. Можем ее записать в частном. 184-184=0. Деление выполнено без остатка.
Значение частного чисел 184 и 23 равно 8.
Рассмотрим более сложные случаи деления.
Найдем значение частного чисел 768 и 24.
Первое неполное делимое – 76 десятков. Значит, в частном будут 2 цифры.
Определим первую цифру частного. Разделим 76 на 24. Чтобы легче было подобрать цифру частного, разделим 76 не на 24, а на 20. То есть нужно 76 разделить на 10, будет 7 (остаток 6). И 7 разделим на 2, получится 3 (остаток 1). 3 – это пробная цифра частного. Сначала проверим, подойдет ли она. Умножим 24*3=72 . 76-72=4. Остаток меньше делителя. Значит, цифра 3 подошла и теперь мы ее можем записать на месте десятков частного. 72 пишем под первым неполным делимым, между ними ставим знак минус, под чертой записываем остаток.
И 7 разделим на 2, получится 3 (остаток 1). 3 – это пробная цифра частного. Сначала проверим, подойдет ли она. Умножим 24*3=72 . 76-72=4. Остаток меньше делителя. Значит, цифра 3 подошла и теперь мы ее можем записать на месте десятков частного. 72 пишем под первым неполным делимым, между ними ставим знак минус, под чертой записываем остаток.
Продолжим деление. Перепишем в строку с остатком цифру 8, следующую за первым неполным делимым. Получим следующее неполное делимое – 48 единиц. Разделим 48 на 24. Чтобы было легче подобрать цифру частного, разделим 48 не на 24, а на 20. То есть разделим 48 на 10, будет 4 (остаток 8). И 4 разделим на 2, будет 2. Это пробная цифра частного. Мы должны сначала проверить, подойдет ли она. Умножим 24*2=48. Мы видим, что цифра 2 подошла и, значит, можем ее записать на месте единиц частного. 48-48=0, деление выполнено без остатка.
Значение частного чисел 768 и 24 равно 32.
Найдем значение частного чисел 15344 и 56.
Первое неполное делимое – 153 сотни, значит, в частном будут три цифры.
Определим первую цифру частного. Разделим 153 на 56. Чтобы легче было подобрать цифру частного, разделим 153 не на 56, а на 50. Для этого разделим 153 на 10, будет 15 (остаток 3). И 15 разделим на 5, будет 3. 3 – это пробная цифра частного. Помните: ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 56*3=168. 168 больше, чем 153. Значит, в частном будет меньше, чем 3. Проверим, подойдет ли цифра 2. Умножим 56*2=112. 153-112=41. Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.
Образуем следующее неполное делимое. 153-112=41. Переписываем в ту же строку цифру 4, следующую за первым неполным делимым. Получаем второе неполное делимое 414 десятков. Разделим 414 на 56. Чтобы удобнее было подобрать цифру частного, разделим 414 не на 56, а на 50. 414:10=41(ост.4). 41:5=8(ост.1). Помните: 8 – это пробная цифра. Проверим ее. 56*8=448. 448 больше, чем 414, значит, в частном будет меньше, чем 8. Проверим, подойдет ли цифра 7. Умножим 56 на 7, получится 392. 414-392=22. Остаток меньше делителя. Значит, цифра подошла и в частном на месте десятков можем записать 7.
Проверим ее. 56*8=448. 448 больше, чем 414, значит, в частном будет меньше, чем 8. Проверим, подойдет ли цифра 7. Умножим 56 на 7, получится 392. 414-392=22. Остаток меньше делителя. Значит, цифра подошла и в частном на месте десятков можем записать 7.
Пишем в строку с новым остатком 4 единицы. Значит следующее неполное делимое – 224 единицы. Продолжим деление. Разделим 224 на 56. Чтобы легче было подобрать цифру частного, разделим 224 на 50. То есть сначала на 10, будет 22 (остаток 4). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 224-224=0, деление выполнено без остатка.
Значение частного чисел 15344 и 56 равно 274.
Пример на деление с остатком
Чтобы провести аналогию, возьмем пример, похожий на пример выше, и отличающийся лишь последней цифрой
Найдем значение частного чисел 15345:56
Делим сначала точно так же, как в примере 15344:56, пока не дойдем до последнего неполного делимого 225. Разделим 225 на 56. Чтобы легче было подобрать цифру частного, разделим 225 на 50. То есть сначала на 10, будет 22 (остаток 5). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 225-224=1, деление выполнено с остатком.
Значение частного чисел 15345 и 56 равно 274 (остаток 1).
Деление с нулем в частном
Иногда в частном одним из чисел получается 0, и дети зачастую пропускают его, отсюда неправильное решение. Разберем, откуда может взяться 0 и как его не забыть.
Найдем значение частного чисел 2870:14
Первое неполное делимое — 28 сотен. Значит в частном будет 3 цифры. Ставим под уголок три точки. Это важный момент. Если ребенок потеряет ноль, останется лишняя точка, которая заставит задуматься, что где-то упущена цифра.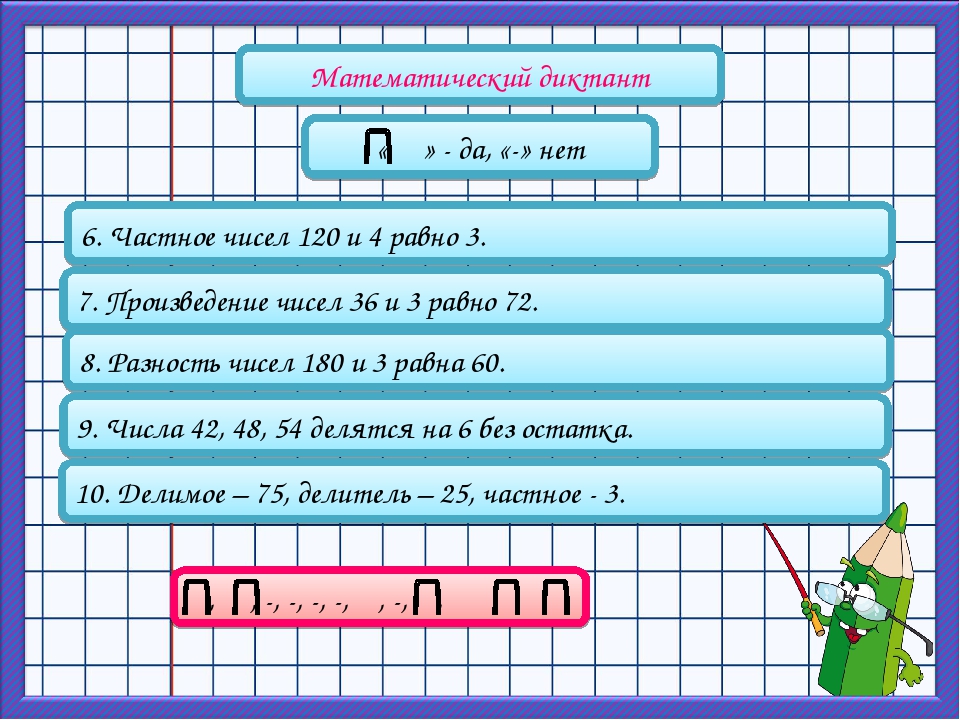
Определим первую цифру частного. Разделим 28 на 14. Подбором получается 2. Проверим, подойдет ли цифра 2. Умножим 14*2=28. Цифра 2 подходит, ее можно записать на месте сотен в частном. 28-28=0.
Получился нулевой остаток. Мы обозначили его розовым для наглядности, но записывать его не нужно. Переписываем в строку с остатком цифру 7 из делимого. Но 7 не делится на 14 с получением целого числа, поэтому записываем на месте десятков в частном 0.
Теперь переписываем в ту же строку последнюю цифру делимого (количество единиц).
70:14=5 Записываем вместо последней точки в частном цифру 5. 70-70=0. Остатка нет.
Значение частного чисел 2870 и 14 равно 205.
Деление нужно непременно проверить умножением.
Примеры на деление для самопроверки
Найдите первое неполное делимое и определите количество цифр в частном.
3432:66 2450:98 15145:65 18354:42 17323:17
Усвоили тему, а теперь потренируйтесь решить несколько примеров столбиком самостоятельно.
1428: 42 30296: 56 254415: 35 16514: 718
Удобно проводить особым методом, который получил название вычитание столбиком или вычитание в столбик . Этот способ вычитания оправдывает свое название, так как уменьшаемое, вычитаемое и разность записываются в столбик. Промежуточные вычисления также проводятся в столбиках, соответствующих разрядам чисел.
Удобство вычитания натуральных чисел столбиком заключается в простоте вычислений. Вычисления сводятся к использованию таблицы сложения и применению свойств вычитания.
Давайте разберемся, как выполняется вычитание столбиком. Процесс вычитания будем рассматривать вместе с решением примеров. Так будет понятнее.
Навигация по странице.
Что необходимо знать для вычитания столбиком?
Для вычитания натуральных чисел столбиком необходимо знать, во-первых, как выполняется вычитание с помощью таблицы сложения .
Наконец, не помешает повторить определение разряда натуральных чисел .
Вычитание столбиком на примерах.
Начнем с записи. Сначала записывается уменьшаемое. Под уменьшаемым располагается вычитаемое. Причем делается это так, что цифры оказываются одна под другой, начиная справа. Слева от записанных чисел ставится знак минус, а внизу проводится горизонтальная линия, под которой будет записан результат после проведения необходимых действий.
Приведем несколько примеров правильных записей при вычитании столбиком. Запишем в столбик разность 56−9 , разность 3 004−1 670 , а так же 203 604 500−56 777 .
Итак, с записью разобрались.
Переходим к описанию процесса вычитания столбиком. Его суть заключается в последовательном вычитании значений соответствующих разрядов. Сначала вычитаются значения разряда единиц, далее – значения разряда десятков, далее – значения разряда сотен и т.д. Результаты записываются под горизонтальной линией на соответствующих местах. Число, которое образуется под линией после завершения процесса, является искомым результатом вычитания двух исходных натуральных чисел.
Представим схему, иллюстрирующую процесс вычитания столбиком натуральных чисел.
Приведенная схема дает общую картину вычитания натуральных чисел столбиком, однако она не отражает всех тонкостей. С этими тонкостями разберемся при решении примеров. Начнем с самых простых случаев, а дальше будем постепенно продвигаться к более сложным случаям, пока не разберемся со всеми нюансами, которые могут встретиться при вычитании столбиком.
Пример.
Для начала вычтем столбиком из числа 74 805 число 24 003 .
Решение.
Запишем эти числа так, как этого требует метод вычитания столбиком:
Начинаем с вычитания значений разрядов единиц, то есть, вычитаем из числа 5 число 3 . Из таблицы сложения имеем 5−3=2 . Записываем полученные результат под горизонтальную черту в этом же столбике, в котором находятся числа 5 и 3 :
Теперь вычитаем значения разряда десятков (в нашем примере они равны нулю).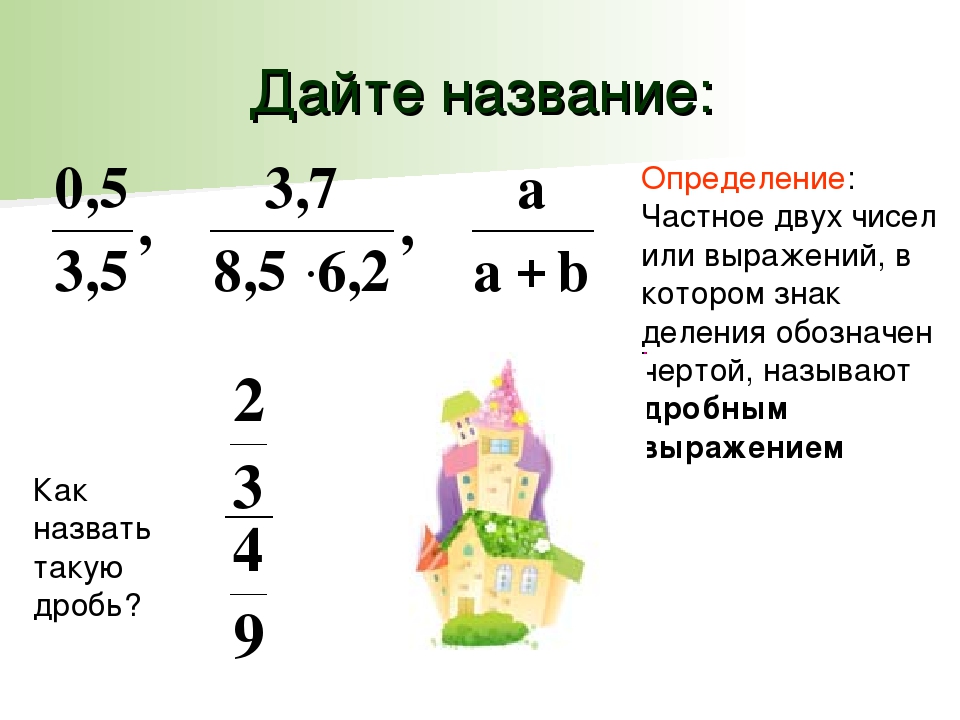 Имеем 0−0=0 (это свойство вычитания мы упоминали в предыдущем пункте). Записываем полученный нуль под линию в том же столбике:
Имеем 0−0=0 (это свойство вычитания мы упоминали в предыдущем пункте). Записываем полученный нуль под линию в том же столбике:
Идем дальше. Вычитаем значения разряда сотен: 8−0=8 (по свойству вычитания, озвученному в предыдущем пункте). Теперь наша запись примет следующий вид:
Переходим к вычитанию значений разряда тысяч: 4−4=0 (это свойств вычитания равных натуральных чисел). Имеем:
Осталось вычесть значения разряда десятков тысяч: 7−2=5 . Записываем полученное число под черту на нужное место:
На этом вычитание столбиком завершено. Число 50 802 , которое получилось внизу, является результатом вычитания исходных натуральных чисел 74 805 и 24 003 .
Рассмотрим следующий пример.
Пример.
Отнимем столбиком от числа 5 777 число 5 751 .
Решение.
Делаем все так же, как в предыдущем примере – вычитаем значения соответствующих разрядов. После завершения всех шагов запись примет следующий вид:
Под чертой получили число, в записи которого слева находятся цифры 0 . Если эти цифры 0 отбросить, то получим результат вычитания исходных натуральных чисел. В нашем случае отбрасываем две цифры 0 , получившиеся слева. Имеем: разность 5 777−5 751 равна 26 .
До этого момента мы вычитали натуральные числа, записи которых состоят из одинакового количества знаков. Сейчас на примере разберемся, как вычитаются столбиком натуральные числа, когда в записи уменьшаемого больше знаков, чем в записи вычитаемого.
Пример.
Вычтем из числа 502 864 число 2 330 .
Решение.
Записываем уменьшаемое и вычитаемое в столбик:
По очереди вычитаем значения разряда единиц: 4−0=4 ; далее – десятков: 6−3=3 ; далее – сотен: 8−3=5 ; далее – тысяч: 2−2=0 . Получаем:
Теперь, чтобы завершить вычитание столбиком, нам еще нужно вычесть значения разряда десятков тысяч, а дальше – значения разряда сотен тысяч. Но из значений этих разрядов (в нашем примере из чисел 0 и 5 ) нам вычитать нечего (так как вычитаемое число 2 330 не имеет цифр в этих разрядах). Как же быть? Очень просто – значения этих разрядов просто переписываются под горизонтальную линию:
Но из значений этих разрядов (в нашем примере из чисел 0 и 5 ) нам вычитать нечего (так как вычитаемое число 2 330 не имеет цифр в этих разрядах). Как же быть? Очень просто – значения этих разрядов просто переписываются под горизонтальную линию:
На этом вычитание столбиком натуральных чисел 502 864 и 2 330 завершено. Разность равна 500 534 .
Осталось рассмотреть случаи, когда на некотором шаге вычитания столбиком значение разряда уменьшаемого числа меньше, чем значение соответствующего разряда вычитаемого. В этих случаях приходится «занимать» из старших разрядов. Давайте разберемся с этим на примерах.
Пример.
Вычтем столбиком из числа 534 число 71 .
Решение.
На первом шаге вычитаем из 4 число 1 , получаем 3 . Имеем:
На следующем шаге нам нужно вычитать значения разряда десятков, то есть, из числа 3 нужно вычесть число 7 . Так как 3, то мы не можем выполнить вычитание этих натуральных чисел (вычитание натуральных чисел определяется лишь когда вычитаемое не больше, чем уменьшаемое). Что же делать? В этом случае мы берем 1 единицу из старшего разряда и «размениваем» ее. В нашем примере «размениваем» 1 сотню на 10 десятков. Чтобы наглядно отразить наши действия, поставим жирную точку над числом в разряде сотен, а над числом в разряде десятков запишем число 10 , используя другой цвет. Запись примет следующий вид:
Прибавляем полученные после «размена» 10 десятков к 3 имеющимся десяткам: 3+10=13 , и из этого числа вычитаем 7 . Имеем 13−7=6 . Это число 6 записываем под горизонтальной чертой на свое место:
Переходим к вычитанию значений разряда сотен. Здесь мы видим над числом 5 точку, которая означает, что из этого числа мы брали единицу «на размен». То есть, сейчас мы имеем не 5 , а 5−1=4 . От числа 4 больше ничего отнимать не нужно (так как исходное вычитаемое число 71 не содержит цифр в разряде сотен). Таким образом, под горизонтальную черту записываем число 4 :
От числа 4 больше ничего отнимать не нужно (так как исходное вычитаемое число 71 не содержит цифр в разряде сотен). Таким образом, под горизонтальную черту записываем число 4 :
Итак, разность 534−71 равна 463 .
Иногда при вычитании столбиком «разменивать» единицы из старших разрядов приходится несколько раз. В подтверждение этих слов разберем решение следующего примера.
Пример.
Отнимем от натурального числа 1 632 число 947 столбиком.
Решение.
На первом же шаге нам нужно вычесть из числа 2 число 7 . Так как 2,то сразу приходится «разменивать» 1 десяток на 10 единиц. После этого из суммы 10+2 вычитаем число 7 , получаем (10+2)−7=12−7=5
:
На следующем шаге нам нужно вычесть значения разряда десятков. Мы видим, что над числом 3 стоит точка, то есть, мы имеем не 3 , а 3−1=2 . И от этого числа 2 нам нужно отнять число 4 . Так как 2, то опять приходится прибегать к «размену». Но сейчас уже размениваем 1 сотню на 10 десятков. При этом имеем (10+2)−4=12−4=8
:
Теперь вычитаем значения разряда сотен. Из числа 6 была занята единица на предыдущем шаге, поэтому имеем 6−1=5 . От этого числа нам нужно отнять число 9 . Так как 5, то нам нужно «разменять» 1 тысячу на 10 сотен. Получаем (10+5)−9=15−9=6
:
Остался последний шаг. Из единицы в разряде тысяч мы занимали на предыдущем шаге, поэтому имеем 1−1=0 . От полученного числа нам ничего больше отнимать не нужно. Это число и записываем под горизонтальную черту:
Калькулятор в столбик для Андроид устройств станет замечательным помощником для современных школьников. Программа не только дает правильный ответ на математическое действие, но и наглядно демонстрирует его пошаговое решение. Если же вам нужны более сложные калькуляторы – можете посмотреть или же продвинутый инженерный калькулятор.
Особенности
Главной особенностью программы является уникальность расчета математических операций. Отображение процесса вычислений столбиком дает возможность школьникам более подробно с ним ознакомиться, понять алгоритм решения, а не просто получить готовый результат и переписать его в тетрадь. Эта особенность имеет огромное преимущество перед другими калькуляторами, т.к. достаточно часто в школе учителя требуют расписать промежуточные вычисления, чтобы удостовериться, что школьник производит их в уме и действительно понимает алгоритм решения задач. Кстати, у нас есть еще одна программа похожего рода – .
Чтобы начать пользоваться программой, необходимо скачать калькулятор в столбик на Андроид. Сделать это можно на нашем сайте абсолютно бесплатно без дополнительных регистраций и смс. После установки откроется главная страница в виде тетрадного листа в клетку, на котором, собственно, и будут отображаться результаты вычислений и их подробное решение. Внизу располагается панель с кнопками:
- Цифры.
- Знаки арифметических действий.
- Удаление раннее введенных символов.
Ввод осуществляется по тому же принципу, что и на . Все отличие состоит только в интерфейсе приложения – все математические вычисления и их результат отображаются в виртуальной ученической тетради.
Приложение позволяет быстро и правильно выполнить стандартные для школьника математические вычисления столбиком:
- умножение;
- деление;
- сложение;
- вычитание.
Приятным дополнением в приложении является функция ежедневного напоминания о домашнем задании по математике. Хотите – делайте домашки. Для ее включения следует зайти в настройки (нажать кнопку в виде шестеренки) и установить галочку о напоминании.
Достоинства и недостатки
- Помогает школьнику не просто быстро получить правильный результат математических вычислений, но и понять сам принцип расчета.
- Очень простой, интуитивно понятный интерфейс для каждого пользователя.

- Установить приложение можно даже на самое бюджетное Андроид устройство с операционной системой 2.2 и более поздней версией.
- Калькулятор сохраняет историю проведенных математических вычислений, которую можно в любой момент очистить.
Калькулятор ограничен в математических операциях, поэтому применить его для сложных расчетов, с какими мог бы справиться инженерный калькулятор, не получится. Однако учитывая назначение самого приложения – наглядно продемонстрировать учащимся младшей школы принцип расчета в столбик, считать это недостатком не стоит.
Приложение также станет отличным помощником не только для школьников, но и для родителей, которые желают заинтересовать своего ребенка математикой и научить его правильно и последовательно производить вычисления. Если Вы уже пользовались приложением Калькулятор в столбик, оставьте свои впечатления ниже в комментариях.
Научить ребенка делению столбиком просто. Необходимо объяснить алгоритм этого действия и закрепить пройденный материал.
- Согласно школьной программе, деление столбиком детям начинают объяснять уже в третьем классе. Ученики, которые схватывают все «на лету», быстро понимают эту тему
- Но, если ребенок заболел и пропустил уроки математики, или он не понял тему, тогда родители должны самостоятельно малышу объяснить материал. Нужно максимально доступно донести до него информацию
- Мамы и папы во время учебного процесса ребенка должны быть терпеливыми, проявляя такт по отношению к своему чаду. Ни в коем случае нельзя кричать на ребенка, если у него что-то не получается, ведь так можно отбить у него всю охоту к занятиям
Важно: Чтобы ребенок понял деление чисел, он должен досконально знать таблицу умножения. Если малыш плохо знает умножение, он не поймет деление.
Во время домашних дополнительных занятий можно пользоваться шпаргалками, но ребенок должен выучить таблицу умножения, прежде чем, приступать к теме «Деление».
Итак, как объяснить ребенку деление столбиком :
- Постарайтесь сначала объяснить на маленьких цифрах. Возьмите счетные палочки, например, 8 штук
- Спросите у ребенка, сколько пар в этом ряду палочек? Правильно — 4. Значит, если разделить 8 на 2, получится 4, а при делении 8 на 4 получится 2
- Пусть ребенок сам разделит другое число, например, более сложное: 24:4
- Когда малыш освоил деление простых чисел, тогда можно переходить к делению трехзначных чисел на однозначные
Деление всегда дается детям немного сложнее, чем умножение. Но усердные дополнительные занятия дома помогут малышу понять алгоритм этого действия и не отставать от сверстников в школе.
Начинайте с простого — деление на однозначное число:
Важно: Просчитайте в уме, чтобы деление получилось без остатка, иначе ребенок может запутаться.
Например, 256 разделить на 4:
- Начертите на листе бумаги вертикальную линию и разделите ее с правой части пополам. Слева напишите первую цифру, а справа над чертой вторую
- Спросите у малыша, сколько четверок помещается в двойке — нисколько
- Тогда берем 25. Для наглядности отделите это число сверху уголком. Опять спросите у ребенка, сколько помещается четверок в двадцати пяти? Правильно — шесть. Пишем цифру «6» в правом нижнем углу под линией. Ребенок должен использовать таблицу умножения для правильного ответа
- Запишите под 25 цифру 24, и подчеркните, чтобы записать ответ — 1
- Опять спрашивайте: в единице сколько помещается четверок — нисколько. Тогда сносим к единице цифру «6»
- Получилось 16 — сколько четверок помещается в этом числе? Правильно — 4. Записываем «4» рядом с «6» в ответе
- Под 16 записываем 16, подчеркиваем и получается «0», значит мы разделили правильно и ответ получился «64»
Письменное деление на двузначное число
Когда ребенок освоил деление на однозначное число, можно двигаться дальше. Письменное деление на двузначное число чуть сложнее, но если малыш поймет, как производится это действие, тогда ему не составит труда решать такие примеры.
Письменное деление на двузначное число чуть сложнее, но если малыш поймет, как производится это действие, тогда ему не составит труда решать такие примеры.
Важно: Снова начинайте объяснять с простых действий. Ребенок научится правильно подбирать цифры и ему будет легко делить сложные числа.
Выполните вместе такое простое действие: 184:23 — как нужно объяснять:
- Разделим сначала 184 на 20, получается примерно 8. Но мы не пишем цифру 8 в ответ, так как это пробная цифра
- Проверяем, подходит 8 или нет. Умножаем 8 на 23, получается 184 — это именно то число, которое у нас стоит в делителе. Ответ будет 8
Важно: Чтобы ребенок понял, попробуйте вместо восьмерки взять 9, пусть он умножит 9 на 23, получается 207 — это больше, чем у нас в делителе. Цифра 9 нам не подходит.
Так постепенно малыш поймет деление, и ему будет легко делить более сложные числа:
- Разделим 768 на 24. Определите первую цифру частного — делим 76 не на 24, а на 20, получается 3. Записываем 3 в ответ под чертой справа
- Под 76 записываем 72 и проводим линию, записываем разность — получилось 4. Эта цифра делится на 24? Нет — сносим 8, получается 48
- Цифра 48 делится на 24? Правильно — да. Получается 2, записываем эту цифру в ответ
- Получилось 32. Теперь можно проверить — правильно ли мы выполнили действие деления. Сделайте умножение в столбик: 24х32, получается 768, значит все правильно
Если ребенок научился выполнять деление на двузначное число, тогда необходимо перейти к следующей теме. Алгоритм деления на трехзначное число такой же, как и алгоритм деления на двузначное число.
Например:
- Разделим 146064 на 716. Берем сначала 146 — спросите у ребенка делится это число на 716 или нет. Правильно — нет, тогда берем 1460
- Сколько раз число 716 поместится в числе 1460? Правильно — 2, значит пишем эту цифру в ответе
- Умножаем 2 на 716, получается 1432.
 Записываем эту цифру под 1460. Получается разность 28, записываем под чертой
Записываем эту цифру под 1460. Получается разность 28, записываем под чертой - Сносим 6. Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2. Сносим еще цифру 4
- Делим 2864 на 716. Берем по 3 — мало, по 5 — много, значит получается 4. Умножаем 4 на 716, получается 2864
- Запишите 2864 под 2864, получается в разности 0. Ответ 204
Важно: Для проверки правильности выполнения деления, умножьте вместе с ребенком в столбик — 204х716=146064. Деление выполнено правильно.
Пришло время ребенку объяснить, что деление может быть не только нацело, но и с остатком. Остаток всегда меньше делителя или равен ему.
Деление с остатком следует объяснять на простом примере: 35:8=4 (остаток 3):
- Сколько восьмерок помещается в 35? Правильно — 4. Остается 3
- Делится эта цифра на 8? Правильно — нет. Получается, остаток 3
После этого ребенок должен узнать, что можно продолжать деление, дописывая 0 к цифре 3:
- В ответе стоит цифра 4. После нее пишем запятую, так как добавление нуля говорит о том, что число будет с дробью
- Получилось 30. Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
- Сносим к цифре 6 цифру 0. Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4
- К цифре 4 дописываем 0 и делим на 8, получается 5 — записываем в ответ
- Вычитаем 40 из 40, получается 0. Итак, ответ: 35:8=4,375
Совет: Если ребенок что-то не понял — не злитесь. Пусть пройдет пару дней и снова постарайтесь объяснить материал.
Уроки математики в школе также будут закреплять знания. Пройдет время и малыш будет быстро и легко решать любые примеры на деление.
Алгоритм деления чисел заключается в следующем:
- Сделать прикидку числа, которое будет стоять в ответе
- Найти первое неполное делимое
- Определить число цифр в частном
- Найти цифры в каждом разряде частного
- Найти остаток (если он есть)
По такому алгоритму выполняется деление как на однозначные числа, так и на любое многозначное число (двузначное, трехзначное, четырехзначное и так далее).
Занимаясь с ребенком, чаще ему задавайте примеры на выполнение прикидки. Он должен быстро в уме подсчитать ответ. Например:
- 1428:42
- 2924:68
- 30296:56
- 136576:64
- 16514:718
Для закрепления результата можно использовать такие игры на деление:
- «Головоломка». Напишите на листе бумаги пять примеров. Только один из них должен быть с правильным ответом.
Условие для ребенка: Среди нескольких примеров, только один решен правильно. Найди его за минуту.
Видео: Игра арифметика для детей сложение вычитание деление умножение
Видео: Развивающий мультфильм Математика Изучение наизусть таблицы умножения и деления на 2
Как вычитать столбиком
Вычитание многозначных чисел обычно выполняют столбиком, записывая числа друг под другом (уменьшаемое сверху, вычитаемое снизу) так, чтобы цифры одинаковых разрядов стояли друг под другом (единицы под единицами, десятки под десятками и т. д.). Слева между числами ставится знак действия. Под вычитаемым проводят черту. Вычисление начинают с разряда единиц: из единиц вычитают единицы, затем из десятков — десятки и т. д. Результат вычитания записывают под чертой:
Рассмотрим пример, когда в каком-либо разряде цифра уменьшаемого меньше цифры вычитаемого:
От 2 мы не можем отнять 9, что нам делать в этом случае? В разряде единиц у нас нехватка, но в разряде десятков у уменьшаемого аж 7 десятков, поэтому мы можем один из этих десятков перекинуть в разряд единиц:
В разряде единиц у нас было 2, мы перекинули десяток, стало 12 единиц. Теперь мы легко можем от 12 отнять 9. Записываем под чертой в разряде единиц 3. В разряде десятков у нас было 7 единиц, одну из них мы перекинули в простые единицы, осталось 6 десятков. Записываем под чертой в разряде десятков 6. В результате мы получили число 63:
Вычитание столбиком обычно не записывают так подробно, вместо этого, над цифрой разряда, у которого будет занята единица, ставят точку, чтобы не запоминать, у какого разряда надо будет дополнительно вычесть единицу:
При этом говорят так: из 2 вычесть 9 нельзя, занимаем единицу, из 12 вычитаем 9 — получим 3, пишем 3, в разряде десятков у нас было 7 единиц, мы одну перекинули, осталось 6, пишем 6 .
Теперь рассмотрим вычитание столбиком из чисел, содержащих нули:
Начинаем вычитать. От 7 отнимаем 3, пишем 4. От нуля мы не можем отнять 5, поэтому мы вынуждены занять единицу в старшем разряде, но в старшем разряде у нас тоже 0, поэтому и для этого разряда мы вынуждены занять в более старшем разряде. Занимаем единицу из разряда тысяч, получаем 10 сотен:
Одну из единиц разряда сотен мы занимаем в младший разряд, получаем 10 десятков. Из 10 вычитаем 5, пишем 5:
В разряде сотен у нас осталось 9 единиц поэтому, от 9 отнимаем 6, пишем 3. В разряде тысяч у нас была единица, но мы её потратили на младшие разряды, поэтому здесь остаётся нуль (его записывать не надо). В результате мы получили число 354:
Такая подробная запись решения была приведена, чтобы было проще понять, как выполняется вычитание столбиком из чисел содержащих нули. Как уже упоминалось, на практике решение обычно записывается так:
А все упомянутые действия выполняются в уме. Чтобы было легче выполнять вычитание, запомните простое правило:
Если при вычитании столбиком над нулём стоит точка, нуль превращается в 9.
Калькулятор вычитания столбиком
Данный калькулятор поможет вам выполнить вычитание чисел столбиком. Просто введите уменьшаемое и вычитаемое и нажмите кнопку Вычислить.
Внеклассное занятие «День птиц» — коррекционная школа, мероприятия
Тема урока: «Деление трёхзначного числа на однозначное».
Цель урока: Создание условий для усвоения алгоритма деления трёхзначного числа на однозначное через различные виды деятельности учащихся.
Задачи урока.
Образовательные:
— расширение понятийной базы за счёт включения в неё новых элементов; освоение алгоритма деления трёхзначного числа на однозначное; умение
вычислять частное; совершенствование вычислительных навыков, навыков устного счёта; совершенствование умения работать в коллективе, в
паре и самостоятельно.
Развивающие:
— развитие наблюдательности, внимания, памяти, логического мышления; активизация умственной деятельности; развитие коммуникативных умений.
Воспитательные:
— воспитание умения слушать, общаться, стремление сознательно соблюдать дисциплину; воспитание ответственности и добросовестного отношения к
работе, уважительных и доброжелательных отношений к товарищам; пропаганда здорового образа жизни
Формируемые УУД:
Регулятивные УУД:
— работать по предложенному плану, инструкции; выдвигать свои гипотезы на основе учебного материала; осуществлять самоконтроль.
Познавательные УУД:
— раскрывать значение понятия «частное», «произведение», «сумма», «разность» и использовать их в активном словаре;
— определять условия письменного деления трехзначного числа на однозначное без перехода через разряд и обосновывать свое мнение;
— -определять порядок письменного деления трехзначного числа на однозначное и обосновывать свое мнение;
Коммуникативные УУД:
— формулировать высказывание, используя математические термины, в рамках учебного диалога;
— согласовывать позиции и находить общее решение;
— адекватно использовать речевые средства для представления результата деятельности.
Личностные УУД: устанавливать связь между целью деятельности и её результатом; определять общие для всех правила поведения; уметь осознанно и внимательно читать задания; выражать способность к самооценке на основе критерия успешности учебной деятельности.
1.Самоопределение к деятельности. Мотивирование к учебной деятельности.
— Закройте глаза и представьте ту оценку, которую хотели бы получить на уроке, нарисуйте ее в воздухе перед собой.
— Очень захотите получить ее и приложите для этого все усилия.
— Я желаю вам удачи. Давайте вместе постараемся.
2. Актуализация и фиксирование индивидуального затруднения в пробном учебном действии. Создание ситуации успеха.
Актуализация и фиксирование индивидуального затруднения в пробном учебном действии. Создание ситуации успеха.
— Откройте тетради, запишите число и классная работа.
— На следующей строчке запишите последнюю цифру сегодняшнего числа. 9
— В следующей клетке запишите цифру, показывающую порядковый номер текущего дня.2
-Рядом запишите последнюю цифру предыдущего года.5
— Какое число у вас получилось? 925
— Что вы о нём можете сказать?
-Оно натуральное, некруглое, стоит на 925 месте в ряду натуральных чисел, ему предшествует число 924 за ним стоит число 926. Сумму цифр этого числа 16. Оно трехзначное. В нем 9 сотен, 2 десятка, 5 единиц.
Запишите самостоятельно другие трехзначные числа, используя эти цифры. Цифры в записи числа не должны повторяться.
— Какие числа у вас получились? взаимопроверка (+_)
925 952 529 592 295 259 — доска
— Что означает цифра 9 в подчеркнутых числах?
952 925 529 592 295 259
— В числе 952 – сотни,
в числе 295 – десятки,
в числе 529 – единицы.
— Отчего это зависит?
— От места, которое цифра занимает в записи числа
— Чем похожи все эти числа?
-Они трехзначные.
— Какие задания вы можете предложить для выполнения с трехзначными числами?
— Назвать числа в порядке убывания и возрастания, назвать последующие и предыдущие числа, сравнить, сложить, вычесть, представить в виде суммы разрядных слагаемых.
-Запишите в порядке возрастания
259 295 529 592 925 952
-Запишите 259 в виде суммы разрядных слагаемых
259 =200+50+9
925=900+20+5
Взаимопроверка
3.Постановка цели и задач урока. Мотивация учебной деятельности учащихся
Выполним вычисления по алгоритму, заданному блок-схемой. Расшифруйте слово
Расшифруйте слово
а
да нет
х 2 :5
Х
а | 200 | 250 | 90 | 50 | 100 | 400 | 300 |
х | 400 | 50 | 180 | 100 | 200 | 80 | 60 |
д | е | л | е | н | и | е |
х | 200 | 50 | 400 | 80 | 180 | 60 | 100 |
н | е | д | и | л | е | е |
-Какое слово у вас получилось?
-Кто догадался какая будет тема сегоднешнего урока?
-Какие цели мы поставим перед собой на уроке?
4. Построение проекта выхода из затруднения (цель и тема, способ, план, средство).
Доска
40:2 153:9 420:60
974:2 72:9 952:2
-На какие две группы можно разбить данные выражения?
(табличное и внетабличное деление)
40:2=20 974:2=487 (учитель)
72:9=8 153:9=17 (ребенок)
420:60=7 952:2=476 (ребенок)
5. Реализация построенного проекта.
Открываем учебник 2 части на странице 20 № 296 и прочитаем алгоритм решения примера 248 и 2 столбиком.
Алгоритм письменного деления трехзначного числа на однозначное
АЛГОРИТМ ПИСЬМЕННОГО ДЕЛЕНИЯ
Выделяем первое неполное делимое.
Определяем количество цифр в значении частного.
Подбираем первую цифру в значении частного.
Умножаем число, записанное этой цифрой, на делитель.
Вычитаем полученный результат из неполного делимого и находим остаток.
Убеждаемся , что остаток меньше делителя.
Записываем цифру следующего разряда делимого рядом с остатком.
Повторяем пункты 3, 4, 5, 6, 7.
6. Первичное закрепление
— Используя алгоритм, решим примеры, записав действия столбиком.
стр 21 девочки, мальчики
696:3=232 609:3=203
864:2=432 840:4=210
-А сейчас решаем примеры у доски
7. Самостоятельная работа с самопроверкой по эталону
1)А теперь решим примеры на стр. 25 № 302 на деление трёхзначных чисел, используя известный лгоритм,
92:4=23
575:5=113
847:7=121
-Проверили результаты примеров на доске.
8. Включение в систему знаний и повторений
— Где нам может пригодиться умение умножать трёхзначное число на однозначное?
Послушайте задачу.
За сезон одна пальма дала 128 литров кокосового сока, а вторая – в 2 раза меньше. Сколько всего литров сока собрали с двух пальм?
— О чем говорится в задаче?
— Прочитайте задачу еще раз, чтобы составить краткое условие.
— Что известно?
— Что запишем в краткое условие?
— Прочитай вопрос задачи.
— Можно ли сразу ответить на главный вопрос? Почему?
— А можно узнать? Как?
I п.- 128 л — ? л
II п. — ? л в 2 р. м.
— Сколько всего литров сока собрали с двух пальм?
— Нет. Мы не знаем, сколько литров сока дала вторая пальма.
Мы не знаем, сколько литров сока дала вторая пальма.
1) 128 : 2 = 64 (л) – со II пальмы
2) 128 + 64 = 291 (л)
Ответ: 291 л сока собрали с двух пальм.
Обсудите в паре решение и запишите в тетрадь.
2) Решение уравнения
859 – b = 124 : 4
— Проверьте решение по образцу
859 – b = 124 : 4
859 – b = 31
b = 859 – 31
b = 828
859 – 828 = 124 :4
31=31
Ответ: b = 828
9. Рефлексия деятельности
(итог урока) и домашнее задание
Самооценки
Чему сегодня научились? 9) 2)
– Что у вас получилось лучше всего?
– Что было интересного на уроке?
– Какое задание понравилось больше?
– Понравилось ли вам работать в группе? Почему?
– Как бы оценили своё настроение после урока?
(PDF) О кратности покрытия ориентированными многоугольниками
Ш К О Л А В « К В А Н Т Е » 27
Однако наши приключения только начи-
наются. Прежде всего стоит спросить, глубо-
ка ли и широка ли щель – та, которая
имеется под мирно спящем на столе телом.
Это зависит от механическах свойств и рель-
ефа поверхности соприкасающихся тел.
Когда мы кладем реальное шероховатое тело,
то сначала оно касается другого тела одной
точкой, потом, чуть повернувшись, второй,
затем, еще чуть повернувшись, третьей, а
еще чуть опускается, расширяя площади так
называемого истинного контакта вокруг этих
точек, причем итоговая суммарная площадь
всех контактных площадок должна быть
такой, чтобы материал выдерживал вес вер-
хнего тела. Заметим, что при соприкоснове-
нии могли возникнуть еще контактные обла-
сти, кроме первых трех. И что деформирова-
лись оба тела, причем распределение дефор-
маций зависело от характеристик шерохова-
тости и твердости обеих поверхностей.
Если мы кладем, например, стальной куб
с ребром 10см, масса которого примерно
8кг, а вес 80Н, на стальную поверхность,
то площадь истинного контакта при прочно-
сти материала 82
5 10 Н м
составит, как лег-
ко посчитать, 2
0,16 мм . Это ничтожно малая
доля – 16 миллионных! – от геометрической
площади контакта, которая составляет
2
10000 мм . Ситуация, когда площадь ис-
тинного контакта составляет малую долю
от геометрической, является для техники
постоянной и вездесущей. И она влечет мно-
жество разных проблем. Так, если через
контакт нужно передавать тепло или элект-
рический ток, им приходится протискивать-
ся через эти маленькие пятнышки. При пере-
даче тепла это влечет увеличение перепада
температур между деталями или, при фикси-
рованном перепаде температур, уменьшение
потока тепла. При протекании электричес-
кого тока маленькие контактные площадки
из-за высокой плотности тока в них перегре-
ваются, контакты могут свариваться, пла-
виться, даже испаряться. И это еще только
начало проблем. Например, именно поведе-
ние контактов определяет сухое трение и
химические процессы, идущие на контакте
твердых тел.
Но сейчас нас интересует щель под телом,
которое лежит на поверхности. Для твердых
материалов оная щель, как мы уже понима-
ем, занимает почти все пространство под
телом. Про мягкие тела поговорим чуть
позже, а сейчас вопрос: как у этой щели дела
с толщиной, пролезет ли туда молекула?
Оптические поверхности имеют идеальную
поверхность с точностью
, т.е. от
1/10 до 1/100 длины волны видимого света
– от 50 до 5нм. Это чудовищно мало: если
учесть, что при нормальном давлении рас-
стояние между молекулами в газе порядка
3нм, и привести в соприкосновение такие
поверхности, то в щели по ширине смогут
расположиться от 20 до 2 молекул. Однако
Однако
этого вполне достаточно для давления –
молекулы мечутся, как безумные, за секунду
сталкиваясь со стенками от 6 до 60 миллиар-
дов раз, и благополучно передают им им-
пульс. Попутно заметим, что в некотором
смысле (например, для движения вдоль
щели) они ведут себя, как при «высоком
вакууме» – сталкиваются в основном со
стенками, а не друг с другом.
Кстати, когда в книгах заводят речь о
диффузии в твердых телах, рассказ начина-
ют с того, что исследователи сначала надолго
прижимают свинец к золоту, а потом изуча-
ют, проникли ли атомы золота в свинец и
наоборот. Но почему берут именно эти ме-
таллы? От каких свойств металлов зависит
количество проникших атомов? В частности,
от тех, от которых зависит площадь истинно-
го контакта, площадь «пятнышек». А она
тем больше, чем металл тяжелее, если он
просто лежит, а не прижат дополнительной
силой, и чем он мягче – мягкий металл
прижимается плотнее, по большей площади.
А что произойдет, если одно из веществ
настолько мягкое, что площадь истинного
контакта оказывается сравнимой с геометри-
ческой? Тогда тела прижимаются друг к
другу весьма большими силами атмосферно-
го давления, и рассоединить их должно быть
трудно. Почему же нам легко удается отде-
лить от стола прижатую к нему резинку?
Ответ – потому, что она вся мягкая, при
прижатии она деформируется вся, отчасти
распластывается, и отделяем мы ее понемно-
гу, плавно уменьшая геометрическую пло-
щадь контакта, а не всю сразу. Вот если бы
мы сделали жесткую деталь с тонким мягким
покрытием и прижали этим покрытием к
жесткой поверхности, то отделить ее от этой
поверхности стало бы труднее. Например,
говорят, что подводную лодку может «при-
Видео с вопросом: деление трехзначных чисел на двузначные числа
Стенограмма видеозаписи
София вычисляет, что 432, разделенное на 12, равно 36. Таким образом, задача состоит из трех частей. Воспользуйтесь разработкой Софии, чтобы найти 216, разделенное на 12. Используйте аналогичный подход, чтобы найти 432, разделенное на 24. И, наконец, теперь воспользуйтесь разработкой Софии, чтобы вычислить 864, разделенное на шесть.
Таким образом, задача состоит из трех частей. Воспользуйтесь разработкой Софии, чтобы найти 216, разделенное на 12. Используйте аналогичный подход, чтобы найти 432, разделенное на 24. И, наконец, теперь воспользуйтесь разработкой Софии, чтобы вычислить 864, разделенное на шесть.
Итак, в трех разных частях этой задачи нас просят вычислить три разных деления.Но каждый раз нам говорят использовать то, что мы уже знаем, чтобы найти ответ. Мы видим, что нам говорят использовать наработку Софии или использовать аналогичный подход. Итак, где София занимается спортом? Что нам нужно использовать, чтобы найти ответы на эти вопросы?
Что ж, нам дан факт в первом предложении. София вычисляет, что 432 делить на 12 равно 36. Итак, давайте внимательно рассмотрим каждый шаг и воспользуемся этим фактом, который нам уже известен, чтобы помочь нам. Во-первых, нас просят использовать вычисления Софии, чтобы найти ответ на 216, разделенный на 12.Что общего и в чем разница в этих двух расчетах?
Ну, в обоих вычислениях делитель или число, на которое мы делим, одинаковы. Мы делим оба числа на 12. Разница заключается между двумя дивидендами, первым числом в каждом вычислении. Давайте внимательно посмотрим на эти числа. Можем ли мы увидеть связь между 432 и 216? 216 — половина 432. Если дивиденд уменьшится вдвое, как это повлияет на ответ? Иногда набросок гистограммы может помочь нам понять, что происходит с числами, когда они меняются при делении.
В первом вычислении дивиденд равен 432. И если мы разделим это на 12, нам скажут, что каждая часть стоит 36. Итак, что мы ожидали бы увидеть, если бы начали с дивиденда, который был вдвое меньше большой. Мы все еще делим на 12 равных частей, но на этот раз каждая из них вдвое меньше. Мы знаем, что 36, разделенное на два, равняется 18. Итак, мы использовали метод Софии, чтобы найти ответ на 216, разделенный на 12. Если у нас есть первое число в делении, а все остальное остается прежним, то ответ будет следующим. вдвое.
Давайте посмотрим на вторую часть проблемы. Опять же, мы воспользуемся разработкой Софии, чтобы помочь нам. На этот раз нам нужно найти ответ на 432, разделенное на 24. Что такое же и в чем разница в этих двух вычислениях на этот раз? На этот раз число, на которое мы делим, дивиденд, остается неизменным в обоих делениях. Итак, если мы снова попробуем нарисовать модель стержня, мы увидим, что у обеих моделей стержня есть большой стержень стоимостью 432.
Разница заключается в количестве, на которое мы делим.В расчетах Софии нам говорят, что она делит на 12. Но в расчетах нам нужно вычислить, нам нужно разделить на 24. Какая связь между 12 и 24? Итак, 24 — это двойное число 12. Что произойдет с ответом, если мы удвоим число, на которое делим?
Вот как выглядит каждая часть, если мы разделим на 12. Но если мы разделим число на вдвое больше частей, они станут вдвое меньше. Итак, они будут стоить половину от 36, что, как мы знаем, равно 18. Итак, если мы удвоим число, на которое делим, или делитель, в вопросе о делении, но оставим другое число прежним, ответ будет половина.
Наконец, давайте используем все, что мы узнали до сих пор, чтобы вычислить последнюю часть задачи — 864, разделенное на шесть. На этот раз в расчетах нет ничего прежнего. Но между ними есть связи. Давайте подумаем, как каждое число повлияет на ответ. Представим, что мы делили на 12, а не на шесть. Мы видим, что наше начальное число увеличилось вдвое, 432 удвоились и равняются 864. Итак, если мы разделим удвоенную сумму на 12, мы ожидаем, что ответ будет удвоенным 36.И удвоение 36 равно 72.
Но есть еще одно изменение, которое нам нужно сделать. Мы не делим 864 на 12. Нам нужно разделить это на шесть. Шесть составляет половину от 12. Итак, мы разделим 864 на половину меньшего количества частей. Это означает, что каждая деталь будет стоить вдвое дороже, потому что их меньше. Двойное 72 равно 144. Итак, мы нашли ответ на три различных деления, используя числовой факт, чтобы помочь нам. 432, разделенное на 24, также равняется 18. А 864, разделенное на шесть, равняется 144.
рупий Aggrawal 2019 за 6 класс по математике Глава 3
Стр. № 45:
Вопрос 1:
Запишите следующие три целых числа после 30999.
Ответ:
Следующие три целых числа после 30999 — 31000, 31001 и 31002.
Стр. № 45:
Вопрос 2:
Запишите три целых числа, которые встречаются непосредственно перед 10001.
Ответ:
Три целых числа, встречающиеся непосредственно перед 10001, следующие:
10001 — 1 = 10000
10000 — 1 = 9999
9999 — 1 = 9998
∴ Три целых числа непосредственно перед 10001 — это 10000, 9999 и 9998.
Стр. № 45:
Вопрос 3:
Сколько целых чисел между 1032 и 1209?
Ответ:
Число целых чисел от 1032 до 1209 = (1209 — 1032) — 1
= 177 — 1
= 176
Стр. № 45:
Вопрос 4:
Какое наименьшее целое число?
Ответ:
0 (ноль) — наименьшее целое число.
Все натуральные числа вместе с 0 называются целыми числами.
Стр. № 45:
Вопрос 5:
Укажите преемника:
(i) 2540801
(ii) 9999
(iii) 50904
(iv) 61639
(v) 687890
(vi) 5386700
(vii) 6475999
(viii) 9999999
Ответ:
(i) Преемник 2540801 = 2540801 + 1 = 2540802
(ii) Преемник 9999 = 9999 + 1 = 10000
(iii) Преемник 50904 = 50904 + 1 = 50905
(iv) Преемник 61639 = 61639 + 1 = 61640
(v) Преемник 687890 = 687890 + 1 = 687891
(vi) Преемник 5386700 = 5386700 + 1 = 5386701
(vii) Преемник 6475999 = 6475999 + 1 = 6476000
(viii) Преемник 9999999 = 9999999 + 1 = 10000000
Стр. № 46:
Вопрос 6:
Запишите предшественник:
(i) 97
(ii) 10000
(iii) 36900
(iv) 7684320
(v) 1566391
(vi) 2456800
(vii) 100000
(viii) 1000000
Ответ:
(i) Предшественник 97 = 97 — 1 = 96
(ii) Предшественник 10000 = 10000 — 1 = 9999
(iii) Предшественник 36900 = 36900 — 1 = 36899
(iv) Предшественник 7684320 = 7684320 — 1 = 7684319
(v) Предшественник 1566391 = 1566391 — 1 = 1566390
(vi) Предшественник 2456800 = 2456800 — 1 = 2456799
(vii) Предшественник 100000 = 100000 — 1 = 99999
(viii) Предшественник 1000000 = 1000000 — 1 = 999999
Страница № 46:
Вопрос 7:
Запишите три последовательных целых числа непосредственно перед 7510001.
Ответ:
Три последовательных целых числа непосредственно перед 7510001 выглядят следующим образом:
7510001 — 1 = 7510000
7510000 — 1 = 7509999
7509999 — 1 = 7509998
∴ Три последовательных числа перед 7510001 — это 7510000, 7509999 и 7509998.
Страница № 46:
Вопрос 8:
Напишите (T) для истинного и (F) для ложного против каждого из следующих утверждений:
(i) Ноль — наименьшее натуральное число.
(ii) Ноль — наименьшее целое число.
(iii) Каждое целое число является натуральным числом.
(iv) Каждое натуральное число является целым числом.
(v) 1 — наименьшее целое число.
(vi) Натуральное число 1 не имеет предшественника.
(vii) Целое число 1 не имеет предшественника.
(viii) Целое число 0 не имеет предшественника.
(ix) Предшественник двузначного числа никогда не бывает однозначным числом.
(x) Преемником двузначного числа всегда является двузначное число.
(xi) 500 является предшественником 499.
(xii) 7000 является преемником 6999.
Ответ:
(i) Неверно. 0 — не натуральное число, 1 — наименьшее натуральное число.
(ii) Верно.
(iii) Неверно. 0 — целое, но не натуральное число.
(iv) Верно. Натуральные числа включают 1,2,3 …, которые являются целыми числами.
(v) Неверно. 0 — наименьшее целое число.
(vi) Верно. Предшественником 1 является 1 — 1 = 0, что не является натуральным числом.
(vii) Неверно. Предшественником 1 является 1 — 1 = 0, что является целым числом.
(viii) Верно. Предшественником 0 является 0 — 1 = -1, что не является целым числом.
(ix) Неверно. Предшественником двузначного числа может быть однозначное число. Например, предшественник 10 равен 10 — 1, то есть 9.
(x) False. Преемник двузначного числа не всегда является двузначным числом. Например, преемником 99 является 99 + 1, т. Е. 100.
(xi) Ложь. Предшественник 499 — 499 — 1, т.е.е., 498.
(xii) Верно. Преемником 6999 является 6999 + 1, то есть 7000.
Страница № 48:
Вопрос 1:
Заполните пропуски, чтобы каждое из следующих утверждений соответствовало действительности:
(i) 458 + 639 = 639 + ……
(ii) 864 + 2006 = 2006 + ……
(iii ) 1946 + …… = 984 + 1946
(iv) 8063 + 0 = ……
(v) 53501 + (574 + 799) = 574 + (53501 + …… )
Ответ:
(i) 458 + 639 = 639 + 458
(ii) 864 + 2006 = 2006 + 864
(iii) 1946 + 984 = 984 + 1946
(iv) 8063 + 0 = 8063
(v) 53501 + ( 574 + 799) = 574 + (53501 + 799)
Страница № 48:
Вопрос 2:
Добавьте следующие числа и проверьте, изменив порядок добавления:
(i) 16509 + 114
(ii) 2359 + 548
(iii) 19753 + 2867
Ответ:
(i) 16509 + 114 = 16623
Изменяя порядок слагаемых, мы получаем:
114 + 16509 = 16623
∴ 16509 + 114 = 114 + 16509
(ii) 2359 + 548 = 2907
. порядок слагаемых:
548 + 2359 = 2907
∴ 2359 + 548 = 548 + 2359
(iii) 19753 + 2867 = 22620
. Изменив порядок слагаемых, мы получаем:
2867 + 19753 = 22620
∴ 19753 + 2867 = 2867 + 19753
Страница № 48:
Вопрос 3:
Найдите сумму: (1546 + 498) + 3589.
Также найдите сумму: 1546 + (498 + 3589).
Равны ли две суммы?
Состояние имущества удовлетворено.
Ответ:
У нас есть:
(1546 + 498) + 3589 = 2044 + 3589 = 5633
Кроме того, 1546 + (498 + 3589) = 1546 + 4087 = 5633
Да, две суммы равны.
Ассоциативное свойство сложения выполнено.
Страница № 48:
Вопрос 4:
Определите каждую из приведенных ниже сумм, используя подходящую перестановку.
(i) 953 + 707 + 647
(ii) 1983 + 647 + 217 + 353
(iii) 15409 + 278 + 691 + 422
(iv) 3259 + 10001 + 2641 + 9999
(v) 1 + 2 + 3 + 4 + 96 + 97 + 98 + 99
(vi) 2 + 3 + 4 + 5 + 45 + 46 + 47 + 48
Ответ:
(i) 953 + 707 + 647
953 + (707 + 647) (Используя ассоциативное свойство сложения)
= 953 + 1354
= 2307
(ii) 1983 + 647 + 217 + 353
(1983 + 647) + (217 +353) (Используя ассоциативное свойство сложения)
= 2630 + 570
= 3200
(iii) 15409 + 278 + 691 + 422
(15409 + 278) + (691 + 422) (Используя ассоциативное свойство сложение)
= 15687 + 1113
= 16800
(iv) 3259 + 10001 + 2641 + 9999
(3259 + 10001) + (2641 + 9999) (Используя ассоциативное свойство сложения)
= 13260 + 12640
= 25900
(v) 1 + 2 + 3 + 4 + 96 + 97 + 98 + 99
(1 + 2 + 3 + 4) + (96 + 97 + 98 + 99) (Используя ассоциативное свойство сложения)
= (10 ) + (390)
= 400
(vi) 2 + 3 + 4 + 5 + 45 + 46 + 47 + 48
(2 + 3 + 4 + 5) + (45 + 46 + 47 + 48) (Используя ассоциативное свойство additio п)
= 14 + 186
= 200
Страница № 48:
Вопрос 5:
Найдите сумму кратким методом:
(i) 6784 + 9999
(ii) 10578 + 99999
Ответ:
(i) 6784 + 9999
= 6784 + (10000 — 1)
= (6784 + 10000) — 1 (Используя ассоциативное свойство сложения)
= 16784 — 1
= 16783
(ii) 10578 + 99999
= 10578 + (100000 — 1)
= (10578 + 100000) — 1 (Используя ассоциативное свойство сложения)
= 110578 — 1
= 110577
Страница № 48:
Вопрос 6:
Для любых целых чисел a , b , c , правда ли, что ( a + b ) + c = a + ( c + b )? Назови причины.
Ответ:
Для любых целых чисел a, b и c, имеем:
( a + b ) + c = a + ( b + c )
Пусть a = 2, b = 3 и c = 4 [мы можем принимать любые значения для a, b и c ]
LHS = ( a + b ) + c
= (2 + 3) + 4
= 5 + 4
= 9
RHS = a + ( c + b )
= a + ( b + c ) [ ∵ Целые числа подчиняются закону коммутативности]
= 2 + (3 + 4)
= 2 + 7
= 9
∴ Это показывает, что ассоциативность (вдобавок) является одним из свойств целых чисел.
Страница № 48:
Вопрос 7:
Завершите каждый из следующих магических квадратов, указав недостающие числа:
(i)
| 2 | 15 | 16 | |
| 9 | 12 | ||
| 7 | 10 | ||
| 14 | 17 |
| 18 | 17 | 4 | |
| 14 | 11 | ||
| 9 | 10 | ||
| 19 | 16 |
Ответ:
В магическом квадрате сумма каждой строки равна сумме каждого столбца и суммы каждой главной диагонали.Используя эту концепцию, мы имеем:
(i)
| 4 | 9 | 2 |
| 3 | 5 | 7 |
| 8 | 1 | 6 |
(ii)
| 16 | 2 | 12 |
| 6 | 10 | 14 |
| 8 | 18 | 4 |
(iii)
| 2 | 15 | 16 | 5 |
| 9 | 12 | 11 | 6 |
| 13 | 8 | 7 | 10 |
| 14 | 3 | 4 | 17 |
(iv)
| 7 | 18 | 17 | 4 |
| 8 | 13 | 14 | 11 |
| 12 | 9 | 10 | 15 |
| 19 | 6 | 5 | 16 |
Страница № 48:
Вопрос 8:
Запишите (T) для истинного и (F) для ложного для каждого из следующих утверждений:
(i) Сумма двух нечетных чисел является нечетным числом.
(ii) Сумма двух четных чисел является четным числом.
(iii) Сумма четного и нечетного числа является нечетным числом.
Ответ:
(i) F (ложь). Сумма двух нечетных чисел не может быть нечетным числом. Пример: 3 + 5 = 8, что является четным числом.
(ii) T (верно). Сумма двух четных чисел является четным числом. Пример: 2 + 4 = 6, что является четным числом.
(iii) T (правда). Сумма четного и нечетного числа является нечетным числом.Пример: 5 + 4 = 9, что является нечетным числом.
Стр. № 49:
Вопрос 1:
Выполните следующие вычитания. Проверьте свои результаты по соответствующим дополнениям.
(i) 6237 — 694
(ii) 21205 — 10899
(iii) 100000 — 78987
(iv) 1010101 — 656565
Ответ:
(i) Вычитание: 6237 — 694 = 5543
Сложение: 5543 + 694 = 6237
(ii) Вычитание: 21205 — 10899 = 10306
Сложение: 10306 + 10899 = 21205
(iii) Вычитание: 100000 — 78987 = 21013
Сложение: 21013 + 78987 = 100000
(iv) Вычитание: 1010101 — 656565 = 353536
Сложение: 353536 + 656565 = 1010101
Стр. № 49:
Вопрос 2:
Замените каждый * правильной цифрой в каждом из следующих пунктов:
(i)
(ii)
(iii)
(iv)
Ответ:
(i) 917 — * 5 * = 5 * 8
⇒ 917-359 = 558
(ii) 6172 — ** 69 = 29 **
⇒ 6172-3269 = 2903
(iii) 5001003 — ** 6987 = 484 ****
⇒ 5001003 — 155987 = 4845016
(iv) 1000000 — **** 1 = * 7042 *
⇒ 1000000 — 29571 =
9
Стр. № 49:
Вопрос 3:
Найдите разницу:
(i) 463 — 9
(ii) 5632 — 99
(iii) 8640 — 999
(iv) 13006 — 9999
Ответ:
(i) 463 — 9
= 463 — 10 + 1
= 464 — 10
= 454
(ii) 5632 — 99
= 5632 — 100 + 1
= 5633 — 100
= 5533
(iii) 8640 — 999
= 8640 — 1000 + 1
= 8641 — 1000
= 7641
(iv) 13006 — 9999
= 13006 — 10000 + 1
= 13007 — 10000
= 3007
Страница № 50:
Вопрос 4:
Найдите разницу между наименьшим числом из 7 цифр и наибольшим числом из 4 цифр.
Ответ:
Наименьшее семизначное число = 1000000
Наибольшее четырехзначное число = 9999
∴ Их разница = 1000000 — 9999
= 1000000 — 10000 + 1
= 1000001 — 10000
= 9
Страница № 50:
Вопрос 5:
Рави открыл свой счет в банке, вложив 136000 рупий.На следующий день он снял с него 73129 рупий. Сколько денег осталось на его счету?
Ответ:
Деньги, внесенные Рави = 1,36,000 рупий
Деньги, снятые Рави = 73,129 рупий
Деньги, оставшиеся на его счете = деньги, внесенные — снятые деньги
= (136000 — 73129)
= 62871 рупий
∴ 62 871 рупий осталось в Счет Рави.
Страница № 50:
Вопрос 6:
Г-жа Саксена сняла 100000 рупий со своего банковского счета. Она купила телевизор за 38750 рупий, холодильник за 23890 рупий и украшения на сумму 35560 рупий. Сколько денег осталось у нее?
Ответ:
Деньги, снятые миссис Саксена = 100000 рупий
Стоимость телевизора = 38750 рупий
Стоимость холодильника = 23890 рупий
Стоимость украшений = 35560 рупий
Всего потраченных денег = (38750 + 23890 + 35560) = 98200
рупий Остались деньги = деньги сняты — потрачены
= (100000 — 98200)
= 1800
∴ 1800 рупий осталось у миссис Саксена.
Страница № 50:
Вопрос 7:
Население города составляло 110 500 человек. За год оно увеличилось на 3608 человек за счет новорожденных. Однако 8973 человека умерли или покинули город в течение года. Какова была численность населения в конце года?
Ответ:
Население города = 110500
Прирост населения = 110500 + 3608 = 114108
Количество человек, которые умерли или покинули город = 8973
Население на конец года = 114108 — 8973 = 105135
∴ Население на конец года будет 105135.
Страница № 50:
Вопрос 8:
Найдите целое число n , когда:
(i) n + 4 = 9
(ii) n + 35 = 101
(iii) n -18 = 39
(iv) n — 20568 = 21403
Ответ:
(i) n + 4 = 9
⇒ n = 9-4 = 5
(ii) n + 35 = 101
⇒ n = 101-35 = 66
(iii) n — 18 = 39
⇒ n = 18 + 39 = 57
(iv) n — 20568 = 21403
⇒ n = 21403 + 20568 = 41971
Страница № 53:
Вопрос 1:
Заполните пропуски, чтобы каждое из следующих утверждений соответствовало действительности:
(i) 246 × 1 =……
(ii) 1369 × 0 = …….
(iii) 593 × 188 = 188 × …….
(iv) 286 × 753 = ….. . × 286
(v) 38 × (91 × 37) = …… × (38 × 37)
(vi) 13 × 100 × …… = 1300000
(vii) 59 × 66 + 59 × 34 = 59 × (…… + ……)
(viii) 68 × 95 = 68 × 100 — 68 × …….
Ответ:
(i) 246 × 1 = 246
(ii) 1369 × 0 = 0
(iii) 593 × 188 = 188 × 593
(iv) 286 × 753 = 753 × 286
(v) 38 × (91 × 37 ) = 91 × (38 × 37)
(vi) 13 × 100 × 1000 = 1300000
(vii) 59 × 66 + 59 × 34 = 59 × (66 + 34)
(viii) 68 × 95 = 68 × 100 — 68 × 5
Страница № 53:
Вопрос 2:
Укажите свойство, используемое в каждом из следующих утверждений:
(i) 19 × 17 = 17 × 19
(ii) (16 × 32) — целое число
(iii) (29 × 36) × 18 = 29 × (36 × 18)
(iv) 1480 × 1 = 1480
(v) 1732 × 0 = 0
(vi) 72 × 98 + 72 × 2 = 72 × (98 + 2)
(vii) 63 × 126 — 63 × 26 = 63 × (126 — 26)
Ответ:
(i) Закон коммутативности при умножении
(ii) Свойство замыкания
(iii) Ассоциативность умножения
(iv) Мультипликативная идентичность
(v) Свойство нуля
(vi) Закон распределения над сложением
(vii) Закон распределения умножения на вычитание
Страница № 53:
Вопрос 3:
Найдите значение каждого из следующих параметров, используя различные свойства:
(i) 647 × 13 + 647 × 7
(ii) 8759 × 94 + 8759 × 6
(iii) 7459 × 999 + 7459
(iv) 9870 × 561 — 9870 × 461
(в) 569 × 17 + 569 × 13 + 569 × 70
(vi) 16825 × 16825 — 16825 × 6825
Ответ:
(i) 647 × 13 + 647 × 7
= 647 × (13 + 7)
= 647 × 20
= 12940 (Используя свойство распределения)
(ii) 8759 × 94 + 8759 × 6
= 8759 × (94 + 6)
= 8759 × 100
= 875900 (Используя свойство распределения)
(iii) 7459 × 999 + 7459
= 7459 × (999 + 1)
= 7459 × 1000
= 7459000 (Используя распределительное свойство)
(iv) 9870 × 561 — 9870 × 461
= 9870 × (561 — 461)
= 9870 × 100
= 987000 (с использованием распределительного свойства)
(v) 569 × 17 + 569 × 13 + 569 × 70
= 569 × (17+ 13+ 70)
= 569 × 100
= 56900 (Используя свойство распределения)
(vi) 16825 × 16825 — 16825 × 6825
= 16825 × (16825 — 6825)
= 16825 × 10000
= 168250000 (При использовании дистрибутивного пр оперти)
Страница № 53:
Вопрос 4:
Определите каждый из следующих продуктов путем подходящей перестановки:
(i) 2 × 1658 × 50
(ii) 4 × 927 × 25
(iii) 625 × 20 × 8 × 50
(iv) 574 × 625 × 16
(v) 250 × 60 × 50 × 8
(vi) 8 × 125 × 40 × 25
Ответ:
(i) 2 × 1658 × 50
= (2 × 50) × 1658
= 100 × 1658
= 165800
(ii) 4 × 927 × 25
= (4 × 25) × 927
= 100 × 927
=
(iii) 625 × 20 × 8 × 50
= (20 × 50) × 8 × 625
= 1000 × 8 × 625
= 8000 × 625
= 5000000
(iv) 574 × 625 × 16
= 574 × (625 × 16)
= 574 × 10000
= 5740000
(v) 250 × 60 × 50 × 8
= (250 × 8) × (60 × 50)
= 2000 × 3000
= 6000000
(vi) 8 × 125 × 40 × 25
= (8 × 125) × (40 × 25)
= 1000 × 1000
= 1000000
Страница № 53:
Вопрос 5:
Найдите каждый из следующих продуктов, используя законы распределения:
(i) 740 × 105
(ii) 245 × 1008
(iii) 947 × 96
(iv) 996 × 367
(v) 472 × 1097
(vi) ) 580 × 64
(vii) 439 × 997
(viii) 1553 × 198
Ответ:
(i) 740 × 105
= 740 × (100 + 5)
= 740 × 100 + 740 × 5 (используя распределительный закон умножения над сложением)
= 74000 + 3700
= 77700
(ii) 245 × 1008
= 245 × (1000 + 8)
= 245 × 1000 + 245 × 8 (Используя распределительный закон умножения над сложением)
= 245000 + 1960
= 246960
(iii) 947 × 96
= 947 × (100 — 4)
= 947 × 100 — 947 × 4 (Используя распределительный закон умножения над вычитанием)
=
=
(iv) 996 × 367
= 367 × (1000-4)
= 367 × 1000 — 367 × 4 (с использованием распределительного закона умножения над вычитанием)
= 367000 × 1468
= 365532
(v) 472 × 1097
= 472 × (1000 + 97)
= 472 × 1000 + 472 × 97 (с использованием распределительного закон умножения над сложением)
= 472000 + 45784
= 517784
(vi) 580 × 64 9004 7 = 580 × (60 + 4)
= 580 × 60 + 580 × 4 (Используя распределительный закон умножения над сложением)
= 34800 + 2320
= 37120
(vii) 439 × 997
= 439 × (1000 — 3)
= 439 × 1000 — 439 × 3 (Используя распределительный закон умножения над вычитанием)
= 439000 — 1317
= 437683
(viii) 1553 × 198
= 1553 × (200 — 2)
= 1553 × 200 — 1553 × 2 (используя распределительный закон умножения над вычитанием)
= 310600 — 3106
= 307494
Страница № 53:
Вопрос 6:
Найдите каждый из следующих продуктов, используя законы распределения:
(i) 3576 × 9
(ii) 847 × 99
(iii) 2437 × 999
Ответ:
Распределительное свойство умножения над сложением утверждает, что a ( b + c ) = ab + ac
Распределительное свойство умножения над вычитанием утверждает, что a ( b — c ) = ab — ac
(i) 3576 × 9
= 3576 × (10 — 1)
= 3576 × 10 — 3576 × 1
= 35760 — 3576
= 32184
(ii) 847 × 99
= 847 × (100 — 1)
= 847 × 100 — 847 × 1
= 84700 — 847
= 83853
(iii) 2437 × 999
= 2437 × (1000 — 1)
= 2437 × 1000 — 2437 × 1
= 2437000 — 2437
= 2434563
Страница № 54:
Вопрос 7:
Найдите продукты:
(i)
(ii)
(iii)
(iv)
Ответ:
(i)
458 × 67 = 30686
(ii)
3709 × 89 = 330101
(iii)
4617 × 234 = 1080378
(iv)
15208 × 542 = 8242736
Страница № 54:
Вопрос 8:
Найдите произведение наибольшего трехзначного числа и наибольшего пятизначного числа.
Ответ:
Наибольшее трехзначное число = 999
Наибольшее пятизначное число = 99999
∴ Произведение двух чисел = 999 × 99999
= 999 × (100000 — 1) (согласно распределительному закону)
= 99
0 — 999
= 99899001
Страница № 54:
Вопрос 9:
Автомобиль движется с постоянной скоростью 75 км в час.Какое расстояние он преодолеет за 98 часов?
Ответ:
Равномерная скорость автомобиля = 75 км / ч
Расстояние = скорость × время
= 75 × 98
= 75 × (100 — 2) (Используя закон распределения)
= 75 × 100 — 75 × 2
= 7500 — 150
= 7350 км
∴ Пройденное расстояние за 98 ч составляет 7350 км.
Страница № 54:
Вопрос 10:
Дилер приобрел 139 видеомагнитофонов.Если стоимость каждого набора составляет 24350 рупий, найдите стоимость всех наборов вместе.
Ответ:
Стоимость 1 набора видеомагнитофонов = 24350 рупий
Стоимость 139 наборов видеомагнитофонов = 139 × 24350
= 24350 × (140 — 1) (с учетом распределительной собственности)
= 24350 × 140 — 24350
= 3409000 — 24350
= рупий.3384650
∴ Стоимость всех комплектов видеомагнитофонов составляет 33,84 650 рупий.
Страница № 54:
Вопрос 11:
Жилищным кооперативом построено 197 домов. Если стоимость строительства каждого дома составляет 450000 рупий, какова общая стоимость строительства всех домов?
Ответ:
Стоимость строительства 1 дома = 450000 рупий
Стоимость строительства 197 таких домов = 197 × 450000
= 450000 × (200 — 3)
= 450000 × 200 — 450000 × 3 [Использование распределительного свойства умножения над вычитанием]
=
000 — 1350000
= 88650000
∴ Общая стоимость строительства 197 домов составляет 8,86,50 000 рупий.
Страница № 54:
Вопрос 12:
Для школы закуплено 50 стульев и 30 классных досок. Если каждый стул стоит 1065 рупий, а каждая доска — 1645 рупий, найдите общую сумму счета.
Ответ:
Стоимость стула = 1065 рупий
Стоимость доски = 1645 рупий
Стоимость 50 стульев = 50 × 1065 = 53250 рупий
Стоимость 30 классных досок = 30 × 1645 = 49350 рупий
∴ Общая сумма счета = стоимость 50 стульев + стоимость 30 досок
= (53250 + 49350)
= 1,02,600
Страница № 54:
Вопрос 13:
В школе шесть секций VI класса, по 45 учеников в каждой секции.Если ежемесячная плата с каждого студента составляет 1650 рупий, найдите общий ежемесячный сбор с Класса VI.
Ответ:
Количество учеников в 1 секции = 45
Количество учеников в 6 разделах = 45 × 6 = 270
Ежемесячная плата с 1 ученика = 1650
рупий ∴ Общий ежемесячный сбор с VI класса = 1650 рупий × 270 = 4,45 500
Страница № 54:
Вопрос 14:
Произведение двух целых чисел равно нулю.К чему вы пришли?
Ответ:
Если произведение двух целых чисел равно нулю, то одно из них определенно равно нулю.
Пример: 0 × 2 = 0 и 0 × 15 = 0
Если произведение целых чисел равно нулю, то оба они могут быть равны нулю.
, т.е. 0 × 0 = 0
Теперь 2 × 5 = 10. Здесь произведение будет ненулевым, потому что умножаемые числа не равны нулю.
Страница № 54:
Вопрос 15:
Заполните пропуски:
(i) Сумма двух нечетных чисел равна…… количество.
(ii) Произведение двух нечетных чисел является …… числом.
(iii) a ≠ 0 и a × a = a ⇒ a =?
Ответ:
(i) Сумма двух нечетных чисел является четным числом. Пример: 3 + 5 = 8, что является четным числом.
(ii) Произведение двух нечетных чисел является нечетным числом. Пример: 5 × 7 = 35, что является нечетным числом.
(iii) a ≠ 0 и a × a = a
Дано: a × a = a
⇒ a = aa = 1 , a ≠ 0
Страница № 56:
Вопрос 1:
Разделите и проверьте свой ответ на соответствующее умножение в каждом из следующих случаев:
(i) 1936 ÷ 36
(ii) 19881 ÷ 47
(iii) 257796 ÷ 341
(iv) 612846 ÷ 582
(v) 34419 ÷ 149
(vi) 39039 ÷ 1001
Ответ:
(i)
Дивиденд = 1936, делитель = 36, коэффициент = 53, остаток = 28
Проверка: делитель × коэффициент + остаток = 36 × 53 + 28
= 1936
= дивиденд
Следовательно, дивиденд = делитель × коэффициент + Остаток
Проверено.
(ii) 19881 ÷ 47
Дивиденд = 19881, делитель = 47, коэффициент = 423, остаток = 0
Проверка: делитель × коэффициент + остаток = 47 × 423 + 0
= 19881
= дивиденд
Следовательно, дивиденд = Делитель × Частное + остаток
Проверено.
(iii)
Дивиденд = 257796, делитель = 341, коэффициент = 756, остаток = 0
Проверка: делитель × коэффициент + остаток = 341 × 756 + 0
= 257796
= дивиденд
Следовательно, дивиденд = делитель × коэффициент + Остаток
Проверено.
(iv) 612846 ÷ 582
Дивиденд = 612846, Делитель = 582, Частное = 1053, Остаток = 0
Проверка: Делитель × Частное + Остаток = 582 × 1053 + 0
= 612846
= Дивиденд
Следовательно, Дивиденд = делитель × частное + остаток
подтверждено.
(v) 34419 ÷ 149
Дивиденд = 34419, Делитель = 149, Частное = 231, Остаток = 0
Проверка: Делитель × Частное + Остаток = 149 × 231 + 0
= 34419
= Дивиденд
Следовательно, Дивиденд = Делитель × Частное + Остаток
Проверено.
(vi) 39039 ÷ 1001
Дивиденд = 39039, делитель = 1001, коэффициент = 39, остаток = 0
Проверка: делитель × коэффициент + остаток = 1001 × 39 + 0
= 39039
= дивиденд
Следовательно, Дивиденд = делитель × частное + остаток
подтверждено.
Страница № 56:
Вопрос 2:
Разделите и найдите частное и остаток.Проверьте свой ответ.
(i) 6971 ÷ 47
(ii) 4178 ÷ 35
(iii) 36195 ÷ 153
(iv)
(v) 23025 ÷ 1000
(vi) 16135 ÷ 875
Ответ:
(i) 6971 ÷ 47
Частное = 148 и остаток = 15
Проверка: делитель × частное + остаток = 47 × 148 + 15
= 6971
= дивиденды
∴ дивиденды = делитель × частное + остаток
подтверждено.
(ii) 4178 ÷ 35
Дивиденд = 119 и остаток = 13
Проверка: делитель × частное + остаток = 35 × 119 + 13
= 4178
= дивиденд
∴ дивиденд = делитель × частное + остаток
Проверено.
(iii) 36195 ÷ 153
Частное = 236 и остаток = 87
Проверка: делитель × частное + остаток = 153 × 236 + 87
= 36195
= дивиденды
∴ дивиденды = делитель × частное + остаток
подтверждено.
(iv)
Частное = 233 и остаток = 375
Проверка: делитель × частное + остаток = 400 × 233 + 375
=
= дивиденды
∴ дивиденды = делитель × частное + остаток
подтверждено.
(v) 23025 ÷ 1000
Частное = 23 и остаток = 25
Проверка: делитель × частное + остаток = 1000 × 23 + 25
= 23025
= дивиденды
∴ дивиденды = делитель × частное + остаток
подтверждено.
(vi) 16135 ÷ 875
Частное = 18 и остаток = 385
Проверка: делитель × частное + остаток = 875 × 18 + 385
= 16135
= дивиденды
∴ дивиденды = делитель × частное + остаток
подтверждено.
Страница № 56:
Вопрос 3:
Найдите значение
(i) 65007 ÷ 1
(ii) 0 ÷ 879
(iii) 981 + 5720 ÷ 10
(iv) 1507 — (625 ÷ 25)
(v) 32277 ÷ (648 — 39)
(vi) (1573 ÷ 1573) — (1573 ÷ 1573)
Ответ:
(i) 65007 ÷ 1 = 65007
(ii) 0 ÷ 879 = 0
(iii) 981 + 5720 ÷ 10
= 981 + (5720 ÷ 10) (в соответствии со свойством DMAS)
= 981 + 572
= 1553
(iv) 1507 — (625 ÷ 25) (Следуя собственности BODMAS)
= 1507-25
= 1482
(v) 32277 ÷ (648-39) (Следуя собственности BODMAS)
= 32277 ÷ (609)
= 53
(vi) (1573 ÷ 1573) — (1573 ÷ 1573) (Следуя свойству BODMAS)
= 1 — 1
= 0
Страница № 56:
Вопрос 4:
Найдите целое число n такое, что n ÷ n = n .
Ответ:
Дано: n ÷ n = n
⇒ nn = n
⇒ n = n 2
т. Е. Целое число n равно n. 2 .
∴ Целое число должно быть 1.
Страница № 56:
Вопрос 5:
Произведение двух чисел — 504347.Если одно из чисел 317, найдите другое.
Ответ:
Пусть x и y будут двумя числами.
Произведение двух чисел = x × y = 504347
Если x = 317, то имеем:
317 × y = 504347
⇒ y = 504347 ÷ 317
3535 9000 y = 1591
∴ Другое число — 1591.
Страница № 56:
Вопрос 6:
При делении 59761 на определенное число получается 189, а остаток — 37. Найдите делитель.
Ответ:
Дивиденд = 59761, частное = 189, остаток = 37 и делитель =?
Дивиденд = делитель × частное + остаток
⇒ 59761 = делитель × 189 + 37
⇒ 59761-37 = делитель × 189
⇒ 59724 = делитель × 189
⇒ Делитель = 59724 ÷ 189
Следовательно, делитель = 316
Страница № 56:
Вопрос 7:
При делении 55390 на 299 остаток равен 75.Найдите частное, используя алгоритм деления.
Ответ:
Здесь Дивиденд = 55390, Делитель = 299 и остаток = 75
Нам нужно найти частное.
Теперь, дивиденд = делитель × частное + остаток
⇒ 55390 = 299 × частное + 75
⇒ 55390 — 75 = 299 × частное
⇒ 55315 = 299 × частное
⇒ частное = 55315 ÷ 299
Следовательно, частное = 55315 ÷ 299
185
Страница № 56:
Вопрос 8:
Какое наименьшее число нужно вычесть из 13601, чтобы получить число, в точности делимое на 87?
Ответ:
Сначала разделим 13601 на 87.
Остаток = 29
Итак, 29 нужно вычесть из 13601, чтобы получить число, точно делимое на 87.
т.е. 13601 — 29 = 13572
Теперь у нас есть:
∴ 29 нужно вычесть из 13601 чтобы оно делилось на 87.
Страница № 56:
Вопрос 9:
Какое наименьшее число нужно добавить к 1056, чтобы получить число, точно делимое на 23?
Ответ:
Сначала разделим 1056 на 23.
Требуемое число = 23-21 = 2
Итак, 2 нужно добавить к 1056, чтобы оно делилось на 23.
т.е. 1056 + 2 = 1058
Теперь у нас есть:
∴ 1058 — это делится в точности на 23.
Страница № 56:
Вопрос 10:
Найдите наибольшее четырехзначное число, делящееся на 16.
Ответ:
Нам нужно найти наибольшее четырехзначное число, делящееся на 16.
Наибольшее четырехзначное число = 9999
Следовательно, делимое = 9999
Делитель = 16
Здесь мы получаем остаток = 15
Следовательно, 15 необходимо вычесть из 9999, чтобы получить наибольшее четырехзначное число, которое делится на 16
т.е. 9999-15 = 9984
Таким образом, 9984 — это наибольшее четырехзначное число, которое делится на 16.
Страница № 56:
Вопрос 11:
Разделите наибольшее пятизначное число на 653.Проверьте свой ответ по алгоритму деления.
Ответ:
Наибольшее пятизначное число = 99999
Дивиденд = 99999, Делитель = 653, Частное = 153 и остаток = 90
Проверка: Делитель × Частное + Остаток
= 653 × 153 + 90
= 99909 + 90
= 99999
= Дивиденд
∴ Дивиденд = делитель × коэффициент + остаток
подтверждено.
Страница № 56:
Вопрос 12:
Найдите наименьшее 6-значное число, которое в точности делится на 83.
Ответ:
Наименьшее шестизначное число = 100000
Здесь делимое = 100000 и делитель = 83
Чтобы найти наименьшее шестизначное число, точно делимое на 83, мы должны прибавить к деленному 83-68 = 15.
То есть, 100000 + 15 = 100015
Итак, 100015 — это наименьшее шестизначное число, которое точно делится на 83.
Страница № 56:
Вопрос 13:
1 дюжина бананов стоит 29 рупий.Сколько дюжин можно купить за 1392 рупий?
Ответ:
Стоимость 1 дюжины бананов = 29
рупий Количество дюжин, купленных за 1392 рупий = 1392 ÷ 29
Следовательно, 48 дюжин бананов можно купить за Rs. 1392.
Страница № 56:
Вопрос 14:
19625 деревьев высажено поровну в 157 рядов.Найдите количество деревьев в каждом ряду.
Ответ:
Количество деревьев, посаженных в 157 рядов = 19625
Деревьев, посаженных в 1 ряд = 19625 ÷ 157
∴ В каждом ряду высажено 125 деревьев.
Страница № 56:
Вопрос 15:
Население города составляет 517530 человек. Если сообщается, что каждый пятнадцатый является грамотным, узнайте, сколько грамотных людей в городе.
Ответ:
Население города = 517530
Считается грамотным 115 человек, т.е. 115 × 517530 = 517530 ÷ 15
∴ В данном городе 34502 неграмотных.
Страница № 56:
Вопрос 16:
Себестоимость 23 цветных телевизоров составляет 570055 рупий. Определите себестоимость каждого телевизора, если каждый из них стоит одинаково.
Ответ:
Себестоимость 23 цветных телевизоров = 5 70 055 рупий
Себестоимость 1 телевизора = 570055 ÷ 23
∴ Себестоимость одного телевизора составляет 24 785 рупий.
Страница № 56:
Вопрос 1:
Наименьшее целое число —
(a) 1
(b) 0
(c) 2
(d) ни одно из этих
Ответ:
(b) 0
Наименьшее целое число равно 0.
Страница № 56:
Вопрос 2:
Наименьшее число из 4 цифр, которое точно делится на 9, равно
(a) 1018
(b) 1026
(c) 1009
(d) 1008
Ответ:
(d) 1008
(a)
Следовательно, 1018 не делится точно на 9.
(b)
Следовательно, 1026 точно делится на 9.
(c)
Следовательно, 1009 не делится точно на 9.
(d)
Следовательно, 1008 точно делится на 9.
(b) и (d) точно делятся на 9, но (d ) — наименьшее число, которое в точности делится на 9.
Стр. № 57:
Вопрос 3:
Наибольшее число из 6 цифр, которое точно делится на 16, равно
(a) 999980
(b) 999982
(c) 999984
(d) 999964
Ответ:
(c) 999984
(a)
Следовательно, 999980 не может точно делиться на 16.
(b)
Следовательно, 999982 не делится точно на 16.
(c)
Следовательно, 999984 точно делится на 16.
(d)
Следовательно, 999964 не делится на 16.
наибольшее шестизначное число, которое точно делится на 16, — это 999984.
Стр. № 57:
Вопрос 4:
Какое наименьшее число нужно вычесть из 10004, чтобы получить число, точно делимое на 12?
(а) 4
(б) 6
(в) 8
(г) 20
Ответ:
(c) 8
Здесь мы должны указать, какое наименьшее число следует вычесть из 10004, чтобы получить число, точно делимое на 12
Итак, сначала мы разделим 10004 на 12.
Остаток = 8
Итак, 8 следует вычесть из 10004, чтобы получить число, точно делимое на 12.
т.е. 10004-8 = 9996
Следовательно, 9996 точно делится на 12.
Стр. № 57:
Вопрос 5:
Какое наименьшее число нужно прибавить к 10056, чтобы получить число, точно делимое на 23?
(а) 5
(б) 18
(в) 13
(г) 10
Ответ:
(a) 18
Здесь мы должны указать, что какое наименьшее число нужно добавить к 10056, чтобы получить число, точно делимое на 23
Итак, сначала мы разделим 10056 на 23
Остаток = 5
Требуемое число = 23-5 = 18
Итак, 18 нужно прибавить к 10056, чтобы получить число, точно делимое на 23.
, то есть 10056 + 18 = 10074
Следовательно, 10074 точно делится на 23.
Стр. № 57:
Вопрос 6:
Какое целое число является ближайшим к 457, деленному на 11?
(а) 450
(б) 451
(в) 460
(г) 462
Ответ:
(d) 462
(a)
Следовательно, 450 не делится на 11.
(b)
Следовательно, 451 делится на 11.
(c)
Следовательно, 460 не делится на 11.
(d)
Следовательно, 462 делится на 11.
Здесь даны числа в вариантах (b) и (d) делятся на 11. Однако нам нужно целое число, ближайшее к 457, которое делится на 11.
Итак, 462 — это целое число, ближайшее к 457 и делимое на 11.
Стр. № 57:
Вопрос 7:
Сколько целых чисел между 1018 и 1203?
(a) 185
(b) 186
(c) 184
(d) ни один из этих
Ответ:
(c) 184
Количество целых чисел = (1203 — 1018) — 1
= 185 — 1
= 184
Стр. № 57:
Вопрос 8:
При делении числа на 46 получается частное 11 и остаток 15.Номер
(а) 491
(б) 521
(в) 701
(г) 679
Ответ:
(b) 521
Делитель = 46
Частное = 11
Остаток = 15
Дивиденд = делитель × частное + остаток
= 46 × 11 + 15
= 506 + 15
= 521
Стр. № 57:
Вопрос 9:
В сумме деления получается дивиденд = 199, частное = 16 и остаток = 7.Делитель
(а) 11
(б) 23
(в) 12
(г) ни один из этих
Ответ:
(c) 12
Дивиденд = 199
Частное = 16
Остаток = 7
Согласно алгоритму деления имеем:
Дивиденд = делитель × частное + остаток
⇒ 199 = делитель × 16 + 7
⇒ 199-7. = делитель × 16
⇒ Делитель = 192 ÷ 16
Стр. № 57:
Вопрос 10:
7589 -? = 3434
(а) 11023
(б) 4245
(в) 4155
(г) ни один из этих
Ответ:
(а) 11023
7589 -? = 3434
⇒ 7589 — x = 3434
⇒ x = 7589 + 3434
⇒ x = 11023
Стр. № 57:
Вопрос 11:
587 × 99 =?
(а) 57213
(б) 58513
(в) 58113
(г) 56413
Ответ:
(c) 58113
587 × 99
= 587 × (100 — 1)
= 587 × 100 — 587 × 1 [Использование распределительного свойства умножения над вычитанием]
= 58700 — 587
= 58113
Стр. № 57:
Вопрос 12:
4 × 538 × 25 =?
(а) 32280
(б) 26900
(в) 53800
(г) 10760
Ответ:
(в) 53800
4 × 538 × 25
= (4 × 25) × 538
= 100 × 538
= 53800
Стр. № 57:
Вопрос 13:
24679 × 92 + 24679 × 8 =?
(a) 4
(b) 1233950
(c) 2467900
(d) ни один из этих
Ответ:
(c) 2467900
Используя свойство распределения, мы имеем:
24679 × 92 + 24679 × 8
= 24679 × (92 + 8)
= 24679 × 100
= 2467900
Стр. № 57:
Вопрос 14:
1625 × 1625 — 1625 × 625 =?
(а) 1625000
(б) 162500
(в) 325000
(г) 812500
Ответ:
(a) 1625000
Используя свойство распределения, мы имеем:
1625 × 1625 — 1625 × 625
= 1625 × (1625 — 625)
= 1625 × 1000
= 1625000
Стр. № 57:
Вопрос 15:
1568 × 185 — 1568 × 85 =?
(a) 7840
(b) 15680
(c) 156800
(d) ни один из этих
Ответ:
(c) 156800
Используя свойство распределения, мы имеем:
1568 × 185 — 1568 × 85
= 1568 × (185 — 85)
= 1568 × 100
= 156800
Стр. № 57:
Вопрос 16:
(888 + 777 + 555) = (111 ×?)
(а) 120
(б) 280
(в) 20
(г) 140
Ответ:
(c) 20
(888 + 777 + 555) = (111 ×?)
⇒ (888 + 777 + 555) = 111 × (8 + 7 + 5) [Взяв 111 обычных]
= 111 × (20) = 2220
Стр. № 57:
Вопрос 17:
Сумма двух нечетных чисел равна
(a) нечетное число
(b) четное число
(c) простое число
(d) кратное 3
Ответ:
(б) четное число
Сумма двух нечетных чисел является четным числом.
Пример: 5 + 3 = 8
Стр. № 57:
Вопрос 18:
Произведение двух нечетных чисел:
(a) нечетное число
(b) четное число
(c) простое число
(d) ни одно из этих
Ответ:
(a) нечетное число
Произведение двух нечетных чисел является нечетным числом.
Пример: 5 × 3 = 15
Стр. № 57:
Вопрос 19:
Если a — целое число, такое что a + a = a , то a =?
(a) 1
(b) 2
(c) 3
(d) ни один из этих
Ответ:
(d) ни один из этих
Дано: a — целое число, такое что a + a = a .
Если a = 1, то 1+ 1 = 2 ≠ 1
Если a = 2, то 2 + 2 = 4 ≠ 2
Если a = 3, то 3 + 3 = 6 ≠ 3
Стр. № 57:
Вопрос 20:
Предшественником 10000 является
(a) 10001
(b) 9999
(c) ни один из этих
Ответ:
(b) 9999
Предшественник 10000 = 10000 — 1 = 9999
Стр. № 57:
Вопрос 21:
Преемником 1001 является
(a) 1000
(b) 1002
(c) ни один из этих
Ответ:
(b) 1002
Преемник 1001 = 1001 + 1 = 1002
Стр. № 57:
Вопрос 22:
Наименьшее четное целое число —
(a) 0
(b) 2
(c) ни одно из этих
Ответ:
(b) 2
Наименьшее четное целое число равно 2.Ноль (0) не является ни четным, ни нечетным числом.
Стр. № 59:
Вопрос 1:
Сколько целых чисел между 1064 и 1201?
Ответ:
Число целых чисел от 1201 до 1064 = (1201 — 1064) — 1
= 137 — 1
= 136
Стр. № 59:
Вопрос 2:
Заполните пустые поля.
1000000 — **** 1 * 7042 *
Ответ:
1000000
— **** 1
* 7042 *
Тогда имеем:
1000000
-29571
9
Стр. № 59:
Вопрос 3:
Используйте закон распределения, чтобы найти значение
1063 × 128 — 1063 × 28.
Ответ:
Используя закон распределения, мы имеем:
1063 × 128 — 1063 × 28
= 1063 × (128 — 28)
= 1063 × 100
= 106300
Стр. № 59:
Вопрос 4:
Найдите произведение наибольшего 5-значного числа и наибольшего 3-значного числа, используя закон распределения.
Ответ:
Наибольшее пятизначное число = 99999
Наибольшее трехзначное число = 999
Используя закон распределения, мы имеем:
Продукт = 99999 × 999
= 99999 × (1000 — 1) [При использовании закона распределения]
= 99999 × 1000 — 99999 × 1
= 99999000 — 99999
= 99899001
OR
999 × 99999
= 999 × (100000 — 1) [При использовании закона распределения]
= 999 × 100000 — 999 × 1
= 99
0 — 999
= 99899001
Стр. № 59:
Вопрос 5:
Разделите 53968 на 267 и проверьте результат с помощью алгоритма деления.
Ответ:
Дивиденд = 53968, Делитель = 267, Частное = 202 и остаток = 34
Проверка: Частное × Делитель + Остаток
= 267 × 202 + 34
= 53934 + 34
= 53968
= Дивиденд
∴ Дивиденд Частное × делитель + остаток
Проверено.
Стр. № 59:
Вопрос 6:
Найдите наибольшее шестизначное число, делящееся на 16.
Ответ:
Наибольшее шестизначное число = 999999
Остаток = 15
Наибольшее шестизначное число, делимое на 16 = 999999-15 = 999984
∴ 999984 делится на 16.
Стр. № 59:
Вопрос 7:
Себестоимость 23 телевизоров составляет 570055 рупий. Найдите стоимость каждого такого набора.
Ответ:
Себестоимость 23 телевизоров = 5,70 055 рупий
Себестоимость 1 телевизора = 570055 ÷ 23
∴ Стоимость одного телевизора составляет 24 785 рупий.
Стр. № 59:
Вопрос 8:
Какое наименьшее число нужно вычесть из 13801, чтобы получить число, в точности делимое на 87?
Ответ:
Мы должны найти наименьшее число, которое нужно вычесть из 13801, чтобы получить число, точно делимое на 87
Итак, сначала мы разделим 13801 на 87
Остаток = 55
Число 55 следует вычесть из 13801, чтобы получить число делимое на 87.
т.е. 13801 — 55 = 13746
∴ 13746 делится на 87.
Стр. № 59:
Вопрос 9:
Значение (89 × 76 + 89 × 24) равно
(а) 890
(б) 8900
(в) 89000
(г) 10420
Ответ:
(b) 8900
(89 × 76 + 89 × 24)
= 89 × (76 + 24) [Использование распределительного свойства умножения над сложением]
= 89 × 100
= 8900
Стр. № 59:
Вопрос 10:
При делении числа на 53 получаем частное 8 и остаток 5.Номер
(a) 419
(b) 423
(c) 429
(d) ни один из этих
Ответ:
(c) 429
Делитель = 53, Частное = 8, Остаток = 5 и Дивиденд =?
Теперь, дивиденд = частное × делитель + остаток
= 8 × 53 + 5
= 429
Стр. № 59:
Вопрос 11:
Целое число, не имеющее предшественника:
(a) 1
(b) 0
(c) 2
(d) ни одно из этих
Ответ:
(b) 0
Целое число, не имеющее предшественника, равно 0.
то есть 0-1 = -1, что не является целым числом.
Стр. № 59:
Вопрос 12:
67 + 33 = 33 + 67 является примером
(a) свойство закрытия
(b) ассоциативное свойство
(c) коммутативное свойство
(d) распределительное свойство
Ответ:
(c) Коммутативное свойство
67 + 33 = 33 + 67 является примером коммутативного свойства сложения.
Стр. № 59:
Вопрос 13:
Присадка, обратная 36:
(a) 136
(b) 0
(c) −36
(d) ни одно из этих
Ответ:
(c) -36
Аддитивная величина, обратная 36, равна -36.
т.е. 36 + (−36) = 0
Стр. № 59:
Вопрос 14:
Что из следующего не равно нулю?
(а) 0 × 0
(б) 02
(в) 8 — 82
(г) 2 + 0
Ответ:
(г) 2 + 0
(а) 0 × 0 = 0
(б) 0/2 = 0
(в) 8-82 = 02 = 0
(г) 2 + 0 = 2
Стр. № 59:
Вопрос 15:
Предшественником наименьшего трехзначного числа является
(a) 999
(b) 100
(c) 101
(d) 99
Ответ:
(d) 99
Наименьшее трехзначное число = 100
∴ Предшественник 100 = 100 — 1 = 99
Стр. № 59:
Вопрос 16:
Число целых чисел между наименьшим целым числом и наибольшим двузначным числом составляет
(a) 88
(b) 98
(c) 99
(d) 101
Ответ:
(b) 98
Наименьшее целое число = 0
Наибольшее двузначное число = 99
Число целых чисел от 0 до 99 = (99-0) — 1 = 98
Стр. № 59:
Вопрос 17:
Заполните пустые поля.
(i) Наименьшее натуральное число ….
(ii) Наименьшее целое число ….
(iii) Деление на …… не определено.
(iv) …… целое число, которое не является натуральным числом.
(v) …… целое число, которое не является натуральным числом.
Ответ:
(i) Наименьшее натуральное число — 1.
(ii) Наименьшее целое число — 0.
(iii) Деление на 0 не определено.
(iv) 0 — целое число, которое не является натуральным числом.
(v) 1 — мультипликативное тождество для целых чисел.
Страница № 60:
Вопрос 18:
Запишите «T» для истинного и «F» для ложного в каждом из следующих значений:
(i) 0 — наименьшее натуральное число.
(ii) Каждое натуральное число является целым числом.
(iii) Каждое целое число является натуральным числом.
(iv) 1 не имеет целых предшественников.
Ответ:
(i) F (ложь). 0 не является натуральным числом.
(ii) T (верно).
(iii) F (ложно). 0 — целое, но не натуральное число.
(iv) F (ложь). 1-1 = 0 предшествует 1, которое является целым числом.
Страница № 60:
Вопрос 19:
Сопоставьте следующие столбцы с целыми числами:
| колонка A | колонка B |
| (а) 137 + 63 = 63 + 137 | (i) Ассоциативность умножения |
| (b) (16 × 25) — это число | (ii) Коммутативность умножения |
| (в) 365 × 18 = 18 × 365 | (iii) Распределительный закон умножения по сложению |
| (г) (86 × 14) × 25 = 86 × (14 × 25) | (iv) Коммутативность сложения |
| (д) 23 × (80 + 5) = (23 × 80) + (23 × 5) | (v) Свойство замыкания для умножения |
Ответ:
| Столбец A | Столбец B |
| (а) 137 + 63 = 63 + 137 | (iv) Коммутативность сложения |
| (b) (16 × 25) — это число | (v) Свойство замыкания для умножения |
| (в) 365 × 18 = 18 × 365 | (ii) Коммутативность умножения |
| (г) (86 × 14) × 25 = 86 × (14 × 25) | (i) Ассоциативность умножения |
| (д) 23 × (80 + 5) = (23 × 80) + (23 × 5) | (iii) Распределительный закон умножения по сложению |
Просмотреть решения NCERT для всех глав класса 6
Тест 1 — Oswal Publishers
НОМЕРА
Число — это набор цифр 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.
ВИДЫ НОМЕРОВ
Натуральное число
Набор всех положительных чисел, начинающихся с 1, называется натуральными числами. Обозначаются они N.
.N = {1, 2, 3, 4, 5, 6, ..}
Целое число
Натуральные числа, включая ноль, называются целыми числами и обозначаются буквой W.
Вт = {0, 1, 2, 3, 4, 5, 6, ..}
Примечание |
Каждое натуральное число является целым числом, но каждое целое число не является натуральным числом. |
Четное число
Число, которое делится на 2, называется четным числом.
Пример: 2, 4, 6, 8, 10, 12,…
Нечетное число
Число, которое не делится на 2, называется нечетным числом.
Пример: 1, 3, 5, 7, 9, 11, 13,…
Простое число
Число, которое делится на 1 и само число, называется простым числом. Всегда больше 1.
Пример: 2, 3, 5, 7, 11, 13, 17, 19,…
Мы знаем, что 2 — четное число.Поэтому 2 называется четным простым числом.
Пример: Сколько простых чисел от 1 до 100?
Решение:
Между 1 и 100 25 простых чисел.
Это 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 и 97.
Метод нахождения простого числа больше 100
Рассмотрим данное число как.
Шаг 1. Найдите ближайшее целое число, большее чем.
Шаг 2: Проверьте, делится ли число на любое простое число, которое меньше или нет.
Шаг 3: Если да, не является простым числом, в противном случае — простым числом.
Пр. 1 Узнайте, является ли число 305 простым или нет.
Решение:
Ближайшее целое число 18
то есть
Простые числа меньше 18 — это 17, 13, 11, 7, 5, 3 и 2.
305 делится на 5. Значит, это не простое число.
Составное число
Число, не являющееся простым числом, называется составным числом.
Пример: 4, 6, 8, 9, 12, 14, 15,…
Составные числа всегда больше 1.
Примечание |
1 не является ни простым, ни составным. |
Сопоставимые числа
Если HCF двух чисел равен 1, то эти числа называются взаимно простыми числами.
Пример: (3, 11), (5, 7), (2, 9) и т. Д.
H.C.F чисел 3 и 11 равно 1. Таким образом, они являются взаимно простыми числами.
Аналогично, (5, 7) и (2, 9) также являются взаимно простыми числами.
Целые числа
Множество всех положительных и отрицательных чисел, включая 0, называется целыми числами и обозначается Z.
Z = {…, — 5, -4, -3, -2, -1,0,1,2,3,4,5, …}
Целые положительные числа: {1, 2, 3, 4, 5,…}
Целые отрицательные числа: {-1, -2, -3, -4,…}
Неотрицательные целые числа: {0, 1, 2, 3, 4, 5,…}
Неположительные целые числа: {0, -1, -2, -3, -4,…}
Где 0 не является ни положительным, ни отрицательным.
Рациональное число
Число в форме называется рациональным числом, где p и q — целые числа, а q 0.
Рациональные числа обозначены Q.
Пример:
Иррациональное число
Число называется иррациональным, если его нельзя выразить в виде, где p и q — целые числа, а q 0.
Пример: и т. Д.
Реальное число
Набор всех рациональных и иррациональных чисел известен как действительное число.Обозначается буквой Р.
.Порядковый номер
В серии чисел, если каждое число больше предыдущего на 1, то последовательность чисел называется последовательными числами.
Пример: 5, 6, 7, 8 или 789, 790, 791, 792, 793 или 1001, 1002, 1003.
ЗНАЧЕНИЕ ЛИЦА И МЕСТО
Каждая цифра числа имеет номинал и разряд.
Мест можно представить как
Ten Crores | 100000000 | 2 |
кроров | 10000000 | 1 |
Десять лакхов | 1000000 | 7 |
лакхов | 100000 | 5 |
Десять тысяч | 10000 | 1 |
тыс. | 1000 | 6 |
сот | 100 | 7 |
Десятки | 10 | 0 |
Единицы | 1 | 1 |
Число 217516701 можно прочитать как «Двадцать один крор семьдесят пять лакхов шестнадцать тысяч семьсот один».
Номинал цифры — это та же цифра, которая не зависит от положения цифры.
Разрядное значение цифры представляет время положения цифры, т. Е. Увеличивается в степени 10, начиная с разряда единицы.
Пример: В 2046 году номинальная стоимость 4 равна 4, а разрядная цифра 4 равна.
Точно так же номинал 0 равен 0, а разряд 0 равен.
Номинальная стоимость 6 — 6, разрядная цифра 6 -.
Номинальная стоимость 2 — 2, разрядная стоимость 2 -.
Расширенная форма
Любое число может быть расширено с помощью разрядов.
Например, 2046 в развернутой форме —
.ДОПОЛНЕНИЕ
Сложение чисел путем деления разрядов
Пример: 3267 + 531
Шаг 1: Разделите числа на сотни, десятки и единицы.
3267 = 3000 + 200 + 60 + 7
531 = 500 + 30 + 1
Шаг 2: сложите числа
3000 + 200 + 60 + 7 + 500 + 30 + 1 = 3000 + 700 + 90 + 8
= 3798
Следовательно, 3267 + 531 = 3798.
Сложение чисел с одинаковыми цифрами в порядке возрастания
Пример: 4 + 44 + 444 + 4444 + 44444
Шаг 1: Возьмите обычную цифру и посчитайте количество цифр в каждом номере.
4 (1 + 11 + 111 + 1111 + 11111)
Шаг 2: Составьте цифры, считая цифры как одно число.
Т.е. 1 = 1, 11 = 2, 111 = 3, 1111 = 4, 11111 = 5
Тогда номер будет 12345
Шаг 3: Умножьте число на 4, тогда мы получим
.
Следовательно, 4 + 44 + 444 + 4444 + 44444 = 49380.
Добавление одинаковых цифр с десятичными знаками
Пример: 0,7 + 0,77 + 0,777 + 0,7777 + 0,77777
Шаг 1. Возьмите обычную цифру из чисел
.7 (0,1 + 0,11 + 0,111 + 0,1111 + 0,11111)
Шаг 2: Сначала решите сложение внутри скобки.
0,1 + 0,11 + 0,111 + 0,1111 + 0,11111 = 0,54321
Шаг 3: Умножьте результат шага 2 на 7.
Следовательно, 0.7 + 0,77 + 0,777 + 0,7777 + 0,77777 = 3,80247
Пр. 2 7,7 + 77,77 + 777,777 + 7777,7777
Мы можем вынести 7 наружу, так как это общее для всех чисел, тогда получим
= 8641,0247
Сложение смешанных дробных чисел
Пример:
Шаг 1. Сложите целые числа
2 + 1 + 3 + 5 = 11
Шаг 2: сложите дробные значения
LCM 3, 4, 2 и 5 — это 60
Шаг 3: сложите результаты как шага 1, так и шага 2.
.
ВЫЧИСЛЕНИЕ
Вычитание чисел путем деления на разряды
Пример: 867 — 531
Шаг 1: Разделите число на сотни и десятки.
867 = 800 + 67
531 = 500 + 31
Шаг 2: вычтите 500 из 800 и 31 из 67
800–500 = 300
67 — 31 = 36
Шаг 3: Добавьте результаты
300 + 36 = 336.
УМНОЖЕНИЕ
Умножение 2-значных чисел
Пример:
Шаг 1. Умножьте цифры единицы
Шаг 2: Умножьте последнюю цифру первого значения на первую цифру второго значения и наоборот.Затем сложите результаты.
Шаг 3: Запишите последнюю цифру перед ответом на шаг 1 и перенесите первую цифру на следующий шаг.
Шаг 4: Умножьте первую цифру первого значения на первую цифру второго значения.
Следовательно,.
Умножение 3-значных чисел
Пример:
Шаг 1:
Шаг 2:
Шаг 3:
Шаг 4:
Шаг 5:
Следовательно,
Умножение на 9
Поставьте ноль после последней цифры числа и вычтите исходное число из этого числа.
Пр. 3 В чем ценность?
Решение:
Умножение на 11
Шаг 1: Напишите 0 перед первой цифрой множимого.
Шаг 2: Оставьте последнюю цифру числа множимого в результате как есть.
Шаг 3: Добавьте последовательные цифры множимого к его предыдущей цифре, затем поместите последнюю цифру результата перед результатом шага 2. Если есть перенос, добавьте его к следующей цифре.
Пр. 4 В чем ценность?
Решение:
Шаг 1:
Шаг 2:
_ _ _ _ _ _ _ 7
Шаг 3: 1 + 7 = 8
_ _ _ _ _ _ 87
4 + 1 = 5
_ _ _ _ _ 587
2 + 4 = 6
_ _ _ _ 6587
6 + 2 = 8
_ _ _ 86587
5 + 6 = 11 (1 — перед 8, 1 — перенос)
_ _ 186587
9 + 5 + 1 = 15 (5 — перед 1, 1 — перенос)
_ 5186587
0 + 9 + 1 = 10
105186587
Следовательно,.
Умножение на 12
Шаг 1: Напишите 0 перед первой цифрой множимого.
Шаг 2: Удвойте последнюю цифру множимого и поместите последнюю цифру результата в ответ. Если перенос есть, то перенаправьте его к следующему шагу.
Шаг 3: Перейти влево к следующей цифре множимого, затем удвоить ее и прибавить к предыдущим цифрам. Сложите перенос из предыдущего шага, запишите последнюю цифру результата и отправьте перенос на следующий шаг.
Шаг 4: Повторите шаг 3 для последовательных цифр.
Пр. 5 В чем ценность?
Решение:
Шаг 1:
Шаг 2:
= _ _ _ _ _ _ _ 4 [Перенести 1]
Шаг 3:
= _ _ _ _ _ _ 04 [Перенести 1]
Шаг 4:
= _ _ _ _ _ 004 [Перенести 1]
= _ _ _ _ 9004 [Перенести 0]
= _ _ _ 49004 [Перенести 1]
= _ _ 749004 [Перенести 1]
= _ 4749004 [Перенести 2]
= 114749004
Следовательно, 0.
Умножение на 13
Шаг 1: Напишите 0 перед первой цифрой множимого.
Шаг 2: Утроите последнюю цифру множимого и поместите последнюю цифру результата в ответ. Если перенос есть, то перенаправьте его к следующему шагу.
Шаг 3: Перейти влево к следующей цифре множимого, затем утроить ее и прибавить к предыдущим цифрам. Сложите перенос из предыдущего шага, запишите последнюю цифру результата и отправьте перенос на следующий шаг.
Шаг 4: Повторите шаг 3 для последовательных цифр.
Пр. 6 В чем ценность?
Решение:
Шаг 1:
Шаг 2:
= _ _ _ _ _ _ _ 1 [Перенести 2]
Шаг 3:
= _ _ _ _ _ _ 21 [Перенести 1]
Шаг 4:
= _ _ _ _ _ 421 [Перенести 1]
= _ _ _ _ 1421 [Перенести 1]
= _ _ _ 11421 [Перенести 2]
= _ _ 311421 [Carry 2]
= _ 4311421 [Carry 3]
= 124311421
Следовательно, 0.
Умножение числа на 25
Шаг 1. Замените 25 на 100/4.
Шаг 2: Разделите полученное число на 4.
Шаг 3: Умножьте результат на 100, чтобы получить ответ.
Пр. 7 В чем ценность?
Решение:
Шаг 1:
Шаг 2:
Шаг 3:
Следовательно,.
ОТДЕЛЕНИЕ
Есть несколько простых способов решить двузначное и трехзначное деление.
Деление на 2-значное число
Пример: 82964 91
Шаг 1: Поместите 9 в столбец делителя и 1 поверх флага, а затем выделите одно место для остатка в правом конце делимого.
Шаг 2: Поскольку первая цифра делимого меньше первой цифры частного, возьмите первые 2 цифры и затем разделите их на 9.
Т.е. Частное = 9, а остаток 1. Поместите остаток перед третьей цифрой делимого, т. Е. 9.
Шаг 3: Теперь 19 — это дивиденд. Умножьте последнюю цифру частного на цифру-флаг, затем вычтите результат из делимого.
Т.е. , то 19 — 9 = 10
Затем разделите 10 на 9.
Частное = 1, а остаток = 1. Поместите остаток перед 6 от дивиденда.
Шаг 4: Теперь 16 — дивиденд. Умножьте последнюю цифру частного на цифру-флаг, затем вычтите результат из делимого.
Т.е. , то 16-1 = 15
Затем разделите 15 на 9.
Частное = 1, а остаток = 6. Поместите остаток перед 4 от дивиденда.
Шаг 5: Теперь 64 — это дивиденд. Умножьте последнюю цифру частного на цифру-флаг, затем вычтите результат из делимого.
Т.е. , то 64 — 1 = 63
Затем разделите 63 на 9.
Частное = 7 и остаток = 0.
Следовательно, частное 911,7
Таким образом,
Деление на 3-х значное число
Пример:
Шаг 1:
Шаг 2:
Частное = 2 и остаток = 1
Шаг 3:
Вычтите дивиденд из произведения первой цифры флаговой цифры и последней цифры частного.
Частное = 1 и остаток = 2
Шаг 4:
Вычтите дивиденд из перекрестного умножения двух флаговых цифр и последних двух частных, чтобы получить фактический дивиденд.
Частное = 2 и остаток = 3
Шаг 5:
Вычтите дивиденд из перекрестного умножения двух флаговых цифр и последних двух частных, чтобы получить фактический дивиденд.
Частное = 4 и остаток = 4
Шаг 6:
Вычтите дивиденд из перекрестного умножения двух флаговых цифр и последних двух частных, чтобы получить фактический дивиденд.
Частное = 4 и остаток = 0
Следовательно, это частное.
ПРОВЕРКА ДЕЛИМОСТИ
«Делится на» означает «когда вы делите одно число на другое, результатом является целое число.
делимость на 2
Числа, заканчивающиеся цифрами 0, 2, 4, 6, 8, делятся на 2.
Пример: 15086 делится на 2, так как его последняя цифра — 6.
15085 не делится на 2, так как его последняя цифра не заканчивается на 0, 2, 4, 6 и 8.
делимость на 3
Если сумма цифр числа делится на 3, то число делится на 3.
Пр. 8 Определите, делится ли 15086 на 3 или нет.
Решение:
Сумма цифр = 1 + 5 + 0 + 8 + 6 = 20
20 не делится на 3.
Итак, 15086 не делится на 3.
Пр. 9 Определите, делится ли 97531245 на 3 или нет.
Решение:
Сумма цифр = 9 + 7 + 5 + 3 + 1 + 2 + 4 + 5 = 36
36 делится на 3.
Итак, 97531245 делится на 3.
делимость на 4
Если две последние цифры числа делятся на 4, то число делится на 4.
Пр. 10 Определите, делится ли314 на 4 или нет.
Решение:
Последние две цифры данного номера314 равны 14.
Мы знаем, что 14 не делится на 4.
Итак,314 также не делится на 4.
Пр. 11 Определите, делится ли 98764392 на 4 или нет.
Решение:
Последние две цифры данного номера 98764392 — 92.
92 делится на 4.
Итак, 98764392 также делится на 4.
делимость на 5
Число, оканчивающееся на 0 или 5, полностью делится на 5.
Пр. 12 Делится ли число 856214680 на 5?
Решение:
Да, число 856214680 делится на 5, так как его последнее число заканчивается на 0.
Делимость на 6
Проверить делимость на 2 и 3.
Пр. 13 Делится ли число 8572146 на 6?
Решение:
Чтобы найти делимость на 6, нам нужно проверить, делится ли число на 2 и 3 или нет.
Для делимости на 2: последняя цифра данного числа 8572146 — 6, что делится на 2.
Для делимости на 3: сумма цифр в данном числе 8572146 равна
8 + 5 + 7 + 2 + 1 + 4 + 6 = 33
33 делится на 3.
Следовательно, число 8572146 делится на 6 так же, как и на 2 и 3.
делимость на 7
Шаг 1. Умножьте последнюю цифру на 2.
Шаг 2: Вычтите результат из оставшихся цифр.
Шаг 3. Проверьте, делится ли ответ на 7 или нет. Если оно делимое, то и исходное число будет делимым.
Пр. 14 Определите, делится ли число 2478 на 7 или нет.
Решение:
Чтобы проверить делимость на 7, умножьте последнюю цифру на 2 и вычтите результат из оставшихся цифр.
для 2478,
Тогда 247-16 = 231
231 делится на 7.
Следовательно, 2479 делится на 7.
делимость на 8
Если последние три цифры числа делятся на 8, то число делится на 8.
Пр. 15 Узнайте, делится ли число 57
на 8 или нет.
Решение:
Мы знаем, что если последние три цифры числа делятся на 8, то это целое число также делится на 8.
Последние 3 цифры числа 57
— 952.
952 делится на 8.
Следовательно, 57
делится на 8.
делимость на 9
Если сумма цифр числа делится на 9, то число делится на 9.
Пр. 16 Определите, делится ли 6574123058 на 9 или нет.
Решение:
Чтобы найти делимость числа на 9, мы должны сложить цифры числа.
Сумма цифр 6574123058
= 6 + 5 + 7 + 4 + 1 + 2 + 3 + 0 + 5 + 8 = 41
41 не делится на 9.
Итак, 6574123058 не делится на 9.
Делимость на 10
Число, оканчивающееся на 0, делится на 10.
Пример: 1874620 делится на 10.
65247900 делится на 10.
1856975 не делится на 10.
6784305 не делится на 10.
Делимость на 11
Число считается делимым на 11, если разница между суммой цифр в нечетных разрядах числа и суммой цифр в четных разрядах того же числа равна либо «0», либо «числу, делящемуся на 11». ‘.
Пр. 17 Делится ли число 4984177 на 11?
Решение:
Сумма нечетных цифр — Сумма четных цифр
= (7 + 1 + 8 + 4) — (7 + 4 + 9)
= 20-20 = 0
Итак, 4984177 делится на 11.
Делимость на 12
Число, которое делится как на 4, так и на 3, можно разделить на 12.
Пр. 18 Делится ли число
572 на 12?
Решение:
Чтобы проверить делимость на 12, сначала мы должны проверить делимость 3 и 4.
Для делимости на 3: сумма цифр в данном числе
572 равна
9 + 6 + 1 + 2 + 4 + 5 + 7 + 2 = 36
36 делится на 3.
Для делимости на 4: последние 2 цифры данного числа равны 72, что делится на 4.
Следовательно, число
572 делится на 12.
делимость на 13
Шаг 1. Умножьте последнюю цифру на 4.
Шаг 2: Добавьте результат к оставшимся цифрам.
Шаг 3. Проверьте, делится ли ответ на 13 или нет.Если оно делимое, то и исходное число будет делимым.
Пр. 19 Узнайте, делится ли число 6877 на 13 или нет.
Решение:
Последняя цифра данного номера — 7.
Затем умножаем 4 на 7, получаем 28
Добавляем 28 к оставшемуся числу 687, получаем
687 + 28 = 715
715 делится на 13.
Итак, 6877 также делится на 13.
делимость на 14
Число, которое делится как на 2, так и на 7, можно разделить на 14.
Пр. 20 Делится ли число 85708 на 14?
Решение:
Чтобы проверить делимость на 14, сначала мы должны проверить делимость 2 и 7.
Для делимости на 2: последняя цифра данного числа 85708 — 8, что делится на 2.
Для делимости на 7: последнюю цифру умножьте на 2, а затем вычтите результат из оставшихся цифр.
8570 — 16 = 8554, что делится на 7.
Следовательно, число 85708 делится на 14, как на 2 и 7.
делимость на 15
Число, которое делится как на 3, так и на 5, можно разделить на 15.
Пр. 21 Делится ли число 5 на 15?
Решение:
Чтобы проверить делимость на 15, сначала мы должны проверить делимость 3 и 5.
Для делимости на 3: сумма цифр в данном числе 5 равна
5 + 9 + 1 + 2 + 8 + 5 = 30
30 делится на 3.
Для делимости на 5: число 5 заканчивается на 5, поэтому 5 делится на 5.
Следовательно, число 5 делится на 15 так же, как и на 3 и 5.
делимость на 17
Шаг 1. Умножьте последнюю цифру на 5.
Шаг 2: Вычтите результат из оставшихся цифр.
Шаг 3. Проверьте, делится ли ответ на 17 или нет. Если оно делимое, то и исходное число будет делимым.
Пр. 22 Делится ли число 8526 на 17?
Решение:
Чтобы проверить делимость на 17, умножьте последнюю цифру на 5 и вычтите результат из оставшихся цифр.
для 8526,
Тогда 852-30 = 822
822 не делится на 17.
Следовательно, 8526 не делится на 17.
делимость на 19
Шаг 1. Умножьте последнюю цифру на 2.
Шаг 2: Добавьте результат к оставшимся цифрам.
Шаг 3. Проверьте, делится ли ответ на 19 или нет. Если оно делимое, то и исходное число будет делимым.
Пр. 23 Делится ли число 8626 на 19?
Решение:
Умножьте последнюю цифру на 2
Затем добавляем результат к оставшимся цифрам, получаем
862 + 12 = 874, что делится на 19.
Итак, число 8626 делится на 19.
Алгоритм деления
делится на для всех значений
делится на, если четно.
делится на, если нечетное.
Пр. 24 При делении 42361 на определенное число получается 61, а остаток — 45. Что такое делитель?
Решение:
Мы знаем,
Пр.25 Какое наименьшее число нужно прибавить к 6148, чтобы получить число, точно делимое на 13?
Решение:
Частное = 472, остаток = 12
Требуемое число для добавления = 13 — 12 = 1.
Проверка:
6148 + 1 = 6149
Разделив 6149 на 13, мы получим частное = 473, а остаток = 0.
Следовательно, 1 — это наименьшее число, которое нужно добавить к 6148, чтобы получить число, точно делимое на 13.
Пр. 26 Какое наименьшее число нужно вычесть из 6148, чтобы получить число, точно делимое на 13?
Решение:
Частное = 472, остаток = 12
Требуемое число для вычитания = 12.
Т.е. 6148 — 12 = 6136
Разделив 6136 на 13, мы получим частное = 472, а остаток = 0.
Следовательно, 12 — это наименьшее число, которое необходимо вычесть из 6148, чтобы получить число, точно делимое на 13.
ЦИФРА БОЛЬШОГО ЭКСПОНЕНТА ЕДИНИЦЫ
Чтобы найти цифру большого показателя степени, где — основание, а — показатель степени, выполните действия, указанные ниже.
Шаг 1. Разделите показатель степени на 4.
Шаг 2: Если мы получим остаток 0, то
Последняя цифра будет 6 для последней цифры основания как 2, 4, 6, 8.
Последняя цифра будет 1, когда последняя цифра основания 3, 7, 9.
Если остаток ненулевой, то
Последняя цифра будет последней цифрой, где — последняя цифра основания, а r — остаток.
Пр. 27 Какая последняя цифра в расширении?
Решение:
Разделим 352 на 4, остаток будет 0.
Поскольку последняя цифра основания — 8, а 352 делится на 4, цифра единицы — 6.
Пр. 28 Найдите цифру единицы.
Решение:
Чтобы найти цифру единицы, нам нужно разделить 2147 на 4.
Частное = 536 и остаток = 3
Последняя цифра основания и остатка,
Следовательно, цифра единицы = цифра единицы.
Пр. 29 Что мы получим в остатке при делении на 5?
Решение:
Цифра в единицах = Цифры в единицах
Цифра единицы не заканчивается ни на 0, ни на 5.
не делится на 5.
УРОВЕНЬ — ЛЕГКО
1.Если полностью делится на 3, наименьшее значение A равно
.2. Какой будет остаток при делении на 30?
(а) 1 | (б) 10 |
(в) 29 | (г) 30 |
3.Разница между местом и номиналом 0 в числе 2017 составляет
(а) 0 | (б) 99 |
(в) 100 | (г) 101 |
4.Разница между разрядными значениями двух троек в числе
8.(а) 9997 | (б) 2970 |
(в) 29997 | (г) 29970 |
5.
(а) 801069 | (б) 81069 |
(в) 80169 | (г) 8010609 |
6.Какое число делится на 13?
(а) 1954 | (б) 1101 |
(в) 1872 | (г) 1517 |
7. Умножьте последнюю цифру на 2 и прибавьте результат к оставшимся цифрам, чтобы найти делимость какого числа?
(а) 19 | (б) 13 |
(в) 17 | (г) 14 |
8.Выберите простое число.
(а) 802 | (б) 803 |
(в) 809 | (г) 807 |
9. Найдите значение позиции «K» в числе 4K1396. Предположим, K — четное простое число
.(а) 20000 | (б) 200 |
(в) 200000 | (г) 2000 |
10.У Таншики 265476 флагов. 7542 флага оранжевого цвета, остальные — фиолетового цвета. Сколько у нее фиолетовых флагов?
(а) 252834 | (б) 257934 |
(в) 247934 | (г) 246222 |
11. Разница между значением разряда и номиналом 9 в числе 429861 составляет
.(а) 8381 | (б) 8991 |
(в) 8101 | (г) 7931 |
12.8340 — 3215 — 1132 =?
(а) 3992 | (б) 3963 |
(в) 3923 | (г) 3993 |
13. Какое из следующих чисел делится на 3?
(а) 267851 | (б) 632817 |
(в) 547191 | (г) 2 |
14.Найдите наименьшее значение *, при котором 6876 * 22 делится на 3.
15. Какое из следующих чисел делится на 4?
782(а) | (б) 47829654 |
(в) 47820264 | (г) 48724838 |
16.Кое из следующих чисел делится на 8?
(а) 5368 | б) 1986 |
(в) 2897 | (г) 2018 |
17.8325 делится на ___________.
(а) 9 | (б) 7 |
(в) 13 | (г) 11 |
18. Сумма всех тех простых чисел, которые не больше 17, равна
.(а) 59 | (б) 58 |
(в) 41 | (г) 42 |
19.Количество целых чисел от 100 до 600, которые делятся на 4 и 6, равно
.(а) 40 | (б) 42 |
(в) 41 | (г) 50 |
20. Найдите наибольшее число, при вычитании из 10000 остаток делится на 32, 36, 48 и 50.
(а) 8272 | (б) 7408 |
(в) 9136 | (г) 8674 |
21.337,62 + 8,591 + 34,4 равно
(а) 370.611 | (б) 380.511 |
(в) 380.611 | (г) 426.97 |
22. Найдите сумму
23. Значение (?) В уравнении
365.089 -? + 89,72 = 302,35 равно
(а) 152.456 | (б) 152.459 |
(с) 153.456 | (г) 153,459 |
24. Число девочек в классе в пять раз превышает число мальчиков. Что из следующего не может быть общим количеством детей в классе?
(а) 24 | (б) 30 |
(в) 35 | (г) 54 |
25.
(а) 2709.18 | б 2079.08 |
(в) 2907,28 | (г) 2790,80 |
(e) Ни один из этих |
26,333,33 + 33,33 + 3,3 =?
(а) 369.69 | б) 369.96 |
(в) 396.96 | (г) 396,69 |
(e) Ни один из этих |
27.
(а) 2862 | (б) 2682 |
(в) 2286 | (г) 2268 |
(e) Ни один из этих |
28,8052 — 9883 + 6048 =? 25
(а) 168.68 | б) 186.68 |
(в) 186,86 | г 168.86 |
(e) Ни один из этих |
29,8536 + 5824 =? 40
(а) 336 | (б) 359 |
(в) 363 | (г) 395 |
(e) Ни один из этих |
30,566,91 + 551,34 + 114,98 =?
(а) 1233.23 | (б) 1222,33 |
(в) 1223,45 | (г) 1235,88 |
(e) Ни один из этих |
31,3463 295 — 18611 =? + 5883
(а) 9 | (б) 887071 |
(в) 989090 | (г) 899060 |
(e) Ни один из этих |
32.
(а) 2477 | (б) 2478 |
(в) 2467 | (г) 2476 |
(e) Ни один из этих |
33.
(а) 15,8 | (б) 14,6 |
(в) 17,4 | (г) 17,2 |
(д) 16.4 |
34,302,46 + 395,72 — 123,47 =?
(а) 576,77 | (б) 547,17 |
(в) 547,77 | (г) 574,71 |
е) 577,71 |
35.
(а) 353.2184 | б) 353.2854 |
(с) 331.54 | (г) 313,2854 |
e) 331.2854 |
36.
(а) 4242 | (б) 4155 |
(в) 1123 | (г) 11023 |
(e) Ни один из этих |
37.
(а) 1250 | (б) 1300 |
(в) 1375 | (г) 1200 |
(e) Ни один из этих |
38.
(а) 1865113 | (б) 1775123 |
(в) 1765113 | (г) 1675123 |
(e) Ни один из этих |
39.
(а) | (б) |
(в) | (г) |
(e) Ни один из этих |
40.
(а) 2436 | (б) 2801 |
(в) 2801 | (г) 2071 |
(e) Ни один из этих |
41.
(а) | (б) |
(в) | (г) |
(e) Ни один из этих |
42.
(а) 4494 | б) 561,75 |
(в) 2247 | (г) 280,875 |
(e) Ни один из этих |
43.
(а) 37 | (б) 333 |
(в) 111 | (г) 84 |
(e) Ни один из этих |
44.
(а) 75 | (б) 51,5 |
(в) 57,5 | (г) 5,25 |
(e) Ни один из этих |
45.
(а) 273258 | (б) 273268 |
(в) 273348 | (г) 273358 |
46.Сколько из следующих чисел делится на 132?
264, 396, 462, 792, 968, 2178, 5184, 6336
47. Какое из следующих чисел в точности делится на 11?
(а) 235641 | (б) 245642 |
(в) 315624 | (г) 415624 |
48.
(а) 420 | (б) 460 |
(в) 500 | (г) 540 |
(e) Ни один из этих |
49.Какая единица измерения?
50. Количество простых чисел меньше 100 —
[C.D.S 2017-I]
(а) 25 | (б) 26 |
(в) 27 | (г) 28 |
51. делится на
[C.D.S. 2016-I]
(а) 5 | (б) 7 |
(в) 10 | (г) 12 |
52.Семизначное число 876p37q делится на 225. Значения p и q могут быть соответственно
.[C.D.S. 2015-II]
(а) 9, 0 | (б) 0, 0 |
(в) 1, 5 | (г) 9, 5 |
53. Цифра в месте единицы продукта 81 × 82 × 83 × 84 ×… × 99 равна
[C.D.S. 2015-I]
54. Какое максимальное значение m, если число N = 35 × 45 × 55 × 60 × 124 × 75 делится на?
[С.D.S. 2015-I]
55. Последняя цифра в расширении —
.[C.D.S. 2015-I]
56. Каков остаток от деления на 7?
[C.D.S. 2014-II]
(а) 1 | (б) 2 |
(в) 3 | (г) 4 |
57. Какой остаток получается при делении 1421 × 1423 × 1425 на 12?
[С.D.S. 2015-I]
58.p, q и r — простые числа, такие что p
[C.D.S. 2014-II]
(а) 1 | (б) 2 |
(в) 3 | (d) Ни один из этих |
59. Какое количество делителей числа 360?
[С.D.S. 2014-II]
(а) 12 | (б) 18 |
(в) 24 | (d) Этих нет |
60. Каков остаток от деления на 7?
[C.D.S. 2014-I]
(а) 1 | (б) 2 |
(в) 4 | (d) Ни один из этих |
61.Если m и n натуральные числа, то это
[C.D.S. 2014-II]
(а) Всегда иррационально | (b) Иррационально, если n не является m-й степенью целого числа |
(c) Иррационально, если m не является n-й степенью целого числа | (d) Иррационально, если m и n не взаимно просты |
62. Если x — положительное четное целое число, а y — отрицательное нечетное целое число, то
[С.D.S. 2014-II]
(a) Целое нечетное | (б) Целое четное |
(c) Рациональное число | (d) Ни один из этих |
63. Пара рациональных чисел от 1/4 до 3/4 равна
.[C.D.S. 2014-I]
64. Какая последняя цифра?
[C.D.S. 2014-I]
(а) 0 | (б) 4 |
(в) 8 | (d) Ничего из вышеперечисленного |
65.делится на
[C.D.S. 2014-I]
(а) Только 10 | (б) Только 20 |
(c) И 10, и 20 | (d) Ни 10, ни 20 |
УРОВЕНЬ — СЛОЖНЫЙ
66. Какое наименьшее число следует заменить на * в числе 56771 * 2, чтобы число полностью делилось на 8?
67. делится на
(а) 10 | (б) 11 |
(в) 13 | (г) 17 |
68.Какое из следующих чисел в точности делится на 17?
(а) 1071 | (б) 2153 |
(в) 4065 | (г) 1849 |
69.8
1256 на какое число в точности делится?
(а) 19 | (б) 11 |
(в) 17 | (г) 13 |
70.Какое из следующих чисел является простым?
(а) 621 | (б) 317 |
(в) 539 | (г) 493 |
71. Какое наименьшее число нужно прибавить к 39417, чтобы получить число, точно делимое на 19?
72. Какое наименьшее число нужно вычесть из 27537, чтобы получить число, в точности делимое на 17?
(а) 2 | (б) 3 |
(в) 14 | (г) 12 |
73.Если, что равно?
74. Предположение: число ABCDE делится на 11.
Утверждение I: E — D + C — B + A делится на 11.
Ведомость II: E — D + C — B + A = 0
Что из следующего верно?
(а) Только я | (б) Только II |
(c) И I, и II | (d) Ни I, ни II |
75.Какое наименьшее число нужно прибавить к 4000, чтобы получить число, точно делимое на 19?
(а) 11 | (б) 13 |
(в) 10 | (г) 9 |
76. Минимальное количество из 4 цифр при увеличении на 5 полностью делится на 12, 15, 20 и 35. Число равно
(а) 1275 | (б) 1265 |
(в) 1235 | (г) 1255 |
77.Двузначное число становится само собой, когда его цифры меняются местами. Разница цифр — одна. Найдите номер.
[Констебль полиции Дели, 2014]
(а) 54 | (б) 63 |
(в) 43 | (г) 32 |
78. Четыре простых числа записаны в порядке возрастания их величин. Произведение первых трех — 385, а последних трех — 1001.Наибольшее данное простое число —
.[AFCAT, 2017]
(а) 11 | (б) 13 |
(в) 17 | (г) 19 |
79. На экзамене студенту было предложено найти определенный номер. По ошибке он это обнаружил. Его ответ был на 150 больше, чем правильный. Найдите номер.
[AFCAT, 2016]
(а) 180 | (б) 280 |
(в) 380 | (г) 480 |
80.7 добавляется к определенному числу, сумма умножается на 5, произведение делится на 9 и 3 вычитается из частного. Остающийся остаток — 12. Какое число?
[AFCAT, 2014]
(а) 20 | (б) 30 |
(в) 40 | (г) 5 |
81,10 прибавляется к определенному числу, сумма умножается на 7, произведение делится на 5 и 5 вычитается из частного.Остается половина от 88. Какое число?
[AFCAT, 2014]
(а) 21 | (б) 20 |
(в) 25 | (г) 30 |
82. Если что равно?
83. Если и 8a + 5b = 22, то значение a равно
84. Если (a — b) на 6 больше, чем (c + d) и (a + b) на 3 меньше, чем (c — d), то значение (a — c) равно
(а) 0.5 | (б) 1.0 |
(в) 1,5 | (г) 2,0 |
85. Мальчика попросили умножить число на 25. Вместо этого он умножил число на 52 и получил ответ на 324 больше, чем правильный ответ. Число, которое нужно умножить, было
.(а) 12 | (б) 15 |
(в) 25 | (г) 32 |
86.Сумма двух нечетных чисел равна 38, а их произведение — 325. Что в три раза больше большего числа?
[Специалист IBPS (ИТ), CWE, 2014]
(а) 42 | (б) 39 |
(в) 75 | (г) 72 |
(д) 78 |
87. Какая единица измерения используется в продукте?
88.Пусть двузначное число в k раз больше суммы его цифр. Если число, образованное перестановкой цифр, в m раз превышает сумму цифр, то значение m равно
.[C.D.S. 2016-I]
(а) 9 — к | (б) 10 — к |
(в) 11 — к | (д) к — 1 |
89. Рассмотрим следующие утверждения в отношении двух разных ненулевых целых чисел p и q
1.Чтобы быть меньше, q должно быть отрицательным.
2. Чтобы быть больше, и p, и q должны быть положительными.
Какое из приведенных выше утверждений является правильным?
[C.D.S. 2016-I]
(a) 1 только | (б) 2 только |
(c) И 1, и 2 | (d) Ни 1, ни 2 |
90.Цифра в месте единицы результирующего числа выражения —
.[C.D.S. 2015-II]
91. Число при делении на 7 оставляет остаток 3, а полученное частное при делении на 11 дает остаток 6. Если такое же число при делении на 11 дает остаток m, а полученное частное при делении на 7 дает остаток n . Каковы значения m и n соответственно?
[C.D.S. 2015-II]
(а) 1 и 4 | (б) 4 и 1 |
(с) 3 и 6 | (г) 6 и 3 |
92.Какое количество возможных пар (P, Q), если число 357P25Q делится как на 3, так и на 5?
[C.D.S. 2015-I]
(а) 7 | (б) 6 |
(в) 5 | (d) Ничего из вышеперечисленного |
93. Умножение трехзначного числа XY5 на цифру Z дает X 215. Чему равно X + Y + Z?
[C.D.S. 2014-II]
(а) 13 | (б) 15 |
(в) 17 | (г) 18 |
94.Сколько пар натуральных чисел m и n удовлетворяют уравнению, где n — нечетное целое число меньше 60?
[C.D.S. 2014-II]
95. Сколько пар X и Y возможно в числе 763X4Y2, если число делится на 9?
[C.D.S. 2014-II]
(а) 8 | (б) 9 |
(в) 10 | (г) 11 |
96.Рассмотрим следующие утверждения:
I. 7710312401 делится на 11.
II. 173 — простое число.
Какое из приведенных выше утверждений является правильным?
(а) Только я | (б) Только II |
(c) И I, и II | (d) Ни I, ни II |
97. Рассмотрите следующие утверждения:
I. Чтобы получить простые числа меньше 121, мы должны отбросить все кратные 2, 3, 5 и 7.
II. Каждое составное число меньше 121 делится на простое число меньше 11.
Какое из приведенных выше утверждений является правильным?
(а) Только я | (б) Только II |
(c) И I, и II | (d) Ни I, ни II |
98. Когда натуральное число n делится на 4, остаток равен 3. Каков остаток от деления 2n на 4?
99.Трехзначное число делится на 11, и его цифра на месте единицы равна 1. Это число на 297 больше, чем число, полученное путем перестановки цифр. Какой номер?
(а) 121 | (б) 231 |
(в) 561 | (г) 451 |
100. Что можно сказать о расширении, где n — положительное целое число?
(a) Последняя цифра 4 | (b) Последняя цифра 8 |
(c) Последняя цифра 2 | (d) Последние две цифры равны нулю |
1.(в) | 2. (а) | 3. (а) | 4. (г) | 5. (а) | 6. (в) | 7. (а) | 8. (в) | 9. (а) | 10. (б) |
11. (б) | 12. (г) | 13. (б) | 14. (в) | 15.(в) | 16. (а) | 17. (а) | 18. (б) | 19. (в) | 20. (в) |
21. (в) | 22. (в) | 23. (б) | 24. (в) | 25. (а) | 26. (б) | 27. (а) | 28.(а) | 29. (б) | 30. (а) |
31. (а) | 32. (г) | 33. (а) | 34. (г) | 35. (г) | 36. (б) | 37. (г) | 38. (в) | 39. (г) | 40. (г) |
41.(б) | 42. (г) | 43. (а) | 44. (в) | 45. (а) | 46. (а) | 47. (г) | 48. e) | 49. (в) | 50. (а) |
51. (г) | 52. (г) | 53. (а) | 54.(в) | 55. (г) | 56. (г) | 57. (в) | 58. (б) | 59. (в) | 60. (в) |
61. (б) | 62. (в) | 63. (г) | 64. (в) | 65. (в) | 66. (г) | 67.(а) | 68. (а) | 69. (б) | 70. (б) |
71. (б) | 72. (в) | 73. (б) | 74. (в) | 75. (г) | 76. (б) | 77. (а) | 78. (б) | 79. (б) | 80.(а) |
81. (в) | 82. (г) | 83. (в) | 84. (в) | 85. (а) | 86. (в) | 87. (в) | 88. (в) | 89. (в) | 90. (г) |
91. (а) | 92. (а) | 93.(а) | 94. (г) | 95. (г) | 96. (в) | 97. (в) | 98. (б) | 99. (г) | 100. (г) |
УРОВЕНЬ — ЛЕГКО
1.
По приведенным данным, целиком делится на 3.
Следовательно, наименьшее значение A равно 2.
Следовательно, делится в точности на 3.
2. Для любого четного натурального числа n в точности делится на.
полностью делится на (29 + 1), т.е. 30.
Разделив на 30, мы получим 1 в качестве остатка.
3. Номинальное значение 0 равно 0.
Разрядное значение 0 равно
Следовательно, разница между местом и номиналом равна 0.
4. Разница = 30000 — 30 = 29970
5.
6. Возьмем из вариантов 1872,
Его последняя цифра — 2.
Умножение на 4
Добавьте к оставшемуся числу 187 + 8 = 195
195 делится на 13.
Итак, данное число 1872 делится на 13.
7. Умножьте последнюю цифру на 2 и прибавьте результат к оставшимся цифрам, чтобы найти делимость 19.
Для 13 умножьте последнюю цифру на 4 и прибавьте результат к оставшимся цифрам.
Для 17 умножьте последнюю цифру на 5 и вычтите результат из оставшихся цифр.
Для 14 число должно делиться как на 2, так и на 7.
8. Вариант (а), 802 — четное число, которое делится на 2. Таким образом, это не простое число.
Вариант (б), ближайшее целое число 29
то есть
Простые числа меньше 29 — это 23, 19, 17, 13, 11, 7, 5, 3 и 2.
803 делится на 11. Значит, это не простое число.
Вариант (в), ближайшее целое число 29
то есть
Простые числа меньше 29 — это 23, 19, 17, 13, 11, 7, 5, 3 и 2.
809 не делится ни на одно из этих простых чисел. Итак, это простое число.
Следовательно, вариант (c) — правильный ответ.
9. Дано K четное простое число. Итак, K = 2
Потому что мы знаем, что 2 — единственное четное простое число.
Итак, имеем
4К 1396 421396
Чтобы получить разряд «K», мы должны посчитать количество цифр после 2.
После 2 четыре цифры.
Следовательно, значение позиции «K» равно 20000.
10. Общее количество флагов = 265476
Количество оранжевых флажков = 7542
Количество фиолетовых флагов = 265476 — 7542 = 257934
Следовательно, у Таншики 257934 фиолетовых флага
11. Разрядность 9 — номинал 9 = 9000 — 9 = 8991
12. 8340 — 3215 — 1132 = 3993
13. Сумма цифр в 632817, т.е. 6 + 3 + 2 + 8 + 1 + 7 = 27, что делится на 3.
14. Мы знаем, что сумма цифр в числе делится на 3, тогда число также делится на 3.
Заменить * на п.
6 + 8 + 7 + 6 + p + 2 + 2 = 31 + p, что делится на 3.
Наименьшее значение, которое нужно добавить к 31, чтобы число делилось на 3, равно 2. То есть. р = 2.
Когда 2 ставится на место *, данное число становится 6876222 и делится на 3.
15. Последние две цифры данного числа составляют 62, что не делится на 4.
Следовательно, 47820262 делится на 4.
16. В 5368 последние три цифры — 368, которые можно разделить на 8.
Следовательно, 5368 делится на 8.
17. Сумма цифр 8325 = 8 + 3 + 2 + 5 = 18, что делится на 9.
Следовательно, 8325 делится на 9.
18. Обязательная сумма всех простых чисел (не больше 17)
= 2 + 3 + 5 + 7 + 11 + 13 + 17 = 58
19. НОК 4 и 6 = 12
Требуемое количество целых чисел
=
20. НОК 32, 36, 48, 54 = 864
Требуемое число = 10000 — 864 = 9136
21.
22.
23 365,089 — х + 89,72 = 302,35
454,809 — 302,350 = х
х = 152,459
24. Вариант (а), 6x = 24
Вариант (б), 6x = 30
Вариант (в), но
Следовательно, 35 не может быть общим количеством детей в классе.
25.
= 2709,18
26.? = 333,33 + 33,33 + 3,3
= 369,96
27.
= 11952–9090
= 2862
28.8052 — 9883 + 6048 =? 25
29. 8536 + 5824 =? 40
14360 =? 40
30.? = 566,91 + 551,34 + 114,98
= 1233,23
31. 3463 295 — 18611 =? + 5883
1021585 — 18611 =? + 5883
1002974 =? + 5883
? = 1002974 — 5883
= 9
32. 4003 (70 + 7) — 21015
280210 + 28021 — 21015
287216 =? 116
? = 287216 116 = 2476
33.
34.? = 302,46 + 395,72 — 123,47
= 698,18 — 123,47
= 574,71
35.
0,2254 + 313,06 =?
? = 313,2854
36. Пусть
Затем,
37. Пусть
Затем,
38. Пусть
Затем,
39. Дана сумма
40. Данное выражение
41.
42.Данное выражение
43. Данное выражение
44. Данное выражение
45.
46.
Ясно, что 968 не делится на 3
Ни одно из 462 и 2178 не делится на 4.
5184 не делится на 11.
Каждый из оставшихся четырех членов делится на каждое из 4, 3 и 11. Итак, таких чисел 4.
47., не делится на 11.
, не делится на 11.
, не делится на 11.
, Итак, 415624 делится на 11.
48. Данное выражение
49. Цифра в единицах = Цифра в единицах
Но, единица измерения
Цифра в
50. 25 простых чисел меньше 100. Это: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61. , 67,71, 73, 79, 83, 89 и 97.
51. Размер дивидендов составляет
.Здесь четное n делится как на (7 + 5), так и на (7-5)
делится на 12 и 2.Следовательно, он делится на 12 и 2.
Итак, вариант (d) верен
52. 876p37q делится на 225 или.
q должно быть 5, а сумма всех цифр должна быть разделена на 9.
p = 0 или 9.
Следовательно, вариант (d) — правильный ответ.
53,81 × 82 × 83 × 84 ×… × 99
Можно записать как = 81 × 82 × 83 ×… × 90 ×… × 99
Когда мы умножаем любое число на 10, то в результирующем числе всегда остается ноль на месте единицы.
54.
= 6,
, т.е. максимальное число 5 равно 6.
55. => Последняя цифра 7
Мы знаем, что 7 повторяет свою единичную цифру 4 раза. =>
Блок из 7 × 7 × 7 × 7 = 2401.
Теперь 256 полностью разделено на 4, поэтому последняя цифра = 1
56.
Мы знаем, что =, тогда его остаток равен 1
.
57. Когда мы делим 1421, 1423 и 1425 на 12, тогда 5, 7 и 9 являются остатками соответственно.
58. Простые числа меньше 13 равны 2, 3, 5, 7, 11.
Также, используя условие, и является простым числом
Следовательно, существуют только две возможные пары, то есть (3, 5, 11) и (5, 7, 11).
59,360 = × × 5
Количество делителей = (3 + 1) (2 + 1) (1 + 1)
= 4 × 3 × 2 = 24
60. Остаток от
61. Если m и n натуральные числа, то иррационально, если n не является степенью целого числа.
62. Если положительное четное целое и отрицательное нечетное целое число, то является рациональным числом.
63. и.
Только вариант (d) с и лежит между 0,25 и 0,75.
64. Здесь 7 и 3 повторяют свою единичную цифру четыре раза.
= + =
= 9 + 9 = 18. Итак, его единичная цифра = 8
.65. Мы знаем, что если n — нечетные числа, то оно делится на a + b.
Итак,. Теперь 40 делится как на 10, так и на 20.
Значит, число делится на 10 и 20.
УРОВЕНЬ — СЛОЖНЫЙ
66. Правило делимости числа 8: последние три цифры должны делиться на 8.
Заменить * на 5, так как 152 полностью делится на 8.
67.
, что делится на 10
68. Проверим вариант (а) 1071, последняя цифра 1.
Умножить последнюю цифру на 5
Вычтем из оставшегося числа 107 — 5 = 102.
102 делится на 17.
Итак, число 1071 делится на 17.
69. Найти делимость на 11:
Сумма нечетных цифр — сумма четных цифр = 0 или кратная 11.
Сумма нечетных цифр — Сумма четных цифр
= (8 + 3 + 7 + 1 + 5) — (9 + 7 + 0 + 2 + 6)
= 24–24 = 0
Следовательно, данное число 8
1256 делится на 11.
70. Вариант (а), ближайшее целое число 25
то есть
Простые числа меньше 25 — это 23, 19, 17, 13, 11, 7, 5, 3 и 2.
621 делится на 23. Значит, это не простое число.
Вариант (б), ближайшее целое число 18
то есть
Простые числа меньше 18 — это 17, 13, 11, 7, 5, 3 и 2.
317 не делится ни на одно из этих простых чисел. Итак, это простое число.
Вариант (в), ближайшее целое число 24
то есть
Простые числа меньше 24 — это 23, 19, 17, 13, 11, 7, 5, 3 и 2.
539 делится на 11.Итак, это не простое число.
Вариант (г), ближайшее целое число 23
то есть
Простые числа меньше 23 — это 19, 17, 13, 11, 7, 5, 3 и 2.
493 делится на 17. Значит, это не простое число.
Следовательно, вариант (б) — правильный ответ.
71. Частное = 2074, остаток = 11
Требуемое число для добавления = 19 — 11 = 8.
72. Частное = 1619, остаток = 14
Требуемое число для вычитания = 14.
Т.е. 27537 — 14 = 27523
Разделив 27523 на 17, мы получим частное = 1619, а остаток = 0.
Следовательно, 14 — это наименьшее число, которое необходимо вычесть из 27537, чтобы получить число, точно делимое на 17.
73. Дано
Следовательно,
74. Мы знаем, что если разница суммы нечетных цифр и суммы четных цифр равна 0 или кратна 11, то число делится на 11.
Данный номер есть.
Здесь или кратно 11.
Следовательно, оба утверждения верны.
75. Разделив 4000 на 19, получим остаток 10.
Требуемое число для добавления = 19-10 = 9
76. Минимальное количество из 4 цифр = 1000
НОК 12, 15, 20, 35 = 420
Требуемый номер:
(минимум)
= 1260 + 5 = 1265
77. Пусть единица и разряды десятков числа будут x и y соответственно.
Тогда число 10y + x
По вопросу
6 (10x + y) = 5 (10y + x)
55x — 44y = 0
5x — 4y = 0 и y — x = 1
Решение обоих уравнений, x = 4, y = 5
Следовательно, число
78.
Произведение двух средних чисел = 77
Самое большое простое число
79. Пусть искомое число = х
По вопросу
80.Предположим, что число =
Затем,
81. Допустим, номер
.Затем,
7x + 45 = 220
7x = 220 — 45 = 175
82.
21a = 15a + 15b
6a = 15b
83.
11b = 22
б = 2
84.а — б = с + г + 6 → (я)
a + b = c — d — 3 → (ii)
Добавление ур. (i) и (ii)
2a = 2c + 3
2a — 2c = 3
2 (а — в) = 3
85. Пусть число
86. Первое число = x
Второе число = 38 — x
х (38 — х) = 325 = 25 (38-25)
х = 25
Требуемый ответ = = 75
87. Цифра
Единичная цифра
Единичная цифра Единичная цифра
Единичная цифра
Единичная цифра Единичная цифра -.
Единичная цифра Единичная цифра
Требуемая цифра = Цифра единицы в
88. Пусть двузначное число
Согласно вопросу,
1-е условие,…. (1)
2-е условие,…. (2)
Складывая (1) и (2), получаем
Вариант (c) правильный.
89,1. Если
1 верно
2. Если
должно быть положительным также положительным (2) верно
И 1, и 2 верны.
90.
Посмотреть выкройку:
Итак, при нечетной степени 4 мы получаем цифру единицы как «4», а при четной степени 4 мы получаем цифру единицы как «6».
=> цифра 6
=> цифра единицы — 4
=> цифра единицы будет (6 + 4 = 10) нулем.
91. Это пример последовательного деления. Пусть число будет N. Число и последовательные частные, последовательные делители и соответствующие остатки приведены в таблице ниже:
Коэффициенты | N | ||
Делители | 7 | 11 | |
остаток | 3 | 6 |
Одно значение N равно.
В целом N = 77K + 45
т.е. m = 1
и, и n = 4
92. Дан номер 357P25Q.
Если он делится на 3, тогда сумма цифр должна быть разделена на 3, а если она делится на 5, то ее единица измерения должна быть 0 или 5.
= 3 + 5 + 7 + P + 2 + 5 + Q
Случай Q = 0 ⇒ 3 + 5 + 7 + P + 2 + 5 + 0 = 22 + P
Возможные значения P = 2, 5, 8
Случай, когда Q = 5 ⇒ 3 + 5 + 7 + P + 2 + 5 + 5 = 27 + P
Возможные значения P = 0, 3, 6, 9
Возможные пары (P, Q) = (2, 0), (5, 0), (8, 0) (0, 5), (3, 5) (6, 5) (9, 5)
Общее количествопар = 7.
93. Здесь трехзначное число =
.Итак, может принимать значения 1, 3, 5, 7 и 9. Но только 9 ему удовлетворяет, тогда = 1, = 3 и = 9
Значение X + Y + Z = 1 + 3 + 9 = 13
94. данное уравнение,
⇒
.⇒
.⇒
.… (i)
Здесь as и — положительные целые числа, поэтому n> 48. Но это нечетное целое число меньше 60, поэтому возможные значения = 49, 51, 53, 55, 57 и 59.
Но если положить = 53, 55 и 59 в уравнение. (i) получаем нецелые значения
Положив = 49, 51 и 57, мы получим значение = 588, 204 и 76 соответственно.
Следовательно, существует три возможных пары m, удовлетворяющих уравнению.
95. Если сумма всех цифр делится на 9, то число делится на 9
Данный номер
Данное число делится на 9.
Итак,
⇒
.Ясно, что LHS делится на 9, если
Теперь сумма и в 5, тогда возможные пары: (1, 4), (4, 1), (2, 3) (3, 2), (0, 5) и (5, 0).
Если сумма и равна 14, тогда возможными парами являются (5, 9), (9, 5), (6, 8), (8, 6) и (7, 7).
Всего возможных пар 11.
96. Ведомость I:
.Правило делимости числа 11: разница между суммой четных знаков и суммой нечетных знаков равна 0 или это число делится на 11.
Разница = Сумма нечетного места — Сумма четного места
, делится на 11.
Заявление II:
173 — это квадрат примерно 13.Итак, ниже 13 простые числа 2, 3, 5, 7, 11
Итак, 173 не делится на 2, 3, 5, 7 и 11. Итак, это простое число.
Итак, оба утверждения I и II верны.
97. Оба приведенных утверждения верны. Поскольку 121 — это квадрат 11. Итак, чтобы получить простые числа меньше 121, мы отвергаем все кратные простых чисел меньше 11, то есть 2, 3, 5 и 7.
Аналогично, каждое составное число меньше 121 делится на простое число меньше 11 i.е., 2, 3, 5 и 7.
98. Когда число n делится на 4, остаток равен 3. Теперь число удваивается, тогда остаток также удваивается.
Итак, остаток = 6. Но остаток никогда не превышает своего делителя. Итак, остаток = 6-4 = 2
99. При выборе варианта (d) обратная цифра 451 будет 154. Теперь 154 + 297 = 451 равно исходному числу.
100.
Следовательно, последние две цифры всегда равны нулю.
% PDF-1.6 % 3291 0 объект> эндобдж xref 3291 343 0000000016 00000 н. 0000015202 00000 п. 0000015340 00000 п. 0000015531 00000 п. 0000015576 00000 п. 0000015708 00000 п. 0000015955 00000 п. 0000015993 00000 п. 0000016071 00000 п. 0000019037 00000 п. 0000019195 00000 п. 0000019610 00000 п. 0000019834 00000 п. 0000020043 00000 п. 0000022714 00000 п. 0000022774 00000 п. 0000022840 00000 п. 0000022910 00000 п. 0000023008 00000 п. 0000023065 00000 п. 0000023159 00000 п. 0000023216 00000 п. 0000024385 00000 п. 0000025545 00000 п. 0000025603 00000 п. 0000026723 00000 п. 0000027899 00000 н. 0000029029 00000 н. 0000029087 00000 н. 0000030213 00000 п. 0000031386 00000 п. 0000032507 00000 п. 0000032565 00000 п. 0000033689 00000 п. 0000034865 00000 п. 0000035985 00000 п. 0000036043 00000 п. 0000037161 00000 п. 0000038339 00000 п. 0000039462 00000 п. 0000039520 00000 н. 0000040634 00000 п. 0000041806 00000 п. 0000042928 00000 п. 0000042986 00000 п. 0000044110 00000 п. 0000045281 00000 п. 0000046446 00000 н. 0000046504 00000 п. 0000047669 00000 п. 0000048834 00000 п. 0000049994 00000 н. 0000050051 00000 н. 0000051206 00000 п. 0000052382 00000 п. 0000053544 00000 п. 0000053601 00000 п. 0000054768 00000 п. 0000055946 00000 п. 0000057069 00000 п. 0000057126 00000 п. 0000058290 00000 п. 0000059467 00000 п. 0000060592 00000 п. 0000060649 00000 п. 0000061772 00000 п. 0000062954 00000 п. 0000064117 00000 п. 0000064174 00000 п. 0000065334 00000 п. 0000066502 00000 п. 0000067633 00000 п. 0000067690 00000 н. 0000068810 00000 п. 0000069986 00000 п. 0000071115 00000 п. 0000071172 00000 п. 0000072305 00000 п. 0000073487 00000 п. 0000074609 00000 п. 0000074665 00000 п. 0000075790 00000 п. 0000076975 00000 п. 0000078137 00000 п. 0000078193 00000 п. 0000079355 00000 п. 0000079458 00000 п. 0000079514 00000 п. 0000079615 00000 п. 0000079671 00000 п. 0000080805 00000 п. 0000080860 00000 п. 0000081979 00000 п. 0000082035 00000 п. 0000083154 00000 п. 0000084330 00000 п. 0000085454 00000 п. 0000085510 00000 п. 0000086627 00000 н. 0000086683 00000 п. 0000087819 00000 п. 0000087875 00000 п. 0000089016 00000 п. 0000089072 00000 н. 0000089128 00000 п. 0000089184 00000 п. 00000 00000 п. 00000 00000 п. 00000
00000 п. 0000000000 п. 00000
00000 п. 00000
00000 п. 00000
00000 п. 00000 00000 п. 00000 00000 п. 00000
00000 п. 0000000000 п. 00000
00000 п. 00000 00000 н. 0000100000 н. 00001
00000 н. 00001
00000 н. 00001 00000 н. 00001 00000 н. 00001
00000 н. 00001 00000 н. 00001
00000 н. 00001
00000 н. 0000198624 00000 н. 0000198682 00000 н. 0000198740 00000 н. 0000199860 00000 н. 0000199918 00000 н. 0000201044 00000 н. 0000201102 00000 н. 0000202240 00000 н. 0000202298 00000 н. 0000203434 00000 н. 0000203492 00000 н. 0000204628 00000 н. 0000204686 00000 н. 0000205826 00000 н. 0000205884 00000 н. 0000207020 00000 н. 0000207078 00000 н. 0000207136 00000 н. 0000207194 00000 н. 0000208327 00000 н. 0000208385 00000 н. 0000208443 00000 н. 0000208501 00000 н. 0000208559 00000 н. 0000208617 00000 н. 0000208675 00000 н. 0000208733 00000 н. 0000208791 00000 н.
| 00000 п.
0000097501 00000 п.
0000097557 00000 п.
0000098689 00000 п.
0000098745 00000 п.
0000099881 00000 п.
0000099937 00000 н.
0000099993 00000 н.
0000100050 00000 н.
0000101197 00000 н.
0000101254 00000 н.
0000102389 00000 н.
0000102446 00000 н.
0000103592 00000 п.
0000103648 00000 н.
0000104797 00000 н.
0000104853 00000 н.
0000105987 00000 п.
0000106043 00000 н.
0000106099 00000 н.
0000106156 00000 п.
0000106213 00000 н.
0000106270 00000 н.
0000107401 00000 п.
0000107458 00000 н.
0000108594 00000 п.
0000108651 00000 п.
0000109784 00000 н.
0000109841 00000 н.
0000109898 00000 п.
0000111022 00000 н.
0000111079 00000 п.
0000112214 00000 н.
0000112271 00000 н.
0000113404 00000 н.
0000113461 00000 н.
0000114598 00000 н.
0000114655 00000 н.
0000115787 00000 н.
0000115844 00000 н.
0000116996 00000 н.
0000117053 00000 п.
0000118190 00000 н.
0000118247 00000 н.
0000119387 00000 н.
0000119444 00000 н.
0000120589 00000 н.
0000120646 00000 н.
0000121782 00000 н.
0000121839 00000 н.
0000121896 00000 н.
0000123013 00000 н.
0000123070 00000 н.
0000124198 00000 п.
0000124255 00000 н.
0000124312 00000 н.
0000124369 00000 н.
0000124426 00000 н.
0000125550 00000 н.
0000125607 00000 н.
0000126738 00000 н.
0000127924 00000 н.
0000129038 00000 н.
0000129095 00000 н.
0000130210 00000 н.
0000131387 00000 н.
0000132513 00000 н.
0000132570 00000 н.
0000133692 00000 н.
0000133749 00000 н.
0000134881 00000 н.
0000134938 00000 н.
0000136076 00000 н.
0000136133 00000 п.
0000137264 00000 н.
0000137321 00000 н.
0000138449 00000 н.
0000138506 00000 н.
0000138563 00000 н.
0000138620 00000 н.
0000139763 00000 н.
0000139820 00000 н.
0000140954 00000 н.
0000141011 00000 н.
0000142145 00000 н.
0000142202 00000 н.
0000143348 00000 п.
0000143405 00000 н.
0000144539 00000 н.
0000144596 00000 н.
0000145731 00000 н.
0000145788 00000 н.
0000146928 00000 н.
0000146985 00000 п.
0000148124 00000 н.
0000148181 00000 п.
0000148238 00000 п.
0000148295 00000 н.
0000149435 00000 н.
0000149492 00000 н.
0000150629 00000 н.
0000150686 00000 н.
0000151821 00000 н.
0000151878 00000 н.
0000151935 00000 н.
0000151992 00000 н.
0000153117 00000 н.
0000153174 00000 н.
0000154301 00000 н.
0000155474 00000 н.
0000156591 00000 н.
0000156648 00000 н.
0000157764 00000 н.
0000157821 00000 н.
0000158953 00000 н.
0000159010 00000 н.
0000160150 00000 н.
0000160207 00000 н.
0000161347 00000 н.
0000161404 00000 н.
0000162545 00000 н.
0000162602 00000 н.
0000162659 00000 н.
0000162716 00000 н.
0000163847 00000 н.
0000163904 00000 н.
0000165043 00000 н.
0000165100 00000 н.
0000166233 00000 н.
0000166290 00000 н.
0000166347 00000 н.
0000167474 00000 н.
0000167531 00000 н.
0000168652 00000 н.
0000168709 00000 н.
0000169847 00000 н.
0000169904 00000 н.
0000171037 00000 н.
0000171094 00000 н.
0000171151 00000 н.
0000172274 00000 н.
0000172331 00000 н.
0000173449 00000 н.
0000174622 00000 н.
0000175743 00000 н.
0000175800 00000 н.
0000176928 00000 н.
0000176985 00000 н.
0000178119 00000 н.
0000178176 00000 н.
0000178233 00000 н.
0000178291 00000 н.
0000179430 00000 н.
0000179488 00000 н.
0000180625 00000 н.
0000180683 00000 н.
0000180740 00000 н.
0000181862 00000 н.
0000181919 00000 н.
0000183047 00000 н.
0000183104 00000 п.
0000184236 00000 п.
0000184293 00000 н.
0000185427 00000 н.
0000185484 00000 н.
0000185541 00000 н.
0000186669 00000 н.
0000186727 00000 н.
0000187852 00000 н.
0000189029 00000 н.
00001 00000 н. 00001 00000 н. 00001 00000 н. 00001 00000 н. 00001 00000 н. 00001 00000 н. 00001 |



 Записываем эту цифру под 1460. Получается разность 28, записываем под чертой
Записываем эту цифру под 1460. Получается разность 28, записываем под чертой
Leave A Comment