Проект 7. Супернебоскреб

Давайте начнем с того, что вычислим, на какой высоте жильцы супернебоскреба будут находиться в невесомости.

Поскольку Земля вращается вокруг своей оси с периодом Т = 24 ч, ее угловая скорость равна

Ясно, что с такой же угловой скоростью вращается и жилец супернебоскреба. А значит, он движется с центростремительным ускорением, равным по величине: a = ω2(R + h), где R — радиус земли, а h — высота над поверхностью Земли.

На жильца массой m, находящегося на высоте h над поверхностью Земли, действуют, вообще говоря, две силы: сила тяготения, где R — радиус Земли, а M — масса Земли (рис. 7.1), и сила нормальной реакции N. Равнодействующая этих сил и сообщает жильцу центростремительное ускорение.

Согласно второму закону Ньютона можем записать:

Из формулы (7.1) видно, что N всегда меньше F

т, и чем больше h, тем меньше N. В условиях невесомости N = 0, тогда

Подставим численные значения: М = 6,0·1024 кг, G = 6,67·1011 (H·м2/кг2), ω ≈ 7,27·10–5 рад/c. Получим:

= 35906076 м ≈ 35,9·103 км.

Как видим, высота, на которой достигается невесомость, примерно в 6 раз больше радиуса Земли, но ничего: уж если строиться — так строиться с размахом!

Главное, чисто теоретически барон прав: в супернебоскребе можно действительно выбрать себе для проживания этаж, на котором всегда существует невесомость!

Если подняться на высоту, большую, чем 35,9 тысяч километров, то сила нормальной реакции, рассчитанная по формуле (7.1), станет отрицательной величиной. Это значит, что для того, чтобы сообщить жильцу центростремительное ускорение, силы тяготения будет уже недостаточно и силе нормальной реакции придется ей «помогать» (рис.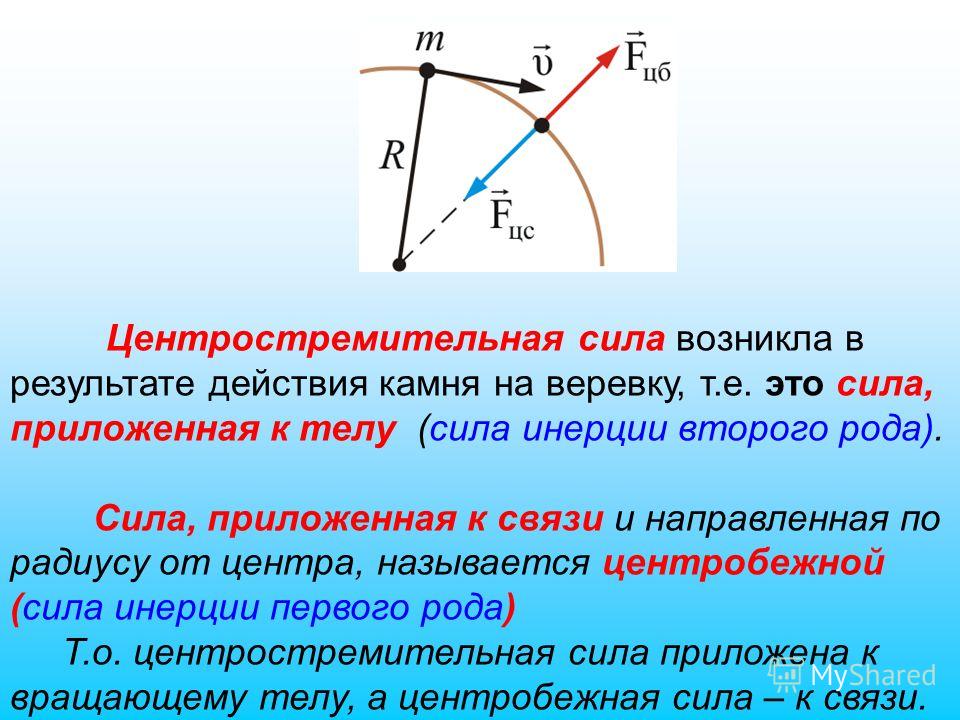

 7.2). При этом «верх» и «низ» для жильца как бы поменяются местами: он сможет спокойно стоять на потолке, на потолок нужно будет поставить и всю необходимую мебель.

Профессор в данном случае прав: речь идет именно о центробежном эффекте: во вращающейся системе отсчета (на карусели, например) все тела как бы отбрасываются от центра к периферии.

Абсолютно прав и Инженер: верхние этажи здания находятся в открытом космосе, поэтому, если супернебоскреб не будет абсолютно герметичным, жильцы на верхних этажах погибнут от полного отсутствия воздуха. Причем герметичным надо сделать не только весь небоскреб, но желательно и каждый этаж в отдельности.

Прав и Бизнесмен: в таком доме отличные условия для тренировки космонавтов!

Далее: Проект 8. Запуск спутника на орбиту без затрат энергии

F = f — Орбитальное движение планет

13 августа, 2016 — 12:21

#1

Fermer05

Не в сети

F = f — Орбитальное движение планет

F = f — Орбитальное движение планет 

Планеты удерживаются на орбите благодаря гравитационной (F) и центробежной (f) силам, которые должны быть взаимно уравновешаны. 
F = f. 
F = G×m1×m2/r2. 
f = m×v2/r. 
Благодаря гравитационной силе планеты не срываются с орбиты, а благодаря центробежной силе планеты не падают на Солнце. 
Полагаю, орбитальное движение планет должно опиратся на равенство F = f. 

http://www.mikesokol.narod.ru/ris9.gif

Считается, что планеты движутся по орбите благодаря только гравитационной силе, без участия центробежной силы. Считается, что центробежная сила (сила инерции) это сила классической механики и что в небесной механике ее не существует, а центростремительная сила (гравитационная сила), это сила небесной механики. . 
Центробежная сила, направлена от центра вращения, а центростремительная сила направлена к центру вращения, а формула у них общая f = m×v2/r. 
Гравитационная сила http://goo.gl/scq3m5 
Центробежная сила http://goo.gl/XXuw9I 

Наводящие вопросы: 
1. Если гравитационная и центростремительная сила, это одно и тоже явление природы, так почему у них разные формулы 
F = G×m1×m2/r2. 
f = m×v2/r.
http://www.physic-in-web.ru/study-22-1.html 
2. Почему в интернете нету описания орбитального движения планет? 
3. Почему в интернете не возможно найти статью о практическом применении формулы центростремительной силы? 
4. Почему в законе всемирного тяготения, об орбитальном движении планет ничего не пишется http://goo.gl/uarUo8 
5. Почему в формуле закона всемирного тяготения F = G×m1×m2/r2, отсутствует величина орбитальной скорости. 
6. Какую тайну природы, раскрывает закон всемирного тяготения?
—————————— 

Зако́н всемирного тяготе́ния—гласит, что сила гравитационного притяжения между двумя материальными точками пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними. 
 
И ни слова, о центростремительной и центробежной силе и орбитальном вращении планет.

Физика — 10

  1. Почему ускорение при равномерном движении тела по окружности называется центростремительным, или нормальным ускорением?
  2. Вычислите модуль центростремительного ускорения Земли, вращающейся вокруг Солнца (радиус орбиты Земли R = 1,5 ⋅ 10
    8    км).
  3. С какой линейной скоростью вращается Земля вокруг Солнца (радиус орбиты Земли R = 1,5 ⋅ 108км)?
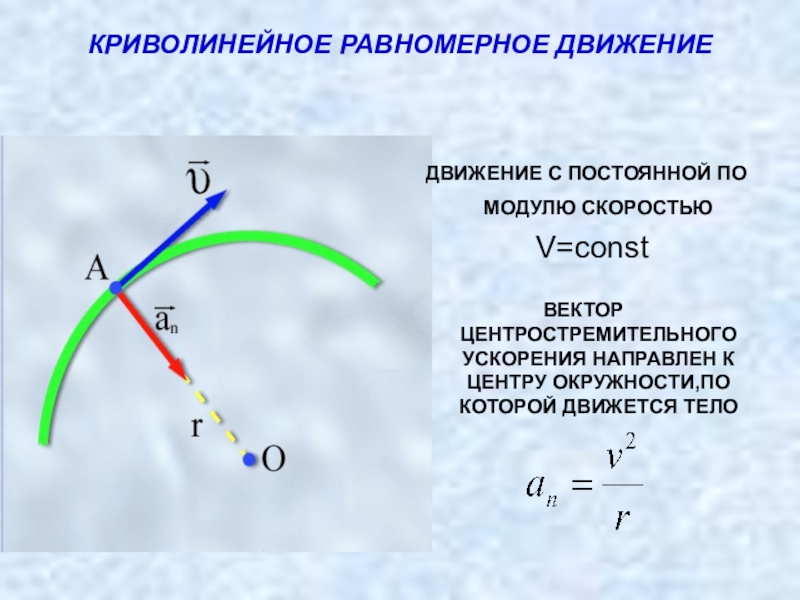
ЧТО ВЫ УЗНАЛИ? Дайте определения нижеприведенных понятий и величин: “угол поворота”, “угловая скорость”, “линейная скорость”, “центростремительное ускорение”, “период вращения”, “частота вращения”.

• ПРОЕКТ • Постройте “КАРТУ ПОНЯТИЙ” равномерного движения по окружности.

Задачи к I главе

1.1.

Определите координаты материальной точки на плоскости ХОУ, зная, что модуль его радиус-вектора, образующего с осью ОХ угол 30°, равен 5 м.

1.2.

Координаты материальной точки М равны xM = 1 м и yM = 1,5 м, а координаты точки N равны xN = 3 м и yN = — 2 м. Определите:
a) модуль вектора, соединяющего точки М и N;

b) проекции этого вектора на оси ОХ и ОУ;
c) угол между этим вектором и осью ОХ.

1.3.

Векторы взаимно перпендикулярны (рис.1).
Определите:
a) результирующий вектор;
b) модуль результирующего вектора.

1.4.

Определите проекции представленных на рисунке (рис.2) векторов на координатные оси ОХ и ОY.

1.5.

Спортсмен, бегая во время тренировки по круговой траектории радиусом 60 м, пробежал 10 кругов. Определите путь, пройденный спортсменом. Чему равен модуль его перемещения (π = 3)?

В результате перехода спутника Земли с одной круговой орбиты на другую его центростремительное ускорение уменьшается. Как изменяются в результате этого перехода потенциальная энергия спутника в поле т

В результате перехода спутника Земли с одной круговой орбиты на другую его центростремительное ускорение уменьшается. 2}{\mathrm R}\;\;\mathrm{где}\;\mathrm v\;\;\mathrm{линейная}\;\mathrm{скорость}\;\mathrm{движения}\;\mathrm{точки}(\mathrm{тела}\;\mathrm{по}\;\mathrm{окружности}$$

На тело движущееся по кривой(окружности в частности) действует центростремительное ускорение (оно показывает быстроту изменения направления движения) чем больше радиус дуги или линейная скорость тем меньше центростремительное ускорение (тк за равные промежутки времени точка(тело) меньше «поворачивает» .

И так, спутник движется по круговой орбите, перешел на другую круговую орбиту, его центростремительное ускорение уменьшилось. Это одновременно свидетельствует о том что радиус его орбиты увеличился а скорость уменьшилась (если бы изменилось что-то одно то не выполнялся бы закон сохранения энергии или орбита не была бы круговой).

Потенциальная энергия -это часть механической энергии системы в поле консервативных сил (силы — работа которых зависит только от координат (начальных и конечных положений тел, или расстояний между ними.))

$${\mathrm E}_\mathrm p=\mathrm{mgh}$$ радиус орбиты это высота над поверхностью, он увеличился, а значит и энергия тоже возросла.

12

Что такое центростремительное ускорение? | Sci-Blog

Центростремительное ускорение сопровождает нас по всюду. Оно заставляет нашу Землю вращаться вокруг Солнца,а сила тяжести позволяет нам существовать на этой планете.Так и что же такое центростремительное ускорение?

Центростремительное ускорение – это то, как быстро изменяется тангенциальная скорость, или проще говоря скорость, с которой движется орбитальное тело. Он включает в себя как величину, так и направление изменения тангенциальной скорости. Когда объект движется с круговым движением , ускорение всегда указывает прямо в центр круга. Он имеет величину, связанную с угловой скоростью и скоростью объекта.

Если тело движется по прямой линии, то его ускорение описывает скорость изменения скорости. Если объект движется по круговой траектории, то центростремительное ускорение объясняет, как быстро изменяется его тангенциальная скорость. Тангенциальная скорость – это мера того, насколько быстро объект меняет направление или движется по кругу, а также фактическую скорость, с которой он движется.

Центростремительное ускорение является вектором, что означает, что оно имеет величину и направление. Направление всегда указывает внутрь к центру круга, потому что это направление, в котором вращающийся объект всегда ускоряется. Это часто сбивает с толку понятие, потому что объект, подвергающийся круговому движению, кажется, не ускоряется к центру круга. Это потому, что, согласно законам Ньютона, ускорение объекта всегда происходит в направлении действия силы. Чтобы объект двигался по кругу, должна быть сила, исходящая из центра круга, так что это направление ускорения.

Центростремительное ускорение тесно связано с центростремительной силой . Согласно законам Ньютона, центростремительная сила равна центростремительному ускорению, умноженному на массу объекта. Другими словами, центростремительная сила – это общая сила, действующая на объект, который заставляет его двигаться по кругу.

Примером кругового движения является луна, вращающаяся вокруг Земли. Когда луна вращается, она находится под действием силы тяжести Земли. Это означает, что он постоянно «падает» к Земле и, следовательно, имеет центростремительное ускорение, направленное к центру Земли, даже если он сохраняет скорость, достаточную для того, чтобы оставаться на круговой орбите.

Ваш вес меняется между полюсами и экватором? (Средний)

Привет, я учусь в седьмом классе в Вашингтоне. У меня был такой вопрос: Земля вращается, поэтому у экватора Земли центробежная сила больше, чем у Северного полюса, потому что экватор вращается быстрее. Итак, если бы вы жили на экваторе, разве вы не весили бы меньше, чем кто-то, живущий на Северном полюсе, потому что есть большая сила, пытающаяся оторвать вас от Земли? Спасибо за ваше время и усилия.Я очень ценю это.

Вы правы, что из-за центробежной силы вы будете весить на экваторе немного меньше, чем на полюсах. Однако постарайтесь не думать о центробежной силе как о силе; на самом деле происходит то, что объекты, которые движутся, любят двигаться по прямой, и поэтому требуется некоторая сила, чтобы заставить их двигаться по кругу. (Центробежная сила — это фиктивная сила, которая проявляется в уравнениях движения объекта во вращающейся системе отсчета, например, на экваторе Земли.)

Итак, некоторая часть силы тяжести (центростремительная сила) используется для того, чтобы заставить вас двигаться по кругу на экваторе (вместо того, чтобы улетать в космос), а на полюсе в этом нет необходимости. Центростремительное ускорение на экваторе определяется как квадрат, умноженный на четыре числа пи, умноженных на радиус Земли, деленный на квадрат периода вращения (4 × π 2 × R / T 2 ). Период вращения Земли — звездные сутки (86164,1 секунды, чуть меньше 24 часов), а экваториальный радиус Земли составляет около 6378 км.Это означает, что центростремительное ускорение на экваторе составляет около 0,03 м / с 2 (квадратных метров в секунду). Сравните это с ускорением свободного падения, которое составляет около 9,8 м / с 2 , и вы увидите, насколько это незначительный эффект — на экваторе вы будете весить примерно на 0,3% меньше, чем на полюсах!

Есть дополнительный эффект из-за сжатия Земли. Земля не совсем сферическая, а, скорее, немного похожа на «сжатую» сферу (технически сплюснутый сфероид) с радиусом на экваторе, немного большим, чем радиус на полюсах.(Эту форму можно объяснить эффектом центробежного ускорения на материал, из которого состоит Земля, точно так, как описано выше.) Это дает эффект небольшого увеличения вашего веса на полюсах (поскольку вы находитесь близко к центру Земли. и сила тяжести зависит от расстояния) и немного уменьшая ее на экваторе.

Принимая во внимание оба вышеупомянутых эффекта, ускорение свободного падения составляет 9,78 м / с 2 на экваторе и 9,83 м / с 2 на полюсах, так что вы весите около 0. На полюсах на 5% больше, чем на экваторе.

Вот еще несколько страниц, на которых обсуждается это явление:

Последний раз эта страница обновлялась Шоном Маршаллом 20 сентября 2015 года.

механика | Определение, примеры, законы и факты

Механика , наука, изучающая движение тел под действием сил, включая особый случай, когда тело остается в покое. В первую очередь проблема движения — это силы, которые тела действуют друг на друга.Это приводит к изучению таких тем, как гравитация, электричество и магнетизм, в зависимости от природы задействованных сил. Учитывая силы, можно искать способ, которым тела движутся под действием сил; это предмет собственно механики.

Британская викторина

Викторина «Все о физике»

Кто был первым ученым, проведшим эксперимент по управляемой цепной ядерной реакции? Какая единица измерения для циклов в секунду? Проверьте свою физическую хватку с помощью этой викторины.

Исторически механика была одной из первых возникших точных наук. Его внутренняя красота как математической дисциплины и ранний замечательный успех в количественном учете движений Луны, Земли и других планетных тел оказали огромное влияние на философскую мысль и послужили толчком для систематического развития науки.

Механику можно разделить на три части: статика, которая имеет дело с силами, действующими на покоящееся тело и в нем; кинематика, описывающая возможные движения тела или системы тел; и кинетика, которая пытается объяснить или предсказать движение, которое произойдет в данной ситуации.В качестве альтернативы механику можно разделить по типу изучаемой системы. Простейшей механической системой является частица, определяемая как настолько маленькое тело, что его форма и внутренняя структура не имеют значения в данной задаче. Более сложным является движение системы из двух или более частиц, которые действуют друг на друга и, возможно, испытывают силы, действующие со стороны тел вне системы.

Принципы механики были применены к трем общим областям явлений.Движение таких небесных тел, как звезды, планеты и спутники, можно предсказать с большой точностью за тысячи лет до того, как они произойдут. (Теория относительности предсказывает некоторые отклонения от движения в соответствии с классической или ньютоновской механикой; однако они настолько малы, что их можно наблюдать только с помощью очень точных методов, за исключением задач, затрагивающих всю или большую часть обнаруживаемой Вселенной. ) Как вторая область, обычные объекты на Земле вплоть до микроскопических размеров (движущиеся со скоростью намного ниже скорости света) должным образом описываются классической механикой без значительных исправлений.Инженер, проектирующий мосты или самолеты, может с уверенностью использовать ньютоновские законы классической механики, даже если силы могут быть очень сложными, а вычислениям не хватает прекрасной простоты небесной механики. Третья область явлений включает поведение материи и электромагнитного излучения в атомном и субатомном масштабах. Хотя вначале были достигнуты ограниченные успехи в описании поведения атомов в терминах классической механики, эти явления должным образом рассматриваются в квантовой механике.

Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишись сейчас

Классическая механика занимается движением тел под действием сил или равновесием тел, когда все силы уравновешены. Этот предмет можно рассматривать как разработку и применение основных постулатов, впервые сформулированных Исааком Ньютоном в его Philosophiae Naturalis Principia Mathematica (1687), широко известном как Principia . Эти постулаты, называемые законами движения Ньютона, изложены ниже.Их можно использовать для предсказания с большой точностью самых разных явлений, от движения отдельных частиц до взаимодействий очень сложных систем. В этой статье обсуждается множество этих приложений.

В рамках современной физики классическую механику можно понять как приближение, вытекающее из более глубоких законов квантовой механики и теории относительности. Однако такой взгляд на место объекта сильно недооценивает его важность в формировании контекста, языка и интуиции современной науки и ученых.Наш современный взгляд на мир и место человека в нем прочно укоренен в классической механике. Более того, многие идеи и результаты классической механики выживают и играют важную роль в новой физике.

Центральными понятиями классической механики являются сила, масса и движение. Ни сила, ни масса не были четко определены Ньютоном, и оба они были предметом многих философских спекуляций со времен Ньютона. Оба они наиболее известны своими эффектами. Масса — это мера склонности тела сопротивляться изменениям в состоянии движения.С другой стороны, силы ускоряют тела, то есть они изменяют состояние движения тел, к которым они приложены. Взаимодействие этих эффектов — основная тема классической механики.

Хотя законы Ньютона фокусируют внимание на силе и массе, три другие величины приобретают особое значение, потому что их общее количество никогда не меняется. Эти три величины — энергия, (линейный) импульс и угловой момент. Любой из них может быть перемещен из одного тела или системы тел в другое.Кроме того, энергия может менять форму, будучи связанной с единственной системой, проявляясь как кинетическая энергия, энергия движения; потенциальная энергия, энергия позиции; тепло или внутренняя энергия, связанная со случайными движениями атомов или молекул, составляющих любое реальное тело; или любая комбинация из трех. Тем не менее полная энергия, импульс и угловой момент во Вселенной никогда не меняются. Этот факт выражается в физике, говоря, что энергия, импульс и угловой момент сохраняются.Эти три закона сохранения вытекают из законов Ньютона, но сам Ньютон их не выражал. Их нужно было обнаружить позже.

Примечательно то, что, хотя законы Ньютона больше не считаются фундаментальными и даже не совсем правильными, три закона сохранения, вытекающие из законов Ньютона — сохранение энергии, импульса и углового момента — остаются в точности верными даже в квантовая механика и теория относительности. Фактически, в современной физике сила больше не является центральным понятием, а масса — лишь одним из множества атрибутов материи.2 r.ac = ω2r.

Чтобы вычислить ускорение байкера, найдите изменение вектора скорости Δv⃗ = v⃗ (θ + Δθ) −v⃗ (θ) \ Delta \ vec {v} = \ vec {v} (\ theta + \ Delta \ theta) — \ vec {v} (\ theta) Δv = v (θ + Δθ) −v (θ), когда велосипед движется на угол Δθ. \ Delta \ theta.Δθ.

Увеличивая небольшой участок траектории, проверьте векторы, используемые для вычисления:

Чтобы найти разницу, выровняйте v⃗ (θ + Δθ) \ vec {v} (\ theta + \ Delta \ theta) v (θ + Δθ) и −v⃗ (θ) — \ vec {v} (\ theta) −v (θ) кончик к хвосту:

Сначала заметьте, что разность Δv⃗ \ Delta \ vec {v} Δv указывает прямо к центру круга.

Далее, очевидно, что угол между двумя векторами равен Δθ \ Delta \ thetaΔθ.

Длина разности Δv⃗ \ Delta \ vec {v} Δv определяется (приблизительно) длиной дуги, проходящей через v⃗ \ vec {v} v при ее повороте на Δθ \ Delta \ thetaΔθ. Используя s = θr, s = \ theta r, s = θr,

Δv⃗≈Δθ∣v∣. \ Delta \ vec {v} \ приблизительно \ Delta \ theta \ lvert v \ rvert.Δv≈Δθ∣v∣.

Деление обеих сторон на Δt, \ Delta t, Δt,

Δv⃗Δt≈ΔθΔt = ωv. \ Frac {\ Delta \ vec {v}} {\ Delta t} \ приблизительно \ frac {\ Delta \ theta} {\ Delta t} = \ omega v.2} {R}} ac = Rv2 и указывает прямо на центр круговой траектории. □ _ \ квадрат □

Хотя эта демонстрация показательна, она была несколько надуманной. Многие ограничения сохраняются на движение: радиус остается постоянным, скорость изменения радиуса остается постоянной, угловое ускорение отсутствует.

На самом деле существует гораздо более простой метод вычисления всех четырех ускорений, которые могут возникнуть во вращающихся системах отсчета, который включает использование теоремы Де Муавра.

Центростремительная сила, вес, напряжение


и экваториальная выпуклость Земли. Дональд Э. Симанек
Заявление об ограничении ответственности: Этот документ, как и многие другие на этом веб-сайте, является попыткой донести информацию сложная физика на языке, максимально простом, концептуальном и нематематическом. Это, конечно, трудный способ сделать это. Если бы мы использовали полномасштабное векторное исчисление аргументы могли бы быть намного компактнее и точнее.Читатель сильно настоятельно рекомендовал проконсультироваться с такими методами лечения в хороших учебниках.

Центростремительная сила.

Ускорение тела — это изменение его скорости, деленное на длительность этого изменения. a = ΔV / Δt . Поскольку скорость является вектором, любое изменение ее размера или направления , или обоих, требует ускорения. Тело, движущееся по кривой траектории, ускоряется, даже если его скорость постоянна.Следовательно, из закона Ньютона мы знаем, что результирующая сила, действующая на него, не равна нулю.

На схеме показано тело, движущееся с постоянной скоростью V по криволинейной траектории радиусом R . Показаны два положения, во время которых тело переместилось на расстояние S по дуге. В начале временного интервала скорость тела равна В 1 . В конце интервала это V 2 .Мы даем им отличительные индексы, потому что они имеют разные направления, даже хотя у них одинаковый размер. За это время тело перемещается на угол на . На справа показана векторная диаграмма связи между этими скоростями и их векторной разностью, ΔV .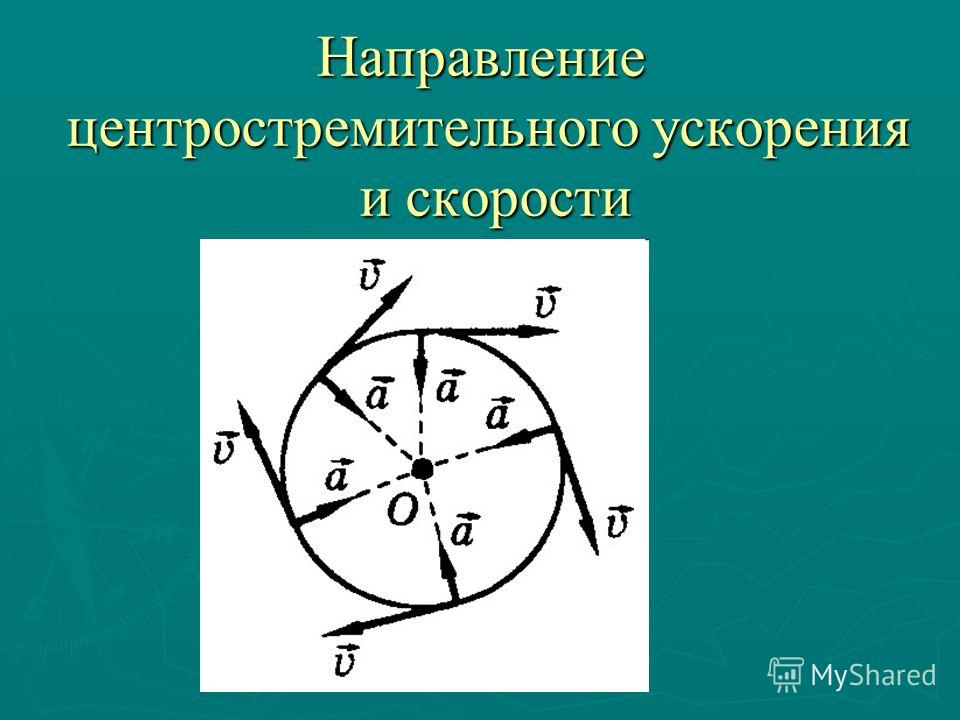

Теперь рассмотрим предельный случай, когда временной интервал становится очень маленьким, приближаясь к нулю. Угол также приближается к нулю. На диаграммах есть два одинаковых, очень тонких треугольника.Мы можем написать:

ΔS / R = ΔV / V

Итак: В δS = R ΔV

и: В (ΔS / Δt) = R (ΔV / Δt) .

Но В = ΔS / Δt , и a = ΔV / Δt , поэтому мы можем написать:

V 2 = R a , что превращается в a = V 2 / R .

Поскольку угловая скорость тела, движущегося по окружности, равна ω = VR , мы можем записать это ускорение как a = ω 2 R .(Эти формулы полезны даже в тех случаях, когда тело движется по извилистой траектории с переменной скоростью. В этом случае мы интерпретируем R, V и ω как мгновенные значения этих величин в указанной точке.)

Из закона Ньютона F = м a мы можем сказать, что сила, вызывающая ускорение, равна F = mV 2 / R = mω 2 R .

Направление вектора ускорения и силы в любой момент направлено внутрь к центру дуги и, следовательно, перпендикулярно вектору скорости в этот момент, который всегда касается кривой.

В случае извилистого движения мы можем связать эту силу и ускорение с внутренней (радиальной) составляющей любой результирующей силы, действующей на тело (массой м ). Пока это простая физика. Концептуальная проблема возникает, когда мы даем этим силам и ускорениям названия: центростремительное ускорение и центростремительная сила .

Центростремительная сила — это не какой-то новый вид силы, а просто удобное название радиальной составляющей суммы всех реальных сил, действующих на тело.

Более полное рассмотрение показало бы, что это уравнение центростремительной силы полезно для любого вида движения по кривой любого вида. Это не ограничивается кругами. Он также не ограничен постоянной скоростью по пути. Это работает, потому что любой физический путь таков, что достаточно малая его часть очень хорошо аппроксимирует круговую дугу. В расчетах мы берем предел, когда дуга становится нулевой длины, и говорим о связи между мгновенным радиусом дуги в этой точке кривой, мгновенной скоростью в этой точке и мгновенным ускорением в этой точке.Соотношение по-прежнему оказывается a = V 2 / R . И если чистая сила имеет касательную к дуге составляющую, это вызывает увеличение или уменьшение скорости тела по этой дуге.

Напряжение.

Упругие тела могут деформироваться под действием приложенных сил. Силы связи, удерживающие молекулы в положении равновесия в твердых и жидких телах действует нечто вроде пружин. Если пружина растягивается, растягивая молекулы дальше друг от друга, эти силы связи увеличиваются в размере.Они также увеличиваются в размере, когда молекулы сближаются. Мы можем смоделировать это поведение, как показано на рисунке, с пружиной, представляющей такой силы, действующие между кусками материи. Для наших ограниченных целей мы можем предположить, что Пружина по поведению приблизительно гуковская, то есть подчиняется закону Гука. В Закон говорит, что натяжение пружины T изменяется на величину ΔT = — KΔL где k — коэффициент упругости пружины, а ΔL — изменение его длины, измеренное от его исходного положения.Если напряжение увеличивается, длина пружины уменьшается. Если натяжение уменьшается, пружина длина увеличивается.

Предположим, что масса самой пружины ничтожна по сравнению с массой двух блоков материи. Следовательно, натяжение пружины оказывает равное усилие. размер на каждом из них, как показано.

F 2 и F 1 представляют силу тяжести на верхних и нижних блоках.В равновесии нижний блок должен испытывать восходящую силу F 1 + F 2 (от того, что поддерживает его снизу). Если бы они были равны по размеру, то для равновесия натяжение T также будет такого же размера.

Теперь предположим, что верхний блок стал меньше по массе. Натяжение пружины должно стать пропорционально меньшим для достижения статического равновесия. Поэтому длина пружины должна увеличиваться, немного разделяя два блока.

То же самое произошло бы, если бы какое-то дополнительное неоднородное гравитационное поле было прикладывалась к системе, так что она оказывала большую направленную вниз силу на нижний блок, чем на верхний. Натяжение пружины уменьшится, а ее длина увеличится. Но что, если такое внешнее поле вызовет более сильную направленную вверх силу на верхний блок, чем на нижнем? Опять же, натяжение пружины уменьшится, и ее длина уменьшится. увеличивать.Это становится важным, когда обсуждают земные приливы из-за неоднородной гравитационной поля с Луны.

Масса.

Вес может быть определен как сила, необходимая для удержания объекта в относительном состоянии покоя. к его окрестностям. Это определение согласуется с большинством разговорных толкований. слова (сюрприз!).

На рисунке изображен человек массой м , стоящий на весах на поверхности. земли.Весы воздействуют на его ступни с силой размером Вт , направленной вверх. Мы называем эту шкалу чтение «веса» человека. Если бы Земля была неподвижной, человек бы быть в равновесии, и у нас будет W = mg , где mg — сила тяжести на мужчину.

Думайте о масштабах как о пружине между массами. Он реагирует на стресс между ноги и пол.

Влияние вращения Земли на вес.

Но если Земля вращается, человек, весы и земля под ней движутся с скорость V по круговой траектории радиусом R , где R — радиус Земли.Эти объекты больше не находятся в статическом равновесии. У всех есть ускорение a = v 2 / R к центру Земли. Это центростремительное ускорение изменяет направление скорости, но не меняет своего размера, потому что вектор ускорения всегда направлен к центру круга и, следовательно, перпендикулярно к телу скорость в любое время.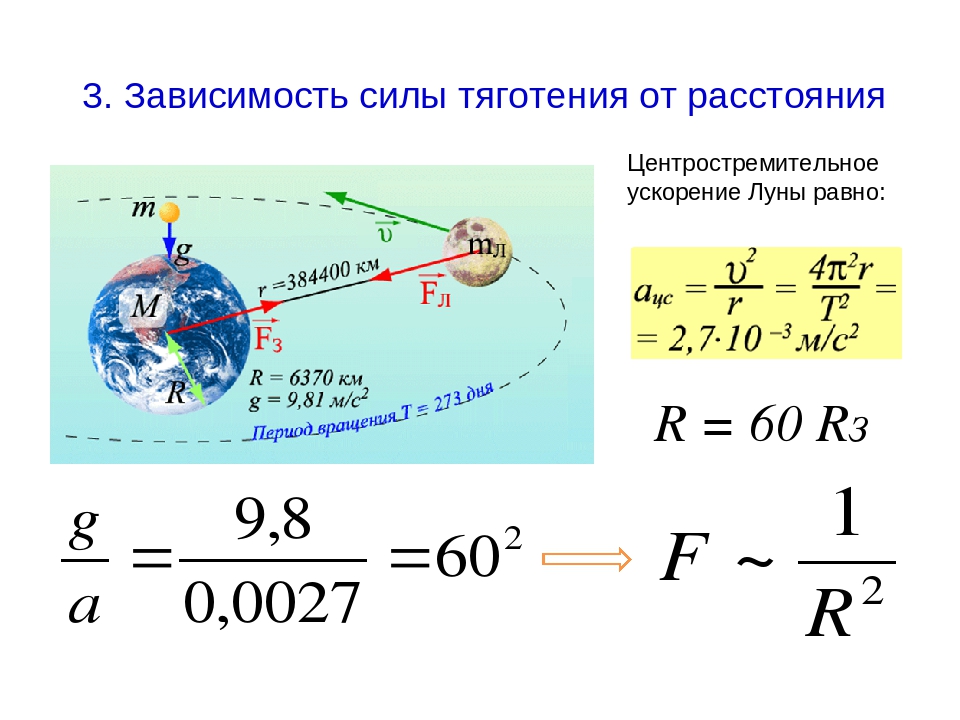

Размер человека относительно радиуса Земли на этой диаграмме сильно преувеличен.Относительные размеры сил тоже.

Закон Ньютона говорит нам, что когда тело массы m имеет ускорение a , чистая сила на корпусе должна составлять F = м a . Таким образом, величина чистой силы, действующей на этого человека, должна быть F = ma = mv 2 / R .

На рисунке показаны векторы силы W и м g , которые являются только силы действуют на человека.Вектор F — их сумма. W направлено по радиусу Земли. Являясь радиальным компонентом чистой силы (в данном случае — это чистая сила), ее размер составляет a = v 2 / R (центростремительная сила). Теперь сравните эти два случая. На невращающейся Земле вес человека был размером м г . Помните, что вес объекта — это сила, необходимая для его поддержки. я.е. усилие, прилагаемое весами вверх. Когда Земля вращается, это сила на меньше на , чем раньше. Сила контакта между ногами мужчины и масштаб уменьшен. Но все другие подобные стрессовые силы также снижаются внутри человека, в пружинах весов, в теле самой Земли. Это вызывает небольшой декомпрессия этих материалов, расслабление пружины в весах. Фактически, все тело земли немного расширяется, и человек и чешуя перемещаются наружу немного от оси вращения, пока силы не придут в равновесие с требованиями вращательной устойчивости на новом радиусе.Это причина экваториальной выпуклости. Земли из-за собственного осевого вращения.

Как мы уже говорили, диаграммы сильно преувеличены. Несложный расчет показывает, что центростремительный разгон всего 0,3% от г . Таким образом, чистая сила составляет всего 0,3% от Вт . Вес мужчины (учтенный на весах) на 0,3% меньше, чем был бы на один вес. полюсов Земли. Результирующая релаксация напряжений в материалах является причиной экваториальной выпуклости Земля, что делает экваториальный радиус на 43 километра больше полярного.

Дихотомия «причина и следствие».

Здесь мы можем столкнуться с сложной дилеммой интерпретации. Снижение веса на экватора просто из-за меньшей гравитационной силы на большем радиусе? Либо это просто из-за уменьшения напряжения между ступней и весами? Это еще один неудачное следствие использования языка «причина и следствие» в чем-то слишком сложно для такого упрощенного описания. Это также ловушка для учителей, которые позируют вопросы с несколькими вариантами ответов на экзаменах.

Предположим, кто-то говорит, что снижение веса произошло исключительно за счет увеличения радиуса. экватора и немного меньшего гравитационного поля на большем радиусе. Тогда, если бы Земля была идеально твердой и не было бы экваториальной выпуклости, из этого можно сделать логический вывод, что, поскольку радиус не меняется, то вес (зарегистрированный на весах) не меняется. Но это ложь. Вес уменьшится, как и должно быть, из-за радиального ускорения из-за кругового движения и закон Ньютона F = м a .

Если кто-то говорит, что снижение веса связано с уменьшением стресса вызванное растяжением материалов Земли, масштаба и человека, мы должны согласиться, это то, что измеряет механизм весов, и это наше определение веса. Но это снижение стресса также является причиной растяжения. Земли, и для увеличенного радиуса на экваторе. А это, в свою очередь, уменьшает гравитационная сила, создаваемая Землей на большем расстоянии.Суть в том, что что сила тяжести уменьшается, а напряжение уменьшается, , но не пропорционально . Сказать, что только одна из этих вещей является «причиной» любой другой, слишком упрощенно. быть полезным. И попытаться объяснить экваториальную выпуклость без упоминания снижение напряжения в материалах — это своего рода обман.

Здесь нужна «центробежная сила»?

Обратите внимание, что в этом обсуждении нам никогда не приходилось вводить термин «центробежная сила».Этот термин полезен только тогда, когда кто-то решает анализировать проблему, используя вращающуюся неинерциальную систему отсчета.

Неинерциальные системы координат

«Инерциальная» система координат не ускоряется. Как мы можем быть уверены, что система координат не ускоряется, когда кажется, что все во Вселенной движется и ускоряется под действием гравитатональных сил других тел? Один из способов — определить все реальные силы, действующие на тело. Если их векторная сумма на теле равна нулю, то тело не ускоряется.Другое определение «инерциальной системы отсчета» — это система отсчета, при которой тело, закрепленное в этой системе координат, строго подчиняется второму закону Ньютона, F = м a .

Но инерционные системы очень редки. Мы действительно сталкиваемся со многими ситуациями, когда «для всех практических целей» система кажется инерциальной системой отсчета. На поверхности Земли лабораторию часто можно рассматривать как инерциальную систему отсчета для чистого ускорения комнаты, поскольку она переносится осевым вращением Земли и ее вращением вокруг Солнца, а также движением солнечной системы в галактике. , так далее., очень мало по сравнению с большими ускорениями, которые мы изучаем. Мы действительно включаем эффект осевого вращения, «корректируя» гравитационную силу, чтобы включить центростремительное ускорение. И если мы имеем дело с очень крупномасштабными движениями воздуха и воды, мы должны также включить эффекты Кориолиса из-за ускорения нашей системы отсчета.

Это сводится к тому, что если чистая сила, действующая на тело в нашей системе отсчета F net, действительная = м a + F extra , мы пытаемся определить этот дополнительный член силы, а затем вычтите его из «реальных» сил и продолжайте использовать эту «исправленную» форму законов Ньютона.Это эквивалентно определению −F extra как «фиктивной» силы, добавлению ее к действительному члену силы и, таким образом, сохранению закона Ньютона, используя его «как если бы» мы решали задачу в инерциальной системе отсчета.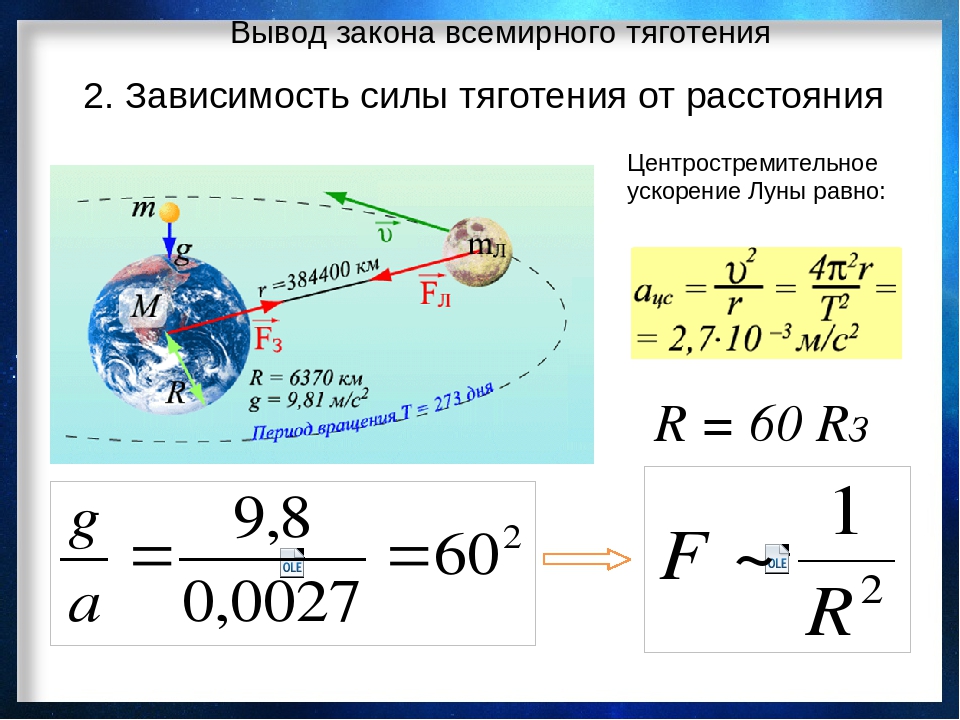

В системе отсчета, центрированной в центре Земли и вращающейся вместе с Землей, одна из этих фиктивных сил, действующих на тело на поверхности земли, называется «центробежной» силой. Это просто отрицательная сила центростремительной силы, действующей на это тело.Он направлен наружу от центра Земли. Другими важными силами на поверхности Земли являются силы Кориолиса, которые имеют большое значение при работе с огромными массами воздуха или воды в метеорологии, океанографии и баллистике на большие расстояния.

Эта длинная преамбула приводит к часто задаваемому вопросу. «Когда мы используем термин центростремительная сила, означает ли это, что мы решаем задачу в неинерциальной системе отсчета?» Нет, это не так. Напротив, центростремительная сила, действующая на объект, — это просто радиальная составляющая суммы действительных сил на него.«Центростремительная сила» используется в первую очередь, когда мы решаем задачу, в которой что-то движется по орбите вокруг фиксированной точки, и мы используем фиксированную (инерциальную) систему координат с центром в этой точке. Мы можем знать, что если векторная сумма всех сил, действующих на тело, зафиксированное в этой системе отсчета, действительно добавляется к нулю. Планетарные орбиты — хороший тому пример. Обычно в этих случаях мы используем инерциальную полярную систему координат.

Но когда мы решаем зафиксировать нашу систему координат на теле, которое, как мы знаем, ускоряется, так что координаты также ускоряются (возможно, претерпевают и вращение, и линейное ускорение), тогда мы обнаруживаем, что действительные силы, которые мы измеряем, действующие на тело, закрепленное в этом (движущаяся) рамка делать , а не , добавить к нулю.

Большая часть путаницы в отношении приливов возникает из-за того, что мы не можем указать, принимаем ли мы инерциальную систему отсчета или ускоряющуюся систему отсчета. Это также может возникнуть из-за того, что инерциальные системы отсчета могут быть декартовыми или полярными. Полярные координаты не ограничиваются вращающимися кадрами.

Приложение и резюме

Вопросы о центростремительной и центробежной силе наверняка вызовут споры среди учителей физики, и я сам испытываю к этому сильные чувства.

В Википедии есть две страницы, на которые стоит обратить внимание: Центробежная сила. Обязательно перейдите по ссылке «Центробежная сила (вращающаяся система отсчета)».

центростремительной сила определяется как радиальная составляющая результирующей силы на теле, когда положение тела представлено в полярной системе координат (координаты быть радиусом от фиксированного центра и угла от фиксированного угла отсчета). Это просто метка, позволяющая отличить радиальную составляющую от тангенциальной составляющей чистой силы.Но это полезное имя, поскольку оно фигурирует в очень полезном уравнении: F = м v 2 / r . Это уравнение не является физическим законом. Это определение.

Центростремительная сила, являющаяся составной частью общей силы, действующей на тело, является «реальной» силой. Реальные силы — это силы, действующие на тело из-за других идентифицируемых материальных объектов: гравитация, электрическое притяжение и отталкивание, магнитные силы, контактные силы (деформация от контакта, а также силы из-за трения и сопротивления качению).

В школьных учебниках иногда можно встретить центробежную силу, «определяемую» как силу реакции на центростремительную силу. Я страстно осуждаю эту вводящую в заблуждение идею, потому что она ни для чего не нужна и бесполезна. Кроме того, это вызывает беспокойство и замешательство, когда студенты идут в колледж и изучают определение центробежной силы, используемой при работе с вращающимися системами отсчета.

Почему? Силы реакции определяются в физике третьим законом Ньютона. Сила, которую тело B оказывает на тело A, равна по размеру и противоположна по направлению силе, которую A оказывает на B. Эти силы иногда называют «силами реакции», но из этого определения ничего не следует понимать. Важным моментом является то, что две силы в этом законе действуют на различных тел . Таким образом, в случае качания массы по кругу центростремительная сила — это натяжение струны, действующей внутрь на массу. Сила реакции на это — это сила, которую масса оказывает на струну.Эти двое равны по размеру и противоположны по направлению.

Но учебники, злоупотребляющие этой физикой, заявляют, что сила противодействия центростремительной силе, действующей внутрь на массу, — это центробежная сила, направленная наружу, которую ось (ось вращения) оказывает на струну в центре круга. Если тело A является осью вращения, S — струной, а M — массой, это не соответствует определению третьего закона Ньютона. Ось не оказывает силы на массу; строка делает. Масса не оказывает силы на ось; строка делает.Эта интерпретация полностью игнорирует строку. Для этого может быть оправдание. В задачах, где струна имеет незначительную массу по сравнению с другими элементами в системе, струна в идеале рассматривается как масса нулевого размера. В учебниках инженерного дела это иногда называют «осевой центробежной силой», «реактивной центробежной силой» или «центробежной инерционной реакцией».

Вращающиеся системы отсчета полезны, они используются инженерами-механиками и астрономами или кем-либо, кто должен делать фактические вычисления на основе данных, измеренных во вращающихся системах отсчета.Это практическая стратегия, поскольку преобразование данных в инерциальную систему отсчета перед выполнением физики было бы утомительным и неудобным. Центробежная сила — это фиктивная сила, используемая для упрощения таких расчетов. Этот подход редко используется во вводных курсах, поэтому лучше не упоминать его там. Тем не менее, он нравится наивным студентам (и некоторым авторам учебников), потому что кажется, что он соответствует ощущению «выброшенного наружу», когда кто-то находится на вращающейся платформе, как на карусели, или в автомобиле, движущемся по крутому повороту. .Это «приятное» объяснение для студентов, которым никогда не придется на самом деле делать какие-либо серьезные вычисления, используя эту концепцию.

Фактически, то, что человек чувствует в подобной ситуации, является результатом того, что автомобиль прилагает силу, перпендикулярную вашему движению, которая заставляет ваше собственное движение отклоняться от прямолинейного движения на изогнутую траекторию. Это физиологическое ощущение. Но это, конечно, возникает из-за реальных сил давления в вашем теле, стимулирующих нервы. Эти сенсорные ощущения указывают только на размер сил, но не на их направление.

Центробежная сила — это не реальная сила, действующая на тело из-за какого-либо другого физического объекта. Вот почему мы называем это «фиктивной силой». Решение задачи во вращающейся системе координат не меняет физику задачи. Природе все равно, какую систему координат мы выберем.

Любая задача, решаемая во вращающейся системе координат, может быть решена в фиксированной системе координат без использования концепции центробежной силы. Результаты, полученные двумя методами, конечно, должны быть идентичными.

Предупреждение: полярная система координат может быть фиксированной инерциальной системой координат. Вращающаяся система координат может быть полярной или декартовой. «полярный» и «вращающийся» не синонимы.

Если выбранные вами координаты не вращаются, термин «центробежная сила» не подходит. Если вы не знаете, вращаются ли ваши координаты, вам необходимо изучить основы, чтобы выяснить это, потому что, если вы продолжите, не зная этого факта, у вас есть 50-50 шансов испортить проблему, и любая попытка ее обсудить. приведет к путанице для всех.

Ньютон F = м a применяется только в инерциальных (фиксированных, неускоряющих) системах координат. Другими словами, слово «инерциальная» применимо к любой системе координат, для которой верен закон Ньютона. Это также означает «любая система координат, которая не ускоряется». Система координат, движущаяся с ускорением, является неинерциальной системой.

Когда вы решаете задачу во вращающейся неинерциальной системе, вы должны изменить закон Ньютона, чтобы он читался как F реальный + F центробежный + F кориолис = m a , где F центробежный и F Coriolis — это фиктивные «корректирующие» силы для компенсации использования неинерциальной системы координат, и это силы , а не , обусловленные физическим влиянием других реальных объектов.(Во вращающейся системе координат, в которой ускоряет , нужно добавить еще одну фиктивную силу, «силу Эйлера».)

Многие дискуссии, которые я вижу по этому поводу в Интернете, часто являются необдуманными мнениями, которые люди предлагают, не глядя на более широкую картину. Действительно, многие учителя не имели достаточной информации об этом в колледжах и университетах. Обычно он занимает главу в университетском курсе классической механики под названием «Неинерциальные системы». Хорошую трактовку можно найти в превосходной (и классической) книге Джерри Мариона «Классическая динамика частиц и систем» (Academic Press, 1965, и более поздние издания).См. Главу 12 «Движение в неинерциальной системе отсчета». Это должно быть в любой хорошей университетской библиотеке. В Соединенных Штатах (ненавижу признавать) большинство учителей средней школы никогда не проходили такой курс, поэтому совершенно невиновны в стандартных методах решения задач в неинерциальной системе отсчета Земли (часто используемых в гидродинамике океана и метеорологии как а также в дальнобойной баллистике ракет и космических аппаратов) и в астрофизике. Инженеры также используют эти методы при работе с гироскопическими эффектами.

Последняя редакция, апрель 2020 г.

Вернитесь к Приливным заблуждениям.

Вернитесь на главную страницу Дональда Симанека.

РЕШЕНИЕ: Вычислить центростремительное ускорение…

Стенограмма видео

всем, Это вопрос номер шестьдесят седьмой из пятой главы. Эта задача требует от нас вычислить центростремительное ускорение Земли на ее орбите вокруг Солнца и результирующую силу, действующую на Землю, а затем определить, что движет силой, действующей на Землю.Итак, мы определили центростремительное ускорение на протяжении всей главы как r, равное V в квадрате над нашим, которое в этом асе будет на орбите Земли. И мы также определили, что это равно двум pi r за чаем, чтобы мы могли заменить это и возвести в квадрат, потому что у нас нет Но у нас есть все в этом выражении справа над нашим e Oh, а затем мы Могу, ммм, переставить, что немного объединить световые элементы и распределить два незаметных распределения квадрата. Таким образом, мы получаем четыре пи в квадрате нашей орбиты Земли, поднятой к земной орбите над t в квадрате.Хорошо. И тогда мы также знаем, что согласно F, согласно второму закону Ньютона f равно и Хорошо, так что продолжаем, Sulphur, а? С нашими номерами. Таким образом, a равно четырем умноженным на квадрат пи. Гм, лучи земной орбиты, которые мы знаем. Одна точка нам говорят одну целую пять раз на одиннадцатом метре, и вы делите это на t в квадрате, которое мы собираемся преобразовать один год в секунду. Таким образом, вы делаете это, умножая на восемьдесят шесть тысяч четыреста три целых одна пять десятых, умножая на семь в квадрате секунд, и это дает вам X и ускорение, когда вы вставляете это в пять целых девять целых семь десятков с минус тремя метрами на секунду в квадрате.Ладно, это ускорение. И теперь мы можем вычислить силу, просто умножив эти пять целых девять и семь десятых на минус три метра в секунду, возведенных в квадрат на массу, как мы сказали, что составляет пять целых девять семь десятых, на двадцать четвертый килограмм, последний из земли, и это даст нам силы три целых пять десятых, подъемов с десяти до двадцати новым владельцам. Это наша сила. И, конечно же, мы знаем, что объект, проявляющий эту силу, — это солнце. Это самая большая вещь в окрестностях Земли, на полюсах и по его гравитационной силе

.

Что такое равномерное круговое движение?

В этой статье мы рассмотрим, как применить как векторы, так и геометрию кругов и треугольников для равномерного кругового движения.Примеры такого движения включают орбиты небесных объектов, таких как планеты и звезды. Мы выводим ускорение таких объектов, а также, согласно второму закону движения Ньютона, силу, действующую на них.

Ключевые термины

o Равномерное круговое движение

o Центростремительное ускорение

o Центростремительная сила

o Напряжение

Цели

o Вывести формулу центростремительного ускорения объектов при равномерном круговом движении

o Использование центростремительного ускорения для решения задач, связанных с объектами, находящимися в равномерном круговом движении

Начнем!

Согласно второму закону движения Ньютона, результирующая сила, действующая на объект, заставляет объект ускоряться в направлении этой чистой силы.Случаи линейного движения, например, объект, который выпущен с некоторой высоты над землей и может упасть под действием силы тяжести, обычны для нашей повседневной жизни. Кроме того, однако, также распространены случаи кругового движения. Мы рассмотрим, как подойти к таким проблемам (например, как Луна, вращающаяся вокруг Земли) и как понять их с точки зрения сил, ускорения и векторов.

Если мы посмотрим в небо (по крайней мере, в определенное время дня и месяца), мы сможем увидеть Луну, вращающуюся вокруг Земли.Очевидно, Луна движется вокруг Земли. Из-за силы тяжести Луна «притягивается» к Земле, но (к счастью) никогда с ней не сталкивается. Эта ситуация является одним из примеров кругового движения (или почти кругового — мы предположим, что оно достаточно близко, чтобы можно было пренебречь любыми отклонениями от идеальной круглости), когда объект испытывает суммарную силу, но в результате не движется линейно. Давайте посмотрим, почему Луна движется по кругу вокруг Земли (и почему объекты в других подобных ситуациях ведут себя именно так).

Мы знаем из второго закона движения Ньютона, что объект, испытывающий общую силу, испытывает ускорение. В случае Луны, вращающейся вокруг Земли (или любого объекта, вращающегося вокруг другого объекта, к которому она притягивается некоторой силой), результирующая сила на Луне всегда направлена ​​к Земле. Проиллюстрируем эту ситуацию схемой. Сила гравитации на Луне показана как F g .

Если и Земля, и Луна изначально находились в состоянии покоя, то сила гравитации заставила бы Луну ускориться к Земле (с катастрофическими результатами).Но что, если бы у Луны была начальная скорость? Подумайте, что бы произошло, если бы Луна имела некоторую скорость — , касательную к поверхности Земли, но никакие силы не действовали бы ни на одно из тел.

Очевидно, Луна просто продолжит свой курс, независимо от присутствия Земли. Но поскольку Земля оказывает на Луну гравитационную силу, Луна ускоряется по направлению к Земле. Если луна уже имеет скорость v , как показано выше, ускорение силы тяжести заставляет путь Луны изгибаться внутрь, как показано ниже.

Если скорость v Луны слишком велика по величине для данного расстояния от Земли, курс Луны слегка изгибается, но она продолжает удаляться от Земли. Если скорость на таком расстоянии слишком мала по величине, Луна в конечном итоге столкнется с Землей. Однако, если скорость правильная, траектория Луны будет кривой, так что она будет поддерживать постоянную орбиту, всегда сохраняя определенное расстояние от Земли (например, в текущих отношениях Луны и Земли).Давайте теперь рассмотрим случай, когда Луна поддерживает постоянную орбиту вокруг Земли. Аналогичная ситуация — мяч, крутящийся на конце веревки; обе ситуации показаны ниже.

Хотя расчет необходим для точного определения ускорения (и, следовательно, силы), действующего на объект при равномерном круговом движении (когда объект движется по кругу с постоянной скоростью), тем не менее мы можем получить правильный результат как следует.Давайте посмотрим на крошечный отрезок времени, Δ t, , в течение которого движущийся объект перемещается на небольшое расстояние по своей круговой траектории. Угол, образованный на этой крошечной части пройденного пути, составляет θ, , а расстояние объекта от центра (его кругового пути) составляет r. Предположим, что угол θ крошечный и что рисунок ниже не в масштабе — мы сделали его немного больше для ясности.

Мы можем соединить концы радиусов длиной r , чтобы образовать равнобедренный треугольник, как показано ниже.Обратите внимание, что если угол θ мал, как мы предполагали, то длина дуги с очень близка к длине неизвестной стороны третьей стороны треугольника. Таким образом, мы просто аппроксимируем эту третью сторону как имеющую длину s . На основе геометрии круга мы знаем, что длина дуги s , ограниченная углом θ в окружности радиуса r , равна просто rθ.

Теперь вернемся к скорости объекта, как вначале, так и через небольшой промежуток времени Δ t. Ускорение объекта — это просто скорость его изменения скорости во времени, которую мы можем выразить как изменение скорости (Δ v ), деленное на прошедшее время (Δ t ). В терминах v 1 и v 2 мы можем записать следующее выражение:

Теперь мы можем применить наше понимание векторов, чтобы показать v 2 — v 1 графически. Но поскольку скорости v 1 и v 2 касательны к окружности и равны по величине, они образуют равнобедренный треугольник с углом θ между ними, как показано ниже.

Обратите внимание, что, поскольку Δ v направлено к центру движения, ускорение также направлено к центру (по мере того, как θ становится все меньше и меньше, это становится все более и более очевидным — потому что мы использовали большую θ на диаграмме для ясности, похоже, что Δ v точек немного смещено от направления к центру).Поскольку треугольник, образованный векторами, и треугольник, образованный радиусами движения, имеют одинаковый угол θ , и поскольку оба треугольника равнобедренные, они похожи. В результате отношение r к s должно быть равно отношению скорости v объекта (величина v 1 или v 2 ) к величина Δ v. Мы можем записать это выражение следующим образом:

Теперь, поскольку расстояние, пройденное объектом за время Δ t , составляет с и поскольку объект имеет скорость v, , мы можем записать следующее выражение:

Другими словами, скорость объекта — это расстояние с , деленное на время Δ t , необходимое для прохождения этого расстояния.Объединим предыдущие два выражения, чтобы исключить s .

Вспомните наше определение a. Также имеет место следующее (в силу взятия величины обеих сторон векторного выражения для a ).

Затем, продолжая манипулировать выражением выше,

Таким образом, мы получили ускорение объекта, движущегося равномерно по кругу. Это ускорение, a c , называется центростремительным ускорением . Согласно второму закону движения Ньютона, центростремительная сила ( F c ) тогда будет следующей для объекта массой м .

Помните, что центростремительное ускорение (и, следовательно, сила) равно , всегда направлено к центру круговой траектории и, следовательно, всегда перпендикулярно скорости объекта.Следующие ниже практические задачи дают вам возможность применить результаты, полученные нами выше.

Практическая задача : Расчетная масса Земли составляет 5,98 10 24 кг. Если он движется по круговой орбите с радиусом 1,50 10 11 метров вокруг Солнца и завершает свой оборот один раз в год (предположим, что год составляет 365 дней), каково его центростремительное ускорение?

Решение : Мы уже можем утверждать на основе того, что мы знаем о равномерном круговом движении, что центростремительное ускорение Земли всегда направлено к Солнцу.Чтобы найти это ускорение, мы должны использовать полученную выше формулу:

Радиус r, известен нам на основании информации, содержащейся в постановке задачи. Нам нужно только вычислить скорость Земли. Напомним, что (средняя) скорость — это просто пройденное расстояние, разделенное на прошедшее время. Орбита Земли равна 2 πr, , а время, необходимое Земле для завершения этой орбиты, составляет 365 дней (один год).Давайте переведем год в секунды, чтобы наш результат был в единицах СИ.

Обратите внимание, что каждая дробь в правой части равна единице, поскольку (например) 24 часа равны одному дню.

Длина орбиты, с, следующая.

Затем мы можем написать символьное выражение для a c .

Давайте подставим числа, чтобы получить окончательный результат.

Обратите внимание, что центростремительное ускорение очень мало — менее 0,01 метра в секунду в квадрате. Тем не менее, если мы рассмотрим массу Земли, мы обнаружим, что центростремительная сила (гравитационное притяжение Солнца к Земле) огромна: около 3.56 10 22 ньютонов! (Для справки, человек с массой 100 кг — около 220 фунтов на поверхности Земли — весит около 980 ньютонов.)

Практическая задача : Натянутая струна (которая считается безмассовой) испытывает натяжение T , параллельное струне и равное по величине приложенной к ней тянущей силе. Предмет массой 0,5 кг на конце нити длины 0.5 метров вращается вокруг фиксированной точки так, чтобы плоскость вращения была параллельна земле. Если скорость объекта составляет 8 метров в секунду, что составляет Тл?

Решение : Сначала мы хотим вычислить центростремительное ускорение, a c , а затем центростремительную силу, F c . Нарисуем схему ситуации. Натяжение T возникает из-за того, что объект оказывает тянущее усилие на струну (вы можете почувствовать эту силу, когда находитесь в поворачивающемся транспортном средстве — вам кажется, что вас отбрасывает наружу!).Кроме того, натяжение равно центростремительной силе.

Центростремительное ускорение объекта:

Центростремительная сила и, следовательно, натяжение T, всегда направлены к центру пути объекта. Эта сила следующая:

Таким образом, натяжение струны составляет 64 ньютона (около 14. 4 фунта силы).

Механика с анимацией и фильмом.

Приведенная ниже анимация представлена ​​в модуле «Круговое движение» и воспроизводится здесь для тех, кто хочет просмотреть ее в замедленном режиме.

Автомобиль движется с постоянной скоростью по холму, на вершине которого радиус кривизны в вертикальной плоскости составляет 30 м, как показано. Найдем критическую скорость v крит , при которой автомобиль теряет контакт с дорогой.

Автомобиль движется по дороге с постоянной скоростью по кругу.Следовательно, на вершине холма его ускорение направлено вниз, и его величина составляет v 2 / r. Какие на него нисходящие силы? Его вес — одна из таких сил. Как правило, существует также нисходящая составляющая силы, которую воздух оказывает на автомобиль *. В нашем случае эта вторая сила ничтожна по сравнению с весом. (См. Раздел «Сопротивление воздуха» для получения верхнего предела.)

Итак, на вершине холма вес является единственной силой, направленной вниз, и поэтому максимальное ускорение вниз равно g, которое, как мы видели в модуле Projectile, равно 9.8 м.с −2 . Теперь центростремительное ускорение вниз, когда автомобиль находится на вершине холма, составляет v 2 / r, и это ускорение не может быть больше g. Итак, критические ускорение и скорость равны

    a крит = v крит 2 / r = g.
Преобразование этого уравнения дает критическую скорость:
    v крит = √ (rg) = 17 мс −1 = 62 тыс.
Обратите внимание, что, соприкасаясь с дорогой, автомобиль вращается в вертикальной плоскости с угловой скоростью ω = v / r.В точке, где он теряет контакт с дорогой, силы, действующие на колеса, малы, как и крутящие моменты (которые мы встретим, когда перейдем к вращению). Следовательно, машина, находясь в воздухе, продолжает вращаться с этой скоростью. Это вращение добавляет дополнительную опасность маневру, что является лишь одной из причин совета, который редко дается в физике, что здесь следует доверять расчетам, а не проводить эксперимент.