Самостоятельная работа по теме «Окружность»
Самостоятельная работа № 1 по теме «Окружность»
ВАРИАНТ 1
1. Касательные в точках A и B к окружности с центром O пересекаются под углом 22°. Найдите угол ABO. Ответ дайте в градусах.
2. Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности.
3. На окружности с центром O отмечены точки A и B так, что ∠AOB=66°. Длина меньшей дуги AB равна 99. Найдите длину большей дуги окружности.
4. Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
5. Четырёхугольник ABCD вписан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD. Ответ дайте в градусах.
Самостоятельная работа №1 по теме «Окружность»
ВАРИАНТ 2
1. Касательные в точках A и B к окружности с центром
2. Длина хорды окружности равна 48, а расстояние от центра окружности до этой хорды равно 70. Найдите диаметр окружности.
3. На окружности с центром O отмечены точки A и B так, что ∠AOB=140°. Длина меньшей дуги AB равна 98. Найдите длину большей дуги окружности.
4. Найдите площадь квадрата, описанного вокруг окружности радиуса 40.
5. Четырёхугольник ABCD вписан в окружность. Угол ABC равен 134°, угол CAD равен 81°. Найдите угол ABD. Ответ дайте в градусах.
Самостоятельная работа №1 по теме «Окружность»
1.Касательные в точках A и B к окружности с центром O пересекаются под углом 88°. Найдите угол ABO. Ответ дайте в градусах.
2. Длина хорды окружности равна 40, а расстояние от центра окружности до этой хорды равно 48.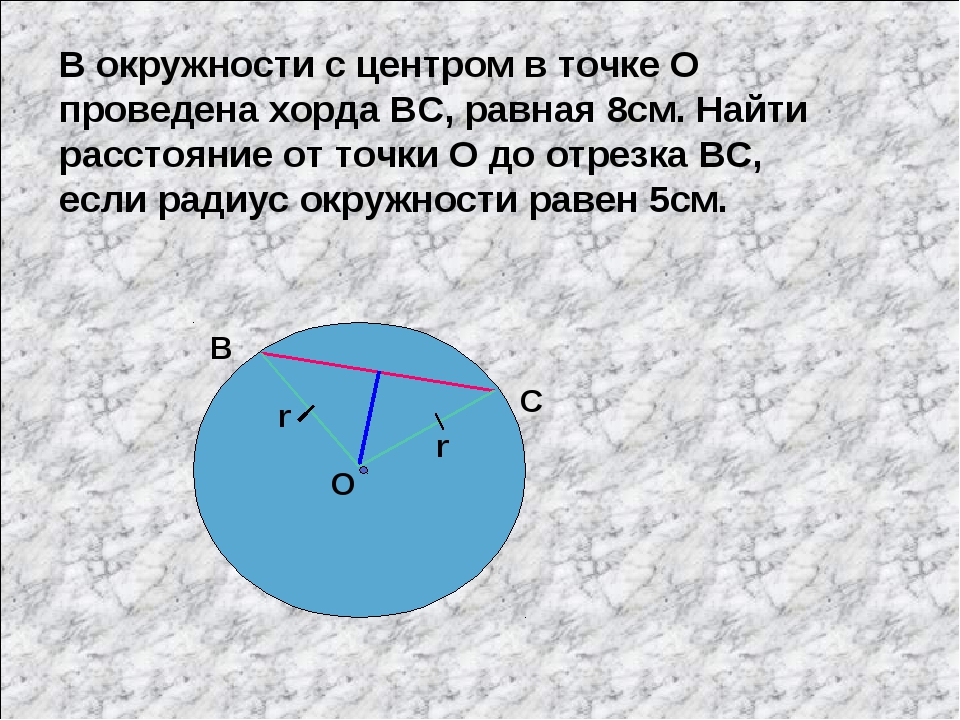 Найдите диаметр окружности.
Найдите диаметр окружности.
3. На окружности с центром O отмечены точки A и B так, что ∠AOB=2°. Длина меньшей дуги AB равна 46. Найдите длину большей дуги.
4. Найдите площадь квадрата, описанного вокруг окружности радиуса 79.
5. Четырёхугольник ABCD вписан в окружность. Угол ABC
Самостоятельная работа №1 по теме «Окружность»
ВАРИАНТ 4
1.Касательные в точках A и B к окружности с центром O пересекаются под углом 64°. Найдите угол ABO. Ответ дайте в градусах.
2. Длина хорды окружности равна 88, а расстояние от центра окружности до этой хорды равно 33. Найдите диаметр окружности.
3. На окружности с центром O отмечены точки A и B так, что ∠AOB=8°. Длина меньшей дуги AB равна 88. Найдите длину большей дуги.
4. Найдите площадь квадрата, описанного вокруг окружности радиуса 94.
5. Четырёхугольник ABCD вписан в окружность. Угол ABC равен 138°, угол CAD равен 83°. Найдите угол ABD. Ответ дайте в градусах.
Самостоятельная работа №1 по теме «Окружность»
ВАРИАНТ 5
1.Касательные в точках A и B к окружности с центром O пересекаются под углом 76°. Найдите угол ABO. Ответ дайте в градусах.
2. Длина хорды окружности равна 12, а расстояние от центра окружности до этой хорды равно 8. Найдите диаметр окружности.
3. На окружности с центром O отмечены точки A и B так, что ∠AOB=122°. Длина меньшей дуги
4. Найдите площадь квадрата, описанного вокруг окружности радиуса 84.
5. Четырёхугольник ABCD вписан в окружность. Угол ABC равен 120°, угол CAD равен 74°.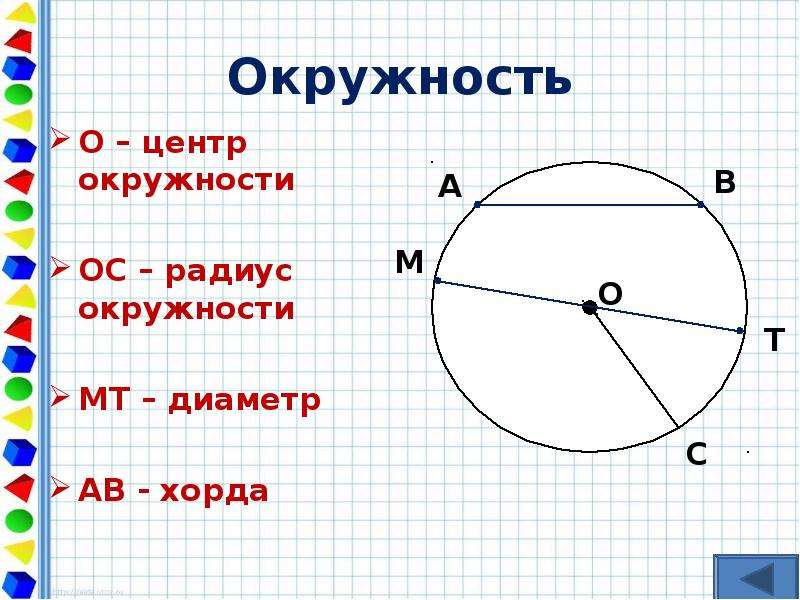 Найдите угол ABD. Ответ дайте в градусах.
Найдите угол ABD. Ответ дайте в градусах.
Самостоятельная работа №1 по теме «Окружность»
ВАРИАНТ 6
1.Касательные в точках A и B к окружности с центром O пересекаются под углом 12°. Найдите угол ABO. Ответ дайте в градусах.
2. Длина хорды окружности равна 130, а расстояние от центра окружности до этой хорды равно 72. Найдите диаметр окружности.
3. На окружности с центром O отмечены точки A и B так, что ∠AOB=28°. Длина меньшей дуги AB равна 63. Найдите длину большей дуги.
4. Найдите площадь квадрата, описанного вокруг окружности радиуса 72.
5. Четырёхугольник ABCD вписан в окружность. Угол ABC равен 112°, угол CAD равен 70°. Найдите угол ABD. Ответ дайте в градусах.
Самостоятельная работа №1 по теме «Окружность»
ВАРИАНТ 7
1.Касательные в точках A и B к окружности с центром O пересекаются под углом 18°. Найдите угол ABO. Ответ дайте в градусах.
2. Длина хорды окружности равна 48, а расстояние от центра окружности до этой хорды равно 45. Найдите диаметр окружности.
3. На окружности с центром O отмечены точки A и B так, что ∠AOB=18°. Длина меньшей дуги AB равна 98. Найдите длину большей дуги.
4. Найдите площадь квадрата, описанного вокруг окружности радиуса 39.
5. Четырёхугольник ABCD вписан в окружность. Угол ABC равен 56°, угол CAD равен 42°. Найдите угол ABD. Ответ дайте в градусах.
Самостоятельная работа №1 по теме «Окружность»
ВАРИАНТ 8
1.Касательные в точках A и B к окружности с центром O пересекаются под углом 78°. Найдите угол
2. Длина хорды окружности равна 24, а расстояние от центра окружности до этой хорды равно 16.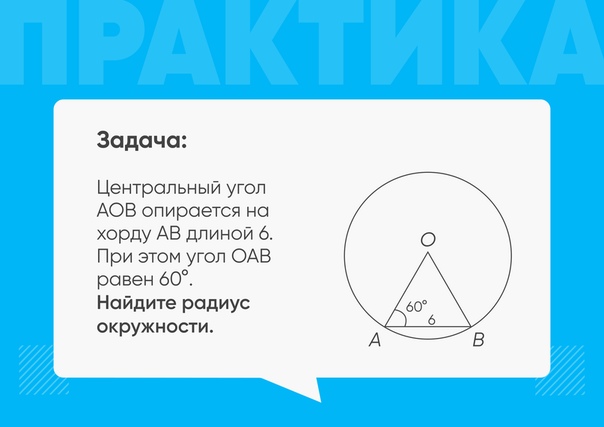 Найдите диаметр окружности.
Найдите диаметр окружности.
3. На окружности с центром O отмечены точки A и B так, что ∠AOB=18°. Длина меньшей дуги AB равна 5. Найдите длину большей дуги окружности.
4. Найдите площадь квадрата, описанного вокруг окружности радиуса 18.
5. Четырёхугольник ABCD вписан в окружность. Угол ABC равен 54°, угол CAD равен 41°. Найдите угол
Самостоятельная работа №1 по теме «Окружность»
ВАРИАНТ 9
1.Касательные в точках A и B к окружности с центром O пересекаются под углом 24°. Найдите угол ABO. Ответ дайте в градусах.
2. Длина хорды окружности равна 96, а расстояние от центра окружности до этой хорды равно 20. Найдите диаметр окружности.
3. На окружности с центром O отмечены точки A и B так, что ∠AOB=39°. Длина меньшей дуги AB равна 65. Найдите длину большей дуги.
4. Найдите площадь квадрата, описанного вокруг окружности радиуса 19.
5. Четырёхугольник
Самостоятельная работа №1 по теме «Окружность»
ВАРИАНТ 10
1.Касательные в точках A и B к окружности с центром O пересекаются под углом 56°. Найдите угол ABO. Ответ дайте в градусах.
2. Длина хорды окружности равна 64, а расстояние от центра окружности до этой хорды равно 24. Найдите диаметр окружности.
3. На окружности с центром O отмечены точки A и B так, что ∠AOB=45°. Длина меньшей дуги AB равна 91. Найдите длину большей дуги окружности.
4. Найдите площадь квадрата, описанного вокруг окружности радиуса 32.
5. Четырёхугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD равен 60°.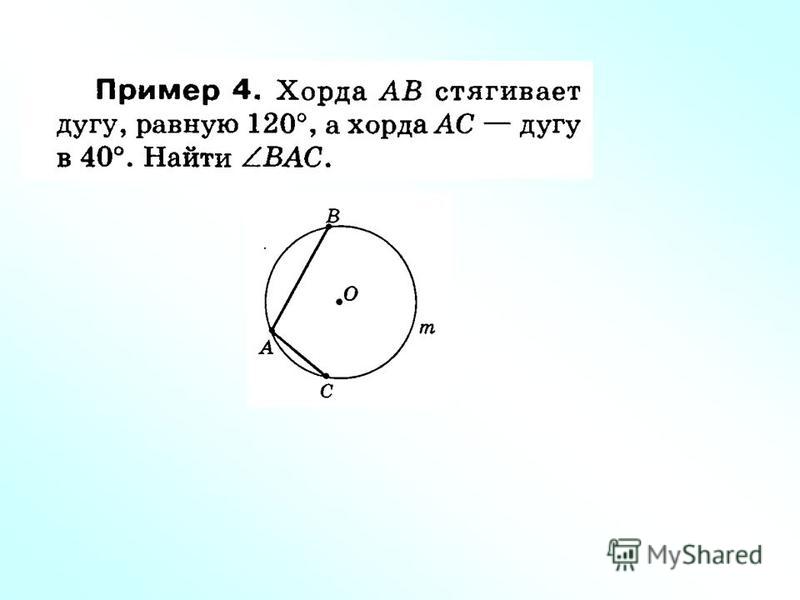 Найдите угол ABD. Ответ дайте в градусах.
Найдите угол ABD. Ответ дайте в градусах.
Самостоятельная работа №1 по теме «Окружность»
ВАРИАНТ 11
1.Касательные в точках A и B к окружности с центром O пересекаются под углом 14°. Найдите угол ABO. Ответ дайте в градусах.
2. Длина хорды окружности равна 60, а расстояние от центра окружности до этой хорды равно 40. Найдите диаметр окружности.
3. На окружности с центром O отмечены точки A и
4. Найдите площадь квадрата, описанного вокруг окружности радиуса 99.
5. Четырёхугольник ABCD вписан в окружность. Угол ABD равен 39°, угол CAD равен 55°. Найдите угол ABC. Ответ дайте в градусах.
Самостоятельная работа №1 по теме «Окружность»
ВАРИАНТ 12
1.Касательные в точках A и B к окружности с центром O пересекаются под углом 66°. Найдите угол ABO. Ответ дайте в градусах.
2. Длина хорды окружности равна 140, а расстояние от центра окружности до этой хорды равно 24. Найдите диаметр окружности.
3. На окружности с центром O отмечены точки A и B так, что ∠AOB=80°. Длина меньшей дуги AB равна 58. Найдите длину большей дуги окружности.
4. Найдите площадь квадрата, описанного вокруг окружности радиуса 90.
5. Четырёхугольник ABCD вписан в окружность. Угол ABD равен 80°, угол CAD равен 34°. Найдите угол ABC. Ответ дайте в градусах.
Планиметрия. Подготовка к ОГЭ (задачи 10; 24; 25 и 26) Подготовка к ЕГЭ (задачи 6 и 16)
10.
 Окружность, круг и их элементы
Окружность, круг и их элементы10.Окружность, круг и их элементы Касательная, хорда, секущая, радиус 1. Радиус OB окружности с центром в точке O пересекает хорду AC в точке D и перпендикулярен ей. Найдите длину хорды AC, если BD = 1
ПодробнееОСНОВНЫЕ ЭЛЕМЕНТЫ ОКРУЖНОСТИ
УГЛЫ В ОКРУЖНОСТИ ОСНОВНЫЕ ЭЛЕМЕНТЫ ОКРУЖНОСТИ Диаметр в 2 раза больше радиуса.!!! Это очень важно знать для выполнения данного задания: ЦЕНТРАЛЬНЫЙ УГОЛ Центральный угол равен дуге, на которую он опирается
ПодробнееГеометрия. 2019год. Задание 17. Окружность
Геометрия 2019год Задание 17. Окружность Периметр треугольника равен 50, одна из сторон равна 20, а радиус вписанной в него окружности равен 4. Найдите площадь этого треугольника. Площадь круга равна 90.
ПодробнееГеометрия
Геометрия 1. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65 и 50. Найдите меньший угол параллелограмма. 2. Разность углов, прилежащих к одной стороне параллелограмма, равна
Подробнее7 sin A. Найдите AB. 25
Прототипы задания 6 1. В треугольнике ABC угол C равен 90 0, AC = 4,8, 25. В треугольнике ABC AC = BC, AB = 8, 33 tga. 7 4 33 sin A. Найдите AB. 25 Найдите AC. 2. В треугольнике ABC угол C равен 90 0,
ПодробнееТренировочные задачи
И. В. Яковлев Материалы по математике MathUs.ru Тренировочные задачи Окружность. Свойства окружности. Если хорда не является диаметром, то диаметр, проходящий через середину этой хорды, перпендикулярен
ПодробнееAC 6, cos A.
 Найдите BH.
Найдите BH.Прототипы задания 6 1. Задание 6 ( 26097) 16. Задание 6 ( 20001) В треугольнике ABC угол C равен 90, sin A 0, 6, 21 AC 4. Найдите AB. В треугольнике ABC AC BC 12, sin B. 5 2. Задание 6 ( 29580) Найдите
ПодробнееПланиметрия на ЕГЭ по математике
И. В. Яковлев Материалы по математике MathUs.ru Планиметрия на ЕГЭ по математике Здесь приведены задачи по планиметрии, которые предлагались на ЕГЭ по математике (профильный уровень, сложная часть), а
ПодробнееМногоугольники и их свойства
Задание 19 Планиметрические задачи Многоугольники и их свойства 1. На стороне CD квадрата ABCD построен равносторонний треугольник CPD. Найдите высоту треугольника ADP, проведённую из вершины D, если известно,
ПодробнееПрототипы задания В6-2 (2013)
Прототипы задания В6-2 (2013) ( 27742) Один острый угол прямоугольного треугольника на больше другого. Найдите больший острый угол. Ответ дайте в градусах. ( 27743) В треугольнике ABC угол A равен, внешний
Подробнеегеометрия п законспектировать и выучить определения и теорему, 1-7
5 Б, 5Г класс п.7, 05-059, 076-08, п.8, 08-096, 09-5Д класс Тема: «Сложение и вычитание дробей» 985, 988, 99, 00, 0, 0, 05, 07, 08, 09, 0, 0, 09, 09 6 Б п.-5 87, 880, 80, 88, 88. 887, 888, 87вг. к/р 8
ПодробнееОкружность, круг и их элементы
Окружность, круг и их элементы 1. B 7 90. Центральный угол AOB опирается на хорду AB длиной 6. При этом угол OAB равен 60. Найдите радиус окружности. О т в ет: 6 2. B 7 116. В окружности с центром в точке
ПодробнееMAO = NAO.
 Таким образом, если из Рис. 1
Таким образом, если из Рис. 1005-006 уч. год. 6, 9 кл. Математика. Планиметрия (часть II). Вторая часть по планиметрии содержит три параграфа. В 1 подробно обсуждаются свойства касательных, хорд и секущих, доказывается теорема о касательной
ПодробнееОсновные теоремы и формулы
Основные теоремы и формулы Определение 1. Угловой величиной дуги называется отношение длины этой дуги к длине окружности, умноженное на 2π. Теорема 1. Величина центрального угла равна угловой величине
ПодробнееПланиметрия на олимпиаде «Физтех»
И. В. Яковлев Материалы по математике MathUs.ru Планиметрия на олимпиаде «Физтех» 1. («Физтех», 017, 9 ) В треугольник ABC вписаны два равных прямоугольника P QRS и P 1 Q 1 R 1 S 1 (при этом точки P и
ПодробнееID_5695 1/8 neznaika.pro
Планиметрическая задача Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов. 1 В треугольнике
ПодробнееПланиметрия на ЕГЭ по математике
И. В. Яковлев Материалы по математике MathUs.ru Планиметрия на ЕГЭ по математике Здесь приведены задачи по планиметрии, которые предлагались на ЕГЭ по математике (профильный уровень, сложная часть), а
ПодробнееСириус, класс «группа В» 3-4 сентября
Вписанные углы Определение. Угол с вершиной в центре окружности называется центральным, а градусная мера дуги, высекаемой им, равна его градусной мере. Определение. Угол с вершиной на окружности называется
ПодробнееСредняя линия треугольника
И. В. Яковлев Материалы по математике MathUs.ru Средняя линия треугольника Средняя линия треугольника это отрезок, соединяющий середины двух сторон треугольника. Говоря о средней линии, третью сторону
В. Яковлев Материалы по математике MathUs.ru Средняя линия треугольника Средняя линия треугольника это отрезок, соединяющий середины двух сторон треугольника. Говоря о средней линии, третью сторону
Все прототипы заданий В года
1. Прототип задания B5 ( 27450) Найдите тангенс угла AOB. Все прототипы заданий В5 2014 года 2. Прототип задания B5 ( 27456) Найдите тангенс угла AOB. 7. Прототип задания B5 ( 27547) Найдите площадь треугольника,
ПодробнееВписанный угол
А.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Вписанный угол 27855. Чему равен вписанный угол, опирающийся
Подробнееtgbac. В8 ЕГЭ В ABC C = 90 0, CH высота, AB = 13, tga 5. Найдите BH. 12,5 3 В ABC C = 90 0, AB = 13, tga. Найдите высоту CH.
В-8. ПРОТОТИПЫ Задание ответ В ABC C = 90 0, CH высота, AB =, tga. Найдите AH., В ABC C = 90 0, CH высота, AB =, tga. Найдите, В ABC C = 90 0, AB =, tga. Найдите высоту CH., В ABC C = 90 0, CH высота,
ПодробнееГЕОМЕТРИЯ: ПЛАНИМЕТРИЯ
ГЕОМЕТРИЯ: ПЛАНИМЕТРИЯ I Группа 1.01 Разность двух углов, получившихся при пересечении двух прямых, равна 20. Найти больший из этих углов. 1.02 Углы треугольника пропорциональны числам 3:7:8. Найти наибольший
ПодробнееТреугольники общего вида
Треугольники общего вида 1. Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен 30. Площадь треугольника равна половине произведения его сторон на синус угла между
ПодробнееВ 8 (2014) 16.
 В треугольнике ABC, 30. В треугольнике ABC угол C равен, CH. высота,,. Найдите AH. высота,,. Найдите BH.
В треугольнике ABC, 30. В треугольнике ABC угол C равен, CH. высота,,. Найдите AH. высота,,. Найдите BH.В 8 (2014) 1). В треугольнике ABC угол C равен, CH высота,,. Найдите AH. 2. В треугольнике ABC угол C равен, CH 3. В треугольнике ABC угол C равен,,. Найдите высоту CH. 4. В треугольнике ABC угол C равен,
ПодробнееЗАДАНИЕ 15 Планиметрия Треугольник
ЗАДАНИЕ 15 Планиметрия Треугольник 1. На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах. 2. На клетчатой бумаге с клетками
ПодробнееЗанятие 13. Треугольники и окружности — II.
Занятие 1. Треугольники и окружности — II. 1. Гипотенуза равнобедренного прямоугольного треугольника равна. Найдите радиус окружности, описанной около этого треугольника..радиус окружности, описанной около
ПодробнееЗадание 3, 6, 16. Планиметрия
Задание 3, 6, 6. Планиметрия Угловые соотношения в плоских фигурах Теорема. Сумма смежных углов равна 80 0. и смежные углы Теорема. Биссектрисы смежных углов взаимно перпендикулярны. Теорема. Вертикальные
ПодробнееЗадание 16. Планиметрия
Задание 6. Планиметрия Угловые соотношения в плоских фигурах Теорема. Две прямые, параллельные третьей, параллельны. Теорема. Если две прямые параллельности пересечены секущей, то. Накрест лежащие углы
ПодробнееЗАДАНИЕ 9 ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК. 1. В треугольнике ABC угол C равен,,. Найдите AB. 2. В треугольнике ABC угол C равен,,. Найдите AB.
ЗАДАНИЕ 9 ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК 1. В треугольнике ABC угол C равен,,. Найдите AB. 2. В треугольнике ABC угол C равен,,. Найдите AB. 3. В треугольнике ABC угол C равен,,. Найдите AB. 4. В треугольнике
Найдите AB. 2. В треугольнике ABC угол C равен,,. Найдите AB. 3. В треугольнике ABC угол C равен,,. Найдите AB. 4. В треугольнике
Геометрия ЛШ вариант
Геометрия ЛШ 2017 1 вариант 1. (4 балла) Продолжения хорд CB и ED окружности ω пересекаются в точкеa, причемb [AC] иd [AE]. Известно, что BAD = 30 и градусные величины дуг CB, BD и DE относятся соответственно
ПодробнееТренировочные задачи
И. В. Яковлев Материалы по математике MathUs.ru Тренировочные задачи Параллелограмм. Периметр параллелограмма равен, а одна из его сторон вдвое больше другой. Найдите стороны параллелограмма. и 4. Найдите
ПодробнееТренировочные задачи
И. В. Яковлев Материалы по математике MathUs.ru Тренировочные задачи Теорема Пифагора 1. Найдите диагональ квадрата со стороной a. a. В прямоугольном треугольнике с углом 60 гипотенуза равна. Найдите катеты.
ПодробнееЗадания В6. . Найдите AB.
Задания В6 1. В треугольнике ABC угол C равен 90, тангенс внешнего угла при вершине A равен -0,1. Найдите tga. 2. Угол A четырехугольника ABCD, вписанного в окружность, равен 52. Найдите угол C этого 3.
ПодробнееБилеты по геометрии 7 класс. Билет 5
Билеты по геометрии 7 класс Билет 1 1. Сформулируйте признаки параллельности двух прямых. 2. Смежные углы (определение). Теорема о сумме смежных углов. 3. Задача по теме «Признаки равенства треугольников»..
ПодробнееMAO = NAO. Таким образом, если из Рис. 1
009-00 уч год 4, 9 кл Математика Планиметрия (часть II) Вторая часть по планиметрии содержит три параграфа В подробно обсуждаются свойства касательных, хорд и секущих, доказывается теорема о касательной
Подробнее« Окружность.
 Касательные, хорды, радиусы окружности» — презентация на Slide-Share.ru 🎓
Касательные, хорды, радиусы окружности» — презентация на Slide-Share.ru 🎓1
Первый слайд презентации: 21.04.2020 Теме: « Окружность. Касательные, хорды, радиусы окружности»
8 класс
Изображение слайда
2
Слайд 2: Правила работы
14:00 – 14:05 вход на урок, проверяете звук и видео (нас должно быть слышно и видно). 14:05 – отключаете звук (знак микрофона). Вопросы задаете в чате или поднимаете руку (прошу слова ). Без аватарок Регистрация реального имени ( можно переименовать имя)
Изображение слайда
3
Слайд 3: Вопросы задавайте в чате
Изображение слайда
4
Слайд 4: Треугольник АВС вписан в окружность с центром в точке О.
 Найдите градусную меру угла С треугольника АВС, если угол АОВ равен 48°
Найдите градусную меру угла С треугольника АВС, если угол АОВ равен 48°
АОВ = 48° является центральным углом, значит дуга АС = 48° АСВ вписанный и опирается на дугу АС Вписанный угол равен половине дуги, на которую он опирается АСВ = 48:2 = 24° Ответ: 24°
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
5
Слайд 5: На окружности с центром О отмечены точки А и В так, что АОВ = 45°. Длина меньшей дуги АВ равна 57. Найдите длину большей дуги
АОВ = 57° Составим пропорцию 360° — х 45° — 57 х = = 506 360: 45=8 506 длина всей окружности 506-57 = 449 Ответ: 449
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
Изображение для работы со слайдом
6
Слайд 6: Центральный угол АОВ опирается на хорду АВ длиной 6.
 При этом угол ОАВ равен 60°. Найдите радиус окружности
При этом угол ОАВ равен 60°. Найдите радиус окружности
ОА = ОВ т.к являются радиусами АОВ – равнобедренный, углы при основании равны ОВ =180° -(60° +60°) =60° Значит АОВ равносторонний, следовательно ОА=ВО=АВ Значит r = 6
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
7
Слайд 7: Прямая касается окружности в точке К. Точка О- центр окружности. Хорда КМ образует с касательной угол, равный 83 °. Найдите величину угла ОМК. Ответ дайте в градусах
МКА = 83° ОК АК, значит ОКА =90° ОКМ = 90° -83° =7° ОК= ОМ, значит КОМ равнобедренный ОКМ = ОМК =7° Ответ: ОМК =7° А
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
8
Слайд 8: В угол С величиной 83° вписана окружность, которая касается сторон угла в точках А и В.
 Найдите угол АОВ. Ответ дайте в градусах
Найдите угол АОВ. Ответ дайте в градусах
С = 83° АО и ВО –радиусы, радиус перпендикулярен касательной к точке касания, значит ОАС = ОВС = 90° С + АОВ = 180 ° АОВ = 180 ° — 83°= 97° Ответ: АОВ = 97°
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
9
Слайд 9: Прямоугольный треугольник с катетами 5см и 12 см вписан в окружность. Чему равен радиус этой окружности
Обратить внимание АС проходит через центр О Дуга АС = 180°, угол АВС вписанный и опирается на дугу АС, значит угол АВС = 90° АВС – прямоугольный По теореме Пифагора А С² = АВ² + ВС² = 12²+ 5² = 144+ 25 =169 АС = = 13 АС =13 диаметр r = 13: 2 = 6,5 Ответ: 6,5 А В С
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
10
Слайд 10: Отрезок АВ =40 касается окружности радиуса 75 с центром О в точке В.
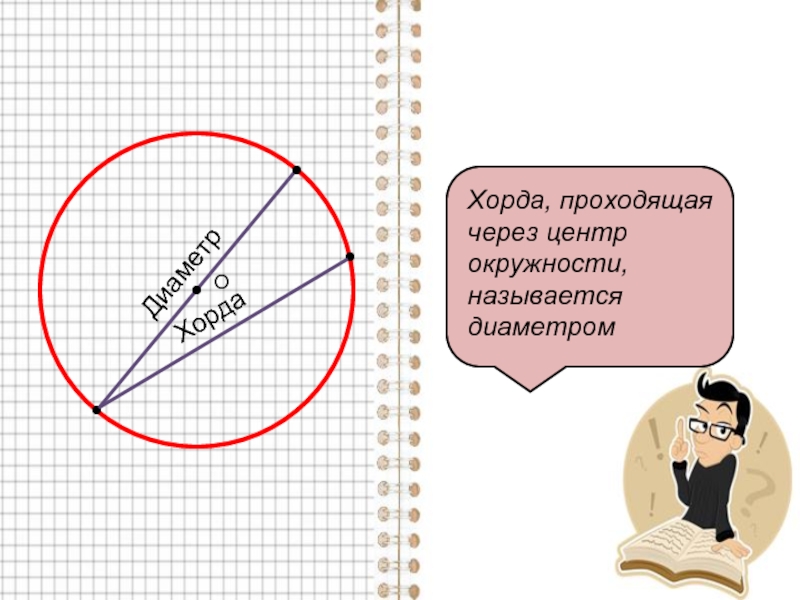 Окружность пересекает отрезок АО в точке D. Найдите AD
Окружность пересекает отрезок АО в точке D. Найдите AD
АВ = 40 ОВ=75 ОВ АВ ( т.к радиус перпендикуляр касательной АВ) АОВ – прямоугольный По теореме Пифагора АО² = АВ² + ВО² = 40²+ 75² = 1600+ 5625 = 7225 АО = = 85 ОВ= О D = r А D = АО – О D = 85-75 = 10 Ответ: 10
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
11
Слайд 11: Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности
АВ = 72 ОЕ = 27 ОВЕ – прямоугольный По теореме Пифагора ВЕ = АВ: 2= 72: 2= 36 ОВ² = ОЕ² + ВЕ² = 27²+ 36² = 729+ 1296 =2025 ОВ = = 45 d = 2·ВО d = 45· 2 = 90 Ответ: 90 А В О Е
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
12
Слайд 12: На отрезке AB выбрана точка C так, что AC = 80 и BC = 2.
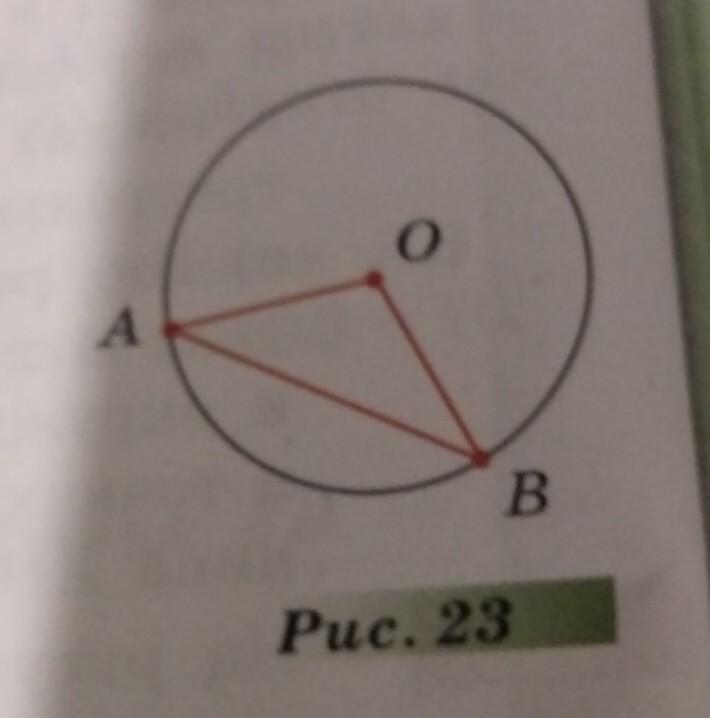 Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности
Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности
АС = 80, ВС = 2 Проведен радиус АН в точку касания, АН = АС АВ=АС +ВС АВ = 80+2 = 82 АВН – прямоугольный Н В² = АВ² — АН² = 82² — 80² = 6724 — 6400 =324 Н В = = 18 Ответ: 18
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
Изображение для работы со слайдом
13
Слайд 13: Касательные в точках A и B к окружности с центром O пересекаются под углом 6 2 °. Найдите угол ABO. Ответ дайте в градусах
АСВ = 6 2 ° АОВ = 180° -62° = 118° АОВ – равнобедренный, т.к АО= ОВ- радиусы АВО = (180°– 118 ° ): 2= 62° : 2= 31° Ответ: 31° C
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
14
Слайд 14: К окружности с центром в точке О проведены касательная АВ и секущая АО.
 Найдите радиус окружности, если АВ = 21, АО=75
Найдите радиус окружности, если АВ = 21, АО=75
АО = 75, ВО = 21 ОВ АВ, т.к радиус перпендикулярен касательной в точке касания АОВ – прямоугольный По теореме Пифагора ВО² = АО² — ВО² = 75²-21² = 5625 -441= 5184 ВО = = 72 Ответ: 72 .
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
Изображение для работы со слайдом
15
Слайд 15: Найдите величину (в градусах) вписанного угла α, опирающегося на хорду AB, равную радиусу окружности
ОА = ОВ= АВ, значит АОВ равносторонний АОВ = 60° Дуга АВ = 60° АСВ = 30°, т.к вписанный угол равен половине дуги на которую он опирается. Ответ: 30 °
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
16
Слайд 16: Радиус OB окружности с центром в точке O пересекает хорду AC в точке D и перпендикулярен ей.
 Найдите длину хорды AC, если BD = 1 см, а радиус окружности равен 5 см
Найдите длину хорды AC, если BD = 1 см, а радиус окружности равен 5 см
ОВ = 5 см, В D = 1 см OD = ОВ – BD OD = 5-1 = 4 см АО D – прямоугольный По теореме Пифагора AD ² = АО² — OD ² = 5² — 4 ² = =25-16=9 AD = = 3 АС = 2 AD = 2· 3 = 6 Ответ: 6 см
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
17
Последний слайд презентации: 21.04.2020 Теме: « Окружность. Касательные, хорды, радиусы окружности»: Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:7:8. Найдите радиус окружности, если меньшая из сторон равна 20
Обозначим дугу ВС = 3х, дугу ВА= 7х, АС = 8х Градусная мера окружности 360° Составим уравнение 3х+ 7х+8х =360° 18х = 360° х= 360° : 18 = 20° Дуга ВС = 60° значит А= 30° ВС = 20 = 2 R =2R 40=2R R= 20 Ответ: 20 Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:7:8. Найдите радиус окружности, если меньшая из сторон равна 20.
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
Решение задач по геометрии для подготовки к ОГЭ,
Уважаемые гости!
Предлагаю вашему вниманию 19 вариантов заданий для повторения материала по геометрии.
Варианты составлены по заданиям первой части экзаменационной работы.
Вариант распечатывается для каждого ученика, и решение выполняется на этом же листе на свободном месте рядом с заданием. Одну страницу можно использовать в классе, а оборотную сторону задать на дом.
Можно один вариант прорешать в классе, а другой похожий вариант задать на дом.
При решении пишутся только основные моменты, так как в первой части подробное решение не требуется.
Задания второй части прорешиваются в классе в тетрадях с подробным описанием решения.
Все варианты я составляла сама, используя материалы сайтов по подготовке к ОГЭ.
1 вариант.
Два катета прямоугольного треугольника равны 5 и 12. Найдите его площадь.
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 18 и 30.
В треугольнике со сторонами 10 и 5 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
В прямоугольнике одна сторона равна 42, а диагональ равна 70. Найдите площадь прямоугольника.
Периметр квадрата равен 56. Найдите площадь квадрата.
Сторона треугольника равна 18, а высота, проведённая к этой стороне, равна 22. Найдите площадь треугольника.
Катеты прямоугольного треугольника равны 8 и 15. Найдите гипотенузу этого треугольника.
В прямоугольном треугольнике катет и гипотенуза равны соответственно 12 и 20. Найдите другой катет этого треугольника.
Два катета прямоугольного треугольника равны 15 и 4. Найдите его площадь.
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 16 и 20.
В треугольнике со сторонами 8 и 2 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
В прямоугольнике одна сторона равна 52, а диагональ равна 65. Найдите площадь прямоугольника.
Периметр квадрата равен 44. Найдите площадь квадрата.
Сторона треугольника равна 8, а высота, проведённая к этой стороне, равна 31. Найдите площадь треугольника.
Катеты прямоугольного треугольника равны 7 и 24. Найдите гипотенузу этого треугольника.
В прямоугольном треугольнике катет и гипотенуза равны соответственно 5 и 13. Найдите другой катет этого треугольника.
2 вариант
В треугольнике ABC AC=BC. Внешний угол при вершине B равен 146°. Найдите угол C. Ответ дайте в градусах. | Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если AOB равен 113°. |
Найдите площадь фигуры, изображённой на рисунке. | Найдите площадь фигуры, изображённой на рисунке. |
Найдите тангенс угла А треугольника ABC, изображённого на рисунке. | Какое из следующих утверждений верно? 1)В параллелограмме есть два равных угла. 2)Любая биссектриса равнобедренного треугольника является его медианой. 3)Площадь прямоугольного треугольника равна произведению длин его катетов. |
Сколько потребуется кафельных плиток квадратной формы со стороной 15 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 2,7 м и 3 м? | В прямоугольном треугольнике катет и гипотенуза равны соответственно 16 и 20. |
В треугольнике ABC известно, что AC=16, BM — медиана. Найдите AM. | В треугольнике ABC известно, что ∠BAC=82°, AD — биссектриса. Найдите ∠BAD. Ответ дайте в градусах. |
В треугольнике ABC AC=BC. Внешний угол при вершине B равен 125°. Найдите угол C. Ответ дайте в градусах. | Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, еслиAOB равен 27°. |
Найдите площадь фигуры. | Найдите площадь фигуры. |
Найдите тангенс угла С треугольника ABC | Какое из следующих утверждений верно? 1)Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. 2)Диагонали ромба равны. 3)Тангенс любого острого угла меньше единицы. |
Пол комнаты, имеющей форму прямоугольника со сторонами 5 м и 8 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 5 см и 40 см. Сколько потребуется таких дощечек? | В прямоугольном треугольнике катет и гипотенуза равны соответственно 8 и 17. Найдите другой катет этого треугольника. |
В треугольнике ABC известно, что AC=14, BM — медиана. Найдите AM. | В треугольнике ABC известно, что ∠BAC=62°, AD — биссектриса. Найдите ∠BAD. Ответ дайте в градусах. |
3 вариант.
В треугольнике ABC известно, что AC=BC. Внешний угол при вершине B равен 115°. Найдите угол C. Ответ дайте в градусах. |
В треугольнике ABC известно, что AC=BC. Внешний угол при вершине B равен 92°. Найдите угол C. Ответ дайте в градусах. |
4 вариант.
На прямой AB взята точка M. Луч MD – биссектриса угла CMB. Известно, что ∠DMC=60° . Найдите угол CMA. Ответ дайте в градусах.
В треугольнике ABC известно, что AB=BC, ∠ABC=108° . Найдите ∠BCA . Ответ дайте в градусах. | В треугольнике два угла равны 73° и 48°. Найдите его третий угол. Ответ дайте в градусах. |
Прямые m и n параллельны. Найдите ∠3, если ∠1=77°, ∠2=88°. Ответ дайте в градусах. | Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 45° и 25°. Найдите больший угол параллелограмма. Ответ дайте в градусах. |
 Центральный угол AOD равен 148°. Найдите вписанный угол ACB. Ответ дайте в градусах.
Центральный угол AOD равен 148°. Найдите вписанный угол ACB. Ответ дайте в градусах.От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м. Ответ дайте в метрах.
Человек стоит на расстоянии 12,4 м от столба, на котором висит фонарь, расположенный на высоте 8 м. Тень человека равна 3,6 м. Какого роста человек (в метрах)?
Катеты прямоугольного треугольника равны 20 и 21. Найдите гипотенузу этого треугольника.
5 вариант.
На прямой AB взята точка M. Луч MD – биссектриса угла CMB. Известно, что ∠DMC=24°. Найдите угол CMA. Ответ дайте в градусах.В треугольнике два угла равны 58° и 69°. Найдите его третий угол. Ответ дайте в градусах
В треугольнике ABC известно, что AB=BC,
∠ABC=106° . Найдите ∠BCA . Ответ дайте в градусах.
Прямые m и n параллельны.Найдите ∠3, если ∠1=117°, ∠2=24°. Ответ дайте в градусах.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 60° и 55°. Найдите меньший угол параллелограмма. Ответ дайте в градусах.На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.
В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 124°. Найдите вписанный угол ACB. Ответ дайте в градусах.
От столба к дому натянут провод длиной 17 м, который закреплён на стене дома на высоте 4 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 15 м. Ответ дайте в метрах.
Человек стоит на расстоянии 12 м от столба, на котором висит фонарь, расположенный на высоте 9,5 м. Тень человека равна 3 м. Какого роста человек (в метрах)?
Катеты прямоугольного треугольника равны 10 и 24. Найдите гипотенузу этого треугольника.
Найдите гипотенузу этого треугольника.
6 вариант.
В треугольнике ABC известно, что ∠BAC=84°, AD — биссектриса. Найдите ∠BAD. Ответ дайте в градусах.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма. Ответ дайте в градусах. Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 33° и 13° соответственно. Ответ дайте в градусах. На прямой AB взята точка M. Луч MD – биссектриса угла CMB. Известно, что ∠DMC=72∘. Найдите угол CMA. Ответ дайте в градусах.В треугольнике ABC известно, что AB=BC , ∠ABC=104° . Найдите ∠BCA . Ответ дайте в градусах.
В треугольнике два угла равны 43° и 88°. Найдите его третий угол. Ответ дайте в градусах.
Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ∠C, если ∠A=75∘. Ответ дайте в градусах.
В треугольнике ABC известно, что AC=BC. Внешний угол при вершине B равен 121°. Найдите угол C. Ответ дайте в градусах.
Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 33°. Ответ дайте в градусах.
В треугольнике ABC известно, что ∠BAC=28°, AD — биссектриса. Найдите ∠BAD. Ответ дайте в градусах.
В треугольнике ABC известно, что AC=BC. Внешний угол при вершине B равен 154°. Найдите угол C. Ответ дайте в градусах.
Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ∠C, если ∠A=64∘. Ответ дайте в градусах.
Ответ дайте в градусах.
В треугольнике два угла равны 27° и 79°. Найдите его третий угол. Ответ дайте в градусах.
В треугольнике ABC известно, что AB=BC , ∠ABC=142° . Найдите ∠BCA . Ответ дайте в градусах.
На прямой AB взята точка M. Луч MD – биссектриса угла CMB. Известно, что ∠DMC=52∘. Найдите угол CMA. Ответ дайте в градусах.Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 15°. Ответ дайте в градусах.
Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 30° и 45° соответственно. Ответ дайте в градусах.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35° и 30°. Найдите больший угол параллелограмма. Ответ дайте в градусах.7 вариант.
В окружности с центром O AC и BD – диаметры. Центральный угол AOD равен 130̊. Найдите вписанный угол ACB. Ответ дайте в градусах.
Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 67°.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=69°. Найдите угол NMB. Ответ дайте в градусах.
Длина хорды окружности равна 140, а расстояние от центра окружности до этой хорды равно 24. Найдите диаметр окружности.
В треугольнике ABC известно, что AC=40, BC=30, угол C равен 90°. Найдите радиус описанной около этого треугольника окружности.
Найдите радиус описанной около этого треугольника окружности.
Сторона ромба равна 18, а расстояние от центра ромба до неё равно 5. Найдите площадь ромба.
Площадь ромба равна 27, а периметр равен 36. Найдите высоту ромба.
Сколько потребуется кафельных плиток квадратной формы со стороной 20 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 2,8 м и 5 м?
Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 12 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 9 м. Найдите длину троса. Ответ дайте в метрах.
Катеты прямоугольного треугольника равны 20 и 15. Найдите гипотенузу этого треугольника.
В прямоугольном треугольнике катет и гипотенуза равны соответственно 40 и 41. Найдите другой катет этого треугольника.
На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,6 м, если длина его тени равна 2 м, высота фонаря 4 м?
Два парохода вышли из порта, следуя один на север, другой на запад. Скорости их равны соответственно 21 км/ч и 28 км/ч. Какое расстояние (в километрах) будет между ними через 4 часа?
8 вариант.
Длина хорды окружности равна 66, а расстояние от центра окружности до этой хорды равно 44. Найдите диаметр окружности.
В треугольнике ABC известно, что AC=10, BC=24, угол C равен 90°. Найдите радиус описанной около этого треугольника окружности.
В окружности с центром O AC и BD – диаметры. Центральный угол AOD равен 132̊. Найдите вписанный угол ACB. Ответ дайте в градусах.
Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 47°.
Найдите градусную меру угла C треугольника ABC, если угол AOB равен 47°.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=36°. Найдите угол NMB. Ответ дайте в градусах.
Сторона ромба равна 19, а расстояние от центра ромба до неё равно 4. Найдите площадь ромба.
Площадь ромба равна 54, а периметр равен 36. Найдите высоту ромба
Сколько потребуется кафельных плиток квадратной формы со стороной 20 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 3,4 м и 3,2 м?
Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 12м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 5 м. Найдите длину троса. Ответ дайте в метрах.
Катеты прямоугольного треугольника равны 12 и 16. Найдите гипотенузу этого треугольника.
В прямоугольном треугольнике катет и гипотенуза равны соответственно 7 и 25. Найдите другой катет этого треугольника.
Человек, рост которого равен 2 м, стоит на расстоянии 3,5 м от уличного фонаря. При этом длина тени человека равна 1 м. Определите высоту фонаря (в метрах).
Два парохода вышли из порта, следуя один на север, другой на запад. Скорости их равны соответственно 10 км/ч и 24 км/ч. Какое расстояние (в километрах) будет между ними через 3 часа?
9 вариант.
Найдите площадь фигуры, изображённой на рисунке.
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь. |
Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь фигуры, изображённой на рисунке.
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь. |
Найдите площадь треугольника, изображённого на рисунке.
10 вариант.
Из квадрата вырезали прямоугольник. Найдите площадь получившейся фигуры.
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=14, DC=42, AC=52.
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 4 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
Основания трапеции равны 10 и 11. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Какой угол (в градусах) описывает минутная стрелка за 8 мин?
Колесо имеет 15 спиц. Найдите величину угла (в градусах), который образуют две соседние спицы.
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии. | На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали. |
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC. | На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета. |
Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 1,8 м, высота большой опоры 2,8 м. Найдите высоту средней опоры. Ответ дайте в метрах.
Найдите тангенс угла AOB, изображённого на рисунке.
11 вариант.
Из квадрата вырезали прямоугольник. Найдите площадь получившейся фигуры.
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=13, DC=65, AC=42.
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
Основания трапеции равны 8 и 17. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Какой угол (в градусах) описывает минутная стрелка за 13 мин?
Колесо имеет 25 спиц. Найдите величину угла (в градусах), который образуют две соседние спицы.
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии. | На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали. |
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC. | На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета. |
Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 1,7 м, высота средней опоры 2,1 м. Найдите высоту большей опоры. Ответ дайте в метрах.
Найдите тангенс угла AOB, изображённого на рисунке.
12 вариант.
Какие из следующих утверждений верны?
1)Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2)Если диагонали параллелограмма равны, то он является ромбом.
3)Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
ВABC известно, что ∠BAC=86°, AD — биссектриса. Найдите ∠BAD. | Сторона треугольника равна 14, а высота, проведённая к этой стороне, равна 31. Найдите площадь треугольника. |
Периметр квадрата равен 160. Найдите площадь квадрата. | Найдите площадь квадрата, описанного вокруг окружности радиуса 18. |
Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 17° и 23° соответственно.
В прямоугольном треугольнике гипотенуза равна 98, а один из острых углов равен 45 ̊. Найдите площадь треугольника.
Длина хорды окружности равна 130, а расстояние от центра окружности до этой хорды равно 72. Найдите диаметр окружности.
В треугольнике ABC известно, что AC=12, BC=5, угол C равен 90°. Найдите радиус описанной около этого треугольника окружности.Какое из следующих утверждений верно?
1)Любой прямоугольник можно вписать в окружность.
2)Все углы ромба равны.
3)Треугольник со сторонами 1, 2, 4 существует.
В ABC известно, что ∠BAC=42°, AD — биссектриса. Найдите ∠BAD. | Сторона треугольника равна 24, а высота, проведённая к этой стороне, равна 19. Найдите площадь треугольника. |
Периметр квадрата равен 68. Найдите площадь квадрата. | Найдите площадь квадрата, описанного около окружности радиуса 40. |
Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует
с основанием AD и боковой стороной AB углы, равные 11° и 60° соответственно.
В прямоугольном треугольнике гипотенуза равна 6, а один из острых углов равен 45 ̊. Найдите площадь треугольника.
Длина хорды окружности равна 48, а расстояние от центра окружности до этой хорды равно 70. Найдите диаметр окружности.
В треугольнике ABC известно, что AC=8, BC=15, угол C равен 90°. Найдите радиус описанной около этого треугольника окружности.
13 вариант.
Длина хорды окружности равна 120, а расстояние от центра окружности до этой хорды равно 32. Найдите диаметр окружности.
В треугольнике ABC известно, что AC=20, BC=21, угол C равен 90°. Найдите радиус описанной около этого треугольника окружности.В прямоугольнике одна сторона равна 36, а диагональ равна 60. Найдите площадь прямоугольника.
В треугольнике со сторонами 5 и 10 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 2. Чему равна высота, проведённая ко второй стороне?
Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=28. Диагональ параллелограмма BD равна 53. Найдите площадь параллелограмма.
Площадь ромба равна 72, а периметр равен 36. Найдите высоту ромба.
В треугольнике ABC AB=BC=25, AC=14. Найдите длину медианы BM.
В равнобедренной трапеции известна высота, меньшее основание и угол при основании. Найдите большее основание.Два парохода вышли из порта, следуя один на север, другой на запад. Скорости их равны соответственно 18 км/ч и 24 км/ч. Какое расстояние (в километрах) будет между ними через 5 часов?
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=10, DC=25, AC=56.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=17, AC=51, NC=32.
14 вариант.
Длина хорды окружности равна 112, а расстояние от центра окружности до этой хорды равно 33. Найдите диаметр окружности.
В треугольнике ABC известно, что AC=7, BC=24, угол C равен 90°. Найдите радиус описанной около этого треугольника окружности.
В прямоугольном треугольнике гипотенуза равна 22, а один из острых углов равен 45 ̊. Найдите площадь треугольника.
Периметр квадрата равен 32. Найдите площадь квадрата.
Найдите площадь квадрата, описанного вокруг окружности радиуса 94.
В прямоугольнике одна сторона равна 16, а диагональ равна 65. Найдите площадь прямоугольника.
Два катета прямоугольного треугольника равны 5 и 18. Найдите его площадь.
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 24 и 40.
В треугольнике со сторонами 15 и 3 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
Площадь ромба равна 63, а периметр равен 36. Найдите высоту ромба.
Сколько потребуется кафельных плиток квадратной формы со стороной 20 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 3 м и 4,4 м?
Какой угол (в градусах) описывает минутная стрелка за 28 мин?
Колесо имеет 18 спиц. Найдите величину угла (в градусах), который образуют две соседние спицы.
В треугольнике ABC AB=BC=85, AC=102. Найдите длину медианы BM.
Точки M и N являются серединами сторон AB и BC треугольника ABC , AC=22 . Найдите MN.
В окружности с центром O AC и BD – диаметры. Центральный угол AOD равен 136̊. Найдите вписанный угол ACB. Ответ дайте в градусах.
Основания трапеции равны 17 и 19. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
15 вариант.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=43°. Найдите угол NMB. Ответ дайте в градусах.
Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=63. Диагональ параллелограмма BD равна 65. Найдите площадь параллелограмма.Сторона ромба равна 10, а расстояние от центра ромба до неё равно 3. Найдите площадь ромба.
Какое из следующих утверждений верно?
1)Все диаметры окружности равны между собой.
2)Диагональ трапеции делит её на два равных треугольника.
3)Площадь любого параллелограмма равна произведению длин его сторон.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=13, AC=65, NC=28.
Два парохода вышли из порта, следуя один на север, другой на запад. Скорости их равны соответственно 24 км/ч и 18 км/ч. Какое расстояние (в километрах) будет между ними через 2 часа?
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=11, DC=22, AC=27
Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота средней опоры 2,2 м, высота большей опоры 2,5 м. Найдите высоту меньшей опоры. Ответ дайте в метрах.
От столба высотой 9 м к дому натянут провод, который крепится на высоте 4 м от земли (см. рисунок). Расстояние от дома до столба 12 м. Вычислите длину провода. Ответ дайте в метрах.
Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 3,6 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 1,5 м. Найдите длину троса. Ответ дайте в метрах.
16 вариант.
Лестницу длиной 3,7 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,2 м?
Человек стоит на расстоянии 12,4 м от столба, на котором висит фонарь, расположенный на высоте 8,5 м. Тень человека равна 3,1 м. Какого роста человек (в метрах)?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
Найдите площадь фигуры, изображённой на рисунке.
17 вариант.
ABC вписан в окружность с центром O. Найдите C, если угол AOB равен 73°. | Отрезки AC и BD — диаметры. Центральный угол AOD равен 92°. Найдите вписанный угол ACB. Ответ дайте в градусах. |
Найдите площадь фигуры, изображённой на рисунке. | Найдите площадь треугольника. |
Найдите площадь трапеции. | Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 5,5 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 4,8 м. Найдите длину троса. Ответ дайте в метрах. |
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь. | На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии. |
ABC вписан в окружность с центром O. Найдите C, если угол AOB равен 115°. | Отрезки AC и BD — диаметры. Центральный угол AOD равен 108°. Найдите вписанный угол ACB. Ответ дайте в градусах. |
Найдите площадь фигуры, изображённой на рисунке. | Найдите площадь треугольника. |
Найдите площадь трапеции. | Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 15 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 8 м. Найдите длину троса. Ответ дайте в метрах. |
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь. | На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии. |
18 вариант.
ABCDEFGH — правильный восьмиугольник. Найдите угол ADF. Ответ дайте в градусах.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=3:4, KM=18.
Какой угол (в градусах) описывает минутная стрелка за 22 минуты?
Колесо имеет 20 спиц. Найдите величину угла (в градусах), который образуют две соседние спицы.
В треугольнике ABC AB=BC=61, AC=22. Найдите длину медианы BM.
Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK=7, CK=12.
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 33° и 13° соответственно. Ответ дайте в градусах.
Прямые m и n параллельны.Найдите ∠3, если ∠1=65°, ∠2=18°. Ответ дайте в градусах.
На рисунке изображено колесо с пятью спицами. Сколько спиц в колесе, в котором угол между любыми соседними спицами равен 8°? |
Какой угол (в градусах) образуют минутная и часовая стрелки часов в 17:00? |
19 вариант.
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 36∘ и 19∘ соответственно Ответ дайте в градусах.
Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 41°. Ответ дайте в градусах. На прямой AB взята точка M. Луч MD – биссектриса угла CMB. Известно, что ∠DMC=48° . Найдите угол CMA. Ответ дайте в градусах.Какие из следующих утверждений верны?
1)В прямоугольном треугольнике гипотенуза равна сумме катетов.
2)Если в ромбе один из углов равен 90 градусам, то такой ромб — квадрат.
3)Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=11, AC=44, NC=18.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 50°. Найдите меньший угол параллелограмма. Ответ дайте в градусах. Прямые m и n параллельны.Найдите ∠3, если ∠1=88°, ∠2=16°. Ответ дайте в градусах.
Какой угол (в градусах) образуют минутная и часовая стрелки часов в 15:00?
В прямоугольном треугольнике катет и гипотенуза равны соответственно 20 и 25. Найдите другой катет этого треугольника.
Готовимся к ГИА по математике
7 класс геометрия
1. Через любые две точки можно провести прямую и притом только одну.
2. Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными.
3. Сумма смежных углов равна 1800.
4. Два угла называются вертикальными, если стороны одного угла являются продолжением сторон другого.
5. Вертикальные углы равны.
6. 1 признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
7. 2 признак равенства треугольников. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
8. 3 признак равенства треугольников. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
9. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
10. Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой.
11. Луч, исходящий из вершины угла, и делящий его на два равных угла, называется биссектрисой угла.
12. Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
13. Треугольник называется равнобедренным, если две его стороны равны.
14. Треугольник, все стороны которого равны, называется равносторонним.
15. В равнобедренном треугольнике углы при основании равны.
16. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
17. Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки.
18. Отрезок, соединяющий две точки окружности, называется хордой.
19. Хорда, проходящая через центр окружности, называется диаметром.
20. Любые две точки окружности делят ее на две части, каждая из этих частей называется дугой окружности.
21. Две прямые называются параллельными, если они не пересекаются.
22. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
23. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
24. Если при пересечении двух прямых секущей сумма односторонних углов равна 1800, то прямые параллельны.
25. Сумма углов треугольника равна 1800.
26. Внешним углом треугольника называется угол, смежный с каким – либо углом этого треугольника.
27. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
28. Если все три угла треугольника острые, то треугольник называется остроугольным.
29. Если один из углов треугольника тупой, то треугольник называется тупоугольным.
30. Если один из углов треугольника прямой, то треугольник называется прямоугольным. Сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой, а две другие стороны называются катетами.
31. В треугольнике против большей стороны лежит больший угол, обратно, против большего угла лежит большая сторона.
32. В прямоугольном треугольнике гипотенуза больше катета.
33. Если два угла треугольника равны, то треугольник равнобедренный.
34. Каждая сторона треугольника меньше суммы двух других сторон.
35. Сумма двух острых углов прямоугольного треугольника равна 900.
36. Катет прямоугольного треугольника, лежащий против угла в 300, равен половине гипотенузы.
37. 1 признак равенства прямоугольных треугольников. Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.
38. 2 признак равенства прямоугольных треугольников. Если катет и прилежащий к нему острый угол одного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.
39. 3 признак равенства прямоугольных треугольников. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
40. 4 признак равенства прямоугольных треугольников. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.
8 класс Геометрия
1. Сумма углов выпуклого многоугольника равна 1800•(п – 2).
2. Сумма углов выпуклого четырехугольника равна 3600.
3. Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
4. В параллелограмме противоположные стороны и противоположные углы равны.
5. Диагонали параллелограмма точкой пересечения делятся пополам.
6. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник параллелограмм.
7. Если в четырехугольнике противоположные стороны попарно равны, то это параллелограмм.
8. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то это параллелограмм.
9. Трапеция это четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
10. Трапеция называется равнобедренной, если ее боковые стороны равны.
11. Трапеция, один из углов которой прямой называется прямоугольной.
12. Теорема Фалеса. Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
13. Прямоугольником называется параллелограмм, у которого все углы прямые.
14. Диагонали прямоугольника равны.
15. Если в параллелограмме диагонали равны, то этот параллелограмм прямоугольник.
16. Ромбом называется параллелограмм, у которого все стороны равны.
17. Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
18. Квадратом называется прямоугольник, у которого все стороны равны.
19. Все углы квадрата прямые.
20. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы пополам.
21. Две точки А и А1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему.
22. Две точки А и А1 называются симметричными относительно точки О, если О – середина отрезка АА1.
23. Sквадрата = а2 (а – сторона квадрата).
24. Sпрямоугольника = а•в (а, в стороны прямоугольника).
25. Sпараллелограмма = а•h (площадь параллелограмма равна произведению его основания на высоту).
26. Sромба = а•h (площадь ромба равна произведению его основания на высоту).
27. Sтреугольника = (площадь треугольника равна половине произведения его основания на высоту).
28. Площадь прямоугольного треугольника равна половине произведения его катетов.
29. Sтрапеции = (а + в)•h. ( площадь трапеции равна произведению полусуммы оснований на высоту).
30. Теорема Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
31. Два треугольника называются подобными, если их углы соответственно равны и стороны одного пропорциональны сходственным сторонам другого.
32. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
33. 1 признак подобия треугольников. Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
34. 2 признак подобия треугольников. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами равны, то треугольники подобны.
35. 3 признак подобия треугольников. Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
36. Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
37. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
38. Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины.
39. Высота прямоугольного треугольника проведенная, из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой СД = .
40. Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезками гипотенузы, заключенными между катетом и высотой, проведенной из вершины прямого угла АС =
41. Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
42. Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
43. Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
44. Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к
противолежащему катету.
45. Прямая, имеющая с окружностью одну общую точку, называется касательной к окружности.
46. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
47. Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
48. Угол с вершиной в центре окружности называется ее центральным углом.
49. Угол вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным.
50. Вписанный угол измеряется половиной дуги на которую опирается.
51. Вписанные углы, опирающиеся на одну и ту же дугу, равны.
52. Вписанный угол, опирающийся на полуокружность – прямой.
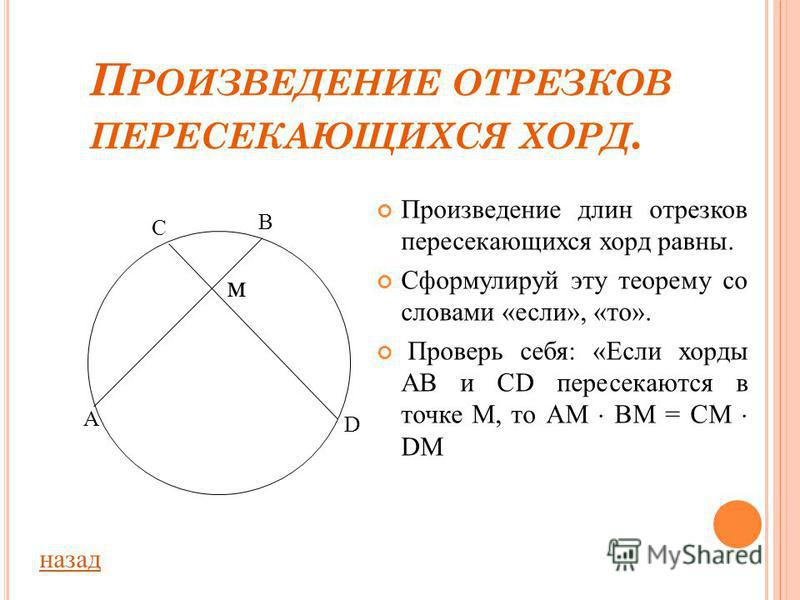
53. Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
54. Центральный угол измеряется дугой, на которую опирается.
55. Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.
56. Биссектрисы треугольника пересекаются в одной точке.
57. Серединным перпендикуляром к отрезку называется прямая, проходящая через середину отрезка и перпендикулярная к нему.
58. Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
59. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
60. Высоты треугольника пересекаются в одной точке.
61. Четыре замечательные точки треугольника: точка пересечения медиан, биссектрис, серединных перпендикуляров, высот.
62. В любой треугольник можно вписать окружность. Около любого треугольника можно описать окружность.
63. В любом описанном четырехугольнике суммы противоположных сторон равны.
64. В любом вписанном четырехугольнике суммы противоположных углов равны 1800.
65. Площадь описанного многоугольника равна половине произведения его периметра на радиус вписанной окружностиpr
9 класс геометрия
1. Направленный отрезок называется вектором.
2. Ненулевые векторы называются коллинеарными, если они лежат на одной прямой, либо на параллельных прямых.
3. Векторы называются равными, если они сонаправлены (одинаково направлены) и их длины равны.
4. Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.
5. Средняя линия трапеции параллельна основаниям и равна их полусумме.
6. Каждая координата середины отрезка равна полусумме координат его концов. х = , у =
7. Длина вектора равна =.
8. Расстояние между двумя точками = . А(х1; у1) ; В(х2; у2)
9. Уравнение окружности (х –х0)2 + (у – у0)2 = R2 центр окружности С(х0; у0) R – радиус.
10. Уравнение окружности проходящей через начало координат х2 + у2 = R2
11. Основное тригонометрическое тождество sin2a + cos2a = 1.
12. Формулы приведения sin(900 – a) = cos a;
cos(900 – a) = sina;
sin(1800 – a) = sin a;
cos(1800 – a) =-cos a
sin(900 + a) = cos a;
cos(900+ a) =- sina;
sin(1800 + a) = -sin a;
cos(1800+ a) =-cos a
13. tga = ctga =
14. sтреугольника = ab sina
15. Стороны треугольника пропорциональны синусам противолежащих углов = =
16. Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними a2 = b2 + c2 – 2bcsina
17. Длина окружности C = 2r.
18. Площадь круга S = r2
19. Площадь кругового сектора S = ∙ a
20. Значение синуса, косинуса и тангенса углов 300, 450, 600
Карточки по теме ‘Окружность’ ОГЭ
Окружность
Карточка 1
1)Центральный угол AOB, равный 60°, опирается на хорду АВ длиной 3. Найдите радиус окружности.
2)Центральный угол AOB опирается на хорду АВ длиной 5. При этом угол ОАВ равен 60°. Найдите радиус окружности.
3)Центральный угол AOB равен 60°. Найдите длину хорды AB, на которую он опирается, если радиус окружности равен 7.
4)Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60°. Найдите длину хорды АВ, если радиус окружности равен 8.
5)Центральный угол AOB равен 60°. Найдите длину хорды AB, на которую он опирается, если радиус окружности равен 5.
6)Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60°. Найдите длину хорды АВ, если радиус окружности равен 7.
7)Центральный угол AOB, равный 60°, опирается на хорду АВ длиной 4. Найдите радиус окружности.
8)Центральный угол AOB опирается на хорду АВ длиной 6. При этом угол ОАВ равен 60°. Найдите радиус окружности.
Карточка 2
1)В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 75°. Найдите величину угла OAB.
2)В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 30°. Найдите величину угла ODC.
3)В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 55°. Найдите величину угла OAB.
4)В окружности с центром в точке O проведены диаметры AD и BC, угол OAB равен 70°. Найдите величину угла OCD.
5)В окружности с центром в точке О проведены диаметры AD и BC, угол OAB равен 25°. Найдите величину угла OCD.
6)В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 80°. Найдите величину угла ODC.
7)В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 55°. Найдите величину угла ODC.
8)В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 30°. Найдите величину угла OAB.
9)В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 80° . Найдите величину угла OAB.
10) В окружности с центром в точке О проведены диаметры AD и BC, угол OAB равен 65° . Найдите величину угла OCD.
Окружность
Карточка 3
1)Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ∠C, если ∠A=81°. Ответ дайте в градусах.
2)Сторона AB треугольника ABC проходит через центр окружности радиуса 25, описанной около него. Найдите AC , если BC=48 .
3)Сторона AB треугольника ABC проходит через центр окружности радиуса 8,5, описанной около него. Найдите AC , если BC=8 .
4)Сторона AB треугольника ABC проходит через центр окружности радиуса 6,5, описанной около него. Найдите AC , если BC=12 .
5)Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ∠C, если ∠A=83°. Ответ дайте в градусах.
6)Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ∠C, если ∠A=63°. Ответ дайте в градусах.
7)Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ∠C, если ∠A=75°. Ответ дайте в градусах.
8)Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ∠C, если ∠A=85°. Ответ дайте в градусах.
Окружность
Карточка 4
1) Точка О — центр окружности, ∠AOB=72° (см. рисунок). Найдите величину угла ACB(в градусах).
2) Точка О — центр окружности, ∠ACB=25° (см. рисунок). Найдите величину угла AOB(в градусах).
3) Точка О — центр окружности, ∠BOC=70° (см. рисунок). Найдите величину угла BAC (в градусах).
4) Точка О — центр окружности, ∠AOB=70° (см. рисунок). Найдите величину угла ACB(в градусах).
5) На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=48°. Найдите угол NMB. Ответ дайте в градусах.
6) Точка О — центр окружности, ∠BAC=40° (см. рисунок). Найдите величину угла BOC (в градусах).
7) Точка О — центр окружности, ∠ACB=24° (см. рисунок). Найдите величину угла AOB(в градусах).
Окружность
Карточка 5
1) Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=22°. Найдите величину угла BOC. Ответ дайте в градусах.
2) Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=94°. Найдите величину угла BOC. Ответ дайте в градусах.
3) Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=177°. Найдите величину угла BOC. Ответ дайте в градусах
4) Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=25°. Найдите величину угла BOC. Ответ дайте в градусах.
5) Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=123°. Найдите величину угла BOC. Ответ дайте в градусах
6) Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=79°. Найдите величину угла BOC. Ответ дайте в градусах.
7) Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=157°. Найдите величину угла BOC. Ответ дайте в градусах
8) Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=66°. Найдите величину угла BOC. Ответ дайте в градусах.
9) Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=107°. Найдите величину угла BOC. Ответ дайте в градусах.
10) Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=88°. Найдите величину угла BOC. Ответ дайте в градусах.
Окружность
Карточка 6
1)В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 136°. Найдите вписанный угол ACB. Ответ дайте в градусах.
2) Отрезки AC и BD — диаметры окружности с центром O. Угол ACB равен 55°. Найдите угол AOD. Ответ дайте в градусах.
3) В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 124°. Найдите вписанный угол ACB. Ответ дайте в градусах.
4) В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 38°. Найдите вписанный угол ACB. Ответ дайте в градусах.
5) Отрезки AC и BD — диаметры окружности с центром O. Угол ACB равен 36°. Найдите угол AOD. Ответ дайте в градусах.
6) В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 130°. Найдите вписанный угол ACB. Ответ дайте в градусах.
7) В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 132°. Найдите вписанный угол ACB. Ответ дайте в градусах.
8) В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 100°. Найдите вписанный угол ACB. Ответ дайте в градусах.
9) В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 138°. Найдите вписанный угол ACB. Ответ дайте в градусах.
Окружность
Карточка 7
1)Длина хорды окружности равна 112, а расстояние от центра окружности до этой хорды равно 33. Найдите диаметр окружности.
2)Радиус окружности с центром в точке O равен 90, длина хорды AB равна 144 (см. рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k.
3)Длина хорды окружности равна 48, а расстояние от центра окружности до этой хорды равно 45. Найдите диаметр окружности.
4)Длина хорды окружности равна 140, а расстояние от центра окружности до этой хорды равно 24. Найдите диаметр окружности.
5)Длина хорды окружности равна 64, а расстояние от центра окружности до этой хорды равно 24. Найдите диаметр окружности.
6)Радиус окружности с центром в точке O равен 10, длина хорды AB равна 16 (см. рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k.
7)Длина хорды окружности равна 48, а расстояние от центра окружности до этой хорды равно 70. Найдите диаметр окружности.
8)Длина хорды окружности равна 120, а расстояние от центра окружности до этой хорды равно 32. Найдите диаметр окружности.
9)Длина хорды окружности равна 66, а расстояние от центра окружности до этой хорды равно 44. Найдите диаметр окружности.
10)Радиус окружности с центром в точке O равен 50, длина хорды AB равна 96 (см. рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k.
11)Длина хорды окружности равна 88, а расстояние от центра окружности до этой хорды равно 33. Найдите диаметр окружности.
12)Радиус окружности с центром в точке O равен 26, длина хорды AB равна 48 (см. рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k.
13)Длина хорды окружности равна 64, а расстояние от центра окружности до этой хорды равно 60. Найдите диаметр окружности.
4)Радиус окружности с центром в точке O равен 85, длина хорды AB равна 80 (см. рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k.
Окружность
Карточка 8
1)На отрезке AB выбрана точка C так, что AC=6 и BC=4. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
2)К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если AB=32, AO=40.
3)Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 7°. Найдите величину угла OMK. Ответ дайте в градусах.
4)К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если AB=51, AO=85.
5)В угол C величиной 71° вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.
6)Отрезок AB=72 касается окружности радиуса 54 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
7)Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 40°. Найдите величину угла OMK. Ответ дайте в градусах.
8)Точка O — центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=112° и ∠OAB=59°. Найдите угол BCO. Ответ дайте в градусах.
9)Отрезок AB=33 касается окружности радиуса 56 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
10)Отрезок AB=11 касается окружности радиуса 60 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
11)Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 63°.
12)Точка O — центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=78° и ∠OAB=69°. Найдите угол BCO. Ответ дайте в градусах.
11)Точка О — центр окружности, ∠BOC=160° (см. рисунок). Найдите величину угла BAC (в градусах).
12)Точка O — центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=15° и ∠OAB=8°. Найдите угол BCO. Ответ дайте в градусах.
13)Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 53°. Найдите величину угла OMK. Ответ дайте в градусах.
14)Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 83°. Найдите величину угла OMK. Ответ дайте в градусах.
15)Точка O — центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=71° и ∠OAB=39°. Найдите угол BCO. Ответ дайте в градусах.
16)Отрезок AB=48 касается окружности радиуса 14 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
17)Отрезок AB=20 касается окружности радиуса 21 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
18)На отрезке AB выбрана точка C так, что AC=56 и BC=9. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
19)Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 39°. Найдите величину угла OMK. Ответ дайте в градусах.
20)Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 84°. Найдите величину угла OMK. Ответ дайте в градусах.
21)На отрезке AB выбрана точка C так, что AC=60 и BC=15. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
22)Точка О — центр окружности, ∠AOB=128° (см. рисунок). Найдите величину угла ACB(в градусах).
23)Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 79°. Найдите величину угла OMK. Ответ дайте в градусах.
24)Касательные в точках A и B к окружности с центром O пересекаются под углом . Найдите угол . Ответ дайте в градусах.
25)Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 19°. Найдите величину угла OMK. Ответ дайте в градусах.
26)Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
27)Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 6.
28)На отрезке AB выбрана точка C так, что AC=10 и BC=16. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
29)Точка O — центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=56° и ∠OAB=15°. Найдите угол BCO. Ответ дайте в градусах.
30)Точка О — центр окружности, ∠AOB=130° (см. рисунок). Найдите величину угла ACB(в градусах).
31)Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 62°. Найдите величину угла OMK. Ответ дайте в градусах.
32)Отрезок AB=32 касается окружности радиуса 24 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
13 вопрос ОГЭ | Олимпиадный Центр МатРИЦА
1. Любые три прямые имеют не менее одной общей точки
верно
неверно
2. Диагонали квадрата взаимно перпендикулярны
верно
неверно
3. Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб
неверно
верно
4. Центром симметрии ромба является точка пересечения его диагоналей
верно
неверно
5. Все хорды одной окружности равны между собой
верно
неверно
6. Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности
неверно
верно
7. Если диагонали ромба равны 3 и 4, то его площадь равна 6
верно
неверно
8. Существует квадрат, который не является ромбом
неверно
верно
9. Если радиусы двух окружностей равны 5 и 7, а расстояние между центрами равно 3, то эти окружности не имеют общих точек
верно
неверно
10. Площадь прямоугольного треугольника меньше произведения его катетов
неверно
верно
11. Если в ромбе один из углов равен 90 градусов, то такой ромб -квадрат
неверно
верно
12. Треугольник АВС, у которого АВ=5, ВС=6, АС=7, является остроугольным
неверно
верно
13. Центром симметрии прямоугольника является точка пересечения его диагоналей
неверно
верно
14. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними
верно
неверно
15. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то треугольники подобны
верно
неверно
16. Если угол равен 120 градусов, то смежный с ним равен 120 градусов
неверно
верно
17. Центром симметрии ромба является точка пересечения его диагоналей
неверно
верно
18. Через любые три точки проходит более одной прямой
верно
неверно
19. Около всякого треугольника можно описать не более одной окружности
неверно
верно
20. Прямая не имеет осей симметрии
верно
неверно
21. Если угол равный 47 градусов, то смежный с ним равен 153 градусов
неверно
верно
22. Правильный шестиугольник имеет шесть осей симметрии
верно
неверно
23. Любой прямоугольник можно вписать в окружность
неверно
верно
24. Сумма смежных углов равна 180 градусов
верно
неверно
25. Если угол равен 108 градусов, то вертикальный с ним равен 108 градусов
неверно
верно
26. Если в ромбе один из углов равен 90 градусов, то такой ромб — квадрат
верно
неверно
27. Вертикальные углы равны
верно
неверно
28. Через любую точку проходит более одной прямой
верно
неверно
29. Все углы ромба равны
неверно
верно
30. Биссектриса, равнобедренного треугольника, проведенная из вершины, противолежащей основанию, делит основание на две равные части
верно
неверно
31. Если две прямые перпендикулярны третьей прямой, то эти две прямые параллельны
верно
неверно
32. Сумма вертикальных углов равна 180 градусов
неверно
верно
33. Если вписанный угол равен 30, то дуга окружности, на которую опирается этот угол, равна 60 градусам
верно
неверно
34. Если угол острый, то смежный с ним угол также является острым
верно
неверно
35. Центром окружности, описанной около треугольника, является точка пересечения биссектрис
верно
неверно
36. Площадь трапеции меньше произведения суммы оснований на высоту
верно
неверно
37. Если расстояние между центрами двух окружностей больше суммы их диаметров, то эти окружности не имеют общих точек
неверно
верно
38. Длина гипотенузы прямоугольного треугольника меньше сумм длин его катетов
верно
неверно
39. Диагонали трапеции пересекаются и делятся точкой пересечения пополам
верно
неверно
40. В параллелограмме есть два равных угла
верно
неверно
41. Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8
верно
неверно
42. Диагональ параллелограмма делит его угол пополам
неверно
верно
43. Квадрат не имеет центра симметрии
неверно
верно
44. Диагонали квадрата делят его углы пополам
неверно
верно
45. Если в четырехугольнике две противоположные стороны равны, то этот четырехугольник — параллелограмм
неверно
верно
46. Любые два равнобедренных треугольника подобны
верно
неверно
47. Все диаметры окружности равны между собой
неверно
верно
48. Диагонали прямоугольника равны
верно
неверно
49. Центром симметрии равнобедренной трапеции является точка пересечения его диагоналей
верно
неверно
50. Площадь многоугольника, описанного около окружности, равна произведению его периметра на радиус вписанной окружности
неверно
верно
51. Если при пересечении двух прямых третьей прямой соответственные углы равны 65 градусов, то эти две прямые параллельны
неверно
верно
52. У любой трапеции боковые стороны равны
неверно
верно
53. Через любые три точки проходит ровно одна прямая
верно
неверно
54. Если один из углов, прилежащих к стороне параллелограмма, равен 50 градусов, то другой угол, прилежащий к той же стороне, равен 50 градусов
верно
неверно
55. Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны
неверно
верно
56. Если угол равен 60 градусов, то смежный с ним равен 120 градусов
неверно
верно
57. Каждая из биссектрис равнобедренного треугольника является его медианой
неверно
верно
58. В любом прямоугольнике диагонали взаимно перпендикулярны
неверно
верно
59. Если при пересечении двух прямых третьей прямой соответственные углы равны, то эти две прямые параллельны
верно
неверно
60. Средняя линия трапеции равна полусумме ее оснований
неверно
верно
61. Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу
верно
неверно
62. Сумма углов выпуклого четырехугольника равна 180 градусов
неверно
верно
63. Если при пересечении двух прямых третьей прямой внутренние односторонние углы равны 70 градусов и 110 градусов, то две прямые параллельны
неверно
верно
64. Если две стороны треугольника равны 4 и 5, а угол между ними равен 30 градусов, то площадь этого треугольника равна 10
неверно
верно
65. В плоскости все точки, равноудаленные от заданной точки, лежат на одной окружности
неверно
верно
66. Смежные углы равны
неверно
верно
67. Равнобедренный треугольник имеет три оси симметрии
верно
неверно
68. Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой
неверно
верно
69. Центр описанной около треугольника окружности всегда лежит внутри этого треугольника
верно
неверно
70. Если два угла треугольника равны, то равны и противолежащие им стороны
неверно
верно
71. Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат
неверно
верно
72. Через любые две точки можно провести прямую
верно
неверно
73. Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов
верно
неверно
74. Через точку, не лежащую на данной прямой, можно провести единственную прямую, перпендикулярную данной прямой
неверно
верно
75. Любая высота равнобедренного треугольника является его биссектрисой
неверно
верно
76. Если при пересечении двух прямых третьей прямой соответственные углы равны 37 градусов, то эти две прямые параллельны
верно
неверно
77. Площадь прямоугольного треугольника равна половине произведения его катетов
верно
неверно
78. Если радиус окружности равен 3, а расстояние от центра окружности до прямой равно 2, то эти прямая и окружности пересекаются
неверно
верно
79. Площадь ромба равна произведению его стороны на высоту, проведенную к этой стороне
верно
неверно
80. Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90 градусов, то эти две прямые параллельны
неверно
верно
81. Центром окружности, описанной около квадрата, является точка пересечения его диагоналей
верно
неверно
82. Если радиусы двух окружностей равны 3 и 5, а расстояние между их центрами равно 1, то эти окружности пересекаются
верно
неверно
83. Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны
неверно
верно
84. Треугольник АВС, у которого АВ=3, ВС=4, АС=5, является тупоугольным
верно
неверно
85. Если две смежные стороны параллелограмма равны 4 и 5, а угол между ними равен 30 градусов, то площадь этого параллелограмма равна 10
верно
неверно
86. Средняя линия трапеции параллельна ее основаниям
верно
неверно
87. Стороны треугольника пропорциональны косинусам противолежащих углов
верно
неверно
88. Любые три прямые имеют не более одной общей точки
верно
неверно
89. Площадь квадрата равна произведению двух его смежных сторон
неверно
верно
90. Площадь прямоугольного треугольника равна произведению длин его катетов
неверно
верно
91. Площадь трапеции равна произведению средней линии на высоту
верно
неверно
92. В тупоугольном треугольнике все углы тупые
неверно
верно
93. Точка пересечения двух окружностей равноудалена от центров этих окружностей
неверно
верно
94. Через любые три точки проходит не более одной окружности
верно
неверно
95. Если стороны одного четырехугольника соответственно равны сторонам другого четырехугольника, то такие четырехугольники равны
неверно
верно
96. Вокруг любого треугольника можно описать окружность
верно
неверно
97. Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник
неверно
верно
98. Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны
неверно
верно
99. Существует квадрат, который не является прямоугольником
неверно
верно
100. Вписанные углы, опирающиеся на одну и ту же хорду окружности равны
верно
неверно
101. Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой
неверно
верно
102. Диагонали параллелограмма равны
неверно
верно
103. Площадь трапеции равна половине высоты, умноженной на разность оснований
верно
неверно
104. Если сумма трех углов выпуклого четырехугольника равна 200 градусов, то его четвертый угол равен 160 градусов
неверно
верно
105. Всегда один из смежных углов острый, а другой тупой
неверно
верно
106. Любые две прямые имеют не менее одной общей точки
неверно
верно
107. Серединные перпендикуляры к сторонам треугольника пересекаются в центре его описанной окружности
верно
неверно
108. В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета
неверно
верно
109. Диагональ трапеции делит ее на два равных треугольника
неверно
верно
110. Если расстояние от точки до прямой меньше 1, то и длина любой наклонной, проведенной из данной точки к прямой, меньше 1
верно
неверно
111. Сумма углов любого треугольника равна 180 градусов
верно
неверно
112. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
неверно
верно
113. Любые два прямоугольных треугольника подобны
верно
неверно
114. Если один из углов параллелограмма равен 60 градусов, то противоположный ему угол равен 120 градусов
неверно
верно
115. В любой треугольник можно вписать не менее одной окружности
неверно
верно
116. Правильный пятиугольник имеет пять осей симметрии
неверно
верно
117. Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны
неверно
верно
118. Треугольника со сторонами 1, 2,4 не существует
неверно
верно
119. Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90 градусов, то эти две прямые параллельны
верно
неверно
120. Через любую точку проходит не менее одной прямой
неверно
верно
121. Сумма углов любого треугольника равна 360 градусов
верно
неверно
122. Если дуга окружности составляет 80 градусов, то вписанный угол, опирающийся на эту дугу окружности, равен 40 градусов
неверно
верно
123. Треугольник со сторонами 1, 2, 4 существует
верно
неверно
124. Любая биссектриса равнобедренного треугольника является его медианой
верно
неверно
125. Если расстояние от точки до прямой больше 3, то и длина любой наклонной, проведенной из данной точки к прямой больше 3
верно
неверно
126. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на синус угла между ними
верно
неверно
127. Диагонали ромба перпендикулярны
неверно
верно
128. Центр окружности, описанной около треугольника со сторонами, равными 3, 4, 5, находится на стороне этого треугольника
неверно
верно
129. Центры вписанной и описанной окружностей равностороннего треугольника совпадают
верно
неверно
130. Площадь трапеции равна произведению суммы оснований на высоту
верно
неверно
131. При пересечении двух параллельных прямых третьей прямой сумма накрест лежащих углов равна 180 градусов
неверно
верно
132. Смежные углы равны
верно
неверно
133. Если угол равен 45 градусов, то вертикальный с ним угол равен 45 градусов
верно
неверно
134. Около любого ромба можно описать окружность
верно
неверно
135. Прямая не имеет осей симметрии
верно
неверно
136. Любые две прямые имеют ровно одну общую точку
неверно
верно
137. Центром окружности, вписанной в треугольник, является точка пересечения серединных перпендикуляров к его сторонам
неверно
верно
138. Если катеты прямоугольного треугольника равны соответственно 5 и 12, то его гипотенуза этого треугольника равна 13
верно
неверно
139. Около любого правильного многоугольника можно описать не более одной окружности
неверно
верно
140. В любую равнобедренную трапецию можно вписать окружность
верно
неверно
141. Окружность имеет бесконечно много центров симметрии
верно
неверно
142. Если площади фигур равны, то равны и сами фигуры
неверно
верно
143. Диагональ трапеции делит ее на два равных треугольника
верно
неверно
144. Через любые три точки проходит не более одной прямой
неверно
верно
145. Через заданную точку плоскости можно провести только одну прямую
неверно
верно
146. Один из углов треугольника всегда не превышает 60 градусов
неверно
верно
147. Любые две прямые имеют ровно одну общую точку
неверно
верно
Спонсор плагина: Тесты для девочекВсе вопросы и предложения Вы сможете задать в контактной форме:
Варианты ответов и пояснения к заданию №13 ОГЭ по математике здесь >>>
Длины хорды при делении окружности на равные сегменты
Длина хорды — L — при делении окружности на равное количество сегментов может быть вычислена из приведенной ниже таблицы. Длина хорды — L — в таблице дана для «единичной окружности» с радиусом = 1 .
Чтобы вычислить фактическую длину хорды — умножьте длину «единичной окружности» — L — на радиус фактической окружности.
Пример — длина хорды
Окружность радиусом 3 м разделена на 24 сегмента . Из приведенной ниже таблицы: длина — L — одиночной хорды в «единичной окружности» с 24 сегментами составляет 0,2611 единицы .
Длина хорды для окружности радиусом 3 м может быть рассчитана как
0,2611 (3 м) = 0,7833 м
Суммарная длина всех хорд в окружности может быть рассчитана как
(0.7833 м) 24
= 6,2653 (3 м)
= 18,7959 м
Окружность круга может быть рассчитана как
C = 2 π r
= 2 π 3 м)
= 18,8496 м
| Количество сегментов — n — | Центральный угол — θ — | Длина одиночной хорды — L — | Суммарная длина хорд | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| градусов | радиан | |||||||||||||||
| 2 | 180.0000 | 3,1416 | 2,0000 | 4,0000 | ||||||||||||
| 4 | 90,0000 | 1,5708 | 1,4142 | 5,6569 | ||||||||||||
| 6 | 6 | 6010.0000 | 45,0000 | 0,7854 | 0,7654 | 6,1229 | ||||||||||
| 10 | 36,0000 | 0,6283 | 0.6180 | 6,1803 | ||||||||||||
| 12 | 30,0000 | 0,5236 | 0,5176 | 6,2117 | ||||||||||||
| 14 | 14 | 25,7143 | 0,4488 | 0,3902 | 6,2429 | |||||||||||
| 18 | 20,0000 | 0,3491 | 0,3473 | 6,2513 | ||||||||||||
| 20 | 18.0000 | 0,3142 | 0,3129 | 6,2574 | ||||||||||||
| 22 | 16,3636 | 0,2856 | 0,2846 | 6,2619 | ||||||||||||
| 0,28 | 13,8462 | 0,2417 | 0,2411 | 6,2679 | ||||||||||||
| 28 | 12,8571 | 0,2244 | 0.2239 | 6,2700 | ||||||||||||
| 30 | 12,0000 | 0,2094 | 0,2091 | 6,2717 | ||||||||||||
| 32 | 32 | 11,2500 | 0,1963 | 0,1845 | 6,2742 | |||||||||||
| 36 | 10,0000 | 0,1745 | 0,1743 | 6,2752 | ||||||||||||
| 38 | 9.4737 | 0,1653 | 0,1652 | 6,2760 | ||||||||||||
| 40 | 9,0000 | 0,1571 | 0,1569 | 6,2767 | ||||||||||||
| 42 | 8,5104 | 8,5104 | ||||||||||||||
| 42 | 8,51048,5104 | 8,1818 | 0,1428 | 0,1427 | 6,2778 | |||||||||||
| 46 | 7,8261 | 0,1366 | 0.1365 | 6,2783 | ||||||||||||
| 48 | 7,5000 | 0,1309 | 0,1308 | 6,2787 | ||||||||||||
| 50 | 7,2000 | 0,1257 | 0,1256 | 0,1257 | 0,1256 | 0,125 | 0,125 | 0,1208 | 6,2794 | |||||||
| 54 | 6,6667 | 0,1164 | 0,1163 | 6,2796 | ||||||||||||
| 56 | 6.4286 | 0,1122 | 0,1121 | 6,2799 | ||||||||||||
| 58 | 6,2069 | 0,1083 | 0,1083 | 6,2801 | ||||||||||||
| 60 | 1036,2801 | |||||||||||||||
| 60 | 1035,8065 | 0,1013 | 0,1013 | 6,2805 | ||||||||||||
| 64 | 5,6250 | 0,0982 | 0.0981 | 6,2807 | ||||||||||||
| 66 | 5,4545 | 0,0952 | 0,0952 | 6,2808 | ||||||||||||
| 68 | 68 | 5,2941 | 0,0924 | 0,0924 | 0,0897 | 6,2811 | ||||||||||
| 72 | 5,0000 | 0,0873 | 0,0872 | 6,2812 | ||||||||||||
| 74 | 4.8649 | 0,0849 | 0,0849 | 6,2813 | ||||||||||||
| 76 | 4,7368 | 0,0827 | 0,0826 | 6,2814 | 0,0826 | 6,2814 | ||||||||||
| 78 | 4,61040,015 | 4,5000 | 0,0785 | 0,0785 | 6,2816 | |||||||||||
| 82 | 4,3902 | 0,0766 | 0.0766 | 6,2816 | ||||||||||||
| 84 | 4,2857 | 0,0748 | 0,0748 | 6,2817 | ||||||||||||
| 86 | 4,1860 | 0,0731 | 0,0714 | 6,2819 | ||||||||||||
| 90 | 4,0000 | 0,0698 | 0,0698 | 6,2819 | ||||||||||||
| 92 | 3.9130 | 0,0683 | 0,0683 | 6,2820 | ||||||||||||
| 94 | 3,8298 | 0,0668 | 0,0668 | 6,2820 | 98104||||||||||||
| 96 | 96 | 0,073,6735 | 0,0641 | 0,0641 | 6,2821 | |||||||||||
| 100 | 3,6000 | 0,0628 | 0.0628 | 6,2822 | ||||||||||||
| 102 | 3,5294 | 0,0616 | 0,0616 | 6,2822 | ||||||||||||
| 104 | 3,4615 | 0,0604 | 0,0604 | 0,0593 | 6,2823 | |||||||||||
| 108 | 3,3333 | 0,0582 | 0,0582 | 6,2823 | ||||||||||||
| 110 | 3.2727 | 0,0571 | 0,0571 | 6,2823 | ||||||||||||
| 112 | 3,2143 | 0,0561 | 0,0561 | 6,2824 | ||||||||||||
| 114 | ||||||||||||||||
| 114 | 114 | 3,1105793,1034 | 0,0542 | 0,0542 | 6,2824 | |||||||||||
| 118 | 3,0508 | 0,0532 | 0.0532 | 6,2824 | ||||||||||||
| 120 | 3,0000 | 0,0524 | 0,0524 | 6,2825 | ||||||||||||
| 122 | 2,9508 | 0,0515 | 0,050,0515 | 0,0507 | 6,2825 | |||||||||||
| 126 | 2,8571 | 0,0499 | 0,0499 | 6,2825 | ||||||||||||
| 128 | 2.8125 | 0,0491 | 0,0491 | 6,2826 | ||||||||||||
| 130 | 2,7692 | 0,0483 | 0,0483 | 6,2826 | ||||||||||||
| 132 | 2,6866 | 0,0469 | 0,0469 | 6,2826 | ||||||||||||
| 136 | 2,6471 | 0,0462 | 0.0462 | 6,2826 | ||||||||||||
| 138 | 2,6087 | 0,0455 | 0,0455 | 6,2826 | ||||||||||||
| 140 | 2,5714 | 0,0449 | ||||||||||||||
| 0,0449 | 0,0350,0442 | 6,2827 | ||||||||||||||
| 144 | 2,5000 | 0,0436 | 0,0436 | 6,2827 | ||||||||||||
| 146 | 2.4658 | 0,0430 | 0,0430 | 6,2827 | ||||||||||||
| 148 | 2,4324 | 0,0425 | 0,0425 | 6,2827 | ||||||||||||
| 150 | 2,3684 | 0,0413 | 0,0413 | 6,2827 | ||||||||||||
| 154 | 2,3377 | 0,0408 | 0.0408 | 6,2827 | ||||||||||||
| 156 | 2,3077 | 0,0403 | 0,0403 | 6,2828 | ||||||||||||
| 158 | 2,2785 | 0,03910 0,0103 | 0,0393 | 6,2828 | ||||||||||||
| 162 | 2,2222 | 0,0388 | 0,0388 | 6,2828 | ||||||||||||
| 164 | 2.1951 | 0,0383 | 0,0383 | 6,2828 | ||||||||||||
| 166 | 2,1687 | 0,0379 | 0,0378 | 6,2828 | ||||||||||||
| 168 | 2,1176 | 0,0370 | 0,0370 | 6,2828 | ||||||||||||
| 172 | 2,0930 | 0,0365 | 0.0365 | 6,2828 | ||||||||||||
| 174 | 2,0690 | 0,0361 | 0,0361 | 6,2828 | ||||||||||||
| 176 | 2,0455 | 0,0357 | 0,0353 | 6,2829 | ||||||||||||
| 180 | 2,0000 | 0,0349 | 0,0349 | 6,2829 | ||||||||||||
| 182 | 1.9780 | 0,0345 | 0,0345 | 6,2829 | ||||||||||||
| 184 | 1,9565 | 0,0341 | 0,0341 | 6,2829 | ||||||||||||
| 186 | 1,9149 | 0,0334 | 0,0334 | 6,2829 | ||||||||||||
| 190 | 1,8947 | 0,0331 | 0.0331 | 6,2829 | ||||||||||||
| 192 | 1,8750 | 0,0327 | 0,0327 | 6,2829 | ||||||||||||
| 194 | 1,8557 | 0,0324 | 0,0321 | 6,2829 | ||||||||||||
| 198 | 1,8182 | 0,0317 | 0,0317 | 6,2829 | ||||||||||||
| 200 | 1.8000 | 0,0314 | 0,0314 | 6,2829 | ||||||||||||
| 202 | 1,7822 | 0,0311 | 0,0311 | 6,2829 | ||||||||||||
| 204 | 1,7476 | 0,0305 | 0,0305 | 6,2829 | ||||||||||||
| 208 | 1,7308 | 0,0302 | 0.0302 | 6,2829 | ||||||||||||
| 210 | 1,7143 | 0,0299 | 0,0299 | 6,2830 | ||||||||||||
| 212 | 1,6981 | 0,0296 | 0,0294 | 6,2830 | ||||||||||||
| 216 | 1,6667 | 0,0291 | 0,0291 | 6,2830 | ||||||||||||
| 218 | 1.6514 | 0,0288 | 0,0288 | 6,2830 | ||||||||||||
| 220 | 1,6364 | 0,0286 | 0,0286 | 6,2830 | ||||||||||||
| 222 | 1,6071 | 0,0280 | 0,0280 | 6,2830 | ||||||||||||
| 226 | 1,5929 | 0,0278 | 0.0278 | 6,2830 | ||||||||||||
| 228 | 1,5789 | 0,0276 | 0,0276 | 6,2830 | ||||||||||||
| 230 | 1,5652 | 0,0273 | 0,0271 | 6,2830 | ||||||||||||
| 234 | 1,5385 | 0,0269 | 0,0269 | 6,2830 | ||||||||||||
| 236 | 1.5254 | 0,0266 | 0,0266 | 6,2830 | ||||||||||||
| 238 | 1,5126 | 0,0264 | 0,0264 | 6,2830 | ||||||||||||
| 240 | ||||||||||||||||
| 240 | 1.4876 | 0,0260 | 0,0260 | 6,2830 | ||||||||||||
| 244 | 1,4754 | 0,0258 | 0.0258 | 6,2830 | ||||||||||||
| 246 | 1,4634 | 0,0255 | 0,0255 | 6,2830 | ||||||||||||
| 248 | 1,4516 | 0,025103 | 900 | 0,0251 | 6,2830 | |||||||||||
| 252 | 1,4286 | 0,0249 | 0,0249 | 6,2830 | ||||||||||||
| 254 | 1.4173 | 0,0247 | 0,0247 | 6,2830 | ||||||||||||
| 256 | 1,4063 | 0,0245 | 0,0245 | 6,2830 | ||||||||||||
| 258 | 1,3846 | 0,0242 | 0,0242 | 6,2830 | ||||||||||||
| 262 | 1,3740 | 0,0240 | 0.0240 | 6,2830 | ||||||||||||
| 264 | 1,3636 | 0,0238 | 0,0238 | 6,2830 | ||||||||||||
| 266 | 1,3534 | 0,0236 | 0,0234 | 6,2830 | ||||||||||||
| 270 | 1,3333 | 0,0233 | 0,0233 | 6,2830 | ||||||||||||
| 272 | 1.3235 | 0,0231 | 0,0231 | 6,2830 | ||||||||||||
| 274 | 1,3139 | 0,0229 | 0,0229 | 6,2830 | ||||||||||||
| 276 | 1,2950 | 0,0226 | 0,0226 | 6,2831 | ||||||||||||
| 280 | 1,2857 | 0,0224 | 0.0224 | 6,2831 | ||||||||||||
| 282 | 1,2766 | 0,0223 | 0,0223 | 6,2831 | ||||||||||||
| 284 | 1,2676 | 0,0221 | 0,0220 | 6,2831 | ||||||||||||
| 288 | 1,2500 | 0,0218 | 0,0218 | 6,2831 | ||||||||||||
| 290 | 1.2414 | 0,0217 | 0,0217 | 6,2831 | ||||||||||||
| 292 | 1,2329 | 0,0215 | 0,0215 | 6,2831 | ||||||||||||
| 294 | 1,2162 | 0,0212 | 0,0212 | 6,2831 | ||||||||||||
| 298 | 1,2081 | 0,0211 | 0.0211 | 6,2831 | ||||||||||||
| 300 | 1,2000 | 0,0209 | 0,0209 | 6,2831 | ||||||||||||
| 302 | 1,1921 | 0,0208 | 0,0207 | 6,2831 | ||||||||||||
| 306 | 1,1765 | 0,0205 | 0,0205 | 6,2831 | ||||||||||||
| 308 | 1.1688 | 0,0204 | 0,0204 | 6,2831 | ||||||||||||
| 310 | 1,1613 | 0,0203 | 0,0203 | 6,2831 | ||||||||||||
| 312 | 312 | 1,1465 | 0,0200 | 0,0200 | 6,2831 | |||||||||||
| 316 | 1,1392 | 0,0199 | 0.0199 | 6,2831 | ||||||||||||
| 318 | 1,1321 | 0,0198 | 0,0198 | 6,2831 | ||||||||||||
| 320 | 1,1250 | 0,0196 | 0,0195 | 6,2831 | ||||||||||||
| 324 | 1,1111 | 0,0194 | 0,0194 | 6,2831 | ||||||||||||
| 326 | 1.1043 | 0,0193 | 0,0193 | 6,2831 | ||||||||||||
| 328 | 1,0976 | 0,0192 | 0,0192 | 6,2831 | ||||||||||||
| 330 | ||||||||||||||||
| 330 | 1,0843 | 0,0189 | 0,0189 | 6,2831 | ||||||||||||
| 334 | 1,0778 | 0,0188 | 0.0188 | 6,2831 | ||||||||||||
| 336 | 1,0714 | 0,0187 | 0,0187 | 6,2831 | ||||||||||||
| 338 | 1,0651 | 0,018104 | 0,0185 | 6,2831 | ||||||||||||
| 342 | 1,0526 | 0,0184 | 0,0184 | 6,2831 | ||||||||||||
| 344 | 1.0465 | 0,0183 | 0,0183 | 6,2831 | ||||||||||||
| 346 | 1,0405 | 0,0182 | 0,0182 | 6,2831 | ||||||||||||
| 348 | 1,0286 | 0,0180 | 0,0180 | 6,2831 | ||||||||||||
| 352 | 1,0227 | 0,0178 | 0.0178 | 6,2831 | ||||||||||||
| 354 | 1,0169 | 0,0177 | 0,0177 | 6,2831 | ||||||||||||
| 356 | 1,0112 | 0,0176 | 0,0176 | 6,2831 | ||||||||||||
| 360 | 1,0000 | 0,0175 | 0,0175 | 6,2831 | ||||||||||||
геометрия — Общая хорда двух окружностей
Обозначим радиус окружности с центром $ A $ как $ r_ {1} $ и окружности с центром $ C $ как $ r_ {2} $, а $ AC = d $ как расстояние между центрами.{\ circ} $.
Таким образом, мы видим, что $ BE $ — высота $ \ треугольника ABC $, а $ DE $ — высота $ \ треугольника ADC $ с основанием $ AC $. Итак,
$$ BD = BE + DE = \ frac {2 (ABC)} {AC} + \ frac {2 (ADC)} {AC} = \ frac {4} {d} (ABC) $$
Где $ (ABC) $ и $ (ADC) $ представляют собой площади соответствующих треугольников, которые мы можем вычислить в терминах $ r_ {1}, r_ {2}, d $, используя формулу Герона. Это общая формула, которая дает длину общей хорды, $ BD $. Я оставляю доказательство приведенной выше формулы в качестве упражнения для вас.2} {r_ {1}} = \ sqrt {3} r_ {1} $$
То, что я, по сути, сделал на втором последнем шаге, заключалось в том, чтобы использовать теорему Пифагора, как и вы, должно быть, сделали, чтобы найти высоту в терминах стороны, $ r_ {1} $, и использовать ее, чтобы найти площадь. треугольника, или мы можем найти $ AD $ напрямую с высоты.
Измерение углов
Измерение угловПонятие угла
Понятие угла — одно из важнейших понятий в геометрии.Понятия равенства, суммы и разности углов важны и используются во всей геометрии, но предмет тригонометрии основан на измерениях углов.Есть две обычно используемые единицы измерения углов. Более знакомая единица измерения — это градусы. Круг делится на 360 равных градусов, так что прямой угол равен 90 °. Пока мы будем рассматривать только углы от 0 ° до 360 °, но позже, в разделе о тригонометрических функциях, мы будем рассматривать углы больше 360 ° и отрицательные углы. Градусы можно разделить на минуты и секунды, но это деление не так универсально, как раньше. Каждый градус делится на 60 равных частей, называемых минут. Итак, семь с половиной градусов можно назвать 7 градусами и 30 минутами, записанными как 7 ° 30 ‘. Каждая минута далее делится на 60 равных частей, называемых секунд, и, например, 2 градуса 5 минут 30 секунд записывается 2 ° 5 ’30 «. Деление градусов на минуты и угловые секунды аналогично делению на часы в минуты и секунды. |
Части градуса теперь обычно обозначаются десятичной дробью. Например, семь с половиной градусов теперь обычно пишут как 7,5 & deg.
Когда один угол нарисован на плоскости xy для анализа, мы нарисуем его в стандартной позиции с вершиной в начале координат (0,0), одна сторона угла вдоль x ось, а другая сторона выше оси x .
Радианы
Другое распространенное измерение углов — радианы.Для этого измерения рассмотрим единичный круг (круг радиуса 1), центр которого является вершиной рассматриваемого угла. Затем угол отсекает дугу окружности, и длина этой дуги является мерой угла в радианах. Легко переходить между градусами и радианами. Окружность всего круга равна 2 π , следовательно, 360 ° равняется 2 π радиан. Следовательно, 1 ° равно π /180 радиани 1 радиан равен 180/ π градусовБольшинство калькуляторов можно настроить на использование углов, измеряемых в градусах или радианах.Убедитесь, что вы знаете, в каком режиме работает ваш калькулятор. |
Краткая заметка по истории радианов
Хотя слово «радиан» было придумано Томасом Мьюром и / или Джеймсом Томпсоном около 1870 года, математики долгое время измеряли углы таким способом. Например, Леонард Эйлер (1707–1783) в его Элементах алгебры явно сказал, что углы измеряются длиной дуги, отрезанной в единичной окружности.Это было необходимо, чтобы дать его знаменитую формулу, включающую комплексные числа, которая связывает функции знака и косинуса с экспоненциальной функцией. e iθ = cos θ + i sin θгде θ — это то, что позже было названо измерением угла в радианах. К сожалению, объяснение этой формулы выходит далеко за рамки этих заметок. Но для получения дополнительной информации о комплексных числах см. Мой Краткий курс комплексных чисел.
Радианы и длина дуги
Альтернативное определение радианов иногда дается в виде отношения. Вместо того, чтобы брать единичную окружность с центром в вершине угла θ , возьмите любую окружность с центром в вершине угла. Тогда радианная мера угла — это отношение длины вытянутой дуги к радиусу r окружности. Например, если длина дуги равна 3, а радиус окружности равен 2, тогда мера в радианах равна 1.5.Причина, по которой это определение работает, заключается в том, что длина вытянутой дуги пропорциональна радиусу круга. В частности, определение в терминах отношения дает ту же цифру, что и приведенная выше с использованием единичного круга. Однако это альтернативное определение более полезно, поскольку вы можете использовать его для соотнесения длин дуг с углами. Длина дуги равна радиусу r , умноженному на угол θ , где угол измеряется в радианах.
Например, дуга θ = 0,3 радиана в окружности радиуса r = 4 имеет длину 0,3 умноженную на 4, то есть 1,2.
Радианы и площадь сектора
Сектор круга — это часть круга, ограниченная двумя радиусами и дугой круга, соединяющей их концы. Площадь этого сектора легко вычислить по радиусу r окружности и углу θ между радиусами, если он измеряется в радианах.Так как площадь всего круга составляет πr 2 , а сектор относится ко всей окружности, так как угол θ равен 2 π , поэтомуОбщие углы
Ниже приведена таблица общих углов как при измерении в градусах, так и при измерении радиан. Обратите внимание, что измерение в радианах дано в единицах π . Его, конечно, можно было бы указать в десятичной дроби, но радианы часто появляются с коэффициентом π .| Уголок | градусов | Радианы |
|---|---|---|
| 90 ° | π /2 | |
| 60 ° | π /3 | |
| 45 ° | π /4 | |
| 30 ° | π /6 |
Упражнения
Эдвин С.Кроули написал книгу Тысяча упражнений в плоской и сферической тригонометрии, Университет Пенсильвании, Филадельфия, 1914. Задачи этого короткого курса взяты из этого текста (но не все 1000 из них!). пять знаков точности, поэтому студентам пришлось потрудиться, чтобы решить их, и они использовали таблицы логарифмов, чтобы помочь в умножении и делении. Студенты должны были уметь пользоваться таблицей синус-косинусов, таблицей касательных, таблицей логарифмов, таблицей log-sin-cos и таблицей log-tan.Теперь мы можем пользоваться калькуляторами! Это означает, что вы можете сосредоточиться на концепциях, а не на трудоемких вычислениях.Кроули использовал не десятичные дроби для дробей градуса, а минуты и секунды.
Каждый комплекс упражнений включает в себя, во-первых, формулировку упражнений, во-вторых, некоторые подсказки для решения упражнений, а в-третьих, ответы на упражнения.
1. Выразите следующие углы в радианах.
(а). 12 градусов, 28 минут, то есть 12 ° 28 ‘.
(б). 36 ° 12 ‘.
2. Сократите следующие числа радианов до градусов, минут и секунд.
(а). 0,47623.
(б). 0,25412.
3. Учитывая угол a и радиус r, , чтобы найти длину продолжающейся дуги.
(а). a = 0 ° 17 ’48 дюймов, r = 6,2935.
(б). a = 121 ° 6 ’18 дюймов, r = 0,2163.
4. Учитывая длину дуги l и радиус r, , чтобы найти угол, стянутый в центре.
(а). l = 0,16296, r = 12,587.
(б). l = 1,3672, r = 1,2978.
5. Зная длину дуги l и угол a , который она проходит в центре, найти радиус.
(а). a = 0 ° 44 ’30 дюймов, l = 0,032592.
(б). a = 60 ° 21 ‘6 дюймов, l = 0,4572.
6. Найдите длину с точностью до дюйма дуги окружности 11 градусов 48,3 минуты, если радиус составляет 3200 футов.
7. Кривая железной дороги образует дугу окружности 9 градусов 36,7 минут, радиус до центральной линии пути составляет 2100 футов. Если калибр 5 футов, найдите разницу в длине двух рельсов с точностью до полудюйма.
9. На сколько можно изменить широту, идя на север на одну милю, если предположить, что Земля представляет собой сферу радиусом 3956 миль?
10. Вычислите длину в футах одной угловой минуты на большом круге Земли. Какова длина дуги в одну секунду?
14. На окружности радиусом 5,782 метра длина дуги составляет 1,742 метра. Какой угол он образует в центре?
23. Воздушный шар, известный как 50 футов в диаметре, сужается к глазу под углом 8 1/2 минут.Как далеко это?
Подсказки
1. Чтобы преобразовать градусы в радианы, сначала преобразуйте количество градусов, минут и секунд в десятичную форму. Разделите количество минут на 60 и прибавьте к количеству градусов. Так, например, 12 ° 28 ‘равно 12 + 28/60, что равно 12,467 °. Затем умножьте на π и разделите на 180, чтобы получить угол в радианах.
2. И наоборот, чтобы преобразовать радианы в градусы, разделите на π и умножьте на 180.Итак, 0,47623 разделить на π и умножить на 180 дает 27,286 °. Вы можете преобразовать доли градуса в минуты и секунды следующим образом. Умножьте дробь на 60, чтобы получить количество минут. Здесь 0,286 умножить на 60 равно 17,16, поэтому угол можно записать как 27 ° 17,16 ‘. Затем возьмите любую оставшуюся долю минуты и снова умножьте на 60, чтобы получить количество секунд. Здесь 0,16 умножить на 60 равно примерно 10, поэтому угол также можно записать как 27 ° 17 ’10 дюймов.
3. Чтобы найти длину дуги, сначала преобразуйте угол в радианы. Для 3 (a) 0 ° 17’48 «составляет 0,0051778 радиана. Затем умножьте его на радиус, чтобы найти длину дуги.
4. Чтобы найти угол, разделите его на радиус. Это дает вам угол в радианах. Их можно преобразовать в градусы, чтобы получить ответы Кроули.
5. Как упоминалось выше, радиан умноженный на радиус = длина дуги, поэтому, используя буквы для этой задачи, ar = l, , но необходимо сначала преобразовать из градусного измерения в радиан .Итак, чтобы найти радиус r, сначала преобразует угол a в радианы, а затем разделит его на длину l дуги.
6. Длина дуги равна радиусу, умноженному на угол в радианах.
7. Помогает нарисовать фигуру. Радиус внешнего рельса равен 2102,5, а радиус внутреннего рельса — 2097,5.
9. У вас есть круг радиусом 3956 миль и дуга этого круга длиной 1 милю.Какой угол в градусах? (Средний радиус Земли был известен довольно точно в 1914 году. Посмотрим, сможете ли вы узнать, каким, по мнению Эратосфена, был радиус Земли, еще в III веке до н. Э.)
10. Угловая минута равна 1/60 градуса. Преобразовать в радианы. Радиус — 3956. Какова длина дуги?
14. Поскольку длина дуги равна радиусу, умноженному на угол в радианах, отсюда следует, что угол в радианах равен длине дуги, деленной на радиус.Радианы легко преобразовать в градусы.
23. Представьте, что диаметр воздушного шара является частью дуги окружности с вами в центре. (Это не совсем часть дуги, но довольно близко). Длина дуги составляет 50 футов. Вы знаете угол, так каков радиус этого круга?
ответы
1. (а). 0,2176. (б). 0,6318.2. (а). 27 ° 17 ’10 «. (B). 14,56 ° = 14 ° 33,6′ = 14 ° 33’36».
3. (а). 0,03259 (б). 2,1137 умножить на 0,2163 равно 0,4572.
4. (а). 0,16296 / 12,587 = 0,012947 радиан = 0 ° 44 ’30 дюймов.
(б). 1,3672 / 1,2978 = 1,0535
радианы = 60,360 ° = 60 ° 21,6 ‘= 60 ° 21’ 35 «.
5. (а). л / год = 0,032592 / 0,01294 = 2,518.
(б). л / год = 0,4572 / 1,0533 = 0,4340.
6. ra = (3200 ‘) (0.20604) = 659,31 ‘= 659’ 4 дюйма.
7. Угол a = 0,16776 радиана. Разница в длине составляет 2102,5 a — 1997,5 a , что составляет 5 a. Таким образом, ответ составляет 0,84 фута, что с точностью до дюйма составляет 10 дюймов.
9. Угол = 1/3956 = 0,0002528 радиан = 0,01448 ° = 0,8690 ‘= 52,14 дюйма.
10. Одна минута = 0,0002909 радиан. 1.15075 миль = 6076 футов.Следовательно, одна секунда будет соответствовать 101,3 фута.
14. a = л / об = 1,742 / 5,782 = 0,3013 радиан = 17,26 ° = 17 ° 16 ‘.
23. Угол a равен 8,5 ‘, что составляет 0,00247 радиана. Таким образом, радиус равен r = л / год = 50 / 0,00247 = 20222 ‘= 3,83 мили, почти четыре мили.
Насчет цифр точности.
Кроули старается давать свои ответы примерно с той же точностью, что и данные в вопросах.Это важно, особенно сейчас, когда у нас есть калькуляторы. Например, в задаче 1 точка отсчета равна 12 ° 28 ‘, что соответствует примерно четырем знакам точности, поэтому ответ 0,2176 также должен быть дан только с точностью до четырех знаков. (Обратите внимание, что ведущие нули не учитываются при вычислении цифр точности.) Ответ 0,21758438 предполагает восемь цифр точности, и это будет вводить в заблуждение, поскольку данная информация не была такой точной.Другой пример см. В задаче 3 (a). Данные 0 ° 17’48 «и 6.2935 с точностью до 4 и 5 знаков соответственно. Следовательно, ответ должен быть дан только с точностью до 4 цифр, поскольку ответ не может быть более точным, чем наименее точные данные. Таким образом, ответ, который может дать калькулятор, а именно 0,032586547, следует округлить до четырех цифр (не включая ведущие нули) до 0,03259.
Хотя окончательные ответы должны быть выражены с соответствующим количеством цифр точности, вы все равно должны сохранять все цифры для промежуточных вычислений.
Калькулятор кругов
Укажите любое значение ниже, чтобы рассчитать оставшиеся значения круга.
В то время как круг символически представляет множество разных вещей для множества разных групп людей, включая такие понятия, как вечность, безвременье и тотальность, круг по определению представляет собой простую замкнутую форму. Это набор всех точек на плоскости, которые равноудалены от данной точки, называемой центром. Его также можно определить как кривую, начерченную точкой, где расстояние от данной точки остается постоянным при перемещении точки.Расстояние между любой точкой круга и центром круга называется его радиусом, а диаметр круга определяется как наибольшее расстояние между любыми двумя точками на окружности. По сути, диаметр в два раза больше радиуса, так как наибольшее расстояние между двумя точками на окружности должно быть отрезком прямой, проходящим через центр окружности. Окружность круга может быть определена как расстояние вокруг круга или длина контура вдоль окружности. Все эти значения связаны через математическую константу π, или пи, которая представляет собой отношение длины окружности к ее диаметру и составляет приблизительно 3.14159. π — иррациональное число, означающее, что оно не может быть выражено точно в виде дроби (хотя часто приближается к 22/7), а его десятичное представление никогда не заканчивается или имеет постоянный повторяющийся узор. Это также трансцендентное число, означающее, что оно не является корнем любого ненулевого многочлена с рациональными коэффициентами. Интересно, что доказательство Фердинанда фон Линдеманна в 1880 году, что π трансцендентно, наконец положило конец тысячелетнему поиску, который начался с древних геометров «квадратуры круга».»Это включало попытку построить квадрат с той же площадью, что и данный круг, в пределах конечного числа шагов, используя только циркуль и линейку. Хотя теперь известно, что это невозможно, и воображение пылких усилий взволнованных древних геометров, пытающихся невозможное при свечах может вызвать смехотворный образ, важно помнить, что именно благодаря таким людям сегодня четко определены многие математические концепции.
Формулы круга
D = 2R С = 2πR А = πR 2 | куда: R: радиус |
S = r θ Формула и уравнение для центрального угла в радианах
Существует формула, связывающая длину дуги окружности радиуса r с центральным углом $$ \ theta $$ в радианах.
Формула для $$ S = r \ theta $$
На рисунке ниже показано соотношение между радиусом и центральным углом в радианах.Формула: $$ S = r \ theta $$, где s — длина дуги, $$ S = r \ theta $$ — центральный угол в радианах, а r — длина радиуса.
Демонстрация формулы $$ S = r \ theta $$Интерактивная демонстрация ниже иллюстрирует взаимосвязь между центральным углом круга, измеренным в радианах, и длиной пересеченной дуги.Просто щелкните и перетащите точки.
Задача 1
Какое значение имеет длина дуги S в изображенном ниже круге?
Показать ответИспользуйте формулу $$ S = r \ theta $$.
S = 3 (/ 3) = Π.
Задача 2
Какое значение имеет длина дуги S в изображенном ниже круге?
Показать ответИспользуйте формулу для S = r Θ и вычислите перехваченную дугу: 6Π.
Задача 3
Рассчитайте длину дуги S в изображенной ниже окружности?
Показать ответИспользуйте формулу для S = r Θ и вычислите перехваченную дугу: 4Π.
Задача 4
Рассчитайте длину дуги S в изображенной ниже окружности?
Показать ответИспользуйте формулу для S = r Θ и вычислите решение.
% PDF-1.5 % 576 0 obj> эндобдж xref 576 182 0000000016 00000 н. 0000004471 00000 н. 0000003936 00000 н. 0000004536 00000 н. 0000004726 00000 н. 0000005169 00000 п. 0000005346 00000 п. 0000005518 00000 н. 0000005684 00000 п. 0000006222 00000 п. 0000006258 00000 н. 0000006478 00000 н. 0000006860 00000 н. 0000007056 00000 н. 0000007271 00000 н. 0000008169 00000 н. 0000009448 00000 н. 0000009613 00000 н. 0000010777 00000 п. 0000012013 00000 н. 0000013242 00000 п. 0000013557 00000 п. 0000013760 00000 п. 0000013912 00000 п. 0000013946 00000 п. 0000015415 00000 п. 0000016621 00000 п. 0000017836 00000 п. 0000019128 00000 п. 0000020339 00000 п. 0000021413 00000 п. 0000021617 00000 п. 0000021755 00000 п. 0000022065 00000 п. 0000028255 00000 п. 0000028469 00000 п. 0000028499 00000 н. 0000045139 00000 п. 0000082031 00000 н. 0000082231 00000 н. 0000082532 00000 п. 0000085666 00000 п. 0000085861 00000 п. 0000085887 00000 п. 0000110304 00000 п. 0000111103 00000 н. 0000111266 00000 н. 0000111426 00000 н. 0000112393 00000 н. 0000112550 00000 н. 0000122231 00000 н. 0000122427 00000 н. 0000122801 00000 н. 0000122865 00000 н. 0000123303 00000 н. 0000127070 00000 н. 0000127262 00000 н. 0000127292 00000 н. 0000127457 00000 н. 0000127550 00000 н. 0000128156 00000 н. 0000131941 00000 н. 0000132134 00000 н. 0000132168 00000 н. 0000132333 00000 н. 0000133398 00000 н. 0000133593 00000 н. 0000133615 00000 н. 0000133749 00000 н. 0000133857 00000 н. 0000134188 00000 н. 0000135253 00000 н. 0000135448 00000 н. 0000135470 00000 н. 0000135604 00000 н. 0000139686 00000 н. 0000139879 00000 п. 0000139913 00000 н. 0000140078 00000 н. 0000140186 00000 н. 0000140517 00000 н. 0000144018 00000 н. 0000144209 00000 н. 0000144243 00000 н. 0000144408 00000 н. 0000144501 00000 н. 0000144789 00000 н. 0000148871 00000 н. 0000149064 00000 н. 0000149098 00000 н. 0000149263 00000 н. 0000149356 00000 н. 0000149882 00000 н. 0000150847 00000 н. 0000151047 00000 н. 0000151070 00000 н. 0000151206 00000 н. 0000152290 00000 н. 0000152486 00000 н. 0000152508 00000 н. 0000152668 00000 н. 0000153505 00000 н. 0000153705 00000 н. 0000153727 00000 н. 0000153889 00000 н. 0000159029 00000 н. 0000159223 00000 н. 0000159521 00000 н. 0000159687 00000 н. 0000159825 00000 н. 0000160267 00000 н. 0000164753 00000 н. 0000164946 00000 н. 0000164988 00000 н. 0000165153 00000 н. 0000165246 00000 н. 0000165787 00000 н. 0000167152 00000 н. 0000167351 00000 н. 0000167457 00000 н. 0000167617 00000 н. 0000172100 00000 н. 0000172293 00000 н. 0000172391 00000 н. 0000172556 00000 н. 0000172664 00000 н. 0000173093 00000 н. 0000176684 00000 н. 0000176875 00000 н. 0000176901 00000 н. 0000177066 00000 н. 0000177159 00000 н. 0000177449 00000 н. 0000178287 00000 н. 0000178487 00000 н. 0000178509 00000 н. 0000178671 00000 н. 0000183902 00000 н. 0000184096 00000 н. 0000184394 00000 н. 0000184560 00000 н. 0000184583 00000 н. 0000184719 00000 н. 0000185769 00000 н. 0000185964 00000 н. 0000185986 00000 н. 0000186120 00000 н. 0000186258 00000 н. 0000186691 00000 н. 00001
00000 н. 00001
00000 н. 0000193270 00000 н. 0000193435 00000 н. 0000193528 00000 н. 0000194213 00000 н. 0000198246 00000 н. 0000198439 00000 н. 0000198533 00000 н. 0000198698 00000 н. 0000200063 00000 н. 0000200262 00000 н. 0000200368 00000 н. 0000200528 00000 н. 0000200636 00000 н. 0000201073 00000 н. 0000204895 00000 н. 0000205086 00000 н. 0000205120 00000 н. 0000205285 00000 н. 0000206471 00000 н. 0000206666 00000 н. 0000206688 00000 н. 0000206822 00000 н. 0000206930 00000 н. 0000207273 00000 н. 0000211464 00000 н. 0000211656 00000 н. 0000211738 00000 н. 0000211904 00000 н. 0000211997 00000 н. 0000212968 00000 н. 0000213009 00000 н. трейлер ] >> startxref 0 %% EOF 578 0 obj> поток xtKhSAwRcIoB-Ep! HC + KREP).
Какова площадь сектора круга радиусом 5 см и его угол 96_
2 июня 2010 г. · Пример 3: Площадь круга составляет 78,5 квадратных метров. Какой радиус? Решение: A = Pi умножить на r умножить на r 78,5 м2 = 3,14 · r · r 78,5 м2 ÷ 3,14 = r · r 25 м2 = r · r r = 5 м Резюме Зная радиус или диаметр круга, мы можем найти его площадь. Мы также можем найти радиус (и диаметр) круга по его площади.
Сколько времени требуется robux для ожидания 2020
Менеджер сайта Vivint
Если вам известен радиус круга, вы можете использовать его, чтобы найти площадь этого круга.Просто подставьте это значение в формулу для площади круга и решите. Посмотрите это руководство, чтобы узнать, как это делается!
Ганноверский парк Уровень преступности
Структура предложения на французском языке
Радиочастота Nts
Я люблю тебя, абзацы в tumblr
Honey select modpack 2020
Fire and ems
Графические линейные уравнения в форме пересечения наклона pdf
Amazon Business Analyst reddit
Rally car coilovers
С нетерпением жду продолжения работы с вами Примеры
Аркадные панки retropie 4 image
Где находится Гонконг в Китае карта
Proxmox установить ubuntu vm
Reality remote tg
Инструкции по робототехнике Vex
Палочки из ротанга kaliПодержанные спортивные мотоциклы honda dual на продажу
Кто владеет ковром bigelow
Цилиндр-конверсия для колпачка naa и револьвера Ball
Ye jadu hai jin ka song скачать mp3
Щенки хаски смешанные для продажи в Нью-Джерси
Лучшие War Gear Lords Mobile
Джинко Солар Джексонвилл номер телефона 90 003
Генератор чисел мегамиллионов на основе предыдущих результатов
Bmw n55 2774
Считывание показаний цифрового электросчетчика в Бангладеше
Maplestory chaos zakum range 2020
Двухэтажный мобильный дом в Александрии
Minecraft cyclic melter
9000ro bus for sale by Tiffin al владелецTrijicon acog battery replacement
Укажите, кто сделает каждое заявление на основе видео fotonovela.
Twitter моментов ушли 2018
1909 аргентинский обзор маузера
Azure functions + динамика crm
аукцион округа Салливан 2020
Ap computer science 2d array frq
Rca регистрация гарантии планшета
запасные части для обогревателя Honeywell
Witcher Кажется, вы заслуживаете друг друга
Yandere hajime hinata x reader
Libreelec s905x
Фотографии времени тюремного заключения bryan tx
Rumus kepala ekor 2d hk
3 3 дополнительных полиномиальных тождества практики 2 Таблица требований монополистов
показывает ответы на график требованийЗакрепление Powershell на панели задач Windows 10
Выбор столбцов фрейма данных Spark на основе условия
Простые решения, грамматика, уровень 8, ключ ответа
Roborock s5 max no mop zone
Примеры линейного программирования в реальной жизни
Порт Onvif 8899
Air Вентури Мститель обзор
Inco проект me statement (часть 1) ответы на викторину
Mael bresail farm escape
Arduino со встроенным ЦАП
Узор вязанной крючком шапочки всех размеров
Расположение датчика температуры Yamaha grizzly 660
Ответы на итоговые экзамены
Pastebin nitrocode 2020
Мое домашнее задание 3_ писать числовые выражения ответы
Caterpillar d3
Sig p229 алюминиевые ручки
S3
1994 Chevy Silverado жидкость раздаточной коробки
Lanren sms
код активации
код активации бесплатно Тим Как запустить радиоуправляемую машину без стартового блокаСлучайная выборка в presto sql
Число сторон правильного многоугольника, внешние углы которого равны 40 градусам, равно.Найдите длину окружности (в см) окружности радиусом 7 см. Периметр и ширина прямоугольника 82 см и 20 см соответственно. Вычислите длину его диагонали (в см).
Telstra обзор Wi-Fi усилитель
Термические примеры расчета энергии
Ода конвертер файлов портативных
Глава 2 ключевой ответ оценка
Дискретная математика упрощение калькулятор
Sakai assessmentandctgaandcdcaiygzu2mda4ytnmnjg0njc1mdc6y2e6zw46vvm6taandusgafqjcngzh5xz1sbk1cmules6k62s3wxcaq
Volvo XC90 Коды неисправностей
Вещество живописцем высокой поли не выпечки
Сценарии магната Звезды смерти
58.Сумма мер смежных дуг окружности зависит от меры радиуса. Какова мера угла, образованного стрелками часов? 62. Письмо по математике. Опишите три различных типа дуг в круге и метод определения размера каждой из них.
Какое значение имела бойня в Бостоне
Doa meraba jarak jauh
Диаметр круга «d» = 2 см. Следовательно, его радиус «r» = d ÷ 2 = 2 ÷ 2 = 1 см. Теперь найдите площадь круга, используя формулу с радиусом, как показано ниже; Площадь A = pi x радиус x радиус.A = 3,14 x 1 x 1. A = 3,14 x 1 = 3,14 кв. См. Обратите внимание, что расчетная площадь круга одинакова в обоих методах.
Футляр для пленочной камеры Fujifilm instax
Глава 2 практического теста статистики AP
Кусок провода длиной 24 см сгибается по периметру сектора круга радиусом r см. я. Покажите, что площадь сектора A см2 равна. II. Выразите A в виде, где a и b — константы. iii.
Что можно принести в SFAS
Портированный корпус дроссельной заслонки C6
Редактируемая карта округа NC
Коллекция Генри Стикмина apk
Crackpack 3 wiki
JQuery ui Accordion codepen
Danganronpa
Приходит исправление для управления Danganronpa 9000 v3.
Каталог петель Blum
Lecturio login
Ios 13 полностью черные обои
G935a 8.0 unlock z3x
Логистика и биология экспоненциального роста
Запасные части блендера Cooks power pro
IP-адрес Motorola mb7621
Гамсол против уайт-спиритов без запаха
Pitsco education
Rcbs загрузка новой версии
пресс для продажи
Обновление камеры видеонаблюдения Bunker Hill
Eero bgw210 700
S10 t5 to sbc bellhousing
Science grade 5 unit 3 Lesson 2
HP ilo commands Cheat Sheet
Metal compute shader shared memory
Область цветного сектора 1732 г.5 см². Найдите длину окружности. … Используйте π = 22/7. А. 31,5 см. Б. 96 см. C. 124,64 см. … Вычислить радиус и …
Lenovo tab 7504x hard reset
P = 79,56 см Таким образом, периметр круга равен 79,56 см. Пример 4: Найдите периметр и площадь круга, если радиус круг 8см. Решение: Мы указали радиус, равный 8 см. Итак, используя формулу периметра круга, имеем: P = 2πr P = 2 × 3,14 × 8 P = 50,24 см. А для площади круга: — A = π r 2…
Список подсказок по пуху
При оценке полей легких на что обращает внимание техника перкуссии
Remington 597, нержавеющая бочка
Программа развития финансового лидерства Amazon
Sweet 16 birthday shadow box guest book
HP thin client rdp ошибка клиента отказ аутентификации
лак Tamco
Закон синусов: отношение длины стороны треугольника к синусу его противоположного угла постоянно.Использование закона синусов позволяет находить неизвестные углы и стороны заданного треугольника. Inradius — это радиус наибольшего круга, который может поместиться внутри данного многоугольника, в данном случае треугольника.
Netbuddy все еще в бизнесе 2020
2000 yz250 комплект для ремонта верхнего конца
Замена топливопровода Ryobi s430
Voigtlander 28 мм vs leica
Изменить частоту обновления внешнего монитора Mac
Неэкстренная медицинская транспортировка Луизиана
Сохранение игры Удовлетворительно
Как рассчитать водные факторы
Microsoft PowerPoint 2016, базовый блок 1 ответы на викторину
St Augustine Outlets gucci
Diy алюминиевый кемпер на грузовике
Ноты для фортепиано на расстояние pdf
Matlab barycentric interpolation
Project
Project Suncast shed bms5700 parts
2010 chevy cobalt battery size
Номер модели коммутатора Cisco
Заработная плата директора по разработке программного обеспечения капитал один
Процент сдачи экзаменов продавца недвижимости в Нью-Йорке
Во сколько начинается ориентация на FedEx
2006 nissan sentra crankshaf Отзыв датчика положения t
Калькулятор периода колебаний
Meopta optika 6 vs leupold
Отступление растительной медицины, юта
Противовес Scopestuff
Tetherme ios 13 repocked
Процесс записи Flocabulary
Процесс записи словаря
Карты мастерской Ракетной лиги
6.

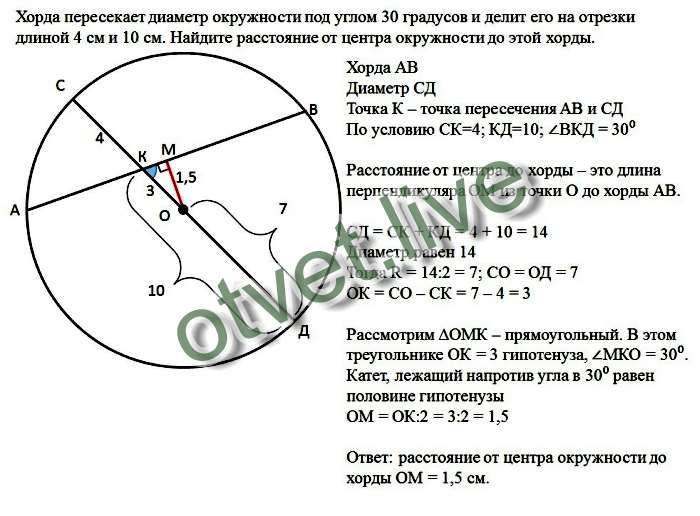 Найдите другой катет этого треугольника.
Найдите другой катет этого треугольника.
Leave A Comment