Что такое производная
Производная — главнейшее понятие математического анализа. Она характеризует изменение функции аргумента x в некоторой точке. При этом и сама производная является функцией от аргумента x
Производной функции в точке называется предел (если он существует и конечен) отношения приращения функции к приращению аргумента при условии, что последнее стремится к нулю.
То есть,
(1)
Наиболее употребительны следующие обозначения производной:
Пример 1. Пользуясь определением производной, найти производную функции
.
Решение. Из определения производной вытекает следующая схема её вычисления.
Дадим аргументу приращение (дельта) и найдём приращение функции:
.
Вычислим предел этого отношения при условии, что приращение аргумента стремится к нулю, то есть требуемую в условии задачи производную:
К понятию производной привело изучение Галилео Галилеем закона свободного падения тел, а в более широком смысле — задачи о мгновенной скорости неравномерного прямолинейного движения точки.
Однако движение свободно падающего тела явно неравномерное. Скорость v падения
постоянно возрастает. И средней скорости уже недостаточно для характеристики быстроты движения на различных участках пути.
Такая характеристика тем точнее, чем меньше промежуток времени .
Поэтому вводится следующее понятие: мгновенной скоростью прямолинейного движения (или скоростью в данный момент времени
(при условии, что этот предел существует и конечен).
Так выясняется, что мгновенная скорость есть предел отношения приращения функции s(t) к приращению аргумента t при Это и есть производная, которая в общем виде записывается так:.
.
Пример 2. Найти производную функции
Решение. Из определения производной вытекает следующая схема для её вычисления.
Шаг 1. Дадим аргументу приращение и найдём
Шаг 2. Найдём приращение функции:
Шаг 3. Найдём отношение приращения функции к приращению аргумента:
Шаг 4. Вычислим предел этого отношения при , то есть производную:
Касательной к графику функции в точке М называется предельное положение секущей МР при , или, что то же при .
Из определения следует, что для существования касательной достаточно, чтобы существовал предел
,
причём предел равен углу наклона касательной к оси .
Теперь дадим точное определение касательной.
где — угол наклона касательной к оси абсцисс, т.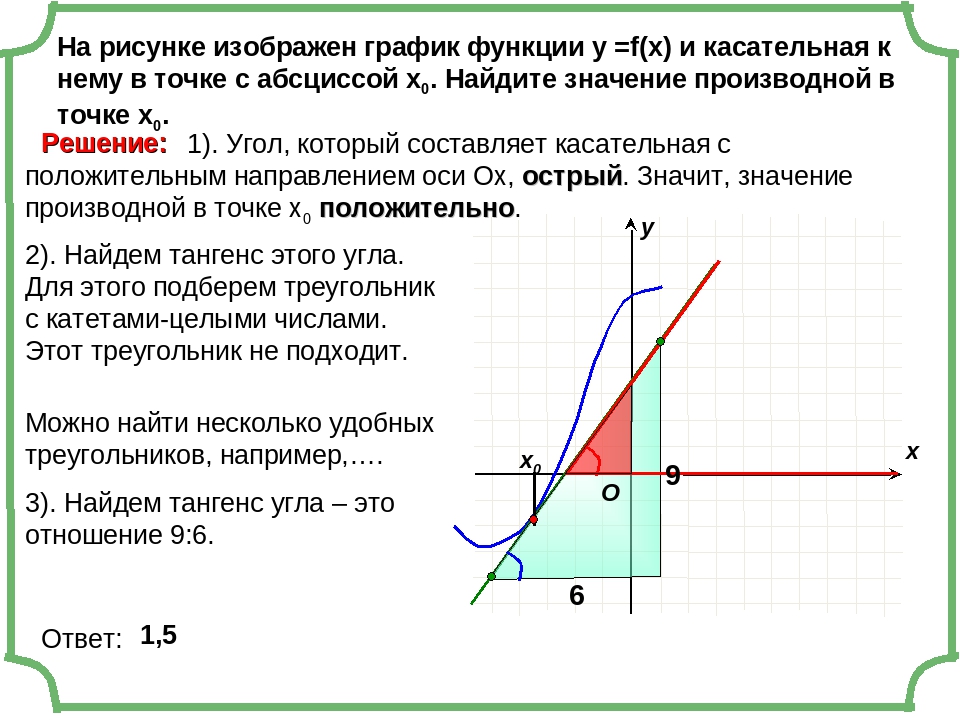 е. угловой коэффициент касательной.
е. угловой коэффициент касательной.
Пример 3. Найти производную функции и значение этой производной при .
Решение. Воспользуемся схемой, приведённой в примере 1.
Шаг 1.
Шаг 2.
Шаг 3.
Шаг 4.
Выражение под знаком предела не определено при (неопределённость вида 0/0), поэтому преобразуем его, избавившись от иррациональности в числителе и затем сократив дробь:
Найдём значение производной при :
Весь блок «Производная»
Наименьшее значение производной. Производная функции
Производная функции — одна из сложных тем в школьной программе. Не каждый выпускник ответит на вопрос, что такое производная.
В этой статье просто и понятно рассказано о том, что такое производная и для чего она нужна
Запомним определение:
Производная — это скорость изменения функции.
На рисунке — графики трех функций. Как вы думаете, какая из них быстрее растет?
Ответ очевиден — третья. У нее самая большая скорость изменения, то есть самая большая производная.
Вот другой пример.
Костя, Гриша и Матвей одновременно устроились на работу. Посмотрим, как менялся их доход в течение года:
На графике сразу все видно, не правда ли? Доход Кости за полгода вырос больше чем в два раза. И у Гриши доход тоже вырос, но совсем чуть-чуть. А доход Матвея уменьшился до нуля. Стартовые условия одинаковые, а скорость изменения функции, то есть
Интуитивно мы без труда оцениваем скорость изменения функции. Но как же это делаем?
На самом деле мы смотрим, насколько круто идет вверх (или вниз) график функции. Другими словами — насколько быстро меняется у с изменением х. Очевидно, что одна и та же функция в разных точках может иметь разное значение производной — то есть может меняться быстрее или медленнее.
Производная функции обозначается .
Покажем, как найти с помощью графика.
Нарисован график некоторой функции . Возьмем на нем точку с абсциссой . Проведём в этой точке касательную к графику функции. Мы хотим оценить, насколько круто вверх идет график функции. Удобная величина для этого — тангенс угла наклона касательной .
Производная функции в точке равна тангенсу угла наклона касательной, проведённой к графику функции в этой точке.
Обратите внимание — в качестве угла наклона касательной мы берем угол между касательной и положительным направлением оси .
Иногда учащиеся спрашивают, что такое касательная к графику функции. Это прямая, имеющая на данном участке единственную общую точку с графиком, причем так, как показано на нашем рисунке. Похоже на касательную к окружности.
Найдем . Мы помним, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Из треугольника :
Мы нашли производную с помощью графика, даже не зная формулу функции. Такие задачи часто встречаются в ЕГЭ по математике под номером .
Есть и другое важное соотношение. Вспомним, что прямая задается уравнением
Величина в этом уравнении называется угловым коэффициентом прямой . Она равна тангенсу угла наклона прямой к оси .
.
Мы получаем, что
Запомним эту формулу. Она выражает геометрический смысл производной.
Другими словами, производная равна тангенсу угла наклона касательной.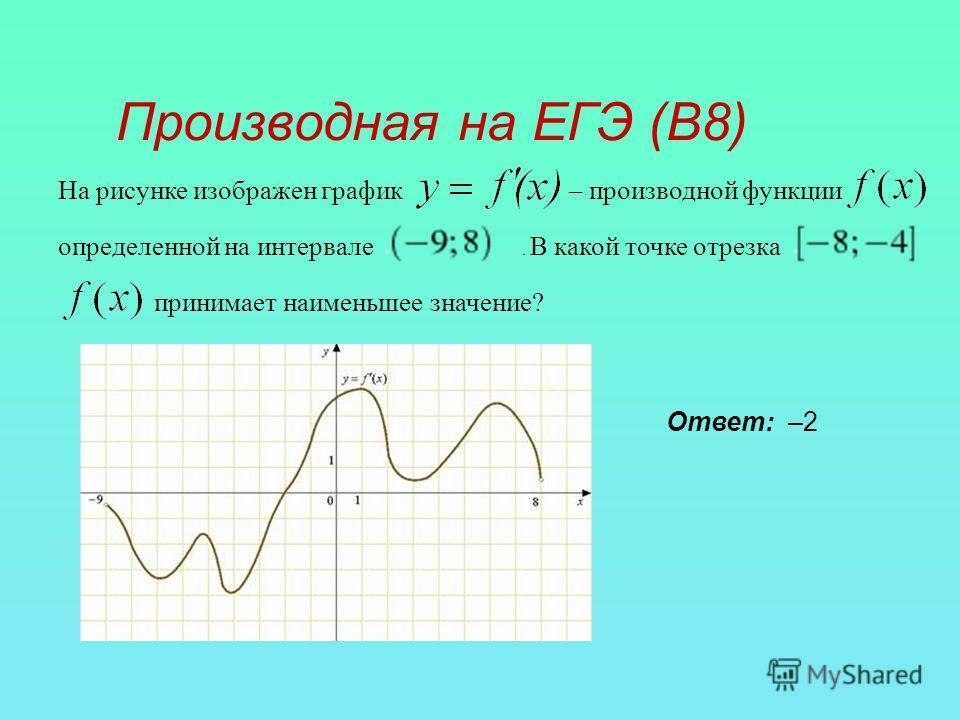
Мы уже сказали, что у одной и той же функции в разных точках может быть разная производная. Посмотрим, как же связана производная с поведением функции.
Нарисуем график некоторой функции . Пусть на одних участках эта функция возрастает, на других — убывает, причем с разной скоростью. И пусть у этой функции будут точки максимума и минимума.
В точке функция возрастает. Касательная к графику, проведенная в точке , образует острый угол с положительным направлением оси . Значит, в точке производная положительна.
В точке наша функция убывает. Касательная в этой точке образует тупой угол с положительным направлением оси . Поскольку тангенс тупого угла отрицателен, в точке производная отрицательна.
Вот что получается:
Если функция возрастает, ее производная положительна.
Если убывает, ее производная отрицательна.
А что же будет в точках максимума и минимума? Мы видим, что в точках (точка максимума) и (точка минимума) касательная горизонтальна. Следовательно, тангенс угла наклона касательной в этих точках равен нулю, и производная тоже равна нулю.
Точка — точка максимума. В этой точке возрастание функции сменяется убыванием. Следовательно, знак производной меняется в точке с «плюса» на «минус».
В точке — точке минимума — производная тоже равна нулю, но ее знак меняется с «минуса» на «плюс».
Вывод: с помощью производной можно узнать о поведении функции всё, что нас интересует.
Если производная положительна, то функция возрастает.
Если производная отрицательная, то функция убывает.
В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».
В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».
Запишем эти выводы в виде таблицы:
| возрастает | точка максимума | убывает | точка минимума | возрастает | |
| + | 0 | — | 0 | + |
Сделаем два небольших уточнения. Одно из них понадобится вам при решении задач ЕГЭ. Другое — на первом курсе, при более серьезном изучении функций и производных.
Одно из них понадобится вам при решении задач ЕГЭ. Другое — на первом курсе, при более серьезном изучении функций и производных.
Возможен случай, когда производная функции в какой-либо точке равна нулю, но ни максимума, ни минимума у функции в этой точке нет. Это так называемая :
В точке касательная к графику горизонтальна, и производная равна нулю. Однако до точки функция возрастала — и после точки продолжает возрастать. Знак производной не меняется — она как была положительной, так и осталась.
Бывает и так, что в точке максимума или минимума производная не существует. На графике это соответствует резкому излому, когда касательную в данной точке провести невозможно.
А как найти производную, если функция задана не графиком, а формулой? В этом случае применяется
Этот раздел содержит задачи ЕГЭ по математике на темы, связанные с исследованием функций и их производных.
В демонстрационных вариантах ЕГЭ 2020 года они могут встретиться под номером 14 для базового уровня и под номером 7 для профильного уровня.
Посмотрите внимательно на эти три графика функций.
Заметили ли вы, что эти функции в некотором смысле «родственники»?
Например, на тех участках, где график зеленой функции расположен выше нуля, красная функция возрастает. На тех участках, где график зеленой функции ниже нуля, красная функция убывает.
Аналогичные замечания можно сделать относительно красного и синего графиков.
Также можно заметить, что нули зеленой функции (точки x = −1 и x = 3) совпадают с точками экстремумов красного графика: при x = −1 на красном графике мы видим локальный максимум, при х = 3 на красном графике локальный минимум.
Нетрудно заметить, что локальные максимумы и минимумы синего графика достигаются в тех же точках, где красный график проходит через значение y = 0.
Можно сделать еще несколько выводов об особенностях поведения этих графиков, потому что они действительно связаны между собой.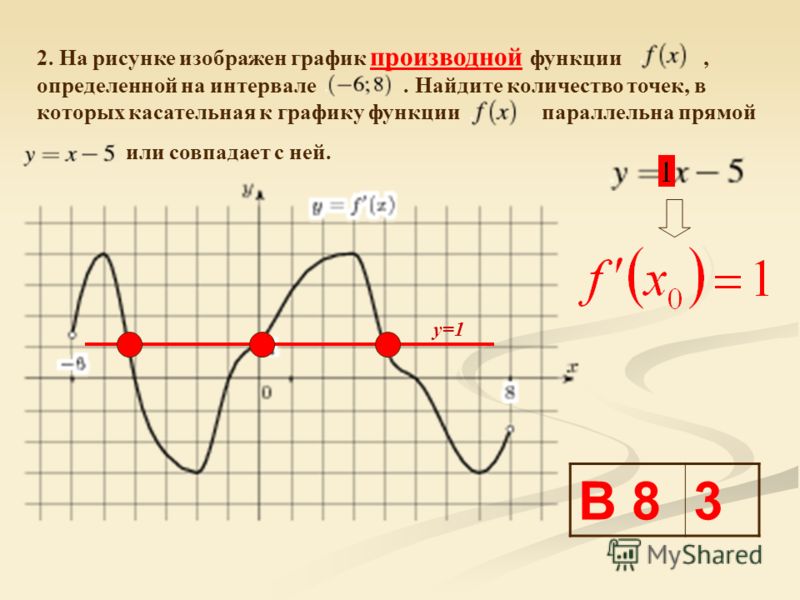 Посмотрите на формулы функций, расположенные под каждым из графиков, и путем вычислений убедитесь, что каждая предыдущая является производной для последующей и, соответственно, каждая следующая является одной из превообразных предыдущей функции.
Посмотрите на формулы функций, расположенные под каждым из графиков, и путем вычислений убедитесь, что каждая предыдущая является производной для последующей и, соответственно, каждая следующая является одной из превообразных предыдущей функции.
φ 1 (x ) = φ» 2 (x ) φ 2 (x ) = Φ 1 (x )
φ 2 (x ) = φ» 3 (x ) φ 3 (x ) = Φ 2 (x )
Вспомним, что мы знаем о производной:
Производная функции y = f (x ) в точке х выражает скорость изменения функции в точке x .
Физический смысл производной заключается в том, что производная выражает скорость протекания процесса, описываемого зависимостью y = f(x).
Геометрический смысл производной заключается в том, что её значение в рассматриваемой точке равняется угловому коэффициенту касательной, проведенной к графику дифференцируемой функции в этой точке.
А теперь пусть красного графика на рисунке нет. Допустим, что и формулы функций нам неизвестны.
Могу ли я спросить вас о чем то, связанном с поведением функции φ 2 (x ), если известно, что она является производной функции φ 3 (x ) и первообразной функции φ 1 (x )?
Могу. И на многие вопросы можно дать точный ответ, ведь мы знаем, что производная является характеристикой скорости изменения функции, поэтому можем судить о некоторых особенностях поведения одной из этих функций, глядя на график другой.
Прежде, чем отвечать на следующие вопросы, прокрутите страницу вверх так, чтобы скрылся верхний рисунок, содержащий красный график. Когда ответы будут даны, верните его обратно, чтобы проверить результат. И только после этого смотрите моё решение.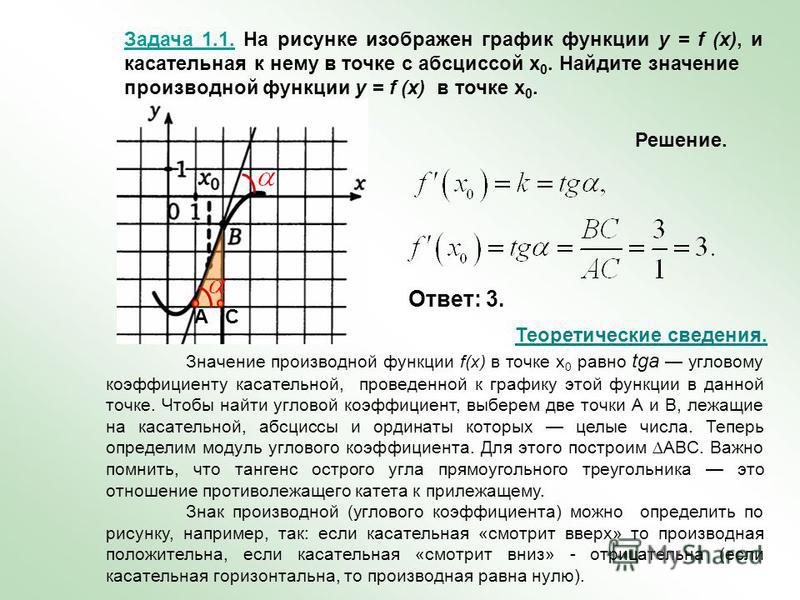
1) Пользуясь графиком производной φ» 2 (x ) (в нашем случае это зеленый график), определите какое из 2-ух значений функции больше φ 2 (−3) или φ 2 (−2)?
По графику производной видно, что на участке [−3;−2] её значения строго положительны, значит функция на этом участке только возрастает, поэтому значение функции в левом конце x = −3 меньше, чем её значение в правом конце x = −2.
Ответ: φ 2 (−3) φ 2 (−2)
2) Пользуясь графиком первообразной Φ 2 (x ) (в нашем случае это синий график), определите какое из 2-ух значений функции больше φ 2 (−1) или φ 2 (4)?
По графику первообразной видно, что точка x = −1 находится на участке возрастания, следовательно значение соответсвующей производной положительно. Точка x = 4 находится на участке убывания и значение соответствующей производной отрицательно. Поскольку положительное значение больше отрицательного, делаем вывод — значение неизвестной функции, которая как раз и является производной, в точке 4 меньше, чем в точке −1.
Ответ: φ 2 (−1) > φ 2 (4)
Подобных вопросов по отсутствующему графику можно задать много, что обуславливает большое разноообразие задач с кратким ответом, построенных по такой же схеме. Попробуйте решить некоторые из них.
Задачи на определение характеристик производной по графику функции.
Рисунок 1.
Рисунок 2.
Задача 1
y = f (x ), определенной на интервале (−10,5;19). Определите количество целых точек, в которых производная функции положительна.
Определите количество целых точек, в которых производная функции положительна.
Производная функции положительна на тех участках, где функция возрастает. По рисунку видно, что это промежутки (−10,5;−7,6), (−1;8,2) и (15,7;19). Перечислим целые точки внутри этих интервалов: «−10″,»−9», «−8″,»0», «1»,»2″, «3»,»4″, «5»,»6″, «7»,»8″, «16»,»17″, «18». Всего 15 точек.
Ответ: 15
Замечания.
1. Когда в задачах о графиках функций требуют назвать «точки», как правило, имеют в виду только значения аргумента x , которые являются абсциссами соответствующих точек, расположенных на графике. Ординаты этих точек — значения функции, они являются зависимыми и могут быть легко вычислены при необходимости.
2. При перечислении точек мы не учитывали края интервалов, так как функция в этих точках не возрастает и не убывает, а «разворачивается». Производная в таких точках не положительна и не отрицательна, она равна нулю, поэтому они называются стационарными точками. Кроме того, мы не рассматриваем здесь границы области определения, потому что в условии сказано, что это интервал.
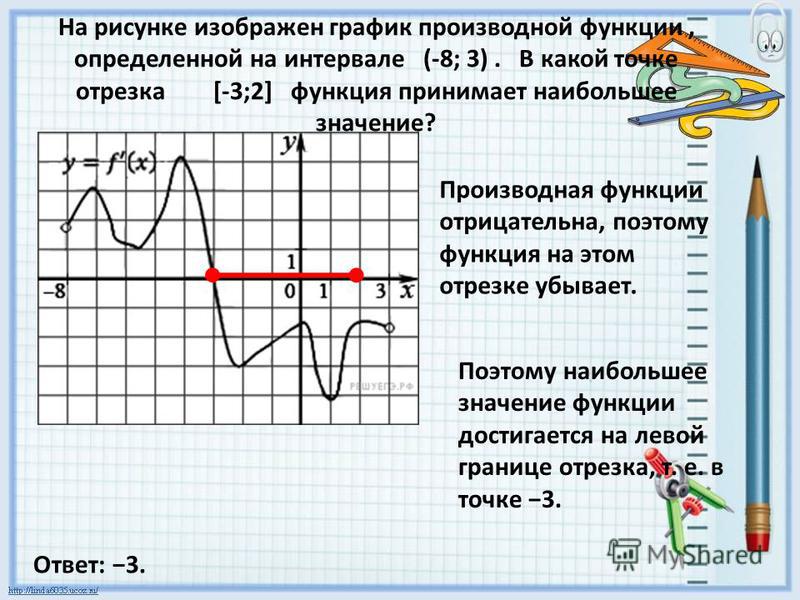
Задача 2
На рисунке 1 изображен график функции y = f (x ), определенной на интервале (−10,5;19). Определите количество целых точек, в которых производная функции f » (x ) отрицательна.
Производная функции отрицательна на тех участках, где функция убывает. По рисунку видно, что это промежутки (−7,6;−1) и (8,2;15,7). Целые точки внутри этих интервалов: «−7″,»−6», «−5″,»−4», «−3″,»−2», «9»,»10″, «11»,»12″, «13»,»14″, «15». Всего 13 точек.
Ответ: 13
См. замечания к предыдущей задаче.
Для решения следующих задач нужно вспомнить еще одно определение.
Точки максимума и минимума функции объединяются общим названием — точки экстремума .
В этих точках производная функции либо равна нулю, либо не существует (необходимое условие экстремума ).
Однако необходимое условие — это признак, но не гарантия существования экстремума функции. Достаточным условием экстремума является смена знака производной: если производная в точке меняет знак с «+» на «−», то это точка максимума функции; если производная в точке меняет знак с «−» на «+» , то это точка минимума функции; если в точке производная функции равна нулю, либо не существует, но знак производной при переходе через эту точку не меняется на противоположный, то указанная точка не является точкой экстремума функции. Это может быть точка перегиба, точка разрыва или точка излома графика функции.
Задача 3
На рисунке 1 изображен график функции y = f (x ), определенной на интервале (−10,5;19). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней.
Вспомним, что уравнение прямой имеет вид y = kx + b , где k — коэффициент наклона этой прямой к оси Ox . В нашем случае k = 0, т.е. прямая y = 6 не наклонена, а параллельна оси Ox . Значит искомые касательные также должны быть параллельны оси Ox и также должны иметь коэффициент наклона 0. Таким свойством касательные обладают в точках экстремумов функций. Поэтому для ответа на вопрос нужно просто посчитать все точки экстремумов на графике. Здесь их 4 — две точки максимума и две точки минимума.
Ответ: 4
Задача 4
Функции y = f (x ), определенной на интервале (−11;23). Найдите сумму точек экстремума функции на отрезке .
На указанном отрезке мы видим 2 точки экстремума. Максимум функции достигается в точке x 1 = 4, минимум в точке x 2 = 8.
x 1 + x 2 = 4 + 8 = 12.
Ответ: 12
Задача 5
На рисунке 1 изображен график функции y = f (x ), определенной на интервале (−10,5;19).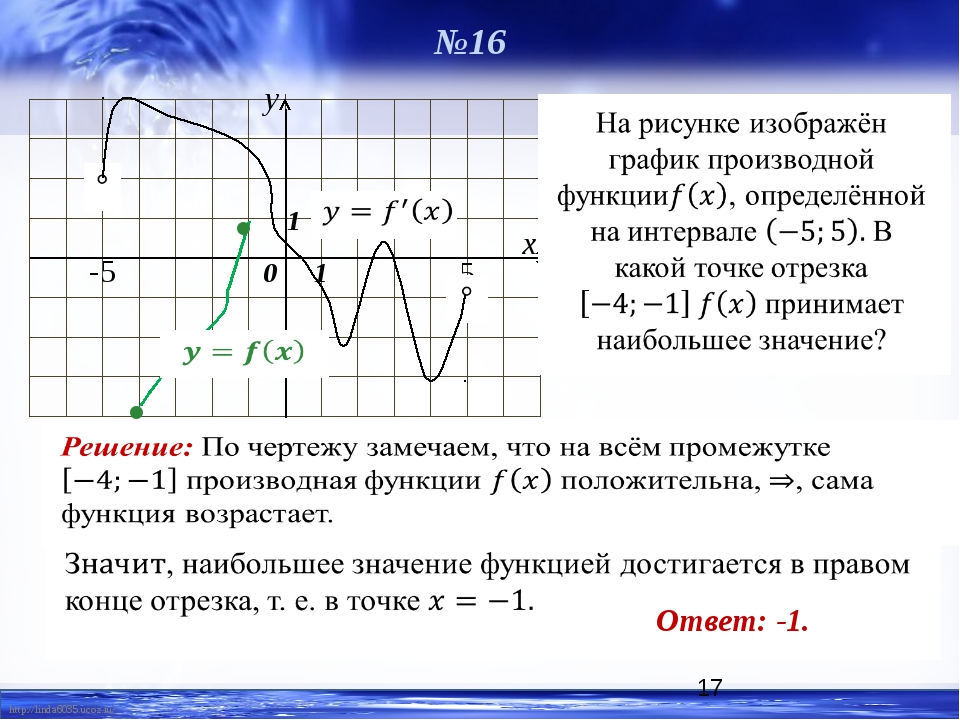 Найдите количество точек, в которых производная функции f » (x ) равна 0.
Найдите количество точек, в которых производная функции f » (x ) равна 0.
Производная функции равна нулю в точках экстремума, которых на графике видно 4:
2 точки максимума и 2 точки минимума.
Ответ: 4
Задачи на определение характеристик функции по графику её производной.
Рисунок 1.
Рисунок 2.
Задача 6
На рисунке 2 изображен график f » (x ) — производной функции f (x ), определенной на интервале (−11;23). В какой точке отрезка [−6;2] функция f (x ) принимает наибольшее значение.
На указанном отрезке производная нигде не была положительной, следовательно функция не возрастала. Она убывала или проходила через стационарные точки. Таким образом, наибольшего значения функция достигала на левой границе отрезка: x = −6.
Ответ: −6
Замечание: По графику производной видно, что на отрезке [−6;2] она равна нулю трижды: в точках x = −6, x = −2, x = 2. Но в точке x = −2 она не меняла знака, значит в этой точке не могло быть экстремума функции. Скорее всего там была точка перегиба графика исходной функции.
Задача 7
На рисунке 2 изображен график f » (x ) — производной функции f (x ), определенной на интервале (−11;23). В какой точке отрезка функция принимает наименьшее значение.
На отрезке производная строго положительна, следовательно функция на этом участке только возрастала. Таким образом, наименьшего значения функция достигала на левой границе отрезка: x = 3.
Ответ: 3
Задача 8
На рисунке 2 изображен график f » (x ) — производной функции f (x ), определенной на интервале (−11;23).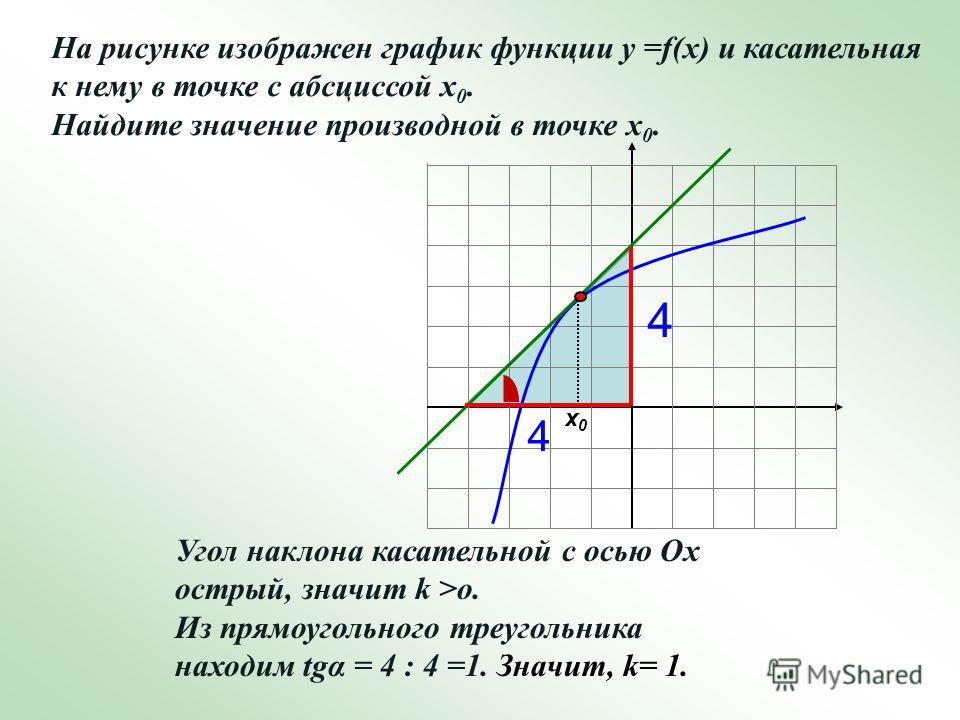 Найдите количество точек максимума функции f (x ), принадлежащих отрезку [−5;10].
Найдите количество точек максимума функции f (x ), принадлежащих отрезку [−5;10].
Согласно необходимому условию экстремума максимум функции может быть в точках, где её производная равна нулю. На заданном отрезке это точки: x = −2, x = 2, x = 6, x = 10. Но согласно достаточному условию он точно будет только в тех из них, где знак производной меняется с «+» на «−». На графике производной мы видим, что из перечисленных точек такой является только точка x = 6.
Ответ: 1
Задача 9
На рисунке 2 изображен график f » (x ) — производной функции f (x ), определенной на интервале (−11;23). Найдите количество точек экстремума функции f (x ), принадлежащих отрезку .
Экстремумы функции могут быть в тех точках, где её производная равна 0. На заданном отрезке графика производной мы видим 5 таких точек: x = 2, x = 6, x = 10, x = 14, x = 18. Но в точке x = 14 производная не поменяла знак, следовательно её надо исключить из рассмотрения. Таким образом, остаются 4 точки.
Ответ: 4
Задача 10
На рисунке 1 изображен график f » (x ) — производной функции f (x ), определенной на интервале (−10,5;19). Найдите промежутки возрастания функции f (x ). В ответе укажите длину наибольшего из них.
Промежутки возрастания функции совпадают с промежутками положительности производной. На графике мы видим их три — (−9;−7), (4;12), (18;19). Самый длинный из них второй. Его длина l = 12 − 4 = 8.
Ответ: 8
Задача 11
На рисунке 2 изображен график f » (x ) — производной функции f (x ), определенной на интервале (−11;23). Найдите количество точек, в которых касательная к графику функции f (x ) параллельна прямой y = −2x − 11
или совпадает с ней.
Найдите количество точек, в которых касательная к графику функции f (x ) параллельна прямой y = −2x − 11
или совпадает с ней.
Угловой коэффициент (он же тангенс угла наклона) заданной прямой k = −2. Нас интересуют параллельные или совпадающие касательные, т.е. прямые с таким же наклоном. Исходя из геометрического смысла производной — угловой коэффициент касательной в рассматриваемой точке графика функции, пересчитываем точки, в которых производная равна −2. На рисунке 2 таких точек 9. Их удобно считать по пересечениям графика и линии координатной сетки, проходящей через значение −2 на оси Oy .
Ответ: 9
Как видите, по одному и тому же графику можно задать самые разнообразные вопросы о поведении функции и её производной. Также один тот же вопрос можно отнести к графикам разных функций. Будьте внимательны при решении этой задачи на экзамене, и она покажется Вам очень легкой. Другие виды задач этого задания — на геометрический смысл первообразной — будут рассмотрены в другом разделе.
Сергей Никифоров
Если производная функции знакопостоянна на интервале, а сама функция непрерывна на его границах, то граничные точки присоединяются как к промежуткам возрастания, так и к промежуткам убывания, что полностью соответствует определению возрастающих и убывающих функций.
Фарит Ямаев 26.10.2016 18:50
Здравствуйте. Как же (на каком основании) можно утверждать, что в точке, где производная равна нулю, функция возрастает. Приведите доводы. Иначе, это просто чей-то каприз. По какой теореме? А также доказательство. Спасибо.
Служба поддержки
Значение производной в точке не имеет прямого отношения к возрастанию функции на промежутке. Рассмотрите, например, функции — все они возрастают на отрезке
Владлен Писарев 02.11.2016 22:21
Если функция возрастает на интервале (а;b) и определена и непрерывна в точках а и b, то она возрастает на отрезке . Т.е. точка x=2 входит в данный промежуток.
Т.е. точка x=2 входит в данный промежуток.
Хотя, как правило возрастание и убывание рассматривается не на отрезке, а на интервале.
Но в самой точке x=2, функция имеет локальный минимум. И как объяснять детям, что когда они ищут точки возрастания (убывания), то точки локального экстремума не считаем, а в промежутки возрастания (убывания) — входят.
Учитывая, что первая часть ЕГЭ для «средней группы детского сада», то наверное такие нюансы- перебор.
Отдельно, большое спасибо за «Решу ЕГЭ» всем сотрудникам- отличное пособие.
Сергей Никифоров
Простое объяснение можно получить, если отталкиваться от определения возрастающей/убывающей функции. Напомню, что звучит оно так: функция называется возрастающей/убывающей на промежутке, если большему аргументу функции соответствует большее/меньшее значение функции. Такое определение никак не использует понятие производной, поэтому вопросов о точках, где производная обращается в ноль возникнуть не может.
Ирина Ишмакова 20.11.2017 11:46
Добрый день. Здесь в комментариях я вижу убеждения, что границы включать нужно. Допустим, я с этим соглашусь. Но посмотрите, пожалуйста, ваше решение к задаче 7089. Там при указании промежутков возрастания границы не включаются. И это влияет на ответ. Т.е. решения заданий 6429 и 7089 противоречат друг другу. Проясните, пожалуйста, эту ситуацию.
Александр Иванов
В заданиях 6429 и 7089 совершенно разные вопросы.
В одном про промежутки возрастания, а в другом про промежутки с положительной производной.
Противоречия нет.
Экстремумы входят в промежутки возрастания и убывания, но точки, в которых производная равна нулю, не входят в промежутки, на которых производная положительна.
A Z 28.01.2019 19:09
Коллеги, есть понятие возрастания в точке
(см. Фихтенгольц например)
и ваше понимание возрастания в точке x=2 противочет классическому определению.
Возрастание и убывание это процесс и хотелось бы придерживаться этого принципа.
В любом интервале, который содержит точку x=2, функция не является возрастающей. Поэтому включение данный точки x=2 процесс особый.
Обычно, чтобы избежать путаницы о включении концов интервалов говорят отдельно.
Александр Иванов
Функция y=f(x) называется возрастающей на некотором промежутке, если бо́льшему значению аргумента из этого промежутка соответствует бо́льшее значение функции.
В точке х=2 функция дифференцируема, а на интервале (2; 6) производная положительна, значит, на промежутке }
Значение производной многочлена по методу Горнера
| Заданная функция |
До последнего был уверен, что если известен многочлен вида
и необходимо узнать значение производной например 5 порядка в какой либо точке, необходимо сначала вычислить эту производную (пятого порядка), а потом уже подставив значение, рассчитать производную.
Оказывается есть более простой и алгоритмически легкий способ, нахождения производной в точке.
Для этого нам понадобится методика описанная в материалах: Разложить многочлен по степеням и Метод Горнера. Деление многочлена.
Да, да, оказывается метод Горнера с успехом решает поставленную задачу.
Рассмотрим пример:
Вычислить производную третьего порядка при х=3 следующего многочлена
1. Разделим заданный многочлен на
Получим и остаток 19.
Число 19 есть значение функции если мы подставим туда x=3
2. Разделим снова на
Получим и остаток 25.
Так как это первая проивзодная, то умножим полученный результат на 1!(один факториал)=1. Получили то же число 25
Число 25 это значение первой производной от заданной функции при x=3. То есть если мы вычислим первую производную
То есть если мы вычислим первую производную
и подставим туда значение 3 получим тот же ответ = 25.
3. Разделим снова на
получим и остаток 13.
Умножим это число на 2! (два факториал) =2 и мы получим значение производной функции второго порядка при х=3
Это число =26
4. Производная третьего порядка вычисляется в данном случае просто, так как далее уже делить невозможно, то это и является остатком. Его необходимо умножить на 3!(три факториал)=6
И получим, что производная третьего порядка при заданном многочлене при x=3 равна 12.
Таким незамысловатым способом мы можем находить значения любой производной любого полинома.
Алгоритм прост, но при многочленах со степенями выше 10, мы сталкиваемся с необходимостью вычислять факториалы выше 10, что очень трудоемко, так как факториал от 10 равен 3628800, а факториал от 16 уже 20922789888000
Но нам на пользу приходит одно из свойств методики Горнера, которое гласит: Если мы умножим какую либо функцию на число то и остаток отделения возрастет во столько же раз.
Поэтому нам достаточно умножать полученные коэффиценты полинома от деления на числа 1,2,3,4,5 и т.д. в зависимости от того какую производную мы вычислем в данный момент и вычислить остаток.
Калькулятор работает и в поле комплексных чисел, поэтому решим вот такой пример.
Есть функция
Необходимо узнать все возможные производные этой функции при x=i
Несложно убедится что решая это вручную, можно допустить оплошность и пойти по неверному пути.
Намного проще воспользоватся ботом и через XMPP клиент написать
propol 2 1-5i 0 -7 i 2 -9 -1;i
и мы получим все результаты
Найдены значения производной полинома
0 производная.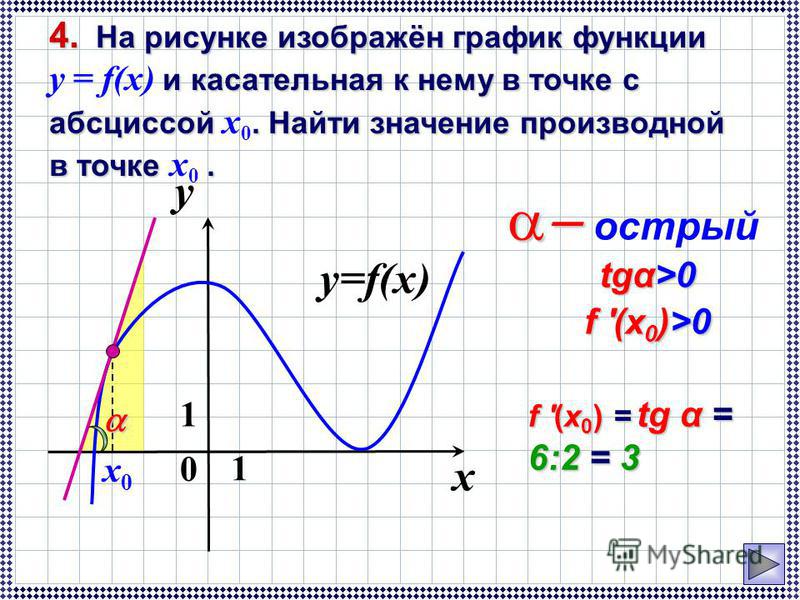 Значение функции -10-6i
Значение функции -10-6i
1 производная. Значение функции 7+35i
2 производная. Значение функции 112-66i
3 производная. Значение функции -180-282i
4 производная. Значение функции -528+120i
5 производная. Значение функции -1440+720i
6 производная. Значение функции 720+6480i
7 производная. Значение функции 10080
Логичный вопрос — а что же такое нулевая производная?
Ответим — это исходная функция. А значение -10-6i получается если бы мы -i подставили в исходную функцию
Попробуем решить другое уравнение
знаем чему же равна четвертая производная функциипри х=2+i
Полином 17-ой степени.. это серъезно как и вычисление при комплексном аргументе.
Что ж попробуем
| Заданная функция | ||||||||||||||||||||||||||||||||||||||
|
при значении x=2+i значение функции при взятии четвертой производной будет
| 4 | 13006113720-5465417040i |
Что еще можно заметить?
Что необходимо внимательно смотреть на расчеты.
В нашем примере при взятии 17 призводной получается число 24.898
хотя должно конечно же быть где 17! это факториал от 17 = 355687428096000Это небольшая недоработка (ошибка при вычислении больших производных) будет испарвлена в ближайшее время. Но вычисления производных не выше 10 порядка, бот осуществляет правильно.
Удачных расчетов!
- Из показательной в алгебраическую. Подробно >>
Производная
youtube.com/embed/zUxNObUaPQg?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>
Производная – отношение приращения функции к приращению ее аргумента при приращении аргумента стремящемся…
ЭЙ-ЭЙ, СТОЙТЕ!!! Куда вы побежали-то? Сейчас легко и просто всё объясню! Приготовьтесь, текста будет много. Зато понятно и наглядно. Так же в конце будут разобраны примеры из ЕГЭ.
Понятие производной на интервале
Пусть у нас есть некоторая линейная функция, определенная на промежутке \([a;b]\). Что значит слово «определенная»? Это значит, что для любого \(x\) из этого промежутка значений мы можем найти соответствующий \(y\) (смотрите, например, следующий график).
Возьмем на этом промежутке \([a;b]\) некоторое значение аргумента — \(x_A\). Ему соответствует точка \(A\) на графике и значение функции \(y_A\).
Теперь дадим выбранному значению \(x_A\) некоторое приращение \(∆x\). Эта запись — \(∆x\) — читается как «дельта икс» и означает величину изменения икса.
То есть мы увеличиваем значение \(x_A\) на \(∆x\). Тогда мы сдвинемся по оси \(x\) и попадем в некое \(x_B\) равное \(x_A+∆x\).
Очевидно, что «расстояние» между \(x_B\) и \(x_A\) равно как раз \(∆x\) (см. график), то есть приращению аргумента. И это приращение аргумента есть «длина» интервала, который мы рассматриваем.
Значению аргумента \(x_B\) соответствует точка \(B\) на графике и значение функции \(y_B\).
Давайте обозначим «расстояние» между \(y_B\) и \(y_A\) как некоторое \(∆y\) (аналогично тому, как это было сделано на оси \(x\)).
Что такое \(∆y\)? Подумайте – был аргумент равный \(x_A\), ему соответствовало значение функции \(y_A\).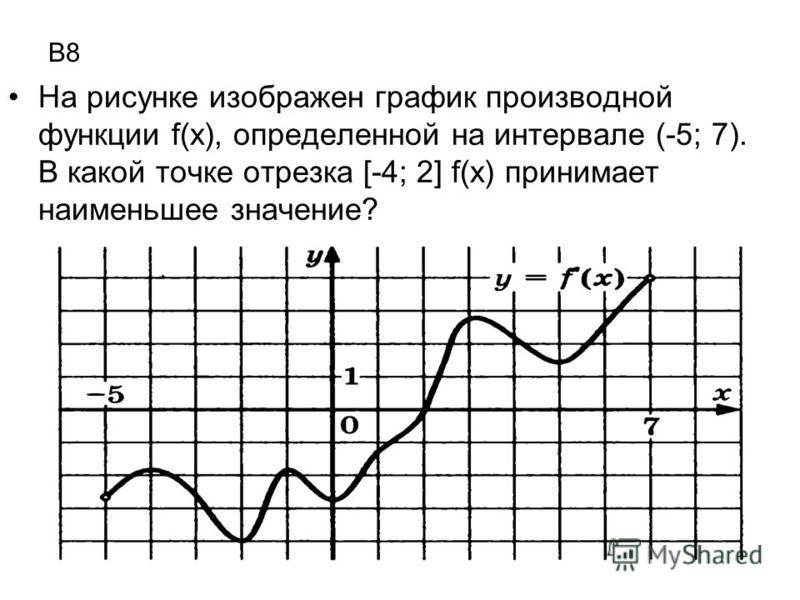 Потом мы аргумент увеличили на \(∆x\) (до \(x_B\)), при этом значение функции тоже выросло до \(y_B\). Что такое тогда \(∆y\) равное разности между \(y_B\) и \(y_A\)? Верно, это приращение значения функции при соответствующем приращении аргумента!
Потом мы аргумент увеличили на \(∆x\) (до \(x_B\)), при этом значение функции тоже выросло до \(y_B\). Что такое тогда \(∆y\) равное разности между \(y_B\) и \(y_A\)? Верно, это приращение значения функции при соответствующем приращении аргумента!
Так вот — если мы теперь разделим \(∆y\) на \(∆x\), то получим производную функции на интервале \(∆x\) (от \(x_A\) до \(x_B\)). В этом суть понятия «производная» на интервале – это просто число, которое получится, если поделить длину отрезка ∆y на длину соответствующего ему отрезка \(∆x\).
Производная на интервале — это отношение приращения функции на интервале к ширине этого интервала (то есть приращению аргумента).
Внимание! Это определение не математически строгое, а «по смыслу», для понимания.
То есть, производная на интервале показывает насколько сильно изменилась функция по отношению к некоторому изменению аргумента этой функции. Или по-другому: производная на интервале характеризует скорость роста функции на этом интервале.
Действительно, посмотрите два графика ниже.
На первом графике при росте аргумента с \(3\) до \(4\), функция выросла с \(1\) до \(4\). Значит:
\(∆x=x_B-x_A=4-3=1\),
\(∆y=y_B-y_A=4-1=3\),
т.е. значение производной на интервале \((3;4)\) равно \(\frac{∆y}{∆x}=\frac{3}{1}=3\)
На втором графике при росте аргумента с \(3\) до \(4\), функция выросла с \(2\) до \(3\). Значит:
\(∆x=x_B-x_A=4-3=1\),
\(∆y=y_B-y_A=4-1=3\),
т.е. значение производной на интервале \((3;4)\) равно \(\frac{∆y}{∆x}=\frac{1}{1}=1.\)
Легко заметить, что график слева «круче», а график справа – более «пологий», т.е. \(f(x)\) растет быстрее, чем \(g(x)\). И производная слева – больше, чем справа. Это логично, ведь фактически производная – это дробь \(\frac{∆y}{∆x}\), а если числитель дроби увеличить, то и значение всей дроби тоже растет.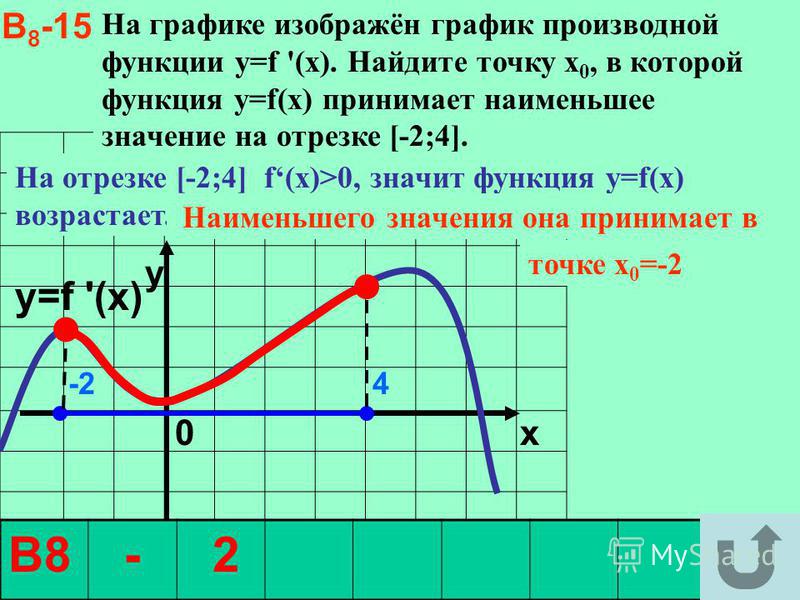
Производная на интервале характеризует скорость роста функции. Чем больше производная – тем быстрее растет функция на интервале.
Хорошо, теперь вопрос на засыпку тем, кто читал внимательно. А что будет с производной, если график линейной функции падает?
Давайте рассмотрим эту ситуацию.
Функция \(f(x)\) падает, то есть при росте аргумента, значение функции становиться все меньше.
Действительно, при росте аргумента с \(2\) до \(3\), функция упала с \(4\) до \(1\). Значит, \(∆x=x_B-x_A=3-2=1\),
\(∆y=y_B-y_A=1-4=-3\).
Тогда значение производной на интервале \((3;4)\) равно \(\frac{∆y}{∆x}=\frac{-3}{1}=-3\).
То есть, если функция на интервале падает – производная станет отрицательна.
Причем, чем круче падает функция, тем больше по модулю будет значение производной. Посмотрите на графики ниже, и вы в этом сами убедитесь.
На первом графике при росте аргумента с \(2\) до \(3\), функция упала с \(4\) до \(1\). Значит:
\(∆x=x_B-x_A=3-2=1\),
\(∆y=y_B-y_A=1-4=-3\),
т.е. значение производной на интервале \((2;3)\) равно \(\frac{∆y}{∆x}=\frac{-3}{1}=-3\).
На втором графике при росте аргумента с \(2\) до \(3\), функция упала с \(2\) до \(1\). Значит:
\(∆x=x_B-x_A=3-2=1\),
\(∆y=y_B-y_A=1-2=-1\),
т.е. значение производной на интервале \((2;3)\) равно \(\frac{∆y}{∆x}=\frac{-1}{1}=-1\).
Если функция падает – производная на интервале отрицательна.
Осталось рассмотреть последнюю ситуацию — а если функция в точке не возрастает и не убывает? Что будет с производной в этом случае? Смотрите график ниже.
Вот, например, функция, имеющая прямолинейный участок, параллельный оси \(x\) на интервале \((2;4)\). Понятно, что если мы рассмотрим этот интервал, то изменение функции \(∆y\) на нем равно нулю, ведь на нем функция не растет и не падает и для любой точки равна \(2\).
Понятно, что если мы рассмотрим этот интервал, то изменение функции \(∆y\) на нем равно нулю, ведь на нем функция не растет и не падает и для любой точки равна \(2\).
И тогда производная равна \(\frac{∆y}{∆x}=\frac{0}{∆x}=0\).
Если функция не растет и не падает – производная на интервале равна \(0\).
Понятие производной в точке
Хорошо, мы разобрали производную на интервале для линейной функции. А если функция отличается от прямой?
Первый порыв ответить: «да какая разница, делаем также!» — неверен. Дело в том, что на прямой была не важна длина рассматриваемого интервала, ведь для неё значение производной – постоянная величина на любом интервале. Смотрите на график ниже:
Если мы рассмотрим интервал по иксу с \(2\) до \(4\), то на нем прирост значения функции – с \(1\) до \(3\). То есть, \(∆x=4-2=2\), \(∆y=3-1=2\), т.е. значение производной на интервале \((2;4)\) равно \(\frac{∆y}{∆x}=\frac{2}{2}=1\).
Если мы рассмотрим интервал по иксу с \(2\) до \(3\), то на нем прирост значения функции – с \(1\) до \(2\). То есть, \(∆x=3-2=1\), \(∆y=2-1=1\), т.е. значение производной на интервале \((2;3)\) равно \(\frac{∆y}{∆x}=\frac{1}{1}=1\).
И на любом другом интервале будет тоже самое — и на \((2;5)\), и на \((3;4)\), и на \((3;5)\) – производная везде равна \(1\). Это и логично, ведь скорость роста функции везде одинакова.
Теперь давайте посмотрим график некоторой нелинейной функции.
Если мы рассмотрим интервал по иксу с \(2\) до \(5\), то на нем прирост значения функции – с \(1\) до \(4\). То есть, \(∆x=5-2=3\), \(∆y=4-1=3\), т.е. значение производной на интервале \((2;5)\) равно \(\frac{∆y}{∆x}=\frac{3}{3}=1\).
Если же мы рассмотрим интервал по иксу с \(2\) до \(4\), то на нем прирост значения функции – с \(1\) до \(2\).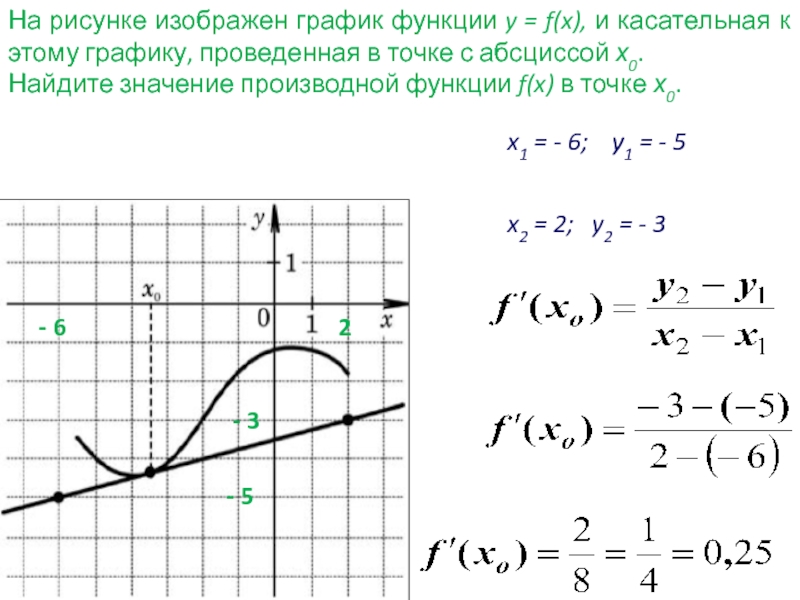 2\), построенный на компьютере с высокой точностью, на интервале от \(-5\) до \(5\). Видно, что график ну очень далек от прямой.
2\), построенный на компьютере с высокой точностью, на интервале от \(-5\) до \(5\). Видно, что график ну очень далек от прямой.
А если рассмотреть тот же график, но на более узком интервале?
Вот тот же график, но уже на интервале от \(0\) до \(2\). Видно, что он изрядно «распрямился».
А вот он же на интервале от \(1\) до \(1,1\). Визуально он уже мало отличается от прямой, хотя на самом деле очень небольшое искривление все же есть. Понятно, что если сжимать интервал еще сильнее, то вскоре график будет практически неотличим от прямой.
Таким образом, вся вышеописанная логика вполне применима и для нелинейных графиков, но только на очень маленьких интервалах. А что мы получим, если будем БЕСКОНЕЧНО уменьшать ширину интервал? Мы будем сжимать его до точки. А что такое «ширина интервала»? Это ни что иное как \(∆x\)! Значит, чтобы найти производную в точке, мы должны посмотреть приращение функции на бесконечно малом (или, говоря более научно, стремящемся к нулю) приращении аргумента. Именно так в математике и вводится понятие производной в точке:
Производная в точке – есть отношение приращения функции к соответствующему приращению ее аргумента при приращении аргумента, стремящемся к нулю.
Таким образом, вся описанная выше логика дифференцирования линейных функций, применима для бесконечно малых участков функций нелинейных. Значит, и все сделанные ранее выводы будут верны. Например, если нелинейная функция в точке (точнее, на бесконечно малом интервале в окрестности этой точки) возрастает, то производная в точке будет положительна. А если функция в точке убывает — производная будет отрицательна.
Остается вопрос – а есть ли на нелинейных функциях точки, где производная равна нулю? Ответ – да, в точках экстремумов. Помните, что это за точки такие?
Экстремумы – это точки максимумов и минимумов функции.
 2 (x+1)-15\).Она имеет максимум при \(x=1\) и минимум при \(x=5\).
2 (x+1)-15\).Она имеет максимум при \(x=1\) и минимум при \(x=5\).И в этих точках функция действительно не растет и не падает.
Давайте посмотрим на большем масштабе, чтобы в этом убедится.
Вот окрестность точки максимума \(x=1\) с очень маленьким шагом.
А это окрестность точки минимума \(x=5\) с очень маленьким шагом.
Думаю, комментарии излишни. Вообще говоря, чтобы понять, что в максимумах и минимумах функция «останавливается» достаточно просто внимательно об этом подумать.
Вдумайтесь, как образуется, допустим, максимум? Функция растет, растет, но после какой-то точки начинает падать. Значит, функция меняет «направление движения» на противоположное. Но это невозможно сделать без остановки! Попробуйте бежать в одну сторону, а потом взять и резко побежать в обратную (не просто повернуть, а именно в противоположную сторону). Вы в любом случае остановитесь при смене направления хоть на долю секунды. Также и функции. С минимумом — аналогично.
Таким образом, получается, что в окрестности точек минимума и максимума функция идет параллельно оси \(x\). И в них производная равна нулю. Слово «в окрестности», употребленное выше, означает «очень-очень близко возле точки». Например, промежуток \((1,99999; 2,00001)\) можно назвать окрестностью точки со значением \(2\).
Подведем итоги:
— Чем больше значение производной функции в точке – тем быстрее в этой точке растет функция.
— Если производная в точке положительна, функция в этой точке растет, если производная в точке отрицательна, функция в ней падает.
— В точках максимумов и минимумов функции – производная равно \(0\).
Эти принципы стоит запомнить (а еще лучше просто понять), потому что с их помощью можно решать огромное количество задач на производные, в том числе и из ЕГЭ.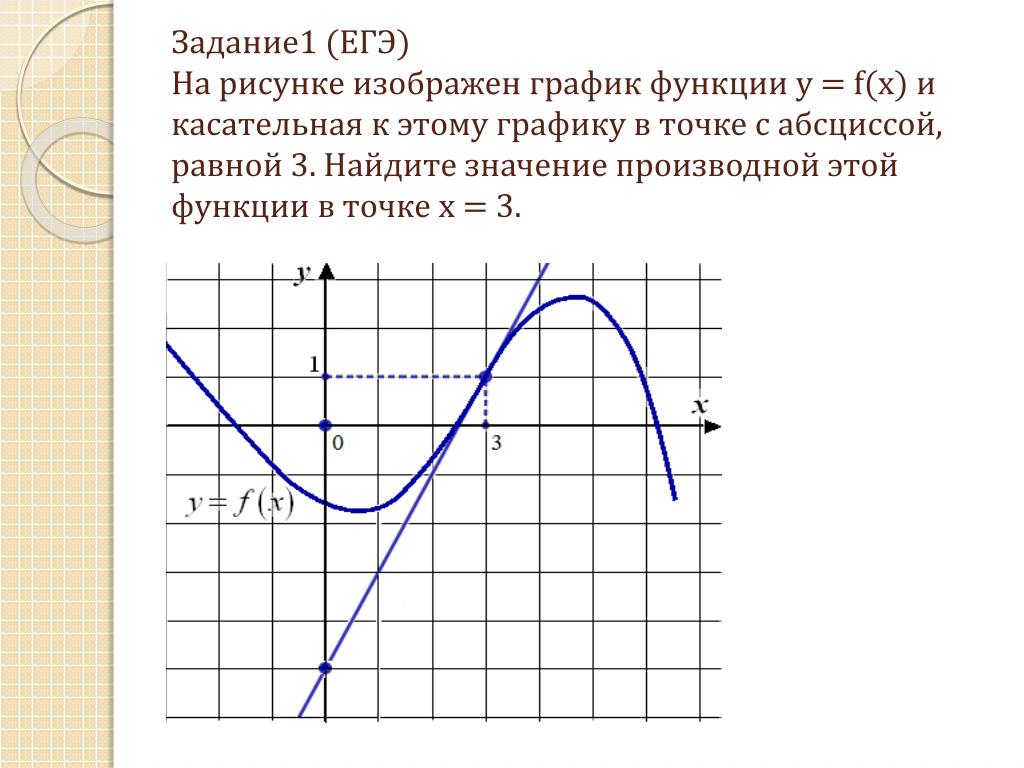
Пример (ЕГЭ). На рисунке изображен график функции, определенной на интервале \((-3;7)\). Определите количество целых точек, в которых производная данной функции отрицательна.
Решение: Начинаем анализировать. Где производная будет отрицательна? Там, где функция падает, то есть от точки А до точки В и от точки С до точки D.
При этом в задаче просят найти количество ЦЕЛЫХ точек. А что такое «целая точка»? Это такая точка графика, у которой икс целое число (например, \(-5\), \(0\) или \(17\), но не \(3,25\) или \(0,7\)).
То есть нам нужны именно такие точки на участках АВ и CD графика. Всего их четыре (обозначены на графике красным ромбом). Обратите внимание, что точка С в ответ не входит, так как это точка максимума и в ней производная равно \(0\), а ноль неотрицателен.
Ответ: 4.
Пример (ЕГЭ). На рисунке изображен график функции \(y=f(x)\) и отмечены точки \(−2\), \(1\), \(3\) и \(9\). В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Решение: Давайте думать.
В точке с координатой \(-2\) функция убывает (падает), значит производная будет отрицательна (ведь она показывает, как раз изменение функции).
В точке с координатой \(1\) – функция медленно растет, значит производная будет, во-первых, положительна, а во-вторых, мала по значению (ведь рост медленный).
В точке с координатой \(3\) – максимум, значит функция не растет и не падает, следовательно, производная будет равна нулю.
И наконец, в точке \(9\) – функция растет и быстро (по крайней мере, быстрее, чем в точке \(1\)). Значит здесь производная положительна и велика.
Таким образом, с учетом всех предыдущих рассуждений, делаем вывод: наибольшее значение производной будет в точке \(9\).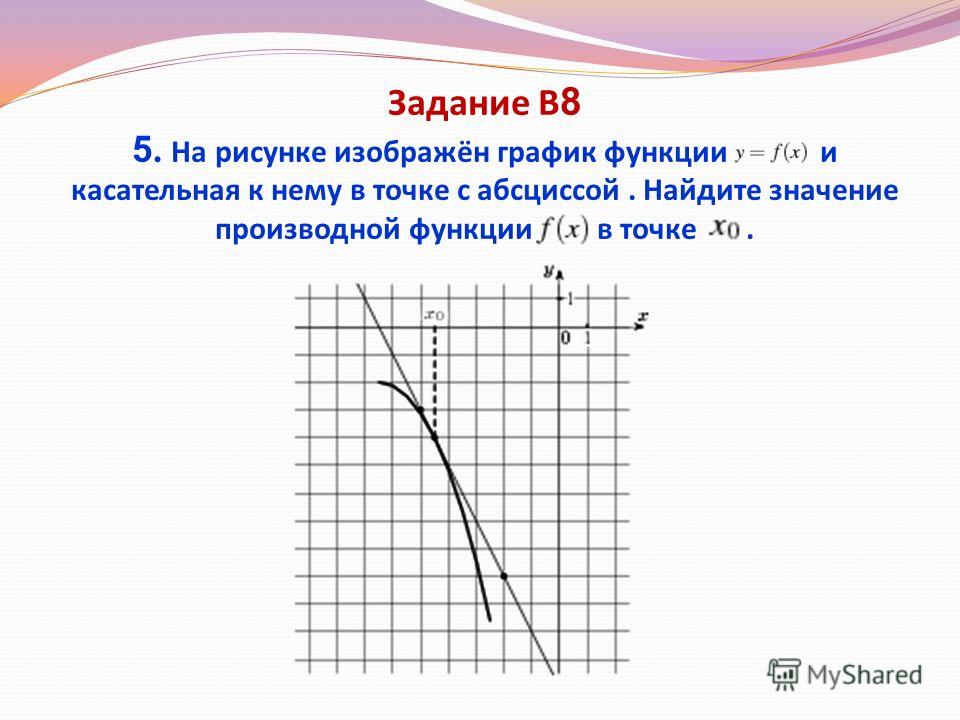
Ответ: \(9\).
Довольно часто в практике попадаются обратные задачи – когда дан график производной, а анализировать надо график функции. Вот, например, такая задача из ЕГЭ:
Пример (ЕГЭ). На рисунке изображен график \(y'(x)\) -производной для функции \(y(x)\). Найдите количество точек экстремумов функции \(y(x)\) на изображенном интервале.
Решение: Экстремумы – это точки минимумов и максимумов функции. Но у нас дан график производной, а не функции. А что происходит с производной в тех точках, где на функции минимум или максимум?
Верно, в этих точках производная равна нулю. Значит, нам нужны все точки, где значение производной ноль! Это точки А, B, C, D и Е. Всего их \(5\), это и есть ответ задачи.
Ответ: \(5\).
Пример (ЕГЭ). На рисунке изображен график \(y'(x)\) — производной для функции \(y(x)\) определенной на интервале \((−7; 7)\). Найдите промежутки возрастания функции \(y(x)\). В ответе укажите длину наибольшего из них.
Решение: Мы знаем, что если функция возрастает – производная положительна, а если падает – то отрицательна. Однако верно и обратное:
— если производная положительна – функция растет,
— если производная отрицательна – функция падает.
Исходя из этого становиться очевидно, что исходная функция \(y(x)\) возрастает на участках \((-5;-2)\) и \((1;6)\) – они выделены зеленым. И длина наибольшего из них равна \(5\).
Ответ: \(5\).
ПРОИЗВОДНАЯ | Энциклопедия Кругосвет
Содержание статьиПРОИЗВОДНАЯ – производной функции y = f(x), заданной на некотором интервале (a, b) в точке x этого интервала, называется предел, к которому стремится отношение приращения функции f в этой точке к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю.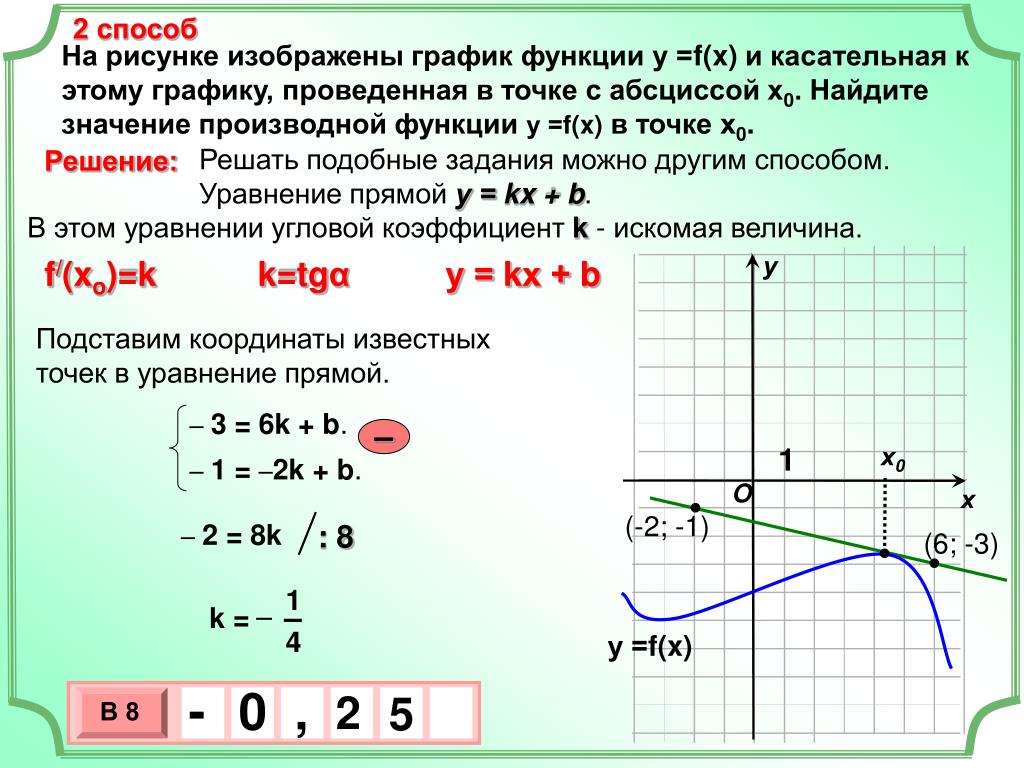
Производную принято обозначать так:
.
Широко употребляются и другие обозначения:
Предел , где рассматривается только Dx > 0 или только Dx f в точке x. О функции f, заданной на отрезке [a, b] принято говорить, что она имеет на этом отрезке производную, если она имеет производную в любой точке интервала (a, b) и, кроме того, правую производную в точке a и левую в точке b.
Понятие производной возникло как результат многовековых усилий, направленных на решение таких задач, как задача о проведении касательной к кривой, о вычислении скорости неравномерного движения, задачи о вычислении площади криволинейной фигуры. В работах Исаака Ньютона и Готфрида Вильгельма Лейбница эта деятельность получила определенное теоретическое завершение. Ньютон и Лейбниц создали общие методы дифференцирования и интегрирования функций и доказали важную теорему, носящую их имя, устанавливающую тесную связь между операциями дифференцирования и интегрирования. Однако современное изложение этих вопросов существенно отличается от того, как они излагались во времена Ньютона и Лейбница. Современный математический анализ базируется на понятии предела, которое было дано (наряду с другими важнейшими понятиями – непрерывность, интеграл и т.д.) в работах французского математика Огюстена Луи Коши.
Мгновенная скорость.
Пусть точка M движется по прямой. Расстояние s движущейся точки, отсчитываемое от некоторого начального ее положения M0 , зависит от времени t , т.е. s есть функция времени t: s = f(t). Пусть в некоторый момент времени t движущаяся точка M находилась на расстоянии s от начального положения M0, а в некоторый следующий момент t + Dt оказалась в положении M1 – на расстоянии s + Ds от начального положения (см.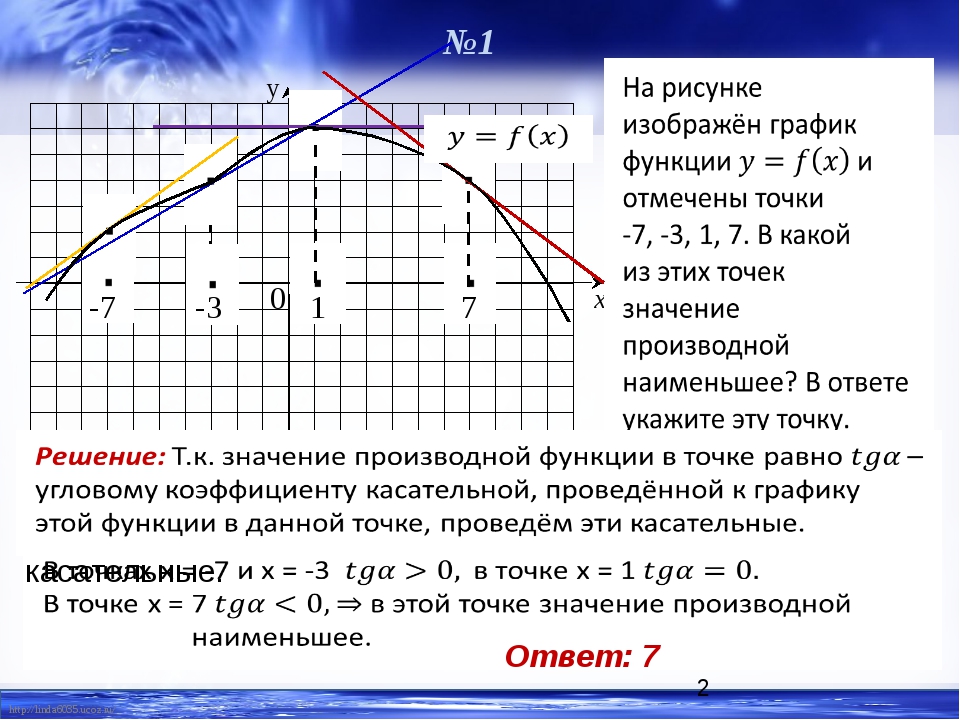 рис.).
рис.).
Таким образом, за промежуток времени Dt расстояние s изменилось на величину Ds. В этом случае говорят, что за промежуток времени Dt величина s получила приращение Ds.
Отношение представляет собой среднюю скорость движения точки за время Dt:
.
Средняя скорость не может во всех случаях точно охарактеризовать быстроту перемещения точки M в момент времени t. Если, например, тело в начале промежутка Dt перемещалось очень быстро, а в конце очень медленно, то средняя скорость не сможет отразить указанных особенностей движения точки и дать представление об истинной скорости ее движения в момент t. Чтобы точнее выразить истинную скорость с помощью средней скорости, надо взять меньший промежуток времени Dt. Наиболее полно характеризует скорость движения точки в момент t тот предел, к которому стремится средняя скорость при Dt ® 0. Этот предел называют скоростью движения в данный момент:
.
Таким образом, скоростью движения в данный момент называется предел отношения приращения пути Ds к приращению времени Dt, когда приращение времени стремится к нулю. Так как
,
то.
Геометрическое значение производной. Касательная к графику функции.
Построение касательных – одна из тех задач, которые привели к рождению дифференциального исчисления. Первый опубликованный труд, относящийся к дифференциальному исчислению и принадлежащий перу Лейбница, имел название Новый метод максимумов и минимумов, а также касательных, для которого не служат препятствием ни дробные, ни иррациональные величины, и особый для этого род исчисления.
Пусть кривая есть график функции y = f(x) в прямоугольной системе координат (см. рис.).
При некотором значении x функция имеет значение y = f(x).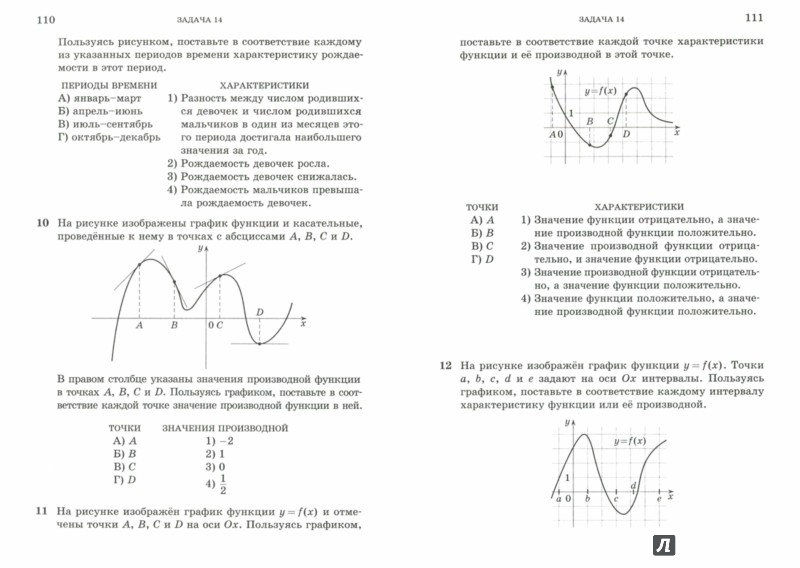 Этим значениям x и y на кривой соответствует точка M0(x, y). Если аргументу x дать приращение Dx, то новому значению аргумента x + Dx соответствует новое значение функции y+Dy = f(x + Dx). Соответствующей ему точкой кривой будет точка M1(x + Dx, y + Dy). Если провести секущую M0M1 и обозначить через j угол, образованный секущей с положительным направлением оси Ox, из рисунка непосредственно видно, что .
Этим значениям x и y на кривой соответствует точка M0(x, y). Если аргументу x дать приращение Dx, то новому значению аргумента x + Dx соответствует новое значение функции y+Dy = f(x + Dx). Соответствующей ему точкой кривой будет точка M1(x + Dx, y + Dy). Если провести секущую M0M1 и обозначить через j угол, образованный секущей с положительным направлением оси Ox, из рисунка непосредственно видно, что .
Если теперь Dx стремится к нулю, то точка M1 перемещается вдоль кривой, приближаясь к точке M0, и угол j изменяется с изменением Dx. При Dx ® 0 угол j стремится к некоторому пределу a и прямая, проходящая через точку M0 и составляющая с положительным направлением оси абсцисс угол a, будет искомой касательной. Ее угловой коэффициент:
.
Следовательно, f´(x) = tga
т.е. значение производной f´(x) при данном значении аргумента x равняется тангенсу угла, образованного касательной к графику функции f(x) в соответствующей точке M0(x,y) с положительным направлением оси Ox.
Дифференцируемость функций.
Определение. Если функция y = f(x) имеет производную в точке x = x0, то функция дифференцируема в этой точке.
Непрерывность функции, имеющей производную. Теорема.
Если функция y = f(x) дифференцируема в некоторой точке x = x0, то она в этой точке непрерывна.
Таким образом, в точках разрыва функция не может иметь производной. Обратное заключение неверно, т.е. из того, что в какой-нибудь точке x = x0 функция y = f(x) непрерывна не следует, что она в этой точке дифференцируема.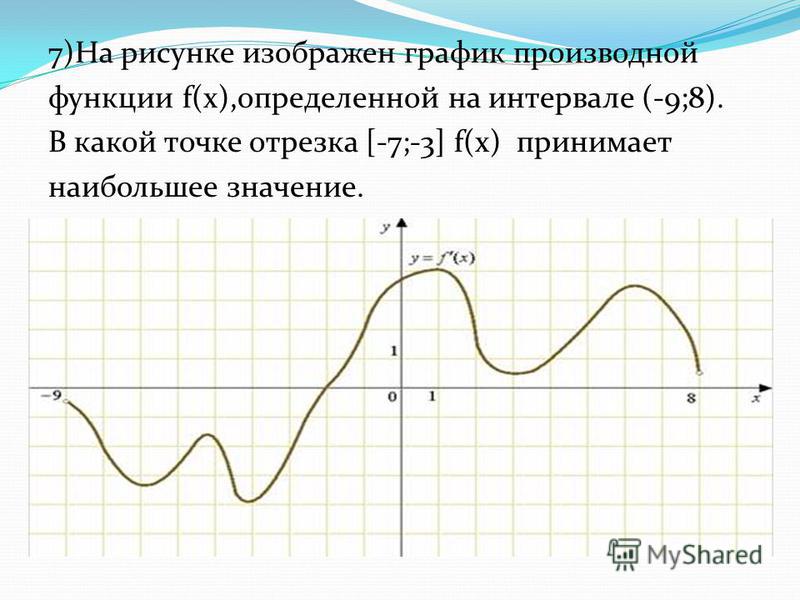 Например, функция y = |x| непрерывна для всех x (–Ґ х x = 0 не имеет производной. В этой точке не существует касательной к графику. Есть правая касательная и левая, но они не совпадают.
Например, функция y = |x| непрерывна для всех x (–Ґ х x = 0 не имеет производной. В этой точке не существует касательной к графику. Есть правая касательная и левая, но они не совпадают.
Некоторые теоремы о дифференцируемых функциях. Теорема о корнях производной (теорема Ролля). Если функция f(x) непрерывна на отрезке [a,b], дифференцируема во всех внутренних точках этого отрезка и на концах x = a и x = b обращается в нуль (f(a) = f(b) = 0), то внутри отрезка [a,b] существует, по крайней мере одна, точка x = с, a c b, в которой производная fў(x) обращается в нуль, т.е. fў(c) = 0.
Теорема о конечных приращениях (теорема Лагранжа). Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема во всех внутренних точках этого отрезка, то внутри отрезка [a, b] найдется по крайней мере одна точка с, a c b, что
f(b) – f(a) = f ў(c)(b – a).
Теорема об отношении приращений двух функций (теорема Коши). Если f(x) и g(x) – две функции, непрерывные на отрезке [a, b] и дифференцируемые во всех внутренних точках этого отрезка, причем gў(x) нигде внутри этого отрезка не обращается в нуль, то внутри отрезка [a, b] найдется такая точка x = с, a c b, что
.
Производные различных порядков.
Пусть функция y = f(x) дифференцируема на некотором отрезке [a, b]. Значения производной f ў(x), вообще говоря, зависят от x, т.е. производная f ў(x) представляет собой тоже функцию от x.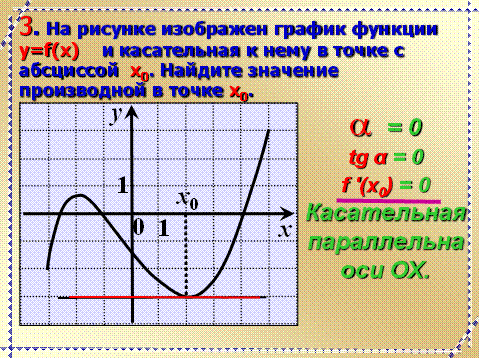 При дифференцировании этой функции получается так называемая вторая производная от функции f(x), которая обозначается f ўў (x).
При дифференцировании этой функции получается так называемая вторая производная от функции f(x), которая обозначается f ўў (x).
Производной n-го порядка от функции f(x) называется производная (первого порядка) от производной n-1—го и обозначается символом y(n) = (y(n – 1))ў.
Дифференциалы различных порядков.
Дифференциал функции y = f(x), где x – независимая переменная, есть dy = f ў(x)dx, некоторая функция от x, но от x может зависеть только первый сомножитель f ў(x), второй же сомножитель (dx) является приращением независимой переменной x и от значения этой переменной не зависит. Так как dy есть функция от x, то можно определить дифференциал этой функции. Дифференциал от дифференциала функции называется вторым дифференциалом или дифференциалом второго порядка этой функции и обозначается d2y:
d(dx) = d2y = f ўў(x)(dx)2.
Дифференциалом n-го порядка называется первый дифференциал от дифференциала n-1—го порядка:
dny = d(dn–1 y) = f(n)(x)dx(n).
Частная производная.
Если функция зависит не от одного, а от нескольких аргументов xi (i изменяется от 1 до n, i = 1, 2,… n), f(x1, x2,… xn), то в дифференциальном исчислении вводится понятие частной производной, которая характеризует скорость изменения функции нескольких переменных, когда изменяется только один аргумент, например, xi . Частная производная 1-ого порядка по xi определяется как обычная производная, при этом предполагается, что все аргументы, кроме xi, сохраняют постоянные значения. Для частных производных вводятся обозначения
Для частных производных вводятся обозначения
fxn, или
Определенные таким образом частные производные 1-ого порядка (как функции тех же аргументов) могут, в свою очередь, также иметь частные производные, это частные производные второго порядка и т.д. Взятые по разным аргументам такие производные называются смешанными. Непрерывные смешанные производные одного порядка не зависят от порядка дифференцирования и равны между собой.
Анна Чугайнова
Геометрический смысл производной
Геометрический смысл производной. Задачи на экзамене связанные данной темой у выпускников вызывают некоторые затруднения. Большинство же из них, на самом деле, очень просты. В этой статье разберём задания, в которых требуется найти производную при заданном графике функции и касательной к графику в определённой точке
*При чём в этих задачах на эскизе явно отмечены как минимум две точки, через которые эта касательная проходит. Что нужно знать для решения?
Геометрический смысл производной
Построим произвольный график некой функции y = f (x) на координатной плоскости, построим касательную в точке xо, обозначим угол между прямой о осью ox как α (альфа)
Из курса алгебры известно, что уравнение прямой имеет вид:
То есть производная функции y = f(x) в точке x0 равна угловому коэффициенту касательной:
А угловой коэффициент в свою очередь равен тангенсу угла α (альфа), то есть:
Угол α (альфа) может быть меньше, больше 90 градусов или равен нулю.
Проиллюстрируем, два случая:
1. Угол наклона касательной больше 90 градусов (тупой угол).
2. Угол наклона касательной равен нулю градусов (касательная параллельна оси ох).
То есть задачи, в которых дан график функции, касательная к этому графику в определённой точке, и требуется найти производную в точке касания, сводятся к нахождению углового коэффициента касательной (либо тангенса угла наклона касательной, что одно и тоже).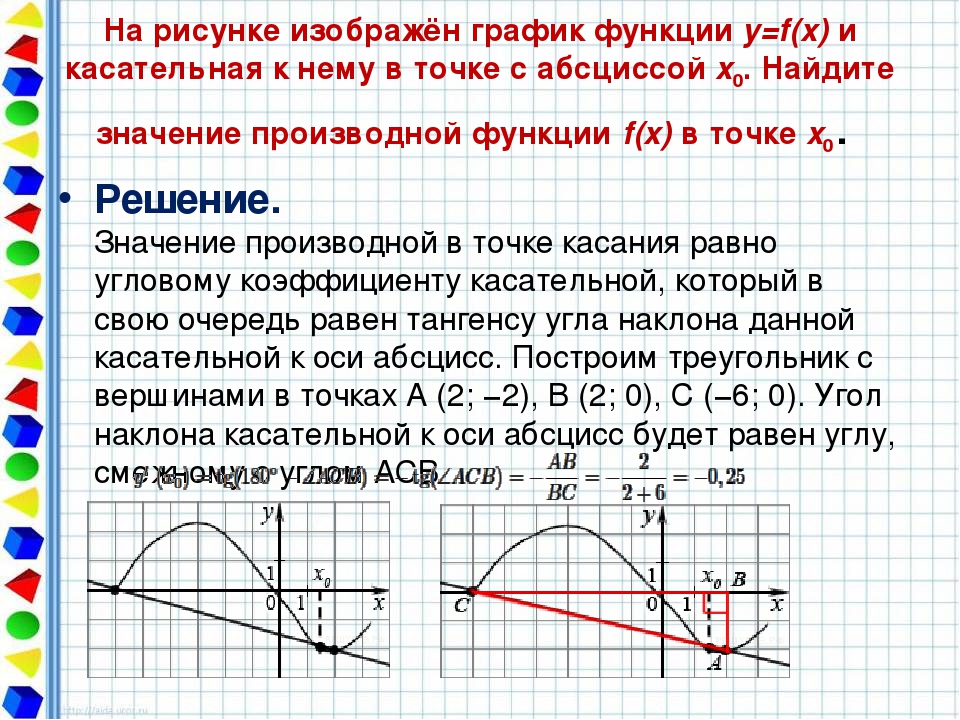
Ниже рассмотрим решение таких задач через нахождение тангенса угла между касательной и осью абсцисс (осью ох), ещё один способ решения (нахождение производной через угловой коэффициент) рассмотрим в недалёком будущем. Также будем рассматривать задачи, где требуется знание свойств производной для чтения графика функции. Не пропустите!
Обратите внимание, что на координатной плоскости обозначены две точки через которые проходит касательная – это очень важный момент (можно сказать ключевой в этих задачах).
Что ещё потребуется — это знание формулы приведения для тангенса тупого угла.
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции y = f(x) в точке x0.
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Для того, чтобы найти тангенс этого угла, построим прямоугольный треугольник, где отрезок ограниченный двумя точками на графике, будет являться гипотенузой, а катеты параллельны осям. В данной задаче это точки (–5; –4), (1; 5).
Напомню: тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему.
Катеты определяем по числу клеток.
Угол наклона касательной к оси абсцисс равен углу BAC, так как катет АС параллелен оси ох. Значит
Ответ: 1,5
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции y = f(x) в точке x0.
Задача аналогична предыдущей. Так же строим прямоугольный треугольник, где отрезок ограниченный двумя точками на графике, будет являться гипотенузой. В данной задаче это точки (–5; –7), (3; 3).
Катеты также определяем по числу клеток.
Угол наклона касательной к оси абсцисс равен углу ВАС, так как катет АС параллелен оси ох. Значит
Ответ: 1,25
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции y = f(x) в точке x0.
Строим прямоугольный треугольник, где отрезок ограниченный двумя точками на графике, будет являться гипотенузой. В данной задаче это точки (–3; 3) и (5; 11). Из точки (5;11) построим продолжение катета так, чтобы получился внешний угол.
Так как CD параллельна оси ох, то угол ABD равен углу наклона касательной к оси ох. Таким образом, мы будем вычислять тангенс угла ABD. Отметим, что он больше 90 градусов, поэтому здесь необходимо воспользоваться формулой приведения для тангенса:
Значит
*Длины катетов считаем по количеству клеток.
Ответ: -1,75
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции y = f(x) в точке x0.
Решите задачу самостоятельно.
Ответ: -1,75
На рисунке изображен график функции y = f(x). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 10. Найдите значение производной функции в точке х0 = 10.
Построим касательную, проходящую через начало координат и точку графика с абсциссой равной 10. Обозначим угол наклона касательной как альфа, а смежный с ним угол как бета.
Значение производной в точке х0 = 10 равно тангенсу угла наклона касательной к оси абсцисс. То есть, для нахождения производной достаточно вычислить тангенс угла альфа. Воспользуемся формулой приведения:
Тангенс угла бета можем найти из прямоугольного треугольника, катеты которого равны 6 и 10:
Ответ: — 0,6
На первый взгляд задачи, связанные с использованием производной входящие в ЕГЭ по математике, довольно разнообразны. Но на самом деле для их решения нужно изучить совсем небольшой «кусочек» теории. На этом всё. Второй способ решения представленных задач обязательно разберем. Надеюсь, статья была полезна.
На этом всё! Успеха вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
§ 1. Производная
Пусть значения переменных х и у связаны уравнением
F(x, y) = 0. (1)
Если функция y = f(x), определенная на некотором интервале (а,в), такая, что уравнение (1) при подстановке в него вместо у выражения f(x) обращается в тождество, то говорят, что уравнение (1) задает функцию y = f(x) неявно или что функция y = f(x) есть неявная функция.
Укажем правило нахождения производной неявной функции, не преобразовывая ее в явную, то есть не представляя в виде y = f(x), так как часто это преобразование бывает технически сложным или невозможным.
Для нахождения производной у’х неявной функции, нужно продифференцировать по х обе части равенства (1), учитывая, что у есть функция от х. Затем из полученного равенства выразить у’х.
Затем из полученного равенства выразить у’х.
Пример 1. Вычислить у’х.
У5+ху-х2 = 0
Продифференцируем обе части по х. Получим 5у4у’+у+ху’-2х=0. Выразим у’. y‘(5у4+х) = 2х-у, у’ = (2х-у)/(5у4+х).
Пример 2.
tg(x+y) = xy
Продифференцируем обе части по х. Получим или . Отсюда или . Окончательно .
Заметим, что производная неявной функции выражается через х и у, то есть получается равенство
y‘ = g(x, y) (2)
Для вычисления второй производной неявной функции, нужно продифференцировать обе части равенства (2) по х и затем подставить выражение g(x, y) вместо y’.
Аналогично можно вычислить производные любого порядка неявной функции.
Пример. х2+у2—1=0. Найти у».
Продифференцируем обе части данного равенства по х, получим 2х+2уу’ = 0, откуда у’ = —. Продифференцируем обе части последнего равенства по х, получим или . Подставим , вместо у’. .
Определение безопасности
Что такое ценная бумага?
Термин «ценная бумага» относится к взаимозаменяемому оборотному финансовому инструменту, имеющему определенную денежную ценность. Он представляет собой долю собственности в публично торгуемой корпорации через акции; отношения кредитора с государственным органом или корпорацией, представленные владельцем облигации этого юридического лица; или права собственности, представленные опционом.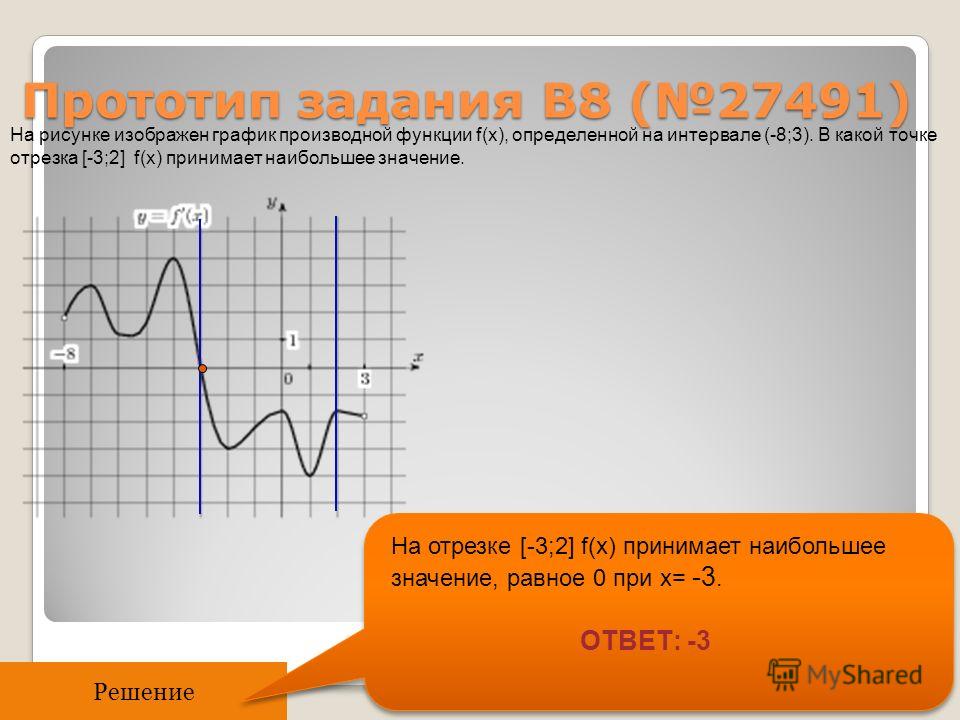
Ключевые выводы
- Ценные бумаги — это взаимозаменяемые и обращающиеся финансовые инструменты, используемые для привлечения капитала на государственных и частных рынках.
- Существует три основных типа ценных бумаг: долевые, предоставляющие право собственности держателям; задолженность — в основном ссуды, погашаемые периодическими платежами; и гибриды, сочетающие в себе аспекты долга и капитала.
- Публичные продажи ценных бумаг регулируются SEC.
- Саморегулируемые организации, такие как NASD, NFA и FINRA, также играют важную роль в регулировании производных ценных бумаг.
Понимание ценных бумаг
Ценные бумаги можно разделить на два различных типа: акции и долги.Однако некоторые гибридные ценные бумаги сочетают в себе элементы как акций, так и долга.
Подготовка к экзамену Series 6: что такое ценная бумага?
Долевые ценные бумаги
Долевые ценные бумаги представляют собой долю владения, принадлежащую акционерам в юридическом лице (компании, товариществе или трасте), реализованную в форме акций акционерного капитала, которые включают акции как простых, так и привилегированных акций.
Держатели долевых ценных бумаг, как правило, не имеют права на регулярные выплаты — хотя долевые ценные бумаги часто выплачивают дивиденды, — но они могут получить прибыль от прироста капитала при продаже ценных бумаг (при условии, что они выросли в цене).
Долевые ценные бумаги действительно дают держателю определенный контроль над компанией на пропорциональной основе посредством права голоса. В случае банкротства они разделяют только остаточные проценты после выплаты всех обязательств перед кредиторами. Иногда они предлагаются в качестве оплаты натурой.
Долговые ценные бумаги
Долговая ценная бумага представляет собой заемные деньги, которые необходимо вернуть, с условиями, которые определяют размер кредита, процентную ставку и дату погашения или продления.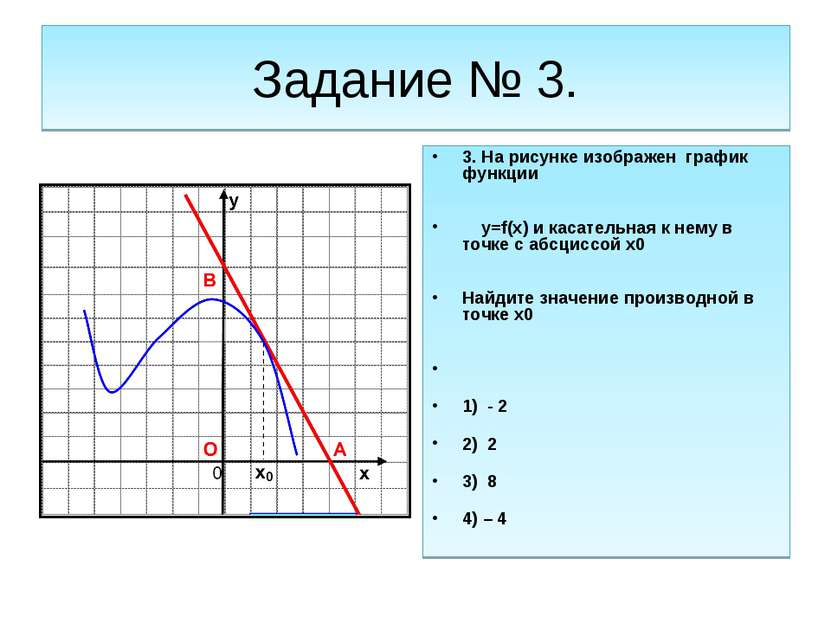
Долговые ценные бумаги, которые включают государственные и корпоративные облигации, депозитные сертификаты (CD) и обеспеченные ценные бумаги (такие как CDO и CMO), как правило, дают их держателю право на регулярную выплату процентов и погашение основной суммы (независимо от результатов деятельности эмитента. ), наряду с любыми другими оговоренными договорными правами (которые не включают право голоса).
Обычно они выпускаются на фиксированный срок, по истечении которого они могут быть погашены эмитентом.Долговые ценные бумаги могут быть обеспеченными (обеспеченными залогом) или необеспеченными, и, если они не обеспечены, могут иметь приоритет по контракту перед другим необеспеченным субординированным долгом в случае банкротства.
Гибридные ценные бумаги
Гибридные ценные бумаги, как следует из названия, сочетают в себе некоторые характеристики как долговых, так и долевых ценных бумаг. Примеры гибридных ценных бумаг включают варранты на акции (опционы, выпущенные самой компанией, которые дают акционерам право покупать акции в течение определенного периода времени и по определенной цене), конвертируемые облигации (облигации, которые могут быть конвертированы в обыкновенные акции компании-эмитента. ) и привилегированные акции (акции компании, выплаты процентов, дивидендов или другие выплаты на капитал могут иметь приоритет над выплатами других акционеров).
Хотя привилегированные акции технически классифицируются как долевые ценные бумаги, они часто рассматриваются как долговые ценные бумаги, поскольку «ведут себя как облигации». Привилегированные акции предлагают фиксированную ставку дивидендов и являются популярным инструментом для инвесторов, стремящихся к заработку. По сути, это ценные бумаги с фиксированным доходом.
Как торгуют ценными бумагами
Публично торгуемые ценные бумаги котируются на фондовых биржах, где эмитенты могут запрашивать листинги ценных бумаг и привлекать инвесторов, обеспечивая ликвидный и регулируемый рынок для торговли. Неформальные электронные торговые системы стали более распространенными в последние годы, и теперь ценные бумаги часто торгуются «внебиржевой» или напрямую между инвесторами через Интернет или по телефону.
Неформальные электронные торговые системы стали более распространенными в последние годы, и теперь ценные бумаги часто торгуются «внебиржевой» или напрямую между инвесторами через Интернет или по телефону.
Первичное публичное размещение акций (IPO) представляет собой первую крупную продажу компанией долевых ценных бумаг населению. После IPO любые вновь выпущенные акции, хотя и проданные на первичном рынке, называются вторичным размещением. В качестве альтернативы ценные бумаги могут быть предложены частным образом ограниченной и квалифицированной группе в рамках так называемого частного размещения — важное различие с точки зрения как законодательства о компаниях, так и регулирования ценных бумаг.Иногда компании продают акции в сочетании с публичным и частным размещением.
На вторичном рынке, также известном как вторичный рынок, ценные бумаги просто передаются как активы от одного инвестора к другому: акционеры могут продавать свои ценные бумаги другим инвесторам за наличные деньги и / или прирост капитала. Таким образом, вторичный рынок дополняет первичный. Вторичный рынок менее ликвиден для частных ценных бумаг, поскольку они не торгуются на открытом рынке и могут быть переданы только квалифицированным инвесторам.
Инвестиции в ценные бумаги
Лицо, создающее ценные бумаги для продажи, называется эмитентом, а те, кто их покупает, конечно же, инвесторы. Как правило, ценные бумаги представляют собой инвестиции и средство, с помощью которого муниципалитеты, компании и другие коммерческие предприятия могут привлекать новый капитал. Компании могут зарабатывать большие деньги, когда становятся публичными, например, продавая акции при первичном публичном размещении (IPO).
Органы власти города, штата или округа могут собрать средства для конкретного проекта, разместив выпуск муниципальных облигаций.В зависимости от рыночного спроса или структуры ценообразования учреждения привлечение капитала с помощью ценных бумаг может быть предпочтительной альтернативой финансированию с помощью банковского кредита.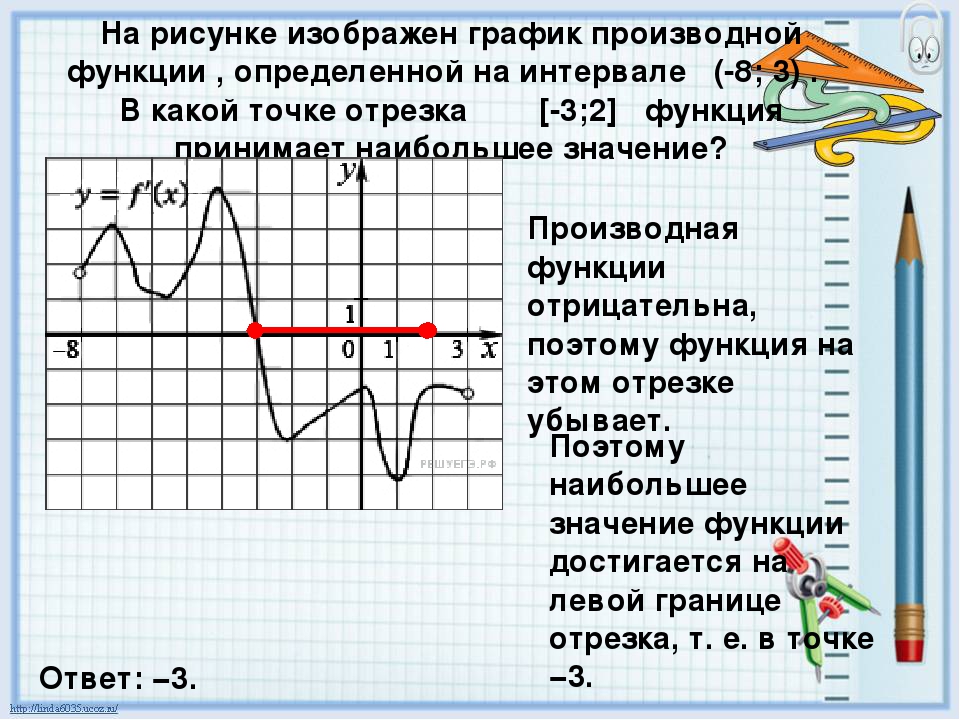
С другой стороны, покупка ценных бумаг на заемные деньги, действие, известное как покупка с маржей, является популярным инвестиционным методом. По сути, компания может предоставить права собственности в форме денежных средств или других ценных бумаг либо при создании, либо в случае неисполнения обязательств, чтобы выплатить свой долг или другое обязательство другому лицу. В последнее время количество таких залоговых соглашений растет, особенно среди институциональных инвесторов.
Регулирование ценных бумаг
В США публичное предложение и продажа ценных бумаг регулирует Комиссия по ценным бумагам и биржам США (SEC).
Публичные предложения, продажи и торги ценными бумагами США должны быть зарегистрированы и зарегистрированы в отделах государственных ценных бумаг SEC. Саморегулируемые организации (СРО) в брокерской отрасли также часто занимают регулирующие позиции. Примеры СРО включают Национальную ассоциацию дилеров по ценным бумагам (NASD) и Регулирующий орган финансовой индустрии (FINRA).
Определение предложения ценных бумаг было установлено Верховным судом в деле 1946 года. В своем решении суд выводит определение ценной бумаги на основе четырех критериев — наличие инвестиционного контракта, создание общего предприятия, обещание прибыли эмитентом и использование третьей стороны для продвижения предложения.
Остаточные ценные бумаги
Остаточные ценные бумаги — это разновидность конвертируемых ценных бумаг, то есть они могут быть преобразованы в другую форму, обычно в обыкновенные акции.Конвертируемая облигация, например, представляет собой остаточную ценную бумагу, поскольку позволяет держателю облигации конвертировать ценную бумагу в обыкновенные акции. У привилегированных акций также может быть возможность конвертации. Корпорации могут предлагать остаточные ценные бумаги для привлечения инвестиционного капитала, когда конкуренция за фонды высока.
Когда остаточная ценная бумага конвертируется или исполняется, это увеличивает количество находящихся в обращении обыкновенных акций.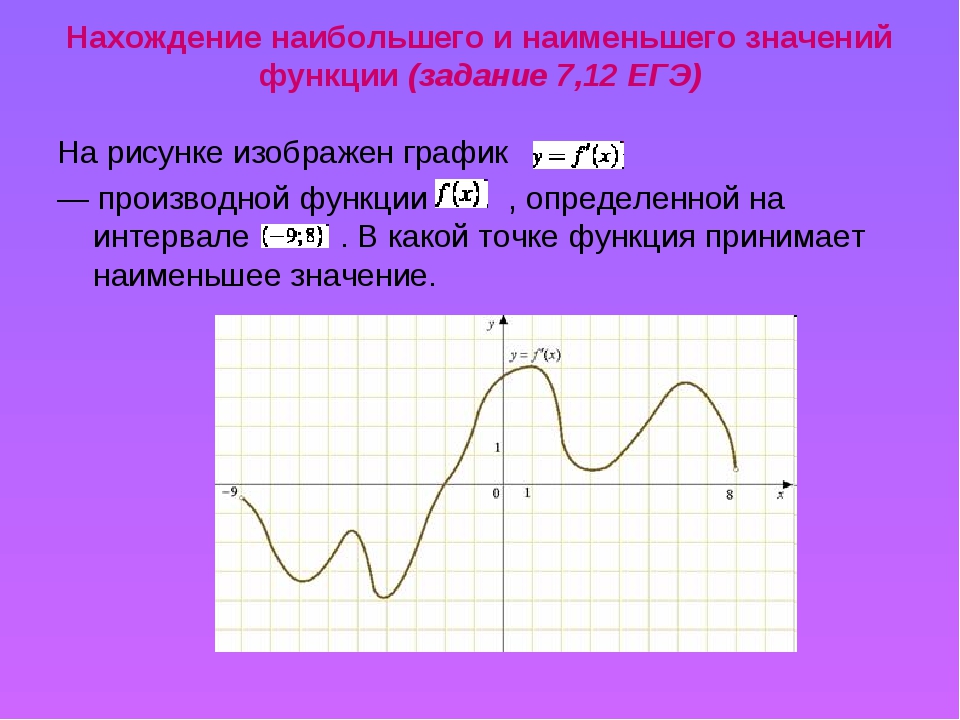 Это может также привести к снижению общего пула акций и их стоимости. Разбавление также влияет на показатели финансового анализа, такие как прибыль на акцию, потому что прибыль компании должна быть разделена на большее количество акций.
Это может также привести к снижению общего пула акций и их стоимости. Разбавление также влияет на показатели финансового анализа, такие как прибыль на акцию, потому что прибыль компании должна быть разделена на большее количество акций.
Напротив, если публично торгуемая компания принимает меры по сокращению общего количества своих акций в обращении, считается, что компания консолидировала их. Чистый эффект этого действия — увеличение стоимости каждой отдельной акции. Часто это делается для привлечения большего количества или более крупных инвесторов, таких как паевые инвестиционные фонды.
Прочие виды ценных бумаг
Сертифицированные ценные бумаги — это ценные бумаги, представленные в бумажной форме. Ценные бумаги также могут храниться в системе прямой регистрации, в которой акции регистрируются в бездокументарной форме.Другими словами, трансфер-агент хранит акции от имени компании без физических сертификатов.
Современные технологии и политики в большинстве случаев устранили необходимость в сертификатах и в необходимости ведения эмитентом полного реестра безопасности. Разработана система, в которой эмитенты могут депонировать единый глобальный сертификат, представляющий все находящиеся в обращении ценные бумаги, в универсальный депозитарий, известный как Депозитарная трастовая компания (DTC). Все ценные бумаги, торгуемые через DTC, хранятся в электронной форме.Важно отметить, что документарные и бездокументарные ценные бумаги не различаются с точки зрения прав или привилегий акционера или эмитента.
Ценные бумаги на предъявителя — это ценные бумаги, которые являются оборотными и дают акционеру права по ценной бумаге. Они передаются от инвестора к инвестору, в некоторых случаях путем одобрения и доставки. С точки зрения собственности ценные бумаги на предъявителя до электронных средств всегда были разделены, то есть каждая ценная бумага представляла собой отдельный актив, юридически отличный от других ценных бумаг того же выпуска.
В зависимости от рыночной практики разделенные ценные бумаги могут быть взаимозаменяемыми или (реже) не взаимозаменяемыми, что означает, что при кредитовании заемщик может вернуть активы, эквивалентные либо исходному активу, либо конкретному идентичному активу в конце кредита. В некоторых случаях ценные бумаги на предъявителя могут использоваться для уклонения от уплаты налогов и, таким образом, иногда могут рассматриваться как эмитенты, акционеры, так и органы налогового регулирования негативно. Они редко встречаются в США.
Именные ценные бумаги имеют имя держателя и другие необходимые реквизиты, которые эмитент ведет в реестре.Перевод именных ценных бумаг осуществляется путем внесения изменений в реестр. Зарегистрированные долговые ценные бумаги всегда неделимы, то есть весь выпуск представляет собой один актив, причем каждая ценная бумага является частью целого. Неделимые ценные бумаги взаимозаменяемы по своей природе. Доли вторичного рынка также всегда неразделимы.
Письменные ценные бумаги не зарегистрированы в SEC и не могут быть проданы публично на рынке. Письменная гарантия — также известная как ограниченная ценная бумага, буквенная бумага или буквенная облигация — продается непосредственно эмитентом инвестору.Термин происходит от требования SEC к «инвестиционному письму» от покупателя, в котором говорится, что покупка предназначена для инвестиционных целей и не предназначена для перепродажи. При переходе из рук в руки эти буквы часто требуют формы 4.
Ценные бумаги кабинета министров котируются на крупной финансовой бирже, такой как NYSE, но активно не торгуются. Удерживаемые неактивной толпой инвесторов, они, скорее всего, будут облигациями, чем акциями. «Кабинет» относится к физическому месту, где заказы на облигации исторически хранились вне торгового зала.В шкафах обычно хранятся лимитные заказы, и заказы хранятся до тех пор, пока срок их действия не истечет или они не будут выполнены.
Эмиссионные ценные бумаги: примеры
Рассмотрим случай XYZ, успешного стартапа, заинтересованного в привлечении капитала для ускорения своего следующего этапа роста. До сих пор собственность стартапа была разделена между двумя его основателями. У него есть несколько вариантов доступа к капиталу. Он может выходить на публичные рынки, проводя IPO, или может собирать деньги, предлагая свои акции инвесторам в ходе частного размещения.
До сих пор собственность стартапа была разделена между двумя его основателями. У него есть несколько вариантов доступа к капиталу. Он может выходить на публичные рынки, проводя IPO, или может собирать деньги, предлагая свои акции инвесторам в ходе частного размещения.
Первый метод позволяет компании увеличить капитал, но он обременен огромными комиссиями и требованиями раскрытия информации. В последнем методе акции торгуются на вторичных рынках и не подлежат контролю со стороны общественности. В обоих случаях, однако, происходит распределение акций, которое уменьшает долю учредителей и предоставляет права собственности инвесторам. Это пример долевой ценной бумаги.
Затем рассмотрим правительство, заинтересованное в сборе денег для возрождения своей экономики.Он использует облигации или долговое обеспечение для увеличения этой суммы, обещая регулярные выплаты держателям купона.
Наконец, рассмотрим случай стартапа ABC. Он привлекает деньги от частных инвесторов, включая семью и друзей. Основатели стартапа предлагают своим инвесторам конвертируемую вексель, которая конвертируется в акции стартапа на более позднем мероприятии. Большинство таких мероприятий финансируются. По сути, банкнота является долговым залогом, потому что это кредит, предоставленный инвесторами основателям стартапа.
На более позднем этапе банкнота превращается в капитал в виде заранее определенного количества акций, которые дают инвесторам долю компании.Это пример гибридной безопасности.
деривативов и опционов: в чем разница?
Деривативы и опционы: обзор
Производный инструмент — это финансовый контракт, стоимость, риск и базовая временная структура которого определяется базовым активом. Опционы представляют собой одну категорию производных инструментов и дают держателю право, но не обязательство, купить или продать базовый актив. Доступны опционы для многих инвестиций, включая акции, валюты и товары.
Деривативы — это контракты между двумя или более сторонами, в которых стоимость контракта основана на согласованной базовой ценной бумаге или наборе активов, таких как индекс S&P. Типичные базовые ценные бумаги для деривативов включают облигации, процентные ставки, товары, рыночные индексы, валюты и акции.
Типичные базовые ценные бумаги для деривативов включают облигации, процентные ставки, товары, рыночные индексы, валюты и акции.
У производных финансовых инструментов есть цена и дата истечения срока или дата расчетов, которые могут быть в будущем. В результате производные финансовые инструменты, включая опционы, часто используются в качестве инструментов хеджирования для компенсации риска, связанного с активом или портфелем.
В течение многих лет производные инструменты использовались для хеджирования рисков в сельскохозяйственной отрасли, когда одна сторона может заключить соглашение о продаже сельскохозяйственных культур или скота другому контрагенту, который соглашается купить эти культуры или скот по определенной цене в конкретную дату. Эти двусторонние контракты были революционными при первом введении, заменив устные договоренности и простое рукопожатие.
Ключевые выводы
- Деривативы — это контракты между двумя или более сторонами, в которых стоимость контракта основана на согласованной базовой ценной бумаге или наборе активов.
- Деривативы включают свопы, фьючерсные контракты и форвардные контракты.
- Опционы представляют собой одну категорию производных финансовых инструментов и дают держателю право, но не обязательство, купить или продать базовый актив.
- Опционы, как и деривативы, доступны для многих инвестиций, включая акции, валюты и товары.
Опции
Когда большинство инвесторов думают об опционах, они обычно думают об опционах на акции, которые представляют собой производные инструменты, стоимость которых определяется базовыми акциями.Опцион на акции представляет собой право, но не обязанность, купить или продать акцию по определенной цене, известной как цена исполнения, в дату истечения срока или до нее. Опционы продаются по цене, называемой премией. Опцион колл дает держателю право купить базовую акцию, в то время как опцион пут дает держателю право продать базовую акцию.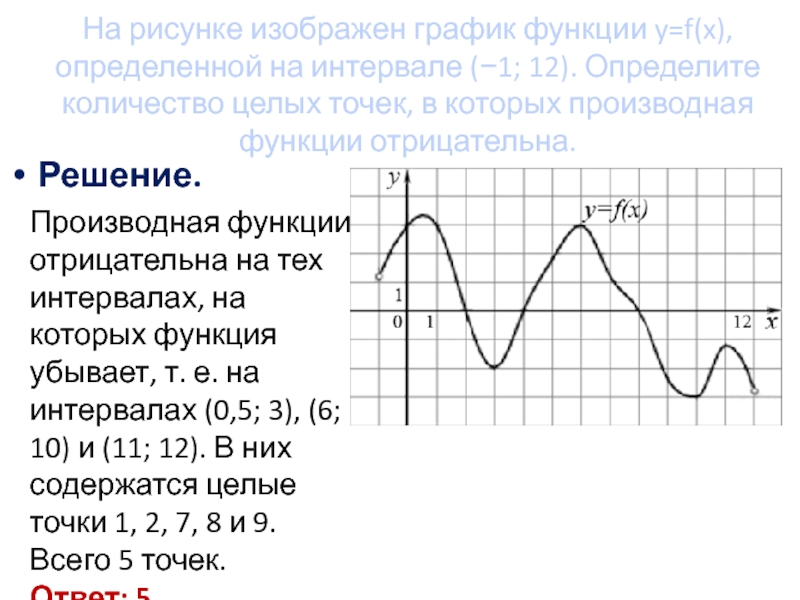
Если опцион исполняется держателем, продавец опциона должен поставить покупателю 100 акций базовых акций по каждому контракту.Опционы на акции торгуются на биржах и рассчитываются через централизованные клиринговые палаты, обеспечивая прозрачность и ликвидность — два критических фактора, когда трейдеры или инвесторы открывают сделки с деривативами.
Опционы американского типа могут быть исполнены в любой момент до даты истечения срока, в то время как опционы европейского типа могут быть исполнены только в день истечения срока его действия. Основные индикаторы, включая S&P 500, активно торгуют опционами европейского типа. Большинство опционов на акции и биржевые фонды (ETF) на биржах являются американскими опционами, в то время как лишь несколько индексов с широкой базой имеют опционы американского типа.Биржевые фонды представляют собой корзину ценных бумаг, таких как акции, которые отслеживают базовый индекс.
Деривативы
Фьючерсные контракты — это производные инструменты, стоимость которых определяется на основе базового денежного товара или индекса. Фьючерсный контракт — это соглашение о покупке или продаже определенного товара или актива по заранее установленной цене и в заранее установленное время или дату в будущем.
Например, стандартный фьючерсный контракт на кукурузу представляет собой 5000 бушелей кукурузы, а стандартный фьючерсный контракт на сырую нефть представляет собой 1000 баррелей нефти.Существуют фьючерсные контракты на такие разнообразные активы, как валюты и погода.
Другой тип производного инструмента — это соглашение о свопе. Своп — это финансовое соглашение между сторонами об обмене последовательностью денежных потоков в течение определенного периода времени. Свопы процентных ставок и валютные свопы являются распространенными типами соглашений о свопах. Например, процентные свопы — это соглашения об обмене одной серии процентных платежей на другую в зависимости от основной суммы.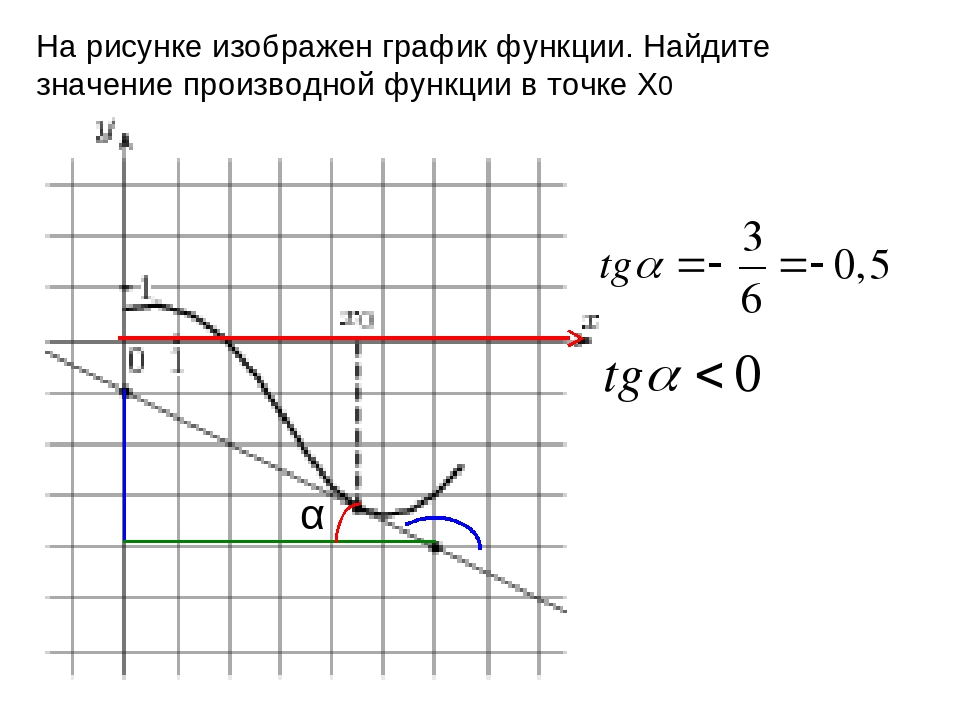 Одной компании могут потребоваться выплаты с плавающей процентной ставкой, а другой — по фиксированной ставке.Соглашение о свопе позволяет двум сторонам обмениваться денежными потоками.
Одной компании могут потребоваться выплаты с плавающей процентной ставкой, а другой — по фиксированной ставке.Соглашение о свопе позволяет двум сторонам обмениваться денежными потоками.
Свопы обычно торгуются на внебиржевой основе, но постепенно переходят на централизованные биржи. Финансовый кризис 2008 года привел к новым финансовым положениям, таким как Закон Додда-Франка, который создал новые обмены свопами для поощрения централизованной торговли.
Есть несколько причин, по которым инвесторы и корпорации торгуют своповыми деривативами. К наиболее распространенным относятся:
- Изменение инвестиционных целей или сценариев погашения.
- Воспринимаемая финансовая выгода от перехода на новые или альтернативные денежные потоки.
- Необходимость хеджирования или снижения риска, связанного с погашением ссуды с плавающей процентной ставкой.
Форвардные контракты
Форвардный контракт — это контракт на торговлю активом, часто валютами, в будущее время и по указанной цене. Форвардный контракт похож на фьючерсный, за исключением того, что форвардные контракты могут быть настроены таким образом, чтобы срок их действия истекал в определенную дату или на определенную сумму.
Например, если американская компания должна получать поток платежей в евро каждый месяц, суммы необходимо конвертировать в доллары США. Каждый раз, когда происходит обмен, применяется другой обменный курс с учетом преобладающего курса евро к США. курс доллара. В результате компания может получать разные суммы в долларах каждый месяц, несмотря на то, что сумма в евро является фиксированной из-за колебаний обменного курса.
Форвардный контракт позволяет компании фиксировать текущий обменный курс для каждого месяца платежей в евро.Каждый месяц компания получает евро, они конвертируются по курсу форвардного контракта. Контракт заключается с банком или брокером и позволяет компании иметь предсказуемые денежные потоки.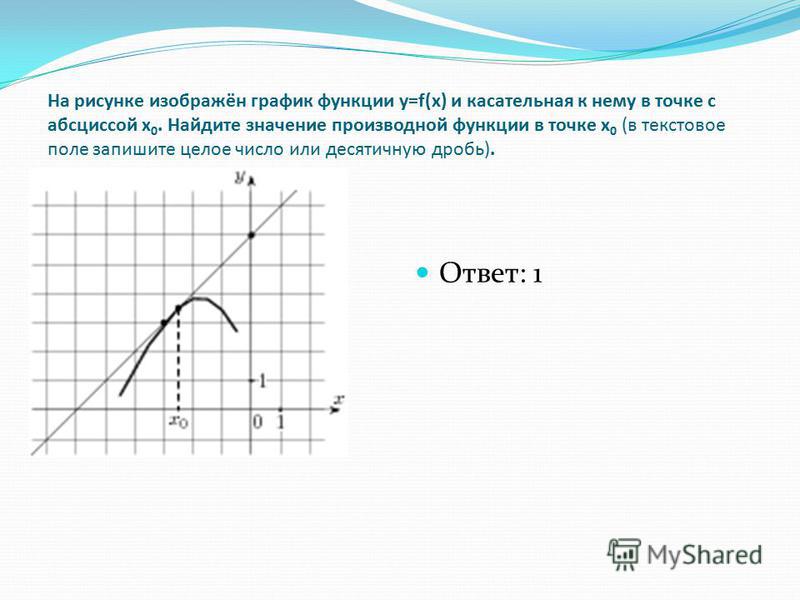
Форвардный контракт может использоваться как для спекуляций, так и для хеджирования, хотя его нестандартный характер делает его особенно подходящим для хеджирования. Форвардные контракты торгуются на внебиржевой основе, то есть между банками и брокерами, поскольку они представляют собой индивидуальные соглашения между двумя сторонами. Поскольку они не торгуются на бирже, форвардные контракты имеют более высокий риск дефолта контрагента.В результате форвардные контракты не так легко доступны розничным трейдерам и инвесторам, как фьючерсные контракты.
Ключевые отличия
Одно из основных различий между опционами и производными инструментами заключается в том, что держатели опционов имеют право, но не обязаны выполнять договор или обменять на акции базовой ценной бумаги.
С другой стороны, деривативы обычно являются юридически обязывающими контрактами, в соответствии с которыми после заключения сторона должна выполнить требования контракта.Конечно, многие опционы и деривативы могут быть проданы до истечения срока их действия, поэтому обмена физическим базовым активом нет.
Однако для любого контракта, который был расторгнут или продан до истечения срока его действия, держатель рискует понести убытки из-за разницы между ценой покупки и продажи контракта.
Определение валютных фьючерсов
Что такое валютные фьючерсы?
Валютные фьючерсы — это торгуемые на бирже фьючерсные контракты, которые определяют цену в одной валюте, по которой другая валюта может быть куплена или продана в будущем.Валютные фьючерсные контракты являются юридически обязательными, и контрагенты, которые все еще держат контракты на дату истечения срока, должны поставить валютную сумму по указанной цене в указанную дату поставки. Валютные фьючерсы могут использоваться для хеджирования других сделок или валютных рисков или для спекуляции на движениях цен в валютах.
Валютные фьючерсы можно противопоставить нестандартным валютным форвардным контрактам, которые торгуются на внебиржевом рынке.
Ключевые выводы
- Валютные фьючерсы — это фьючерсные контракты на валюты, которые определяют цену обмена одной валюты на другую в будущем.
- Курс валютных фьючерсных контрактов определяется на основе спотовых курсов валютной пары.
- Валютные фьючерсы используются для хеджирования риска получения платежей в иностранной валюте.
Основы валютных фьючерсов
Первый валютный фьючерсный контракт был создан на Чикагской товарной бирже в 1972 году, и сегодня это крупнейший рынок валютных фьючерсов в мире. Валютные фьючерсные контракты оцениваются по рыночной цене ежедневно. Это означает, что трейдеры несут ответственность за наличие достаточного капитала на своем счете для покрытия прибыли и убытков, возникающих после открытия позиции.Фьючерсные трейдеры могут отказаться от своих обязательств по покупке или продаже валюты до даты поставки контракта. Это делается путем закрытия позиции. За исключением контрактов с мексиканским песо и южноафриканским рандом, валютные фьючерсные контракты физически поставляются четыре раза в год: в третью среду марта, июнь, сентябрь и декабрь.
Цена валютных фьючерсов определяется при открытии сделки.
Например, покупка фьючерса на евро на валюту U.S. Exchange по цене 1,20 означает, что покупатель соглашается купить евро по цене 1,20 доллара США. Если он допустит истечение срока действия контракта, он несет ответственность за покупку 125 000 евро по цене 1,20 доллара США. Каждый фьючерс на евро на Чикагской товарной бирже (CME) стоит 125 000 евро, поэтому покупателю придется покупать именно столько. С другой стороны, продавец контракта должен будет поставить евро и получить доллары США.
Большинство участников фьючерсных рынков — это спекулянты, которые закрывают свои позиции до истечения срока действия фьючерсов.Они не доставляют физическую валюту. Скорее, они зарабатывают или теряют деньги в зависимости от изменения цен самих фьючерсных контрактов.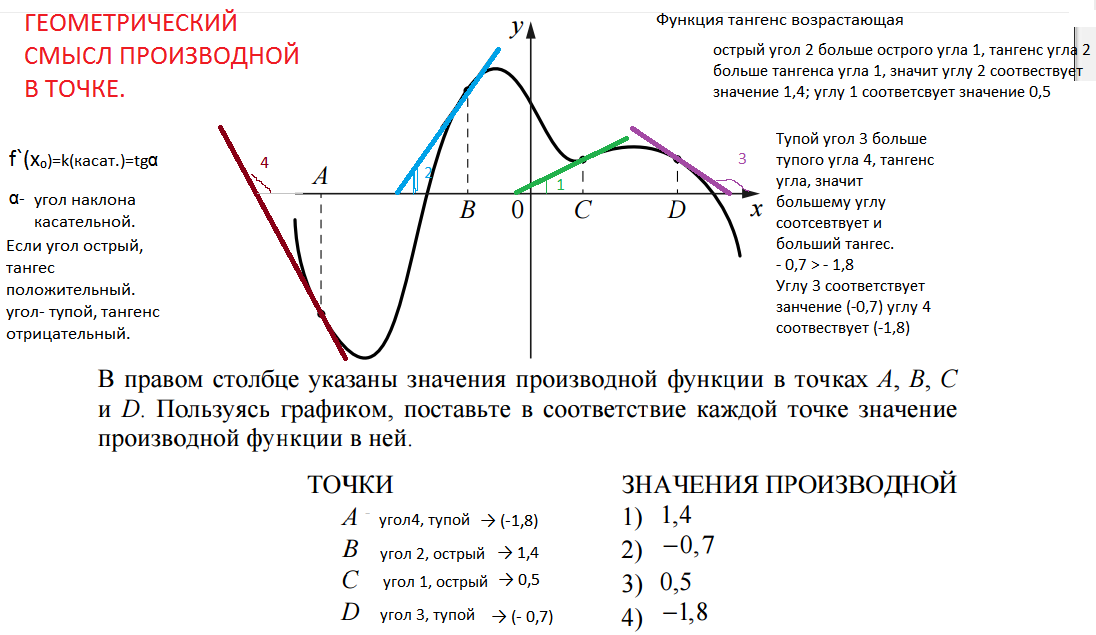
Ежедневный убыток или прибыль по фьючерсному контракту отражается на торговом счете. Это разница между ценой входа и текущей ценой фьючерса, умноженная на контрактную единицу, которая в приведенном выше примере равна 125000. Если, например, контракт упадет до 1,19 или вырастет до 1,21, это будет представлять прибыль или убыток в размере 1250 долларов по одному контракту, в зависимости от того, на какой стороне сделки находится инвестор.
Разница между спотовой и фьючерсной ставками
Спот-курс валюты — это текущий котируемый курс, по которому валюта в обмен на другую валюту может быть куплена или продана. Две задействованные валюты называются «парой». Если инвестор или хеджер проводит сделку по спот-курсу валюты, обмен валют происходит в момент, когда была совершена сделка, или вскоре после нее. Поскольку валютные форвардные курсы основаны на валютных курсах спот, валютные фьючерсы имеют тенденцию меняться по мере изменения спотовых курсов.
Если курс спот валютной пары увеличивается, фьючерсные цены на валютную пару имеют высокую вероятность повышения. С другой стороны, если спот-курс валютной пары снижается, фьючерсные цены имеют высокую вероятность снижения. Однако это не всегда так. Иногда курс спот может двигаться, но фьючерсы, срок действия которых истекает в отдаленные сроки, — нет. Это связано с тем, что изменение курса спот может рассматриваться как временное или краткосрочное и, таким образом, вряд ли повлияет на долгосрочные цены.
Пример валютного фьючерса
Предположим, что гипотетическая компания XYZ, базирующаяся в Соединенных Штатах, сильно подвержена валютному риску и желает застраховаться от предполагаемого поступления 125 миллионов евро в сентябре. До сентября компания могла продавать фьючерсные контракты на полученные евро. Контракт на фьючерсы Euro FX составляет 125 000 евро. Они продают фьючерсы на евро, потому что они американская компания, и им не нужны евро. Следовательно, поскольку они знают, что получат евро, они могут продать их сейчас и зафиксировать курс, по которому эти евро можно обменять на U. С. долларов.
С. долларов.
Компания XYZ продает 1 000 фьючерсных контрактов на евро для хеджирования предполагаемого поступления. Следовательно, если евро обесценивается по отношению к доллару США, прогнозируемая выручка компании защищена. Они зафиксировали свой курс, поэтому они могут продавать свои евро по фиксированному курсу. Однако компания теряет любые выгоды, которые могут возникнуть в случае повышения курса евро. Они по-прежнему вынуждены продавать свои евро по цене фьючерсного контракта, что означает отказ от прибыли (относительно цены в августе), которую они имели бы, если бы не продали контракты.
Определение риска контрагента
Что такое риск контрагента?
Риск контрагента — это вероятность или вероятность того, что один из участников сделки может не выполнить свои договорные обязательства. Риск контрагента может существовать в кредитных, инвестиционных и торговых операциях.
Ключевые выводы
- Риск контрагента — это вероятность или вероятность того, что один из участников операции может не выполнить свои договорные обязательства.Риск контрагента может существовать в кредитных, инвестиционных и торговых операциях.
- Числовое значение кредитного рейтинга заемщика отражает уровень риска контрагента для кредитора или кредитора.
- Инвесторы должны рассмотреть компанию, выпускающую облигации, акции или страховой полис, чтобы оценить, существует ли риск дефолта или контрагента.
Понимание риска контрагента
Во всех финансовых операциях существует разная степень риска контрагента.Риск контрагента также известен как риск дефолта. Риск неисполнения обязательств — это вероятность того, что компании или частные лица не смогут произвести необходимые платежи по своим долговым обязательствам. Кредиторы и инвесторы подвержены риску дефолта практически при всех формах предоставления кредитов. Риск контрагента — это риск, который обе стороны должны учитывать при оценке контракта.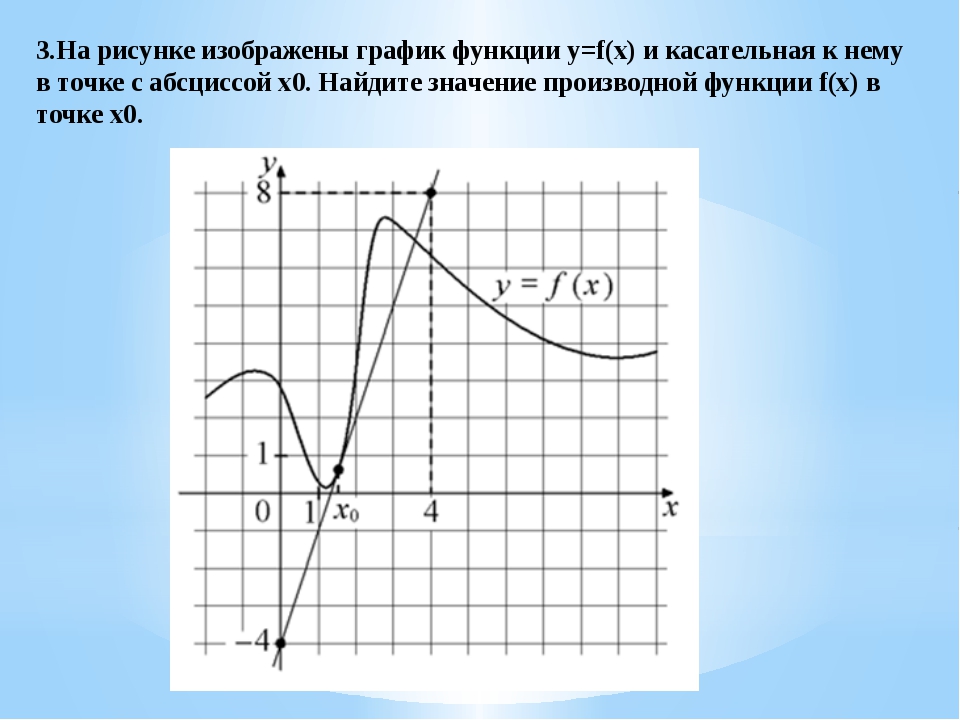
Риск контрагента и премии за риск
Если одна сторона имеет более высокий риск неисполнения обязательств, к сделке обычно прилагается премия для компенсации другой стороне.Премия, добавленная из-за риска контрагента, называется премией за риск.
В розничных и коммерческих финансовых операциях кредитные отчеты часто используются кредиторами для определения кредитного риска контрагента. Кредитные рейтинги заемщиков анализируются и контролируются, чтобы определить уровень риска для кредитора. Кредитный рейтинг — это числовое значение кредитоспособности человека или компании, которое основано на многих переменных.
Кредитный рейтинг человека колеблется от 300 до 850, и чем он выше, тем более надежным в финансовом отношении человек считается для кредитора.Числовые значения кредитных рейтингов перечислены ниже:
- Отлично: 750 и выше
- Хорошо: от 700 до 749
- Ярмарка: от 650 до 699
- Плохо: от 550 до 649
- Плохо: 550 и ниже
Многие факторы влияют на кредитный рейтинг, включая историю платежей клиента, общую сумму долга, длину кредитной истории и использование кредита, которое представляет собой процент от общего доступного кредита заемщика, который используется в настоящее время. Числовое значение кредитного рейтинга заемщика отражает уровень риска контрагента для кредитора или кредитора.Заемщик с кредитным рейтингом 750 будет иметь низкий риск контрагента, в то время как заемщик с кредитным рейтингом 450 будет нести высокий риск контрагента.
Если у заемщика низкий кредитный рейтинг, кредитор, скорее всего, потребует более высокую процентную ставку или премию из-за риска неисполнения обязательств по долгу. Компании, выпускающие кредитные карты, например, взимают процентную ставку свыше 20% для лиц с низким кредитным рейтингом, одновременно предлагая процентную ставку 0% для клиентов, которые имеют отличную кредитную историю или высокие кредитные рейтинги. Если заемщик просрочивает платежи на срок 60 дней или более или превышает кредитный лимит карты, компании, выпускающие кредитные карты, обычно прибегают к надбавке за риск или «ставке штрафа», что может повысить процентную ставку по карте до более чем 29% в год.
Если заемщик просрочивает платежи на срок 60 дней или более или превышает кредитный лимит карты, компании, выпускающие кредитные карты, обычно прибегают к надбавке за риск или «ставке штрафа», что может повысить процентную ставку по карте до более чем 29% в год.
Инвесторы должны рассмотреть компанию, выпускающую облигации, акции или страховой полис, чтобы оценить, существует ли риск дефолта или контрагента.
Риск инвестиционного контрагента
Финансовые инвестиционные продукты, такие как акции, опционы, облигации и производные финансовые инструменты, несут в себе риск контрагента.Облигациям присваиваются рейтинги таких агентств, как Moody’s и Standard and Poor’s, от AAA до статуса мусорных облигаций для измерения уровня риска контрагента. Облигации с более высоким риском контрагента приносят более высокую доходность. Когда риск контрагента минимален, премии или процентные ставки низкие, как, например, для фондов денежного рынка.
Например, компания, предлагающая бросовые облигации, будет иметь высокую доходность, чтобы компенсировать инвесторам дополнительный риск того, что компания может не выполнить свои обязательства. И наоборот, U.S. Казначейские облигации имеют низкий риск контрагента и, следовательно,; рейтинг выше, чем корпоративный долг и бросовые облигации. Однако казначейские облигации обычно приносят более низкую доходность, чем корпоративный долг, поскольку существует меньший риск дефолта.
Примеры риска контрагента
Когда риск контрагента неправильно рассчитан и сторона не выполняет свои обязательства, надвигающийся ущерб может быть серьезным. Например, дефолт по такому количеству обеспеченных долговых обязательств (CDO) стал основной причиной обвала рынка недвижимости в 2008 году.
Субстандартный риск
Ипотечные кредиты секьюритизируются в CDO для инвестиций и поддерживаются базовыми активами. Одним из основных недостатков CDO до экономического краха было то, что они содержали субстандартные и низкокачественные ипотечные кредиты, в результате чего CDO получали такие же высокие рейтинги, как и корпоративный долг.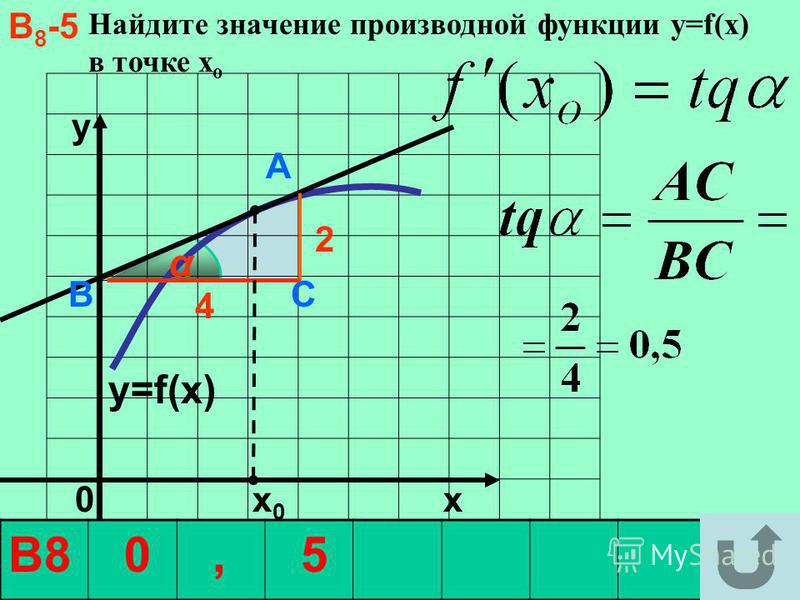
Высокий кредитный рейтинг CDO позволил им получить институциональные инвестиции, поскольку средства требуются для инвестирования только в долговые обязательства с высоким рейтингом. Когда заемщики начали не выплачивать ипотечные платежи, пузырь на рынке недвижимости лопнул, оставив инвесторов, банки и перестраховщиков на крючке, неся огромные убытки.Рейтинговые агентства получили много вины за обвал, который в конечном итоге привел к обвалу финансового рынка, который определил медвежий рынок 2007–2009 годов.
AIG и страховой риск
AIG или American International Group предлагает страховые продукты для недвижимости, предприятий и частных лиц. Компании потребовалась помощь правительства США во время финансового кризиса. Для тех, кто был застрахован в AIG, они внезапно столкнулись с увеличением контрагентского риска. В результате инвесторы должны учитывать компанию, выпускающую облигации, акции или страховой полис, чтобы оценить, существует ли риск контрагента.
Определение производной
Что такое производный инструмент?
Производный инструмент — это контракт между двумя или более сторонами, стоимость которого основана на согласованном базовом финансовом активе (например, ценной бумаге) или наборе активов (например, индексе). Общие базовые инструменты включают облигации, товары, валюты, процентные ставки, рыночные индексы и акции.
Ключевые выводы
- Производный инструмент — это контракт между двумя или более сторонами, стоимость которого основана на согласованном базовом финансовом активе, индексе или ценной бумаге.
- Фьючерсные контракты, форвардные контракты, опционы, свопы и варранты обычно являются производными финансовыми инструментами.
- Деривативы могут использоваться либо для снижения риска (хеджирование), либо для принятия риска с ожиданием соразмерного вознаграждения (спекуляция).
Общие сведения о производных финансовых инструментах
Деривативы — это вторичные ценные бумаги, стоимость которых основывается (производная) исключительно на стоимости первичной ценной бумаги, с которой они связаны, называемой базой.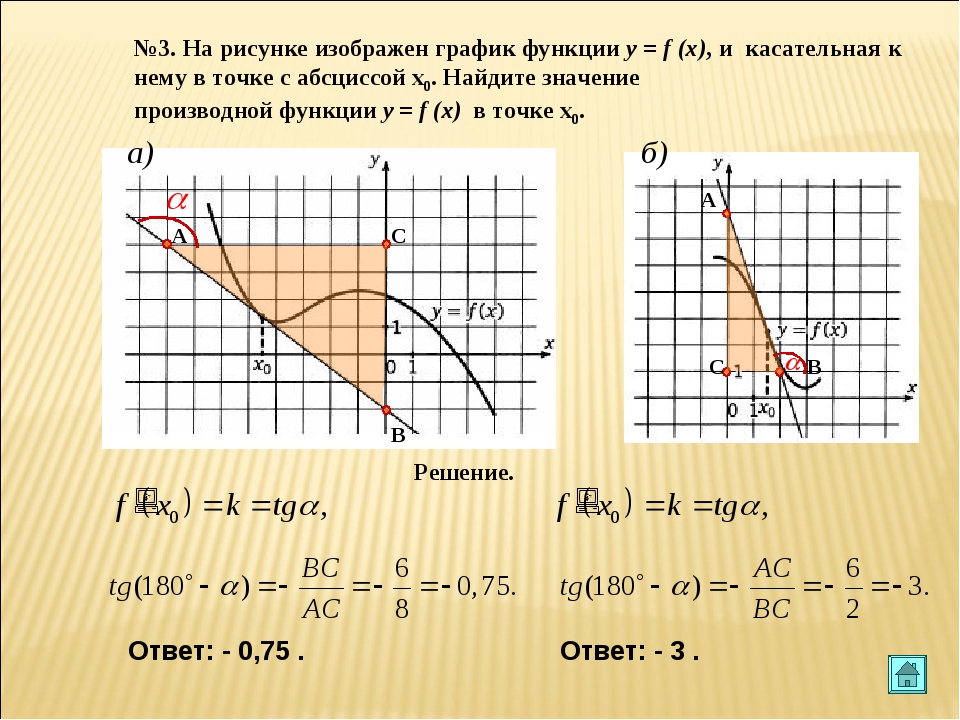 Обычно производные финансовые инструменты считаются передовым инвестированием.
Обычно производные финансовые инструменты считаются передовым инвестированием.
Существует два класса производных продуктов: «блокировка» и «опцион». Блокирующие продукты (например, свопы, фьючерсы или форварды) с самого начала связывают соответствующие стороны согласованными условиями в течение срока действия контракта. С другой стороны, опционные продукты (например, опционы на акции) предлагают держателю право, но не обязательство, купить или продать базовый актив или ценную бумагу по определенной цене в дату истечения срока действия опциона или до нее. В то время как стоимость производного инструмента основана на активе, владение производным инструментом не означает владение активом.Фьючерсные контракты, форвардные контракты, опционы, свопы и варранты обычно являются производными финансовыми инструментами.
Фьючерсные контракты
Например, фьючерсный контракт является производным инструментом, потому что его стоимость зависит от доходности базового актива. Фьючерсный контракт — это контракт на покупку или продажу товара или ценной бумаги по заранее определенной цене и в заранее установленную дату в будущем. Фьючерсные контракты стандартизированы по определенным объемам и срокам истечения. Фьючерсные контракты можно использовать с сырьевыми товарами, такими как нефть и пшеница, а также с драгоценными металлами, такими как золото и серебро.
Опционы на акции
Опцион на акции или акции — это разновидность производных финансовых инструментов, поскольку их стоимость «производная» от стоимости лежащих в их основе акций. Опционы бывают разных форм: звонки и путы. Опцион колл дает держателю право купить базовую акцию по заранее установленной цене (называемой ценой исполнения) и в заранее установленную дату, указанную в контракте (называемую датой истечения срока). Опцион пут дает держателю право продать акции по заранее установленной цене и дате, указанным в контракте.За опцион, называемый опционной премией, взимается предоплата.
Уравнение риска и вознаграждения часто считается основой инвестиционной философии, и производные финансовые инструменты могут использоваться либо для снижения риска (хеджирование), либо для спекуляций, где будет учитываться уровень риска по сравнению с вознаграждением. Например, трейдер может попытаться получить прибыль от ожидаемого падения цены индекса, такого как S&P 500, продавая (или открывая короткую позицию) соответствующий фьючерсный контракт. Производные инструменты, используемые в качестве хеджирования, позволяют передавать риски, связанные с ценой базового актива, между сторонами, участвующими в контракте.
Биржи производных финансовых инструментов и регулирование
Некоторые деривативы торгуются на национальных фондовых биржах и регулируются Комиссией по ценным бумагам и биржам США (SEC). Другие деривативы торгуются на внебиржевом рынке (OTC), что подразумевает индивидуальные договоренности между сторонами.
Фьючерс
Большинство деривативов торгуются на биржах. Например, товарные фьючерсы торгуются на фьючерсной бирже, которая представляет собой рынок, на котором покупаются и продаются различные товары.Брокеры и коммерческие трейдеры являются членами биржи и должны быть зарегистрированы в Национальной фьючерсной ассоциации (NFA) и Комиссии по торговле товарными фьючерсами (CFTC).
CFTC регулирует фьючерсные рынки и является федеральным агентством, которому поручено регулировать рынки таким образом, чтобы рынки функционировали справедливо. Надзор может включать предотвращение мошенничества, злоупотреблений в торговле и регулирование брокерских фирм.
Опции
Опционные контракты торгуются на Чикагской бирже опционов (CBOE), которая является крупнейшим в мире рынком опционов.Члены этих бирж регулируются SEC, которая контролирует рынки, чтобы гарантировать, что они функционируют должным образом и справедливо.
Внебиржевые транзакции
Важно отметить, что правила могут несколько отличаться в зависимости от продукта и его обмена.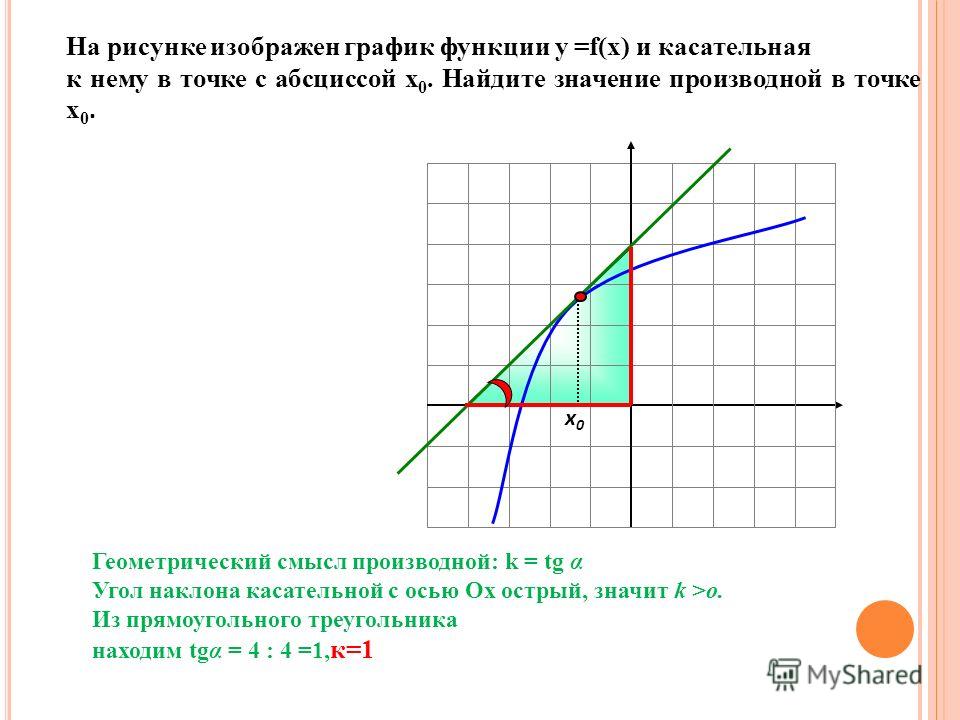 На валютном рынке, например, торговля осуществляется через внебиржевой рынок (OTC), то есть между брокерами и банками, а не на официальной бирже. Две стороны, такие как корпорация и банк, могут договориться об обмене одной валюты на другую по определенному курсу в будущем.Банки и брокеры регулируются SEC. Однако инвесторы должны знать о рисках, связанных с внебиржевыми рынками, поскольку транзакции не имеют центрального рынка или такого же уровня регулирующего надзора, как транзакции, совершаемые через национальную биржу.
На валютном рынке, например, торговля осуществляется через внебиржевой рынок (OTC), то есть между брокерами и банками, а не на официальной бирже. Две стороны, такие как корпорация и банк, могут договориться об обмене одной валюты на другую по определенному курсу в будущем.Банки и брокеры регулируются SEC. Однако инвесторы должны знать о рисках, связанных с внебиржевыми рынками, поскольку транзакции не имеют центрального рынка или такого же уровня регулирующего надзора, как транзакции, совершаемые через национальную биржу.
Двусторонние производные инструменты
Товарный фьючерсный контракт — это контракт на покупку или продажу заранее определенного количества товара по заранее установленной цене на определенную дату в будущем. Товарные фьючерсы часто используются для хеджирования или защиты инвесторов и предприятий от неблагоприятных изменений цен на товар.
Например, товарные деривативы используются фермерами и мукомольниками для обеспечения определенной степени «страховки». Фермер заключает контракт, чтобы зафиксировать приемлемую цену на товар, а мельник заключает контракт, чтобы зафиксировать гарантированную поставку товара. Хотя и фермер, и мельник снизили риск за счет хеджирования, оба по-прежнему подвержены риску изменения цен.
Пример товарного производного инструмента
Например, в то время как фермер получает определенную цену на товар, цены могут вырасти (из-за, например, нехватки из-за погодных явлений), и фермер в конечном итоге потеряет любой дополнительный доход, который мог бы быть получен. .Точно так же цены на товар могут упасть, и мельнику придется платить за товар больше, чем он бы в противном случае.
Например, предположим, что в апреле 2020 года фермер заключает фьючерсный контракт с мельником на продажу 5000 бушелей пшеницы по цене 4,404 доллара за бушель в июле. На дату истечения срока в июле 2017 года рыночная цена пшеницы упадет до 4,350 доллара, но мельник должен покупать по контрактной цене 4,404 доллара, что выше преобладающей рыночной цены в 4 доллара.350. Вместо 21 750 долларов (4,350 x 5 000) мельник заплатит 22 020 долларов (4,404 x 5 000), в то время как фермер возмещает цену, превышающую рыночную.
Однако, если бы цена поднялась до 5 долларов за бушель, хеджирование мельника позволило бы закупить пшеницу по контрактной цене 4,404 доллара по сравнению с преобладающей ценой в 5 долларов на дату истечения июльского срока. Фермер, с другой стороны, продал бы пшеницу по более низкой цене, чем преобладающая рыночная цена в 5 долларов.
Преимущества деривативов
Давайте воспользуемся историей вымышленной фермы, чтобы изучить механику нескольких разновидностей производных.Гейл, владелица Healthy Hen Farms, обеспокоена недавними колебаниями цен на курицу или нестабильностью на рынке курятины из-за сообщений о птичьем гриппе. Гейл хочет защитить свой бизнес от очередного приступа плохих новостей. Поэтому она встречается с инвестором, который заключает с ней фьючерсный контракт.
Инвестор соглашается платить 30 долларов за птицу, когда птица будет готова к убою через шесть месяцев, независимо от рыночной цены. Если в это время цена будет выше 30 долларов, инвестор получит выгоду, поскольку он сможет покупать птиц по цене ниже рыночной и продавать их на рынке по более высокой цене с прибылью.Если цена упадет ниже 30 долларов, Гейл получит выгоду, потому что она сможет продать своих птиц по цене, превышающей текущую рыночную цену, или больше, чем та, которую она получила бы за птиц на открытом рынке.
Деривативы и хеджирование
Заключая фьючерсный контракт, Гейл защищена от изменений цен на рынке, поскольку она зафиксировала цену в 30 долларов за птицу. Она может проиграть, если цена на птичье бешенство вырастет до 50 долларов за птицу, но она будет защищена, если цена упадет до 10 долларов после новостей о вспышке птичьего гриппа.Хеджируя фьючерсным контрактом, Гейл может сосредоточиться на своем бизнесе и уменьшить беспокойство по поводу колебаний цен.
Важно помнить, что, когда компании хеджируют, они не спекулируют на цене товара. Напротив, хеджирование — это просто способ каждой стороны управлять риском. Каждая сторона имеет свою прибыль или маржу, встроенную в цену, и хеджирование помогает защитить эту прибыль от потери рыночными колебаниями цены на товар. Независимо от того, станет ли цена товара выше или ниже цены фьючерсного контракта к истечению срока, обе стороны хеджировали свою прибыль по сделке, заключив контракт друг с другом.
Производный своп
Производные финансовые инструменты также могут использоваться с продуктами с процентной ставкой. Производные инструменты на процентную ставку чаще всего используются для хеджирования процентного риска. Риск процентной ставки может возникнуть, когда изменение процентных ставок вызывает изменение стоимости базового актива.
Ссуды, например, могут быть выданы как ссуды с фиксированной ставкой (одинаковая процентная ставка в течение срока ссуды), в то время как другие могут быть выданы как ссуды с переменной ставкой, то есть ставка колеблется в зависимости от процентных ставок на рынке.Некоторые компании могут захотеть перевести свои ссуды с переменной ставки на фиксированную.
Например, если у компании действительно низкая ставка, они могут захотеть заблокировать ее, чтобы защитить себя в случае повышения ставок в будущем. У других компаний может быть долг с высокой фиксированной ставкой по сравнению с текущим рынком, и они захотят поменять или поменять эту фиксированную ставку на текущую, более низкую переменную ставку на рынке. Обмен может быть осуществлен посредством процентного свопа, при котором две стороны обмениваются своими платежами, так что одна сторона получает плавающую ставку, а другая — фиксированную.
Пример процентного свопа
Продолжая наш пример с Healthy Hen Farms, предположим, что Гейл решила, что пора вывести Healthy Hen Farms на новый уровень. Она уже приобрела все небольшие фермы рядом с ней и хочет открыть собственный перерабатывающий завод. Она пытается получить больше финансирования, но кредитор, Ленни, отвергает ее.
Причина отказа Ленни в финансировании заключается в том, что Гейл профинансировала поглощение других ферм за счет огромной ссуды с переменной ставкой, и Ленни обеспокоен тем, что, если процентные ставки вырастут, она не сможет выплатить свои долги.Он говорит Гейл, что даст ей ссуду только в том случае, если она сможет конвертировать ссуду в ссуду с фиксированной ставкой. К сожалению, другие ее кредиторы отказываются изменять ее текущие условия ссуды, потому что надеются, что процентные ставки также вырастут.
Гейл повезло, когда она встречает Сэма, владельца сети ресторанов. У Сэма есть ссуда с фиксированной ставкой примерно такого же размера, что и у Гейл, и он хочет преобразовать ее в ссуду с переменной ставкой, потому что надеется, что процентные ставки в будущем снизятся.
По тем же причинам кредиторы Сэма не изменят условия ссуды.Гейл и Сэм решают поменяться кредитами. Они заключают сделку, по которой платежи Гейл идут на ссуду Сэма, а его выплаты идут на ссуду Гейл. Хотя названия ссуд не изменились, их контракт позволяет им обоим получить ссуду того типа, который они хотят.
Сделка немного рискованна для них обоих, потому что, если один из них не выполнит свои обязательства или обанкротится, другой будет возвращен обратно в свой старый заем, который может потребовать оплаты, к которой Гейл или Сэм могут быть не готовы. Однако это позволяет им изменять свои ссуды в соответствии со своими индивидуальными потребностями.
Кредитный производный инструмент
Кредитный производный инструмент — это договор между двумя сторонами, который позволяет кредитору или кредитору передать риск неисполнения обязательств третьей стороне. Контракт переносит кредитный риск того, что заемщик может не выплатить ссуду. Однако ссуда остается на балансе кредитора, но риск переходит к другой стороне. Кредиторы, такие как банки, используют кредитные деривативы для устранения или снижения риска невыполнения ссуды из своего общего ссудного портфеля и взамен уплачивают авансовый сбор, называемый премией.
Пример кредитного производного инструмента
Ленни, банкир Гейл, вносит дополнительный капитал по выгодной процентной ставке, и Гейл уезжает счастливая. Ленни тоже доволен, потому что его деньги там окупаются, но он также немного обеспокоен тем, что Сэм или Гейл могут потерпеть неудачу в их бизнесе.
Что еще хуже, друг Ленни Дейл приходит к нему и просит денег на открытие собственной кинокомпании. Ленни знает, что у Дейла много залога и что кредит будет под более высокий процент из-за более нестабильного характера киноиндустрии, поэтому он ругает себя за то, что одолжил весь свой капитал Гейл.
К счастью для Ленни, деривативы предлагают другое решение. Ленни превращает ссуду Гейл в производный финансовый инструмент и продает его спекулянту со скидкой по отношению к истинной стоимости. Хотя Ленни не видит полной отдачи от ссуды, он получает свой капитал обратно и может снова выдать его своему другу Дейлу. Ленни настолько нравится эта система, что он продолжает использовать свои ссуды как кредитные деривативы, получая скромную прибыль в обмен на меньший риск дефолта и большую ликвидность.
Опционные контракты
Спустя годы Healthy Hen Farms стала публичной корпорацией (HEN) и крупнейшим производителем мяса птицы в Америке.Гейл и Сэм оба с нетерпением ждут выхода на пенсию.
За эти годы Сэм купил довольно много акций HEN. Фактически, он вложил в компанию более 100 000 долларов. Сэм нервничает, потому что он обеспокоен тем, что еще одно потрясение, возможно, еще одна вспышка птичьего гриппа, может уничтожить огромную часть его пенсионных денег. Сэм начинает искать кого-нибудь, чтобы снять риск с его плеч. Ленни теперь экстраординарный финансист и активный писатель или продавец опционов, соглашается помочь ему.
Ленни описывает сделку, называемую пут-опционом, по которой Сэм платит Ленни комиссию или премию за право (но не обязательство) продать Lenny the HEN акции через год по их текущей цене в 25 долларов за акцию. Если цены на акции резко упадут, Ленни защитит Сэма от потери его пенсионных сбережений.
Healthy Hen Farms остается стабильной до тех пор, пока Сэм и Гейл не выведут свои деньги на пенсию. Ленни получает прибыль от гонораров и своей быстрорастущей карьеры финансиста. Ленни в порядке, потому что он собирает гонорары и может справиться с риском.
Итог
Этот рассказ показывает, как производные финансовые инструменты могут перемещать риск (и сопутствующее вознаграждение) от не склонных к риску лиц, ищущих его. Хотя Уоррен Баффет однажды назвал деривативы «финансовым оружием массового уничтожения», деривативы могут быть очень полезными инструментами при условии их правильного использования. Как и все другие финансовые инструменты, у деривативов есть свои плюсы и минусы, но они также обладают уникальными свойствами. потенциал для повышения функциональности финансовой системы в целом.
Страница не найдена
- Образование
Общий
- Словарь
- Экономика
- Корпоративные финансы
- Рот ИРА
- Акции
- Паевые инвестиционные фонды
- ETFs
- 401 (к)
Инвестирование / Торговля
- Основы инвестирования
- Фундаментальный анализ
- Управление портфелем
- Основы трейдинга
- Технический анализ
- Управление рисками
- Рынки
Новости
- Новости компании
- Новости рынков
- Торговые новости
- Политические новости
- Тенденции
Популярные акции
- Яблоко (AAPL)
- Тесла (TSLA)
- Amazon (AMZN)
- AMD (AMD)
- Facebook (FB)
- Netflix (NFLX)
- Симулятор
Симулятор
- Завести аккаунт
- Присоединяйтесь к игре
Мой симулятор
- Моя игра
- Создать игру
- Твои деньги
Личные финансы
- Управление благосостоянием
- Бюджетирование / экономия
- Банковское дело
- Кредитные карты
- Домовладение
- Пенсионное планирование
- Налоги
- Страхование
Обзоры и рейтинги
- Лучшие онлайн-брокеры
- Лучшие сберегательные счета
- Лучшие домашние гарантии
- Лучшие кредитные карты
- Лучшие личные займы
- Лучшие студенческие ссуды
- Лучшее страхование жизни
- Лучшее автострахование
- Советники
Ваша практика
- Управление практикой
- Продолжая образование
- Карьера финансового консультанта
- Инвестопедия 100
Управление благосостоянием
- Портфолио Строительство
- Финансовое планирование
- Академия
Популярные курсы
- Инвестирование для начинающих
- Станьте дневным трейдером
- Торговля для начинающих
- Технический анализ
Курсы по темам
- Все курсы
- Курсы трейдинга
- Курсы инвестирования
- Финансовые профессиональные курсы
Представлять на рассмотрение
Извините, страница, которую вы ищете, недоступна.Вы можете найти то, что ищете, используя наше меню или параметры поиска.
дома- О нас
- Условия эксплуатации
- Словарь
- Редакционная политика
- Рекламировать
- Новости
- Политика конфиденциальности
- Связаться с нами
- Карьера
- Уведомление о конфиденциальности Калифорнии
- #
- А
- B
- C
- D
- E
- F
- грамм
- ЧАС
- я
- J
- K
- L
- M
- N
- О
- п
- Q
- р
- S
- Т
- U
- V
- W
- Икс
- Y
- Z
Страница не найдена
- Образование
Общий
- Словарь
- Экономика
- Корпоративные финансы
- Рот ИРА
- Акции
- Паевые инвестиционные фонды
- ETFs
- 401 (к)
Инвестирование / Торговля
- Основы инвестирования
- Фундаментальный анализ
- Управление портфелем
- Основы трейдинга
- Технический анализ
- Управление рисками
- Рынки
Новости
- Новости компании
- Новости рынков
- Торговые новости
- Политические новости
- Тенденции
Популярные акции
- Яблоко (AAPL)
- Тесла (TSLA)
- Amazon (AMZN)
- AMD (AMD)
- Facebook (FB)
- Netflix (NFLX)
- Симулятор
Симулятор
- Завести аккаунт
- Присоединяйтесь к игре
Мой симулятор
- Моя игра
- Создать игру
- Твои деньги
Личные финансы
- Управление благосостоянием
- Бюджетирование / экономия
- Банковское дело
- Кредитные карты
- Домовладение
- Пенсионное планирование
- Налоги
- Страхование
Обзоры и рейтинги
- Лучшие онлайн-брокеры
- Лучшие сберегательные счета
- Лучшие домашние гарантии
- Лучшие кредитные карты
- Лучшие личные займы
- Лучшие студенческие ссуды
- Лучшее страхование жизни
- Лучшее автострахование
- Советники
Ваша практика
- Управление практикой
- Продолжая образование
- Карьера финансового консультанта
- Инвестопедия 100
Управление благосостоянием
- Портфолио Строительство
- Финансовое планирование
- Академия
Популярные курсы
- Инвестирование для начинающих
- Станьте дневным трейдером
- Торговля для начинающих
- Технический анализ
Курсы по темам
- Все курсы
- Курсы трейдинга
- Курсы инвестирования
- Финансовые профессиональные курсы
Представлять на рассмотрение

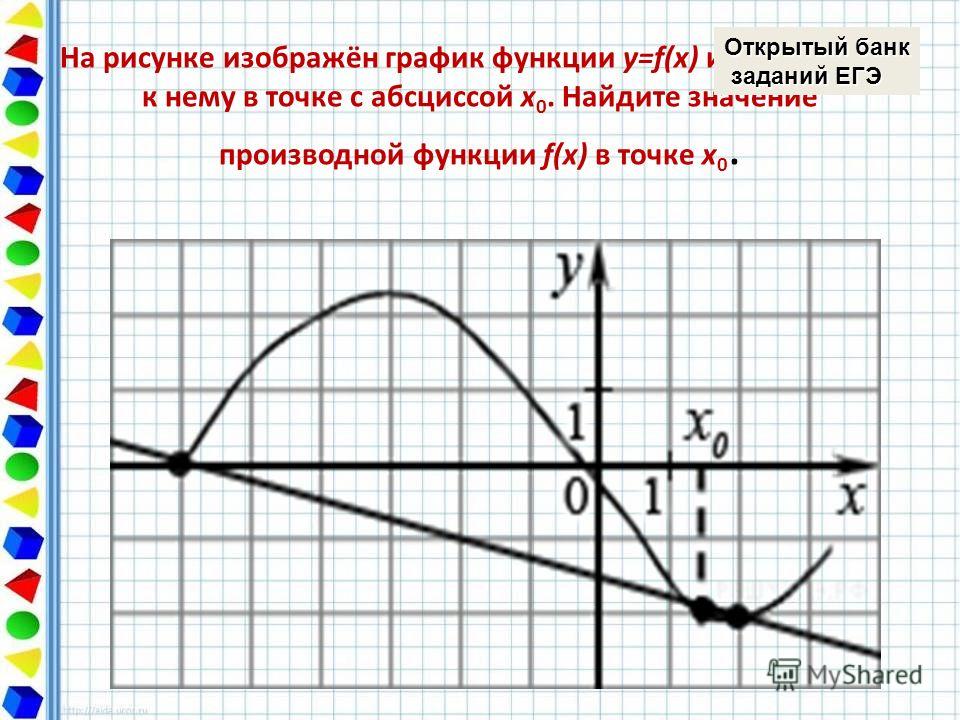 393813225728E+14+5293047513600i
393813225728E+14+5293047513600i
Leave A Comment