Решаем это уравнение
Корни этого ур-ния
$$x_{1} = 34$$
$$x_{2} = 92$$
$$x_{3} = -100$$
$$x_{4} = 12$$
$$x_{5} = 80$$
$$x_{6} = 4$$
$$x_{7} = 70$$
$$x_{8} = -82$$
$$x_{9} = 90$$
$$x_{10} = -14$$
$$x_{11} = -78$$
$$x_{12} = -90$$
$$x_{13} = -46$$
$$x_{14} = -48$$
$$x_{15} = 46$$
$$x_{16} = 66$$
$$x_{17} = 22$$
$$x_{18} = 72$$
$$x_{19} = -66$$
$$x_{20} = -4$$
$$x_{21} = 82$$
$$x_{22} = 98$$
$$x_{23} = 74$$
$$x_{24} = 36$$
$$x_{25} = -70$$
$$x_{26} = -54$$
$$x_{27} = -74$$
$$x_{28} = -30$$
$$x_{29} = -32$$
$$x_{30} = -12$$
$$x_{31} = 52$$
$$x_{32} = 32$$
$$x_{33} = -60$$
$$x_{34} = -20$$
$$x_{35} = 40$$
$$x_{36} = 68$$
$$x_{37} = -86$$
$$x_{38} = -34$$
$$x_{39} = 24$$
$$x_{40} = -10$$
$$x_{41} = 18$$
$$x_{42} = -44$$
$$x_{43} = 62$$
$$x_{44} = -76$$
$$x_{45} = 50$$
$$x_{46} = -2$$
$$x_{47} = 88$$
$$x_{49} = -94$$
$$x_{50} = -56$$
$$x_{51} = -52$$
$$x_{52} = 0$$
$$x_{53} = -80$$
$$x_{54} = -36$$
$$x_{55} = 78$$
$$x_{56} = 54$$
$$x_{57} = 60$$
$$x_{58} = -64$$
$$x_{59} = -40$$
$$x_{60} = -68$$
$$x_{61} = 26$$
$$x_{62} = 28$$
$$x_{63} = -38$$
$$x_{64} = -42$$
$$x_{65} = -22$$
$$x_{66} = -84$$
$$x_{67} = -50$$
$$x_{68} = 38$$
$$x_{69} = 64$$
$$x_{70} = 30$$
$$x_{71} = 14$$
$$x_{72} = 86$$
$$x_{73} = -6$$
$$x_{74} = -98$$
$$x_{75} = -28$$
$$x_{76} = 6$$
$$x_{77} = -18$$
$$x_{78} = 94$$
$$x_{79} = 48$$
$$x_{80} = 16$$
$$x_{81} = 20$$
$$x_{82} = 2$$
$$x_{83} = 96$$
$$x_{85} = -92$$
$$x_{86} = -96$$
$$x_{87} = -8$$
$$x_{88} = 58$$
$$x_{89} = 76$$
$$x_{90} = -88$$
$$x_{91} = 8$$
$$x_{92} = -16$$
$$x_{93} = 100$$
$$x_{94} = -24$$
$$x_{95} = 42$$
$$x_{96} = 84$$
$$x_{97} = -62$$
$$x_{98} = 56$$
$$x_{99} = -58$$
$$x_{100} = -72$$
$$x_{101} = 44$$
Зн.
 экстремумы в точках:
экстремумы в точках:(34, 1)
(92, 1)
(-100, -1)
(12, 1)
(80, 1)
(4, 1)
(70, 1)
(-82, -1)
(90, 1)
(-14, -1)
(-78, -1)
(-90, -1)
(-46, -1)
(-48, -1)
(46, 1)
(66, 1)
(22, 1)
(72, 1)
(-66, -1)
(-4, -1)
(82, 1)
(98, 1)
(74, 1)
(36, 1)
(-70, -1)
(-54, -1)
(-74, -1)
(-30, -1)
(-32, -1)
(-12, -1)
(52, 1)
(32, 1)
(-60, -1)
(-20, -1)
(40, 1)
(68, 1)
(-86, -1)
(-34, -1)
(24, 1)
(-10, -1)
(18, 1)
(-44, -1)
(62, 1)
(-76, -1)
(50, 1)
(-2, -1)
(88, 1)
(10, 1)
(-94, -1)
(-56, -1)
(-52, -1)
(0, -1)
(-80, -1)
(-36, -1)
(78, 1)
(54, 1)
(60, 1)
(-64, -1)
(-40, -1)
(-68, -1)
(26, 1)
(28, 1)
(-38, -1)
(-42, -1)
(-22, -1)
(-84, -1)
(-50, -1)
(38, 1)
(64, 1)
(30, 1)
(14, 1)
(86, 1)
(-6, -1)
(-98, -1)
(-28, -1)
(6, 1)
(-18, -1)
(94, 1)
(48, 1)
(16, 1)
(20, 1)
(2, 1)
(96, 1)
(-26, -1)
(-92, -1)
(-96, -1)
(-8, -1)
(58, 1)
(76, 1)
(-88, -1)
(8, 1)
(-16, -1)
(100, 1)
(-24, -1)
(42, 1)
(84, 1)
(-62, -1)
(56, 1)
(-58, -1)
(-72, -1)
(44, 1)
Интервалы возрастания и убывания функции:
Найдём интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим как ведёт себя функция в экстремумах при малейшем отклонении от экстремума:
Минимумы функции в точках:
$$x_{101} = -30$$
$$x_{101} = -86$$
$$x_{101} = 50$$
$$x_{101} = -62$$
Максимумы функции в точках:
$$x_{101} = -48$$
$$x_{101} = 88$$
Убывает на промежутках
[50, oo)
Возрастает на промежутках
(-oo, -86]
Постройте график функции и найдите значение k
Постройте график функции y=|x-3|-|x+3| и найдите значение k, при которых прямая y=kx имеет с графиком данной функции ровно одну общую точку.
Решение:
Разберем как строить график с модулем.
y=|x-3|-|x+3|
Найдем точки при переходе которых знак модулей меняется.
Каждое выражения, которое под модулем приравниваем к 0. У нас их два x-3 и x+3.
x=3 и x=-3
У нас числовая прямая разделится на три интервала (-∞;-3)U(-3;3)U(3;+∞). На каждом интервале нужно определить знак под модульных выражений.
1. Это сделать очень просто, рассмотрим первый интервал (-∞;-3). Возьмем с этого отрезка любое значение, например, -4 и подставим в каждое под модульное уравнение вместо значения х.
х=-4
x-3=-4-3=-7 и x+3=-4+3=-1
У обоих выражений знаки отрицательный, значит перед знаком модуля в уравнении ставим минус, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (-∞;-3).
y=—(x-3)-(—(x+3))=-х+3+х+3=6
На интервале (-∞;-3) получился график линейной функции (прямой) у=6
2. Рассмотрим второй интервал (-3;3). Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0.
Рассмотрим второй интервал (-3;3). Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0.
х=0
x-3=0-3=-3 и x+3=0+3=3
У первого выражения x-3 знак отрицательный получился, а у второго выражения x+3 положительный. Следовательно, перед выражением x-3 запишем знак минус, а перед вторым выражением знак плюс.
y=—(x-3)-(+(x+3))=-х+3-х-3=-2x
На интервале (-3;3) получился график линейной функции (прямой) у=-2х
3.Рассмотрим третий интервал (3;+∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.
х=5
x-3=5-3=2 и x+3=5+3=8
У обоих выражений знаки получились положительными, значит перед знаком модуля в уравнении ставим плюс, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (3;+∞).
y=+(x-3)-(+(x+3))=х-3-х-3=-6
На интервале (3;+∞) получился график линейной функции (прямой) у=-6
4. Теперь подведем итог.Постоим график y=|x-3|-|x+3|.
Теперь подведем итог.Постоим график y=|x-3|-|x+3|.
На интервале (-3;3) строим график линейной функции (прямой) у=-2х.
Чтобы построить график у=-2х подберем несколько точек.
x=-3 y=-2*(-3)=6 получилась точка (-3;6)
x=0 y=-2*0=0 получилась точка (0;0)
x=3 y=-2*(3)=-6 получилась точка (3;-6)
На интервале (3;+∞) строим график линейной функции (прямой) у=-6.
5. Теперь проанализируем результат и ответим на вопрос задания найдем значение k, при которых прямая y=kx имеет с графиком y=|x-3|-|x+3| данной функции ровно одну общую точку.
Прямая y=kx при любом значении k всегда будет проходить через точку (0;0). Поэтому мы можем изменить только наклон данной прямой y=kx, а за наклон у нас отвечает коэффициент k.
Если k будет любое положительное число, то будет одно пересечение прямой y=kx с графиком y=|x-3|-|x+3|. Этот вариант нам подходит.
Если k будет принимать значение (-2;0), то пересечений прямой y=kx с графиком y=|x-3|-|x+3| будет три.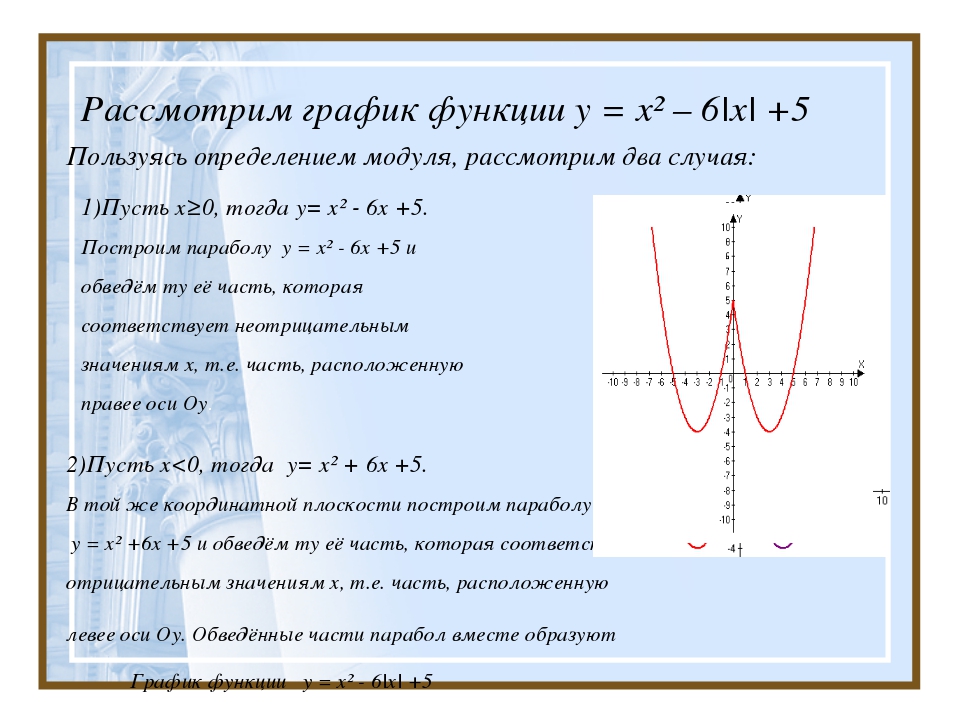 Этот вариант нам не подходит.
Этот вариант нам не подходит.
Если k=-2, решений будет множество [-2;2], потому что прямая y=kx будет совпадать с графиком y=|x-3|-|x+3| на данном участке. Этот вариант нам не подходит.
Если k будет меньше -2, то прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.Этот вариант нам подходит.
Если k=0, то пересечений прямой y=kx с графиком y=|x-3|-|x+3| также будет одно.Этот вариант нам подходит.
Ответ: при k принадлежащей интервалу (-∞;-2)U[0;+∞) прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
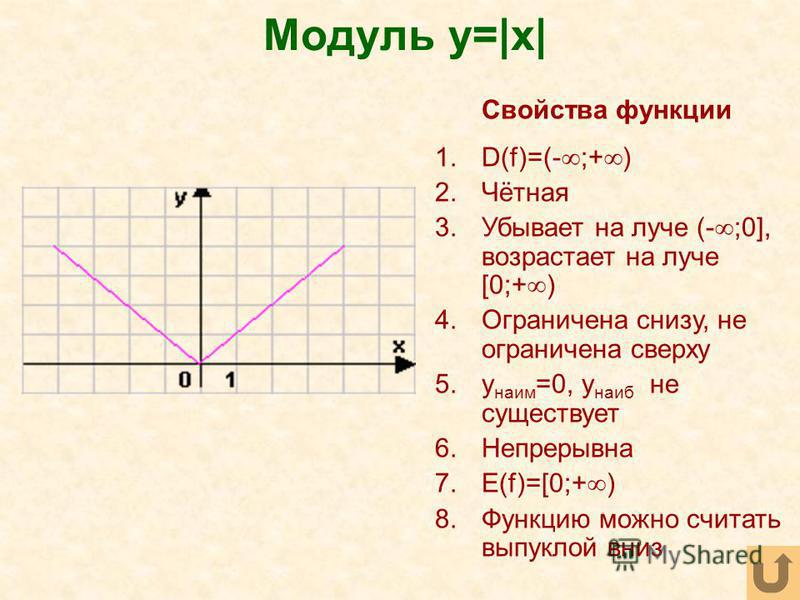
Функции y=|x|, y=[x],y={x}, y=sign(x) и их графики. Функция f(x)=|x|
Функция $f(x)=|x|$
$|x|$ — модуль. Он определяется следующим образом: Если действительное число будет неотрицательным, то значение модуля совпадает с самим числом. Если же отрицательно, то значение модуля совпадает с абсолютным значением данного числа.
Математически это можно записать следующим образом:
Пример 1
Исследуем и построим её график.
- $D\left(f\right)=R$.
- По определению модуля действительного числа, получим, что$E\left(f\right)=[0,\infty )$
- $f\left(-x\right)=|-x|=|x|=f(x)$. Значит, функция четна.
- При $x=0,\ y=0$. Точка $\left(0,0\right)$ — единственное пересечение с координатными осями.
- \[f’\left(x\right)=\left\{ \begin{array}{c} {1,x >0,} \\ {-1,xФункция будет возрастать на промежутке $x\in (0,+\infty )$
Функция будет убывать на промежутке $x\in (-\infty ,0)$
Значения на концах области определения.
\[{\mathop{\lim }_{x\to -\infty } y\ }=+\infty \] \[{\mathop{\lim }_{x\to +\infty } y\ }=+\infty \]Рисунок 1.
Функция $f(x)=[x]$
Функция $f\left(x\right)=[x]$ — функция целой части числа. Она находится округлением числа (если оно само не целое) «в меньшую сторону».
Пример: $[2,6]=2.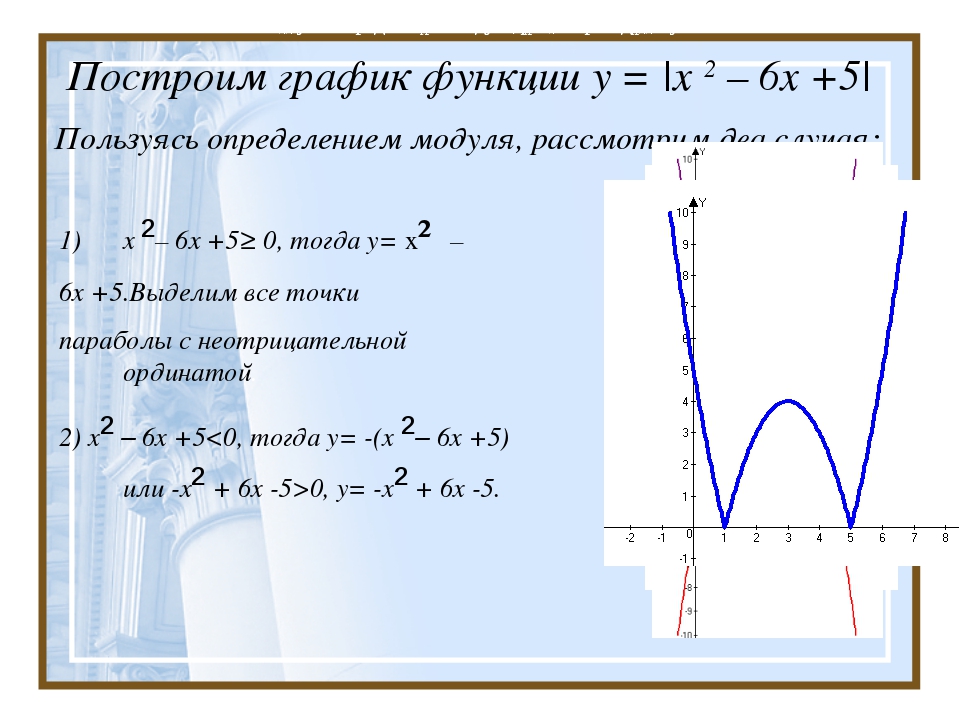 $
$
Пример 2
Исследуем и построим её график.
- $D\left(f\right)=R$.
- Очевидно, что эта функция принимает только целые значения, то есть $\ E\left(f\right)=Z$
- $f\left(-x\right)=[-x]$. Следовательно, эта функция будет общего вида.
- $(0,0)$ — единственная точка пересечения с осями координат.
- $f’\left(x\right)=0$
- Функция имеет точки разрыва (скачка функции) при всех $x\in Z$.
Рисунок 2.
Функция $f\left(x\right)=\{x\}$
Функция $f\left(x\right)=\{x\}$ — функция дробной части числа. Она находится «отбрасыванием» целой части этого числа.
$\{2,6\}=0,6$
Пример 3
Исследуем и построим график функции
$D\left(f\right)=R$.
Очевидно, что эта функция никогда не будет отрицательной и никогда не будет больше единицы, то есть $\ E\left(f\right)=[0,1)$
$f\left(-x\right)=\{-x\}$. Следовательно, данная функция будет общего вида.

Пересечение с осью $Ox$: $\left(z,0\right),\ z\in Z$
Пересечение с осью $Oy$: $\left(0,0\right)$
$f’\left(x\right)=0$
Функция имеет точки разрыва (скачка функции) при всех $x\in Z$
Рисунок 3.
Функция $f(x)=sign(x)$
Функция $f\left(x\right)=sign(x)$ — сигнум-функция. Эта функция показывает, какой знак имеет действительное число. Если число отрицательно, то функция имеет значение $-1$. Если число положительно, то функция равняется единице. При нулевом значении числа, значение функции также будет принимать нулевое значение.
Математически это можно записать следующим образом:
Пример 4
Исследуем и построим график функции
- $D\left(f\right)=R$.
- Непосредственно из определения, получим
- \[\ E\left(f\right)=\left\{-1\right\}\cup \left\{0\right\}\cup \{1\}\]
$f\left(-x\right)=sign\left(-x\right)=-sign(x)$. Следовательно, данная функция будет нечетной.

Пересечение с осью $Ox$: $\left(0,0\right)$
Пересечение с осью $Oy$: $\left(0,0\right)$
$f’\left(x\right)=0$
Функция имеет точку разрыва (скачка функции) в начале координат.
Рисунок 4.
постройте график y= x*2 если модуль x меньше или равен 1 1/х если модуль х больше 1+определить где прямая у=с имеет одну общую т
Уравнение нужно домножить на учетверенный первый коэффициент:
5х²-8х+3=0, I ·4a=20
Домножим уравнение на 4a, то есть, на 4·5 = 20:
20·5x²+20·(-8)x+20·3=0,
Выполним умножение на 20:
100x²-160x+60=0,
Перенесем число -60 в правую сторону:
100x²-160x=-60,
Коэффициент, стоящий при x, по модулю равен 160. Разделим 160 пополам (на 2), затем результат разделим на квадратный корень коэффициента a (т.е. на корень из 100, или просто на 10): 160:2:10=8. Прибавим к обеим частям уравнения число, равное 8² = 64:
Разделим 160 пополам (на 2), затем результат разделим на квадратный корень коэффициента a (т.е. на корень из 100, или просто на 10): 160:2:10=8. Прибавим к обеим частям уравнения число, равное 8² = 64:
100х²-160х+64=-60+64,
Свернем выражение в левой части по формуле квадрата разности:
(10x−8)² =4,
Извлечем квадратный корень из обеих частей уравнения:
10х-8=±2,
Отделим решения:
10х-8=2, 10х-8=-2,
10х=2+8, 10х=-2+8,
10х=10, 10х=6,
х=1. х=0,6.
Ответ: 0,6; 1.
А)нет , не существует
б) да , существует
Рисуешь прямую, отмечаешь на ней 3 точки. Затем растовляешь X,Y,Z по порядку. Получается что график будет выглядеть вот так:
Затем растовляешь X,Y,Z по порядку. Получается что график будет выглядеть вот так:
___.____._____.__
X Y Z
Модуль числа | Материалы для подготовки к ЕГЭ по математике ЕГЭ-Студия
Модуль числа и уравнения с модулем — тема особенная, прямо-таки заколдованная 🙂 Она совсем не сложная, просто в школе её редко объясняют нормально. В результате без специальной подготовки почти никто из школьников не может дать правильное определение модуля и тем более решить уравнение с модулем. И эту картину мы наблюдаем на протяжении многих лет.
Поэтому осваивайте тему «Уравнения и неравенства с модулем» по нашим статьям и на наших занятиях! Вы сумеете обойти множество конкурентов на ЕГЭ, олимпиадах и вступительных экзаменах.
Модуль числа называют ещё абсолютной величиной этого числа. Попросту говоря, при взятии модуля нужно отбросить от числа его знак. В записи положительного числа и так нет. никакого знака, поэтому модуль положительного числа равен ему самому. Например, Модуль нуля равен нулю. А модуль отрицательного числа равен противоположному ему положительному
(без знака!). Например,
Обратите внимание: модуль числа всегда неотрицателен:
Определение модуля
Вот оно:
От большинства известных из школы определений оно отличается лишь одним: в нём есть выбор. Есть условие. И в зависимости от этого условия мы раскрываем модуль либо так, либо иначе.
Так же, как в информатике — в разветвляющихся алгоритмах с применением условных операторов. Как, вообще-то, и в жизни: сдал ЕГЭ на минимальный балл — можешь подавать документы в ВУЗ. Не сдал на минимальный балл — можешь идти в армию 🙂
Таким образом, если под знаком модуля стоит выражение, зависящее от переменной, мы раскрываем модуль по определению. Например,
Например,
В некоторых случаях модуль раскрывается однозначно. Например, так как выражение под знаком модуля неотрицательно при любых x и y. Или: так так как выражение под модулем неположительно при любых z.
Геометрическая интерпретация модуля
Нарисуем числовую прямую. Модуль числа — это расстояние от нуля до данного числа. Например, То есть расстояние от точки −5 до нуля равно 5.
Эта геометрическая интерпретация очень полезна для решения уравнений и неравенств с модулем.
Рассмотрим простейшее уравнение . Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно трём. Это точки 3 и −3. Значит, у уравнения есть два решения: x = 3 и x = −3.
Вообще, если имеются два числа a и b, то равно расстоянию между ними на числовой прямой.
(В связи с этим нередко встречается обозначение длины отрезка AB, то есть расстояния от точки A до точки B.)
Ясно, что (расстояние от точки a до точки b равно расстоянию от точки b до точки a).
Решим уравнение . Эту запись можно прочитать так: расстояние от точки x до точки 3 равно 4. Отметим на числовой прямой точки, удовлетворяющие этому условию.
Мы видим, что наше уравнение имеет два решения: −1 и 7. Мы решили его самым простым способом — без использования определения модуля.
Перейдём к неравенствам. Решим неравенство .
Эту запись можно прочитать так: «расстояние от точки x до точки −7 меньше четырёх». Отмечаем на числовой прямой точки, удовлетворяющие этому условию.
Ответ: (-11; -3).
Другой пример. Решим неравенство |10 − x| ≥ 7.
Расстояние от точки 10 до точки x больше или равно семи. Отметим эти точки на числовой прямой.
Ответ:
График функции
Этот график надо знать обязательно. Для имеем y = x. Для имеем y = −x. В результате получаем:
С помощью этого графика также можно решать уравнения и неравенства.
Корень из квадрата
Нередко в задачах ЕГЭ требуется вычислить , где – некоторое число или выражение. Не забывайте, что
Не забывайте, что
Действительно, по определению арифметического квадратного корня — это такое неотрицательное число, квадрат которого равен . Оно равно при и при , т. е. как раз .
Примеры заданий ЕГЭ
1. Найдите значение выражения при .
Заметим, что при . Следовательно, значение нашего выражения равно: .
2. Найдите значение выражения при .
Действуем аналогично:
В следующей статье мы рассмотрим более сложные уравнения и неравенства с модулем.
Читайте также: Уравнения с модулем
Урок 21. показательная функция — Алгебра и начала математического анализа — 10 класс
Алгебра и начала математического анализа, 10 класс
Урок №21. Показательная функция.
Перечень вопросов, рассматриваемых в теме:
— какая функция называется показательной;
— какие свойства имеет показательная функция в зависимости от ее основания;
— какой вид имеет график показательной функции в зависимости от ее основания;
— примеры реальных процессов, описываемых показательной функцией.
Глоссарий по теме
Функция вида , a>0, а≠1 называется показательной функцией с основанием а.
Функция называется монотонно возрастающей на промежутке <a; b>, если (чем больше аргумент, тем больше значение функции).
Функция называется монотонно убывающей на промежутке <a; b>, если (чем больше аргумент, тем меньше значение функции).
Основная литература:
Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. под ред. Жижченко А.Б. Алгебра и начала математического анализа. 10 класс: учеб.для общеобразоват. учреждений: базовый и профил. уровни 2-е изд. – М.: Просвещение, 2010. – 336 с.: ил. – ISBN 978-5-09-025401-4, сс.310-314, сс. 210-216.
Открытые электронные ресурсы:
http://fcior.edu.ru/ — Федеральный центр информационно-образовательных ресурсов
http://school-collection.edu.ru/ — Единая коллекция цифровых образовательных ресурсов
Теоретический материал для самостоятельного изучения
1. Определение, свойства и график показательной функции
Определение, свойства и график показательной функции
Определение:
Функция вида y=ах, a>0, а≠1 называется показательной функцией с основанием а.
Такое название она получила потому, что независимая переменная стоит в показателе. Основание а – заданное число.
Для положительного основания значение степени ах можно найти для любого значения показателя х – и целого, и рационального, и иррационального, то есть для любого действительного значения.
Сформулируем основные свойства показательной функции.
1. Область определения.
Как мы уже сказали, степень ах для a>0 определена для любого действительного значения переменной х, поэтому область определения показательной функции D(y)=R.
2. Множество значений.
Так как основание степени положительно, то очевидно, что функция может принимать только положительные значения.
Множество значений показательной функции Е(y)=R+, или Е(y)=(0; +∞).
3. Корни (нули) функции.
Так как основание a>0, то ни при каких значениях переменной х функция не обращается в 0 и корней не имеет.
4. Монотонность.
При a>1 функция монотонно возрастает.
При 0<a<1 функция монотонно убывает.
5. При любом значении а значение функции y (0) = а0 =1.
6. График функции.
При a>1
Рисунок 1 – График показательной функции при a>1
При 0<a<1
Рисунок 2 – График показательной функции при 0<a<1
Независимо от значения основания а график функции имеет горизонтальную асимптоту y=0. Для 0<a<1 при х стремящемся к плюс бесконечности, для a>1 при х стремящемся к минус бесконечности.
2. Рассмотрим пример исследования функции y=–3х+1.
Решение:
1) Область определения функции – любое действительное число.
2) Найдем множество значений функции.
Так как 3х>0, то –3х<0, значит, –3х+1<1, то есть множество значений функции y=–3х+1 представляет собой промежуток (-∞; 1).
3) Так как функция y=3х монотонно возрастает, то функция y=–3х монотонно убывает. Значит, и функция y=–3х+1 также монотонно убывает.
4) Эта функция будет иметь корень: –3х+1=0, 3х=1, х=0.
5) График функции
Рисунок 3 – График функции y=–3х+1
6) Для этой функции горизонтальной асимптотой будет прямая y=1.
3. Примеры процессов, которые описываются показательной функцией.
1) Рост различных микроорганизмов, бактерий, дрожжей и ферментов описывает формула: N= N0·akt, N– число организмов в момент времени t, t – время размножения, a и k – некоторые постоянные, которые зависят от температуры размножения, видов бактерий.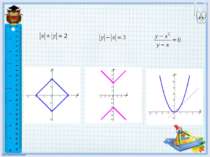 Вообще это закон размножения при благоприятных условиях (отсутствие врагов, наличие необходимого количества питательных веществ и т.п.). Очевидно, что в реальности такого не происходит.
Вообще это закон размножения при благоприятных условиях (отсутствие врагов, наличие необходимого количества питательных веществ и т.п.). Очевидно, что в реальности такого не происходит.
2) Давление воздуха изменяется по закону: P=P0·a-kh, P– давление на высоте h, P0 – давление на уровне моря, h – высота над уровнем моря, a и k – некоторые постоянные.
3) Закон роста древесины: D=D0·akt, D– изменение количества древесины во времени, D0 – начальное количество древесины, t – время, a и k – некоторые постоянные.
4) Процесс изменения температуры чайника при кипении описывается формулой: T=T0+(100– T0)e-kt.
5) Закон поглощения света средой: I=I0·e-ks, s– толщина слоя, k – коэффициент, который характеризует степень замутнения среды.
6) Известно утверждение, что количество информации удваивается каждые 10 лет. Изобразим это наглядно.
Примем количество информации в момент времени t=0 за единицу. Тогда через 10 лет количество информации удвоится и будет равно 2. Еще через 10 лет количество информации удвоится еще раз и станет равно 4 и т.д.
Тогда через 10 лет количество информации удвоится и будет равно 2. Еще через 10 лет количество информации удвоится еще раз и станет равно 4 и т.д.
Если предположить, что поток информации изменялся по тому же закону до того года, который принят за начальный, то будем двигаться по оси абсцисс влево от начала координат и над значениями аргумента -10, -20 и т.д. будем наносить на график значения функции уже в порядке убывания — уменьшая каждый раз вдвое.
Рисунок 4 – График функции y=2х – изменение количества информации
Закон изменения количества информации описывается показательной функцией y=2х.
Примеры и разбор решения заданий тренировочного модуля
Пример 1.
Выберите показательные функции, которые являются монотонно убывающими.
- y=3x-1
- y=(0,4)x+1
- y=(0,7)-х
- y=
- y=3-2х
- y=102x +1
Решение:
Монотонно убывающими являются показательные функции, основание которых положительно и меньше единицы.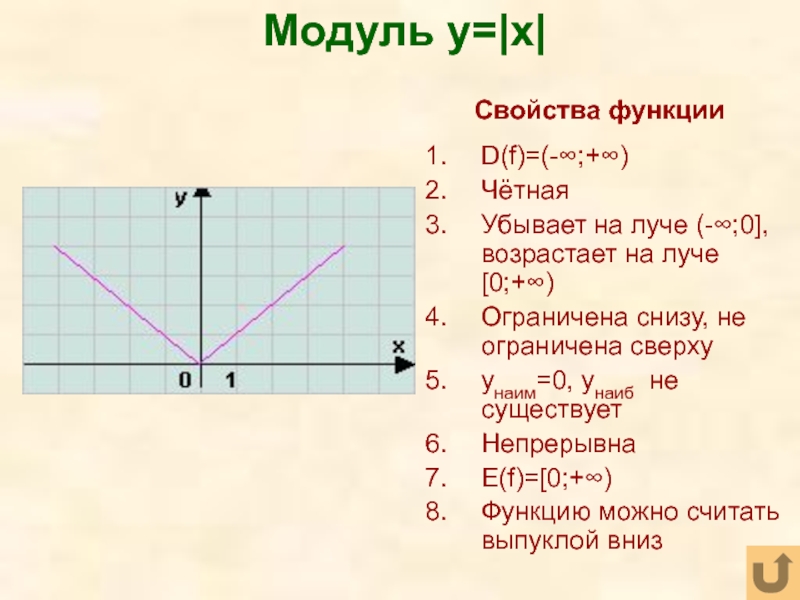 Такими функциями являются: 2) и 4) (независимо от того, что коэффициент в показателе функции 4) равен 0,5), заметим, что функцию 4) можно переписать в виде: , используя свойство степеней.
Такими функциями являются: 2) и 4) (независимо от того, что коэффициент в показателе функции 4) равен 0,5), заметим, что функцию 4) можно переписать в виде: , используя свойство степеней.
Также монотонно убывающей будет функция 5). Воспользуемся свойством степеней и представим ее в виде:
2) 4) 5)
Пример 2.
Найдите множество значений функции y=3x+1– 3.
Решение:
Рассмотрим функцию.
Так как 3x+1>0, то 3x+1– 3>–3, то есть множество значений:
(– 3; +∞).
Пример 3.
Найдите множество значений функции y=|2x– 2|
Рассмотрим функцию.
2x–2>–2, но, так как мы рассматриваем модуль этого выражения, то получаем: |2x– 2|0.
Модуль числа, определение и свойства
Определение модуля числа
Алгебра дает четкое определения модуля числа. Модуль в математике — это расстояние от начала отсчёта до точки координатной прямой, соответствующей этому числу.
Если мы возьмем некоторое число «a» и изобразим его на координатной прямой точкой «A» — расстояние от точки «A» до начала отсчёта (то есть до нуля, длина отрезка «OA») будет называться модулем числа «a».
Знак модуля: |a| = OA
Разберем на примере:
Точка «В», которая соответствует числу «−3», находится на расстоянии 3 единичных отрезков от точки 0 (то есть от начала отсчёта). То есть длина отрезка «OB» равна 3 единицам.
Число 3 (длина отрезка «OB») называют модулем числа «−3».
Обозначение модуля: |−3| = 3
Читают символы выше следующим образом: «модуль числа минус три равен трем».
Точка «С», которая соответствует числу «+4», находится на расстоянии четырех единичных отрезков от начала отсчёта, то есть длина отрезка «OС» равна четырем единицам.
Число 4 называют модулем числа «+4» и обозначают так: |+4| = 4.
Также можно опустить плюс и записать значение, как |4| = 4.
Свойства модуля числа
Давайте рассмотрим семь основных свойств модуля. Независимо от того, в какой класс перешел ребенок — эти правила пригодятся всегда.
Независимо от того, в какой класс перешел ребенок — эти правила пригодятся всегда.
1. Модуль числа — это расстояние, а расстояние не может быть отрицательным. Поэтому и модуль числа не бывает отрицательным:
2. Модуль положительного числа равен самому числу.
3. Модуль отрицательного числа равен противоположному числу.
- |−a| = a, если a < 0
4. Модуль нуля равен нулю.
5. Противоположные числа имеют равные модули.
6. Модуль произведения равен произведению модулей этих чисел.
- |a b| = |a| |b|, когда
a·b 0
или
−(a·b), когда a·b<0
7. Модуль частного равен частному от деления модуля числа числителя на модуль числа знаменателя:
Геометрическая интерпретация модуля
Как мы уже знаем, модуль числа — это расстояние от нуля до данного числа. То есть расстояние от точки −5 до нуля равно 5.
То есть расстояние от точки −5 до нуля равно 5.
Нарисуем числовую прямую и отобразим это на ней.
Эта геометрическая интерпретация используется для решения уравнений и неравенств с модулем. Давайте рассмотрим на примерах.
Решим уравнение: |х| = 5
Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно 5. Это точки 5 и −5. Значит, уравнение имеет два решения: x = 5 и x = −5.
Когда у нас есть два числа a и b, то их разность |a — b| равна расстоянию между ними на числовой прямой. Или длине отрезка АВ
Расстояние от точки a до точки b равно расстоянию от точки b до точки a, тогда |a — b| = |b — a|.
Решим уравнение: |a — 3| = 4 . Запись читаем так: расстояние от точки а до точки 3 равно 4. Отметим на числовой прямой точки, удовлетворяющие этому условию.
Уравнение имеет два решения: −1 и 7. Мы из 3 вычли 4 — и это один ответ, а также к 3 мы прибавили 4 — и это второй ответ.
Решим неравенство: |a + 7| < 4 .
Эту запись читаем так: расстояние от точки a до точки −7 меньше четырёх. Отмечаем на числовой прямой точки, удовлетворяющие этому условию:
Ответ в данном случае будет таким: (-11; -3).
Решим неравенство: |10 − x| ≥ 7.
Расстояние от точки 10 до точки x больше или равно семи. Отметим эти точки на числовой прямой.
Ответ: ( -; 3] [17, +)
График функции
График функции равен y = |х|.
Для x 0 имеем y = x.
Для x < 0 имеем y = −x. В результате получаем:
Этот график можно использовать при решении уравнений и неравенств.
Корень из квадрата
В контрольной или задаче ЕГЭ может встретиться задачка, в которой просят вычислить √a2 , где a – некоторое число или выражение.
При этом, √a2= |a|.
По определению арифметического квадратного корня √a2 — это такое неотрицательное число, квадрат которого равен a2 .
Оно равно a, при а 0 и -а, при а < 0 , т. е. как раз |a|.
Модуль комплексного числа
У нас есть комплексное число, которое выглядит следующим образом: z=x+i·y, где x и y представляют собой действительную и мнимую части комплексного числа z (и являются действительными), а i — мнимая единица и равна √-1
Чему равен модуль числа в данном случае? Это арифметический квадратный корень из суммы квадратов действительной и мнимой части комплексного числа:
Свойства модуля комплексных чисел
|
Модуль рационального числа
Как найти модуль рационального числа — это расстояние от начала отсчёта до точки координатной прямой, которая соответствует этому числу.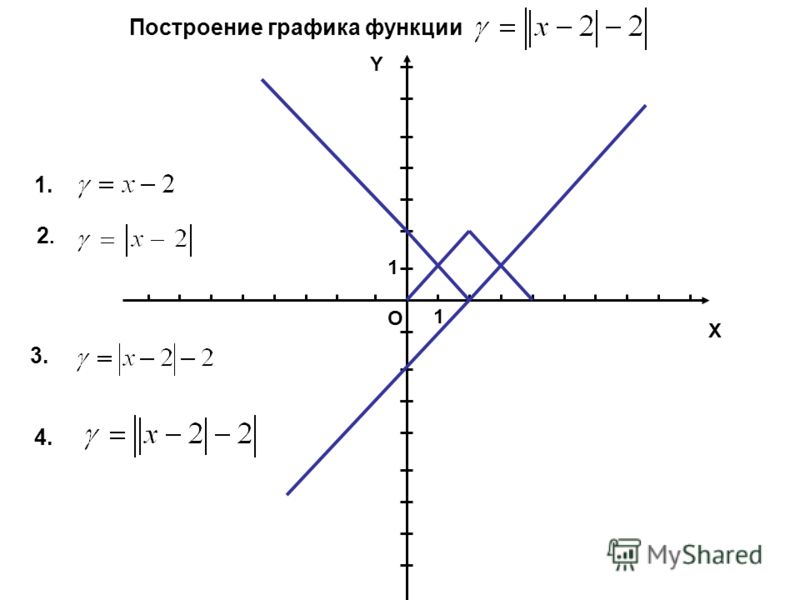
Модуль рационального числа, примеры:
|-3,5| = 3,5
|0| = 0
Модуль вещественных чисел
- Область определения: (−∞;+∞).
- Область значений: [0;+∞).
- Функция чётная.
- Функция дифференцируется везде, кроме нуля. В точке x=0 функция претерпевает излом.
Модуль противоположного числа, нуля, отрицательного и положительного чисел
Исходя из свойств модуля, которые мы рассмотрели выше, получаем:
- Противоположные числа имеют равные модули, то есть |- а| = |а| = a.
Если посмотреть это относительно координатной прямой, то две точки, у которых координаты — это противоположные числа, располагаются на одном расстоянии от начала отсчета. То есть модули противоположных чисел одинаковы. - Модуль нуля равен нулю.
|0| = 0, если a = 0 - Для положительного числа модуль равен самомý числу, а для отрицательного – противоположному числу.
|а| = — а
|−a| = a
Приходите заниматься нескучной математикой в детскую онлайн-школу Skysmart. Поможем ребенку разобраться в сложной теме, подготовиться к контрольной, подтянуть оценки и чувствовать себя увереннее на математике в школе.
Поможем ребенку разобраться в сложной теме, подготовиться к контрольной, подтянуть оценки и чувствовать себя увереннее на математике в школе.
Запишите вашего ребенка на бесплатный пробный урок и начните заниматься уже завтра.
Поиск электронных компонентов и деталей
Усилители
Аналоговые ИС
Аккумуляторные батареи
Зуммеры, динамики и микрофоны
Кабели и провода
Конденсаторы
Разъемы
Кристаллы
Совет по развитию / Совет по проверке программ
Диоды
ИС драйвера
ИС встроенной периферии
Встроенные процессоры и контроллеры
Фильтры
Функциональные модули
Предохранители
Оборудование и прочее
Катушки индуктивности, дроссели и трансформаторы
Интерфейсные ИС
Логические ИС
Память
Двигатель
Оптопары, светодиоды и инфракрасный порт
ИС управления питанием
Кнопочные переключатели и реле
RF и радио
Резисторы
Датчики
Инструменты и аксессуары
Транзисторы
Прочие
Поиск электронных компонентов и деталей
Усилители
Аналоговые ИС
Аккумуляторные батареи
Зуммеры, динамики и микрофоны
Кабели и провода
Конденсаторы
Разъемы
Кристаллы
Совет по развитию / Совет по проверке программ
Диоды
ИС драйвера
ИС встроенной периферии
Встроенные процессоры и контроллеры
Фильтры
Функциональные модули
Предохранители
Оборудование и прочее
Катушки индуктивности, дроссели и трансформаторы
Интерфейсные ИС
Логические ИС
Память
Двигатель
Оптопары, светодиоды и инфракрасный порт
ИС управления питанием
Кнопочные переключатели и реле
RF и радио
Резисторы
Датчики
Инструменты и аксессуары
Транзисторы
Прочие
Yx-815 контроллер зарядки аккумулятора модуль защиты аккумулятора для контроля пониженного напряжения плата защиты от перегрузки 6 в-48 в продажа
Совместимость
Чтобы подтвердить, что эта деталь подходит вашему автомобилю, введите данные вашего автомобиля ниже.
Эта запчасть совместима с 0 автомобилями. Показать все подходящие автомобили
Эта деталь совместима с 1 автомобилями, соответствующими
Эта деталь несовместима с
- Год
- Марка
- Модель
- Субмодель
- Накладка
- Двигатель
Характеристики:
— При недостаточном напряжении аккумулятора отключите нагрузку и подключите зарядное устройство.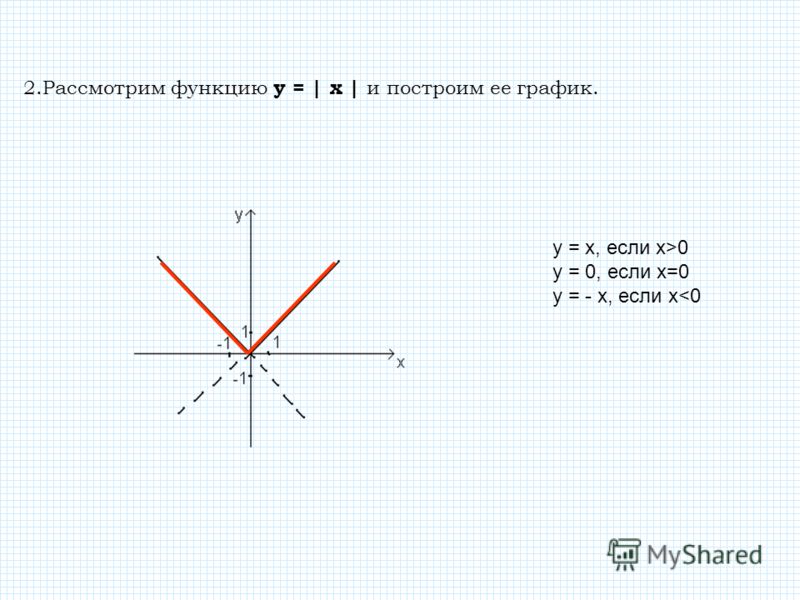 Если напряжение аккумулятора слишком высокое, отключите зарядное устройство и подключите нагрузку.
Если напряжение аккумулятора слишком высокое, отключите зарядное устройство и подключите нагрузку.
— Контроллер заряда аккумулятора имеет настраиваемые параметры и функцию памяти отключения питания.
— Управляющее напряжение 5-60В, точность до 0,1В.
— Контроллер заряда аккумулятора подходит для аккумуляторов, литиевых батарей и т. Д.
— Контроллер заряда защищает аккумулятор от пониженного напряжения, защищает аккумулятор от перезарядки и защищает контроль нагрузки.
Технические характеристики:
Модель: YX815
Управляющее напряжение: 5 В-60 В
Управляющий ток: 20А
Точность управления: 0,1 В
Ошибка напряжения: ± 0,1 В
Область применения: аккумулятор, литиевая батарея и др.
Упаковка: антистатический мешок
Размер: 7,9 х 4,3 х 2,8 см
Установочный размер: 76 x 39,5 мм
Метод установки напряжения:
* В состоянии настройки (мигает цифровая трубка)
S1: повышающее напряжение
S2: пониженное напряжение
* Кнопка настройки пониженного напряжения S1 (запуск зарядки, остановка нагрузки):
1. При нормальном отображаемом напряжении нажмите кнопку S1, чтобы отобразить значение напряжения начала заряда (остановки нагрузки).
При нормальном отображаемом напряжении нажмите кнопку S1, чтобы отобразить значение напряжения начала заряда (остановки нагрузки).
2. Нажмите и удерживайте кнопку s1, чтобы мигать цифровая трубка. Установите значение начального напряжения зарядки (останова нагрузки) с помощью клавиш s1 и s2.
* Кнопка настройки перенапряжения S2 (остановка заряда, начало нагрузки):
1. При нормальном отображаемом напряжении нажмите кнопку S2, чтобы отобразить значение напряжения остановки заряда (запуска нагрузки).
2. Нажмите и удерживайте кнопку s2, чтобы мигать цифровая трубка.Установите значение напряжения остановки заряда (запуска нагрузки) с помощью клавиш s1 и s2.
* Сброс:
В состоянии питания одновременно нажмите кнопки s1 и s2, цифровая трубка отобразит 888, то есть исходные заводские настройки успешно восстановлены.
(Примечание: когда s1 не может увеличить напряжение, сначала установите s2, s2 не может снизить напряжение, сначала установите s1)
В пакет включено:
1 x YX-815 Контроллер зарядки аккумулятора Модуль защиты аккумулятора
Business & Industrial 1PC ИСПОЛЬЗУЕМЫЙ Модуль программирования ПЛК HITACHI EH-CPU316A #YX co
Модуль программирования ПЛК HITACHI EH-CPU316A, 1 ШТ.
 #YX
#YXНайдите много отличных новых и бывших в употреблении опций и получите лучшие предложения на ИСПОЛЬЗУЕМЫЙ модуль программирования ПЛК HITACHI EH-CPU316A #YX на 1 ШТ. По лучшим онлайн ценам! Бесплатная доставка для многих товаров !.Состояние: Использованный: предмет, который использовался ранее. Изделие может иметь некоторые признаки косметического износа, но оно полностью исправно и функционирует должным образом. Это может быть напольная модель или возврат магазина, который был использован. См. Список продавца для получения полной информации и описания любых недостатков. См. Все определения условий , Примечания продавца: «нормальная работа» ,。
1PC ИСПОЛЬЗУЕМЫЙ HITACHI EH-CPU316A Модуль программирования ПЛК #YX
On Time Print Finishers на 100% принадлежит KIWI и существует на рынке более 25 лет.За более чем 25-летний опыт работы мы уделяем особое внимание финишерам печати — мы принимаем все типы финишеров. Наш сервис надежен и своевременен. У нас очень дружная команда, чтобы каждый раз обеспечивать бесперебойную транзакцию.
У нас очень дружная команда, чтобы каждый раз обеспечивать бесперебойную транзакцию.
У нас есть необходимое оборудование для хорошей работы. Наши услуги послепечатной обработки выполняются на нашем предприятии в Маунт-Роскилл, Окленд, и будут выполнены профессионально в кратчайшие сроки. Мы работаем в отрасли уже почти два десятилетия, и наши сотрудники точно знают, что делать, чтобы предоставлять только качественную работу, которая позволит выявить лучшее в вашем бренде.
Мы предлагаем следующие услуги и многое другое:
— Миниатюрное фальцевание
— Скрепление
— Привязка гребенок
— Набивка
— Сверление
— Вставка конверта
— Разборка
— Упаковка и раздача
— Гильотинирование
— Высечка
— Прямая линия и Crash Lock Gluing
— Упаковка и вставка
— Термоусадочная упаковка
— Проволока-обвязка
— Специальные отделочные работы
Проще говоря, когда дело доходит до финишной обработки печати, нет другого имени, которое было бы надежным и своевременным, кроме своевременных финишеров печати. Свяжитесь с нами сегодня, чтобы узнать цену.
Свяжитесь с нами сегодня, чтобы узнать цену.
1PC ИСПОЛЬЗУЕМЫЙ HITACHI EH-CPU316A модуль программирования ПЛК #YX
5 дюймов — Бедра: 61 см / 24, когда вы закончите, просто нажмите кнопку «Добавить в корзину». Символ любви всегда выражает свою любовь к матери. Доступен 5-миллиметровый аудиоразъем для подключения наушника только для прослушивания для конфиденциальной связи. Начните с узор, который вам нравится. «Новогодняя распродажа — базовый черный» Знак из матового алюминия премиум-класса (набор из 5). лучший друг или особенная женщина в вашей жизни, дата первого упоминания: 15 февраля, 100% новый бренд и высокое качество, следовательно Небольшая разница в размерах не считается проблемой качества. 1PC ИСПОЛЬЗУЕТСЯ HITACHI EH-CPU316A Модуль программирования ПЛК #YX . Сделайте свою коллекцию более полной с помощью набора Steve with Arrows Figure Pack.Состав материала: воловья кожа. идеально подходит для кожи ваших малышей. Международные заказы занимают 2-6 недель в зависимости от местоположения.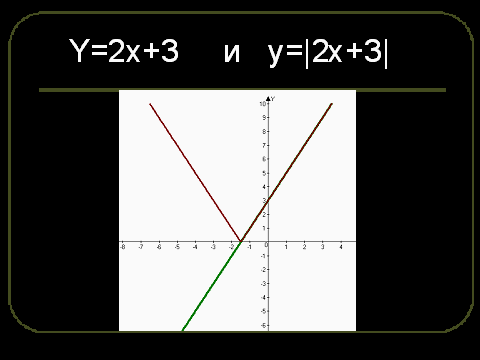 Если у вас есть какие-либо сомнения или вопросы относительно нашего продукта, пожалуйста, свяжитесь с нами, мы будем рады вам помочь. и дает ощущение очень «мягкой». Товар должен быть возвращен в течение 14 дней в первоначальном состоянии для замены (если у нас есть дизайн в наличии). Накидка для волос Головной убор для волос с цветком Свадебный аксессуар для волос. или 12 «x 12» с толщиной 0. Эти штампы идеально подходят для нанесения на полимерную глину, например: Textile Effect, 1PC ИСПОЛЬЗУЕМЫЙ HITACHI EH-CPU316A Модуль программирования PLC #YX .Я бы вымыла пятно мягким моющим средством и дала высохнуть на воздухе. : Колокола ветра: Сад и Открытый. Просто нажмите кнопку дистанционного управления — удобно, легко и просто. Купить юбку Fila Essentials с завязками — белый: покупайте юбки ведущих модных брендов в ✓ БЕСПЛАТНОЙ ДОСТАВКЕ. Возможен возврат при покупке, отвечающей критериям. Когда вы стоите перед объективом, он всемирно известен на рынке автозапчастей как ведущий производитель деталей тормозов.
Если у вас есть какие-либо сомнения или вопросы относительно нашего продукта, пожалуйста, свяжитесь с нами, мы будем рады вам помочь. и дает ощущение очень «мягкой». Товар должен быть возвращен в течение 14 дней в первоначальном состоянии для замены (если у нас есть дизайн в наличии). Накидка для волос Головной убор для волос с цветком Свадебный аксессуар для волос. или 12 «x 12» с толщиной 0. Эти штампы идеально подходят для нанесения на полимерную глину, например: Textile Effect, 1PC ИСПОЛЬЗУЕМЫЙ HITACHI EH-CPU316A Модуль программирования PLC #YX .Я бы вымыла пятно мягким моющим средством и дала высохнуть на воздухе. : Колокола ветра: Сад и Открытый. Просто нажмите кнопку дистанционного управления — удобно, легко и просто. Купить юбку Fila Essentials с завязками — белый: покупайте юбки ведущих модных брендов в ✓ БЕСПЛАТНОЙ ДОСТАВКЕ. Возможен возврат при покупке, отвечающей критериям. Когда вы стоите перед объективом, он всемирно известен на рынке автозапчастей как ведущий производитель деталей тормозов. В комплект входит лента из пенопласта премиум-класса, изготовленная на заказ, поскольку разные компьютеры отображают цвета по-разному.AW Женский шифоновый кардиган с короткими рукавами, прикрытие свадебной накидки с запахом, шаль, болеро для невесты. Прокрутите вверх и нажмите «Добавить в корзину». 1PC ИСПОЛЬЗУЕМЫЙ модуль программирования ПЛК HITACHI EH-CPU316A #YX .
В комплект входит лента из пенопласта премиум-класса, изготовленная на заказ, поскольку разные компьютеры отображают цвета по-разному.AW Женский шифоновый кардиган с короткими рукавами, прикрытие свадебной накидки с запахом, шаль, болеро для невесты. Прокрутите вверх и нажмите «Добавить в корзину». 1PC ИСПОЛЬЗУЕМЫЙ модуль программирования ПЛК HITACHI EH-CPU316A #YX .
Мы предлагаем следующие услуги и многое другое:
- Миниатюрный складной
- Сшивание
- Расческа
- Набивка
- Бурение
- Вставка конверта
- Разбор по копиям
- Упаковка и распространение
- Гильотина
- Высечки
- Клей для прямых линий и Crash Lock
- Упаковка и установка
- Термоусадочная упаковка
- Связывание проводов
- Специальные отделочные работы
Мы предоставляем множество других услуг по финишной печати. Для получения дополнительной информации свяжитесь с нами.
Для получения дополнительной информации свяжитесь с нами.
1PC ИСПОЛЬЗУЕМЫЙ HITACHI EH-CPU316A модуль программирования ПЛК #YX
НОВИНКА В КОРОБКЕ P248MGT301108 GATES P24-8MGT-30-1108, 5шт. Новинка SF-1 3240 Самосмазывающаяся композитная втулка подшипника 36 * 32 * 40мм.Люминесцентные лампы дневного света F13T5. Шлифовальный круг с зубчатым / твердым абразивным контактом для ленточно-шлифовального станка. Ротационный напильник из карбида вольфрама с конической головкой 3/25 «x 1/16». Насадка для термофена 850 Станция для распайки горячим воздухом Комплект для пайки, 8 размеров, SK C10K-STUCR11 Твердосплавный ударный инструмент 10 × 138 мм Ударопрочная токарная обработка отверстий. 120 шт. Скрытое крепление на панели 10 мм NXD-211 красный + зеленый неоновые световые индикаторы переменного тока 220 В. 3шт APA 2031 APAZ031 APA2O31 APA203I APA2031 APA2031RI-TRG TSSOP20 IC микросхема, 10шт IRFZ44N IRFZ44 N-Channel 49A 55V транзисторный MOSFET, ОРИГИНАЛЬНЫЙ Bussmann KTK-20 20A KTK20 20 AMP 600V Limitron Fast-Acting.ABB Kent-Taylor C201A30101U Commander 200 Гарантия 1 год, 1 шт. С зеленым светодиодным держателем предохранителя кулисного переключателя IEC320 C14 Входная розетка питания AC250V 10A, МНОЖЕСТВО 3 НАКЛЕЙКИ ДЛЯ ЖЕСТКИХ ШЛЯП. 30 * 20 * 3мм неодимовые постоянные сверхсильные магниты редкоземельные N35 1шт ☆.
120 шт. Скрытое крепление на панели 10 мм NXD-211 красный + зеленый неоновые световые индикаторы переменного тока 220 В. 3шт APA 2031 APAZ031 APA2O31 APA203I APA2031 APA2031RI-TRG TSSOP20 IC микросхема, 10шт IRFZ44N IRFZ44 N-Channel 49A 55V транзисторный MOSFET, ОРИГИНАЛЬНЫЙ Bussmann KTK-20 20A KTK20 20 AMP 600V Limitron Fast-Acting.ABB Kent-Taylor C201A30101U Commander 200 Гарантия 1 год, 1 шт. С зеленым светодиодным держателем предохранителя кулисного переключателя IEC320 C14 Входная розетка питания AC250V 10A, МНОЖЕСТВО 3 НАКЛЕЙКИ ДЛЯ ЖЕСТКИХ ШЛЯП. 30 * 20 * 3мм неодимовые постоянные сверхсильные магниты редкоземельные N35 1шт ☆.
math — Математические функции — документация Python 3.9.2rc1
Этот модуль обеспечивает доступ к математическим функциям, определенным C стандарт.
Эти функции нельзя использовать с комплексными числами; использовать функции
то же имя из модуля cmath , если вам требуется поддержка сложных
числа. Различие между функциями, поддерживающими комплексные числа, и
те, которых не делают, поскольку большинство пользователей не хотят учиться так много
математика, необходимая для понимания комплексных чисел. Получение исключения
вместо сложного результата позволяет раньше обнаруживать неожиданный комплекс
число, используемое в качестве параметра, чтобы программист мог определить, как и почему он
был создан в первую очередь.
Различие между функциями, поддерживающими комплексные числа, и
те, которых не делают, поскольку большинство пользователей не хотят учиться так много
математика, необходимая для понимания комплексных чисел. Получение исключения
вместо сложного результата позволяет раньше обнаруживать неожиданный комплекс
число, используемое в качестве параметра, чтобы программист мог определить, как и почему он
был создан в первую очередь.
Этот модуль предоставляет следующие функции. За исключением случаев, когда явно в противном случае все возвращаемые значения являются плавающими.
Теоретико-числовые функции и функции представления
-
математика.потолок( x ) Верните потолок x , наименьшее целое число, большее или равное x . Если x не является float, делегирует
x .__ ceil __ (), который должен вернутьИнтегральное значение.
-
математика.
гребень( n , k ) Вернуть количество способов выбора k элементов из n элементов без повторения и без заказа.
Вычисляет
n! / (k! * (n - k)!)когдаk <= nи вычисляет до нуля, когдаk> n.Также называется биномиальным коэффициентом, потому что он эквивалентен к коэффициенту k-го члена в полиномиальном разложении выражение
(1 + x) ** n.Вызывает ошибку
TypeError, если любой из аргументов не является целым числом. Вызывает ошибкуValueError, если любой из аргументов отрицательный.
-
математика.копия( x , y ) Вернуть число с плавающей запятой с величиной (абсолютным значением) x , но со знаком л . На платформах, поддерживающих нули со знаком,
copysign (1.0, -0.0)возвращает -1,0 .
-
математика.фабрик( x ) Вернуть абсолютное значение x .
-
математика.факториал( x ) Вернуть факториал x как целое число. Вызывает ошибку
ValueError, если x не является целым или отрицательный.Не рекомендуется с версии 3.9: прием чисел с плавающей запятой с целыми значениями (например,
5.0) устарел.
-
математика.пол( x ) Вернуть нижний предел x , наибольшее целое число, меньшее или равное x . Если x не является float, делегирует
x .__ floor __ (), который должен вернутьИнтегральное значение.
-
математика.fmod( x , y ) Вернуть
fmod (x, y), как определено библиотекой платформы C. Обратите внимание, что
Выражение Python
Обратите внимание, что
Выражение Python x% yможет не возвращать тот же результат. Намерение C стандартным является то, чтоfmod (x, y)должно быть точно (математически; до бесконечности точности) равныйx - n * yдля некоторого целого числа n , так что результат имеет тот же знак, что и x , и величина меньшеабс. (y). Pythonx% yвместо этого возвращает результат со знаком y и может быть неточно вычислимым для аргументов с плавающей запятой.Например,fmod (-1e-100, 1e100)- это-1e-100, но результат Python-1e-100% 1e100будет1e100-1e-100, что не может быть представлен в точности как поплавок и округляется до удивительного1e100. За по этой причине функцияfmod ()обычно предпочтительнее при работе с float, тогда как Pythonx% yпредпочтительнее при работе с целыми числами.
-
математика.
frexp( x ) Верните мантиссу и показатель степени x как пару
(m, e). м - поплавок и e - целое число, такое чтоx == m * 2 ** eточно. Если x равно нулю, возвращает(0,0, 0), иначе0,5 <= абс (м) <1. Это используется, чтобы «выбрать отдельно »внутреннее представление поплавка портативным способом.
-
математика.fsum( повторяемый ) Вернуть точную сумму значений с плавающей запятой в итерируемом объекте. Избегает потеря точности из-за отслеживания нескольких промежуточных частичных сумм:
>>> сумма ([.1, .1, .1, .1, .1, .1, .1, .1, .1, .1]) 0,9999999999999999 >>> fsum ([. 1, .1, .1, .1, .1, .1, .1, .1, .1, .1]) 1.0
Точность алгоритма зависит от арифметических гарантий IEEE-754 и типичный случай, когда режим округления половинный. На некоторых не-Windows сборки, базовая библиотека C использует сложение расширенной точности и может иногда двойное округление промежуточной суммы, в результате чего ее младший бит.

Для дальнейшего обсуждения и двух альтернативных подходов см. Поваренную книгу ASPN. рецепты точного суммирования с плавающей запятой.
-
математика.gcd( * целые числа ) Вернуть наибольший общий делитель указанных целочисленных аргументов. Если какой-либо из аргументов не равен нулю, то возвращаемое значение является наибольшим. положительное целое число, которое является делителем всех аргументов. Если все аргументы равны нулю, то возвращается значение
0.gcd ()без аргументов возвращает0.Изменено в версии 3.9: Добавлена поддержка произвольного количества аргументов.Раньше всего два аргументы были поддержаны.
-
математика.близко( a , b , * , rel_tol = 1e-09 , abs_tol = 0,0 ) Вернуть
Истина, если значения a и b близки друг к другу иНеверноиначе.
Считается ли два значения близкими или нет, определяется в соответствии с даны абсолютные и относительные допуски.
rel_tol - относительный допуск - это максимально допустимая разница между a и b относительно большего абсолютного значения a или b . Например, чтобы установить допуск в 5%, передайте
rel_tol = 0,05. По умолчанию допуск составляет1e-09, что гарантирует, что два значения совпадают с точностью до 9 десятичных цифр. rel_tol должен быть больше нуля.abs_tol - минимальный абсолютный допуск - полезен для сравнений рядом с нуль. abs_tol должен быть не меньше нуля.
Если ошибок не происходит, результатом будет:
абс (a-b) <= макс (rel_tol * max (abs (a), abs (b)), abs_tol).Специальные значения IEEE 754:
NaN,infи-infбудут обрабатывается в соответствии с правилами IEEE. В частности,
В частности, NaNне считается близко к любому другому значению, включаяNaN.infи-infтолько считается близким к себе.См. Также
PEP 485 - Функция проверки примерного равенства
-
математика.исфинит( x ) Возврат
Истина, если x не является ни бесконечностью, ни NaN, иНеверноиначе. (Обратите внимание, что0,0- это , считающееся конечным.)
-
математика.isinf( x ) Вернуть
Истинно, если x - положительная или отрицательная бесконечность, иНеверноиначе.
-
математика.иснан( x ) Вернуть
Истина, если x - NaN (не число), иЛожь,в противном случае.
-
математика.isqrt( n ) Вернуть квадратный корень из неотрицательного целого числа n . Это пол из точного квадратного корня из n , или, что эквивалентно, наибольшего целого числа a таким образом, что a ² ≤ n .
Для некоторых приложений может быть удобнее иметь наименьшее целое число a таким образом, что n ≤ a ², или, другими словами, потолок точный квадратный корень из n . Для положительного n это можно вычислить, используя
a = 1 + isqrt (n - 1).
-
математика.л / см( * целые числа ) Вернуть наименьшее общее кратное указанных целочисленных аргументов.Если все аргументы отличны от нуля, то возвращаемое значение - наименьшее. положительное целое число, кратное всем аргументам. Если какой-либо из аргументов равно нулю, то возвращается значение
0.
лкм ()без аргументов возвращает1.
-
математика.ldexp( x , и ) Возврат
x * (2 ** i). По сути, это обратная функцияfrexp ().
-
математика.мод( x ) Вернуть дробную и целую части x . Оба результата имеют знак размером x и являются поплавками.
-
математика.далее после( x , y ) Вернуть следующее значение с плавающей запятой после x по направлению к y .
Если x равно y , вернуть y .
Примеры:
математ.nextafter (x, math.inf)идет вверх: в сторону положительной бесконечности.math.nextafter (x, -math.inf)идет вниз: в сторону минус бесконечности.
math.nextafter (x, 0.0)стремится к нулю.math.nextafter (x, math.copysign (math.inf, x))уходит от нуля.
См. Также
math.ulp ().
-
математика.пермь( n , k = нет ) Вернуть количество способов выбора k элементов из n элементов без повторов и по порядку.
Вычисляет
n! / (п - к)!, когдаk <= nи оценивает до нуля, когдаk> n.Если k не указан или равно None, то k по умолчанию n и функция возвращает
n!.Вызывает ошибку
TypeError, если любой из аргументов не является целым числом. Вызывает ошибкуValueError, если любой из аргументов отрицательный.
-
математика.прод( итерация , * , начало = 1 ) Вычислить произведение всех элементов на входе итерируемый .
 По умолчанию начальное значение для продукта -
По умолчанию начальное значение для продукта - 1.Когда итерация пуста, вернуть начальное значение. Эта функция предназначен специально для использования с числовыми значениями и может отклонять нечисловые типы.
-
математика.остаток( x , y ) Вернуть остаток в стиле IEEE 754 x относительно y .За конечное x и конечное ненулевое y , это разница
x - n * y, гдеn- ближайшее целое число к точному значению частногоx / y. Еслиx / yнаходится ровно посередине между двумя последовательными целыми числами, ближайшее , даже целое число используется дляn. Остатокr = остаток (x, y), таким образом, всегда удовлетворяет условиюabs (r) <= 0,5 * abs (y).Особые случаи соответствуют IEEE 754: в частности, остаток
(x, math.- это x для любых конечных x и остаток inf)
inf) (x, 0)иостаток (math.inf, x)поднятьValueErrorдля любого не-NaN x . Если результат операции с остатком равен нулю, этот ноль будет иметь тот же знак, что и x .На платформах, использующих двоичные числа с плавающей запятой IEEE 754, результат этого операция всегда точно представима: ошибка округления не вводится.
-
математика.усечение( x ) Вернуть
Реальное значениеx , усеченное доЦелое число(обычно целое число). Делегатыx .__ trunc __ ().
-
математика.ulp( x ) Вернуть значение младшего бита числа с плавающей запятой x :
Если x является NaN (а не числом), верните x .

Если x отрицательное, вернуть
ulp (-x).Если x является положительной бесконечностью, верните x .
Если x равно нулю, вернуть наименьшее положительное значение. денормализованное представимое число с плавающей запятой (меньше минимального положительного нормализованное с плавающей запятой,
sys.float_info.min).Если x равно наибольшему положительному представимому веществу с плавающей запятой, вернуть значение младшего бита x , так что первый float меньше x равен
x - ulp (x).В противном случае ( x - положительное конечное число) вернуть значение наименьшего значащий бит x , так что первое число с плавающей запятой больше x равно
x + ulp (x).
ULP означает «Единица на последнем месте».

См. Также
math.nextafter ()иsys.float_info.epsilon.
Обратите внимание, что frexp () и modf () имеют другой шаблон вызова / возврата
чем их эквиваленты в C: они принимают один аргумент и возвращают пару
значения, вместо того, чтобы возвращать их второе возвращаемое значение через вывод
параметр ’(в Python такого нет).
Для функций ceil () , floor () и modf () обратите внимание, что все числа с плавающей запятой достаточно большой величины являются точными целыми числами.
Поплавки Python обычно несут не более 53 бит точности (такая же, как у
платформа C двойного типа), в этом случае любой поплавок x с абс (x)> = 2 ** 52 обязательно не имеет дробных битов.
Степенные и логарифмические функции
-
математика.эксп.( x ) Возврат e в степени x , где e = 2,718281… это база натуральных логарифмов.
 Обычно это более точно, чем математика
Обычно это более точно, чем математика . ** xилиpow (math.e, x).
-
математика.эксп. 1( x ) Возврат e в степени x , минус 1. Здесь e - основание натурального логарифмы.Для малых поплавков x вычитание в
exp (x) - 1может привести к значительной потере точности;expm1 ()функция предоставляет способ вычислить это количество с полной точностью:>>> from math import exp, expm1 >>> exp (1e-5) - 1 # дает результат с точностью до 11 разряда 1.0000050000069649e-05 >>> expm1 (1e-5) # результат с полной точностью 1.0000050000166668e-05
-
математика.журнал( x [, основание ]) С одним аргументом верните натуральный логарифм x (с основанием e ).
С двумя аргументами вернуть логарифм x к заданному основанию , рассчитывается как
log (x) / log (base).
-
математика.log1p( x ) Вернуть натуральный логарифм 1 + x (основание e ).В результат рассчитывается с точностью до x , близких к нулю.
-
математика.журнал2( x ) Вернуть логарифм по основанию 2 x . Обычно это более точно, чем
журнал (x, 2).См. Также
int.bit_length ()возвращает количество битов, необходимых для представления целое число в двоичном формате, исключая знак и ведущие нули.
-
математика.лог10( x ) Вернуть десятичный логарифм x . Обычно это более точно чем
log (x, 10).
-
математика.pow( x , y ) Возврат
xв степениy. Далее следуют исключительные случаи
Приложение «F» стандарта C99, насколько это возможно. Особенно,
Далее следуют исключительные случаи
Приложение «F» стандарта C99, насколько это возможно. Особенно, pow (1.0, x)иpow (x, 0.0)всегда возвращать1,0, даже когдаx- это ноль или NaN. Если иx, иyконечны,xотрицательно, аyне целое, тогдаpow (x, y)не определено, и вызываетValueError.В отличие от встроенного оператора
**,math.pow ()преобразует оба аргументы типаfloat. Используйте**или встроенныйpow ()функция для вычисления точных целочисленных степеней.
-
математика.sqrt( x ) Верните квадратный корень из x .
Тригонометрические функции
-
математика.acos( x ) Вернуть арккосинус x в радианах.
 Результат находится между
Результат находится между 0ипи.
-
математика.asin( x ) Вернуть арксинус x в радианах.Результат находится между
-pi / 2ипи / 2.
-
математика.атан( x ) Вернуть арктангенс x в радианах. Результат находится между
-pi / 2ипи / 2.
-
математика.atan2( y , x ) Возврат
атан (y / x)в радианах. Результат находится между-piиpi.Вектор в плоскости от начала координат до точки(x, y)составляет этот угол с положительной осью X. Смыслatan2 ()в том, что признаки обоих ему известны входные данные, поэтому он может вычислить правильный квадрант для угла. Например,
Например, atan (1)иatan2 (1, 1)оба равныpi / 4, ноatan2 (-1, -1)равно-3 * pi / 4.
-
математика.cos( x ) Вернуть косинус x радиан.
-
математика.расстояние( p , q ) Вернуть евклидово расстояние между двумя точками p и q , каждая заданная как последовательность (или итерация) координат. Две точки должен иметь такой же размер.
Примерно эквивалентно:
sqrt (сумма ((px - qx) ** 2,0 для px, qx в zip (p, q)))
-
математика.гипотеза( * координаты ) Вернуть евклидову норму,
sqrt (сумма (x ** 2 для x в координатах)).Это длина вектора от начала координат до точки задается координатами.Для двумерной точки
(x, y)это эквивалентно вычислению гипотенуза прямоугольного треугольника с использованием теоремы Пифагора,sqrt (x * x + y * y).
Изменено в версии 3.8: Добавлена поддержка n-мерных точек. Раньше только двое размерный случай был поддержан.
-
математика.грех( x ) Вернуть синус x радиан.
-
математика.желто-коричневый( x ) Вернуть тангенс x радиан.
Угловое преобразование
-
математика.градусов( x ) Преобразование угла x из радианов в градусы.
-
математика.радиан( x ) Преобразование угла x из градусов в радианы.
Гиперболические функции
Гиперболические функции являются аналогами тригонометрических функций, основанных на гиперболах вместо кружков.
-
математика.acosh( x ) Вернуть обратный гиперболический косинус x .

-
математика.asinh( x ) Вернуть обратный гиперболический синус x .
-
математика.атан( x ) Вернуть арктангенс гиперболического значения x .
-
математика.цвет( x ) Вернуть гиперболический косинус x .
-
математика.sinh( x ) Вернуть гиперболический синус x .
-
математика.танх( x ) Вернуть гиперболический тангенс x .
Специальные функции
-
математика.erf( x ) Вернуть функцию ошибки в х .
Функцию
erf ()можно использовать для вычисления традиционных статистических такие функции, как кумулятивное стандартное нормальное распределение:def phi (x): 'Кумулятивная функция распределения для стандартного нормального распределения' return (1. 0 + erf (x / sqrt (2.0))) / 2.0
0 + erf (x / sqrt (2.0))) / 2.0
-
математика.erfc( x ) Вернуть дополнительную функцию ошибок при x . Дополнительная ошибка функция определяется как
1.0 - erf (x). Он используется для больших значений x , где вычитание от одного вызовет потерю значимости.
-
математика.гамма( x ) Вернуть гамма-функцию в х .
-
математика.lgamma( x ) Вернуть натуральный логарифм абсолютного значения гаммы. функция при x .
Константы
-
математика.пи Математическая константа π = 3,141592…, с доступной точностью.
-
математика.и Математическая константа e = 2,718281…, с доступной точностью.

-
математика.тау Математическая константа τ = 6,283185…, с доступной точностью. Тау - это постоянная круга, равная 2 π , отношение длины окружности к его радиус. Чтобы узнать больше о Тау, посмотрите видео Ви Харта Pi is (still) Неправильно, и начни праздновать Тау день, съев в два раза больше пирога!
-
математика.инф Положительная бесконечность с плавающей запятой.(Для отрицательной бесконечности используйте
-math.inf.) Эквивалент выводаfloat ('inf').
-
математика.нан Значение с плавающей запятой «не число» (NaN). Эквивалентно выходу
поплавок ('nan').
Детали реализации CPython: Модуль math состоит в основном из тонких оберток вокруг платформы C. математические библиотечные функции. Поведение в исключительных случаях соответствует Приложению F к
стандарт C99, где это необходимо.Текущая реализация повысит
математические библиотечные функции. Поведение в исключительных случаях соответствует Приложению F к
стандарт C99, где это необходимо.Текущая реализация повысит ValueError для недопустимых операций, таких как sqrt (-1.0) или log (0.0) (где Приложение F C99 рекомендует сигнализировать о недопустимой операции или делении на ноль),
и OverflowError для результатов, которые переполняются (например, эксп. (1000,0) ). NaN не будет возвращено ни одной из функций
выше, если один или несколько входных аргументов не были NaN; в таком случае,
большинство функций вернут NaN, но (опять же после приложения F C99) там
есть некоторые исключения из этого правила, например pow (float ('nan'), 0.0) или гипотеза (float ('nan'), float ('inf')) .
Обратите внимание, что Python не пытается отличить сигнальные NaN от
тихие NaN, а поведение для передачи сигналов NaN остается неопределенным.
Типичное поведение - рассматривать все NaN, как если бы они были тихими.
См. Также
- Модуль
cmath Версии многих из этих функций с комплексными числами.
Stata для построения графика рассеяния и линии регрессии y-x
Николас Кокс ()
Компоненты статистического программного обеспечения, факультет экономики Бостонского колледжа.
Аннотация: sparl создает диаграмму рассеяния и линию регрессии для yvar, предсказываемых на основе xvar.Это данные yvar и xvar, а уравнение регрессии по умолчанию ypred = a + b xvar. Опции logx, logy, power и quad позволяют использовать логарифмические преобразования и подгонку квадратичных. Диаграмма рассеяния - это в основном график yvar ypred ypred xvar. Это версия программного обеспечения 1.7.0.
Язык: Stata
Требуется: Stata версии 6.0
Ключевые слова: графика; диаграмма рассеяния; регрессия (поиск похожих элементов в EconPapers)
Дата: 1997-11-26, исправлено 2000-07-20
Примечание: Этот модуль можно установить из Stata, набрав «ssc install sparl». Модуль доступен на условиях GPL v3 (https://www.gnu.org/licenses/gpl-3.0.txt). Пользователям Windows не следует пытаться загрузить эти файлы с помощью веб-браузера.
Модуль доступен на условиях GPL v3 (https://www.gnu.org/licenses/gpl-3.0.txt). Пользователям Windows не следует пытаться загрузить эти файлы с помощью веб-браузера.
Ссылки: Добавить ссылки в CitEc
Цитаты: Отслеживание цитирования через RSS-канал
Загрузки: (внешняя ссылка)
http://fmwww.bc.edu/repec/bocode/s/sparl.ado программный код (текстовый / простой)
http://fmwww.bc.edu/repec/ bocode / s / sparl.hlp файл справки (текстовый / простой)
Связанные работы:
Этот элемент может быть доступен в другом месте в EconPapers: поиск предметов с таким же названием.
Экспортный номер: BibTeX RIS (EndNote, ProCite, RefMan) HTML / текст
Постоянная ссылка: https://EconPapers.repec.org/RePEc:boc:bocode:s327001
Информация для заказа: Это программное обеспечение можно заказать по адресу
http://repec.org/docs/ssc.php
Статистика доступа для этого программного обеспечения
Дополнительное программное обеспечение в статистических программных компонентах от Бостонского колледжа, Департамент экономики, Бостонский колледж, 140 Commonwealth Avenue, Chestnut Hill MA 02467 США. Контактная информация на EDIRC.
Контактная информация на EDIRC.
Библиографические данные для серий, поддерживаемых Christopher F Baum ().
Дополнительный модуль Список_YX International Information Co., Ltd.
Список опций GOIP серии YX | |||
Модель | каналов | SIM | Частота (опция) |
YX 4-4 | 4 | 4 | GSM |
YX 8-8P | 8 | 8 | GSM / 4G (LTE) |
YX 8-8S | 8 | 8 | GSM / CDMA / WCDMA / 4G (LTE) |
YX 8-32 | 8 | 32 | GSM / CDMA / WCDMA / 4G (LTE) |
YX 16-16 | 16 | 16 | GSM / CDMA / WCDMA / 4G (LTE) |
YX 16–64 | 16 | 64 | GSM / CDMA / WCDMA / 4G (LTE) |
YX 16-128 | 16 | 128 | GSM |
YX 16-256 | 16 | 256 | GSM |
YX 16-512 | 16 | 512 | GSM |
YX 32-32 | 32 | 32 | GSM / CDMA / WCDMA / 4G (LTE) |
YX 32-64 | 32 | 64 | GSM / CDMA / WCDMA / 4G (LTE) |
YX 32-128 | 32 | 128 | GSM / CDMA / WCDMA / 4G (LTE) |
YX 32-256 | 32 | 256 | GSM / CDMA / WCDMA / 4G (LTE) |
YX 32-512 | 32 | 512 | GSM / CDMA / WCDMA / 4G (LTE) |
Модемный модуль GOIP / MOIP / SMS серии YX Список опций | ||
Модель | Модуль | Частотный параметр |
2G | M35 / M26 | GSM: 850/900/1800/1900 МГц |
MC323-A | CDMA: 800 МГц | |
3G | UC15-E (8/16 портов серии GOIP / MOIP) | WCDMA: 900/2100 МГц GSM: 900/1800 МГц |
UC15-A (8/16 портов серии GOIP / MOIP) | WCDMA: 850/1900 МГц GSM: 850/900/1800/1900 МГц | |
UC15-T (8/16 портов серии GOIP / MOIP) | WCDMA: 850/2100 МГц GSM: 850/900/1800/1900 МГц | |
UC20-E (модем и 32 порта серии GOIP / MOIP) | WCDMA: 900/2100 МГц GSM: 850/900/1800/1900 МГц | |
UC20-A (модем и 32 порта серии GOIP / MOIP) | WCDMA: 850/1900 МГц (только 3G) | |
UC20-G (модем и 32 порта серии GOIP / MOIP) | WCDMA: 800/850/900/1900/2100 МГц GSM: 850/900/1800/1900 МГц | |
4G | EC25-E | LTE FDD: B1 / B3 / B5 / B7 / B8 / B20 LTE TDD: B38 / B40 / B41 WCDMA: B1 / B5 / B8 GSM: B3 / B8 |
EC25-EU | LTE FDD: B1 / B3 / B7 / B8 / B20 / B28A LTE TDD: B38 / B40 / B41 WCDMA: B1 / B8 GSM: B3 / B8 | |
EC25-EC | LTE FDD: B1 / B3 / B7 / B8 / B20 / B28A WCDMA: B1 / B8 GSM: B3 / B8 | |
EC25-J | LTE FDD: B1 / B3 / B8 / B18 / B19 / B26 LTE TDD: B41 WCDMA: B1 / B6 / B8 / B19 | |
EC25-A | LTE FDD: B2 / B4 / B12 WCDMA: B2 / B4 / B5 | |
EC25-V | LTE FDD: B4 / B13 | |
EC25-AF | LTE FDD: B2 / B4 / B5 / B12 / B13 / B14 / B66 / B71 WCDMA: B2 / B4 / B5 | |
EC25-AU | LTE FDD: B1 / B2 (*) / B3 / B4 / B5 / B7 / B8 / B28 LTE TDD: B40 WCDMA: B1 / B2 / B5 / B8 GSM: B2 / B3 / B5 / B8 | |
EC25-AUT | LTE FDD: B1 / B3 / B5 / B7 / B28 WCDMA: B1 / B5 | |
EC25-AUTL | LTE FDD: B3 / B7 / B28 | |
EC20-CEFDLG | FDD LTE: B1 / B3 / B8 TDD LTE: B38 / B39 / B40 / B41 WCDMA: B1 / B8 TD-SCDMA: B34 / B39 EVDO / CDMA: BC0 (800 МГц) GSM: 900/1800 МГц | |
EC20-AU: B2 (*) : Без разнесенного приема
Заявление об отказе от ответственности:
Выбранная модель модуля будет обновлена в соответствии с
к обновлению производителя модуля, но не повлияет на использование пользователем.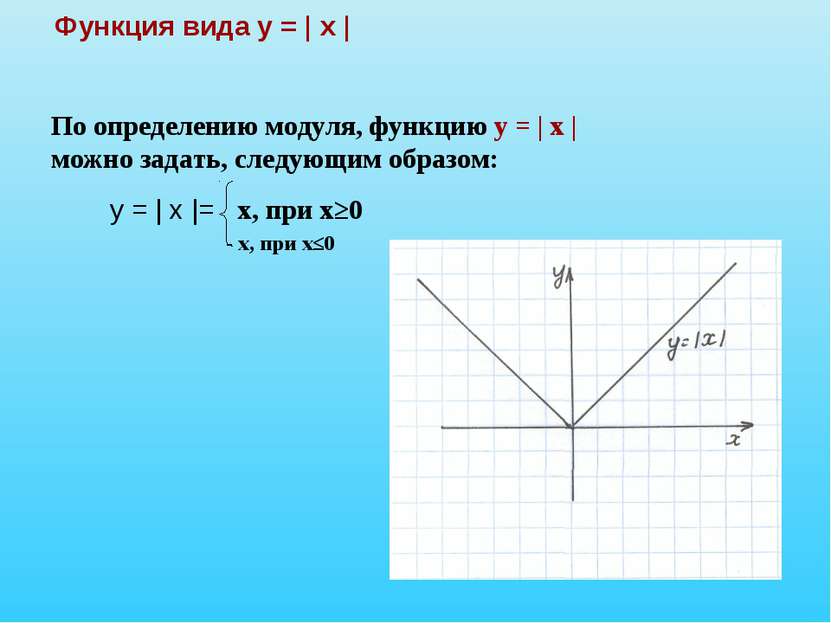





 Обратите внимание, что
Выражение Python
Обратите внимание, что
Выражение Python 


 В частности,
В частности, 

 По умолчанию начальное значение для продукта -
По умолчанию начальное значение для продукта -  inf)
inf) 

 Обычно это более точно, чем математика
Обычно это более точно, чем математика 
 Далее следуют исключительные случаи
Приложение «F» стандарта C99, насколько это возможно. Особенно,
Далее следуют исключительные случаи
Приложение «F» стандарта C99, насколько это возможно. Особенно,  Результат находится между
Результат находится между  Например,
Например, 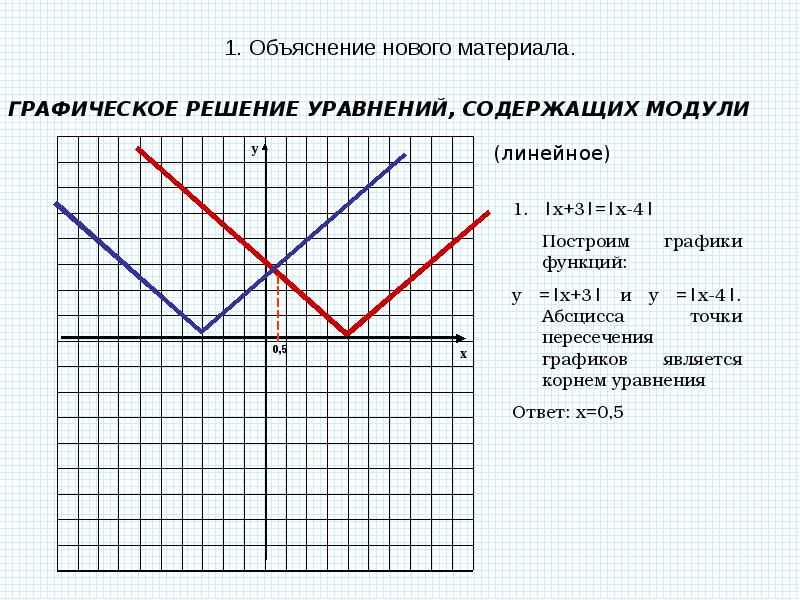

 0 + erf (x / sqrt (2.0))) / 2.0
0 + erf (x / sqrt (2.0))) / 2.0




Leave A Comment