Трапеция
\[{\Large{\text{Произвольная трапеция}}}\]
Определения
Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны трапеции называются её основаниями, а две другие стороны – боковыми сторонами.
Высота трапеции – это перпендикуляр, опущенный из любой точки одного основания к другому основанию.
Теоремы: свойства трапеции
1) Сумма углов при боковой стороне равна \(180^\circ\).
2) Диагонали делят трапецию на четыре треугольника, два из которых подобны, а два другие – равновелики.

Доказательство
1) Т.к. \(AD\parallel BC\), то углы \(\angle BAD\) и \(\angle ABC\) – односторонние при этих прямых и секущей \(AB\), следовательно, \(\angle BAD +\angle ABC=180^\circ\).
2) Т.к. \(AD\parallel BC\) и \(BD\) – секущая, то \(\angle DBC=\angle
BDA\) как накрест лежащие.
Также \(\angle BOC=\angle AOD\) как вертикальные.
Следовательно, по двум углам \(\triangle BOC \sim \triangle AOD\).
Докажем, что \(S_{\triangle AOB}=S_{\triangle COD}\). Пусть \(h\) – высота трапеции. Тогда \(S_{\triangle ABD}=\frac12\cdot h\cdot AD=S_{\triangle ACD}\). Тогда: \[S_{\triangle AOB}=S_{\triangle ABD}-S_{\triangle AOD}=S_{\triangle ACD}-S_{\triangle AOD}=S_{\triangle COD}\]
Определение
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Теорема
Средняя линия трапеции параллельна основаниям и равна их полусумме.

Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем параллельность.

Проведем через точку \(M\) прямую \(MN’\parallel AD\) (\(N’\in CD\)). Тогда по теореме Фалеса (т.к. \(MN’\parallel AD\parallel BC, AM=MB\)) точка \(N’\) — середина отрезка \(CD\). Значит, точки \(N\) и \(N’\) совпадут.
2) Докажем формулу.
Проведем \(BB’\perp AD, CC’\perp AD\). Пусть \(BB’\cap MN=M’, CC’\cap MN=N’\).

Тогда по теореме Фалеса \(M’\) и \(N’\) — середины отрезков \(BB’\) и \(CC’\) соответственно. Значит, \(MM’\) – средняя линия \(\triangle ABB’\), \(NN’\) — средняя линия \(\triangle DCC’\). Поэтому: \[MM’=\dfrac12 AB’, \quad NN’=\dfrac12 DC’\]
Т.к. \(MN\parallel AD\parallel BC\) и \(BB’, CC’\perp AD\), то \(B’M’N’C’\) и \(BM’N’C\) – прямоугольники. По теореме Фалеса из \(MN\parallel AD\) и \(AM=MB\) следует, что \(B’M’=M’B\). Значит, \(B’M’N’C’\) и \(BM’N’C\) – равные прямоугольники, следовательно, \(M’N’=B’C’=BC\).
Таким образом:
\[MN=MM’+M’N’+N’N=\dfrac12 AB’+B’C’+\dfrac12 C’D=\] \[=\dfrac12 \left(AB’+B’C’+BC+C’D\right)=\dfrac12\left(AD+BC\right)\]
Теорема: свойство произвольной трапеции
Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.

Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем, что точки \(P\), \(N\) и \(M\) лежат на одной прямой.

Проведем прямую \(PN\) (\(P\) – точка пересечения продолжений боковых сторон, \(N\) – середина \(BC\)). Пусть она пересечет сторону \(AD\) в точке \(M\). Докажем, что \(M\) – середина \(AD\).
Рассмотрим \(\triangle BPN\) и \(\triangle APM\). Они подобны по двум углам (\(\angle APM\) – общий, \(\angle PAM=\angle PBN\) как соответственные при \(AD\parallel BC\) и \(AB\) секущей). Значит: \[\dfrac{BN}{AM}=\dfrac{PN}{PM}\]
Рассмотрим \(\triangle CPN\) и \(\triangle DPM\). Они подобны по двум углам (\(\angle DPM\) – общий, \(\angle PDM=\angle PCN\) как соответственные при \(AD\parallel BC\) и \(CD\) секущей). Значит: \[\dfrac{CN}{DM}=\dfrac{PN}{PM}\]
Отсюда \(\dfrac{BN}{AM}=\dfrac{CN}{DM}\). Но \(BN=NC\), следовательно, \(AM=DM\).
2) Докажем, что точки \(N, O, M\) лежат на одной прямой.

Пусть \(N\) – середина \(BC\), \(O\) – точка пересечения диагоналей. Проведем прямую \(NO\), она пересечет сторону \(AD\) в точке \(M\). Докажем, что \(M\) – середина \(AD\).
\(\triangle BNO\sim \triangle DMO\) по двум углам (\(\angle OBN=\angle ODM\) как накрест лежащие при \(BC\parallel AD\) и \(BD\) секущей; \(\angle BON=\angle DOM\) как вертикальные). Значит: \[\dfrac{BN}{MD}=\dfrac{ON}{OM}\]
Аналогично \(\triangle CON\sim \triangle AOM\). Значит: \[\dfrac{CN}{MA}=\dfrac{ON}{OM}\]
Отсюда \(\dfrac{BN}{MD}=\dfrac{CN}{MA}\). Но \(BN=CN\), следовательно, \(AM=MD\).
\[{\Large{\text{Равнобедренная трапеция}}}\]
Определения
Трапеция называется прямоугольной, если один из ее углов – прямой.
Трапеция называется равнобедренной, если ее боковые стороны равны.
Теоремы: свойства равнобедренной трапеции
1) У равнобедренной трапеции углы при основании равны.
2) Диагонали равнобедренной трапеции равны.
3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.
Доказательство
1) Рассмотрим равнобедренную трапецию \(ABCD\).

Из вершин \(B\) и \(C\) опустим на сторону \(AD\) перпендикуляры \(BM\) и \(CN\) соответственно. Так как \(BM\perp AD\) и \(CN\perp AD\), то \(BM\parallel CN\); \(AD\parallel BC\), тогда \(MBCN\) – параллелограмм, следовательно, \(BM = CN\).
Рассмотрим прямоугольные треугольники \(ABM\) и \(CDN\). Так как у них равны гипотенузы и катет \(BM\) равен катету \(CN\), то эти треугольники равны, следовательно, \(\angle DAB = \angle CDA\).
2) 
Т.к. \(AB=CD, \angle A=\angle D, AD\) – общая, то по первому признаку \(\triangle ABD=\triangle ACD\). Следовательно, \(AC=BD\).
3) Т.к. \(\triangle ABD=\triangle ACD\), то \(\angle BDA=\angle CAD\). Следовательно, треугольник \(\triangle AOD\) – равнобедренный. Аналогично доказывается, что и \(\triangle BOC\) – равнобедренный.
Теоремы: признаки равнобедренной трапеции
1) Если у трапеции углы при основании равны, то она равнобедренная.
2) Если у трапеции диагонали равны, то она равнобедренная.
Доказательство
Рассмотрим трапецию \(ABCD\), такую что \(\angle A = \angle D\).

Достроим трапецию до треугольника \(AED\) как показано на рисунке. Так как \(\angle 1 = \angle 2\), то треугольник \(AED\) равнобедренный и \(AE = ED\). Углы \(1\) и \(3\) равны как соответственные при параллельных прямых \(AD\) и \(BC\) и секущей \(AB\). Аналогично равны углы \(2\) и \(4\), но \(\angle 1 = \angle 2\), тогда \(\angle 3 = \angle 1 = \angle 2 = \angle 4\), следовательно, треугольник \(BEC\) тоже равнобедренный и \(BE = EC\).
В итоге \(AB = AE — BE = DE — CE = CD\), то есть \(AB = CD\), что и требовалось доказать.
2) Пусть \(AC=BD\). Т.к. \(\triangle AOD\sim \triangle BOC\), то обозначим их коэффициент подобия за \(k\). Тогда если \(BO=x\), то \(OD=kx\). Аналогично \(CO=y \Rightarrow AO=ky\).

Т.к. \(AC=BD\), то \(x+kx=y+ky \Rightarrow x=y\). Значит \(\triangle AOD\) – равнобедренный и \(\angle OAD=\angle ODA\).
Таким образом, по первому признаку \(\triangle ABD=\triangle ACD\) (\(AC=BD, \angle OAD=\angle ODA, AD\) – общая). Значит, \(AB=CD\), чтд.
Свойства трапеции
Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
Что такое трапеция?
СОДЕРЖАНИЕ СТАТЬИ
 |
Трапеция – такой четырехугольник, у которого две стороны параллельны, а две другие – нет. |
Параллельные стороны называются – основания, а непараллельные стороны называются боковые стороны.
Вот, смотри:

Оказывается, трапеция (как и треугольник) бывает равнобедренная.
 |
Если боковые стороны равны, то она называется равнобедренной, или равнобокой. |
И тут возникает вопрос: а могут ли у трапеции быть равными ОСНОВАНИЯ??? И ответ: а вот и нет — тогда это получится НЕ трапеция, а параллелограмм, потому что две стороны окажутся параллельны и равны (вспоминаем признаки параллелограмма…)
Свойства трапеции
Свойства трапеции… Какие они и что же ты должен знать о них?
 |
Сумма углов при каждой боковой стороне трапеции равна 180°. (у нас на рисунке и ) |
Почему так? Ну, конечно, просто потому, что основания – параллельны, а боковая сторона – секущая. Вот и получается, что и – внутренние односторонние углы при параллельных и и секущей . Поэтому . И точно так же и – внутренние односторонние углы при тех же параллельных и , но секущая теперь – .
Видишь: главное, что играет роль – это параллельность оснований. Давай разберем еще некоторые свойства трапеции.
Как у всякого четырехугольника, у трапеции есть диагонали. Их две – посмотри на рисунки:
 |
 |
Ну вот, а теперь снова порассуждаем об углах.
 |
Опять и – параллельные, а диагональ – секущая. Поэтому . |
А теперь – сразу 2 диагонали и 4 угла:
 |
|
Что из этого может следовать? Очень важный факт: треугольники и – подобны по двум углам.
Их коэффициент подобия равен отношению оснований: .
Средняя линия трапеции
Для начала – что же такое средняя линия трапеции?
 |
Средняя линия трапеции – это отрезок, который соединяет середины боковых сторон трапеции. |
Оказывается, длину этой средней линии можно выразить через длины оснований трапеции. А именно, имеет место такая формула:
 |
, то есть |
| Длина средней линии трапеции равна полусумме (то есть половине суммы) длин оснований |
А ещё:
| Средняя линия трапеции параллельна ее основаниям |
Трапеция, вписанная в окружность.
Даже если ты ещё не изучал темы «Окружность. Вписанный угол» и «Вписанный четырехугольник», тебе будет полезно (и, надеюсь, интересно) узнать следующий удивительный факт:
 |
Если трапецию можно вписать в окружность, то она – равнобокая. |
Доказывать это мы не будем (здесь во всяком случае), а вот запомнить – хорошо бы – пригодится!
Подведём итог – он короткий.
Самое важное, что есть в трапеции – две параллельные стороны и BCE свойства трапеции именно этим и определяются.
Так что, если у тебя в задаче трапеция – используй параллельность – всё получится!
ТРАПЕЦИЯ. СРЕДНИЙ УРОВЕНЬ
Трапеция. Основные понятия и определения
| Трапеция – четырёхугольник, у которого две стороны параллельны, а две другие – нет. |

Параллельные стороны называются основаниями, а непараллельные – боковыми сторонами.
 |
Если боковые стороны трапеции равны, то она называется равнобедренной или равнобокой. |
Свойства трапеции
Свойства трапеции… Какие они и что же ты должен о них знать? Рассмотрим основные свойства трапеции.
Первое свойство трапеции
 |
Сумма угловпри каждой боковой стороне трапеции равна . |
Почему? и – параллельны, а и – секущие, поэтому:
Второе свойство трапеции
 |
Треугольники и подобны по двум углам. ( и – как накрест лежащие) |
Коэффициент подобия треугольников и равен отношению оснований:
Третье свойство трапеции
Сначала сформулируем основное определение, которое тебе нужно знать для понимания этого свойства трапеции:
 |
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон. |
А теперь формула:
А вот и само третье свойство трапеции:
| Средняя линия трапеции равна полусумме оснований и параллельна им. |
А это почему? Ту чуть – чуть сложнее – потребуется провести аж одну лишнюю линию!

Итак, проведём . Тогда четырехугольник – параллелограмм. Возьмём середину стороны и середину стороны . Оба: и – снова параллелограммы ( и ; и ). Ну вот, значит , да ещё .
Поедем дальше.
 |
Проведём — среднюю линию в . Знаем, что и |
Что же из всего этого следует?
 |
|
Вот и доказали!
Четвертое свойство трапеции
 |
Если трапеция вписана в окружность, то она равнобокая. |
Почему? Подробнее смотри в теме «Вписанный четырехугольник», а тут – двумя строчками:
(трапеция же!)
(вписанный четырехугольник)
. Ну, и так же .
Пятое свойство трапеции
 |
В ЛЮБОЙ трапеции следующие четыре точки лежат на одной прямой: 1) – точка пересечения продолжений боковых сторон; 2) и – середины оснований; 3) – точка пересечения диагоналей. |
Эту теорему доказывать не будем – не пугайся.
Заметим только, что ВЕРНО и ОБРАТНОЕ:
| Если в каком – нибудь четырехугольнике какие – нибудь три из перечисленных четырёх точек окажутся на одной прямой – то четырёхугольник этот – ТРАПЕЦИЯ. |
Шестое свойство трапеции
 |
Биссектрисы углов при боковой стороне трапеции перпендикулярны. |
Седьмое свойство трапеции
Здесь мы ещё раз увидим, как полезно в трапеции бывает провести линию, параллельную или боковой стороне, или диагонали – сразу появляется новый взгляд. Один раз мы уже так делали – в пункте про среднюю линию. А теперь ты узнал новый факт, который относительно часто встречается в задачах.
 |
В трапеции с перпендикулярными диагоналями |
Давай докажем! Это уже целая задача, которая вполне может попасться прямо на экзамене!
Ну вот, и ты теперь старайся с помощью новых знаний и методов решать задачки про трапецию – они обычно не слишком сложные. Главное, твёрдо помнить все свойства трапеции и не забывать о параллельности оснований и иногда (в задачах посложнее) бывает полезно провести что-то параллельное или соединить боковые стороны.

Проведём и .
Обозначим ; .
Тогда:
- – прямоугольный
Значит, (медиана, проведенная к гипотенузе, равна её половине).
То есть .
Но ведь (так как — параллелограмм) .
ТРАПЕЦИЯ. КРАТКОЕ ИЗЛОЖЕНИЕ И ОСНОВНЫЕ ФОРМУЛЫ
Трапеция – четырёхугольник, у которого две стороны параллельны (они называются основания), а две другие – нет (это боковые стороны).
 |
|
 |
|
- Средняя линия параллельна основаниям: .
- Длина средней линии трапеции равна полусумме длин оснований: .
 |
|
- Треугольники, образованные основаниями трапеции и отрезками диагоналей
( и ) подобны по двум углам с коэффициентом подобия равным отношению оснований: . - Площади треугольников, образованных боковыми сторонами и отрезками диагоналей трапеции, равны: .
 |
|
Свойства равнобедренной трапеции:
- диагонали равны: ;
- углы при основании равны: ;
- сумма противолежащих углов равна : .
 |
|
Стороны и диагональ равнобокой трапеции связаны соотношением: .
Площадь трапеции равна полусумме оснований, умноженной на высоту: .
ОСТАВШИЕСЯ 2/3 СТАТЬИ ДОСТУПНЫ ТОЛЬКО УЧЕНИКАМ YOUCLEVER!
Стать учеником YouClever,
Подготовиться к ОГЭ или ЕГЭ по математике по цене «чашка кофе в месяц»,
А также получить бессрочный доступ к учебнику «YouClever», Программе подготовки (решебнику) «100gia», неограниченному пробному ЕГЭ и ОГЭ, 6000 задач с разбором решений и к другим сервисам YouClever и 100gia.
можно кликнув по этой ссылке.
Замечательное свойство трапеции — подготовка к ЕГЭ по Математике
Анна Малкова
Замечательное свойство трапеции. Точка пересечения диагоналей трапеции, точка пересечения продолжений ее боковых сторон и середины оснований лежат на одной линии.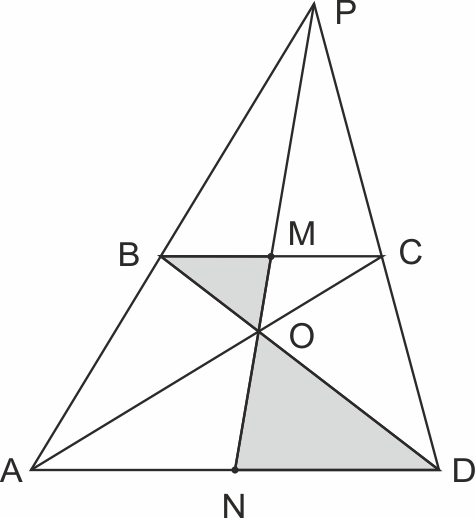
Дана трапеция ABCD, , N — середина AD, M — середина BC, . Докажем, что точки M, N, O, P лежат на одной прямой.
Задача не так уж и проста, да и сама формулировка необычна: доказать, что четыре точки лежат на одной прямой. Как это сделать?
Во-первых, разобьем задачу на две более простых. Во-вторых – немного переформулируем.
1) Докажем, что середина основания AD лежит на прямой, соединяющей середину основания BC и точку пересечения диагоналей.
2) Докажем, что середина основания AD лежит на прямой, соединяющей середину основания BC и точку пересечения продолжений боковых сторон.
Начнем с пункта 1.
Пусть M — середина BC, O – точка пересечения диагоналей трапеции, .
Докажем, что N – середина AD.
по двум углам ( как вертикальные, как накрест лежащие при параллельных основаниях трапеции), тогда .
Аналогично, ( как вертикальные, как накрест лежащие при параллельных основаниях трапеция), отсюда .
Отсюда . Это значит, что N – середина AD.
Теперь пункт 2.
Проведем PM – медиану треугольника BPC. Пусть прямые AD и PM пересекаются в точке N. Докажем, что N – середина AD
по двум углам (угол P – общий, как соответственные при параллельных основаниях трапеции), отсюда .
аналогично, .
Получим: , значит, N – середина AD.
Таким образом, точки M,O,N,P лежат на одной прямой, что и требовалось доказать.
Трапеция. Свойства, признаки, площадь. Средняя линия трапеции
Трапеция — четырехугольник, у которого две стороны параллельны, а две другие — нет.
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны.
Если боковые стороны равны, трапеция называется равнобедренной.
Площадь трапеции равна произведению полусуммы оснований на высоту:
Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции. Средняя линия трапеции параллельна основаниям, а длина ее равна полусумме оснований:
Как видим, теория очень проста. А задачи, в которых применяются свойства трапеции, весьма разнообразны. В этой статье разобраны и стандартные задачи (номер и ), и более интересные.
. Найдите высоту трапеции , опущенную из вершины , если стороны квадратных клеток равны .
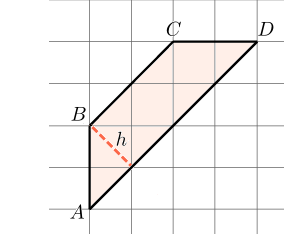
Высота трапеции — это отрезок, перпендикулярный ее основаниям. Проведем высоту из вершины .
Ответ: .
. Основания трапеции равны и , боковая сторона, равная , образует с одним из оснований трапеции угол . Найдите площадь трапеции.
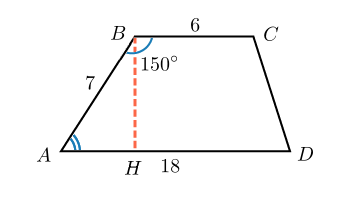
Это стандартная задача. Углы и — односторонние, значит, их сумма равна , и тогда угол равен . Из треугольника найдем высоту . Катет, лежащий напротив угла в , равен половине гипотенузы. Получаем, что и площадь трапеции равна .
. Основания трапеции равны и . Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.
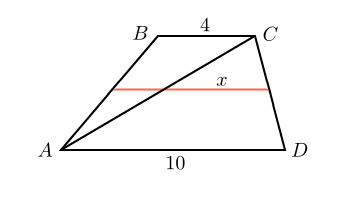
Скажите, что вы видите на чертеже? Можно сказать, что изображена трапеция , и в ней проведена средняя линия. А можно увидеть и другое — два треугольника, и , в которых проведены средние линии.
Мы помним, что средняя линия треугольника — это отрезок, соединяющий середины двух его сторон. Средняя линия треугольника параллельна третьей его стороне и равна половине этой стороны.
Из треугольника находим: .
Ты нашел то, что искал? Поделись с друзьями!
В следующей задаче мы тоже воспользуемся свойством средней линии треугольника.
. Основания трапеции равны и . Найдите отрезок, соединяющий середины диагоналей трапеции.
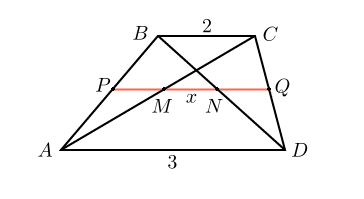
Проведем — среднюю линию трапеции, . Легко доказать, что отрезок , соединяющий середины диагоналей трапеции, лежит на средней линии. Дальше все просто. Найдем отрезки и , являющиеся средними линиями треугольников и , а затем отрезок . Он равен .
. Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного , отсекает треугольник, периметр которого равен . Найдите периметр трапеции.
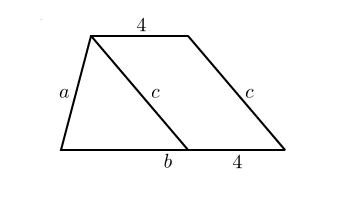
Периметр треугольника равен сумме его сторон, то есть .
Периметр трапеции равен .
Заметим, что периметр трапеции на 8 больше, чем периметр треугольника. Значит, он равен 15 + 8 = 23.
Ответ: .
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Основные определения и свойства трапеций
| Тип утверждения | Фигура | Рисунок | Формулировка |
| Определение | Трапеция |  | Трапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны. Параллельные стороны трапеции называют основаниями, а непараллельные стороны – боковыми сторонами трапеции |
| Определение | Диагонали трапеции |  | Диагоналями трапеции называют отрезки, соединяющие противоположные вершины трапеции |
| Определение | Высота трапеции |  | Высотой трапеции называют перпендикуляр, опущенный из любой точки одного оснований трапеции на другое основание или его продолжение |
| Свойство | Точка пересечения диагоналей |  | Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой Более подробно об этом свойстве |
| Определение | Средняя линия трапеции |  | Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции |
| Свойство | Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме Посмотреть доказательство | ||
| Свойство | Биссектрисы углов при боковой стороне трапеции |  | Биссектрисы углов при боковой стороне трапеции перпендикулярны |
| Трапеция |
 Определение: Трапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны. Параллельные стороны трапеции называют основаниями, а непараллельные стороны – боковыми сторонами трапеции |
| Диагонали трапеции |
 Определение: Диагоналями трапеции называют отрезки, соединяющие противоположные вершины трапеции |
| Высота трапеции |
 Определение: Высотой трапеции называют перпендикуляр, опущенный из любой точки одного оснований трапеции на другое основание или его продолжение |
| Точка пересечения диагоналей |
 Свойство: Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой Более подробно об этом свойстве |
| Средняя линия трапеции |
 Определение: Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции Свойство: Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме Посмотреть доказательство |
| Биссектрисы углов при боковой стороне трапеции |
 Свойство: Биссектрисы углов при боковой стороне трапеции перпендикулярны |
Подробнее со свойствами средней линии трапеции можно ознакомиться в разделе нашего справочника «Средняя линия трапеции».
В разделе нашего справочника «Типы четырёхугольников» представлена схема классификации трапеций. В том же разделе представлена таблица, в которой описаны всевозможные типы трапеций.
Свойства и признаки равнобедренных трапеций
| Тип утверждения | Фигура | Рисунок | Формулировка |
| Определение | Равнобедренная трапеция |  | Равнобедренной трапецией называют трапецию, у которой боковые стороны равны. |
| Свойство | Равенство углов при основании |  | Если трапеция является равнобедренной, то углы при каждом из её оснований равны. |
| Признак | Если у трапеции углы при одном из оснований равны, то углы равны и при другом основании, а трапеция является равнобедренной. | ||
| Свойство | Равенство диагоналей |  | Если трапеция является равнобедренной, то её диагонали равны. |
| Признак | Если у трапеции диагонали равны, то она является равнобедренной | ||
| Свойство | Углы, которые диагонали образуют с основаниями |  | Если трапеция является равнобедренной, то её диагонали образуют равные углы с каждым из её оснований. |
| Признак | Если диагонали трапеции образуют равные углы с одним из оснований, то диагонали образуют равные углы и с другим основанием, а трапеция является равнобедренной. | ||
| Свойство | Описанная окружность |  | Если трапеция является равнобедренной, то около неё можно описать окружность. |
| Признак | Если около трапеции можно описать окружность, то она является равнобедренной. | ||
| Свойство | Высоты трапеции |  | Основания высот равнобедренной трапеции, опущенных из вершин меньшего основания, делят большее основание на отрезки, один из которых равен меньшему основанию, а два других – полуразности оснований |
| Определение: Равнобедренная трапеция | |
 | Равнобедренной трапецией называют трапецию, у которой боковые стороны равны. |
| Свойство: равенство углов при основании | |
 | Если трапеция является равнобедренной, то углы при каждом из её оснований равны. |
| Признак: равенство углов при основании | |
 | Если у трапеции углы при одном из оснований равны, то углы равны и при другом основании, а трапеция является равнобедренной. |
| Свойство: равенство диагоналей | |
 | Если трапеция является равнобедренной, то её диагонали равны. |
| Признак: равенство диагоналей | |
 | Если у трапеции диагонали равны, то она является равнобедренной |
| Свойство: углы, которые диагонали образуют с основаниями | |
 | Если трапеция является равнобедренной, то её диагонали образуют равные углы с каждым из её оснований. |
| Признак: углы, которые диагонали образуют с основаниями | |
 | Если диагонали трапеции образуют равные углы с одним из оснований, то диагонали образуют равные углы и с другим основанием, а трапеция является равнобедренной. |
| Свойство: описанная окружность | |
 | Если трапеция является равнобедренной, то около неё можно описать окружность. |
| Признак: описанная окружность | |
 | Если около трапеции можно описать окружность, то она является равнобедренной. |
| Свойство: высоты трапеции | |
 | Основания высот равнобедренной трапеции, опущенных из вершин меньшего основания, делят большее основание на отрезки, один из которых равен меньшему основанию, а два других – полуразности оснований |
| Равнобедренная трапеция |
 Определение: Равнобедренной трапецией называют трапецию, у которой боковые стороны равны. |
| Равенство углов при основании |
 Свойство: Если трапеция является равнобедренной, то углы при каждом из её оснований равны. Признак: Если у трапеции углы при одном из оснований равны, то углы равны и при другом основании, а трапеция является равнобедренной. |
| Равенство диагоналей |
 Свойство: Если трапеция является равнобедренной, то её диагонали равны. Признак: Если у трапеции диагонали равны, то она является равнобедренной. |
| Углы, которые диагонали образуют с основаниями |
 Свойство: Если трапеция является равнобедренной, то её диагонали образуют равные углы с каждым из её оснований. Признак: Если диагонали трапеции образуют равные углы с одним из оснований, то диагонали образуют равные углы и с другим основанием, а трапеция является равнобедренной. |
| Описанная окружность |
 Свойство: Если трапеция является равнобедренной, то около неё можно описать окружность. Признак: Если около трапеции можно описать окружность, то она является равнобедренной. |
| Высоты трапеции |
 Свойство: Основания высот равнобедренной трапеции, опущенных из вершин меньшего основания, делят большее основание на отрезки, один из которых равен меньшему основанию, а два других – полуразности оснований |

На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Основания трапеции параллельны некоторой плоскости.Верно ли что боковые стороны трапеции так же параллельны этой плоскости? Ответ объясните.
АВ²=АС²-(3АВ)² АВ²+9АВ²=АС²
10АВ²=АС²
АВ=√АС²/10=√4*10/10=2
АВ=2
Ответ:
решение представлено на фото
Найдём площадь основания пирамиды:
Sabc=((4^2)*корень из 3)/25=0,64корень из 3
Объем пирамиды:
Vsabc=1/3×0,64корень из 3+5корень из 3=3,2
Ответ:3.2
1) угол 4
он смежный с углом 2 — их сумма 180
2)угол 1
он смежный с углом 2 — их сумма 180
3) угол 5
он односторонний с углом 2 — их сумма 180
4) угол 8
угол 2 с углом 7 накрест лежащие — они равны
угол 7 и 8 смежные -их сумма 180
Развёрнутый угол равен 180°. Тогда первый угол равен 180 * 0.2(20% = 0.2) = 36°. Второй угол равен 180 * 0.6 = 108°. Третий угол равен 180 * 0.8 = 144°
Свойства трапеций и воздушных змеев
Теперь, когда мы видели несколько типов четырехугольники, которые параллелограммы, давайте узнаем о фигурах, не обладающих свойствами параллелограммов. Напомним, что параллелограммы были четырехугольниками, противоположные стороны были параллельны. В этом разделе мы рассмотрим четырехугольники, противоположные стороны могут пересекаться в какой-то момент.Мы изучим два типа четырехугольников. называются трапеции и воздушных змеев . Начнем наше исследование с изучения некоторые свойства трапеций.
Трапеции
Определение: Трапеция — это четырехугольник с ровно одной парой параллелей. Стороны.
Поскольку у трапеции должна быть ровно одна пара параллельных сторон, нам потребуется докажите, что одна пара противоположных сторон параллельна, а другая не находится в нашем двухколоночные геометрические доказательства.Если мы забудем доказать, что одна пара противоположных стороны не параллельны, мы не исключаем возможность того, что четырехугольник — параллелограмм. Следовательно, этот шаг будет абсолютно необходим, когда мы будем работать. на разные упражнения с трапециями.
Прежде чем мы углубимся в наше изучение трапеций, необходимо выучить названия различных частей этих четырехугольников, чтобы уточнить его стороны и углы.Все трапеции состоят из двух основных частей: основания и ножек . Противоположные стороны трапеции, параллельные друг другу, называются основаниями. Остальные стороны трапеции, которые пересекаются в некоторой точке при удлинении, называются ножками трапеции.
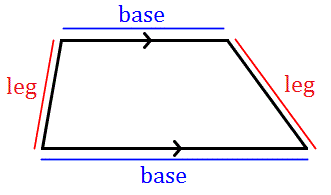
Верхняя и нижняя стороны трапеции проходят параллельно друг другу, поэтому они основания трапеции.Другие стороны трапеции будут пересекаться, если их удлинить, так что они ноги трапеции.
Отрезок, соединяющий середины ног трапеции, называется отрезком. мидсегмент . Длина этого сегмента всегда равна половине суммы основания трапеции, или
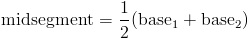
Рассмотрим трапецию ABCD, показанную ниже.
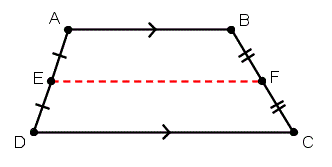
Средний сегмент EF , показанный красным, имеет длину
. 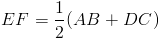
Размер среднего сегмента зависит только от длины трапеции. основы. Тем не менее, есть важная особенность некоторых трапеций: полагается исключительно на свои ноги. Давайте теперь посмотрим на эти трапеции.
Равнобедренные трапеции
Определение: Равнобедренная трапеция — это трапеция, ноги которой совпадают.
По определению, если в четырехугольнике есть ровно одна пара параллельных прямых, тогда четырехугольник — трапеция. Определение равнобедренной трапеции добавляет еще одно уточнение: ноги трапеции должны быть конгруэнтными.
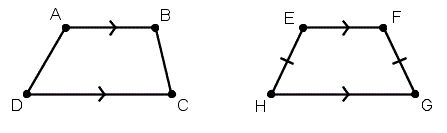
ABCD не является равнобедренной трапецией, потому что AD и BC не совпадают. Потому что EH и FG конгруэнтны, трапеция EFGH — равнобедренная трапеция.
Есть несколько теорем, которые помогут нам доказать, что трапеция равнобедренная. Эти свойства перечислены ниже.
(1) Трапеция является равнобедренной тогда и только тогда, когда углы основания совпадают.
(2) Трапеция равнобедренная тогда и только тогда, когда диагонали совпадают.
(3) Если трапеция равнобедренная, то ее противоположные углы являются дополнительными.
Воздушные змеи
Определение: Воздушный змей — это четырехугольник с двумя разными парами смежных стороны, которые совпадают.
Напомним, что параллелограммы также имели пары равных сторон.Однако их конгруэнтные стороны всегда были противоположными сторонами. Воздушные змеи имеют две пары совпадающих сторон, которые встречаются в двух разных точках. Давайте посмотрим на иллюстрацию ниже, чтобы понять, что как выглядит воздушный змей.
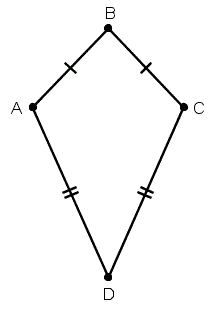
Отрезок AB прилегает к отрезку BC и конгруэнтен ему. Сегменты AD и CD также смежные и конгруэнтные.
У воздушных змеев есть несколько свойств, которые помогут нам отличить их от других четырехугольников.
(1) Диагонали воздушного змея пересекаются под прямым углом.
(2) Воздушные змеи имеют ровно одну пару противоположных углов, которые совпадают.
Эти два свойства показаны на диаграмме ниже.
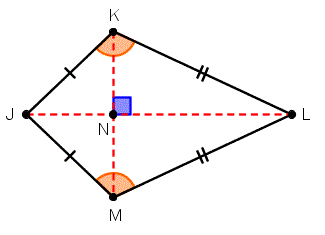
Обратите внимание, что на пересечении диагоналей образуется прямой угол, который в точке N.Также мы видим, что? K ?? M. Это наша единственная пара совпадающих углов, потому что ? J и? L имеют разные меры.
Попрактикуемся в выполнении некоторых задач, требующих использования свойств трапеций. и воздушных змеев, о которых мы только что узнали.
Упражнение 1
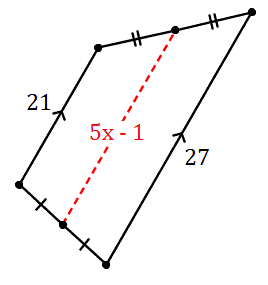
Найдите значение x на трапеции ниже.
Ответ:
Поскольку нам даны длины оснований трапеции, мы можем вычислить какой длины должен быть средний сегмент.Давайте использовать формулу, которую мы использовали дано для среднего сегмента, чтобы понять это. (Помните, что это половина суммы основания.)
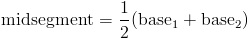
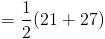
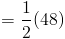
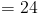
Итак, теперь, когда мы знаем, что длина среднего сегмента составляет 24 , мы можем перейти вперед и установите 24 равным 5x-1 .Переменная разрешима сейчас:
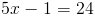
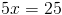
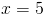
Упражнение 2
Найдите значение y на равнобедренной трапеции ниже.
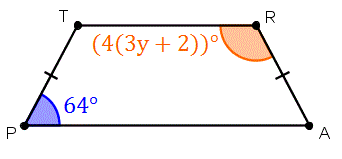
Ответ:
На рисунке нам дана величина только одного угла, поэтому мы должны иметь возможность чтобы вывести больше информации на основе этого элемента.Поскольку четырехугольник равнобедренной трапеции, мы знаем, что углы основания равны. Это означает, что ? A также имеет размер 64 ° .
Теперь давайте разберемся, какая сумма ? A и ? P составляет:
. 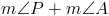
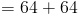
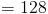
Вместе они имеют в общей сложности 128 ° .Напомним по Polygon Interior Теорема суммы углов гласит, что внутренние углы четырехугольника должны быть 360 ° . Итак, давайте попробуем использовать это так, чтобы помочь нам определить меру ? R . Сначала просуммируем все углы и установим его равным 360 ° .
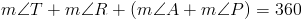
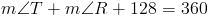
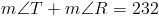
Теперь мы видим, что сумма ? T и ? R составляет 232 ° .Поскольку сегмент TR является другой базой трапеции TRAP , мы знаем, что углы в точках T и R должны совпадать друг другу. Таким образом, если мы определим меры ? T и ? R по переменной x , имеем
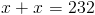
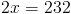
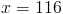
Это значение означает, что размер ? T и ? R равен . 116 ° .Наконец, мы можем установить 116 равным выражению, показанному в ? R для определения стоимости y . У нас
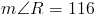
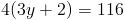
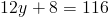
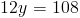
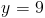
Итак, получаем x = 9 .
Хотя приведенный выше метод был подробным способом решения упражнения, мы могли бы Также как раз использовалось свойство, что противоположные углы равнобедренных трапеций являются дополнительными.Решение таким образом происходит намного быстрее, поскольку нам нужно только найти, что за добавка угла 64 ° составляет. Получаем
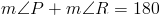
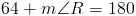
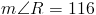
Как только мы дойдем до этой точки в нашей проблеме, мы просто установим 116 равным 4 (3y + 2) и решите, как мы делали раньше.
Упражнение 3
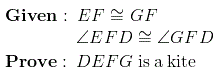
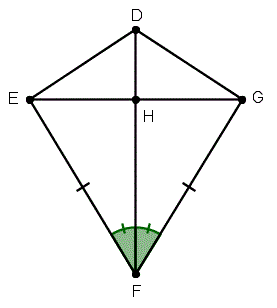
Ответ:
Прочитав задачу, мы видим, что нам предоставили ограниченный объем информации. и хочу сделать вывод, что четырехугольник DEFG — это воздушный змей. Заметь EF и GF совпадают, поэтому, если мы сможем найти способ доказать, что DE и DG совпадают, это даст нам две различные пары смежных сторон, которые конгруэнтны, что является определением воздушного змея.
Нам также известно, что ? EFD и ? GFD совпадают. В прошлом мы узнали несколько теорем сравнения треугольников, которые могут быть применимы в этой ситуации, если мы сможем найти другую сторону или угол, которые совпадают.
Поскольку сегмент DF составляет сторону ? DEF и ? DGF , мы можем использовать рефлексивное свойство , чтобы сказать, что оно конгруэнтно самому себе.Таким образом, согласно постулату SAS у нас есть два совпадающих треугольника.
Далее, мы можем сказать, что сегменты DE и DG совпадают. потому что соответствующие части конгруэнтных треугольников конгруэнтны. Наша новая иллюстрация показано ниже.
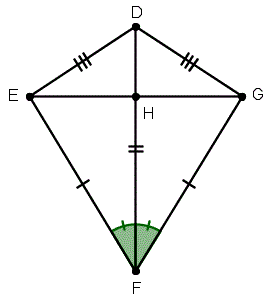
Мы заключаем, что DEFG является воздушным змеем, потому что он имеет две отдельные пары смежных сторон, которые совпадают.Геометрическое доказательство этого упражнения из двух столбцов показано ниже.

Свойства трапеций и равнобедренных трапеций
- Образование
- Математика
- Геометрия
- Свойства трапеций и равнобедренных трапеций
Марк Райан
Трапеция — это четырехугольник с ровно одной парой параллельных сторон (параллельные стороны называются основаниями ). На следующем рисунке изображена трапеция слева и равнобедренная трапеция справа.
Пожалуй, самое сложное свойство обеих диаграмм — наличие дополнительных углов. Из-за того, что стороны параллельны, последовательные углы являются внутренними углами одной стороны и, следовательно, являются дополнительными. (Кстати, все специальные четырехугольники, кроме воздушного змея, содержат следующие друг за другом дополнительные углы.)
Вот вам доказательство равнобедренной трапеции:
Заявление 1 :
Причина выписки 1 : Дано.
Заявление 2 :
Причина утверждения 2 : Ноги равнобедренной трапеции совпадают.
Заявление 3 :
Причина утверждения 3 : Верхние углы основания равнобедренной трапеции совпадают.
Заявление 4 :
Причина выписки 4 : Рефлексивное свойство.
Заявление 5 :
Причина утверждения 5 : SAS или Side-Angle-Side (2, 3, 4)
Заявление 6 :
Причина утверждения 6 : CPCTC (Соответствующие части конгруэнтных треугольников конгруэнтны).
Заявление 7 :
Причина утверждения 7 : Если углы, то стороны.
,Площадь трапеций | Shmoop
Площадь трапеций
До сих пор мы в значительной степени имели дело с вариациями формулы той же площади A = bh . Мы изменили его на A = lw для прямоугольников и даже A = s 2 для квадратов, но по сути это то же самое. Сколько раз можно перемножить два числа?
Пора развлечься. Нет, не супер причудливый, а изрядно причудливый.Как иметь две базы — а не две головы — вместо одной.
Мы говорим ни о чем другом, как о трапециях , которые действительно легко найти. Пока только две из четырех его сторон параллельны друг другу, мы получаем трапецию. Они даже не обязательно должны быть одинаковой длины, а это значит, что другие стороны могут делать все, что захотят, в значительной степени. Совсем ничего похожего на параллелограммы или прямоугольники.
Мы вам сказали. Чумовая. Настолько причудливые, что мы должны называть их Freakazoids.
Все равно они выглядят по-разному. Даже если бы мы могли использовать одно уравнение для вычисления площади для всех, с чего бы мы начали? Это похоже на попытку переехать из Небраски в страну Оз. (Может быть, это не лучший пример. Объезд через Канзас, и мы золотые.)
Давайте возьмем общую характеристику всех трапеций: параллельные стороны. Мы знаем, что две параллельные линии всегда будут на одинаковом расстоянии друг от друга, поэтому назовем это расстояние высотой . Для единообразия мы будем использовать h для высоты… снова.
Мы знаем, что две параллельные стороны не будут иметь одинаковую длину, потому что тогда у нас будет параллелограмм. Поэтому мы назовем эти две стороны базами , b 1 и b 2 . (Иногда вы увидите B и b вместо b 1 и b 2 . Это просто разные способы различения двух оснований.) Наша формула площади для любой трапеции с высотой h и баз b 1 и b 2 is:
A = ½ ( b 1 + b 2 ) h
К счастью, мы может игнорировать шаткие стороны, которые не параллельны друг другу.
Пример задачи
Если основания трапеции имеют длину 4 и 5 при высоте 2, какова площадь трапеции?
Используя уравнение для площади трапеции, все, что нам нужно сделать, это указать длину оснований и высоту.
A = ½ ( b 1 + b 2 ) h
A = ½ (4 + 5) × 2
A = ½ × 9 × 2
A = 9 единиц 2
Пример задачи
Найдите высоту трапеции, которая имеет площадь 7 единиц 2 и основания 7 единиц и 21 единицу в длину.
Мы можем использовать ту же формулу площади для трапеции. На этот раз вместо решения для A мы можем решить для высоты h . Замените 21 единицу на b 1 , 7 единиц на b 2 и 7 единиц 2 на A . Вы знаете, что делать.
A = ½ ( b 1 + b 2 ) h
7 = ½ (21 + 7) h
7 = ½ × 28 × h
0.5 = h
Высота трапеции 0,5 единицы.
Какими бы причудливыми ни были трапеции, вы, наверное, уже знаете, что они бывают разных типов. Равнобедренные трапеции предприняли некоторые попытки сделать их нормальными, сделав две непараллельные стороны одинаковой длины. Правые трапеции имеют сторону, которая образует прямые углы с обоими основаниями.
Знание этих конкретных типов трапеций не меняет формулы для расчета площади.По-прежнему A = ½ ( b 1 + b 2 ) h . С другой стороны, это может быть полезно, если вам прямо не даны b 1 , b 2 и h .
Пример задачи
Какова площадь и периметр этой трапеции?
Это правая трапеция, поэтому мы можем рассматривать ее как прямоугольник и прямоугольный треугольник, соединенные вместе. Гипотенуза треугольника равна 5, и мы можем найти один из катетов, вычитая маленькое основание из большого, что дает нам длину 3.
Мы знаем гипотенузу и один из катетов прямоугольного треугольника. Можете ли вы сказать «теорема Пифагора»? Конечно, можем. Просто замените a на 3, b на h и c на 5.
a 2 + b 2 = c 2
3 2 + h 2 = 5 2
h 2 = 16
h = 4 единицы
Высота этой трапеции равна 4, и мы знаем, что ее основания 8 и 11.Поиск области должен быть легким.
A = ½ ( b 1 + b 2 ) h
A = ½ (8 + 11) × 4
A = ½ × 19 × 4
А = 38 штук 2
Ну, все хорошо, а что с периметром? Мы знаем, что периметр — это просто сложение всех сторон. Мы уже знаем три стороны (два основания и неперпендикулярная сторона). К счастью для нас, высота равна одной из сторон для правой трапеции.
P = b 1 + b 2 + h + s
P = 8 + 11 + 4 + 5
P = 28 единиц
Площадь трапеции
Напомним, что площадь треугольника равна половине основания, умноженной на высоту. 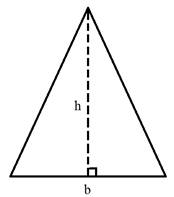
Теперь давайте посмотрим, что произойдет, если мы срежем вершину треугольника.

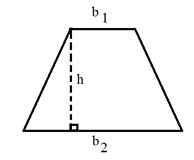
Новая форма — трапеция . Трапеция — это четырехугольник, у которого есть только одна пара противоположных сторон, параллельных друг другу. Мы должны взять среднее значение оснований, а затем умножить на высоту. Это означает, что нам нужно сложить основания и разделить их на 2.Потом умножим на высоту.

Определите площадь следующих трапеций.
1.)
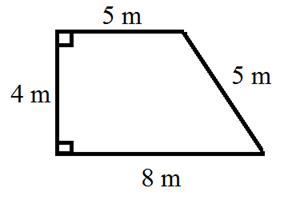
Обязательно используйте параллельные стороны в качестве оснований, а высота — это кусок, который образует прямой угол с параллельными сторонами.
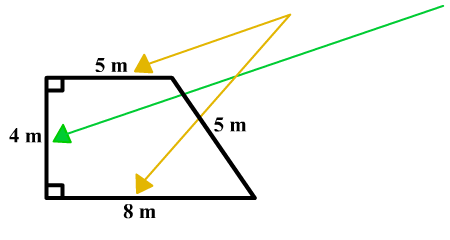
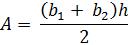
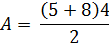
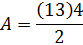
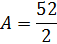
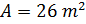
2.)
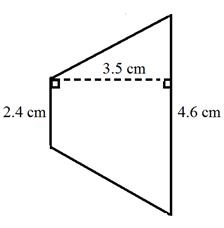
Эта трапеция находится на боку. Высота соединяет две базы.
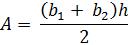
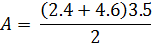
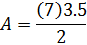
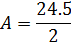
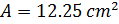
3. Площадь трапеции составляет 168 дюймов 2 . Определите высоту .
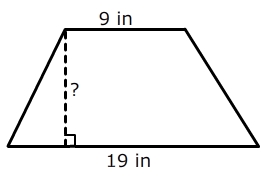
В этом примере задана площадь, поэтому мы будем работать в обратном направлении, чтобы определить высоту.
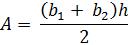
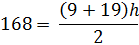
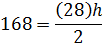
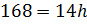
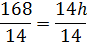
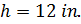
Обратите внимание, что в этом примере высота обозначена в дюймах, а не в дюймах в квадрате.Высота одномерная, а площадь двухмерная. Поэтому высота обозначается в дюймах, а площадь — в квадратных дюймах.
Давайте рассмотрим
Чтобы определить площадь трапеции, выполните три шага.
1.) Добавляем базы.2.) Умножьте сумму на высоту.
3.) Разделите произведение на 2.
4.) Обязательно пометьте область словом «единицы в квадрате».
,
Leave A Comment