В данной публикации мы рассмотрим, каким образом можно посчитать периметр трапеции и разберем примеры решения задач.
Формула вычисления периметра
Периметр (P) трапеции равняется сумме длин всех ее сторон.
P = a + b + c + d
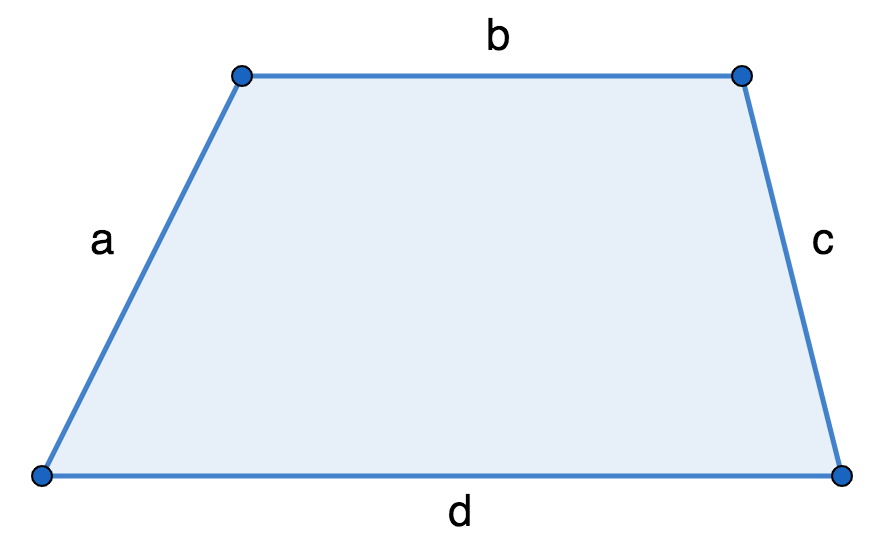
- b и d – основания трапеции;
- a и с – ее боковые стороны.
Периметр равнобедренной трапеции
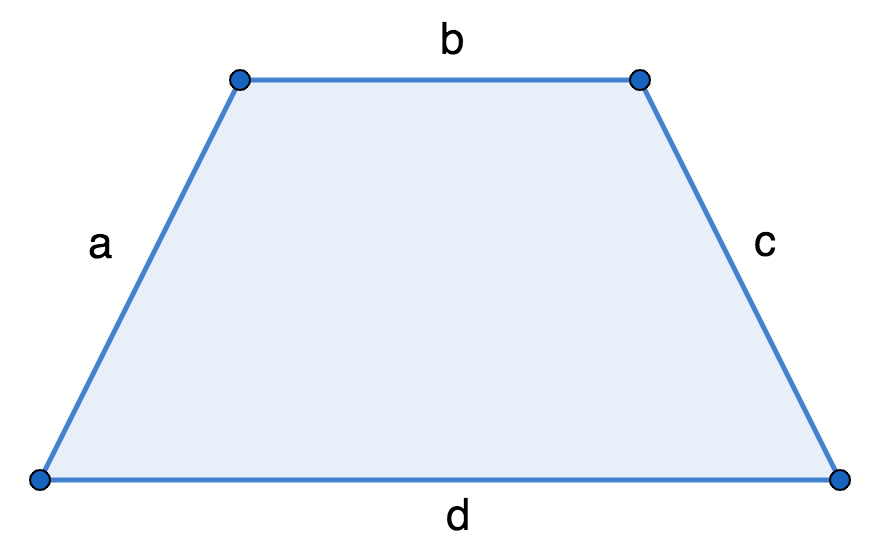
В равнобедренной трапеции боковые стороны равны (a=c), из-за чего ее, также, называют равнобокой. Периметр считается так:
P = 2a + b + d или P = 2с + b + d
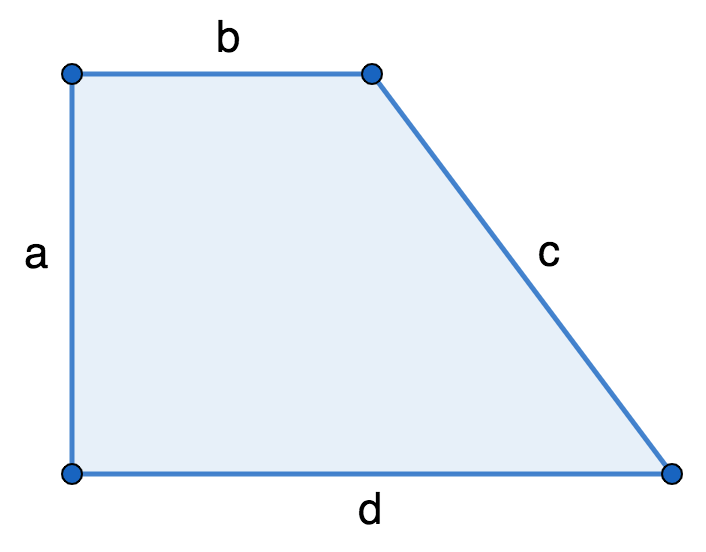
Периметр прямоугольной трапеции
Для расчета периметра используется такая же формула, что и для разносторонней трапеции.
P = a + b + c + d
Примеры задач
Задание 1
Найдите периметр трапеции, если ее основания равны 7 и 10 см, а боковые стороны – 4 и 5 см.
Решение:
Используем стандартную формулу, подставив в нее известные нам длины сторон: P = 7 см + 10 см + 4 см + 5 см = 26 см.
Задание 2
Периметр равнобедренной трапеции равняется 22 см. Найдите длину боковой стороны, если основания фигуры равны 3 см и 9 см.
Решение:
Как мы знаем, периметр равнобедренной трапеции вычисляется по формуле: P = 2a + b + d, где а – боковая сторона.
Ее длина, умноженная на два равна: 2a = P – b – d = 22 см – 3 см – 9 см = 10 см.
Следовательно, длина боковой стороны составляет: a = 10 см / 2 = 5 см.
Формула периметра трапеции
Трапе́ция (от др. -греч. τράπέζιου — «столик» ; τράπεζα — «стол, еда» ) — четырёхугольник, у которого ровно одна пара противолежащих сторон параллельна. Иногда трапеция определяется как четырёхугольник, у которого произвольная пара противолежащих сторон параллельна, в этом случае параллелограмм является частным случаем трапеции
Периметр произвольной трапеции
Периметр произвольной трапеции, в которой AB=a, BC=b, CD=c, AD=d, имеет вид:
\[ \LARGE P_{ABCD} = a + b + c + d \]
где:
P — периметр трапеции
a, b, c, d — стороны трапеции
Периметр равнобокой трапеции
Равнобедренная трапеция — это трапеция у котрой боковые стороны равны.
Периметр произвольной трапеции, в которой AB=CD=a, BC=b, AD=c, имеет вид:
\[ \LARGE P_{ABCD} = 2 \cdot a + b + c \]
где:
a, b, c, d — стороны трапеции
Признаки равнобедренной трапеции
Трапеция будет равнобедренной если выполняется одно из этих условий:
1. Углы при основе равны: ∠ABC = ∠BCD и ∠BAD = ∠ADC
2. Диагонали равны: AC = BD
3. Одинаковые углы между диагоналями и основаниями: ∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC
4. Сумма противоположных углов равна 180°: ∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°
5. Вокруг трапеции можно описати окружность
Также можно найти периметр трапеции, не зная длин оснований, но имея среднюю линию m. Средняя линия по определению представляет собой полусумму оснований трапеции, поэтому умножив ее на два, можно подставить ее вместо оснований в формулу периметра: \( P = 2 \cdot m + c + d \).
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Трапеция — Формулы | Свойства
Для расчёта всех основных параметров трапеции воспользуйтесь калькулятором.
Виды трапеции
- Произвольная трапеция – это четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна)
- Прямоугольная трапеция – это такая трапеция, у которой есть прямые углы при боковой стороне
Свойства трапеции
- Средняя линия трапеции (FE) параллельна основаниям и равна их полусумме $$ FE = {AB + DC \over 2} $$
- Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне
Например: биссектриса AH отсекает на основании DC отрезок DH , который равен боковой стороне AD - Треугольники AOB и DOC, образованные отрезками диагоналей и основаниями трапеции, подобны
- Треугольники AOD и BOC, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь
- В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон (AD + BC = AB + DC)
- Отрезок (KL), соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии, т.е. $$ KL = {DC — AB \over 2} $$
- Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой
- Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности
Свойства и признаки равнобедренной трапеции
- В равнобедренной трапеции углы при любом основании равны (∠ADC = ∠DCB и ∠DAB = ∠ABC)
- В равнобедренной трапеции длины диагоналей равны (AC = BD)
- Если трапецию можно вписать в окружность, то трапеция – равнобедренная
- Около равнобедренной трапеции можно описать окружность
Формулы площади произвольной трапеции
Площадь трапеции через основания и высоту
$$ S = {AB + DC \over 2} * AG $$Площадь трапеции через среднюю линию и высоту
$$ S = FE * AG $$Площадь трапеции через диагонали и угол между ними
$$ S = {AC * BD \over 2} * sin(∠AOD) = {AC * BD \over 2} * sin(∠AOB) $$Площадь трапеции через четыре стороны
$$ S = {DC + AB \over 2} * \sqrt{AD^2 — ({(DC — AB)^2 + AD^2 — BC^2 \over 2 * (DC — AB)})^2} $$Формулы площади равнобедренной трапеции
Площадь трапеции через стороны
$$ S = {DC + AB \over 2} * \sqrt{AD^2 — {(DC — AB)^2 \over 4}} $$Площадь трапеции через стороны и угол
$$ S = AD * sin(∠ADC) * (DC — AD * cos(∠ADC)) $$ $$ S = AD * sin(∠ADC) * (AB + AD * cos(∠ADC)) $$Площадь трапеции через диагонали и угол между ними
$$ S = {AC^2 \over 2} * sin(∠AOD) = {AC^2 \over 2} * sin(∠BOC) $$Площадь трапеции через среднюю линию, боковую сторону и угол при основании
$$ S = FE * AD * sin(∠ADC) = FE * AD * sin(∠DAB) $$Площадь трапеции если в нее вписана окружность
$$ S = {4 * R_В^2 \over sin(∠ADC)} = {4 * R_В^2 \over sin(∠DAB)} $$ $$ S = {AB * DC \over sin(∠ADC)} = {AB * DC \over sin(∠DAB)} $$Формулы сторон произвольной трапеции
Основание через другое основание и среднюю линию
$$ AB = 2 * FE — DC $$ $$ DC = 2 * FE — AB $$Основание через другое основание, диагонали и угол между ними
$$ DC = {AC * BD \over AG} * sin(∠AOD) — AB $$ $$ AB = {AC * BD \over AG} * sin(∠AOD) — DC $$Длины сторон
$$ DC = AB + AG * (ctg(∠ADC) + ctg(∠BCD)) $$ $$ AB = DC — AG * (ctg(∠ADC) + ctg(∠BCD)) $$ $$ DC = AB + AD * cos(∠ADC) + BC * cos(∠BCD) $$ $$ AB = DC — AD * cos(∠ADC) — BC * cos(∠BCD) $$ $$ AD = {AG \over sin(∠ADC)} $$ $$ BC = {AG \over sin(∠BCD)} $$Формулы сторон равнобедренной трапеции
Длины сторон
$$ AD = {AG \over sin(∠ADC)} $$ $$ AD = {DC — AB \over 2 * cos(∠ADC)} $$ $$ DC = AB + 2 * AG * ctg(∠ADC) $$ $$ AB = DC — 2 * AG * ctg(∠ADC) $$ $$ DC = AB + 2 * AB * cos(∠ADC) $$ $$ AB = DC — 2 * AB * cos(∠ADC) $$Длина основания через диагональ, боковую сторону и другое основание
$$ DC = {AC^2 — DA^2 \over AB} $$ $$ AB = {AC^2 — DA^2 \over DC} $$Длина боковой стороны через диагональ и основания
$$ AD = \sqrt{AC^2 — AB * DC} $$Длина основания через высоту, другое основание, диагонали и угол между ними
$$ DC = {AC^2 \over AG} * sin(∠AOD) — AB $$ $$ AB = {AC^2 \over AG} * sin(∠AOD) — DC $$Длина основания через высоту, другое основание и площадь трапеции
$$ DC = {2 * S \over AG} — AB $$ $$ AB = {2 * S \over AG} — DC $$Длина боковой стороны через площадь трапеции, среднюю линию и угол при основании
$$ AD = {S \over FE * sin(∠ADC)} = {S \over FE * sin(∠DAB)} $$Длина боковой стороны через площадь трапеции, основания и угол при основании
$$ AD = {2 * S \over (AB + DC) * sin(∠ADC)} $$ $$ AD = {2 * S \over (AB + DC) * sin(∠DAB)} $$Формулы сторон прямоугольной трапеции
Длины оснований
$$ DC = AB + BC * cos(∠BCD) = AB + AD * ctg(∠BCD) $$ $$ AB = DC — BC * cos(∠BCD) = DC — AD * ctg(∠BCD) $$ $$ DC = AB + \sqrt{BC^2 — AD^2} $$ $$ AB = DC — \sqrt{BC^2 — AD^2} $$Длина основания через боковую сторону, другое основание, диагонали и угол между ними
$$ DC = {AC * BD \over AD} * sin(∠AOD) — AB $$ $$ AB = {AC * BD \over AD} * sin(∠AOD) — DC $$Длина основания через площадь трапеции, другое основание и высоту
Высота в прямоугольной трапеции равна стороне, которая перпендикулярна основаниям (AD = AG) $$ DC = {2 * S \over AD} — AB $$ $$ AB = {2 * S \over AD} — DC $$Формулы диагоналей произвольной трапеции
Длина диагоналей через четыре стороны
$$ BD = \sqrt{BC^2 + DC * AB — {DC * (BC^2 — AD^2) \over DC — AB}} $$ $$ AC = \sqrt{AD^2 + DC * AB — {DC * (AD^2 — BC^2) \over DC — AB}} $$Длина диагоналей по теореме косинусов
$$ BD = \sqrt{DC^2 + BC^2 — 2 * DC * BC * cos(∠BCD)} $$ $$ AC = \sqrt{DC^2 + AD^2 — 2 * DC * AD * cos(∠ADC)} $$Длина диагоналей через высоту
$$ BD = \sqrt{AG^2 + (DC — AG * ctg(∠BCD))^2} $$ $$ BD = \sqrt{AG^2 + (AB + AG * ctg(∠ADC))^2} $$ $$ BD = \sqrt{DC^2 + BC^2 — 2 * DC * \sqrt{BC^2 — AG^2}} $$ $$ AC = \sqrt{AG^2 + (DC — AG * ctg(∠ADC))^2} $$ $$ AC = \sqrt{AG^2 + (AB + AG * ctg(∠BCD))^2} $$ $$ AC = \sqrt{DC^2 + AD^2 — 2 * DC * \sqrt{AD^2 — AG^2}} $$Длина диагоналей через стороны и другую диагональ
$$ BD = \sqrt{AD^2 + BC^2 + 2 * DC * AB — AC^2} $$ $$ AC = \sqrt{AD^2 + BC^2 + 2 * DC * AB — BD^2} $$Длина диагоналей через высоту, основания, другую диагональ и угол между диагоналей
$$ BD = {AG * (DC + AB) \over AC * sin(∠AOD)} $$ $$ AC = {AG * (DC + AB) \over BD * sin(∠AOD)} $$ $$ sin(∠AOD) = sin(∠AOB) $$Длина диагоналей через площадь трапеции, другую диагональ и угол между диагоналей
$$ BD = {2 * S \over AC * sin(∠AOD)} $$ $$ AC = {2 * S \over BD * sin(∠AOD)} $$ $$ sin(∠AOD) = sin(∠AOB) $$Длина диагоналей через среднюю линию, высоту, другую диагональ и угол между диагоналей
$$ BD = {2 * FE * AG \over AC * sin(∠AOD)} $$ $$ AC = {2 * FE * AG \over BD * sin(∠AOD)} $$ $$ sin(∠AOD) = sin(∠AOB) $$Формулы диагоналей равнобедренной трапеции
Длина диагоналей через стороны
$$ AC = \sqrt{AD^2 + AB * DC} $$Длина диагоналей по теореме косинусов
$$ AC = \sqrt{DC^2 + AD^2 — 2 * DC * AD * cos(∠ADC)} $$ $$ AC = \sqrt{DC^2 + AD^2 + 2 * DC * AD * cos(∠DAB)} $$ $$ AC = \sqrt{AB^2 + AD^2 — 2 * AB * AD * cos(∠DAB)} $$ $$ AC = \sqrt{AB^2 + AD^2 + 2 * AB * AD * cos(∠ADC)} $$Длина диагоналей
$$ AC = \sqrt{AG^2 + FE^2} $$ $$ AC = \sqrt{AG^2 + {(DC + AB)^2 \over 4 }} $$ $$ AC = \sqrt{{AG * (AB + DC) \over sin(∠AOD)}} = \sqrt{{2 * S \over sin(∠AOD)}} = \sqrt{{2 * FE * AG \over sin(∠AOD)}} $$Длина диагоналей через высоту основание и угол при основании
$$ AC = \sqrt{AG^2 + (DC — AG * ctg(∠ADC))^2} $$ $$ AC = \sqrt{AG^2 + (AB + AG * ctg(∠ADC))^2} $$Длина диагоналей через сторону и высоту
$$ AC = \sqrt{DC^2 + AD^2 — 2 * DC * \sqrt{AD^2 — AG^2}} $$Формулы диагоналей прямоугольной трапеции
$$ BD = \sqrt{AD^2 + AB^2} $$ $$ AC = \sqrt{AC^2 + DC^2} $$Формулы средней линии произвольной трапеции
Длина средней линии через основания
$$ FE = {DC + AB \over2} $$Длина средней линии через основание, высоту и углы при нижнем основании
$$ FE = DC — AG * {ctg(∠ADC) + ctg(∠BCD) \over 2} $$ $$ FE = AB + AG * {ctg(∠ADC) + ctg(∠BCD) \over 2} $$Длина средней линии через диагонали, высоту и угол между диагоналями
$$ FE = {AC * BD \over 2 * AG} * sin(∠AOD) $$ $$ FE = {AC * BD \over 2 * AG} * sin(∠AOB) $$Длина средней линии через площадь и высоту
$$ FE = {S \over AG} $$Формулы средней линии равнобедренной трапеции
Длина средней линии через основания
$$ FE = {DC + AB \over2} $$Длина средней линии через основание, высоту и углы при нижнем основании
$$ FE = DC — AG * ctg(∠ADC) = AB + AG * ctg(∠ADC) $$Длина средней линии через основания, боковую сторону и высоту
$$ FE = DC — \sqrt{AD^2 — AG^2} = AB + \sqrt{AD^2 — AG^2} $$Длина средней линии через диагонали, высоту и угол между диагоналями
$$ FE = {AC^2 \over 2 * AG} * sin(∠AOD) = {AC^2 \over 2 * AG} * sin(∠AOB) $$Длина средней линии через площадь и боковую сторону
$$ FE = {S \over AD * sin(∠ADC)} $$Формулы средней линии прямоугольной трапеции
Длина средней линии через основания, высоту и угол при нижнем основании
$$ FE = DC — AG * {ctg(∠BCD) \over 2} $$ $$ FE = AB + AG * {ctg(∠BCD) \over 2} $$Длина средней линии через основания, боковую сторону и угол при нижнем основании
$$ FE = DC — BC * {cos(∠BCD) \over 2} $$ $$ FE = AB + BC * {cos(∠BCD) \over 2} $$Длина средней линии через основания и боковые стороны
$$ FE = DC — {\sqrt{BC^2 — AD^2} \over 2} $$ $$ FE = AB + {\sqrt{BC^2 — AD^2} \over 2} $$Длина средней линии через диагонали, высоту и угол между диагоналями
$$ FE = {AC * BD \over 2 * AG} * sin(∠AOD) $$ $$ FE = {AC * BD \over 2 * AG} * sin(∠AOB) $$Формулы высоты произвольной трапеции
Длина высоты через четыре стороны
$$ AG = \sqrt{AD^2 — ({(DC — AB)^2 + AD^2 — BC^2 \over 2 * (DC — AB)})^2} $$Длина высоты через боковую сторону и прилегающий угол к основанию
$$ AG = AD * sin(∠ADC) = BC * sin(∠BCD) $$Длина высоты через диагонали и углы между ними
$$ AG = {AC * BD \over AB + DC} * sin(∠AOD) $$ $$ AG = {AC * BD \over AB + DC} * sin(∠AOB) $$Длина высоты через среднюю линию, диагонали и углы между ними
$$ AG = {AC * BD \over 2 * FE} * sin(∠AOD) $$ $$ AG = {AC * BD \over 2 * FE} * sin(∠AOB) $$Длина высоты через площадь и основания
$$ AG = {2 * S \over AB + DC} $$Длина высоты через площадь и среднюю линию
$$ AG = {S \over FE} $$Формулы высоты равнобедренной трапеции
Длина высоты через по сторонам
$$ AG = \sqrt{AD^2 — {(DC — AB)^2 \over 4}} $$Длина высоты через боковую сторону и прилегающий угол к основанию
$$ AG = AD * sin(∠ADC) $$Длина высоты через основания и прилегающий угол к основанию
$$ AG = {DC — AB \over 2} * tg(∠ADC) $$Длина высоты через диагонали и углы между ними
$$ AG = {AC^2 \over AB + DC} * sin(∠AOD) $$ $$ AG = {AC^2 \over AB + DC} * sin(∠AOB) $$Длина высоты через площадь и основания
$$ AG = {2 * S \over AB + DC} $$Длина высоты через площадь и среднюю линию
$$ AG = {S \over FE} $$Формулы боковых сторон прямоугольной трапеции
Сторона AD
Сторона AD в прямоугольной трапеции равна высоте, поэтому все формулы высоты произвольной трапеции актуальны для стороны AD прямоугольной трапеции.Сторона BC по трём сторонам
$$ BC = \sqrt{AD^2 + (DC — AB)^2} $$Сторона BC через основания и угол ∠BCD
$$ BC = {DC — AB \over cos(∠BCD)} $$Сторона BC через Сторону AD
$$ BC = {AD \over sin(∠BCD)} $$Сторона BC через площадь, среднюю линию и угол ∠BCD
$$ BC = {S \over FE * sin(∠BCD)} $$Сторона BC через площадь, основания и угол ∠BCD
$$ BC = {2 * S \over (AB + DC) * sin(∠BCD)} $$Все формулы средней линии трапеции
Трапеция это фигура, которая имеет четыре стороны, две из которых параллельны, а две другие, нет. Параллельные стороны называются — верхнее основание и нижнее основание. Две другие, называются боковыми сторонами.
Средняя линия трапеции — отрезок соединяющий середины боковых сторон и расположен параллельно к основаниям. Длина средней линии, равна полу сумме оснований.
1. Формула средней линии трапеции через основания

b — верхнее основание
a — нижнее основание
m— средняя линия
Формула средней линии, (m ):

2. Формулы средней линии через основание, высоту и углы при нижнем основании

b — верхнее основание
a — нижнее основание
α, β — углы трапеции
h — высота трапеции
m — средняя линия
Формулы средней линии трапеции, (m):


3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями

α, β — углы между диагоналями
d1 , d2 — диагонали трапеции
h — высота трапеции
m — средняя линия
Формулы средней линии трапеции, (m ):

4. Формула средней линии трапеции через площадь и высоту

S — площадь трапеции
h — высота трапеции
m — средняя линия
Формула средней линии трапеции, (m):

Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Площадь трапеции
Площадь трапеции, формулы и калькулятор для вычисления площади в режиме онлайн и сводная таблица с формулами площади трапеции. Приведены формулы для всех типов трапеций и частные случаи для равнобедренных трапеций.
Таблица с формулами площади трапеции (в конце страницы)
— Вычисления (показано) (скрыто)
— примечания (показано) (скрыто)
Площадь для всех видов трапеции
1
Площадь трапеции по высоте и двум основаниям

… подготовка …
a — основание
b — основание
h — высота
2
Площадь трапеции по высоте и средней линии
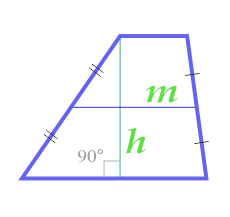
… подготовка …
m — средняя линия
h — высота
3
Площадь трапеции по четырем сторонам

… подготовка …
a — основание
b — основание
c — сторона
d — сторона
4
Площадь трапеции по диагонали и углу между диагоналями
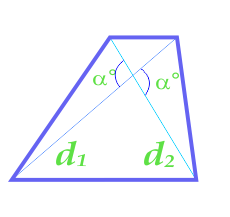
… подготовка …
d1 — диагональ
d2 — диагональ
α° — угол между диагоналями
5
Площадь трапеции через ее основания и углы при основании

… подготовка …
a — основание
b — основание
α° — угол при основании
β° — угол при основании
Площадь равнобедренной трапеции
6
Площадь равнобедренной трапеции через ее стороны

… подготовка …
a — сторона
b — сторона
c — сторона
7
Площадь равнобедренной трапеции через малое основание, боковую сторону и угол при большем основании

… подготовка …
a — основание
c — сторона
α° — угол при основании
8
Площадь равнобедренной трапеции через большее основание, боковую сторону и угол при большем основании

… подготовка …
b — основание
c — сторона
α° — угол при основании
9
Площадь равнобедренной трапеции через основания и угол при основании

… подготовка …
a — основание
b — основание
α° — угол при основании
10
Площадь равнобедренной трапеции через диагонали и угол между диагоналями

… подготовка …
α° — угол между диагоналями
11
Площадь равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
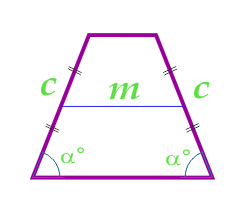
… подготовка …
m — средняя линия
c — сторона
α° — угол между сторонами
Площадь равнобедренной трапеции по радиусу вписанной окружности и углу между сторонами

Данная формула применима только для равнобедренных трапеций, в которые можно вписать окружность.
… подготовка …
r — радиус вписанной окружности
α° — угол между сторонами
13
Площадь равнобедренной трапеции через два ее основания и радиус вписанной окружности
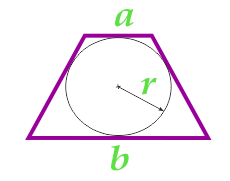
Данная формула применима только для равнобедренных трапеций, в которые можно вписать окружность.
… подготовка …
a — основание
b — основание
r — радиус вписанной окружности
14
Площадь равнобедренной трапеции через ее основания и угол при большем основании

Данная формула применима только для равнобедренных трапеций, в которые можно вписать окружность.
… подготовка …
a — основание
b — основание
α° — угол при основании
15
Площадь равнобедренной трапеции через стороны

Данная формула применима только для равнобедренных трапеций, в которые можно вписать окружность.
… подготовка …
a — основание
b — основание
c — сторона
16
Площадь равнобедренной трапеции через основания и среднюю линию
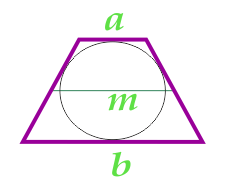
Данная формула применима только для равнобедренных трапеций, в которые можно вписать окружность.
… подготовка …
a — основание
b — основание
m — средняя линия
Примечание:
Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Таблица с формулами площади трапеции
В зависимости от известных исходных данных и вида трапеции, площадь трапеции можно вычислить по различным формулам.
Определения
Площадь трапеции – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой, образованной четырьмя последовательно соединенными отрезками (сторонами), два из которых параллельны друг другу
Трапеция – это геометрическая фигура, образованная четырьмя последовательно соединенными отрезками (сторонами), два из которых параллельны друг другу.
Основания трапеции – это параллельные стороны трапеции. Трапеция имеет большое и малое основание.
Средняя линия трапеции – это отрезок соединяющий середины боковых сторон трапеции и при этом всегда параллельный основаниям трапеции.
Высота трапеции – это отрезок проведенный между основаниями трапеции под углом 90 градусов к каждому из снований.
Сумма углов трапеции равна 360 градусов.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т.д.
Все формулы сторон трапеции
1. Формула длины основания трапеции через среднюю линию

a — нижнее основание
b — верхнее основание
m — средняя линия
Формулы длины оснований :


2. Формулы длины сторон через высоту и углы при нижнем основании

a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α, β — углы трапеции
h — высота трапеции
Формулы всех четырех сторон трапеции:






3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями

a — нижнее основание
b — верхнее основание
d1 , d2 — диагонали трапеции
α , β — углы между диагоналями
h — высота трапеции
Формулы длины сторон трапеции:


Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Все формулы площади трапеции. Найти онлайн
Формулы площади трапеции
Внимание! Десятичную дробь надо писать с точкой, а не с запятой!
Трапеция — четырехугольник, две противоположные стороны которого параллельны между собой, а две другие не параллельны. Параллельные стороны трапеции называются основаниями, а непараллельные — боковыми сторонами.
Площадь трапеции через основания и высоту
 $$S= \frac{a+b}{2}h $$
\(S\) — площадь трапеции
$$S= \frac{a+b}{2}h $$
\(S\) — площадь трапеции\(a\) — основание
\(b\) — основание
\(h\) — высота
\(a =\) \(b =\) \(h =\)
Площадь трапеции через высоту и среднюю линию
 $$S= mh $$
\(S\) — площадь трапеции
$$S= mh $$
\(S\) — площадь трапеции\(h\) — высота
\(m\) — средняя линия трапеции
\(h =\) \(m =\)
Площадь трапеции через четыре стороны
 $$S= \frac{a+b}{2} \sqrt{c^2-\left( \frac{(b-a)^2+c^2-d^2}{2(b-a)} \right)^2}$$
\(S\) — площадь трапеции
$$S= \frac{a+b}{2} \sqrt{c^2-\left( \frac{(b-a)^2+c^2-d^2}{2(b-a)} \right)^2}$$
\(S\) — площадь трапеции\(a, b, c, d\) — стороны
\(a =\) \(b =\)
\(c =\) \(d =\)
Площадь трапеции через диагонали и угол между ними
 $$S= \frac{1}{2}d_1d_2sin \alpha $$
\(S\) — площадь трапеции
$$S= \frac{1}{2}d_1d_2sin \alpha $$
\(S\) — площадь трапеции\(d_1, d_2\) — диагонали
\(\alpha\) — угол между диагоналями \(d_1\) и \(d_2\)
\(d_1 =\) \(d_2 =\) \(\alpha = \)
Для равнобедренной трапеции
Площадь равнобедренной трапеции через радиус вписанной окружности и угол
 $$S= \frac{4r^2}{sin \alpha}$$
\(S\) — площадь трапеции
$$S= \frac{4r^2}{sin \alpha}$$
\(S\) — площадь трапеции\(r\) — радиус вписанной окружности
\(\alpha\) — угол
\(r =\) \(\alpha =\)
Трапеция — это четырехугольник, в котором ровно одна пара противоположных сторон параллельна. Рассмотрим следующую трапецию, высота и длина которой известны.
Периметр трапеции — это просто сумма длин его сторон.
$ периметр = AB + BC + CD + DA $
Чтобы найти площадь трапеции, разбиваем ее на параллелограмм и треугольник, как показано на диаграмме.
$ \ begin {собрано}
область \ слева ({trapezium \, ABCD} \ right) = область \ left ({{\ text {triangle}} \, ADE} \ right) + область \ left ({{ \ text {параллелограмм}} \, ABCE} \ right) \\
= \ frac {1} {2} \ раз DE \ времена h + EC \ времена h \\
\ end {собрано} $
с противоположные стороны параллелограмма равны, $ EC = AB = {b_1} $
$ DE = DC — EC = {b_2} — {b_1} $
$ \ Площадь правой стрелки \ left ({trapezium \, ABCD} \ справа) = \ frac {h} {2} \ times \ left ({DE + 2EC} \ right) = \ frac {h} {2} \ times \ left ({{b_2} — {b_1} + 2 {b_1) }} \ right) = \ frac {h} {2} \ left ({{b_1} + {b_2}} \ right) $
Давайте рассмотрим пример, чтобы увидеть, как использовать эти формулы.2} $. Если его высота составляет 4 см, а непараллельные стороны — 6 см и 5 см, оцените его периметр.
Опции:
(a) 21 $, см $
(b) 25000 $, см $
(c) $ 27 \, см $
(d) ни один из этих
Ответ: (a)
Решение:
$ {\ text {area}} = \ frac {h} {2} \ left ({{b_1} + {b_2}} \ right) \ Rightarrow 20 = \ frac {4} {2} \ раз \ влево ({{b_1} + {b_2}} \ right) \ Rightarrow {b_1} + {b_2} = 10 \, см $
$ {\ text {периметр}} = 6 + 5 + {b_1} + {b_2} = 11 + 10 = 21 \, см $
,
координаты его Вершины.
Попробуй это Перетащите любую вершину трапеции ниже. Она останется трапециевидной, а площадь и периметр будут рассчитаны. Вы также можете перетащить исходную точку в (0,0) или переместить сам прямоугольник.
Площадь
Площадь трапеции рассчитывается путем умножения средней ширины на высоту. См. Определение трапеции (координатная геометрия), чтобы увидеть, как длина стороны и высота найдены. (Обратите также внимание, что средняя длина равна средней ширине.)
Как формула: где
b1, b2 — длины двух оснований (BC и AD),
a — высота трапеции
На рисунке выше, перетащите любую вершину трапеции и обратите внимание, как вычисляется площадь.
Периметр
Периметр трапеции — это просто сумма всех четырех сторон. Поскольку они не имеют никакого отношения друг к другу, для этого нет формулы. Просто найдите четыре длины сторон и сложите их. Длина каждой стороны определяется с помощью методов, описанных в Расстояние между двумя точками (с учетом их координат) которые используются, чтобы найти расстояние между конечными точками каждой стороны.
Пример
Найдите площадь и периметр трапеции на рисунке выше.Сначала нажмите «сброс» и «показать высоту».Площадь
- Во-первых, нам нужна длина двух оснований (параллельных сторон).
Они определяются путем расчета расстояния между конечными точками отрезков линий.
(См. Расстояние между двумя точками). Делая это, мы видим, что
BC = 22 и AD = 47
- Тогда нам нужна высота. Это перпендикулярное расстояние между основаниями. Как описано в
Трапеция (координатная геометрия) Есть несколько способов сделать это
в зависимости от того, вращается ли трапеция или нет.Делая это, мы видим, что
высота = 21
- Наконец, мы рассчитываем площадь как высоту, умноженную на среднюю ширину (средняя базовая длина): Что согласуется с расчетной цифрой выше.
Периметр
- Периметр является суммой четырех сторон длины.
Таким образом, они находятся путем расчета расстояния между конечными точками отрезков линий.
(См. Расстояние между двумя точками). Делая это, мы видим, что
BC = 22 AD = 47 AB = 22 CD = 28
- Наконец мы добавляем их, чтобы получить периметр
22 + 22 + 28 + 47 = 119
Что согласуется с расчетной цифрой выше.
Повернутый корпус
На рисунке выше трапециевидные основания параллельны оси X, что облегчает вычисления. Если вы нажмете «повернуто», это не будет иметь место. Все методы, описанные выше, все еще будут работать, но вы должны использовать правильный метод для определения расстояния между двумя точками, и высота, которая требует правильного метода для нахождения перпендикулярного расстояния от точки до линии. ВидетьЧто попробовать
- Нажмите «скрыть детали» и «повернуть», затем перетащите вершины трапеции вокруг, чтобы создать произвольный размер.
- Из координат угловых точек рассчитайте площадь и периметр трапеции.
- Затем нажмите «показать детали», чтобы проверить свой результат. (Результаты, показанные выше, округлены до целых чисел для ясности)
Ограничения
В целях ясности в апплете выше координаты округлены до целых чисел, а длины округлены до одного десятичного знака. Это может привести к тому, что расчеты будут немного отклонены.
Для более см. Учебные заметки
Другие темы координатной геометрии
(C) 2011 Copyright Math Открытая ссылка.
Все права защищены
Свойства трапеции
Определения и формулы для периметра трапеции, площади трапеции, свойств сторон и углов трапеции, свойств сторон и углов равнобедренной трапеции
Просто прокрутите вниз или нажмите на то, что вы хотите, и я буду прокручивать вниз для вас!
| Периметр трапеции: | |
| Чтобы найти периметр трапеции, просто сложите все длины сторон: Периметр = a + b + c + B |
| |
| Площадь трапеции: | |
| Найти площадь трапеции… Чем длиннее основание (внизу), тем больше B, а меньшим основанием (вверху) мало … |
| Да, это формула … Но давайте посмотрим, откуда она взялась! | |
Возьмите две копии трапеции (одну синюю трапецию и одну зеленую трапецию) … Наклоните одну вверх дном и склейте их вместе … Теперь у вас есть параллелограмм. Площадь параллелограмма = основание х высота Но это вдвое больше, чем нам нужно.Итак, умножьте на 1/2! |

Трапеция
(Переход к области трапеции или периметру трапеции)
Трапеция представляет собой 4-стороннюю плоскую форму с прямыми сторонами, имеющую , пару противоположных сторон, параллельных (отмечены стрелками ниже):
| Трапеция | равнобедренная трапеция |
трапеция:
| имеет пару параллельных сторон | |
— это равнобедренной трапеции , когда она имеет равных углов с параллельной стороны | |
| называется « трапеция » в Великобритании (см. Ниже) |
Играть с трапецией:
Параллельные стороны являются «основаниями»
Две другие стороны «ноги»
Расстояние (под прямым углом) от одной базы до другой называется «высотой»
Площадь трапеции
Район представляет собой среднее значение двух базовых длин в раз больше высоты : Площадь = a + b 2 × ч |
Пример: две базы трапеции имеют высоту 6 м и 4 м и высоту 3 м.Какова его площадь?
Площадь = 6 м + 4 м 2 × 3 м = 5 м × 3 м = 15 м 2
Инструмент Площадь многоугольника при рисовании полезен, когда вы можете нарисовать трапецию.
Периметр трапеции
Периметр — это расстояние по краям.
Периметр сумма всех сторон длины : Периметр = a + b + c + d |
Пример: трапеция имеет длину стороны 5 см, 12 см, 4 см и 15 см, каков ее периметр?
Периметр = 5 см + 12 см + 4 см + 15 см = 36 см
медиана трапеции
Медиана (также называемая средней линией или средним сегментом) — это отрезок на полпути между двумя основаниями. Длина медианы — это средняя из двух базовых длин: m = a + b 2 |
Вы можете вычислить площадь, когда вы знаете медиану, это просто медиана, умноженная на высоту:
Площадь = MH
Трапеция
Трапеция (Великобритания: трапеция) представляет собой четырехугольник без параллельных сторон.
США и Великобритания поменяли свои определения, например:
| Трапеция | Трапеция | |
| США: | пара параллельных сторон | НЕТ параллельных сторон |
| Великобритания: | НЕТ параллельных сторон | пара параллельных сторон |





Leave A Comment