
Курс повышения квалификации
Курс повышения квалификации

Курс профессиональной переподготовки
Учитель математики и информатики
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:

Общая информация
Номер материала: ДВ-119159
Вам будут интересны эти курсы:
Оставьте свой комментарий
Мы уже знакомы с понятием степени с целым показателем. Давайте разберемся, что такое степень с рациональным показателем.
Рациональный показатель – это выражение вида \(\frac{p}{q}\), где \(p\)-некоторое целое число, а \(q\) – натуральное число, причем \(q\ge2\).
Определение
Положительное число \(a\) в рациональной степени \(\frac{p}{q}\) является арифметическим корнем степени \(q\) из числа \(a\) в степени \(p\):
Обращаем ваше внимание, что
$$ \sqrt[q]{p}=(\sqrt[p]{a})^p,$$Неважно в каком порядке – сначала извлечь корень или возвести в степень, от этого смысл выражения не теряется. Как удобнее, так и считайте.
Пример 1 $$ 8^{\frac{2}{3}}=\sqrt[3]{8^2}=(\sqrt[3]{8})^2=2^2=4; $$ $$ 3^{\frac{1}{5}}=\sqrt[5]{3}; $$ $$ 5^{\frac{3}{2}}=\sqrt{5^3};$$ $$ 7^{-\frac{5}{6}}=\sqrt[6]{7^{-5}}.$$Теорема
Пусть есть некоторое положительное число \(a\) и целое число \(p\), тогда справедливы следующие соотношения:
$$1.\; a^{\frac{p}{q}}=(a^{\frac{1}{q}})^p,$$ $$2.\; a^{\frac{p}{q}}=a^{\frac{p*k}{q*k}},$$ $$ 3.\;a^p= a^{\frac{pq}{q}}, $$где \(k\) и \(q\) – натуральные числа большие 1.
Давайте попробуем их доказать:
Из определения степени с рациональным показателем следует, что:
$$ a^{\frac{p}{q}}=\sqrt[q]{a^p}=(\sqrt[p]{a})^p=(a^{\frac{1}{q}})^p,$$Опять из определения и свойства корня n-й степени следует:
$$ a^{\frac{p}{q}}=\sqrt[q]{a^p}=\sqrt[q*k]{a^{p*k}}= a^{\frac{p*l}{q*k}}, $$Третья формула на наш взгляд очевидна, просто сократить степень справа и получите исходное выражение.
Пример 2 $$a)\;8^{\frac{4}{3}}=(8^{\frac{1}{3}})^4=2^4=16;$$ $$б)\;4^{\frac{15}{5}}=4^{\frac{3}{1}}=4^3=64;$$ $$в)\;3^{-\frac{6}{2}}=3^{-3}=\frac{1}{3^3}=\frac{1}{27}.$$Свойства степени с рациональным показателем
Пусть \(a\) и \(b\) – некоторые положительные числа, а числа \(m\) и \(n\) – рациональные числа. Тогда выполняются соотношения:
$$ 1. \;a^m*a^n=a^{m+n}. $$При умножении степеней с рациональным показателем и одинаковым основанием их показатели степени складываются.
$$2. \; a^m:a^n=a^{m-n}.$$При делении степеней с рациональным показателем и одинаковым основанием их показатели степени вычитаются.
$$3. \; (a^m)^n=a^{m*n}.$$При возведении степени с рациональным показателем в степень с рациональным показателем их показатели перемножаются.
$$4. \; (a*b)^n=a^n*b^n.$$Степень с рациональным показателем от произведения двух положительных чисел равна произведению степеней этих множителей.
$$ 5.\; (\frac{a}{b})^n=\frac{a^n}{b^n}.$$Степень с рациональным показателем от частного двух положительных чисел равна частному степеней этих чисел.
И еще два очень важных свойства степеней. Они вам понадобятся при решении показательных уравнений и неравенств.
Пусть опять есть некоторое положительное число \(a>1\) и рациональные числа \(n\) и \(m\).
$$6.\;$$При \(n \gt 0\) \(a^n \gt 1\),
При \(n \lt 0\) \(0 \lt a^n \lt 1\).
$$7.$$Если же \(a \gt 1\) и \(n \gt m\), то
$$ a^n>a^m.$$Если \( 0 \lt a \lt 1 \) и \(n \gt m\), то
$$ a^n \lt a^m.$$Разберем несколько примеров:
Пример 3 $$ 3^{-\frac{3}{4}}*3^{-\frac{1}{4}}=3^{-\frac{3}{4}-\frac{1}{4}}=3^{-1}=\frac{1}{3};$$ $$ 2^{\frac{1}{2}}:2^{\frac{1}{4}}=2^{\frac{1}{2}-\frac{1}{4}}=2^{\frac{1}{4}}=\sqrt[4]{3};$$ $$ (5^{-\frac{1}{2}})^{-4}=5^{(-\frac{1}{2})*(-4)}=5^2=25; $$ $$ (0,125)^{-\frac{2}{3}}*8^{-\frac{2}{3}}=(0,125*8)^{-\frac{2}{3}}=1^{-\frac{2}{3}}=1; $$ $$ (4,4)^{\frac{1}{3}}:(0,55)^{\frac{1}{3}}=(\frac{4,4}{0,55})^{\frac{1}{3}}=8^{\frac{1}{3}}=\sqrt[3]{8}=2;$$ $$ 3^{\frac{1}{3}} \lt 3^{\frac{1}{2}},$$Так как основание степени больше единицы \(3 \gt 1\) и \(\frac{1}{3} \lt \frac{1}{2}\).
$$ (\frac{1}{5})^{\frac{1}{3}} \gt (\frac{1}{5})^{\frac{1}{2}}, $$Так как \(0 \lt \frac{1}{5} \lt 1\) и \(\frac{1}{3} \lt \frac{1}{2}\)
Вариант 1
1.Вычислить: (2-1 + 3-1)(2-1 — 3-1) + (2-1 20)-4 : 23
2.Найдите значение выражения
3.Упростить выражение 4 — (2
4.Вычислите +
5) Упростить выражение
6.Вычислить
Вариант 2
1.Вычислить: (3-1 + 3-1)(3-1 — 4-1) + (3-1 30)-4 : 33
2.Найдите значение выражения
3.Упростить выражение 4 — (2
4.Вычислите -1,5 – 7,5
5) Упростить выражение
6.Вычислить
Видеоурок 1: Степень с рациональным показателем
Видеоурок 2: Степень с рациональным показателем. Решение примеров
Лекция: Степень с рациональным показателем и её свойства
 Степень с рациональным показателем
Степень с рациональным показателем
Степень с рациональным показателем — это та, в показателе которой находится конечная обыкновенная или десятичная дробь.
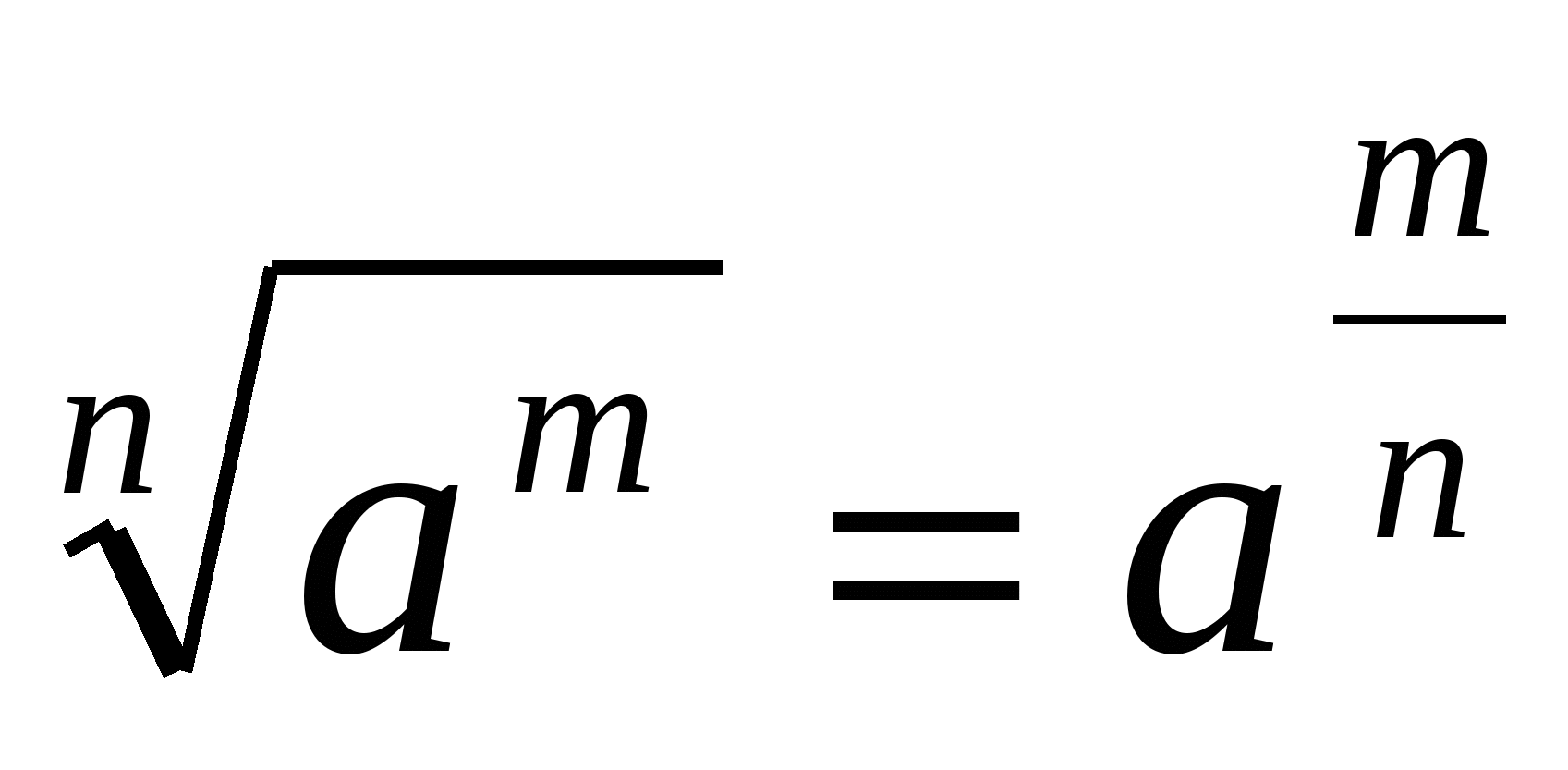
Любую степень с рациональным показателем можно представить в виде корня, чья степень будет равна знаменателю дроби, находящейся в показателе степени, а числитель будет степенью подкоренного выражения.
 Свойства степени с рациональным показателем
Свойства степени с рациональным показателем
Все, перечисленные ниже степени используются для рациональных чисел p, q и для положительных a, b.
1. Если Вам необходимо умножить две степени с рациональными показателями, которые имеют одинаковые основания, то в таком случае основание необходимо оставить без изменения, а показатели сложить.
ap * aq = ap+q.
Например:
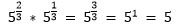
2. Если необходимо разделить две степени c рациональными показателями, которые имеют одинаковые основания, то в таком случае основание необходимо оставить без изменения, а показатели вычесть.
ap / aq = ap—q .
Например,
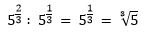
3. Если необходимо возвести одну степень в другую, основанием результата останется то же число, а показатели степени перемножаются.
(ap )q = ap*q
Например,
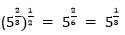
4. Если в некоторую степень необходимо возвести произведение произвольных чисел, то можно воспользоваться неким распределительным законом, при котором получим произведение различных оснований в одной и той же степени.
(a * b)p = ap * bp
5. Аналогичное свойство можно применять для деления степеней, иначе говоря, для возведения обыкновенной двоби в степень.
(a / b)p = ap / bq
6. Если некоторая дробь имеет отрицательный рациональный показатель степени, то для избавления от знака минуса, её следует перевернуть.
Например,
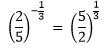
Очень важно помнить, что знак степени не влияет на знак выражения при возведении в степень.
Практическая работа по темам
«Степень с рациональным показателем, корень n-ой степени»
Вариант 1
Вариант 2
Задание 1. Вычислить:
а) 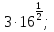 б)
б) 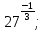 в)
в) 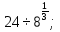
г) 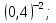 д)
д) 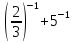 .
.
Задание 2. Вычислить:
а) 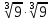 ; б)
; б) 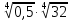 ; в)
; в) 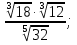
г) 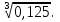
Задание 3. Найдите значение выражения 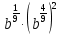
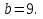
Задание 4. Найдите значение выражения 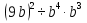 при
при 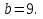
Задание 5. Найдите значение выражения 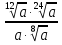
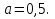
Задание 6. Вычислить: 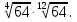
Задание 1. Вычислить:
а) 5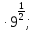 б)
б) 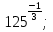 в) 81
в) 81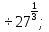
г) 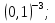 д)
д) 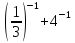 .
.
Задание 2. Вычислить:
а) 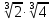 ; б)
; б) 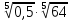
в) 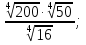 г)
г) 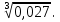
Задание 3. Найдите значение выражения 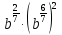 при
при 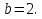
Задание 4. Найдите значение выражения 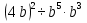
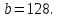
Задание 5. Найдите значение выражения 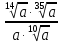 при
при 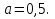
Задание 6. Вычислить: 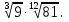
Вариант 3
Вариант 4
Задание 1. Вычислить:
а) 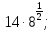 б)
б) 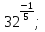 в)
в) 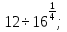
г) 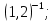 д)
д) 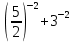
Задание 2. Вычислить:
а) 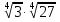 ; б)
; б) 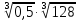 ;
;
в) 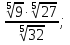 г)
г) 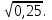
Задание 3.
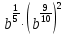 при
при 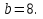
Задание 4. Найдите значение выражения 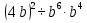 при
при 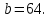
Задание 5. Найдите значение выражения 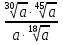 при
при 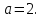
Задание 6. Вычислить: 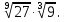
Задание 1. Вычислить:
а) 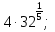 б)
б) 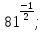 в) 3
в) 3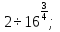
г) 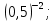 д)
д) 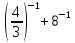 .
.
Задание 2. Вычислить:
а) 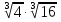 ; б)
; б) 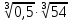 ;
;
в) 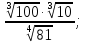 г)
г) 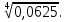
Задание 3. Найдите значение выражения 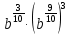 при
при 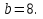
Задание 4. Найдите значение выражения 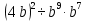 при
при 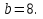
Задание 5. Найдите значение выражения 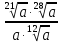 при
при 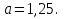
Задание 6. Вычислить: 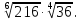
Время выполнения – 45 минут
Практическая работа по темам
«Степень с рациональным показателем, корень n-ой степени»
Вариант 5
Вариант 6
Задание 1. Вычислить:
а) 7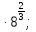 б)
б) 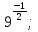 в)
в) 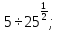
г) 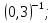 д)
д) 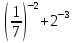 .
.
Задание 2. Вычислить:
а) 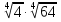 ; б)
; б) 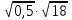 ; в)
; в) 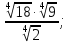
г) 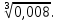
Задание 3. Найдите значение выражения 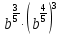 при
при 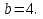
Задание 4. Найдите значение выражения 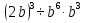 при
при 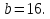
Задание 5. Найдите значение выражения 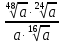 при
при 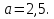
Задание 6. Вычислить: 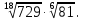
Задание 1. Вычислить:
а) 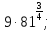 б)
б) 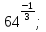 в)
в) 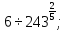
г) 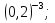 д)
д) 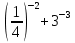 .
.
Задание 2. Вычислить:
а) 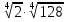 ; б)
; б) 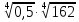 ;
;
в) 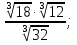 г)
г) 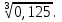
Задание 3. Найдите значение выражения 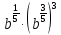 при
при 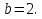
Задание 4. Найдите значение выражения 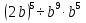 при
при 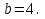
Задание 5. Найдите значение выражения 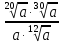 при
при 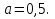
Задание 6. Вычислить: 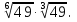
Вариант 7
Вариант 8
Задание 1. Вычислить:
а) 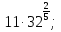 б)
б) 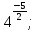 в)
в) 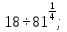
г) 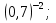 д)
д) 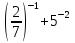 .
.
Задание 2. Вычислить:
а) 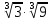 ; б)
; б) 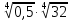 ; в)
; в) 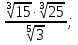
г) 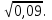
Задание 3. Найдите значение выражения 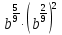 при
при 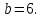
Задание 4. Найдите значение выражения 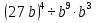 при
при 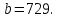
Задание 5. Найдите значение выражения 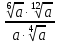 при
при 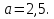
Задание 6. Вычислить: 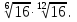
Задание 1. Вычислить:
а) 10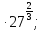 б)
б) 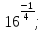 в)
в) 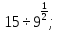
г) 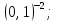 д)
д) 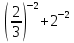 .
.
Задание 2. Вычислить:
а) 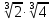 ; б)
; б) 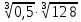 ;
;
в) 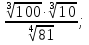 г)
г) 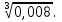
Задание 3. Найдите значение выражения 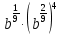 при
при 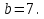
Задание 4. Найдите значение выражения 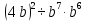 при
при 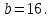
Задание 5. Найдите значение выражения 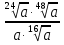 при
при 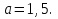
Задание 6. Вычислить: 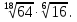
Время выполнения – 45 минут
Контрольная работа по алгебре в 9 классе
«Степень с рациональным показателем»
Цель работы: выявить уровень соответствия знаний учащихся требованиям современного стандарта
Кодификатор элементов содержания к уровню подготовке учащихся 9 классов для проведения контрольной работы по теме
«Степень с рациональным показателем»
№ задания
Элементы содержания, проверяемые заданиями контрольной работы
Кол-во баллов
1.
Степень с рациональным показателем
1
Формула разности квадратов
1
Свойства степеней
1
2.
Корень натуральной степени
1
Действия с рациональными числами
1
3.
Корень натуральной степени
1
Решение дробно-рационального неравенства
1
4.
Свойства арифметического корня
1
Приведение подобных слагаемых
1
5.
Степень с целым показателем
1
Степень с рациональным показателем
1
Степень с нулевым показателем
1
Арифметические действия с положительными и отрицательными числами
1
6.
Степень с рациональным показателем
1
Вынесение общего множителя за скобки
1
Сокращение дробей
1
7.
Степень с рациональным показателем
1
Свойства степеней
1
Действия с рациональными числами
1
Всего
19
Критерии оценивания:
«5»- 17-19 баллов «4»-14-16 баллов
«3»-10-13 баллов «2»-12 и менее баллов
Контрольная работа №2
Степень с рациональным показателем
Вариант 1
А1. Вычислите 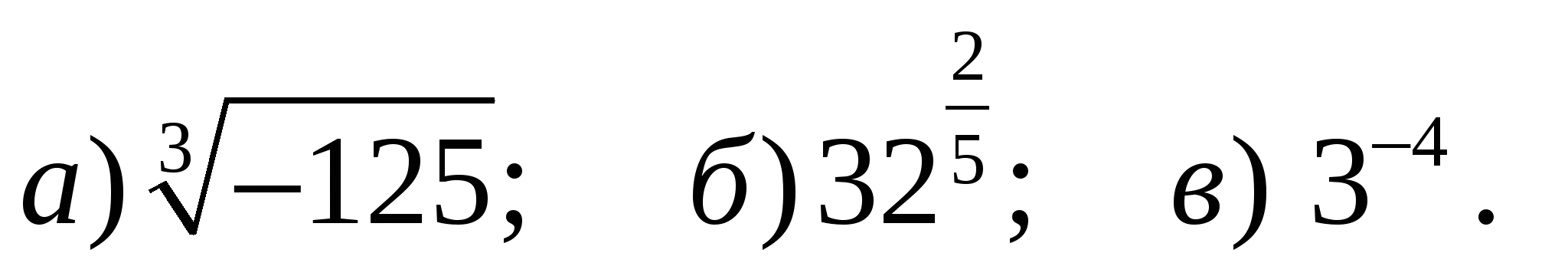
А2. Вычислите:
а) 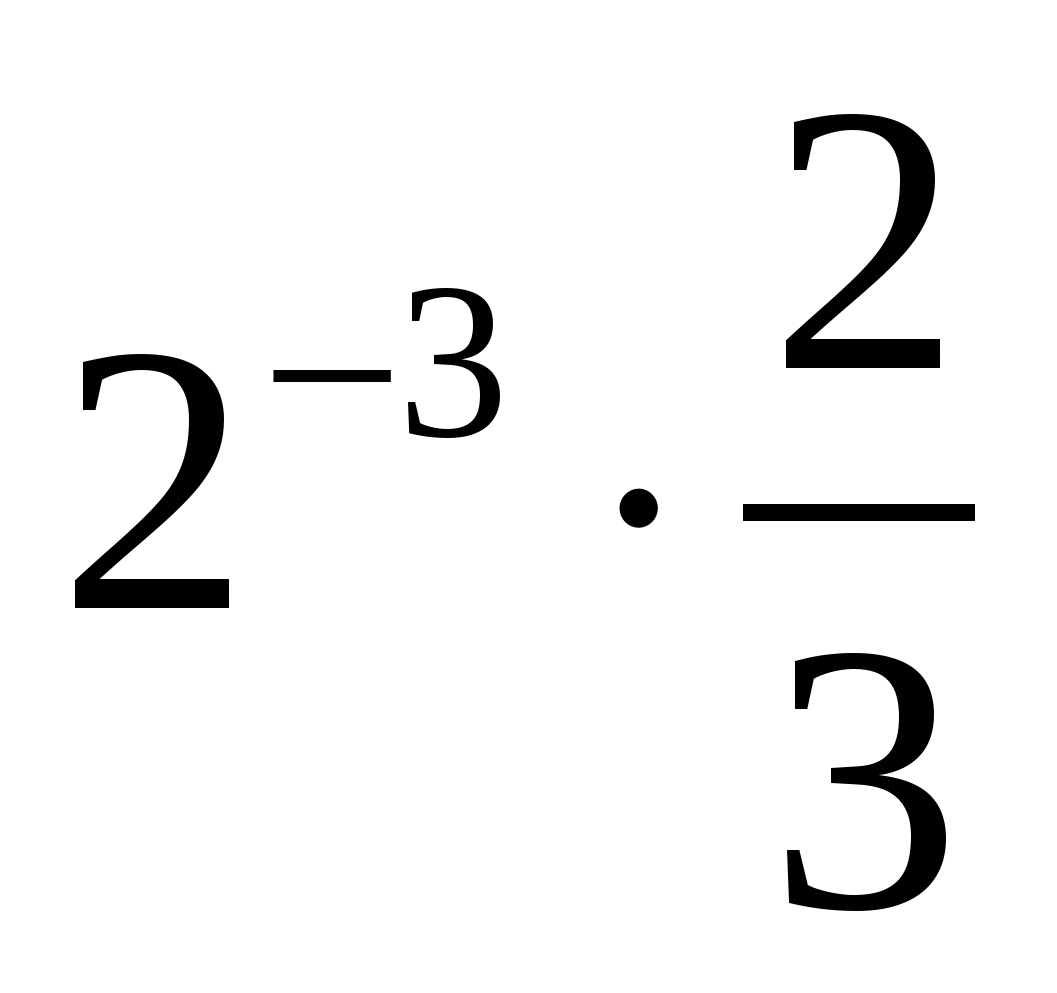 ; б)
; б) 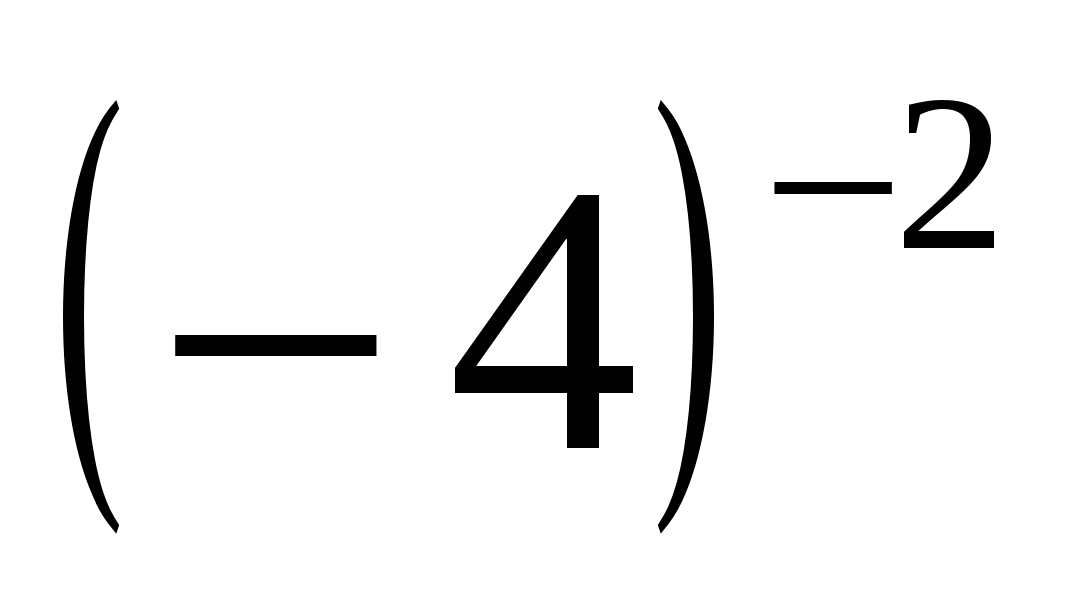 ; в)
; в) 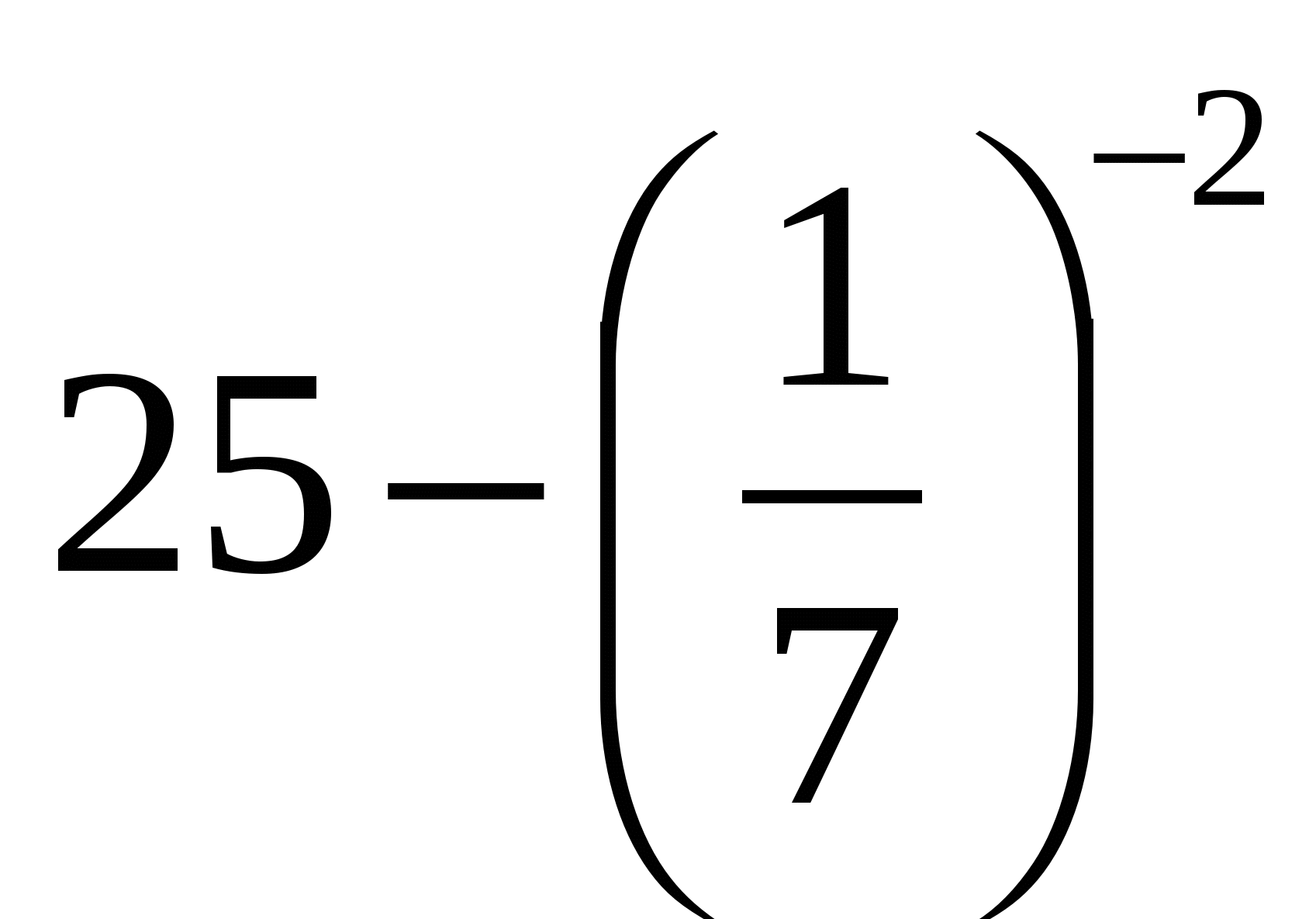 .
.
А3. Вычислите : а) 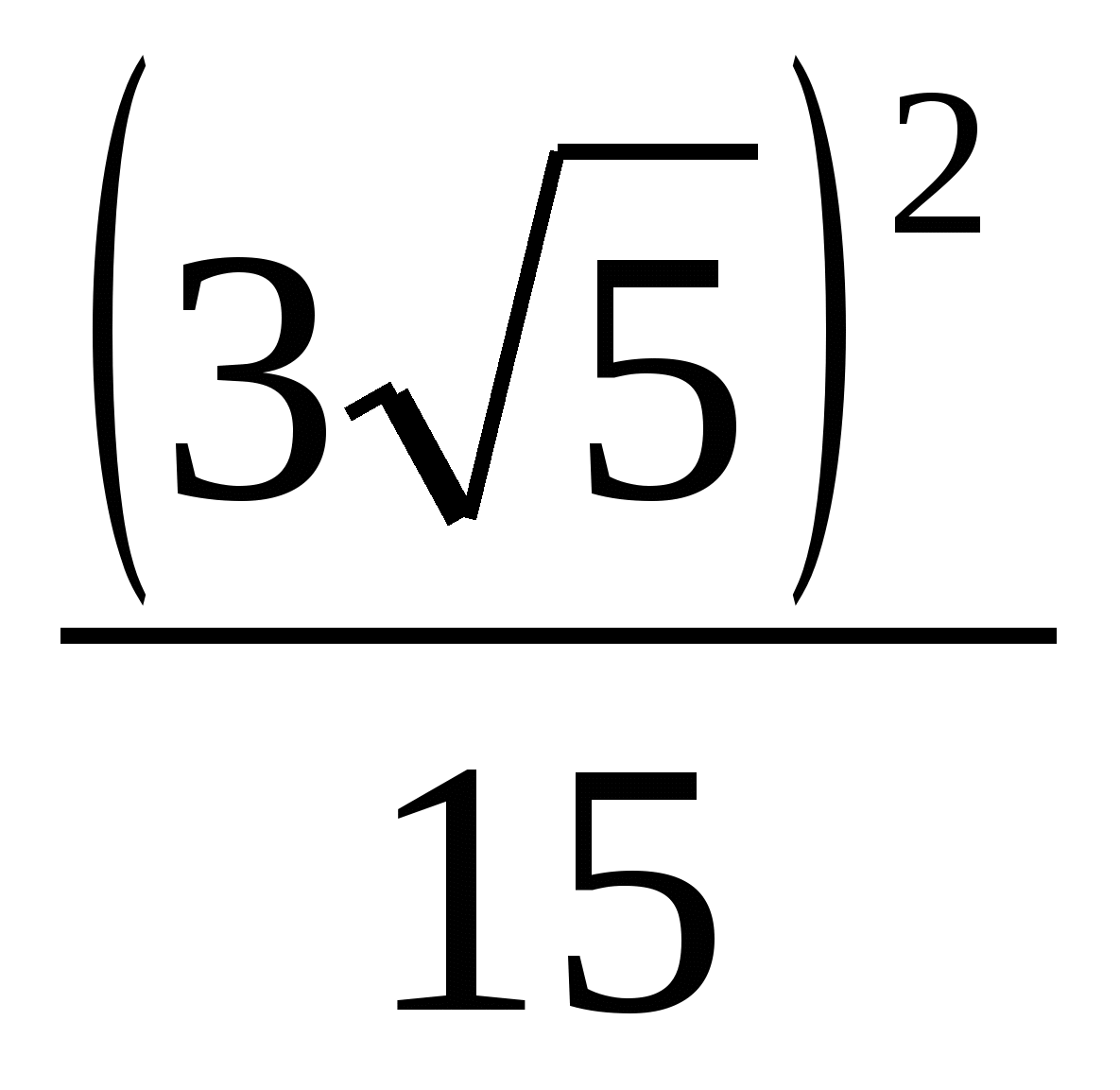 ; б)
; б) 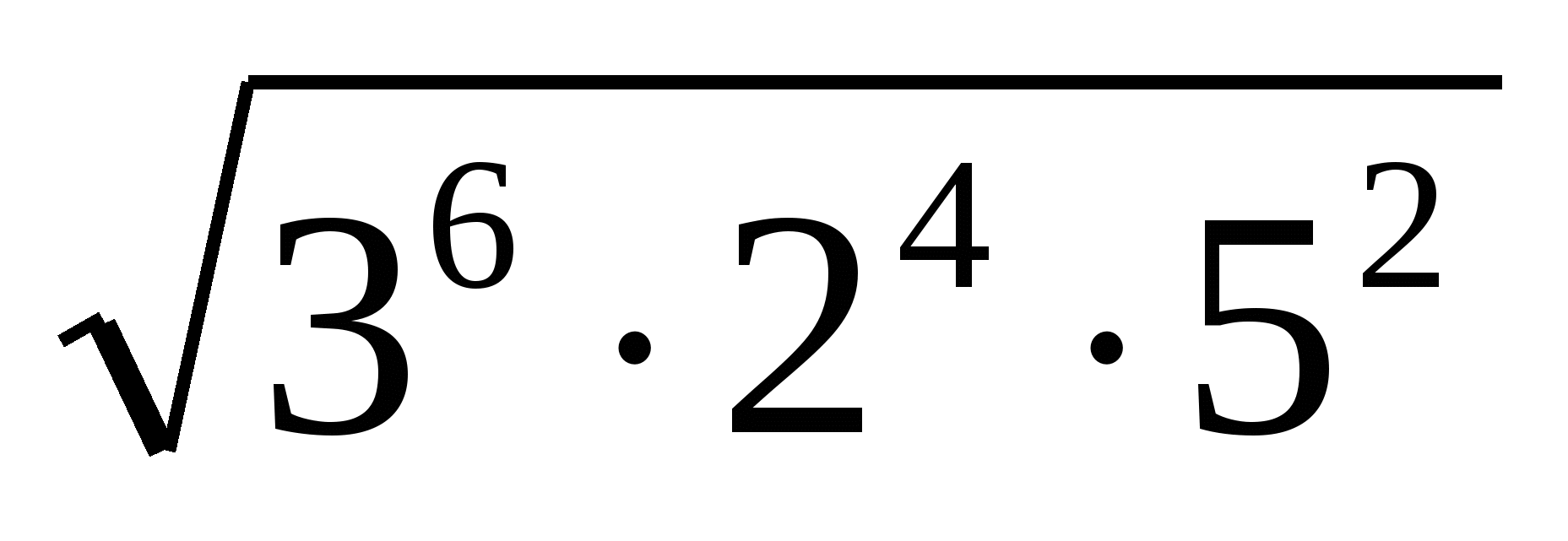 в)
в) 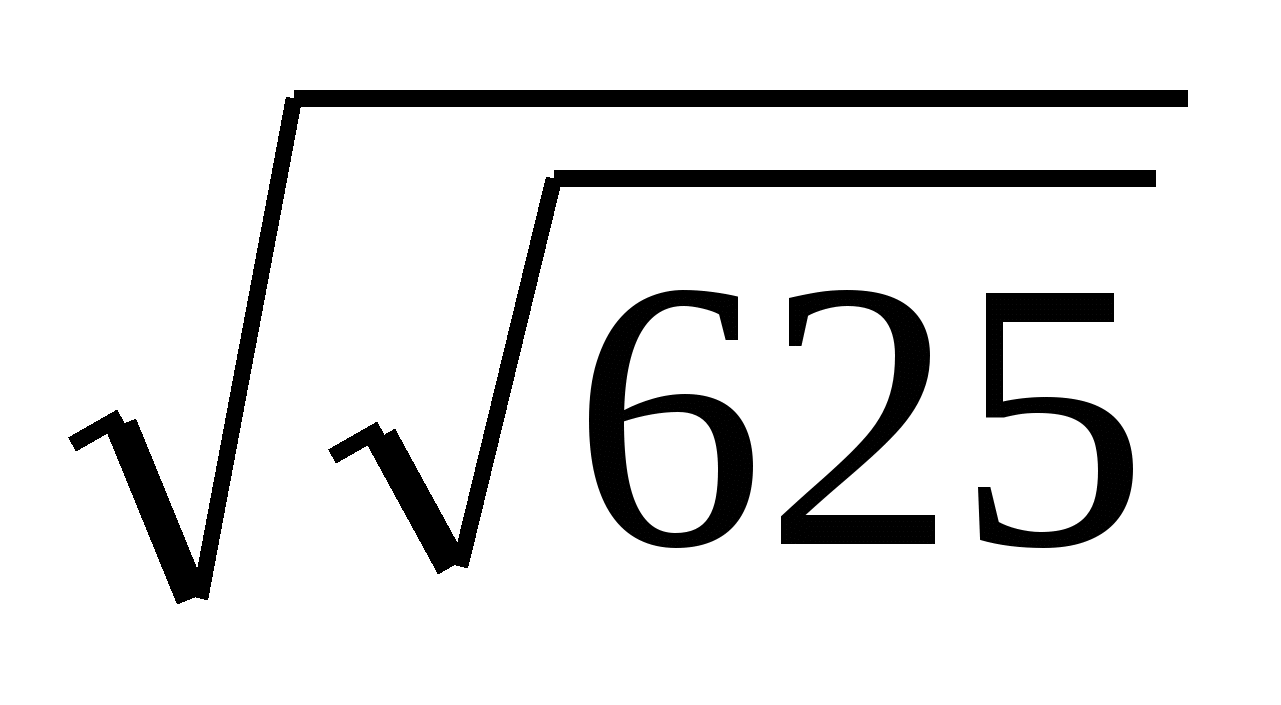 .
.
А4. Упростите выражение: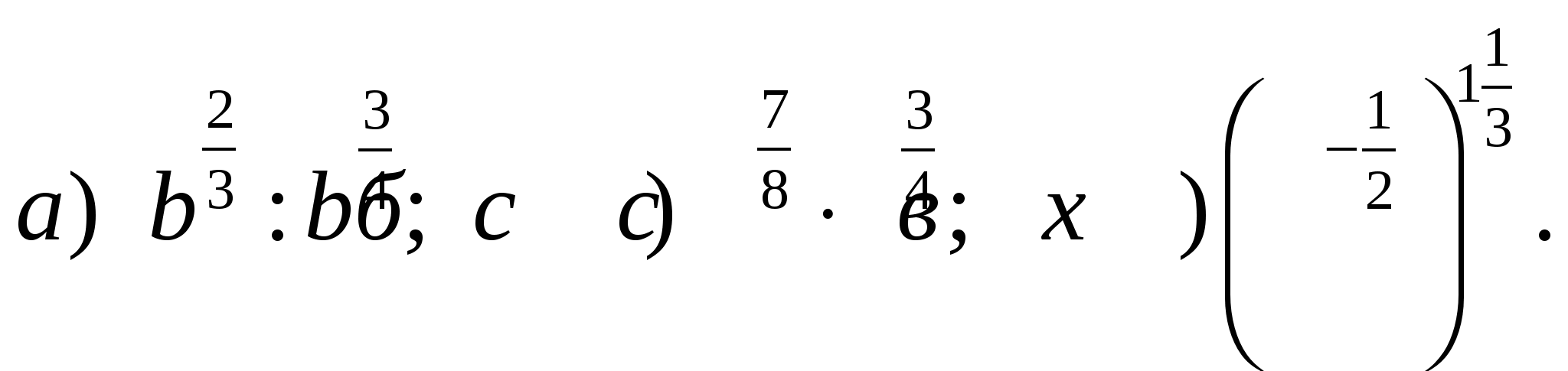
А5. Вынесите множитель из под знака корня: 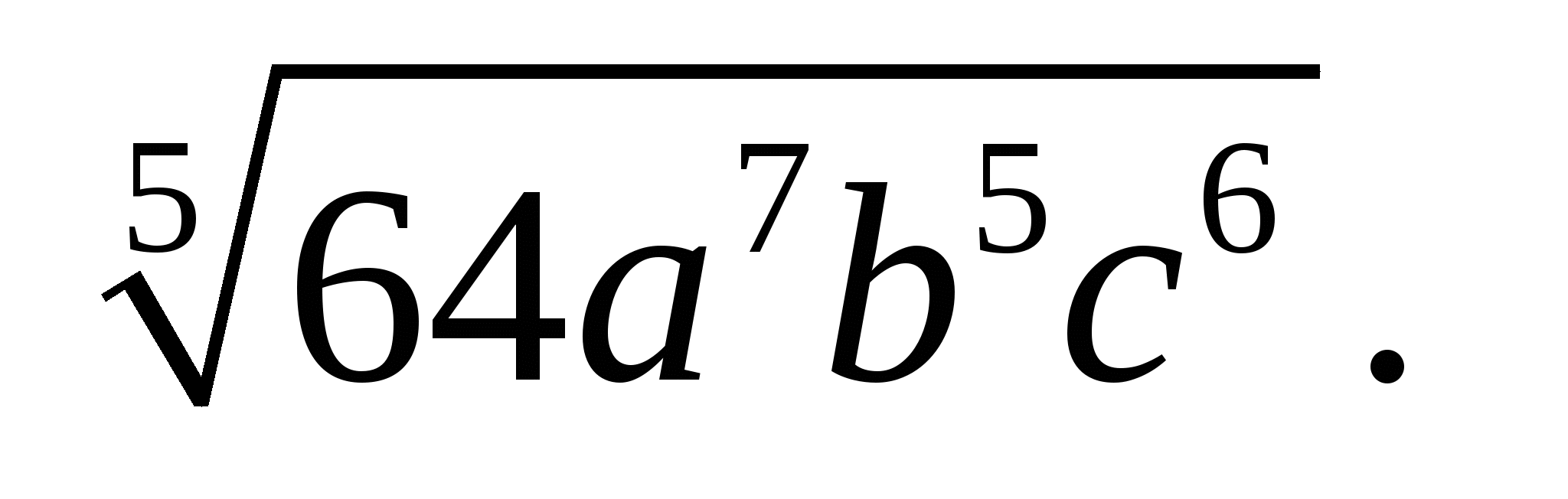
В1.Вычислите значение выражения 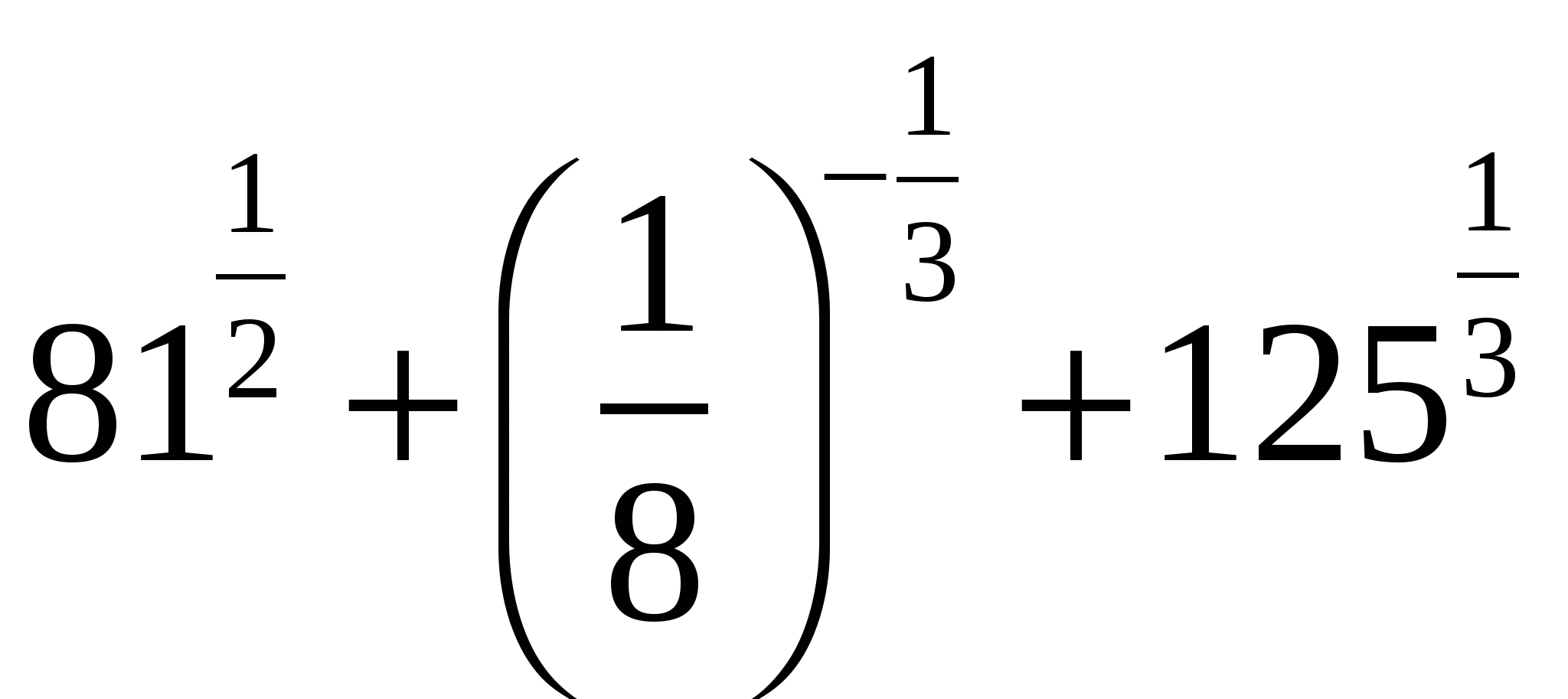 .
.
В2. Упростите выражение 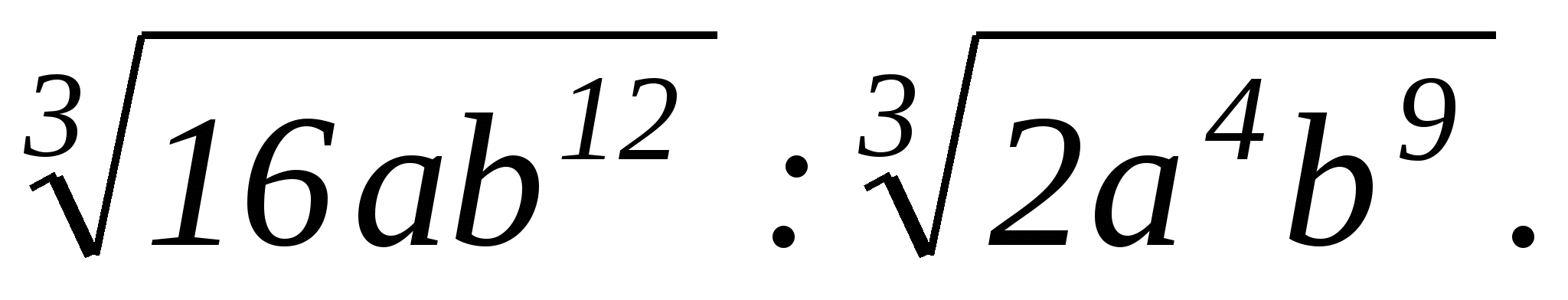
В3. Представьте в виде десятичной дроби 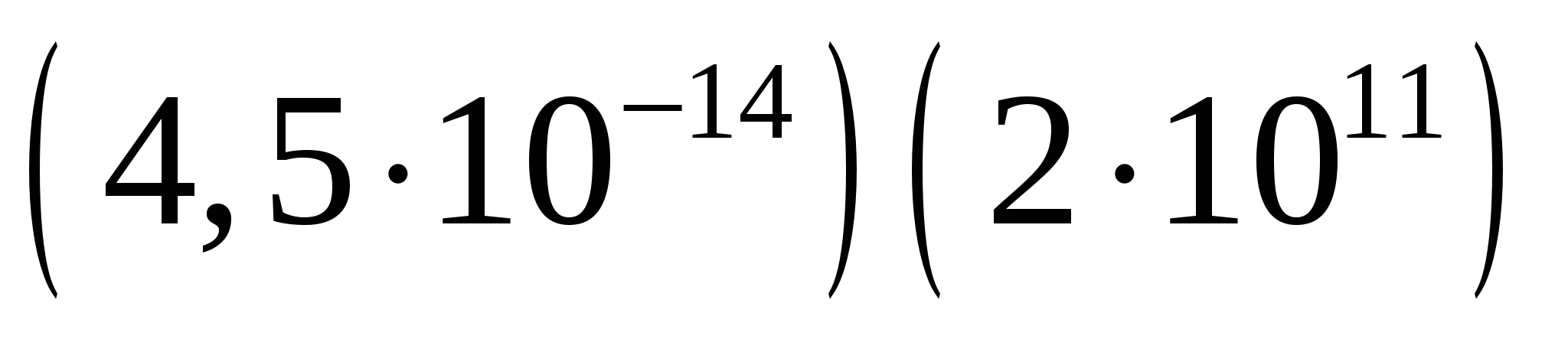 .
.
В 4. Запишите выражение 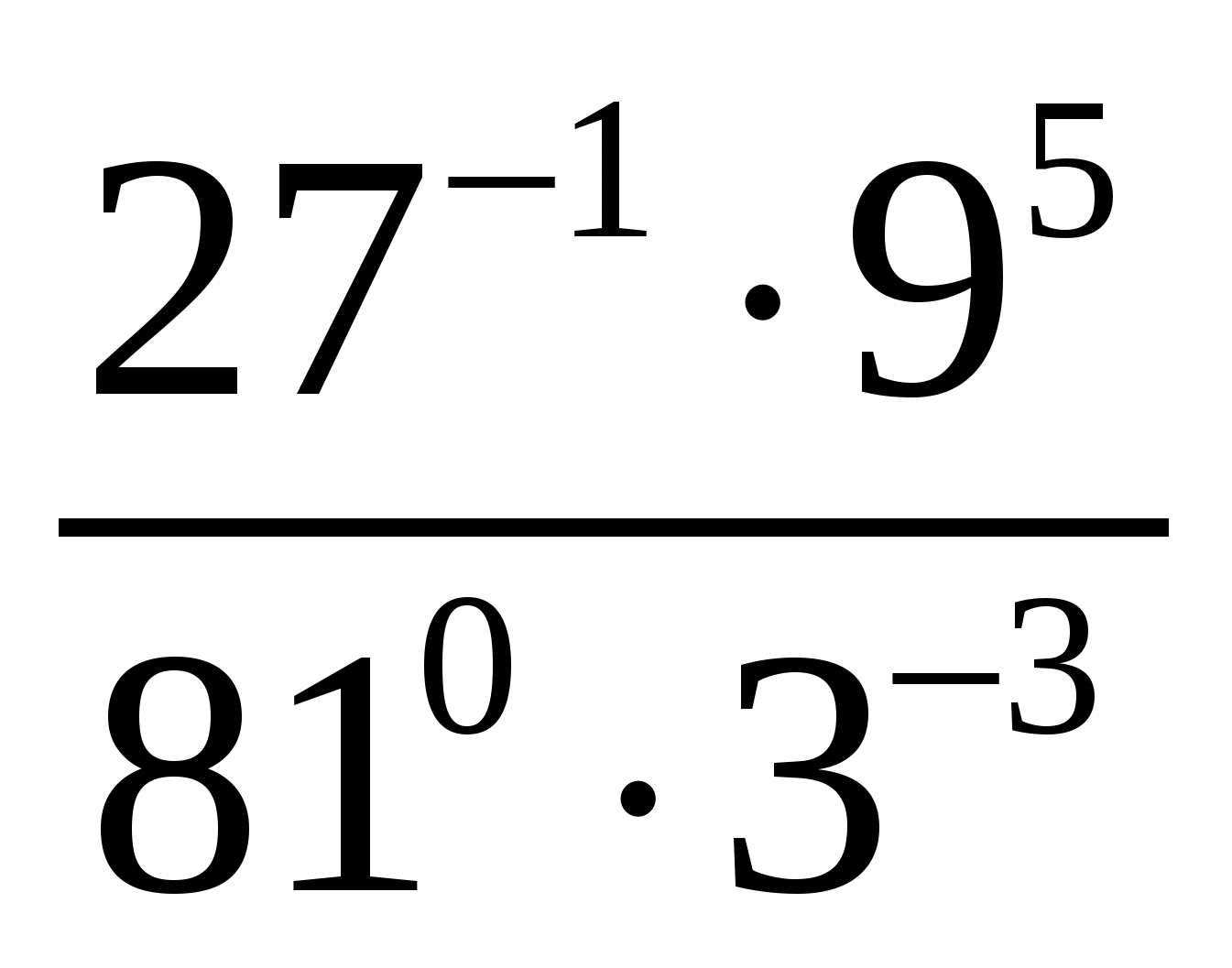 в виде степени числа 3.
в виде степени числа 3.
В5. Сократите дробь : а) 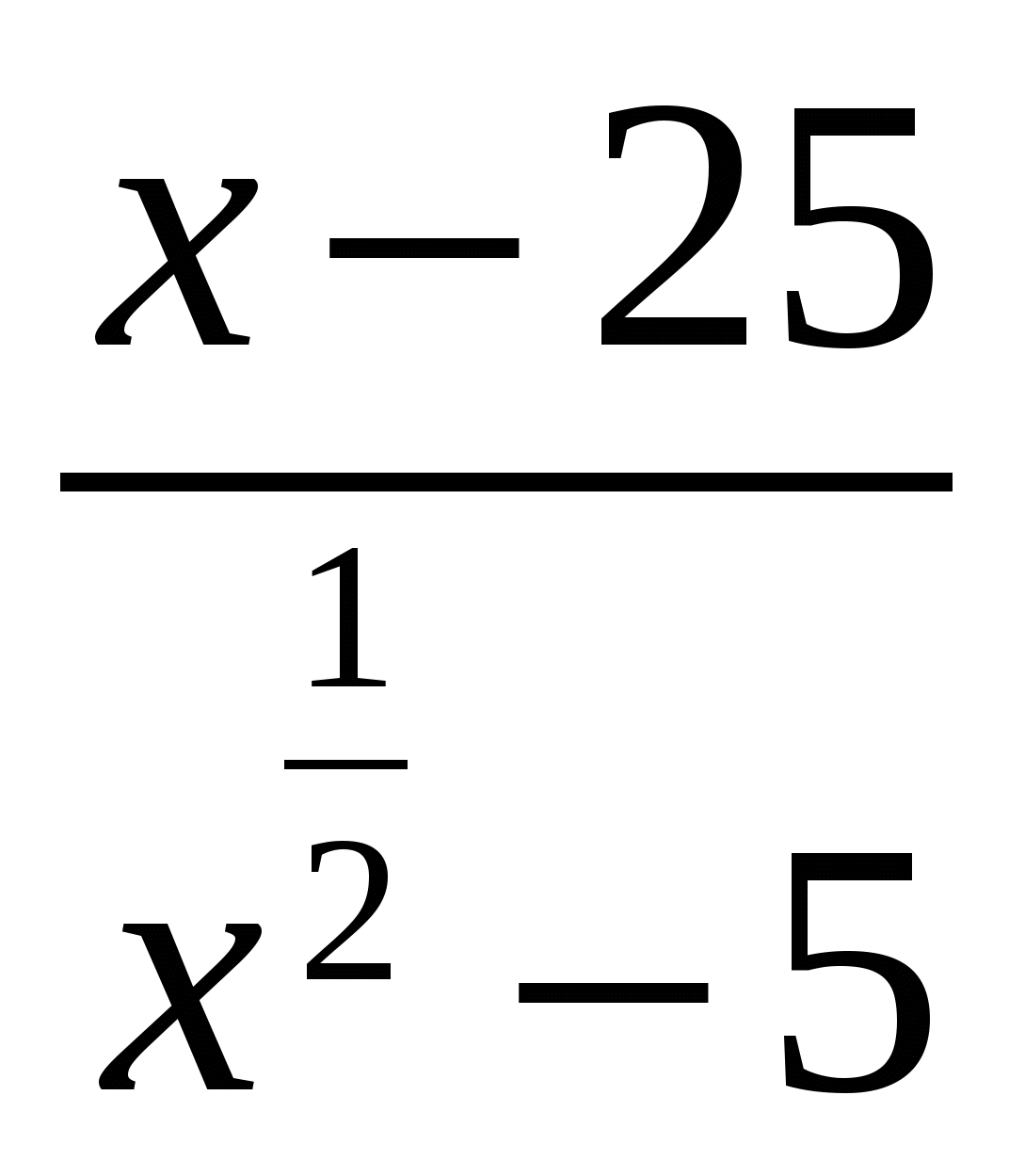 б)
б)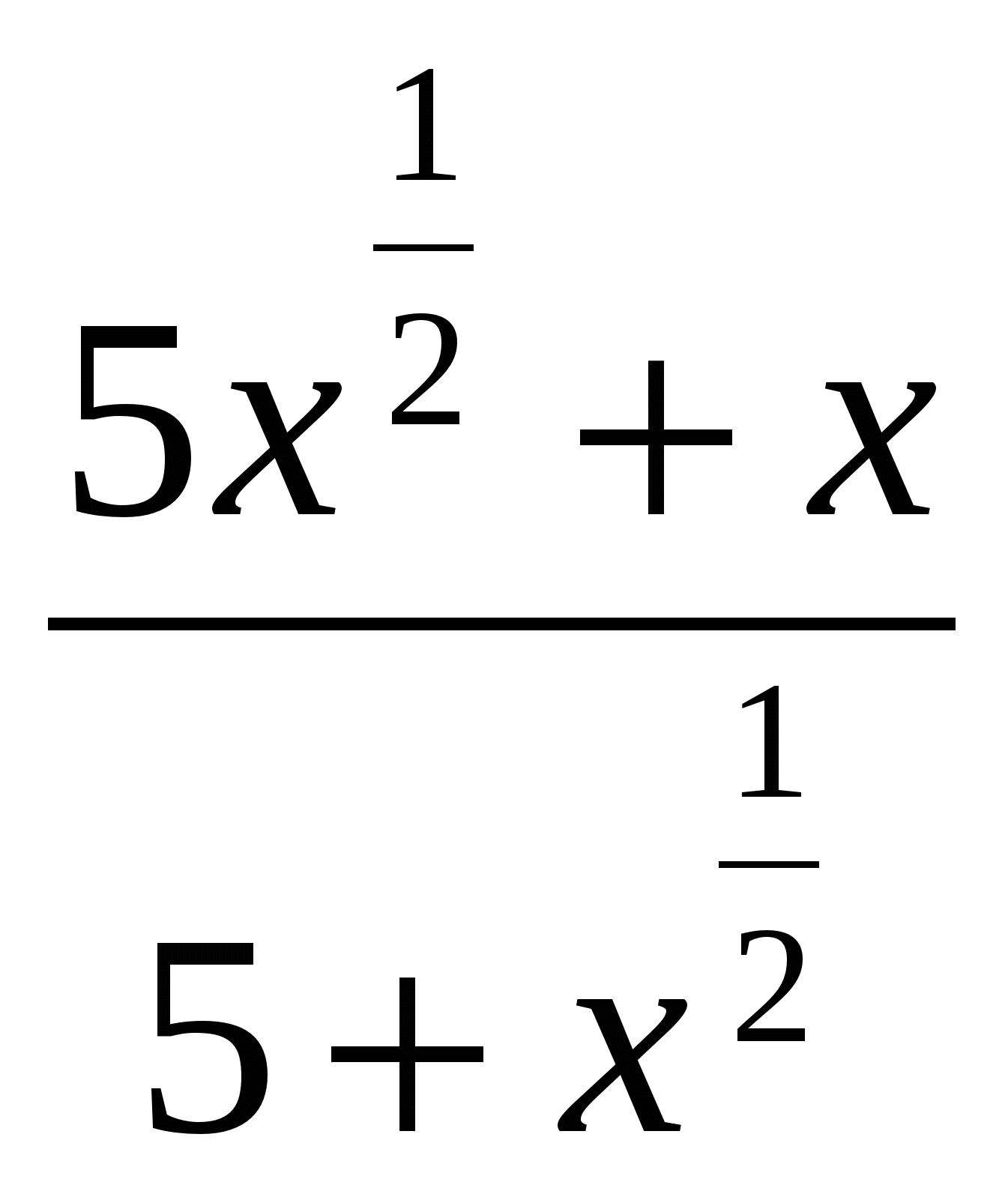
В6. Решите уравнение: а)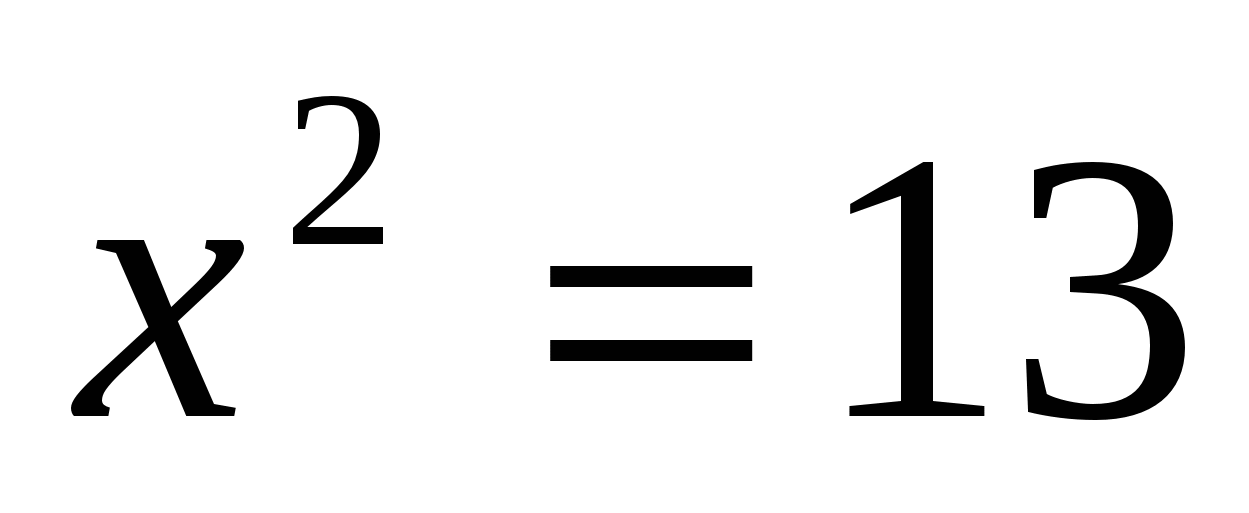 ; б)
; б)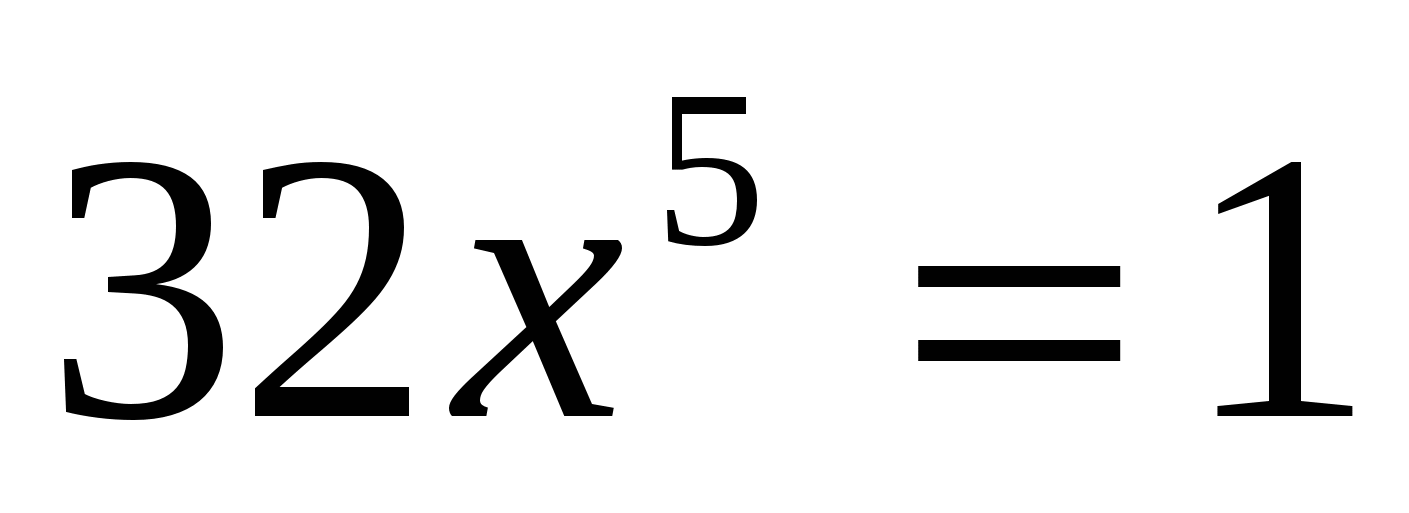 ; в)
; в)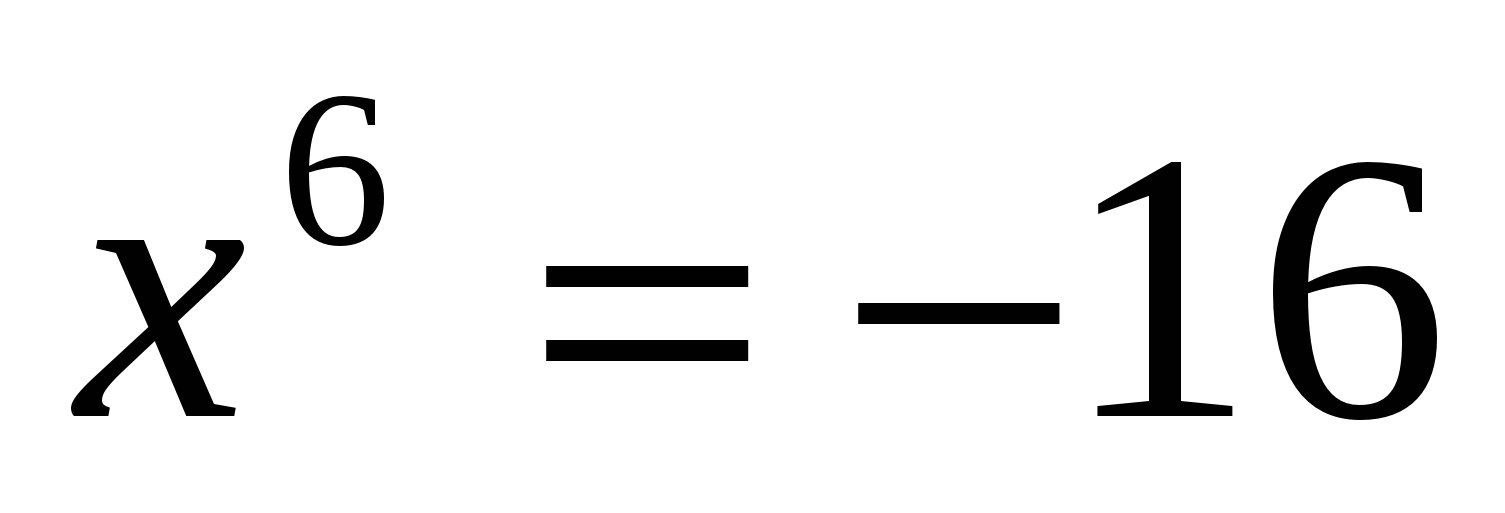 ; г)
; г)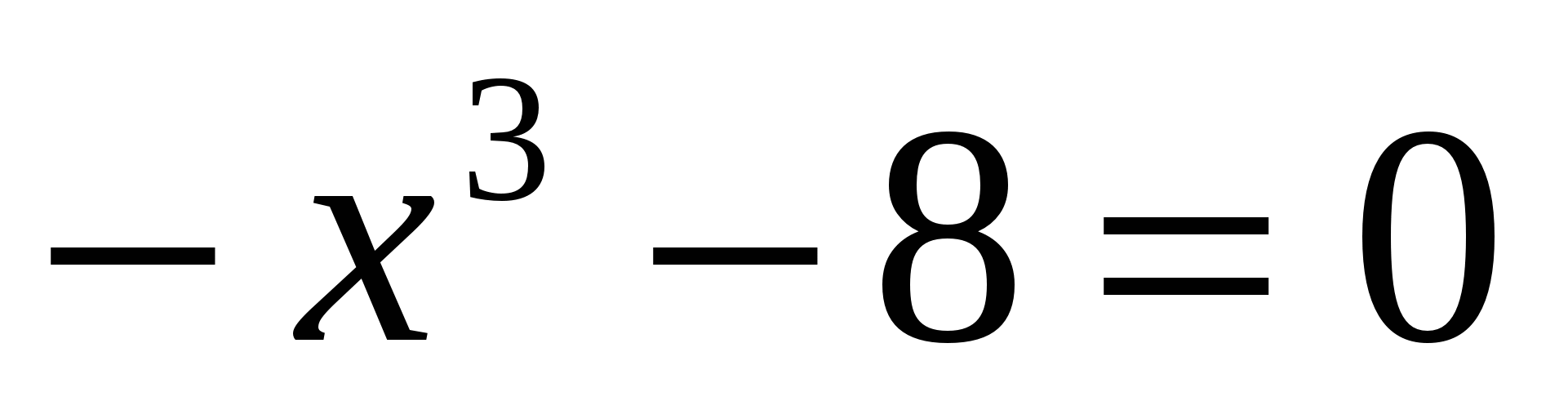 .
.
С1. Решить уравнения: а) б)
в) г)
Контрольная работа №2
Степень с рациональным показателем
Вариант 2
А1. Вычислите 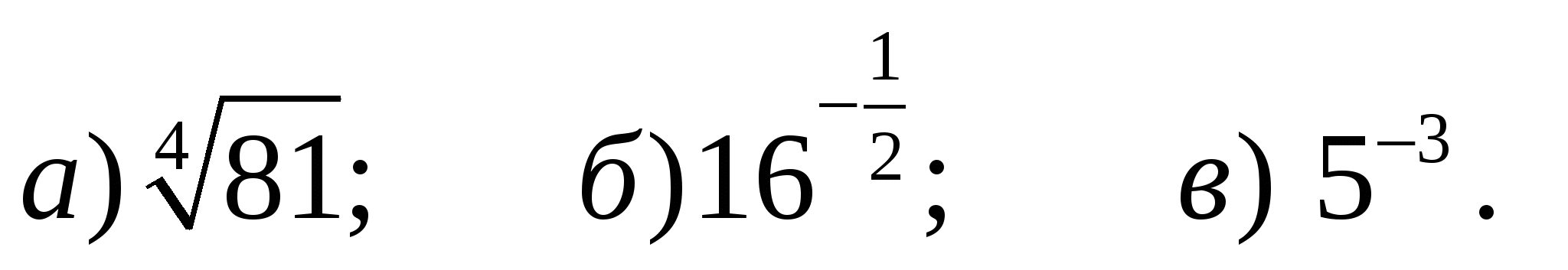
А2. Вычислите:
а) 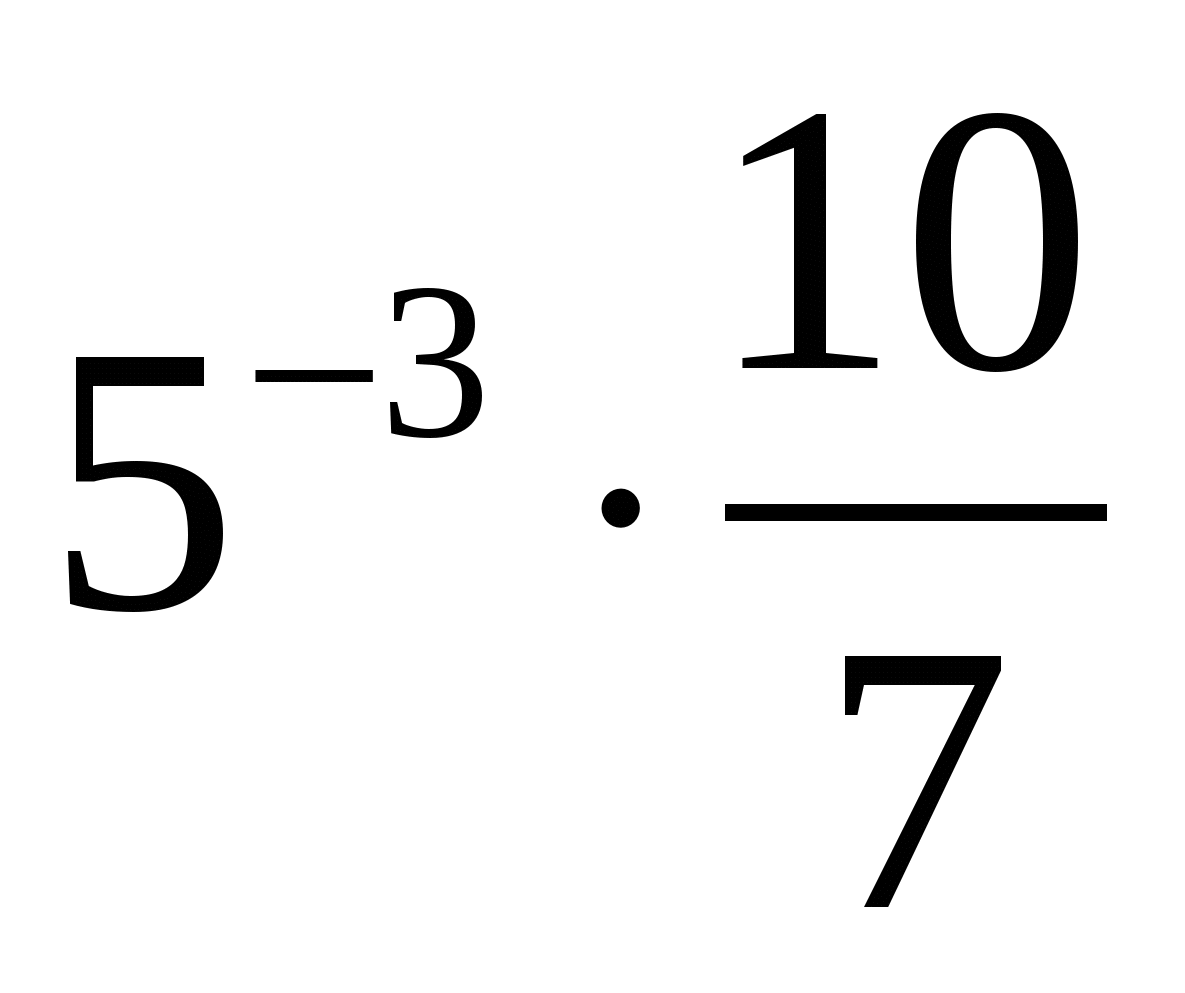 ; б)
; б) 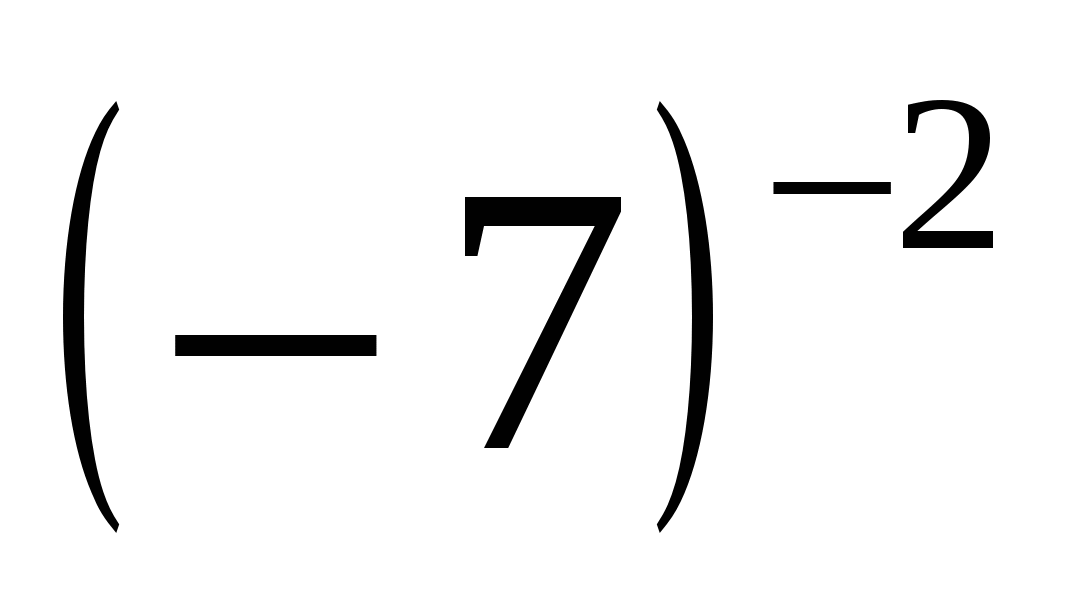 ; в)
; в) 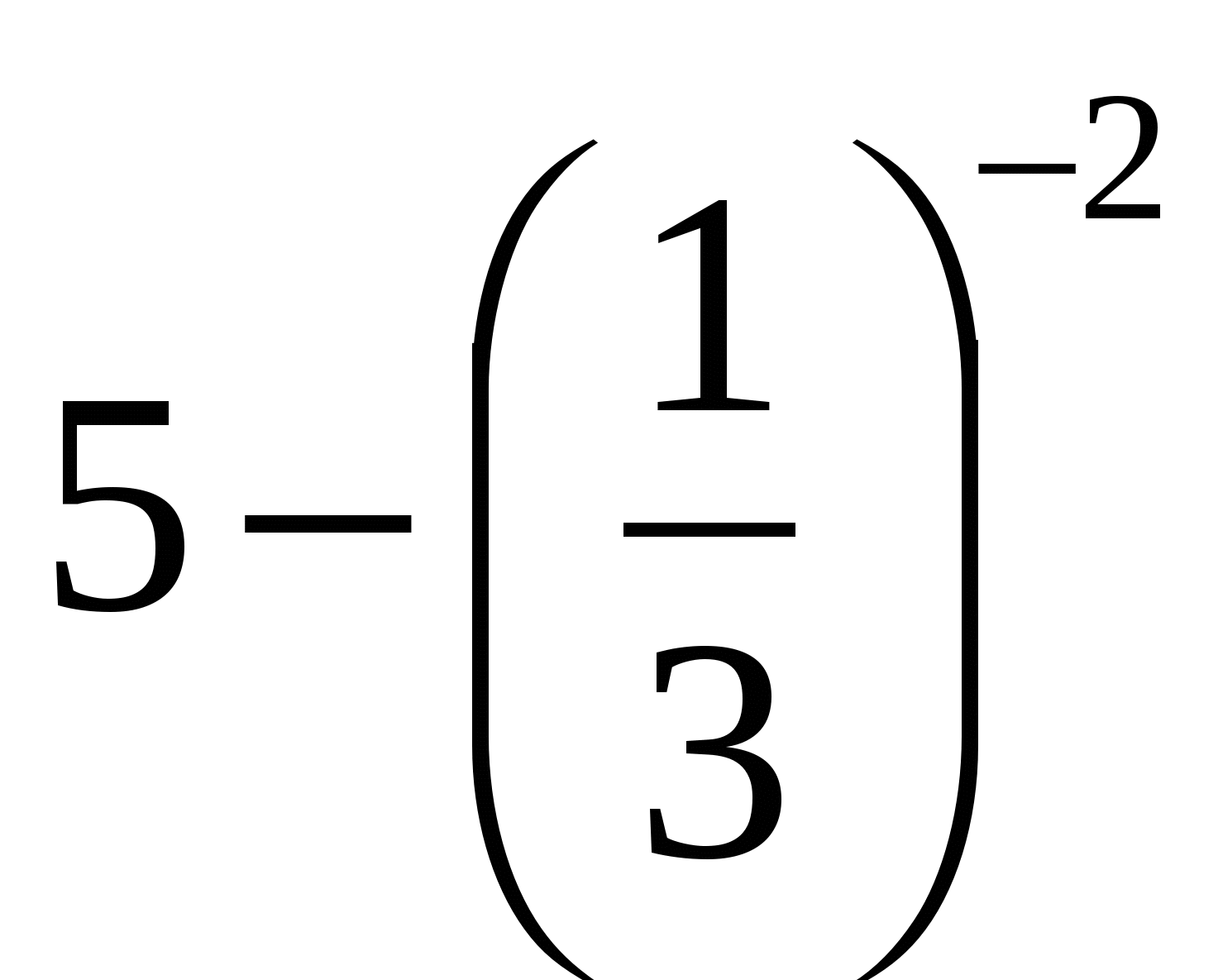 .
.
А3. Вычислите : а) 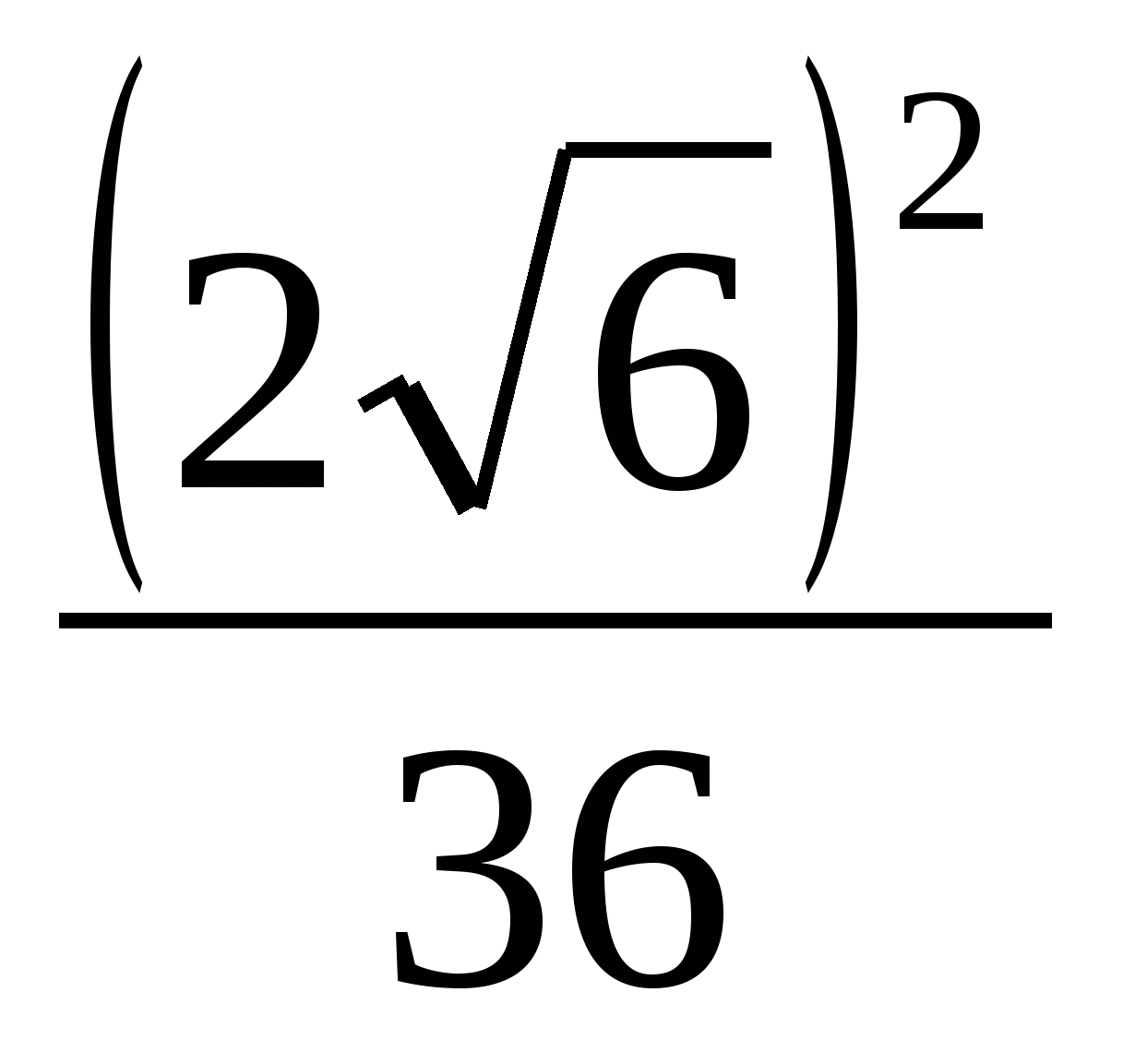 ; б)
; б) 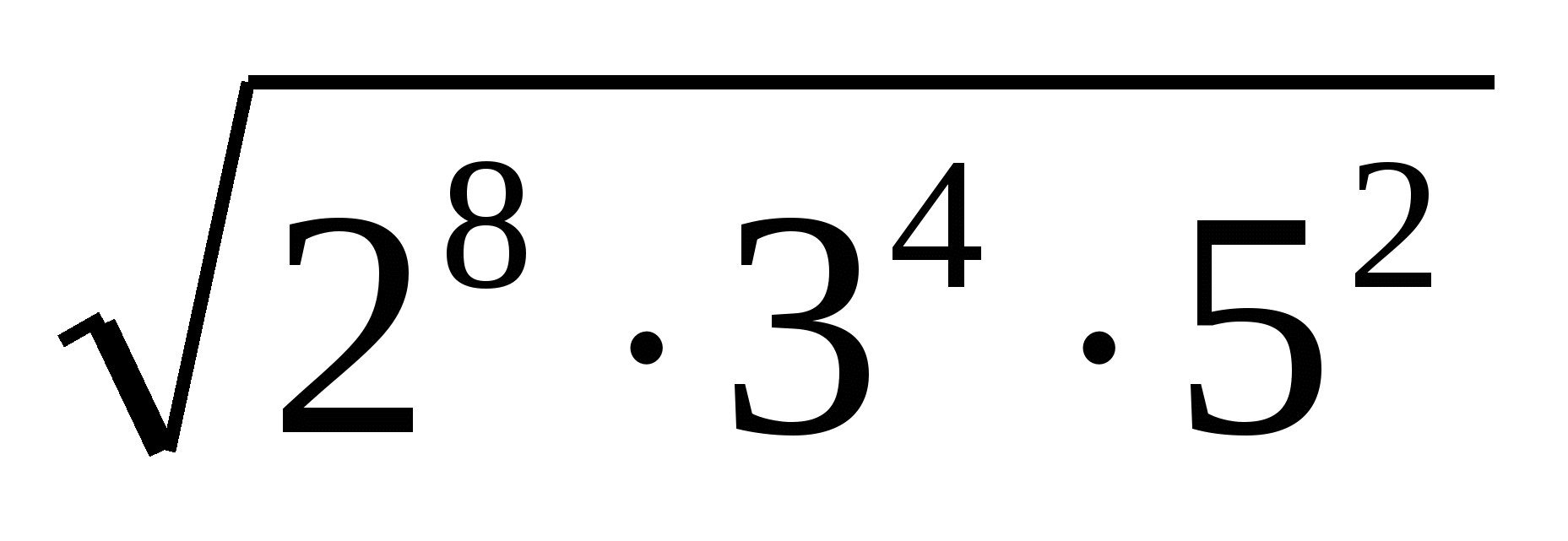 в)
в)  .
.
А4. Упростите выражение: 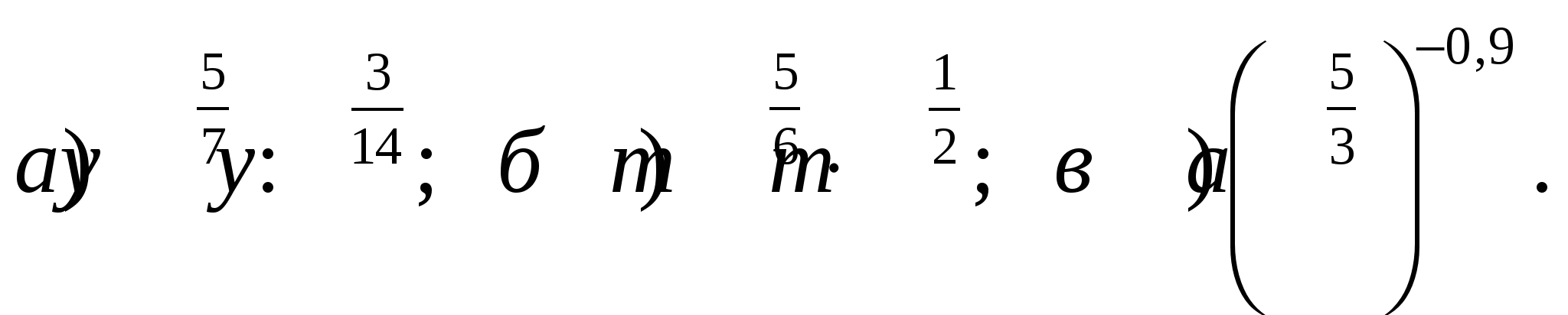
А5. Вынесите множитель из — под знака корня: 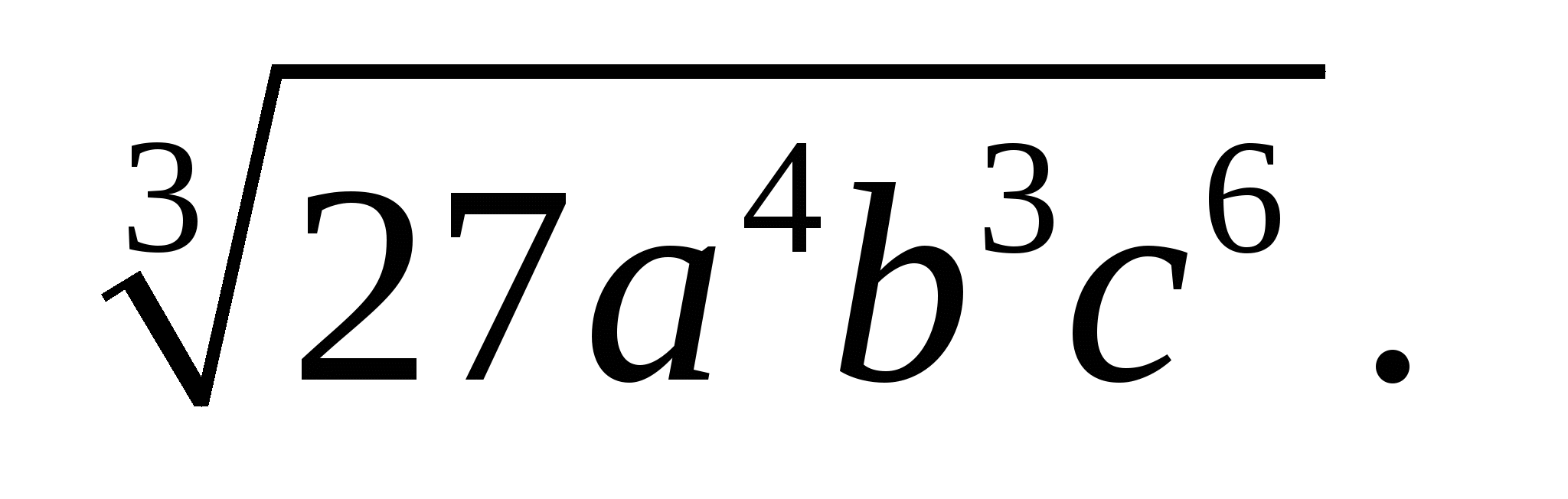
В1.Вычислите значение выражения 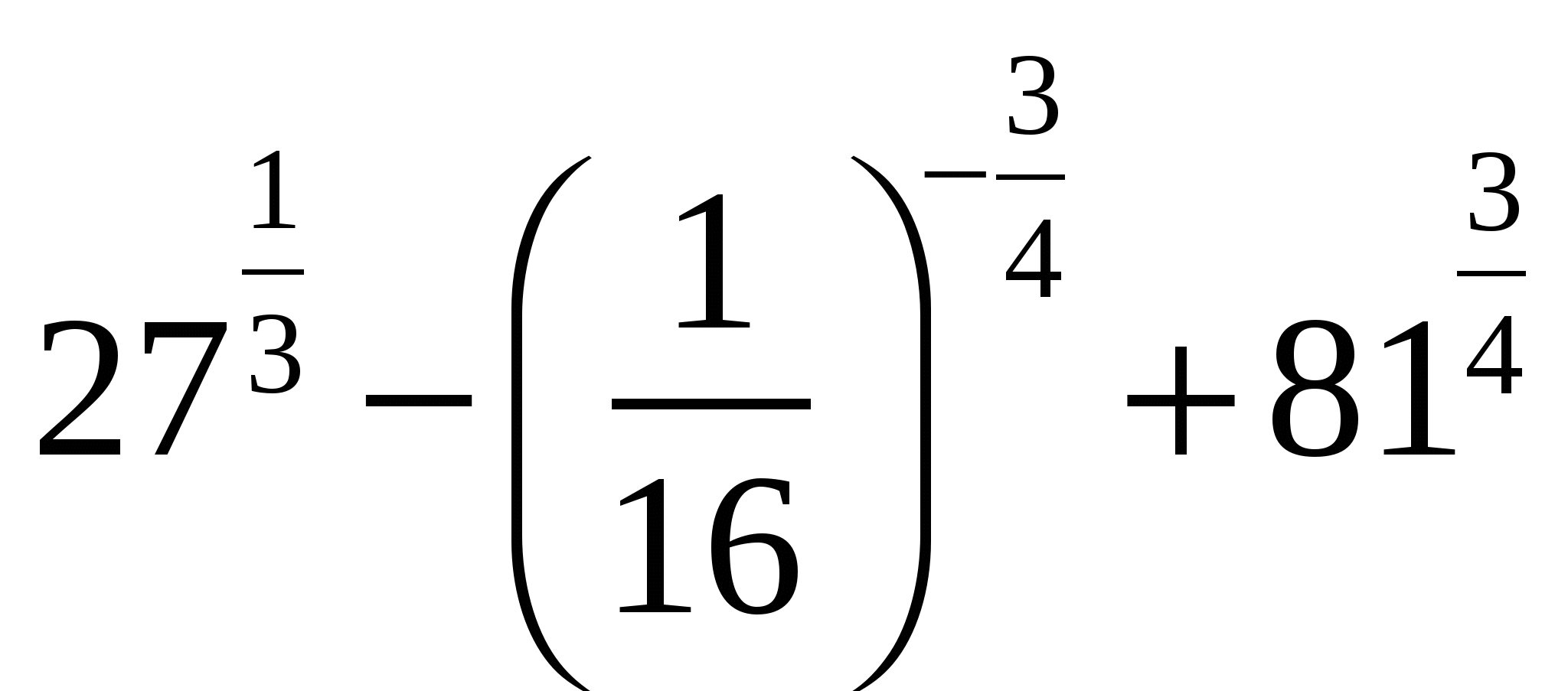 .
.
В2.Упростите выражение 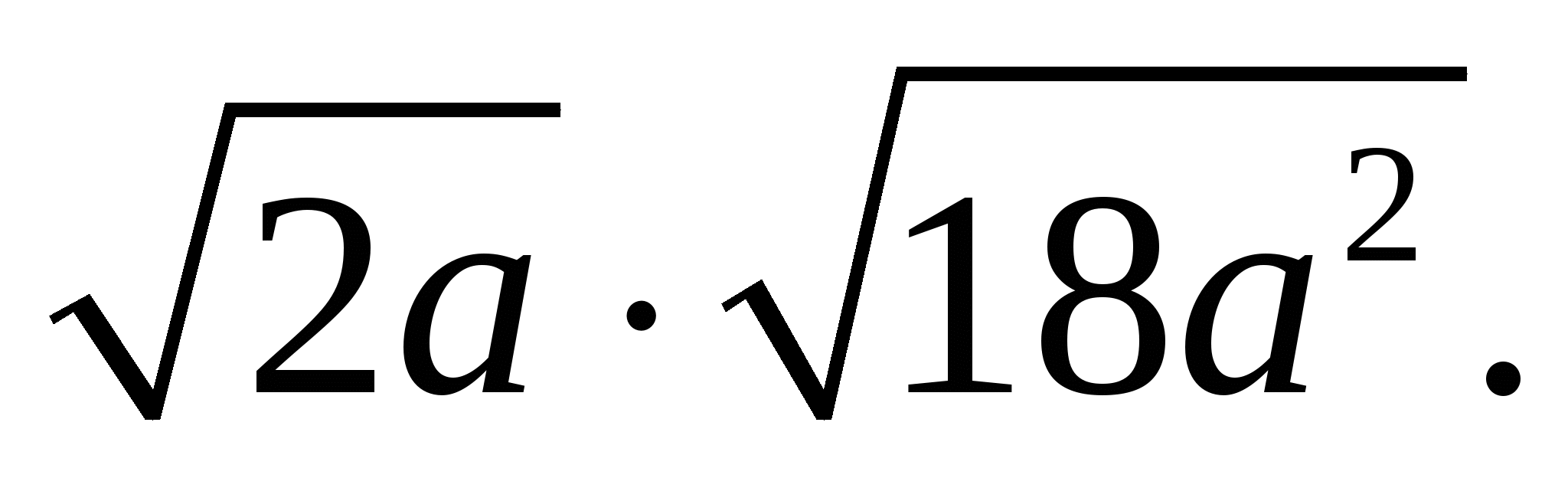
В3. Представьте в виде десятичной дроби 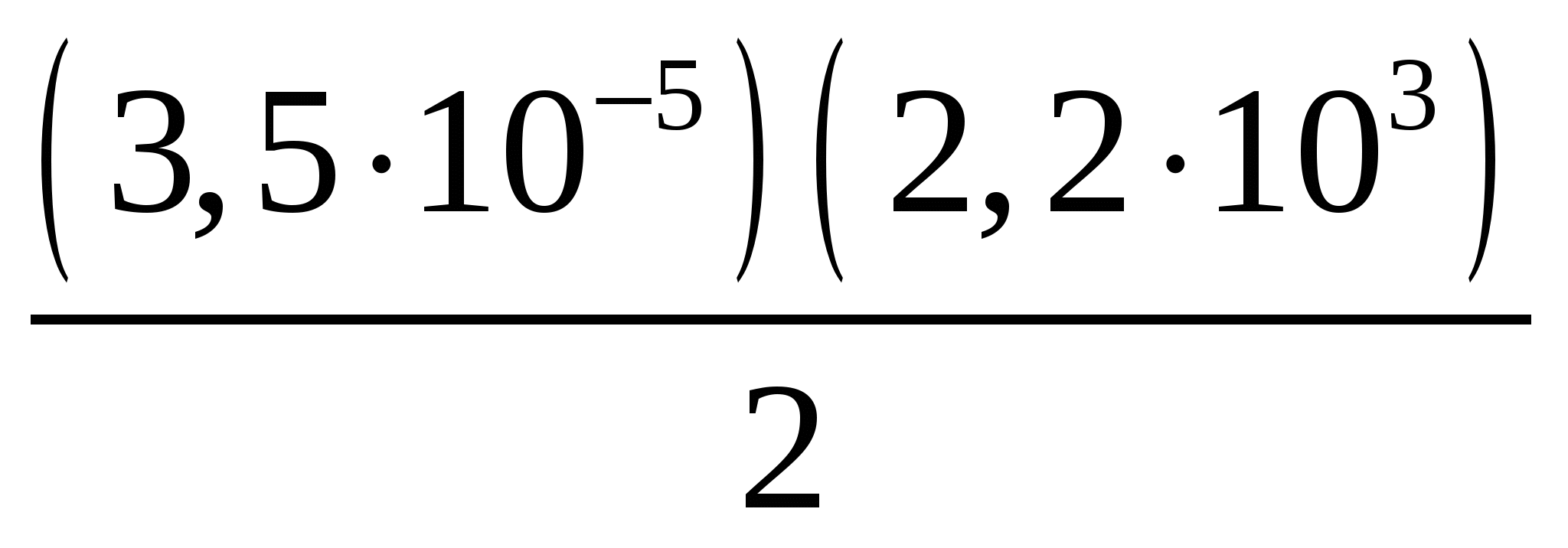 .
.
В4. Запишите выражение 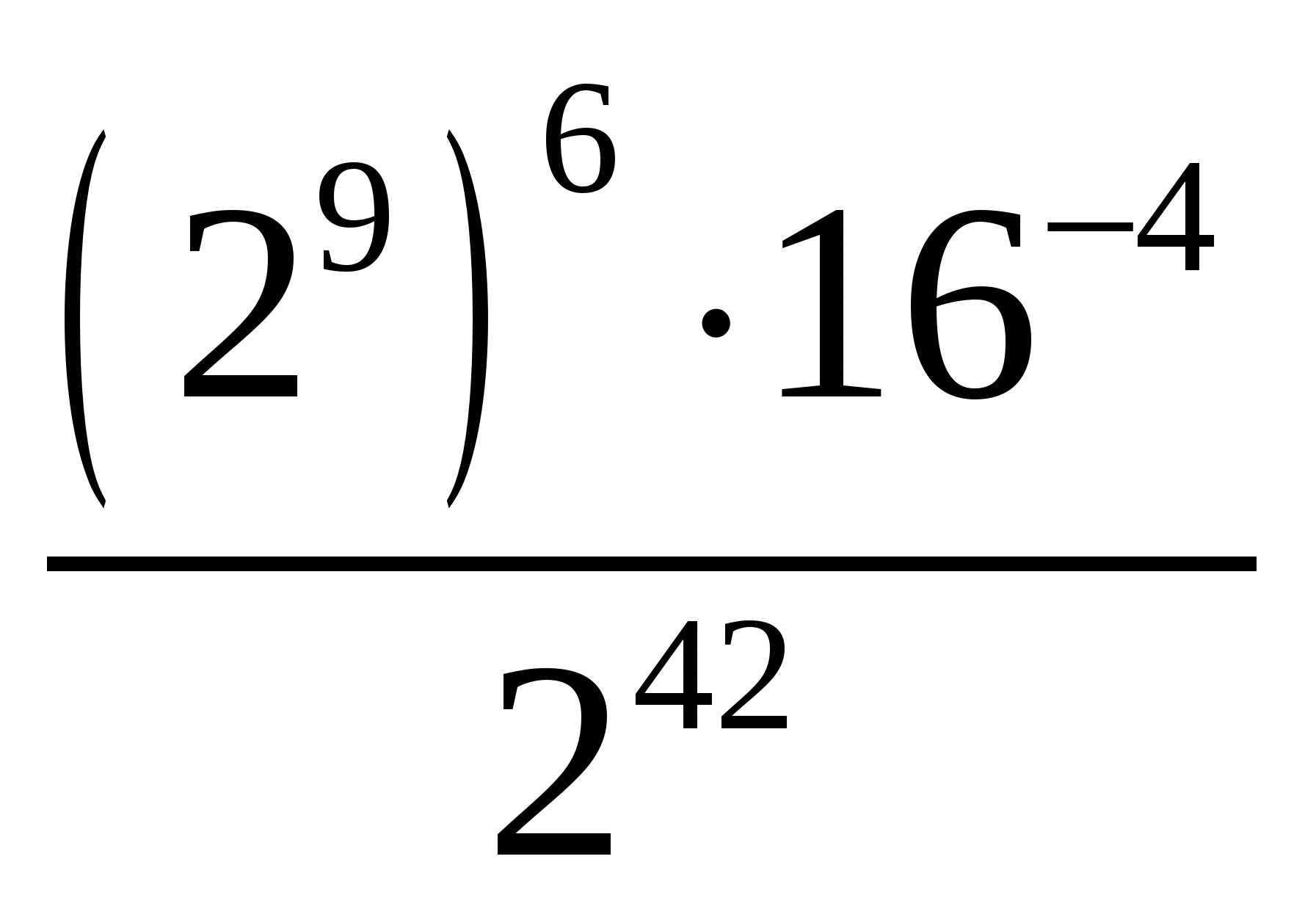 в виде степени числа 2.
в виде степени числа 2.
В5. Сократите дробь: а)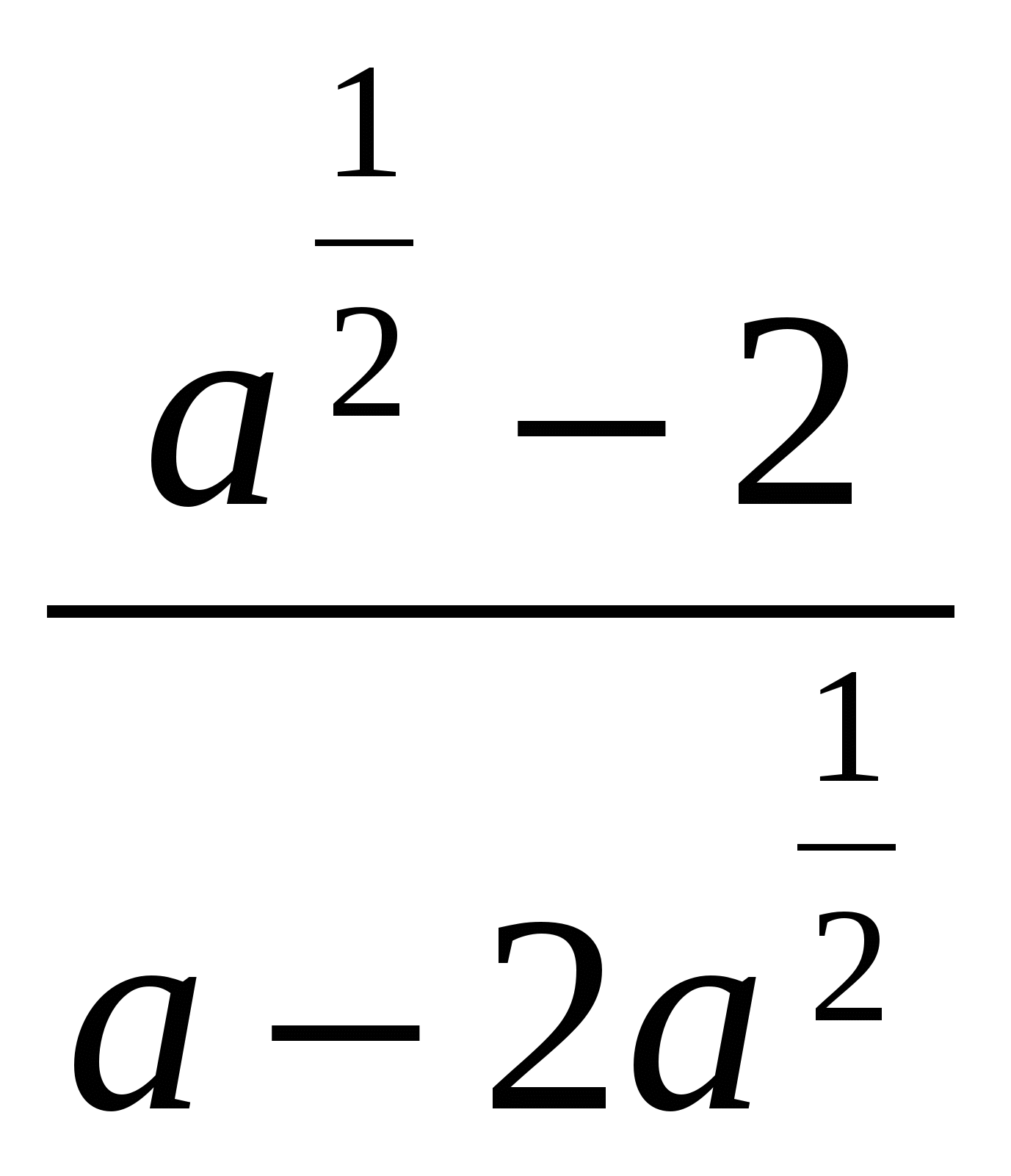 , б)
, б)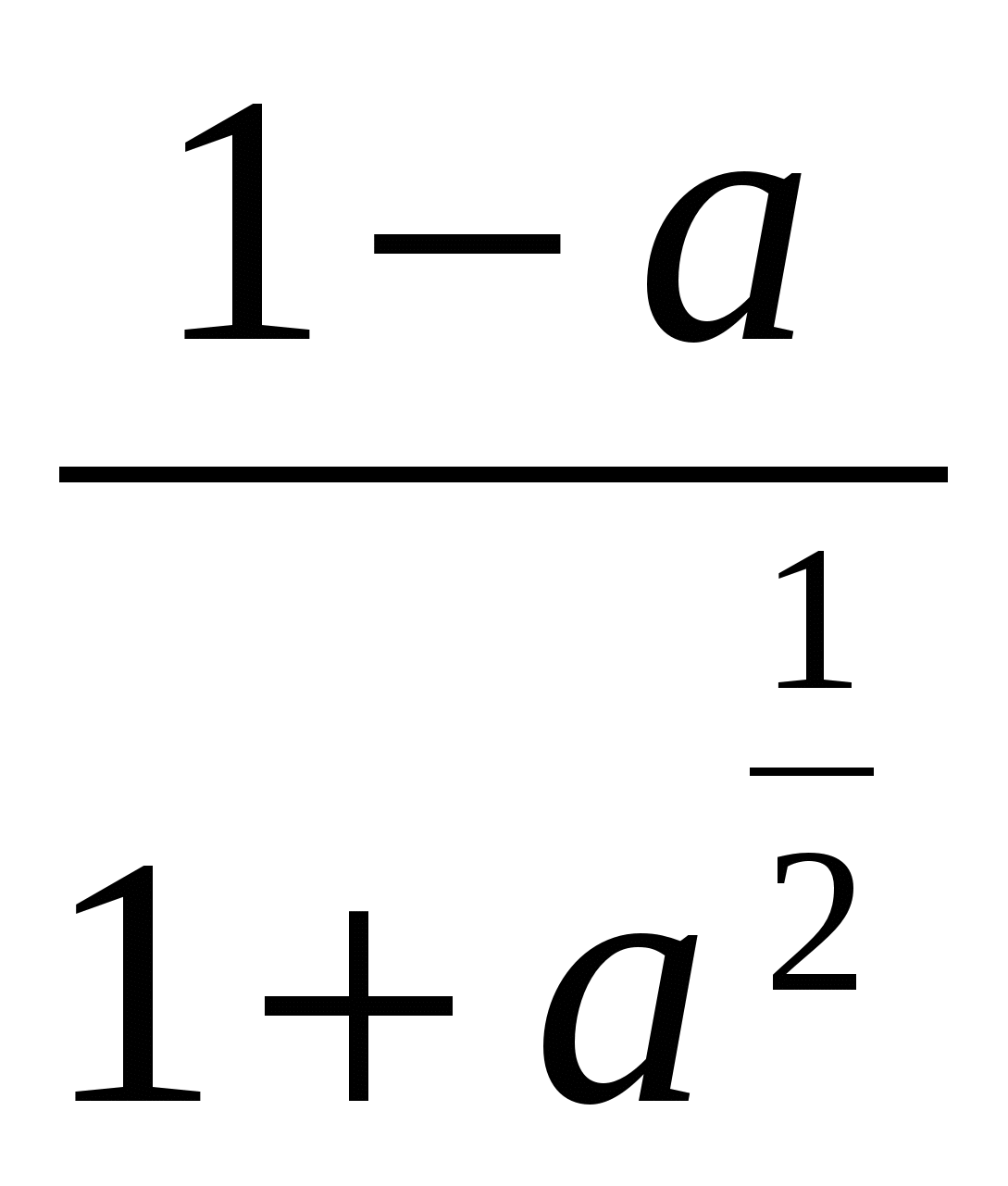 ,
,
В6. Решите уравнение: а)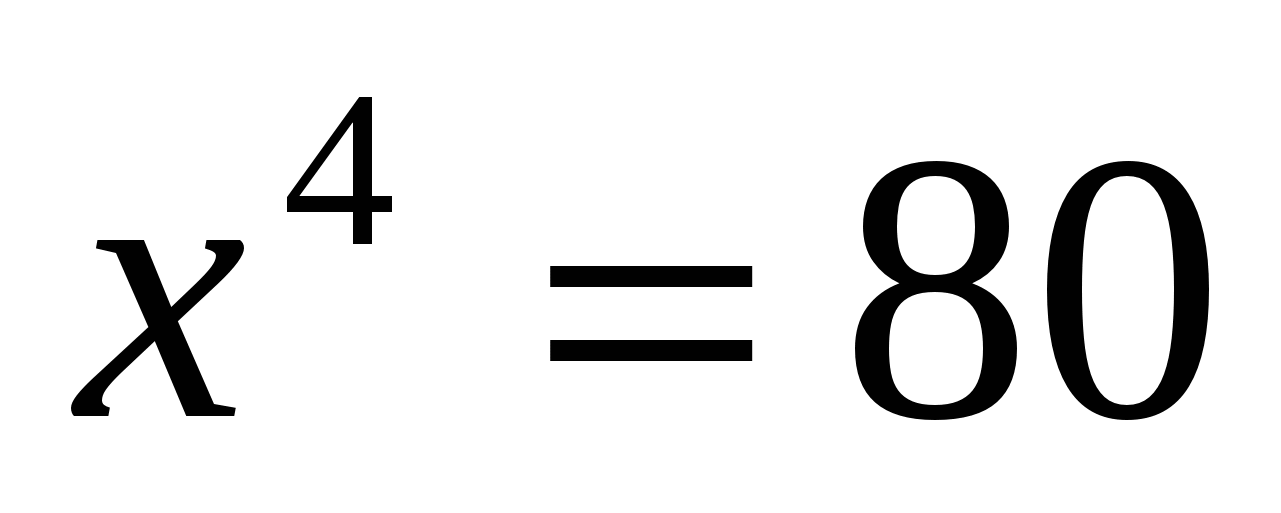 ; б)
; б)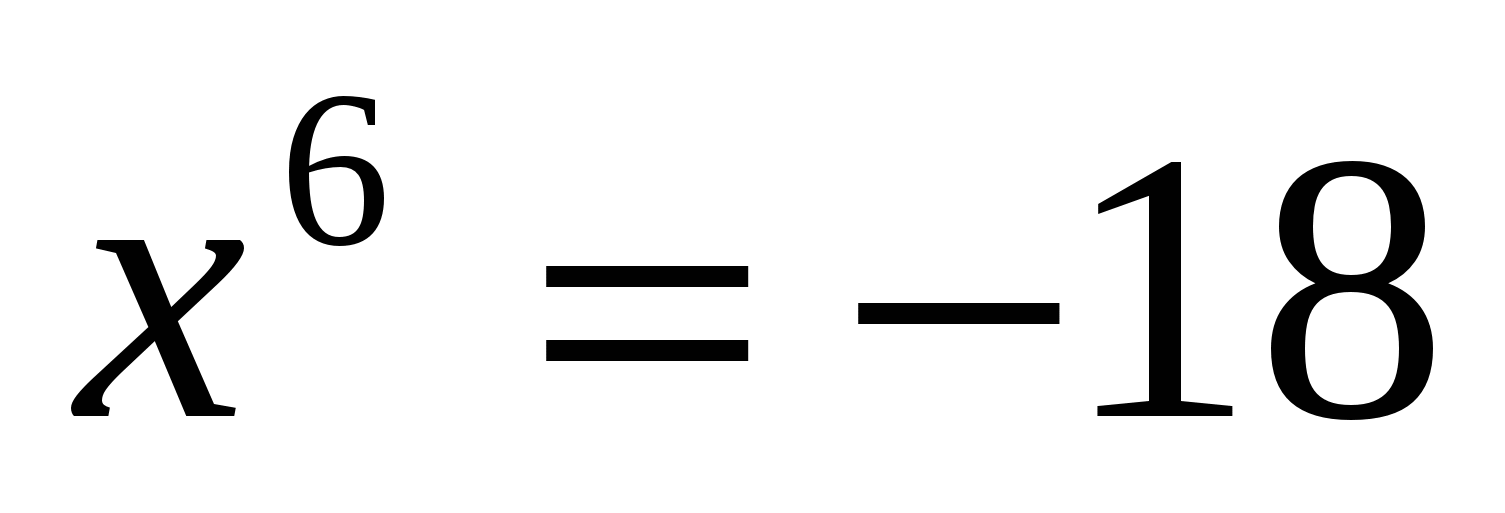 ; в)
; в)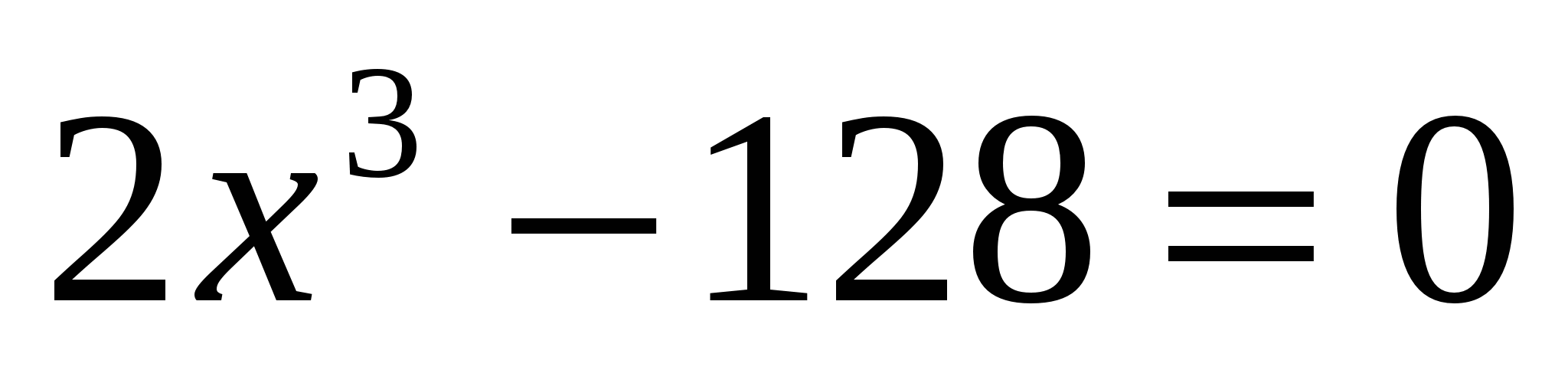 ; г)
; г)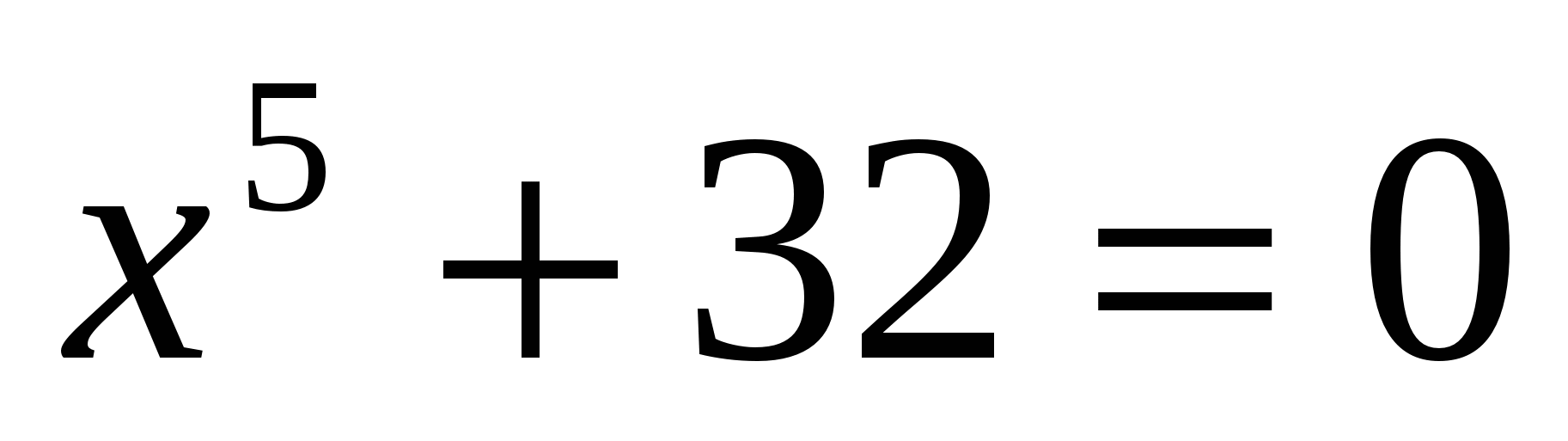 .
.
С1. Решите уравнения: а) б)
в) г)
Тема: «Степень с рациональным показателем»
Математика-это музыка разума.
Музыка-это математика чувств.
(Джеймс Джозеф Сильвестр)
Урок повторения и обобщения материала.
Цели урока:
Обобщение и систематизация знаний, умений, навыков.
Актуализация опорных знаний в условиях сдачи ЕГЭ.
Контроль и самоконтроль знаний, умений, навыков с помощью тестов.
Развитие умения сравнивать, обобщать.
План урока.
Формулировка цели урока.
Устная работа: «Дополни предложение», «Найди ошибку».
Математический диктант.
Решение серии примеров на основе демонстрационного варианта ЕГЭ.
Работа по учебнику.
Физминутка.
Самостоятельная работа на основе демонстрационного варианта ЕГЭ.
Задание на дом.
Подведение итогов урока.
Оборудование: проектор.
1. Друзья! Перед вашими глазами часть высказывания английского математика Джеймса Джозефа Сильвестра (1814–1897) о математике “Математика – это музыка разума”. Не правда ли, как романтично?
Вопрос. А как вы думаете, как определил он музыку?
“Музыка – это математика чувств”.
К чувствам мы можем отнести различного рода переживания. В этом году одной из причин ваших и моих переживаний является успешная сдача ЕГЭ и, как следствие, поступление в ВУЗ. Очень хочется, чтобы преобладали положительные эмоции. Должна быть уверенность, а это наши знания и навыки. Сегодня на уроке мы продолжим подготовку к ЕГЭ, повторяя и обобщая понятие степени.
Итак, тема сегодняшнего урока – «Степень с рациональным показателем».
2. Устная работа
Дополните предложения:
При умножении степеней с одинаковыми основаниями: показатели складываются
При делении степеней с одинаковыми основаниями : показатели вычитаются
Степень степени равна: произведению показателей
Степень числа а, не равного нулю с нулевым показателем равна :1
Степень произведения равна :произведению степеней
Степень дроби равна :дроби степеней
Степень с дробным показателем m/n есть:

2. «Найди ошибку»:
1. Имеют смысл выражения:
а)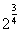 б)
б)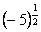 в)
в) 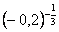 с)
с) 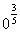 д)
д) 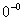
3. Уравнение имеет три корня
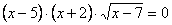 (нет, корень один: 7, т.к.
(нет, корень один: 7, т.к.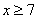 )
)
3. Математический диктант
Вариант 1
1. представьте выражение в виде степени с рациональным показателем
а) 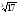 ; б)
; б) 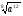 .
.
2. представьте выражение в виде корня из числа или выражения
а) 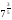 ; б)
; б) 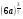 .
.
3. вычислите:
а) 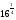 ; б)
; б) 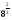 в)
в) 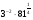 .
.
Вариант 2
1. представьте выражение в виде степени с рациональным показателем
а) 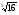 ; б)
; б) 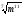 ;
;
2. представьте выражение в виде корня из числа или выражения
а) 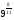 ; б)
; б) 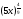 .
.
3. вычислите:
а) 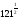 ; б)
; б) 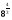 в)
в) 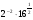 .
.
Матрица ответов:
Задание 1
Задание 2
Задание 3
Вариант 1
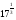
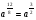

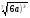
2
4
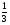
Вариант 2

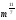
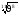
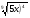
11
16
1
Решение серии примеров на основе демонстрационного варианта ЕГЭ
Задания выполняются на доске, с последующей проверкой ответов. (три человека по три примера, одновременно)
Найдите значение выражения
27∙253:502=
98∙411:367=
34∙58:154=
79∙1110:779=
 при x=3
при x=3
 при x=9
при x=9
 при x=5
при x=5
5. Работа по учебнику: №436(а,б), №441(а,б)
6. Физминутка.
6.Самостоятельная работа на основе демонстрационного варианта ЕГЭ с последующей проверкой на доске.
А теперь самое время потренироваться: перед вами примеры из демонстрационного варианта ЕГЭ.
Вы их видите как на доске, так и на листочках. Ваша задача – быстро решить и заполнить таблицы с ответами. Соответствие букв и чисел перед вами. Правильно вычислив или упростив выражения в таблице, вы прочтёте то, что необходимо вам при сдаче ЕГЭ.
1 вариант – удача;
2 вариант — знания;
3 вариант – уверенность.
7.Задание на дом п.34, №436(в,г), №441(в,г).
8.Подведение итогов урока.
Итак, сегодня на уроке мы увидели насколько широко понятие степени используется при сдаче ЕГЭ. Закрепить полученные навыки вы сможете, выполнив домашнюю работу
алгебра — рациональные экспоненты
Пол Заметки ОнлайнНоты Быстрая навигация Скачать
- Перейти к
- Ноты
- Проблемы с практикой
- Проблемы с назначением
- Показать / Скрыть
- Показать все решения / шаги / и т. Д.
- Скрыть все решения / шаги / и т. Д.
- Разделы
- Целочисленные экспоненты
- Радикалы
- глав
- Решение уравнений и неравенств
- Классы
- Алгебра
- Исчисление I
- Исчисление II
- Исчисление III
- Дифференциальные уравнения
- Дополнительно
- Обзор алгебры и триггеров
- Распространенные математические ошибки
- Комплексное число праймер
- Как изучать математику
- Шпаргалки и таблицы
- Разное
- Свяжитесь со мной
- Справка и настройка MathJax
- Мои ученики
- Примечания Загрузки
- Полная книга
- Текущий Глава
- Текущий раздел
- Практика Проблемы Загрузки
- Complete Book — Проблемы только
- Complete Book — Решения
- Текущая глава — только проблемы
- Текущая глава — Решения
- Текущий раздел — только проблемы
- Текущий раздел — Решения
- Проблемы с назначением Загрузки
- Полная книга
- Текущий Глава
- Текущий раздел
- Другие предметы
- Получить URL для загрузки элементов
- Распечатать страницу в текущей форме (по умолчанию)
- Показать все решения / шаги и распечатать страницу
- Скрыть все решения / шаги и распечатать страницу
- Дом
- Классы
- алгебра
- Предварительные
- Целочисленные экспоненты
- Рациональные экспоненты
- Радикалы
- полиномов
- Факторинг Полиномы
- Rational Expressions
- Комплексные числа
- Решение уравнений и неравенств
- Решения и комплекты решений
- линейных уравнений
- приложений линейных уравнений
- уравнений с более чем одной переменной
- Квадратичные уравнения — Часть I
- Квадратичные уравнения — Часть II
- Квадратичные уравнения: краткое изложение
- Приложения квадратичных уравнений Уравнения
- , приводимые к квадратичной форме
- Уравнения с радикалами
- линейных неравенств
- Полиномиальное неравенство
- Рациональное неравенство
- Уравнения абсолютной стоимости
- Абсолютное неравенство в значениях
- Графика и функции
- График
- Линии
- Круги
- Определение функции
- Графические функции
- Объединение функций
- Обратные функции
- общих графиков
- Линии, окружности и кусочные функции
- Параболы
- Эллипсы
- Гипербол
- Разные функции
- Преобразования
- Симметрия
- Рациональные функции
- полиномиальных функций
- делительных полиномов
- Предварительные
правил для рациональных экспонентов
Правила для рациональных экспонентов До этого момента у нас были только целые показатели (положительные или отрицательные целые числа), поэтому пришло время ввести два новых правила, которые имеют дело с рациональными (или дробными) показателями. Эти правила помогут упростить радикалы с разными индексами, переписав задачу с рациональными показателями. Вот новые правила вместе с примером или двумя из того, как применить каждое правило:Пример 1 — Перепишите, используя радикалы.
| Шаг 1 : Применить определение. |
Пример 2 — Перепишите, используя рациональные показатели.
| Шаг 1 : Применить определение. |
Нажмите здесь для практических проблем
Пример 3 — Перепишите, используя радикалы.
| Шаг 1 : Применить определение. |
Нажмите здесь для практических проблем
Пример 4 — Перепишите, используя рациональные показатели.
| Шаг 1 : Применить определение. |
Нажмите здесь для практических проблем
Ниже приведен полный список правил для показателей, а также несколько примеров каждого правила:
| Правило нулевого экспонента: a 0 = 1, это говорит о том, что все, что поднято до нулевой степени, равно 1. | |
| Правило мощности (полномочия на полномочия): ( м ) n = млн , это говорит о том, что для увеличения мощности до мощности необходимо умножить показатели. Есть несколько других правил, которые согласуются с правилом власти, таких как правило продукта к полномочиям и правило отношения к полномочиям. | |
| Отрицательный показатель степени Правило : здесь говорится, что отрицательные показатели в числителе перемещаются в знаменатель и становятся положительными показателями.Отрицательные показатели в знаменателе перемещаются в числитель и становятся положительными показателями. Перемещайте только отрицательные показатели. | |
| Правило продукта : м , n = м + n , это говорит о том, что для умножения двух показателей на одну и ту же базу вы сохраняете базу и добавляете силы. | |
| Факторное правило : здесь говорится, что для деления двух показателей на одну и ту же базу вы сохраняете базу и вычитаете силы.Это похоже на сокращение фракций; когда вы вычитаете полномочия, поместите ответ в числитель или знаменатель в зависимости от того, где была расположена высшая сила. Если в знаменателе находится высшая сила, поместите разницу в знаменателе и наоборот, это поможет избежать отрицательных показателей. | |
| Определение : это говорит о том, что если показатель степени является дробной, то проблема может быть переписана с использованием радикалов.Обратите внимание, что знаменатель дроби становится индексом радикала. | |
| Определение : это говорит о том, что если показатель степени является дробной, то проблема может быть переписана с использованием радикалов. Обратите внимание, что знаменатель дроби становится индексом радикала, а числитель становится степенью внутри радикала. |
Рациональные показатели — Полный курс по алгебре
29
Дробный показатель
Экспоненциальная форма против радикальной формы
Отрицательный показатель степени
Оценки
Правила экспонентов
НАСТОЯЩИЙ СИМВОЛ, как мы видели, символизирует одно число, которое является квадратным корнем из и .Под этим символом мы подразумеваем кубический корень из и . Это тот номер, третья сила которого и .
Например,
потому что
8 = 2 3 .
В этом символе («кубический корень из 8») 3 называется индексом радикала. В общем
означает a = b n .
Эквивалентно,
Читать « n -й корень из а «.
Например,
— шестой корень из 64 — это 2,
, потому что 64 — это шестая степень 2.
Если индекс опущен, как в, индекс понимается как 2.
| Примеры 1. | = | 11. | |
| = | 2, потому что 2 5 = 32. | ||
| = | 10, потому что 10 4 = 10000. | ||
| = | -2, потому что (-2) 5 = -32. | ||
Мы видим, что, если индекс нечетный , то радиканд может быть отрицательным. Но если индекс четный, радиканд не может быть отрицательным. Там нет такого действительного числа, например, как.
Задача 1. Оцените каждое следующее — если оно реально.
| а) | = | 3 | б) | = | −3 | в) | = | 2 |
| г) | = | не настоящий. | е) | = | −5 |
| е) | = | 1 | г) | = | не настоящий. | ч) | = | -1 |
| Проблема 2Доказательство: |
| Подсказка : умножить числитель и знаменатель на |
Дробный показатель
Какой смысл мы можем иметь символ? Оказывается, мы должны идентифицировать себя с.
=.
Почему? Потому что должны подчиняться правилам экспонентов.И когда это происходит, он подчиняется тому же формальному правилу, которое определяет, а именно
() 2 = a .
Ибо согласно силовому правилу:
() 2 = · 2 = a 1 = a .
Поэтому мы должны идентифицировать себя с.
В общем
=
Знаменатель дробного показателя
равен индексу радикала.
| Пример 2. | 8 означает кубический корень из 8, что составляет 2. |
| 81 означает четвертый корень 81, что составляет 3. | |
| (-32) означает пятый корень из -32, который равен -2. | |
8 — экспоненциальная форма кубического корня из 8.
— это его радикальная форма.
Задача 3. Оцените следующее.
Задача 4. Выразить каждый радикал в экспоненциальной форме
Затем, какой смысл мы можем придать этому символу и ?
Опять же, согласно правилу умножения показателей:
a = ( a ) 2 = ( a 2 ).
То есть
Например,
8 = (8) 2 = 2 2 = 4.
8 равно кубическому корню из 8 в квадрате.
Опять же:
Знаменатель дробного показателя
указывает корень .
Хотя 8 = (8 2 ), чтобы оценить дробную степень, более эффективно сначала получить корень, потому что мы будем брать корень меньшего числа.
В общем
Задача 5. Оцените следующее.
Задача 6. Выразить каждый радикал в экспоненциальной форме.
Отрицательный показатель степени
Число с отрицательным показателем определяется как обратное значение этого числа с положительным показателем.
a −v — это , взаимное из a v .
Следовательно,
Задача 7. Выразите каждое из следующего с отрицательным показателем степени.
Задача 8. Выразить в радикальной форме.
Оценки
В уроке об экспонентах мы увидели, что −2 4 — отрицательное число. Это негатив 2 4 .
Ибо знак минус означает отрицательный знак числа, следующего за ним.А число, которое следует за -2 4 , равно 2 4 .
[(−2) 4 — положительное число. Урок 13.]
Точно так же,
−8 — это , отрицательное из 8:
−8 = −2 2 = −4.
(−8), с другой стороны, является положительным числом:
(−8) = (−2) 2 = 4.
Задача 9. Оцените следующее.
| а) | 9 -2 | = | 1 9 2 | = | 1 81 | б) | 9 | = | 3 | в) | 9 | = | 1 3 |
| г) | −9 | = | −3 | е) | −9 2 | = | −81 | е) | (−9) 2 | = | 81 | |||
| г) | −9 −2 | = | — | 1 81 | ч) | (−9) -2 | = | 1 81 | я) | −27 | = | −9 | ||
| к) | (−27) | = | 9 | к) | 27 | = | 1 9 | л) | (−27) | = | 1 9 |
| Задача 10.Оценить |
Это ответ 16/25 с положительным показателем.
Таким образом, это квадратный корень из 25/16, то есть 5/4, возведенный в 3-ю степень: 125/64.
Правила экспонентов
Показатель степени теперь может быть любым рациональным числом. Рациональные показатели u, v будут подчиняться обычным правилам.
| a u a v | = | a u + v | Same Base |
| = | a u — v | ||
| ( ab ) u | = | a u b u | Мощность изделия |
| ( a u ) v | = | a uv | Мощность власти |
| = | Мощность дроби | ||
Пример 3Перепишите в экспоненциальной форме и примените правила.
См. Навык в арифметике, сложении и вычитании дробей.
Задача 11. Применение правил экспонент.
| а) | 4 · 4 = 4 = 4 = 2 |
| б) | 8 8 | = 8 = 8 = 2 |
| в) | (10) | = 10 = 10 −3 знак равно | 1 1000 |
Задача 12.Выразите каждый радикал в экспоненциальной форме и примените правила экспонент.
| а) | x знак равно x · x = х = х |
| б) | x 2 знак равно x 2 · x = х = х |
| в) | = | ( х + 1) = ( x + 1) |
Теперь мы можем понять, что правила для радикалов — в частности,
— правила экспонент.Как таковые, они относятся только к факторам.
Задача 13. Докажите:
= ( ab ) = a · b = ·
Чтобы решить уравнение, которое выглядит следующим образом:
For, x · = x 1 = x .
Задача 14.Решить за х .
| а) | x | = | 8 | б) | x | = | −32 | ||||||
| x | = | 8 | = | 4 | x | = | (−32) | = | −8 | ||||
| в) | ( x — 1) | = | 64 | г) | x 7 | = | 5 | |||
| x — 1 | = | 64 | x | = | ||||||
| x | = | 256 + 1 = 257 | ||||||||
| е) | x | = | 7 | е) | = | 5 | |||
| x | = | 7 5 | x | = | 5 = | ||||
Следующий урок: Комплексные числа
Содержание | Дом
Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.
Даже 1 доллар поможет.
Copyright © 2020 Lawrence Spector
Вопросы или комментарии?
E-mail: [email protected]
,
градусов (выражения)
«Степень» может означать несколько вещей в математике:
- В геометрии градус (°) — это способ измерения углов,
- Но здесь мы посмотрим, что означает степень в Алгебра .
В алгебре «Степень» иногда называют «Заказ»
Степень полинома (с одной переменной)
Полином выглядит так:
| пример многочлена у этого есть 3 члена |
Степень (для многочлена с одной переменной, например x ):
— , крупнейший показатель этой переменной.
Больше примеров:
| 4x | Степень составляет 1 (переменная без показателя степени фактически имеет показатель степени 1) | |
| 4x 3 — x + 3 | Степень составляет 3 (наибольший показатель x) | |
| x 2 + 2x 5 — x | Степень составляет 5 (наибольший показатель x) | |
| z 2 — z + 3 | Степень 2 (самый большой показатель степени z) |
названий степеней
Когда мы знаем степень, мы также можем дать ей имя!
| Степень | Имя | Пример |
|---|---|---|
| 0 | Константа | 7 |
| 1 | Линейный | х + 3 |
| 2 | Quadratic | x 2 −x + 2 |
| 3 | куб. | x 3 −x 2 +5 |
| 4 | Quartic | 6x 4 −x 3 + x − 2 |
| 5 | Quintic | x 5 −3x 3 + x 2 +8 |
Пример: y = 2x + 7 имеет степень 1, поэтому это линейное уравнение
Пример: 5w 2 — 3 имеет степень 2, поэтому он квадратичный
Уравнения высшего порядка , как правило, труднее решить:
- Линейные уравнения легко решить
- Квадратичные уравнения немного сложнее , чтобы решить
- Кубические уравнения снова сложнее, но есть формулы , чтобы помочь
- Квартические уравнения также могут быть решены, но формулы очень сложны
- У квинтических уравнений нет формул, а иногда может быть неразрешимым !
градусов многочлена с более чем одной переменной
Когда многочлен имеет более одной переменной, нам нужно взглянуть на каждый член .Термины разделены знаками + или -:
| пример многочлена с несколькими переменными |
За каждый семестр :
- Найти степень по , сложив в ней показатели каждой переменной ,
наибольшая такая степень является степенью полинома.
Пример: какова степень этого полинома:
Проверка каждого термина:
- 5xy 2 имеет степень 3 (x имеет показатель степени 1, y имеет 2 и 1 + 2 = 3)
- 3x имеет степень 1 (x имеет показатель степени 1)
- 5y 3 имеет степень 3 (у имеет показатель степени 3)
- 3 имеет степень 0 (без переменной)
Наибольшая степень из них равна 3 (фактически два члена имеют степень 3), поэтому полином имеет степень 3
Пример: какова степень этого полинома:
4z 3 + 5y 2 z 2 + 2yz
Проверка каждого термина:
- 4z 3 имеет степень 3 (z имеет показатель степени 3)
- 5y 2 z 2 имеет степень 4 (y имеет показатель степени 2, z имеет 2 и 2 + 2 = 4)
- 2yz имеет степень 2 (у имеет показатель степени 1, z имеет 1 и 1 + 1 = 2)
Наибольшая степень из них равна 4, поэтому полином имеет степень 4
Записываем
Вместо того, чтобы сказать « степень (что угодно) составляет 3 », мы пишем это так:
Когда выражение является дробью
Мы можем определить степень рационального выражения (в виде дроби), взяв степень вершины (числитель) и вычтя степень дна (знаменатель).
Вот три примера:
Вычисление других типов выражений
Предупреждение: передовые идеи впереди!
Иногда мы можем определить степень выражения, разделив …
- логарифм функции по
- логарифм переменной
… затем сделайте это для больших и больших значений, чтобы увидеть, где ответ «движется».
(более правильно, мы должны установить предел до бесконечности ln (f (x)) / ln (x) , но я просто хочу сохранить это простым здесь).
Вот пример:
Пример: Какова степень (3 плюс квадратный корень из x)?
Попробуем увеличить значения x:
| x | ln () | ln (x) | ln () / ln (x) |
|---|---|---|---|
| 2 | 1,48483 | 0,69315 | 2,1422 |
| 4 | 1.60944 | 1,38629 | 1,1610 |
| 10 | 1,81845 | 2,30259 | 0,7897 |
| 100 | 2,56495 | 4,60517 | 0,5570 |
| 1 000 | 3,54451 | 6,90776 | 0,5131 |
| 10000 | 4.63473 | 9,21034 | 0,5032 |
| 100 000 | 5,76590 | 11,51293 | 0,5008 |
| 1 000 000 | 6,91075 | 13,81551 | 0,5002 |
Глядя на стол:
- при x становится больше, чем ln () / ln (x) становится все ближе и ближе к 0.5
Таким образом, степень составляет 0,5 (другими словами, 1/2)
(Примечание: это хорошо согласуется с x ½ = квадратный корень из x, см. Дробные показатели)
Некоторые значения степени
| Выражение | Степень |
|---|---|
| бревно (х) | 0 |
| е х | ∞ |
| 1 / х | -1 |
| 1/2 |

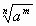
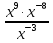 при x=3
при x=3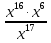 при x=9
при x=9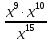 при x=5
при x=5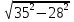
Leave A Comment