Радиус окружности с центром: Радиус окружности с центром в точке O равен 85, длина хорды AB равна 80. Найдите расстояние

Радиус окружности — что такое, формула, как найти ⚪

Поможем понять и полюбить математику

Начать учиться

210.2K

Решить задачу можно по-разному: посчитать на калькуляторе, взять алгоритм из похожей задачки, списать у одноклассника. Самый эффективный и радостный — запомнить формулу и прийти к ответу самому. В этой статье расскажем про способы поиска радиуса окружности.

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.

Круг — часть плоскости, которая лежит внутри окружности. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.

Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.

Возможно тебе интересно узнать — как найти длину окружности?

Узнай, какие профессии будущего тебе подойдут

Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас

Формула радиуса окружности

Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.

Если известна площадь круга

, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Если известна длина

, где C — длина окружности.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Если известен диаметр окружности

, где D — диаметр.

Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.

Если известна диагональ вписанного прямоугольника

R = d : 2, где d — диагональ прямоугольника.

Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:

, где a, b — стороны вписанного прямоугольника.

Если известна сторона описанного квадрата

, где a — сторона квадрата.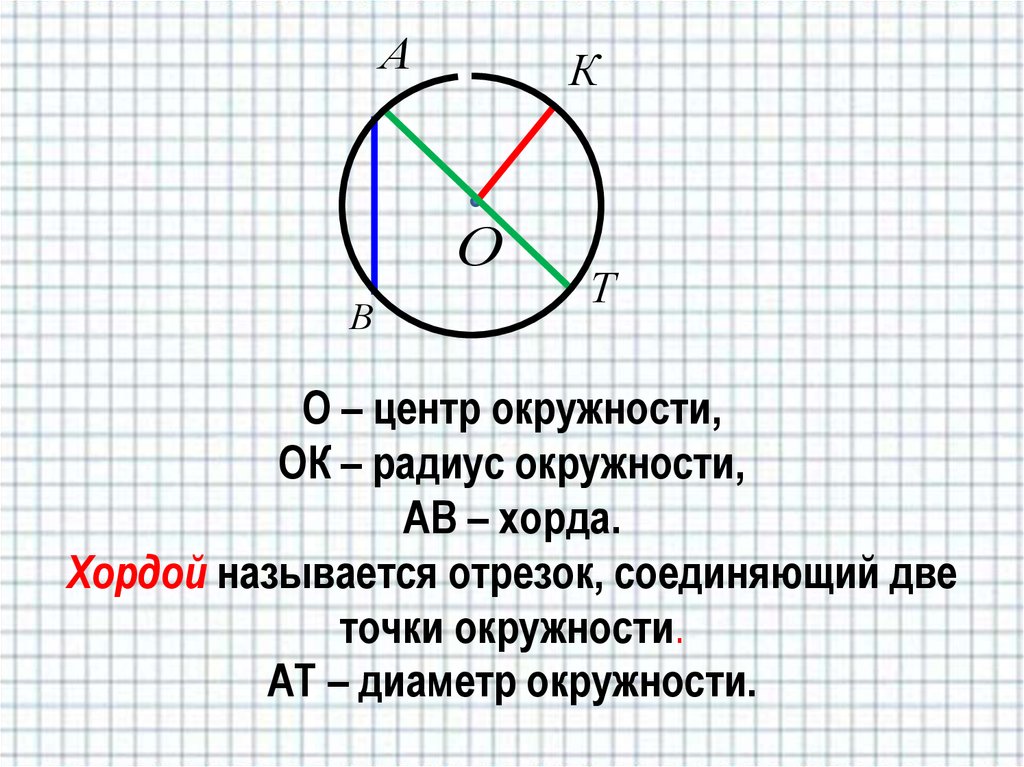

Сторона описанного квадрата равна диаметру окружности.

Если известны стороны и площадь вписанного треугольника

, где a, b, с — стороны треугольника, S — площадь треугольника.

Если известна площадь и полупериметр описанного треугольника

, где S — площадь треугольника, p — полупериметр треугольника.

Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.

Если известна площадь сектора и его центральный угол

, где S — площадь сектора круга, α — центральный угол.

Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.

Если известна сторона вписанного правильного многоугольника

, где a — сторона правильного многоугольника, N — количество сторон.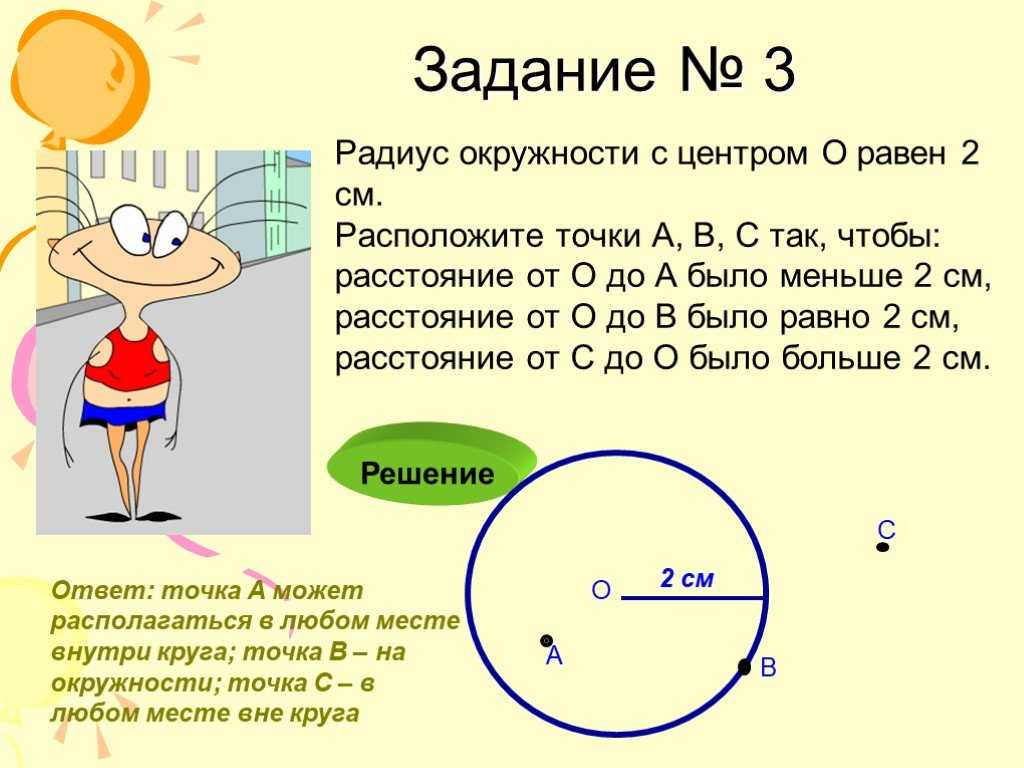

В правильном многоугольнике все стороны равны.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Лидия Казанцева

Автор Skysmart

К предыдущей статье

Как найти периметр квадрата

К следующей статье

517.8K

Теорема Пифагора

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс

Окружность, радиус, диаметр, число Пи, сектор, касательная

Окружность — геометрическое место точек плоскости, расстояние от которых до центра окружности равно.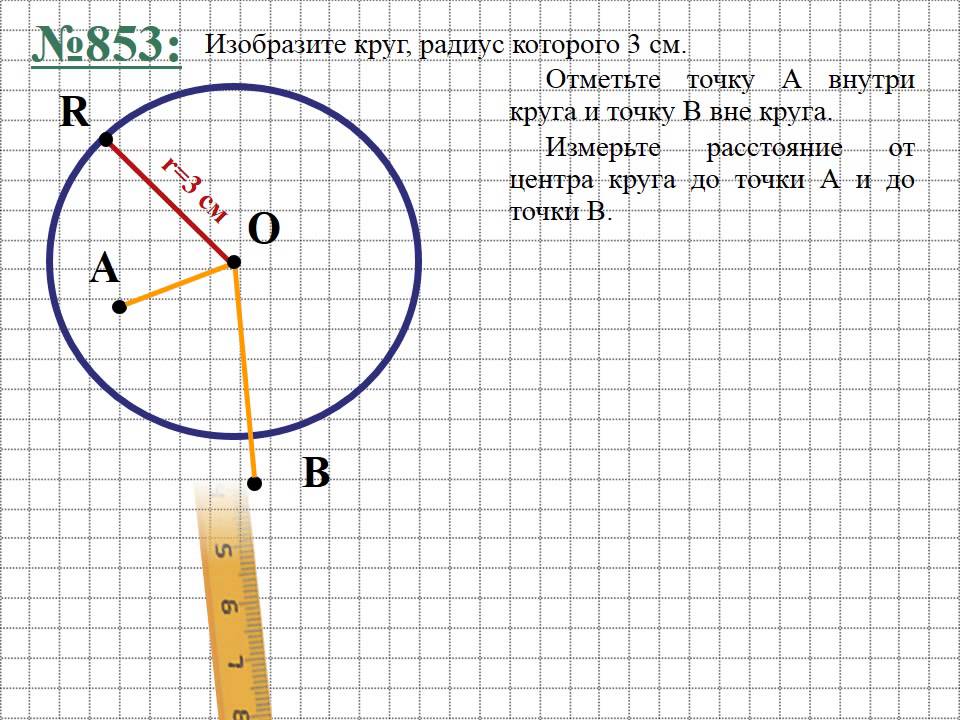

Центр окръжности

Радиус: расстояние от центра окружности до его границы.

Диаметр: наибольшее расстояние от одной границы окружности до другой. Диаметр равен двум радиусам.

$d = 2\cdot r$

Периметр (длина окружности): длина границы окружности.

Длина окружности $= \pi \cdot$ диаметр $= 2 \cdot \pi \cdot$ радиус
Длина окружности $= \pi \cdot d = 2 \cdot \pi \cdot r$

$\pi$ — pi: число, равное 3,141592… или $\approx \frac{22}{7}$, то есть отношение $\frac{\text{длины окружности}}{\text{диаметр}}$ любого окружности.

Дуга: изогнутая линия, которая является частью окружности.

Дуги окружности измеряется в градусах или радианах.
Например: 90° или $\frac{\pi}{2}$ — четверть круга,
180° или $\pi$ — половина круга.
Сумма всех дуг окружности составляет 360° или $2\pi$

Хорда: отрезок прямой, соединяющей две точки на окружности.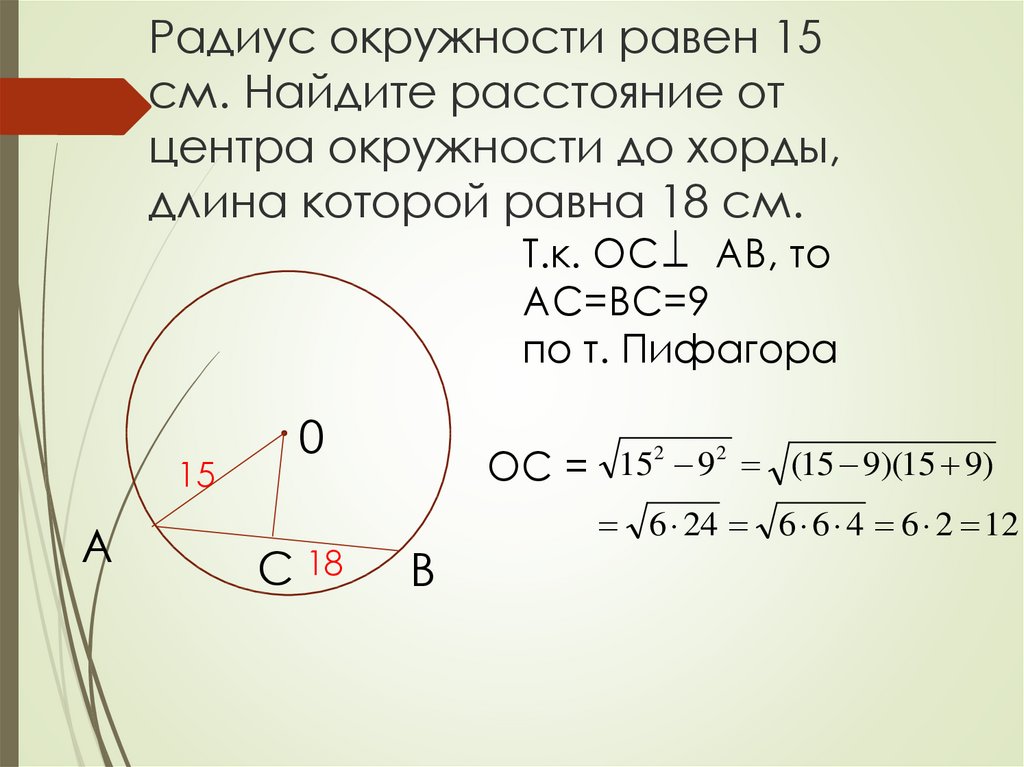 \circ$

Хорды

Если две хорды пересекаются внутри окружности, как на рисунке выше, тогда:

$AX \cdot XB = CX \cdot XD$

Как найти центр и радиус окружности из ее уравнения — Криста Кинг Математика

Какова стандартная форма уравнения окружности?

В этом уроке мы рассмотрим, как написать уравнение окружности в стандартной форме, чтобы найти центр и радиус окружности.

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее. 92???

где ???r??? это радиус и ???(h,k)??? является центром.

Иногда, чтобы написать уравнение окружности в стандартной форме, вам нужно заполнить квадрат дважды, один раз для ???x??? и один раз для ???y???.

Приведение уравнения окружности к стандартной форме и определение ее центра и радиуса по стандартной форме

92=\фракция{19}{6}???

Центр круга ???(h,k)??? ???(-1,0)??? а радиус равен ???\sqrt{19/6}???.

Исключить ???-\sqrt{19/6}??? потому что радиус не может быть отрицательным.

Получить доступ к полному курсу Алгебра 2

Начать

Изучение математикиКриста Кинг 30 мая 2021 г. математика, изучение онлайн, онлайн-курс, онлайн-математика, алгебра, алгебра 2, алгебра II, круг, уравнение окружности, центр и радиус, центр и радиус окружности, стандартная форма уравнение окружности

0 лайков

Как найти центр и радиус окружности (3 метода) – JDM Educational

Окружности используются в математике и в повседневной жизни. Однако знание того, как найти центр или радиус из другой заданной информации, также может быть полезным.

Итак, как найти центр и радиус круга? Чтобы найти центр и радиус окружности, запишите уравнение окружности в стандартной форме. Мы также можем использовать три точки на окружности (или две точки, если они находятся на противоположных концах диаметра), чтобы найти центр и радиус. Кроме того, мы можем использовать центр и одну точку на окружности, чтобы найти радиус.

Конечно, полезно ознакомиться со стандартной формой уравнения окружности, чтобы вы могли легко работать с этими различными ситуациями.

В этой статье мы поговорим о том, как найти центр и радиус окружности по информации о ней (например, ее уравнению или точкам на окружности). Мы также рассмотрим несколько примеров, чтобы прояснить концепции.

Начнем.

Проблемы с математикой?

Ищете репетитора?

Как найти центр и радиус окружности

Способ, которым мы находим центр и радиус окружности, зависит от информации, которую мы получили:

Из уравнения : с уравнением в стандартной форме, мы можем легко найти центр и радиус круга. В противном случае нам нужно будет заполнить квадрат для переменной x или y (или обеих) для преобразования в стандартную форму.
С двумя точками : по двум точкам на окружности на противоположных концах диаметра мы можем найти центр. Мы также можем найти радиус, учитывая центр и одну точку на окружности, используя формулу расстояния.
С тремя точками : по трем точкам на окружности мы можем найти центр и радиус окружности, решив систему трех уравнений с тремя неизвестными (a, b и r).

В некоторых ситуациях мы можем найти центр и радиус круга, имея информацию о точках на круге.

Начнем с нахождения центра окружности по заданному уравнению.

Найти центр круга из уравнения

Чтобы найти центр круга из уравнения, мы всегда хотим преобразовать его в стандартную форму.

Как найти формулу экспоненты…

Включите JavaScript

Как найти формулу показательной функции

Помните, что уравнение окружности в стандартной форме задается как:

( x – a) ² + (y – b) ² = r ²

, где (a, b) – центр окружности, а r – радиус окружности.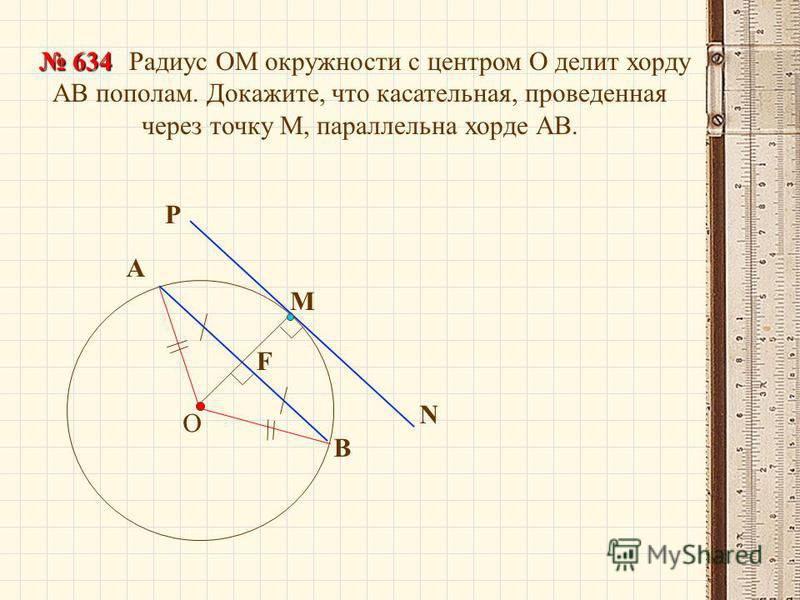

Если нам дано уравнение не в стандартной форме, нам нужно сначала заполнить квадрат для одной или обеих переменных (x и y).

Пример 1: Центр окружности из уравнения в стандартной форме

Допустим, мы хотим найти центр окружности, заданной уравнением

(x – 2) ² + (y + 4) ² = 9

Сравнивая это со стандартной формой выше, мы видим, что a = 2 и b = -4 (остерегайтесь этих отрицательных знаков: y — (-4) такое же, как y + 4 ).

Итак, центр окружности (a, b) = (2, -4).

Пример 2. Центр круга из уравнения путем заполнения квадрата одной переменной

Допустим, мы хотим найти центр окружности, заданной уравнением 004 Этот круг не стандартной формы, поэтому мы знаем, что нам нужно будет заполнить квадрат хотя бы для одной переменной.

Переставив члены таким образом, чтобы переменные сгруппировались, мы получим:

(x ² + 6x) + (y ² + 10y + 25) = 27

Легко видеть, что выражение с переменной y, y ² + 10y + 25, представляет собой трехчлен с полным квадратом, (y + 5) ² :

(x ² + 6x ) + (y + 5) ² = 27

Теперь нам просто нужно дополнить квадрат выражения с переменной x, x ² + 6x. Помните, что для завершения квадрата мы берем половину коэффициента x и возводим результат в квадрат, а затем прибавляем его к обеим сторонам.

Здесь x-коэффициент равен 6, поэтому половина этого числа дает нам результат 3. Возведение результата в квадрат дает нам 3 ² = 9.

Итак, мы добавляем 9 к обеим частям уравнения, чтобы получить:

(x ² + 6x + 9) + (y + 5) ² = 27 + 9 9 0034

Обратите внимание, что мы сгруппировали +9 слева с членами x. Это позволяет нам разложить на множители еще один идеальный квадратный трехчлен:

(x + 3) ² + (y + 5) ² = 36

Теперь у нас есть уравнение окружности в стандартной форме. Сравнивая его с приведенным выше общим уравнением, мы находим, что a = -3 и b = -5.

Итак, центр окружности (a, b) = (-3, -5).

Пример 3: Центр круга из уравнения, заполнив квадрат для двух переменных

, скажем, мы хотим найти центр круга, заданный уравнением

x ² + y ² + x ² + y ² + x ² + y ² + x ² + у 8x + 12y = 12

Этот круг не имеет стандартной формы, поэтому мы знаем, что нам нужно заполнить квадрат для обеих переменных.

Переставив члены так, чтобы переменные сгруппировались вместе, мы получаем:

(x ² + 8x) + (y ² + 12y) = 12

Сначала нам нужно заполнить квадрат выражения с переменной x, x ^{2 9 0190 + 8х. Помните, что для завершения квадрата мы берем половину коэффициента x и возводим результат в квадрат, а затем прибавляем его к обеим сторонам.}

Здесь x-коэффициент равен 8, поэтому половина этого дает нам результат 4. Возведение результата в квадрат дает нам 4 ² = 16.

Итак, мы добавляем 16 к обеим частям уравнения, чтобы получить:

(x ² + 8x + 16) + (y ² + 12y) = 12 + 16

Обратите внимание, что мы сгруппировали +12 слева с членами x. Это позволяет нам разложить как совершенный квадратный трехчлен:

(x + 4) ² + (y ² + 12y) = 28

Теперь нам нужно завершить квадрат для выражения с переменная у, у ² + 12у. Помните, что для завершения квадрата мы берем половину коэффициента x и возводим результат в квадрат, а затем прибавляем его к обеим сторонам.

Здесь x-коэффициент равен 12, поэтому половина этого числа дает нам результат 6. Возведение результата в квадрат дает нам 6 ² = 36.

Итак, мы добавляем 36 к обеим частям уравнения, чтобы получить:

(x ² + 8x + 16) + (y ² + 12y + 36) = 28 + 36

Обратите внимание, что мы сгруппировали +36 слева с у условия. Это позволяет нам разложить как совершенный квадратный трехчлен:

(x + 4) ² + (y + 6) ² = 64

Теперь у нас есть уравнение окружности в стандартной форме. Сравнивая его с приведенным выше общим уравнением, мы находим, что a = -4 и b = -6.

Итак, центр окружности (a, b) = (-4, -6).

Найти центр окружности с двумя точками (на концах диаметра)

Имея две точки на окружности, мы можем найти центр.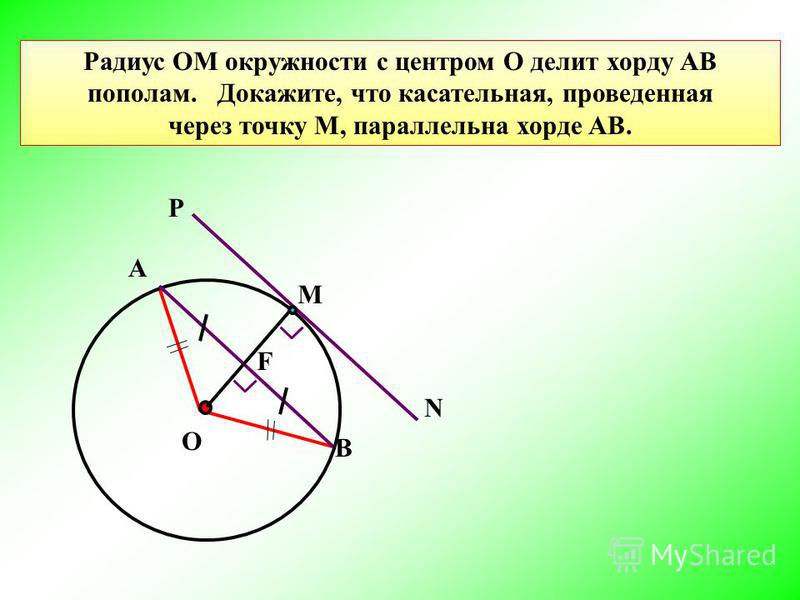 Если они не лежат на одном диаметре, то у нас недостаточно информации, и мы можем указать только все семейство окружностей, а не одну конкретную окружность.

Однако по двум точкам на окружности, лежащим на концах диаметра, мы можем найти центр окружности.

Центр круга будет в середине любого диаметра, нарисованного на круге.
Все, что нам нужно сделать, это найти середину отрезка между двумя точками на диаметре.
Помните, что для отрезка с концами (x ₁ , y ₁ ) и (x ₂ , y ₂ ) формула средней точки определяется как:
(х _м , у _м ) = ((х ₁ + х ₂ ) / 2, (у ₁ + у _{2 904 06 ) / 2)}
В основном, x _m — это среднее значение координат x конечных точек, а y _m — это среднее значение координат y конечных точек.
Давайте попробуем на примере, чтобы увидеть, как это работает.
Пример: найти центр окружности с двумя точками на диаметре
Допустим, мы хотим найти центр окружности с точками (0, 0) и (6, -8) в качестве концов диаметра.
Использование формулы средней точки для нахождения центра окружности дает нам:
(x _м , y _м ) = ((x ₁ + x ₂ ) / 2, (у ₁ + у ₂ ) / 2)
(х _м , у _м ) = ((0 + 6) / 2, (0 + -8) / 2) 9016 2
( х _м , у _м ) = (6 / 2, -8/ 2)
(х _м , у _м ) = (3, -4) 9016 2
Итак, центр этого круга находится в точке (3, -4).
Мы также можем найти радиус окружности, если захотим. Это просто половина диаметра, который определяется формулой расстояния:
D = √((x ₂ – x ₁ ) ² + (y ₂ – y ₁ ) ² )
D = √((6 – 0) ² + (-8 – 0) ² )
D = √( (6) ² + (-8) ² )
D = √(36 + 64)
D = √(100)
D = 10
Таким образом, диаметр равен 10, и радиус равен 5.
Помните, что диаметр Окружность — это длина самой длинной прямой линии, которую можно провести между двумя точками окружности. Радиус равен половине длины диаметра.
Проблемы с математикой?
Ищете репетитора?
Найти центр окружности по трем точкам
Чтобы найти центр окружности по трем точкам, мы можем просто подставить значения x и y из каждой точки в уравнение окружности.
Тогда мы можем установить все 3 уравнения равными друг другу (все они равны r ² , или квадрату радиуса).
Затем мы можем написать отдельные уравнения, упростить их и одновременно решать линейные уравнения.
Давайте рассмотрим пример.
Пример: найти центр окружности по трем точкам
Допустим, нам даны точки (-1, -3), (-2, 4) и (5, 5) на окружности.
Подставим каждую из этих точек по очереди в стандартную форму окружности:
(x – a) ² + (y – b) ² = r ²
Для первой точки (-1, -3) получаем: 9000 5
( -1 – а) ² + (-3 – б) ² = r ²
Для второй точки (-2, 4) получаем:
(-2 — а ) ² + (4 – б) ² = r ²
Для третьей точки (5, 5) получаем:
(5 – а) ² + (5 – b) ² = r ²
Мы можем положить любые две левые части равными друг другу, поскольку все правые части равны r ² (независимо от значения р).
Приравняв первые две левые части, получим:
(-1 – a) ² + (-3 – b) ² = (-2 – a) ² + (4 – b) ) ²
1 + 2а + а ² + 9 + 6б + б ² = 4 + 4а + а ² + 16 – 8б + б ²
1 + 2а + а ² + 9 + 6б = 4 + 4а + а ² + 16 – 8б [вычесть b ² с обеих сторон ]
1 + 2a + 9 + 6b = 4 + 4a + 16 – 8b [вычесть ² с обеих сторон]
10 + 2a + 6b = 20 + 4a – 8b [объединить постоянные члены на обе стороны]
-10 – 2a + 14b = 0 [собрать все термины на одной стороне и объединить подобные термины]
5 + a – 7b = 0 [разделить на -2 с обеих сторон]
Приравняв первую и третью левую части, получим:
(-1 – a) ² + ( — 3 – б) ² = (5 – а) ² + (5 – б) ²
1 + 2а + а ² + 9 + 6б + б ² = 25 – 10а + а ² + 25 – 10б + б ²
1 + 2а + а ² + 9 + 6б = 25 – 10а + а ² + 25 – 10b [вычесть b ² с обеих сторон]
1 + 2a + 9 + 6b = 25 – 10a + 25 – 10b [вычесть a ² с обеих сторон]
10 + 2a + 6b = 50 – 10a – 10b [объединить постоянные члены с обеих сторон]
-40 + 12a + 16b = 0 [собрать все члены с одной стороны и объединить одинаковые члены]
-10 + 3a + 4b = 0 [разделить на 4 с обеих сторон]
Теперь мы можем решить следующую систему методом исключения:
5 + a – 7b = 0
-10 + 3a + 4b = 0
Для этого умножьте первое уравнение на -3, чтобы получить:
-15 – 3а + 21b = 0
-10 + 3a + 4b = 0
Теперь сложите два уравнения, чтобы получить:
-25 + 0a + 25b = 0
1 = б
Итак, при b = 1 находим:
5 + a – 7b = 0
5 + а – 7(1) = 0
5 + а – 7 = 0
а – 2 = 0
а = 2
Итак, центр окружность находится в точке (a, b) = (1, 2). Затем мы можем использовать центр и любую точку на окружности, чтобы найти радиус, используя формулу расстояния (подробнее об этом методе ниже).
Найдите радиус круга из уравнения
Чтобы найти радиус круга из уравнения, мы всегда хотим преобразовать его в стандартную форму.
Помните, что уравнение окружности в стандартной форме задается формулой:

(x – a) ² + (y – b) ² = r ²
90 171
где ( a, b) — центр окружности, r — радиус окружности.
Если нам дано уравнение не в стандартной форме, нам нужно сначала заполнить квадрат для одной или обеих переменных (x и y).
Пример 1: центр окружности из уравнения в стандартной форме
Допустим, мы хотим найти радиус окружности, заданной уравнением приведение этого к стандартной форме выше мы видим, что r = 7 (поскольку r ² = 49 — не забудьте взять квадратный корень, чтобы найти r).
Итак, радиус окружности равен r = 7.
Пример 2. Радиус окружности из уравнения путем заполнения квадрата
Допустим, мы хотим найти радиус окружности, заданный уравнением
x ² + y ² + 8x + 12y + 12 = 24
Этот круг не имеет стандартной формы, поэтому мы знаем, что нам нужно заполнить квадрат хотя бы для одной переменной.
Переставив члены таким образом, чтобы переменные сгруппировались, мы получим:
(x ² + 8x) + (y ² + 12y) = 24 – 12
9015 9 (х ² + 8х) + (у ² + 12у) = 12
Чтобы завершить возведение в квадрат переменной x, x ² + 8x, мы возьмем половину от 8, чтобы получить 4, и возведем этот результат в квадрат, чтобы получить 16. Прибавим 16 к обеим частям:
(x ² + 8x + 16) + (y ² + 12y) = 12 + 16
(x ² + 8x + 16) + (y ² + 12y) = 28
Теперь нам нужно чтобы разложить выражение x на множители, x ² + 8x + 16. Это идеальный квадратный бином: (x + 4) ² .
(x + 4) ² + (y ² + 12y) = 28
половина из 12, чтобы получить 6 , и возведите этот результат в квадрат, чтобы получить 36. Добавим 36 к обеим частям:

(x + 4) ² + (y ² + 12y + 36) = 28 + 36

90 033 (х + 4) ² + (y ² + 12y + 36) = 64

Теперь нам нужно разложить выражение y на множители, y ² + 12y + 36. Это идеальный квадратный бином: (y + 6) ² .

(х + 4) ² + (у + 6) ² = 64
(х + 4) ² + (у + 6) 9 0189 2 = 8 ²

Мы также переписали 64 как 8 ² , так как это соответствует r ² в правой части уравнения окружности в стандартной форме.

Теперь мы знаем, что радиус окружности равен r = 8.

Найти радиус окружности по данным центра и точки

Если мы знаем центр окружности и одну точку на окружности, мы можем найти радиус с помощью формулы расстояния.

(Помните, что радиус — это расстояние между центром окружности и любой точкой на окружности.)

Давайте рассмотрим пример того, как это сделать.

Пример: нахождение радиуса окружности по центру и точке на окружности

Предположим, что вам дан центр окружности в точках (4, 3) и точка на окружности в точках (16, 12) . Используя формулу расстояния, мы получаем:

D = √((х ₂ – х ₁ ) ² + (у ₂ – у ₁ ) ² )
D = √((16 – 4 ) ² + (12 – 3) ² )
D = √((12) ² + (9) ² )
Д = √(144 + 81)
D = √(225)
D = 15

Итак, радиус окружности равен 15.

Найдите радиус окружности с двумя точками на окружности

В этом случае мы не можем решить для одного круга, так как у нас недостаточно информации. Вместо этого мы получили бы целое семейство окружностей, содержащих обе точки.

Если у нас также есть центр или третья точка на окружности, мы можем найти радиус (используя формулу расстояния с центром в качестве одной точки и одной из точек на окружности в качестве другой точки).

Затем мы можем использовать центр и радиус, чтобы записать уравнение окружности в стандартной форме.

Заключение

Теперь вы знаете, как найти центр и радиус круга в различных ситуациях. Вы также знаете, как использовать формулы средней точки и расстояния в качестве сокращений, чтобы сделать ваши вычисления немного проще.

Вы можете узнать о длине окружности и площади круга в моей статье здесь.