Встретились четыре друга и каждый поздоровался друг с другом, сколько всего было рукопожатий?…(вопрос из учебника математики второго класса) — Обсуждай
Встретились четыре друга и каждый поздоровался друг с другом, сколько всего было рукопожатий?…(вопрос из учебника математики второго класса) — ОбсуждайАл
Александр
Встретились четыре друга и каждый поздоровался друг с другом, сколько всего было рукопожатий?…(вопрос из учебника математики второго класса) вопрос друг класс математика рукопожатие учебник
1197
115
2
Ответы
VR
Vladimir Rakivnenko
В комбинаторике это называется «Количество сочетаний без повторений», потому что когда Петя пожал руку Васе, это всё равно, что Вася — Пете.
Сочетание без повторений: сколькими способами можно из n (эн) различных элементов выбрать m (эм) элементов (m≤n) без упорядочения? — число способов равно числу сочетаний из n элементов по m
C(nm) = n! / m!(n-m)!
C (4,2) = 1*2*3*4 / (1*2)*(1*2) , сокращая одинаковые множители, получаем 3*4/1*2 = 6
Источник: Комбинаторика, школьный курс
0
Ал
Александр
Браво маэстро!.. Такого исчерпывающего и полноценного ответа ещё не было!..
1
VR
Vladimir Rakivnenko
Я в хорошей школе учился. Помню — я сразу не смог решить эту задачу, потом наша славная учительница по математике объяснила (9 класс) как это решается. По окончании школы я поступил в МИФИ и частенько однокашников озадачивал — вот нас здесь столько-то сидит за столом в пивнушке, сколько раз мы чокнемся бокалами друг с другом?. .. )))
.. )))
1
Ал
Александр
В нынешней школе детей учат «устной» сообразительности, все ваши формулы уже не к чему!.. В этом примере достаточно понять, что одно рукопожатие — это поздоровались сразу два друга из всех четырёх!..
1
VR
Vladimir Rakivnenko
До встречи! ))
1
Наталья Попова
6 раз получается. Первый поздоровался 3 раза. Второй -2 раза. Третий -1 раз. Четвертый — ни разу. Все здоровались с ним.
0
Ал
Александр
Так ещё никто не отвечал!. . Вы мадам и правы, и нет!.. Как это четвёртый ни разу?!.. Каждый из них пожал руку остальным троим, но рукопожатий всего было шесть, это верно!.. Одно рукопожатие, это поздоровались двое!
. Вы мадам и правы, и нет!.. Как это четвёртый ни разу?!.. Каждый из них пожал руку остальным троим, но рукопожатий всего было шесть, это верно!.. Одно рукопожатие, это поздоровались двое!
1
Наталья Попова
Это по идее, что-четвертый ни с кем. Достаточно вспомнить футбол. Чемпионат Европы, например. Где 16 команд разделены на 4 подгруппы, в каждой подгруппе 4 команды и они на предварительном этапе должны сыграть все друг с другом. Как ни крути, получается только 6 матчей в подгруппе. И логически получается, что с одной из команд играют все три остальные. А она огрызается.
1
Ал
Александр
Хорошо, согласен!..
1
Сергей Петрович
Если больше никто не подойдет то скорее всего 6.
0
Луиза Бальтазар
Умные люди – странный предмет, в интернете их куча, но нигде больше нет.
0
Александр Емельянов + 7Я +Инструктор Туризма
Прикинул… 6-8…не больше….
1
Ал
Александр
1
Александр Емельянов + 7Я +Инструктор Туризма
ШЕСТЬ….
1
Ал
Александр
1
Александр Емельянов + 7Я +Инструктор Туризма
1
Видмет Лапатыч Бизульо
Первый с тремя, второй с двумя, третий с одним. Щетадь лень.
Щетадь лень.
0
Ал
Александр
1
Елена Алексеева
Насколько помню математику, будет 6 рукопожатий…
0
Ал
Александр
1
Елена Алексеева
1
ЛМ
Люси Марево
Во втором классе учишься? Молодец!))))
0
Ал
Александр
Внучка, во втором классе учится!.
1
ЛМ
Люси Марево
И ты…подтягивайся за внучкой!….))))))))))
1
Тт
Тт
насчитала 6! Если нет — на фиг эту математику))))
0
Ал
Александр
1
Ли
Лида
ЕСЛИ СЧИТАТЬ КАЖДОГО ДРУГА С КАЖДЫМ ДРУГОМ-16.
0
Ал
Александр
Нет мадам, Вам кол!. .
.
1
Ли
Лида
Я знаю! А ты ,Потешился?! Оценщик!
1
Ал
Александр
Похоже туговато у Вас с математикой, мадам!..
1
Ли
Лида
можно и без математики узнать, что 6!
1
ЕТ
Евгения Трусова
пересчитала 3,2,1 и получилось 6
0
Ал
Александр
1
ЕС
Евгения Силантьева (Елистратова)
Бедные дети.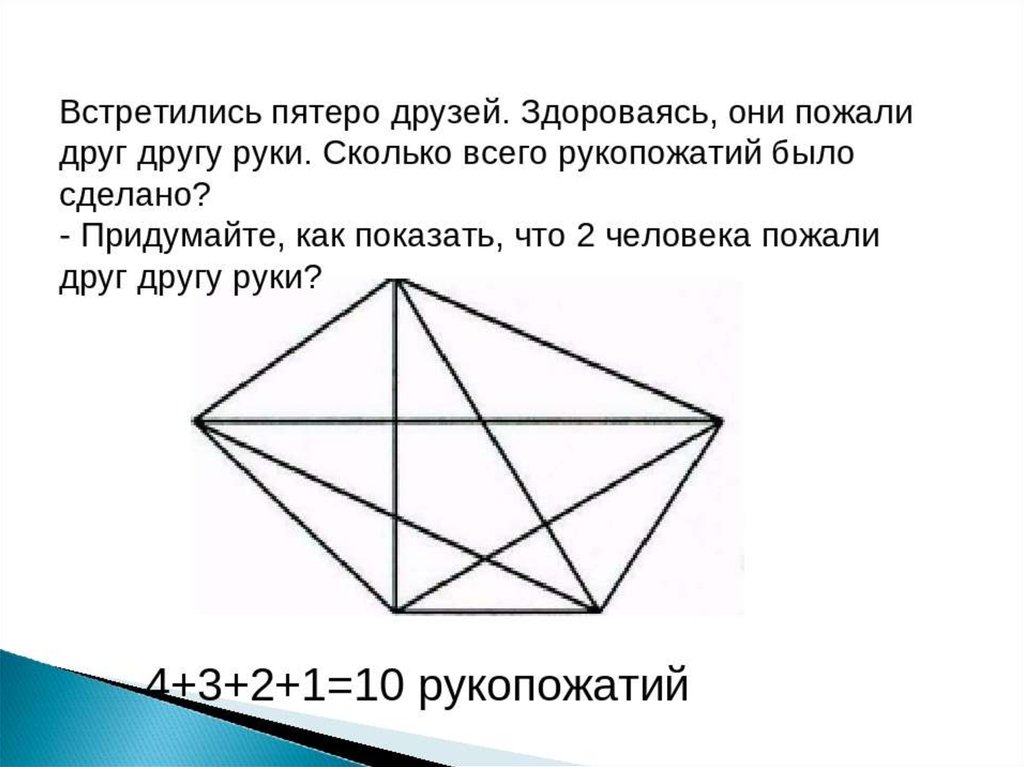 ..ну,6, наверное…
..ну,6, наверное…
0
Ал
Александр
Дааааааааааааааааа!!!!!!!!!!!!!!!!!!!!!
1
ЕС
Евгения Силантьева (Елистратова)
Ух ты…Можно и на ЕГЭ пойти рискнуть…
1
Наталия
ваш ребенок как ответил?
0
Наталия
я вам довкряю
1
Ал
Александр
1
Наталия
фу, какой!
1
Ал
Александр
Ага, я такой!. .
.
1
Наталия
ужас
1
ВМ
Валентина Маршакова
4 в четвёртой степени
0
ВМ
Валентина Маршакова
Ты как мой папа
1
ВМ
Валентина Маршакова
6
1
Ал
Александр
Да, я такой, я дважды папа и четырежды дед!.. Во — как!
1
ВМ
Валентина Маршакова
Везёт!
1
Ал
Александр
А-то!. .
.
1
SB
Svetlana Barisheva (Chernishova)
Точно 6, просчиталась
0
Ал
Александр
1
ГА
Галина Александрова
16.или я старая неуч.
0
Ал
Александр
Или!
1
ГА
Галина Александрова
Наобум написала.
1
Мира Донна
4!))
1
ГА
Галина Александрова
Не обменялись по шеренге.
1
ТТ
Тина Тим
Наверное 6.Не знаю.
0
Людмила Склярова
Да наверно одно!
0
Ал
Александр
Такого ответа, ещё не было!..
1
Людмила Склярова
Красота,я первая!
1
Ал
Александр
Но ответ не верный!
1
ЛА
Ледовская Анна
Наверное, шесть
0
Ал
Александр
1
Кс
Ксюша
6. .я так думаю)))
.я так думаю)))
0
Ал
Александр
1
Кс
Ксюша
ой..вы пажарный?)))
1
Ал
Александр
Ну, вообще то, пОжарный!.. Что, не похож?..
1
Кс
Ксюша
похож)))
1
Ал
Александр
Это хорошо, или плохо?…
1
Кс
Ксюша
)))
1
ОК
Ольга Красноперова
3 рукопожатия?
0
Ал
Александр
Нет
1
Следующая страница
Комбинаторика.
 Расчёт количества вариантов. Формулы перемножения и сложения количества вариантов
Расчёт количества вариантов. Формулы перемножения и сложения количества вариантов1. Задание на урок:
Запустите презентацию и внимательно её изучите.Презентация вас познакомит с темой урока и основными
понятиями, раскрывающими тему урока. А также в конце
урока есть задачи на повторение. Если, что- то непонятно, то
вы можете найти информацию в интернете, либо задать
вопрос Лидии Александровне по почте в электронном
дневнике.
Пора за работу! У вас всё получится.
2. Тема урока: Расчёт количества вариантов
3. Встретились 6 друзей и каждый пожал руку каждому своему другу. Сколько было рукопожатий?
Встретились 6 друзей и каждыйпожал руку каждому своему
другу. Сколько было
рукопожатий?
В науке и практике часто встречаются такие задачи,
решая которые приходится составлять различные
комбинации из конечного числа элементов и
подсчитывать число комбинаций. Такие задачи
получили название комбинаторных задач, а раздел
математики, в котором рассматриваются подобные
задачи, называют комбинаторикой.

Комбинат орика
–
эт о раздел
мат емат ики,
посвященный
решению
задач
на
перебор
различных вариант ов, удовлет воряющих какимлибо условиям.
Здесь изучают ся вопросы о т ом, сколько
различных комбинаций, подчиненных т ем или
иным условиям, можно сост авит ь из заданных
объект ов.
Слово «комбинаторика» происходит от латинского
слова combinare, которое означает «соединять,
сочетать».
Методы комбинаторики находят широкое
применение в физике, химии, биологии, экономике
и других областях знаний.
5
Из истории комбинаторики
С комбинаторными задачами люди столкнулись в
глубокой древности. В Древнем Китае увлекались
составлением магических квадратов. В Древней Греции
занимались теорией фигурных чисел.
Комбинаторные задачи возникли и в связи с
такими играми, как шашки, шахматы, домино, карты,
кости и т.д. Комбинаторика становится наукой лишь в 18
в. – в период, когда возникла теория вероятности.
6
В Древней Греции
подсчитывали число различных
комбинаций длинных и коротких
слогов в стихотворных размерах,
занимались теорией фигурных
чисел, изучали фигуры, которые
можно составить из частей и т.д.
Со временем появились различные игры
(нарды, карты, шашки, шахматы и т. д.)
В каждой из этих игр приходилось
рассматривать различные сочетания
фигур, и выигрывал тот, кто их лучше
изучал,
знал
выигрышные
комбинации
и
умел
избегать
проигрышных.
7
Готфрид Вильгельм Лейбниц
(1.07.1646 — 14.11.1716)
Комбинаторику, как
самостоятельный раздел
математики первым стал
рассматривать немецкий
ученый Г. Лейбниц в своей
работе «Об искусстве
комбинаторики»,
опубликованной в 1666г. Он
также впервые ввел термин
«Комбинаторика».
Леонард Эйлер
(1707-1783)
рассматривал задачи о
разбиении чисел, о
паросочетаниях, циклических
расстановках, о построении
магических и латинских
квадратов, положил начало
совершенно новой области
исследований, выросшей
впоследствии в большую и
важную науку—топологию,
которая изучает общие
свойства пространства и
фигур.

8
Методы решения комбинаторных задач
1. Правило суммы.
2.
Правило произведения
9
10. Расчет количества вариантов: формулы перемножения и сложения количества вариантов.
11. Правило суммы
Если пересечение конечных множеств Аи В пусто, то число элементов в их
объединении равно сумме чисел элементов
множеств А и В :
А
В
n A и В n( А) n( B)
12. Задача №1.
На одной полке книжного шкафастоит 30 различных книг, а на другой
– 40 различных книг (не такие как на
первой). Сколькими способами
можно выбрать одну книгу.
Решение:
30 + 40 = 70 (способами).
13. Правило умножения.
Если множества А и В конечны, точисло N возможных пар (а; в), где
а из А, в из В равно
произведению чисел элементов
этих множеств:
N = n (A) *n (B)
14. Задача № 2
Пусть существует 3кандидата на пост
командира и 2 на пост
инженера. Сколькими
способами можно
сформировать экипаж
корабля, состоящий из
командира и инженера?
1
1
2
1
2
2
1
3
2
Решение:
3 * 2 = 6 (способ).

Повторение.
(Три задачи с решениями просмотреть
всем. Особенно тем, кто сдаёт экзамен)
№1 (Демоверсия ФИПИ – 2020)
В одной из кодировок Unicode каждый символ кодируется 16 битами.
Вова написал текст (в нём нет лишних пробелов):
«Ёж, лев, слон, олень, тюлень, носорог, крокодил, аллигатор – дикие
животные».
Ученик вычеркнул из списка название одного из животных. Заодно он
вычеркнул ставшие лишними запятые и пробелы – два пробела не должны
идти подряд.
При этом размер нового предложения в данной кодировке оказался на 16
байт меньше, чем размер исходного предложения. Напишите в ответе
вычеркнутое название животного.
Решение:
1.
2.
3.
4.
5.
По условию: 1 символ – 16 бит = 2 байта (1 байт = 8 бит).
Размер нового предложения на 16 байт меньше, чем размер исходного
предложения.
16/2 = 8 (символов) – было вычеркнуто (удалено из текста).
Важно! При удалении слова нужно удалить один пробел и лишнюю
запятую.

8 символов – 2 символа = 6 символов (содержит вычеркнутое слово).
Ответ: тюлень
№4 (А.Г. Минак, вариант №3)
В одной из кодировок Unicode каждый символ кодируется 2 байтами. Иван написал
текст
(в нем нет лишних пробелов):
«Январь, февраль, март, апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь,
декабрь – месяцы года».
Ученик вычеркнул из списка название одного месяца. Заодно он вычеркнул ставшие
лишними запятые и пробелы – два пробела не должны идти подряд. При этом размер
нового предложения в данной кодировке оказался на 128 бит меньше, чем размер
исходного предложения. Среди месяцев, имеющих одинаковое количество букв, Иван
вычеркивает последний по порядку. Напишите в ответе вычеркнутое название месяца.
Решение:
1.
2.
По условию: 1 символ – 2 байта = 16 бит (1 байт = 8 бит).
Размер нового предложения на 128 бит меньше, чем размер исходного
предложения.
3. 128/16 = 8 (символов) – было вычеркнуто (удалено из текста).
4. Важно! При удалении слова нужно удалить один пробел и лишнюю
запятую.
5. 8 символов – 2 символа = 6 символов (содержит вычеркнутое слово).
6. По условию: среди месяцев, имеющих одинаковое количество букв, Иван
вычеркивает последний по порядку
Ответ: ноябрь
№5
В кодировке КОИ-8 каждый символ кодируется 8 битами.
Витя написал текст (в нём нет лишних пробелов):
«Футбол, волейбол, регби, гандбол, теннис, бейсбол, гольф – спортивные игры с
мячом».
Ученик решил добавить в список названий ещё одной игры с мячом — баскетбол. При
этом он добавил в текст необходимую запятую и пробел.
На сколько байт при этом увеличился размер нового предложения в данной
кодировке?
В ответе укажите только одно число — количество байт.
Решение:
1.
2.
3.
4.
5.
По условию: 1 символ – 8 бит = 1 байт (1 байт = 8 бит).
Добавленное слово: баскетбол содержит 9 символов.
Важно! При добавлении слова нужно добавить один пробел и одну
запятую.

9 символов + 2 символа = 11 символов (содержит добавленное слово,
запятая и пробел).
11 символов * 1 байт = 11 байт
Ответ: 11
20. Домашнее задание
1.Решайте задачи в рабочей тетради и вышлите мне для
проверки фото с решениями из тетради.
Домашнее задание по новой
теме:
Решите задачу по формуле и графически:
1.
Имеется 3 вида конвертов и 4 вида марок.
Сколько существует вариантов выбора конверта с
маркой?
22. Домашнее задание по повторению
1. В одной из кодировок Unicode каждый символ кодируется 16битами.
Вова написал текст (в нём нет лишних пробелов):
«Чиж,
грач,
стриж,
гагара,
пингвин,
ласточка,
жаворонок, свиристель, буревестник, вертиголовка –
птицы».
Ученик вычеркнул из списка название одной птицы. Заодно он
вычеркнул ставшие лишними запятые и пробелы – два пробела
не должны идти подряд.
При этом размер нового предложения в данной кодировке
оказался на 18 байт меньше, чем размер исходного
предложения.
 Напишите в ответе вычеркнутое название птицы.
Напишите в ответе вычеркнутое название птицы.2.
В одной из кодировок Unicode каждый символ
кодируется 16 битами.
Вова написал текст (в нём нет лишних пробелов):
«Чиж, грач, стриж, гагара, пингвин, ласточка,
жаворонок,
свиристель,
буревестник,
вертиголовка – птицы».
Ученик вычеркнул из списка название одной птицы. Заодно
он вычеркнул ставшие лишними запятые и пробелы –
два пробела не должны идти подряд.
При этом размер нового предложения в данной кодировке
оказался на 12 байт меньше, чем размер исходного
предложения. Напишите в ответе вычеркнутое название
птицы.
Рукопожатие | NZ Maths
Цель
Это упражнение по решению задач сосредоточено на алгебре.
Цели достижения
NA3-8: соедините элементы последовательных шаблонов с их порядковым номером и используйте таблицы, графики и диаграммы, чтобы найти отношения между последовательными элементами числовых и пространственных шаблонов.
Разработка АО и другие учебные ресурсы
Студенческая деятельность
Шесть деловых людей встречаются за обедом и обмениваются рукопожатием.
Сколько рукопожатий?
Конкретные результаты обучения
Опишите словами правила шаблона.
Определите структуру треугольных чисел.
Разработайте и используйте стратегии решения проблем для математического исследования ситуаций (систематический список, рисование картинок, использование оборудования).
Описание математики
Математика, используемая в этой задаче, зависит от подхода, используемого для ее решения. Если учащиеся ищут закономерности, начиная с более простых случаев (2 человека и т. д.), задача связана с треугольными числами.
Необходимые материалы
- Копи-мастер задачи (маори)
- Копи-мастер задачи (английский)
Деятельность
Проблема
Шесть деловых людей встречаются за обедом и обмениваются рукопожатием. Сколько рукопожатий?
Сколько рукопожатий?
Последовательность обучения
- Представьте задачу, предложив трем ученикам разыграть людей, которые встречаются и обмениваются рукопожатием.
- Подсчитайте и запишите количество рукопожатий. Обсудите другие способы убедить других в том, что рукопожатий было 3 (например, нарисуйте рисунок).
- Поставьте задачу для работы учащихся в парах или малых группах.
- Придумайте способы решения более крупной проблемы (разыграйте ее, составьте список и найдите закономерность). Перечислите их на доске, чтобы студенты могли их обдумать.
- Во время работы учащиеся задают вопросы, которые фокусируют их мышление на систематической работе и поиске закономерностей.
Как вы отслеживаете рукопожатия? (диаграмма, список)
Как вы думаете, сколько рукопожатий было бы, если бы вы добавили еще одного человека?
Что вы заметили в отношении количества рукопожатий и количества людей?
Как бы вы могли записать свою работу, чтобы найти закономерность? - Делитесь результатами.

Добавочный номер
Сколько рукопожатий будет на собрании, если люди приходят парами и пожимают руки всем, кроме своих партнеров.
Решение
Если два человека обмениваются рукопожатием, то это одно рукопожатие.
Если три человека обмениваются рукопожатиями, то получается 3 рукопожатия.
Если четыре человека обмениваются рукопожатиями, то 3 + 3 = 6 рукопожатий.
Если пять человек пожимают друг другу руки, то есть еще 4 рукопожатия, поэтому 6 + 4 = 10.
На 6 человек приходится еще 5 рукопожатий, поэтому 10 + 5 = 15. руки со всеми остальными. Если нас 6 человек, то каждому нужно сделать по 5 рукопожатий. Но каждый раз, когда происходит рукопожатие, участвуют 2 человека. Это означает, что вам нужно только ½ (6 x 5) = 15,
Решение для расширения
6 человек = 12 рукопожатий (15 – 3 = 12, вычесть 3 для рукопожатий между партнерами).
Приложения
Добавить в план
Третий уровень
Если \\[20\\] человек пожмут друг другу руки.
 Сколько рукопожатий будет всего?
Сколько рукопожатий будет всего?Дата последнего обновления: 19 апреля 2023
•
Всего просмотров: 247.8k
•
Просмотров сегодня: 2.17k
Ответ 9Подсказка 1} \справа)}}{2}\] . Это потому, что каждый из «n» человек может пожать руку \[n — 1\] людям, и они не пожмут руку себе. Рукопожатие между двумя людьми не должно засчитываться дважды.
Полный пошаговый ответ :
Пусть количество людей, которые обмениваются рукопожатием, равно «n». Поскольку человек не будет пожимать руку самому себе, значит, «n» человек могут пожать руку \[n — 1\] людям.
Рукопожатие между двумя людьми не должно засчитываться дважды. Когда человек позволяет «а» пожать руку другому человеку, пусть «б» и когда «б» пожимает руку «а», то это не будет считаться еще одним рукопожатием, это то же самое рукопожатие.
Следовательно, формула для количества рукопожатий, возможных с «n» людьми, приведена ниже:
\[\dfrac{{n \times \left( {n — 1} \right)}}{2}\]
Эта формула можно использовать для любого количества людей.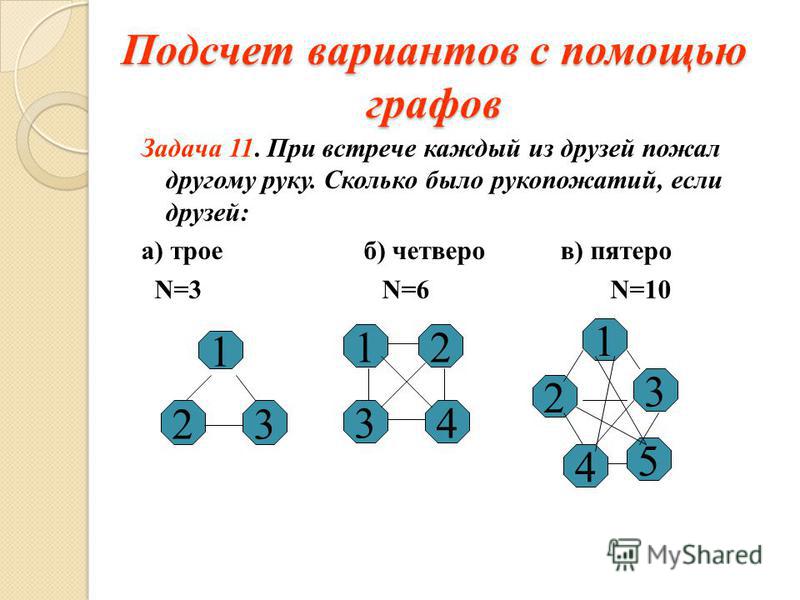


Leave A Comment