Задание №12. Уравнения — профильный ЕГЭ по математике
Задание 12 Профильного ЕГЭ по математике – это решение уравнений. Чаще всего, конечно, это тригонометрические уравнения. Но встречаются и другие типы – показательные, логарифмические, комбинированные.
Сейчас задание 12 Профильного ЕГЭ на решение уравнения состоят из двух пунктов: собственно решения и отбора корней на определенном отрезке.
Что нужно знать, чтобы справиться с этой задачей на ЕГЭ? Вот необходимые темы для повторения.
Задачи из сборников Ященко, 2021 год
Квадратные уравнения
Показательные уравнения
Логарифмические уравнения
Модуль числа
Уравнения с модулем
Тригонометрический круг
Формулы тригонометрии
Формулы приведения
Простейшие тригонометрические уравнения 1
Простейшие тригонометрические уравнения 2
Тригонометрические уравнения
Что необходимо помнить при решении уравнений?
1) Помним про область допустимых значений уравнения! Если в уравнении есть дроби, корни, логарифмы или арксинусы с арккосинусами — сразу записываем ОДЗ. А найдя корни, проверяем, входят они в эту область или нет. Есть в уравнении есть — помним, что он существует, только если
А найдя корни, проверяем, входят они в эту область или нет. Есть в уравнении есть — помним, что он существует, только если
2) Стараемся записывать решение в виде цепочки равносильных переходов.
3) Если есть возможность сделать замену переменной — делаем замену переменной! Уравнение сразу станет проще.
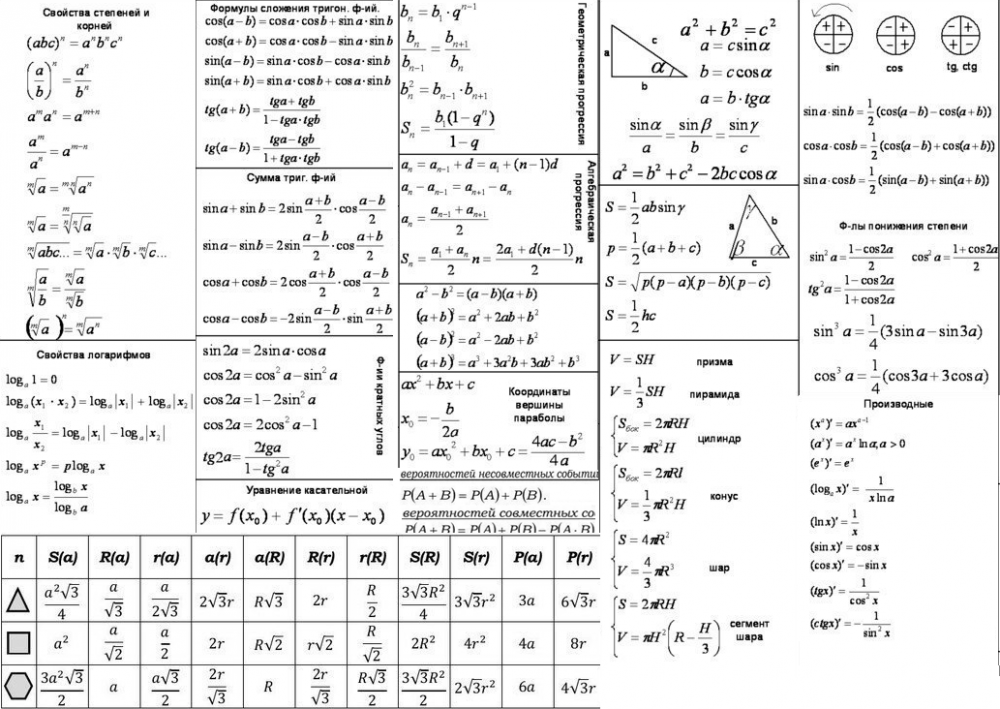
4) Если еще не выучили формулы тригонометрии — пора это сделать! Много формул не нужно. Самое главное — тригонометрический круг, формулы синусов и косинусов двойных углов, синусов и косинусов суммы (разности), понижения степени. Формулы приведения не надо зубрить наизусть! Надо знать, как они получаются.
5) Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.
Например, вы нашли серию решений , где — целое, а найти надо корни на отрезке На указанном промежутке лежит точка . От нее и будем отсчитывать. Получим:
От нее и будем отсчитывать. Получим:
6) Получив ответ, проверьте его правильность. Просто подставьте найденные решения в исходное уравнение!
Давайте потренируемся.
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
Упростим левую часть по формуле приведения.
Вынесем за скобки. Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
б) Отметим на тригонометрическом круге найденные серии решений и отрезок
Видим, что указанному отрезку принадлежат решения
Ответ:
Как отбирать решения с помощью тригонометрического круга?
Например, вы нашли серию решений , где — целое, а найти надо корни на отрезке На указанном промежутке лежит точка От нее и отсчитываем.
Получим:
2. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Это уравнение — комбинированное. Кроме тригонометрии, применяем свойства степеней.
а)
Степени равны, их основания равны. Значит, равны и показатели.
Это ответ в пункте (а).
б) Отберем корни, принадлежащие отрезку
Отметим на тригонометрическом круге отрезок и найденные серии решений.
Видим, что указанному отрезку принадлежат точки и из серии
Точки серии не входят в указанный отрезок.
А из серии в указанный отрезок входит точка
Ответ в пункте (б):
3. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
а)
Применим формулу косинуса двойного угла:
Перенесем всё в левую часть уравнения и разложим по формуле разности квадратов.
Обратите внимание: мы отметили серии решений на тригонометрическом круге. Это помогло нам увидеть, как их записать одной формулой.
Это помогло нам увидеть, как их записать одной формулой.
б) Для разнообразия отберем корни на отрезке с помощью двойного неравенства.
Сначала серия
Теперь серия
Ответ: .
Какой способ отбора корней лучше — с помощью тригонометрического круга или с помощью двойного неравенства? У каждого из них есть «плюсы» и «минусы».
Пользуясь тригонометрическим кругом, вы не ошибетесь. Вы видите и интервал, и сами серии решений. Это наглядный способ.
Зато, если интервал больше, чем один круг, удобнее отбирать корни с помощью двойного неравенства. Например, надо найти корни из серии на отрезке Это больше 10 кругов! Конечно, в таком случае лучше решить двойное неравенство.
4. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Самое сложное здесь — область допустимых значений (ОДЗ). Условие заметно сразу. А условие появляется, поскольку в уравнении есть
ОДЗ:
Уравнение равносильно системе:
Отберем решения с помощью тригонометрического круга.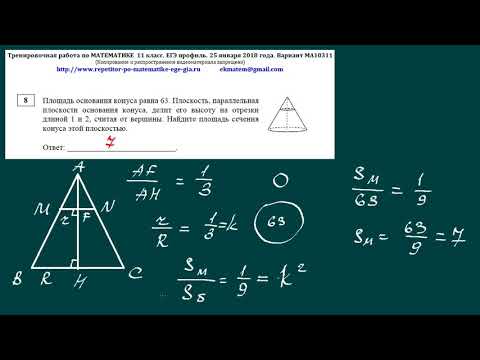 Нам нужны те серии решений, для которых , то есть те, что соответствуют точкам справа от оси .
Нам нужны те серии решений, для которых , то есть те, что соответствуют точкам справа от оси .
Ответ в пункте а)
б) Отметим на тригонометрическом круге найденные серии решений и отрезок
Как обычно, ориентируемся на начало круга. Видим, что указанному промежутку принадлежат точки
и
5. а) Решите уравнение
б) Найдите корни, принадлежащие отрезку
Выражение под корнем должно быть неотрицательно, а произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
Это значит, что уравнение равносильно системе:
Решим эту систему с помощью тригонометрического круга. Отметим на нем углы, для которых или . Заметим, что среди них находятся и углы, для которых
Числа серии не могут быть корнями исходного уравнения, т.к. для этих чисел не выполнено условие . Остальные серии решений нас устраивают.
Тогда в ответ в пункте (а) войдут серии решений:
б) Отберем корни, принадлежащие отрезку любым способом — с помощью тригонометрического круга или с помощью двойного неравенства.
На отрезке нам подходит корень .
На отрезке нам подходят корни .
На отрезке — корни
Ответ в пункте б):
Благодарим за то, что пользуйтесь нашими материалами. Информация на странице «Задание №12. Уравнения u0026#8212; профильный ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена: 08.04.2023
Показательные уравнения | Материалы для подготовки к ЕГЭ по математике ЕГЭ-Студия
Рассмотрим уравнение 2x = 8. В какую степень надо возвести 2, чтобы получить 8? Ясно, что в степень 3.
Более того, x = 3 — единственное решение данного уравнения.
Простейшее показательное уравнение — это уравнение вида
| ax = b, | (1) |
где a > 1 или 0 < a < 1.
Если b > 0, то уравнение (1) имеет решение, и притом единственное. Действительно, при a > 1 показательная функция монотонно возрастает, а при 0 < a < 1 — монотонно убывает; в любом случае она принимает каждое своё значение ровно один раз.
А вот если b ⩽ 0, то уравнение (1) не имеет решений: ведь показательная функция может принимать только положительные значения.
Любое показательное уравнение после соответствующих преобразований сводится к решению одного или нескольких простейших.
В задачах достаточно представить левую и правую части в виде степеней с одинаковым основанием.
1.
Вспоминаем, что 125 = 53. Уравнение приобретает вид: 5x−7 = 5−3.
В силу монотонности показательной функции показатели степени равны: x − 7 = −3, откуда x = 4.
2.
Поскольку , уравнение можно записать в виде:
Дальнейшее ясно:
Теперь рассмотрим более сложные уравнения.
3.
Здесь лучше всего вынести за скобку двойку в наименьшей степени:
4.
Делаем замену
Тогда и относительно t мы получаем квадратное уравнение: Его корни: и
В первом случае имеем: откуда
Во втором случае: решений нет.
Ответ: 3.
5.
Замечаем, что а :
Делим обе части на положительную величину :
Делаем замену:
Полученное квадратное уравнение имеет корни −1 и .
В случае
решений нет.
В случае
имеем единственный корень
Ответ:
Вообще, показательные уравнения вида
называются однородными. Для них существует стандартный приём решения — деление обеих частей на (эта величина не равна нулю, так как показательная функция может принимать только положительные значения). Именно этим приёмом мы в данной задаче и воспользовались.
Для них существует стандартный приём решения — деление обеих частей на (эта величина не равна нулю, так как показательная функция может принимать только положительные значения). Именно этим приёмом мы в данной задаче и воспользовались.
С однородными уравнениями, кстати, мы уже встречались — в тригонометрии. Это были уравнения вида
Их мы решали похожим приёмом — делением на
Спасибо за то, что пользуйтесь нашими статьями. Информация на странице «Показательные уравнения» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена: 07.04.2023
Математика в фокусе | K-8 Singapore Math Curriculum
МАТЕМАТИКА В ФОКУСЕ ® : SINGAPORE MATH ® BY MARSHALL CAVENDISH ®
Сделайте классы математики лучше, чем когда-либо Math in Focus помогает учащимся в Классы K–8 изучают язык математики.
Запрос информации
Получить образец Американское издание эффективной учебной программы по математике в Сингапуре. , позитивный настрой и уверенность, необходимые для достижения успеха.- Создан на основе исследований с упором на решение проблем
Сингапурская учебная программа по математике признает навыки решения задач центральными в обучении.
- Визуальные модели способствуют пониманию
Конкретно-графический-абстрактный подход программы строит математическое концептуальное понимание с помощью манипуляций, диаграмм, моделей и абстрактных символов.

- Справедливость и доступ в каждом классе
От строительных лесов по математике до непревзойденной цифровой поддержки, Math in Focus обеспечивает равенство для каждого учащегося.
ОПЫТ СТУДЕНТОВ
- Интерактивные ресурсы обеспечивают рост
Визуальные модели помогают учащимся развивать способность визуализировать математические ситуации, что является ключом к успешному решению задач.

- Практическое обучение привлекает учащихся
Практические занятия по математике и математические манипуляции позволяют учащимся конкретизировать понятия.
- Онлайн-доступ из любого места
Студенты могут выполнять тесты и взаимодействовать с электронными книгами, видео, мини-играми и виртуальными манипуляторами из любого места на Ed , учебной платформе HMH.

ОПЫТ УЧИТЕЛЯ
Встроенная поддержка упрощает обучение
Каждый урок включает в себя пошаговое планирование, учебные материалы и профессиональное развитие.
Инструменты для дифференциации
Ресурсы для дифференцированного обучения математике помогают учителям удовлетворять потребности стремящихся, на уровне, продвинутых и многоязычных учащихся.

Полезные данные способствуют росту
Суммарное и формативное оценивание по математике измеряют прогресс учащихся, оценивают истинное мастерство и выявляют пробелы в обучении.
Пара Math in Focus с Дополнительные онлайн-практики и инструкции Waggle для постоянной поддержки.
- Адаптивная математическая практика
Waggle ® выходит за рамки адаптивного обучения, чтобы персонализировать практику и обучение, дополняя Math in Focus: Singapore Math для поддержки студентов на всех уровнях.
 Waggle назначает соответствующие упражнения и инструкции на основе результатов Growth Measure ® , или учителя могут назначать контент, соответствующий оглавлению Math in Focus .
Waggle назначает соответствующие упражнения и инструкции на основе результатов Growth Measure ® , или учителя могут назначать контент, соответствующий оглавлению Math in Focus .
Управляемое внедрение
ПрограммыHMH включают в себя постоянную поддержку внедрения с помощью путей достижения успеха учителя, которые персонализированы для каждого учителя, обеспечивая успех в первые 30 дней обучения.

Уголок учителя
Уголок учителя по Ed предлагает годовой доступ к профессиональному обучению с живыми мероприятиями и контентом по запросу, которые помогают учителям в реализации программ, организации занятий и изучении передового опыта.
Членство и курсы коучинга
Получите индивидуальную помощь в обучении от опытных тренеров, которая предоставляется онлайн или лично, чтобы отслеживать цели учителей.

Поддержка лидера
Лидеры получают целевую поддержку для внедрения инноваций и решения проблем в своем округе.
Math in Focus получил высокий рейтинг ESSA, основанный на особом количестве и качестве профессионального обучения, которое учителя получают в рамках Программа Math in Focus .

Запрос информации
Получить образец Информация и ресурсыДоступ к соответствующим статьям, исследованиям и вебинарам.
- Артикул
- Исследования
- Вебинары
- Ресурсы
Поддержка учителей в продвижении математического дискурса в классе
Учебная программа, включающая математический дискурс на ежедневных уроках, имеет несколько преимуществ в обучении.

Энди Кларк
Math in Focus Классы 1-курс 3 США Консультант и курс 2-курс 3 писательИспользование увлекательных и систематических задач для повышения мастерства в математике
Учитель объясняет, почему не только увлекательные, но и систематические задания могут помочь учащимся обобщить свое обучение, чтобы продемонстрировать мастерство.

Susan Resnick
Math in Focus 1-й курс 3, консультант в США, 1-й курс, рецензент, 2-й ускоренный курс и 3-й курс, писательСочетание концептуального и процедурного понимания в математике
При таком подходе учителя могут помочь учащимся стать уверенными, творческими и настойчивыми учениками.

Лаура Гиффорд
Math in Focus®: Singapore Math® by Marshall Cavendish®: Research Evidence Base
- Тип отчета: База данных исследований
- Уровень: Начальный, средний
- Демонстрирует обоснование
- Математика
Математика в фокусе: исследование эффективности, 3, 4 и 5 классы
- Тип отчета: Исследование эффективности, исследование, проведенное третьей стороной
- Уровень: Элементарный
- Регион: Средний Запад, Северо-Восток
- Район Город: Городской, пригородный, сельский
- Демонстрирует обоснование
- Математика
Математика в центре внимания: рандомизированное контрольное исследование (РКИ), 3–5 классы
- Тип отчета: Исследование эффективности, исследование, проведенное третьей стороной
- Уровень: Элементарный
- Регион: Запад
- Район Город: Городской, пригородный, сельский
- Размер района: Большой
- Веские доказательства
- Математика
Математика в фокусе: Исследование эффективности математики в средних классах Сингапура
- Тип отчета: Исследование эффективности, исследование, проведенное третьей стороной
- Уровень: Середина
- Регион: Северо-Восток, Запад
- Район Город: Пригородный, сельский
- Размер района: Большой, Маленький
- Демонстрирует обоснование
- Математика
Singapore Math®: визуальный подход к решению задач
Использование увлекательных и систематических заданий для развития обобщения и мастерства
Способствовать студенческому дискурсу, более глубокому пониманию математических концепций и решению задач
Решение задач в Singapore Math®
Посмотрите на сингапурский подход к обучению решению проблем и почему он так успешен.

История успеха
Сила учебной программы Singapore Math® зависит от постоянных изменений, основанных на текущих исследованиях и передовом опыте. Узнайте, как он изменился за эти годы.
Узнайте, как Math in Focus повышает успеваемость по математике.
запросить информацию
получить образецподписаться
Magma Math — математическая платформа K-12
Magma Math — это математическая платформа, предназначенная для помощи учителям в принятии более обоснованных учебных решений в классе и создания возможностей для более глубокого обсуждения и сотрудничества между учащимися.
Расписание демонстрации
Почему Magma?
Узнайте, как думают ученики
Magma Math смещает акцент с получения окончательного ответа на полное решение, позволяя учителям понять мыслительный процесс учащихся.
Дифференциальные задания
Разработка формирующих оценок и заданий с использованием библиотеки Magma Math из 15 000 математических задач. Каждый доступен в 3 уровнях сложности.
140 различных языков
Язык не должен быть барьером в математике. Студенты могут выбрать доступ к контенту на 140 различных языках.
Выявление и устранение пробелов в обучении по мере их возникновения
Magma Math показывает, с чем борются отдельные учащиеся, а также профиль уровня понимания вашего класса в целом.
Демонстрация расписания
Когда учителя используют Magma
Математический дискурс
Magma — отличная платформа для углубления математических знаний учащихся и развития разнообразных навыков решения задач.
Формирующее оценивание
Эффективно оценивайте учащихся с помощью входных и выходных билетов. Magma даст вам информацию, необходимую для выявления пробелов.
Индивидуальная практика
Один размер не подходит для всех в образовании. Вот почему Magma позволяет вам и ученикам практиковаться в нужных задачах в нужное время.
Вот почему Magma позволяет вам и ученикам практиковаться в нужных задачах в нужное время.
Запланировать демонстрацию
Наша служба поддержки всегда готова помочь вам. 24/7.
Преподаватели имеют доступ к круглосуточной поддержке нашей команды, персонализированному профессиональному развитию и подключены к глобальному образовательному сообществу Magma.
Как цифровой математический инструмент должен работать
Учащиеся лучше учатся, показывая свою работу
Преподаватели могут перенаправить свое время с выставления оценок на содействие более глубокому изучению математики
Учащиеся получают немедленную обратную связь, которая дает им независимость как учащимся
Администраторы могут расслабиться благодаря кросс-платформенной совместимости
Запланировать демонстрацию
«Покажи свою работу!»
Математика — это больше, чем просто практика множественного выбора.
Каждый шаг в учебном процессе раскрывает историю.




 Waggle назначает соответствующие упражнения и инструкции на основе результатов Growth Measure ® , или учителя могут назначать контент, соответствующий оглавлению Math in Focus .
Waggle назначает соответствующие упражнения и инструкции на основе результатов Growth Measure ® , или учителя могут назначать контент, соответствующий оглавлению Math in Focus .
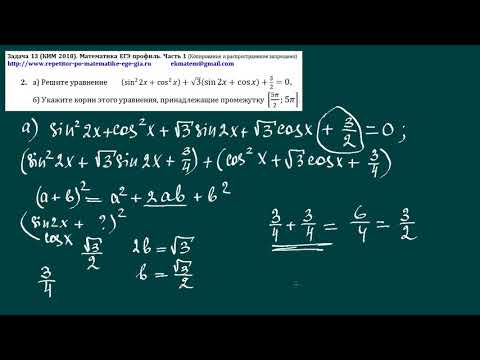


Leave A Comment