Формула равнодействующей силы
Формула равнодействующей силыСила выступает в качестве количественной меры взаимодействия тел. Это важная физическая величина, так как в инерциальной системе отсчета любое изменение скорости тела может происходить только при взаимодействии с другими телами. Иначе говоря, при действии на тело силы.
Взаимодействия тел могут иметь разную природу, например, существуют электрические, магнитные, гравитационные и другие взаимодействия. Но при исследовании механического движения тела природа сил, вызывающих у тела ускорение значения не имеет. Проблемой происхождения взаимодействия механика не занимается. Для любого взаимодействия численной мерой становится сила. Силы разной природы измеряют в одних единицах (в Международной системе единиц в ньютонах), при этом используют одни и те же эталоны. В виду такой универсальности механика занимается исследованием и описанием движения тел, которые испытывают воздействия сил любой природы.
Результатом действия силы на тело является ускорение тела (изменение скорости его движения) или (и) его деформация.
Сложение сил
Сила — это векторная величина. Кроме модуля она имеет направление и точку приложения. Независимо от природы все силы складываются как векторы.
Пусть, металлический шарик удерживается упругой пружиной и его притягивает магнит(рис.1). Тогда на него действуют две силы: сила упругости со стороны пружины (${\overline{F}}_u$) и магнитная сила (${\overline{F}}_m$) со стороны магнита. Считаем, что их величины известны. При совместном действии данных, сил шарик будет находиться в состоянии покоя, если на него воздействовать третьей силой ($\overline{F}$), которая удовлетворяет равенству:
\[\overline{F}=-\left({\overline{F}}_u+{\overline{F}}_m\right)\left(1\right).\]
Этот опыт дает возможность сделать вывод о том, что несколько сил, действующих на одно тело можно заменить одной равнодействующей, при этом не важна природа сил. Равнодействующая получается как результат векторного суммирования сил, действующих на тело.
Определение и формула равнодействующей силы
И так, векторная сумма всех сил, оказывающих действие на тело в один и тот же момент времени, называют равнодействующей силой ($\overline{F}$):
\[\overline{F}={\overline{F}}_1+{\overline{F}}_2+\dots +{\overline{F}}_N=\sum\limits^N_{i=1}{{\overline{F}}_i}\ \left(2\right).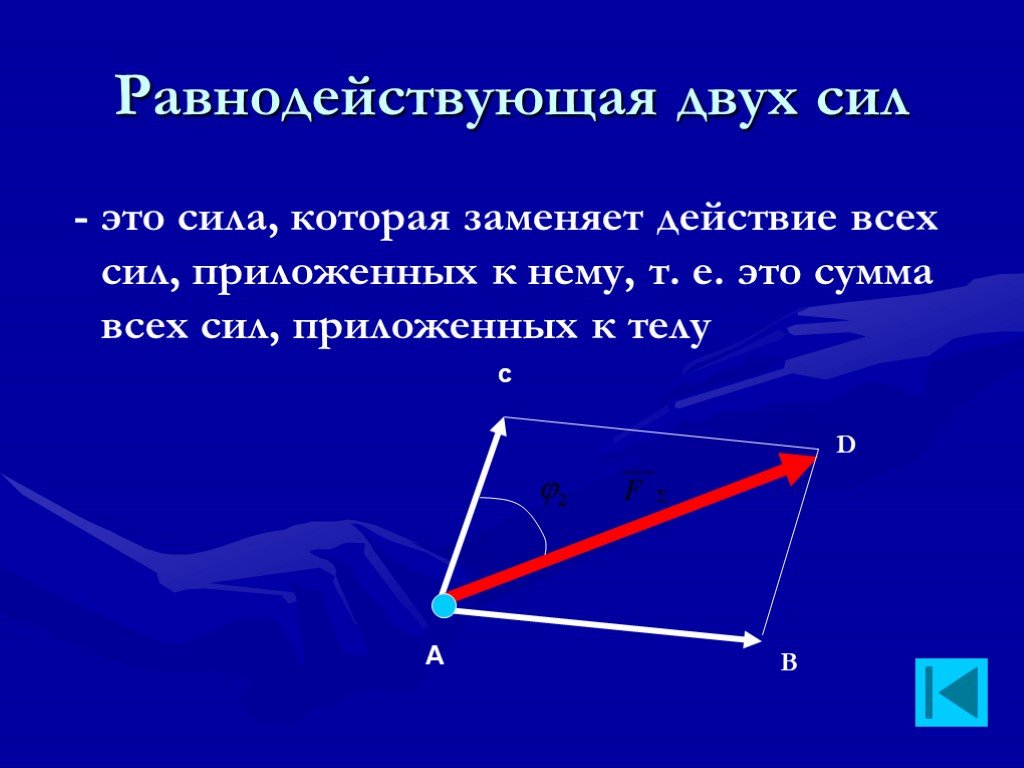 N_{i=1}{{\overline{F}}_i}=m\overline{a}\left(3\right).\]
N_{i=1}{{\overline{F}}_i}=m\overline{a}\left(3\right).\]
Формула (3) означает, что равнодействующая всех сил, приложенных к телу, может быть равна нулю, в том случае, если происходит взаимная компенсация сил. Тогда тело перемещается с постоянной скоростью или находится в состоянии покоя в инерциальной системе отсчета. Можно сказать обратное, если тело движется равномерно и прямолинейно в инерциальной системе отсчета, то на него не действуют силы или их равнодействующая равна нулю.
При решении задач и указании на схемах сил, действующих на тело, при движении тела с постоянным ускорением, равнодействующую силу направляют по ускорению и изображают длиннее, чем противоположно ей направленную силу (сумму сил). При равномерном движении (или если тело находится в состоянии покоя) длина векторов сил, имеющих противоположные направления одинакова (равнодействующая равна нулю).
Исследуя условия задачи, необходимо определить, какие силы оказывают действие на тело, будут учитываться в равнодействующей, какие силы не оказывают существенного влияния на движение тела и их можно отбросить. 2_1+2F_1F_1{\cos \alpha \to \ }{\cos \alpha =-\frac{1}{2}.\ }\]
2_1+2F_1F_1{\cos \alpha \to \ }{\cos \alpha =-\frac{1}{2}.\ }\]
Решением полученного тригонометрического уравнения являются углы:
\[\alpha =\frac{2\pi }{3}+\pi n\ ;;\ \alpha =\frac{4\pi }{3}+\pi n\ \left(где\ n-целое\ число\right).\ \]
Исходя из рисунка (рис.2) нам подходит ответ $\alpha =\frac{2\pi }{3}$.
Ответ. $\alpha =\frac{2\pi }{3}$
Пример 2
Задание. Чему равна равнодействующая сила, если на тело действуют силы, представленные на рис.3.
Решение. Равнодействующую силу найдем векторным суммирование используя правило многоугольника. Последовательно каждый следующий вектор силы отложим от конца предыдущего. В результате вектор равнодействующей всех сил будет иметь началом точку, из которой выходит первый вектор (у нас вектор ${\overline{F}}_1$), ее конец будет приходить в точку, где заканчивается последний вектор (${\overline{F}}_4$). В результате получим рис.
В результате построения получен замкнутый многоугольник, это означает, что равнодействующая сил, приложенных к телу равна нулю.
Ответ. $\overline{R}=0$
Читать дальше: формула силы Архимеда.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
основные понятия и определения, измерение и нахождение, обозначение в физике
Физика
12.11.21
12 мин.
Равнодействующая (результирующая) сила — это векторная величина, используемая в физической механике при изучении законов взаимодействия нескольких тел. Она была открыта английским физиком Исааком Ньютоном во второй половине XVII столетия. Эта величина равна сумме всех сил, оказывающих непосредственное воздействие на физическое тело. Она изучается на уроках физики в 9 классе.
Оглавление:
- Основные характеристики
- Сложение величин
- Условия равновесия рычага
- Фундаментальные взаимодействия
- Второй закон Ньютона
- Нахождение силы
- Пример решения задачи
Равнодействующая (результирующая) сила — это векторная величина, используемая в физической механике при изучении законов взаимодействия нескольких тел.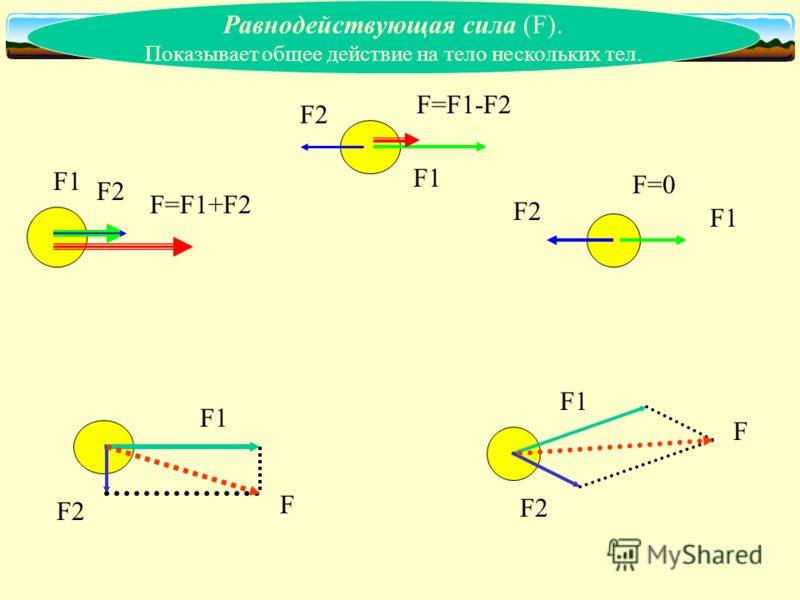 Она была открыта английским физиком Исааком Ньютоном во второй половине XVII столетия. Эта величина равна сумме всех сил, оказывающих непосредственное воздействие на физическое тело. Она изучается на уроках физики в 9 классе.
Она была открыта английским физиком Исааком Ньютоном во второй половине XVII столетия. Эта величина равна сумме всех сил, оказывающих непосредственное воздействие на физическое тело. Она изучается на уроках физики в 9 классе.
Основные характеристики
Равнодействующую силу характеризуют три основных параметра:
- модуль;
- направление;
- точка приложения.
В системе СИ единицей измерения этой величины является Ньютон (H). Также она может измеряться в кг*м/с2. Проекции равнодействующей силы на декартовой плоскости могут быть как положительными, так и отрицательными. Модуль и направление вектора не зависят от выбранной системы отсчета.
Для подробного описания данной векторной величины необходимо знать основные особенности нахождения векторной суммы и условия равновесия рычага.
Сложение величин
Если на физическое тело действуют одновременно два предмета, то оно начинает двигаться с ускорением.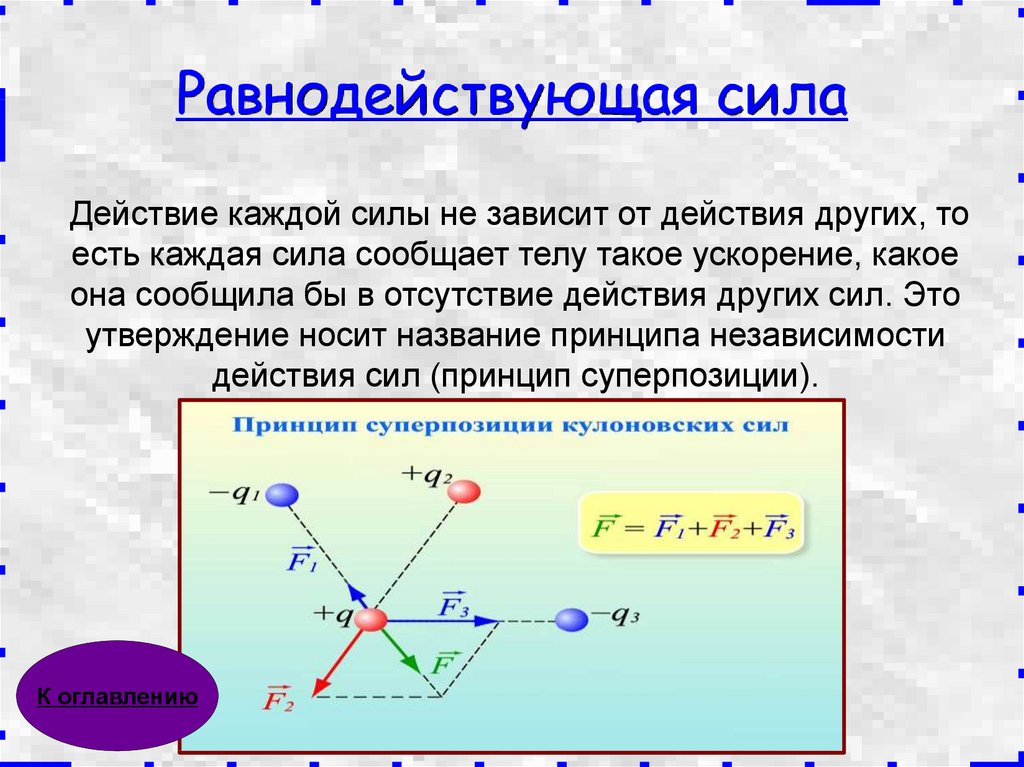 Они могут иметь разную массу и размер. В этом случае объекты, действующие на физическое тело, суммируются по правилу сложения векторных величин. Вектор суммы этих величин будет являться результирующей силой. Прямая, проходящая через точку соприкосновения векторов, называется линией действия. Если объекты действуют на физическое тело перпендикулярно друг другу, то равнодействующая сила будет приложена к их точке пересечения. В противном случае она будет рассчитываться по формуле: F 1 l 1 = F 2 l 2.
Они могут иметь разную массу и размер. В этом случае объекты, действующие на физическое тело, суммируются по правилу сложения векторных величин. Вектор суммы этих величин будет являться результирующей силой. Прямая, проходящая через точку соприкосновения векторов, называется линией действия. Если объекты действуют на физическое тело перпендикулярно друг другу, то равнодействующая сила будет приложена к их точке пересечения. В противном случае она будет рассчитываться по формуле: F 1 l 1 = F 2 l 2.
Условия равновесия рычага
При изучении основных условий равновесия рычага в физике вводится понятие «Момент силы». Оно характеризует меру механического воздействия, способного изменить траекторию поворота физического тела. Условия равновесия зависят от разновидности движения:
- Поступательное: при перемещении объект не изменяет свою форму и размерные характеристики.
- Вращение: движение тела по кругу. В этом случае траекторией всех точек движущегося объекта являются дуги окружностей с единым центром — точкой вращения.

Если во время движения тело сохраняет свою форму, то оно находится в равновесии. В этом случае вектор суммы равен 0. При вращении тело находится в покое, если соблюдается общее условие равновесия. Геометрическая и алгебраическая сумма всех моментов сил, приложенных к объекту, должны равняться 0.
Фундаментальные взаимодействия
Равнодействующая сила зависит от 4 видов фундаментальных взаимодействий:
- Гравитационное: характерно для всех материальных объектов, имеющих вес. Оно основано на законе Всемирного тяготения, созданного Исааком Ньютоном. С помощью гравитационного взаимодействия описывается движение планет Солнечной системы. В этом случае между 2 телами действует сила притяжения. Гравитационное взаимодействие обуславливается гравитонами — элементарными частицами, из которых состоит большинство макрообъектов.
- Электромагнитное: характерно для электрически заряженных объектов. При движении тел возникают электрическое и магнитное поля.
 В результате тела, находящие на близком расстоянии, начинают притягиваться или отталкиваться. Характер электромагнитного взаимодействия определяется знаком заряда. При изменении агрегатного состояния тела начинают двигаться в противоположных направлениях. Электромагнитное взаимодействие основано на законах электродинамики и электростатики, описывающих связь между магнитными и электрическими полями.
В результате тела, находящие на близком расстоянии, начинают притягиваться или отталкиваться. Характер электромагнитного взаимодействия определяется знаком заряда. При изменении агрегатного состояния тела начинают двигаться в противоположных направлениях. Электромагнитное взаимодействие основано на законах электродинамики и электростатики, описывающих связь между магнитными и электрическими полями. - Сильное: возникает между адронами и кварками — фундаментальными бесструктурными частицами. Оно обеспечивает баланс между отрицательными и положительными частицами в ядерных реакциях. Сильное взаимодействие отличается небольшим радиусом действия, равным атому ядра.
- Слабое: характеризует основные разновидности бета-взаимодействий. Радиус его действия составляет 10−18 м. В процессе слабого взаимодействия принимают участие лептоны и кварки, обладающих проникающей способностью. Они могут обмениваться тепловой энергией и квантами.
Интенсивность фундаментальных взаимодействий рассчитывается в единицах энергии, называемых электрон-вольтами.
Второй закон Ньютона
Второй закон Ньютона является одним из основных правил динамики. Он действует только в инерциальных системах отсчета. На основе этого закона ученый смог выявить следующие закономерности:
- Ускорения тел, на которые воздействуют объекты с одинаковым весом, обратно пропорциональны их массам.
- Если к физическому объекту приложены 2 силы с разными модулями и направлениями, то его ускорение будет прямо пропорционального его массе.
При помощи этих утверждений Ньютон сформулировал следующее определение: сила, воздействующая на тело, равна произведению его массы на ускорение.
На основе второго закона Ньютона была выявления формула равнодействующей силы: F = ma. В этом выражении m является массой, характеризующей инертные свойства физического тела, a — ускорение, определяющее интенсивность изменения скорости движения объекта. Результирующая сила равна 0, если она компенсируется иной мерой физического воздействия, противоположной по направлению и одинаковой по модулю. Если эта физическая величина не равна 0, то тело движется с ускорением. Это значит, что оно не находится в равновесии.
Результирующая сила равна 0, если она компенсируется иной мерой физического воздействия, противоположной по направлению и одинаковой по модулю. Если эта физическая величина не равна 0, то тело движется с ускорением. Это значит, что оно не находится в равновесии.
Нахождение силы
Чтобы найти результирующую силу, необходимо выполнить следующий алгоритм действий:
- Обозначить все величины, оказывающие воздействие на физический объект. Для обозначения чаще всего используется латинская буква F. В физике основные переменные не могут обозначаться при помощи символов русского алфавита. Важно показать, что силы являются векторными величинами. Для этого нужно над буквой нарисовать стрелку.
- Построить координатные оси и обозначить на них координаты тела.
- Отметить проекции векторов на оси. На основе графика нужно записать уравнение движения.
Если на графике присутствуют участки, где тело движется равномерно или находится в равновесии, то сумма проекций равняется 0. Если есть участки, где объект снижает или повышает свою скорость, то результирующая сила должна определяться при помощи массы на ускорение. При знании этой величины человек сможет определить работу тела по формуле: W F = 0 n W (Fk).
Если есть участки, где объект снижает или повышает свою скорость, то результирующая сила должна определяться при помощи массы на ускорение. При знании этой величины человек сможет определить работу тела по формуле: W F = 0 n W (Fk).
Пример решения задачи
Даны силы тяжести, трения и реакции опоры. Также известна мера механического воздействия на тело. Объект движется по горизонтальной поверхности. Необходимо найти вектор направления результирующей силы.
Для решения этой задачи необходимо построить оси координат и обозначить на них все величины, воздействующие на тело. При черчении графика важно знать, в каком направлении движется объект. На следующем рисунке изображена координатная плоскость с обозначенными векторами.
После построения графика необходимо найти проекции на следующие оси:
- Ox: F x = F, F x тр = -Fxтр, N x = 0, F т = 0.
- Oy: F y = 0, F y тр = 0, N y = N, F т = — F т.

После этого необходимо записать уравнение:
- Ox: F — F тр = 0.
- Oy: N — F т = 0.
Тело движется с ускорением. Его прижимают силы тяжести, трения и упругости. Вектор ускорения направлен вниз. Это обусловлено мерой механического воздействия, оказывающего давление на объект. Из этого следует, что вектор равнодействующей силы также направлен вниз.
Не успеваете написать работу?
Заполните форму и узнайте стоимость
Вид работыПоиск информацииДипломнаяВКРМагистерскаяРефератОтчет по практикеВопросыКурсовая теорияКурсовая практикаДругоеКонтрольная работаРезюмеБизнес-планДиплом MBAЭссеЗащитная речьДиссертацияТестыЗадачиДиплом техническийПлан к дипломуКонцепция к дипломуПакет для защитыСтатьиЧасть дипломаМагистерская диссертацияКандидатская диссертацияКонтактные данные — строго конфиденциальны!
Указывайте телефон без ошибок! — потребуется для входа в личный кабинет.
* Нажимая на кнопку, вы даёте согласие на обработку персональных данных и соглашаетесь с политикой конфиденциальности
Подтверждение
Ваша заявка принята.
Ей присвоен номер 0000.
Просьба при ответах не изменять тему письма и присвоенный заявке номер.
В ближайшее время мы свяжемся с Вами.
Ошибка оформления заказа
Кажется вы неправильно указали свой EMAIL, без которого мы не сможем ответить вам.
Пожалуйста проверте заполнение формы и при необходимости скорректируйте данные.
Результирующая сила – x-engineer.org
Содержание
- Введение
- Определение
- Диаграмма
- Формула
- Примеры
- Результирующая сила нескольких сил
- Калькулятор
Введение
Представьте, что система на один и тот же объект (или точку) одновременно действуют несколько сил, имеющих разные направления и величины. Сумма всех этих сил называется 9.0023 результирующая сила . «Сумма» всех сил также может быть разницей в зависимости от направления каждой силы. Давайте рассмотрим несколько простых примеров для лучшего понимания.
Сумма всех этих сил называется 9.0023 результирующая сила . «Сумма» всех сил также может быть разницей в зависимости от направления каждой силы. Давайте рассмотрим несколько простых примеров для лучшего понимания.
Изображение: Диаграмма результирующей силы – парашютист
Если представить парашютиста, когда он (она) выпрыгивает из самолета, на него (на нее) действуют две силы. Сила веса F веса [Н], притягивающая парашютиста к поверхности Земли под действием силы тяжести, и сила сопротивления воздуха F воздушное сопротивление [N], которое противодействует движению парашютиста по воздуху и пытается его (ее) замедлить. Как видите, сила веса и сила сопротивления воздуха имеют противоположные направления, а значит, равнодействующая R [N] будет разностью между ними.
Если считать, что положительное направление сил направлено к поверхности, то формула равнодействующей силы:0025
Результат говорит нам о том, что парашютист будет продолжать падать к поверхности Земли, потому что его тянет вниз результирующая сила.
Назад
Определение
Результирующая сила – это конечная сила, действующая на объект (тело) после суммирования векторным сложением всех отдельных сил, действующих на тело. Другими словами, равнодействующая сила — это единственная сила, которая оказывает на тело такое же воздействие, как две или более сил, действующих одновременно.
Давайте посмотрим на другой пример.
Изображение: Диаграмма результирующей силы – противоположные направления сил
В точке P действуют две силы: сила F 1 [Н], тянущая вправо, и сила F 2 [Н], тянущая вправо левый. Поскольку для F 1 больше, чем сила F 2 , результирующая сила R [Н] будет иметь то же направление, что и F 1 , а величина равна разнице между F 1 и F 2 .
R = F 1 – F 2 = 10 – 5 = 5 N
Что произойдет, если две силы действуют в одном направлении?
Изображение: Диаграмма результирующей силы – одинаковые направления сил
В этом примере обе силы F 1 и F 2 тянут точку вправо.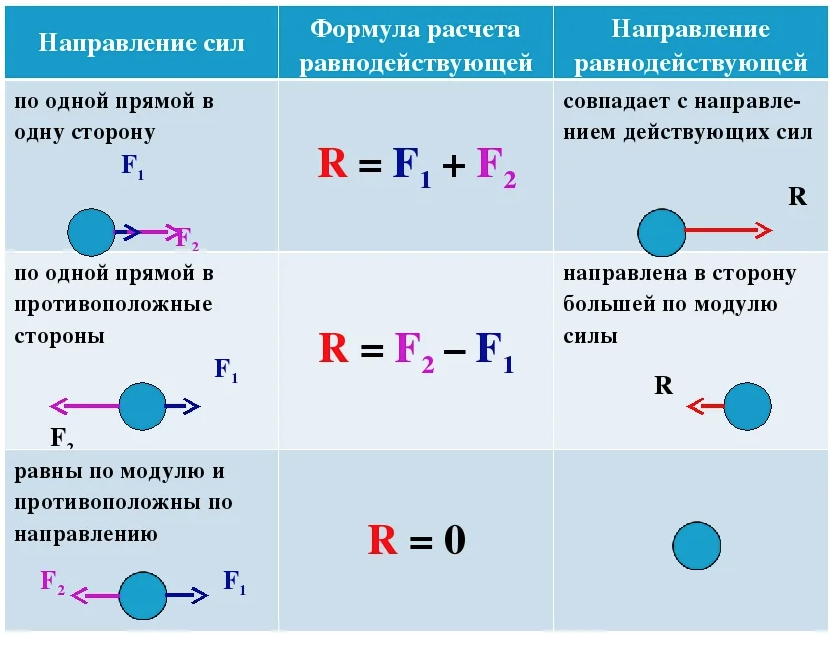 В этом случае результирующая сила R будет иметь то же направление, что и F 1 или F 2 , а ее величина будет равна сумме двух сил.
В этом случае результирующая сила R будет иметь то же направление, что и F 1 или F 2 , а ее величина будет равна сумме двух сил.
R = F 1 + F 2 = 10 + 5 = 15 Н
Единицей измерения результирующей силы является Ньютон [Н], а символ результирующей силы обычно Р.
Далее мы собираемся подробнее остановимся на расчете результирующей силы.
Назад
Диаграмма
В механике мы имеем дело с двумя типами величин (переменных): скалярными и векторными переменными. Скалярные переменные имеют только величину, например: длина, масса, температура, время. Переменные вектора имеют величину и направление, например: скорость, сила, крутящий момент. Направление вектора определяется углами действия силы по каждой оси. Векторные переменные обычно представляются жирным шрифтом со стрелками сверху.
На тело или точку могут действовать несколько сил, каждая из которых имеет свое направление и величину.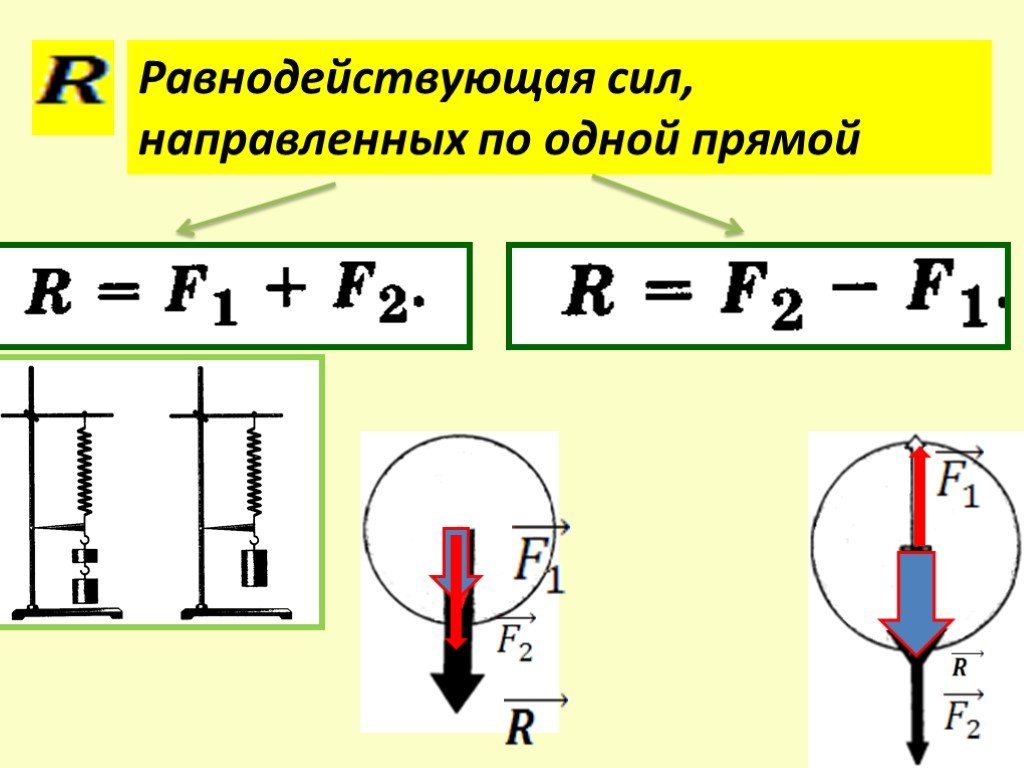 В технике основное внимание уделяется результирующей силе, действующей на тело. Равнодействующую действующих сил (действующих в одной плоскости) можно найти с помощью закон параллелограмма , правило треугольника или правило многоугольника .
В технике основное внимание уделяется результирующей силе, действующей на тело. Равнодействующую действующих сил (действующих в одной плоскости) можно найти с помощью закон параллелограмма , правило треугольника или правило многоугольника .
Две или более сил действуют одновременно если их направления пересекаются через общую точку. Например, две параллельные силы F 1 и F 2 действуют на одну и ту же точку P . Чтобы найти их равнодействующую R , мы можем применить закон параллелограмма или правило треугольника .
\[\ overrightarrow{R} = \overrightarrow{F_1} + \overrightarrow{F_2}\]
Если на одну и ту же точку действует несколько сил, мы можем применить правило многоугольника , чтобы найти их равнодействующую.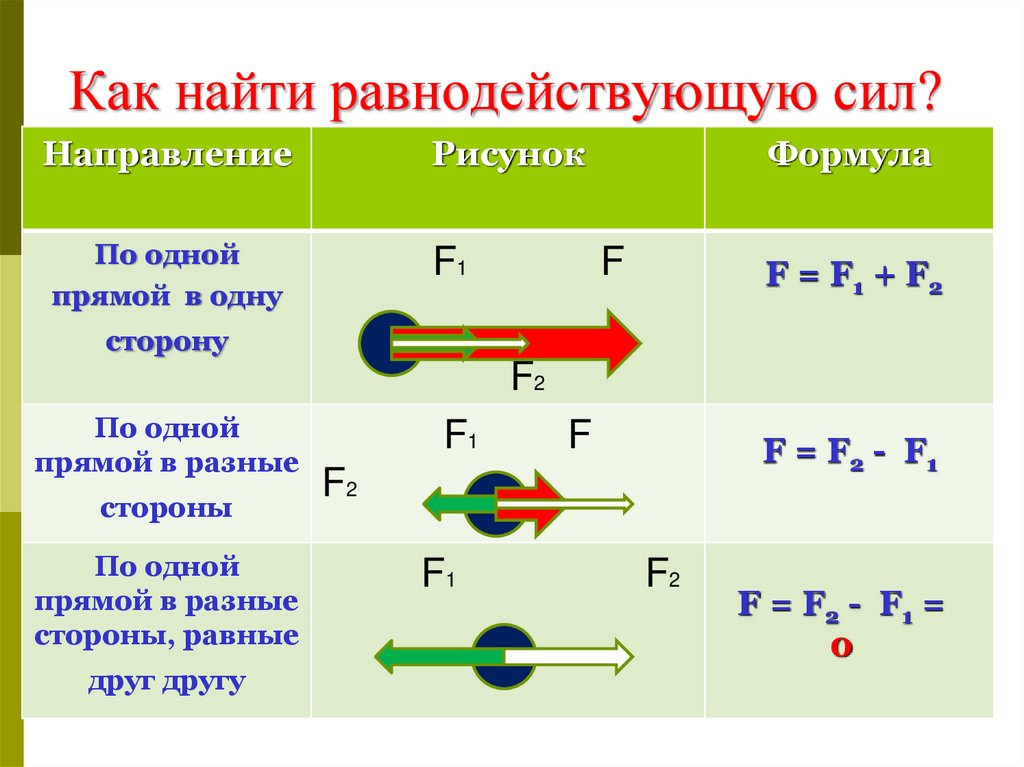
\[\overrightarrow{R} = \overrightarrow{F_1} + \overrightarrow{F_2} + \overrightarrow{F_3} + \overrightarrow{F_4}\]
Результирующая сила может быть определена также для трех- системы размерных сил , используя правило многоугольника.
\[\overrightarrow{R} = \overrightarrow{F_1} + \overrightarrow{F_2} + \overrightarrow{F_3}\]
Закон параллелограмма, правило треугольника и правило многоугольника — это геометрических методов нахождения равнодействующая силы. Мы можем изобразить равнодействующую силы, но точно не знаем ее величины и направления.
Чтобы вычислить величину и направление равнодействующей силы или вычислить значение той или иной составляющей силы, мы можем использовать закон синусов и закон косинусов.
Диагональ параллелограмма PBCA является равнодействующей силой R, которая образует два разносторонних треугольника с силами F 1 и F 2 .
Поскольку сумма всех углов внутри треугольника равна 180°, мы можем записать γ как функцию 9{\circ} – \alpha – \beta)} \tag{3}\]
Результирующая сила также может быть рассчитана аналитически , используя проекции силы. Используя метод проецирования силы , мы можем рассчитать величину и углы направления результирующей силы.
На изображении выше у нас есть результирующая сила R и ее проекции на каждую ось:
F x – проекция R на ось x
F у – проекция R на ось y
F z – проекция R на ось z
α – угол между R и ось х
β – угол между R и осью y
γ – угол между R и осью z
Если в одной точке действуют несколько сил, вычислим равнодействующую их проекции на каждую ось:
92}}\end{split} \]
Метод проецирования силы также можно использовать для копланарных (оси x, y) расчетов равнодействующей силы.
Вернуться назад
Примеры
Пример 1 . Учитывая силы F 1 = 2,91 Н , F 2 = 2,67 Н , F 3 = 2,47 Н и F 9002 9 4 = 2,23 N и углы α = 60° и β = 30° , рассчитать результирующую силу R и его угол γ с осью x.
Шаг 1 . Чтобы получить представление о том, как может выглядеть результирующая сила, мы можем применить правило многоугольника.
Как видите, величина равнодействующей почти равна силе F 3 . Кроме того, угол γ должен быть примерно равен α . Это геометрическое решение полезно, потому что мы знаем, каких результатов следует ожидать от аналитического решения.
Шаг 2 . Рассчитайте проекции силы на каждую ось.
\[ \begin{split}
F_x &= F_1 + F_2 \cdot \text{cos}(\alpha) – F_3 \cdot \text{cos}(\beta) &= 2. 2} = 2,48 \text{N}\] 9{\circ}\]
2} = 2,48 \text{N}\] 9{\circ}\]
Как и ожидалось, аналитическое решение (проекция сил) дает те же результаты, что и геометрическое решение (правило многоугольника).
Пример 2 . Даны силы F 1 = 6,12 Н , F 2 = 4,32 Н , F 3 = 1,84 Н и их углы α = 16° , β = 22° , γ = 36° , вычислить равнодействующую силы R и ее углы α R , β R , γ R с осями x, y и z. Силы представляют собой диагонали с каждой стороны прямоугольного параллелепипеда.
Шаг 1 . Рассчитайте проекции силы на каждую ось.
\[ \begin{split}
F_x &= F_1 \cdot \text{cos}(\alpha) + F_2 \cdot \text{cos}(\beta) &= 9.89 \text{ N}\\
F_y &= F_1 \cdot \text{cos} \left ( \frac{\pi}{2} – \alpha \right ) + F_3 \cdot \text{cos} \left ( \frac{\pi}{2} – \gamma \right ) &= 2,77 \text{ N}\\ 9\circ}{\pi}, \text{ if } F_{x}<0 \text{ and } F_{y}<0\\
\end{matrix}\right. \]
\]
Пример 3 . В качестве примера возьмем систему сил из Упражнение 1 и вычислим результирующую силу и ее угол с горизонтальной осью ( O-x ).
Чтобы этот метод работал, все углы должны быть привязаны к горизонтальной оси, O-x .
Силы и углы следующие:
- F 1 = 2,91 с.ш., α 1 = 0°
- F 2 = 2,67 с.ш., α 2 = 60°
- F 3 = 2,47 N, α 3 = 150°
- F 4 = 2,23 Н, α 4 = 270°
Этап 1 . Вычислить горизонтальную составляющую результирующей
\[F_{x} = 2,91 \cdot \cos (0) + 2,67 \cdot \cos (60) + 2,47 \cdot \cos (150) + 2,23 \cdot \cos (270) ) = 2,106 \text{ N}\]
Наблюдение: если вычисления выполняются на ручном калькуляторе программного приложения, аргумент 9Функция 0123 cos() должна быть указана в радианах, например:
\[\cos \left ( 60 \cdot \frac{\pi}{180} \right )\]
Шаг 2 . Вычислить вертикальную составляющую результирующей
Вычислить вертикальную составляющую результирующей
\[F_{y} = 2,91 \cdot \sin (0) + 2,67 \cdot \sin (60) + 2,47 \cdot \sin (150) + 2,23 \cdot \sin (270) ) = 1,32 \text{ N}\]
Наблюдение: если вычисления выполняются на ручном калькуляторе программного приложения, аргумент функции sin() должен быть задан в радианах, например: 9{\circ}\]
Этот метод можно распространить на любое количество сил, если известны значения сил и углы.
Вы также можете проверить свои результаты, используя калькулятор ниже.
Назад
Калькулятор
| F 1 [N] | F 2 [N] | F 9 0029 3 [Н] | Ф 4 [Н] | Ф 5 [Н] |
| α 1 [°] | α 2 [°] | α 3 [°] | α 4 9 0030 [°] | α 5 [°] |
| Горизонтальная сила, F x [Н] = | ||||
| Вертикальная сила, F y [Н] = | ||||
| Угол силы, γ [°] = | ||||
| Результирующая сила, R [Н] = | ||||
Используйте приведенный выше калькулятор для расчета и оценки различного распределения сил.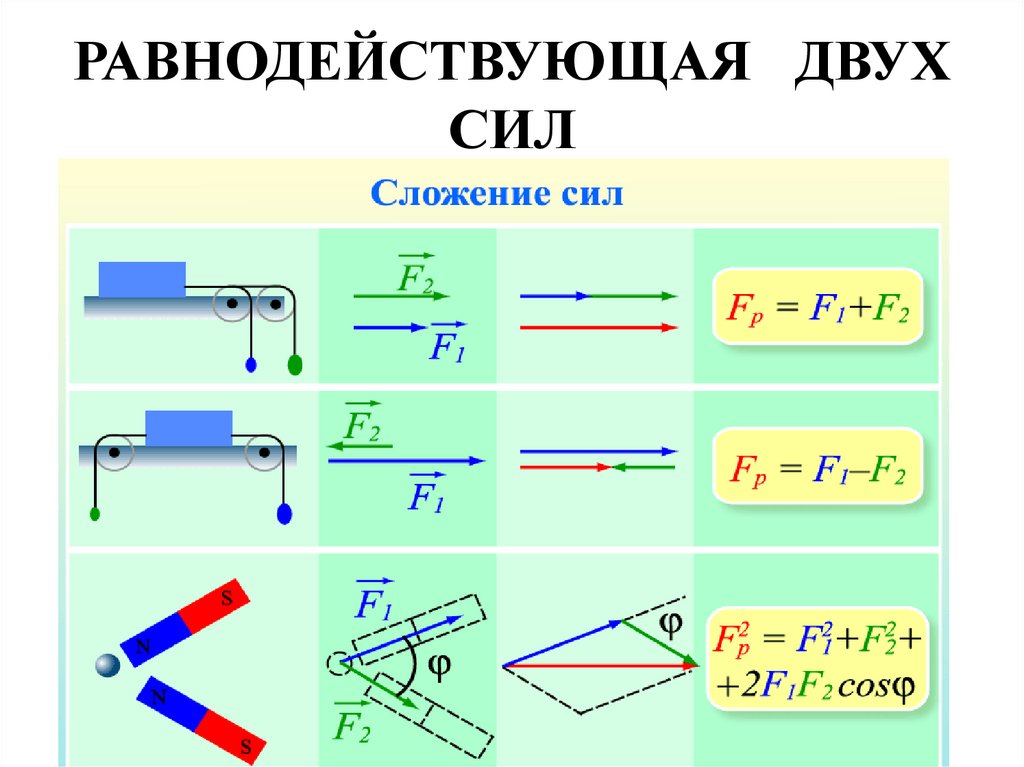 Наведя указатель мыши на линейные силы, вы увидите их координаты, которые представляют компоненты F x [Н] и F y [Н].
Наведя указатель мыши на линейные силы, вы увидите их координаты, которые представляют компоненты F x [Н] и F y [Н].
Не забудьте поставить лайк, поделиться и подписаться!
Определение, формула, примеры [Примечания GATE]
Что такое результирующая сила?
Суммарная действующая сила, действующая на тело во всех направлениях, известна как результирующая сила. Результирующая сила также должна быть равна нулю, когда объект покоится или движется с той же скоростью. Поскольку все силы действуют в одном направлении, результирующая сила должна быть одинаковой.
Теорема Пифагора также может вычислить результирующую силу, если одна сила перпендикулярна другой или если две силы действуют в противоположных направлениях. Приведенная ниже формула используется для расчета равнодействующей силы.
Результирующая сила Определение
«Разница между силами, воздействующими на объект, когда действует система сил, известна как результирующая сила».
Можно комбинировать силы, приложенные к одной и той же части тела, для получения одного и того же результата. Однако нельзя сочетать силы с разными местами приложения и сохранять одинаковое воздействие на тело. Система сил, действующих на твердое тело, объединяется путем перемещения сил в одну и ту же точку приложения и расчета соответствующих крутящих моментов. Результирующий крутящий момент силы получается путем сложения этих сил и крутящих моментов.
Загрузить Формулы для машиностроения ВОРОТ — Проектирование машин
Формула результирующей силы
Теорема Пифагора вычисляет результирующую силу, когда две силы действуют перпендикулярно. Формула для результирующей силы выглядит следующим образом:
F R = F 1 + F 2 + F 3
Где,
9002 2 Три силы, действующие на объект в одном направлении, равны F 1 , Ф 2 и Ф 3 .Как найти результирующую силу?
Используя второй закон Ньютона, мы можем определить результирующую силу, если мы знаем массу «m» объекта и ускорение «a», вызванное действующими на него силами. Действительно, второй закон Ньютона утверждает, что только сила F заставляет объект с массой m ускоряться.
Действительно, второй закон Ньютона утверждает, что только сила F заставляет объект с массой m ускоряться.
F = ma
Это наша результирующая сила, F. Таким образом, мы можем написать:
R = ma
Это означает, что результирующая сила R имеет то же направление, что и a, а величина равна произведению ma .
Первый закон движения Ньютона
Первый закон движения гласит, что объект в состоянии покоя «имеет тенденцию оставаться в покое, а объект в движении имеет тенденцию оставаться в движении, если на него не действует несбалансированная сила».
Если есть неравномерная сила, то будет и результирующая сила, которая заставит объект ускоряться. Второй закон Ньютона гласит, что величина и направление неуравновешенной силы, а также масса объекта будут определять величину и направление ускорения.
Загрузить формулы для GATE Машиностроение — технология производства и материалы
Второй закон движения Ньютона
Согласно второму закону движения Ньютона сила тела равна его массе, умноженной на его ускорение (a).


 В результате тела, находящие на близком расстоянии, начинают притягиваться или отталкиваться. Характер электромагнитного взаимодействия определяется знаком заряда. При изменении агрегатного состояния тела начинают двигаться в противоположных направлениях. Электромагнитное взаимодействие основано на законах электродинамики и электростатики, описывающих связь между магнитными и электрическими полями.
В результате тела, находящие на близком расстоянии, начинают притягиваться или отталкиваться. Характер электромагнитного взаимодействия определяется знаком заряда. При изменении агрегатного состояния тела начинают двигаться в противоположных направлениях. Электромагнитное взаимодействие основано на законах электродинамики и электростатики, описывающих связь между магнитными и электрическими полями.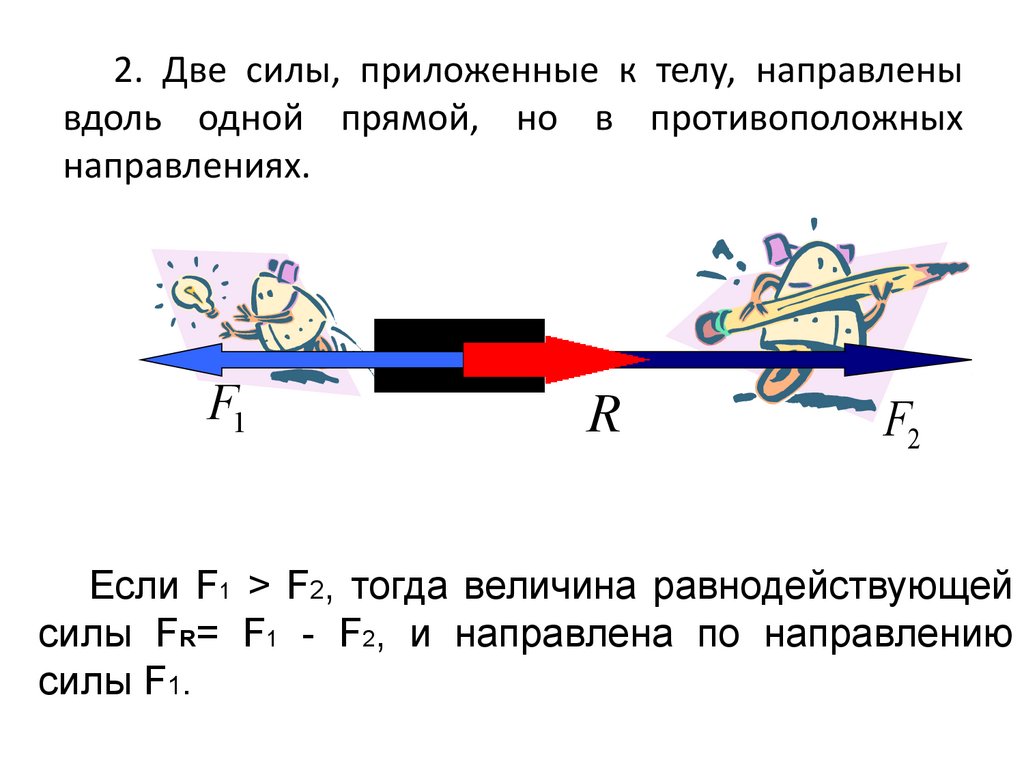

Leave A Comment