1) f(x)<0 при x<1 2) Наибольшее значение функции равно 3 3) f(0)>f(4) Ответ: 12 36. B 3 № 314676. На рисунке изображён график квадратичной функции y = f(x). Какие из следующих утверждений о данной функции неверны? Запишите их номера в порядке возрастания. 1) Функция возрастает на промежутке (−∞; −1]. 2) Наибольшее значение функции равно 8. 3) f(−4) ≠ f(2). Ответ: 23 37. B 3 № 314681. На рисунке изображён график квадратичной функции y=f(x) . Какие из следующих утверждений о данной функции неверны? Запишите их номера. 1) Функция убывает на промежутке [1; +∞) 2) Наименьшее значение функции равно – 4 3) f(−2)<f(3) Ответ: 13 38. B 3 № 314684. На рисунке изображён график квадратичной функции y=f( x ) . Какие из следующих утверждений о данной функции неверны? Запишите их номера. 1) Функция возрастает на промежутке [2; +∞) 2) f(x)>0 при −1<x<5 3) f(0)<f(4) Ответ: 1 39. Графики
Формулы
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам: Ответ: 321 40. B 3 № 314703. На рисунке изображён график квадратичной функции y = f(x). Какие из следующих утверждений о данной функции неверны? Запишите их номера. 1) f(−1) = f(3). 2) Наибольшее значение функции равно 3. 3) f(x)>0 при −1<x<3. Ответ: 2 41. B 3 № 314704. Какие из следующих утверждений о данной функции неверны? Запишите их номера. 1) Наибольшее значение функции равно 9. 2) f(0)>f(1). 3) f( x )>0 при x<0. Ответ: 3 42. B 3 № 314706. На рисунке изображён график квадратичной функции y = f(x). Какие из следующих утверждений о данной функции неверны? Запишите их номера. 1) f(x)<0 при −1<x<5. 2) Функция возрастает на промежутке [2; +∞). 3) Наименьшее значение функции равно −5. Ответ: 3 43. B 3 № 314707. На рисунке изображён график квадратичной функции y = f(x). Какие из следующих утверждений о данной функции неверны? Запишите их номера. 1) Функция убывает на промежутке [−1; +∞). 2) f(−3)<f(0). 3) f(x)<0 при −4<x<2. Ответ: 12 44. B 3 № 314709. На рисунке изображён график квадратичной функции y=f(x). Какие из следующих утверждений о данной функции неверны? Запишите их номера. 1) Наибольшее значение функции равно 9 2) Функция убывает на промежутке ( −∞; 2 ] 3) f(x)<0 при x<2 Ответ: 23 45. B 3 № 314711. На рисунке изображён график квадратичной функции y = f(x). Какие из следующих утверждений о данной функции неверны? Запишите их номера. 1) Функция возрастает на промежутке [1; +∞). 2) f(−2) = f(2). 3) Наименьшее значение функции равно –4. Ответ: 2 46. B 3 № 314712. На рисунке изображён график квадратичной функции y=f(x). Какие из следующих утверждений о данной функции неверны? Запишите их номера. 1) Функция возрастает на промежутке [2; +∞) 2) f( −1 )<f( 5 ) 3) Наименьшее значение функции равно −9 Ответ: 23 47. B 3 № 314718. На рисунке изображён график квадратичной функции y=f(x). Какие из следующих утверждений о данной функции неверны? Запишите их номера. 1) f( −2) = f(2) 2) f(x)>0 при x<−4 и при x>2 3) Наименьшее значение функции равно −9 Ответ: 1 48. КОЭФФИЦИЕНТЫ А) Б) В) ГРАФИКИ Запишите в ответ цифры, расположив их в порядке, соответствующем буквам: Ответ: 321 49. B 3 № 316316. На рисунке изображены графики функций вида . Установите соответствие между графиками и знаками коэффициентов и ГРАФИКИ КОЭФФИЦИЕНТЫ 1) 2) 3) Запишите в ответ цифры, расположив их в порядке, соответствующем буквам: Ответ: 214 50. B 3 № 316342. Установите соответствие между функциями и их графиками. ФУНКЦИИ А) Б) В) ГРАФИКИ Запишите в ответ цифры, расположив их в порядке, соответствующем буквам: Ответ: 142 51. ФУНКЦИИ Б) В) ГРАФИКИ Запишите в ответ цифры, расположив их в порядке, соответствующем буквам: Ответ: 413 52. B 3 № 333087. На рисунке изображён график функции вида . Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются. Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.
Ответ: Ответ: 23 |
Свойства графиков функций 9 класс
6. На рисунке изображён график функции y = ax2 + bx + c . Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются.
На рисунке изображён график функции y = ax2 + bx + c . Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются.
| УТВЕРЖДЕНИЯ | ПРОМЕЖУТКИ | |
А) функция возрастает на промежутке | 1) [-4;3] 2) [1;2] 3) [-4;-3] 4) [-6;-4] |
8. На рисунке изображён график функции y = ax2 + bx + c . Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются. Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.
| УТВЕРЖДЕНИЯ | ПРОМЕЖУТКИ | |
А) функция возрастает на промежутке Б) функция убывает на промежутке | 1) [1;2] 2) [0;2] 3) [-1;0] 4) [-2;3] |
10.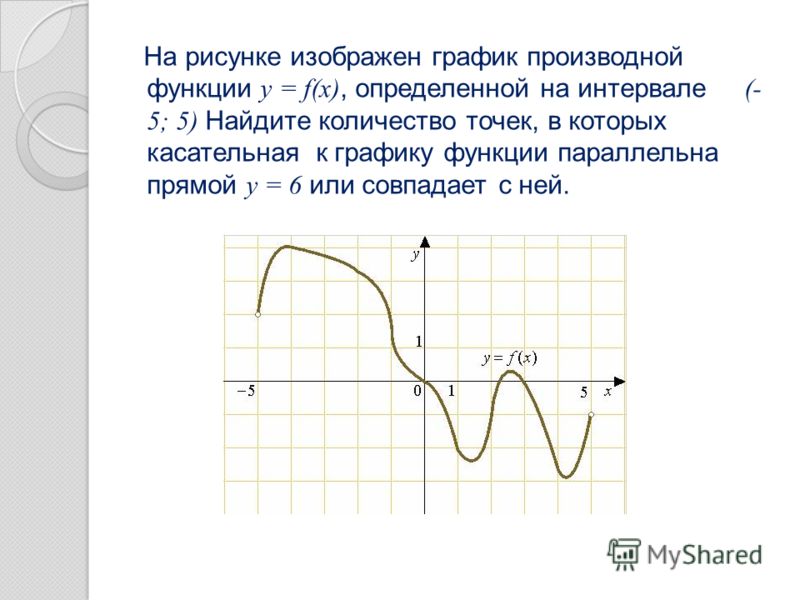
На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) f( −2) = f(2)
2) f(x)>0 при x<−4 и при x>2
3) Наименьшее значение функции равно −9
14.
На рисунке изображён график квадратичной функции y = f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) f(−1) = f(3).
2) Наибольшее значение функции равно 3.
3) f(x)>0 при −1<x<3.
16.
На рисунке изображён график квадратичной функции y = f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) f(x) < 0 при x < 1
2) Наибольшее значение функции равно 3
3) f(0) > f(4)
Если ответов несколько, запишите их в порядке возрастания
18.
На рисунке изображён график квадратичной функции
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Наибольшее значение функции равно 9
2) Функция убывает на промежутке ( −∞; 2 ]
3) f(x)<0 при x<2
24.
На рисунке изображён график квадратичной функции y = f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) f(x)<0 при −1<x<5.
2) Функция возрастает на промежутке [2; +∞).
3) Наименьшее значение функции равно −5.
25.
На рисунке изображён график квадратичной функции y = f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Функция убывает на промежутке [−1; +∞).
2) f(−3)<f(0).
3) f(x)<0 при −4<x<2.
28.
На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Функция возрастает на промежутке [2; +∞)
2) f( −1 ) < f( 5 )
3) Наименьшее значение функции равно −9
29.
На рисунке изображён график квадратичной функции y = f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера в порядке возрастания.
1) Функция возрастает на промежутке (−∞; −1].
2) Наибольшее значение функции равно 8.
3) f(−4) ≠ f(2).
Расширенная справка по геометрии
Студенты, нуждающиеся в помощи по продвинутой геометрии, получат большую пользу от нашей интерактивной программы. Мы разбираем все ключевые элементы, чтобы вы могли получить адекватную помощь по продвинутой геометрии.
Имея под рукой обязательные концепции изучения и актуальные практические вопросы, вы мгновенно получите много помощи по продвинутой геометрии.
Получите помощь сегодня с нашей обширной коллекцией важной информации Advanced Geometry.
Мы разбираем все ключевые элементы, чтобы вы могли получить адекватную помощь по продвинутой геометрии.
Имея под рукой обязательные концепции изучения и актуальные практические вопросы, вы мгновенно получите много помощи по продвинутой геометрии.
Получите помощь сегодня с нашей обширной коллекцией важной информации Advanced Geometry.
Вы когда-нибудь задавались вопросом: «Когда мне когда-нибудь понадобится это знать?» во время изучения курса геометрии? Как оказалось, изучение концепций геометрии на самом деле очень важно во многих профессиях и может применяться даже в самых простых проектах, связанных с образом жизни, таких как создание террасы или развешивание рамок для картин. Это правда, что для некоторых изучение и понимание концепций геометрии может быть очень сложным, и курсы Advanced Geometry выводят эту сложность на совершенно новый уровень. Будь то в старшей школе или в колледже, инструменты обучения Varsity Tutors Learn by Concept могут помочь упростить сложное содержание углубленной геометрии для вас, независимо от вашего возраста или уровня образования. Инструмент «Learn by Concept» — это всеобъемлющий бесплатный онлайн-ресурс для обучения, который позволяет вам точно оценить свои сильные и слабые стороны при подготовке к тесту, поиске общей помощи или просто оттачивании навыков. Нужен ли вам репетитор по геометрии в Филадельфии, репетитор по геометрии в Милуоки или репетитор по геометрии в Портленде, работа один на один с экспертом может стать именно тем, что вам нужно для учебы.
Инструмент «Learn by Concept» — это всеобъемлющий бесплатный онлайн-ресурс для обучения, который позволяет вам точно оценить свои сильные и слабые стороны при подготовке к тесту, поиске общей помощи или просто оттачивании навыков. Нужен ли вам репетитор по геометрии в Филадельфии, репетитор по геометрии в Милуоки или репетитор по геометрии в Портленде, работа один на один с экспертом может стать именно тем, что вам нужно для учебы.
Инструмент «Изучение по понятиям» разбивает основные понятия расширенной геометрии на три основных предмета, включая координатную геометрию, плоскую геометрию и объемную геометрию. Вы можете начать бесплатное занятие по продвинутой геометрии прямо с основных предметов, чтобы оценить, какой контент требует вашего внимания больше всего. Например, если вы обнаружите, что вам нужна помощь с четырехугольниками в плоской геометрии, вы можете выбирать между подтемами воздушные змеи, ромбы и трапеции. После того, как вы выбрали одну из этих подтем, вы можете углубиться еще глубже. Например, в рамках темы о ромбах есть еще один слой подтем, которые включают в себя понятия о том, как найти площадь ромба и как найти длину диагонали ромба. У каждой темы есть несколько подтем, а затем дополнительно у каждой подтемы есть еще несколько более узких тем. Этот целенаправленный контент обеспечивает специализированный опыт обучения, удобный для пользователя и разработанный для простоты и эффективности. Varsity Tutors предлагает такие ресурсы, как бесплатный вопрос дня по продвинутой геометрии , который поможет вам в самостоятельном обучении, или вы можете подумать о преподавателе геометрии.
Например, в рамках темы о ромбах есть еще один слой подтем, которые включают в себя понятия о том, как найти площадь ромба и как найти длину диагонали ромба. У каждой темы есть несколько подтем, а затем дополнительно у каждой подтемы есть еще несколько более узких тем. Этот целенаправленный контент обеспечивает специализированный опыт обучения, удобный для пользователя и разработанный для простоты и эффективности. Varsity Tutors предлагает такие ресурсы, как бесплатный вопрос дня по продвинутой геометрии , который поможет вам в самостоятельном обучении, или вы можете подумать о преподавателе геометрии.
Интерактивная программа Advanced Geometry содержит примеры вопросов по каждому предмету или подтеме. Эти примеры вопросов представлены в формате множественного выбора. Представлено несколько ответов с несколькими вариантами ответов, за которыми следует правильный ответ и подробное объяснение того, почему этот ответ был лучшим выбором. Подробные пояснения показывают формулы и все действия, когда это необходимо, что делает средство обучения эффективным ресурсом для самостоятельного изучения. Кроме того, ответы с несколькими вариантами ответов случайным образом перемешиваются и даются в другом порядке каждый раз, когда вы повторно посещаете определенную концепцию в инструменте «Узнать по концепции». Этот аспект переназначения ценен, когда речь идет о доказательстве истинного понимания концепции, а не о запоминании правильного ответа из предыдущей попытки. В дополнение к разделу справки по базовой геометрии и урокам геометрии вы также можете рассмотреть некоторые из наших карточек для углубленного изучения геометрии.
Кроме того, ответы с несколькими вариантами ответов случайным образом перемешиваются и даются в другом порядке каждый раз, когда вы повторно посещаете определенную концепцию в инструменте «Узнать по концепции». Этот аспект переназначения ценен, когда речь идет о доказательстве истинного понимания концепции, а не о запоминании правильного ответа из предыдущей попытки. В дополнение к разделу справки по базовой геометрии и урокам геометрии вы также можете рассмотреть некоторые из наших карточек для углубленного изучения геометрии.
Другие бесплатные средства обучения университетских преподавателей, которые помогают в изучении концепций продвинутой геометрии, включают карточки, которые очень эффективны при запоминании формул, упражнение «Вопрос дня», которое обеспечивает быстрый ежедневный обзор с новым вопросом каждый день и практические тесты. . Эти средства обучения дополняют друг друга, а также являются эффективными и действенными инструментами сами по себе. Средства обучения делают обучение увлекательным, даже если вы имеете дело со сложными предметами, такими как продвинутая геометрия!
Расширенная геометрия
Координатная геометрия
Графики
Как построить график функции
Как построить логарифм
Как построить график квадратичной функции
Как построить график двухшагового неравенства
Как построить график экспоненциальной функции
Как построить график упорядоченной пары
Как построить график комплексных чисел
Как построить график обратной вариации
Трансформация
Как найти преобразование для уравнения аналитической геометрии
Плоская геометрия
Четырехугольники
Воздушные змеи
Как найти площадь воздушного змея
Как найти длину диагонали воздушного змея
Ромбы
Как найти площадь ромба
Как найти длину диагонали ромба
Трапеции
Как найти площадь трапеции
Как найти длину диагонали трапеции
Твердотельная геометрия
Конусы
Как найти площадь поверхности конуса
Тетраэдры
Как найти диагональ тетраэдра
Как найти длину ребра
Как найти площадь поверхности тетраэдра
Как найти объем тетраэдра
Обратные функции
Обратные функции
|
Содержание: Эта страница соответствует § 1. 7 (стр. 150) текста.
7 (стр. 150) текста.
Предполагаемые проблемы из текста
стр.158 #1-4, 5, 8, 9, 12, 13, 15, 18, 21, 22, 27, 31, 34, 37, 46, 48, 51, 71, 74, 83
Определение обратной функции
Графики обратных функций
Существование инверсии
Нахождение инверсий
Определение обратной функции
Прежде чем определить обратную функцию, нам нужно иметь правильный ментальный образ функции.
Рассмотрим функцию f(x) = 2x + 1. Мы знаем, как вычислить f при 3, f(3) = 2*3 + 1 = 7. В этом разделе помогает думать о f как о преобразовании 3 в 7, а f о преобразовании 5 в 11 и т. д.
Теперь, когда мы думаем о f как о «действии» на числа и их преобразовании, мы можем определить обратную функцию
f как функцию, которая «отменяет» то, что сделал f. Другими словами, функция, обратная f, должна вернуть 7 к
3, и вернуть -3 обратно в -2 и т. д.
д.
Пусть g(x) = (x — 1)/2. Тогда g(7) = 3, g(-3) = -2 и g(11) = 5, поэтому g, похоже, отменяет то, что сделал f, по крайней мере для этих трех значений. Чтобы доказать, что g является обратным значением f, мы должны показать, что это верно для любого значения x в домен ф. Другими словами, g должен вернуть f(x) обратно к x для всех значений x в области определения f. Итак, g(f(x)) = x должно выполняться для всех x в области определения f. Способ проверки этого условия состоит в том, чтобы убедиться, что формула для g(f(x)) упрощается до х.
г (f (х)) = г (2х + 1) = (2х + 1 -1)/2 = 2х/2 = х.
Это упрощение показывает, что если мы выберем любое число и позволим f воздействовать на него, то применение g к результату восстанавливает наш исходный номер. Нам также нужно увидеть, что этот процесс работает в обратном порядке, или что f также отменяет то, что делает g.
f(g(x)) = f((x — 1)/2) = 2(x — 1)/2 + 1 = x — 1 + 1 = x.
Обозначив f -1 , обратную f, мы только что показали, что g = f -1 .
Определение:
Пусть f и g — две функции. Если
f(g(x)) = x и g(f(x)) = x,
, то g является обратным значением f, а f является обратным значением g.
Упражнение 1:
(a) Откройте калькулятор Java и введите формулы для f и g. Обратите внимание, что вы берете куб корень путем повышения до (1/3), и вам нужно ввести показатель степени как (1/3), а не десятичное приближение. Таким образом, текст для поля g будет 9(1/3)
Используйте калькулятор для вычисления f(g(4)) и g(f(-3)). g является обратным f, но из-за округления ошибка, калькулятор может не вернуть точное значение, с которого вы начали. Попробуйте f(g(-2)). Ответы будут разными для разные компьютеры. Однако на нашей тестовой машине функция f(g(4)) вернула 4; g(f(-3)) вернул 3; но f(g(-2)) вернул -1,9999999999999991, что довольно близко к -2.
Калькулятор может дать нам хорошее представление о том, что g является обратным значением f, но мы не можем проверить все возможные значения. х.
(b) Докажите, что g является обратной величиной f, упростив формулы для f(g(x) и g(f(x)).
Вернуться к содержанию
Графики обратных функций
Мы видели примеры отражений в плоскости. Отражение точки (a,b) относительно оси x равно (a,-b), а отражение (a,b) относительно оси y равно (-a,b). Теперь мы хотим подумать о линии y = x.
Отражение точки (a,b) относительно прямой y = x есть точка (b,a) .
Пусть f(x) = x 3 + 2. Тогда f(2) = 10 и точка (2,10) находится на графике f. Обратное f должно
вернуть 10 к 2, т. е. f -1 (10)=2, поэтому точка (10,2) находится на графике f -1 . Смысл
(10,2) есть отражение на линии y = x точки (2,10). То же самое можно сделать для всех точек на
графики f и f -1 .
График f -1 является отражением относительно линии y = x графика f.
- Видео: x 3 + c Анимированный Gif, Файл MS Avi, или Real Видео файл
- Видео: x 2 + c Анимированный Gif, Файл MS Avi, или Реальный Видео файл
Вернуться к содержанию
Существование инверсии
Некоторые функции не имеют обратных функций. Например, рассмотрим f(x) = x 2 . Есть два числа
что f принимает значение 4, f(2) = 4 и f(-2) = 4. Если бы f было обратным, то тот факт, что f(2) = 4, подразумевал бы, что
обратная функция f возвращает 4 обратно в 2. С другой стороны, поскольку f(-2) = 4, обратная функция f должна преобразовать 4 в -2.
Следовательно, не существует функции, обратной f.
Посмотрите на ту же задачу с точки зрения графиков. Если бы у f была обратная, то ее график был бы отражением график f относительно прямой y = x. График f и его отражение относительно y = x нарисованы ниже.
Обратите внимание, что отраженный график не проходит тест вертикальной линии, так что это не график функции.
Это обобщается следующим образом: функция f имеет обратную тогда и только тогда, когда ее график отражается относительно линия y = x, результатом является график функции (проходит тест вертикальной линии). Но это можно упростить. Прежде чем отражать график, мы можем сказать, будет ли какая-либо вертикальная линия пересекаться более одного раза. как горизонтальные линии пересекают исходный график!
Проверка горизонтальной линии
Пусть f — функция.
Если любая горизонтальная линия пересекает график f более одного раза, то f не имеет обратной.
Если ни одна горизонтальная линия не пересекает график функции f более одного раза, то функция f имеет обратную.
Свойство наличия инверсии очень важно в математике, и у него есть имя.
Определение : Функция f является однозначной тогда и только тогда, когда f имеет обратную.
Следующее определение эквивалентно, и оно чаще всего дается для взаимно однозначного ответа.
Альтернативное определение : Функция f является однозначной , если для каждого a и b в своей области определения f(a) = f(b) влечет a = b.
Упражнение 2:
(1/3) (кубический корень из х). Ответ
Вернуться к содержанию
Нахождение инверсий
Пример 1. Сначала рассмотрим простой пример f(x) = 3x + 2 .
График функции f представляет собой линию с наклоном 3, поэтому он проходит тест горизонтальной линии и имеет обратную сторону.
Требуется два шага, чтобы вычислить f по числу x. Сначала умножаем x на 3, затем прибавляем 2.
Думая об обратной функции как об отмене действия f, мы должны отменить эти шаги в обратном порядке.
Шаги, необходимые для оценки f -1 , заключаются в том, чтобы сначала отменить прибавление 2 путем вычитания 2. Затем мы отменяем умножение на 3 делением на 3.
Следовательно, f -1 (х) = (х — 2)/3.
Этапы поиска обратной функции f.
- Замените f(x) на y в уравнении, описывающем функцию.
- Развязка x и y. Другими словами, замените каждый x на y и наоборот.
- Решите для y.
- Заменить y на f -1 (x).
Пример 2. f(x) = 6 — x/2
| Этап 1 | у = 6 — х/2. |
| Шаг 2 | х = 6 — у/2. |
| Этап 3 | х = 6 — у/2. у/2 = 6 — х. у = 12 — 2х. |
| Этап 4 | ж -1 (х) = 12 — 2х. |
Шаг 2 часто сбивает учащихся с толку. Мы могли бы пропустить шаг 2 и найти x вместо y, но тогда мы получили бы с формулой в y вместо x. Формула будет та же, но переменная будет другой. Избегать это мы просто меняем роли x и y, прежде чем решить.
Пример 3. f(x) = x 3 + 2
Это функция, с которой мы работали в упражнении 1. Из ее графика (показанного выше) видно, что она имеет обратный. (На самом деле в упражнении 1 дано обратное значение)
Этап 1 у = х 3 + 2. Этап 2 х = у 9(1/3).
Упражнение 3:
График f(x) = 1 — 2x 3 , чтобы увидеть, что у него есть обратный.

 B 3 № 314688. Установите соответствие между графиками функций и формулами, которые их задают.
B 3 № 314688. Установите соответствие между графиками функций и формулами, которые их задают.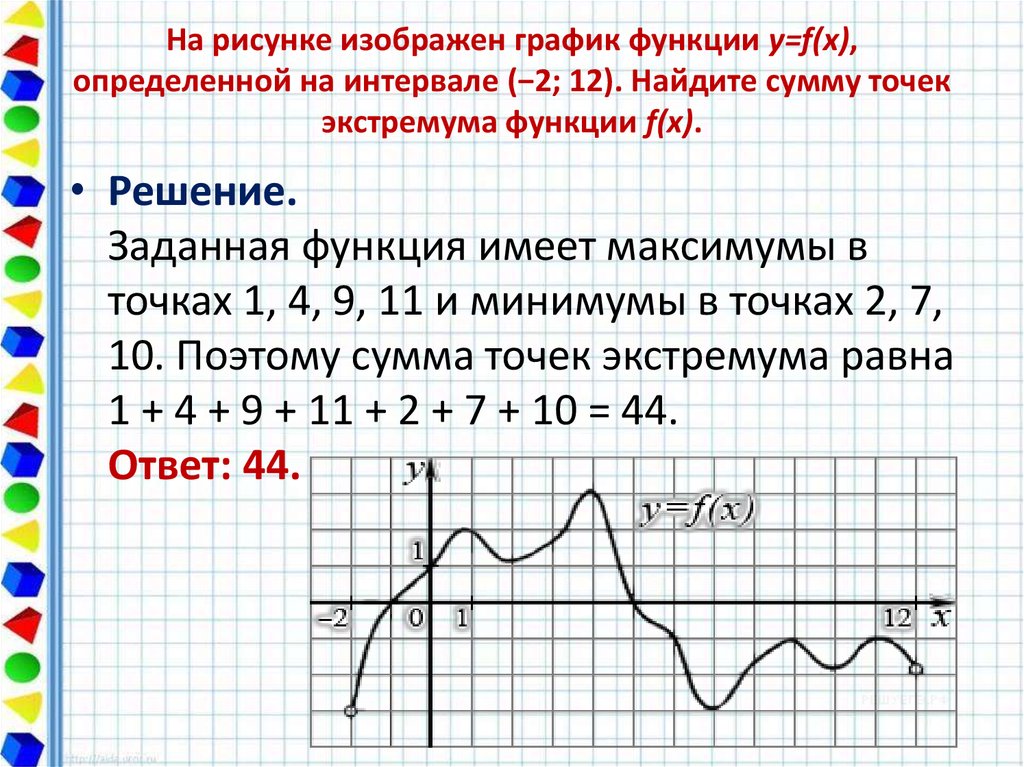 На рисунке изображён график квадратичной функции y = f(x).
На рисунке изображён график квадратичной функции y = f(x).
 B 3 № 316226. На рисунке изображены графики функций вида . Установите соответствие между знаками коэффициентов и и графиками.
B 3 № 316226. На рисунке изображены графики функций вида . Установите соответствие между знаками коэффициентов и и графиками. B 3 № 316368. Установите соответствие между функциями и их графиками.
B 3 № 316368. Установите соответствие между функциями и их графиками.



Leave A Comment