КОМИТЕТ ОБРАЗОВАНИЯ, КУЛЬТУРЫ И СПОРТА АДМИНИСТРАЦИИ ГОРОДА КИРОВСКА » Страница не найдена
КОМИТЕТ ОБРАЗОВАНИЯ, КУЛЬТУРЫ И СПОРТА АДМИНИСТРАЦИИ ГОРОДА КИРОВСКА » Страница не найденаОшибка 404. Страница не найдена.
Ничего не найдено. Вы можете посмотреть по ссылкам в меню или воспользоваться формой поиска.
Найти:
Новое на сайте »
- Премия #МЫ_ВМЕСТЕ
- ЕГЭ по истории и химии в досрочный период прошел в штатном режиме
- Досрочный период ЕГЭ 6 апреля продолжат экзамены по информатике и ИКТ и обществознанию
- ЕГЭ по обществознанию и информатике и ИКТ в досрочный период прошел без нарушений
- Специалисты региона отработали процедуру проведения устной части ЕГЭ по иностранным языкам (раздел «Говорение»)
- ЕГЭ по английскому языку (раздел «Говорение») в досрочный период прошел без сбоев
- ЕГЭ по русскому языку в досрочный период прошел без нарушений
- Досрочный период ЕГЭ-2023 продолжит экзамен по математике профильного уровня
- Самый массовый экзамен досрочного периода пройдет 23 марта
Страницы »
- #6425 (без названия)
- #6317 (без названия)
- #1499 (без названия)
- «Коррекционный педагог»
- «Сердце отдаю детям-2023»
- 2015- 2016 учебный год
- 2020
- 2021 год
- 2022-2023 учебный год
- Аналитическая информация
- Банк лучших педагогических и управленческих практик
- В сфере культуры
- В сфере культуры
- В сфере образования
- В сфере образования
- В сфере физической культуры и спорта
- В сфере физической культуры и спорта
- Виртуальная приемная
- Воспитатель года
- Воспитатель года города Кировска — 2022
- Всероссийские проверочные работы
- Всероссийское военно-патриотическое детско-юношеское общественное движение «Юнармия»
- Главная
- Государственная итоговая аттестация
- Дистанционное обучение
- ДОКУМЕНТЫ
- КУЛЬТУРА
- Дорожная карта в сфере культуры
- Дорожная карта в сфере образования, физической культуры и спорта
- Дошкольное образование
- Законодательно- нормативная база по персональным данным, обрабатываемым в информационных системах
- Интернет — ресурсы в сфере физической культуры и спорта
- Интернет- ресурсы в сфере культуры
- Интернет- ресурсы в сфере образования
- Информационно- аналитические материалы
- Информационные материалы
- Информационные материалы
- Информация о сроках и местах подачи заявлений на участие в ГИА, апелляций, о порядке информирования о результатах ГИА
- Карта сайта
- Каталог полезных ссылок
- Комитет образования, культуры и спорта администрации города Кировска
- Общие сведения
- Уставные документы
- Структура, состав и контакты сотрудников
- Основные задачи, функции и полномочия Комитета образования, культуры и спорта
- План работы
- Конкурс «Большая перемена»
- Конкурсное распределение муниципальных услуг
- Конкурсы
- СЕРДЦЕ ОТДАЮ ДЕТЯМ -2023
- Контакты
- Контакты сотрудников
- Материалы
- Материалы августовской педагогической конференции
- Материалы августовской педагогической конференции 30.
 08.2021 года.
08.2021 года. - Материалы августовской педагогической конференции от 15.09.2017
- МАУО «Кировский комбинат школьного питания»
- Мероприятия в основной и средней школе
- Методические материалы
- Методические материалы
- Методические мероприятия
- Молодёжная политика
- Муниципальные документы
- Муниципальный опорный центр
- На 2021 год
- На 2022 год
- на 2023 год
- Направления работы сотрудников
- Научно-исследовательское, научно-техническое творчество школьников
- Национальные, региональные исследования
- Начальное, основное и среднее общее образование
- Наши сотрудники
- Независимая оценка качества
- Нормативно- правовая база
- Нормативно- правовая база
- О сертификате дополнительного образования
- Образование
- Организация питания
- Основная деятельность
- Оценка качества услуг в сфере культуры
- Оценка качества услуг в сфере образования
- Подготовка к ЕГЭ
- Подготовка к экзаменам
- Приказы
- Приказы Комитета образования, культуры и спорта
- Приказы Министерства образования и науки Мурманской области
- Присвоение разрядов, категорий
- Присвоение судейских категорий
- Профилактика правонарушений
- Профильное обучение
- Психологическая служба в системе образования г.
 Кировска
Кировска- Методические рекомендации
- Новости
- Нормативно-правовая документация
- Развитие и поддержание интереса к чтению
- Развитие и поддержание интереса к чтению
- Реализация Концепции математического образования
- Реализация концепции развития предметной области «Технология
- Реализация Концепции развития школьных информационно-библиотечных центров
- Реализация предметных областей ОРКСЭ и ОДНКНР
- Региональные документы
- РЕГИОНАЛЬНЫЕ ДОКУМЕНТЫ
- Результаты
- Результаты
- Результаты контроля в сфере информатизации образования
- Родителям о ВПР
- Российское движение школьников
- Система методической работы
- Система мониторинга качества дошкольного образования
- Система мониторинга эффективности руководителей образовательных организаций
- Система обеспечения профессионального развития педагогических работников
- Система организации воспитания обучающихся
- Система оценки качества подготовки обучающихся
- Система работы со школами с низкими результатами обучения и/или школами, функционирующими в неблагоприятных социальных условиях
- Соглашения о сотрудничестве
- Структура Комитета образования, культуры и спорта администрации города Кировска
- Учитель года города Кировска — 2021
- Учитель года города Кировска — 2022
- Учреждения культуры
- Учреждения культуры
- Учреждения образования
- Учреждения спорта
- Учреждения спорта
- ФГОС
- ФГОС для детей с ОВЗ
- ФГОС ДО
- ФГОС начального общего образования
- ФГОС общего образования
- ФГОС основного общего образования
- ФГОС среднего общего образования
- ФГОС среднего общего образования
- Федеральные государственные образовательные стандарты
- Финансовая грамотность
- Электронные услуги
- Электронные услуги в сфере культуры
- Электронные услуги в сфере образования
- Электронные услуги в сфере физической культуры и спорта
- Национальный проект «Образование»
- Нормативно — правовая база
- Нормативно-правовые акты
- Правовая база предоставления муниципальных услуг, стандарты качества
- Профессиональные конкурсы, лучшие педагогические и управленческие практики
- Административные регламенты
- Ведомственные и муниципальные программы
- Сведения о контрольных мероприятиях и их результатах
- Воспитательная компонента, мероприятия
- Официальные выступления руководства
- Материалы августовской педагогической конференции 14.
 09.2018
09.2018
- Материалы августовской педагогической конференции 14.
- Отчет о деятельности
- Отчет о деятельности МКУ «Управление социального развития г. Кировска»
- Подведомственные учреждения
- Учреждения образования
- ОБРАЗОВАНИЕ
- КУЛЬТУРА
- ФГОС дошкольного образования
- Конкурсное распределение муниципальных услуг
- Календарь официальных физкультурных и спортивных мероприятий г. Кировска
- Дорожная карта
- ФИЗИЧЕСКАЯ КУЛЬТУРА И СПОРТ
- Методические рекомендации
- Государственная итоговая аттестация
- Документы
- «Горячая» линия по вопросам государственной итоговой аттестации
- Пункт регистрации на ЕГЭ выпускников прошлых лет, обучающихся СПО
- Информатизация образования
- Автоматизированные информационные системы
- Аналитическая информация
- Информационная безопасность
- Информационные материалы
- Территориальная психолого — медико — педагогическая комиссия
- Нормативно — правовые акты
- Для родителей
- Оценка качества подготовки обучающихся (ГИА, ВПР, исследования качества подготовки обучающихся)
- Реализация Концепции преподавания русского языка и литературы
- Реализация Концепции преподавания русского языка и литературы
- Одаренные дети, социальная активность
- 2014- 2015 учебный год
- Всероссийская олимпиада школьников
- 2020-2021 учебный год
- Мероприятия в начальной школе
- 2016 год
- 2016 год
- Муниципальные олимпиады
- 2016 год
- Управление качеством образования
- Отдых и оздоровление детей
- Документы
- Отдых и оздоровление
- Отдых и оздоровление детей в трудной жизненной ситуации
- Вакансии в образовательных организациях
- Обращения граждан
- Общая информация
- Формы обращений
- Виртуальная приемная
- Обзоры обращений
Профильная и базовая математика: какую сдавать?
ЭКЗАМЕНЫ
18. 10.2019
10.2019
Какая разница между профильным ЕГЭ по математике и базовым вариантом экзамена? Какой из них выбрать? Отвечаем на самые распространенные вопросы.
В чем разница между профильной и базовой математикой?
Выпускники имеют право выбрать один из двух вариантов экзамена по математике.
Профильная математика обязательна для тех, кому математика нужна для поступления в вуз. Речь идет о технических специальностях и ряде гуманитарных, таких как экономика. Более простая базовая математика подойдет тем, кто поступает на сугубо гуманитарные специальности и в вузе ее изучать не будет.
Что такое профильная математика?
Профильная математика — сложный экзамен, который оценивается по стобалльной шкале. Минимум, который был необходим для сдачи этого экзамена в 2019 году, — 27 баллов. Чтобы получить пятерку нужно было набрать 72 балла.Экзамен по профильной математике охватывает всю школьную программу и состоит из 19 заданий.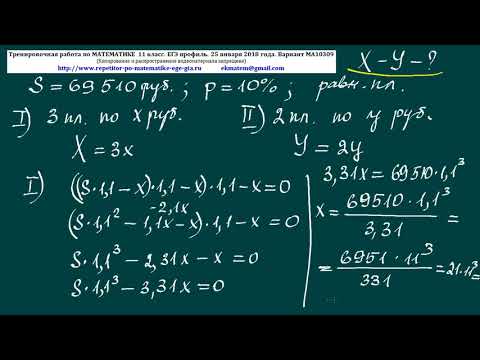 Задачи с 1 по 8 относительно просты, и для них достаточно краткого ответа, задания с 9 по 12 — сложнее (все они проверяются автоматически). Остальные задания имеют высокий уровень сложности и требуют развернутого решения.
Задачи с 1 по 8 относительно просты, и для них достаточно краткого ответа, задания с 9 по 12 — сложнее (все они проверяются автоматически). Остальные задания имеют высокий уровень сложности и требуют развернутого решения.
Что такое базовая математика?
ЕГЭ по базовой математике оценивается по пятибалльной системе. Чтобы сдать экзамен на тройку и получить аттестат, достаточно верно решить 7 заданий из 20 (так было в 2019 году). Задания базового экзамена на порядок легче, чем профильные задачи. По уровню сложности с профильным ЕГЭ могут сравниться только задания 17–20.
Можно ли получить медаль, не сдавая профильную математику?
Да, можно. Если вы гуманитарий, и не планируете поступать в технический вуз, а до медали вам рукой подать, — смело сдавайте базовую математику на пятерку и получайте отличный аттестат.
Можно ли сдать базовую математику в 10 классе, а в 11 классе — профильную?
Нет, перестраховаться не получится. Если вы решите сдавать базовую математику в 10 классе и сдадите ее не на двойку (то есть наберете удовлетворительны балл), то в 11 классе вас на профильную математику уже не допустят — ведь формально вы аттестованы.
Если провалил профильную математику, можно ли пересдавать уже базовую?
Да, можно. Если вы переоценили свои силы и профильная математика оказалась вам не по зубам, вы можете аттестоваться с помощью базового экзамена в резервные сроки. Чтобы сдать экзамен с первого раза и успешно, готовьтесь к нему в Ростелеком Лицее. Вы научитесь решать типовые задачи и познакомитесь со всеми темами, которые могут вам попасться на ЕГЭ по математике.
Автор: Редакция Лицея
Подпишитесь на нашу рассылку
Мы вышлем в подарок словарь плеоназмов для подготовки к ЕГЭ!Раз в две недели мы будем присылать вам полезные статьи, чек-листы и учебные материалы.
2023 Challenge: Ежегодный вызов
Что такое испытание «Годовой номер»?
Какие математические символы или операции разрешены?
Дополнительный вызов
Как я могу использовать этот вызов в своем классе?
Вызов 2023 года
Бесплатная загрузка рабочего листа задач 2023 года
Цифровая версия конкурса 2023 года
Проблемы прошлого года
Вызов 2022 года
Вызов 2019 года
Вызов 2018 года
Вызов 2017 года
Вызов 2016 года
Решения головоломок
Больше задач и головоломок на основе чисел
Этот пост в блоге содержит партнерские ссылки Amazon. Как партнер Amazon, я получаю небольшую комиссию от соответствующих покупок. Это бесплатно для вас. Спасибо за вашу поддержку Math = Love!
Как партнер Amazon, я получаю небольшую комиссию от соответствующих покупок. Это бесплатно для вас. Спасибо за вашу поддержку Math = Love!
Задача «Число года» — это простая в объяснении головоломка, которая увлечет вас на несколько часов. Используя цифры текущего года ровно по одному разу, можете ли вы написать математическое выражение для каждой цифры от 1 до 100? Вы можете использовать любой математический символ или операцию по вашему выбору.
Что такое испытание «Годовой номер»?
Цель задания — использовать цифры текущего года (2023) ровно один раз вместе с любым математическим символом или операцией по вашему выбору, чтобы составить выражения, эквивалентные числам от 1 до 100.
Какие математические символы или операции разрешены?
Конкатенация
- Вы можете соединять цифры вместе, чтобы образовать большее число. Например, 2 и 0 можно объединить, чтобы получить 20. 2 и 3 можно объединить, чтобы получить 23 или 32.
Десятичные точки
- Десятичные точки могут быть размещены между цифрами, такими как 2.
 0 или 2.2.
0 или 2.2.
Основные арифметические операции
- Дополнение
- Вычитание 92 +20 за 29.
- Допускаются квадратные корни. Это не считается использованием цифры 2.
Другие математические символы
- Факториалы. Мне нравится использовать это упражнение как способ познакомить моих учеников с концепцией факториалов. Факториал числа — это произведение всех положительных целых чисел меньше или до числа.
- 0! = 1 [ ЭТОТ ФАКТ ОЧЕНЬ ПОЛЕЗЕН В ЭТОМ ЗАДАЧЕ! ]
- 1! = 1
- 2! = 2 * 1 = 2
- 3! = 3 * 2 * 1 = 6
- 4! = 4 * 3 * 2 * 1 = 24
- 5! = 5 * 4 * 3 * 2 * 1 = 120
- Двойные факториалы. Двойные факториалы похожи на факториалы, но они предполагают умножение только на числа, имеющие ту же четность (четную или нечетную), что и исходное число. [ ПРИМЕЧАНИЕ. Desmos не вычисляет двойные факториалы. Он просто дважды применяет факториальную функцию.
 ]
]- 4!! = 4 * 2 = 8
- 5!! = 5 * 3 * 1 = 15
- 6!! = 6 * 4 * 2 = 48
- Нужен обзор того, как работают факториалы? Я создал бесплатную печатную таблицу факториалов, в которой рассматриваются концепции факториала и двойного факториала, а также предоставляется удобная таблица значений факториала для справки.
- Я также создал бесплатный плакат факториала для печати, который вы можете распечатать и повесить в своем классе, чтобы учащиеся могли на него ссылаться.
- Я видел, как некоторые люди использовали функции пола и потолка в этом испытании, но я никогда не позволял ни своим ученикам, ни себе делать это. Мне всегда казалось, что это слишком похоже на «обман».
В конце концов, помните, что это испытание может быть таким, каким вам нужно. Не стесняйтесь изменять правила, чтобы удовлетворить потребности ваших учеников!
Дополнительное испытание
Хотите еще больше испытаний? Сколько чисел вы сможете найти, если будете каждый раз ставить цифры по порядку?
Как я могу использовать этот вызов в своем классе?
С 2016 года я использую в своем классе различные формы ежегодного конкурса чисел.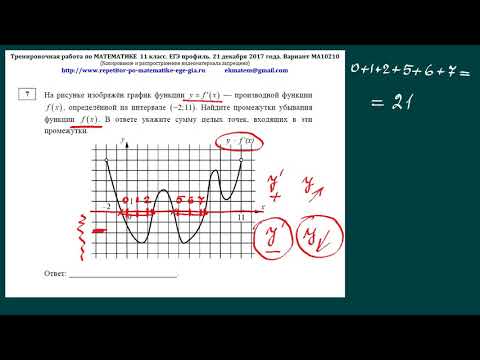 На протяжении многих лет конкурс принимал различные формы. В 2019 году, я превратил ежегодное числовое соревнование в групповое соревнование.
На протяжении многих лет конкурс принимал различные формы. В 2019 году, я превратил ежегодное числовое соревнование в групповое соревнование.
В течение нескольких лет (2016–2018) я оформлял ежегодное числовое задание в виде бесплатной доски объявлений для печати. Совсем недавно я сделал печатный лист с заданиями, в котором учащиеся могли записывать каждое найденное решение.
ПРЕДУПРЕЖДЕНИЕ
Некоторые проблемы года решить легче, чем другие. Убедитесь, что учащиеся понимают, что они могут не найти все решения!
2023 Задача
Когда я использую ежегодную задачу по числам со своими учениками средней школы по математике, я предлагаю им найти математические выражения для как можно большего числа чисел от 1 до 100. Я создал для них бесплатный печатный лист, который они могут заполнять, находя решения для различных чисел.
В некоторые годы в задаче можно найти больше чисел, чем в другие годы.
В зависимости от возраста и математических способностей ваших учеников, а также от количества времени, которое вы хотели бы посвятить этому занятию, вы можете предложить своим ученикам найти только подмножество чисел.
В этом году я создал 6 разных версий Вызова 2023, которые вы можете распечатать и использовать со своими учениками. Предложите своим ученикам найти числа 1–10, 1–20, 1–30, 1–40, 1–50 или 1–100, используя цифры 2023 года. числа на нем, а затем попытайтесь найти как можно больше решений, используя тип математических операций, которые, как вы ожидаете, будут использовать ваши ученики при решении. Как только вы увидите, сколько задач вы можете решить самостоятельно, вы сможете решить, какой уровень сложности подойдет вашим ученикам.
1-100 Challenge
1-50 Challenge
1-40 Challenge
1-30 Challenge
1-20 Challenge
1-10 Challenge
Если вы ищете новый способ отпраздновать новый год , посмотрите мою головоломку 2023 года!
Цифровая версия Challenge 2023
Крейг Винске создал версию Desmos Challenge 2023.
Задачи прошлого года
Задачи 2022 года
Сегодня был первый день нового семестра. Я предложил своим ученикам задание «Вызов 2022», чтобы их мозг снова занялся математикой без необходимости сразу переходить к содержанию в первый же день.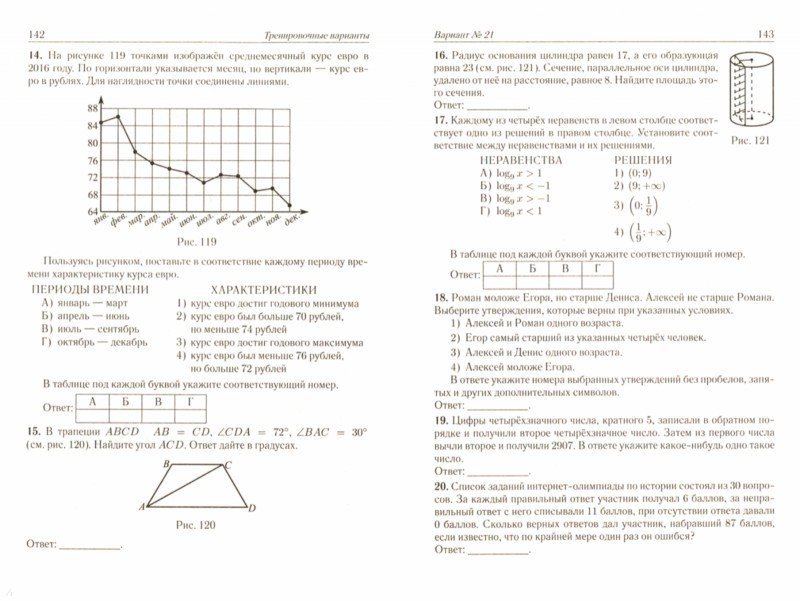
Что такое Challenge 2022?
Цель задания — использовать цифры 2022 (2, 0, 2 и 2) ровно по одному разу вместе с любым математическим символом или операцией по вашему выбору, чтобы составить выражения, эквивалентные числам от 1 до 100.
Впервые я узнал об этом типе ежегодных числовых испытаний в 2016 году. Сначала я начал с создания больших плакатов, которые можно было повесить на доску объявлений с заданием для учащихся. В 2019 году я все изменил и сделал групповой конкурс на 2019 годИспытание.
В 2020 году я решил, что иметь только две двойки и два нуля — это слишком ограничительно, поэтому я не стал участвовать в «Вызове 2020» со студентами. Мы начали 2021 учебный год с дистанционного обучения, поэтому челлендж 2021 тоже не состоялся.
В этом году я не был уверен, какую часть «Вызова 2022» смогут выполнить мои ученики, но все же решил попробовать. Я также решил изменить ситуацию в этом году и выполнить ежегодную задачу с числами в виде рабочего листа.
На самом деле я начал урок с вопроса ACT с факториалами. Большинство моих студентов никогда раньше не сталкивались с факториалами, и я знал, что мы добьемся гораздо большего успеха, если сможем извлечь выгоду из того факта, что 0! = 1.
Мы решили задачу ACT, я научил их слову «факториал», а затем предложил им использовать их новое понимание факториалов для определения значения 0!.
После обнаружения 0! равно 1, я сказал им, что этот факт может пригодиться сегодня, и раздал рабочий лист «Вызов-2022».
На данный момент мы обсудили направления. Я намеренно оставил указания расплывчатыми, так как считаю, что учащимся лучше всего начать с задания, а затем позволить им начать задавать вопросы.
Это когда я говорю им, что конкатенация (например, объединение 2 и 0 для образования 20) разрешена. Я также даю им идеи различных математических символов, которые они могут использовать, таких как круглые скобки, десятичные точки, факториал и показатели степени.
Предостережение относительно показателей степени состоит в том, что показатель степени имеет значение как одну из цифр. Некоторым учащимся также приходит в голову, что им нужно хранить цифры 2, 0, 2 и 2 в таком порядке.
NCTM называет это «Годовой игрой» и поощряет учащихся по возможности сохранять цифры в исходном порядке. Я думал, что вызов этого года был достаточно сложным, чтобы не поощрять это ограничение.
Чтобы дать моим ученикам немного дополнительной мотивации для участия в деятельности в первый день после каникул, я решил сразить свои классы друг с другом в соревновании. Я сказал им, что в зависимости от того, какой классный период найдет наибольшее количество решений задачи, выиграют печеньки.
Очевидно, подростки любят поесть, потому что я обнаружил, что мои ученики увлечены и весьма конкурентоспособны. Мой дневной класс даже дошел до того, что записал все их результаты на доске, чтобы убедиться, что ученики не работают с числами, которые уже были решены другой группой.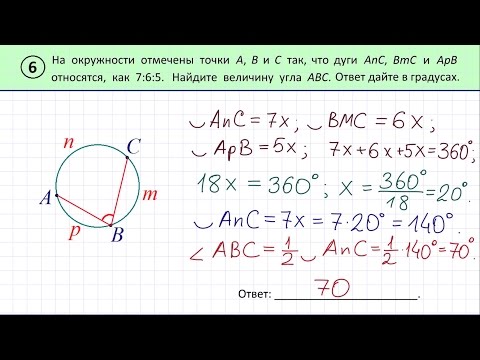
Они также утверждали, что их класс находился в невыгодном положении, поскольку в нем было вдвое меньше учеников, чем в некоторых других моих классах. Вместо этого они хотели, чтобы я изменил правила, чтобы они основывались на пропорциях.
Сколько решений оказалось действительно возможным найти? Моим ученикам удалось найти решения для 45 различных чисел от 1 до 100.
Возможны все числа от 1 до 10. Итак, если вы хотите использовать это упражнение в качестве разминки в классе, вы можете предложить учащимся найти выражения для первых десяти чисел.
Решений становится очень мало после 50. Таким образом, вы можете также отредактировать задачу, чтобы найти только числа от 1 до 50.
Я знаю, что вы можете использовать функции пола и потолка, чтобы найти гораздо больше решений, но это подход всегда казался мне немного «обманом». Итак, я никогда не говорил своим ученикам о функциях пола и потолка как опции.
Мне не терпится узнать, сколько решений найдут ваши ученики!
2019 Challenge
Несмотря на то, что сейчас середина лета, я только сейчас начинаю вести блог о мероприятии, которое мы провели в январе. Да, это в значительной степени подводит итог тому, как продвигается блог в этом году. Я чувствую, что почти каждый пост начинается с извинения за то, что пост запоздал.
Да, это в значительной степени подводит итог тому, как продвигается блог в этом году. Я чувствую, что почти каждый пост начинается с извинения за то, что пост запоздал.
Итак, без лишних извинений, я хочу поделиться с вами Вызовом 2019 года. У нас еще есть несколько месяцев 2019 годаслева, так что я думаю, пост еще не слишком запоздал.
Начинать весенний семестр с задания, основанного на новом календарном году, стало традицией в моем классе. Давайте совершим небольшое путешествие по переулку памяти.
Вызов 2016 года
Вызов 2017 года
Вызов 2018 года
У меня были планы разместить Вызов 2019 года в качестве доски объявлений, прежде чем мы пошли на рождественские каникулы. Этого не произошло. Затем наш первый день после Рождества был отменен из-за гололеда.
Это означало, что наша обычная двухдневная неделя после возвращения во второй семестр стала однодневной. Я никак не мог начать новый контент в один день недели, поэтому я решил взять вызов 2019 года, который я планировал поставить как своего рода головоломку для тех, кто раньше финиширует, и превратить его в занятие для всего класса.
Примечание. Обычно я использую это как «Добро пожаловать в новый семестр!» деятельности, но вы могли бы так же легко использовать это как «Добро пожаловать в новый учебный год!» активность в августе/сентябре.
Если вы не знакомы с задачей, цель состоит в том, чтобы использовать цифры 2019 (2, 0, 1 и 9) ровно один раз каждую вместе с любым математическим символом или операцией по вашему выбору, чтобы создать выражения, эквивалентные числа от 1 до 100.
Я дал им список некоторых возможных математических операторов, чтобы заставить их мозги двигаться.
Мне нравится использовать это задание, чтобы познакомить учащихся с одним из моих любимых слов: конкатенация.
Конкатенация означает, что 2 и 0 можно объединить, чтобы получить число 20.
Мои ученики еще не познакомились с понятием факториала, поэтому я дал краткий урок о том, как он выглядит и что означает. Мы начали с попытки заполнить эту диаграмму.
Мы начали с того, что попытались заполнить эту таблицу всем классом на доске. Было интересно слышать, как развиваются теории студентов по мере раскрытия каждого нового ответа.
Было интересно слышать, как развиваются теории студентов по мере раскрытия каждого нового ответа.
Раньше я размещал задание, представлял его своим ученикам и позволял им заполнить как можно больше вариантов решения. По ходу первого дня задача становилась все более и более сложной, поскольку уже были заявлены более простые числа, которые можно было получить простым сложением и вычитанием с, возможно, небольшим добавлением умножения.
Мне нужно было заинтересовать шесть целых классов учеников, поэтому я решил, чтобы каждый класс начал задание с самого начала. Именно тогда мне пришла в голову идея вытащить свою диаграмму из 100 чисел, которую я купил в прошлом году на Amazon.
Затем я провел некоторое время с резаком для бумаги и картоном, чтобы вырезать набор квадратов разного цвета для каждой из шести групп, в которых расположены мои столы. Я сделал эти квадраты того же размера, что и 1 -100 карточек, которые вписываются в мою таблицу из 100 чисел.
Группы будут работать вместе, чтобы найти как можно больше выражений, равных числам от 1 до 100. Когда группа находит выражение для невостребованного числа, они предлагают свое решение, чтобы проверить его.
Когда группа находит выражение для невостребованного числа, они предлагают свое решение, чтобы проверить его.
Если бы это было правильно, они бы поместили один из своих квадратов карточек поверх числа, чтобы «заявить» его для своей команды.
К концу 50-минутного периода доска будет выглядеть примерно так:
В некотором смысле эта структура деятельности была лучше, чем мои доски объявлений прошлого. И это также оставляло желать лучшего. Позвольте мне попытаться отразить.
Приспособление к групповому соревнованию имело некоторые непредвиденные последствия.
Некоторые группы оказались НАМНОГО более гиперконкурентными, чем я ожидал.
В одной группе один из членов команды постоянно стоял рядом с таблицей из 100 чисел, чтобы, как только они вычислили число и проверили свое решение, они могли отметить его цветом для своей команды. Это означало, что этот студент вообще не занимался математикой, что не входило в мои намерения.
Я попытался бороться с этим, потребовав на другом уроке, чтобы только один человек из каждой группы мог покинуть свое место. Это решило предыдущую проблему, но создало другую.
Это решило предыдущую проблему, но создало другую.
Один учащийся из группы, как правило, проводил все время, поднося ответы к моему столу и проверяя их, прежде чем отмечать их числа в таблице. Это означало, что все еще был студент, который в основном вообще не занимался математикой.
Еще одним недостатком соревновательной командной природы этой деятельности было то, что некоторые группы, как правило, полностью сдавались, осознавая ТОЛЬКО то, насколько далеко они отстали от других команд.
Некоторые ученики начали играть в игры на своих телефонах вместо участия в мероприятии, потому что знали, что их группа НЕ выиграет.
Чтобы избежать этого в будущем, я могу предложить учащимся убрать карточки с таблицы после их решения и положить их в небольшую коробку или корзину для каждой команды.
Таким образом, каждый по-прежнему может видеть, какие числа остаются неразгаданными, но они не могут легко увидеть, насколько они впереди или позади других команд.
Мне очень понравился тот факт, что превращение этого занятия в групповое в конечном итоге привлекло гораздо больший процент моих учеников, чем мое предыдущее использование задания с досрочно закончившими.
Однако компромисс заключался в том, что мои ученики не обязательно учились друг у друга так много, как в прошлом. Это было связано с тем, что раньше учащиеся писали свои решения для каждого числа на доске объявлений.
Часто учащиеся брали решение для одного числа и в конечном итоге слегка изменяли его, чтобы получить другое число. Обычно это включает добавление символа факториала к 0 для получения 1 или чего-то подобного.
Часто учащиеся видели решение, написанное на доске, и задавали вопросы о нем, думая, что оно неверно. Это стало отличным обучающим моментом.
Если я сделаю это снова, я могу написать от 1 до 100 на доске, и пусть учащиеся напишут свои решения рядом с каждым числом в качестве шага в процессе. Это сохраняет соревновательный аспект, в то же время поощряя студентов учиться друг у друга. Это также легко стирается между занятиями.
Это также легко стирается между занятиями.
Мне нужно многое обдумать, прежде чем я решу, как мне поступить с Вызовом 2020 года. Меня больше всего беспокоит не структура действия, а то, что делать с тем фактом, что у нас есть только две двойки и два 0 для использования. Если у вас есть какие-либо идеи, я буду рад их услышать!
Я закончу этот довольно длинный и бессвязный пост в блоге одним из моих любимых решений проблемы 2019 года.
Вызов 2018
Завтра будет наш первый день возвращения. Сегодня профессиональный день, поэтому я не увижу своих учеников до пятницы. Я не совсем уверен, как я отношусь к тому, что у меня будет только один день в неделю с детьми, но я думаю, мы посмотрим, что из этого получится.
Я с нетерпением жду возможности начать одну из моих ежегодных традиций — Challenge 2018. Это ежегодное задание, в котором учащиеся должны использовать цифры даты текущего года, чтобы составить каждое число от одного до ста. Например, 28 + 10 = 38.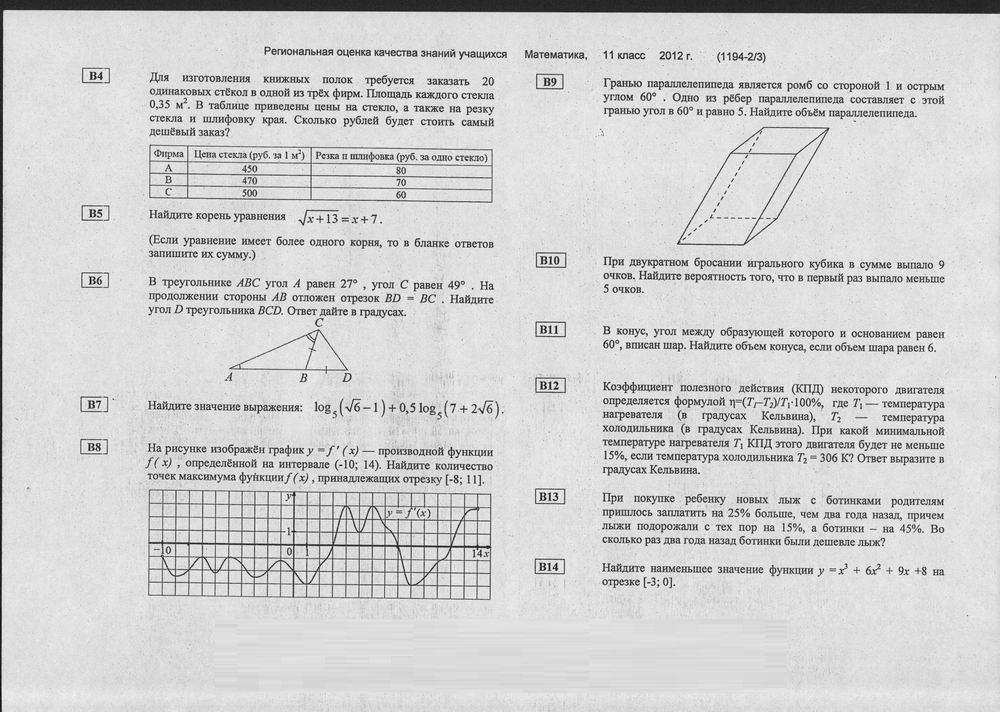 Или 28 + 1 + 0! = 30,
Или 28 + 1 + 0! = 30,
Вы можете прочитать о том, как я подходил к этому вызову в предыдущие годы, в моих постах о вызовах 2016 и 2017. Первоначально я узнал об этой задаче от Джереми Дентона, который узнал о задаче от мистера Коллинза.
Каждый год я распечатываю задание на картоне 11 x 17.
В прошлом году я использовал магниты, чтобы повесить задание на доску для сухого стирания.
Мой проектор умирает и ненадежен, поэтому моя доска для сухого стирания в данный момент занимает первое место в моем классе. Итак, я решил снова вернуться к использованию своей доски объявлений в этом году.
Я использовал свои обычные шаблоны 11 x 17, в которых есть пробелы для написания решения и имя человека, придумавшего решение, рядом с каждым числом. Мне просто нужно было обновить инструкции, чтобы сказать, что используйте цифры 2, 0, 1 и 8 вместо 2, 0, 1 и 7.
Я решил добавить визуальные напоминания о том, какие операции разрешены, чтобы оживить мою доску объявлений.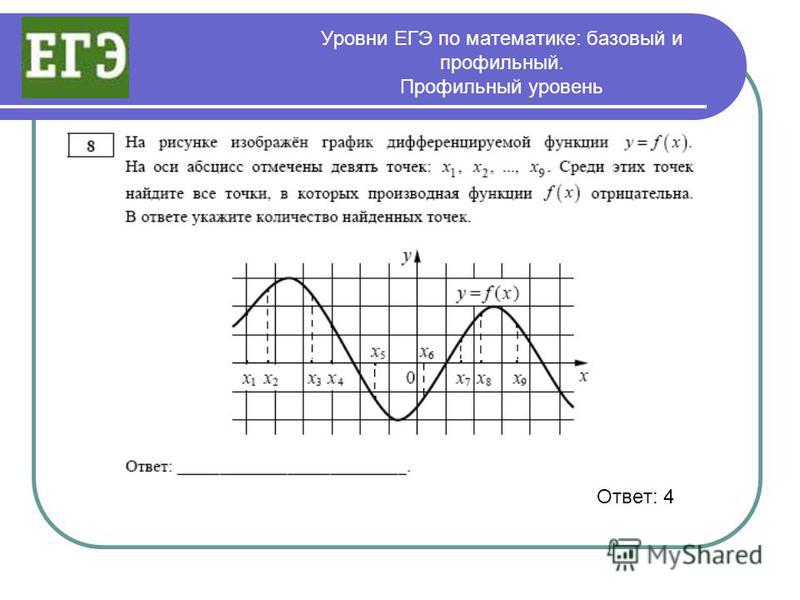 немного.
немного.
Вот подробная инструкция:
Хотите присоединиться к своим ученикам? Я загрузил файлы ниже. Они отформатированы для печати на картоне размером 11 x 17. Если у вас есть доступ только к бумаге формата Letter, вы можете распечатать их в стиле плаката через Adobe.
Нажмите «Плакат». Затем масштабируйте до 95% с перекрытием 0,001 дюйма. Это позволит вам распечатать весь комплект доски объявлений на бумаге формата Letter. У вас будет еще немного сборки!
С Новым 2018 годом!
Вызов на 2017 год
Я очень рад наступающему 2017 году, потому что это означает, что пришло время для нового ежегодного номера – «Вызова на 2017 год».
Я разработал шаблон для печати на карточках 11 x 17 – моей идеальной бумаге для изготовления классных плакатов и дисплеев!
В прошлом году я разместил эту доску объявлений для конкурса 2016 года:
Я отредактировал файлы для 2017 года вместо 2016 года. Я также изменил шрифт на свою нынешнюю навязчивую идею Wellfleet!
Для каждого целого числа от 1 до 100 включительно учащимся предоставляется место для записи решения. Справа также есть место, где учащиеся могут написать свое имя, чтобы показать, кто нашел решение.
Справа также есть место, где учащиеся могут написать свое имя, чтобы показать, кто нашел решение.
ВСЕ решения должны быть проверены мной перед добавлением на плакаты!
Последняя страница файла содержит инструкции. Учащихся просят составить каждое целое число от 1 до 100, используя только цифры 2017 года. Повторение цифр не допускается. Студенты могут использовать любой математический символ или операцию.
Что мне нравится в этом задании, так это то, что оно побуждает учащихся узнавать о факториалах, с которыми они вообще не сталкивались.
В прошлом году было интересно наблюдать за тем, как учащиеся справляются с этой задачей. Мы не доделали его в прошлом году, но не всегда удается найти решения для каждого числа. Количество возможных решений зависит от года!
Задание на 2016 год
Я рад представить своим ученикам ежегодное числовое задание, основанное на цифрах 2016 года. Вы можете подыграть цифрам года, в котором живете в настоящее время, если будете читать это в будущем.
Новый семестр означает новые изменения в моем классе. Скажем так, это изменение взволновало некоторых моих учеников, а некоторых раздражало. В восторге от нового вызова. Раздражает, что липкой доски больше нет.
После того, как в течение семестра студенты приклеивали стикеры (со своим именем) на доску каждый раз, когда они впервые набирали высший балл в викторине, у меня была доска объявлений с КУЧЕЙ стикеров.
Что хорошего в помощниках? Я не должен был снимать все это сам!!!
Так что же вместо него?
Вызов 2016 года. Потому что это… ну вы знаете… 2016 год. Цель состоит в том, чтобы учащиеся составили числа от 1 до 100, используя только цифры 2, 0, 1 и 6. Учащиеся могут складывать/вычитать/умножать/делить, использовать круглые скобки, возведения в степень, факториалы, квадратные корни и т. д. желания.
Впервые я узнал о вызове от Джереми Дентона в Твиттере:
Комментарий к этому твиту привел меня к этому сообщению в блоге г-на Коллинза о вызове 2015 года.
Мне, конечно, пришлось напечатать свою версию, чтобы она поместилась на бумаге американского размера. Некоторое время назад моя мама купила мне пачку карточек 11 x 17, которые я хорошо применил в классе.
Я решил, что напечатав задание на этой большой бумаге, я спасу свой рассудок, когда дело дойдет до того, чтобы его повесить.
Вот как в итоге выглядела доска объявлений Challenge 2016:
У каждого числа есть место для записи уравнения и место для ученика, который нашел решение, чтобы подписать свое имя.
Вот инструкции для испытания номера года. Создайте каждое число, используя цифры 2, 0, 1 и 6 (или цифры текущего года, если вы читаете это из будущего). Повторение цифр не допускается. Вы можете использовать любой математический символ или операцию. Совет: 0! = 1,
Итак, прошел один день. И я очень впечатлен ответом, который я получил от своих детей. Скажем так, я не привыкла к тому, что дети, толпящиеся вокруг моих досок объявлений со своими калькуляторами, ведут бурные дискуссии. Я мог бы привыкнуть к этому!
Я мог бы привыкнуть к этому!
Вот результаты на данный момент:
Первая страница почти полностью заполнена. Остальным страницам еще предстоит заполниться. Но это хорошо. Я знаю, что с этого момента прогресс будет НАМНОГО медленнее.
Решения головоломок
Я намеренно не делаю ответы на печатные математические головоломки, которыми я делюсь в своем блоге, доступными в Интернете, потому что я стремлюсь предоставить своим ученикам опыт обучения, который не может использовать Google. Я хотел бы, чтобы другие учителя могли использовать эти головоломки в своих классах, а решения не были бы легко найдены в Интернете.
Однако я понимаю, что мы, учителя, занятые люди, и иногда нам нужно быстро обратиться к ключу ответа, чтобы увидеть, правильно ли ученик решил головоломку или правильно ли он интерпретировал инструкции.
Если вы учитель, который использует эти головоломки в своем классе, пришлите мне электронное письмо по адресу sarah@mathequalslove. net с информацией о том, чему вы учите и где вы учите. Я буду рад направить вам ключ ответа.
net с информацией о том, чему вы учите и где вы учите. Я буду рад направить вам ключ ответа.
Другие задачи и головоломки на основе чисел
Не пора ли отвлечься от математики?
Два года назад Джули Уорд, координатор программы по математике в государственных школах Кембриджа в штате Массачусетс, взглянула на результаты тестов восьмиклассников округа за предыдущий учебный год: 70 процентов белых учащихся сдали государственные тесты по математике, хотя только 10 процентов чернокожих студентов имели. Углубившись в данные, она обнаружила, что цифры были частью закономерности, неизменной из года в год.
Сотрудники Кембриджа начали пытаться понять, почему существуют такие расовые различия в успеваемости по математике, вспоминает Мануэль Фернандес, директор старшей школы на Кембридж-стрит, который говорит, что он и его сотрудники заметили сильную корреляцию с тем, как ученики были распределены по математическим курсам. .
«Со временем вы получите математические курсы более низкого уровня, заполненные чернокожими и латиноамериканскими детьми, и математические курсы высокого уровня с белыми и азиатскими детьми», — сказал он. «Студенты усваивают это — они считают, что умные дети — это белые дети. Наши сотрудники сказали, что мы не можем продолжать разделять наших студентов таким образом».
«Студенты усваивают это — они считают, что умные дети — это белые дети. Наши сотрудники сказали, что мы не можем продолжать разделять наших студентов таким образом».
Отслеживание — практика разделения учащихся по воспринимаемым способностям на разные классы — особенно широко распространена и вызывает споры в математике. По данным Brookings Institution, только на уроках математики в восьмом классе 75% американских школьников посещают классы, основанные на способностях, что делает математику наиболее популярным курсом в школах. Решения об отслеживании варьируются от школы к школе, но обычно основаны на результатах тестов и оценках, а также на рекомендациях учителей, которые, как показывают некоторые исследования, могут быть предвзятыми.
Учащиеся усваивают это: они считают, что умные дети — это белые дети. Наши сотрудники сказали, что мы не можем продолжать разделять наших студентов таким образом.
За последние несколько лет школы и округа по всей стране, в том числе в Кембридже, Сан-Франциско и Эскондидо, штат Калифорния, отказались от отслеживания математики, признав, что эта практика может привести к неравенству между учащимися со значительными последствиями по мере их прогресса. через школу. Учащиеся младших классов получают менее строгую и насыщенную учебную программу по математике, что со временем может повлиять на их математические знания. Отслеживание также может помешать долгосрочным достижениям учащихся: алгебра I — это начальный курс, который учащиеся должны пройти, чтобы поступить в старшие классы средней школы и колледжа по математике, а во многих случаях — вообще продолжить учебу в колледже, особенно в местных колледжах. .
через школу. Учащиеся младших классов получают менее строгую и насыщенную учебную программу по математике, что со временем может повлиять на их математические знания. Отслеживание также может помешать долгосрочным достижениям учащихся: алгебра I — это начальный курс, который учащиеся должны пройти, чтобы поступить в старшие классы средней школы и колледжа по математике, а во многих случаях — вообще продолжить учебу в колледже, особенно в местных колледжах. .
Исследования показывают, что отслеживание математики также не является эффективной практикой для повышения успеваемости учащихся. Метаанализ 2016 года почти 100-летнего исследования показал, что группировка между классами или отслеживание не приносят пользы учащимся ни с высокими, ни с низкими показателями успеваемости, хотя полное повышение успеваемости может привести к тому, что уже хорошо успевающие учащиеся превзойдут академические успехи. сверстники того же возраста. Кроме того, дети четко осознают, какое место они занимают в контролируемых классах, и определяют себя как «умных» или «неумных» в зависимости от их положения — убеждения, которые могут остаться с ними на всю жизнь, согласно многочисленным исследованиям.
Напротив, классы, в которых учащиеся объединены в группы со смешанными способностями, а учителя воспитывают в себе установку на рост, могут иметь противоположный эффект. Исследования показывают, что учащиеся в округах, которые отказались от учебы и возлагают большие надежды на всех учащихся, набрали более высокие баллы по тестам штата. Эти округа также помогли сотрудникам и учащимся усвоить установку на рост и идею о том, что все учащиеся могут учиться и совершенствоваться.
Предоставление доступа всем учащимся
Еще пять лет назад учащиеся восьмого класса в округе Сан-Франциско, где проживает 56 000 учащихся, обычно распределялись по алгебре I или общей математике восьмого класса в зависимости от оценок и рекомендаций учителя. С 2008 по 2010 год почти 80 процентов чернокожих и латиноамериканских учащихся были переведены на курс общей математики, а 55 процентов азиатских и белых восьмиклассников были помещены на курс алгебры I более высокого уровня. Из чернокожих и латиноамериканцев, изучающих алгебру I, более половины должны были повторить курс.
К старшей школе цифры не улучшились: среди выпускников средней школы 2014 года менее 25 процентов всех учащихся владели алгеброй II, но результаты были еще хуже для чернокожих и латиноамериканских учащихся, всего 5 процентов которые были опытными.
Системы слежения за математикой, такие как старая система Сан-Франциско, неэффективны отчасти потому, что только некоторые учащиеся имеют доступ к контенту, который им необходим для роста в качестве изучающих математику, а другие нет, согласно заявлению Национального совета учителей математики. NCTM указывает на низкие национальные баллы по математике на протяжении десятилетий, необходимость дополнительной математики в колледже для 50 процентов студентов и плохую успеваемость американских студентов на международных тестах по математической грамотности как свидетельство того, что нынешняя практика подрывает доступ студентов к обучению.
©Twenty20/Wandeaw
При поддержке учителей и руководителей школ округ Сан-Франциско отменил отслеживание по математике в восьмом классе в 2014–15 учебном году и вместо этого обязал всех учащихся сдавать алгебру I в девятом классе. Результаты были поразительны: количество повторных экзаменов по алгебре I упало для всех расовых и этнических групп в среднем с 40 до 10 процентов, включая учащихся, изучающих английский язык, и учащихся из малообеспеченных семей. Для чернокожих учащихся процент повторения снизился с 52 процентов до 19 процентов.процентов, а для латиноамериканских студентов — с 57 до 14 процентов. В то же время чернокожие и латиноамериканские учащиеся зачисляются на продвинутые математические курсы средней школы по более высоким ставкам.
Результаты были поразительны: количество повторных экзаменов по алгебре I упало для всех расовых и этнических групп в среднем с 40 до 10 процентов, включая учащихся, изучающих английский язык, и учащихся из малообеспеченных семей. Для чернокожих учащихся процент повторения снизился с 52 процентов до 19 процентов.процентов, а для латиноамериканских студентов — с 57 до 14 процентов. В то же время чернокожие и латиноамериканские учащиеся зачисляются на продвинутые математические курсы средней школы по более высоким ставкам.
«В Сан-Франциско была сильная команда тренеров по математике и лидеров, которые знали, что им говорят исследования, и решили взяться за это», — сказала Джо Боалер, профессор математического образования Стэнфордского университета и исследователь, работавшая с округом. «Что изменилось, так это сообщения, которые получают дети — им больше не говорят, что у них фиксированный мозг».
Точно так же на Кембридж-стрит, где в прошлом году отменили математику в восьмом классе, вдвое больше учеников сдали общий экзамен по математике, а 95 процентов заявили, что хотят изучать математику с отличием в старшей школе. В следующем году все восьмые классы округа откажутся от математики. «Речь шла о предоставлении всем учащимся доступа к ускоренному учебному плану», — говорит учитель математики восьмого класса с Кембридж-стрит Кендал Шварц.
В следующем году все восьмые классы округа откажутся от математики. «Речь шла о предоставлении всем учащимся доступа к ускоренному учебному плану», — говорит учитель математики восьмого класса с Кембридж-стрит Кендал Шварц.
Содействие развитию мышления — для учителей
Однако система отслеживания влияет гораздо больше, чем на размещение учащихся, и может укреплять устоявшиеся — и ошибочные — представления о математических способностях учащихся.
В большей степени, чем другие предметы, математика может быть камнем преткновения для родителей и педагогов, многие из которых считают, что ученик либо усваивает материал (является «математиком»), либо нет. Тем не менее, в традиционных классах, где делается упор на скорость выполнения механических задач, учащиеся, которые «понимают это», часто являются теми, кто больше практикуется или просто хорошо запоминает.
Педагоги часто могут подкрепить эти предположения. Исследования показали, что белые учителя, как правило, меньше ожидают от чернокожих учеников, чем белые, и что чернокожие учащиеся с меньшей вероятностью будут рекомендованы для одаренных или продвинутых математических классов, чем белые учащиеся, даже чернокожими учителями, что может повлиять на размещение в системе отслеживания.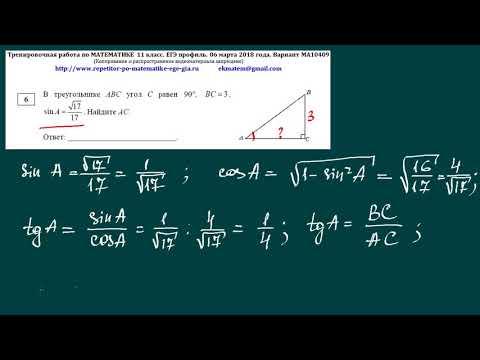 система на основе.
система на основе.
Эти решения о распределении по математике могут оказать значительное влияние на то, как учащиеся видят себя и успевают по математике. Дети, особенно в средней школе, усваивают свое место на уроках математики, а те, кто считает себя плохо успевающими, склонны отделяться и поддаваться воспринимаемому образу или стереотипу своей группы.
@Twenty20/JosiEpic
«Математика — это одно из мест, где мы помогаем вам понять, хорошо вы в ней разбираетесь или нет», — говорит Лиззи Халл Барнс, руководитель отдела математики округа Сан-Франциско. «Статус в классе очень важен для того, как он проявляется в математике».
Но математический склад ума не обязательно должен оставаться неизменным ни у преподавателей, ни у учащихся. В одном из исследований стэнфордского исследователя Дэйва Паунеску студенты, получившие сообщение с установкой на рост — о том, что их интеллект может расти с практикой, — освоили новые математические концепции с большей готовностью, чем студенты, получившие общее поощрение. Хотя переход к установке на рост может показаться расплывчатым, конкретные стратегии, такие как работа учащихся в разнородных группах и визуальное представление их мышления, а также подчеркивание того, что «никто не хорош во всех способах работы, но каждый хорош в некоторых из них», может помочь.
Хотя переход к установке на рост может показаться расплывчатым, конкретные стратегии, такие как работа учащихся в разнородных группах и визуальное представление их мышления, а также подчеркивание того, что «никто не хорош во всех способах работы, но каждый хорош в некоторых из них», может помочь.
Например, в Кембриджских классах, которые недавно перестали ориентироваться, сосредоточение внимания на решении проблем и групповой работе над сложными задачами помогло укрепить уверенность среди учащихся с разным уровнем способностей, говорит учитель математики седьмого класса Стивен Абреу. «У нас меньше студентов, ожидающих, пока «умный ребенок» ответит на вопрос, и больше разных типов учащихся, которые делятся тем, что они замечают», — сказал Абреу.
Получение согласия
Округа и школы не могут просто отвлечься и предполагать, что за ними последуют отличные результаты. Округи, которые успешно отказались от отслеживания, должны были работать как с педагогами, так и с родителями, чтобы адаптироваться к новой системе, особенно в отношении статуса и предполагаемых преимуществ отслеживания с семьями и учащимися.
Округи и школы, которые отвлекают скептиков, объясняя преимущества всем учащимся и доказывая это результатами, по словам Аби Лиф, специалиста по математике школьного округа Эскондидо Юнион в Южной Калифорнии, перешедшего на смешанный, не- отслеживал уроки математики для девятых и десятых классов в 2013 году. Эскондидо отвлекся, когда появились Единые базовые государственные стандарты, поэтому это было частью более широких разговоров о том, как соответствовать стандартам, сказал Лиф, добавив, что учителя подчеркивают, что «все дети умны, у всех людей в классе есть что предложить, и делать это быстрее — не всегда лучше».
Это дает взрослым новый опыт математики, и они строят представление о том, что возможно.
Ее округ также обеспечил значительный уровень профессионального развития педагогов, включая поддержку со стороны внешних консультантов, и призвал учителей сотрудничать в небольших группах, чтобы помочь изменить отношение педагогов к математике.

 08.2021 года.
08.2021 года.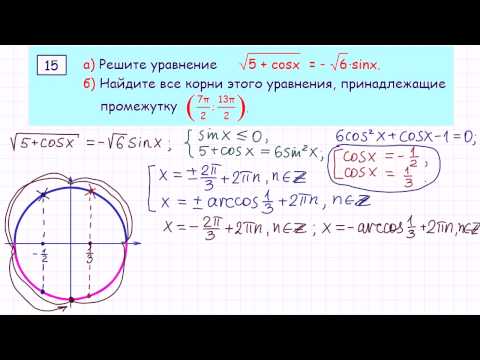 Кировска
Кировска 09.2018
09.2018 0 или 2.2.
0 или 2.2. ]
]
Leave A Comment