Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
помогите плиз , решить задачу!!! в первой связке на 56 шаров больше, чем во второй. сколько шаров в каждой связке, если во второй связке в 5 раз меньше шаров, чем в первой?
сколько шаров в каждой связке, если во второй связке в 5 раз меньше шаров, чем в первой?
Саша, Юра и Олег вместе сделали для новогодних гирлянд 48 бумажных фонариков. Олег сделал 12 фонариков. Сколько фонариков сделал Саша, если он сделал на 6 фонариков меньше, чем Юра?
5 класс Жучка тяжелее кошки в 3 раза, мышка легче кошки в 10 раз, репка тяжелее мышки в 60 раз. Во сколько раз репка тяжелее Жучки? Ответ Обоснуйте Помогите пожалуйста
При посеве подсолнуха на 1000м2 расходуют 1кг семян. Хватит ли 500гр семян, чтобы засеять участок прямоугольной формы длиной 80м и шириной 6м при такой же норме расхода
Полый алюминиевый куб с ребром…
Пользуйтесь нашим приложением
Информатика — B15 Математика
B15.1 B15.2 B15.3 B15.4 B15.5 B15. 6 B15.7 B15.8 B15.9 B15.10
6 B15.7 B15.8 B15.9 B15.10
B15.11 B15.12 B15.13 B15.14 B15.15 B15.16 B15.17 B15.18 B15.19 B15.20
B15.21 B15.22 B15.23 B15.24 B15.25 B15.26 B15.27 B15.28 B15.29 B15.30
B15.31
Справочные материалы от Д. Гущина
№1
Центральный угол на 36∘ больше острого вписанного угла, опирающегося на ту же дугу окружности.
Найдите вписанный угол. Ответ дайте в градусах.
Ответ дайте в градусах.
Решение
Пусть вписанный ∠ AСB=x, тогда центральный ∠AOB=2x (т.к. вписанный угол равен половине центрального угла, опирающиеся а одну дугу)
|∠ACB-∠AOB|=|x-2x|=x=36
Ответ 36
№2
Диагонали ромба равны 16 и 30. Найдите длину стороны ромба.
Решение
Найдем сторону по теореме Пифагора.
первая диагональ -\(\) вторая-\(\)
\(\)
=>a=17
Ответ 17
№3
В треугольнике ABC угол C равен 90°, cosB=\(\). AB=29. Найдите AC.
Решение
\(\)
\(\)
sinB=\(\)
AC=AB*sinB=21
Ответ 21
№4
В треугольнике ABC угол C равен 90°, tgA=\(\)
Найдите sin A.
Решение
tgA=\(\)=>CB=3x AB=4x
По теореме Пифагора
AC=\(\)=5x
=>sinA=\(\)
Ответ 0,6
№5
В прямоугольном треугольнике гипотенуза равна 5, синус одного из острых углов равен \(\).
Найдите прилежащий к этому углу катет.
Решение
см №3
Ответ 1,4
№6
В прямоугольном треугольнике АВС катеты равны 15 и 6. Найдите тангенс острого угла при большем катете.
Решение
Тангенс при меньшем угле-меньше.
\(\)
Ответ 0,4
№7
Найдите косинус острого угла равнобедренной трапеции, основания которой равны 37 и 49, а боковые стороны — 15.
Решение
построим высоту равнобедренной трапеции BH. Получим прямоугольный треугольник ABH.
Гипотенуза треугольника- боковая сторона трапеции (AB)
малый катет равен полуразности оснований трапеции AH=(AD-BC):2=(49-37):2=6
=> \(\)
Ответ 0,4
№8
В треугольнике угол при одной из вершин равен 46°, внешний угол при другой вершине равен 127°
Найдите третий угол. Ответ дайте в градусах.
Ответ дайте в градусах.
Решение
треугольник угол А, угол B и угол C
угол A=46
угол B=180-127 (тк внешний =127)
угол C=180-A-B=180-46-180+127=127-46=81
Ответ: 81
№9
В треугольнике ABC угол C равен 90∘, sinA=\(\), AC=\(\). Найдите AB.
Решение
см №3
Ответ 28
№10
В треугольнике ABC угол A равен 90∘, tgB=\(\), AC=5. Найдите BC.
Решение
см №4
Ответ 10
№11
В треугольнике ABC угол C равен 90∘, tgA=\(\), BC=4. Найдите AB.
Решение
см №4
Ответ 12
№12
В треугольнике ABC угол C равен 90∘, AC=3, sinA=\(\). Найдите BC.
Решение
см №3
Ответ 2,25
№13
В треугольнике ABC угол C равен 90∘, AB=40, AC=\(\). Найдите sinA.
Найдите sinA.
Решение
\(\)
\(\) тк a+b=\(\)
=> \(\)
Ответ 0,7
№14
В треугольнике ABC угол C равен 90∘, cosA=\(\). Найдите tgA
Решение
см №4
Ответ 2
№15
Два угла треугольника равны 74∘ и 41∘. Найдите угол (острый), который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах.
Решение
Ответ 65
№16
В треугольнике ABC угол C равен 90∘, AB=14,AC=\(\). Найдите sinA.
Решение
см №4
Ответ 0,5
№17
В треугольнике ABC AB=BC, AC=24, cos∠C=\(\). Найти высоту BH.
Решение
Треугольник ABC-равнобедренный, следовательно высота BH проведенная к основанию треугольника является также медианой.
=>CH=AH=AC:2=12
\(\) => треугольник HBC-египетский =>BH=\(\)12=4*4=16
Ответ 16
№18
Прямые, содержащие высоту CH и биссектрису AD треугольника ABC, пересекаются в точке O, ∠BAD=63∘. Найдите угол OAC. Ответ дайте в градусах.
Решение
Отметим, что угол BAC = 2*(угол BAD) = 2*\(\) = \(\) — то есть это тупой угол. Поэтому чертеж выглядит так, как изображено на рисунке.
угол OAC=угол HAO+угол HAC
угол BAD=углу HAO=\(\) (вертикальные)
угол HAC=\(\)-угол СAB=\(\)
OAC=63+54=\(\)
Ответ 117
№19
Основания равнобедренной трапеции равны 78 и 60. Тангенс острого угла равен \(\). Найдите высоту трапеции.
Решение
см №4, №7
Ответ 2
№20
В равнобедренном треугольнике ABC угол при вершине C равен 30∘, а боковые стороны AC=BC=72.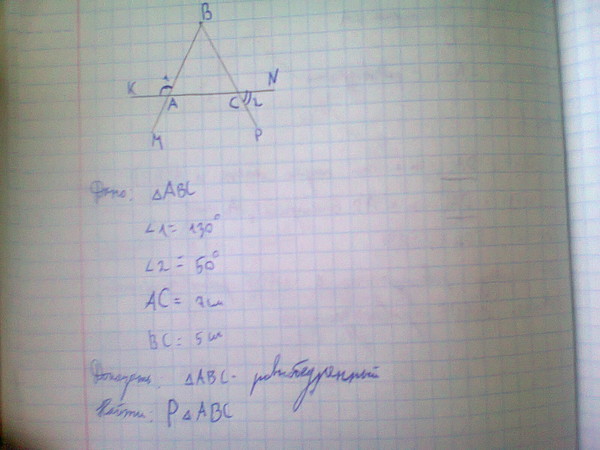 Найдите высоту AH.
Найдите высоту AH.
Решение
Ответ 36
№21
Хорда AB делит окружность на две части, градусные величины которых относятся как 13 к 59. Под каким углом видна эта хорда из точки C, если она принадлежит меньшей дуге окружности? Ответ дайте в градусах.
Решение
Ответ 147,5
№22
Вокруг четырехугольника ABCD можно описать окружность. Найдите угол CAD, если ∠ABC=50∘и ∠ABD=33∘. Ответ дайте в градусах.
Решение
Ответ 17
№23
В параллелограмме ABCD cos∠BAD=\(\) . Найдите sin∠ADC.
Решение ∠ ADC = 180° — ∠ BAD. Следовательно, sin ∠ ADC = sin∠ BAD = √(1- cos² ∠ BAD) = √(1-624/625) = √(1/625) = 1/25.
Ответ 1/25 = 0,04
№24
Найдите медиану треугольника ABC, проведенную из вершины B, если AB=AC=\(\), BC=\(\).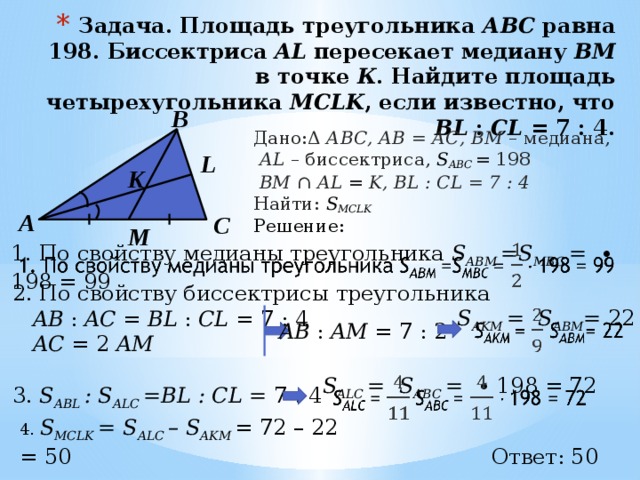
Решение
Ответ 3
№25
В треугольнике ABC отрезок AD — биссектриса угла A, угол C равен 24∘, угол CAD равен 29∘. Найдите угол B. Ответ дайте в градусах.
Решение
Ответ 98
№26
В прямоугольном треугольнике ABC с прямым углом C, гипотенуза AB равна \(\), а sinA=0,2. Найдите длину высоты CH.
Решение
Ответ 9,6
№27
Биссектрисы углов B и C параллелограмма ABCD пересекаются на стороне AD в точке E. Сторона AB равна 2. Найдите BC.
Решение
Ответ 4
№28
В прямоугольном треугольнике ABC с прямым углом C, тангенс внешнего угла при вершине A равен \(\) , сторона BC равна 3. Найдите сторону AB.
Решение
см №8, потом №4
Ответ 7
№29
Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 36∘? Ответ дайте в градусах.
Решение
Сумма противолежащих углов равнобедренной трапеции равна \(\)
Пусть ∠A=x∘=> ∠C=\(\)
∠A+∠C=2x+36=180
2x=180-36=144
x=72=> больший угол C=x+36=72+36=108
Ответ 108
№30
Биссектриса тупого угла D параллелограмма ABCD делит сторону AB в отношении 5 к 8, считая от вершины A. Найдите большую сторону параллелограмма, если его периметр равен 18.
Решение
Пусть K– точка пересечения биссектрисы DKи отрезка AB (см. рисунок).
1. Углы KDCи DKA равны (накрест лежащие углы при DC || AB и секущей DK. Углы KDCи KDAравны, так как KD– биссектриса. Значит углы DKA и KDA тоже равны.
2. В треугольнике DKAуглы при основании DKравны (см. п.1). Значит, этот треугольник равнобедренный и DA = AK.
3. Обозначим длину стороны DA (меньшей из сторон) через x; длину стороны ABчерез y. По доказанному (см. п.2) AK = AG = x. Следовательно, KB = y-xи по условию задачи получаем:
По доказанному (см. п.2) AK = AG = x. Следовательно, KB = y-xи по условию задачи получаем:
x: (y-x) = 5 : 8 (1)
Так как, периметр параллелограмма равен 18, получаем:
2*(x+y) = 18 (2)
4. Решаем систему (1) — (2). Из (1) :
8*x = 5*(y-x)
8x = 5y– 5x
5y = 13x
y= (13/5)*x (3)
Подставляем из (3) в (2)
2 * (x+ (13/5)*x) = 18
(18/5)*x = 9
x= 2,5
Из (3) находим: y = (13/5)*2,5 = 13/2 = 6,5
Ответ 6,5
№31
Сторона AB тупоугольного треугольника ABC в \(\) раз больше радиуса описанной около него окружности. Найдите угол C . Ответ дайте в градусах.
Решение
Ответ
В треугольнике ABC угол B равен 20, а угол C равен 40, длина биссектрисы угла A равна 2.
 Какова величина BC — AB?
Какова величина BC — AB?Геометрические треугольники
Дев С.
спросил 10.03.17В треугольнике ABC угол B равен 20, а угол C равен 40. При этом длина биссектрисы угла A равна 2. Какова величина BC — AB?
Подписаться І 2
Подробнее
Отчет
2 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Наталья Л. ответил 17.03.23
Репетитор
5 (2)
Экспертное репетиторство по математике — тесты, математические соревнования, планирование колледжа
Об этом репетиторе ›
Об этом репетиторе ›
Это задача «Кенгуру по математике» для 7-8 классов.
Продлите сторону CA за точку A, пока она не станет равной CB, назовите эту точку B’, таким образом, BC=B’C и треугольник CBB’ равнобедренный. угол CB’B равен 80.
Пусть D основание биссектрисы угла из вершины A. Найдите все углы. Обратите внимание, что треугольник ADB и треугольник AB’B равны по ASA, сторона AB является общей. Таким образом, AB’ (что равно BC-AB) = AD =2.
Голосовать за 0 голос против
Отчет
Исаак С. ответил 10.03.17
Репетитор
4.9 (757)
Репетитор по физике, химии, математике и компьютерному программированию
Об этом репетиторе ›
Об этом репетиторе ›
Чтобы решить эту задачу, нужно найти длины BC и AB и затем вычесть их.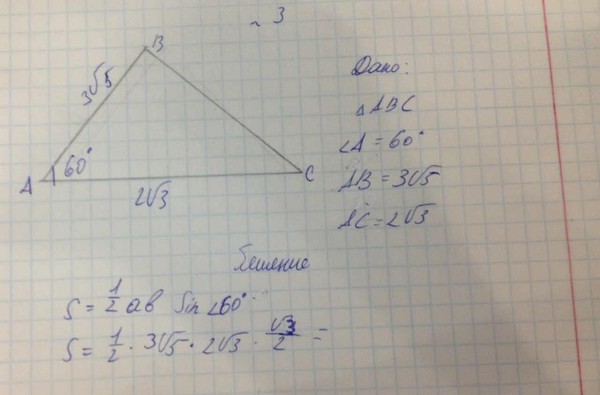
Во-первых, угол в точке А равен 120 градусов, так как три заданных угла должны быть равны 180 градусам.
Обозначим биссектрису AP, где P — точка окончания на BC. Тогда биссектриса делит треугольник ABC на два треугольника. В треугольнике ABP закон синусов можно использовать для решения для AB. Угол в точке P равен 100 градусам, потому что угол в точке A равен 60 (половина от 120), а угол в точке B равен 20 (данные).
Итак, sin 20/2 = sin 100/AB => AB = 2*sin 100/sin 20 = 5,759
Теперь мы можем использовать закон синусов треугольника ABC, чтобы найти BC sin 120/BC = sin 40/AB => BC = 5,759 * sin 120/sin 40 = 7,759. ВС — АВ = 7,759 — 5,759 = 2,000
Голосовать за 0 голос против
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.
Задайте вопрос бесплатно
Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.
ИЛИ
Найдите онлайн-репетитора сейчас
Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.
Свойства треугольника | mathtestpreparation.com
вернуться к Геометрия
Прямоугольный треугольник
Прямоугольный треугольник — это треугольник, внутри которого есть прямой угол.
Равнобедренный прямоугольный треугольник
Равнобедренный прямоугольный треугольник — это треугольник, в котором две стороны равны по размеру.
В треугольнике ABC, если AC = BC и угол C = 90 o , то треугольник ABC является равнобедренным прямоугольным треугольником.
Теорема о биссектрисе угла
Свойство биссектрисы угла состоит в том, что расстояния от точки биссектрисы угла до обеих сторон треугольника равны.
На рисунке выше AD — это биссектриса угла, которая делит угол A пополам. P — точка, лежащая на AD. Тогда PE = PF. То есть, если точка P лежит на биссектрисе угла AD, то PE = PF
Свойство равнобедренного треугольника
У равнобедренного треугольника два угла при основании равны.
В треугольнике ABC, если AB = AC, то треугольник ABC равнобедренный. В треугольнике ABC AB напротив угла C и AC напротив угла B. Если AB = AC, то угол C = угол B. То есть, если AB = AC, то угол B = угол C.
Свойство биссектрисы равнобедренного треугольника
Биссектриса угла при вершине равнобедренного треугольника делит его основание пополам и перпендикулярна его основанию.
В треугольнике ABC, если AB = AC, то треугольник ABC равнобедренный. Если AD — биссектриса угла, то угол 1 = углу 2. Если AB = AC и угол 1 = углу 2, то BD = DC и AD перпендикулярен BC.
Свойство внутренних углов равностороннего треугольника
Если треугольник равносторонний, то каждый из внутренних углов равен 60 градусам
В треугольнике ABC, если AB = BC = AC, то угол A = угол B = угол C = 60 o
Определение равнобедренного треугольника
Если два угла треугольника равны, то стороны, противолежащие этим углам также равны.
В треугольнике ABC, если угол B = углу C, то AB = AC. Тогда треугольник ABC равнобедренный. В треугольнике равные углы противолежащие равным сторонам.
Определить равносторонний треугольник
Если три угла треугольника равны, то треугольник является равносторонним.
В треугольнике ABC, если угол A = угол B = угол C, то AB = BC = AC. Тогда треугольник ABC равнобедренный.
Определить равносторонний треугольник
Если угол равнобедренного треугольника равен 60 градусов, то треугольник равносторонний.
Если треугольник ABC равнобедренный и угол A или угол B или угол C = 60 o , то треугольник ABC равнобедренный.
Неравенства относительно сторон и углов в теореме треугольника
Если две стороны треугольника неравны, то неравны и углы, противолежащие этим сторонам, и больший угол, противолежащий большей стороне.
В треугольнике ABC, если AC > AB, то угол B > угол C. В треугольнике ABC AC напротив угла B и AB напротив угла C.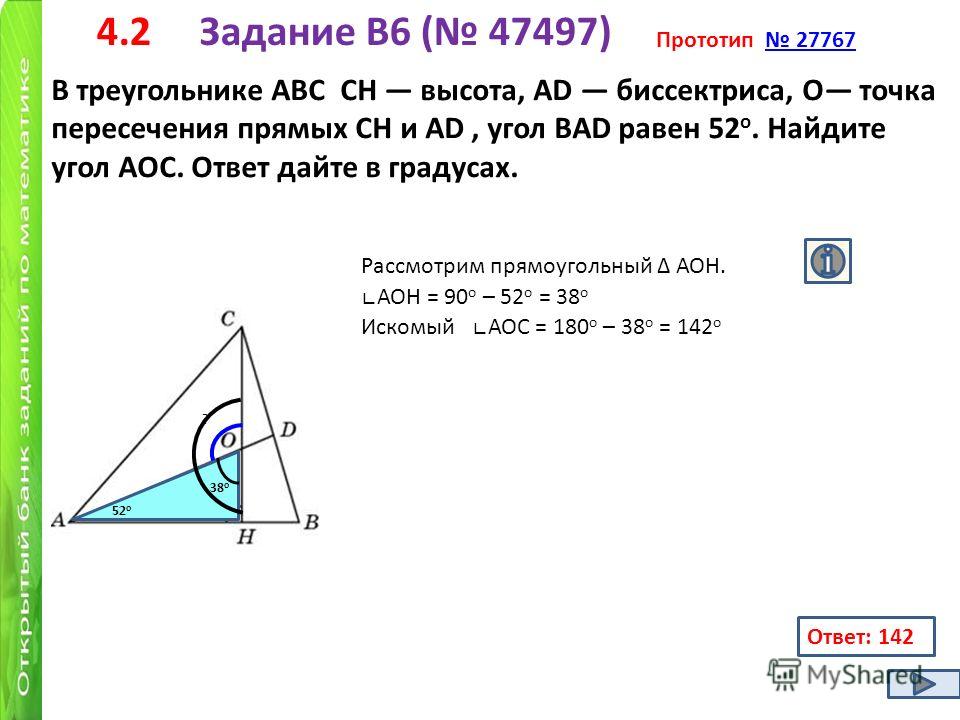 В треугольнике большая сторона противоположна большему углу.
В треугольнике большая сторона противоположна большему углу.
Неравенства относительно сторон и углов в треугольнике
Если два угла треугольника неравны, то неравны и стороны, противолежащие этим углам, и более длинные стороны, противоположные большему углу.
В треугольнике ABC, если угол B больше угла C, то AC больше угла AB. Примечание: угол B против AC и угол C против AB. В треугольнике против большей стороны лежит больший угол.
Биссектриса отрезка
Если прямая перпендикулярна отрезку и пересекает отрезок в его середине, то эта прямая называется биссектрисой отрезка.
На рисунке выше линия l перпендикулярна отрезку AB. АО = БО. Прямая l является серединным перпендикуляром к AB.
Свойство биссектрисы отрезка
Расстояние от точки биссектрисы отрезка до двух концов отрезка равно.
На рисунке выше, если прямая l является серединным перпендикуляром к AB, а точка P лежит на прямой l, то PA = PB.
Обратная теорема о биссектрисе отрезка
Если расстояния от точки до двух концов отрезка равны, то точка лежит на серединном перпендикуляре к отрезку.
На рисунке выше, если PA = PB. тогда точка P лежит на серединном перпендикуляре к AB.
Пример 1
На приведенном выше рисунке, если AB = AC и градусная мера угла A равна 98 o , какова градусная мера угла 1?
- Раствор
- Так как AB = AC (Дано), то треугольник ABC равнобедренный.
- угол B = угол ACB = (180 o — угол A)/2 = (180 о — 98 о )/2 = 41 о
- Так как угол 1 является внешним углом треугольника ABC, то
- угол 1 = угол B + угол A = 41 o + 98 o = 139 o
Пример 2
На рисунке ниже, если градусная мера угла A равна 70 o , а градусная мера угла C равна 50 o , найдите соотношение между AB и AC.
- Решение
- В треугольнике ABC угол B = 180 o — (угол A + угол C) = 180 o — (70 + 50 o ) = 180 o — 120 o = 120 o 5
- Так как угол B = 60 o и угол A = 50 o
- , поэтому AC > AB
- примечание: угол B против AC и угол C против AB
Пример 3
На рисунке ниже треугольник со сторонами разной величины.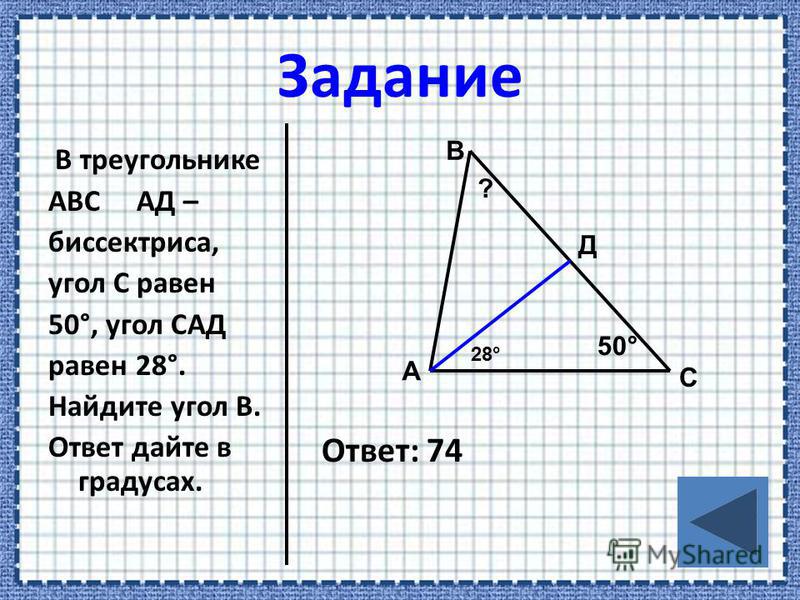

Leave A Comment