§7. Примеры решения задач
2012-2013 уч. год, № 2, 9 кл. Физика. Кинематика
мощью теоремы Пифагора: v = | vx | 2 + vy | 2 . В соответствии с системой | |||
уравнений | (19) в этот | момент (при | t =τ ) имеем: vx = v0 cosα, | |||
vy = v0sinα − gτ = −v0sinα. | Следовательно, | |||||
v = v | 2cos2α + v 2sin2α = v | 0 | (так как cos2 α +sin2 α =1 ). | |||
0 | 0 |
|
|
|
| |
Направление скорости тела в момент падения составляет угол α с направлением оси Ox. Этот угол отсчитывается по часовой стрелке от направления оси Ox.
Пусть при t =τ1 | тело достигло максимальной | высоты. | В этот | мо- | |||||
мент vy =0, y = H. | Соответствующие уравнения систем (19) и (20) | ||||||||
дают: |
|
|
|
| gτ12 |
|
| ||
0 = v0 sinα − gτ1 , H =(v0 sinα)τ1 − |
|
| |||||||
| 2 | . |
|
| |||||
Отсюда последовательно находим: τ1 = | v | 0 | sinα | , H = | v 2 sin2 α | . | |||
|
|
| 0 | ||||||
|
| g |
| 2g | |||||
|
|
|
|
|
|
|
| ||
Видим, что τ = 2τ1.
Уравнение траектории получим, исключив из системы (20) время t :
y(x) = − |
| g | x2 + tgα x. График траектории тела представляет | |
2v0 | 2 cos2 α | |||
|
|
собой участок параболы, ветви которой направлены вниз.
Задача 1. Два маленьких стальных шарика брошены одновременно из одной и той же точки с поверхности земли с начальными скоростями
v01 =5 м/c и v02 =8 м/c, направленными под углами α1 =80o и α2 = 20o к горизонту соответственно. Чему равно расстояние между
шариками, спустя время t = 13 c после броска?
Траектории шариков лежат в одной вертикальной плоскости. Сопротивлением воздуха
пренебречь. Решение. Шарики движутся в поле тя-
жести Земли с постоянным ускорением | g |
(сопротивлением воздуха пренебрегаем). | Рис. 20 |
© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич
21
2012-2013 уч. год, № 2, 9 кл. Физика. Кинематика
r |
| r |
|
| r |
|
| r |
|
|
| r |
|
|
|
|
| r |
| r |
|
| r |
|
|
| r |
|
|
| ||||||||||
|
|
|
|
|
|
|
| gt2 |
|
|
|
|
|
|
|
|
|
|
| gt | 2 |
| ||||||||||||||||||
r (t) имеем: |
| r (t) = r |
| + v | + |
|
| , |
|
|
| r (t) | = r | + v | 02 | + |
|
|
| . | ||||||||||||||||||||
|
|
|
|
| ||||||||||||||||||||||||||||||||||||
2 |
|
| 1 |
|
| 01 |
| 01 |
|
|
| 2 |
|
|
|
|
| 2 |
|
|
|
| 02 |
|
|
|
|
| 2 |
|
|
| ||||||||
Искомое |
| расстояние l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||
|
| равно модулю |
|
| разности радиус-векторов | |||||||||||||||||||||||||||||||||||
шариков в | момент времени t = |
| 1 |
| c. | |||||||||||||||||||||||||||||||||||
3 | ||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
одной и той же точки, то r01 = r02 , следовательно: |
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
| l = |
|
| rr1(t) −rr2(t) |
| = |
| vr01−vr02 |
| t. |
|
|
|
|
|
| |||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||
(Остальные слагаемые при вычитании радиус-векторов уничтожились.) | ||||||||||||||||||||||||||||||||||||||||
В свою очередь по теореме косинусов (см. рис. 20): |
| |||||||||||||||||||||||||||||||||||||||
|
|
|
| vr |
| −vr |
| = |
|
|
| v | 2 | + v | 2 | −2v | 01 | v | 02 | cos(α | 1 | −α | 2 | ). | ||||||||||||||||
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||
|
|
|
| 01 |
| 02 |
|
| 01 |
|
| 02 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||
Подставляя | в это | равенство числовые значения входящих в него ве- | ||||||||||||||||||||||||||||||||||||||
личин, получим |
| vr01 −vr02 |
|
|
| =7 м/c. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||
Тогда искомое |
| расстояние между | шариками |
| в |
|
| момент времени | ||||||||||||||||||||||||||||||||
t = | 1 | c будет равно l =7 |
| м |
|
| 1 | c = | 7 | м ≈ 2,3м. |
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||
|
|
|
| 3 |
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
| c | 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||
Задача 2. | Два тела брошены вертикально вверх с поверхности | |||||||||||||||||||||||||||||||||||||||
земли из одной точки вслед друг за другомr с интервалом времени τ, с одинаковыми начальными скоростями v0 . Пренебрегая сопротивлением воздуха, определить через сколько времени они «встретятся»? Про-
комментируйте решение для v0 < g τ2 .
Решение. Направим ось Oy вертикально вверх, начало отсчёта по-
местим в точку бросания. Отсчёт времени будем вести, начиная с момента бросания первого тела. Начальные условия движения тел:
1) t0 =0, y01 =0, vy01 = v0 ; 2) t0 =τ, y02 =0, vy02 = v0 . Проекции ускорений тел при отсутствии сопротивления воздуха равны: ay1= ay 2 = −g. Урав-
нения движения тел в проекциях на ось Oy с учётом начальных условий имеют вид:
y1 (t) = v0t − gt22 , y2 (t) = v0 (t −τ) − g(t −2 τ)2 . (Заметим, что y2 =0 при 0 <t ≤τ. )
Для наглядности изобразим графики этих функций на одном чертеже (рис. 21). Из чертежа видно, что «встреча» произойдёт в некоторый
момент времени tx в точке A, | где пересекаются графики y1(t) и | |||||||
y2 (t). |
| y1 (tx ) = y2 (tx ), то есть | ||||||
v0tx − | gt | 2 | = v0 (tx | −τ) − | g(t | x | −τ)2 | . |
2 |
|
|
| 2 | ||||
|
|
|
|
|
|
| ||
© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич
22
2012-2013 уч. год, № 2, 9 кл. Физика. Кинематика
Решая это уравнение относительно tx , находим: tx = vg0 +τ2 . Про-
анализируем полученное выражение при v0 < gτ / 2. Известно (см.
Пример 7), что время полёта тела, брошенного вертикально, равно
2v0 / g. Поэтому, если v0 < gτ / 2, то τ > 2v0 / g. Это означает, что сна-
Это означает, что сна-
чала упадёт на землю первое тело, а только затем будет брошено вверх второе. Иными словами, тела «встретятся» в точке бросания.
y |
|
| A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
y (t) |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
| y1(t) |
| y2(t) |
|
|
|
| |||
|
|
|
|
| ||||||||
O |
| τ | zx | 2 v0 t |
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
| |||||
|
|
|
| g |
|
|
|
|
|
|
|
|
|
|
| Рис. |
|
|
|
| Рис. 22 | ||||
Задача 3. Мальчик, находясь на плоском склоне горы с углом наклона ϕ =30o , бросает камень в сторону подъёма горы, сообщив ему
начальную скорость v0 , направленную под углом β =60o к горизон-
ту. На каком расстоянии от мальчика упадёт камень? Сопротивлением воздуха пренебречь.
Решение. Выберем систему отсчёта так, как показано на рис. 22, поместив начало отсчёта O в точку бросания. В этой системе отсчё-
та начальная скорость камня составляет с осью Ox угол α =β −ϕ =30o. Начальные условия: x0 =0, y0 =0, v0x = v0 cosα, v0y = v0 sinα. Проекции ускорения камня в отсутствие сопротивления воздуха равны (см. рис. 22): ax = −g sinϕ, ay = −g cosϕ. Здесь мы учли, что угол между
вектором g и перпендикуляром к поверхности горы равен углу наклона горы ϕ =30o (почему?), кроме того, по условию задачиϕ =α.
Запишем уравнения системы (14) с учётом начальных условий:
x(t) =(v0 | cosα)t −(g sinϕ) | t2 | , | y(t) =(v0 sinα)t −(g cosϕ) | t2 | . |
|
| |||||
| 2 |
| 2 |
| ||
© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич
23
2012-2013 уч. год, № 2, 9 кл. Физика. Кинематика |
|
|
| ||||
| Время полёта τ камня найдём из последнего уравнения, зная, что | ||||||
|
| y(τ) =0, cosϕ = | 3 , | sinα = 1 . |
| ||
|
|
|
| 2 | 2 |
| |
А именно τ = 2 v0 . (Значение τ =0 мы отбросили, т. к. оно не связа- | |||||||
|
| 3 g |
|
|
|
| |
но с вопросом задачи). |
| в уравнение для x(t), |
| ||||
| Подставляя найденное значение τ | определим | |||||
искомое расстояние (иными словами, дальность полёта): |
| ||||||
|
|
| l = x(τ) = | 2 v 2 | . |
| |
|
|
| 0 |
| |||
|
|
|
| 3 g |
|
| |
uur | Задача 4. Массивная платформа движется с постоянной скоростью | ||||||
V0 | по горизонтальному полу. | ||||||
удар по мячу. Модуль начальной скорости мяча относительно плат- | |||||||
формы равен u = 2V , причём вектор | u составляет угол α =60o с гори- | ||||||
|
| 0 |
|
|
|
| |
зонтом (рис. 23). На какую максимальную высоту над полом поднимет- | |||||||
ся мяч? На каком расстоянии от края платформы будет находиться мяч | |||||||
в момент приземления. Высотой платформы и сопротивлением воздуха | |||||||
пренебречь. Все скорости лежат в |
|
| y | ||||
одной | вертикальной | плоскости. | u | g | |||
| |||||||
(ФЗФТШ при МФТИ, 2009.) |
|
|
| ||||
| Решение. Для описания движе- | α |
| ||||
ния мяча и платформы введём сис- | V0 | ||||||
тему отсчёта, связанную с полом. |
|
| |||||
/ / / / / / / / / / / / / / / / / / / / / | |||||||
Ось Ox направим горизонтально в | x |
| O | ||||
направлении удара, а ось Oy − вер- |
| Рис. 23 |
| ||||
тикально вверх (рис. |
|
|
|
| |||
Движение мяча происходит с постоянным ускорением a, причём ax = 0, ay = −g, где g − величина ускорения свободного падения.
Проекции начальной скорости v0 мяча на оси Ox и Oy равны: v0,x =V0,x +ux = −V0 +2V0 cos60o = −V0 +V0 =0,
v | =V | +u | y | =0 + 2V sin 60o = | 3V . |
0,y | 0, y |
| 0 | 0 |
Равенство нулю горизонтальной скорости мяча означает, что его движение происходит только по вертикали, и он упадёт в точке удара.
Максимальную высоту подъёма (ymax ) и время полёта мяча найдём
© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич
24
Выберем систему координат. Искомое расстояние. Проекция ускорения
По этой ссылке вы найдёте полный курс лекций по математике:
| Решение задач по математике |
Задача 1. с после броска? Траектории шариков лежат в одной вертикальной плоскости. Сопротивлением воздуха пренебречь. Решение. Шарики движутся в поле тяже- yi сти Земли с постоянным ускорением g (со- v~-v л противлением воздуха пренебрегаем).
с после броска? Траектории шариков лежат в одной вертикальной плоскости. Сопротивлением воздуха пренебречь. Решение. Шарики движутся в поле тяже- yi сти Земли с постоянным ускорением g (со- v~-v л противлением воздуха пренебрегаем).
Выберем систему координат так, как показано на рис. 20, начало отсчёта поместим в точку бросания. Для радиус-векторов шарики Выберем систему координат. Искомое расстояние. Проекция ускорения Искомое расстояние / равно модулю разности радиус-векторов шариков в момент времени / = — с . Так как шарики были брошены из од- 3 ной и той же точки, то /*0| = г02, следовательно: / = . (Остальные слагаемые при вычитании радиус-вектопов уничтожились.)
В свою очередь по теореме косинусов (см. рис. 20): Подставляя в это равенство числовые значения входящих в него величин, получим \v0l -v02\ = 7м/с. Тогда искомое расстояние между шариками в момент времени * Задача 2. Два тела брошены вертикально вверх с поверхности земли из одной точки вслед друг за другом с интервалом времени г, с одинаковыми начальными скоростями v0. условие «встречи»: у, (О = Уг (Л)»то есть = v0 ft -г) 2 ‘ 2 Решая это уравнение относительно /v, находим: tx = — + —. Проанализируем по- g 2 лученное выражение при Известно (см. Пример 7), что время полёта тела, брошенного вертикально, равно 2v0/g.
условие «встречи»: у, (О = Уг (Л)»то есть = v0 ft -г) 2 ‘ 2 Решая это уравнение относительно /v, находим: tx = — + —. Проанализируем по- g 2 лученное выражение при Известно (см. Пример 7), что время полёта тела, брошенного вертикально, равно 2v0/g.
Поэтому, если v0 2v0/g. Это означает, что сначала упадёт на землю первое тело, а только затем будет брошено вверх второе. Иными словами, тела «встретятся» в точке бросания. Задача 3. Мальчик, находясь на плоском склоне горы с углом наклона (р- 30°, бросает камень в сторону подъёма горы, сообщив ему начальную скорость v0, направленную под углом /? = 60° к горизонту. На каком расстоянии от мальчика упадёт камень? Сопротивлением воздуха пренебречь. Решение.
Выберем систему отсчёта так, как показано на рис. 22, поместив начало отсчёта О в точку бросания.
В этой системе отсчёта начальная скорость камня составляет с осью Ох угол а = ft-(p = 30°. Начальные условия: Рис 22 Проекции ускорения камня в отсутствие сопротивления воздуха равны (см. >)—, y(t) = (v0sina)t-(gcosp)—.
>)—, y(t) = (v0sina)t-(gcosp)—.
Время полёта г камня найдём из последнего уравнения, зная, что Выберем систему координат. Искомое расстояние. Проекция ускорения А именно г = —=—. (Значение г = 0 мы отбросили, т. к. оно не связа-V3 g но с вопросом задачи). Подставляя найденное значение г в уравнение для .г(/), определим искомое расстояние (иными словами, дальность полёта): 3 g Задача 4. Массивная платформа движется с постоянной скоростью К0 по горизонтальному полу.
Возможно вам будут полезны данные страницы:
| Допускаемые напряжения условие прочности |
| Односторонние пределы, правосторонний предел, левосторонний |
| Площадь криволинейной трапеции 2 |
| Стехиометрические соотношения в химии |
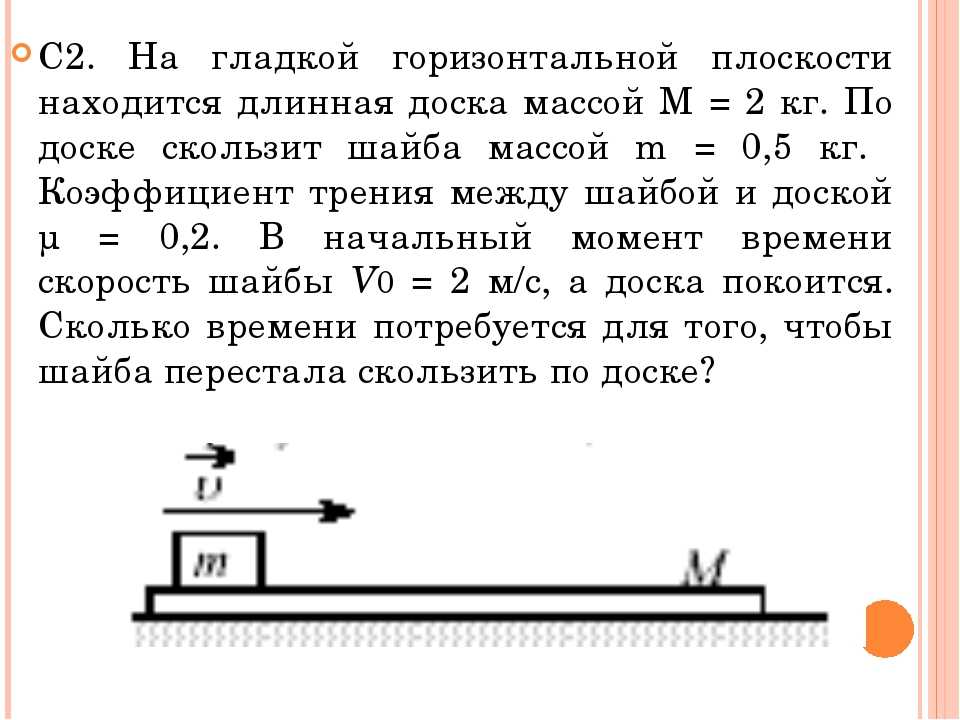
С заднего края платформы производится удар по мячу. Модуль начальной скорости мяча относительно платформы равен у\ u = 2VQ9 причём вектор и составляет угол а = 60° с горизонтом (рис. 23). На какую максимальную высоту над полом поднимется мяч? На каком расстоянии от края платформы будет находиться мяч в момент _ j. w_ ,0 приземления. Высотой платформы и со-противлением воздуха пренебречь. Все скорости лежат в одной вертикальной плоскости. (ФЗФТШ при МФТИ, 2009.)
23). На какую максимальную высоту над полом поднимется мяч? На каком расстоянии от края платформы будет находиться мяч в момент _ j. w_ ,0 приземления. Высотой платформы и со-противлением воздуха пренебречь. Все скорости лежат в одной вертикальной плоскости. (ФЗФТШ при МФТИ, 2009.)
Решение. Для описания движения мяча и платформы введём систему отсчёта, связанную с полом. Ось Ох направим горизонтально в направлении удара, а ось Оу — вертикально вверх (рис. 23). Движение мяча происходит с постоянным ускорением а, причём ах = 0, aY = -g, где g — величина ускорения свободного падения. Проекции начальной скорости v0 мяча на оси Ох и Оу равны: v0,x = V0, + = -К + 2F0 • cos 60° = -V0 + V0 = 0, % = К,- + =10 + • sin 60° = >/3F0.
Равенство нулю горизонтальной скорости мяча означает, что его движение происходит только по вертикали, и он упадёт в точке удара. Максимальную высоту подъёма (ynvix) и время полёта мяча найдём из законов кинематики равноускоренного движения: а/ Выберем систему координат. проекция вертикальной скорости обращается в ноль vY = 0 , а в момент приземления мяча t = Гполёта его координата по оси Оу обращается в ноль у = 0 , имеем:
проекция вертикальной скорости обращается в ноль vY = 0 , а в момент приземления мяча t = Гполёта его координата по оси Оу обращается в ноль у = 0 , имеем:
ЗУ- т = 1 полета 2 g 2 g — S За время полёта мяча платформа сместится на расстояние полета 8 У шах которое и является искомым расстоянием между мячом и платформой в момент приземления мяча. Контрольные вопросы 1. На рис. 24 показана траектория движения тела. Его начальное положение обозначено точкой А, конечное — точкой С. Чему равны проекции перемещения тела на оси Ох и Оу, модуль перемещения и пройденный телом путь? 2. Тело движется равномерно и прямолинейно на плоскости хОу.
Его координаты в зависимости от времени изменяются в соответствии с уравнениями: (величины измерены в СИ). Запишите уравнение у = у(х) траектории тела. Чему равны начальные координаты тела и его координаты через 2 с после начала движения? 3. Стержень АВ, ориентированный вдоль оси Ох, движется с постоянной скоростью v = 0,1 м/с в положительном направлении оси. Передним концом стержня является точка А, задним — точка В.
Передним концом стержня является точка А, задним — точка В.
Чему равна длина стержня, если в момент времени tA = 1 Ос после начала движения координата точки А равна х,=3м, а в момент времени tB- 30с координата точки В равна *Л=4,5м? (МИЭТ, 2006 г.) 4. Как при движении двух тел определяется их относительная скорость? 5. Автобус и мотоцикл находятся друг от друга на расстоянии L = 20 км . Если они будут двигаться в одном направлении с некоторыми скоростями г\ и v2 соответственно, то мотоцикл догонит автобус через время / = 1 час.
| Чему равна скорость мотоцикла |
относительно автобуса? 6. Что называют средней путевой скоростью тела? 7. Первый час пути поезд проехал со скоростью 50 км/ч , следующие 2 часа он ехал со скоростью 80 км/ч . Найдите среднюю скорость поезда за эти 3 часа. Выберите правильный вариант ответа и обоснуйте свой выбор: 1) 60 км/ч; 2) 65 км/ч; 3) 70 км/ч; 4) 72 км/ч; 5) 75 км/ч. (РГТУ им. К. Э. Циолковского (МАТИ), 2006 г.) 8. Одну пятую часть пути автомобиль ехал со скоростью г\ = 40 км/ч , а оставшийся путь — со скоростью v2 = 60 км/ч .
(РГТУ им. К. Э. Циолковского (МАТИ), 2006 г.) 8. Одну пятую часть пути автомобиль ехал со скоростью г\ = 40 км/ч , а оставшийся путь — со скоростью v2 = 60 км/ч .
Найдите среднюю скорость автомобиля на всем пути. (МИФИ, 2006 г.) 9. Материальная точка начинает двигаться по оси Ох по закону *(/) = 5 + 4/-2г(м). На каком расстоянии от начала координат скорость точки будет равна нулю? (МГТУ им. Н. Э. Баумана, 2006 г.) 10. Конькобежец, разогнавшись до скорости v0 = 5 м/с, начал скользить прямолинейно и равнозамедленно. Спустя время t = 20 с модуль скорости конькобежца стал равен v = 3 м/с.
Чему равно ускорение конькобежца? Задачи 1. Пешеход треть всего пути бежал со скоростью v{ =9км/ч, треть всего времени шёл со скоростью v2 =4 км/ч , а оставшуюся часть шел со скоростью, равной средней скорости на всем пути. Найдите эту скорость. (ЗФТШ при МФТИ, 2001 г.) 2. Тело, двигаясь равноускоренно и прямолинейно из состояния покоя, прошло расстояние S за время г. Какую скорость имело тело в тот момент, когда оно прошло расстояние S/n , где п — некоторое положительное число? (МИФИ, 2006 г. ) 3. Тело падает без начальной скорости и достигает поверхности земли через 4с. С какой высоты падало тело?
) 3. Тело падает без начальной скорости и достигает поверхности земли через 4с. С какой высоты падало тело?
Сопротивлением воздуха пренебречь. Выберите правильный вариант ответа и обоснуйте свой выбор: 1) 20м; 2) 40 м; 3) 80м;4) 120м;5) 160 м. (РГТУ им. К. Э. Циолковского (МАТИ), 2006 г.) 4. Камень, брошенный с поверхности земли вертикально вверх, упал на землю через Т = 2с. Определите путь 5, пройденный камнем за время г = 1,5с после броска. Сопротивлением воздуха пренебречь. Ускорение свободного падения принять равным g = 10м/с2. (МИЭТ, 2006 г.)
Выберем систему координат. Искомое расстояние. Проекция ускорения 5. Из одной точки на высоте h от поверхности земли брошены с одинаковыми скоростями камень А вертикально вверх и камень В вертикально вниз. Известно, что камень А достиг верхней точки своей траектории одновременно с падением камня В на землю. Какой максимальной высоты (считая от поверхности земли) достиг камень А? Сопротивление воздуха не учитывать. (МФТИ, 1997 г.) 6.
Камень брошен горизонтально со склона горы, образующего угол а = 45° с горизонтом (рис. 25). Чему равна начальная скорость v0 камня, если он упал на склон на расстоянии / = 50 м от точки бросания? Сопротивлением воздуха пренебречь. 7. Тело брошено горизонтально. Через 3 с после броска угол между направлением полной скорости и направлением полного ускорения стал равным 60°. Определите величину полной скорости тела в этот момент времени.
Сопротивлением воздуха пренебречь. (РГУ нефти и газа им. И. М. Губкина, 2006 г.) Указание. Под полной скоростью и полным ускорением понимайте просто скорость и ускорение тела. 8. Снаряд разорвался на несколько осколков, полетевших во все стороны с одинаковыми скоростями. Осколок, полетевший вертикально вниз, достиг земли за время . Осколок, полетевший вертикально вверх, упал на землю через время t2. Сколько времени падали осколки, полетевшие горизонтально?
Сопротивление воздуха не учитывать. (МФТИ, 1997 г.) 9. Камень, брошенный под углом к горизонту, достиг наибольшей высоты 5 м. Найдите полное время полёта камня. Сопротивлением воздуха пренебречь. (РГУ нефти и газа им. И. М. Губкина, 2006 г.) 10. Камень, брошенный с поверхности земли под углом а = 30° к горизонту, дважды побывал на одной и той же высоте h спустя время =3с и =5с после начала движения. Найдите начальную скорость камня v0.
Найдите полное время полёта камня. Сопротивлением воздуха пренебречь. (РГУ нефти и газа им. И. М. Губкина, 2006 г.) 10. Камень, брошенный с поверхности земли под углом а = 30° к горизонту, дважды побывал на одной и той же высоте h спустя время =3с и =5с после начала движения. Найдите начальную скорость камня v0.
Ускорение свободного падения принять равным g = 10м/с2 . Сопротивлением воздуха пренебречь. (Институт криптографии, связи и информатики Академии ФСБ РФ, 2006 г.) 11. С какой скоростью v0 должен вылететь снаряд из пушки в момент старта ракеты, чтобы сбить её? Ракета стартует вертикально с постоянным ускорением я = 4м/с2. Расстояние от пушки до места старта ракеты (они находятся на одном горизонтальном уровне) равно / = 9км. Пушка стреляет под углом « = 45° к горизонту. Сопротивлением воздуха пренебречь.
Нормальная сила и вес — AP Physics 1
Все ресурсы AP Physics 1
7 Диагностические тесты 170 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 Следующая →
AP Physics 1 Справка » Ньютоновская механика » Силы » Удельные силы » Нормальная сила и вес
Кусок железа массой 10 кг находится на склоне под углом 30 градусов к горизонтали. Чему равна нормальная сила, действующая на кусок железа?
Чему равна нормальная сила, действующая на кусок железа?
Возможные ответы:
Правильный ответ:
Объяснение:
Схема системы со свободным телом показана ниже:
– нормальная сила, действующая на блок, – вес блока.
Поскольку является компонентом , мы можем представить его как:
Если вы не понимаете, почему это косинус, а не синус, подумайте о системе практически. Чем пологий уклон, тем больше нормальная сила. Чем меньше становится угол (создавая более пологий наклон), тем больше становится значение косинуса и, следовательно, тем больше становится нормальная сила.
Теперь мы можем просто подставить заданные нами значения:
Сообщить об ошибке
Человек пытается поднять очень тяжелый камень, применяя восходящую силу , но не может поднять его вверх. Вычислите, какая дополнительная сила потребовалась, чтобы поднять камень с земли.
Вычислите, какая дополнительная сила потребовалась, чтобы поднять камень с земли.
Возможные ответы:
Правильный ответ:
Пояснение:
Сначала рассчитайте гравитационную силу, действующую на камень.
Прилагает силу вниз, что означает, что если бы человек приложил хотя бы , то он смог бы поднять его. Вместо этого человек подал заявку только . Это означает, что человеку нужно было приложить дополнительную силу, чтобы поднять камень.
Сообщить об ошибке
Рассмотрим следующую систему:
Если блок ускоряется вниз по склону под углом и скоростью , каков коэффициент кинетического трения между блоком и склоном?
Возможные ответы:
Правильный ответ:
Пояснение:
В этом сценарии действуют две силы: первая — гравитация, а вторая — трение. Мы можем использовать второй закон Ньютона, чтобы решить эту задачу:
Мы можем использовать второй закон Ньютона, чтобы решить эту задачу:
Подставив две силы, которые мы только что упомянули:
Обратите внимание, что сила трения вычитается, потому что она находится в направлении, противоположном силе тяжести. Теперь, подставляя выражения для наших двух сил, получаем:
Если вы не уверены, использовать ли косинус или синус для каждой силы, подумайте о ситуации практически. Чем более пологим становится наклон, тем меньше сила тяжести будет влиять на перемещение блока вниз по плоскости, поэтому используется функция синуса. Кроме того, чем более пологим становится наклон, тем больше становится нормальная сила, поэтому используется функция косинуса .
Сокращая массу из уравнения и переставляя решение для коэффициента трения, мы получаем:
Сообщить об ошибке
Рассмотрим следующую систему:
Если блок движется вниз по склону с постоянной скоростью и коэффициент кинетического трения равен , каков угол наклона?
Возможные ответы:
Правильный ответ:
Объяснение:
В этом сценарии действуют две силы. Первое — гравитация, второе — трение. Оба зависят от угла наклона. Поскольку блок движется с постоянной скоростью, мы знаем, что сила тяжести и силы трения в направлении наклона уравновешивают друг друга, а результирующая сила равна нулю (ускорения нет). Следовательно, мы можем написать:
Первое — гравитация, второе — трение. Оба зависят от угла наклона. Поскольку блок движется с постоянной скоростью, мы знаем, что сила тяжести и силы трения в направлении наклона уравновешивают друг друга, а результирующая сила равна нулю (ускорения нет). Следовательно, мы можем написать:
Подставляя в выражения для каждой силы, получаем:
Если вы не уверены, использовать ли косинус или синус для каждой силы, подумайте о ситуации практически. Чем более пологим становится наклон, тем меньше сила тяжести будет влиять на перемещение блока вниз по плоскости, поэтому используется функция синуса. Кроме того, чем более пологим становится наклон, тем больше становится нормальная сила, поэтому используется функция косинуса .
Сократив массу и найдя угол в одной части уравнения, мы получим:
Это важно знать! Когда объект движется вниз по склону с постоянной скоростью, тангенс угла наклона равен коэффициенту кинетического трения.
Сообщить об ошибке
Рассмотрим следующую систему:
Если , то каков минимальный коэффициент трения покоя, при котором блок остается неподвижным?
Возможные ответы:
Правильный ответ:
Пояснение:
В этом сценарии действуют две силы: сила трения и сила тяжести. Если блок неподвижен, это означает, что две силы компенсируют друг друга. Следовательно, мы можем написать:
Подставив в выражения для каждой силы, получим:
Если вы не уверены, использовать ли косинус или синус для каждой силы, подумайте о ситуации практически. Чем более пологим становится наклон, тем меньше сила тяжести будет влиять на попытку переместить блок вниз по плоскости, отсюда и использование функции синуса. Кроме того, чем более пологим становится наклон, тем больше становится нормальная сила, поэтому используется функция косинуса .
Сообщить об ошибке
Рассмотрим следующую систему. Если , каков коэффициент кинетического трения?
Возможные ответы:
Правильный ответ:
Пояснение:
В этом сценарии действуют две силы: гравитация и трение. Мы можем использовать второй закон Ньютона, чтобы составить выражение с этими силами:
Подставляя выражения для каждой силы, получаем:
Если вы не уверены, использовать ли косинус или синус для каждой силы, подумайте о ситуации практически. Чем более пологим становится наклон, тем меньше сила тяжести будет влиять на перемещение блока вниз по плоскости, поэтому используется функция синуса. Кроме того, чем более пологим становится наклон, тем больше становится нормальная сила, поэтому используется функция косинуса .
Сокращая массу и переставляя коэффициент трения, получаем:
Сообщить об ошибке
Рассмотрим следующую систему:
Если нормальная сила, действующая на блок, и угол наклона равны, какова масса блока?
Возможные ответы:
Правильный ответ:
Объяснение:
Нам нужно составить выражение для нормальной силы, действующей на брусок, чтобы решить эту задачу:
Если вы не уверены, использовать ли синус или косинус, подумайте о системе практически: чем более плоской становится система, тем больше становится нормальная сила; отсюда и использование функции косинуса.
Переставляя массу, получаем:
Сообщить об ошибке
Какова величина нормальной силы, действующей на объект массой 5 кг, который находится под наклоном к горизонтали?
Возможные ответы:
Невозможно определить, не зная высоты объекта от земли
Правильный ответ:
Объяснение:
Напомним, что формула для определения величины нормальной силы на склоне задается следующим образом:
Здесь – величина нормальной силы, это масса объекта, это гравитационная постоянная, а это угол, образованный с горизонтом.
В нашем случае:
Сообщить об ошибке
Предмет массой 10 кг лежит на горизонтальном столе. Какая нормальная сила действует на тело?
Возможные ответы:
Правильный ответ:
Пояснение:
Нормальная сила направлена перпендикулярно силе тяжести (противоположное направление) и равна по величине. Поскольку сила гравитации равна , мы просто умножаем нашу заданную массу и силу гравитации, чтобы получить ответ.
Поскольку сила гравитации равна , мы просто умножаем нашу заданную массу и силу гравитации, чтобы получить ответ.
Сообщить об ошибке
Человек, который взвешивает, стоит в лифте. Затем лифт ускоряется вверх со скоростью . Сколько весит человек при этом ускорении?
Возможные ответы:
Недостаточно информации для решения этой задачи
Вес человека не изменится, он останется равным
75 5
Объяснение:
В этом вопросе нам представлен сценарий, в котором человек, весящий в состоянии покоя, ускоряется вверх. Затем нас просят определить новый вес этого человека, пока он подвергается этому ускорению.
Давайте начнем наш анализ с того, что сначала рассмотрим человека, находящегося в состоянии покоя в лифте. В этой ситуации полезно изобразить диаграмму свободного тела человека и всех сил, действующих на него/нее. В состоянии покоя на этого человека не действует результирующая сила. Поскольку в направлении y нет результирующей силы, это означает, что восходящие силы должны быть точно уравновешены направленными вниз силами. Нисходящая сила, действующая на человека, — это сила гравитации, а восходящая сила — это нормальная сила пола лифта, действующая на человека.
В состоянии покоя на этого человека не действует результирующая сила. Поскольку в направлении y нет результирующей силы, это означает, что восходящие силы должны быть точно уравновешены направленными вниз силами. Нисходящая сила, действующая на человека, — это сила гравитации, а восходящая сила — это нормальная сила пола лифта, действующая на человека.
Другими словами:
Теперь давайте получим выражение, учитывая ускорение лифта вверх. В такой ситуации теперь на человека действует чистая сила, и эта чистая восходящая сила возникает из-за ускорения лифта. Как и в состоянии покоя, направленная вниз сила, действующая на человека, в этом случае по-прежнему является силой тяжести, а восходящая сила, действующая на человека, является нормальной силой пола лифта.
Записав в виде уравнения, мы имеем:
Обратите внимание, что мы находим новое значение нормальной силы, когда лифт ускоряется. Причина, по которой нормальная сила дает нам вес человека, связана с третьим законом Ньютона. Когда лифт ускоряется вверх, лифт оказывает (нормальную) силу на человека, которая по величине равна весу человека, но с обратной направленностью.
Когда лифт ускоряется вверх, лифт оказывает (нормальную) силу на человека, которая по величине равна весу человека, но с обратной направленностью.
Наконец, мы можем вычислить массу человека:
Подстановка соответствующих значений в полученное выше выражение даст нам ответ.
Обратите внимание, что это значение больше, чем вес человека в состоянии покоя. Это связано с первым законом Ньютона. Когда лифт ускоряется вверх, инерция человека сопротивляется этому движению вверх, что заставляет человека чувствовать себя тяжелее. Вы действительно можете попробовать это сами, когда в следующий раз найдете лифт!
Сообщить об ошибке
← Предыдущий 1 2 3 4 Следующий →
Уведомление об авторских правах
Все ресурсы AP Physics 1
7 Диагностические тесты 170 практических тестов Вопрос дня Карточки Learn by Concept
6.5: Трение (Часть 2) — Physics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 5889
- OpenStax
- OpenStax
Трение и наклонная плоскость
Одной из ситуаций, когда трение играет очевидную роль, является объект на склоне. Это может быть ящик, поднимаемый по пандусу к погрузочной площадке, или скейтбордист, спускающийся с горы, но основная физика остается той же. Обычно мы обобщаем наклонную поверхность и называем ее наклонной плоскостью, но затем делаем вид, что поверхность плоская. Рассмотрим пример анализа движения по наклонной плоскости с учетом трения.
Это может быть ящик, поднимаемый по пандусу к погрузочной площадке, или скейтбордист, спускающийся с горы, но основная физика остается той же. Обычно мы обобщаем наклонную поверхность и называем ее наклонной плоскостью, но затем делаем вид, что поверхность плоская. Рассмотрим пример анализа движения по наклонной плоскости с учетом трения.
Пример \(\PageIndex{1}\): Горнолыжник
Лыжник массой 62 кг скользит по заснеженному склону с постоянной скоростью. Найдите коэффициент кинетического трения для лыжника, если известно, что трение равно 45,0 Н.
Стратегия
Величина кинетического трения равна 45,0 Н. Кинетическое трение связано с нормальной силой Н соотношением f k = \(\mu_{k}\)N; таким образом, мы можем найти коэффициент кинетического трения, если мы можем найти нормальную силу, действующую на лыжника. Нормальная сила всегда перпендикулярна поверхности, а поскольку движение перпендикулярно поверхности отсутствует, нормальная сила должна равняться составляющей веса лыжника, перпендикулярной склону. (См. рисунок \(\PageIndex{1}\), который повторяет рисунок из главы о законах движения Ньютона.)
(См. рисунок \(\PageIndex{1}\), который повторяет рисунок из главы о законах движения Ньютона.)
Значимость
Этот результат немного меньше, чем коэффициент, указанный в таблице 6.1 для парафинированной древесины на снегу, но все же приемлем, поскольку значения коэффициентов трения может сильно различаться. В подобных ситуациях, когда объект массы m скользит по склону, образующему угол \(\theta\) с горизонтом, трение определяется выражением f k = \(\mu_{k}\) mg cos \ (\тета\). В этих условиях все объекты скользят вниз по склону с постоянным ускорением.
В подобных ситуациях, когда объект массы m скользит по склону, образующему угол \(\theta\) с горизонтом, трение определяется выражением f k = \(\mu_{k}\) mg cos \ (\тета\). В этих условиях все объекты скользят вниз по склону с постоянным ускорением.
Мы обсудили, что когда объект лежит на горизонтальной поверхности, нормальная сила, поддерживающая его, равна по величине его весу. Кроме того, простое трение всегда пропорционально нормальной силе. Когда предмет находится не на горизонтальной поверхности, как при наклонной плоскости, мы должны найти силу, действующую на предмет, которая направлена перпендикулярно поверхности; это составляющая веса.
Теперь выведем полезное соотношение для расчета коэффициента трения на наклонной плоскости. Обратите внимание, что результат применим только к ситуациям, в которых объект скользит с постоянной скоростью вниз по пандусу.
Объект скользит по наклонной плоскости с постоянной скоростью, если результирующая сила, действующая на объект, равна нулю. Мы можем использовать этот факт для измерения коэффициента кинетического трения между двумя объектами. Как показано в примере \(\PageIndex{1}\), кинетическое трение на склоне равно f k = \(\mu_{k}\) mg cos \(\theta\). Компонент веса вниз по склону равен mg sin \(\theta\) (см. диаграмму свободного тела на рисунке \(\PageIndex{1}\)). Эти силы действуют в противоположных направлениях, поэтому, когда они имеют одинаковую величину, ускорение равно нулю. Записывая это,
Мы можем использовать этот факт для измерения коэффициента кинетического трения между двумя объектами. Как показано в примере \(\PageIndex{1}\), кинетическое трение на склоне равно f k = \(\mu_{k}\) mg cos \(\theta\). Компонент веса вниз по склону равен mg sin \(\theta\) (см. диаграмму свободного тела на рисунке \(\PageIndex{1}\)). Эти силы действуют в противоположных направлениях, поэтому, когда они имеют одинаковую величину, ускорение равно нулю. Записывая это,
\[\mu_{k} мг \cos \theta = mg \sin \theta \ldotp\]
Решая для \(\mu_{k}\), находим, что
\[\mu_{k} = \frac{mg \sin \theta}{mg \cos \theta} = \tan \theta \ldotp\]
Положите монету на книгу и наклоняйте ее, пока монета не будет скользить по книге с постоянной скоростью. Возможно, вам придется слегка постучать по книге, чтобы заставить монету двигаться. Измерьте угол наклона относительно горизонтали и найдите \(\mu_{k}\). Обратите внимание, что монета вообще не начинает скользить, пока не будет достигнут угол, больший \(\theta\), поскольку коэффициент статического трения больше, чем коэффициент кинетического трения. Подумайте, как это может повлиять на значение \(\mu_{k}\) и его неопределенность.
Подумайте, как это может повлиять на значение \(\mu_{k}\) и его неопределенность.
Объяснение трения в атомном масштабе
До сих пор рассматривались более простые аспекты трения, связанные с его макроскопическими (крупномасштабными) характеристиками. За последние несколько десятилетий были достигнуты большие успехи в объяснении трения на атомном уровне. Исследователи обнаружили, что атомарная природа трения, по-видимому, имеет несколько фундаментальных характеристик. Эти характеристики не только объясняют некоторые из более простых аспектов трения, они также несут в себе потенциал для разработки сред, почти свободных от трения, которые могли бы сэкономить сотни миллиардов долларов энергии, которая в настоящее время преобразуется (без необходимости) в тепло.
Рисунок \(\PageIndex{2}\) иллюстрирует одну макроскопическую характеристику трения, которая объясняется микроскопическими (мелкомасштабными) исследованиями. Мы заметили, что трение пропорционально нормальной силе, но не площади контакта, что несколько противоречит здравому смыслу. Когда соприкасаются две шероховатые поверхности, фактическая площадь контакта составляет ничтожную долю от общей площади, потому что соприкасаются только выступающие точки. Когда действует большая нормальная сила, фактическая площадь контакта увеличивается, и мы обнаруживаем, что трение пропорционально этой площади.
Когда соприкасаются две шероховатые поверхности, фактическая площадь контакта составляет ничтожную долю от общей площади, потому что соприкасаются только выступающие точки. Когда действует большая нормальная сила, фактическая площадь контакта увеличивается, и мы обнаруживаем, что трение пропорционально этой площади.
Однако представление в атомном масштабе обещает объяснить гораздо больше, чем более простые особенности трения. В настоящее время определяется механизм образования тепла. Другими словами, почему поверхности нагреваются при трении? По сути, атомы связаны друг с другом, образуя решетки. Когда поверхности трутся, поверхностные атомы прилипают и вызывают вибрацию атомных решеток, по существу создавая звуковые волны, которые проникают в материал. Звуковые волны уменьшаются с расстоянием, и их энергия преобразуется в тепло. Химические реакции, связанные с фрикционным износом, также могут происходить между атомами и молекулами на поверхностях. На рисунке \(\PageIndex{3}\) показано, как кончик зонда, проведенного по другому материалу, деформируется за счет трения атомного масштаба. Сила, необходимая для перетаскивания наконечника, может быть измерена, и установлено, что она связана с напряжением сдвига, которое обсуждается в разделе «Статическое равновесие и эластичность». Изменение касательного напряжения заметно (более чем в 1012 раз) и его трудно предсказать теоретически, но касательное напряжение дает фундаментальное понимание крупномасштабного явления, известного с древних времен, — трения.
Звуковые волны уменьшаются с расстоянием, и их энергия преобразуется в тепло. Химические реакции, связанные с фрикционным износом, также могут происходить между атомами и молекулами на поверхностях. На рисунке \(\PageIndex{3}\) показано, как кончик зонда, проведенного по другому материалу, деформируется за счет трения атомного масштаба. Сила, необходимая для перетаскивания наконечника, может быть измерена, и установлено, что она связана с напряжением сдвига, которое обсуждается в разделе «Статическое равновесие и эластичность». Изменение касательного напряжения заметно (более чем в 1012 раз) и его трудно предсказать теоретически, но касательное напряжение дает фундаментальное понимание крупномасштабного явления, известного с древних времен, — трения.
Моделирование
Описать модель трения на молекулярном уровне. Описывать материю с точки зрения молекулярного движения. Описание должно включать диаграммы для поддержки описания; как температура влияет на изображение; каковы различия и сходства между движением твердых, жидких и газообразных частиц; и как размер и скорость молекул газа соотносятся с повседневными объектами.
Пример \(\PageIndex{2}\): скользящие блоки
Два блока на рисунке \(\PageIndex{4}\) соединены друг с другом невесомой нитью, намотанной на шкив без трения. Когда нижний брусок массой 4,00 кг тянет влево под действием постоянной силы \(\vec{P}\), верхний брусок массой 2,00 кг скользит по нему вправо. Найдите величину силы, необходимой для перемещения блоков с постоянной скоростью. Предположим, что коэффициент кинетического трения между всеми поверхностями равен 0,400.
Рисунок \(\PageIndex{4}\): (a) Каждый блок движется с постоянной скоростью. (b) Диаграммы свободного тела для блоков.
Стратегия
Анализируем движение двух блоков по отдельности. На верхний блок действует контактная сила, создаваемая нижним блоком. Компонентами этой силы являются нормальная сила Н 1 и сила трения -0,400 Н 1 . Другими силами, воздействующими на верхний блок, являются натяжение T струны и вес самого верхнего блока, 19.6 Н. На нижний блок действуют контактные усилия верхнего блока и пола. Первая контактная сила имеет составляющие -N 1 и 0,400 Н 1 , которые представляют собой просто силы реакции на контактные силы, которые нижний блок оказывает на верхний блок. Составляющие контактной силы пола равны Н 2 и 0,400 Н 2 . Другими силами, воздействующими на этот блок, являются −P, сила натяжения T и вес –39,2 Н. Решение Поскольку верхний блок движется горизонтально вправо с постоянной скоростью, его ускорение равно нулю как в горизонтальном, так и в вертикальном направлениях. Из второго закона Ньютона,
\[\сумма F_{x} = m_{2} a_{x}\] \[Т — 0,400\; N_{1} = 0\] | \[\сумма F_{y} = m_{1} a_{y}\] \[N_{1} — 19,6\; N = 0 \ldotp\] |
Решая для двух неизвестных, получаем N 1 = 19,6 Н и T = 0,40 Н 1 = 7,84 Н. Нижний блок также не ускоряет, поэтому применение второго закона Ньютона к этому блоку дает
Нижний блок также не ускоряет, поэтому применение второго закона Ньютона к этому блоку дает
\[\сумма F_{x} = m_{2} a_{x}\] \[Т — Р + 0,400\; N_{1} + 0,400\; N_{2} = 0\] | \[\сумма F_{y} = m_{1} a_{y}\] \[N_{2} — 39,2\; N — N_{1} = 0 \ldotp\] |
Значения N 1 и T были найдены с помощью первой системы уравнений. Подставив эти значения во вторую систему уравнений, мы можем определить N 2 и P. Они равны
\[N_{2} = 58,8\; Н\; и\; Р = 39,2\; N \ldotp\]
Значение
Понимание того, в каком направлении направить силу трения, часто бывает затруднительным. Обратите внимание, что каждая сила трения, отмеченная на рисунке \(\PageIndex{4}\), действует в направлении, противоположном движению соответствующего блока.
Пример \(\PageIndex{3}\): Ящик на разгоняющемся грузовике
Ящик весом 50,0 кг лежит на кузове грузовика, как показано на рисунке \(\PageIndex{5}\). Коэффициенты трения между поверхностями равны \(\mu_{k}\) = 0,300 и \(\mu_{s}\) = 0,400. Найти силу трения на ящике, когда грузовик движется вперед относительно земли со скоростью (а) 2,00 м/с 2 и (б) 5,00 м/с 2 .
Коэффициенты трения между поверхностями равны \(\mu_{k}\) = 0,300 и \(\mu_{s}\) = 0,400. Найти силу трения на ящике, когда грузовик движется вперед относительно земли со скоростью (а) 2,00 м/с 2 и (б) 5,00 м/с 2 .
Стратегия
Силы, действующие на ящик, включают его вес, а также нормальные силы и силы трения, возникающие при контакте с кузовом грузовика. Начнем с предположения, что ящик не скользит. В этом случае на обрешетку действует сила трения покоя fs. Кроме того, ускорения ящика и грузовика равны. 9{2} \ldotp \end{split}\]
Значение
Относительно земли грузовик движется вперед со скоростью 5,0 м/с 2 , а ящик движется вперед со скоростью 2,94 м/с 2 . Следовательно, ящик скользит назад относительно кузова грузовика с ускорением 2,94 м/с 2 — 5,00 м/с 2 = -2,06 м/с 2 .
Пример \(\PageIndex{4}\): Сноубординг
Ранее мы проанализировали ситуацию, когда лыжник движется с постоянной скоростью, чтобы определить коэффициент кинетического трения. Теперь проведем аналогичный анализ для определения ускорения. Сноубордист на рисунке \(\PageIndex{6}\) скользит вниз по склону, наклоненному под углом \(\theta\) = 13° к горизонтали. Коэффициент кинетического трения между доской и снегом равен \(\mu_{k}\) = 0,20. Каково ускорение сноубордиста?
Рисунок \(\PageIndex{6}\): (a) Сноубордист скользит вниз по склону, наклоненному под углом 13° к горизонтали. (b) Диаграмма свободного тела сноубордиста.Стратегия
Силы, действующие на сноубордиста, это его вес и контактная сила склона, которая имеет составляющую по нормали к склону и составляющую вдоль склона (сила кинетического трения). Поскольку она движется вдоль склона, наиболее удобной системой отсчета для анализа ее движения является система с осью x вдоль и осью y, перпендикулярной наклону. В этой системе отсчета как нормальная сила, так и сила трения лежат вдоль осей координат, компоненты веса составляют mg sin θ вдоль склона и mg cos \(\theta\) под прямым углом к склону , а единственное ускорение — вдоль ось x (a у = 0).
В этой системе отсчета как нормальная сила, так и сила трения лежат вдоль осей координат, компоненты веса составляют mg sin θ вдоль склона и mg cos \(\theta\) под прямым углом к склону , а единственное ускорение — вдоль ось x (a у = 0).
Решение
Теперь мы можем применить второй закон Ньютона к сноубордисту:
\[\begin{split} \sum F_{x} & = ma_{x} \\ mg \sin \theta — \mu_{k} N & = ma_{x} \end{split}\] | \[\begin{split} \sum F_{y} & = ma_{y} \\ N — mg \cos \theta &= m(0) \ldotp \end{split}\] |
Из второго уравнения N = mg cos \(\theta\). Подставив это в первое уравнение, находим 9{2} \ldotp \end{split}\]
Значимость
Из этого уравнения следует, что если \(\theta\) достаточно мало или \(\mu_{k}\) достаточно велико, то х отрицательно, то есть сноубордист тормозит.
Упражнение \(\PageIndex{4}\)
Теперь сноубордист движется вниз по склону с уклоном 10,0°. Чему равно ускорение лыжника?
Эта страница под названием 6.5: Friction (Part 2) публикуется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать оглавление
- нет
- Теги
- трение
- Кинетическое трение
- источник@https://openstax.





 Так как шарики были брошены из
Так как шарики были брошены из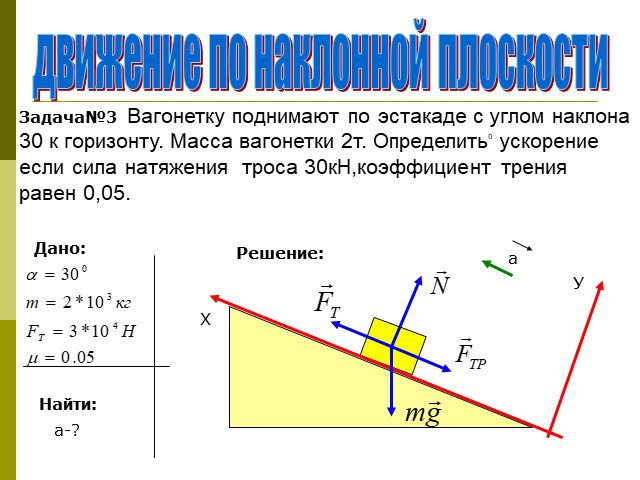



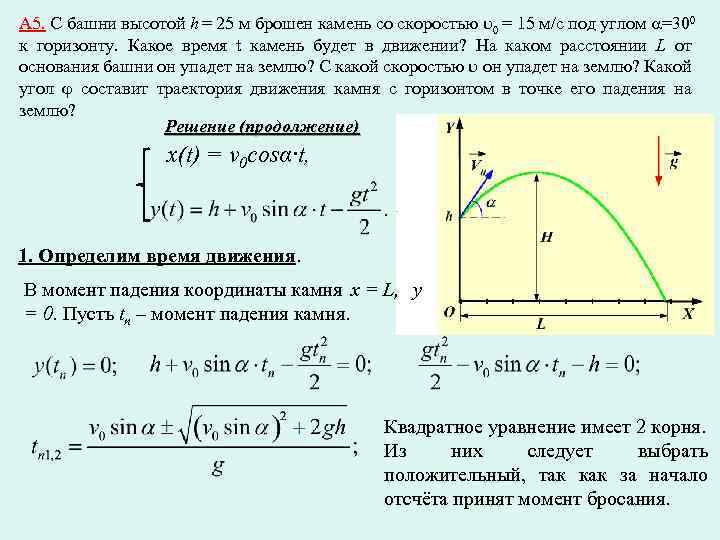
 Таким образом, условие «встречи»:
Таким образом, условие «встречи»: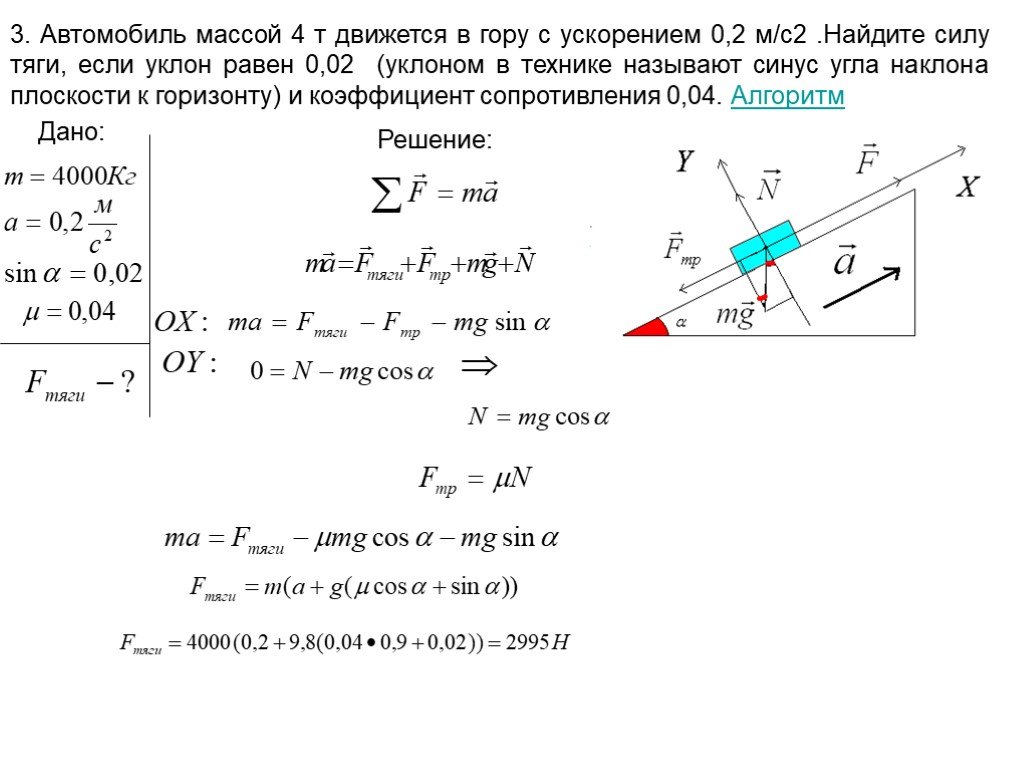 21
21

 С заднего края платформы производится
С заднего края платформы производится
 23).
23).
Leave A Comment