Решение логических задач
Решение
логических задач
Зорина Ольга Александровна
Учитель информатики
МБОУ «СШ №7» г.Новый Уренгой
Зорина Наталья Александровна
Учитель информатики
МБОУ «СШ №1» г.Новый Уренгой
Для какого из приведенных чисел ложно высказывание:
НЕ (число ИЛИ (число чётное)?
1) 48 2) 49 3) 50 4) 51
НЕ (х ИЛИ (х чётное) = (x = 50) ИЛИ (х чётное)
х
x=50
48
49
x чёт
ИЛИ
50
51
1
0
1
0
0
0
1
1
1
1
0
1
Ответ: 2.
Для какого из приведенных чисел истинно высказывание:
НЕ (число 45) И (число нечётное)?
1) 44 2) 45 3) 46 4) 47
НЕ (х 45) И (х нечётное) = (x И (х нечётное)
х
x
44
45
x нечёт
И
46
47
0
1
0
1
1
1
0
0
0
0
1
0
Ответ: 2.
Для какого из приведенных названий животных истинно высказывание:
НЕ (первая буква гласная) И
1) Леопард 2) Ягуар 3) Антилопа 4) Кошка
НЕ (1 гл) И НЕ (посл согл) = (1 согл) И (посл гл)
х
1 согл
Леопард
Ягуар
посл гл
И
Антилопа
Кошка
0
1
0
0
0
0
1
0
0
1
1
1
Ответ: 4.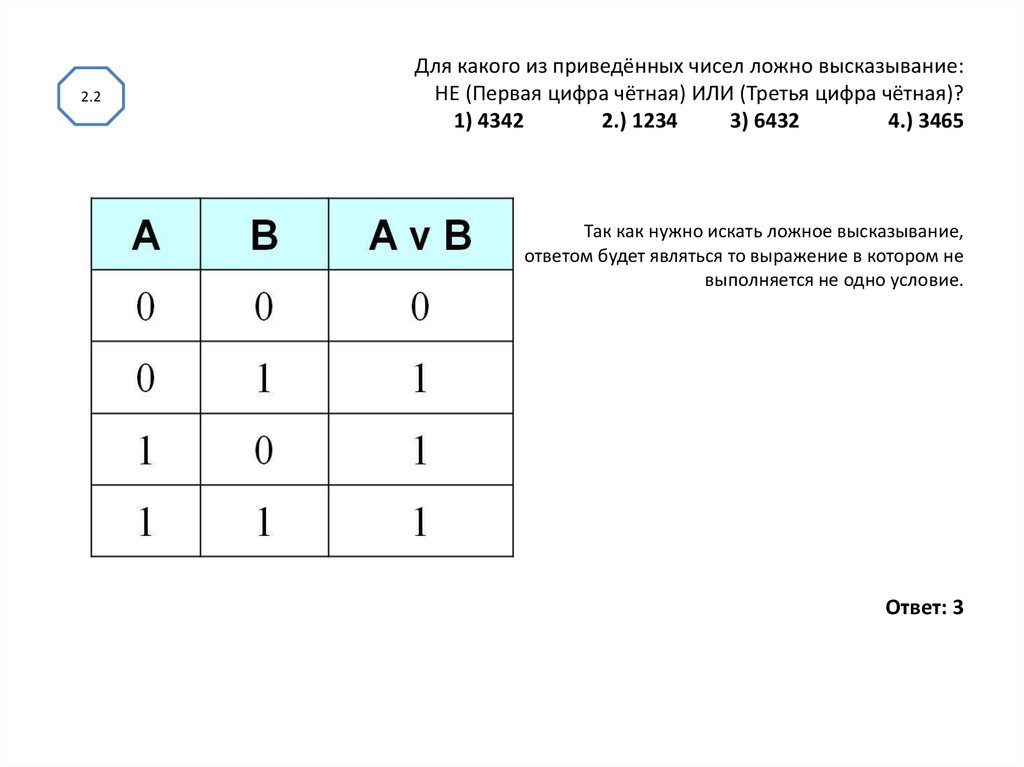
Для какого из приведенных названий птиц истинно высказывание:
НЕ ((первая буква согласная)
1) Коршун 2) Чайка 3) Удод 4) Иволга
НЕ ((1 согл) ИЛИ (посл гл)) = (1 гл) И (посл согл)
х
1 гл
Коршун
Чайка
посл согл
И
Удод
Иволга
1
0
0
0
0
0
1
1
1
1
0
0
Ответ: 3.
Для какого из приведенных чисел истинно высказывание:
НЕ (число И (число нечётное)?
1) 21 2) 30 3) 52 4) 63
НЕ (х И (x нечёт) = (x 30) И (x нечёт)
х
х 30
21
30
х нечёт
И
52
63
1
0
0
0
0
0
0
1
0
1
1
1
Ответ: 4.
Самостоятельная работа
I вариант
- Для какого из приведённых имён истинно высказывание:
НЕ (Первая буква гласная) И (Третья буква согласная)?
1) Елена 2) Полина
3) Кристина 4) Анна
II вариант
- Для какого из приведённых имён истинно высказывание:
НЕ (Первая буква гласная) И (Количество букв 5)?
1) Иван 2) Николай
3) Семён 4) Илларион
I вариант
2. Для какого из приведённых слов истинно высказывание:
(Первая буква гласная) И НЕ (Последняя буква согласная)?
1) слива 2) яблоко
3) банан 4) ананас
II вариант
2. Для какого из приведённых слов истинно высказывание:
НЕ (Первая буква гласная) И (Последняя буква согласная)?
1) слива 2) яблоко
3) банан 4) ананас
I вариант
3.
Для какого из приведённых чисел истинно высказывание:
НЕ (Первая цифра чётная) И (Сумма цифр чётная)?
1) 638 2) 442 3) 357 4) 123
II вариант
3. Для какого из приведённых чисел истинно высказывание:
НЕ (Первая цифра чётная) И НЕ (Сумма цифр чётная)?
1) 638 2) 442 3) 357 4) 123
I вариант
4. Для какого из приведённых чисел истинно высказывание:
НЕ (Число 10000) И (Число нечётное)?
1) 54321 2) 45980 3) 125 4) 24
II вариант
4. Для какого из приведённых чисел истинно высказывание:
НЕ (Число И НЕ (Число чётное)?
1) 54324 2) 4597 3) 46 4) 25
Для какого из приведённых значений числа X истинно высказывание: НЕ (X И (X 1) 6 2) 5 3) 4 4) 3 «
I вариант
5. Для какого из приведённых значений числа X истинно высказывание:
НЕ (X 5) И (X 4)?
1) 4 2) 5 3) 6 4) 7
II вариант
5. Для какого из приведённых значений числа X истинно высказывание:
НЕ (X И (X
1) 6 2) 5 3) 4 4) 3
НЕ ((х
= (х 70) И (х чётное)
70
71 70 и нечётное
72 70 и чётное
Ответ: 72.
25
24 1 1 =1 0 =1
наибольшее
23 1 0 =1 1 =1
Ответ: 24.
НЕ (х
= (х 30) И (х чётное)
30
31 30 и нечётное
32 30 и чётное
Ответ: 32.
НЕ (х
= (х 50) ИЛИ (х нечётное)
50
51 1 1 = 1
50 0 0 = 0
Ответ: 50.
Домашнее задание: решить 5 задач
1)
2)
3)
4)
5)
Не число 50 и число четное. Примеры решения задач
«Комплексные числа» — Название “мнимые числа” ввёл французский математик и философ Р.Декарт. Мнимая единица. Решение. Первым учёным, предложившим ввести числа новой природы, был Джорж Кордано. Комплексные числа. Квадратный корень из положительного числа имеет два значения – положительное и отрицательное. Числа вида a + bi, где a и b – действительные числа, i – мнимая единица, называются комплексными.
«Системы счисления» — ц Перевод из двоичной системы счисления в восьмеричную и шестнадцатеричную. Десятичная система счисления. Позиция цифры в числе называется ее разрядом, а количество цифр в числе его разрядностью.
Количество цифр в СС называется ее основанием. Шестнадцатеричная система счисления. В позиционной системе вес цифры зависит от ее позиции (места) в числе.
«Алгебра высказываний» — Соединение двух высказываний а и в в одно с помощью союза «и». Эквиваленция -. Конъюнкция (логическое умножение) -. Этапы развития логики. Основные операции алгебры высказываний. Простые высказывания будем называть логическими переменными, а сложные логическими функциями. Логики: Слово «логика» обозначает совокупность правил, которым подчиняется процесс мышления.
«Число 4» — 4.Развивать внимание, логическое мышление. 2.Освоение математической символики. 3. Формирование основных понятий: количественные, натуральные числа. Число и цифра 4. Состав числа 4. =1+3=4. 1.Знакомство с числом 4, с цифрой 4. = 3+1=4. Цели и задачи: Закрепление. = 2+2=4.
«Системы счисления» — Восьмеричная система счисления. Какие системы счисления используются для общения с компьютером? Системы счисления. Шестнадцатеричная система счисления.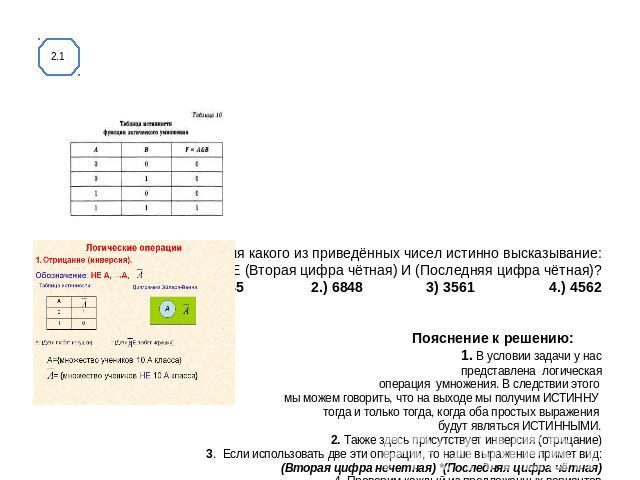
«Урок числа от 1 до 10» — Какие карточки перевернуты? Состав числа 5. Геометрические фигуры. Состав числа 6. Раз, два, три, четыре, пять! Работа в тетрадях. Сказка. Состав числа 7. Работа в тетради. Физкультминутка. 8 Игра «Отпусти рыбку в море». Игра «Прибавляем 1 и вычитаем 1». Будем вместе повторять. А теперь мы отдохнем И опять считать начнем.
Логика широко используется не только в жизни, но и в реализации работы цифровой техники, в том числе и компьютеров. Цифровая техника содержит так называемые логические элементы, которые реализуют те или иные логические операции.
В логике используются простые и составные логические высказывания (повествовательные утверждения), которые могут быть истинными (1 ) или ложными (0 ).
Пример простых высказываний:
- «Москва — столица России» (1)
- «Дважды два — три» (0)
- «Здорово!» (не является высказыванием)
Для объединения нескольких простых высказываний в одно составное используют логические операции.
Существуют три базовые логические операции: И, ИЛИ, НЕ.
Порядок операций:
- действия в скобках, операции сравнения (, ≥, =, ≠)
Рассмотрим каждую из трех операций отдельно.
1. Операция НЕ меняет значение логического высказывания на противоположное. Эта операция носит также названия «инверсия», «логическое отрицание». Знак операции: ¬
Таблица истинности:
| А | НЕ А |
| 0 | 1 |
| 1 | 0 |
2. Операция И для составного высказывания дает истину только тогда, когда истинны все входящие простых высказывания. Данную операцию можно также называть как «логическое умножение» или «конъюнкция». Знак операции: , & , /\
Таблица истинности:
| A | B | A И B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
3.
Операция ИЛИ для составного высказывания дает истину тогда, когда истинно хотя бы одно любое входящее простое высказывание. «Логическое сложение», «дизъюнкция». Знак операции: + , v
| A | B | A ИЛИ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Примеры решения задач
Пример 1.
Для какого из приведённых чисел ложно высказывание:
НЕ (число > 50) ИЛИ (число чётное)?
1) 9 2) 56 3) 123 4) 8
Решение. Сначала выполняем сравнения в скобках, затем операция НЕ, в последнюю очередь — операция ИЛИ.
1) Подставим число 9 в выражение:
НЕ (9 > 50) ИЛИ (9 чётное)
НЕ (ложь) ИЛИ (ложь) = истина ИЛИ ложь = истина
9 нам не подходит, так как по условию мы должны получить ложь.
2) Подставим число 56 в выражение:
НЕ (56 > 50) ИЛИ (56 чётное)
НЕ (истина) ИЛИ (истина) = ложь ИЛИ истина = истина
56 тоже не подходит.
3) Подставим 123:
НЕ (123 > 50) ИЛИ (123 чётное)
НЕ (истина) ИЛИ (ложь) = ложь ИЛИ ложь = ложь
Число 123 подошло.
Эту задачу можно было решить и по-другому:
НЕ (число > 50) ИЛИ (число чётное)
Нам надо получить ложное значение. Мы видим, что операция ИЛИ будет выполняться в последнюю очередь. Операция ИЛИ даст ложь, когда оба выражения НЕ(число) и (число чётное) будут ложны.
Так как условие (число чётное) должно быть равно ложному значению, то сразу отвергаем варианты с числами 56, 8.
Итак, можно решать прямой подстановкой, что долго и может дать ошибку при вычислении выражения; или же можно решать задачу быстро, проанализировав все простые условия.
Ответ: 3)
Пример 2
Для какого из приведённых чисел истинно высказывание:
НЕ (Первая цифра чётная) И НЕ (Последняя цифра нечётная)?
1) 6843 2) 4562 3) 3561 4) 1234
Сначала выполняем сравнения в скобках, затем операции НЕ над скобками, в последнюю очередь — операция И.
Все это выражение должно принимать истинное значение.
Так как операция НЕ меняет смысл высказывания на противоположный, мы может переписать это сложное выражение так:
(Первая цифра нечётная) И (Последняя цифра чётная) = истина
Как известно, логическое умножение И дает истину только тогда, когда истинны все простые высказывания. Таким образом, оба условия должны быть истинными:
(Первая цифра нечётная) = истина (Последняя цифра чётная) = истина
Как видно, подходит только число 1234
Ответ: 4)
Пример 3
Для какого из приведённых имён истинно
высказывание:
НЕ (Первая буква гласная) И (Количество букв > 5)?
1) Иван 2) Николай 3) Семён 4) Илларион
Перепишем выражение:
(Первая буква не гласная) И (Количество букв > 5) = истина
(Первая буква согласная) И (Количество букв > 5) = истина
Определение того, является ли число решением уравнения
Результаты обучения
- Определение того, является ли целое число решением уравнения
- Определить, является ли целое число решением уравнения
Определить, является ли число решением уравнения
Решение уравнения похоже на поиск ответа на головоломку.
Алгебраическое уравнение утверждает, что два алгебраических выражения равны. Решить уравнение означает определить значения переменной, которые делают уравнение истинным утверждением. Любое число, которое делает уравнение истинным, называется решением уравнения. Это ответ на загадку!
Решение уравнения
Решение уравнения — это значение переменной, которое дает истинное утверждение при подстановке в уравнение.
Процесс нахождения решения уравнения называется решением уравнения.
Найти решение уравнения означает найти значение переменной, при котором уравнение становится верным. Можете ли вы узнать решение [латекс]х+2=7?[/латекс] Если вы сказали [латекс]5[/латекс], вы правы! Мы говорим, что [латекс]5[/латекс] является решением уравнения [латекс]х+2=7[/латекс], потому что, когда мы подставляем [латекс]5[/латекс] вместо [латекс]х[/латекс] результирующее утверждение верно.
[латекс]\begin{array}{}\\ \hfill x+2=7\hfill \\ \hfill 5+2\stackrel{?}{=}7\hfill \\ \\ \hfill 7=7 \quad\checkmark \hfill \end{array}[/latex]
Поскольку [latex]5+2=7[/latex] является верным утверждением, мы знаем, что [latex]5[/latex] действительно является решением к уравнению.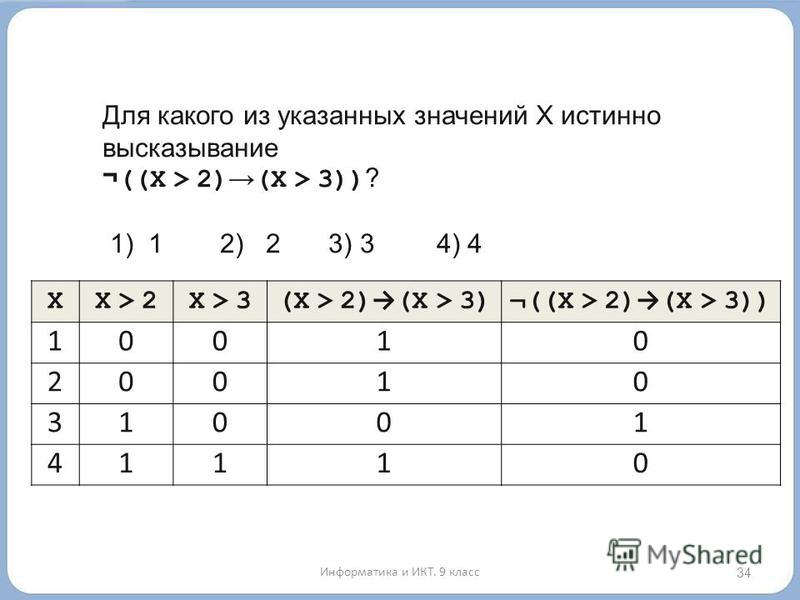
Символ [латекс]\stackrel{?}{=}[/латекс] спрашивает, равна ли левая часть уравнения правой части. Как только мы это узнаем, мы можем перейти на знак равенства [latex]=[/latex] или знак не равенства [latex]\not=[/latex].
Определить, является ли число решением уравнения.
- Подставьте число вместо переменной в уравнении.
- Упростите выражения в обеих частях уравнения.
- Определите, верно ли полученное уравнение.
- Если это правда, число является решением.
- Если это не так, число не является решением.
пример
Определите, является ли [латекс]х=5[/латекс] решением [латекс]6х — 17=16[/латекс].
Решение
Thirteen is not equal to 16 on the right side of the equation.»>Итак, [латекс]х=5[/латекс] не является решением уравнения [латекс]6х — 17=16[/латекс].
попробуйте
пример
Определите, является ли [латекс]у=2[/латекс] решением [латекс]6у — 4=5у — 2[/латекс].
Показать решение
попробуй
Определить, является ли целое число решением уравнения
Шаги, которые мы предпринимаем, чтобы определить, является ли число решением уравнения, одинаковы независимо от того, является ли решение целым или целым числом.
пример
Определите, является ли каждое из следующих решений решением [latex]2x — 5=-13\text{:}[/latex]
1.
[латекс]x=4[/латекс]
2. [латекс]x=-4[/латекс]
3. [латекс]x=-9[/латекс]
Раствор
| 1. Подставьте [латекс]4[/латекс] вместо x в уравнении, чтобы определить, верно ли оно. | |
| [латекс]2x-5=-13[/латекс] | |
| Замените x на [латекс]\цвет{красный}{4}[/латекс]. | [латекс]2(\цвет{красный}{4})-5=-13[/латекс] |
| Умножение. | [латекс]8-5=-13[/латекс] |
| Вычесть. | [латекс]3\не=-13[/латекс] |
Поскольку [латекс]x=4[/латекс] не дает истинного уравнения, [латекс]4[/латекс] не является решением уравнения.
| 2. Подставьте [латекс]−4[/латекс] вместо x в уравнении, чтобы определить, верно ли оно. | |
| [латекс]2x-5=-13[/латекс] | |
| Замените x на [латекс]\цвет{красный}{-4}[/латекс]. | [латекс]2(\цвет{красный}{-4})-5=-13[/латекс] |
| Умножение. | [латекс]-8-5=-13[/латекс] |
| Вычесть. | [латекс]-13=-13\quad\галочка[/латекс] |
Поскольку [латекс]x=-4[/латекс] дает верное уравнение, [латекс]-4[/латекс] является решением уравнения.
The second row states substitute negative 9 for x and has 2 times negative 9 minus 5 equals negative 13 with a question mark above the equal sign. The third row states multiply and has negative 18 minus 5 equals negative 13 with a question mark above the equal sign. The fourth row states subtract and has negative 23 is not equal to negative 13.»>Поскольку [латекс]x=-9[/латекс] не дает истинного уравнения, [латекс]-9[/латекс] не является решением уравнения.
попробуйте
В следующем видео мы покажем больше примеров того, как проверить, является ли целое число решением линейного уравнения.
Понимание оператора If-Else в Python [обновлено]
Принятие решений является важной концепцией любого языка программирования и требуется, когда вы хотите выполнить код, когда выполняется определенное условие. В этом блоге вы узнаете о знаменитом операторе if-else в Python. Мы будем использовать Jupyter Notebook для демонстрации кода.
Существует несколько форм операторов if-else. Давайте рассмотрим их один за другим.
Используется ключевое слово if, за которым следует условие.
Синтаксис:
если условие:
#оператор для выполнения, если условие истинно
Ниже приведен весь рабочий процесс работы операторов if:
Сначала проверяется тестовое выражение. Если выражение истинно, выполняется тело оператора if.
Если оно ложно, оператор, присутствующий после оператора if, выполняется. В любом случае любая строка кода, присутствующая снаружи, если оператор оценивается по умолчанию.
Чтобы лучше понять это, мы будем использовать пример:
а=20
если а>50:
print(«Это тело if»)
print(«Это вне блока if»)
Поскольку 20 не больше 50, оператор внутри блока if не будет выполняться. Вместо этого выполняется оператор, находящийся вне блока if.
В приведенном ниже коде будут выполнены оба оператора печати, поскольку a больше 50.
До сих пор мы могли указывать операторы, которые будут выполняться, если условие истинно. Теперь, если вы хотите оценить операторы, определяющие, является ли условие действительным и является ли отдельный набор операторов ложным, вы можете использовать условный оператор if-else.
Оператор if-else используется для выполнения как истинной, так и ложной части заданного условия. Если условие истинно, выполняется код блока if, а если условие ложно, выполняется код блока else.
Синтаксис:
если (условие):
#Выполняет этот блок, если условие истинно
иначе:
#Выполняет этот блок, если условие ложно
Здесь следует отметить, что Python использует отступы в обоих блоках для определения области действия кода. Другие языки программирования часто используют для этой цели фигурные скобки.
Ниже приведен весь рабочий процесс оператора if-else.
Сначала проверяется тестовое выражение. Если это правда, операторы, присутствующие в теле блока if, будут выполняться. Затем выполняются операторы, представленные ниже блока if. В случае, если тестовое выражение имеет ложные результаты, выполняются операторы, присутствующие в теле else, а затем выполняются операторы ниже if-else.
Ниже приведен пример, который лучше иллюстрирует, как работает if-else:
Поскольку значение «i» делится на два, выполняется оператор if.
Поскольку значение «i» не делится на два, выполняется оператор else.
Давайте теперь посмотрим, что такое вложенный оператор IF и как он работает.
Когда оператор if присутствует внутри другого оператора if, он называется вложенным оператором IF. Такая ситуация возникает, когда вам нужно фильтровать переменную несколько раз.
Синтаксис:
если (условие1):
#Выполняется, если условие1 истинно
если (условие2):
#Выполняется, если условие2 истинно
#Условие2 заканчивается здесь
#Условие1 заканчивается здесь
Во вложенных инструкциях IF вы всегда должны следить за отступом, чтобы определить область действия каждой инструкции. У вас может быть столько уровней вложенности, сколько требуется, но это делает программу менее оптимизированной и, как следствие, более сложной для чтения и понимания. Поэтому вы всегда должны стараться свести к минимуму использование вложенных операторов IF.
Приведенный ниже рабочий процесс демонстрирует, как работают вложенные операторы IF:
Ниже приведен еще один пример, показывающий, как работает вложенный ЕСЛИ: У нас есть число, и мы собираемся проверить, больше оно или меньше 25.
Если число меньше 25, мы проверим, является ли оно нечетное число или четное число. Если число больше 25, мы напечатаем, что число больше 25.
До сих пор с IF и if-else мы видели только бинарный подход. Предположим, у нас есть проблема, которая имеет несколько условий. В этом случае на помощь приходит оператор if-elif-else.
Проверяет условие оператора if. Если это ложно, оператор elif оценивается. Если условие elif ложно, оценивается оператор else.
Синтаксис:
если (условие):
выписка
элиф (состояние):
выписка
.
.
иначе:
Выписка
Ниже приведена блок-схема, показывающая, как работает лестница if-elif-else. Проверяется тестовое выражение1. Если это подтверждается, тело if оценивается. Если оно ложно, то управление переходит к продолжающемуся Test Expression2. Если это правда, выполняется тело elif1. Если оно ложно, проверяется тестовое выражение3. Если это правда, выполняется тело elif2.
Если оно ложно, вычисляется тело else. Затем проверяется любой оператор ниже в if-elif.
Приведенная ниже программа использует лестницу if-elif-else, чтобы проверить, является ли буква гласной или согласной.
Теперь, когда мы рассмотрели основы if, else, elif и вложенных IF, давайте сделаем несколько упражнений.
Что происходит, когда условие «если» не выполняется?
Если условный оператор верен, выполняется блок кода, включенный в оператор if. Но, если условие не выполняется, код внутри фигурных скобок пропускается, и выполняется следующий оператор if. Он показывает ошибку, потому что не соответствует указанному условию if.
Когда «иначе условие» не работает?
Иногда невозможно получить желаемый результат, используя «иначе условие». Это происходит из-за логической ошибки, которая возникает в программе. Это часто происходит, когда программа имеет более двух операторов или условий. Если у вас возникли проблемы с else, это потому, что вы указали оператору, что ‘;’ отмечает заключение вашего оператора if; следовательно, когда он обнаруживает «еще» несколькими шагами позже, он начинает сообщать.
Что означает for Else и While Else в Python?
Python предоставляет удобные функции, такие как for-else и while-else. Блок else можно использовать сразу после цикла for и while. Если оператор break не завершает цикл, будет выполнен блок else.
Синтаксис for-else Python:
для i в диапазоне (n):
#код
еще :
#code
Синтаксис для while-else Python:
в то время как состояние:
#код
иначе:
#код
Что означает == в Python?
Равенство двух объектов сравнивается с помощью оператора ‘==’. В Python один знак равенства ‘=’ присваивает значение переменной, а два знака равенства ‘==’ проверяют, дают ли два выражения одно и то же значение. В общем, вы сравниваете стоимость двух предметов. Если вы хотите оценить, имеют ли два объекта схожие характеристики, и не беспокоитесь о том, где они хранятся в памяти, это все, что вам нужно.
Сокращение Если
Сокращенный оператор — это исполняемый оператор, построенный настолько лаконично, что содержит только одну строку кода.
Например, Python предлагает различные сокращенные операторы, что позволяет нам составлять наш код более компактно и эффективно.
ShortHand Если … иначе
Shorthand — отличный подход к построению небольших операторов if-else, когда вам нужно выполнить только одну строку. Python предоставляет программистам множество синтаксических опций для написания одного и того же кода. Например, вы можете создать оператор if-else в одной строке кода, используя сокращенную функцию if-else.
Формат сокращенной записи, если не указано иное:
оператор 1 если условие еще оператор 2
Операторы Python
Операторы обычно используются для выполнения функций над значениями и атрибутами. Это общие символы, используемые в логических и математических процессах. Например, арифметические операторы могут выполнять основные математические операции. Для сравнения двух значений используются операторы отношения, и результаты являются истинными или ложными в зависимости от критериев.
Булевы или логические операторы: И, ИЛИ и НЕ. Побитовые операторы — это операторы для двоичных чисел.
И
И — это логический оператор в Python. Оператор возвращает ИСТИНА, если оба значения действительны, то есть как слева, так и справа.
ИЛИ
Оператор возвращает значение ИЛИ, если какое-либо из значений верно, это может быть правая или левая сторона.
НЕ
Оператор возвращает истину, если обе части значений ложны.
Ниже приведен пример логических операторов:
р = правда
с = ложь
print((‘p и s есть’, x и y))
print((‘p или s is’, x или y))
print((‘не р есть’, не х))
Выход:
(p и s, False)
(p или s’, True)
(«не p», ложь)
Оператор pass в программировании на Python — это пустой оператор, который можно использовать в качестве пробела для будущего кода. Например, предположим, что у вас есть нереализованный цикл или функция, которую вы собираетесь построить.
Вы можете использовать оператор pass в таких обстоятельствах. Однако есть разница между оператором pass и комментарием; интерпретатор не может игнорировать оператор pass, в то время как комментарий может быть проигнорирован.
Switch case не встроен в Python, но вы можете реализовать их с помощью различных других методов. Например, переключение управления выполнением может быть выполнено с помощью оператора управления. Кроме того, Python разработал структурное сопоставление с образцом, функцию переключения регистра. Используя ключевые слова соответствия и регистра, вы можете применить эту функцию на практике. Вы можете использовать ключевые слова match и case как имена переменных и функций. Оператор switch сравнивает значения переменных со значениями, указанными в операторах case. Оператор case часто является оператором многостороннего перехода.
Лямбда, если еще в Python
Хотя лямбда-функция может иметь много параметров, она имеет только одно выражение. Оценка и возврат выполняются для этого единственного выражения.
Следовательно, лямбда-функции могут использоваться как функциональные объекты. Лямбда-функция вернет значение для каждого заданного данных. Когда условие в данном случае истинно, возвращается блок if; когда оно ложно, возвращается блок else.
Формат лямбда-функции if-else:
лямбда <аргументы> : <оператор1> if <условие> else <оператор2>
Программа для проверки наибольшего из трех чисел
В приведенном выше коде мы сначала проверяем, выше ли «a», чем «b» и «c». Затем мы печатаем «a» как наибольшее число.
В случае, если это неверно, мы затем проверяем, больше ли «b», чем «a» и «c». Если это так, мы печатаем ‘b’ как наибольшее число. В противном случае ‘c’ является наибольшим числом.
Та же программа может быть создана с использованием вложенного оператора IF следующим образом:
Вот еще одно упражнение, позволяющее проверить, делится ли число на два, три или пять.
Проблема с приведенным выше кодом заключается в том, что 12 также делится на три, но мы не можем его напечатать.
Leave A Comment