Самостоятельная работа по теме «Закон Кулона»
МКОУ «Мостовская СОШ»
Самостоятельная работа по теме
«Закон Кулона»
УМК Мякишев Г.Я., Буховцев Б.Б.
10 класс
Составитель: учитель физики
Синяк Татьяна Ивановна
2017г
Вариант-1
1.С какой силой взаимодействуют два точечных заряда 10нКл и 15нКл, находящиеся на расстоянии 5см друг от друга?
2.Два неподвижных точечных заряда действуют друг на друга с силами, модуль которых равен F.Во сколько раз увеличится модуль этих сил, если один заряд увеличить в 4 раза, другой заряд уменьшить в 2 раза, а расстояние между ними оставить прежним?
3.Как направлена (вправо, влево, вверх, вниз) кулоновская сила, действующая на положительный точечный электрический заряд
+ 2q, помещенный в центр квадрата, в вершинах которого находятся заряды +q, +q, — q, — q?
Вариант-2
1. На каком расстоянии друг от друга находятся два заряда 10нКл и 15нКл, если они взаимодействуют с силой 5,4·10-4Н?
На каком расстоянии друг от друга находятся два заряда 10нКл и 15нКл, если они взаимодействуют с силой 5,4·10-4Н?
2.Два неподвижных точечных заряда действуют друг на друга с силами, модуль которых равен F.Во сколько раз увеличится модуль этих сил, если один заряд увеличить в 3 раза, другой заряд уменьшить в 2 раза, а расстояние между ними оставить прежним?
3.Точечный отрицательный заряд q помещен между разноименно заряженными шариками. Куда направлена (вправо, влево, вверх, вниз) равнодействующая кулоновских сил, действующих на заряд q?
Вариант-3
1.Два точечных заряда , находящиеся на расстоянии 5см друг от друга, взаимодействуют с силой5,4·10-4Н. Какова величина второго заряда, если первый заряд равен 10 нКл?
2. Два неподвижных точечных заряда действуют друг на друга с силами, модуль которых равен F.Во сколько раз уменьшится модуль этих сил, если один заряд уменьшить в 5 раз, другой заряд увеличить в 2 раза, а расстояние между ними оставить прежним?
3. Как направлена (вправо, влево, вверх, вниз) кулоновская сила,
Как направлена (вправо, влево, вверх, вниз) кулоновская сила,
действующая на положительный точечный электрический заряд + q, помещенный в центр квадрата, в вершинах
которого находятся заряды +q, +q, — q, — q?
Вариант-4
1.Два точечных заряда , находящиеся на расстоянии 5см друг от друга, взаимодействуют с силой 5,4·10-4Н. Какова величина первого заряда, если второй заряд равен 15 нКл?
2.Два маленьких шарика, обладающих зарядами q каждый, находятся на расстоянии r друг от друга и притягиваются с силой 3F. Какова сила электростатического притяжения двух других шариков, если заряд одного 3q,заряд другого q/3, а расстояние между их центрами 3r?
3.Точечный отрицательный заряд помещен вблизи одинаковых одноименно заряженных шариков .Как направлена (вверх, вниз, влево, вправо, к наблюдателю, от наблюдателя) равнодействующая кулоновских сил, действующих на заряд?
Ответы
Вариант-1
1. 5,4·10-4Н 2.В 2 раза 3.Влево
5,4·10-4Н 2.В 2 раза 3.Влево
Вариант-2
1.5см 2.В 1,5 раза 3.Вправо
Вариант-3
1.15нКл 2.В 2,5 раза 3.Вниз
Вариант-4
1.10нКл 2.F/3 3.Влево
Источники информации
1.Громцева О.И. ЕГЭ. Физика. Высший балл. Самостоятельная подготовка к ЕГЭ/
О. И. Громцева. – М.: Издательство «Экзамен», 2017.
2.Демидова М.Ю. ЕГЭ 2015. – Физика. Типовые тестовые задания/ М.Ю. Демидова, В.А. Грибов, — М.: Издательство «Экзамен», 2015.
Глава 17. Взаимодействие электрических зарядов. Закон Кулона, принцип суперпозиции
Взаимодействие электрических зарядов описывается законом Кулона, который утверждает, что сила взаимодействия двух покоящихся точечных зарядов в вакууме равна
(17.1) |
где и — модули зарядов, — расстояние между ними.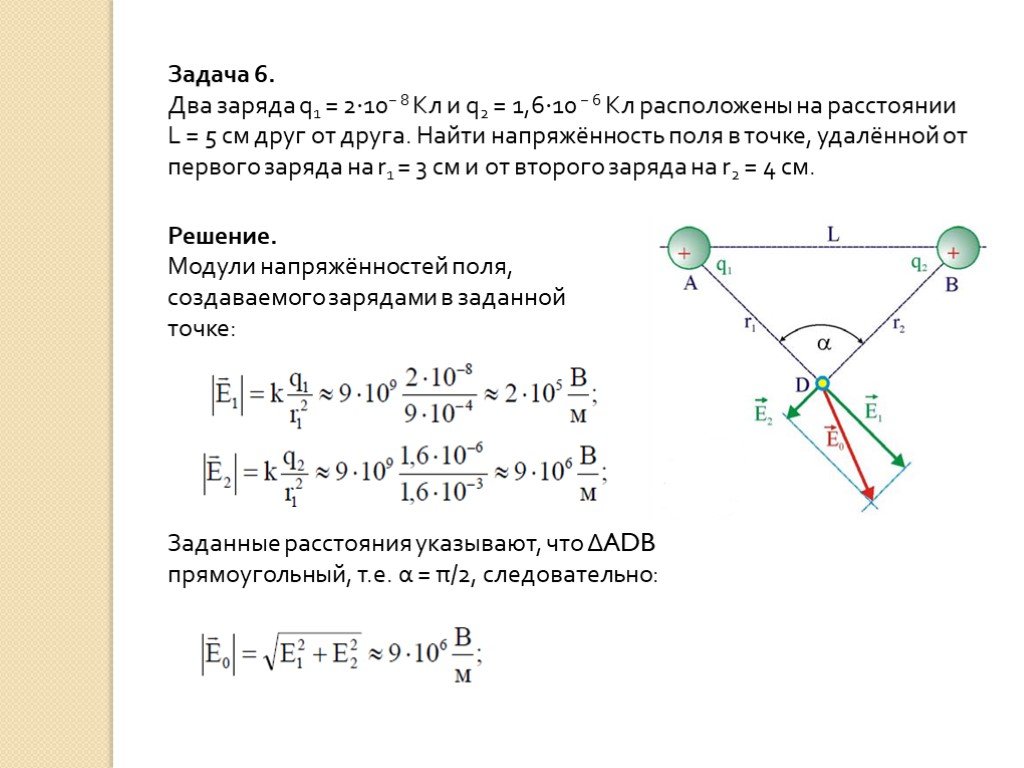 Коэффициент пропорциональности в формуле (17.1) зависит от системы единиц. В международной системе единиц СИ этот коэффициент принято записывать в виде
Коэффициент пропорциональности в формуле (17.1) зависит от системы единиц. В международной системе единиц СИ этот коэффициент принято записывать в виде
(17.2) |
где величина называется электрической постоянной, размерность величины сводится к отношению размерности длины к размерности электрической емкости (Фарада). Электрические заряды бывают двух типов, которые условно принято называть положительным и отрицательным. Как показывает опыт, заряды притягиваются, если они разноименные и отталкиваются, если одноименные.
В любом макроскопическом теле содержится огромное количество электрических зарядов, поскольку они входят в состав всех атомов: электроны заряжены отрицательно, протоны, входящие в состав атомных ядер — положительно. Однако большинство тел, с которыми мы имеем дело, не заряжены, поскольку количество электронов и протонов, входящих в состав атомов, одинаково, а их заряды по абсолютной величине в точности совпадают. Тем не менее, тела можно зарядить, если создать в них избыток или недостаток электронов по сравнению с протонами. Для этого нужно передать электроны, входящие в состав какого-нибудь тела, другому телу. Тогда у первого возникнет недостаток электронов и соответственно положительный заряд, у второго — отрицательный. Такого рода процессы происходят, в частности, при трении тел друг о друга.
Тем не менее, тела можно зарядить, если создать в них избыток или недостаток электронов по сравнению с протонами. Для этого нужно передать электроны, входящие в состав какого-нибудь тела, другому телу. Тогда у первого возникнет недостаток электронов и соответственно положительный заряд, у второго — отрицательный. Такого рода процессы происходят, в частности, при трении тел друг о друга.
Если заряды находятся в некоторой среде, которая занимает все пространство, то сила их взаимодействия ослабляется по сравнению с силой их взаимодействия в вакууме, причем это ослабление не зависит от величин зарядов и расстояния между ними, а зависит только от свойств среды. Характеристика среды, которая показывает, во сколько раз ослабляется сила взаимодействия зарядов в этой среде по сравнению с силой их взаимодействия в вакууме, называется диэлектрической проницаемостью этой среды и, как правило, обозначается буквой . Формула Кулона в среде с диэлектрической проницаемостью принимает вид
(17. |
Если имеется не два, а большее количество точечных зарядов для нахождения сил, действующих в этой системе, используется закон, который называется принципомсуперпозиции1. Принцип суперпозиции утверждает, что для нахождения силы, действующей на один из зарядов (например, на заряд ) в системе из трех точечных зарядов , и надо сделать следующее. Сначала надо мысленно убрать заряд и по закону Кулона найти силу, действующую на заряд со стороны оставшегося заряда . Затем следует убрать заряд и найти силу, действующую на заряд со стороны заряда . Векторная сумма полученных сил и даст искомую силу.
Принцип суперпозиции дает рецепт поиска силы взаимодействия неточечных заряженных тел. Следует мысленно разбить каждое тело на части, которые можно считать точечными, по закону Кулона найти силу их взаимодействия с точечными частями, на которое разбивается второе тело, просуммировать полученные вектора. Ясно, что такая процедура математически очень сложна, хотя бы потому, что необходимо сложить бесконечное количество векторов.
Кроме того, школьник должен знать (без вывода) формулы для силы, действующей на точечный заряд со стороны равномерно заряженной сферы и бесконечной плоскости. Если имеется сфера радиуса , равномерно заряженная зарядом , и точечный заряд , расположенный на расстоянии от центра сферы, то величина силы взаимодействия равна
(17.4) |
если точечный заряд находится снаружи сферы, и
(17.5) |
если заряд находится внутри (причем не обязательно в центре).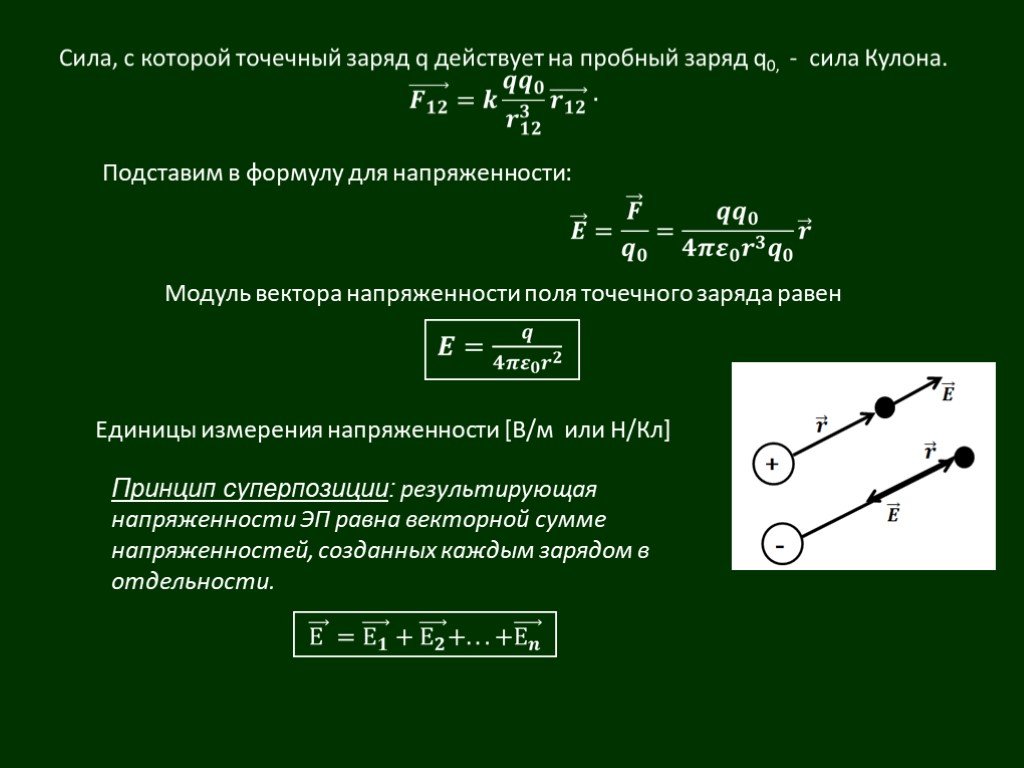 Из формул (17.4), (17.5) следует, что сфера снаружи создает такое же электрическое поле как весь ее заряд, помещенный в центре, а внутри — нулевое.
Из формул (17.4), (17.5) следует, что сфера снаружи создает такое же электрическое поле как весь ее заряд, помещенный в центре, а внутри — нулевое.
Если имеется очень большая плоскость с площадью , равномерно заряженная зарядом , и точечный заряд , то сила их взаимодействия равна
(17.6) |
где величина имеет смысл поверхностной плотности заряда плоскости. Как следует из формулы (17.6) сила взаимодействия точечного заряда и плоскости не зависит от расстояния между ними. Обратим внимание читателя на то, что формула (17.6) является приближенной и «работает» тем точнее, чем дальше точечный заряд находится от ее краев. Поэтому при использовании формулы (17.6) часто говорят, что она справедлива в рамках пренебрежения «краевыми эффектами», т.е. когда плоскость считается бесконечной.
Рассмотрим теперь решение данных в первой части книги задач.
Согласно закону Кулона (17.1) величина силы взаимодействия двух зарядов из
 1.1 выражается формулой
1.1 выражается формулойЗаряды отталкиваются (ответ 2).
Поскольку капелька воды из задачи 17.1.2 имеет заряд ( – заряд протона), то она имеет в избытке электронов по сравнению с протонами. Значит при потере трех электронов их избыток уменьшится, и заряд капельки станет равен (ответ 2).
Согласно закону Кулона (17.1) величина силы взаимодействия двух зарядов при увеличении в раз расстояния между ними уменьшится в раз (
Если заряды двух точечных тел увеличить в раз при неизменном расстоянии между ними, то сила их взаимодействия, как это следует из закона Кулона (17.1), увеличится в раз (задача 17.1.4 — ответ 3).
При увеличении одного заряда в 2 раза, а второго в 4, числитель закона Кулона (17.1) увеличивается в 8 раз, а при увеличении расстояния между зарядами в 8 раз — знаменатель увеличивается в 64 раза. Поэтому сила взаимодействия зарядов из задачи 17.1.5 уменьшится в 8 раз (ответ 4).
Поэтому сила взаимодействия зарядов из задачи 17.1.5 уменьшится в 8 раз (ответ 4).
При заполнении пространства диэлектрической средой с диэлектрической проницаемостью = 10, сила взаимодействия зарядов согласно закону Кулона в среде (17.3) уменьшится в 10 раз (
Сила кулоновского взаимодействия (17.1) действует как на первый, так и на второй заряд, а поскольку их массы одинаковы, то ускорения зарядов, как это следует из второго закона Ньютона, в любой момент времени одинаковы (задача 17.1.7 — ответ 3).
Похожая задача, но массы шариков разные. Поэтому при одинаковой силе ускорение шарика с меньшей массой в 2 раза больше ускорения шарика с меньшей массой , причем этот результат не зависит от величин зарядов шариков (задача 17.1.8 — ответ 2).
Поскольку электрон заряжен отрицательно, он будет отталкиваться от шара (задача 17.1.9). Но поскольку начальная скорость электрона направлена к шару, он будет двигаться в этом направлении, но его скорость будет уменьшаться. В какой-то момент он на мгновение остановится, а потом будет двигаться от шара с увеличивающейся скоростью (ответ 4).
В какой-то момент он на мгновение остановится, а потом будет двигаться от шара с увеличивающейся скоростью (ответ 4).
В системе двух заряженных шариков, связанных нитью (задача 17.1.10), действуют только внутренние силы. Поэтому система будет покоиться и для нахождения силы натяжения нити можно использовать условия равновесия шариков. Поскольку на каждый из них действуют только кулоновская сила и сила натяжения нити, то из условия равновесия заключаем, что эти силы равны по величине.
Отсюда
где (ответ 1).
Система трех шариков в задаче 17.2.1 покоится, поэтому силы натяжения должны компенсировать силы кулоновского отталкивания крайних зарядов. Последние найдем по закону Кулона и принципу суперпозиции. Каждый крайний заряд отталкивается от центрального заряда и другого крайнего. Для суммы этих сил получаем
Этой величине и будет равна сила натяжения нитей (ответ 4).
Для нахождения силы, действующей на заряд — в задаче 17.2.2, используем принцип суперпозиции. На заряд — действуют силы притяжения к левому и правому зарядам (см. рисунок). Поскольку расстояния от заряда — до зарядов одинаковы, модули этих сил равны друг другу и они направлены под одинаковыми углами к прямой, соединяющей заряд — с серединой отрезка — . Поэтому сила, действующая на заряд — направлена вертикально вниз (вектор результирующей силы выделен жирным на рисунке; ответ 4).
Задача 17.2.3 похожа на предыдущую, но изменен знак одного из зарядов. Поэтому сила, действующая на заряд — со стороны правого заряда, не изменившись по величине, изменится по направлению (см. рисунок). Поэтому вектор результирующей силы будет направлен влево (вектор результирующей силы выделен жирным на рисунке; ответ 1). |
|
На каждый заряд в задаче 17.2.4 действуют силы отталкивания со стороны двух других зарядов (см. рисунок), причем значения этих сил одинаковы (из-за равенства величин всех зарядов и расстояний между ними) и равны |
Из-за равенства значений сил-слагаемых параллелограмм сложения сил представляет собой ромб, и, следовательно, вектор результирующей силы направлен вдоль биссектрисы треугольника из зарядов (выделен жирным на рисунке). Поэтому угол, отмеченный на рисунке дугой равен 30°, а значение результирующей силы равно
(ответ 3).
Из формулы (17.6) заключаем, что правильный ответ в задаче 17.2.5 — 4. В задаче 17.2.6 нужно использовать формулу для силы взаимодействия точечного заряда и сферы (формулы (17. 4), (17.5)). Имеем = 0 (ответ 3).
4), (17.5)). Имеем = 0 (ответ 3).
В задаче 17.2.7 необходимо применить принцип суперпозиции к двум сферам. Принцип суперпозиции утверждает, что взаимодействие каждой пары зарядов не зависит от наличия других зарядов. Поэтому каждая сфера действует на точечный заряд независимо от другой сферы, и для нахождения результирующей силы нужно сложить силы со стороны первой и второй сфер. Поскольку точечный заряд расположен внутри внешней сферы, она не действует на него (см. формулу (17.5)), внутренняя действует с силой
где . Поэтому и результирующая сила равна этому выражению (ответ 2)
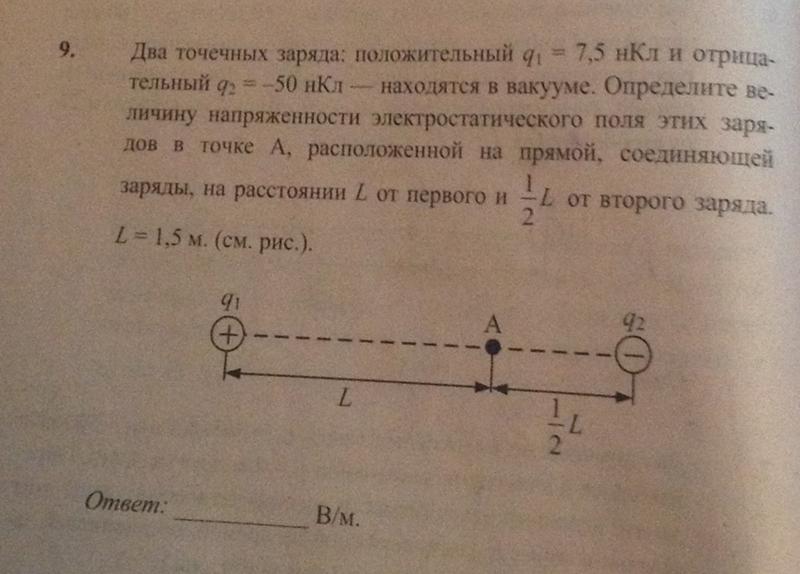
В задаче 17.2.8 также следует использовать принцип суперпозиции. Если заряд поместить в точку , то силы, действующие на него со стороны зарядов и , направлены влево. Поэтому по принципу суперпозиции имеем для равнодействующей силы
где — расстояния от зарядов до исследуемых точек. Если поместить положительный заряд в точку , то силы будут направлены противоположно, и на основании принципа суперпозиции находим результирующую силу
Если поместить положительный заряд в точку , то силы будут направлены противоположно, и на основании принципа суперпозиции находим результирующую силу
В точке на заряд будут действовать силы, направленные направо, и потому
Из этих формул следует, что наибольшей сила будет в точке — ответ 1.
Пусть, для определенности, заряды шариков и в задаче 17.2.9 положительны. Так как шарики одинаковы, заряды после их соединения распределяться между ними равномерно и для сравнения сил, нужно сравнить друг с другом величины
(1) |
которые представляют собой произведения зарядов шариков до и после их соединения. После извлечения квадратного корня сравнение (1) сводится к сравнению среднего геометрического и среднего арифметического двух чисел. А поскольку среднее арифметическое любых двух чисел больше их среднего геометрического, то сила взаимодействия шариков возрастет независимо от величин их зарядов (ответ 1).
А поскольку среднее арифметическое любых двух чисел больше их среднего геометрического, то сила взаимодействия шариков возрастет независимо от величин их зарядов (ответ 1).
Задача 17.2.10 очень похожа на предыдущую, а ответ — другой. Непосредственной поверкой легко убедиться, что сила может как увеличиться, так и уменьшиться в зависимости от величин зарядов. Например, если заряды равны по величине, то после соединения шариков их заряды станут равны нулю, поэтому нулевой будет и сила их взаимодействия, которая, следовательно, уменьшится. Если один из первоначальных зарядов равен нулю, то после соприкосновения шариков заряд одного из них распределится между шариками поровну, и сила их взаимодействия увеличится. Таким образом, правильный ответ в этой задаче — 3.
Линии электрического поля: несколько зарядов
Цели обучения
К концу этого раздела вы сможете:
- Вычислять общую силу (величину и направление), действующую на пробный заряд от более чем одного заряда
- Описать диаграмму электрического поля положительного точечного заряда; отрицательного точечного заряда с удвоенной величиной положительного заряда
- Проведите линии электрического поля между двумя точками с одинаковым зарядом; между двумя точками противоположного заряда.

Чертежи с использованием линий для представления электрических полей вокруг заряженных объектов очень полезны для визуализации силы и направления поля. Поскольку электрическое поле имеет как величину, так и направление, оно является вектором. Как и все векторов , электрическое поле может быть представлено стрелкой, длина которой пропорциональна его величине и которая указывает в правильном направлении. (Например, мы широко использовали стрелки для обозначения векторов силы.)
На рисунке 1 показаны два графических изображения одного и того же электрического поля, создаваемого положительным точечным зарядом В . На рис. 1b показано стандартное представление с использованием сплошных линий. На рис. 1b показаны многочисленные отдельные стрелки, каждая из которых представляет силу, действующую на испытательный заряд q . Силовые линии представляют собой карту бесконечно малых векторов силы.
Рис. 1. Два эквивалентных представления электрического поля, обусловленного положительным зарядом Q . (а) Стрелки, обозначающие величину и направление электрического поля. (b) В стандартном представлении стрелки заменены непрерывными силовыми линиями, имеющими то же направление в любой точке, что и электрическое поле. Близость линий напрямую связана с силой электрического поля. Пробный заряд, помещенный в любом месте, почувствует силу в направлении линии поля; эта сила будет иметь силу, пропорциональную плотности линий (например, вблизи заряда). 92}\\[/latex] и площадь пропорциональна r 2 . Это графическое представление, в котором силовые линии представляют направление, а их плотность (т. е. их плотность или число линий, пересекающих единицу площади) представляет силу, используется для всех полей: электростатического, гравитационного, магнитного и других.
(а) Стрелки, обозначающие величину и направление электрического поля. (b) В стандартном представлении стрелки заменены непрерывными силовыми линиями, имеющими то же направление в любой точке, что и электрическое поле. Близость линий напрямую связана с силой электрического поля. Пробный заряд, помещенный в любом месте, почувствует силу в направлении линии поля; эта сила будет иметь силу, пропорциональную плотности линий (например, вблизи заряда). 92}\\[/latex] и площадь пропорциональна r 2 . Это графическое представление, в котором силовые линии представляют направление, а их плотность (т. е. их плотность или число линий, пересекающих единицу площади) представляет силу, используется для всех полей: электростатического, гравитационного, магнитного и других.
Рис. 2. Электрическое поле, окружающее три различных точечных заряда. а) Положительный заряд. (b) Отрицательный заряд равной величины. в) Больший отрицательный заряд.
Во многих случаях взимается несколько платежей. Полное электрическое поле, создаваемое несколькими зарядами, представляет собой векторную сумму отдельных полей, создаваемых каждым зарядом. В следующем примере показано, как добавить векторы электрического поля. Пример 1. Добавление электрических полей на рис. 3.
Полное электрическое поле, создаваемое несколькими зарядами, представляет собой векторную сумму отдельных полей, создаваемых каждым зарядом. В следующем примере показано, как добавить векторы электрического поля. Пример 1. Добавление электрических полей на рис. 3.
Рис. 3. Электрические поля E 1 и E 2 в начале координат O добавить к E to .
Стратегия
Поскольку электрическое поле является вектором (имеющим величину и направление), мы добавляем электрические поля с помощью тех же векторных методов, что и для других типов векторов. Сначала мы должны найти электрическое поле каждого заряда в интересующей точке, которая в данном случае является началом системы координат (O). Делаем вид, что есть положительный тестовый заряд, 95\text{ N/C}\end{array}\\[/latex]
Четыре цифры были сохранены в этом решении, чтобы проиллюстрировать, что E 1 ровно в два раза больше величины E 2 . Теперь стрелки изображают величины и направления E 1 и E 2 . (См. рис. 3.) Направление электрического поля совпадает с направлением силы, действующей на положительный заряд, поэтому обе стрелки указывают прямо в сторону от создающих их положительных зарядов. Стрелка на 9{\circ}\end{array}\\[/latex]
Теперь стрелки изображают величины и направления E 1 и E 2 . (См. рис. 3.) Направление электрического поля совпадает с направлением силы, действующей на положительный заряд, поэтому обе стрелки указывают прямо в сторону от создающих их положительных зарядов. Стрелка на 9{\circ}\end{array}\\[/latex]
или на 63,4º выше оси x .
Обсуждение
В случаях, когда добавляемые векторы электрического поля не перпендикулярны, можно использовать векторные компоненты или графические методы. Полное электрическое поле, найденное в этом примере, является полным электрическим полем только в одной точке пространства. Чтобы найти полное электрическое поле, обусловленное этими двумя зарядами, во всей области, тот же метод необходимо повторить для каждой точки области. Этой невероятно длительной задачи (в пространстве существует бесконечное количество точек) можно избежать, вычислив полное поле в репрезентативных точках и воспользовавшись некоторыми объединяющими свойствами, отмеченными далее.
Рис. 4. Два положительных точечных заряда q 1 и q 2 создают результирующее электрическое поле, показанное на рисунке. Поле рассчитывается в репрезентативных точках, а затем сглаживаются линии поля в соответствии с правилами, изложенными в тексте.
На рисунке 4 показано, как можно изобразить электрическое поле от двух точечных зарядов, найдя полное поле в репрезентативных точках и нарисовав линии электрического поля, соответствующие этим точкам. Хотя электрические поля от нескольких зарядов более сложны, чем поля одиночных зарядов, легко заметить некоторые простые особенности.
Например, поле слабее между одинаковыми зарядами, о чем свидетельствуют линии, расположенные дальше друг от друга в этой области. (Это связано с тем, что поля от каждого заряда воздействуют на любой заряд, помещенный между ними, противоположными силами.) (См. рис. 4 и рис. 5а.) Кроме того, на большом расстоянии от двух одинаковых зарядов поле становится идентичным полю от одиночного заряда.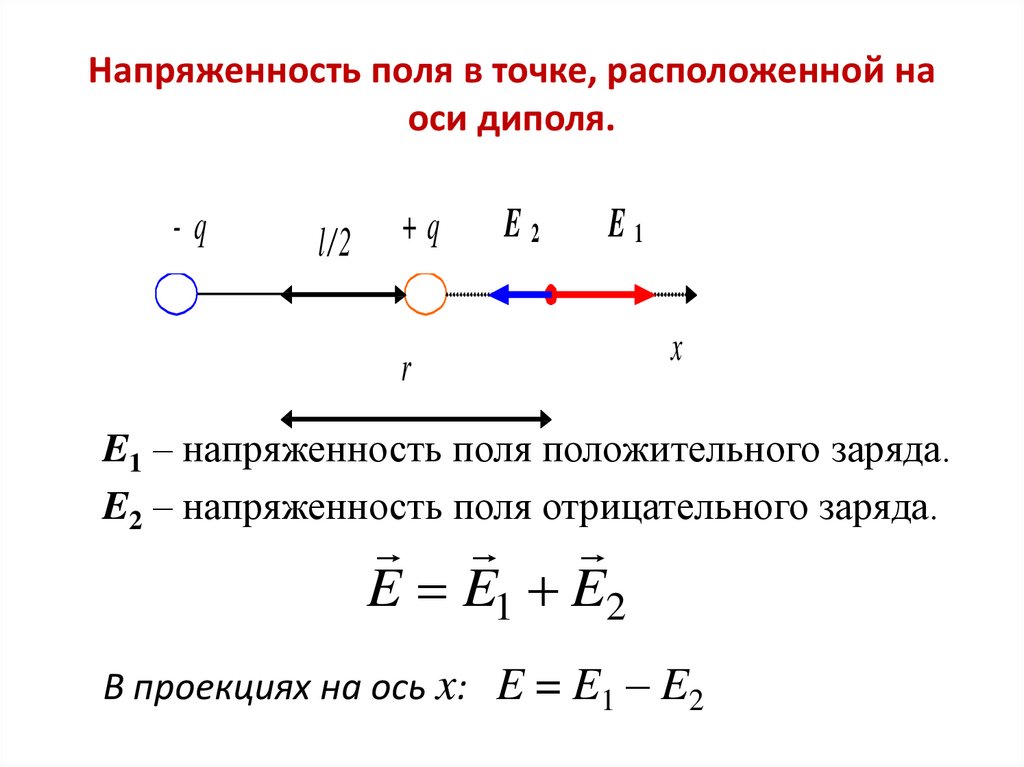 , больший заряд. На рис. 5б показано электрическое поле двух разноименных зарядов. Поле сильнее между зарядами. В этой области поля от каждого заряда имеют одинаковое направление, поэтому их сила складывается. Поле двух разноименных зарядов слабо на больших расстояниях, потому что поля отдельных зарядов направлены в противоположные стороны, и поэтому их силы вычитаются. На очень больших расстояниях поле двух разноименных зарядов выглядит как поле меньшего одиночного заряда.
, больший заряд. На рис. 5б показано электрическое поле двух разноименных зарядов. Поле сильнее между зарядами. В этой области поля от каждого заряда имеют одинаковое направление, поэтому их сила складывается. Поле двух разноименных зарядов слабо на больших расстояниях, потому что поля отдельных зарядов направлены в противоположные стороны, и поэтому их силы вычитаются. На очень больших расстояниях поле двух разноименных зарядов выглядит как поле меньшего одиночного заряда.
Рис. 5. (a) Два отрицательных заряда создают указанные поля. Оно очень похоже на поле, создаваемое двумя положительными зарядами, за исключением того, что направления противоположны. Между зарядами поле явно слабее. Отдельные силы на пробном заряде в этой области направлены в противоположные стороны. (b) Два противоположных заряда создают показанное поле, которое сильнее в области между зарядами.
Мы используем линии электрического поля для визуализации и анализа электрических полей (линии являются графическим инструментом, а не физической сущностью сами по себе). Свойства силовых линий электрического поля для любого распределения заряда можно резюмировать следующим образом:
Свойства силовых линий электрического поля для любого распределения заряда можно резюмировать следующим образом:
- Линии поля должны начинаться на положительных зарядах и заканчиваться на отрицательных зарядах или на бесконечности в гипотетическом случае изолированных зарядов.
- Количество силовых линий, покидающих положительный заряд или входящих в отрицательный заряд, пропорционально величине заряда.
- Сила поля пропорциональна близости линий поля, точнее, пропорциональна количеству линий на единицу площади, перпендикулярных линиям.
- Направление электрического поля касается линии поля в любой точке пространства.
- Линии поля никогда не могут пересекаться.
Последнее свойство означает, что поле уникально в любой точке. Линия поля представляет направление поля; поэтому, если они пересекутся, поле будет иметь два направления в этом месте (невозможно, если поле уникально).
PhET Explorations: Charges and Fields
Перемещайте точечные заряды по игровому полю, а затем просматривайте электрическое поле, напряжения, эквипотенциальные линии и многое другое. Это красочно, это динамично, это бесплатно.
Это красочно, это динамично, это бесплатно.
Нажмите, чтобы запустить симуляцию.
Резюме раздела
- Чертежи линий электрического поля являются полезным визуальным инструментом. Свойства линий электрического поля для любого распределения заряда таковы:
- Линии поля должны начинаться на положительных зарядах и заканчиваться на отрицательных зарядах или на бесконечности в гипотетическом случае изолированных зарядов.
- Количество силовых линий, покидающих положительный заряд или входящих в отрицательный заряд, пропорционально величине заряда.
- Сила поля пропорциональна близости линий поля, точнее, пропорциональна количеству линий на единицу площади, перпендикулярных линиям.
- Направление электрического поля касается линии поля в любой точке пространства.
- Линии поля никогда не могут пересекаться.
Концептуальные вопросы
- Сравните и сопоставьте кулоновское силовое поле и электрическое поле.
 Для этого составьте список из пяти свойств кулоновского силового поля, аналогичных пяти свойствам, перечисленным для силовых линий электрического поля. Сравните каждый пункт в вашем списке свойств кулоновского силового поля со свойствами электрического поля — они одинаковые или разные? (Например, линии электрического поля не могут пересекаться. Верно ли то же самое для линий кулоновского поля?)
Для этого составьте список из пяти свойств кулоновского силового поля, аналогичных пяти свойствам, перечисленным для силовых линий электрического поля. Сравните каждый пункт в вашем списке свойств кулоновского силового поля со свойствами электрического поля — они одинаковые или разные? (Например, линии электрического поля не могут пересекаться. Верно ли то же самое для линий кулоновского поля?) - [ссылка] показывает электрическое поле, распространяющееся на три области, обозначенные I, II и III. Ответьте на следующие вопросы. а) Имеются ли изолированные заряды? Если да, то в каком регионе и каковы их признаки? б) Где поле сильнее? в) Где он слабее всего? г) Где поле наиболее однородно?
Рис. 6.
Задачи и упражнения
- (a) Нарисуйте линии электрического поля вблизи точечного заряда + q . (b) Сделайте то же самое для точечного заряда −3,00 q .
- Нарисуйте линии электрического поля на большом расстоянии от распределения заряда, показанного на рис.
 5a и 5b.
5a и 5b. - На рис. 8 показаны силовые линии электрического поля вблизи двух зарядов [латекс]{q}_{1}[/латекс] и [латекс]{q}_{2}[/латекс]. Каково соотношение их величин? (b) Нарисуйте силовые линии электрического поля на большом расстоянии от зарядов, показанных на рисунке.
Рис. 7. Электрическое поле вблизи двух зарядов.
- Изобразите силовые линии электрического поля вблизи двух противоположных зарядов, где отрицательный заряд в три раза больше по величине, чем положительный. (См. рисунок 7 для аналогичной ситуации).
Глоссарий
электрическое поле: трехмерная карта электрической силы, простирающейся в пространство от точечного заряда сила, создаваемая этим зарядом
вектор: величина, имеющая как величину, так и направление
сложение векторов: математическая комбинация двух или более векторов, включая их величины, направления и положения
18.3 Электрическое поле — физика
Раздел Цели обучения
К концу этого раздела вы сможете делать следующее:
- Вычислять напряженность электрического поля
- Создание и интерпретация рисунков электрических полей
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:
- (5) Учащийся знает природу сил в физическом мире.
 Ожидается, что студент:
Ожидается, что студент:- (С) описать и рассчитать, как величина электрической силы между двумя объектами зависит от их зарядов и расстояния между ними.
Основные термины раздела
| электрическое поле | испытательный заряд |
Поддержка учителей
Поддержка учителей
Спросите учащихся, видели ли они фильмы, в которых используется концепция полей как в силовых полей . Попросите их описать, как работают такие поля. Опишите, как можно рассматривать гравитацию как поле, которое окружает массу и с которым взаимодействуют другие массы. Объясните, что электрические поля очень похожи на гравитационные поля.
Возможно, вы слышали о силовом поле в научно-фантастических фильмах, где такие поля применяют силы в определенных точках в космосе, чтобы удержать злодея в ловушке или защитить космический корабль от вражеского огня. Концепция поля очень полезна в физике, хотя она несколько отличается от того, что вы видите в кино.
Концепция поля очень полезна в физике, хотя она несколько отличается от того, что вы видите в кино.
Поле — это способ концептуализации и отображения силы, которая окружает любой объект и действует на другой объект на расстоянии без видимой физической связи. Например, гравитационное поле, окружающее Землю и все другие массы, представляет гравитационную силу, которая возникла бы, если бы в данной точке поля была помещена другая масса. Майкл Фарадей, английский физик девятнадцатого века, предложил концепцию электрического поля. Если вы знаете электрическое поле, то можете легко рассчитать силу (величину и направление), действующую на любой электрический заряд, который вы поместите в поле.
Электрическое поле создается электрическим зарядом и сообщает нам силу на единицу заряда во всех точках пространства вокруг распределения заряда. Распределение заряда может быть одноточечным; распределение заряда, скажем, по плоской пластине; или более сложное распределение заряда. Электрическое поле распространяется в пространстве вокруг распределения заряда. Теперь рассмотрите возможность размещения пробного заряда в поле. Пробный заряд — это положительный электрический заряд, заряд которого настолько мал, что не возмущает существенно заряды, создающие электрическое поле. Электрическое поле действует на пробный заряд в заданном направлении. Приложенная сила пропорциональна заряду пробного заряда. Например, если мы удвоим заряд пробного заряда, сила, действующая на него, удвоится. Математически говоря, что электрическое поле представляет собой силу на единицу заряда, записывается как
Электрическое поле распространяется в пространстве вокруг распределения заряда. Теперь рассмотрите возможность размещения пробного заряда в поле. Пробный заряд — это положительный электрический заряд, заряд которого настолько мал, что не возмущает существенно заряды, создающие электрическое поле. Электрическое поле действует на пробный заряд в заданном направлении. Приложенная сила пропорциональна заряду пробного заряда. Например, если мы удвоим заряд пробного заряда, сила, действующая на него, удвоится. Математически говоря, что электрическое поле представляет собой силу на единицу заряда, записывается как
E→=F→qtestE→=F→qtest
18.15
где мы рассматриваем только электрические силы. Обратите внимание, что электрическое поле представляет собой векторное поле, направленное в том же направлении, что и сила, действующая на положительный пробный заряд. Единицы электрического поля N/C.
Если электрическое поле создается точечным зарядом или сферой с однородным зарядом, то величина силы между этим точечным зарядом Q и пробным зарядом определяется законом Кулона
F=k|Qqtest|r2F =k|Qqtest|r2
, где используется абсолютное значение, потому что мы учитываем только величину силы. Тогда величина электрического поля равна
Тогда величина электрического поля равна
E=Fqtest=k|Q|r2.E=Fqtest=k|Q|r2.
18,16
Это уравнение дает величину электрического поля, создаваемого точечным зарядом Q . Расстояние r в знаменателе — это расстояние от точечного заряда Q или от центра сферического заряда до интересующей точки.
Если тестовый заряд удалить из электрического поля, электрическое поле все еще существует. Чтобы создать трехмерную карту электрического поля, представьте себе размещение пробного заряда в разных местах поля. В каждом месте измерьте силу, действующую на заряд, и используйте векторное уравнение E→=F→/qtestE→=F→/qtest для расчета электрического поля. Нарисуйте стрелку в каждой точке, где вы поместите пробный заряд, чтобы представить силу и направление электрического поля. Длина стрелок должна быть пропорциональна напряженности электрического поля. Если вы соедините эти стрелки вместе, вы получите линии. На рис. 18.17 показано изображение трехмерного электрического поля, создаваемого положительным зарядом.
Если вы соедините эти стрелки вместе, вы получите линии. На рис. 18.17 показано изображение трехмерного электрического поля, создаваемого положительным зарядом.
Рисунок 18.17 Трехмерное представление электрического поля, создаваемого положительным зарядом.
Поддержка учителей
Поддержка учителей
[BL][OL]Укажите, что все силовые линии электрического поля берут начало от заряда.
[AL]Обратите внимание, что количество линий, пересекающих воображаемую сферу, окружающую заряд, одинаково независимо от того, какой размер сферы вы выберете. Спросите, могут ли учащиеся использовать это, чтобы показать, что количество силовых линий, пересекающих поверхность на единицу площади, показывает, что напряженность электрического поля уменьшается пропорционально обратному квадрату расстояния.
Простое рисование линий электрического поля в плоскости, пересекающей заряд, дает двумерные карты электрического поля, показанные на рис. 18.18. Слева — электрическое поле, создаваемое положительным зарядом, а справа — электрическое поле, создаваемое отрицательным зарядом.
18.18. Слева — электрическое поле, создаваемое положительным зарядом, а справа — электрическое поле, создаваемое отрицательным зарядом.
Обратите внимание, что силовые линии электрического поля направлены от положительного заряда к отрицательному. Таким образом, положительный пробный заряд, помещенный в электрическое поле положительного заряда, будет отталкиваться. Это согласуется с законом Кулона, согласно которому одноименные заряды отталкиваются друг от друга. Если мы поместим положительный заряд в электрическое поле отрицательного заряда, положительный заряд притянется к отрицательному заряду. Противоположное верно для отрицательных тестовых зарядов. Таким образом, направление линий электрического поля согласуется с тем, что мы находим, используя закон Кулона.
Уравнение E=k|Q|/r2E=k|Q|/r2 говорит о том, что электрическое поле становится сильнее по мере приближения к заряду, который его генерирует. Например, на расстоянии 2 см от заряда Q ( r = 2 см) электрическое поле в четыре раза сильнее, чем на расстоянии 4 см от заряда ( r = 4 см). Снова взглянув на рис. 18.17 и рис. 18.18, мы видим, что линии электрического поля становятся более плотными по мере приближения к заряду, который их генерирует. На самом деле плотность линий электрического поля пропорциональна напряженности электрического поля!
Снова взглянув на рис. 18.17 и рис. 18.18, мы видим, что линии электрического поля становятся более плотными по мере приближения к заряду, который их генерирует. На самом деле плотность линий электрического поля пропорциональна напряженности электрического поля!
Рисунок 18.18 Линии электрического поля от двух точечных зарядов. Красная точка слева несет заряд +1 нКл, а синяя точка справа несет заряд -1 нКл. Стрелки указывают направление, в котором будет двигаться положительный пробный заряд. Линии поля сгущаются по мере приближения к точечному заряду.
Карты электрического поля могут быть составлены для нескольких зарядов или для более сложных распределений зарядов. Электрическое поле от нескольких зарядов можно найти, сложив электрические поля от каждого отдельного заряда. Поскольку эта сумма может быть только одним числом, мы знаем, что только одна линия электрического поля может проходить через любую заданную точку. Другими словами, линии электрического поля не могут пересекаться друг с другом.
На рис. 18.19(а) показана двумерная карта электрического поля, создаваемого зарядом + q и соседним зарядом — q . Трехмерная версия этой карты получается путем вращения этой карты вокруг оси, проходящей через оба заряда. Положительный пробный заряд, помещенный в это поле, будет испытывать силу в направлении силовых линий в его местоположении. Таким образом, он будет отталкиваться от положительного заряда и притягиваться к отрицательному заряду. Рисунок 18.19(b) показывает электрическое поле, создаваемое двумя зарядами − q . Обратите внимание, как силовые линии отталкиваются друг от друга и не перекрываются. Положительный пробный заряд, помещенный в это поле, будет притягиваться к обоим зарядам. Если вы находитесь далеко от этих двух зарядов, где далеко значит намного дальше, чем расстояние между зарядами, электрическое поле выглядит как электрическое поле от одного заряда -2 q .
Рисунок 18.19 (а) Электрическое поле, создаваемое точечным положительным зарядом (слева) и точечным отрицательным зарядом той же величины (справа). (б) Электрическое поле, создаваемое двумя равными отрицательными зарядами.
Поддержка учителей
Поддержка учителей
Попросите учащихся интерпретировать карты электрического поля. Где поле сильнее? Где поле слабее? В каком направлении поле увеличивается или уменьшается? Где поле наиболее однородно? Могут ли они проверить, что величина заряда одинакова в данной панели? Чем отличается поле двух отрицательных зарядов от поля положительного и отрицательного зарядов?
Виртуальная физика
Исследование электрического поля
Эта симуляция показывает вам электрическое поле из-за зарядов, которые вы размещаете на экране. Начните с установки верхнего флажка на панели параметров с правой стороны, чтобы отобразить электрическое поле. Перетащите заряды из ведер на экран, перемещайте их и наблюдайте за электрическим полем, которое они образуют. Чтобы более точно увидеть величину и направление электрического поля, перетащите датчик электрического поля или датчик электрического поля из нижнего ведра и перемещайте его по экрану.
Перетащите заряды из ведер на экран, перемещайте их и наблюдайте за электрическим полем, которое они образуют. Чтобы более точно увидеть величину и направление электрического поля, перетащите датчик электрического поля или датчик электрического поля из нижнего ведра и перемещайте его по экрану.
Исследования PhET: заряды и поля. Перемещайте точечные заряды по игровому полю, а затем просматривайте электрическое поле, напряжения, эквипотенциальные линии и многое другое.
Нажмите, чтобы просмотреть содержимое
Два положительных заряда размещены на экране. Какое утверждение описывает электрическое поле, создаваемое зарядами?
Постоянно везде.
Рядом с каждым зарядом ноль.

Между зарядками ноль.
Наибольшая сила на полпути между зарядами.
Смотреть физику
Электростатика (часть 2): интерпретация электрического поля
В этом видеоролике объясняется, как рассчитать электрическое поле точечного заряда и как интерпретировать карты электрического поля в целом. Обратите внимание, что лектор использует d для расстояния между частицами вместо r . Обратите внимание, что точечные заряды бесконечно малы, поэтому все их заряды сосредоточены в одной точке. Когда рассматриваются более крупные заряженные объекты, расстояние между объектами должно измеряться между центрами объектов.
Проверка захвата
Верно или неверно — если точечный заряд имеет силовые линии электрического поля, которые указывают на него, заряд должен быть положительным.
- правда
- ложно
Рабочий пример
Какова плата?
Посмотрите на рисунок электрического поля на рис. 18.20. Какова относительная сила и знак трех зарядов?
Рисунок 18.20 Карта электрического поля трех заряженных частиц.
Стратегия
Мы знаем, что электрическое поле простирается от положительного заряда и заканчивается отрицательным зарядом. Мы также знаем, что количество силовых линий электрического поля, которые касаются заряда, пропорционально заряду. Заряд 1 имеет 12 полей, выходящих из него. В заряд 2 входит шесть силовых линий. В заряд 3 входит 12 силовых линий.
Решение
Линии электрического поля выходят из заряда 1, так что это положительный заряд. Линии электрического поля проходят через заряды 2 и 3, поэтому они являются отрицательными зарядами. Отношение зарядов равно q1:q2:q3=+12:-6:-12q1:q2:q3=+12:-6:-12. Таким образом, величина зарядов 1 и 3 вдвое превышает величину заряда 2.
Линии электрического поля проходят через заряды 2 и 3, поэтому они являются отрицательными зарядами. Отношение зарядов равно q1:q2:q3=+12:-6:-12q1:q2:q3=+12:-6:-12. Таким образом, величина зарядов 1 и 3 вдвое превышает величину заряда 2.
Обсуждение
Хотя мы не можем определить точный заряд каждой частицы, мы можем получить много информации из электрического поля относительно величины и знака зарядов. и где сила пробного заряда будет наибольшей (или наименьшей).
Рабочий пример
Электрическое поле от дверной ручки
Дверная ручка, которую можно принять за сферический металлический проводник, приобретает заряд статического электричества q=-1,5 нКл. q=-1,5 нКл. Чему равно электрическое поле на расстоянии 1,0 см от дверной ручки? Диаметр дверной ручки 5,0 см.
Стратегия
Поскольку дверная ручка является проводником, весь заряд распределяется по внешней поверхности металла.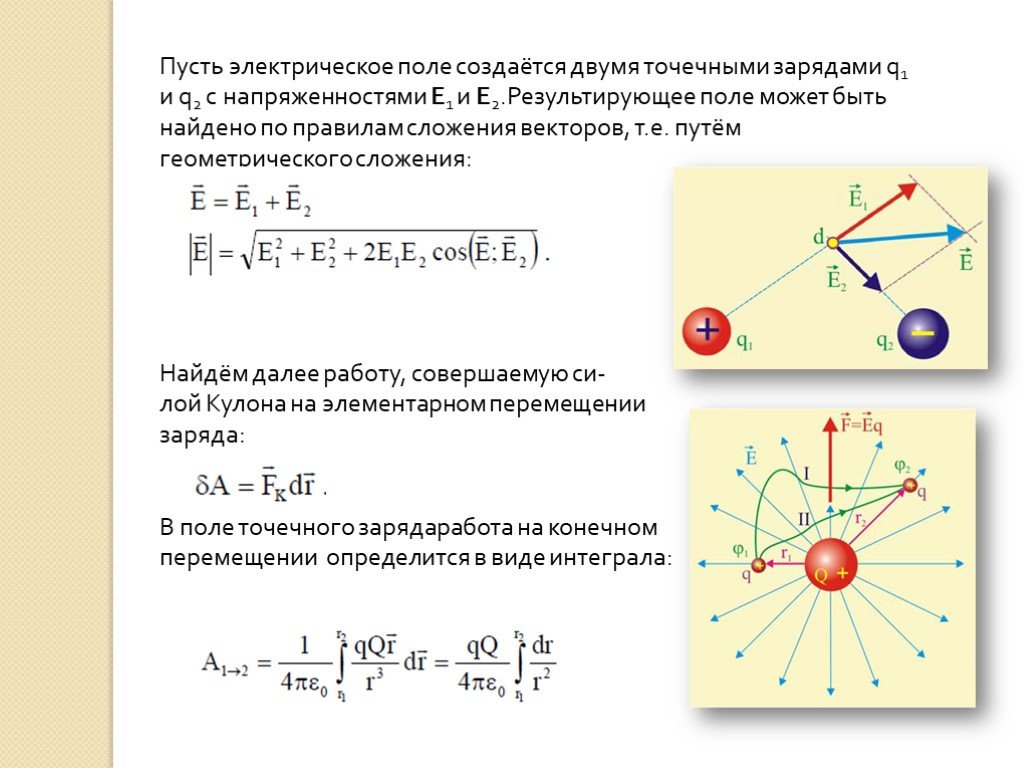 Кроме того, поскольку дверная ручка считается идеально сферической, заряд на поверхности распределяется равномерно, поэтому мы можем рассматривать дверную ручку так, как если бы весь заряд был сосредоточен в центре дверной ручки. Справедливость этого упрощения будет доказана в следующем курсе физики. Теперь нарисуйте дверную ручку и определите вашу систему координат. Используйте +x+x, чтобы указать внешнее направление, перпендикулярное двери, с x=0x=0 в центре дверной ручки (как показано на рисунке ниже).
Кроме того, поскольку дверная ручка считается идеально сферической, заряд на поверхности распределяется равномерно, поэтому мы можем рассматривать дверную ручку так, как если бы весь заряд был сосредоточен в центре дверной ручки. Справедливость этого упрощения будет доказана в следующем курсе физики. Теперь нарисуйте дверную ручку и определите вашу систему координат. Используйте +x+x, чтобы указать внешнее направление, перпендикулярное двери, с x=0x=0 в центре дверной ручки (как показано на рисунке ниже).
Если диаметр дверной ручки 5,0 см, ее радиус 2,5 см. Мы хотим знать электрическое поле на расстоянии 1,0 см от поверхности дверной ручки, что составляет расстояние r = 2,5 см + 1,0 см = 3,5 см, r = 2,5 см + 1,0 см = 3,5 см от центра дверной ручки. Мы можем использовать уравнение E=k|Q|r2E=k|Q|r2, чтобы найти величину электрического поля. Направление электрического поля определяется знаком заряда, который в данном случае отрицателен.
Решение
Введение заряда Q=-1,5 нКл=-1,5×10-9.
Обсуждение
Похоже на огромное электрическое поле. К счастью, требуется электрическое поле примерно в 100 раз сильнее (3×106 Н/Кл3×106 Н/Кл), чтобы заставить воздух разлагаться и проводить электричество. Кроме того, вес взрослого человека составляет около 70 кг × 9,8 м/с2 ≈ 700 Н70 кг × 9,8 м/с2 ≈ 700 Н, так почему вы не чувствуете силы, действующей на протоны в вашей руке, когда вы тянетесь к дверной ручке? Причина в том, что ваша рука содержит равное количество отрицательного заряда, который отталкивает отрицательный заряд дверной ручки. Из-за поляризации в вашей руке может развиться очень небольшая сила, но вы никогда этого не заметите.
Практические задачи
15.
Какова величина электрического поля на расстоянии 20 см от точечного заряда q = 33 нКл?
- 7,4 × 10 3 Н/З
- 1,48 × 10 3 Н/З
- 7,4 × 10 12 Н/З
- 0
16.
Заряд -10 нКл находится в начале. В каком направлении электрическое поле от заряда указывает на x + 10 см?
- Электрическое поле направлено в сторону от отрицательных зарядов.
- Электрическое поле указывает на отрицательные заряды.
- Электрическое поле направлено в сторону положительных зарядов.
- Электрическое поле направлено в сторону от положительных зарядов.
Проверьте свое понимание
17.
Когда силовые линии электрического поля сближаются, что это говорит вам об электрическом поле?
- Электрическое поле обратно пропорционально плотности линий электрического поля.
- Электрическое поле прямо пропорционально плотности линий электрического поля.
- Электрическое поле не связано с плотностью линий электрического поля.
- Электрическое поле обратно пропорционально квадратному корню из плотности силовых линий электрического поля.


 3)
3)

 Для этого составьте список из пяти свойств кулоновского силового поля, аналогичных пяти свойствам, перечисленным для силовых линий электрического поля. Сравните каждый пункт в вашем списке свойств кулоновского силового поля со свойствами электрического поля — они одинаковые или разные? (Например, линии электрического поля не могут пересекаться. Верно ли то же самое для линий кулоновского поля?)
Для этого составьте список из пяти свойств кулоновского силового поля, аналогичных пяти свойствам, перечисленным для силовых линий электрического поля. Сравните каждый пункт в вашем списке свойств кулоновского силового поля со свойствами электрического поля — они одинаковые или разные? (Например, линии электрического поля не могут пересекаться. Верно ли то же самое для линий кулоновского поля?)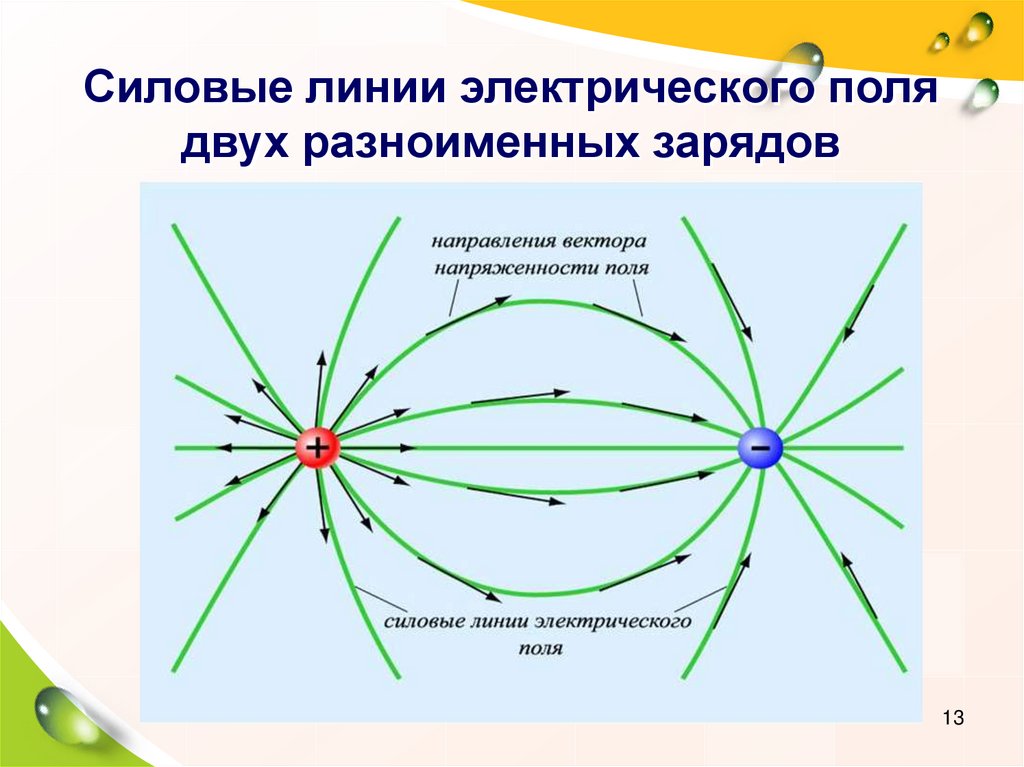 5a и 5b.
5a и 5b. Ожидается, что студент:
Ожидается, что студент:

Leave A Comment