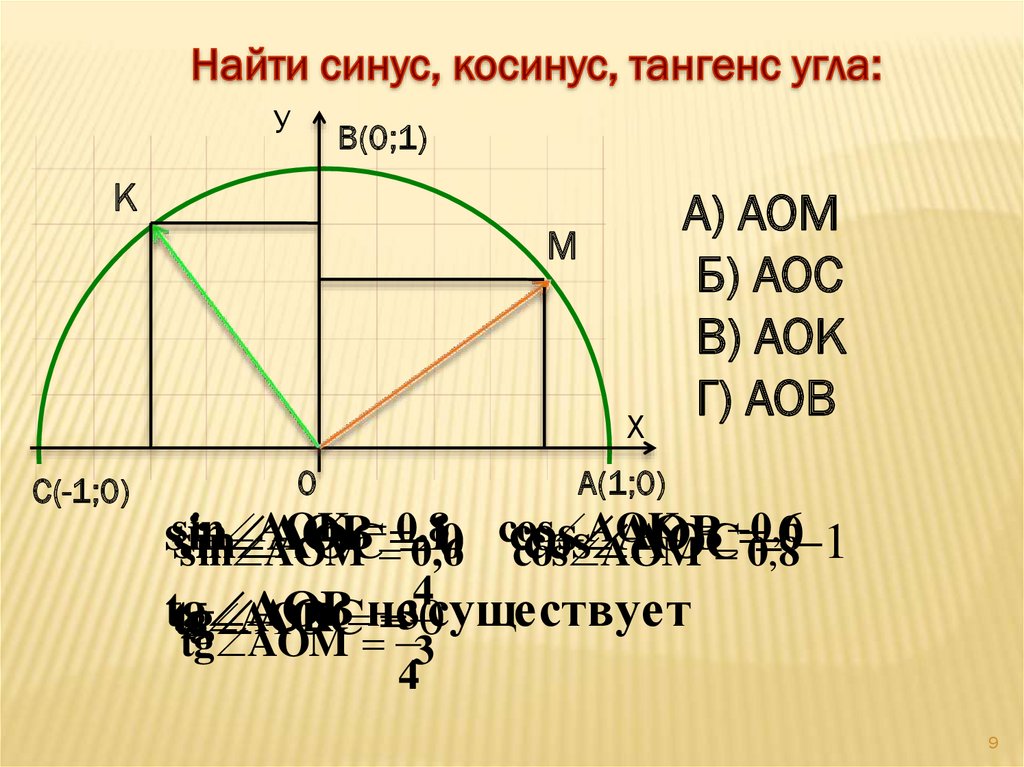
Синус и косинус острого угла
1. Синус и косинус острого угла
Синусом острого угла прямоугольного треугольниканазывается отношение противолежащего к этому углу
катета к гипотенузе. Синус угла А обозначается sin A.
Косинусом острого угла прямоугольного треугольника
называется отношение прилежащего к этому углу катета к
гипотенузе. Косинус угла А обозначается cos A.
По определению,
BC
AC
sin A
, cos A
.
AB
AB
2. Тангенс и котангенс острого угла
Тангенсом острого угла прямоугольного треугольниканазывается отношение противолежащего к этому углу
катета к прилежащему.Тангенс угла А обозначается tg A.
Котангенсом острого угла прямоугольного треугольника
называется отношение прилежащего к этому углу катета к
противолежащему. Котангенс угла А обозначается сtg A.
По определению,
BC
AC
tgA
, ctgA
.
AC
BC
3. Тригонометрические функции
Синус, косинус, тангенс и котангенс называюттригонометрическими функциями острого угла.

Из определения тригонометрических функций следует:
1) катет прямоугольного треугольника равен
гипотенузы на синус противолежащего угла;
произведению
2) катет прямоугольного треугольника
гипотенузы на косинус прилежащего угла;
произведению
равен
3) катет прямоугольного треугольника равен произведению второго
катета на тангенс противолежащего угла;
4) катет прямоугольного треугольника равен произведению второго
катета на котангенс прилежащего угла.
4. Упражнение 1
Найдите значения тригонометрических функцийугла в 30о.
1
3
sin 30 , cos30
,
2
2
Ответ:
3
tg 30
, ctg 30 3.
3
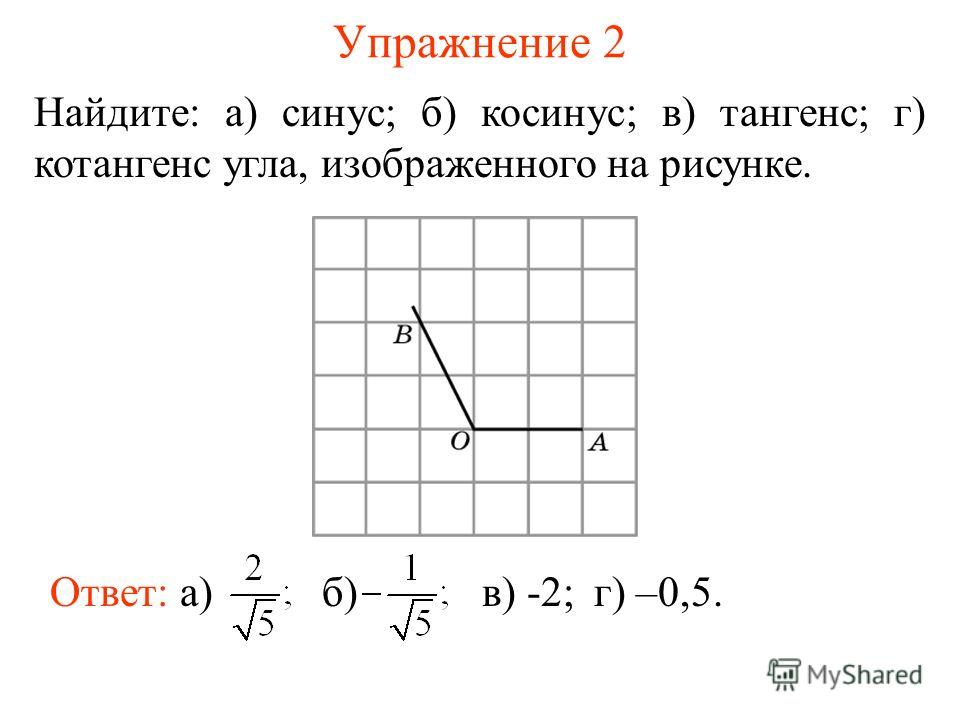
5. Упражнение 2
Найдите значения тригонометрических функцийугла в 45о.
2
2
Ответ: sin 45 2 , cos 45 2 ,
tg 45 1, ctg 45 1.
6. Упражнение 3
Найдите значения тригонометрических функцийугла в 60о.
3
1
Ответ: sin 60
, cos60 ,
2
2
3
tg 60 3, ctg 60
.
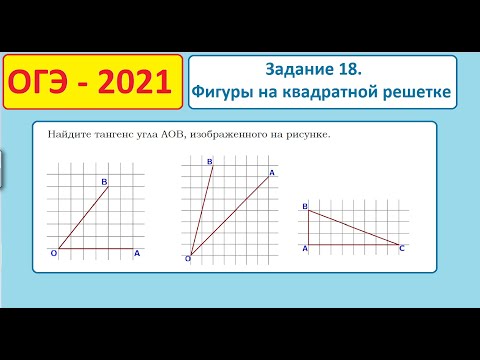
3
7. Упражнение 4
Найдите значения тригонометрических функцийугла AOB, изображенного на рисунке.
2
2
sin AOB
, cos AOB
,
Ответ:
2
2
tg AOB 1, ctg AOB 1.
8. Упражнение 5
Найдите значения тригонометрических функцийугла AOB, изображенного на рисунке.
5
2 5
sin AOB
, cos AOB
,
Ответ:
5
5
tg AOB 0,5, ctg AOB 2.
9. Упражнение 6
Найдите значения тригонометрических функцийугла AOB, изображенного на рисунке.
2 5
5
sin AOB
, cos AOB
,
Ответ:
5
5
tg AOB 2, ctg AOB 0,5.
10. Упражнение 7
Найдите значения тригонометрических функцийугла AOB, изображенного на рисунке.
2
2
sin AOB
, cos AOB
,
Ответ:
2
2
tg AOB 1, ctg AOB 1.
11. Упражнение 8
Найдите значения тригонометрических функцийугла AOB, изображенного на рисунке.
5
2 5
sin AOB
, cos AOB
,
Ответ:
5
5
tg AOB 0,5, ctg AOB 2.
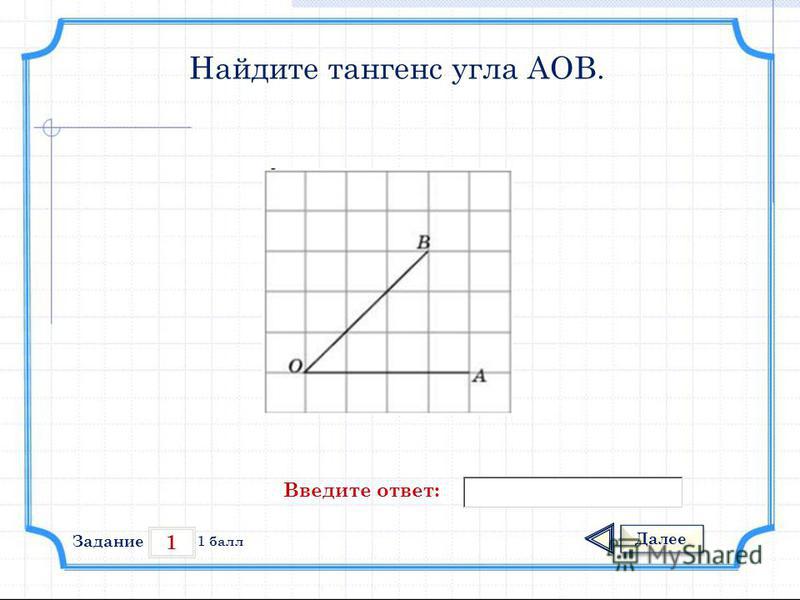
12. Упражнение 9
На клетчатой бумаге изобразите угол, тангенскоторого равен: а) 1; б) 0,5; в) 2; г) 3.
Ответ:
13. Упражнение 10
От луча OA отложите угол, тангенс которогоравен: а) 1/2; б) 1/3; в) 2.
Ответ:
14. Упражнение 11
Может ли синус (косинус) угла быть равен 2 ?Ответ: Нет, значения синуса и косинуса меньше
единицы.
15. Упражнение 12
Может ли тангенс (котангенс) угла быть равен2 ?
Ответ: Да.
16. Упражнение 13
Катеты прямоугольного треугольника равны 12см и 5 см. Найдите все тригонометрические
функции его меньшего угла A.
Ответ:
5
12
sin A , cos A ,
13
13
5
12
tgA , ctgA .
12
5
17. Упражнение 14
В треугольнике ABC угол C равен 90о, CH –высота, AC = 5, AH = 4. Найдите:
а) sin B;
б) cos B.
Ответ: а) 0,8. б) 0,6.
18. Упражнение 15
В треугольнике ABC угол C равен 90о, CH –высота, BC = 5, BH = 3.
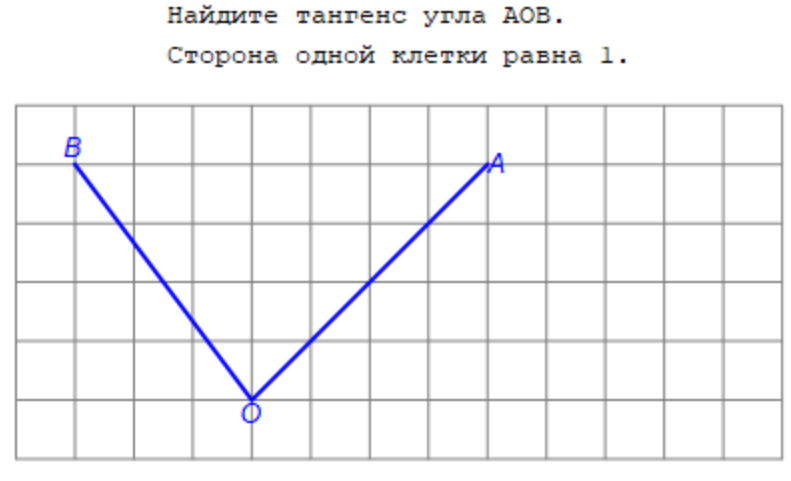 Найдите:
Найдите:а) sin A;
б) cos A.
Ответ: а) 0,6; б) 0,8.
19. Упражнение 16
В треугольнике ABC угол C равен 90о, AC = 5,высота CH равна 3. Найдите sin B.
Ответ: 0,8.
20. Упражнение 17
В треугольнике ABC угол C равен 90о, BC = 5,высота CH равна 4. Найдите sin A.
Ответ: 0,6.
21. Упражнение 18
Высота,проведенная
к
основанию
равнобедренного треугольника, равна 8 см,
основание равно 12 см. Найдите синус и косинус
угла A при основании треугольника.
4
3
Ответ: sin A , cos A .
5
5
22. Упражнение 19
В треугольнике ABCНайдите tg A.
Ответ: 0,75.
AC = BC = 5, AB = 8.
23. Упражнение 20
В треугольнике ABC AC = BC, AB = 5, высота AHравна 4. Найдите sin A.
Ответ: 0,8.
24. Упражнение 21
В треугольнике ABC AC = BC, AB = 5, высота AHравна 4. Найдите cos A.
Ответ: 0,6.
25. Упражнение 22
В треугольнике ABC AC = BC, AB = 5,высота, BH = 3.
 Найдите cos A.
Найдите cos A.Ответ: 0,6.
AH –
26. Упражнение 23
В треугольнике ABC AC = BC, AH – высота, sin A= 0,8. Найдите косинус угла BAH.
Ответ: 0,8.
27. Упражнение 24
В треугольнике ABC AC = BC, AH – высота, sin A= 0,8. Найдите синус угла BAH.
Ответ: 0,6.
28. Упражнение 25
В треугольнике ABC AB = BC, AC = 10, CH –высота, AH = 8. Найдите sin C.
Ответ: 0,6.
29. Упражнение 26
В треугольнике ABC AB = BC, CH — высота, sin C =0,4. Найдите косинус угла ACH.
Ответ: 0,4.
30. Упражнение 31
Мальчик прошел от дома по направлению на восток 800 м. Затемповернул на север и прошел 600 м. Под каким углом к направлению
на запад он должен идти, чтобы вернуться домой? В ответе укажите
целое число градусов. (Используйте таблицу тригонометрических
функций.)
Ответ: 37о.
31. Упражнение 32
Грибник, войдя в лес, в течение двух часов шел в направлении насевер, а затем с той же скоростью в течение полутора часов – на
восток.
 Под каким углом к направлению на юг он должен идти,
Под каким углом к направлению на юг он должен идти,чтобы вернуться к месту, где он вошел в лес? В ответе укажите
целое число градусов. (Используйте таблицу тригонометрических
функций.)
Ответ: 37о.
32. Упражнение 34
Горная железная дорога поднимается на 1 м на каждые 30 м пути.Используя таблицу тригонометрических функций, найдите угол
подъема в градусах. В ответе укажите приближенное значение,
выражаемое целым числом градусов.
Ответ: 2о.
33. Упражнение 35
Человек, пройдя вверх по склону холма 1000 м, поднялся на 90 мнад плоскостью основания холма. Используя таблицу
тригонометрических функций, найдите (в среднем) угол наклона
холма в градусах. В ответе укажите приближенное значение,
выражаемое целым числом градусов.
Ответ: 5о.
34. Упражнение 36
Использую таблицу тригонометрических функций, найдитеприближенное значение угла, под которым виден столб высотой 3
м, находящийся от наблюдателя на расстоянии 100 м.
 В ответе
В ответеукажите целое число градусов.
Ответ: 2о.
35. Упражнение 37
Высота башни главного здания МГУ имени М.В. Ломоносоваравна 240 м. Под каким углом видна эта башня с расстояния 200
м? В ответе укажите приближенное значение, равное целому
числу градусов.
Ответ: 50о.
36. Упражнение 38
Высота Останкинской телевизионной башни – 540 м. Используятаблицу тригонометрических функций, найдите угол в градусах,
под которым видна башня с расстояния 2000 м.
Ответ: 15о.
37. Упражнение 39
Строение высоты 30 м бросает тень длиной 45 м. Используятаблицу тригонометрических функций, найдите угол наклона
солнечных лучей. В ответе укажите приближенное значение,
выражаемое целым числом градусов.
Ответ: 34о.
38. Упражнение 40
Используя таблицу тригонометрических функций, найдите уголнаклона солнечных лучей, если длина тени стоящего человека в
два раза меньше его роста. В ответе укажите приближенное
значение, выражаемое целым числом градусов.
Ответ: 64о.
39. Упражнение 41
Лестница имеет ступеньки, ширина которых равна 30 см, авысота – 18 см. Используя таблицу тригонометрических функций,
найдите угол подъема лестницы. В ответе укажите приближенное
значение, выражаемое целым числом градусов.
Ответ: 31о.
40. Упражнение 42
Ширина дачного домика равна 6 м, ширина одного ската егодвускатной крыши равна 5 м. Используя таблицу
тригонометрических функций, найдите угол между стропилами
крыши и потолком.
Ответ: 53о.
41. Упражнение 43
Ширина футбольных ворот равна 8 ярдам. Расстояние от 11метровой отметки до линии ворот равно 12 ярдам. Найдите угол,под которым видны ворота с 11-метровой отметки. В ответе
укажите целое число градусов.
Ответ: 37о.
42. Таблица тригонометрических функций
sin AA
tg A
A
sin A
tg A
A
sin A
tg A
30′
0,0087
0,0087
30о
1о
0,0175
0,0175
31о
0,035
32о
0,54
0,65
63о
0,56
0,68
64о
0,90
2,02
0,91
2,15
2о
0,035
0,50
0,52
0,53
0,58
60о
0,87
1,73
0,60
61о
0,87
1,80
0,62
62о
0,88
1,88
0,89
1,96
3о
0,05
0,05
33о
4о
0,07
0,07
34о
0,57
0,70
65о
5о
0,09
0,09
35о
6о
0,10
0,11
36о
0,59
0,73
66о
0,91
2,25
7о
0,12
0,12
37о
0,60
0,75
67о
0,92
2,36
0,62
0,78
68о
0,93
2,48
8о
0,14
0,14
38о
9о
0,16
0,16
39о
0,63
0,81
69о
0,93
2,61
10о
0,17
0,18
40о
0,64
0,84
70о
0,94
2,78
0,66
0,87
71о
0,95
2,90
11о
0,19
0,19
41о
12о
0,21
0,21
42о
0,67
0,9
72о
0,95
3,08
13о
0,23
0,23
43о
0,68
0,93
73о
0,96
3,27
0,69
0,97
74о
0,96
3,49
14о
0,24
0,25
44о
15о
0,26
0,27
45о
0,71
1,00
75о
0,97
3,73
16о
0,28
0,29
46о
0,72
1,04
76о
0,97
4,01
0,73
1,07
77о
0,97
4,33
0,74
1,11
78о
0,98
4,71
0,98
5,15
17о
0,29
0,31
47о
18о
0,31
0,32
48о
0,75
1,15
79о
19о
0,33
0,34
49о
20о
0,34
0,36
50о
0,77
1,19
80о
0,98
5,67
21о
0,36
0,38
51о
0,78
1,23
81о
0,99
6,31
0,79
1,28
82о
0,99
7,12
22о
0,37
0,40
52о
23о
0,39
0,42
53о
0,80
1,33
83о
0,992
8,14
24о
0,41
0,45
54о
0,81
1,38
84о
0,994
9,51
0,82
1,43
85о
0,996
11,43
25о
0,42
0,47
55о
26о
0,44
0,49
56о
0,83
1,48
86о
0,998
14,30
27о
0,45
0,51
57о
0,84
1,54
87о
0,999
19,08
0,85
1,60
88о
1,00
28,64
0,86
1,66
89о
1,00
57,29
28о
0,47
0,53
58о
29о
0,48
0,55
59о
9.
 5. Углы (Задачи ЕГЭ база)
5. Углы (Задачи ЕГЭ база)Сайт подготовки к экзаменам Uchus.online
Задачи ЕГЭ база
№7143
Сложность:
20 %
!
На клетчатой бумаге с размером клетки 1×1 изображён острый угол. Найдите тангенс этого угла.
Подпишись на ютуб канал
Подписаться
№4326
Сложность:
21 %
!
На клетчатой бумаге с размером клетки 1×1 изображён угол. Найдите тангенс этого угла.
Подпишись на ютуб канал
Подписаться
№2281
Сложность:
21 %
!
Найдите тангенс угла AOB, изображённого на рисунке.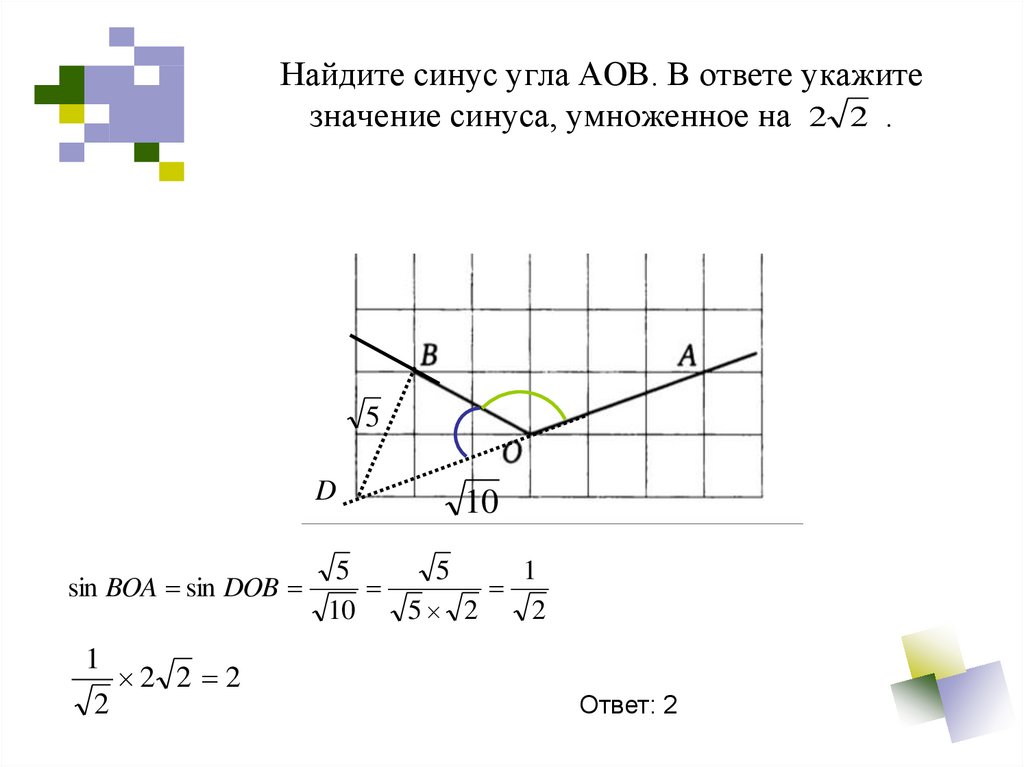
Подпишись на ютуб канал
Подписаться
№628
Сложность:
22 %
!
Найдите тангенс угла, изображенного на рисунке.
Подпишись на ютуб канал
Подписаться
№4151
Сложность:
26 %
!
На клетчатой бумаге с размером клетки 1×1 изображен угол. Найдите тангенс этого угла.
Подпишись на ютуб канал
Подписаться
№5306
Сложность:
34 %
!
На клетчатой бумаге с размером клетки 1× 1 изображен угол. Найдите его градусную меру.
Подпишись на ютуб канал
Подписаться
№630
Сложность:
36 %
!
Найдите величину угла, изображенного на рисунке.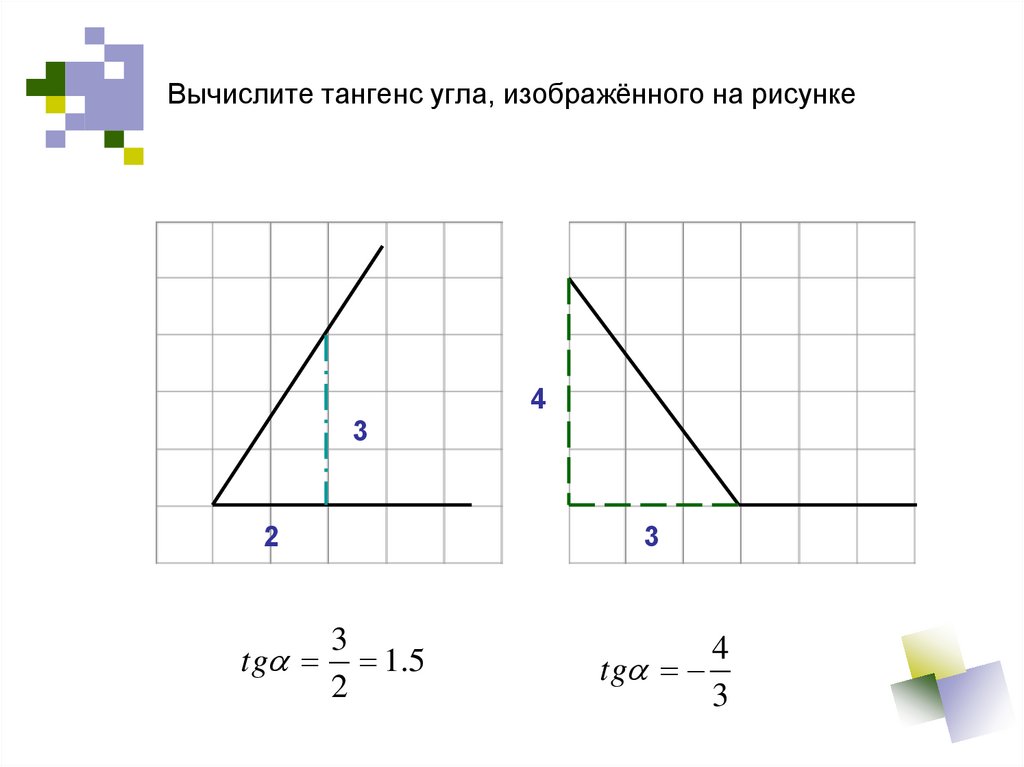
Подпишись на ютуб канал
Подписаться
№637
Сложность:
39 %
!
Найдите величину угла, изображенного на рисунке. Ответ дайте в градусах.
Подпишись на ютуб канал
Подписаться
№4018
Сложность:
43 %
!
Найдите градусную величину дуги \(AC\) окружности, на которую опирается угол \(ABC\). Ответ дайте в градусах.
Подпишись на ютуб канал
Подписаться
№1180
Сложность:
45 %
!
На клетчатой бумаге с размером клетки 1×1 изображен угол. Найдите котангенс этого угла.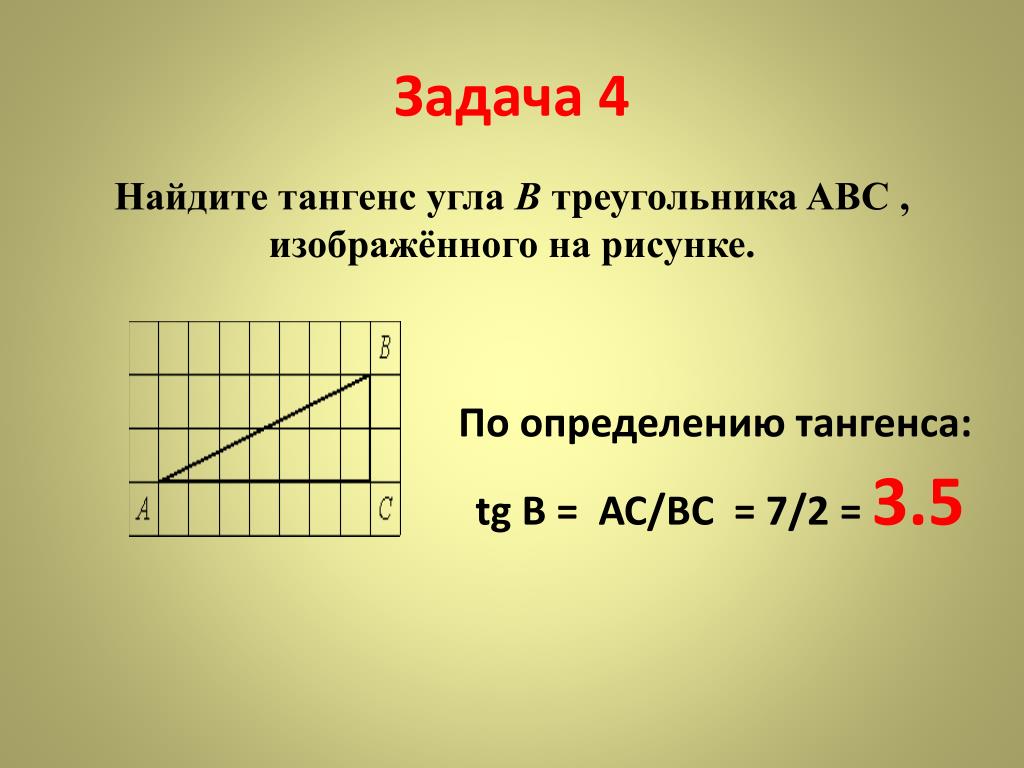
Подпишись на ютуб канал
Подписаться
Загрузка…
2023 ©, ИП Иванов Дмитрий Михайлович- ВК
- Почта
Используйте ваш ВК для того, чтобы войти в систему
Пользуясь сайтом вы автоматически принимаете пользовательское соглашение.
Чтобы выслать код сброса пароля, пожалуйста, введите ваш адрес электронной почты.
 Задать вопрос на форуме
Задать вопрос на форумеОпишите ошибку
Результат вашего теста:
Всего задач в тесте: 0
Вы ответили верно на: 0 (0 %)
Вы ответили неверно на: 0
Открыть
Загрузка…
Формула котангенса — таблица тригонометрических отношений, решенные проблемы и часто задаваемые вопросы
- Формула
- Формула котангенса
Что такое тригонометрия? Дата последнего обновления: 04 апреля 2023 г.
 . Обычно треугольники, принимаемые для тригонометрических расчетов, являются прямоугольными. Тригонометрических соотношений шесть. Это синус, косинус, тангенс, косеканс, секанс и котангенс, и их обычно называют sin, cos, tan, cosec, sec, cot соответственно.
. Обычно треугольники, принимаемые для тригонометрических расчетов, являются прямоугольными. Тригонометрических соотношений шесть. Это синус, косинус, тангенс, косеканс, секанс и котангенс, и их обычно называют sin, cos, tan, cosec, sec, cot соответственно.[Изображение будет загружено в ближайшее время]
Формула загара
Формулы загара взаимозаменяемы. Если длину прилежащей стороны разделить на длину противолежащей стороны, то получится значение котангенса угла прямоугольного треугольника. Угол загара — это обратная формула детской кроватки.
Cot x Formulas
\[Cotx=\frac{AdjacentSide}{OppositeSide}\]
\[Cotx=\frac{1}{tanx}\]
\[Tanx=\frac{sinx}{cosx }\]
Sec Cosec Cot Формула Связь
\[Cotx=\frac{Cosecx}{Secx}\]
Соотношение формулы Cosec Cot
1+ cot2 = cosec2
cosec2 — cot2 = 1
Здесь таблица для вычисления формул тригонометрии для углов: нижеприведенный. Они обычно используются для определения угла наклона в прямоугольном треугольнике. Таблица тригонометрических соотношений содержит значения стандартных тригонометрических углов, таких как 0°, 30°, 45°, 60° и 90°.
Они обычно используются для определения угла наклона в прямоугольном треугольнике. Таблица тригонометрических соотношений содержит значения стандартных тригонометрических углов, таких как 0°, 30°, 45°, 60° и 90°.
Таблица тригонометрических соотношений
Angles (In Degrees) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° | |||||
Angles (In Radians) | 0° | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π | |||||
sin | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 | |||||
cos | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 | |||||
tan | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 | |||||
cot | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ | |||||
COSEC | ∞ | 2 | √2 2 | √2 2 | √2 | √2 | √2 | 2 | 0013 | ∞ | -1 | ∞ | |
sec | 1 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
 0013
0013Решение:
Формула котангенса для вычисления cot x с использованием значения tan x: 1/tan x
Итак,
cot x = 15/6
Значение cot x = 6/5
Задача 2: Найдите значение в кроватке. Если длина прилежащей стороны прямоугольного треугольника равна 6√3 см, а длина прямоугольного треугольника равна 6 см.
Решение:
Ниже приведена формула котангенса для расчета cot.
\[Cot\theta =\frac{AdjacentSide}{OppositeSide}\]
раскладушка = 6√3 / 6
Итак, раскладушка = √3
Значение можно получить из таблицы тригонометрических соотношений.
So, = Cot 30°
Недавно обновленные страницы Часто задаваемые вопросы
Формула процентной доходности — APY, атомная экономика и пример решения
Формула серии – определение, примеры решений и часто задаваемые вопросы
Формула площади поверхности квадратной пирамиды – определение и вопросы
Диагональ формулы квадрата – значение, вывод и примеры решения
Формула дисперсионного анализа – определение, полная форма, статистика и примеры
Формула среднего — методы отклонения, примеры решений и часто задаваемые вопросы
Формула доходности в процентах — APY, атомная экономика и пример решения
Формула серии— определение, примеры решений и часто задаваемые вопросы
Площадь поверхности квадратной пирамиды Формула — определение и вопросы
Актуальные темы
Котангенс — формула, график, область, диапазон
Котангенс — одна из 6 тригонометрических функций.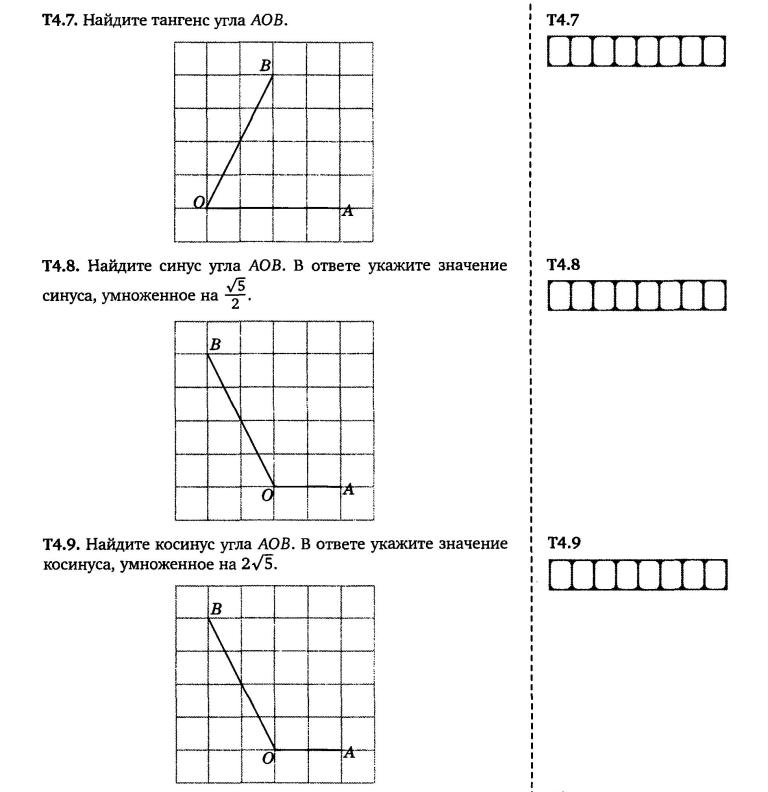 Обычно его называют «кроваткой». Как и другие тригонометрические отношения, формула котангенса также определяется как отношение сторон прямоугольного треугольника. Формула cot x равна отношению основания и перпендикуляра прямоугольного треугольника. Вот 6 основных тригонометрических функций и их сокращения.
Обычно его называют «кроваткой». Как и другие тригонометрические отношения, формула котангенса также определяется как отношение сторон прямоугольного треугольника. Формула cot x равна отношению основания и перпендикуляра прямоугольного треугольника. Вот 6 основных тригонометрических функций и их сокращения.
| Тригонометрическая функция | Аббревиатура |
|---|---|
| Синусоидальная функция | грех |
| Функция косинуса | потому что |
| Касательная функция | желтовато-коричневый |
| Функция косеканса | КСК |
| Функция секущей | сек |
| Функция котангенса | детская кроватка |
Давайте узнаем больше о котангенсе, изучив его определение, формулу cot x, его область определения, диапазон, график, производную и интеграл.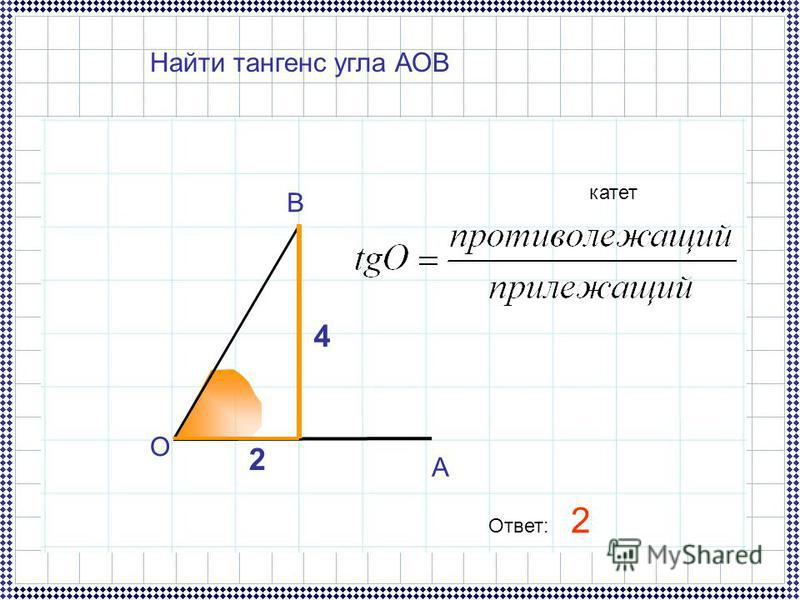
| 1. | Что такое котангенс? |
| 2. | Формула котангенса |
| 3. | Свойства котангенса |
| 4. | Закон котангенса |
| 5. | Период котангенса |
| 6. | Котангенс единичной окружности |
| 7. | Домен, диапазон и график котангенса |
| 8. | Производная и интеграл от котангенса |
| Часто задаваемые вопросы о котангенсе |
Что такое котангенс?
Котангенс — одно из основных тригонометрических соотношений. Фактически это одно из обратных тригонометрических соотношений csc, sec и cot. Обычно его обозначают как «кроватка х», где х — угол между основанием и гипотенузой прямоугольного треугольника.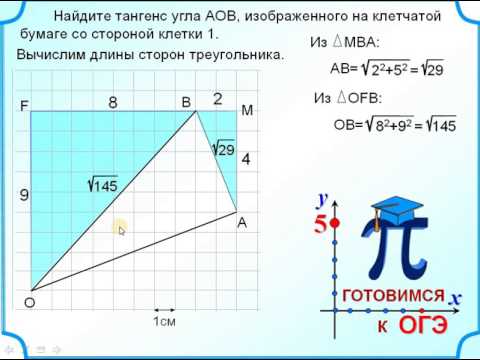 Альтернативные названия котангенса — котангенс и котангенс х. Котангенс угла в прямоугольном треугольнике определяется как отношение прилежащей стороны (стороны, прилежащей к углу) к противолежащей стороне (стороны, противолежащей углу).
Альтернативные названия котангенса — котангенс и котангенс х. Котангенс угла в прямоугольном треугольнике определяется как отношение прилежащей стороны (стороны, прилежащей к углу) к противолежащей стороне (стороны, противолежащей углу).
Формула котангенса
Формула котангенса для угла θ: cot θ = (прилежащая сторона) / (противоположная сторона). . Рассмотрим прямоугольный треугольник ABC, образующий прямой угол в точке B. Тогда AB — сторона, примыкающая к A, а BC — сторона, противолежащая A. Тогда котангенс треугольника A (который записывается как детская кроватка A),
детская кроватка A = (прилегающая сторона A) / (противоположная сторона A) = (AB) / (BC).
Например, если AB = 3 и BC = 4, то кроватка A = 3/4.
Свойства котангенса
Мы уже знаем, что кроватка x = (Смежный) / (Противоположный). Помимо этого, существует несколько других формул отношения котангенса, в которых котангенс может быть записан через другие тригонометрические отношения.
Котангенс относительно Cos и Sin
Мы знаем, что sin θ = (Противоположный) / (Гипотенуза) и cos θ = (Смежный) / (Гипотенуза). Если мы разделим cos θ на sin θ , мы получим
(cos θ) / (sin θ) = (Смежный) / (Гипотенуза) × (Гипотенуза) / (Противоположный)
= (Смежный) / (Противоположный)
= кроватка θ
Следовательно, кроватка θ = (cos θ) / (sin θ) — это формула кроватки x с точки зрения cos и sin.
Котангенс через Tan
Мы знаем, что tan θ = (Противоположный)/(Смежный) и cot θ = (Смежный)/(Противоположный). Таким образом, cot и tan обратны друг другу. Таким образом, мы можем написать cot θ = 1/tan θ и tan θ = 1/cot θ. Таким образом, раскладушка с точки зрения загара есть. раскладушка θ = 1/тангенс θ. Существует еще одна формула для записи кроватки в терминах загара: кроватка θ = тангенс (π/2 — θ) (или) тангенс (90° — θ).
Котангенс через косек
Из одного из тождеств Пифагора csc 2 θ — ctg 2 θ = 1. Отсюда получаем cot 2 θ = csc 2,1. Если взять квадратный корень с обеих сторон, кроватка θ = √(csc 2 θ — 1). Следовательно, детская кроватка в терминах csc равна кроватка θ = √(csc 2 θ — 1)
Отсюда получаем cot 2 θ = csc 2,1. Если взять квадратный корень с обеих сторон, кроватка θ = √(csc 2 θ — 1). Следовательно, детская кроватка в терминах csc равна кроватка θ = √(csc 2 θ — 1)
Закон котангенса
Рассмотрим треугольник ABC, где AB = c, BC = a и CA = b. Закон котангенса похож на закон синусов, но включает половинные углы. Закон котангенса гласит: (cot A/2) / (s — a) = (cot B/2) / (s — b) = (cot C/2) / (s — c). Здесь s — полупериметр треугольника. т. е. s = (a + b + c)/2.
Знак котангенса
Отношение котангенса (разумеется, как tan, так и cot) положительно только в первом и третьем квадрантах. Он отрицателен во втором и четвертом квадрантах. Таким образом,
- раскладушка (π — θ) = — раскладушка θ (2 -й квадрант)
- раскладушка (π + θ) = раскладушка θ (3 -й -й квадрант)
- раскладушка (2π — θ) = — раскладушка θ (4 -й квадрант)
- раскладушка (2π + θ) = раскладушка θ (1 ст квадрант)
Период котангенса
Мы знаем, что все тригонометрические функции являются периодическими функциями. Также из предыдущего раздела мы знаем, что кроватка (2π + θ) = кроватка θ . Но функция котангенса может иметь меньший период π (поскольку функция котангенса положительна в первом и третьем квадранте, где углы в третьем квадранте равны π + угол в первом квадранте). Таким образом, период котангенса равен π. т. е. раскладушка (π + θ) = раскладушка θ .
Также из предыдущего раздела мы знаем, что кроватка (2π + θ) = кроватка θ . Но функция котангенса может иметь меньший период π (поскольку функция котангенса положительна в первом и третьем квадранте, где углы в третьем квадранте равны π + угол в первом квадранте). Таким образом, период котангенса равен π. т. е. раскладушка (π + θ) = раскладушка θ .
Котангенс отрицательного угла
Котангенс отрицательного угла равен отрицательному значению котангенса положительного угла. т. е. кроватка (-x) = -кроватка x для любого x в области. Отсюда можно сделать вывод, что котангенс является нечетной функцией.
Котангенс единичной окружности
Мы знаем, что каждая точка на единичной окружности дает значения cos и sin соответствующего угла. Чтобы найти котангенс соответствующего угла, мы просто делим соответствующее значение cos на соответствующее значение sin, потому что у нас есть формула cot x, определяемая как cot x = (cos x) / (sin x).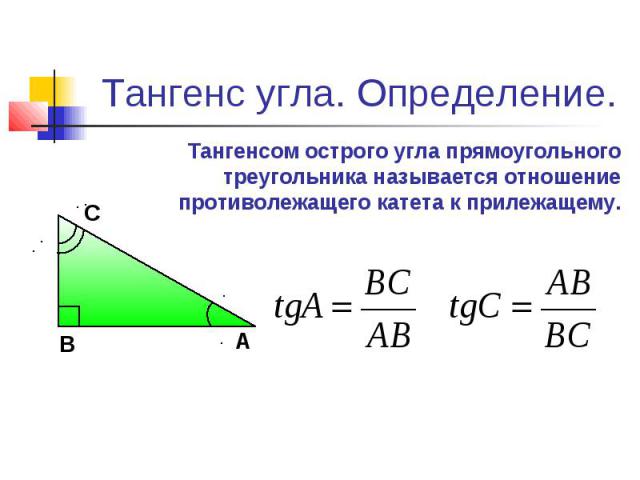 Здесь мы можем видеть значения cot θ для некоторых стандартных углов.
Здесь мы можем видеть значения cot θ для некоторых стандартных углов.
Таким же образом мы можем вычислить котангенс всех углов единичной окружности. Вот единичный круг с функцией котангенса.
Домен, диапазон и график котангенса
В этом разделе давайте посмотрим, как мы можем найти область определения и область значений функции котангенса. Кроме того, мы увидим процесс построения графика в своей области.
Область и диапазон котангенса
В предыдущем разделе мы видели, что кроватка не определена при 0° (0π), 180° (1π) и 360° (2π) (другими словами, котангенс не определен везде, где sin x равен нулю, потому что cot x = (cos x)/(sin x)). Мы знаем, что sin x равен нулю для целых чисел, кратных π, поэтому функция котангенса не определена для всех целых чисел, кратных π. Таким образом, кроватка nπ НЕ определена ни для какого целого числа n. Таким образом, областью определения котангенса является множество всех действительных чисел (R), кроме nπ (где n ∈ Z). Опять же, из единичного круга мы можем видеть, что функция котангенса может давать все действительные числа, и, следовательно, ее областью значений является множество всех действительных чисел (R). Таким образом,
Опять же, из единичного круга мы можем видеть, что функция котангенса может давать все действительные числа, и, следовательно, ее областью значений является множество всех действительных чисел (R). Таким образом,
- Областью определения котангенса является множество действительных чисел, за исключением всех целых чисел, кратных π
- Областью котангенса является множество всех действительных чисел
т. е. cot x : R — {nπ / n ∈ Z} → R
График котангенса
Поскольку функция котангенса НЕ определена для целых чисел, кратных π, на графике есть вертикальные асимптоты для всех кратных π котангенса. Кроме того, из единичного круга (в одном из предыдущих разделов) мы можем видеть, что котангенс равен 0 во всех нечетных кратных π/2. Кроме того, из единичного круга мы можем видеть, что в интервале, скажем (0, π), значения кроватки уменьшаются по мере увеличения углов. Следовательно, ctg — убывающая функция. Таким образом, график функции котангенса выглядит так.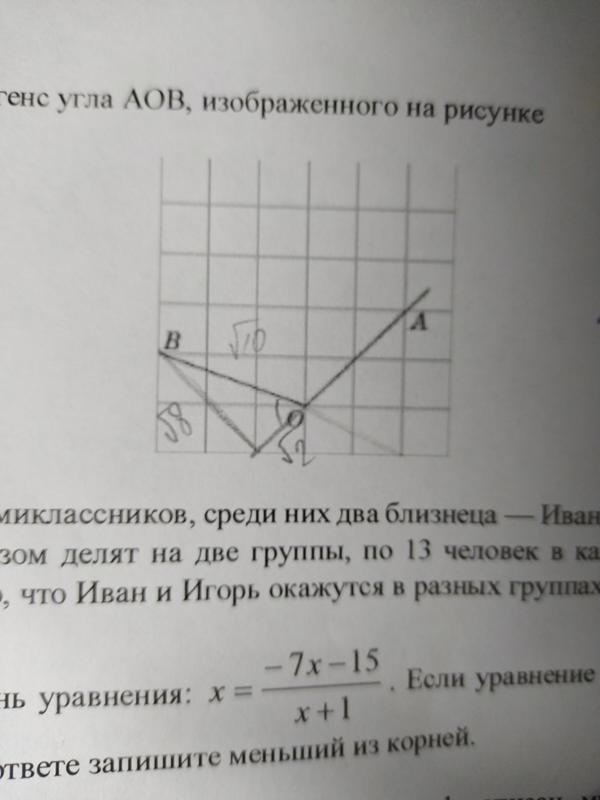
Производная и интеграл от котангенса
Чтобы найти производную и интеграл котангенса, мы используем формулу тождественного котангенса cot x = (cos x) / (sin x). Давайте посмотрим, как.
Производная котангенса
Пусть y = cot x = (cos x) / (sin x). Тогда по правилу частных
y’ = [sin x d/dx(cos x) — cos x d/dx(sin x)] / (sin x) 2
= [sin x (- sin x) — cos x (cos x)] / sin 2 x
= [-sin 2 x — cos 2 x] / sin 2 x
= — [sin 2 x + cos 2 x] / sin 2 x
= — 1/sin 2 x — [Используя тригонометрическое тождество sin 2 x + cos 2 x = 1]
= -csc 2 x — [Поскольку sin x = 1/csc x и csc x = 1/sin x]
Таким образом, производная от cot x равна -csc 2 x.
Интеграл от котангенса
∫ cot x = ∫ (cos x) / (sin x) dx
Вычислим этот интеграл методом подстановки. Для этого пусть sin x = u. Тогда cos x dx = du.
Для этого пусть sin x = u. Тогда cos x dx = du.
Тогда, используя приведенный выше интеграл, получим
∫ (1/u) du = ln |u| + C, где C — постоянная интегрирования.
Замените u = sin x здесь,
∫ cot x dx = ln |sin x| + C
Таким образом, интеграл от cot x равен ln |sin x| + C.
Важные моменты по котангенсу:
- Cot x Формула: cot x = (cos x) / (sin x)
- Некоторые важные формулы котангенса:
детская кроватка x = (cos x)/(sin x)
детская кроватка х = 1/загар х
детская кроватка (-x) = — детская кроватка x
детская кроватка θ = √(csc 2 θ — 1) - Домен cot x равен R — {nπ}, а его диапазон равен R.
- Функция котангенса имеет вертикальные асимптоты при всех кратных π.
Темы по теме:
- Детская кроватка — Формула загара
- Тригонометрия
- Тригонометрический калькулятор
- Калькулятор арккотангенса
- Детская кроватка 53 градуса
- Детская кроватка 18 градусов
- Детская кроватка 1 градус
Часто задаваемые вопросы о котангенсе
Что такое котангенс в тригонометрии?
Котангенс является одним из тригонометрических отношений и определяется как cot x = (прилежащая сторона)/(противоположная сторона) для любого угла x между основанием и гипотенузой в прямоугольном треугольнике.
Что такое формулы котангенса?
Некоторые важные формулы кроватки x:.
- детская кроватка x = (смежный)/(напротив)
- раскладушка x = (cos x)/(sin x)
- детская кроватка х = 1/тан х
- раскладушка (π/2 — x) = tan x
- детская кроватка (π + x) = детская кроватка x
- детская кроватка (2π + x) = детская кроватка x
- детская кроватка (-x) = — детская кроватка x
- раскладушка θ = √csc²θ — 1
Является ли котангенс обратным тангенсу?
Нет, обратным тангенсом является арктангенс. Пишется как загар -1 . Но (tan x) -1 = 1/tan x = кроватка x. (tan x) -1 и tan -1 x НЕ совпадают.
Что такое домен и диапазон котангенса?
Область определения котангенса равна R — {nπ, где n — целое число}, а диапазон значений котангенса равен R. Здесь R — множество всех действительных чисел.
Что является противоположностью формулы котангенса?
Мы не используем терминологию противоположности котангенса.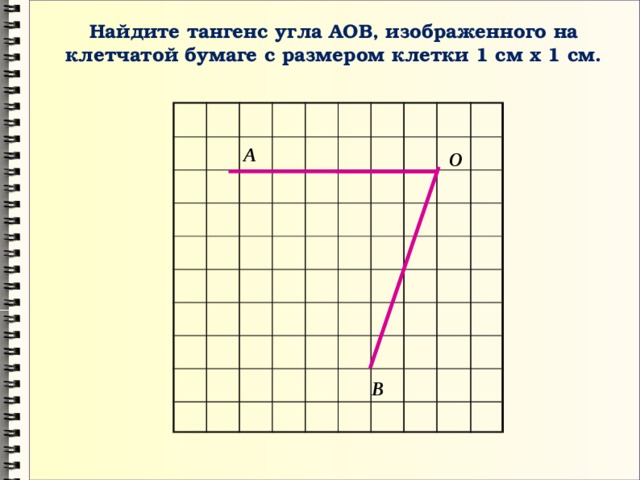

Leave A Comment