Контрольна робота «Теплові явища»

Контрольная работа по теме «Тепловые явления»

Вариант

 

1 (1,5 балла). На сколько изменится внутренняя энергия куска олова массой 2 кг, если его нагреть на 1оС?

2 (1,5 балла). Сколько нужно сжечь газа, чтобы выделилось 115 000 кДж теплоты?

3 (2 балла). В алюминиевый калориметр массой 140 г налили 250 г воды при температуре 15оС. После того, как брусок из свинца массой 100 г нагретый до 100оС поместили в калориметр с водой, там установилась температура 16оС. Составить уравнение теплового баланса и определить удельную теплоёмкость свинца.

4 (3 балла). Сколько спирта надо сжечь, чтобы изменить температуру воды массой 2 кг от 14оС до 50оС, если вся теплота, выделенная спиртом, пойдёт на нагревание воды.

5 (4 балла). На керогазе нагрели 3 кг воды от 25оС до 100оС.

Сколько при этом сожгли керосина, если на нагревание воды ушло 40% выделившейся теплоты?

 

 

 

 

Контрольная работа по теме «Тепловые явления»

Вариант

 

1 (1,5 балла). Какова масса железной детали, если на её нагревание от 20оС до 200оС пошло 20,7 кДж теплоты?

2 (1,5 балла). Сколько спирта надо сжечь, чтобы получить 45 000 кДж теплоты?

3 (2 балла). Вода массой 150 г, налитая в латунный калориметр массой 200 г, имеет температуру 12оС. Найти температуру, которая установится в калориметре, если в воду опустить железную гирю массой 0,5 кг, нагретую до 100

оС.

4 (3 балла). Сколько воды, взятой при температуре 14оС, можно на-греть до 50оС, сжигая спирт массой 30 г и считая, что вся выделяемая при горении спирта энергия идёт на нагревание воды.

5 (4 балла). В медном сосуде массой 0,5 кг нагревают 2л воды, взятой при температуре 10оС. До какой температуры можно нагреть воду за счёт сжигания 50 г спирта? КПД считать равным 50%.

Контрольная работа по теме «Тепловые явления»

Вариант

 

1 (1,5 балла). На сколько градусов повысилась температура 4 л воды, если она получила количество теплоты, равное 168 кДж?

2 (1,5 балла). Какая масса каменного угля была сожжена в печи, если при этом выделилось 60 МДж теплоты?

3 (2 балла). Стальное изделие закалялось нагреванием до температуры 700оС с последующим опусканием в масло массой 2 кг, взятое при температуре 10оС. При этом масло нагрелось до температуры 40оС. Найти массу стального изделия, если изделие охладилось на 30оС при переносе. Удельная теплоёмкость масла 2100 Дж/(кг·К).

4 (3 балла). Сколько дров необходимо сжечь для того, чтобы нагреть 50 л воды в железном котле массой 10 кг от 15

оС до 65оС? Потерями тепла можно пренебречь.

5 (4 балла). На примусе с КПД 40% необходимо вскипятить 4л воды, начальная температура которой 20оС, в алюминиевой кастрюле массой 2 кг. Определить расход керосина на нагревание воды и кастрюли.

 

 

 

Контрольная работа по теме «Тепловые явления»

Вариант

 

1 (1,5 балла). Какое количество теплоты необходимо для нагревания латунной гири массой 200 г от 20оС до 28оС?

2 (1,5 балла

). Сколько энергии выделится при полном сгорании керосина объёмом 5 л?

3 (2 балла). Чтобы охладить деталь из меди, имеющую температуру 100оС, её погрузили в 420 г воды с температурой 15оС. Определите массу детали, если известно, что в процессе теплообмена вода нагрелась на 18оС.

4 (3 балла). На сколько изменится температура воды объёмом 100 л, если считать, что вся теплота, выделяемая при сжигании древесного угля массой 0,5 кг, пойдёт на нагревание воды?

5 (4 балла). Сколько процентов теплоты полезно использовано, если на спиртовке нагрели 400 г воды от 20о

С до 100оС и сожгли при этом 15 г спирта?

Задачи на расчет количества теплоты

Вы можете изучить и скачать доклад-презентацию на тему Задачи на расчет количества теплоты. Презентация на заданную тему содержит 13 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!

Презентации» Физика» Презентация Задачи на расчет количества теплоты

Слайды и текст этой презентации

Слайд 1

Описание слайда:

Задачи на расчет количества теплоты

Слайд 2

Описание слайда:

Условие В алюминиевый калориметр массой 45 г, содержащий 100 г воды при температуре 20°С, поместили чугунную гирю массой 50 г, предварительно нагретую до 100°С. Какая температура установится в калориметре?

Слайд 3

Описание слайда:

Условие В алюминиевый калориметр массой 45 г, содержащий 100 г воды при температуре 20°С, поместили чугунную гирю массой 50 г, предварительно нагретую до 100°С. Какая температура установится в калориметре?

Слайд 4

Описание слайда:

Условие В алюминиевый калориметр массой 45 г, содержащий 100 г воды при температуре 20°С, поместили чугунную гирю массой 50 г, предварительно нагретую до 100°С. Какая температура установится в калориметре?

Слайд 5

Описание слайда:

Условие В алюминиевый калориметр массой 45 г, содержащий 100 г воды при температуре 20°С, поместили чугунную гирю массой 50 г, предварительно нагретую до 100°С.

Какая температура установится в калориметре?

Слайд 6

Описание слайда:

Какие тепловые процессы происходят в задаче? Назовите процессы, которые происходят с каждым из этих тел

Слайд 7

Описание слайда:

Условие В алюминиевый калориметр массой 45 г, содержащий 100 г воды при температуре 20°С, поместили чугунную гирю массой 50 г, предварительно нагретую до 100°С. Какая температура установится в калориметре?

Слайд 8

Описание слайда:

Обсуждение

Слайд 9

Описание слайда:

Решение

Слайд 10

Описание слайда:

Решение

Слайд 11

Описание слайда:

Решение

Слайд 12

Описание слайда:

Решение

Слайд 13

Описание слайда:

Ответ



Tags Задачи на расчет количества теплоты

Похожие презентации

Презентация успешно отправлена!

Ошибка! Введите корректный Email!

Email

Конечная температура после помещения теплого металла в более холодную воду

Конечная температура после помещения теплого металла в более холодную воду

Когда теплый металл помещают в более холодную воду, какой получается конечная температура?

Перейти к расчету конечной температуры при смешивании металла и воды: задачи 1 — 15

Перейти к расчету конечной температуры при смешивании двух проб воды

Назад в меню термохимии

Эти задачи точно такие же, как смешивание двух количеств воды, за одним небольшим исключением: удельные теплоемкости в двух частях уравнения будут разными. Удельная теплоемкость воды останется на уровне 4,184, но значение для металла будет другим. Эти значения сведены в таблицы, а списки выбранных значений есть в большинстве учебников.

Пример #1: Определите конечную температуру, когда кусок железа массой 25,0 г при температуре 85,0 °C помещают в 75,0 г воды при температуре 20,0 °C.

Сначала обсуждение, потом решение. Простите меня, если пункты кажутся очевидными:

а) Более холодная вода будет нагреваться (к ней «притекает» тепловая энергия). Более нагретый металл остынет (из него «вытекает» тепловая энергия).
b) Вся смесь будет иметь температуру ЖЕ . Это очень, очень важно.
c) Энергия, которая «вытекла» (из более теплой воды), равна энергии, которая «втекла» (в более холодную воду)

Ключ решения номер один: Начнем с того, что назовем конечную, конечную температуру «x». Имейте в виду, что И утюг, и вода будут нагреваться до температуры, которую мы называем «х». Кроме того, убедитесь, что вы понимаете, что «x», который мы используем, ЯВЛЯЕТСЯ НЕ Δt, а ОКОНЧАТЕЛЬНОЙ температурой. Это то, для чего мы решаем.

Более нагретое железо понижается с 85,0 до х, значит, его Δt равно 85,0 минус х. Более холодная вода нагревается, поэтому ее Δt равно x минус 20,0.

Последний абзац может немного сбить с толку, поэтому давайте сравним его с числовой строкой:

Чтобы вычислить абсолютное расстояние, это большее значение минус меньшее значение, поэтому от 85,0 до х равно 85,0 минус х, а расстояние от х до 20,0 равно х минус 20,0

Ключевое решение номер два: количество энергии, выходящее из теплой воды, равно количеству энергии, выходящей из холодной воды. Это означает:

q потеря = q усиление

Таким образом, путем подстановки имеем:

(25,0) (85,0 — х)(0,45) = (75,0) (х — 20,0) (4,184)

Найдите х

Обратите внимание на использование удельной теплоты сгорания железа. Это 0,45 Дж на грамм-градус Цельсия.

Учитывая, что 75/25 = 3, получаем:

38,25 — 0,45х = 12,552х — 251,04

тогда

13,002x = 289,29

Ответ

22,25 °С

, если вы не слишком придирчивы к значащим цифрам.

Обратите внимание, что температура железа немного падает, в то время как вода перемещается всего на несколько (в данном случае 2,25) градусов. Это типичная ситуация в этом типе проблемы.

Пример #2: Определите конечную температуру, когда 10,0 г алюминия при 130,0 °C смешиваются с 200,0 г воды при 25,0 °C.

Техника расчета не отличается от Примера №1. Обратите внимание, начальная температура металла выше точки кипения воды. В действительности образец может испарить незначительное количество воды, но мы будем считать, что это не так для расчетов.

Решение:

1) Настройте числа:

q алюминий = q вода

(10) (130 − x) (0,901) = (200,0 )(x − 25) (4,18)

2) Заметив, что 200/10 = 20, получаю:

117,13 — 0,901х = 83,6х — 2090

х = 26,12 °С.

Имейте в виду, что «x» соответствует конечной температуре, а НЕ Δt.

Также я решил эту проблему с 4.18. Выполнение этого с 4.184 дает немного другой ответ. Убедитесь, что вы согласовали со своим учителем значения различных констант, которые он/она хочет, чтобы вы использовали.

Пример №3: Определите конечную температуру, когда 20,0 г ртути при 165,0 °C смешиваются с 200,0 г воды при 60,0 °C. (C p для Hg = 0,14 Дж на грамм-градус Цельсия.)

Мы проигнорируем тот факт, что ртуть жидкая. он не растворяется в воде.

Решение:

(20,0) (165,0 — х) (0,14) = (200,0) (х — 60,0) (4,18)

Заметив, что 200/20 = 10, я получаю:

23,1 — 0,14х = 41,8х — 2508

41,94х = 2531,1

х = 60,35 °С

Обратите внимание, что вода перемещается только на 0,35 градуса. Имейте в виду, что существует большое количество воды по сравнению с ртутью, И что для перемещения воды на один градус требуется гораздо больше энергии, чем для того же количества ртути, перемещаемого на один градус.

Пример №4: 10,0 г воды имеют температуру 59,0 °C. Если в калориметр поместить 3,00 г золота при температуре 15,2 °С, какова будет конечная температура воды в калориметре? (Удельная теплоемкость золота составляет 0,128 Дж/г°С.)

Решение:

1) Настройте следующее:

q вода = q золото

(10,0) (59,0 − x) (4,184) = (3,00) (x − 15,2) (0,128)

2) Алгебра:

2468,56 — 41,84х = 0,384х — 5,8368

42,224х = 2474,3968

х = 58,6 °С

Обратите внимание, что в этом случае вода остывает, а золото нагревается. Это противоположно самой распространенной задаче этого типа, но методика решения та же.

Пример №5: 105,0 мл H 2 O изначально имеет комнатную температуру (22,0 °C). Охлажденный стальной стержень (2,00°С) помещают в воду. Если конечная температура системы 21,5 °С, какова масса стального стержня? (удельная теплоемкость воды = 4,184 Дж/г °C; удельная теплоемкость стали = 0,452 Дж/г °C)

Решение:

(105,0 г) (0,5 °C) (4,184 Дж °C -1 г -1 ) = (x) (19,5 °C) (0,452 Дж °C -1 г -1 )

х = 24,9 г

Пример #6: Кольцо из чистого золота и кольцо из чистого серебра имеют общую массу 15,0 г.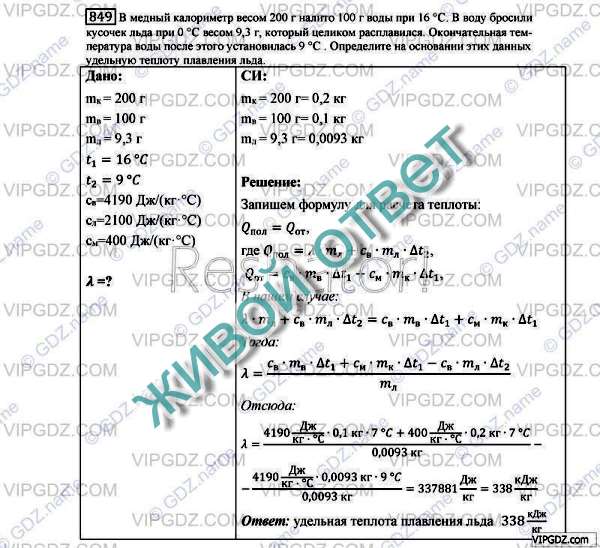 Два кольца нагревают до 62,4°С и опускают в 13,6 мл воды при 22,1°С. Когда достигается равновесие, температура воды составляет 23,9 °С. (Примите плотность воды 0,998 г/мл.)

(а) Какова масса золотого кольца?
(b) Какова масса серебряного кольца?

Комментарий: теплотворная способность доступна во многих местах в Интернете и в учебниках. Вот пример.

Решение:

1) Основное используемое уравнение:

Полученное или потерянное тепло = (масса) (изменение температуры) (удельная теплоемкость)

В более компактной форме: q = (m) (Δt) (C p )

Ниже будут использованы три из них.

2) Две массы, связанные с золотым и серебряным кольцами:

Пусть y = граммы золота
Следовательно, 15,0 − y = грамм серебра

3) Масса воды:

13,6 мл x 0,998 г/мл = 13,5728 г

4) Тепло, получаемое водой:

q = (13,5728 г) x (1,8 °C) (4,184 Дж г¯ 1 °C¯ 1 )

кв = 102,2195 Дж

1,8 получается следующим образом: 23,9 − 22,1

5) Когда золотое кольцо и серебряное кольцо остывают, они высвобождают энергию, которая в сумме составляет 102,2195 Дж. Сумма может быть выражена следующим образом:

(у) (38,5 °С) (0,129 Дж г¯ 1 °С¯ 1 ) + (15 − у) (38,5 °С) (0,235 Дж г¯ 1 °С¯ 1 ) = 102,2195 Дж

Помните, изменение на 1 °C равно изменению на 1 K. Это означает, что 0,129 Дж·г¯ 1  °C¯ 1  — это то же самое, что 0,129 Дж·г¯ 1 К¯ 1

38,5 было получено таким же образом, как и 1,8 чуть выше.

6) Алгебра!

4,9665г + (15 — г) (9,0475) = 102,2195

4,9665г + 135,7125 – 9,0475г = 102,2195

-4,081г = -33,493

г = 8,21 г золота

15,0 − 8,21 = 6,79г Ag

Пример №7: Кольцо массой 8,352 грамма сделано из золота и серебра. Когда кольцо было нагрето до 94,52 °С, а затем брошено в 13,40 г воды при 20,00 °С, температура воды после достижения теплового равновесия составила 22,00 °С. Какова массовая доля золота и серебра в кольце?

Решение:

Теплота, выделяемая серебром, плюс теплота, выделяемая золотом, равняется теплоте, поглощаемой водой.

Установите массу серебра равной «x». Это означает, что масса золота равна 8,352 минус x.

(x) (72,52 °C) (0,235 Дж/г °C) + (8,352 − x) (72,52 °C) (0,129 Дж/г °C) = (13,40 г) (2,00 °C) (4,184 Дж /г °С)

72,52 получается из 94,52 минус 22,00

17,0422х + (8,352 — х) (9,35508) = 112,1312

17,0422х + 78,13362816 — 9,35508х = 112,1312

7,68712x = 33,99757184

х = 4,422667 г

массовых процентов золота: (4,422667 / 8,352) * 100 = 52,95%

Массовая доля серебра: 100,00 − 52,95 = 47,05%

Пример #8: Кубик льда весом 74,0 г при температуре -12,0 °C помещают на блок меди массой 10,5 кг при температуре 23,0 °C, и вся система изолируется от окружающей среды. Через несколько минут лед растаял, и температура системы достигла равновесия. Рассчитайте конечную температуру системы.

Комментарий: не указана ни одна из соответствующих констант. Вам придется искать правильные значения, если вы столкнулись с такой проблемой. Если вы изучите свои источники информации, вы можете обнаружить, что они немного отличаются от значений, которые я использую. Это обычное дело. Многие из используемых значений были определены экспериментально, и разные источники часто содержат немного отличающиеся значения.

Решение:

1) Лед изменяется с −12 до 0:

q = (74,0 г) (12,0 °C) (2,06 Дж/г °C) = 1829,28 Дж

2) Лед тает:

q = (74,0 г / 18,0 г/моль) (6,02) = 24,7489 кДж

3) Жидкая вода подвергается неизвестному повышению температуры до конечного значения x

q = (74,0 г) (x — 0) (4,184 Дж/г°C) = 309,616x

4) Медь теряет тепло и падает до конечного значения x:

q = (10500 г) (23,0 − x) (0,385 Дж/г°C)

5) Количество тепла, отдаваемое медью, равно количеству тепла, полученному водой:

(10500) (23,0 — х) (0,385) = 1829,28 + 24748,9 + 309,616х

Обратите внимание, что кДж от таяния льда используется как Дж, а не кДж. Масса меди выражается в граммах, а не в кг.

(23,0 — х) (4042,5) = 26578,18 + 309,616х

92977,5 — 4042,5х = 26578,18 + 309,616х

66399,32 = 4352,116х

х = 15,2568 °С

x = 15,2 °C (до трех цифр, я следовал правилу округления до 5)

Пример #9: Сколько граммов воды можно нагреть с 25,0 °С до 35,0 °С за счет тепла, выделяемого 85,0 г железа, которое охлаждается с 85,0 °С до 35,0 °С? Удельная теплоемкость железа 0,450 Дж/г °С.

Решение:

1) Сколько тепла теряет утюг?

изменение температуры —> 85,0 °C − 35,0 0 °C = 50,0 °C

q = (масса) (изменение температуры) (удельная теплоемкость)

q = (85,0 г) (50,0 °С) (0,450 Дж/г °С)

q = 1912,5 Дж

2) Предположим, что все 1912,5 Дж идут на нагрев воды:

q = (масса) (изменение температуры) (удельная теплоемкость)

1912,5 Дж = (х) (10,0 °С) (4,184 Дж/г °С)

х = 45,7 г

Обратите внимание, что удельная теплоемкость жидкой воды в тексте задачи не приводится.

3) Эту задачу можно было бы решить, приравняв два уравнения и решив относительно «x»:

(85,0 г) (50,0 °C) (0,450 Дж/г °C) = (x) (10,0 °C) (4,184 Дж/г °C)

Пример #10: Найдите массу жидкости H 2 O при 100,0 °C, которую можно вскипятить в газообразное H 2 O при 100,0 °C блоком алюминия массой 130,0 г при температуре 402,0 °C? Предположим, что алюминий способен кипятить воду до тех пор, пока ее температура не упадет ниже 100,0 °С. Теплоемкость алюминия равна 0,900 Дж г¯ 1 °С¯ 1 , а теплота парообразования воды при 100 °С составляет 40,65 кДж моль¯ 1

Решение:

1) Теплота, которую Al может потерять при переходе от начальной к конечной температуре:

q = m Δt C p

q = (130.) г (302,0 °С) (0,900 Дж г¯ 1 °С¯ 1 ) = 35334 Дж = 35,334 кДж

Для испарения воды доступно 35,334 кДж тепла.

2) Используйте 35,334 кДж и теплоту парообразования воды для вычисления молей, а затем массу испарившейся воды:

q = (ΔH) (моль)

35,334 кДж = (40,65 кДж/моль) (х)

х = 0,869225 молей H 2 O

масса H 2 O = (0,869225 моль) (18,015 г/моль) = 15,659г

Три сига инжира, это 15,6 г

Бонус Пример: 250-граммовый образец металла нагревают до температуры 98,0 °C. Его помещают в 100 г воды в латунный калориметрический стакан с латунной мешалкой. Общая масса чашки и мешалки составляет 50,0 грамм. Начальная температура воды, мешалки и калориметра 20,0 °С. Конечная равновесная температура системы составляет 30,0 °С. Чему равна удельная теплоемкость металлического образца? (Удельная теплоёмкость латуни 0,0920 кал г¯ 1 C¯ 1 .)

Решение:

1) Количество тепла, выделяемого образцом металла, поглощается (а) водой и (б) латунным калориметром и мешалкой. Какое количество теплоты было захвачено водой?

q = m Δt C p

q = (100, г) (10,0 °C) (1,00 г кал. г¯ 1 C¯ 1 )

кв = 1000 кал

Примечание: 1,00 г кал/г¯ 1 C¯ 1 – удельная теплоемкость жидкой воды.

2) Сколько тепла поглотил латунный калориметр и мешалка?

q = m Δt C p

q = (50,0 г) (10,0 °C) (0,092 кал г¯ 1 C¯ 1 )

q = 54,28 кал

3) Суммарное тепло, выделяемое металлическим образцом:

1000 кал + 54,28 кал = 1054,28 кал

4) Определите удельную теплоемкость металлического образца:

q = m Δt C p

1054,28 кал = (250, г) (68,0 °C) (C p )

C p = 0,062 г кал г¯ 1 C¯ 1

Перейти к расчету конечной температуры при смешивании металла и воды задач 1 — 15

Перейти к расчету конечной температуры при смешивании двух проб воды

Назад в меню термохимии

Когда 45 г металла при 100°C бросают в ледяной калориметр, наблюдается уменьшение объема льда на 0,4596×10−6 м3.

Чему равна удельная теплоемкость металла? (L=336×103 Дж/кг и относительная плотность льда =0,917)

Вопрос

Обновлено: 07.09.2019

NN GHOSH-КАЛОРИМЕТРИЯ-Все вопросы

20 видео

РЕКЛАМА

Текст Решение

9 Ответ 0 NA 5 0 Правильный ответ 90 0004 Ответить

Шаг за шагом пошаговое решение от экспертов, которое поможет вам избавиться от сомнений и получить отличные оценки на экзаменах.

Ab Padhai каро бина объявления ке

Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке!

Похожие видео

Небольшое количество воды массой m при температуре θ (в ∘C) выливается на большую массу льда M, находящегося в точке плавления. Если с — удельная теплоемкость воды, L — удельная теплоемкость воды, а L — удельная скрытая теплота плавления льда, то масса расплавленного льда равна

11749502

при 0∘С. В калориметр опускают 50 г металла при 100°С. Установлено, что при достижении теплового равновесия объем содержимого калориметра уменьшается на 0,5×10–6 м3. Вычислите удельную теплоемкость металла. Изменением объема металла пренебречь. Удельная скрытая теплота плавления льда составляет L=300×103 Дж/кг, а его относительная плотность равна 0,9..

15085696

При температуре воздуха -10∘C лед на большом мелководном озере увеличивается на 1 см за 12 минут. Найдите теплопроводность льда. (Плотность льда = 900 кгм-3 и L = 330×103 Дж кг-1)

15634998

Сферический железный шар помещают на большой кусок сухого льда при температуре 0°C. Мяч погружается в лед до половины. Какой была температура утюга?
(Плотность железа =7,7×103кгм3, Плотность льда =920кгм-3 Удельная теплоемкость железа =504Джкг-1К-1, Удельная скрытая теплота плавления льда =336×103Джкг-1) 9(1) )

17686445

1 кг льда при 0°C сжимается при таянии на 91×10−6 м3. Твердое вещество массой 40 г, брошенное при температуре 60°С в ледяной калориметр, вызывает изменение объема на 0273×10-6 м3.
(Удельная теплота плавления льда =336×103 Дж/кг. Рассчитать удельную теплоемкость твердого тела. изменение температуры при погружении в него 10×10-3 кг металла при температуре 100 ∘ С. Относительная плотность льда 0,917. Найдите удельную теплоемкость металла.

17686451

Калориметр содержит лед. Определить теплоемкость калориметра, если для нагревания его вместе с содержимым от 270 К до 270 К требуется 2,1 кДж теплоты, а для повышения его температуры с 272 К до 274 К требуется 69,72 кДж теплоты.
(л льда =336×103 Джкг-1, удельная теплоемкость льда =2100кг-1К-1)

17686466

Термостойкий конверт содержит 100 г льда при температуре 1∘C. Он сжат до 1200 атм. Найдите массу растаявшего льда, если температура плавления льда понизится на 1°С при повышении давления на 138 атм.
(л льда =336×103 Джкг-1 и удельная теплоемкость льда =2100Джкг-1К-1)

17686467

Текст Решение

Сосуд площадью 1 м2, изготовленный из медного листа толщиной 5 мм, наполнен тающего льда и погружен в воду при температуре 100∘C.