«Основные понятия и утверждения геометрии»
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«СРЕДНЯЯ ШКОЛА №29»
г. Нижневартовск
Дидактический материал по теме:
«Основные понятия и утверждения геометрии»
9 класс
Автор:
Султанмуратова Л.М.,
учитель математики
1. Какое
из следующих утверждений верно?
Какое
из следующих утверждений верно?
1) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм – квадрат.
2) Смежные углы равны.
3) Каждая из биссектрис равнобедренного треугольника является его высотой.
2. Какие из следующих утверждений верны?
1) Средняя линия трапеции равна сумме ее оснований.
2) Диагонали ромба перпендикулярны.
3) Площадь треугольника меньше произведения двух его сторон.
3. Какое из следующих утверждений верно?
1) У любой трапеции основания параллельны.
2) Диагонали ромба равны.
3) Точка пересечения двух окружностей равноудалены от центров этих окружностей.
4. Какие из следующих утверждений верны?
1) Один из углов треугольника всегда не превышает 60 градусов.
2) Угол, вписанный в
окружность, равен соответствующему центральному углу, опирающемуся на ту же
дугу.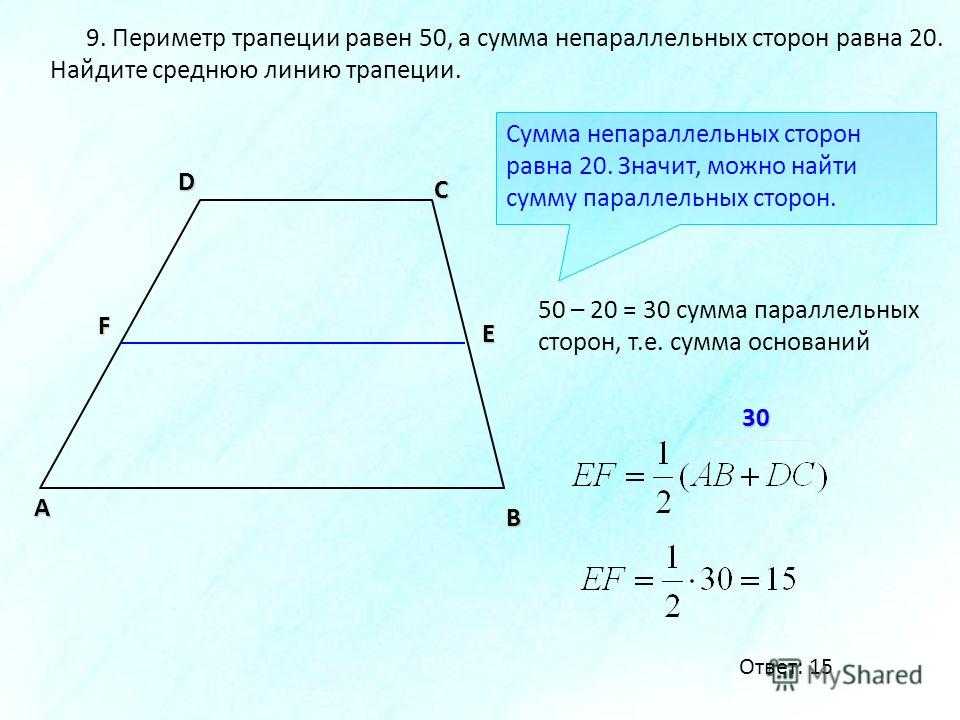
3) Диагонали прямоугольника точкой пересечения делятся пополам.
5. Какие из следующих утверждений верны?
1) Треугольника со сторонами 1,2,3 не существует.
2) Площадь трапеции равна произведению основания трапеции на высоту.
3) Все диаметры окружности равны между собой.
6. Какое из следующих утверждений верно?
1) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.
2) Если стороны одного четырехугольника соответственно равны сторонам другого четырехугольника, то такие четырехугольники равны.
3) Смежные углы равны.
7. Какое из следующих утверждений верно?
1) Если стороны одного четырехугольника соответственно равны сторонам другого четырехугольника, то такие четырехугольники равны.
2) Площадь ромба равна произведению двух его смежных сторон на синус угла между ними.
3) Смежные углы равны.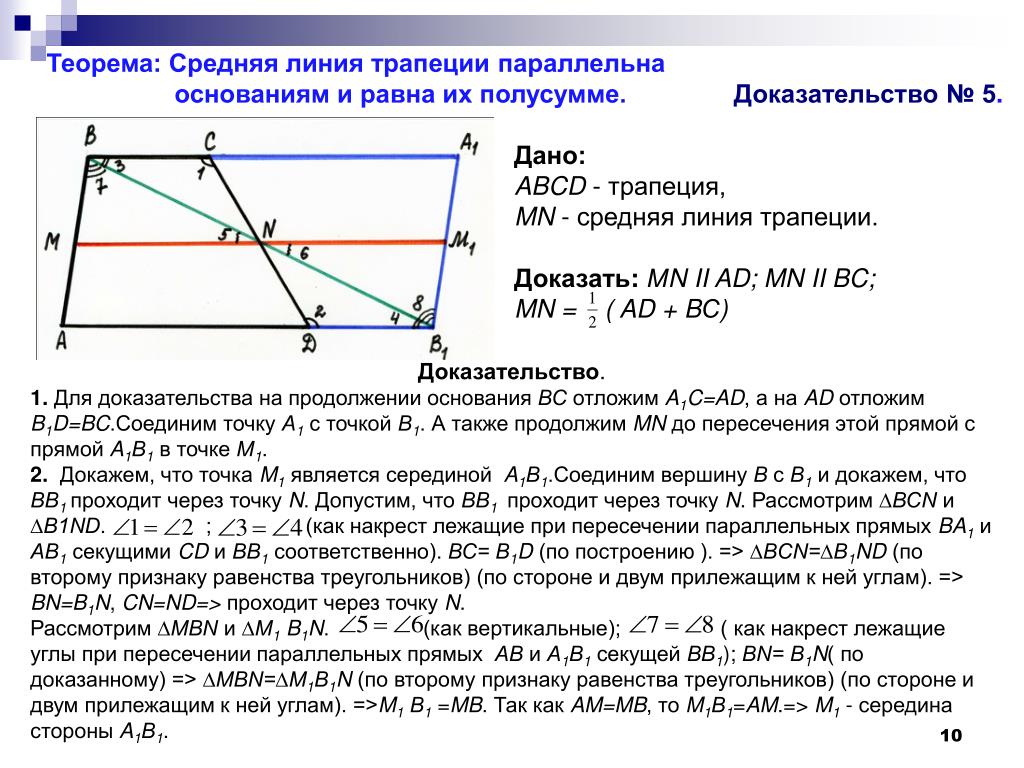
8. Какие из следующих утверждений верны?
1) Смежные углы равны.
2) Площадь квадрата равна произведению двух его смежных сторон.
3) Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
9. Какое из следующих утверждений верно?
1) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
2) Средняя линия трапеции равна сумме ее оснований.
3) Площадь параллелограмма равна половине произведения его диагоналей.
10. Какие из следующих утверждений верны?
1) Сумма углов прямоугольного треугольника равна 90 градусам.
2) Существуют три прямые, которые проходят через одну точку.
3) Диагонали ромба точкой пересечения делятся пополам.
11. Какое из следующих утверждений верно?
1) Тангенс любого острого угла меньше единицы.
2) Средняя линия трапеции
равна сумме ее оснований.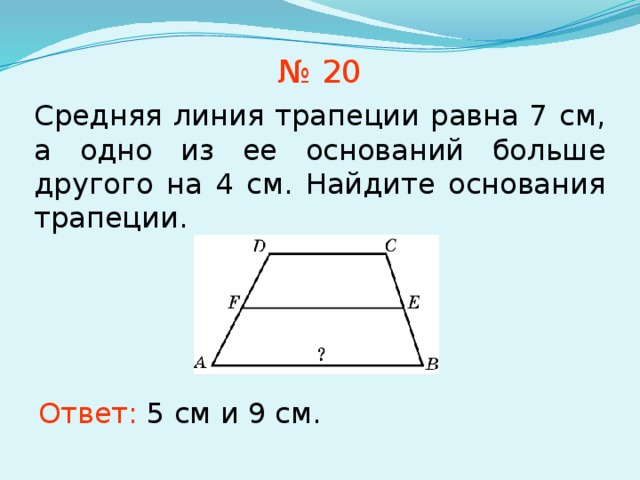
3) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.
12. Какие из следующих утверждений верны?
1) Если точка лежит на биссектрисе угла, то она равноудалена от сторон этого угла.
2) Если в параллелограмме две соседние стороны равны, то такой параллелограмм является ромбом.
3) Касательная к окружности параллельна радиусу, проведенному в точку касания.
13. Какие из следующих утверждений верны?
1) Площадь параллелограмма равна половине произведения его диагоналей.
2) Сумма углов прямоугольного треугольника равна 90 градусам.
3) Биссектрисы треугольника пересекаются в центре его вписанной окружности.
14. Какое из следующих утверждений верно?
1) В параллелограмме есть два равных угла.
2) В тупоугольном треугольнике все углы тупые.
3) Площадь прямоугольного
равна произведению длин всех его сторон.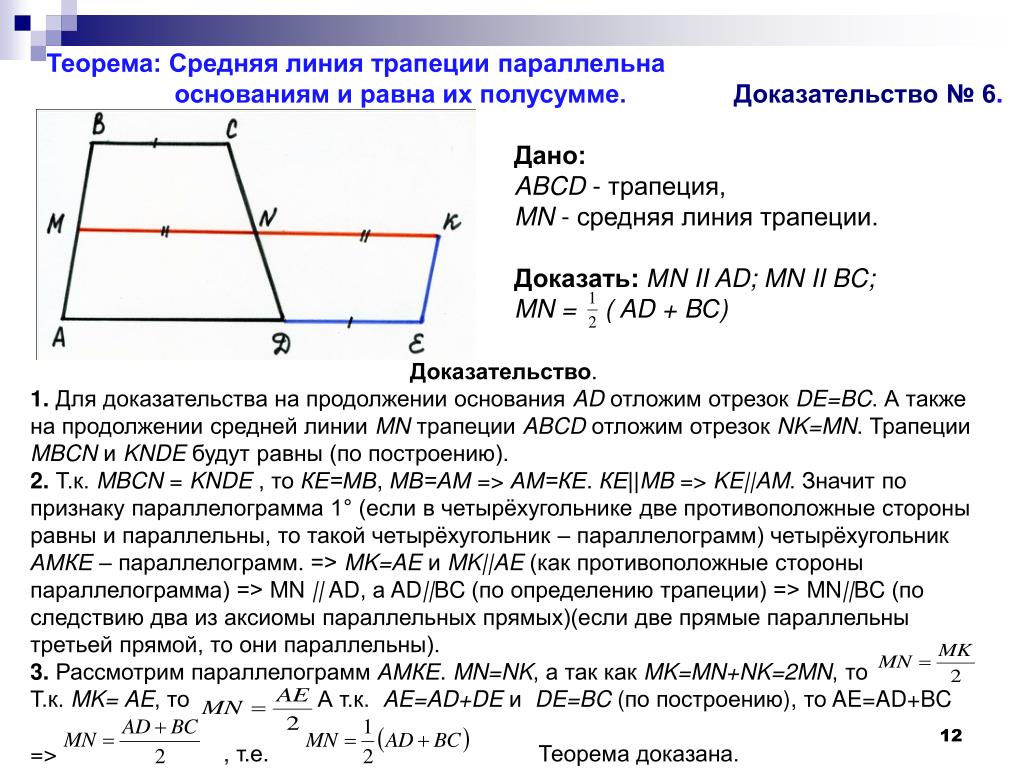
15. Какие из следующих утверждений верны?
1) Один из углов треугольника всегда не превышает 60 градусов.
2) Средняя линия трапеции равна сумме ее оснований.
3) Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
16. Какое из следующих утверждений верно?
1) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника
2) Сумма углов равнобедренного треугольника равна 180 градусов.
3) Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
17. Какое из следующих утверждений верно?
1) Смежные углы равны.
2) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
3) Площадь параллелограмма равна половине произведения его диагоналей.
18. Какие из следующих утверждений верны?
1) Все диаметры окружности
равны между собой.
2) Если в параллелограмме две соседние стороны равны, то такой параллелограмм является ромбом.
3) Сумма углов любого треугольника равна 360 градусам.
19. Какие из следующих утверждений верны?
1) Треугольники со сторонами 1,2,4 не существует.
2) Медиана треугольника делит пополам угол, из которого проведена.
3) Все диаметры окружности равны между собой.
20. Какие из следующих утверждений верны?
1) Сумма углов равнобедренного треугольника равна 180 градусов.
2) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой данной.
3) В прямоугольном треугольнике квадрат гипотенузы равен разности квадратов катетов.
21. Какое из следующих утверждений верно?
1) Касательная к окружности параллельна радиусу, проведенному в точку касания.
2) Диагонали ромба точкой пересечения делятся пополам.
3) Внешний угол треугольника
равен сумме его внутренних углов.
22. Какое из следующих утверждений верно?
1) Если диагонали параллелограмма равны, то это квадрат.
2) Сумма углов равнобедренного треугольника равна 180 градусов.
3) Площадь трапеции равна произведению основания трапеции на высоту.
23. Какие из следующих утверждений верны?
1) Если диагонали параллелограмма равны, то это ромбом.
2) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
3) В любом тупоугольном треугольнике есть острый угол.
24. Какое из следующих утверждений верно?
1) Если диагонали выпуклого четырехугольника равны и перпендикулярны, то этот квадрат.
2) Сумма острых углов прямоугольного треугольника равна 90 градусам.
3) Смежные углы равны.
25. Какое из следующих утверждений верно?
1) Если два угла одного
треугольника равны двум углам другого треугольника, то такие треугольники
подобны.
2) Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.
3) Средняя линия трапеции равна сумме ее оснований.
26. Какое из следующих утверждений верно?
1) Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу.
2) Любой квадрат является прямоугольником
3) Каждая из биссектрис равнобедренного треугольника является его высотой.
27. Какое из следующих утверждений верно?
1) Сумма углов прямоугольного треугольника равна 90 градусам.
2) Отношение площадей подобных треугольников равно коэффициенту подобия.
3) Любой прямоугольник можно вписать в окружность.
28. Какие из следующих утверждений верны?
1) У любой трапеции основания параллельны.
2) Треугольника со сторонами 1,2,4 не существует.
3) Две прямые,
перпендикулярные третьей прямой, перпендикулярны друг другу.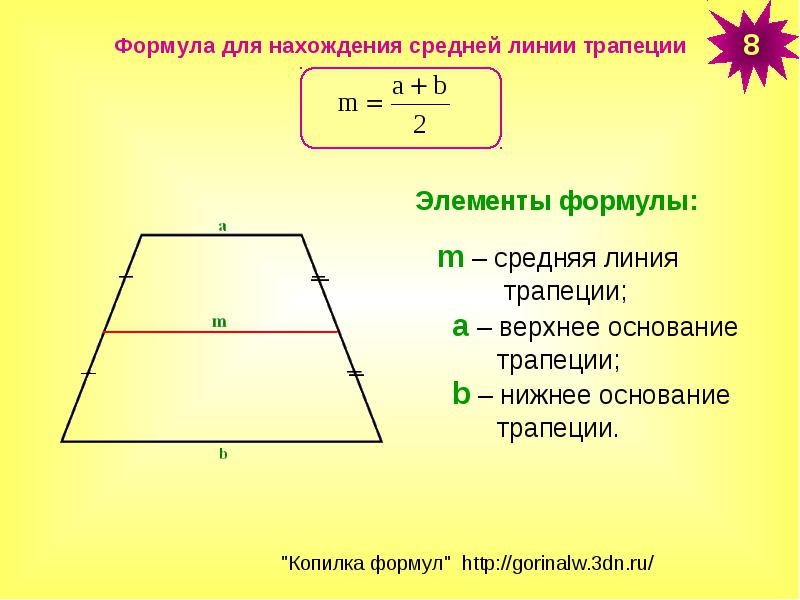
29. Какие из следующих утверждений верны?
1) Площадь треугольника меньше произведения двух его сторон.
2) Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу.
3) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.
30. Какие из следующих утверждений верны?
1) Касательная к окружности параллельна радиусу, проеденному в точку касания.
2) Если в ромбе один из углов равен 90 градусам, то такой ромб – квадрат.
3) Сумма углов равнобедренного треугольника равна 180 градусов.
Ответы:
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
1 | 23 | 1 | 13 | 13 | 1 | 2 | 23 | 1 | 23 | 3 | 12 | 3 | 1 | 13 | 2 | 2 | 12 | 13 | 12 | 2 | 2 | 23 | 2 | 1 | 2 | 3 | 12 | 13 | 23 |
Информационный источник
ОГЭ
(ГИА-9): 3000 задач с ответами по математике; под ред. И. В. Ященко.- М.:
Издательство «Экзамен», издательство МЦНМО, 2015.-463.
И. В. Ященко.- М.:
Издательство «Экзамен», издательство МЦНМО, 2015.-463.
Геометрия — выбор верных утверждений
Приглашаем учителей и учеников на весенний сезон олимпиад. Бесплатная викторина, мгновенные результаты, комфортное участие
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Выбрать материалы
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Выбор верных утверждений
Вопрос 1
Если диагонали параллелограмма перпендикулярны, то этот параллелограмм является ромбом.
Варианты ответов
- верно
- не верно
Вопрос 2
Диагонали ромба равны.
Варианты ответов
- равны
- не равны
Вопрос 3
В треугольнике против большего угла лежит большая сторона.
Варианты ответов
- верно
- не верно
Вопрос 4
Вертикальные углы равны.
Варианты ответов
- верно
- не верно
Вопрос 5
Две прямые, перпендикулярные третьей прямой, перпендикулярны.
Варианты ответов
- верно
- не верно
Вопрос 6
Средняя линия трапеции равна сумме её оснований.
Варианты ответов
- верно
- не верно
Вопрос 7
Все углы ромба равны.
Варианты ответов
- верно
- не верно
Вопрос 8
Все диаметры окружности равны между собой.
Варианты ответов
- верно
- не верно
Пройти тест
Сохранить у себя:
© 2022, Гасанова Айшан Гасангулу кызы 59
Равнобедренная трапеция: определение, формула, свойства, примеры
Что такое равнобедренная трапеция?
Равнобедренная трапеция — это трапеция, у которой верхняя и нижняя стороны параллельны, а остальные две непараллельные стороны имеют одинаковую длину.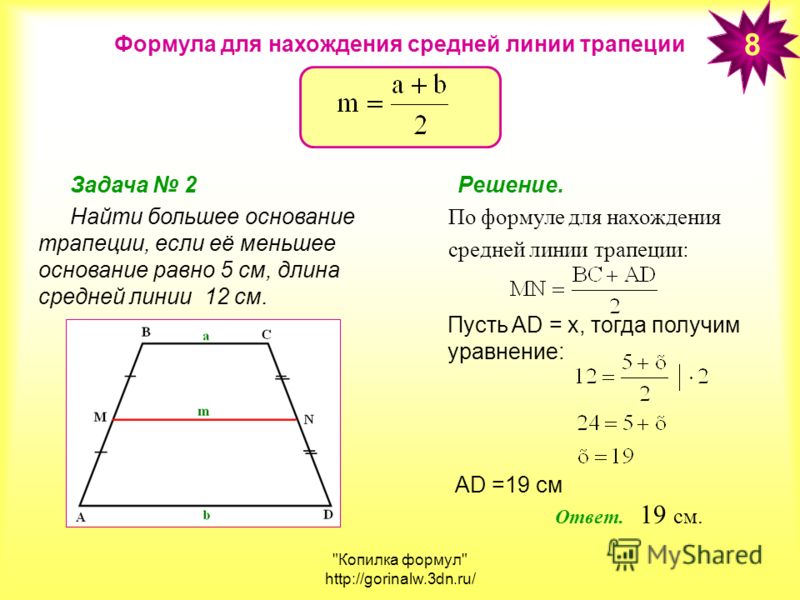
Мы знаем, что трапеция — это четырехугольник с двумя параллельными сторонами и двумя непараллельными сторонами. У равнобедренной трапеции непараллельные стороны равны.
Таким образом, мы можем сказать, что параллельные стороны равнобедренной трапеции не равны, а равные стороны не параллельны. Два угла при основании равнобедренной трапеции равны между собой.
Сумма углов трапеции всегда равна 360 градусов, как и любого четырехугольника.
Взгляните на следующее изображение, чтобы понять форму равнобедренной трапеции.
Равнобедренная трапеция может быть определена как трапеция, у которой непараллельные стороны имеют одинаковую длину; и углы при основании имеют одинаковую величину.
Родственные игры
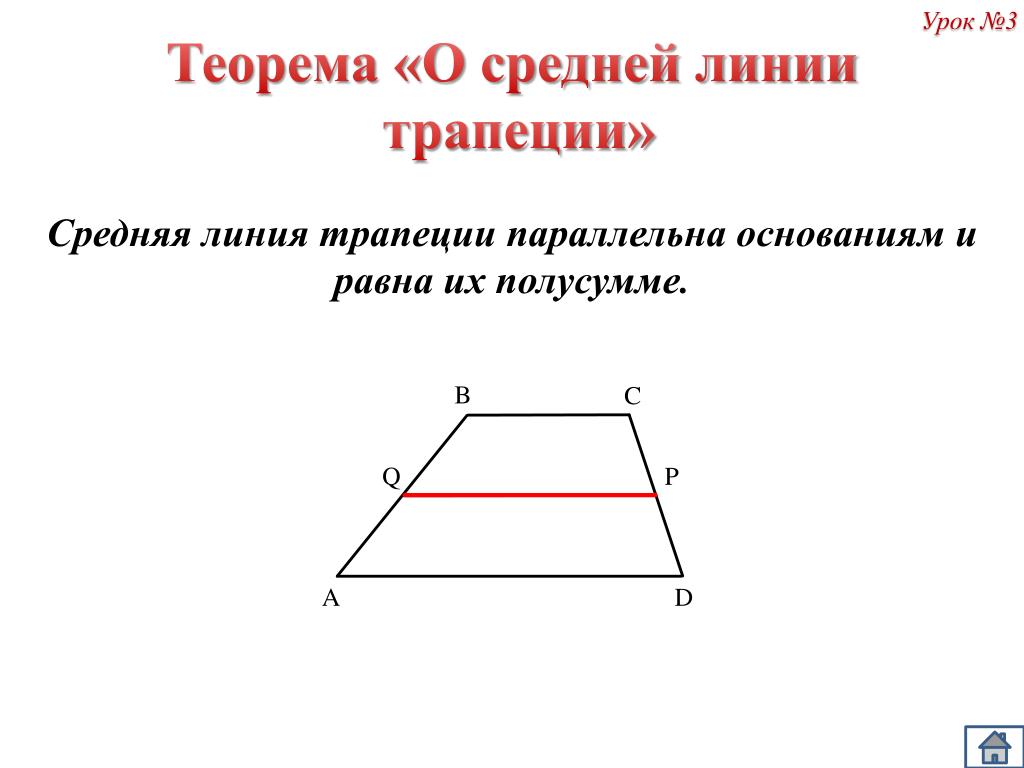
Свойства равнобедренной трапеции
Свойства равнобедренной трапеции обсуждаются ниже. 9\circ$
Похожие рабочие листы
Равнобедренная трапеция: Формулы
Давайте обсудим формулы для нахождения площади и периметра, медианы равнобедренной трапеции.
Медиана равнобедренной трапеции
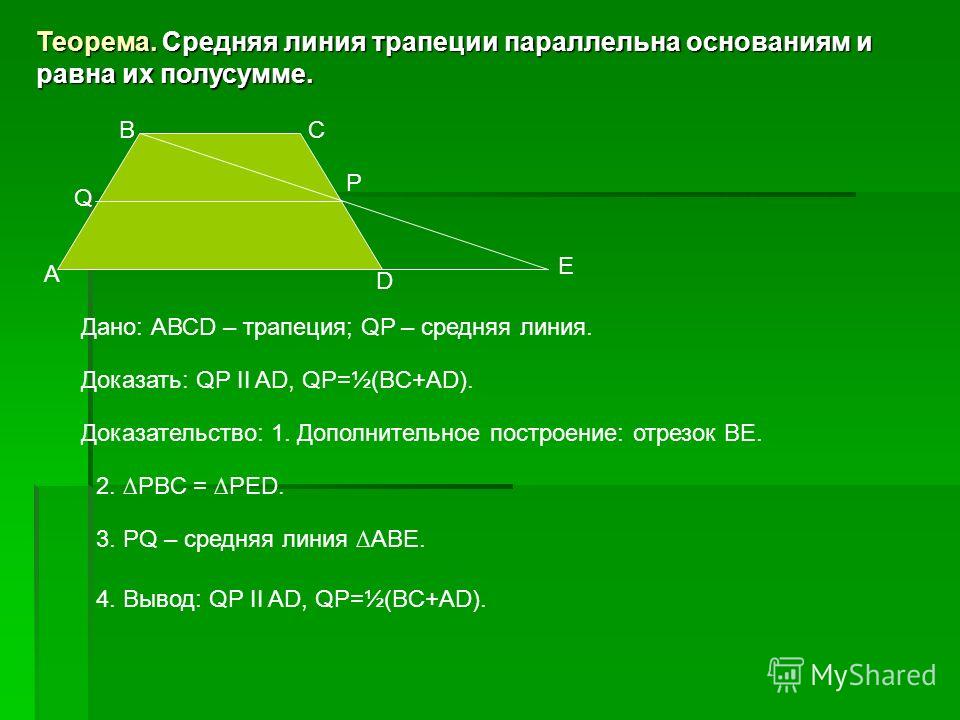
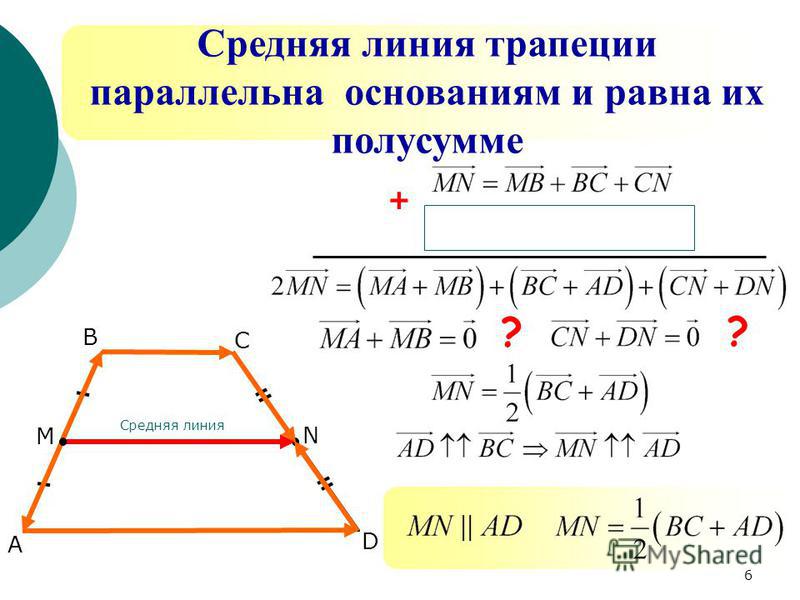
Линия, соединяющая середины непараллельных сторон, образует среднюю линию или медиану. Медиана образует специальную теорему, применимую только к равнобедренным трапециям. Длина средней линии равна половине суммы двух параллельных сторон. Если мы присвоим переменные a и b измерениям параллельных сторон, то длина медианы будет равна:
$Median = \frac{a + b}{2}$
Периметр равнобедренной трапеции Формула
$P = a + b + 2 c$
Где a, b и c — стороны трапеции.
Формула площади равнобедренной трапеции
$A = \frac{1}{2} h (a+b)$
где a и b — длины параллельных сторон, а h — расстояние в перпендикулярном выражении между ними.
Как найти периметр равнобедренной трапеции
Вычисление периметра фигуры просто означает нахождение длины вокруг фигуры. Давайте разберемся с шагами на примере.
Шаг 1: Вызовите формулу. Периметр равнобедренной трапеции равен
$P = a + b + 2c$
Длины сторон нужно просто сложить, потому что периметр равен сумме длин сторон фигуры. Стороны этой равнобедренной трапеции равны по длине, следовательно, вы можете использовать 2c в формуле, поскольку обе стороны одинаковой длины.
Шаг 2: Замените переменные известными значениями.
Шаг 3: Укажите правильную единицу измерения в соответствии с вопросом.
Пример: Найдите периметр данной равнобедренной трапеции.
Здесь $a = 16$ единиц, $b = 26$ единиц, $c = 10$ единиц
Периметр $= 16 + 26 + 10 + 10$
$= 16 + 26 + 2(10) $
$= 62$ единиц
Как найти площадь равнобедренной трапеции
Формула площади равнобедренной трапеции:
$A = \frac{1}{2} h (a + b)$, где a и b — длины основания, h — высота.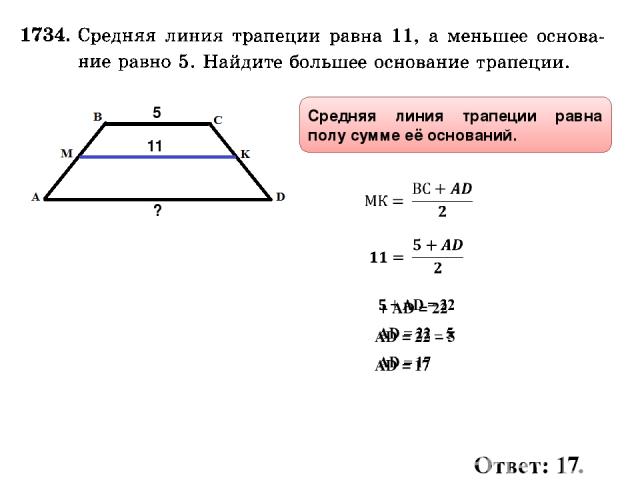
Просто подставьте значения в формулу. Площадь измеряется в квадратных единицах. Итак, примените соответствующую единицу к ответу.
Факты о равнобедренной трапеции
- Сумма внутренних углов равнобедренной трапеции составляет 360 градусов.
- Непараллельные стороны равнобедренной трапеции равны.
- Медиана проходит параллельно обоим основаниям, и ее длина равна сумме длин оснований.
- «Трапеция» — другое название трапеции.
Заключение
В этой статье мы узнали о равнобедренной трапеции, ее свойствах и связанных с ней формулах. Давайте решим несколько примеров, чтобы применить то, что мы узнали!
Решенные примеры
на Isockeles Trapezoid- Предполагая, что Trapezoid Isockeles имеет площадь 128 дюймов 2 и основания, которые составляют 12 дюймов и 20 дюймов, определяют его высоту. 92$
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 34150
- Генри Африк
- CUNY City College of Technology через New York City College of Technology at CUNY Academic3 Works
0 Works
На рисунке \(\PageIndex{1}\) \(b_1\) и \(b_2\) — основания трапеции \(ABCD\), а \(h\) — высота или высота .
Рисунок \(\PageIndex{1}\): трапеция \(ABCD\) с основаниями \(b_1\) и \(b_2\) и высотой \(h\). Формула площади дана в следующей теореме:
Формула площади дана в следующей теореме:Теорема \(\PageIndex{1}\)
Площадь трапеции равна половине произведения ее высоты на сумму оснований.
\[A = \dfrac{1}{2} h(b_1 + b_2)\]
- Доказательство
На рисунке \(\PageIndex{1}\) нарисуйте \(BD\) (см. рисунок \(\PageIndex{2}\)). Обратите внимание, что \(CD = b_2\) — это основание, а \(BF = h\) — это высота \(\треугольника BCD\). Площадь трапеции \(ABCD =\) Площадь \(\треугольника ABD\) + Площадь \(\треугольника BCD\) = \(\dfrac{1}{2} b_1h + \dfrac{1}{2} b_2 h = \dfrac{1}{2} h(b_1 + b_2)\).
Рисунок \(\PageIndex{2}\): Нарисуйте \(BD\). \(CD\) — основание, а \(BF\) — высота \(\треугольника BCD\).
Пример \(\PageIndex{1}\)
Найдите площадь:
Решение
\(A = \dfrac{1}{2} h(b_1 + b_2)= \dfrac{1} {2} (6)(28 + 16) = \dfrac{1}{2} (6)(44) = 132\).

Ответ: \(A = 132\).
Пример \(\PageIndex{2}\)
Найдите площадь и периметр:
Решение 92} \\ {x} & = & {\sqrt{124} = \sqrt{4} \sqrt{31} = 2\sqrt{31}} \end{массив}\]
Площадь = \(\dfrac {1}{2} h(b_1 + b_2) = \dfrac{1}{2} (5\sqrt{3}) (22 + 10) = \dfrac{1}{2} (5\sqrt{3} )(32) = 80\sqrt{3}\).
Периметр = \(22 + 10 + 10 + 2\sqrt{31} = 42 + 2\sqrt{31}\).
Ответ: \(A = 80\sqrt{3}\), \(P = 42 + 2\sqrt{31}\).
1 — 2. Найдите площадь \(ABCD\):
1.
2.
3 — 12. Найдите площадь и периметр \(ABCD\):
3.
4.
5.
6.
7.
8.
99.
99999999999999999999999999999999999999999999999999999999999999999
999999999999 11.12.
13 — 14. Найдите площадь и периметр в ближайшую десятую от \ (ABCD \):
13.

Основания $= 12$ дюймов и 20 дюймов
мы знаем, что площадь равнобедренной трапеции $= A = \frac{1}{2} h(a + b)$
$128 = \frac{1} {2} h(12 + 20)$
Высота $= \frac{128}{16} = 8$ дюймов
2. Вычислите площадь равнобедренной трапеции с высотой 4 дюйма и основанием 3 дюйма и 5 дюймов.
Вычислите площадь равнобедренной трапеции с высотой 4 дюйма и основанием 3 дюйма и 5 дюймов.
Решение: Площадь равнобедренной трапеции$ = \frac{1}{2} (сумма\; параллелей\; сторон) \× высота$
дано, основания $= 3$ дюйма и 5 дюймов, высота $= 4$ дюймов 92$.
3. Вычислите периметр.
Решение:
Периметр равнобедренной трапеции $=$ сумма всех сторон
Периметр равнобедренной трапеции $= 20 + 25 + 30 + 30 = 105$ дюймов.
4. Основания трапеции 2 дюйма и 4 дюйма. Найдите длину средней линии по формуле медианы.
Решение: Медиана равнобедренной трапеции $= \frac{a+b}{2}$.
Где a и b — параллельные стороны трапеции.
Итак, длина средней линии $= \frac{2 + 4}{2} = 3$ дюймов
5. Определить периметр равнобедренной трапеции с основаниями 10 и 15 дюймов и непараллельными сторонами 20 дюймов каждая.
Решение: Периметр равнобедренной трапеции $=$ сумма всех сторон равнобедренной трапеции
Периметр равнобедренной трапеции $= 10 + 15 + 20 + 20 = 65$ дюймов.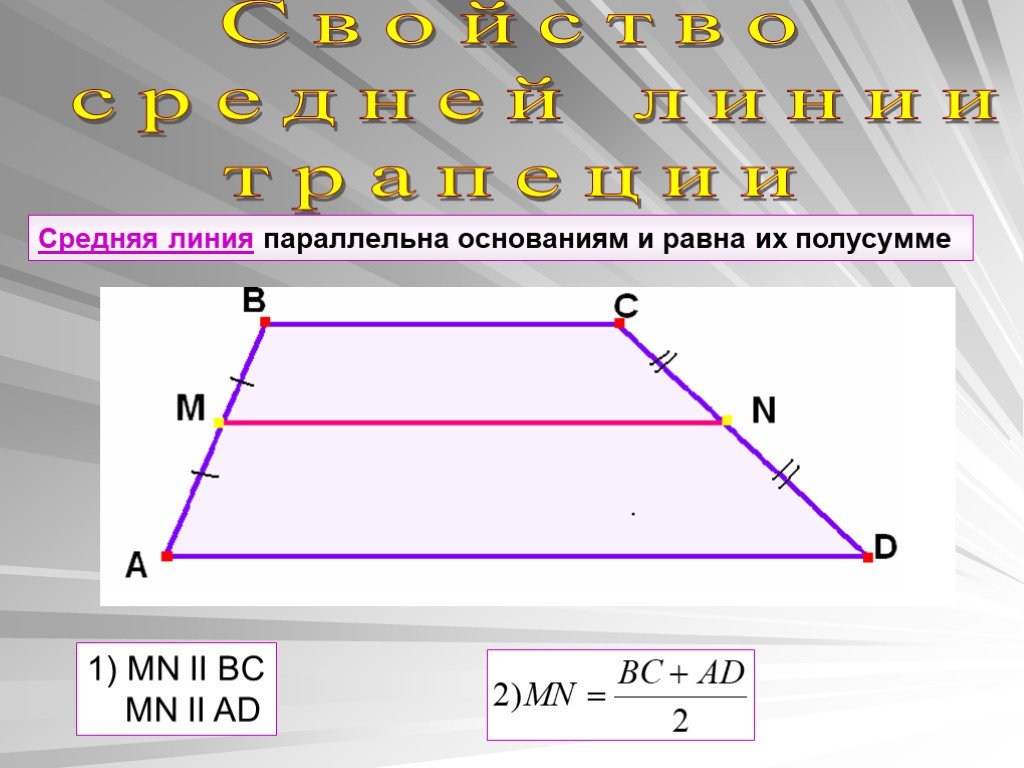
Практические задачи на равнобедренной трапеции
1
Какое из следующих свойств является свойством равнобедренной трапеции?
Противоположные стороны параллельны
Непараллельные стороны равны
И 1, и 2
Только 1
Правильный ответ: непараллельные стороны равны .
2
Противоположные углы равнобедренной трапеции __________________.
конгруэнтный
дополнительный
дополнительный
Ничего из вышеперечисленного
Правильный ответ: дополнительный
Противоположные углы равнобедренной трапеции являются дополнительными.
3
Трапеция имеет ножки по 8 см каждая. Его основания равны 10 см и 15 см соответственно. Вычислить его периметр.
33 дюйма
29 см
41 см
64 см
Правильный ответ: 33 дюйма
Периметр трапеции $=$ Сумма всех ее сторон $= 10 + 8 + 15 + 8 = 33$ дюймов
4
В трапеции основания равны 8 дюймам и 4 дюймам.
 Найдите длину средней линии по формуле медианы.
Найдите длину средней линии по формуле медианы.86 дюймов
6 дюймов
14 дюймов
Нет
Правильный ответ: 6 дюймов
Медиана трапеции $= \frac{1}{2} \times $ Сумма параллельных сторон $= \frac {1}{2} \times (8 + 4) = 6$ дюймов
5
Вычислите площадь равнобедренной трапеции с высотой 6 дюймов и основаниями 8 дюймов и 4 дюйма.
86 квадратных единиц
36 квадратных единиц
14 квадратных единиц
Нет
Правильный ответ: 36 квадратных единиц им дается.
Часто задаваемые вопросы о равнобедренной трапеции
Чем отличается равнобедренная трапеция от трапеции?
У равнобедренной трапеции непараллельные стороны равны, углы при основании равны, диагонали конгруэнтны, а противоположные углы смежны.
Почему трапецию называют равнобедренной?
Isosceles означает «равные ноги». В равнобедренной трапеции непараллельные стороны (или катеты) имеют одинаковую длину. Таким образом, она называется равнобедренной трапецией.
Таким образом, она называется равнобедренной трапецией.
Какими свойствами обладает равнобедренная трапеция?
Число сторон равнобедренной трапеции равно четырем. В то время как два основания (противоположные стороны) параллельны друг другу, две другие стороны равны по длине, но не параллельны друг другу.
Что такое прямая трапеция?
Прямоугольная трапеция — это трапеция, имеющая два смежных прямых угла.
Что такое разносторонняя трапеция?
Трапеция, у которой все четыре стороны имеют разную длину, называется разносторонней трапецией.

 Формула площади дана в следующей теореме:
Формула площади дана в следующей теореме: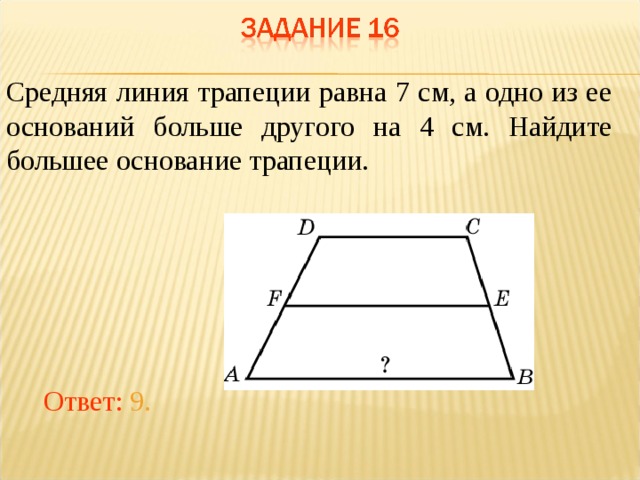
Leave A Comment