​Приведите пример трёхзначного числа, которое при делении дает равные остатки – как решать

Формулировка задачи: Приведите пример трёхзначного натурального числа, которое при делении на M и на N даёт равные ненулевые остатки и первая справа (первая слева, средняя) цифра которого является средним арифметическим двух других цифр. В ответе укажите ровно одно такое число.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 19 (Задачи на цифровую запись числа).

Рассмотрим, как решаются подобные задачи на примере.

Пример задачи:

Приведите пример трёхзначного натурального числа, которое при делении на 4 и на 15 даёт равные ненулевые остатки и первая справа цифра которого является средним арифметическим двух других цифр. В ответе укажите ровно одно такое число.

Решение:

Для удобства назовем наше число abc, где каждая буква обозначает конкретный разряд числа: a – сотни, b – десятки и c – единицы. По условию задачи

c = (a + b) / 2

Кроме этого число abc при делении на 4 и 15 дает равные ненулевые остатки. Это значит, что остаток находится в диапазоне от 1 до 3 (так как наименьший делитель равен 4 и остаток не равен 0). Поскольку при делении на 4 и 15 остатки одинаковы, значит при делении числа abc на произведение чисел

4 ⋅ 15 = 60

остаток получится такой же: 1, 2 или 3.

Попробуем подобрать трехзначные натуральные числа, которые будут соответствовать этому условию. Для этого будем умножать 60 на 1, 2, 3 и т.д. и прибавлять к этим числам возможные остатки. А после этого проверять, является ли крайняя правая цифра средним арифметическим двух остальных.

Умножаем 60 на 1:

60 ⋅ 1 = 60 – двухзначное число, не подойдет

Умножаем 60 на 2:

60 ⋅ 2 = 120

121: (1 + 2) / 2 ≠ 1

122: (1 + 2) / 2 ≠ 2

123: (1 + 2) / 2 ≠ 3

Умножаем 60 на 3:

60 ⋅ 3 = 180

181: (1 + 8) / 2 ≠ 1

182: (1 + 8) / 2 ≠ 2

183: (1 + 8) / 2 ≠ 3

Умножаем 60 на 4:

60 ⋅ 4 = 240

241: (2 + 4) / 2 ≠ 1

242: (2 + 4) / 2 ≠ 2

243: (2 + 4) / 2 = 3

Одно число подобрали: оно равно 243. На этом шаге можно было закончить решение, однако мы проверим какие еще числа подойдут в качестве ответа.

Умножаем 60 на 5:

60 ⋅ 5 = 300

301: (3 + 0) / 2 ≠ 1

302: (3 + 0) / 2 ≠ 2

303: (3 + 0) / 2 ≠ 3

Умножаем 60 на 6:

60 ⋅ 6 = 360

361: (3 + 6) / 2 ≠ 1

362: (3 + 6) / 2 ≠ 2

363: (3 + 6) / 2 ≠ 3

Умножаем 60 на 7:

60 ⋅ 7 = 420

421: (4 + 2) / 2 ≠ 1

422: (4 + 2) / 2 ≠ 2

423: (4 + 2) / 2 = 3

Еще одно число, подходящее по условию задачи: 423.

Умножаем 60 на 8:

60 ⋅ 8 = 480

481: (4 + 8) / 2 ≠ 1

482: (4 + 8) / 2 ≠ 2

483: (4 + 8) / 2 ≠ 3

Умножаем 60 на 9:

60 ⋅ 9 = 540

541: (5 + 4) / 2 ≠ 1

542: (5 + 4) / 2 ≠ 2

543: (5 + 4) / 2 ≠ 3

Умножаем 60 на 10:

60 ⋅ 10 = 600

601: (6 + 0) / 2 ≠ 1

602: (6 + 0) / 2 ≠ 2

603: (6 + 0) / 2 = 3

Число 603 также подойдет в качестве ответа.

Умножаем 60 на 11:

60 ⋅ 11 = 660

661: (6 + 6) / 2 ≠ 1

662: (6 + 6) / 2 ≠ 2

663: (6 + 6) / 2 ≠ 3

Умножаем 60 на 12:

60 ⋅ 12 = 720

721: (7 + 2) / 2 ≠ 1

722: (7 + 2) / 2 ≠ 2

723: (7 + 2) / 2 ≠ 3

Умножаем 60 на 13:

60 ⋅ 13 = 780

781: (7 + 8) / 2 ≠ 1

782: (7 + 8) / 2 ≠ 2

783: (7 + 8) / 2 ≠ 3

Умножаем 60 на 14:

60 ⋅ 14 = 840

841: (8 + 4) / 2 ≠ 1

842: (8 + 4) / 2 ≠ 2

843: (8 + 4) / 2 ≠ 3

Умножаем 60 на 15:

60 ⋅ 15 = 900

901: (9 + 0) / 2 ≠ 1

902: (9 + 0) / 2 ≠ 2

903: (9 + 0) / 2 ≠ 3

Умножаем 60 на 16:

60 ⋅ 16 = 960

961: (9 + 6) / 2 ≠ 1

962: (9 + 6) / 2 ≠ 2

963: (9 + 6) / 2 ≠ 3

Умножаем 60 на 17:

60 ⋅ 17 = 1020 – четырехзначное число, не подойдет.

Таким образом, перебрав все возможные варианты, мы получили 3 числа: 243, 423 и 603.

Ответ: 243 или 423 или 603

Разложение чисел на простые множители: способы и примеры

Поможем понять и полюбить математику

Начать учиться

Некоторые задания в математике кажутся очень легкими, как дважды два или пятью пять. Другие же можно сравнить с ужасным драконом, которого не сможет победить даже самый отважный и сильный рыцарь. 🐉 Давайте сегодня поближе познакомимся с темой «Разложение числа на простые множители» и проверим, на что она похожа: на дракона или же на героя, который поможет нам и защитит от беды.

Зачем раскладывать число на простые множители

А ведь и правда интересно, стоит ли вообще изучать эту тему или в жизни она не пригодится? Насколько полезен навык разложения числа на множители?

Вопрос очень хороший! Математические задачки прекрасно развивают логику и умение мыслить нестандартно, что пригодится в любой профессии.

К тому же в математике многие темы словно ступеньки, ведущие к более объемным и сложным. Вот и предмет нашего обсуждения не исключение.

Когда вы научитесь раскладывать число на простые множители, то:

  • заодно повторите понятие «простые множители»;

  • вспомните тему «Признаки делимости»;

  • сможете находить наименьшее общее кратное;

  • поймете, как можно сокращать дроби и находить общий множитель.

И это только разделы, с которыми вы познакомитесь в 6-м классе. Представляете, сколько еще ждет впереди! Как видно, плюсов от изучения темы достаточно много, — давайте же начнем.

Узнай, какие профессии будущего тебе подойдут

Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас

Вспоминаем, что такое простые множители

Первое, с чем стоит разобраться, — это само понятие «простой множитель».

Помните, что это такое?

Множитель — это число, которое показывает, сколько раз нужно повторить слагаемым какое-нибудь другое число (множимое), чтобы получить произведение.

Так, в примере 2 × 7 = 14 число 2 называют первым множителем, число 7 — вторым множителем, а 14 — произведением, или значением произведения.

В уравнении 5х = 20 число 5 можно назвать известным множителем, х — неизвестным множителем, 20 — значением произведения.

Простое число — это число, которое делится только на само себя и единицу.

Попробуем перечислить все простые числа от 1 до 10: 1, 3, 5, 7.

А число 9 простое? Нет, так как, помимо 1 и 9, число делится на 3.

А число 8? Нет, так как восьмерка делится на 1, 8, 2 и 4.

Как вы думаете, сколько простых чисел существует?

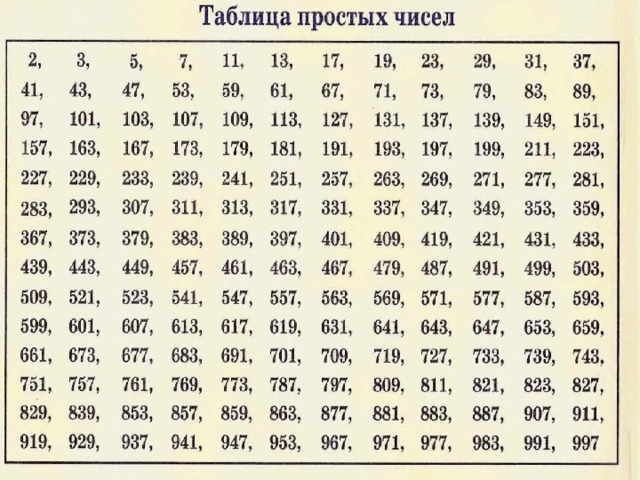
Правильно, бесконечное множество! Разумеется, весь этот числовой ряд выучить не получится. Но есть две хорошие новости: во-первых, нам и не нужно знать все это множество, математики давно составили таблицы простых чисел (от 1 до 100, от 1 до 1 000), которыми мы можем воспользоваться в любой момент. А самое главное, зная алгоритм проверки числа, мы можем самостоятельно установить, является ли оно простым.

Один из способов проверки — метод перебора делителей. Для этого нам необходимо проверить делимость числа на разные другие числа. Если подобрать дополнительные делители для числа получится — оно составное, а если среди его делителей будет только единица и оно само — то простое.

Понятие разложения на простые множители

Итак, с основными понятиями мы разобрались. Что же тогда означает «разложить число на простые множители»?

Разложить на простые множители — значит представить число в виде произведения простых множителей (чисел).

Например:

20 = 2 × 2 × 5;

99 = 11 × 3 × 3;

126 = 2 × 2 × 31;

1 084 = 2 × 2 × 271.

Разложение на простые множители можно сравнить с разменом купюры. Представьте, что вам захотелось купить газировку из автомата, а он принимает только монеты. Вы идете в магазин и просите разменять купюру, продавец выдает вам целую стопку монет разного номинала. Среди всего количества будут повторы: несколько рублевых, парочка пятирублевых, горсть десяток. Теперь можно бежать к автомату: какой напиток возьмем, вишневый или грушевый?

Возможно, кто-то сейчас начал волноваться и переживать, что ошибется при выполнении разложения. Спешим успокоить!

В арифметике есть теорема: любое натуральное число n, большее единицы, можно разложить на произведение простых чисел, причем это разложение единственно с точностью до порядка следования сомножителей.

А значит, каким бы способом разложения вы ни воспользовались, все равно придете к верному ответу — при условии, что все множители в произведении будут простыми.

Практика

Теперь про способы разложения. В школе на уроках математики часто пользуются методом, который заключается в записывании множителей столбиком, этаком последовательном делении. Мы перебираем простые множители по порядку, начиная с числа 2, и делим на них число до тех пор, пока от него не остается единичка.

Задачка 1

Разложим число 52 на простые множители:

  1. Начинаем перебор простых множителей. 52 точно делится на 2, так как является четным: 52 : 2 = 26.

  2. Получившийся ответ 26 также делится на 2: 26 : 2 = 13.

  3. Число 13 не делится ни на 2, ни на 3, ни на 5. Перебирая ряд простых чисел, мы сможем разделить 13 только на само себя, а значит, это число — простое.

Наглядно это записывается таким образом:

Разложение прошло успешно!

52 = 2 × 2 × 13.

«Practice makes perfect», — говорят в Англии, что означает «Практика приводит к совершенству». Давайте продолжим решать задачи и подытожим разбор метода алгоритмом, которым вы сможете воспользоваться на уроках математики.

Задачка 2

Разложим число 63 на простые множители:

  1. Начинаем перебор простых множителей. 63 не делится на 2, а вот на 3 — прекрасно! 63 : 3 = 21.

  2. Число 21 вновь не делится на 2, так как является нечетным. Следующий простой множитель — это 3, проверяем делимость на него: 21 : 3 = 7.

  3. Перебираем ряд простых чисел и делим на них число 7. Без остатка 7 делится только на само себя: 7 : 7 = 1.

63 = 3 × 3 × 7.

Задачка 3

Разложим число 128 на простые множители:

  1. 128 точно делится на 2: 128 : 2 = 64.

  2. Число 64 тоже является четным, а значит, 64 : 2 = 32.

  3. Продолжаем делить на два: 32 : 2 = 16.

  4. Еще немножко: 16 : 2 = 8.

  5. 8 : 2 = 4.

  6. 4 : 2 = 2.

  7. 2 : 2 = 1.

128 = 2 × 2 × 2 × 2 × 2 × 2 × 2, или же 128 = 27. О втором виде записи поговорим чуть ниже.

Задачка 4

Разложим число 37 на простые множители.

Перебирая простые множители от 1 до 37, мы не найдем ни одного числа, кроме самого 37, которое бы делилось на него без остатка. Значит, число 37 простое и разложение провести невозможно.

37 = 37.

Алгоритм разложения числа на множители

Время подвести промежуточный итог и составить алгоритм разложения числа на множители:

  1. В первый столбик записываем исходное число.

  2. Во второй столбик, напротив первого числа, записываем наименьший простой множитель, на который исходное число делится без остатка (идем по порядку ряда простых чисел: 2, 3, 5, 7 и т. д.).

  3. В первый столбик записываем результат деления и вновь ищем наименьший простой множитель, на который это число делится без остатка.

  4. Проводим разложение до тех пор, пока в левом столбике не запишем число 1.

Каноническая запись

В теме «Разложение на простые множители» встречается понятие «канонический вид» или «каноническая запись». Что означают эти страшные слова?

Канонический вид — это такой тип записи, который иначе можно назвать стандартным, общепринятым. То есть такой, что где бы вы ни показали записанное, вас обязательно поймут — и в Индии, и в Китае, и даже в Арктике (при условии, что вы показываете записи математикам, конечно).

Это как показать любому ученому химическую формулу Н2О: это каноническая, общепринятая запись для обозначения молекулы воды.

Но вернемся к простым множителям. Думаем, вы уже заметили, что при разложении могут повторяться одни и те же числа. Так, при разложении числа 128 мы получили аж семь двоек! Для упрощения записи произведение одинаковых множителей записывают с помощью степени.

Степень — это число, которое показывает, сколько раз множитель был умножен сам на себя.

52 = 5 × 5.

73 = 7 × 7 × 7.

104 = 10 × 10 × 10 × 10.

Таким образом, запись разложения на простые множители будет выглядеть так:

63 = 32 × 7;

52 = 22 × 13;

32 = 25.

Применение признаков делимости при разложении на простые множители

Последний нюанс, который нам нужно обсудить, — это применение признаков делимости при разложении на простые множители. Иными словами, как определить, что число делится на 3, или на 7, или на другие числа, не прибегая непосредственно к делению?

Почему это важно? Порой при поиске простых делителей нам приходится перебирать число за числом, что достаточно долго и энергозатратно. Математики (и программисты тоже) всегда стремятся упростить задачу, найти более легкое решение. А зная свойства делимости, как раз можно ускорить процесс разложения.

Для начала давайте вспомним: как определить, на что делится число? Приведем некоторые примеры.

Признак делимости на…

Правило

Примеры

2

Число четное, оканчивается на 0, 2, 4, 6, 8

10, 24, 12 658:

  • 10 : 2 = 5;

  • 24 : 2 = 12;

  • 12 658 : 2 = 6 329

3

Сумма цифр делится на 3

24, 63, 102:

  • 24 : 2 + 4 = 6, а 6 делится на 3, значит, 24 делится на 3;

  • 63 : 6 + 3 = 9, а 9 делится на 3, значит, и 63 делится на 3;

  • 102 : 1 + 0 + 2 = 3, а 3 делится на 3, значит, и 102 делится на 3

4

Последние две цифры — нули или образуют число, которое делится на 4

100, 1 024:

  • 100 : 4 = 25;

  • 1 024 : 24 делится на 4, значит, и 1024 : 4 = 256

5

Оканчивается на 0 или 5

15, 105, 1 200:

  • 15 : 5 = 3;

  • 105 : 5 = 21;

  • 1 200 : 5 = 240

6

Делится на 2 и на 3

36:

  • делится на 2, так как является четным;

  • делится на 3, так как сумма цифр 3 + 6 = 9 делится на 3

72:

  • делится на 2, так как является четным;

  • делится на 3, так как сумма цифр 3 + 6 = 9 делится на 3

7

Разность числа без последней цифры и удвоенной последней цифры делится на 7

343:

  • 34 − 3 × 2 = 34 − 6 = 28;

  • 28 делится на 7, значит, и 343 : 7 = 49

8

Последние три цифры — нули или образуют число, которое делится на 8

9

Сумма цифр делится на 9

  • 252 делится на 9, так как 2 + 5 + 2 = 9;

  • 9 900 делится на 9, так как 9 + 9 + 0 + 0 = 18

10

Оканчивается на 0

  • 50 : 10 = 5;

  • 600 : 10 = 60;

  • 75 460 : 10 = 7 546

Кстати, чтобы определить, делится ли число на составной множитель, нужно проверить, делится ли оно на простые множители, входящие в его состав.

Например, чтобы проверить, делится ли число на 14, нужно определить, можно ли его разделить на 2 и на 7. А число, делящееся на 27, будет делиться одновременно и на 3, и на 9.

Попробуем применить знание о делимости к разложению на множители.

Задачка 5

Разложим на множители число 5 600:

  1. Так как число оканчивается на два нуля, оно точно делится на 100. 100 = 25 × 4 = 5 × 5 × 2 × 2.

  2. Число 56 не делится на 3 (т. к. 5 + 6 = 11), 4, 5, 6, зато делится на 7. 56 = 7 × 8 = 7 × 2 × 2 × 2.

  3. Значит, 5 600 = 56 × 100 = 7 × 8 × 25 × 4 = 7 × 2 × 2 × 2 × 5 × 5 × 2 × 2. В каноническом виде 5 600 = 25 × 52 × 7.

Задачка 6

Разложим на множители число 364:

  1. Оно оканчивается на число 64, которое, в свою очередь, делится на 4. Значит, и само число делится: 364 : 4 = 91.

  2. Число 91 не делится на 2, 3, 4, 5, 6, но делится на 7: 91 : 7 = 13.

  3. 364 = 4 × 7 × 13 = 22 × 7 × 13.

Задачка 7

Разложим на множители число 750:

  1. Число оканчивается на 0, а значит, делится на 10. 10 = 2 × 5.

  2. 75 делится на 3 (7 + 5 = 12): 75 : 3 = 25.

  3. 750 = 75 × 10 = 25 × 3 × 2 × 5 = 5 × 5 × 3 × 2 × 5 = 53 × 2 × 3.

Арифметика как наука завораживает своей простотой и изящностью. Из десяти цифр складывается бесконечное множество чисел, которые взаимодействуют друг с другом, рождая закономерности и правила. Больше о царице наук вы сможете узнать на курсах профильной математики в онлайн-школе Skysmart. На уроках вы получите ответы на вопросы: «Откуда взялось число пи?», «Как получить бесконечную десятичную дробь?», «Что значит округлить по избытку?» и многие другие. Интересно? Тогда с нетерпением ждем вас!

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Дарья Вишнякова

К предыдущей статье

Перпендикулярные прямые

К следующей статье

Возрастание и убывание функции

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

  1. Выявим пробелы в знаниях и дадим советы по обучению

  2. Расскажем, как проходят занятия

  3. Подберём курс

Задача по математике: Цифры — вопрос № 4974, комбинаторика, варианты

Сколько натуральных чисел больше 4000 образовано из чисел 0,1,3,7,9 с неповторяющимися цифрами,

Б) Сколько получится количество натуральных чисел меньше 4000, и могут ли числа повторяться?

Правильный ответ:

a =  144
b =  375

04 b=5+4⋅ 5+4⋅ 5⋅ 5+2⋅ 5⋅ 5⋅ 5=375


Нашли ошибку или неточность? Не стесняйтесь

пишите нам

. Спасибо!

Советы по использованию связанных онлайн-калькуляторов

См. также наш калькулятор перестановок.
Смотрите также наш калькулятор вариаций.
Хотите подсчитать количество комбинаций?

Для решения этой математической задачи вам необходимо знать следующие знания:

  • комбинаторика
  • вариации
  • перестановки 9Основные функции
  • средняя школа
  • Повторная 79734
    Сколько чисел а) меньше 500, б) больше 500 можно составить из цифры 0,1,5,8,9 так, чтобы ни одна цифра не повторялась?
  • Двузначное число 33471
    Сколько двузначных чисел больше 60 можно составить из цифр 0,5,6,7,8,9? Цифры не должны повторяться.
  • Делимые 6615
    Сколько трехзначных чисел можно составить из цифры 1,3,5,7,9, если цифры не могут повторяться в записи чисел? Сколько из них делится на пять?
  • Цифры
    Сколько нечетных четырехзначных чисел можно составить из цифр: 0, 3, 5, 6 и 7? (a) цифры могут повторяться (b) цифры не могут повторяться
  • Трехзначные числа
    Сколько всего трехзначных чисел, состоящих из цифр 0, 2, 5, 7 и делящихся на девять, если цифры могут повторяться?
  • Повторяется 38103
    Сколько пятизначных чисел можно составить из числа 2,3,4,5,6,7,8,9, если цифра в каждом числе может повторяться только один раз?
  • Цифры
    Сколько пятизначных чисел можно составить из чисел 0,3,4, 5 и 7, разделенных на 10, причем цифры повторяются?
  • Трехзначное число
    Сколько трехзначных натуральных чисел можно составить из цифр 0, 1 и 2, если числительные в этих числах повторяются?
  • Сколько 2
    Сколько трехбуквенных слов можно составить из букв A B C D E G H, если повторы: а) не допускаются б) допускаются?
  • Трехзначное число
    Сколько трехзначных натуральных чисел больше 321, если ни одна цифра в этом числе не повторяется?
  • Натуральные числа
    Сколько натуральных чисел меньше 301 можно составить из числа 0,1,2,3,6,7?
  • Треугольник из палочек
    У валуна Боба много палочек длин 3,5 и 7. Он хочет составить треугольники, каждое ребро которых состоит ровно из одной палочки. Сколько неравных треугольников можно составить из палочек?
  • 5 цифр
    У вас есть следующие цифры: 9, 8, 0, 1, 5. Запишите наименьшее, даже пятизначное число, если одна цифра повторяется три раза, а остальные цифры не повторяются. Сумма цифр числа: а) 9 б) 6 в) 8 г) 23
  • Перестановки
    Сколько четырехзначных чисел можно составить из чисел 1,2,3,4,5,6,7, если: а цифры в числе b не должны повторяться, число должно делиться на пять, а числа не должны повторяться c, цифры могут повторяться
  • Пятизначное
    Найдите все пятизначные числа, которые можно составить из числа 12345 так, чтобы числа не повторялись, а затем числа с повторяющимися цифрами. Дайте расчет.
  • Двузначное число 17443
    Сколько всего четных двузначных чисел, которые Мы можем составить из цифр 2, 4 и 7? Цифры могут повторяться в созданном номере.
  • Четырёхзначный 73114
    Сколько четырёхзначных чисел можно составить из цифр 2, 6, 3, 5, 1 и 9, если цифры в числе не повторяются?

Глава 3a.