4 в степени x производная: Найти производную y’ = f'(x) = 4^x (4 в степени х)

2

Производная e x 2x 3. Производная e в степени x и показательной функции

Операция отыскания производной называется дифференцированием.

В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).

Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться таблицей производных и правилами дифференцирования. Для нахождения производной подходит следующий алгоритм.

Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное)

связаны эти функции. Далее производные элементарных функций находим в таблице производных, а формулы производных произведения, суммы и частного — в правилах дифференцирования. Таблица производных и правила дифференцирования даны после первых двух примеров.

Пример 1. Найти производную функции

Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.

Из таблицы производных выясняем, что производная «икса» равна единице, а производная синуса — косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:

Пример 2. Найти производную функции

Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:

Если пока возникают вопросы, откуда что берётся, они, как правило, проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования. К ним мы и переходим прямо сейчас.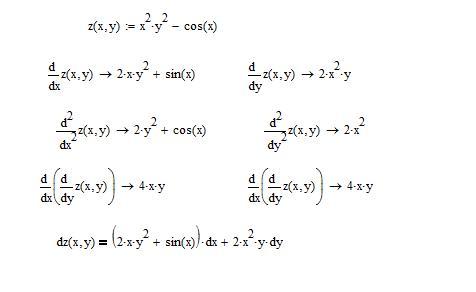

Таблица производных простых функций

1. Производная константы (числа). Любого числа (1, 2, 5, 200…), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто
2. Производная независимой переменной. Чаще всего «икса». Всегда равна единице. Это тоже важно запомнить надолго
3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни.
4. Производная переменной в степени -1
5. Производная квадратного корня
6. Производная синуса
7. Производная косинуса
8. Производная тангенса
9. Производная котангенса
10. Производная арксинуса
11. Производная арккосинуса
12. Производная арктангенса
13. Производная арккотангенса
14. Производная натурального логарифма
15. Производная логарифмической функции
16. Производная экспоненты
17. Производная показательной функции

Правила дифференцирования

1. Производная суммы или разности
2. Производная произведения
2a. Производная выражения, умноженного на постоянный множитель
3. Производная частного
4. Производная сложной функции

Правило 1. Если функции

дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции

причём

т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.

Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны

, т.е.

Правило 2. Если функции

дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение

причём

т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.

Следствие 1. Постоянный множитель можно выносить за знак производной :

Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.

Например, для трёх множителей:

Правило 3. Если функции

дифференцируемы в некоторой точке

и , то в этой точке дифференцируемо и их частное u/v , причём

т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.

Где что искать на других страницах

При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье «Производная произведения и частного функций »

.

Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.

А если при дифференцировании произведения или частного у вас появилось слагаемое u «v , в котором u — число, например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё слагаемое будет равно нулю (такой случай разобран в примере 10).

Другая частая ошибка — механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.

По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .

Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие «Производная суммы дробей со степенями и корнями «.

Если же перед Вами задача вроде , то Вам на занятие «Производные простых тригонометрических функций».

Пошаговые примеры — как найти производную

Пример 3. Найти производную функции

Решение. Определяем части выражения функции: всё выражение представляет произведение, а его сомножители — суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:

Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль. Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как производную «икса». Получаем следующие значения производных:

Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:

Пример 4. Найти производную функции

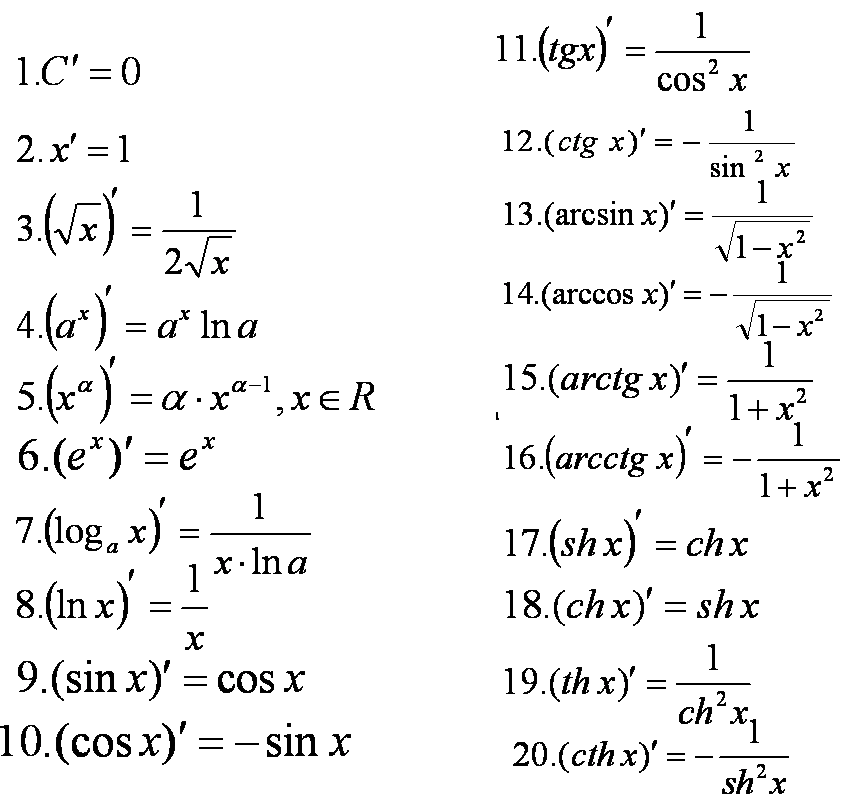Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного: производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:

Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:

Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие

«Производная суммы дробей со степенями и корнями» .

Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок «Производные простых тригонометрических функций» .

Пример 5. Найти производную функции

Решение. В данной функции видим произведение, один из сомножителей которых — квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:

Пример 6.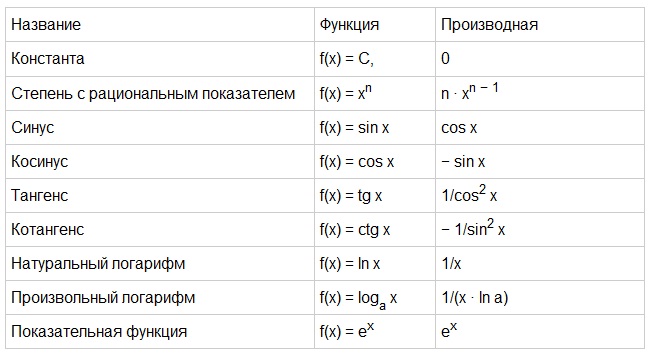 Найти производную функции

Решение. В данной функции видим частное, делимое которого — квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:

Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .

Вычисление производной — одна из самых важных операций в дифференциальном исчислении. Ниже приводится таблица нахождения производных простых функций. Более сложные правила дифференцирования смотрите в других уроках:

• Таблица производных экспоненциальных и логарифмических функций

Приведенные формулы используйте как справочные значения. Они помогут в решении дифференциальных уравнений и задач. На картинке, в таблице производных простых функций, приведена «шпаргалка» основных случаев нахождения производной в понятном для применения виде, рядом с ним даны пояснения для каждого случая.

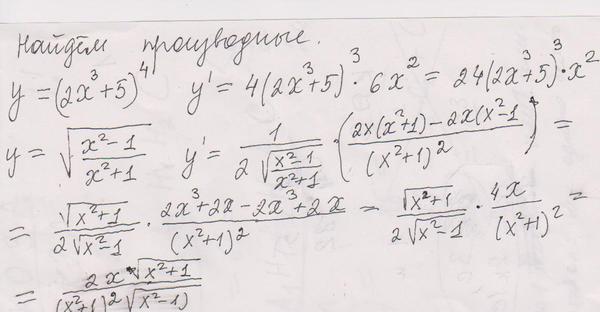
Производные простых функций

1. Производная от числа равна нулю
с´ = 0
Пример:
5´ = 0

Пояснение :
Производная показывает скорость изменения значения функции при изменении аргумента. Поскольку число никак не меняется ни при каких условиях — скорость его изменения всегда равна нулю.

2. Производная переменной равна единице
x´ = 1

Пояснение :
При каждом приращении аргумента (х) на единицу значение функции (результата вычислений) увеличивается на эту же самую величину. Таким образом, скорость изменения значения функции y = x точно равна скорости изменения значения аргумента.

3. Производная переменной и множителя равна этому множителю
сx´ = с
Пример:
(3x)´ = 3
(2x)´ = 2
Пояснение :
В данном случае, при каждом изменении аргумента функции (х ) ее значение (y) растет в с раз. Таким образом, скорость изменения значения функции по отношению к скорости изменения аргумента точно равно величине с .

Откуда следует, что
(cx + b)» = c
то есть дифференциал линейной функции y=kx+b равен угловому коэффициенту наклона прямой (k).

4. Производная переменной по модулю равна частному этой переменной к ее модулю
|x|» = x / |x| при условии, что х ≠ 0
Пояснение :
Поскольку производная переменной (см. формулу 2) равна единице, то производная модуля отличается лишь тем, что значение скорости изменения функции меняется на противоположное при пересечении точки начала координат (попробуйте нарисовать график функции y = |x| и убедитесь в этом сами. Именно такое значение и возвращает выражение x / |x| . Когда x 0 — единице. То есть при отрицательных значениях переменной х при каждом увеличении изменении аргумента значение функции уменьшается на точно такое же значение, а при положительных — наоборот, возрастает, но точно на такое же значение.

5. Производная переменной в степени равна произведению числа этой степени и переменной в степени, уменьшенной на единицу
(x c)»= cx c-1 , при условии, что x c и сx c-1 ,определены а с ≠ 0
Пример:
(x 2)» = 2x
(x 3)» = 3x 2
Для запоминания формулы :
Снесите степень переменной «вниз» как множитель, а потом уменьшите саму степень на единицу. Например, для x 2 — двойка оказалась впереди икса, а потом уменьшенная степень (2-1=1) просто дала нам 2х. То же самое произошло для x 3 — тройку «спускаем вниз», уменьшаем ее на единицу и вместо куба имеем квадрат, то есть 3x 2 . Немного «не научно», но очень просто запомнить.

6. Производная дроби 1/х
(1/х)» = — 1 / x 2
Пример:
Поскольку дробь можно представить как возведение в отрицательную степень
(1/x)» = (x -1)» , тогда можно применить формулу из правила 5 таблицы производных
(x -1)» = -1x -2 = — 1 / х 2

7. Производная дроби с переменной произвольной степени в знаменателе
(1 / x c)» = — c / x c+1
Пример:
(1 / x 2)» = — 2 / x 3

8. Производная корня (производная переменной под квадратным корнем)
(√x)» = 1 / (2√x) или 1/2 х -1/2
Пример:
(√x)» = (х 1/2)» значит можно применить формулу из правила 5
(х 1/2)» = 1/2 х -1/2 = 1 / (2√х)

9. nx. Формулы производных высших порядков.

Производная экспоненты равна самой экспоненте (производная e в степени x равна e в степени x):
(1) (e x )′ = e x .

Производная показательной функции с основанием степени a равна самой функции, умноженной на натуральный логарифм от a :
(2) .

Вывод формулы производной экспоненты, e в степени x

Экспонента — это показательная функция, у которой основание степени равно числу e , которое является следующим пределом:
.
Здесь может быть как натуральным, так и действительным числом. Далее мы выводим формулу (1) производной экспоненты.

Вывод формулы производной экспоненты

Рассмотрим экспоненту, e в степени x :
y = e x .
Эта функция определена для всех . Найдем ее производную по переменной x . По определению, производная является следующим пределом:
(3) .

Преобразуем это выражение, чтобы свести его к известным математическим свойствам и правилам. Для этого нам понадобятся следующие факты:
А) Свойство экспоненты :
(4) ;
Б) Свойство логарифма :
(5) ;
В) Непрерывность логарифма и свойство пределов для непрерывной функции:
(6) .
Здесь — некоторая функция, у которой существует предел и этот предел положителен.
Г) Значение второго замечательного предела:
(7) .

Применяем эти факты к нашему пределу (3). Используем свойство (4):
;
.

Сделаем подстановку . Тогда ; .
В силу непрерывности экспоненты,
.
Поэтому при , . В результате получаем:
.

Сделаем подстановку . Тогда . При , . И мы имеем:
.

Применим свойство логарифма (5):
. Тогда
.

Применим свойство (6). Поскольку существует положительный предел и логарифм непрерывен, то:
.
Здесь мы также воспользовались вторым замечательным пределом (7). Тогда
.

Тем самым мы получили формулу (1) производной экспоненты.

Вывод формулы производной показательной функции

Теперь выведем формулу (2) производной показательной функции с основанием степени a . Мы считаем, что и . Тогда показательная функция
(8)
Определена для всех .

Преобразуем формулу (8). Для этого воспользуемся свойствами показательной функции и логарифма .
;
.
Итак, мы преобразовали формулу (8) к следующему виду:
.

Производные высших порядков от e в степени x

Теперь найдем производные высших порядков. Сначала рассмотрим экспоненту:
(14) .
(1) .

Мы видим, что производная от функции (14) равна самой функции (14). Дифференцируя (1), получаем производные второго и третьего порядка:
;
.

Отсюда видно, что производная n-го порядка также равна исходной функции:
.

Производные высших порядков показательной функции

Теперь рассмотрим показательную функцию с основанием степени a :
.
Мы нашли ее производную первого порядка:
(15) .

Дифференцируя (15), получаем производные второго и третьего порядка:
;
.

Мы видим, что каждое дифференцирование приводит к умножению исходной функции на . Поэтому производная n-го порядка имеет следующий вид:
.

Представлено доказательство и вывод формулы для производной синуса — sin(x). Примеры вычисления производных от sin 2x, синуса в квадрате и кубе. Вывод формулы для производной синуса n-го порядка.

Производная по переменной x от синуса x равна косинусу x:
(sin x)′ = cos x .

Доказательство

Для вывода формулы производной синуса, мы воспользуемся определением производной:
.

Чтобы найти этот предел, нам нужно преобразовать выражение таким образом, чтобы свести его к известным законам, свойствам и правилам. Для этого нам нужно знать четыре свойства.
1) Значение первого замечательного предела:
(1) ;
2) Непрерывность функции косинус:
(2) ;
3) Тригонометрические формулы . Нам понадобится следующая формула:
(3) ;
4) Свойство пределов:
Если и , то
(4) .

Применяем эти правила к нашему пределу. Сначала преобразуем алгебраическое выражение
.
Для этого применим формулу
(3) .
В нашем случае
; . Тогда
;
;
;
.

Теперь сделаем подстановку . При , . Применим первый замечательный предел (1):
.

Сделаем такую же подстановку и используем свойство непрерывности (2):
.

Поскольку пределы, вычисленные выше, существуют, то применяем свойство (4):

.

Формула производной синуса доказана.

Примеры

Рассмотрим простые примеры нахождения производных от функций, содержащих синус. Мы найдем производные от следующих функций:
y = sin 2x; y = sin 2 x и y = sin 3 x .

Пример 1

Найти производную от sin 2x .

Решение

Сначала найдем производную от самой простой части:
(2x)′ = 2(x)′ = 2 · 1 = 2.
Применяем .
.
Здесь .

Ответ

(sin 2x)′ = 2 cos 2x.

Пример 2

Найти производную от синуса в квадрате:
y = sin 2 x .

Решение

Перепишем исходную функцию в более понятном виде:
.
Найдем производную от самой простой части:
.
Применяем формулу производной сложной функции.

.
Здесь .

Можно применить одну из формул тригонометрии. Тогда
.

Ответ

Пример 3

Найти производную от синуса в кубе:
y = sin 3 x .

Производные высших порядков

Заметим, что производную от sin x первого порядка можно выразить через синус следующим образом:
.

Найдем производную второго порядка, используя формулу производной сложной функции :

.
Здесь .

Теперь мы можем заметить, что дифференцирование sin x приводит к увеличению его аргумента на . Тогда производная n-го порядка имеет вид:
(5) .

Докажем это, применяя метод математической индукции.

Мы уже проверили, что при , формула (5) справедлива.

Предположим, что формула (5) справедлива при некотором значении . Докажем, что из этого следует, что формула (5) выполняется для .

Выпишем формулу (5) при :
.
Дифференцируем это уравнение, применяя правило дифференцирования сложной функции:

.
Здесь .
Итак, мы нашли:
.
Если подставить , то эта формула примет вид (5).

Формула доказана.

Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная — одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?

Геометрический и физический смысл производной

Пусть есть функция f(x) , заданная в некотором интервале (a, b) . Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:

Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.

Иначе это можно записать так:

Какой смысл в нахождении такого предела? А вот какой:

производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.

Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.

Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t .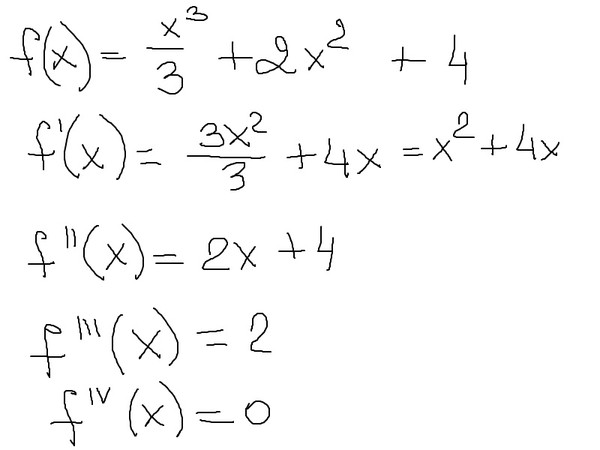 Средняя скорость за некоторый промежуток времени:

Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:

Правило первое: выносим константу

Константу можно вынести за знак производной. Более того — это нужно делать. При решении примеров по математике возьмите за правило — если можете упростить выражение, обязательно упрощайте .

Пример. Вычислим производную:

Правило второе: производная суммы функций

Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.

Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.

Найти производную функции:

Правило третье: производная произведения функций

Производная произведения двух дифференцируемых функций вычисляется по формуле:

Пример: найти производную функции:

Решение:

Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.

В вышеуказанном примере мы встречаем выражение:

В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.

Правило четвертое: производная частного двух функций

Формула для определения производной от частного двух функций:

Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.

С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис . За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.

Мэтуэй | Популярные задачи

92) 9(3x) по отношению к x 92+1

1	Найти производную — d/dx	бревно натуральное х
2	Оценить интеграл	интеграл натурального логарифма x относительно x
3	Найти производную — d/dx
21	Оценить интеграл	интеграл от 0 до 1 кубического корня из 1+7x относительно x
22	Найти производную — d/dx	грех(2x)
23	Найти производную — d/dx
41	Оценить интеграл	интеграл от cos(2x) относительно x
42	Найти производную — d/dx	1/(корень квадратный из х)
43	Оценка интеграла 9бесконечность
45	Найти производную — d/dx	х/2
46	Найти производную — d/dx	-cos(x)
47	Найти производную — d/dx	грех(3x)
68	Оценить интеграл	интеграл от sin(x) по x
69	Найти производную — d/dx	угловой синус(х)
70	Оценить предел	ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х
85	Найти производную — d/dx	лог х
86	Найти производную — d/dx	арктан(х)
87	Найти производную — d/dx	бревно натуральное 5х92

Wolfram|Alpha Примеры: производные

Ого! Wolfram|Alpha не работает без JavaScript.

Пожалуйста, включите JavaScript. Если вы не знаете, как это сделать, вы можете найти инструкции здесь. Как только вы это сделаете, обновите эту страницу, чтобы начать использовать Wolfram|Alpha.

Примеры для

Производные измеряют скорость изменения вдоль кривой по отношению к данной действительной или комплексной переменной. Wolfram|Alpha — отличный ресурс для определения дифференцируемости функции, а также для вычисления производных тригонометрических, логарифмических, экспоненциальных, полиномиальных и многих других типов математических выражений. Дифференциация имеет множество приложений в физике, тригонометрии, анализе, оптимизации и других областях. 94(Ai(t)) Начальная производная второго порядка, Начальная независимая переменная, t , независимая переменная Конец,Начальная функция, Начальная экспонента, Начальная экспонента, — Начальная степень, Начальная база, t , Базовая конечная,Начальная экспонента, 2 , Экспонента Конец , Power End , exponent End , Exponential End , function End , Производная второго порядка Endd2dt2 ⅇ-t2

Частные производные

Найдите частную производную по одной переменной или вычислите смешанные частные производные.