Сила натягу нитки формула через обсяг. Формула сили натягу нитки. Розрахунок натягу троса і реакції опори
визначення
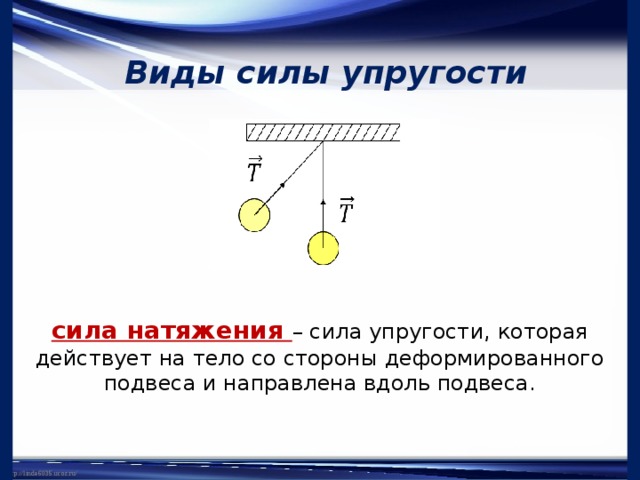
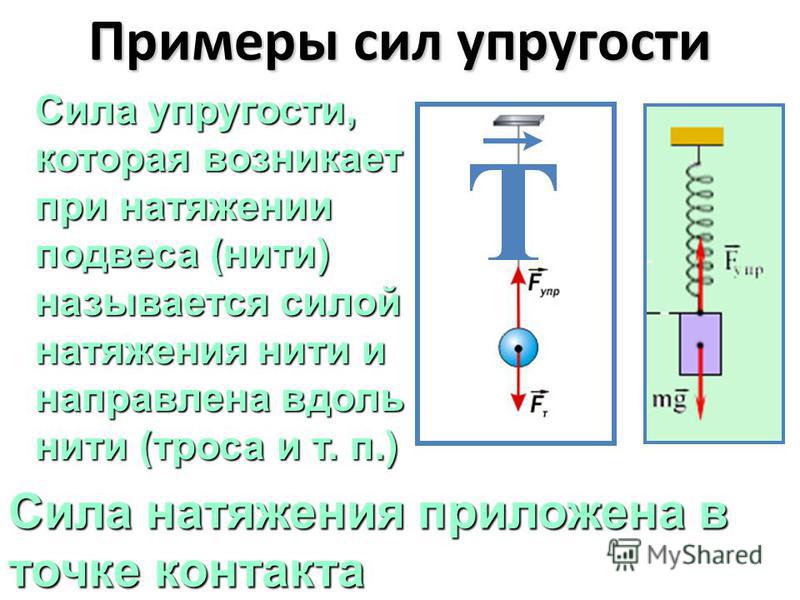
силу натягувизначають як рівнодіюча сил, прикладених до нитки, рівну їй по модулю, але протилежно спрямовану. Усталеного символу (букви), що позначає силу натягу немає. Її позначають і просто і, і. Математично визначення для сили натягу нитки можна записати як:
де = векторна сума всіх сил, які діють на нитку. Сила натягу нитки завжди спрямована по нитці (або підвісу).
Найчастіше в задачах і прикладах розглядають нитка, масою якої можна знехтувати. Її називають невагомою.
Ще одним важливим характеристикою нитки при розрахунку сили натягу є її розтяжність. Якщо досліджується невагома і нерозтяжна нитку, то така нитка вважається просто проводить через себе силу. У тому випадку, коли необхідно враховувати розтягнення нитки, застосовують закон Гука, при цьому:
де k — коефіцієнт жорсткості нитки, — подовження нитки при розтягуванні.
Одиниці виміру сили натягу нитки
Основною одиницею виміру сили натягу нитки (як і будь-якої сили) в системі СІ є: [T] = Н
В СГС: [T] = дин
Приклади розв’язання задач
приклад
Завдання.Невагома, нерозтяжна нитка витримує силу натягу T = 4400Н. З яким максимальним прискоренням можна піднімати вантаж масою m = 400 кг, який підвішують на цю нитку, щоб вона не розірвалася?
Рішення.Зобразимо на рис.1 всі сили, що діють на вантаж, і запишемо другий закон Ньютона. Тіло будемо вважати матеріальною точкою, всі сили доданими до центру мас тіла.
де — сила натягу нитки. Запишемо проекцію рівняння (1.1) на вісь Y:
З виразу (1.2) отримаємо прискорення:
Всі дані в завданні представлені в одиницях системи СІ, проведемо обчислення:
м / с 2
Відповідь. a = 1,2 м / с 2
приклад
Завдання.Шарик, який має масу m = 0,1 кг прикріплений до нитки (рис.2) рухається по колу, розташованої в горизонтальній площині.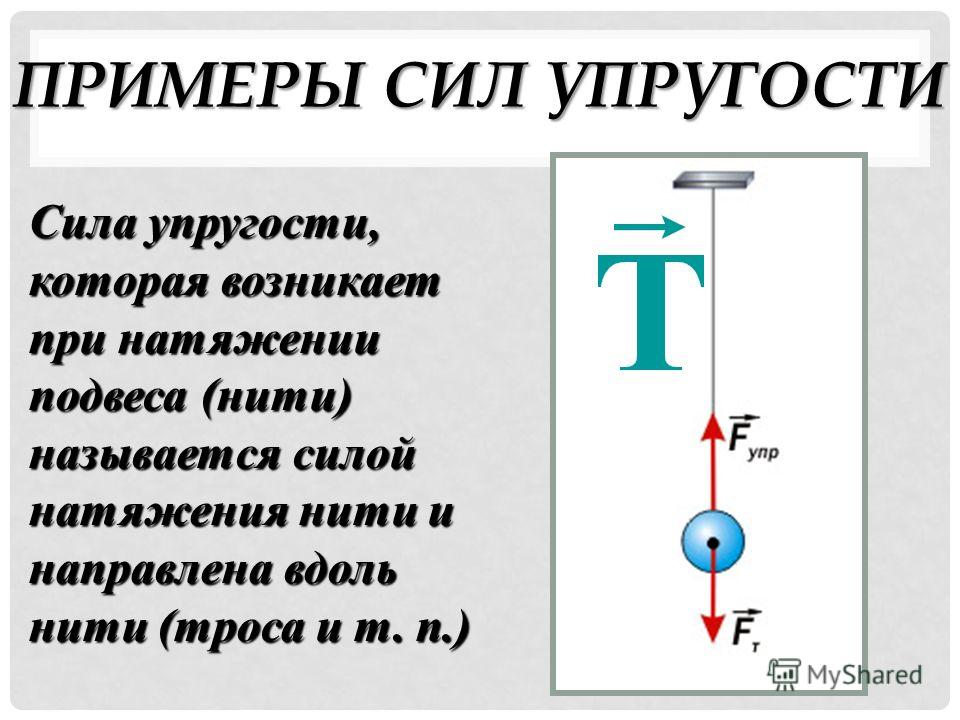 Знайдіть модуль сили натягу нитки, якщо довжина нитки l = 5 м, радіус кола R = 3м.
Знайдіть модуль сили натягу нитки, якщо довжина нитки l = 5 м, радіус кола R = 3м.
Рішення.Запишемо другий закон Ньютона для сил, прикладених до кульки, що обертається по колу з доцентровим прискоренням:
Знайдемо проекції даного рівняння на зазначені на рис.2 осі X і Y.
завдання 10048
Блок, який має форму диска масою m = 0,4 кг, обертається під дією сили натягу нитки, до кінців якої підвішені вантажі масами m 1 = 0,3 кг і m 2 = 0,7 кг. Визначити сили натягу Т 1 і T 2 нитки по обидві сторони блоку.
завдання 13144
На однорідний суцільний циліндричний вал радіусом R = 5 см і масою М = 10 кг намотана легка нитка, до кінця якої прикріплений вантаж масою m = 1 кг. Визначити: 1) залежність s (t), згідно з якою рухається вантаж; 2) силу натягу нитки Т; 3) залежність φ (t), згідно з якою обертається вал; 4) кутову швидкість ω вала через t = 1 с після початку руху; 5) тангенціальне (а τ) і нормальне (а n) прискорення точок, що знаходяться на поверхні вала.
завдання 13146
Через нерухомий блок у вигляді однорідного суцільного циліндра масою m = 0,2 кг перекинута невагома нитка, до кінців якої прикріплені тіла масами m 1 = 0,35 кг і m 2 = 0,55 кг. Нехтуючи тертям в осі блоку, визначте: 1) прискорення вантажу; 2) відношення T 2 / T 1 сил натягу нитки.
завдання 40602
На порожній тонкостінний циліндр маси m намотана нитка (тонка і невагома). Вільний кінець її прикріплений до стелі ліфта, що рухається вниз з прискоренням а л. Циліндр наданий сам собі. Знайти прискорення циліндра щодо ліфта і силу натягу нитки. Під час руху нитка вважати вертикальної.
завдання 40850
Вантаж масою 200 г обертають на нитці довжиною 40 см в горизонтальній площині. Чому дорівнює сила натягу нитки, якщо вантаж робить 36 обертів за одну хвилину.
завдання 13122
У повітрі на шовковій нитці підвішений заряджений кульку масою m = 0,4 м Знизу підносять до нього на відстань r = 2 см різнойменний і рівний за величиною заряд q. В результаті цього сила натягу нитки Т збільшується в n = 2,0 рази. Знайти величину заряду q.
В результаті цього сила натягу нитки Т збільшується в n = 2,0 рази. Знайти величину заряду q.
завдання 15612
Знайти відношення модуля сили натягу нитки математичного маятника в крайньому положенні з модулем сили натягу нитки конічного маятника; довжини ниток, маси важків і кути відхилення маятників однакові.
завдання 16577
Два маленьких однакових кульки масою 1 мкг кожен підвішені на нитках однакової довжини і стикаються. Коли кульки зарядили, вони розійшлися на відстань 1 см, а сила натягу нитки стала рівною 20 ПН. Знайти заряди кульок.
завдання 19285
Встановити закон, згідно з яким змінюється з часом сила натягу F нитки математичного маятника. Маятник коливається по закону α = α max cosωt, маса його m, довжина l.
завдання 19885
На малюнку зображено заряджена нескінченна площина з поверхневою площиною заряду σ = 40 мкКл / м 2 і однойменно заряджений кульку з масою m = l г і зарядом q = 2,56 нКл.
Рух системи тел
Динаміка: руху системи зв’язаних тіл.
Проектування сил декількох об’єктів.
Дія другого закону Ньютона на тіла, які скріплені ниткою
Якщо ти, друже, забув, як силушку проектувати, раджу в своїй голівоньці освіжити.
А для тих, хто все пам’ятає, поїхали!
Завдання 1. На гладкому столі лежать два пов’язаних невагомою і нерастяжимой ниткою бруска з масою 200 г лівого і масою правого 300 м До першого прикладена сила 0,1 Н, до лівого — в протилежному напрямку сила 0,6 Н. З яким прискоренням рухаються вантажі?
Рух відбувається тільки на осі X.
Оскільки до правого вантажу прикладена велика сила, рух даної системи буде направлено вправо, тому направимо вісь так само. Прискорення у обох брусків буде направлено в одну сторону — сторону більшої сили.
Складемо верхнє і нижнє рівняння. У всіх завданнях, якщо немає якихось умов сила натягу у різних тел однакова T₁ і Т ₂.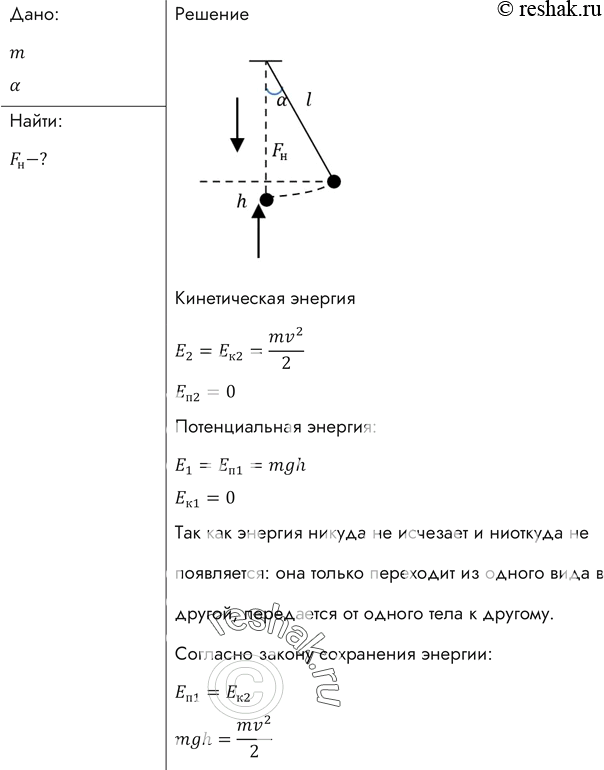
Висловимо прискорення:
Відповідь: 1 м / с?
Завдання 2. Два бруска, пов’язані нерастяжимой ниткою, знаходяться на горизонтальній площині. До них додаються сили F₁ і F₂, складові з горизонтом кути α і β. Знайти прискорення системи і силу натягу нитки. Коефіцієнти тертя брусків про площину однакові і рівні μ. Сили F₁ і F₂ менше сили тяжіння брусків. Система рухається вліво.
Cистема рухається вліво, однак вісь можна направити в будь-яку сторону (справа лише в знаках, можете поексперментіровать на дозвіллі). Для різноманітності направимо вправо, проти руху всієї системи, ми ж любимо мінуси! Спроектуємо сили на Ох (якщо з цим складності -).
За II з. Ньютона спроеціруем сили обох тіл на Ох:
Складемо рівняння і висловимо прискорення:
Висловимо натяг нитки. Для цього прирівняємо прискорення з обох рівнянь системи:
Завдання 3. Через неподівжний блок перекинуті нитка, до якої підвішені три однакових вантажу (два з одного боку і один з іншого) масою 5кг кожен. Знайти прискорення системи. Який шлях пройдуть вантажі за перші 4 з руху?
Знайти прискорення системи. Який шлях пройдуть вантажі за перші 4 з руху?
У цьому завданню можна уявити, що два лівих вантажу скріплені разом без нитки, це позбавить нас від проектування взаємно рівних сил.
Віднімемо від першого рівняння друге:
Знаючи прискорення і те, що початкова швидкість дорівнює нулю, використовуємо формулу шляху для рівноприскореного руху:
Відповідь: 26,64 м
Завдання 4. Два вантажу масами 4 кг і 6 кг з’єднані легкої нерастяжимой ниткою. Коефіцієнти тертя між вантажем і столомμ = 0,2. Визначте прискорення, з яким будуть рухатися вантажі.
Запишемо рух тіл на осі, з Oy знайдемо N для сили тертя (Fтр = μN):
(Якщо складно зрозуміти, які рівняння знадобляться для вирішення завдання, краще запишіть все)
Складемо два нижніх рівняння для того, щоб T скоротилося:
Висловимо прискорення:
Відповідь: 2,8 м / с ²
Завдання 5. На похилій поскості з кутом нахилу 45 ° лежить брускок масою 6 кг.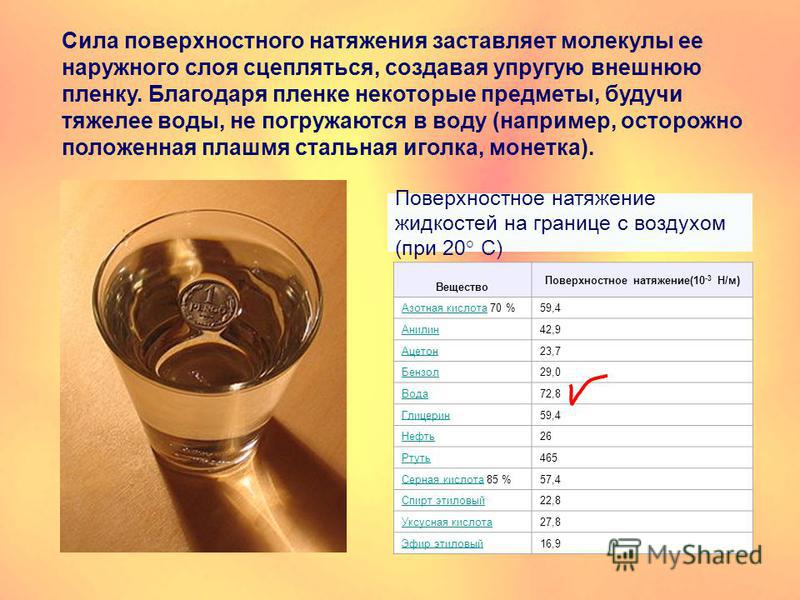 Вантаж масою 4 кг приєднаний до бруска за допомогою нитки і перекинутий через блок. Визначте натяг нитки, якщо коефіцієнт тертя бруска про площину μ = 0,02. При яких значеннях μ система буде в рівновазі?
Вантаж масою 4 кг приєднаний до бруска за допомогою нитки і перекинутий через блок. Визначте натяг нитки, якщо коефіцієнт тертя бруска про площину μ = 0,02. При яких значеннях μ система буде в рівновазі?
Ось направимо довільно і припустимо, що правий вантаж переважує лівий і піднімає його вгору по похилій площині.
З рівняння на вісь Y висловимо N для сили тертя на вісь Х (Fтр = μN):
Вирішимо систему, взявши рівняння для лівого тіла по осі Х і для правого тіла по осі Y:
Висловимо прискорення, щоб залишилася одна невідома T, і знайдемо її:
Система буде в рівновазі. Це означає, що сума всіх сил, що діють на кожне з тіл, буде дорівнює нулю:
Отримали негативний коефіцієнт тертя, значить, рух системи ми вибрали невірно (прискорення, силу тертя). Можна це перевірити, підставивши силу натягу нитки Т в будь-яке рівняння і знайшовши прискорення. Але нічого страшного, значення залишаються тими ж по модулю, але протилежними за напрямком.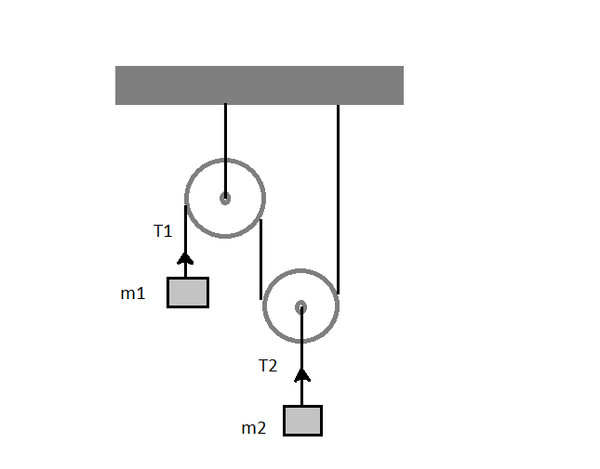
Значить, правильний напрямок сил має виглядати так, а коефіцієнт тертя, при якому система буде в рівновазі, дорівнює 0,06.
Відповідь: 0,06
Завдання 6. На двох похилих площинах знаходиться по вантажу масами 1 кг. Кут між горизонталлю і площинами дорівнює α= 45 ° і β = 30 °. Коефіцієнт тертя у обох площин μ= 0,1. Знайдіть прискорення, з яким рухаються вантажі, і силу натягу нитки. Яким має бути ставлення мас вантажів, щоб вони знаходилися в рівновазі.
У цьому завданню вже будуть потрібні всі рівняння на обидві осі для кожного тіла:
Знайдемо N в обох випадках, підставимо їх у силу тертя і запишемо разом рівняння для осі Х обох тел:
Складемо рівняння і скоротимо на масу:
Висловимо прискорення:
Підставивши в будь-яке рівняння знайдене прискорення, знайдемо Т:
А тепер здолаємо останній пункт і розберемося з співвідношенням мас. Сума всіх сил, що діють на будь-який з тіл, дорівнює нулю для того, щоб система перебувала в рівновазі:
складемо рівняння
Все, що з одного масою, перенесемо в одну частину, все інше — в іншу частину рівняння:
Отримали, що відношення мас повинно бути таким:
Однак, якщо ми припустимо, що система може рухатися в іншому напрямку, тобто правий вантаж буде переважувати лівий, напрямок прискорення і сили тертя зміниться.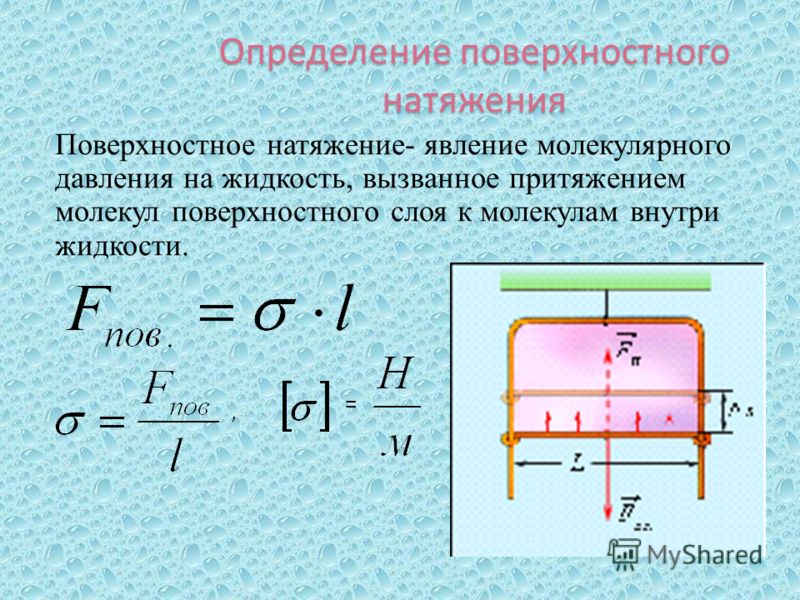 Рівняння залишаться такими ж, а ось знаки будуть іншими, і тоді відношення мас вийде таким:
Рівняння залишаться такими ж, а ось знаки будуть іншими, і тоді відношення мас вийде таким:
Тоді при співвідношенні мас від 1,08 до 1,88 система буде перебувати в спокої.
У багатьох може скластися враження, що співвідношення мас повинно бути якимось конкретним значенням, а не проміжком. Це правда, якщо отстутвует сила тертя. Щоб врівноважувати сили тяжіння під різними кутами, знайдеться тільки один варінт, коли система знаходиться в спокої.
В даному ж випадку сила тертя дає діапазон, в якому, поки сила тертя не буде подолане, руху не почнеться.
Відповідь: від 1,08 до 1,88
популярне визначення
Сила — це дія,яке може змінити стан спокою або руху тіла; отже, він може прискорювати або змінювати швидкість, напрямок або напрямок руху даного тіла. навпаки, напруженість— це стан тіла, яке зазнає дії протидіючих сил, які його притягують.
Вона відома як сила розтягування,яка при впливі на пружне тіло створює напругу; Ця остання концепція має різні визначення, які залежать від галузі знань, з якої вона аналізується.
Канати, наприклад, дозволяють передавати сили від одного тіла до іншого. Коли дві рівні і протилежні сили застосовуються на кінцях мотузки, мотузка стає натягнутою. Коротше кажучи, сили натягу — це кожна з цих сил, яка підтримує канат без руйнування .
фізикаі інженеріяговорять про механічному напрузі,щоб позначити силу на одиницю площі в оточенні матеріальної точки на поверхні тіла. Механічне напруга може бути виражено в одиницях сили, виділених на одиниці площі.
Напруга також є фізичною величиною, яка призводить електрони через провідник в замкнутий електричний ланцюг, яка викликає протікання електричного струму. У цьому випадку напруга можна назвати напругоюабо різницею потенціалів .
З іншого боку, поверхневий натягрідини — це кількість енергії, необхідне для зменшення площі її поверхні на одиницю площі. Отже, рідина чинить опір, збільшуючи її поверхню.
Як знайти силу натягу
Знаючи, що силанатягу — це сила, З якої натягується лінія або струна, можна знайти натяг в ситуації статичного типу, якщо відомі кути ліній. Наприклад, якщо навантаження знаходиться на схилі, а лінія, паралельна останньому, перешкоджає переміщенню вантажу вниз, натяг дозволяється, знаючи, що сума горизонтальних і вертикальних складових задіяних сил повинна давати нуль.
Наприклад, якщо навантаження знаходиться на схилі, а лінія, паралельна останньому, перешкоджає переміщенню вантажу вниз, натяг дозволяється, знаючи, що сума горизонтальних і вертикальних складових задіяних сил повинна давати нуль.
Перший крок для виконання цього розрахунку— намалювати схил і помістити на нього блок маси M. Справа збільшується нахил, і в одній точці він зустрічає стіну, від якої лінія проходить паралельно першому. і зв’язати блок, утримуючи його на місці і створюючи натяг T. Далі ви повинні ототожнити кут нахилу з грецької буквою, яка може бути «альфа», а силу, яку він надає на блок, з буквою N, оскільки мова йде про нормальній силі .
з блоку векторповинен бути намальований перпендикулярно нахилу і вгору, щоб представити нормальну силу, і один вниз (паралельно осі y), Щоб відобразити силу тяжіння. Потім ви починаєте з формул.
Щоб знайти силу, F = M використовується. g , де g — цейого постійне прискорення(В разі сили тяжіння це значення дорівнює 9, 8 м / с ^ 2). Одиницею, яка використовується для результату, є ньютон, який позначається буквою N.У разі нормальної сили його необхідно розкласти по вертикальних і горизонтальних векторах, використовуючи кут, який він утворює з віссю x: Для обчислення вектора вгору gдорівнює косинусу кута, а для вектора в напрямку зліва, до лоно цього.
Одиницею, яка використовується для результату, є ньютон, який позначається буквою N.У разі нормальної сили його необхідно розкласти по вертикальних і горизонтальних векторах, використовуючи кут, який він утворює з віссю x: Для обчислення вектора вгору gдорівнює косинусу кута, а для вектора в напрямку зліва, до лоно цього.
Нарешті, ліва складова нормальної сили повинна бути прирівняна до правого боку напруги T, нарешті, дозволивши напруга.
бібліотекознавство
Щоб добре знати термін бібліотечна справа, яке нас зараз займає, необхідно почати з з’ясування його етимологічного походження. У цьому випадку ми можемо сказати, що це слово походить від грецького, оскільки воно утворено сумою декількох елементів цієї мови: — Іменник «бібліон», яке можна перекласти як «книга». — Слово «техе», яке є синонімом слова «ящик» або «місце, де воно зберігається». Суфікс «-logía», який використовується для позначення «науки, яка вивчає». Це відомо як бібліотечна справа в дисципліні, сфокусованої на
визначення
taxismo
Таксізм перестав бути терміном, прийнятим Королівської іспанської академією (RAE) в своєму словнику.
 Поняття використовується з посиланням на спрямований рух, яке реалізує жива істота, щоб відповісти на стимул, який сприймає. Таксі може бути негативним (коли жива істота віддаляється від джерела стимулу) або позитивним (жива істота наближається до того, що генерує розглянутий стимул). щоб органи
Поняття використовується з посиланням на спрямований рух, яке реалізує жива істота, щоб відповісти на стимул, який сприймає. Таксі може бути негативним (коли жива істота віддаляється від джерела стимулу) або позитивним (жива істота наближається до того, що генерує розглянутий стимул). щоб органивизначення
розширення
Розширення, від латинського expansĭo, є дією і ефектом розширення або розширення (поширення, поширення, розгортання, розгортання, надання більшої амплітуди або створення чогось займає більше місця). Розширення може бути територіальним зростанням нації або імперії від завоювання і анексії нових земель. Наприклад: «Американська експансія дев’ятнадцятого століття була дуже важливою і торкнулася Мекси
визначення
У техніці зустрічається ще один вид розтягнутих елементів, при визначенні міцності яких важливе значення має власну вагу. Це так звані гнучкі нитки. Таким терміном позначаються гнучкі елементи в лініях електропередач, в канатних дорогах, в висячих мостах та інших спорудах.

Нехай (Рис.1) є гнучка нитка постійного перетину, навантажена власною вагою і підвішена в двох точках, що знаходяться на різних рівнях. Під дією власної ваги нитка провисає по деякій кривій АОВ.
Горизонтальна проекція відстані між опорами (точками її закріплення), що позначається, носить назву прольоту.
Нитка має постійний перетин, отже, вага її розподілений рівномірно по її довжині. Зазвичай провисання нитки невелика в порівнянні з її прольотом, і довжина кривої АОВмало відрізняється (не більше ніж на 10%) від довжини хорди АВ. В цьому випадку з достатнім ступенем точності можна вважати, що вага нитки одно- мірно розподілено не по її довжині, а по довжині її проекції на горизонтальну вісь, т. Е. Вздовж прольоту l.
Рис.1.Розрахункова схема гнучкої нитки.
Цю категорію гнучких ниток ми і розглянемо. Приймемо, що інтенсивність навантаження, рівномірно розподіленим по прольоту нитки, дорівнює q.
 Це навантаження, що має розмірність сила / довжина, Може бути не тільки власною вагою нитки, припадає на одиницю довжини прольоту, а й вагою льоду або будь-який інший навантаженням, також рівномірно розподіленим. Зроблене припущення про закон розподілу навантаження значно полегшує розрахунок, але робить його разом з тим наближеним; якщо при точному вирішенні (навантаження розподілено вздовж кривої) кривої провисання буде ланцюгова лінія, то в наближеному вирішенні крива провисання виявляється квадратної параболою.
Це навантаження, що має розмірність сила / довжина, Може бути не тільки власною вагою нитки, припадає на одиницю довжини прольоту, а й вагою льоду або будь-який інший навантаженням, також рівномірно розподіленим. Зроблене припущення про закон розподілу навантаження значно полегшує розрахунок, але робить його разом з тим наближеним; якщо при точному вирішенні (навантаження розподілено вздовж кривої) кривої провисання буде ланцюгова лінія, то в наближеному вирішенні крива провисання виявляється квадратної параболою.Початок координат виберемо в найнижчій точці провисання нитки Про, Положення якої, нам поки невідоме, очевидно, залежить від величини навантаження q, Від співвідношення між довжиною нитки по кривій і довжиною прольоту, а також від відносного положення опорних точок. У точці Продотична до кривої провисання нитки, очевидно, горизонтальна. З цієї дотичній направимо вправо вісь.
Виріжемо двома перетинами на початку координат і на відстані від початку координат (перетин m n) Частина довжини нитки.
 Так як нитка припущена гнучкою, т. Е. Здатної чинити опір лише розтягування, то дія відкинутої частини на решту можливо тільки у вигляді сили, спрямованої по дотичній до кривої провисання нитки в місці розрізу; інший напрямок цієї сили неможливо.
Так як нитка припущена гнучкою, т. Е. Здатної чинити опір лише розтягування, то дія відкинутої частини на решту можливо тільки у вигляді сили, спрямованої по дотичній до кривої провисання нитки в місці розрізу; інший напрямок цієї сили неможливо.На рис.2 представлена вирізана частина нитки з діючими на неї силами. Рівномірно розподілене навантаження інтенсивністю qспрямована вертикально вниз. Вплив лівої відкинутої частини (горизонтальна сила Н) Направлено, з огляду на те, що нитка працює на розтяг, вліво. Дія правої відкинутої частини, сила Т, Направлено вправо по дотичній до кривої провисання нитки в цій точці.
Cоставить рівняння рівноваги вирізаного ділянки нитки. Візьмемо суму моментів всіх сил щодо точки прикладання сили Ті прирівняємо її нулю. При цьому врахуємо, спираючись на наведене на початку допущення, що рівнодіюча розподіленого навантаження інтенсивністю qбуде, і що вона прикладена посередині відрізка. тоді
Рис.
 2.Фрагмент вирізаної частини гнучкої нитки
2.Фрагмент вирізаної частини гнучкої нитки,
Звідси випливає, що крива провисання нитки є параболою. Коли обидві точки підвісу нитки знаходяться на одному рівні, то Величина в даному випадку буде так званої стрілою провисання. Її легко визначити. Так як в цьому випадку, з огляду на симетрії, нижча точка нитки знаходиться посередині пролита, то; підставляючи в рівняння (1) значення і отримуємо:
величина Нназиваєтьсягоризонтальним натягом нитки.
і натяг H, То за формулою (2) знайдемо стрілу провисання. При заданих і натяг Нвизначається формулою (3). Зв’язок цих величин з довжиною нитки по кривій провисання встановлюється за допомогою відомої з математики наближеною формули)Складемо ще одна умова рівноваги вирізаної частини нитки, а саме, прирівняємо нулю суму проекцій всіх сил на вісь:
З цього рівняння знайдемо силу Т натяг в довільній точці
Звідки випливає, що сила Тзбільшується від нижчої точки нитки до опор і буде найбільшою в точках підвісу там, де дотична до кривої провисання нитки становить найбільший кут з горизонталлю.
 При малому провисанні нитки цей кут не досягає великих значень, тому з достатньою для практики ступенем точності можна вважати, що зусилля в нитки постійно і дорівнює її натягу Н. На цю величину зазвичай і ведеться розрахунок міцності нитки. Якщо все ж потрібно вести розрахунок на найбільшу силу у точок підвісу, то для симетричною нитки її величину визначимо наступним шляхом. Вертикальні складові реакцій опор рівні між собою і дорівнюють половині сумарного навантаження на нитку, т. Е.. Горизонтальні складові рівні силі Н, Яка визначається за формулою (3). Повні реакції опор вийдуть як геометричні суми цих складових:
При малому провисанні нитки цей кут не досягає великих значень, тому з достатньою для практики ступенем точності можна вважати, що зусилля в нитки постійно і дорівнює її натягу Н. На цю величину зазвичай і ведеться розрахунок міцності нитки. Якщо все ж потрібно вести розрахунок на найбільшу силу у точок підвісу, то для симетричною нитки її величину визначимо наступним шляхом. Вертикальні складові реакцій опор рівні між собою і дорівнюють половині сумарного навантаження на нитку, т. Е.. Горизонтальні складові рівні силі Н, Яка визначається за формулою (3). Повні реакції опор вийдуть як геометричні суми цих складових:Умова міцності для гнучкої нитки, якщо через Fпозначена площа перетину, має вигляд:
замінивши натяг Нйого значенням за формулою (3), отримаємо:
З цієї формули при заданих,, і можна визначити необхідну стрілу провисання. Рішення при цьому спроститься, якщо в включений лише власну вагу; тоді, де вага одиниці об’єму матеріалу нитки, і
т.
 е. величина Fне ввійде в розрахунок.
е. величина Fне ввійде в розрахунок.Якщо точки підвісу нитки знаходяться на різних рівнях, то, підставляючи в рівняння (1) значення і, знаходимо і:
Звідси з другого виразу визначаємо натяг
а ділячи перше на друге, знаходимо:
Маючи на увазі, що, отримуємо:
Підставивши це значення в формулу певного натягу Н, Остаточно визначаємо:
Два знака в знаменнику вказують на те, що можуть бути дві основні форми провисання нитки. Перша форма при меншому значенні Н(Знак плюс перед другим коренем) дає нам вершину параболи між опорами нитки. При більшому натягу Н(Знак мінус перед другим коренем) вершина параболи розташується лівіше опори А(Рис.1). Отримуємо другу форму кривої. Можлива і третя (проміжна між двома основними) форма провисання, відповідна умові; тоді початок координат поєднується з точкою А. Та чи інша форма буде отримана в залежності від співвідношень між довжиною нитки по кривій провисання АОВ(Рис.
 1) і довжиною хорди АВ.
1) і довжиною хорди АВ.Якщо при підвісці нитки на різних рівнях невідомі стріли провисання і, але відомо натяг Н, То легко отримати значення відстаней аі bі стріл провисання, і. різниця hрівнів підвіски дорівнює:
Підставами в цей вислів значення і, і перетворимо його, маючи на увазі, що:
а так як то
Слід мати на увазі, що при буде мати місце перша форма провисання нитки, при друга форма провисання і при третя форма. Підставляючи значення і в вирази для стріл провисання і, отримуємо величини і:
Тепер з’ясуємо, що станеться із симетричною ниткою, що перекриває проліт, якщо після підвішування її при температурі і інтенсивності навантаження температура нитки підвищитьсядо а навантаження збільшиться до інтенсивності (наприклад, через її зледеніння). При цьому припустимо, що в першому стані задано або натяг, або стріла провисання (Знаючи одну з цих двох величин, завжди можна визначити іншу.)
при підрахунку деформаціїнитки, що є в порівнянні з довжиною нитки малою величиною, зробимо два припущення: довжина нитки «дорівнює її прольоту, а натяг постійно і дорівнює Н.
 При пологах нитках ці припущення дають невелику похибку.
При пологах нитках ці припущення дають невелику похибку.
Продемонструємо можливості теореми Остроградського-Гаусса на кількох прикладах. Поле нескінченної однорідно зарядженої площини Поверхнева густина заряду на довільній площині площею S визначається за формулою: де dq — Заряд, зосереджений на площі dS; dS – фізично нескінченно мала ділянка поверхні. Нехай у всіх точках площини S однакова. Заряд q – позитивний. Напруженість у всіх точках матиме напрямок, перпендикулярний до площини. S(Рис. 2.11). Вочевидь, що у симетричних, щодо площині точках, напруженість буде однакова за величиною і протилежна за напрямом. Уявімо собі циліндр з утворюючими, перпендикулярними площині, та основами Δ S, розташованими симетрично щодо площини (рис.
Застосуємо теорему Остроградського-Гаусса. Потік Ф Е через бічну частину поверхні циліндра дорівнює нулю, т.к. Сумарний потік через замкнуту поверхню (циліндр) дорівнюватиме: Усередині поверхні укладено заряд. Отже, з теореми Остроградського-Гаусса отримаємо: ; звідки видно, що напруженість поля площини S дорівнює:
Отриманий результат залежить від довжини циліндра. Це означає, що на будь-якій відстані від площини Поле двох рівномірно заряджених площин Нехай дві нескінченні площини заряджені різноіменними зарядами з однаковою за величиною щільністю σ (рис. 2.13). Результуюче поле, як було сказано вище, знаходиться як суперпозиція полів, створюваних кожною з площин. Тоді всередині площин
Поза площинаминапруженість поля Отриманий результат справедливий і для площин кінцевих розмірів, якщо відстань між площинами набагато менша за лінійні розміри площин (плоский конденсатор). Між пластинами конденсатора діє сила взаємного тяжіння (на одиницю площі пластин): де S – площа обкладок конденсатора. Т.к. , то
Це формула для розрахунку пондермоторної сили. Поле зарядженого нескінченно довгого циліндра (нитки) Нехай поле створюється нескінченною циліндричною поверхнею радіусу R, зарядженої з постійною лінійною густиною , де dq – заряд, зосереджений на відрізку циліндра (рис. 2.14). З міркування симетрії випливає, що в будь-якій точці буде спрямована вздовж радіуса, перпендикулярно осі циліндра. Представимо навколо циліндра (нитки) коаксіальнузамкнуту поверхню ( циліндр у циліндрі) радіусу rі довжиною l (основи циліндрів перпендикулярно до осі). Для основ циліндрів для бічної поверхні тобто. залежить від відстані r. Отже, потік вектора через поверхню, що розглядається, дорівнює За теоремі Остроградського-Гаусса , звідси
Якщо, т.к. усередині замкнутої поверхні зарядів немає (рис.2.15). Якщо зменшувати радіус циліндра R (при ), можна поблизу поверхні отримати поле з дуже великою напруженістю і, при , отримати нитку. Поле двох коаксіальних циліндрів з однаковою лінійною щільністю λ, але різним знаком Усередині меншого і поза більшим циліндром поле буде відсутнє (рис. 2.16). У зазорі між циліндрами поле визначається так само, як і в попередньому випадку: Це справедливо і для нескінченно довгого циліндра, і для циліндрів кінцевої довжини, якщо зазор між циліндрами набагато менший за довжину циліндрів (циліндричний конденсатор). Поле зарядженої пустотілої кулі Пустотіла куля (або сфера) радіусу R заряджена позитивним зарядом з поверхневою щільністю σ. Поле в даному випадку буде центрально симетричним – у будь-якій точці проходить через центр кулі. і силові лінії перпендикулярні поверхні в будь-якій точці. Уявімо навколо кулі – сферу радіусу r (рис. 2.17). | |||
Что такое предварительная нагрузка болта? — Albany County Fasteners
Болт и гайка используются вместе в качестве сжимающей силы для удержания материалов в соединении. Резьба гайки взаимодействует с резьбой винта, прикладывая усилие к обеим сторонам скрепляемого материала. Это натяжение называется предварительным натягом болта и представляет собой сжатие, создаваемое при затягивании гайки по отношению к болту (или наоборот).
Когда на болт возлагается нагрузка (вес), она ограничивается величиной нагрузки, которую болт может выдержать до разрушения. Однако, когда болт затянут относительно материала, это позволяет болту распределять усилие через материал , поэтому сам болт удерживает только часть нагрузки. Это означает, что болт может выдерживать значительно более высокую нагрузку при правильном натяжении. Это напряжение известно как предварительная нагрузка.
Нагрузка – величина силы, действующей на узел крепежа
Предварительная нагрузка – величина натяжения (сжатия), необходимая для распределения усилия нагрузки по узлу крепежа
Рабочая нагрузка – нагрузка, прикладываемая к узлу, когда он готов к работе
Предварительная нагрузка болта — натяжение, создаваемое при навинчивании гайки на болт для удержания двух материалов вместе. Когда натяжение достигает оптимального предварительного натяга, рабочая нагрузка (нагрузка, добавленная после создания сборки), приложенная к болту, будет распределяться на установочные материалы, поэтому болт не воспринимает всю нагрузку.
Когда натяжение достигает оптимального предварительного натяга, рабочая нагрузка (нагрузка, добавленная после создания сборки), приложенная к болту, будет распределяться на установочные материалы, поэтому болт не воспринимает всю нагрузку.
Результаты предварительного натяга болта:
- Если сборка ослаблена (предварительный натяг приложен неправильно), внешняя нагрузка увеличивает нагрузку только на болт. Это приведет к выходу болта из строя.
- Если сборка тугая (была приложена правильная предварительная нагрузка), нагрузка вызовет деформацию болта только за счет распределения нагрузки между болтом и гайкой.
Болты — невероятные инструменты, но на самом деле они не так прочны, как мы думаем. При первом взгляде на узел болта с прикрепленной к нему рабочей нагрузкой создается впечатление, что болт удерживает всю эту нагрузку сам по себе. Это не вариант.
Когда болт имеет предварительную нагрузку, он может распределять рабочую нагрузку по пластине возле головки болта. Мы будем называть это опорной пластиной. Это означает, что правильно установленный узел болта может выдержать гораздо большую нагрузку, поскольку он распределяет усилие от самого себя. Когда рабочая нагрузка прикладывается к крепежному узлу, который не был предварительно нагружен, вся сила воздействует только на болт, что значительно повышает вероятность его отказа.
Мы будем называть это опорной пластиной. Это означает, что правильно установленный узел болта может выдержать гораздо большую нагрузку, поскольку он распределяет усилие от самого себя. Когда рабочая нагрузка прикладывается к крепежному узлу, который не был предварительно нагружен, вся сила воздействует только на болт, что значительно повышает вероятность его отказа.
Почему предварительная нагрузка болта так важна?
Как обсуждалось выше, без предварительного натяга болта вся конструкция полностью зависела бы от болта, удерживающего вес. При приложении предварительного натяга требуется значительно меньше болтов, так как материал (опорная пластина) будет играть значительно большую роль в удержании рабочей нагрузки. Однако это не панацея; рабочая нагрузка может по-прежнему превышать предварительную нагрузку болтов, что может привести к отказу болтов, отказу опорной пластины или тому и другому.
Простые способы определения предварительного натяга болта
- Использование динамометрического ключа для достижения оптимального крутящего момента
- Хотя это не является точной мерой предварительного натяга болта, если болт затянут с оптимальным крутящим моментом, можно предположить, что он близок к правильному предварительному натягу.
 Причина, по которой этот метод не принимается с готовностью, заключается в том, что крутящий момент будет напрямую зависеть от материала, против которого он вращается. Более грубый материал будет создавать большее трение, что повысит значение крутящего момента при одновременном снижении предварительного натяжения. Обратное тоже верно. Вы можете достичь оптимального крутящего момента, не достигая оптимальной предварительной нагрузки (и наоборот). В конце концов, это зависит от материала, поэтому этот метод не является точным, но является приличным предположением.
Причина, по которой этот метод не принимается с готовностью, заключается в том, что крутящий момент будет напрямую зависеть от материала, против которого он вращается. Более грубый материал будет создавать большее трение, что повысит значение крутящего момента при одновременном снижении предварительного натяжения. Обратное тоже верно. Вы можете достичь оптимального крутящего момента, не достигая оптимальной предварительной нагрузки (и наоборот). В конце концов, это зависит от материала, поэтому этот метод не является точным, но является приличным предположением.
- Хотя это не является точной мерой предварительного натяга болта, если болт затянут с оптимальным крутящим моментом, можно предположить, что он близок к правильному предварительному натягу.
- Используйте шайбы с индикацией предварительного натяга
- Шайбы с индикацией предварительного натяжения — это шайбы, предназначенные для вращения до тех пор, пока к ним не будет приложена определенная нагрузка. Таким образом, как только стиральная машина перестанет вращаться в свободном режиме, предварительная нагрузка будет соблюдена. Это гораздо более простой способ определить, было ли соблюдено правильное сжатие.

- Шайбы с индикацией предварительного натяжения — это шайбы, предназначенные для вращения до тех пор, пока к ним не будет приложена определенная нагрузка. Таким образом, как только стиральная машина перестанет вращаться в свободном режиме, предварительная нагрузка будет соблюдена. Это гораздо более простой способ определить, было ли соблюдено правильное сжатие.
- Используйте индикаторные шайбы прямого натяжения
- Эти шайбы имеют небольшие выступы, которые сглаживаются при достижении предварительного натяга. После сплющивания используется щуп, чтобы убедиться, что стержень болта находится под шайбой не более чем на 50% (в идеале меньше).
- Используйте кремниевые индикаторные шайбы прямого натяжения
- Эти шайбы работают так же, как и шайбы с прямой индикацией натяжения, описанные выше. Эти шайбы имеют небольшие углубления, в которые заливается силиконовая паста. По мере затягивания гайки силикон начинает выходить из боковых сторон шайбы. Чтобы определить, когда достигается оптимальная предварительная нагрузка на шайбе этого типа, количество углублений на шайбе за вычетом одного должно быть снаружи. Например: если есть 6 углублений, то должно быть выставлено как минимум 5. 6 углублений – 1 углубление = 5 (достигнута предварительная нагрузка)
- Затяните до упора, а затем затяните на «X» градусов
- Менее надежный подход — затянуть гайку до упора, а затем затянуть гайку на «Х» градусов.
 Например, рекомендация 90 градусов будет выглядеть следующим образом: Накрутите гайку на сборку до плотного прилегания к материалу. Присоедините гаечный ключ к гайке и поверните ее на четверть оборота (90 градусов). Этот метод даст вам близкую к точной предварительную нагрузку.
Например, рекомендация 90 градусов будет выглядеть следующим образом: Накрутите гайку на сборку до плотного прилегания к материалу. Присоедините гаечный ключ к гайке и поверните ее на четверть оборота (90 градусов). Этот метод даст вам близкую к точной предварительную нагрузку.
- Менее надежный подход — затянуть гайку до упора, а затем затянуть гайку на «Х» градусов.
Что же делает предварительная нагрузка болта?
Предварительное натяжение болта в конечном счете позволяет полностью затянутому болту выжить в тех случаях, когда незатянутый или ослабленный узел может очень быстро выйти из строя. В затянутом состоянии соединение обеспечивает канал, по которому усилие передается на сами материалы сборки. Это означает, что сам болт в сборе находится только под частью силы рабочей нагрузки. Хотя вы не можете посмотреть на болт и увидеть, как происходит эта передача, предварительный натяг позволяет болтам выживать в гораздо более суровых условиях.
- Механические свойства и определения крепежных изделий
- Сокращения крепежа
Ищете другие блоги, подобные этому?
Зарегистрируйтесь, чтобы получать новые блоги прямо на ваш почтовый ящик!
Электронная почта *
Имя *
Фамилия *
Постоянное использование контактов. Пожалуйста, оставьте это поле пустым.
Пожалуйста, оставьте это поле пустым.
Отправляя эту форму, вы соглашаетесь получать маркетинговые электронные письма от: RAW PRODUCTS CORP, 100 Newfield Ave., Edison, NJ, 08837, https://www.albanycountyfasteners.com. Вы можете отозвать свое согласие на получение электронных писем в любое время, используя ссылку SafeUnsubscribe®, расположенную внизу каждого электронного письма. Электронная почта обслуживается Constant Contact

 Поняття використовується з посиланням на спрямований рух, яке реалізує жива істота, щоб відповісти на стимул, який сприймає. Таксі може бути негативним (коли жива істота віддаляється від джерела стимулу) або позитивним (жива істота наближається до того, що генерує розглянутий стимул). щоб органи
Поняття використовується з посиланням на спрямований рух, яке реалізує жива істота, щоб відповісти на стимул, який сприймає. Таксі може бути негативним (коли жива істота віддаляється від джерела стимулу) або позитивним (жива істота наближається до того, що генерує розглянутий стимул). щоб органи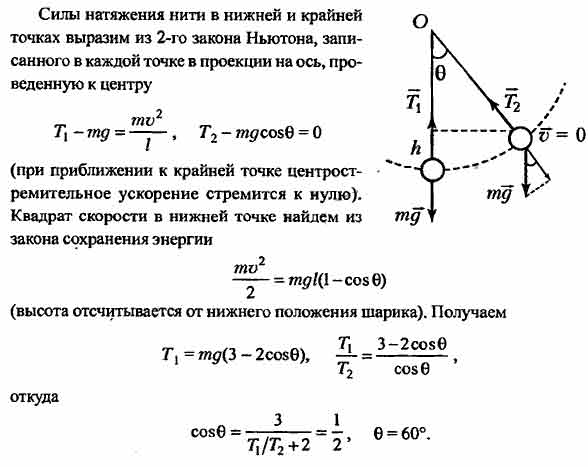
 Це навантаження, що має розмірність сила / довжина, Може бути не тільки власною вагою нитки, припадає на одиницю довжини прольоту, а й вагою льоду або будь-який інший навантаженням, також рівномірно розподіленим. Зроблене припущення про закон розподілу навантаження значно полегшує розрахунок, але робить його разом з тим наближеним; якщо при точному вирішенні (навантаження розподілено вздовж кривої) кривої провисання буде ланцюгова лінія, то в наближеному вирішенні крива провисання виявляється квадратної параболою.
Це навантаження, що має розмірність сила / довжина, Може бути не тільки власною вагою нитки, припадає на одиницю довжини прольоту, а й вагою льоду або будь-який інший навантаженням, також рівномірно розподіленим. Зроблене припущення про закон розподілу навантаження значно полегшує розрахунок, але робить його разом з тим наближеним; якщо при точному вирішенні (навантаження розподілено вздовж кривої) кривої провисання буде ланцюгова лінія, то в наближеному вирішенні крива провисання виявляється квадратної параболою.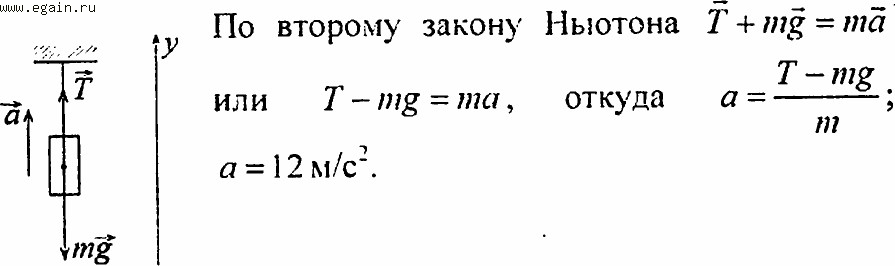 Так як нитка припущена гнучкою, т. Е. Здатної чинити опір лише розтягування, то дія відкинутої частини на решту можливо тільки у вигляді сили, спрямованої по дотичній до кривої провисання нитки в місці розрізу; інший напрямок цієї сили неможливо.
Так як нитка припущена гнучкою, т. Е. Здатної чинити опір лише розтягування, то дія відкинутої частини на решту можливо тільки у вигляді сили, спрямованої по дотичній до кривої провисання нитки в місці розрізу; інший напрямок цієї сили неможливо. 2.Фрагмент вирізаної частини гнучкої нитки
2.Фрагмент вирізаної частини гнучкої нитки При малому провисанні нитки цей кут не досягає великих значень, тому з достатньою для практики ступенем точності можна вважати, що зусилля в нитки постійно і дорівнює її натягу Н. На цю величину зазвичай і ведеться розрахунок міцності нитки. Якщо все ж потрібно вести розрахунок на найбільшу силу у точок підвісу, то для симетричною нитки її величину визначимо наступним шляхом. Вертикальні складові реакцій опор рівні між собою і дорівнюють половині сумарного навантаження на нитку, т. Е.. Горизонтальні складові рівні силі Н, Яка визначається за формулою (3). Повні реакції опор вийдуть як геометричні суми цих складових:
При малому провисанні нитки цей кут не досягає великих значень, тому з достатньою для практики ступенем точності можна вважати, що зусилля в нитки постійно і дорівнює її натягу Н. На цю величину зазвичай і ведеться розрахунок міцності нитки. Якщо все ж потрібно вести розрахунок на найбільшу силу у точок підвісу, то для симетричною нитки її величину визначимо наступним шляхом. Вертикальні складові реакцій опор рівні між собою і дорівнюють половині сумарного навантаження на нитку, т. Е.. Горизонтальні складові рівні силі Н, Яка визначається за формулою (3). Повні реакції опор вийдуть як геометричні суми цих складових: е. величина Fне ввійде в розрахунок.
е. величина Fне ввійде в розрахунок.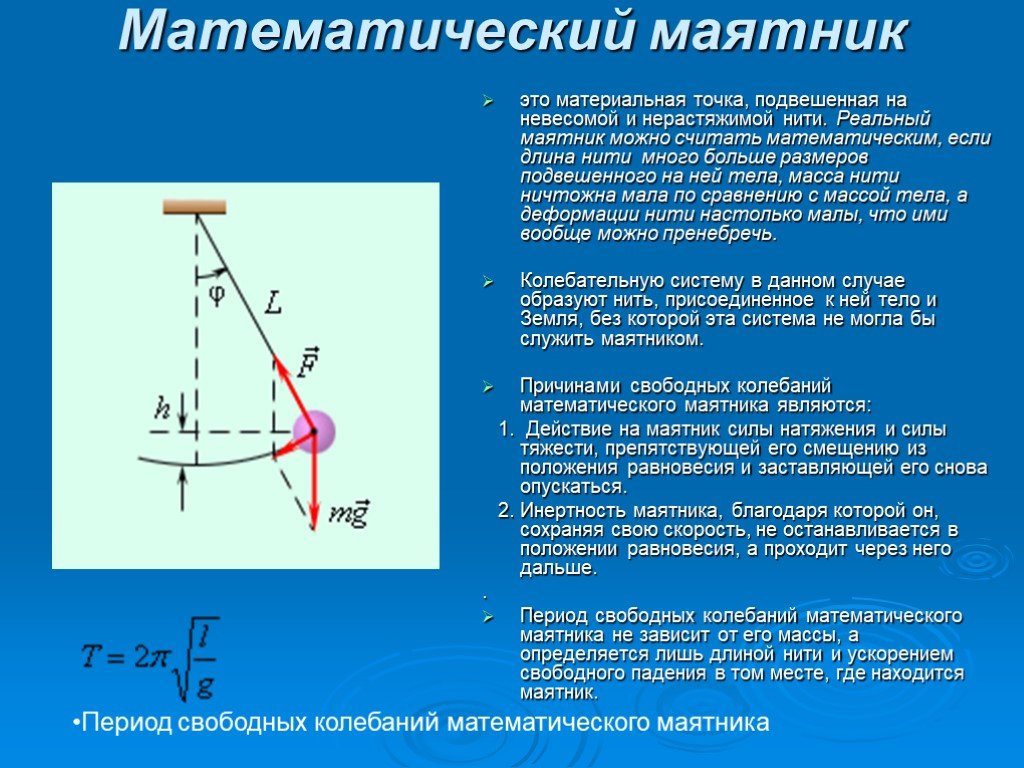 1) і довжиною хорди АВ.
1) і довжиною хорди АВ. При пологах нитках ці припущення дають невелику похибку.
При пологах нитках ці припущення дають невелику похибку. Це означає, що споруди, техніка та інші конструкції зможуть довше зберігати свою цілісність та міцність. Умовно, ці розрахунки та знання можна поділити на 5 основних пунктів, щоб повною мірою зрозуміти, про що йдеться.
Це означає, що споруди, техніка та інші конструкції зможуть довше зберігати свою цілісність та міцність. Умовно, ці розрахунки та знання можна поділити на 5 основних пунктів, щоб повною мірою зрозуміти, про що йдеться. На балці підвішена міцна нитка з вантажем 2 кг. При цьому відсутній вітер, похитування та інші фактори, що так чи інакше впливають на наші розрахунки. Тоді міць натягу дорівнює силі тяжіння. У формулі це можна сказати так: Fн=Fт=м*g, у разі це 9,8*2=19,6 ньютона.
На балці підвішена міцна нитка з вантажем 2 кг. При цьому відсутній вітер, похитування та інші фактори, що так чи інакше впливають на наші розрахунки. Тоді міць натягу дорівнює силі тяжіння. У формулі це можна сказати так: Fн=Fт=м*g, у разі це 9,8*2=19,6 ньютона. Тут потрібне значення означає додаткову міць натягу, v – швидкість обертання підвішеного вантажу, а r – радіус кола, яким обертається вантаж. Останнє значення фактично дорівнює довжині нитки, нехай вона становить 1,7 метра.
Тут потрібне значення означає додаткову міць натягу, v – швидкість обертання підвішеного вантажу, а r – радіус кола, яким обертається вантаж. Останнє значення фактично дорівнює довжині нитки, нехай вона становить 1,7 метра.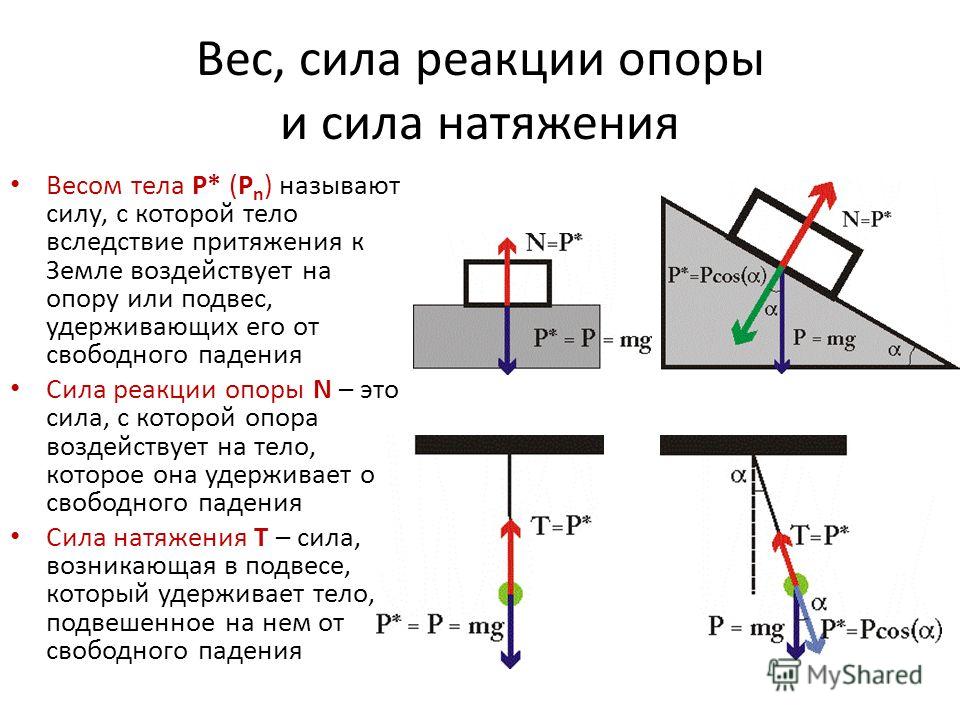 Іншими словами – вантаж стане «легшим», через що ослабне і натяг на мотузку.
Іншими словами – вантаж стане «легшим», через що ослабне і натяг на мотузку. Припустимо, у нас вантаж 2 кг і коефіцієнт тертя дорівнює 0,7 із прискоренням руху 4м/с постійної швидкості. Тепер задіємо всі формули і отримуємо:
Припустимо, у нас вантаж 2 кг і коефіцієнт тертя дорівнює 0,7 із прискоренням руху 4м/с постійної швидкості. Тепер задіємо всі формули і отримуємо: Визначити: 1) залежність s(t), згідно з якою рухається вантаж; 2) силу натягу нитки Т; 3) залежність φ(t), згідно з якою обертається вал; 4) кутову швидкість валу через t = 1 з після початку руху; 5) тангенціальне (а τ) та нормальне (а n) прискорення точок, що знаходяться на поверхні валу.
Визначити: 1) залежність s(t), згідно з якою рухається вантаж; 2) силу натягу нитки Т; 3) залежність φ(t), згідно з якою обертається вал; 4) кутову швидкість валу через t = 1 з після початку руху; 5) тангенціальне (а τ) та нормальне (а n) прискорення точок, що знаходяться на поверхні валу. Чому дорівнює сила натягу нитки, якщо вантаж робить 36 оборотів за одну хвилину.
Чому дорівнює сила натягу нитки, якщо вантаж робить 36 оборотів за одну хвилину.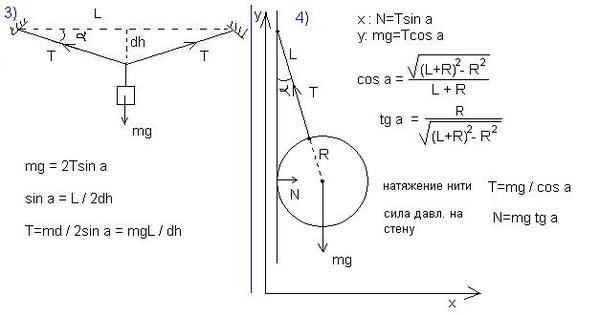
 2.12)
2.12)


 дорівнюватиме подвійному добутку маси на прискорення, так як третій брусок знаходиться на другому і нитка натягу повинна вже рухати два бруски. У такому разі ставлення до дорівнює 2. Правильна відповідь — перша.
дорівнюватиме подвійному добутку маси на прискорення, так як третій брусок знаходиться на другому і нитка натягу повинна вже рухати два бруски. У такому разі ставлення до дорівнює 2. Правильна відповідь — перша.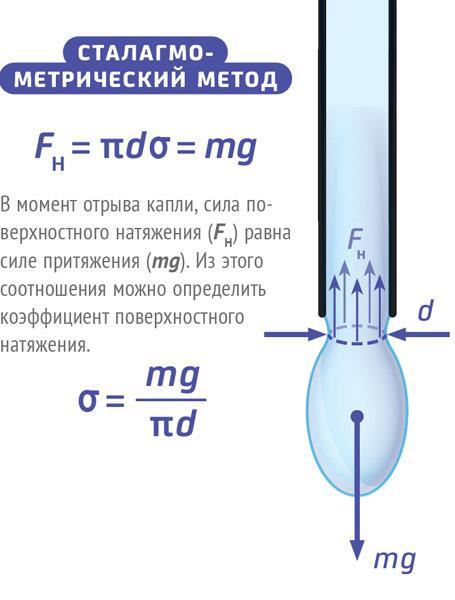 До другого кінця нитки підвішено вантаж масою 0,5 кг (рис. 6). Визначити прискорення, з яким рухається брусок, якщо коефіцієнт тертя бруска об стіл становить 0,35.
До другого кінця нитки підвішено вантаж масою 0,5 кг (рис. 6). Визначити прискорення, з яким рухається брусок, якщо коефіцієнт тертя бруска об стіл становить 0,35. Примушує рухатися цю систему сила тяжіння другого тіла, але заважає руху сила тертя бруска об стіл, у разі:
Примушує рухатися цю систему сила тяжіння другого тіла, але заважає руху сила тертя бруска об стіл, у разі: Але між собою ці сили натягу дорівнюють, становлять вони між собою прямий кут, тому при складанні цих сил виходить квадрат замість звичайного паралелограма. Шукана сила F д є діагоналлю квадрата. Ми бачимо, що для результату нам необхідно знайти силу натягу нитки. Проведемо аналіз: у який бік рухається система із двох зв’язаних брусків? Більш масивний брусок, природно, перетягне легший, брусок 1 зісковзуватиме вниз, а брусок 2 рухатиметься вгору по схилу, тоді рівняння другого закону Ньютона для кожного з брусків виглядатиме:
Але між собою ці сили натягу дорівнюють, становлять вони між собою прямий кут, тому при складанні цих сил виходить квадрат замість звичайного паралелограма. Шукана сила F д є діагоналлю квадрата. Ми бачимо, що для результату нам необхідно знайти силу натягу нитки. Проведемо аналіз: у який бік рухається система із двох зв’язаних брусків? Більш масивний брусок, природно, перетягне легший, брусок 1 зісковзуватиме вниз, а брусок 2 рухатиметься вгору по схилу, тоді рівняння другого закону Ньютона для кожного з брусків виглядатиме: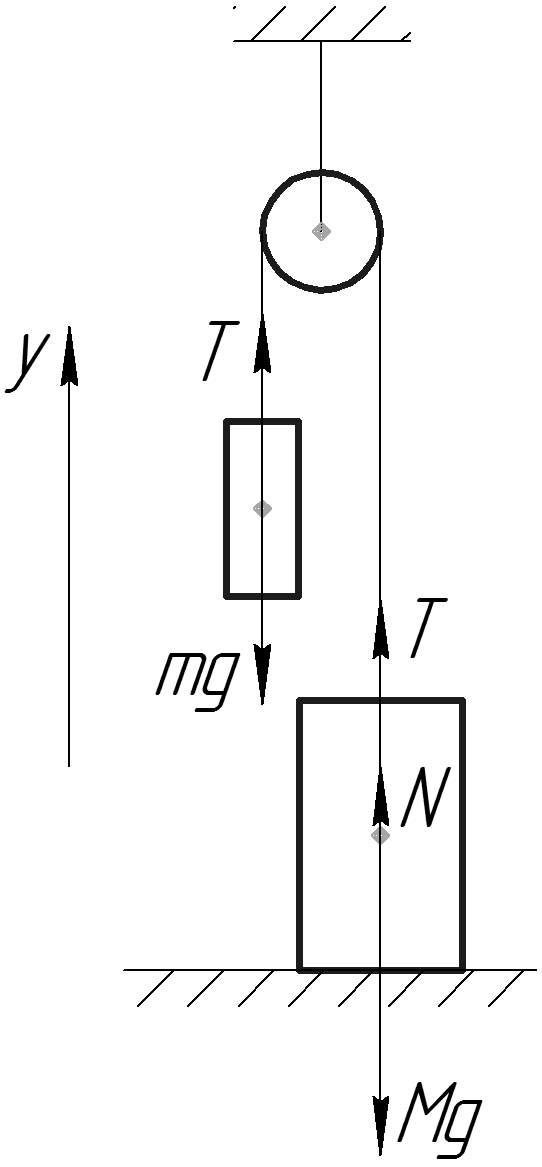
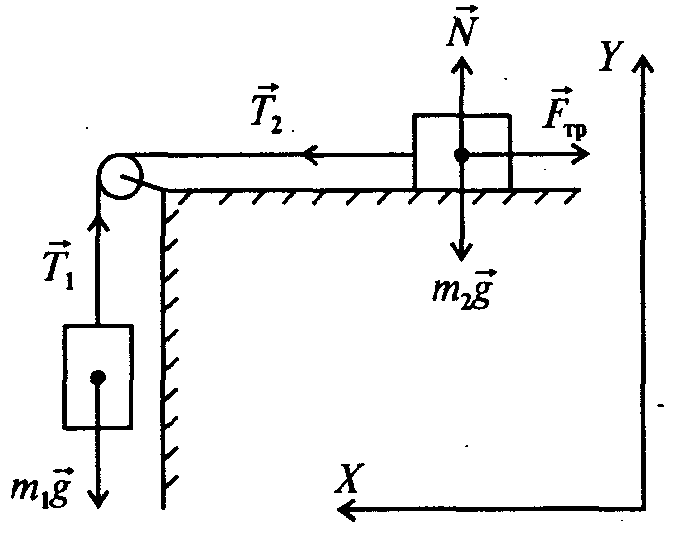 Також згадані інші сили, які будуть розглянуті в інших розділах.
Також згадані інші сили, які будуть розглянуті в інших розділах. Ця сила називається реакцією опори. Назва сили «каже» реагує опора. Ця сила виникає завжди, коли вплив на опору. Природа її виникнення молекулярному рівні. Предмет хіба що деформував звичне становище і зв’язку молекул (всередині столу), вони, своєю чергою, прагнуть повернутися у своє початкове стан, » пручаються » .
Ця сила називається реакцією опори. Назва сили «каже» реагує опора. Ця сила виникає завжди, коли вплив на опору. Природа її виникнення молекулярному рівні. Предмет хіба що деформував звичне становище і зв’язку молекул (всередині столу), вони, своєю чергою, прагнуть повернутися у своє початкове стан, » пручаються » . Коли стискаємо пружину – зменшуємо. Коли перекручуємо чи зрушуємо. У всіх цих прикладах виникає сила, яка перешкоджає деформації – сила пружності.
Коли стискаємо пружину – зменшуємо. Коли перекручуємо чи зрушуємо. У всіх цих прикладах виникає сила, яка перешкоджає деформації – сила пружності.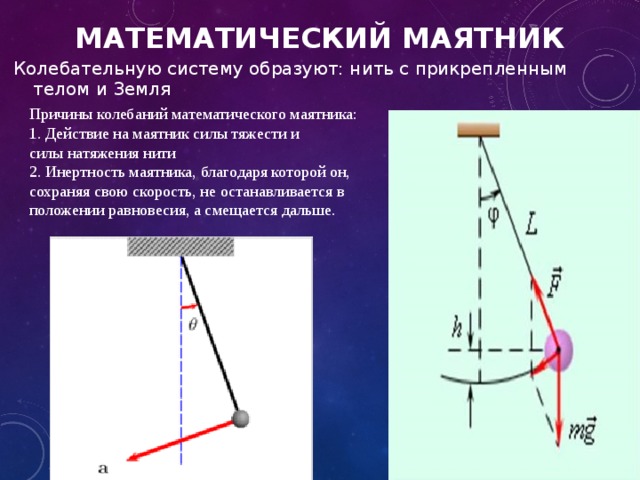 Сила тяжкості — сила, що виникає внаслідок взаємодії із Землею. Вага – результат взаємодії з опорою. Сила тяжіння прикладена у центрі тяжкості предмета, вага — сила, яка прикладена на опору (не предмет)!
Сила тяжкості — сила, що виникає внаслідок взаємодії із Землею. Вага – результат взаємодії з опорою. Сила тяжіння прикладена у центрі тяжкості предмета, вага — сила, яка прикладена на опору (не предмет)!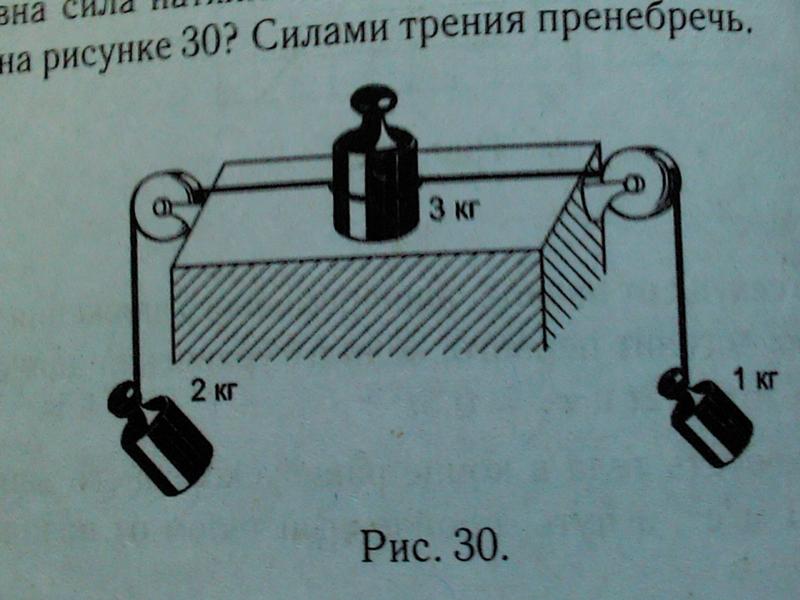
 Тому на схемах різні точки застосування переносять в одну точку — в центр, а тіло зображують схематично кругом або прямокутником.
Тому на схемах різні точки застосування переносять в одну точку — в центр, а тіло зображують схематично кругом або прямокутником. При невеликих швидкостях руху сила опору пропорційна швидкості тіла
При невеликих швидкостях руху сила опору пропорційна швидкості тіла
 Причина, по которой этот метод не принимается с готовностью, заключается в том, что крутящий момент будет напрямую зависеть от материала, против которого он вращается. Более грубый материал будет создавать большее трение, что повысит значение крутящего момента при одновременном снижении предварительного натяжения. Обратное тоже верно. Вы можете достичь оптимального крутящего момента, не достигая оптимальной предварительной нагрузки (и наоборот). В конце концов, это зависит от материала, поэтому этот метод не является точным, но является приличным предположением.
Причина, по которой этот метод не принимается с готовностью, заключается в том, что крутящий момент будет напрямую зависеть от материала, против которого он вращается. Более грубый материал будет создавать большее трение, что повысит значение крутящего момента при одновременном снижении предварительного натяжения. Обратное тоже верно. Вы можете достичь оптимального крутящего момента, не достигая оптимальной предварительной нагрузки (и наоборот). В конце концов, это зависит от материала, поэтому этот метод не является точным, но является приличным предположением.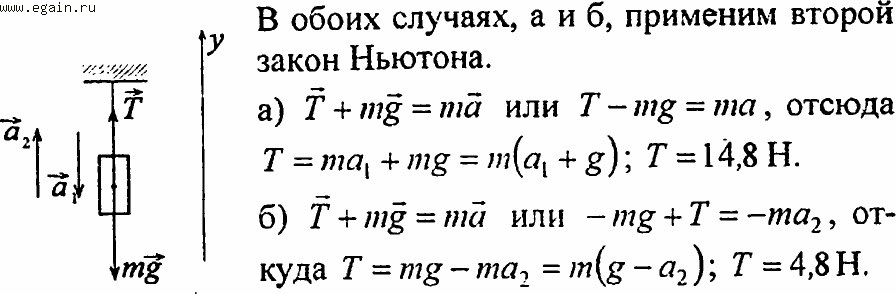
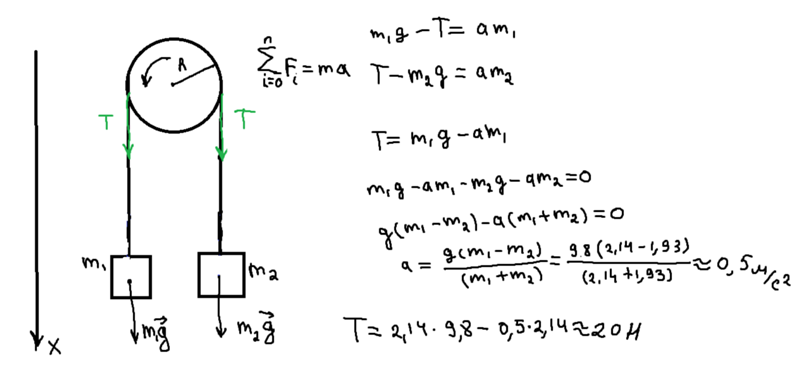 Например, рекомендация 90 градусов будет выглядеть следующим образом: Накрутите гайку на сборку до плотного прилегания к материалу. Присоедините гаечный ключ к гайке и поверните ее на четверть оборота (90 градусов). Этот метод даст вам близкую к точной предварительную нагрузку.
Например, рекомендация 90 градусов будет выглядеть следующим образом: Накрутите гайку на сборку до плотного прилегания к материалу. Присоедините гаечный ключ к гайке и поверните ее на четверть оборота (90 градусов). Этот метод даст вам близкую к точной предварительную нагрузку. Требование предварительной загрузки
Диаграммы — это способ графического отображения результатов совместной работы.
Анализ в ясной и понятной форме.
Требование предварительной загрузки
Диаграммы — это способ графического отображения результатов совместной работы.
Анализ в ясной и понятной форме. Перегрузка болта нехарактерна.
Если предварительная нагрузка, обеспечиваемая болтом, недостаточна, разъединение стыка
и перемещение может привести к возможной усталости болта и
проблемы с самоосвобождением. Чтобы таких проблем не было
очень важно, чтобы была достаточная остаточная сила зажима, действующая
на объединенном интерфейсе после учета эффектов
приложенные силы и потери вложения. Таблица требований к предварительной загрузке
графически иллюстрирует этот момент, когда он смотрит на силы
действует на совместный интерфейс. Такая диаграмма показана ниже для
вышеуказанный сустав.
Перегрузка болта нехарактерна.
Если предварительная нагрузка, обеспечиваемая болтом, недостаточна, разъединение стыка
и перемещение может привести к возможной усталости болта и
проблемы с самоосвобождением. Чтобы таких проблем не было
очень важно, чтобы была достаточная остаточная сила зажима, действующая
на объединенном интерфейсе после учета эффектов
приложенные силы и потери вложения. Таблица требований к предварительной загрузке
графически иллюстрирует этот момент, когда он смотрит на силы
действует на совместный интерфейс. Такая диаграмма показана ниже для
вышеуказанный сустав. Заделка приводит к потере силы зажима, действующей
на суставе. Если можно установить жесткость соединения и болта,
количество этой потери силы может быть определено количественно, если поверхность
определяется шероховатость контактных поверхностей. На приведенном выше графике
ожидается потеря 10 кН. Большие потери при встраивании
может возникать в суставах с коротким хватом, состоящим из многих
интерфейсы.
Требование к осевой силе: в
соединение с предварительным натягом, большая часть приложенной осевой нагрузки снижается
усилие зажима на интерфейсе сустава, а не увеличение
нагрузка в болте (см. предыдущий урок
для объяснения). Величина осевой нагрузки, которая разгружает
интерфейс соединения можно определить по жесткости соединения/болта
расчеты.
Заделка приводит к потере силы зажима, действующей
на суставе. Если можно установить жесткость соединения и болта,
количество этой потери силы может быть определено количественно, если поверхность
определяется шероховатость контактных поверхностей. На приведенном выше графике
ожидается потеря 10 кН. Большие потери при встраивании
может возникать в суставах с коротким хватом, состоящим из многих
интерфейсы.
Требование к осевой силе: в
соединение с предварительным натягом, большая часть приложенной осевой нагрузки снижается
усилие зажима на интерфейсе сустава, а не увеличение
нагрузка в болте (см. предыдущий урок
для объяснения). Величина осевой нагрузки, которая разгружает
интерфейс соединения можно определить по жесткости соединения/болта
расчеты. В этом примере из приложенной силы 15 кН 13,8
кН снижает усилие зажима на границе раздела (оставшиеся 1,2
кН увеличивает нагрузку на болт). Для упрощения при ручных расчетах
завершаются, часто применяется консервативное предположение
что вся приложенная осевая нагрузка уменьшает усилие зажима на
совместный интерфейс.
Требование к сдвигающей силе: большинство
соединений в машиностроении используют сквозные отверстия и
любая сдвигающая нагрузка передается фрикционным сцеплением. Это
сила зажима на поверхности соединения создает силу трения
который сопротивляется любой приложенной сдвигающей нагрузке. На таких шарнирах, если проскальзывает
предотвращается, болты не воспринимают напрямую срезающую нагрузку,
однако они должны обеспечивать достаточную силу зажима, чтобы предотвратить
совместное движение.
В этом примере из приложенной силы 15 кН 13,8
кН снижает усилие зажима на границе раздела (оставшиеся 1,2
кН увеличивает нагрузку на болт). Для упрощения при ручных расчетах
завершаются, часто применяется консервативное предположение
что вся приложенная осевая нагрузка уменьшает усилие зажима на
совместный интерфейс.
Требование к сдвигающей силе: большинство
соединений в машиностроении используют сквозные отверстия и
любая сдвигающая нагрузка передается фрикционным сцеплением. Это
сила зажима на поверхности соединения создает силу трения
который сопротивляется любой приложенной сдвигающей нагрузке. На таких шарнирах, если проскальзывает
предотвращается, болты не воспринимают напрямую срезающую нагрузку,
однако они должны обеспечивать достаточную силу зажима, чтобы предотвратить
совместное движение.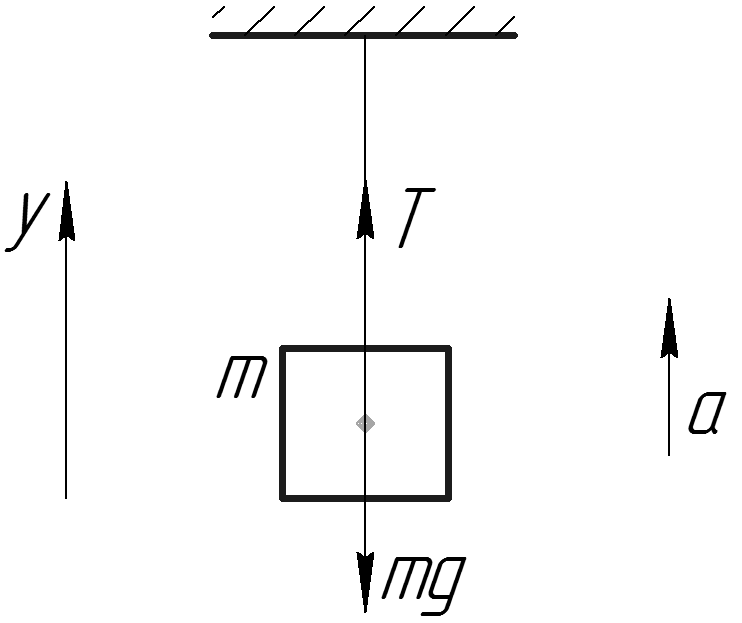 Для этого необходимо усилие смыкания
сила сдвига, деленная на имеющийся коэффициент трения
между суставными поверхностями (для единственной плоскости сдвига, присутствующей
в суставе, показанном выше). Так как коэффициент трения
обычно значительно меньше 1, это требование приводит к
требуется значительно большее усилие смыкания, чем
величина поперечной силы. В этом примере приложенный сдвиг
составляет 4 кН, что, если принять коэффициент трения 0,2
между соединительными пластинами, приводит к минимальной силе зажима
20 кН (т.е. 4/0,2).
Общие требования к предварительной загрузке: это
представляет собой минимальную предварительную нагрузку, которую должен обеспечить
болт. Это сумма убытков от внедрения, сумма
приложенная осевая сила, уменьшающая усилие зажима на суставе
и сила зажима, необходимая для предотвращения проскальзывания соединения
из-за сдвиговой нагрузки.
Для этого необходимо усилие смыкания
сила сдвига, деленная на имеющийся коэффициент трения
между суставными поверхностями (для единственной плоскости сдвига, присутствующей
в суставе, показанном выше). Так как коэффициент трения
обычно значительно меньше 1, это требование приводит к
требуется значительно большее усилие смыкания, чем
величина поперечной силы. В этом примере приложенный сдвиг
составляет 4 кН, что, если принять коэффициент трения 0,2
между соединительными пластинами, приводит к минимальной силе зажима
20 кН (т.е. 4/0,2).
Общие требования к предварительной загрузке: это
представляет собой минимальную предварительную нагрузку, которую должен обеспечить
болт. Это сумма убытков от внедрения, сумма
приложенная осевая сила, уменьшающая усилие зажима на суставе
и сила зажима, необходимая для предотвращения проскальзывания соединения
из-за сдвиговой нагрузки.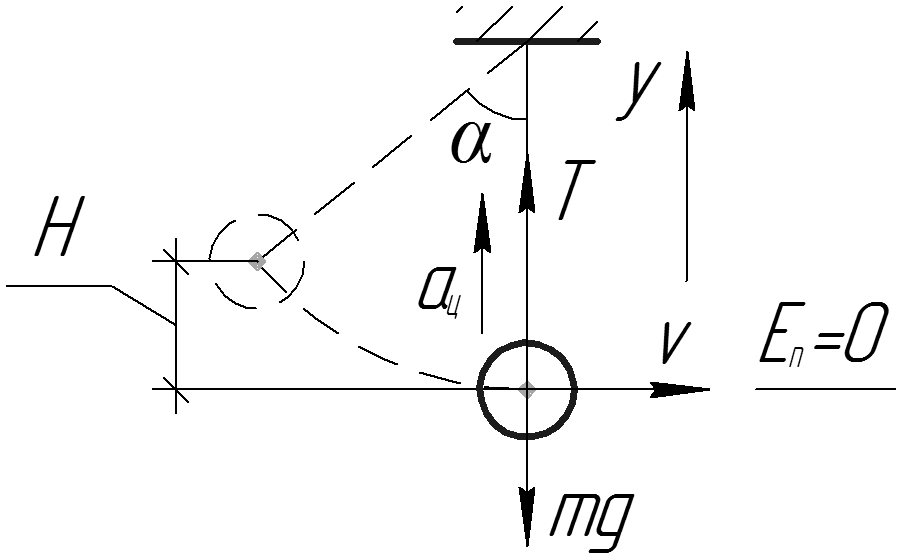 Вариант предварительной нагрузки: в идеале
мире предварительная нагрузка, обеспечиваемая болтом, была бы известна
точное значение и будет одинаковым для каждого затянутого болта.
К сожалению, не существует дешевого способа затягивания болта.
и точно зная значение предварительной нагрузки. Такие методы, как
затяжка болта до определенного значения крутящего момента приводит к изменению
в преднатяге между, видимо, одинаковыми болтами. Это
из-за невозможности приложить крутящий момент к одному и тому же
каждый раз точное значение, изменение допусков отверстий и болтов
но что более важно, изменение коэффициента трения
присутствует в резьбе и под поверхностью гайки/болта. Проектировать
сустав успешно этот разброс в предварительной нагрузке должен быть взят
в учетную запись.
Вариант предварительной нагрузки: в идеале
мире предварительная нагрузка, обеспечиваемая болтом, была бы известна
точное значение и будет одинаковым для каждого затянутого болта.
К сожалению, не существует дешевого способа затягивания болта.
и точно зная значение предварительной нагрузки. Такие методы, как
затяжка болта до определенного значения крутящего момента приводит к изменению
в преднатяге между, видимо, одинаковыми болтами. Это
из-за невозможности приложить крутящий момент к одному и тому же
каждый раз точное значение, изменение допусков отверстий и болтов
но что более важно, изменение коэффициента трения
присутствует в резьбе и под поверхностью гайки/болта. Проектировать
сустав успешно этот разброс в предварительной нагрузке должен быть взят
в учетную запись.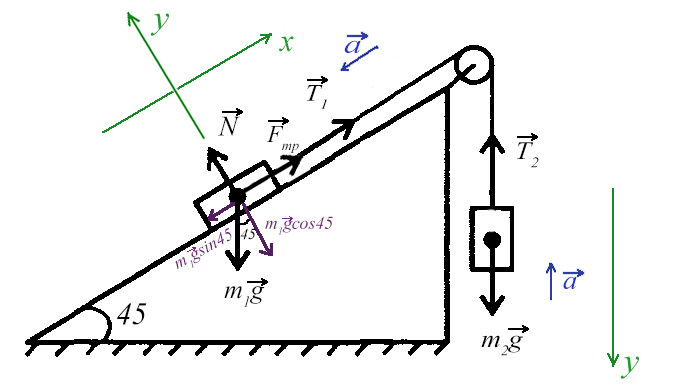 Это можно сделать несколькими способами, но обычно
либо путем определения минимальных/максимальных преднагрузок по знаниям
изменения трения или с помощью коэффициента затяжки.
Это можно сделать несколькими способами, но обычно
либо путем определения минимальных/максимальных преднагрузок по знаниям
изменения трения или с помощью коэффициента затяжки. д.) показано ниже
это диаграмма для изменения метода затяжки на крутящий момент и
угол. Если применить правильно. этот метод последовательно обеспечивает
высокое значение предварительной нагрузки.
д.) показано ниже
это диаграмма для изменения метода затяжки на крутящий момент и
угол. Если применить правильно. этот метод последовательно обеспечивает
высокое значение предварительной нагрузки.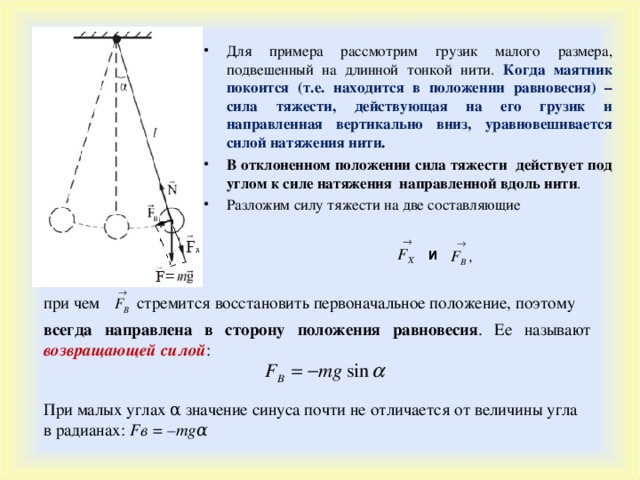
Leave A Comment