{ – 19}}\;Кл\]

Интересно, что заряд частицы равен по модулю двум зарядам электрона \(2e\).

Ответ: 2e.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

8.2.9 Протон описал окружность радиусом 5 см в однородном магнитном поле с индукцией 20 мТл
8.2.11 Электрон движется в однородном магнитном поле с индукцией 0,1 Тл по окружности
8.2.12 Протон движется в однородном магнитном поле с индукцией 1 Тл со скоростью 200000 км/с

Движение заряженных частиц в однородном магнитном поле

Рассмотрим частицу массы m, имеющую положительный заряд q и движущуюся в однородном магнитном поле В. Под однородным магнитным полем мы понимаем поле, величина и направление которого постоянны во всем объеме, в котором движется частица. Мы ввели одно неявное упрощение. Нас не интересует вопрос, какое распределение токов вызывает заданное распределение поля. (Практически однородное поле может быть получено внутри соленоида. ) Мы просто полагаем, что с помощью какой-то токовой системы нам удалось создать такое поле. В этом состоит одно из упрощений, обусловленных введением понятия поля. В результате все расчеты четко разделяются на два этапа.

На первом этапе вычисляется поле по заданному распределению токов.

На втором этапе рассчитывается сила, а затем движение частицы, исходя из заданного распределения поля. Мы предполагаем, что каким-то образом нам удалось в некоторой области пространства создать однородное магнитное поле. Далее мы предполагаем, что в этой области электрическое поле отсутствует (вблизи нет не скомпенсированных зарядов). Тогда сила, испытываемая заряженной частицей в таком однородном магнитном поле, определяется вторым членом в формуле Лоренца:

Величина вектора [v x В] в случае, когда v не перпендикулярен В, равна vBsinθ, где θ — угол между векторами v и В (фиг. 317, а).

Сила Лоренца обращается в нуль, если синус угла между скоростью частицы и магнитным полем равен нулю.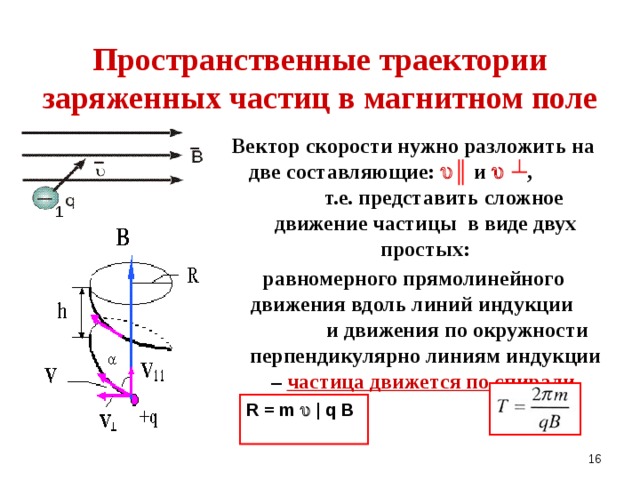 Это происходит, когда частица движется параллельно или антипараллельно направлению поля (фиг. 317, б). Если скорость и магнитное поле заданы, то сила максимальна, когда sinθ = 1, т. е. когда v перпендикулен В, как на фиг. 318; в этом случае:

Рассматривая частный случай, когда заряженная частица движется перпендикулярно направлению поля (фиг. 319), мы по существу ничего не теряем, но зато все наши вычисления упрощаются. В этом случае величина силы, действующей на движущуюся в магнитном поле положительно заряженную частицу1), равна:

а направлена она всегда перпендикулярно скорости, как на фиг. 319. Не проводя никаких вычислений, мы можем сразу же сделать несколько важных качественных выводов, касающихся действия такой силы на заряженную частицу.

1) Если частица заряжена отрицательно, величина силы остается такой же, а ее направление изменяется на противоположное.

Сначала рассмотрим следствие из того утверждения, которое мы повторили несколько раз: сила всегда остается перпендикулярной скорости, даже если скорость непрерывно изменяет свое направление.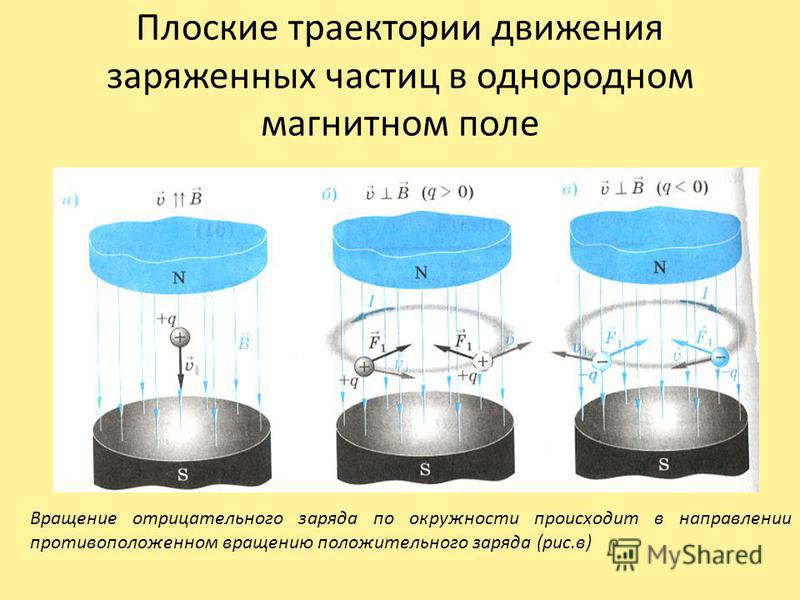 Из определения работы следует, что такая сила не совершает над частицей работы, поэтому кинетическая энергия частицы сохраняется. А, следовательно, мы можем заключить, что в отсутствие других сил скорость частицы, движущейся в магнитном поле, не изменяется. Удивительно, но факт! Тем не менее сила действует и вызывает ускорение тела. Это ускорение изменяет направление движения заряженной частицы, но не ее скорость. При таких условиях заряженная частица будет двигаться по окружности. Мы знаем, что при движении частицы по окружности ее ускорение записывается особенно просто: α=v2/R. В результате получим:

F = ma,

Отсюда

или

Отсюда видно, что, зная величину магнитного поля (его можно либо вычислить по известному распределению внешнего тока, возбуждающего поле, либо измерить с помощью различных приборов, причем, как правило, для его определения используют оба эти метода), заряд летящей частицы и радиус ее траектории, можно определить ее массу.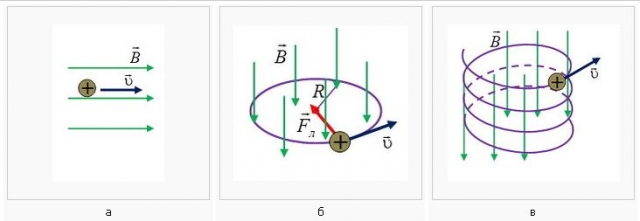

Пример. Частица движется по окружности радиусом R=5,65 см в однородном магнитном поле B=10 Гс со скоростью ν=109 см/с (фиг. 320). Чему равно отношение заряда частицы к ее массе, q/m?

Из уравнения (20.27) имеем:

Это число представляет определенный интерес, так как оно характеризует отношение заряда к массе в случае электрона (как мы увидим позже, это отношение впервые нашел Дж. Дж. Томсон).

НВидимый след образован пузырьками, возникающими в жидком водороде при прохождении заряженной частицы. Если бы заряд частицы изменил знак, а все остальное осталось бы прежним, частица начала бы «раскручиваться» в другую сторону, так как сила изменила бы свое направление. Такие траектории (треки) постоянно наблюдаются на фотографиях, полученных в пузырьковых камерах или камерах Вильсона при изучении элементарных частиц.

Метки: величина векторазарядызаряженные частицымагнитное полемассаоднородное магнитное полеположительный зарядсила Лоренцасинус углаТомсонформула Лоренца

электромагнетизм — Формула радиуса окружности пути заряженной частицы в однородном магнитном поле

спросил

Изменено 1 год, 9 месяцев назад

Просмотрено 60 тысяч раз

$\begingroup$

Заряженная частица $q$ входит в однородное магнитное поле $\vec{B}$ со скоростью $\vec{v}$, образуя с ним угол $\theta$. Поскольку сила Лоренца перпендикулярна скорости, частица будет двигаться по круговой траектории радиуса $r$, что 92}{r}=qvB \sin\theta$$ $$r=\frac{mv\sin\theta}{qB}.$$

Это должно быть потому, что мы учитываем только перпендикулярную составляющую скорости, когда вычисляем магнитную силу, и, следовательно, скорость, к которой перпендикулярна сила, является составляющая скорости, перпендикулярная $\vec{B}$, а не $\vec{v}$.

Какая формула правильная?

  • электромагнетизм
  • магнитные поля

$\endgroup$

$\begingroup$

Ваш вывод верен, и ваша книга неверна, если только $v$ в их уравнении не является составляющей скорости, перпендикулярной магнитному полю?
На приведенной ниже диаграмме предполагается положительный заряд.

Радиус кругового движения определяется уравнением $r=\dfrac{mv\sin\theta}{qB}$, а шаг спирали $p = \dfrac{2\pi mv\cos \тета}{qB}$

$\endgroup$

5

$\begingroup$

Легко видеть, что книжный ответ r = mv/qBsin θ верен.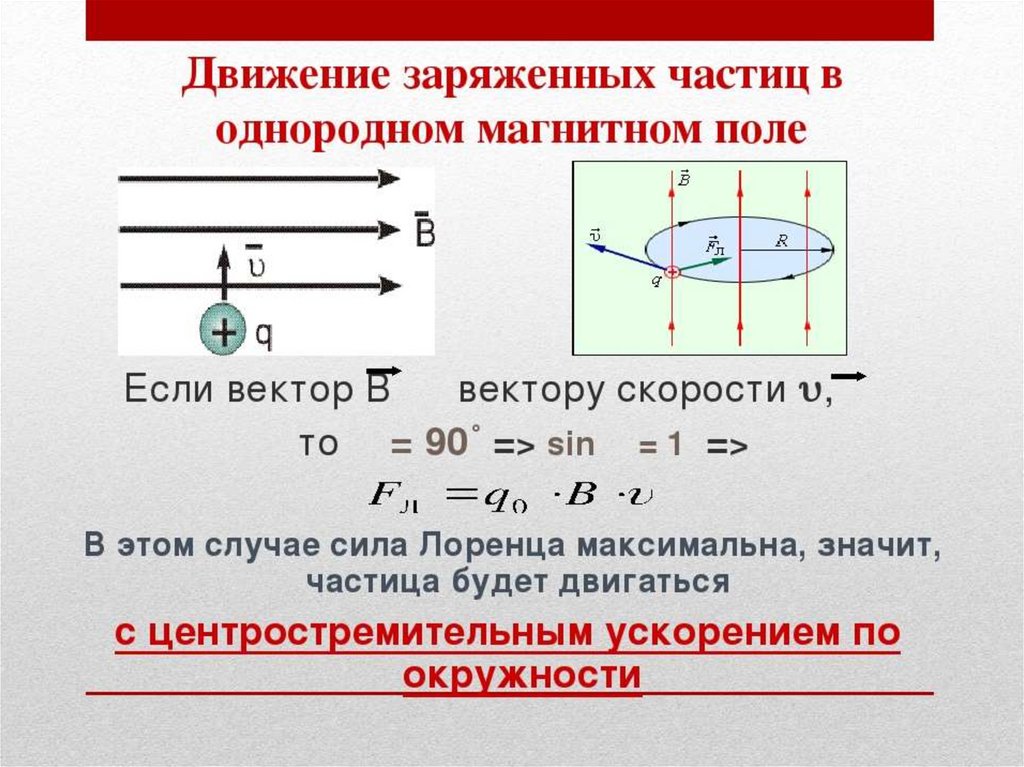

Спросите себя, что происходит с радиусом, когда сила магнитного поля уменьшается. Поскольку составляющая магнитного поля, воздействующая на заряд, меньше 1,0 для любого θ меньше 90 градусов, формула книги правильно описывает, что происходит для углов, отличных от 90 градусов.

Ошибка при умножении скорости на sin θ, а не на магнитное поле, заключается в том, что вы рассматриваете только ту составляющую скорости, которая перпендикулярна полю. Вы ошибочно проигнорировали влияние общей скорости на окружность круга.

Также коэффициент sin θ применяется только к силе, действующей на заряд, движущийся перпендикулярно магнитному полю. Это не относится к силе, необходимой для изменения направления движущейся массы, которая имеет заряд.

$\endgroup$

1

$\begingroup$

.это ответ на вопрос

$\endgroup$

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

AP Физика 2 Справка

  • Войти
  • Биографии репетитора
  • Подготовка к тесту
    СРЕДНЯЯ ШКОЛА
    • ACT Репетиторство
    • SAT Репетиторство
    • Репетиторство PSAT
    • ASPIRE Репетиторство
    • ШСАТ Репетиторство
    • Репетиторство STAAR
    ВЫСШАЯ ШКОЛА
    • Репетиторство MCAT
    • Репетиторство GRE
    • Репетиторство по LSAT
    • Репетиторство по GMAT
    К-8
    • Репетиторство AIMS
    • Репетиторство по HSPT
    • Репетиторство ISEE
    • Репетиторство ISAT
    • Репетиторство по SSAT
    • Репетиторство STAAR
    Поиск 50+ тестов
  • Академическое обучение
    репетиторство по математике
    • Алгебра
    • Исчисление
    • Элементарная математика
    • Геометрия
    • Предварительный расчет
    • Статистика
    • Тригонометрия
    репетиторство по естественным наукам
    • Анатомия
    • Биология
    • Химия
    • Физика
    • Физиология
    иностранные языки
    • французский
    • Немецкий
    • Латинский
    • Китайский мандарин
    • Испанский
    начальное обучение
    • Чтение
    • Акустика
    • Элементарная математика
    прочее
    • Бухгалтерский учет
    • Информатика
    • Экономика
    • Английский
    • Финансы
    • История
    • Письмо
    • Лето
    Поиск по 350+ темам
  • О
    • Обзор видео
    • Процесс выбора наставника
    • Онлайн-репетиторство
    • Мобильное обучение
    • Мгновенное обучение
    • Как мы работаем
    • Наша гарантия
    • Влияние репетиторства
    • Обзоры и отзывы
    • Освещение в СМИ
    • О преподавателях университета

Звоните прямо сейчас, чтобы записаться на обучение:

(888) 888-0446

Учащиеся, нуждающиеся в помощи по AP Physics 2, получат большую пользу от нашей интерактивной программы.

Мы разбираем все ключевые элементы, чтобы вы могли получить адекватную помощь по AP Physics 2. Имея под рукой обязательные концепции обучения и актуальные практические вопросы, AP Physics 2 поможет вам в кратчайшие сроки. Получите помощь сегодня с нашей обширной коллекцией важной информации AP Physics 2.

  • AP Физика 2

  • Электричество и магнетизм

  • Схемы

  • Компоненты схемы

  • Конденсатор Энергия

  • Конденсаторы и емкость

  • Конденсаторы и электрические поля

  • Свойства конденсаторов и диэлектриков

  • Резисторы и сопротивление

  • Свойства цепи

  • Питание цепи

  • Ток и напряжение

  • Закон Ома

  • Другие принципы схемы

  • Удельное сопротивление

  • Понимание принципиальных схем постоянного тока

  • Понимание принципиальных схем RC

  • Электростатика

  • Распределение заряда

  • Электрические поля

  • Электрическая сила между точечными зарядами

  • Электрическая сила в электрическом поле

  • Электрическая потенциальная энергия

  • Закон Гаусса

  • Другие электростатические концепции

  • Баллы

  • Магнетизм и электромагнетизм

  • Электродвижущая сила и магнитный поток

  • Индукция

  • Магнитные поля

  • Магнитная сила

  • Другие концепции магнетизма

  • Правило правой руки для заряда в магнитном поле

  • Правило правой руки для токоведущего провода

  • Соленоиды

  • Жидкости

  • Гидродинамика

  • Уравнение Бернулли

  • Расход

  • Другое гидродинамика

  • Поток Пуазейля

  • Турбулентность

  • Статика жидкости

  • Принцип Архимеда

  • Выталкивающая сила

  • Плотность и удельный вес

  • Давление

  • Оптика

  • Показатель преломления

  • Линзы

  • Увеличение

  • Зеркала

  • Другие принципы оптики

  • Закон Снелла

  • Уравнение тонкой линзы

  • Полное внутреннее отражение

  • Квантовая и ядерная физика

  • Атомная и ядерная физика

  • Атомные модели

  • Уровни энергии электрона

  • Слияние и деление

  • Ядерные силы и взаимодействия

  • Другие принципы ядерной физики

  • Радиоактивный ядерный распад

  • Субатомные частицы

  • Основы квантовой механики

  • Электромагнитный спектр и излучение

  • Массово-энергетический эквивалент

  • Другие принципы квантовой механики

  • Фотоны и фотонная энергия

  • Принципы общей теории относительности

  • Принципы специальной теории относительности

  • Термодинамика

  • Теплопередача и тепловое равновесие

  • Закон идеального газа

  • Кинетическая молекулярная теория

  • Законы термодинамики

  • Другие концепции термодинамики

  • Свойства идеальных газов

  • Работа, энтальпия и внутренняя энергия

  • Волны

  • Эффект Доплера

  • Другие концепты Wave

  • Представление волн как функций синуса и косинуса

  • Щелевые эксперименты

  • Интерференция волн и дифракция

Создание собственного плана проверки теста AP Physics 2 может занять много времени. Часто время, необходимое для создания учебного пособия, может отнять время, которое можно было бы потратить с большей пользой на изучение материала. Если вы только начинаете подготовку, рассмотрите возможность использования ресурса Varsity Tutors Learning Tools Learn by Concept. Learn by Concept представлен в виде интерактивной программы. Когда вы получите доступ к ресурсу AP Physics Learn by Concept, вы обнаружите, что он выходит далеко за рамки того, что вы ожидаете найти в обычном учебном пособии. Нужна ли вам репетиторство по физике в Вирджиния-Бич, репетиторство по физике в Индианаполисе или репетиторство по физике в Силиконовой долине, работа один на один с экспертом может стать именно тем стимулом, в котором нуждается ваша учеба.

Одним из наиболее полезных аспектов Learn by Concept является включение примеров вопросов, ответов и пояснений AP Physics 2. Результатом является упражнение, основанное на вопросах для каждой категории и подкатегории, с которыми вы столкнетесь во время обзора AP Physics. Вы можете просмотреть все темы, затронутые в «Учись по концепции», пытаясь ответить на каждый вопрос, и вы можете сравнить свой ответ с пояснениями, которые сопровождают каждый из примеров вопросов, чтобы еще больше усилить глубину вашей подготовки. Varsity Tutors предлагает ресурсы, такие как бесплатные практические тесты AP Physics 2, которые помогут вам в самостоятельном обучении, или вы можете подумать о репетиторах AP Physics 2 .

Learn by Concept предоставляет вам возможность более глубокого изучения каждой концепции. Например, в категории AP Physics 2 Learn by Concept «Закон Ома» вы найдете вопросы по закону Ома с несколькими вариантами ответов. После того, как вы выберете один из ответов, вам будет показан правильный ответ, сопровождаемый подробным объяснением того, почему этот ответ является правильным. Даже если вы неправильно ответите на первый примерный вопрос AP Physics 2, у вас будет много шансов глубже вникнуть в рассматриваемую концепцию. Интерактивность ресурса Learn by Concept предоставляет вам четкую, краткую и бесплатную практику. В дополнение к справочному разделу AP Physics 2 и репетиторству по AP Physics 2 вы также можете рассмотреть некоторые из наших карточек AP Physics 2 Flashcards.

Еще одним полезным аспектом Learn by Concept является его портативность. Поскольку средство обучения полностью находится в сети, вы сможете использовать ресурс «Учись по концепции» везде, где есть доступ к Интернету. Чтобы сделать просмотр еще более удобным, вы можете загрузить приложение Varsity Tutors’ Learning Tools на свое мобильное устройство или планшет. Это дает вам доступ к бесплатной практике AP Physics 2 в любое время, когда вы готовы повторить.

Некоторые из основных понятий, которые вы можете найти в ресурсе Learn by Concept для AP Physics 2, включают:

— Электричество и магнетизм

— Жидкости

— Квантовая и ядерная физика

— Термодинамика

— Волны

— И многие другие.

Когда вы почувствуете, что хорошо разбираетесь в концепциях AP Physics, охватываемых Learn by Concept, вы можете ознакомиться с некоторыми другими бесплатными учебными материалами, доступными через Учебные инструменты Varsity Tutors.