на рис 8 показаны графики движения точечного тела, движущейся по плоскости XY. Запишите законы движения x(t) и y(t) в аналитическом виде.Определите начальные координаты тела,а также их значения для моментов времени t=0,2 с и 0,4 с.Получите уравнение траектории y(x). Постройте траекторию на плоскости XY.
Последние вопросы
Математика
2 минуты назад
Разделите числа в данном отношении. а) 48 в отношении 3 : 5 d) 50 в отношении 4 : 1 g) 90 в отношении 4 : 5 b) 100 в отношении 7 : 3 с) 56 в отношении 1:6 е) 120 в отношении 5 : 3 f) 75 в отношении 8 : 7 h) 120 в отношении 40 : 20Русский язык
2 минуты назад
Прочитай.Составь и запиши предложение.Синичка,лес,по,летать, зимнийЗаяц,она,дятел,встретить,иЗиньеа, воробей,старый, рассказать,о,лес, жизнь,зима,в даю 10 балловЛитература
2 минуты назад
Как писатели-натуралисты преображают в своих произведениях жизнь животных?Русский язык
2 минуты назад
4. Составь и запиши предложения. Вставь пропу- щенные буквы. В лесу ж…вут и Шоссе — это ш…рокая После дождя Бабушка испекла луж… . беляш… . жи ШИ Л дорога. еж…
Составь и запиши предложения. Вставь пропу- щенные буквы. В лесу ж…вут и Шоссе — это ш…рокая После дождя Бабушка испекла луж… . беляш… . жи ШИ Л дорога. еж…Математика
2 минуты назад
Составьте систему уравнений с двумя неизвестными, решением которых является пара чисел: 1) x=3, y=0; 2) x=0, y=5.Литература
2 минуты назад
4. Как писатели-натуралисты преображают в своих произведениях жизнь животных?Информатика
2 минуты назад
ЗАБИРАЙТЕ БАЛЫно когда нажмёте на синийНемецкий язык
2 минуты назад
Mein Mann machmal auch am Wochenende.
Физика
2 минуты назад
Запропонуйте скільки резисторів заданого опору й яким чином потрібно з’єднати,щоб отримати еквівалентний опір певної величини.Наприклад,скільки й як потрібно з’єднати опорів по 2 Ом, щоб отримати єквівалентний опір 7 ОмМатематика
7 минут назад
3. Реши задачу. Стиральные машины первого поколения расходовали за одну стирку 120 литров воды. За 4 стирки такая стиральная машина тратила столько же воды, сколько современные машины за 10 стирок. Сколько литров воды расходует за один цикл стирки современная стиральная машина? СРОЧНО. дам 20 балловҚазақ тiлi
7 минут назад
-тапсырма. 2(x-3).
РЕШИТЬ ВСЕ ЗАДАНИЯ СРОЧНО ПОЖАЛУЙСТА!! С ОБЪЯСНЕНИЯМИ
2(x-3).
РЕШИТЬ ВСЕ ЗАДАНИЯ СРОЧНО ПОЖАЛУЙСТА!! С ОБЪЯСНЕНИЯМИЛитература
7 минут назад
Опис оповідання спілка рудих(мотив,як шерлок холмс це розгадав)Русский язык
7 минут назад
Используйте данные начало предложения напишите о том что необходимо делать чтобы хорошо учиться подчеркните глаголы необходимое в форме обозначьте есть суффикс»хочется скорее вырасти ,заниматься любимым делом .Папа и мама говорят ,что человек всего добьётся , если он этого очень хочет и хорошо учится в школе . А чтобы хорошо учиться , необходимо ……Русский язык
7 минут назад
Исстория о фантазий людей
Все предметы
Выберите язык и регион
English
United States
Polski
Polska
Português
Brasil
English
India
Türkçe
Türkiye
English
Philippines
Español
España
Bahasa Indonesia
Indonesia
Русский
Россия
How much to ban the user?
1 hour 1 day 100 years
Задания ЕГЭ с ответами.
 Равномерное движение. Относительность движения.
Равномерное движение. Относительность движения.Задание 1 № 101. Может ли график зависимости пути от времени иметь следующий вид?
1) да
2) нет
3) может, если траектория прямолинейная
4) может, если тело возвращается в исходную точку
Решение.
Путь — это физическая величина, показывающая пройденное телом расстояние. Иначе говоря, это длина пройденного участка траектории. По определению, путь есть величина положительная, которая может только возрастать со временем, так что представленный график не может изображать зависимость пути от времени.
Правильный ответ: 2.
Задание 1 № 125. Вертолет поднимается вертикально вверх. Какова траектория движения точки на конце лопасти винта вертолета в системе отсчета, связанной с винтом?
1) точка
2) прямая
3) окружность
4) винтовая линия
Решение.
В системе отсчета, связанной с винтом, точка на конце лопасти не двигается. Следовательно, ее траектория в данной системе отсчета представляет собой точку.
Правильный ответ: 1.
Задание 1 № 126. Два автомобиля движутся по прямому шоссе: первый — со скоростью ν, второй — со скоростью -3 ν. Какова скорость второго автомобиля относительно первого?
1) | 2) | 3) | 4) |
Решение.
Скорость второго автомобиля относительно первого равна ν2 —ν 1=-3 ν- ν= -4ν
Правильный ответ: 2.
Задание 1 № 131. Лодка должна попасть на противоположный берег реки по кратчайшему пути в системе отсчета, связанной с берегом. Скорость течения реки u, а скорость лодки относительно воды ν .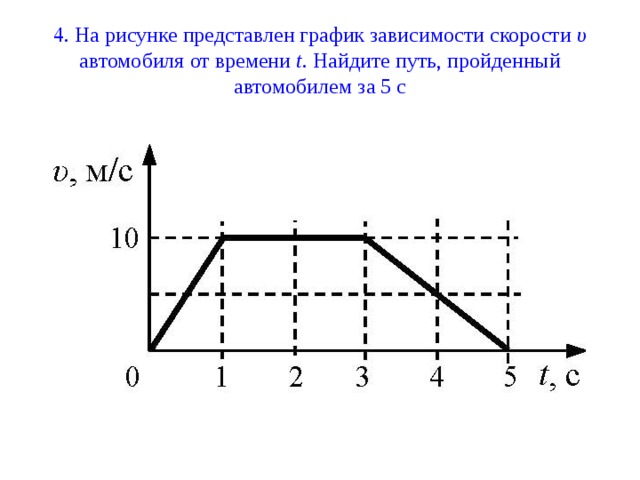 Чему должен быть равен модуль скорости лодки относительно берега?
Чему должен быть равен модуль скорости лодки относительно берега?
1)
2)
3)
4)
Решение.
1 способ: По закону сложения скоростей, вектор скорости лодки относительно берега (неподвижной с.о.) равен сумме скорости лодки относительно воды (подвижной с.о.) и скорости течения воды (переносной скорости). По условию, вектор скорости лодки в системе отсчета, связанной с берегом, должен быть перпендикулярен ему. Построив «треугольник скоростей» из теоремы Пифагора для скорости лодки относительно берега имеем
ν2 — u2
2 способ:
Вектор скорости лодки относительно воды разложим на две компоненты: , где вектор направлен параллельно берегу, а вектор — перпендикулярно берегу. Для того, чтобы лодка в системе отсчета, связанной с берегом, двигалась перпендикулярно к нему, необходимо, чтобы компонента скорости лодки относительно воды вдоль реки в точности компенсировала скорость течения u. Тогда модуль скорости лодки относительно берега будет равен (по теореме Пифагора)
Тогда модуль скорости лодки относительно берега будет равен (по теореме Пифагора)
Правильный ответ: 4.
Задание 1 № 133. На рисунке представлен график зависимости пути S велосипедиста от времени t.
Определите интервал времени после начала отсчета времени, когда велосипедист двигался со скоростью 5 м/с.
1) от 50 с до 70 с
2) от 30 с до 50 с
3) от 10 с до 30 с
4) от 0 до 10 с
Решение.
Для того чтобы по графику зависимости пути от времени найти скорость движения тела в некоторый момент, необходимо вычислить тангенс угла наклона графика в соответствующей точке. Из графика видно, что в интервале от 0 до 10 с скорость велосипедиста была постоянна и равнялась
.
На других интервалах скорость была иная.
Правильный ответ: 4.
Задание 1 № 134. На рисунке представлен график движения автобуса из пункта A в пункт Б и обратно.
Пункт A находится в точке х=0, а пункт Б — в точке х=30 км. Чему равна максимальная скорость автобуса на всем пути следования туда и обратно? (Ответ дайте в километрах в час.)
Решение.
Для того чтобы по графику зависимости координаты от времени найти скорость движения тела в некоторый момент, необходимо вычислить тангенс угла наклона графика в соответствующей точке. Максимальной скорости соответствует максимальный угол наклона. Из приведенного графика видно, что с максимальной скоростью автобус движется из пункта A в пункт Б, скорость его при этом равна: 30-0/0,5=60 км/ч.
Задание 1 № 138. На рисунке приведен график зависимости проекции скорости тела от времени.
Чему равно ускорение тела в интервале времени от 30 до 40 с? (Ответ дайте в метрах в секунду в квадрате.)
Решение.
Из графика видно, что в интервале времени от 30 до 40 с проекция скорости тела не изменялась, а значит, проекция ускорения была равна нулю.
Задание 1 № 317. Пловец плывет по течению реки. Определите скорость пловца относительно берега, если скорость пловца относительно воды 0,4 м/с, а скорость течения реки 0,3 м/с. (Ответ дайте в метрах в секунду.)
Решение.
Вектор скорости пловца относительно берега есть сумма векторов скорости пловца относительно воды и скорости течения реки:. Поскольку пловец плывет по течению реки, получаем, что для величин скоростей выполняется соотношение: 0,4 + 0,3 =0,7 м/с.
Задание 1 № 3354. Четыре тела двигались по оси Ох. В таблице представлена зависимость их координат от времени.
t, с | 0 | 1 | 2 | 3 | 4 | 5 |
x1, м. | 0 | 2 | 4 | 6 | 8 | 10 |
x2, м | 0 | 0 | 0 | 0 | 0 | 0 |
x3, м | 0 | 1 | 4 | 9 | 16 | 25 |
x4, м | 0 | 2 | 0 | -2 | 0 | 2 |
У какого из тел скорость могла быть постоянна и отлична от нуля?
Решение.
Таблица содержит информацию о положениях тел только в отдельные моменты времени. В промежутках между указанными временами тела могли двигаться абсолютно произвольно. Определим тело, скорость которого могла бы быть постоянной и отличной от нуля. При движении с постоянной скоростью координата тела за равные промежутки времени изменяется одинаково. Из таблицы видно, что этому свойству удовлетворяет только первое тело. Значит, скорость первого тела могла быть постоянной и не равной нулю.
Задание 1 № 3357. Вертолет равномерно поднимается вертикально вверх. Какова траектория крайней точки лопасти вертолета в системе отсчета, связанной с корпусом вертолета?
1) прямая линия
2) винтовая линия
3) окружность
4) эллипс
Решение.
Крайняя точка лопасти вертолета двигается по окружности вокруг оси вращения винта. Поскольку ось вращения жестко связана с корпусом вертолета, такую же траекторию описывает эта точка и относительно любой точки корпуса. Правильный ответ 3.
Поскольку ось вращения жестко связана с корпусом вертолета, такую же траекторию описывает эта точка и относительно любой точки корпуса. Правильный ответ 3.
Задание 1 № 3539. На каком из графиков изображена возможная зависимость пройденного пути от времени?
1) А
2) Б
3) В
4) Такой график отсутствует
Решение.
Путь — это физическая величина, показывающая пройденное телом расстояние. Иначе говоря, это длина пройденного участка траектории. По определению, путь есть величина положительная, которая может только возрастать со временем. Этому требованию удовлетворяет только график В.
Правильный ответ: 3.
Задание 1 № 3540. Велосипедист, двигаясь под уклон, проехал расстояние между двумя пунктами со скоростью, равной 15 км/ч. Обратно он ехал вдвое медленнее. Какова средняя путевая скорость на всем пути? (Ответ дайте в километрах в час.)
Какова средняя путевая скорость на всем пути? (Ответ дайте в километрах в час.)
Решение.
Необходимо различать два понятия: среднюю путевую скорость и среднюю скорость по перемещению. Средняя путевая скорость определяется как скорость прохождения пути: . То есть, буквально, надо весь пройденный телом путь разделить на все время, затраченное им на этот путь. Средняя путевая скорость представляет собой число, скаляр.
Разберемся теперь со второй средней скоростью. Средняя скорость по перемещению — это вектор, равный отношению перемещения ко времени, за которое оно совершено: . В нашей конкретной задаче, поскольку велосипедист вернулся в исходную точку, его перемещение равно нулю, а значит, его средняя скорость по перемещению тоже равна нулю.
Вычислим теперь среднюю путевую скорость. Обозначим расстояние между двумя пунктами через ? тогда весь путь пройденный велосипедистом равен . На первую половину пути велосипедист затратил время . На обратную дорогу — время . Все время пути составило . Окончательно, находим, что средняя путевая скорость велосипедиста равна
На первую половину пути велосипедист затратил время . На обратную дорогу — время . Все время пути составило . Окончательно, находим, что средняя путевая скорость велосипедиста равна
.
Задание 1 № 3541. Тело движется прямолинейно вдоль оси x. На графике представлена зависимость координаты тела от времени. В какой момент времени модуль перемещения относительно исходной точки имел максимальное значение? (Ответ дайте в секундах.)
Решение.
Из графика видно, что начальная координата тела равна . Модуль перемещения тела относительно исходной точки в любой момент определяется выражением: . Построим график этой функции и определим ее максимум. Из построенного графика ясно, что модуль перемещения относительно исходной точки максимален при и равен 20 м.
Ответ: 6 с
Задание 1 № 3544. Движение двух велосипедистов заданы уравнениями x1 =2 t и x2 =100- 8 t . Найдите координату x места встречи велосипедистов. Велосипедисты двигаются вдоль одной прямой. (Ответ дайте в метрах.)
Движение двух велосипедистов заданы уравнениями x1 =2 t и x2 =100- 8 t . Найдите координату x места встречи велосипедистов. Велосипедисты двигаются вдоль одной прямой. (Ответ дайте в метрах.)
Решение.
Встреча двух велосипедистов означает, что у них в некоторый момент времени совпадут координаты. Определим, когда именно произойдет встреча, для этого решим уравнение . Теперь не составляет труда определить координату места встречи:
Задание 1 № 3545.
На рисунке приведен график движения x(t) электрокара. Определите по этому графику путь, проделанный электрокаром за интервал времени от t1 = 1 c до t2 = 4 c. (Ответ дайте в метрах.)
Решение.
Путь — это физическая величина, показывающая пройденное телом расстояние. Иначе говоря, это длина пройденного участка траектории. Из графика видно, что в интервале времени от до электрокар двигался в положительном направлении оси . При этом его координата изменилась на . Последнюю, четвертую, секунду электрокар двигался в обратном направлении, изменение его координаты на этом участке равно . Таким образом, путь, пройденный машинкой за интервал времени от до равен .
Иначе говоря, это длина пройденного участка траектории. Из графика видно, что в интервале времени от до электрокар двигался в положительном направлении оси . При этом его координата изменилась на . Последнюю, четвертую, секунду электрокар двигался в обратном направлении, изменение его координаты на этом участке равно . Таким образом, путь, пройденный машинкой за интервал времени от до равен .
Задание 1 № 3548. Пешеход идет по прямолинейному участку дороги со скоростью v. Навстречу ему движется автобус со скоростью 10v. С какой скоростью должен двигаться навстречу пешеходу велосипедист, чтобы модуль его скорости относительно пешехода и автобуса был одинаков?
1)
2)
3)
4)
Решение.
Обозначим искомую скорость велосипедиста через . Тогда, как видно из рисунка, велосипедист приближается к пешеходу со скоростью , а к автобусу — со скоростью .
Приравняв эти две скорости, находим требуемую скорость велосипедиста:
Правильный ответ: 1.
Задание 1 № 3549. Пароход движется по реке против течения со скоростью 5 м/с относительно берега. Определите скорость течения реки, если скорость парохода относительно берега при движении в обратном направлении равна 8 м/с. (Ответ дайте в метрах в секунду.)
Решение.
Обозначим искомую скорость течения реки через , а скорость парохода в стоячей воде — через . Тогда можно составить следующие уравнения. Скорость парохода вниз по течению равна . Скорость парохода вверх по течению: . Решая систему из двух этих уравнений, для скорости течения воды имеем .
Задание 1 № 3734.
Материальная точка движется вдоль оси OX. На рисунке представлен график зависимости проекции скорости этой материальной точки на ось OX от времени. Какой из приведенных ниже графиков может соответствовать зависимости координаты материальной точки от времени?
Какой из приведенных ниже графиков может соответствовать зависимости координаты материальной точки от времени?
1) 1
2) 2
3) 3
4) 4
Решение.
Из графика видно, что проекция скорости материальной точки на ось OX положительна и постоянна, а значит, точка движется равномерно и в положительном направлении оси OX. Единственный график, удовлетворяющий обоим этим требованиям, — это график под номером 1.
Правильный ответ: 1.
Задание 1 № 3783. На рисунке представлены графики зависимости пройденного пути от времени для двух тел. На какую величину Δv скорость второго тела v2 больше скорости первого тела v1? (Ответ дайте в метрах в секунду.)
Решение.
Из графика видно, что для обоих тел пройденный путь линейно зависит от времени, а значит, оба тела двигались с постоянными по величине скоростями.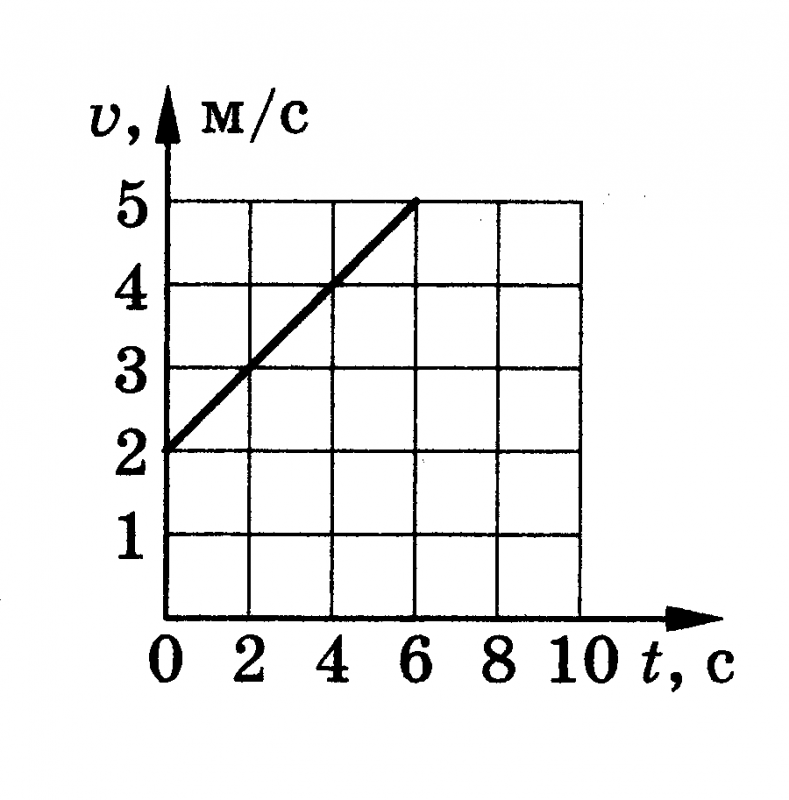 Модуль скорости первого тела равен . Скорость же второго тела: . Следовательно, скорость второго тела больше скорости первого тела на величину
Модуль скорости первого тела равен . Скорость же второго тела: . Следовательно, скорость второго тела больше скорости первого тела на величину
Задание 1 № 3867.
Тела 1 и 2 двигаются вдоль оси x. На рисунке изображены графики зависимости координат движущихся тел 1 и 2 от времени t. Чему равен модуль скорости 1 относительно тела 2? (Ответ дайте в метрах в секунду.)
Решение.
Используя график, определим проекции скоростей обоих тел. Для тела 1 имеем
Для тела 2:
Таким образом модуль скорости одного тела относительно другого равен
Задание 1 № 4077. Автобус везёт пассажиров по прямой дороге со скоростью 10 м/с. Пассажир равномерно идёт по салону автобуса со скоростью 1 м/с относительно автобуса, двигаясь от задней двери к кабине водителя. Чему равен модуль скорости пассажира относительно дороги? (Ответ дайте в метрах в секунду.)
Чему равен модуль скорости пассажира относительно дороги? (Ответ дайте в метрах в секунду.)
Решение.
Согласно закону сложения скоростей, скорость тела относительно «неподвижной системы отсчёта» связана со скоростью этого тела относительно «подвижной системы отсчёта» и скоростью движения «подвижной с. о.» относительно «неподвижной» при помощи следующего соотношения: В данном случае, так как пассажир двигается вдоль автобуса по направлению его движения, для скорости пассажира относительно дороги имеем:
Ответ: 11 м/с
Задание 1 № 4186. Координата материальной точки изменяется с течением времени по закону x=3-2t. Какой из приведённых ниже графиков соответствует этой зависимости?
1) 1
2) 2
3) 3
4) 4
Решение.
Из зависимости видно, что координата убывает со временем, при этом в начальный момент времени координата равна а в начало координат материальная точка попадает в момент времени: Таким образом, зависимости соответствует график под номером 4.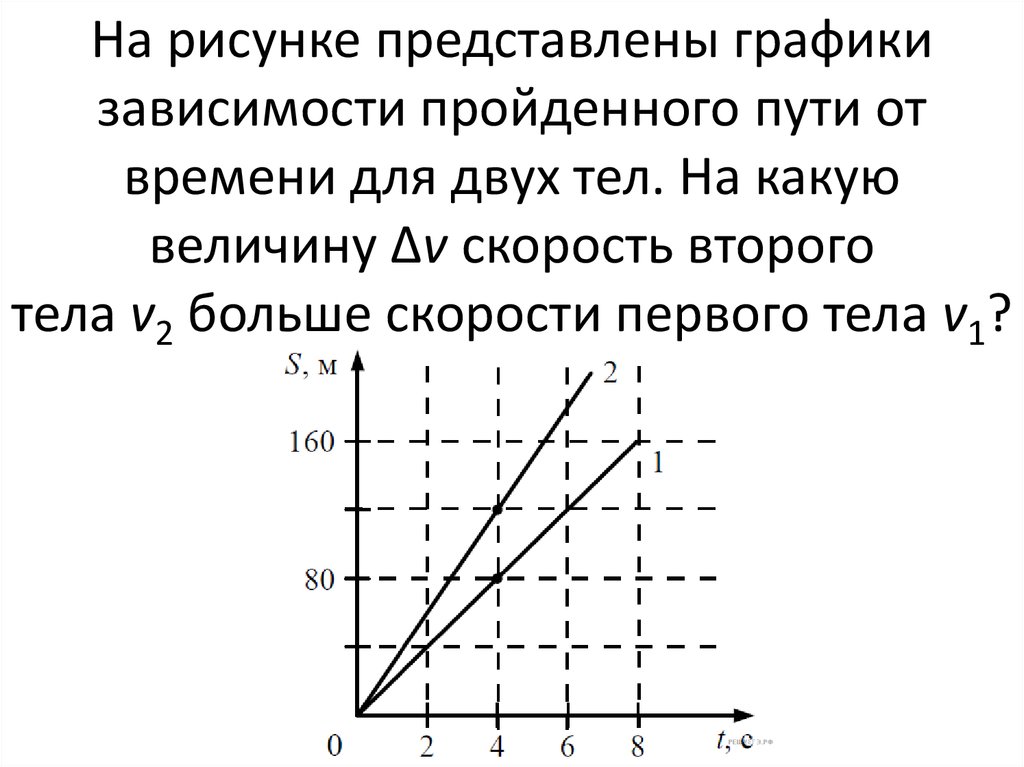
Правильный ответ: 4.
Задание 1 № 4221. Координата материальной точки изменяется с течением времени по закону . x=3+ 2t. Какой из приведённых ниже графиков соответствует этой зависимости?
1)
2)
3)
4)
Решение.
Из зависимости видно, что координата возрастает со временем, при этом в начальный момент времени координата равна , а в момент времени координата равна . Таким образом, зависимости соответствует график под номером 3.
Правильный ответ: 3.
Задание 1 № 4409. По плоскости движутся четыре точечных тела —А, Б, В, Г. x=1+t., y=2 t, и , траектории которых изображены на рисунке. Зависимости координат одного из этих тел от времени имеют вид и . Это тело обозначено буквой
1) А
2) Б
3) В
4) Г
Решение.
На зависимость координат от времени и можно смотреть как на параметрическое задание прямой на плоскости .
Выразим время из первого уравнения и подставим во второе: . Из рисунка видно, что уравнению соответствует прямая .
Правильный ответ: 3
Задание 1 № 4444. По плоскости движутся четыре точечных тела — А,Б В, и Г, траектории которых изображены на рисунке. Зависимости координат одного из этих тел от времени имеют вид x=2t.и . y=1+ t. Это тело обозначено буквой
1) А
2) Б
3) В
4) Г
Решение.
На зависимость координат от времени и можно смотреть как на параметрическое задание прямой на плоскости .
Выразим время из первого уравнения и подставим во второе: . Из рисунка видно, что уравнению соответствует прямая A.
Правильный ответ: 1
Задание 1 № 4934. Два автомобиля движутся по прямому шоссе: первый со скоростью , второй со скоростью относительно шоссе. Скорость первого автомобиля относительно второго равна
1)
2)
3)
4)
Решение.
Скорость первого автомобиля относительно второго равна
.
Правильный ответ: 2.
Графики движения: типы, уравнения и анализ
Для нефизиков карты и спидометры пригодятся при оценке изменения положения или изменения скорости объекта. Но когда вы физик, графики — особенно графики движения — очень важны для определения положения или скорости изменения скорости объекта. Как вы увидите ниже, графики движения помогают нам, студентам-физикам, лучше понять движение тела за определенный период времени.
Типы графиков движения
Существуют три основных типа графиков, используемых для определения движения объекта по прямой линии : графики перемещения-времени, графики скорости-времени и графики ускорения-времени.
График зависимости смещения от времени
На рис. 1 показан график зависимости смещения от времени объекта, движущегося с постоянной скоростью . Для графика «смещение-время» смещение (обозначается d) находится на оси y, а время (обозначается t) — на оси x.
Для графика «смещение-время» смещение (обозначается d) находится на оси y, а время (обозначается t) — на оси x.
Рис. 1. График перемещение-время объекта, движущегося с постоянной скоростью. Usama Adeel — StudySmarter Originals
Из такого графика мы можем получить
- пройденное расстояние в любой момент времени,
- среднюю скорость путем вычисления наклона (градиента) графика и
- мгновенная скорость путем вычисления производной любой точки на кривой.
Чтобы рассчитать наклон p приведенного выше графика, мы используем следующее уравнение:
p=y2-y1x2-x1=∆d∆tm/s
Скорость изменения смещения — это скорость, , поэтому наклон графика смещения-времени — это скорость.
График зависимости скорости от времени
Посмотрите на график зависимости скорости от времени ниже:
Рисунок 2. График зависимости скорости от времени объекта, движущегося с постоянной скоростью. Usama Adeel – StudySmarter Originals
Usama Adeel – StudySmarter Originals
Для графика скорость-время скорость (v) находится на оси y, а время (t) – на оси x. Из этого графика мы можем найти
- скорость в любой момент времени,
- среднее ускорение путем вычисления наклона прямой линии,
- мгновенное ускорение путем взятия производной любой точки на кривой и
- перемещение тела путем вычисления площади под кривой (между линией и осью времени).
Чтобы рассчитать наклон p приведенного выше графика, мы используем следующее уравнение:
p=y2-y1x2-x1=∆v∆tm/s2
Скорость изменения скорости есть ускорение , поэтому наклон графика скорость-время есть ускорение.
Кроме того, площадь под графиком скорость-время дает расстояние, пройденное объектом , то есть смещение.
График зависимости ускорения от времени
Для графика зависимости ускорения от времени ускорение (a) отложено по оси y, а время (t) по оси x. График ускорение-время дает нам ускорение в любой момент времени. Кроме того, 9Площадь 0007 под кривой зависимости ускорения от времени представляет изменение скорости .
Рис. 3. График зависимости ускорения от времени объекта, движущегося с равномерно возрастающим ускорением. Usama Adeel – StudySmarter Originals
Анализ графиков движения без чисел
Ниже мы рассмотрим, как рисовать графики движения для различных сценариев.
Графики движения: объект в состоянии покоя
Для объекта в состоянии покоя перемещение не изменится, что не приведет к изменению скорости, а поскольку скорость не изменится, изменение ускорения будет также быть нулевым.
График смещения-времени для объекта в состоянии покоя Объект в состоянии покоя не будет двигаться.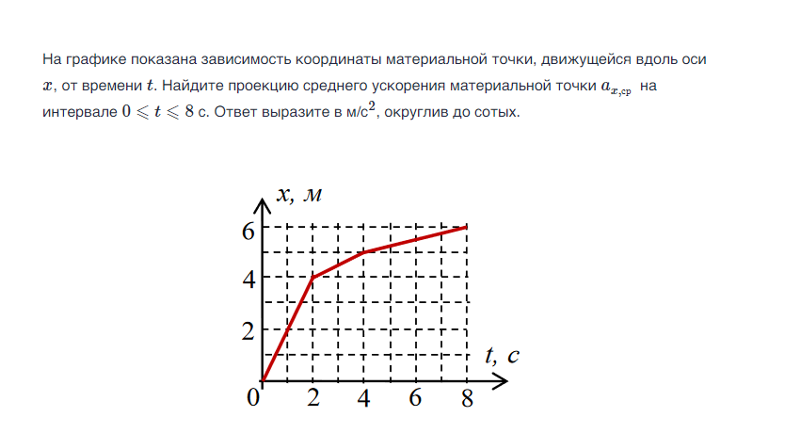 Следовательно, смещение не изменится на за интервал времени, изображенный плоской линией, параллельной оси времени.
Следовательно, смещение не изменится на за интервал времени, изображенный плоской линией, параллельной оси времени.
Рис. 4. График перемещения объекта в состоянии покоя от времени. Usama Adeel — StudySmarter Originals
График зависимости скорости от времени для объекта в состоянии покояСкорость будет равна нулю , потому что смещение объекта не меняется. Следовательно, график для объекта без изменения его скорости во времени может быть показан прямой линией на оси времени.
Рис. 5. График зависимости скорости покоящегося объекта от времени. Usama Adeel — StudySmarter Originals
График ускорения и времени для объекта в состоянии покоя Ускорение будет равно нулю , поскольку скорость объекта не меняется, а график ускорения и времени представляет собой плоскую линию, начинающуюся от начала координат.
Рис. 6. График ускорения объекта в состоянии покоя. Usama Adeel – StudySmarter Originals
Графики движения: объекты, движущиеся с постоянной скоростью (расстояние увеличивается со временем)
Когда объект движется с постоянной скоростью:
- Скорость изменения смещения будет равна при равномерном увеличении .
- Скорость будет представлять собой непрерывную прямую линию с положительным или отрицательным значением в зависимости от направления движения.
- Ускорение будет равно нулю , поэтому через начало координат будет проходить постоянная линия.
Наклон на приведенном ниже графике равен положительному , что указывает на то, что движение происходит в положительном направлении (от начала координат).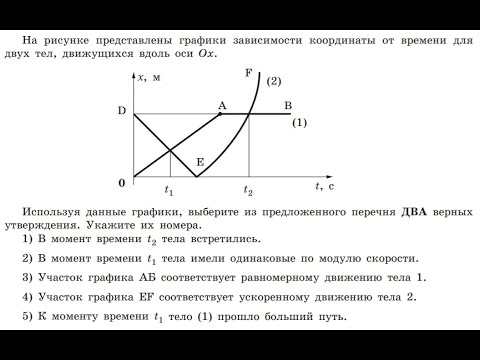 Если бы эта кривая была такой же, но с отрицательным градиентом (к началу координат), она отображала бы смещение в противоположном направлении. Кроме того, перемещение равномерно увеличивается, потому что скорость постоянна.
Если бы эта кривая была такой же, но с отрицательным градиентом (к началу координат), она отображала бы смещение в противоположном направлении. Кроме того, перемещение равномерно увеличивается, потому что скорость постоянна.
Рис. 7. График перемещение-время объекта, движущегося с постоянной скоростью из состояния покоя. Усама Адил – StudySmarter Originals
Вопрос: Какое направление считать положительным или отрицательным?
Ответ: Знак произвольный. Вы можете выбрать любое направление как положительное, так и отрицательное. На рис. линия в положительном направлении .
Рис. 8. График зависимости скорости объекта, движущегося с постоянной скоростью. Usama Adeel — StudySmarter Originals
График зависимости ускорения от времени для объекта, движущегося с постоянной скоростью Чтобы произошло ускорение или замедление, также должно произойти изменение скорости. Рис. 9. График зависимости ускорения объекта, движущегося с постоянной скоростью. Усама Адил – StudySmarter Originals
Усама Адил – StudySmarter Originals
Графики движения: объекты, движущиеся с постоянным ускорением (расстояние увеличивается с течением времени)
Когда объект движется с постоянным ускорением:
- График перемещение-время будет представлять собой кривую с градиентом, который становится возрастающим круче .
- Скорость изменения скорости будет равномерно возрастать.
- Ускорение будет постоянным с положительным значением.
Ниже приведены два графика зависимости смещения от времени. Рисунок 10 соответствует постоянному ускорению , а рисунок 11 соответствует постоянному замедлению .
Рис. 10. График перемещение-время объекта, движущегося с постоянным ускорением. Usama Adeel – StudySmarter Originals
Рис. 11. График перемещение-время объекта, движущегося с постоянным замедлением. Усама Адил – StudySmarter Originals
Если вы возьмете касательные в различных точках обеих вышеприведенных кривых, вы увидите, что наклон графика смещения-времени на рисунке 10 становится все круче и круче. Это указывает на то, что скорость увеличивается . На рисунке 11 градиент постепенно уменьшается , что указывает на то, что скорость уменьшается .
Рис. 12. График перемещение-время объекта, движущегося с постоянным ускорением. Наклон становится круче, что указывает на постоянное ускорение. Усама Адил – StudySmarter Originals
Рис. 13. График перемещение-время объекта, движущегося с постоянным ускорением. Склон становится более пологим, что указывает на постоянное замедление. Usama Adeel – StudySmarter Originals
Usama Adeel – StudySmarter Originals
График скорости от времени для объекта с постоянным ускорением будет представлять собой равномерно возрастающую линию, как показано на рисунке ниже.
Рис. 14. График зависимости скорости объекта, движущегося с постоянным ускорением. Усама Адил – StudySmarter Originals
График ускорение-время для объекта, движущегося с постоянным ускорениемПоскольку ускорение не меняется во времени и является постоянным, график ускорение-время может быть представлен прямой линией.
Рис. 15. График ускорение-время объекта, движущегося с постоянным ускорением. Usame Adeel – StudySmarter Originals
Графики движения: Объект движется с постоянным замедлением (расстояние увеличивается со временем)
Когда объект движется с постоянным замедлением:
- График смещение-время будет представлять собой кривую с градиентом, который становится все более и более горизонтальным.

- Скорость изменения скорости будет равномерно уменьшаться .
- Ускорение будет постоянным , но с отрицательным значением.
Поскольку тело замедляется, кривая приближается к постоянному (неизменному) значению .
Рис. 16. График перемещение-время объекта, движущегося с постоянным замедлением. StudySmarter Originals – Usama Adeel
График зависимости скорости от времени для объекта, движущегося с постоянным замедлениемГрафик зависимости скорости от времени при постоянном замедлении будет представлять собой однородную линию, постоянно уменьшающуюся от некоторого значения.
Рис. 17. График зависимости скорости объекта, движущегося с постоянным замедлением. Усама Адил – StudySmarter Originals
График ускорение-время для объекта, движущегося с постоянным замедлением Постоянная линия с отрицательным ускорением показывает, что объект замедляется с постоянным значением.
Рис. 18. График ускорение-время объекта, движущегося с постоянным замедлением. Usama Adeel – StudySmarter Originals
Графики движения: подбрасывание объекта прямо вверх с возвратом объекта к бросающему
В этом сценарии объект, скажем, мяч, подбрасывается вверх таким образом, что он попадает в руку через некоторое время. Сопротивлением воздуха можно пренебречь, и единственные силы, действующие на мяч, исходят от бросающего (чтобы подбросить мяч вверх) и гравитационного притяжения мяча до тех пор, пока он не приземлится в руке бросающего. Направление вверх считается положительным.
График смещения-времени для предмета, брошенного вертикально вверхГрафик смещения-времени для предмета, брошенного вертикально вверх и затем приземлившегося в руке метателя, показан ниже.
Рис. 19. График перемещения объекта, подброшенного в воздух и захваченного на той же высоте, от времени. Usama Adeel — StudySmarter Originals
Usama Adeel — StudySmarter Originals
Как только мяч подброшен в воздух, его смещение увеличивается, потому что мы приняли направление вверх как положительное. Когда он достигнет вершины, градиент графика смещения-времени на короткое время станет равным нулю, что указывает на то, что мяч меняет свое направление и с этого момента будет двигаться вниз. Поэтому график будет двигаться вниз, пока шарик не достигнет исходного положения.
Но почему график представляет собой кривую, а не прямую линию? Ускорение из-за силы тяжести постоянно, со значением 9,81 м/с 2 . Таким образом, с момента броска мяча и до того, как он будет пойман, замедление за счет силы тяжести и ускорение за счет свободного падения будут постоянными и отличными от нуля.
График зависимости скорости от времени для объекта, брошенного вертикально вверх График зависимости скорости от времени для объекта, брошенного вертикально вверх и приземлившегося в руке метателя, показан ниже.
Рис. 20. График зависимости скорости тела, подброшенного в воздух и пойманного на одной высоте. Usama Adeel – StudySmarter Originals
Мяч брошен вверх с некоторой начальной скоростью u. Когда мяч достигает вершины, его скорость равномерно уменьшается, пока не достигнет нуля, где мяч на короткое время покоится. После этого мяч движется вниз с равномерно возрастающей скоростью.
Поскольку пройденное расстояние вверх и вниз будет одинаковым из-за пренебрежимо малого сопротивления воздуха, начальная скорость будет равна конечной скорости -u. Итак, 9В этом случае площадь 0007 обоих регионов A и B будет равна
.Почему наклон графика становится отрицательным, а не положительным после того, как u достигает нуля? Поскольку направление вверх принимается за положительное, как только направление мяча изменится вверху, движение будет направлено вниз в отрицательном направлении с постоянным ускорением свободного падения.
График времени ускорения для предмета, брошенного вертикально вверх График времени ускорения для предмета, брошенного вертикально вверх и затем приземлившегося в руке метателя, показан ниже.
Рис. 21. График зависимости ускорения объекта, подброшенного в воздух и пойманного на одной высоте. Usama Adeel – StudySmarter Originals
Ускорение является постоянным -9,81 м/с 2 на протяжении всего смещения , поскольку график зависимости скорости от времени равномерно уменьшается.
После того, как мяч подброшен в воздух, сила тяжести действует в направлении, противоположном движению вверх. Поскольку движение вверх считается положительным, сила тяжести будет отрицательной. Как только мяч достигает своей вершины, мяч меняет направление. Следовательно, гравитационная сила по-прежнему будет отрицательной.
Графики движения – ключевые выводы
Существует три основных типа графиков, касающихся линейного движения: график смещения-времени, график скорости-времени и график ускорения-времени
Из графика смещения-времени графика, вы можете рассчитать среднюю скорость и мгновенную скорость, рассчитав наклон графика.

По графику скорость-время можно рассчитать среднее ускорение, найдя наклон графика, и мгновенное ускорение, найдя наклон в определенной точке.
Площадь под графиком скорость-время представляет перемещение.
Область под графиком ускорение-время представляет собой изменение скорости.
Графики положение-время: значение формы
Наше исследование одномерной кинематики было связано с многочисленными средствами, с помощью которых может быть представлено движение объектов. К таким средствам относятся использование слов, использование диаграмм, использование чисел, использование уравнений и использование графиков. Урок 3 посвящен использованию графиков зависимости положения от времени для описания движения. Как мы узнаем, особенности движения объектов демонстрируются формой и наклоном линий на графике зависимости положения от времени. Первая часть этого урока включает в себя изучение взаимосвязи между формой графика p-t и движением объекта.
Противопоставление постоянной и изменяющейся скорости
Для начала рассмотрим автомобиль, движущийся с постоянной скоростью вправо (+), скажем, +10 м/с.
Если представить данные о положении во времени для такого автомобиля, то результирующий график будет похож на график справа. Обратите внимание, что движение, описываемое как постоянная положительная скорость, приводит к линии постоянного и положительного наклона при построении в виде графика положение-время.
Теперь рассмотрим автомобиль, движущийся вправо (+) с изменяющейся скоростью, то есть автомобиль, который движется вправо, но с ускорением или ускорение .
Если представить данные о положении во времени для такого автомобиля, то результирующий график будет похож на график справа. Обратите внимание, что движение, описываемое как изменение положительной скорости, приводит к линии изменения и положительного наклона при построении в виде графика положение-время.
Графики зависимости положения от времени для двух типов движения — постоянной скорости и изменяющейся скорости (ускорения) — представлены следующим образом.
| Постоянная скорость Положительная скорость | Положительная скорость Изменение скорости (ускорение) |
|---|---|
Важность наклона
Формы графиков зависимости положения от времени для этих двух основных типов движения — движения с постоянной скоростью и движения с ускорением (т. е. с изменением скорости) — раскрывают важный принцип. Принцип заключается в том, что наклон линии на графике положение-время дает полезную информацию о скорости объекта. Часто говорят: «Как наклон, так и скорость». Какими бы характеристиками ни обладала скорость, наклон будет одинаковым (и наоборот). Если скорость постоянна, то и наклон постоянен (т. е. прямая линия). Если скорость меняется, то меняется и наклон (т. е. кривая линия). Если скорость положительна, то и наклон положительный (т. е. движение вверх и вправо). Этот самый принцип может быть распространен на любое мыслимое движение.
е. кривая линия). Если скорость положительна, то и наклон положительный (т. е. движение вверх и вправо). Этот самый принцип может быть распространен на любое мыслимое движение.
Противопоставление медленного и быстрого движения
Рассмотрим приведенные ниже графики в качестве примера применения этого принципа относительно наклона линии на графике зависимости положения от времени. График слева представляет объект, который движется с положительной скоростью (обозначается положительным наклоном), постоянной скоростью (обозначается постоянным наклоном) и малой скоростью (обозначается малым наклоном). График справа имеет схожие черты — здесь постоянная положительная скорость (обозначается постоянным положительным наклоном). Однако наклон графика справа больше, чем слева. Этот больший наклон указывает на большую скорость. Объект, представленный графиком справа, движется быстрее, чем объект, представленный графиком слева. Принцип наклона можно использовать для извлечения соответствующих характеристик движения из графика зависимости положения от времени.
| Медленно, вправо(+) Постоянная скорость | Быстро, вправо(+) |
|---|---|
Рассмотрим приведенные ниже графики как еще одно применение этого принципа наклона. График слева представляет объект, который движется с отрицательной скоростью (обозначается отрицательным наклоном), постоянной скоростью (обозначается постоянным наклоном) и малой скоростью (обозначается малым наклоном). График справа имеет схожие черты — здесь постоянная отрицательная скорость (обозначается постоянным отрицательным наклоном). Однако наклон графика справа больше, чем слева. Еще раз, этот больший наклон указывает на большую скорость. Объект, представленный графиком справа, движется быстрее, чем объект, представленный графиком слева.
| Медленно, влево(-) Постоянная скорость | Быстро, влево(-) Постоянная скорость |
|---|---|
В качестве последнего применения этого принципа наклона рассмотрим два графика ниже. На обоих графиках нанесены точки, образующие кривую линию. Изогнутые линии имеют изменяющийся наклон; они могут начинаться с очень небольшого уклона и начинать резко изгибаться (вверх или вниз) к большому наклону. В любом случае кривая линия изменения наклона является признаком ускоренного движения (т. е. изменения скорости). Применяя принцип наклона к графику слева, можно было бы сделать вывод, что объект, изображенный на графике, движется с отрицательной скоростью (поскольку наклон отрицателен). Кроме того, объект стартует с небольшой скоростью (наклон начинается с небольшого наклона) и заканчивается с большой скоростью (наклон становится большим). Это означало бы, что этот объект движется в отрицательном направлении и ускоряется (маленькая скорость превращается в большую скорость). Это пример отрицательного ускорения — движение в отрицательном направлении и ускорение. На графике справа также изображен объект с отрицательной скоростью (поскольку имеется отрицательный наклон). Объект начинается с высокой скорости (наклон изначально большой) и заканчивается с малой скоростью (поскольку наклон становится меньше).
На обоих графиках нанесены точки, образующие кривую линию. Изогнутые линии имеют изменяющийся наклон; они могут начинаться с очень небольшого уклона и начинать резко изгибаться (вверх или вниз) к большому наклону. В любом случае кривая линия изменения наклона является признаком ускоренного движения (т. е. изменения скорости). Применяя принцип наклона к графику слева, можно было бы сделать вывод, что объект, изображенный на графике, движется с отрицательной скоростью (поскольку наклон отрицателен). Кроме того, объект стартует с небольшой скоростью (наклон начинается с небольшого наклона) и заканчивается с большой скоростью (наклон становится большим). Это означало бы, что этот объект движется в отрицательном направлении и ускоряется (маленькая скорость превращается в большую скорость). Это пример отрицательного ускорения — движение в отрицательном направлении и ускорение. На графике справа также изображен объект с отрицательной скоростью (поскольку имеется отрицательный наклон). Объект начинается с высокой скорости (наклон изначально большой) и заканчивается с малой скоростью (поскольку наклон становится меньше).
| Отрицательная (-) скорость Медленно к быстрому | Влево (-) Скорость От быстрого к медленному |
|---|---|
Принцип наклона — невероятно полезный принцип для извлечения релевантной информации о движении объектов, описываемой графиком зависимости их положения от времени. После того, как вы попрактикуетесь в этом принципе несколько раз, он станет очень естественным средством анализа графиков положение-время.
См. анимацию различных движений с сопровождающими графиками
Расследуй! Виджет ниже отображает график положение-время для объекта с указанными характеристиками. Верхний виджет отображает движение объекта, движущегося с постоянной скоростью. Нижний виджет отображает движение ускоряющегося объекта. Просто введите указанные значения, и виджет начертит линию с положением по вертикальной оси и временем по горизонтальной оси. Обязательно обратите внимание на разницу между графиком постоянной скорости и графиком ускоренного движения.
Просто введите указанные значения, и виджет начертит линию с положением по вертикальной оси и временем по горизонтальной оси. Обязательно обратите внимание на разницу между графиком постоянной скорости и графиком ускоренного движения.
Мы хотели бы предложить …
Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего Graph That Motion или наших Graphs and Ramps Interactives. Каждый из них находится в разделе Physics Interactives на нашем веб-сайте и позволяет учащимся применять концепции кинематических графиков (как положение-время, так и скорость-время) для описания движения объектов.
Посетите: Постройте график этого движения || Графики и рампы
Проверьте свое понимание
Используйте принцип наклона для описания движения объектов, изображенных на двух графиках ниже.

 Составь и запиши предложения. Вставь пропу- щенные буквы. В лесу ж…вут и Шоссе — это ш…рокая После дождя Бабушка испекла луж… . беляш… . жи ШИ Л дорога. еж…
Составь и запиши предложения. Вставь пропу- щенные буквы. В лесу ж…вут и Шоссе — это ш…рокая После дождя Бабушка испекла луж… . беляш… . жи ШИ Л дорога. еж…
 2(x-3).
РЕШИТЬ ВСЕ ЗАДАНИЯ СРОЧНО ПОЖАЛУЙСТА!! С ОБЪЯСНЕНИЯМИ
2(x-3).
РЕШИТЬ ВСЕ ЗАДАНИЯ СРОЧНО ПОЖАЛУЙСТА!! С ОБЪЯСНЕНИЯМИ
Leave A Comment