1 задание ЕГЭ по математике профильного уровня 2023: теория и практика
Русский язык Математика (профиль) Математика (база) Обществознание История Биология Физика Химия Английский язык Информатика Литература
Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Задание 7 Задание 8 Задание 9 Задание 10 Задание 11 Задание 12 Задание 13 Задание 14 Задание 15 Задание 16 Задание 17 Задание 18
За это задание ты можешь получить  °$. Найдите угол $ACB$. Ответ дайте в градусах.
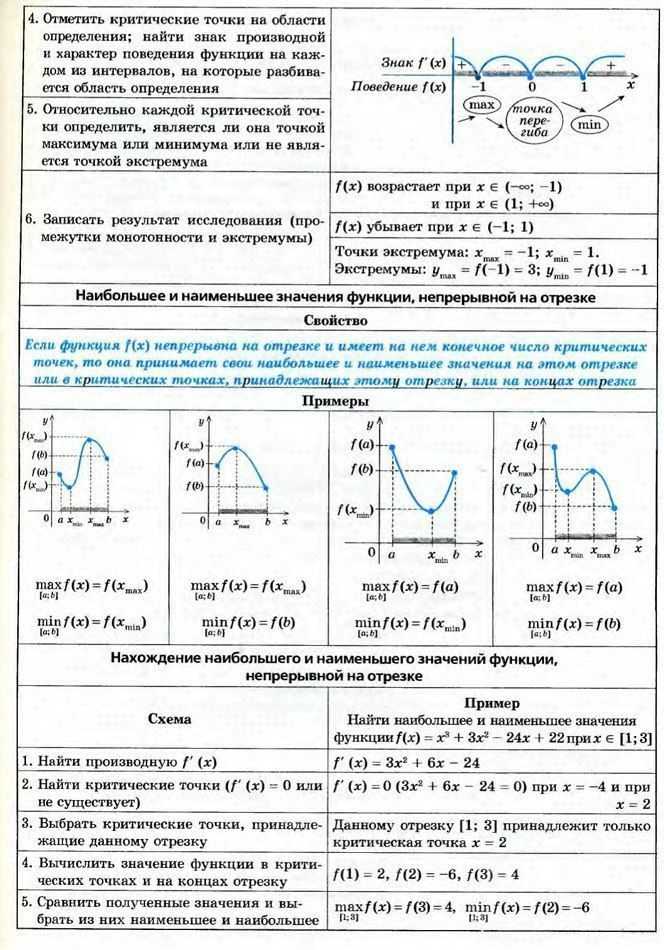
°$. Найдите угол $ACB$. Ответ дайте в градусах.
Решение
$∠C AB = ∠C BA$, как углы между хордой и касательной, они измеряются половиной дуги $AB$, то есть $∠C AB = {1}/{2} ︶ AB$ и $∠C BA = {1}/{2} ︶ AB$.
Отсюда, $∠AC B = 180°- ︶AB = 180° — 48° = 132°$.
Ответ: 132
Показать решение
Бесплатный интенсив
Задача 4
Периметр треугольника равен $73$, а радиус вписанной окружности равен $4$. Найдите площадь этого треугольника.
Решение
$S_{ABC} = p · r$, где $p$ — полупериметр треугольника, а $r$ — радиус вписанной окружности, тогда $S_{ABC} = {73}/{2} · 4 = 146$.
Ответ: 146
Показать решение
Бесплатный интенсив
Задача 5
Периметр треугольника равен $40$, а радиус вписанной окружности равен $3$. 2$
2$
$ x = {9±13}/{2}$
$ x_1 = 11$
$ x_2 = -2$ (не подходит).
Ответ: 11
Показать решение
Бесплатный интенсив
Задача 14
Основания равнобедренной трапеции равны $15$ и $9$. Высота трапеции равна $6$. Найдите тангенс острого угла.
Решение
Рассмотрим трапецию $ABCD$. Пусть $AB = CD, BK$ и $CM$ — высоты. Тогда $AK = MD$ и $AD = BC + 2AK$.
$tg ∠BAD = {BK}/{AK}, AK = {AD — BC}/{2} = {15 — 9}/{2} = 3, BK = 6$ (по условию). $tg ∠BAD = {6}/{3} = 2$.
Ответ: 2
Показать решение
Бесплатный интенсив
Задача 15
Основания равнобедренной трапеции равны $14$ и $6$. Высота трапеции равна $7$. Найдите тангенс острого угла.
Решение
Рассмотрим трапецию $ABCD$. Пусть $AB = CD, BK$ и $CM$ высоты. Тогда $AK = MD$ и $AD = BC + 2AK$. °$. Боковая сторона треугольника равна $7$. Найдите площадь этого треугольника.
°$. Боковая сторона треугольника равна $7$. Найдите площадь этого треугольника.
Решение
Пусть в $▵ ABC$ $∠ C=30°$, $AC=BC=7$ (см. рис.). $S_{ACB}={1} / {2} AC⋅ CB⋅ \sin ∠ ACB={1} / {2}⋅ 7⋅ 7⋅ \sin 30°={1} / {2}⋅ 49⋅ {1} / {2}={49} / {4}=12{,}25$.
Ответ: 12.25
Показать решение
Бесплатный интенсив
Задача 20
Периметр прямоугольника равен $28$, а площадь $48$. Найдите меньшую сторону прямоугольника.
Решение
Пусть $x$ и $y$ — две стороны прямоугольника. Из условия следует система уравнений:
$\{{\table {2(x+y)=28{,}}; {xy=48{.}};}$
Из первого уравнения системы: $x+y=14$
$y=14-x$.
Подставляя выражение для переменной $y$ во второе уравнение системы, получим:
$x(14-x)=48$
$x^2-14x+48=0$
$x_1=8$
$x_2=6$
Тогда $y_1=14-8=6$
$y_2=14-6=8$
Следовательно, меньшая сторона прямоугольника равна $6$.
Ответ: 6
Показать решение
Бесплатный интенсив
Показать еще
Для доступа к решениям необходимо включить уведомления от группы Турбо в вк — это займет буквально 10 секунд. Никакого спама, только самое важное и полезное для тебя. Ты всегда можешь запретить уведомления.
Включить уведомления
Бесплатный интенсив по математике (профильной)
3 огненных вебинара, домашние задания, беседа курса, личный кабинет, связь с преподавателем и многое другое.
Курс стартует 28 марта. Бесплатный интенсив
ЕГЭ по математике – теория
ЕГЭ по математике большинство выпускников считает самым сложным, поэтому к подготовке многие подходят основательно, штудируя теорию от корки до корки.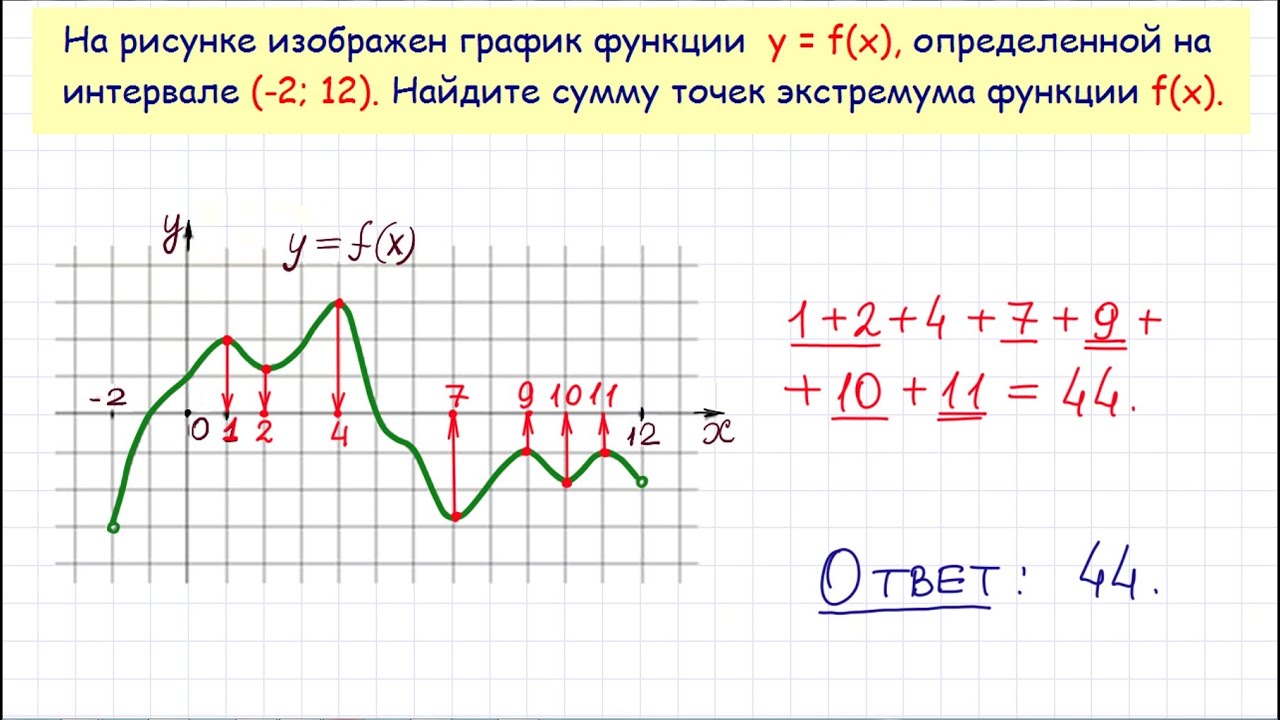 В принципе это правильно, но при ограниченном времени можно обойтись обязательным изучением только тех разделов школьного курса, которые вынесены на ЕГЭ.
В принципе это правильно, но при ограниченном времени можно обойтись обязательным изучением только тех разделов школьного курса, которые вынесены на ЕГЭ.Сейчас существует множество бесплатных инструментов, которые позволяют подготовиться к ЕГЭ и увеличить балл на 40% с минимальными временными затратами. Наиболее эффективными являются подписки на видеокурсы. Попробовать можно с
компанией Twostu
, тем более здесь это ничего не стоит.Содержание
- Где узнать, что будет на экзамене
- Какие математические навыки будут проверяться
- Темы ЕГЭ по математике
- Видео по теме
- Комментарии
Где узнать, что будет на экзамене
Тайны из этого не делается: список теоретическим тем, по которым будут составлены практические задания в КИМах, находится в открытом доступе – в кодификаторе элементов содержания (КЭС). Найти его можно на сайте ФИПИ в разделе «Демоверсии, спецификации, кодификаторы».
Найти его можно на сайте ФИПИ в разделе «Демоверсии, спецификации, кодификаторы».
Представлена теория для ЕГЭ по математике в виде таблицы, в которой детализируются темы по математике, алгебре, геометрии, началам анализа и теории вероятностей.
При подготовке нужно руководствоваться учебниками, одобренными Министерством просвещения (образования) для использования в школах, работающих по аккредитованным государством программам, так как тексты заданий в КИМах, по которым сдается ЕГЭ, составляются в формулировках, принятых именно в этих учебниках. Это поможет избежать неправильного понимания вопросов и, соответственно, неверных решений.
Какие математические навыки будут проверяться
В другом кодификаторе – требований к уровню подготовки выпускников (КТ, он тоже выложен на сайте ФИПИ) – указано то, что к моменту проведения ЕГЭ по математике участники экзамена должны уметь:
- вычислять и преобразовывать выражения;
- решать уравнения и неравенства, задачи на нахождение геометрических величин;
- работать с функциями и векторами;
- находить координаты;
- строить простейшие математические модели и исследовать их;
- применять имеющиеся навыки на практике и в реальной жизни.

На проверку этих умений и направлены экзаменационные задания ЕГЭ по математике. Поэтому подтягивать в первую очередь стоит теорию, необходимую для их выполнения.
Темы ЕГЭ по математике
На экзамене не будет вопросов, выходящих за пределы школьной программы. Всю исчерпывающую информацию можно найти в учебниках.
- Алгебра (числа, степени и корни).
- Основы тригонометрии.
- Логарифмы.
- Преобразования выражений.
- Уравнения и неравенства.
- Функции.
- Начало математического анализа.
- Геометрия.
- Элементы комбинаторики, статистики и теории вероятностей:
- бином Ньютона, формулы числа сочетаний и перестановок;
- вероятность событий;
- числовые характеристики рядов;
- использование вероятности и статистики в решении задач;
- одновременный и поочередный выбор;
- представление данных в таблице и графикой.

Конечно, на ЕГЭ по математике абсолютно все темы попасться не могут, например, в заданиях на функции будут предложены либо квадратичные, либо логарифмические. Но, чтобы подстраховаться и чувствовать себя во всеоружии, стоит изучить всю теорию, и хорошие баллы будут обеспечены.
МАТЕМАТИКА 4400/6400: Теория чисел | Пол Поллак
МАТЕМАТИКА 4400/6400: Теория чисел
MWF, 15:00-15:50, Исследовательский и образовательный центр Бойда, аудитория 323
Весна 2023
Текущие задания/другие материалы курса
Резюме курса на сегодняшний день (в обратном хронологическом порядке)
2 2
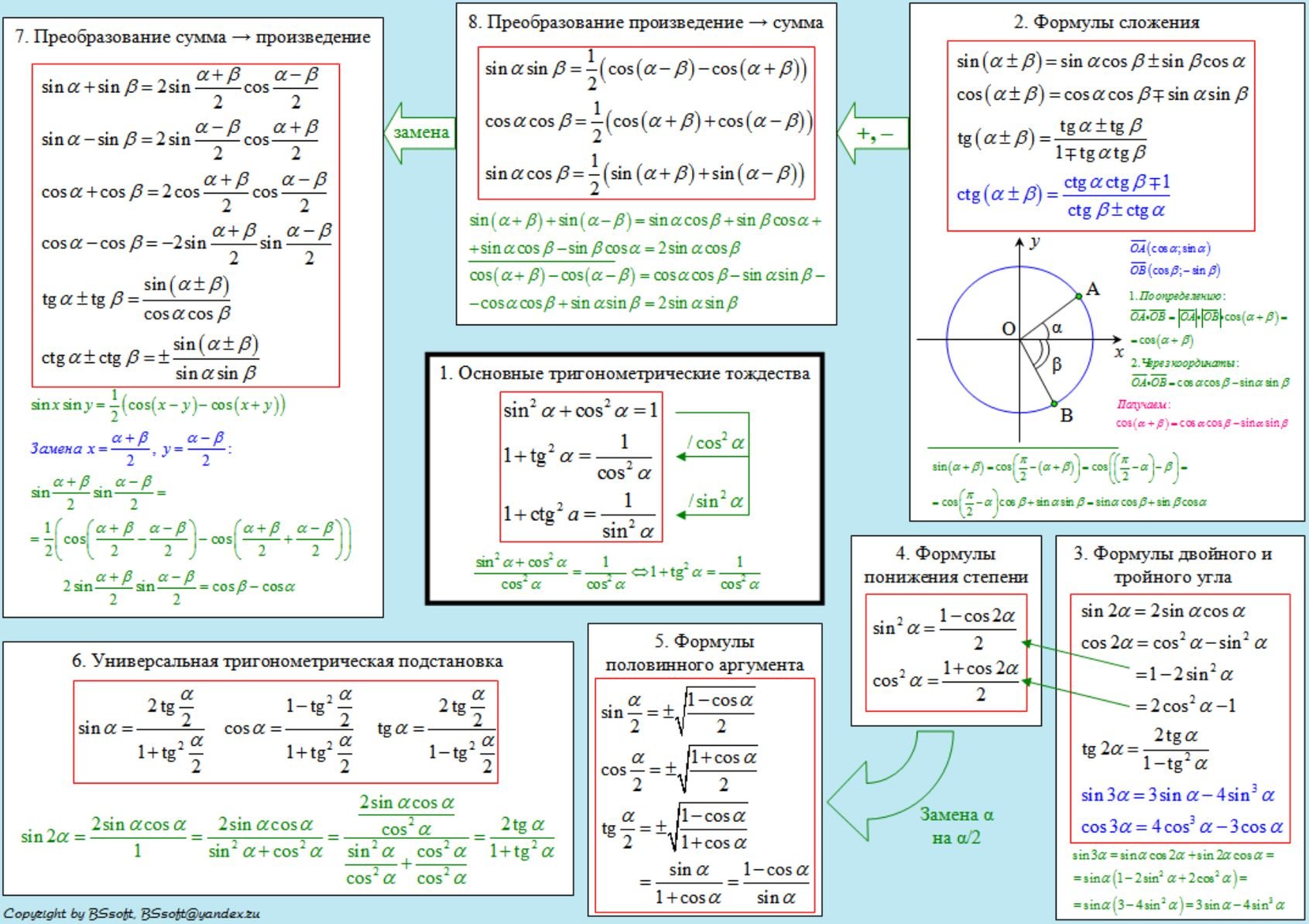 Знакомство с символом Якоби.
Знакомство с символом Якоби. Критерий Гаусса. Примеры критерия Гаусса для вычисления $(\frac{2}{p})$ для $p$ в классах вычетов по модулю $8$.
Критерий Гаусса. Примеры критерия Гаусса для вычисления $(\frac{2}{p})$ для $p$ в классах вычетов по модулю $8$.
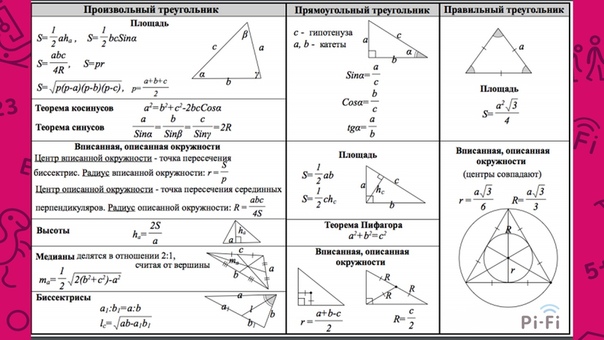 Существование разложений на простые числа в $\mathbb{Z}[i]$. Стратегия доказательства алгоритма деления в $\mathbb{Z}[i]$.
Существование разложений на простые числа в $\mathbb{Z}[i]$. Стратегия доказательства алгоритма деления в $\mathbb{Z}[i]$. Начало обзора уникальной факторизации.
Начало обзора уникальной факторизации.Краткое содержание курса
Теория чисел — это изучение натуральных чисел 1, 2, 3, $\dots$ и связанных с ними объектов. Заманчиво предположить, что такие простые вещи, как счет чисел, должны быть достаточно хорошо поняты. Но это далеко не так! Действительно, теория чисел во многом обязана своим обаянием множеству легко формулируемых задач, которые можно объяснить детям среднего школьного возраста, которые до сих пор не поддаются решению, несмотря на сотни лет усилий величайших математиков мира.
Этот курс предназначен для ознакомления с фундаментальными результатами, с особым вниманием к новаторским достижениям 18-го и 19-го веков. Мы начнем с обзора теории простой факторизации и сравнений, с которыми вы познакомились в MATH 4000. Одной из центральных ранних тем MATH 4000 является изучение линейных сравнений: $ax\equiv b\pmod{m}$. Одной из основных тем этого курса будет изучение квадратичных сравнений. 2\equiv a\pmod{p}$ имеет решение. Например, если $a=3$, это разрешимо при $p=11$ и $p=13$, но не при $p=5$ или $p=7$; какое общее правило? Ответ придет из красивого и глубокого результата Гаусса, 92.$$
Мы также можем говорить о том, как простые числа распределяются на прямой с действительными числами, и об основах алгебраической теории чисел (где изучается система «целых чисел», принадлежащая конечному расширению рациональных чисел).
2\equiv a\pmod{p}$ имеет решение. Например, если $a=3$, это разрешимо при $p=11$ и $p=13$, но не при $p=5$ или $p=7$; какое общее правило? Ответ придет из красивого и глубокого результата Гаусса, 92.$$
Мы также можем говорить о том, как простые числа распределяются на прямой с действительными числами, и об основах алгебраической теории чисел (где изучается система «целых чисел», принадлежащая конечному расширению рациональных чисел).
Рекомендуемый учебник
Книга Левека охватывает все стандартные темы, хорошо раскрывает их и стоит удивительно недорого. Вам , а не нужна книга для этого курса, но это отличное дополнение к любой математической библиотеке.
Даты экзаменов
Есть два промежуточных экзамена в классе, а также выпускной экзамен.
- Промежуточный семестр №1: пятница, 3 марта
- Промежуточный экзамен № 2: среда, 19 апреля.

- Заключительный экзамен: среда, 3 мая, 15:30–18:30 (место уточняется)
Вступительные экзамены не проводятся. Итоговый экзамен в сумме .
Домашнее задание/экзамены/оценка
Ваша оценка состоит из следующих взвешенных компонентов:
- Каждый промежуточный период: 22,5% (всего 45%)
- Домашнее задание: 25%
- Итоговый экзамен: 30%
Задания HW будут содержать задачи, обязательные для всех учащихся, а также отмеченные звездочкой задачи, обязательные только для учащихся MATH 6400. Учащиеся MATH 4400 могут решить эти дополнительные задачи за дополнительные баллы.
Ожидается, что вы будете участвовать в занятиях. В частности, посещаемость этого курса составляет , требуется . Более четырех пропусков без уважительной причины могут привести к исключению вас из курса. Держите меня в курсе всякий раз, когда у вас возникает конфликт, который требует, чтобы вы пропустили урок, и это не должно быть проблемой.
В частности, посещаемость этого курса составляет , требуется . Более четырех пропусков без уважительной причины могут привести к исключению вас из курса. Держите меня в курсе всякий раз, когда у вас возникает конфликт, который требует, чтобы вы пропустили урок, и это не должно быть проблемой.
Все экзамены проводятся в классе, с закрытой тетрадью и закрытыми заметками.
Домашнее задание будет собираться в классе один раз в неделю или две. Запоздалая домашняя работа не принимается. (Если вам необходимо сдать HW раньше, это можно организовать.) В конце семестра ваш самый низкий балл HW будет сброшен.
При выполнении домашних заданий сотрудничество разрешено и даже очень поощряется. Математика не была бы такой увлекательной, если бы мы не могли говорить о ней с другими людьми! Однако копирование (из учебника или другого ученика) и поиск в Интернете не допускаются, и вы должны самостоятельно написать свои собственные окончательные решения. Имейте в виду, что, вступая в UGA, вы уже соглашаетесь соблюдать Кодекс чести UGA, подробно описанный на странице https://honesty.uga.edu/Academic-Honesty-Policy/.
Имейте в виду, что, вступая в UGA, вы уже соглашаетесь соблюдать Кодекс чести UGA, подробно описанный на странице https://honesty.uga.edu/Academic-Honesty-Policy/.
На практике это означает, что вы можете обсуждать домашние задания и их решения со своими одноклассниками, но вы не можете сдавать решение, если не понимаете его сами. Разумное эмпирическое правило состоит в том, что вы должны быть в состоянии объяснить мне свои решения устно (со всеми их кровавыми подробностями), если вас попросят сделать это.
Специальные условия
Учащиеся с ограниченными возможностями, которым могут потребоваться специальные условия, должны связаться со мной как можно скорее. Могут потребоваться соответствующие документы об инвалидности. Для получения дополнительной информации посетите страницу Ресурсного центра по вопросам инвалидности.
Отказ от ответственности
Программа курса представляет собой общий план курса; могут потребоваться отклонения, объявленные классу инструктором.
Как изучать математику в колледже
Body
Введение
Почему у тебя не лучшие оценки по математике? Вы чувствуете, что потратили на это все время, которое от вас можно ожидать, и что вы все еще не получаете результатов? Или ты просто ленивый? Если вам лень, этот материал не для вас. Но если вы пытались, но ваши оценки по-прежнему не показывают ваших способностей, или если вы получали хорошие оценки, но по-прежнему чувствуете, что математика не имеет для вас большого значения, очень вероятно, что вы не знаете, как учиться эффективно. Этот материал призван помочь вам эффективно изучать математику.
Некоторым из вас может показаться, что у вас есть собственные успешные методы обучения, отличные от описанных здесь. В этом случае вам не нужно думать, что вы должны изменить свои методы, хотя вы можете извлечь пользу из сравнения своих методов с этими.
С другой стороны, некоторым из вас может показаться, что предложения на следующих страницах слишком амбициозны, что они потребуют больше времени и усилий, чем вы готовы потратить. Вероятно, вы будете правы. Мы не можем ожидать, что все сделаем идеально, но мы можем сделать все, что в наших силах. Из предложенных предложений вы можете выбрать те, которые могут помочь вам больше всего, и когда вы обнаружите, что ваша работа улучшается, вы можете попробовать другие предложения. Так что смейтесь, если хотите, над этими амбициозными предложениями, но затем попробуйте некоторые из них, честно попробуйте и посмотрите на результаты.
Вероятно, вы будете правы. Мы не можем ожидать, что все сделаем идеально, но мы можем сделать все, что в наших силах. Из предложенных предложений вы можете выбрать те, которые могут помочь вам больше всего, и когда вы обнаружите, что ваша работа улучшается, вы можете попробовать другие предложения. Так что смейтесь, если хотите, над этими амбициозными предложениями, но затем попробуйте некоторые из них, честно попробуйте и посмотрите на результаты.
Как учиться:
- Советы по выполнению домашних заданий
- Как сделать так, чтобы ваши ошибки помогали вам учиться Советы
- Работа в классе: как максимально эффективно использовать свое время в классе, советы
- Как пользоваться советами из учебника
- Советы по просмотру тестов
- Советы по сдаче тестов
Вернуться к началу
Домашнее задание
Существует распространенное заблуждение, что домашнее задание — это прежде всего то, что в конечном итоге нужно сдать учителю. На самом деле домашнее задание — это, прежде всего, средство изучения фундаментальных идей и процессов в математике, а также выработки привычек к аккуратности и точности. То, что передается учителю, является лишь побочным продуктом этого процесса обучения. Следующая четырехступенчатая процедура является предложением для того, чтобы сделать ваше домашнее обучение эффективным:
На самом деле домашнее задание — это, прежде всего, средство изучения фундаментальных идей и процессов в математике, а также выработки привычек к аккуратности и точности. То, что передается учителю, является лишь побочным продуктом этого процесса обучения. Следующая четырехступенчатая процедура является предложением для того, чтобы сделать ваше домашнее обучение эффективным:
- Ориентируйтесь. Подумайте несколько минут, просмотрите свои заметки и просмотрите книгу, чтобы ясно увидеть, над какими идеями вы работали.
- Выстраивайте идеи. Подумайте об идеях, законах и методах дневного задания или урока. Не забывайте знакомиться со всеми новыми словами в вашем математическом словаре. Попытайтесь напомнить себе о любых предупреждениях об ошибках, чтобы избежать их, которые мог упомянуть учитель. Просмотрите все приведенные примеры, чтобы убедиться, что вы действительно понимаете иллюстрируемые концепции.
- Выполнить задание. Подумайте об идеях, которые иллюстрируют упражнения.
 Вы должны расширять свое понимание, а также получать ответы. Следующие советы помогут вам сделать работу лучше:
Вы должны расширять свое понимание, а также получать ответы. Следующие советы помогут вам сделать работу лучше:- Точно получить задание с доски. Выделите в блокноте определенное место, куда вы записываете задание или урок. Если вы не понимаете задание, не стесняйтесь спрашивать.
- Следуйте инструкциям.
- Работайте аккуратно и аккуратно.
- Покажите свою работу полностью, а не только ответ. Это поможет вам и вашему учителю, когда вы проверяете ошибки.
- Всегда проверяйте, правильно ли вы выполнили все простые арифметические действия.
- Выполняйте работу как можно быстрее, пока не забыли все инструкции.
- Если вы застряли, не сдавайтесь! Просмотрите книгу и свои заметки, чтобы найти идеи, связанные с проблемой. Если ваша работа над проблемой кажется совершенно запутанной, иногда полезно полностью отказаться от своей статьи и начать новую. Если вы все еще не можете очистить свое мышление, как можно скорее расспросите учителя о проблемах.

- Помогите кому-нибудь, если можете. Нет лучшего способа изучить тему, чем пытаться ее преподавать! Кроме того, часто бывает полезно обратиться к однокласснику, когда вы не понимаете проблему. Часто они могут объяснить концепцию вам так же (если не лучше), как и учитель.
Вернуться к началу
Как сделать так, чтобы ваши ошибки помогали вам учиться
Что вы делаете, если в вашем домашнем задании или контрольной дается неверный ответ? Выбрасываете ли вы его и забываете, а затем совершаете ту же ошибку в следующий раз? Если вы мудры, эти ошибки вас чему-то научат. Вот что вы можете сделать:
- Проанализируйте ошибку, чтобы определить, что вы сделали не так.
- Если это ошибка по невнимательности, и вы действительно знали, как правильно выполнить работу, запишите ее, и если вы обнаружите, что продолжаете часто делать ошибки по невнимательности, начните работать более внимательно.
- Если вы не можете найти свою ошибку, попросите учителя или одноклассника помочь вам.

- Держите в своей записной книжке страницу под названием «Предупреждение: ошибки, которых следует избегать». На той же странице напишите описание исправленного способа выполнения такого рода упражнений, обязательно подчеркнув важную идею, стоящую за ним.
Вернуться к началу
Классная работа: как максимально эффективно использовать время в классе
- Приготовьтесь. За минуту или две до начала занятия подумайте, над чем вы недавно работали.
- Иметь все необходимое оборудование: книгу, карандаши или ручки, тетрадь, домашнее задание.
- Быстро и точно запишите задание.
- Концентрат. Это требует усилий, если вы из тех, чей ум склонен блуждать.
- Задавайте вопросы, когда не понимаете.
- Слушайте вопросы и ответы других в классе. Когда другой ученик отвечает на вопрос, подумайте, как бы вы ответили на этот вопрос.
- Примите участие в обсуждении класса.
- Не пишите не вовремя. Когда вы делаете заметки, следите за тем, чтобы ничего не пропустить.
 Делая заметки, вы должны попытаться сделать две противоречивые вещи. Один из них — сделать ваши заметки достаточно полными и точными, чтобы впоследствии они были вам полезны. Во-вторых, делайте свои заметки достаточно краткими, чтобы вы могли продолжать слушать то, что говорится в классе.
Делая заметки, вы должны попытаться сделать две противоречивые вещи. Один из них — сделать ваши заметки достаточно полными и точными, чтобы впоследствии они были вам полезны. Во-вторых, делайте свои заметки достаточно краткими, чтобы вы могли продолжать слушать то, что говорится в классе.
Наверх
Как пользоваться учебником
- Используйте указатель и глоссарий в конце книги, особенно если вы забыли значение слова.
- Когда в вашей книге приводится пример для иллюстрации какой-либо идеи, внимательно проанализируйте его на наличие идей, лежащих в его основе, вместо того, чтобы просто пытаться сделать ваши упражнения похожими на пример.
- Если вы не можете выполнить упражнение, перечитайте пояснительный материал в книге и/или просмотрите свои конспекты.
- Максимально используйте подсказки в конце каждой главы.
Вернуться к началу
Как проверять экзамены
- Начинайте просматривать заблаговременно, чтобы у вас было время для тщательной неспешной работы и чтобы вы могли лечь спать пораньше накануне экзамена.

- Обязательно просмотрите свои заметки и примеры, которые там есть. Если они не имеют для вас смысла, вы сделали недостаточно заметок!
- Если есть какие-то формулы, за которые вы отвечаете, составьте их список, а затем потренируйтесь произносить или писать их.
- Используйте обзорные материалы в конце каждой главы. Если у вас возникли проблемы с проблемой, вернитесь к этому разделу книги и переделайте некоторые проблемы там.
- Если бы вы были учителем, какие вопросы вы бы задали на тесте? Подготовьтесь к этим вопросам.
- Поскольку говорится, что «практика делает совершенным», один из лучших способов подготовиться к тесту – решить некоторые задачи, которые вам ранее были заданы. Просмотрите свою домашнюю работу, чтобы убедиться, что вы понимаете процедуру, которую вы использовали в каждом разделе.
- Хорошо отдохните в ночь перед экзаменом!
- НЕ БЕСПОКОИТЬСЯ!
Вернуться к началу
Как сдавать тесты
- Когда вы сдаете тест, придерживайтесь правильного отношения — гордитесь тем, что делаете свою работу как можно лучше.
 Не пытайтесь «обойтись», делая как можно меньше. Имейте уверенность в своих силах.
Не пытайтесь «обойтись», делая как можно меньше. Имейте уверенность в своих силах. - Будьте серьезны и обеспокоены тестом, чтобы сделать все возможное, но не беспокойтесь до тревожности. Один только страх может заставить человека плохо сдать тест, независимо от его способностей и знаний.
- Иметь все необходимое оборудование.
- СЛЕДУЙТЕ ИНСТРУКЦИЯМ. Внимательно прочитайте и внимательно прослушайте любые специальные инструкции, например, где должны быть написаны ответы, любые изменения или исправления и т. д.
- В начале быстро просмотрите весь тест и, если от вас не требуется отвечать на вопросы в указанном порядке, сначала ответьте на те, в которых вы уверены.
- Если вы не можете ответить на вопрос, оставьте его и перейдите к другому, а позже вернитесь к сложному. Часто, начав с чистого листа, вы вдруг гораздо лучше понимаете, что делать.
- Постарайтесь четко показать, что вы делаете. Помните, что учитель не умеет читать мысли, и ваша оценка может зависеть от того, увидит ли учитель по вашей работе, что вы понимаете, что делаете.





 Вы должны расширять свое понимание, а также получать ответы. Следующие советы помогут вам сделать работу лучше:
Вы должны расширять свое понимание, а также получать ответы. Следующие советы помогут вам сделать работу лучше:

 Делая заметки, вы должны попытаться сделать две противоречивые вещи. Один из них — сделать ваши заметки достаточно полными и точными, чтобы впоследствии они были вам полезны. Во-вторых, делайте свои заметки достаточно краткими, чтобы вы могли продолжать слушать то, что говорится в классе.
Делая заметки, вы должны попытаться сделать две противоречивые вещи. Один из них — сделать ваши заметки достаточно полными и точными, чтобы впоследствии они были вам полезны. Во-вторых, делайте свои заметки достаточно краткими, чтобы вы могли продолжать слушать то, что говорится в классе.
 Не пытайтесь «обойтись», делая как можно меньше. Имейте уверенность в своих силах.
Не пытайтесь «обойтись», делая как можно меньше. Имейте уверенность в своих силах.
Leave A Comment