\[x=A{\cos \left({\omega }_0t+\varphi \right)=B{\sin \left({\omega }_0t+{\varphi }_1\right)\ }\ }\left(2\right),\]
где ${\omega }_0=\sqrt{\frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$ и $B$ — амплитуда колебаний; ${(\omega }_0t+\varphi )$ — фаза колебаний; $\varphi $ и ${\varphi }_1$ — начальные фазы колебаний.
Частота и период колебаний пружинного маятника
Косинус (синус) — периодическая функция, смещение $x$ будет принимать одинаковые значения через определенные одинаковые промежутки времени, которые называют периодом колебаний. Обозначают период буквой T.
Еще одной величиной, характеризующей колебания является величина обратная периоду колебаний, ее называют частотой ($\nu $):
\[T=\frac{1}{\nu }\left(3\right).\]
Период связан с циклической частотой колебаний как:
 \]
\]Зная, что для пружинного маятника ${\omega }_0=\sqrt{\frac{k}{m}}$, период колебаний его определим как:
\[T=2\pi \sqrt{\frac{m}{k}}\ \left(5\right).\]
Из выражения (5) мы видим, что период колебаний пружинного маятника зависит от массы груза, находящегося на пружине и коэффициента упругости пружины, но не зависит от амплитуды колебаний (A). Такое свойство колебаний называют изохронностью. Изохронность выполняется до тех пор, пока справедлив закон Гука. При больших растяжениях пружины закон Гука нарушается, при этом возникает зависимость колебаний от амплитуды. Отметим, что формула (5) для вычисления периода колебаний пружинного маятника справедлива при малых колебаниях.
Единицей измерения периода являются единицы времени, в Международной системе единиц это секунды:
\[\left[T\right]=с.\]
Примеры задач на период колебания пружинного маятника
Пример 1
Задание. К упругой пружине прикрепили небольшой груз, при этом пружина растянулась на $\Delta x$=0,09 м. Каким будет период колебаний данного пружинного маятника, если его вывести из равновесия?
К упругой пружине прикрепили небольшой груз, при этом пружина растянулась на $\Delta x$=0,09 м. Каким будет период колебаний данного пружинного маятника, если его вывести из равновесия?
Решение. Сделаем рисунок.
Рассмотрим состояние равновесия пружинного маятника. Груз прикрепили, после этого пружина растянулась на величину $\Delta x$, маятник находится в состоянии равновесия. На груз действуют две силы: сила тяжести и сила упругости. Запишем второй закон Ньютона для состояния равновесия груза:
\[m\overline{g}+{\overline{F}}_u=0\ \left(1.1\right).\]
Запишем проекцию уравнения (1.1) на ось Y:
\[mg=F_u\left(1.2\right).\]
Так как груз по условию задачи небольшой, пружина растянулась не сильно, следовательно выполняется закон Гука, величину силы упругости найдем как:
\[F_u=k\Delta x\ \left(1.3\right).\]
Используя выражения (1.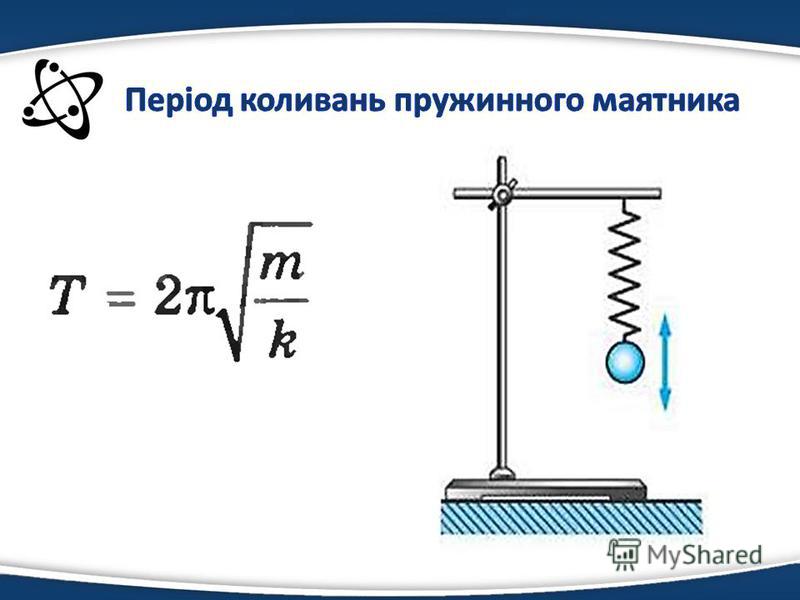
\[T=2\pi \sqrt{\frac{0,09\ \ }{9,8}\ \approx 0,6\ (с)}\]
Ответ. $T$=0,6 с
Пример 2
Задание. Две пружины с жесткостями $k_1$ и $k_2$ соединены последовательно (рис.2), к концу второй пружины присоединен груз массы $m$, Каков период колебаний данного пружинного маятника, если массами пружин можно пренебречь, сила упругости, действующая на груз, подчиняется закону Гука.
Решение.Период колебаний пружинного маятника равен:
\[T=2\pi \sqrt{\frac{m}{k}}\ \left(2.1\right).\]
Если две пружины соединены последовательно, то их результирующая жесткость ($k$) находится как:
\[\frac{1}{k}=\frac{1}{k_1}+\frac{1}{k_2}\to k=\frac{k_1k_2}{k_1{+k}_2}\left(2.2\right).\]
Вместо $k$ в формулу для вычисления периода пружинного маятника подставим правую часть выражения (2.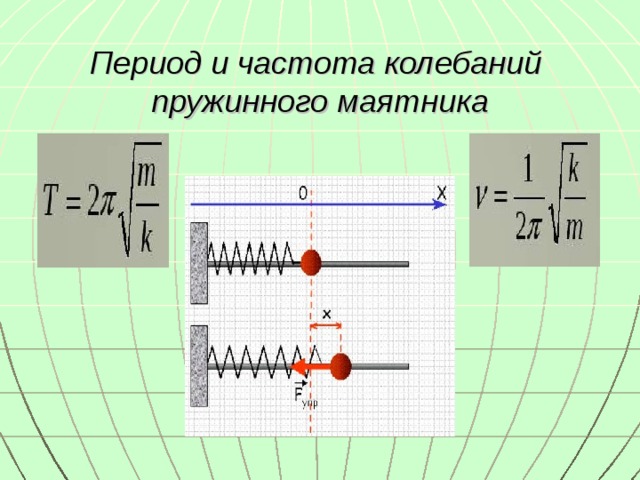 2), имеем:
2), имеем:
\[T=2\pi \sqrt{\frac{m(k_1{+k}_2)}{k_1k_2}}.\]
Ответ. $T=2\pi \sqrt{\frac{m(k_1{+k}_2)}{k_1k_2}}$
Читать дальше: плечо силы.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Период пружинного маятника, теория и онлайн калькуляторы
Период пружинного маятника, теория и онлайн калькуляторыОпределение и основные понятия пружинного маятника
Одной из самых простых систем, в которой можно возбудить механические колебания является система, состоящая из пружины, с коэффициентом упругости $k$, на которой подвешен груз с массой $m$. Пусть система расположена вертикально. На груз действуют сила упругости и сила тяжести, если систему вывести из состояния равновесия и предоставить самой себе, то груз будет совершать колебания.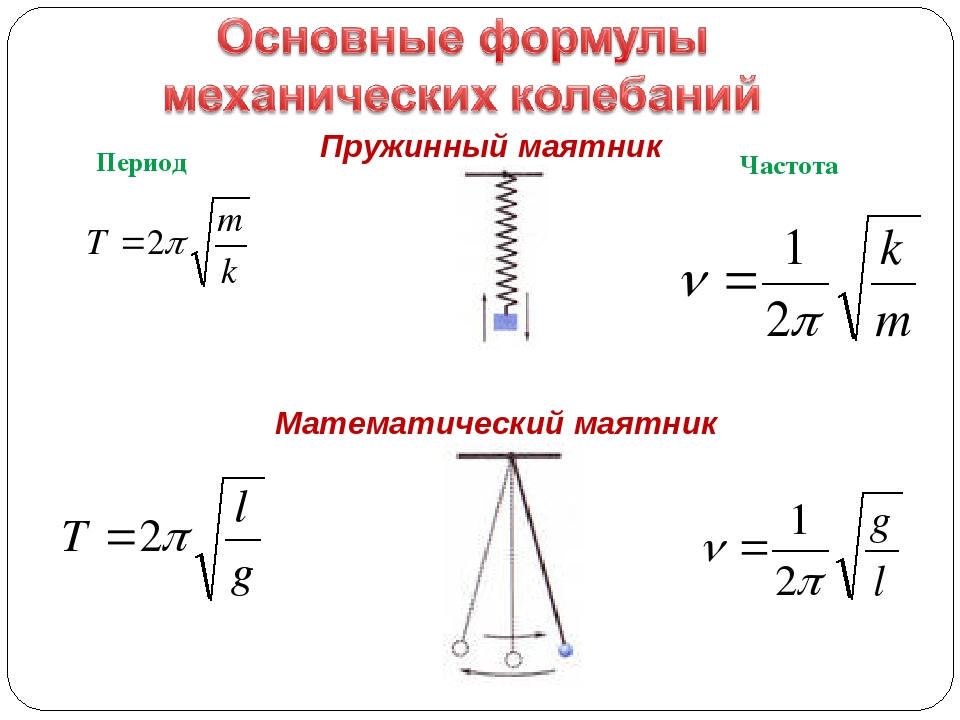
\[x=A{\cos \left({\omega }_0t+\varphi \right)\ }\left(2\right),\]
где ${\omega }_0=\sqrt{\frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$ — амплитуда колебаний; ${(\omega }_0t+\varphi )$ — фаза колебаний; $\varphi $ — начальная фаза колебаний.
Период колебаний пружинного маятника
Косинус является периодической функцией, следовательно, смещение $x$ будет принимать одинаковые значения через определенные одинаковые промежутки времени, которые называются периодом колебаний. Его обозначают буквой.
Другая величина, характеризующая колебания, это величина обратная периоду колебаний, называемая частотой ($\nu $):
\[T=\frac{1}{\nu }\left(3\right).\]
Период связан с циклической частотой колебаний как:
\[T=\frac{2\pi }{{\omega }_0}\left(4\right).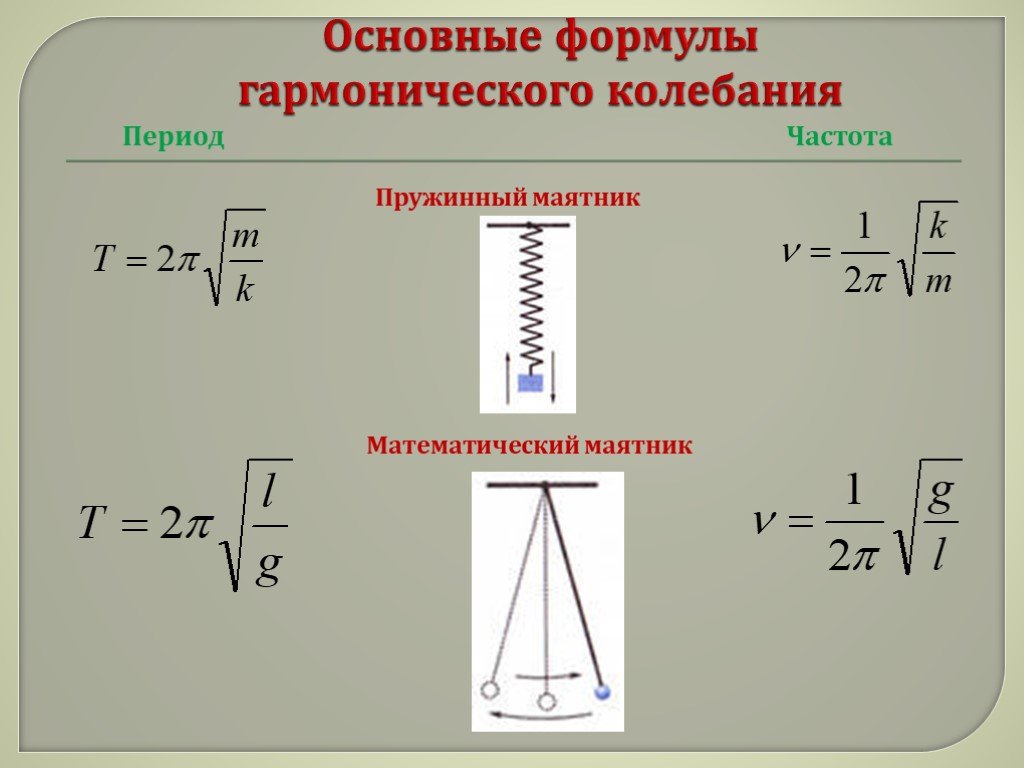 \]
\]
Для пружинного маятника ${\omega }_0=\sqrt{\frac{k}{m}}$, следовательно, период колебаний пружинного маятника равен:
\[T=2\pi \sqrt{\frac{m}{k}}\ \left(5\right).\]
Формула (5), говорит о том, что период колебаний пружинного маятника пропорционален квадратному корню от массы груза, подвешенного к пружине, обратно пропорционален квадратному корню от коэффициента упругости пружины, и не зависит от амплитуды колебаний (A). Это свойство колебаний называется изохронностью. Изохронность реализуется до тех пор, пока справедлив закон Гука. При больших растяжениях пружины закон Гука нарушается, и появляется зависимость периода колебаний от амплитуды. Следует сказать, что выражение (5) для вычисления периода колебаний пружинного маятника справедливо при малых колебаниях.
Единица измерения периода это единицы времени, в Международной системе единиц это секунды:
Примеры задач на колебания пружинного маятника
Пример 1
Задание: Пружинный маятник совершает гармонические колебания. 2}\approx 9,9\ (\frac{Н}{м}).\]
2}\approx 9,9\ (\frac{Н}{м}).\]
Ответ: $k\approx 9,9\frac{Н}{м}$
Читать дальше: плавание тел.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
домашнее задание и упражнения — Влияние магнитного поля на период времени пружинного маятника
спросил
Изменено 3 года, 10 месяцев назад
Просмотрено 772 раза
$\begingroup$
Предположим, что у нас есть пружинный маятник, а рядом магнит. Если предположить, что пружина притягивается к магниту, уменьшается ли период?
Формула периода времени = 2𝜋√m/k Будет ли магнитное поле иметь тот же эффект, что и увеличение g?
- домашние задания и упражнения
- экспериментальная физика
- гармонический осциллятор
$\endgroup$
5
$\begingroup$
Нетехническая версия: магнит тянет груз вниз, и величина этой силы увеличивается по мере растяжения пружины. Пружина тянет массу вверх, и величина этой силы также увеличивается по мере растяжения пружины. Таким образом, действие магнита заключается в уменьшении эффективной жесткости пружины, поскольку магнит действует против пружины. Чистая сила, действующая на массу от пружины и магнита вместе, увеличивается медленнее, чем сила от одной только пружины; Другими словами, добавление магнита в основном эквивалентно замене оригинальной пружины менее жесткой. Поскольку период массы на пружине уменьшается по мере уменьшения жесткости пружины, период колебаний с магнитом будет меньше, чем без магнита.
Пружина тянет массу вверх, и величина этой силы также увеличивается по мере растяжения пружины. Таким образом, действие магнита заключается в уменьшении эффективной жесткости пружины, поскольку магнит действует против пружины. Чистая сила, действующая на массу от пружины и магнита вместе, увеличивается медленнее, чем сила от одной только пружины; Другими словами, добавление магнита в основном эквивалентно замене оригинальной пружины менее жесткой. Поскольку период массы на пружине уменьшается по мере уменьшения жесткости пружины, период колебаний с магнитом будет меньше, чем без магнита.
Техническая версия: Пусть $z$ — вертикальная координата массы, положительная величина $z$ отсчитывается от вниз на от нерастянутого положения пружины. На массу будут воздействовать три силы:
- Гравитация, где $F_g = +mg$;
- Сила пружины, при $F_s = — k z$; и
- Сила $F_m(z)$ со стороны магнита. Эта сила будет (предположительно) направлена вниз для всех значений $z$ и, как правило, будет возрастать по мере увеличения $z$: $dF_m/dz > 0$.

Пусть $z_0$ — координата, в которой система находится в равновесии. В этот момент чистые силы, действующие на массу, должны компенсироваться:
$$
F_g + F_s + F_m = mg — k z_0 + F_m(z_0)= 0.
$$
Теперь представим перемещение массы на небольшое расстояние $\epsilon$ от положения равновесия; другими словами, $z = z_0 + \epsilon$. Поскольку $\ddot{z} = \ddot{\epsilon}$, второй закон Ньютона принимает вид:
\начать{выравнивать}
м \ddot{\epsilon} &= F_g + F_s + F_m \\
&= mg — k(z_0 + \epsilon) + F_m(z_0 + \epsilon) \\
&\приблизительно мг — k z_0 — k \epsilon + F_m(z_0) + F_m'(z_0) \epsilon
\end{выравнивание}
где мы разложили $F_m(z_0 + \epsilon)$ в ряд Тейлора на последнем шаге. Тогда из условия равновесия это сводится к
$$
m \ddot{\epsilon} = -(k — F_m'(z_0)) \epsilon
$$
и поэтому частота колебаний
$$
\omega = \sqrt{ \frac{k — F_m'(z_0)}{m}} < \sqrt{\frac{k}{m}}.
$$
Поскольку угловая частота массы в отсутствие магнита равна $\sqrt{k/m}$, заключаем, что период колебаний увеличивает в присутствии магнита, поэтому период уменьшается .
(Все это предполагает, что $F_m'(z_0) < k$. Если бы это было не так, то положение равновесия было бы неустойчивым.)
$\endgroup$
2
Зарегистрируйтесь или войдите
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
ньютоновская механика — Почему период времени маятника с пружиной постоянной силы $k$ и грузом значительной массы $m$ на Луне такой же, как и на Земле?
Задавать вопрос
спросил
Изменено 2 года, 3 месяца назад
Просмотрено 404 раза
$\begingroup$
Вопрос, с которым я столкнулся сегодня в классе:
Как изменится период времени нагруженной пружины, когда ее доставят на Луну? 9\frac{1}{2}$$
$T$ в этом выражении не зависит от $g$. Таким образом, период времени нагруженной пружины на Луне будет таким же, как и на Земле.
Мои мысли
Я думаю, что значение $k$ для пружины, подвешенной вверх ногами, зависит от гравитационного притяжения. Из закона Гука получаем, что возвращающая сила пружины линейно зависит от перемещения.
$$ F(x) = -k(x) \\ k = \frac{-F(x)}{x} $$
Когда масса подвешена вертикально, $x$ зависит от гравитационного притяжения $g $. 9\frac{1}{4} $$
Таким образом, период времени на Луне будет немного больше, чем на Земле. Может ли кто-нибудь сказать мне, правильно ли я это сделал?
- ньютоновская механика
- ньютоновская гравитация
- гармонический осциллятор
- пружина
- осцилляторы
$\endgroup$
$\begingroup$
Обратите внимание, что масса $m$ и жесткость пружины $k$ на Земле такие же, как и на Луне. Следовательно, период времени пружины не зависит от разницы, вызванной ускорением силы тяжести. Следовательно, он не изменится, когда его доставят на Луну.
Следовательно, он не изменится, когда его доставят на Луну.
Я думаю, что значение 𝑘 для пружины, подвешенной вверх ногами, зависит от гравитационного притяжения
Нет. Это константа. Приведенный вами математический аргумент содержит много ошибок, но достаточно сказать, что период нагруженной пружины не будет отличаться.
Единственное, что будет отличаться, это положение равновесия массы, в этом случае на Луне она будет выше.
$\endgroup$
$\begingroup$
Чтобы проиллюстрировать независимость величины гравитационного поля, можно установить систему пружинных масс на горизонтальном столе, и при отсутствии трения период колебаний все равно будет $2\pi \sqrt{\frac mk}$ при условии, что пружина может подвергаться как сжатию, так и растяжению.
Причина такой независимости в том, что восстанавливающая сила, $F$, зависит от смещения массы из положения равновесия, на нее не действует результирующая сила, которая не является функцией гравитационного поля и массы $m$ , также не зависит от гравитационного поля, поэтому ускорение массы $a=\frac Fm$ не зависит от гравитационного поля.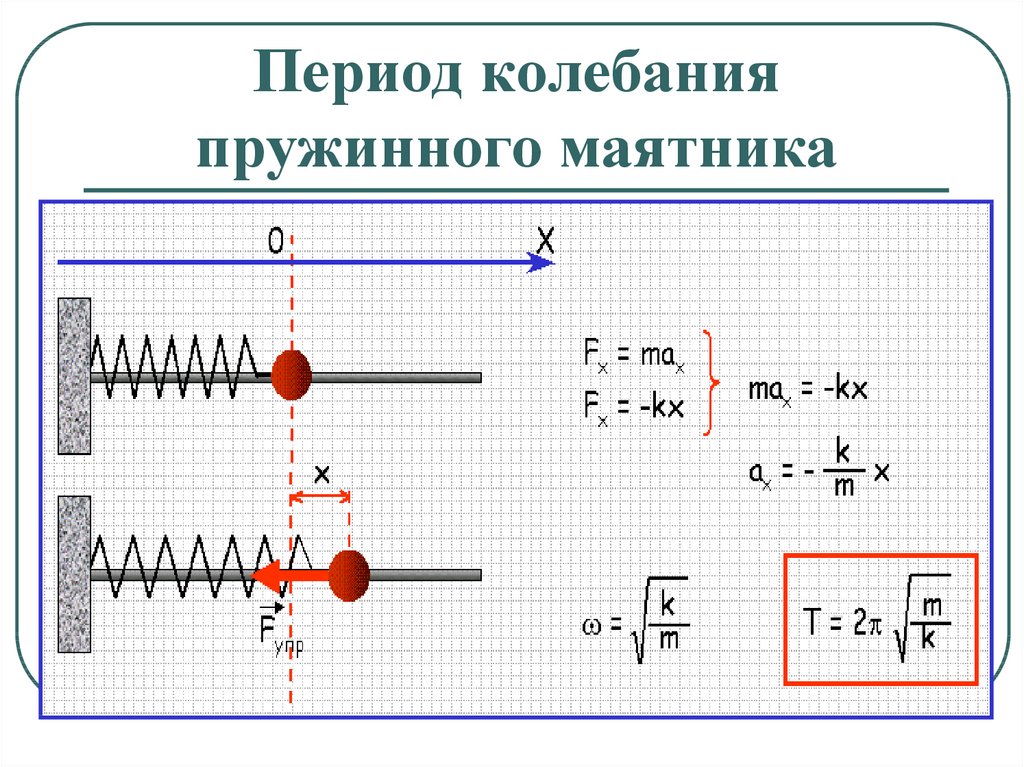
Соотношение $l$ и $g$, которое, по-видимому, показывает зависимость периода от силы гравитационного поля, не показывает этого, потому что $l$ и $g$ не независимы друг от друга и подобны уравнению $kl =mg$, так что $g$ увеличивается вместе с $l$ в той же пропорции.
$\endgroup$
$\begingroup$
… имеем, что возвращающая сила в пружине линейно зависит от смещения. $$F(x) = -k(x) \\ k = \frac{-F(x)}{x}$$
Этот расчет силы неверен.
Собственно сила ($F$) состоит из двух частей:
- Возвращающая сила пружины ($-kx$) который пропорционален текущему смещению ($x$). И константа пружины $k$ по-прежнему остается постоянной.
- Сила гравитации ($mg$) которое не зависит от текущего смещения ($x$)
Итак, у нас есть общая сила $$F=-kx+мг. \tag{1}$$
Согласно второму закону Ньютона ($m\ddot{x}=F$) получаем уравнение движения
$$m\ddot{x}=-kx+mg.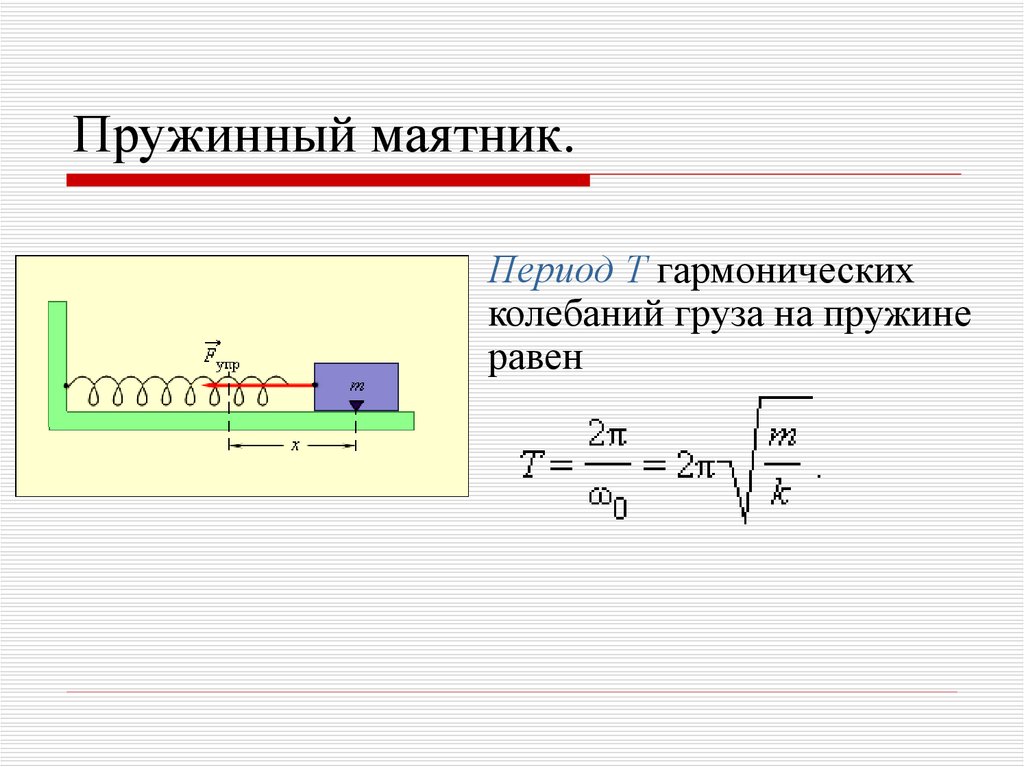

Leave A Comment