Перемещение тела при равноускоренном движении

Прямолинейным равноускоренным движением называется движение, при котором скорость тела за любые равные промежутки времени изменялась на одинаковую величину. И основной характеристикой такого движения являлось ускорение — это физическая векторная величина, характеризующая быстроту изменения скорости.

Как определить координату тела, пройденный путь и перемещение при прямолинейном равноускоренном движении?

Это можно сделать, если рассмотреть прямолинейное равноускоренное движение как набор большого количества очень малых равномерных перемещений тела.

Первым решил задачу местоположения тела в определённый момент времени при ускоренном движении итальянский учёный Галилео Галилей. Галилей использовал наклонную плоскость с гладкой канавкой посередине, по которой скатывались латунные шары. По водным часам он засекал определённый интервал времени и фиксировал расстояния, которые за это время преодолевали шары. Галилей выяснил, что если время увеличить в два раза, то шары прокатятся в четыре раза дальше (т.е. зависимость квадратичная). Это опровергало мнение Аристотеля, что скорость шаров будет постоянной.

Получим формулу для определения перемещения при равноускоренном движении графическим методом.

Известно, что при равноускоренном движении тела, происходящем вдоль координатной оси X, скорость с тече­нием времени не остается постоянной, а меняется со временем согласно формуле

Т. е. скорость является линейной функцией, и поэтому графики скорости имеют вид прямой.

Прямая 1 соответст­вует движению с поло­жительным ускорением (скорость увеличивается), прямая 2 — движе­нию с отрицательным ускорением (скорость убывает).

График скорости разобьем на маленькие прямоугольные участки. Каждый участок будет соответствовать определённой постоянной скорости.

Необходимо определить пройденный путь за первый промежуток времени. Запишем формулу

Теперь посчитаем суммарную площадь всех имеющихся у нас фигур. А сумма площадей при равномерном движении – это полный пройденный путь.

Обратите внимание, от точки к точке скорость будет изменяться, тем самым можно получить путь, пройденный телом именно при прямолинейном равноускоренном движении.

Заметим, что при прямолинейном равноускоренном движении тела, когда скорость и ускорение направлены в одну сторону, модуль перемещения равен пройденному пути, поэтому, когда определяется модуль перемещения, то определяется и пройденный путь.

В данном случае можно говорить, что модуль перемещения будет равен площади фигуры, ограниченной графиком скорости и осью времени.

Фигура, ограниченная графиком скорости и осью времени есть не что иное, как прямоугольная трапеция. Из математики известна формула для нахождения площади трапеции. Площадь трапеции равна произведению половины суммы её оснований на высоту.

Следовательно, перемещение за все время tчисленно равно площади тра­пеции ОАВС. В нашем случае длина одного из оснований численно равна υoх, длина дру­гого — υх. Высота же ее чис­ленно равна t. Отсюда следует, что перемещение равно:

Подставим в эту формулу вместо υ равную ей величину υ0 + at.Тогда

Разделив почленно числитель на знаменатель, получим

Это есть уравнение перемещения в проекциях на ось координат

.

При пользовании этой формулой нужно помнить, что s, υ0 и а могут быть как положительными, так и отрицательными — ведь это проекции векторов пути, начальной скорости и ускорения на ось X.

Теперь вспомним, что пройденный путь, равный в нашем случае модулю перемещения, выражается разностью: s = x – x0

Если в уравнение подставить полученное нами выражение для S, то запишем закон, по которому движется тело при прямолинейном равноускоренном движении:

Это уравнение называется основным кинематическим уравнением равноускоренного движения.

Если тело движется из состояния покоя, график проходит через начало координат, фигура под графиком – прямоугольный треугольник, площадь которого равна половине произведения катетов.

Тогда формула для определения перемещения при­нимает вид:

Это уравнение перемещения при равноускоренном движении без начальной скорости.

Тогда

x = x0 + at2/2

Это кинематическое уравнение равноускоренного движения , без начальной скорости.

Рассмотрим некоторые важные зависимости между величинами равноускоренного движения. Для равноускоренного движения без начальной скорости путь, пройденный телом, пропорционален квадрату времени. Значит, пути, пройденные телом за 1 с, 2 с, 3 с, 4 с будут относиться как квадраты последовательных натуральных чисел.

Для любого равноускоренного движения, пути, пройденные телом  за любые равные промежутки времени, будут относиться как последовательный ряд нечетных чисел.

Основные выводы:

– Перемещение тела за все время t численно равно площади тра­пеции, ограниченной графиком скорости и осью времени.

 — уравнениеперемещения

 — кинематическое уравнение равноускоренного движения

– Для равноускоренного движения без начальной скорости путь, пройденный телом, пропорционален квадрату времени.

– Для любого равноускоренного движения, пути, пройденныетеломза любые равные промежутки времени, будутотноситьсякакпоследовательный ряд нечетных чисел.

videouroki.net

Равноускоренное движение: формулы, примеры

Равноускоренное движение

Равноускоренное движение — это движение с ускорением, вектор которого не меняется по модулю и направлению. Примеры такого движения: велосипед, который катится с горки; камень брошенный под углом к горизонту.

Рассмотрим последний случай более подробно. В любой точке траектории на камень действует ускорение свободного падения g→, которое не меняется по величине и всегда направлено в одну сторону. 

Движение тела, брошенного под углом к горизонту, можно представить в виде суммы движений относительно вертикальной и горизонтальной осей.

Вдоль оси X движение равномерное и прямолинейное, а вдоль оси Y — равноускоренное и прямолинейное. Будем рассматривать проекции векторов скорости и ускорения на оси.

Формулы для равноускоренного движения

Формула для скорости при равноускоренном движении:

v=v0+at.

Здесь v0 — начальная скорость тела, a=const — ускорение.

Покажем на графике, что при равноускоренном движении зависимость v(t) имеет вид прямой линии.

Ускорение можно определить по углу наклона графика скорости. На рисунке выше модуль ускорения равен отношению сторон треугольника ABC.

a=v-v0t=BCAC

Чем больше угол β, тем больше наклон (крутизна) графика по отношению к оси времени. Соответственно, тем больше ускорение тела.

Для первого графика: v0=-2 мс; a=0,5 мс2.

Для второго графика: v0=3 мс; a=-13 мс2.

По данному графику можно также вычислить перемещение тела за время t. Как это сделать?

Выделим на графике малый отрезок времени ∆t. Будем считать, что он настолько мал, что движение за время ∆t можно считать равномерным движением со скоростью, равной скорости тела в середине промежутка ∆t. Тогда, перемещение ∆s за время ∆t будет равно ∆s=v∆t.

Разобьем все время t на бесконечно малые промежутки ∆t. Перемещение s за время t равно площади трапеции ODEF.

s=OD+EF2OF=v0+v2t=2v0+(v-v0)2t.

Мы знаем, что 

zaochnik.com

Перемещение при прямолинейном равноускоренном движении

 

Попытаемся вывести формулу для нахождения проекции вектора перемещения тела, которое двигается прямолинейно и равноускоренно, за любой промежуток времени.

Для этого обратимся к графику зависимости проекции скорости прямолинейного равноускоренного движения от времени.

График зависимости проекции скорости прямолинейного равноускоренного движения от времени

Ниже на рисунке представлен график, для проекции скорости некоторого тела, которое движется с начальной скорость V0 и постоянным ускорением а.

Если бы у нас было равномерное прямолинейное движение, то для вычисления проекции вектора перемещения, необходимо было бы посчитать площадь фигуры под графиком проекции вектора скорости.

Теперь докажем, что и в случае равноускоренного прямолинейного движения проекция вектора перемещения Sx будет определяться таким же образом. То есть проекция вектора перемещения будет равняться площади фигуры под графиком проекции вектора скорости.

Найдем площадь фигуры ограниченную осью оt, отрезками АО и ВС, а также отрезком АС.

 

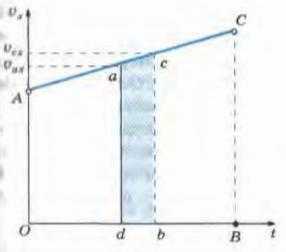
Выделим на оси ot малый промежуток времени db. Проведем через эти точки перпендикуляры к оси времени, до их пересечения с графикос проекции скорости. Отметим точки пересечения a и c. За этот промежуток времени скорость тела поменяется от Vax до Vbx.

Если взять этот промежуток достаточно малым, то можно считать что скорость остается практически неизменной, а следовательно мы будем иметь на этом промежутке дело с равномерным прямолинейным движением. 

Тогда можно считать отрезок ac горизонтальным, а abcd – прямоугольником. Площадь abcd будет численно равна проекции вектора перемещения, за промежуток времени db. Мы можем разбить на такие малые промежутки времени всю площадь фигуры OACB. 

То есть мы получили, что проекция вектора перемещения Sx за промежуток времени, соответствующий отрезку ОВ, будет численно равна площади S трапеции ОACB, и будет определяться по той же формуле, что и эта площадь.

Следовательно,

Так как Vx=V0x+ax*t и S=Sx, полученная формула примет следующий вид:

Мы получили формулу, с помощью которой можем рассчитать проекцию вектора перемещения при равноускоренном движении.

В случае равнозамедленного движения формула примет следующий вид:

Нужна помощь в учебе?



Предыдущая тема: Скорость прямолинейного равноускоренного движения: график скорости
Следующая тема:&nbsp&nbsp&nbspПеремещение при прямолинейном равноускоренном движении без начальной скорости

Все неприличные комментарии будут удаляться.

www.nado5.ru

Равноускоренное движение, вектор ускорения, направление, перемещение. Формулы, определение, законы

Тестирование онлайн

Равноускоренное движение

В этой теме мы рассмотрим очень особенный вид неравномерного движения. Исходя из противопоставления равномерному движению, неравномерное движение — это движение с неодинаковой скоростью, по любой траектории. В чем особенность равноускоренного движения? Это неравномерное движение, но которое

«равно ускоряется». Ускорение у нас ассоциируется с увеличением скорости. Вспомним про слово «равно», получим равное увеличение скорости. А как понимать «равное увеличение скорости», как оценить скорость равно увеличивается или нет? Для этого нам потребуется засечь время, оценить скорость через один и тот же интервал времени. Например, машина начинает двигаться, за первые две секунды она развивает скорость до 10 м/с, за следующие две секунды 20 м/с, еще через две секунды она уже двигается со скоростью 30 м/с. Каждые две секунды скорость увеличивается и каждый раз на 10 м/с. Это и есть равноускоренное движение.

Физическая величина, характеризующая то, на сколько каждый раз увеличивается скорость называется ускорением.

Можно ли движение велосипедиста считать равноускоренным, если после остановки в первую минуту его скорость 7км/ч, во вторую — 9км/ч, в третью 12км/ч? Нельзя! Велосипедист ускоряется, но не одинаково, сначала ускорился на 7км/ч (7-0), потом на 2 км/ч (9-7), затем на 3 км/ч (12-9).

Обычно движение с возрастающей по модулю скоростью называют ускоренным движением. Движение же с убывающей скоростью — замедленным движением. Но физики любое движение с изменяющейся скоростью называют ускоренным движением. Трогается ли автомобиль с места (скорость растет!), или тормозит (скорость уменьшается!), в любом случае он движется с ускорением.

Равноускоренное движение — это такое движение тела, при котором его скорость за любые равные промежутки времени изменяется (может увеличиваться или уменьшаться) одинаково

Ускорение тела

Ускорение характеризует быстроту изменения скорости. Это число, на которое изменяется скорость за каждую секунду. Если ускорение тела по модулю велико, это значит, что тело быстро набирает скорость (когда оно разгоняется) или быстро теряет ее (при торможении). Ускорение — это физическая векторная величина, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.

Определим ускорение в следующей задаче. В начальный момент времени скорость теплохода была 3 м/с, в конце первой секунды скорость теплохода стала 5 м/с, в конце второй — 7м/с, в конце третьей 9 м/с и т.д. Очевидно, . Но как мы определили? Мы рассматриваем разницу скоростей за одну секунду. В первую секунду 5-3=2, во вторую секунду 7-5=2, в третью 9-7=2. А как быть, если скорости даны не за каждую секунду? Такая задача: начальная скорость теплохода 3 м/с, в конце второй секунды — 7 м/с, в конце четвертой 11 м/с.В этом случае необходимо 11-7= 4, затем 4/2=2. Разницу скоростей мы делим на промежуток времени.

Эту формулу чаще всего при решении задач применяют в видоизмененном виде:

Формула записана не в векторном виде, поэтому знак «+» пишем, когда тело ускоряется, знак «-» — когда замедляется.

Направление вектора ускорения

Направление вектора ускорения изображено на рисунках

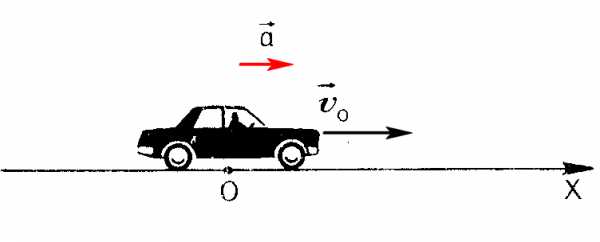
На этом рисунке машина движется в положительном направлении вдоль оси Ox, вектор скорости всегда совпадает с направлением движения (направлен вправо). Когда вектор ускорение совпадает с направлением скорости, это означает, что машина разгоняется. Ускорение положительное.

При разгоне направление ускорения совпадает с направлением скорости. Ускорение положительное.

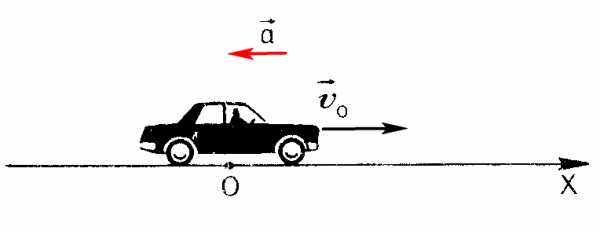
На этом рисунке машина движется в положительном направлении по оси Ox, вектор скорости совпадает с направлением движения (направлен вправо), ускорение НЕ совпадает с направлением скорости, это означает, что машина тормозит. Ускорение отрицательное.

При торможении направление ускорения противоположно направлению скорости. Ускорение отрицательное.

Разберемся, почему при торможении ускорение отрицательное. Например, теплоход за первую секунду сбросил скорость с 9м/с до 7м/с, за вторую секунду до 5м/с, за третью до 3м/с. Скорость изменяется на «-2м/с». 3-5=-2; 5-7=-2; 7-9=-2м/с. Вот откуда появляется отрицательное значение ускорения.

При решении задач, если тело замедляется, ускорение в формулы подставляется со знаком «минус»!!!

Перемещение при равноускоренном движении

Дополнительная формула, которую называют безвременной

Формула в координатах

Связь со средней скоростью

При равноускоренном движении среднюю скорость можно рассчитывать как среднеарифметическое начальной и конечной скорости

Из этого правила следует формула, которую очень удобно использовать при решении многих задач

Соотношение путей

Если тело движется равноускоренно, начальная скорость нулевая, то пути, проходимые в последовательные равные промежутки времени, относятся как последовательный ряд нечетных чисел.

Главное запомнить

1) Что такое равноускоренное движение;
2) Что характеризует ускорение;
3) Ускорение — вектор. Если тело разгоняется ускорение положительное, если замедляется — ускорение отрицательное;
3) Направление вектора ускорения;
4) Формулы, единицы измерения в СИ

Упражнения

Два поезда идут навстречу друг другу: один — ускоренно на север, другой — замедленно на юг. Как направлены ускорения поездов?

Одинаково на север. Потому что у первого поезда ускорение совпадает по направлению с движением, а у второго — противоположное движению (он замедляется).


Поезд движется равноускоренно с ускорением a (a>0). Известно, что к концу четвертой секунды скорость поезда равна 6м/с. Что можно сказать о величине пути, пройденном за четвертую секунду? Будет ли этот путь больше, меньше или равен 6м?

Так как поезд движется с ускорением, то скорость его все время возрастает (a>0). Если к концу четвертой секунды скорость равна 6м/с, то в начале четвертой секунды она была меньше 6м/с. Следовательно, путь, пройденный поездом за четвертую секунду, меньше 6м.


Какие из приведенных зависимостей описывают равноускоренное движение?


Уравнение скорости движущегося тела . Каково соответствующее уравнение пути?


*Автомобиль прошел за первую секунду 1м, за вторую секунду 2м, за третью секунду 3м, за четвертую секунду 4м и т.д. Можно ли считать такое движение равноускоренным?

В равноускоренном движении пути, проходимые в последовательные равные промежутки времени, относятся как последовательный ряд нечетных чисел. Следовательно, описанное движение не равноускоренное.


fizmat.by

Равноускоренное движение, формулы и примеры

Равноускоренное прямолинейное движение

Траектория движения в данном случае — прямая линия.

Основные формулы и кинематические характеристики

Ускорение (по модулю и по направлению).

Скорость тела меняется по закону

   

где начальная скорость движения.

Закон движения в случае равноускоренного движения имеет вид:

   

где радиус-вектор точки в момент времени , радиус-вектор начального положения точки, начальная скорость, ускорение.

В одномерном случае закон движения запишется в виде:

   

Для двумерного случая (движения по плоскости) закон движения в случае равноускоренного движения запишется в виде системы двух уравнений:

   

Также справедлива так называемая формула для определения пути «без времени»:

   

Графическое изображение зависимости кинематических характеристик от времени представлено на рисунках 1-3.

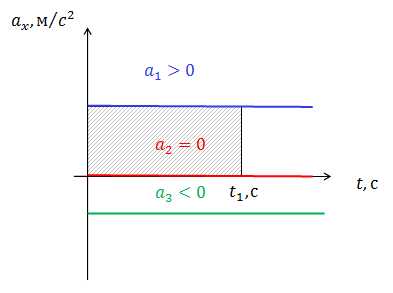
Рис.1. Зависимость ускорения от времени при равноускоренном движении

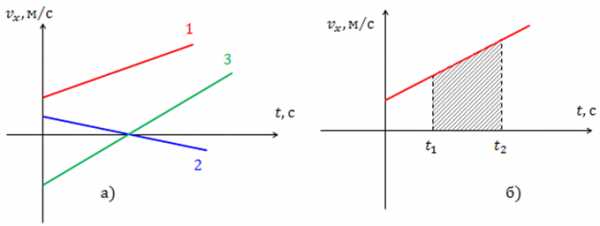
Рис.2. Зависимость скорости от времени при равноускоренном движении: а) закон изменения скорости для различных случаев; б) определение перемещения с помощью графика скорости.

Рис.3. Зависимость перемещения от времени при равноускоренном движении.

На рис.1 изображен график зависимости ускорения от времени при равноускоренном движении. Случай соответствует равноускоренному движению, случай — равнозамедленному движению, случай — равномерному движению. Площадь заштрихованного прямоугольника численно равна средней скорости движения тела.

На рис.2 представлена зависимость скорости от времени при равноускоренном движении. Рис.2 (а) демонстрирует разные случаи движения: 1- тело двигалось в направлении оси равноускоренно; 2 — тело двигалось равнозамедленно в направлении оси , затем остановилось и поменяло направление движения; 3- тело двигалось равноускоренно в направлении, противоположном оси , затем остановилось и стало двигаться в противоположном направлении. Во всех трех случаях тело имело начальные скорости.

По графику скорости можно определить ускорение движущегося объекта как тангенс угла наклона прямой зависимости к оси

Площадь заштрихованной трапеции (рис.2 (б)) численно равна пути, пройденному телом за время

Зависимость перемещения от времени при равноускоренном движении — это квадратичная функция (рис.3). Положение вершины параболы зависит от направлений начальной скорости и ускорения.

Примеры решения задач

ru.solverbook.com

Формула равноускоренного движения

В целом равнопеременным движением называют такое движение тела, при котором ускорение является постоянным.

Примером равноускоренного движения может быть движение тела в поле постоянного земного притяжения при условиях, когда сопротивлением воздуха можно пренебречь.

   

где — ускорение (определяется в м/с), — конечная скорость, — начальная скорость, — время.

Формулы скорости и пути для ускоренного движения:

1. При одномерном равноускоренном движении скорость тела изменяется со временем линейно по закону:

   

2. Формула координаты тела:

   

3. Формула пути:

   

4. Формула пути, если t неизвестно:

   

Примеры решения задач по теме «Равноускоренное движение»

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Перемещение при равноускоренном движении. I уровень

1.9. Графическое представление равноускоренного прямолинейного движения.

Перемещение при равноускоренном движении.

I уровень.
Многие физические величины, описывающие движения тел, с течением времени изменяются. Поэтому для большей наглядности описания движение часто изображают графически.

Покажем, как графически изображаются зависимости от времени кинематических величин, описывающих прямолинейное равноускоренное движения.

Равноускоренное прямолинейное движение — это движение, при котором скорость тела за любые равные промежутки времени изменяется одинаково, т. е. это движение с постоянным по модулю и направлению ускорением.

a=const — уравнение ускорения. Т.е а имеет численное значение, которое не изменяется со временем.

По определению ускорения 

Отсюда мы уже нашли уравнения для зависимости скорости от времени: v = v0 + at.  

Посмотрим, как это уравнение можно использовать для графического представления равноускоренного движения.

Изобразим графически зависимости кинематических величин от времени для трех тел

.

1 тело движется вдоль оси 0Х, при этом увеличивает свою скорость (вектор ускорения а сонаправленн с вектором скорости v). vx >0, ах > 0

2 тело движется вдоль оси 0Х, при этом уменьшает свою скорость (вектор ускорения а не сонаправленн с вектором скорости v). vx >0, ах

2 тело движется против оси 0Х, при этом уменьшает свою скорость (вектор ускорения а не сонаправленн с вектором скорости v). vxах > 0

График ускорения

Ускорение по определению величина постоянная. Тогда для представленной ситуации график зависимости ускорения от времени a(t) будет иметь вид:

Из графика ускорения можно определить как изменялась скорость – увеличивалась или уменьшалась и на какое численное значение изменилась скорость и у какого тела скорость больше изменилась.
График скорости

Если сравнить зависимость координаты от времени при равномерном движении и зависимость проекции скорости от времени при равноускоренном движении, можно увидеть, что эти зависимости одинаковы:

х= х0 + vx t vx= v0x + aхt

Это значит, что и графики зависимостей имеют одинаковый вид.

Для построения этого графика на оси абсцисс откладывают время движения, а на оси ординат — скорость (проекцию скорости) тела. В равноускоренном движении скорость тела с течением времени изменяется.
Перемещение при равноускоренном движении.

При равноускоренном прямолинейном движении скорость тела определяется формулой 

vx= v0x + aхt

В этой формуле υ0 – скорость тела при t = 0 (начальная скорость), a = const – ускорение. На графике скорости υ (t) эта зависимость имеет вид прямой линии (рис. ).

По наклону графика скорости может быть определено ускорение a тела. Соответствующие построения выполнены на рис.  для графика I. Ускорение численно равно отношению сторон треугольника ABC: 


Чем больше угол β, который образует график скорости с осью времени, т. е. чем больше наклон графика (крутизна), тем больше ускорение тела.

Для графика I: υ0 = –2 м/с, a = 1/2 м/с2.

Для графика II: υ0 = 3 м/с, a = –1/3 м/с2.

График скорости позволяет также определить проекцию перемещения s тела за некоторое время t. Выделим на оси времени некоторый малый промежуток времени Δt. Если этот промежуток времени достаточно мал, то и изменение скорости за этот промежуток невелико, т. е. движение в течение этого промежутка времени можно считать равномерным с некоторой средней скоростью, которая равна мгновенной скорости υ тела в середине промежутка Δt. Следовательно, перемещение Δs за время Δt будет равно Δs = υΔt. Это перемещение равно площади заштрихованной полоски (рис. ). Разбив промежуток времени от 0 до некоторого момента t на малые промежутки Δt, получим, что перемещение s за заданное время t при равноускоренном прямолинейном движении равно площади трапеции ODEF. Соответствующие построения выполнены для графика II на рис. 1.4.2. Время t принято равным 5,5 с. 


Так как υ – υ0 = at, окончательная формула для перемещения s тела при равномерно ускоренном движении на промежутке времени от 0 до t запишется в виде: 

Для нахождения координаты y тела в любой момент времени t нужно к начальной координате y0 прибавить перемещение за время t: 

Так как υ – υ0 = at, окончательная формула для перемещения s тела при равномерно ускоренном движении на промежутке времени от 0 до t запишется в виде: 

Для нахождения координаты x тела в любой момент времени t нужно к начальной координате x0 прибавить перемещение за время t: 

При анализе равноускоренного движения иногда возникает задача определения перемещения тела по заданным значениям начальной υ0 и конечной υ скоростей и ускорения a. Эта задача может быть решена с помощью уравнений, написанных выше, путем исключения из них времени t. Результат записывается в виде 



Из этой формулы можно получить выражение для определения конечной скорости υ тела, если известны начальная скорость υ0, ускорение a и перемещение s: 

Если начальная скорость υ0 равна нулю, эти формулы принимают вид 

Следует еще раз обратить внимание на то, что входящие в формулы равноускоренного прямолинейного движения величины υ0, υ, s, a, y0 являются величинами алгебраическими. В зависимости от конкретного вида движения каждая из этих величин может принимать как положительные, так и отрицательные значения.

Пример решения задачи:

Петя съезжает со склона горы из состояния покоя с ускорением 0,5 м/с2 за 20 с и дальше движется по горизонтальному участку. Проехав 40 м, он врезается в зазевавщегося Васю и падает в сугроб, снизив свою скорость до 0м/с. С каким ускорением двигался Петя по горизонтальной поверхности до сугроба? Какова длина склона горы, с которой так неудачно съехал Петя?

 


Дано:

Решение

v01 = 0

a1 = 0,5 м/с2

t1 = 20 с

s2 = 40 м

v2 = 0


Движение Пети состоит из двух этапов: на первом этапе, спускаясь со склона горы, он движется с возрастающей по модулю скоростью; на втором этапе при движении по горизонтальной поверхности его скорость уменьшается до нуля (столкнулся с Васей). Величины, относящиеся к первому этапу движения, запишем с индексом 1, а ко второму этапу с индексом 2.

a2 ?

s1 ?

1 этап.

Уравнение для скорости Пети в конце спуска с горы:

v1 = v01 + a1t1.

В проекциях на ось X получим: 

v1x = a1xt.

Запишем уравнение, связывающее проекции скорости, ускорения и перемещения Пети на первом этапе движения:

или т.к. Петя ехал с самого верха горки с начальной скоростью V01=0

то:

(на месте Пети, я бы поостереглась ездить с таких высоких горок)

Учитывая, что начальная скорость Пети на этом 2 этапе движения равна его конечной скорости на первом этапе:

v02x = v1x, v2x = 0, где v1 – скорость с которой Петя достиг подножия горки и начал двигаться к Васе. V2x — скорость Пети в сугробе.

Используем уравнение и найдем скорость v1

На горизонтальним участе дороги путь Пети рамен:

НО!!! целесообразнее воспользоваться другим уравнением, т.к. нам не известно время жвижения Пети до Васи t2

Ускорение получиться отрицательным – это значит, что Петя очень старался затормозить не об Васю, а несколько раньше.

Ответ: a2 = -1,25 м/с2; s1 = 100 м.

II уровень. Письменно решить задачи.


  1. Поезд метро, отходя от станции, может развить скорость 72 км/ч за 20 с. Определить с каким ускорением удаляется от вас сумка, забытая в вагоне метро. Какой путь при этом она проедет?

  2. Велосипедист, движущийся со скоростью 3 м/с, начинает спускаться с горы с ускорением 0,8 м/с2. Найдите длину го­ры, если спуск занял 6 с.

  3. Начав торможение с ускорением 0,5 м/с2, поезд прошел до остановки 225 м. Какова была его скорость перед началом торможения?

  4. Начав двигаться, футбольный мяч достиг скорости 50 м/с, пройдя путь 50 м и врезался в окно. Определите время, за которое мяч прошел этот путь, и ускорение, с которым он двигался.

  5. Время реакции соседа дяди Олега = 1,5 мин, за это время он сообразит, что случилось с его окном и успеет выбежать во двор. Определите какую скорость должны развить юные футболисты, что бы радостные владельцы окна их не догнали, если до своего подъезда им нужно бежать 350 м.

  6. Два велосипедиста еду навстречу друг другу. Первый, имея скорость 36 км/ч, начал подниматься в гору с ускоре­нием 0,2 м/с2, а второй, имея скорость 9 км/ч, стал спус­каться с горы с ускорением 0,2 м/с2. Через сколько времени и в каком месте они столкнуться из-за своей рассеянности, если длина горы 100 м?

gazya.ru