Чему равен радиус окружности описанной около прямоугольного треугольника: Радиус описанной окружности прямоугольного треугольника

Радиус описанной окружности около прямоугольного треугольника онлайн

С помощю этого онлайн калькулятора можно найти радиус описанной окружности около любого треугольника, в том числе радиус описанной окружности около прямоугольного треугольника. Для нахождения радиуса окружности описанной около треугольника введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Содержание

1. Радиус окружности описанной около прямоугольного треугольника, если известна гипотенуза треугольника
2. Радиус окружности описанной около прямоугольного треугольника, если известны катеты треугольника
3. Радиус окружности описанной около прямоугольного треугольника, если известны катет и противолежащий угол треугольника
4. Радиус окружности описанной около прямоугольного треугольника, если известны катет и прилежащий острый угол треугольника

1.

Радиус окружности описанной около прямоугольного треугольника, если известна гипотенуза треугольника

Пусть известна гипотенуза c прямоугольного треугольника (Рис.1). Найдем радиус описанной окружности около треугольника.

На странице Радиус окружности описанной около треугольника формула радиуса описанной окружности около треугольника по стороне и противолежащему углу имеет вид:

\( \small R=\frac{\large c}{\large 2 \sin C} \)

где C − угол противолежащий гипотенузе прямоугольного треугольника. Поскольку угол, противолежащий гипотенузе − прямой, то получим:

\( \small R=\frac{\large c}{\large 2 \sin 90°}=\frac{\large c}{\large 2}, \)

то есть

\( \small R=\frac{\large c}{\large 2}. \)

(1)

Пример 1. Известна гипотенуза \( \small с=\frac{9}{2} \) прямоугольного треугольника.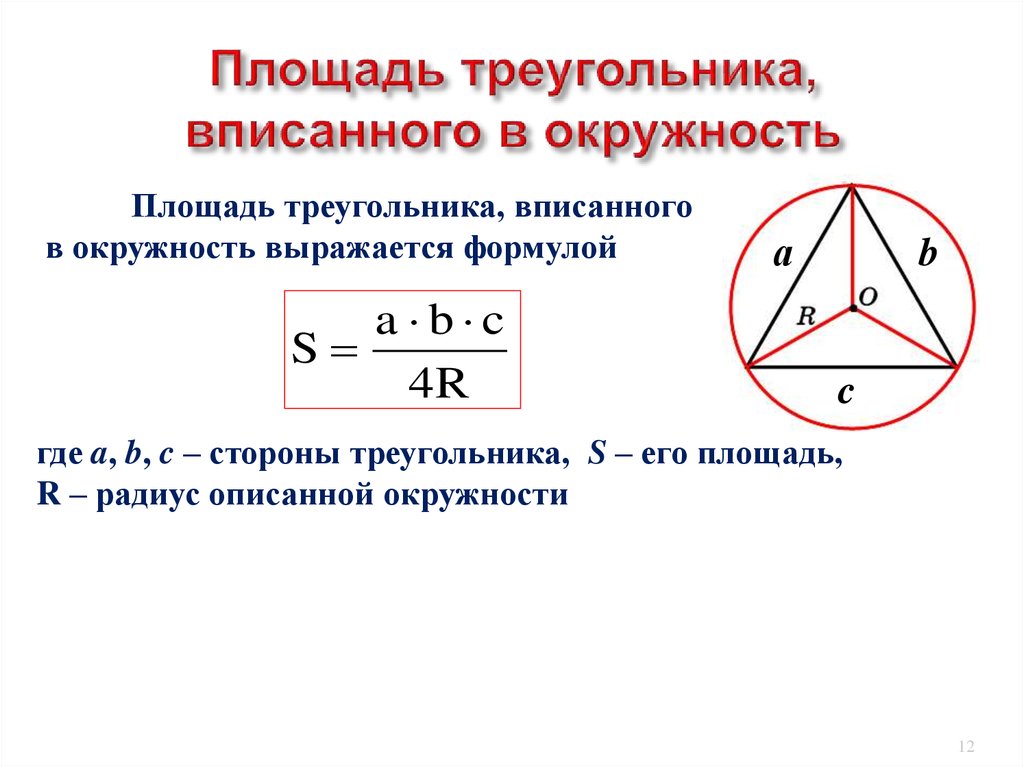 2}}{\large 2}. \)(3)

Пример 2. Катеты прямоугольного треугольника равны: \( \small a=15 , \; b=3.\) Найти радиус окружности описанной около треугольника.

Решение. Для нахождения радиуса окружности описанной около прямоугольного треугольника воспользуемся формулой (3). Подставим значения \( \small a=15 , \; b=3\) в (3):

Ответ:

3. Радиус окружности описанной около прямоугольного треугольника, если известны катет и противолежащий угол треугольника

Формула для вычисления радиуса окружности описанной около прямоугольного треугольника, если известны катет и противолежащий угол треугольника аналогична формуле вычисления радиуса описанной окружности около произвольного треугольника (см. статью на странице Радиус описанной окружности около треугольника онлайн):

4. Радиус окружности описанной около прямоугольного треугольника, если известны катет и прилежащий острый угол треугольника

Пусть известны катет a и прилежащий острый угол B прямоугольного треугольника (Рис. 4). Найдем радиус описанной окружности около треугольника.

Так как треугольник прямоугольный, то сумма острых углов треугольника равна 90°:

\( \small \angle A+\angle B=90°. \)

Откуда:

\( \small \angle A=90°-\angle B. \)

(5)

Подставляя (5) в (4), получим:

\( \small R=\frac{\large a}{\large 2 \sin A}=\frac{\large a}{\large 2 \sin(90°-B)}\) \( \small =\frac{\large a}{\large 2 \cos B} \)

или

\( \small R=\frac{\large a}{\large 2 \cos B}. \)

(6)

Пример 3. Катет прямоугольного треугольника равен: \( \small a=15 ,\) а прилежащий угол равен \( \small \angle B=25°. \) Найти радиус окружности описанной около треугольника.

Решение. Для нахождения радиуса окружности описанной около прямоугольного треугольника воспользуемся формулой (6).

Подставим значения \( \small a=15 , \; \angle B=25° \) в (6):

Ответ:

Смотрите также:

• Радиус описанной окружности около треугольника онлайн
• Радиус описанной окружности около равностороннего треугольника онлайн
• Радиус описанной окружности около равнобедренного треугольника онлайн

Радиус вписанной окружности через высоты треугольника. Формулы радиусов вписанных и описанных окружностей правильных многоугольников

Проблемы беременных

Очень часто при решении геометрических задач приходится совершать действия со вспомогательными фигурами. Например, находить радиус вписанной или описанной окружности и т.д. Данная статья покажет, как находить радиус окружности, описанной около треугольника. Или, иными словами, радиус окружности, в которую вписан треугольник.

Как найти радиус окружности, описанной около треугольника – общая формула

Общая формула выглядит следующим образом: R = abc/4√p(p – a)(p – b)(p – c), где R – радиус описанной окружности, p – периметр треугольника поделенный на 2 (полупериметр). a, b, c – стороны треугольника.

Найти радиус описанной окружности треугольника, если a = 3, b = 6, c = 7.

Таким образом, исходя из вышеприведенной формулы, вычисляем полупериметр:
p = (a + b + c)/2 = 3 + 6 + 7 = 16. => 16/2 = 8.

Подставляем значения в формулу и получаем:
R = 3 × 6 × 7/4√8(8 – 3)(8 – 6)(8 – 7) = 126/4√(8 × 5 × 2 × 1) = 126/4√80 = 126/16√5.

Ответ: R = 126/16√5

Как найти радиус окружности, описанной около равностороннего треугольника

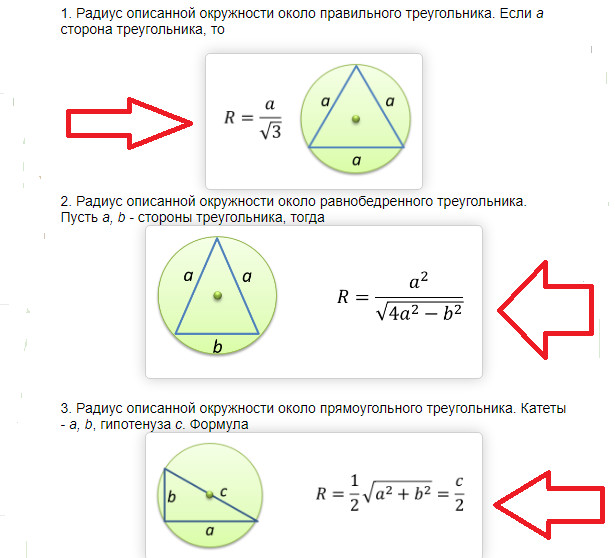
Для нахождения радиуса окружности, описанной около равностороннего треугольника, существует довольно простая формула: R = a/√3, где a – величина его стороны.

Пример: Сторона равностороннего треугольника равна 5. Найти радиус описанной окружности.

Так как у равностороннего треугольника все стороны равны, для решения задачи нужно всего лишь вписать ее значение в формулу. Получим: R = 5/√3.

Ответ: R = 5/√3.

Как найти радиус окружности, описанной около прямоугольного треугольника

Формула выглядит следующим образом: R = 1/2 × √(a² + b²) = c/2, где a и b – катеты и c – гипотенуза.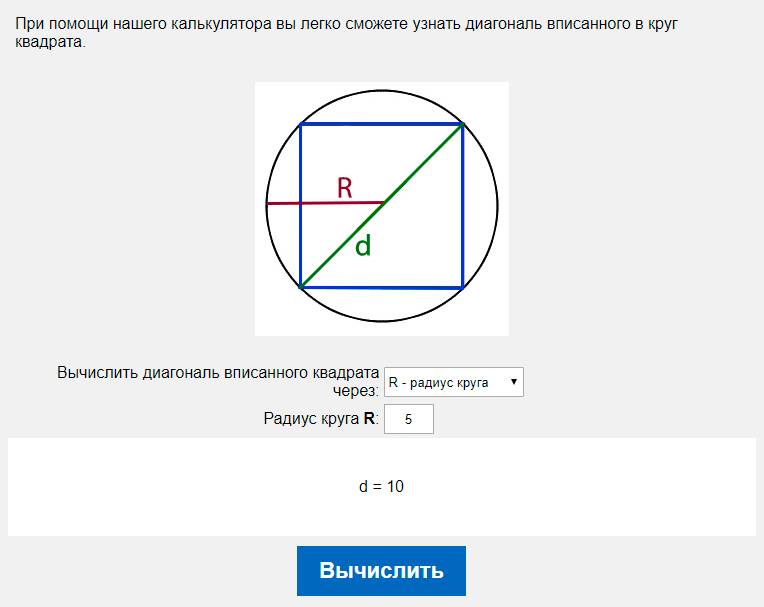 Если сложить квадраты катетов в прямоугольном треугольнике, то получим квадрат гипотенузы. Как видно из формулы, данное выражение находится под корнем. Вычислив корень из квадрата гипотенузы, мы получим саму длину. Умножение получившегося выражения на 1/2 в итоге приводит нас к выражению 1/2 × c = c/2.

Пример: Вычислить радиус описанной окружности, если катеты треугольника равны 3 и 4. Подставим значения в формулу. Получим: R = 1/2 × √(3² + 4²) = 1/2 × √25 = 1/2 × 5 = 2.5.

В данном выражение 5 – длина гипотенузы.

Ответ: R = 2.5.

Как найти радиус окружности, описанной около равнобедренного треугольника

Формула выглядит следующим образом: R = a²/√(4a² – b²), где a – длина бедра треугольника и b – длина основания.

Пример: Вычислить радиус окружности, если его бедро = 7, а основание = 8.

Решение: Подставляем в формулу данные значения и получаем: R = 7²/√(4 × 7² – 8²).

R = 49/√(196 – 64) = 49/√132. Ответ можно записать прямо так.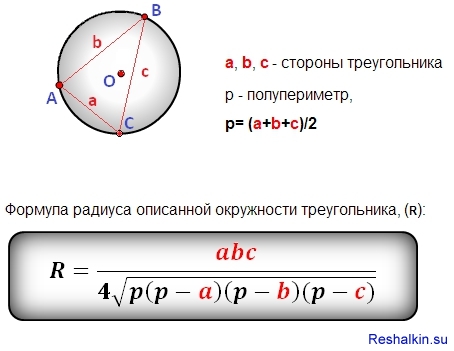

Ответ: R = 49/√132

Онлайн ресурсы для вычисления радиуса окружности

Можно очень легко запутаться во всех этих формулах. Поэтому при необходимости можно воспользоваться онлайн калькуляторами, которые помогут вам в решении задач на нахождение радиуса. Принцип работы таких мини-программ очень прост. Подставляете значение стороны в соответствующее поле и получаете готовый ответ. Можно выбрать несколько вариантов округления ответа: до десятичных, сотых, тысячных и т.д.

В данной статье речь пойдёт о том, как выразить площадь многоугольника, в который можно вписать окружность, через радиус этой окружности. Сразу стоит отметить, что не во всякий многоугольник можно вписать окружность. Однако, если это возможно, то формула, по которой вычисляется площадь такого многоугольника, становится очень простой. Дочитайте эту статью до конца или посмотрите прилагающийся видеоурок, и вы узнаете, как же выразить площадь многоугольника через радиус вписанной в него окружности.

Формула площади многоугольника через радиус вписанной окружности

Нарисуем многоугольник A 1 A 2 A 3 A 4 A 5 , не обязательно правильный, но такой, в который можно вписать окружность. Напомню, что вписанной называется окружность, которая касается всех сторон многоугольника. На рисунке это зелёная окружность с центром в точке

O :

Мы взяли здесь для примера 5-угольник. Но на самом деле это не имеет существенного значения, поскольку дальнейшее доказательство справедливо и для 6-угольника и для 8-угольника и вообще для любого сколь угодно «угольника».

Если соединить центр вписанной окружности со всеми вершинами многоугольника, то он разобьётся на столько треугольников, сколько вершин в данном многоугольнике. В нашем случае: на 5 треугольников. Если же соединить точку O со всеми точками касания вписанной окружности со сторонами многоугольника, то получится 5 отрезков (на рисунке снизу это отрезки

OH 1 , OH 2 , OH 3 , OH 4 и OH 5), которые равны радиусу окружности и перпендикулярны сторонам многоугольника, к которым они проведены. Последнее справедливо, поскольку радиус, проведенный в точку касания, перпендикулярен касательной:

Как же найти площадь нашего описанного многоугольника? Ответ прост. Нужно сложить площади всех полученных в результате разбиения треугольников:

Рассмотрим, чему равна площадь треугольника . На рисунке снизу он выделен жёлтым цветом:

Она равна половине произведения основания

A 1 A 2 на высоту OH 1 , проведённую к этому основанию. Но, как мы уже выяснили, эта высота равна радиусу вписанной окружности. То есть формула площади треугольника принимает вид: , где r — радиус вписанной окружности. Аналогично находятся площади всех оставшихся треугольников. В результате искомая площадь многоугольника оказывается равна:

Видно, что во всех слагаемых этой суммы ест общий множитель , который можно вынести за скобки. В результате получится вот такое выражение:

То есть в скобках осталась просто сумма всех сторон многоугольника, то есть его периметр P .

Чаще всего в этой формуле выражение заменяют просто на p и называют эту букву «полупериметром». В результате, окончательная формула принимает вид:

То есть площадь многоугольника, в который вписана окружность известного радиуса, равна произведению этого радиуса на полупериметр многоугольника. Это и есть тот результат, в которому мы стремились.

Отметит напоследок, что в треугольник, который является частным случаем многоугольника, всегда можно вписать окружность. Поэтому для треугольника эту формулу можно применять всегда. Для остальных многоугольников, с количеством сторон большим 3, сперва нужно убедиться, что в них можно вписать окружность. Если это так, можно смело использовать эту простую формулу и находить по ней площадь этого многоугольника.

Материал подготовил , Сергей Валерьевич

Окружность вписана в треугольник. В данной статье собрал для вас задачи, в которых даётся треугольник с вписанной в него или описанной около него окружностью. В условии ставится вопрос о нахождении радиуса окружности или стороны треугольника.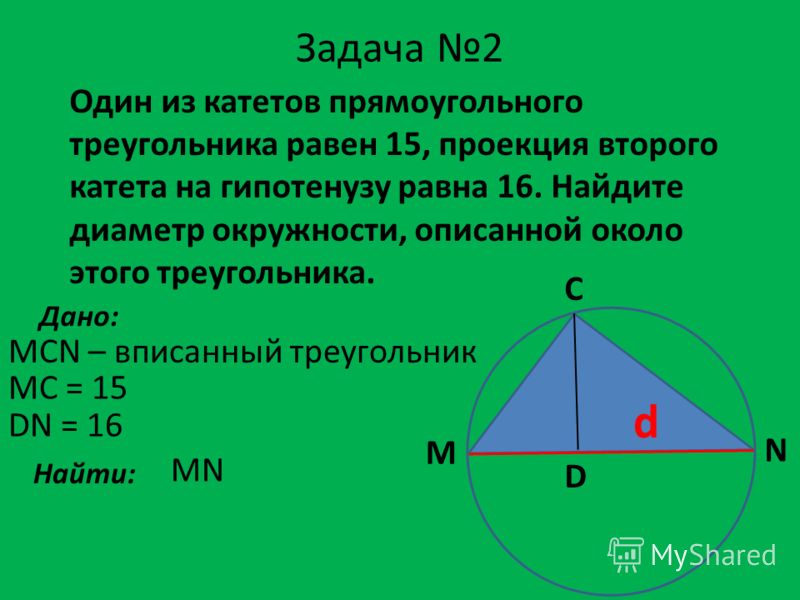

Данные задания удобно решать используя представленные формулы. Рекомендую их выучить, бывают очень полезны не только при решении этого типа заданий. Одна формула выражает связь радиуса вписанной в треугольник окружности с его сторонами и площадью, другая радиус описанной около треугольника окружности также с его сторонами и площадью:

S – площадь треугольника

Рассмотрим задачи:

27900. Боковая сторона равнобедренного треугольника равна 1, угол при вершине, противолежащей основанию, равен 120 0 . Найдите диаметр описанной окружности этого треугольника.

Здесь окружность описана около треугольника.

Первый способ:

Диаметр мы сможем найти, если будет известен радиус. Используем формулу радиуса описанной около треугольника окружности:

где a, b, c – стороны треугольника

S – площадь треугольника

Две стороны нам известны (боковые стороны равнобедренного треугольника), третью мы можем вычислить используя теорему косинусов:

Теперь вычислим площадь треугольника:

*Использовали формулу (2) из .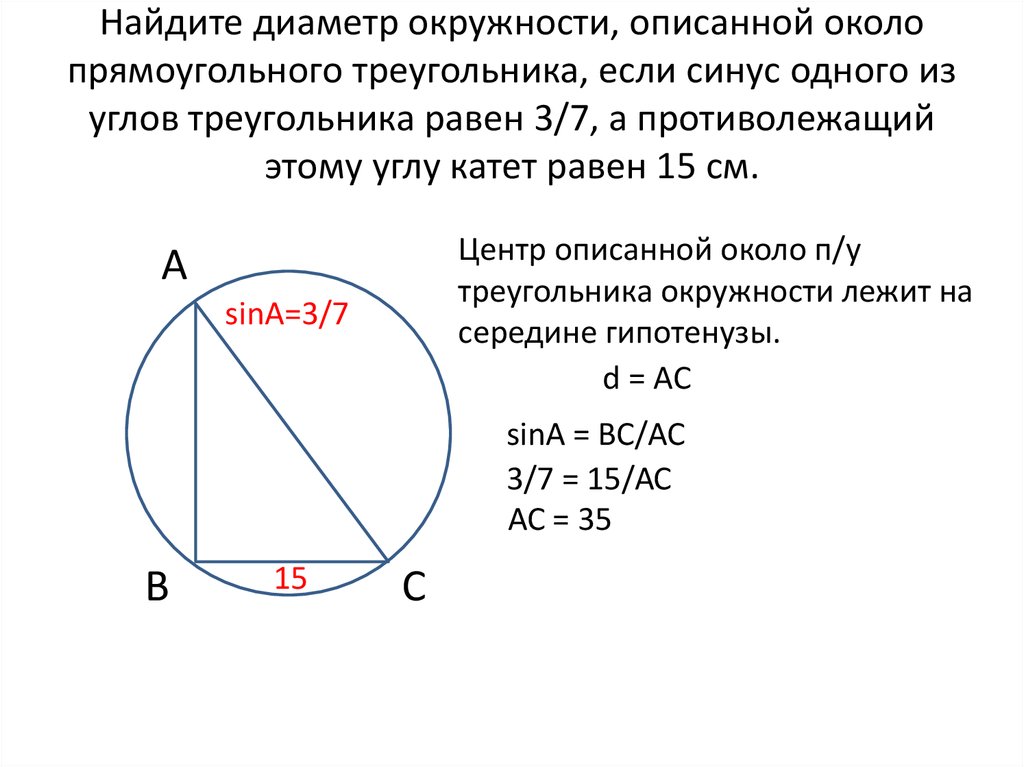

Вычисляем радиус:

Таким образом диаметр будет равен 2.

Второй способ:

Это устные вычисления. Для тех кто имеет навык решения заданий с вписанным в окружность шестиугольником, тот сразу определит, что стороны треугольника АС и ВС «совпадают» со сторонами вписанного в окружность шестиугольника (угол шестиугольника как раз равен 120 0 , как и в условии задачи). А далее на основании того, что сторона вписанного в окружность шестиугольника равна радиусу этой окружности не сложно сделать вывод о том, что диаметр будет равен 2АС, то есть двум.

Подробнее о шестиугольнике посмотрите информацию в (п.5).

Ответ: 2

27931. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 2. Найдите гипотенузу с этого треугольника. В ответе укажите .

где a, b, c – стороны треугольника

S – площадь треугольника

Нам неизвестны ни стороны треугольника, ни его площадь. Обозначим катеты как х, тогда гипотенуза будет равна:

А площадь треугольника будет равна 0,5х 2 .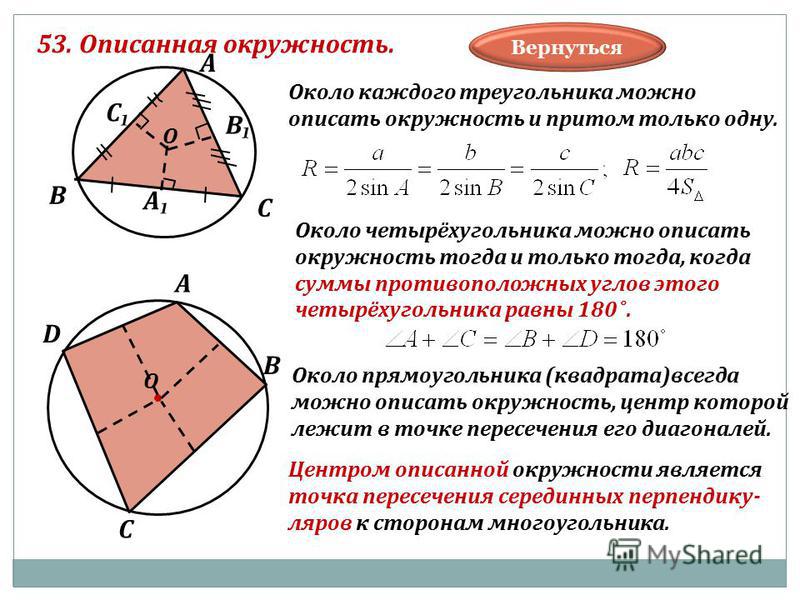

Значит

Таким образом, гипотенуза будет равна:

В ответе требуется записать:

Ответ: 4

27933. В треугольнике ABC АС = 4, ВС = 3, угол C равен 90 0 . Найдите радиус вписанной окружности.

Воспользуемся формулой радиуса окружности вписанной в треугольник:

где a, b, c – стороны треугольника

S – площадь треугольника

Две стороны известны (это катеты), можем вычислить третью (гипотенузу), также можем вычислить и площадь.

По теореме Пифагора:

Найдём площадь:

Таким образом:

Ответ: 1

27934. Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.

Воспользуемся формулой радиуса окружности вписанной в треугольник:

где a, b, c – стороны треугольника

S – площадь треугольника

Известны все стороны, вычислим и площадь. Её мы можем найти по формуле Герона:

Тогда

Таким образом:

Ответ: 1,5

27624.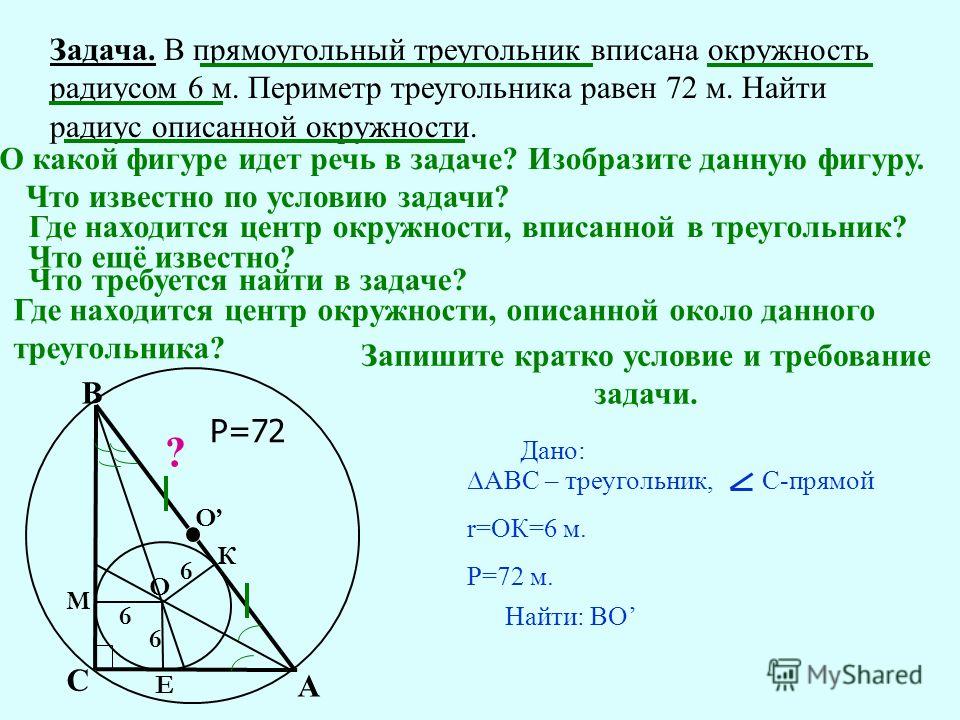 Периметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника. Посмотреть решение

27932. Катеты равнобедренного прямоугольного треугольника равны . Найдите радиус окружности, вписанной в этот треугольник.

Небольшой итог.

Если в условии дан треугольник и вписанная или описанная окружность, и речь идёт о сторонах, площади, радиусе, то сразу вспомните об указанных формулах и пробуйте использовать их при решении. Если не получается, то тогда уже ищите другие способы решения.

На этом всё. Успеха вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Окружность считается вписанной в границы правильного многоугольника, в случае, если лежит внутри него, касаясь при этом прямых, которые проходят через все стороны. Рассмотрим, как найти центр и радиус окружности. Центром окружности будет являться точка, в которой пересекаются биссектрисы углов многоугольника. Радиус рассчитывается: R=S/P; S – площадь многоугольника, Р – полупериметр окружности.

В треугольнике

В правильный треугольник вписывают лишь одну окружность, центр которой называется инцентром; он от всех сторон удалён на одинаковое расстояние и является местом пересечения биссектрис.

В четырёхугольнике

Часто приходится решать, как найти радиус вписанной окружности в эту геометрическую фигуру. Она должна быть выпуклой (если нет самопересечений). Окружность вписать в неё можно только в случае равенства сумм противоположных сторон: AB+CD=BC+AD.

При этом центр вписанной окружности, середины диагоналей, расположены на одной прямой (согласно теореме Ньютона). Отрезок, концы которого находятся там, где пересекаются противоположные стороны правильного четырёхугольника, лежит на этой же прямой, называемой прямой Гаусса. Центром окружности будет точка, в которой пересекаются высоты треугольника с вершинами, диагоналями (по теореме Брокара).

В ромбе

Им считается параллелограмм с одинаковой длиной сторон.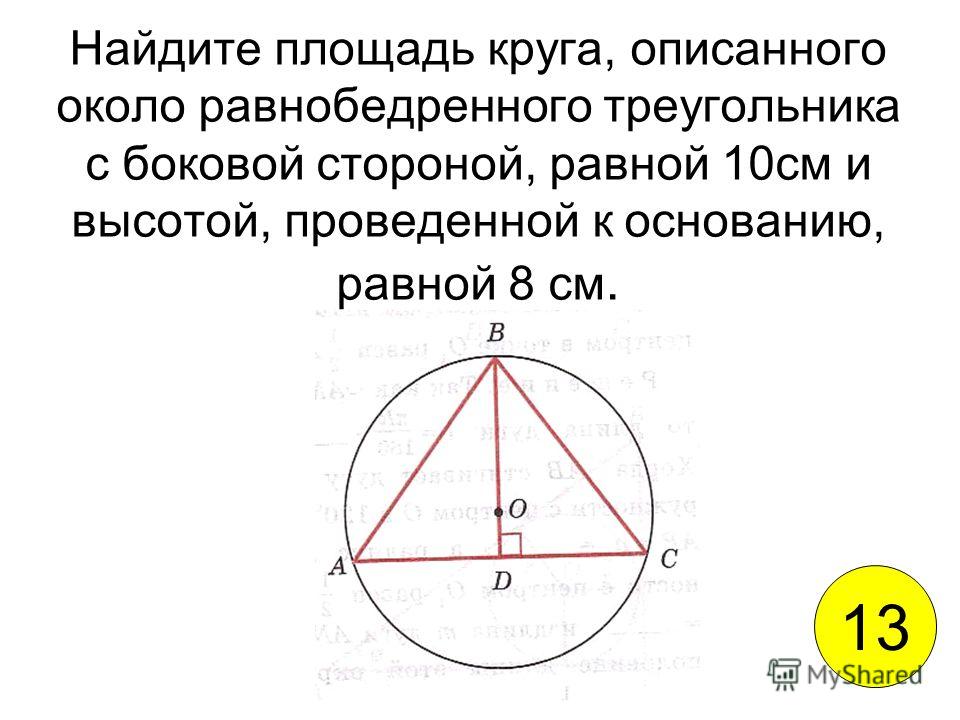 Радиус окружности, вписываемой в него, можно рассчитать несколькими способами.

1. Чтобы сделать это правильно, найдите радиус вписанной окружности ромба, если известна площадь ромба, длина его стороны. Применяется формула r=S/(2Хa). К примеру, если площадь ромба составляет 200 мм кв., длина стороны 20 мм, то R=200/(2Х20), то есть, 5 мм.
2. Известен острый угол одной из вершин. Тогда необходимо использовать формулоу r=v(S*sin(α)/4). Например, при площади в 150 мм и известном угле в 25 градусов, R= v(150*sin(25°)/4) ≈ v(150*0,423/4) ≈ v15,8625 ≈ 3,983 мм.
3. Все углы в ромбе равны. В этой ситуации радиус окружности, вписанной в ромб, будет равен половине длины одной стороны данной фигуры. Если рассуждать по Евклиду, утверждающего, что сумма углов всякого четырёхугольника равна 360 градусов, то один угол будет равен 90 градусам; т.е. получится квадрат.

Окружность, вписанная в треугольник

Существование окружности, вписанной в треугольник

Напомним определение биссектрисы угла .

Определение 1 . Биссектрисой угла называют луч, делящий угол на две равные части.

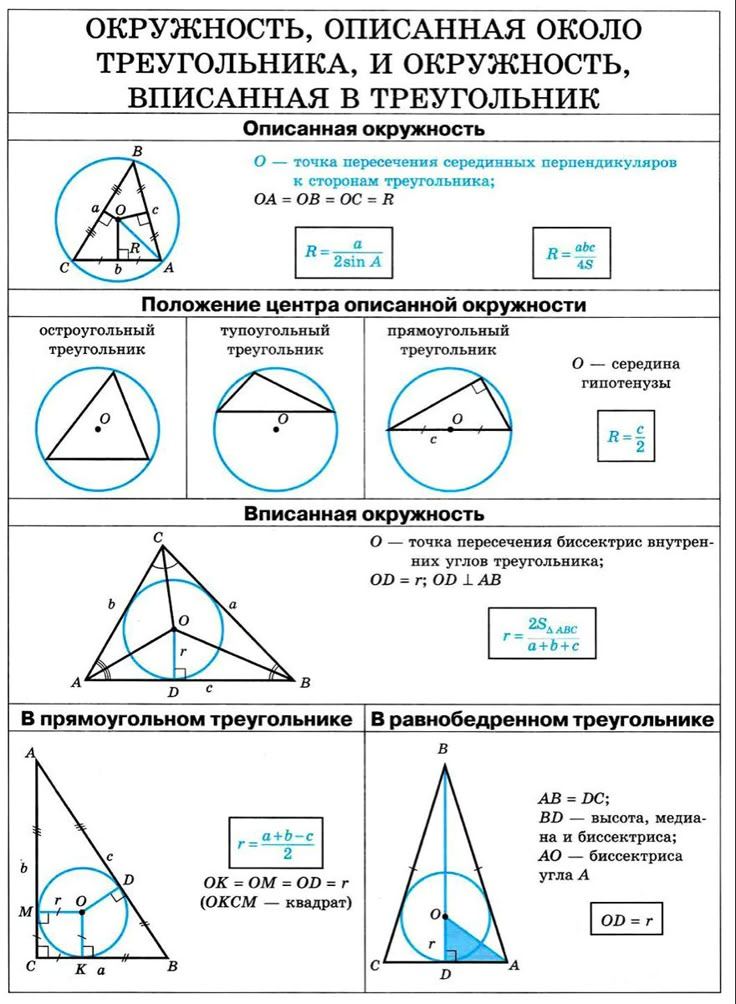
Теорема 1 (Основное свойство биссектрисы угла) . Каждая точка биссектрисы угла находится на одном и том же расстоянии от сторон угла (рис.1).

Рис. 1

Доказательство D , лежащую на биссектрисе угла BAC , и DE и DF на стороны угла (рис.1). Прямоугольные треугольники ADF и ADE равны , поскольку у них равны острые углы DAF и DAE , а гипотенуза AD – общая. Следовательно,

DF = DE,

что и требовалось доказать.

Теорема 2 (обратная теорема к теореме 1) . Если некоторая , то она лежит на биссектрисе угла (рис.2).

Рис. 2

Доказательство . Рассмотрим произвольную точку D , лежащую внутри угла BAC и находящуюся на одном и том же расстоянии от сторон угла.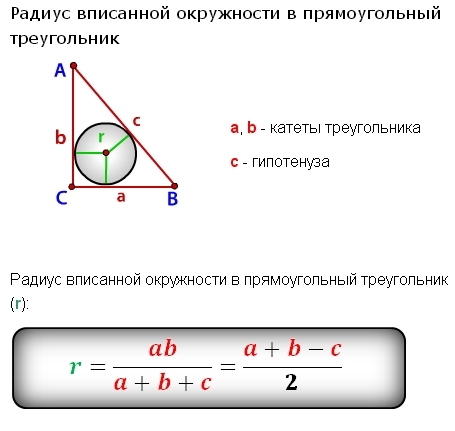 Опустим из точки D перпендикуляры DE и DF на стороны угла (рис.2). Прямоугольные треугольники ADF и ADE равны , поскольку у них равны катеты DF и DE , а гипотенуза AD – общая. Следовательно,

что и требовалось доказать.

Определение 2 . Окружность называют окружностью, вписанной в угол , если она сторон этого угла.

Теорема 3 . Если окружность вписана в угол, то расстояния от вершины угла до точек касания окружности со сторонами угла равны.

Доказательство . Пусть точка D – центр окружности, вписанной в угол BAC , а точки E и F – точки касания окружности со сторонами угла (рис.3).

Рис.3

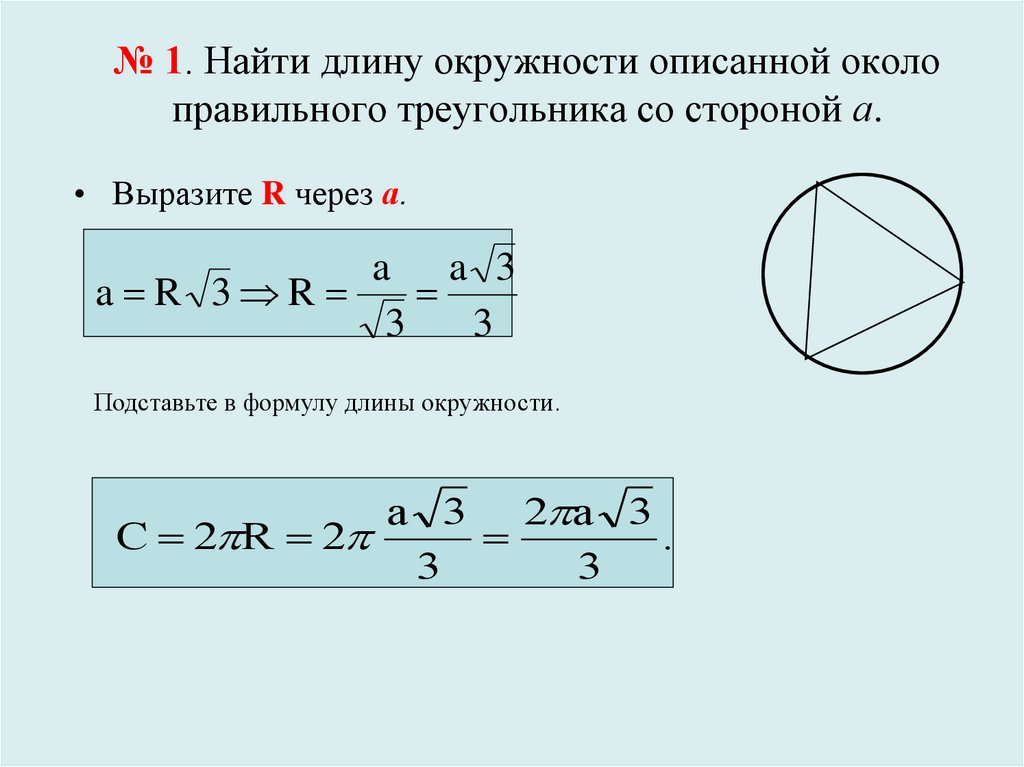
a , b , c – стороны треугольника, 
 S –площадь,

r – радиус вписанной окружности, 
 p – полупериметр

.

Посмотреть вывод формулы

a – боковая сторона равнобедренного треугольника , 
 b – основание, r – радиус вписанной окружности

a r – радиус вписанной окружности

Посмотреть вывод формул

,

где

,

то, в случае равнобедренного треугольника, когда

получаем

что и требовалось.

Теорема 7 . Для справедливо равенство

где a – сторона равностороннего треугольника, r – радиус вписанной окружности (рис. 8).

Рис. 8

Доказательство .

,

то, в случае равностороннего треугольника, когда

b = a,

получаем

что и требовалось.

Замечание . Я рекомендую вывести в качестве упражнения формулу для радиуса окружности, вписанной в равносторонний треугольник, непосредственно, т.е. без использования общих формул для радиусов окружностей, вписанных в произвольный треугольник или в равнобедренный треугольник.

Теорема 8 . Для прямоугольного треугольника справедливо равенство

где a , b – катеты прямоугольного треугольника, c – гипотенуза , r – радиус вписанной окружности.

Доказательство . Рассмотрим рисунок 9.

Рис. 9

Поскольку четырёхугольник CDOF является , у которого соседние стороны DO и OF равны, то этот прямоугольник – . Следовательно,

СВ = СF= r,

В силу теоремы 3 справедливы равенства

Следовательно, принимая также во внимание , получаем

что и требовалось.

Подборка задач по теме «Окружность, вписанная в треугольник».

1.

Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию.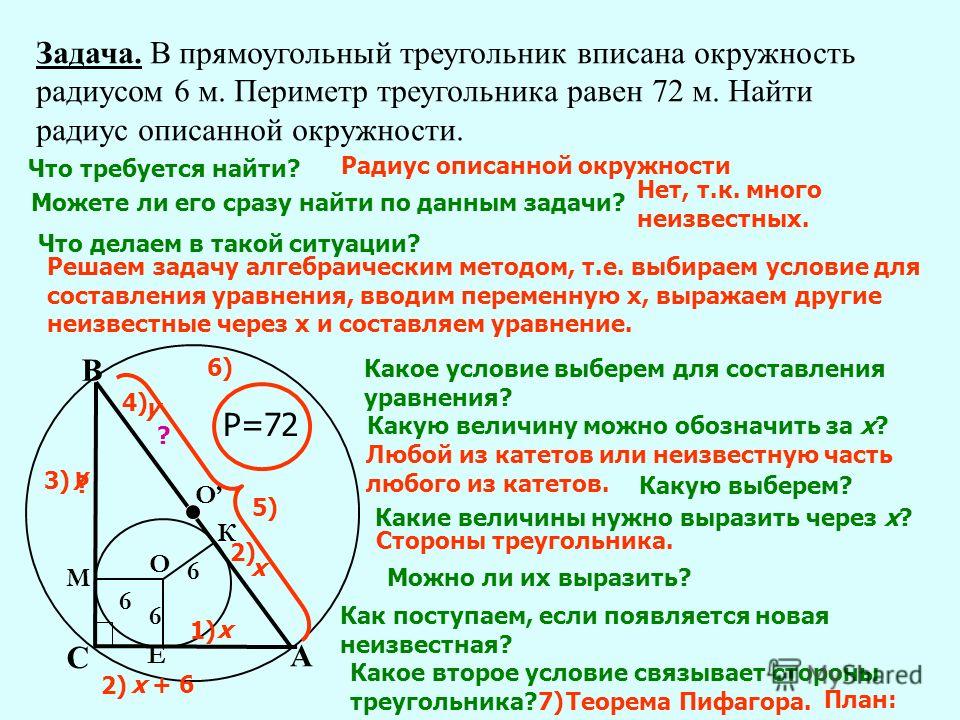 Найдите периметр треугольника.

2.

3

В треугольнике ABC АС=4, ВС=3, угол C равен 90º. Найдите радиус вписанной окружности.

4.

Катеты равнобедренного прямоугольного треугольника равны 2+. Найдите радиус окружности, вписанной в этот треугольник.

5.

Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 2. Найдите гипотенузу c этого треугольника. В ответе укажите с(–1).

Приведем ряд задач из ЕГЭ с решениями.

Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен . Найдите гипотенузу c этого треугольника. В ответе укажите .

Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен . Тогда гипотенуза равна .

Запишем площадь треугольника АВС двумя способами:

Приравняв эти выражения, получим, что . Поскольку , получаем, что . Тогда .

В ответ запишем .

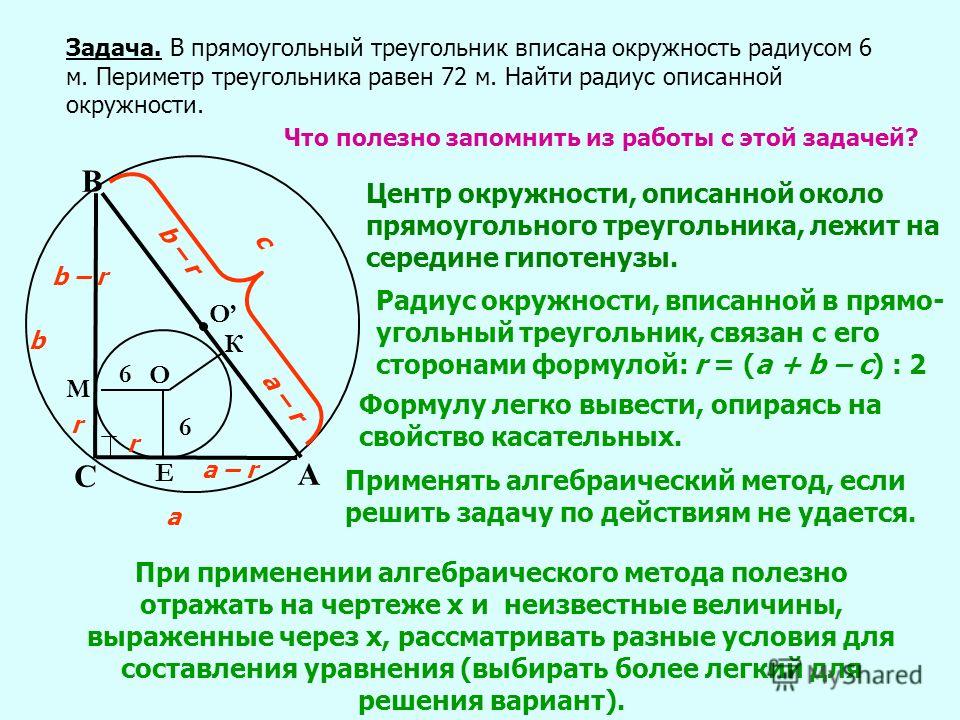
Ответ: .

Задача 2.

1. В произвольном две боковые стороны 10см и 6см (AB и BC). Найти радиусы описанной и вписанной окружностей
Задача решается самостоятельно с комментированием.

Решение:

В .

1) Найти:
2) Доказать: и найти СK
3) Найти: радиусы описанной и вписанной окружностей

Решение:

Задача 6.

Р адиус окружности вписанной в квадрат равен . Найти радиус окружности описанной около этого квадрата. Дано :

Найти : ОС=?
Решение : в данном случае задачу можно решить, воспользовавшись либо теоремой Пифагора, либо формулой для R. Второй случай будет проще, поскольку формула для R выведена из теоремы.

Задача 7.

Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 2. Найдите гипотенузу с этого треугольника. В ответе укажите .

S – площадь треугольника

Нам неизвестны ни стороны треугольника, ни его площадь. Обозначим катеты как х, тогда гипотенуза будет равна:

А площадь треугольника будет равна 0,5х 2 .

Значит

Таким образом, гипотенуза будет равна:

В ответе требуется записать:

Ответ: 4

Задача 8.

В треугольнике ABC АС = 4, ВС = 3, угол C равен 90 0 . Найдите радиус вписанной окружности.

Воспользуемся формулой радиуса окружности вписанной в треугольник:

где a, b, c – стороны треугольника

S – площадь треугольника

Две стороны известны (это катеты), можем вычислить третью (гипотенузу), также можем вычислить и площадь.

По теореме Пифагора:

Найдём площадь:

Таким образом:

Ответ: 1

Задача 9.

Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.

Воспользуемся формулой радиуса окружности вписанной в треугольник:

где a, b, c – стороны треугольника

S – площадь треугольника

Известны все стороны, вычислим и площадь. Её мы можем найти по формуле Герона:

Тогда

найти центр и радиус окружности, описанной вокруг прямоугольного треугольника с вершинами (1,1), (1,4) и (7,4).

РЕШЕНИЕ: найти центр и радиус окружности, описанной вокруг прямоугольного треугольника с вершинами (1,1), (1,4) и (7,4).

Алгебра -> Настраиваемые средства решения задач Word -> Геометрия -> РЕШЕНИЕ: найти центр и радиус окружности, описанной вокруг прямоугольного треугольника с вершинами (1,1), (1,4) и (7,4). Войти

Объявление: Более 600 словесных задач по алгебре на edhelper.com

Задачи Word: GeometryWord РешателиРешатели УрокиУроки Архив ответовОтветы     Щелкните здесь, чтобы просмотреть ВСЕ задачи по геометрии Word Problems Вопрос 809979: найти центр и радиус окружности, описанной вокруг прямоугольного треугольника с вершинами (1,1), (1,4) и (7) ,4). Ответ от KMST(5315)    (Показать источник): Вы можете разместить это решение на ВАШЕМ сайте! Отрезок, соединяющий (1,1) и (1,4), является частью вертикальной линии. Отрезок, соединяющий (1,4) и (7,4), является частью горизонтальной линии. Очевидно, это стороны прямоугольного треугольника, прямой угол лежит в точке (1,4), и отрезок, соединяющий (1,1) и (7,4), является гипотенузой. ЦЕНТР: Если вы изучаете окружности, возможно, вас учили, что угол, вписанный в окружность, измеряет половину центрального угла, опирающегося на ту же дугу. Возможно, вам сказали, что следствие состоит в том, что дуга, проведенная на вписанном прямом угле, равна и делает соответствующую хорду диаметром. В этом случае вы бы поняли, что гипотенуза треугольника — это диаметр, а его середина — центр окружности. Если вы изучаете треугольники, возможно, вас учили, что все три перпендикулярные биссектрисы сторон треугольника пересекаются в центре описанной окружности, то есть в центре описанной окружности. В любом случае вы найдете координаты центра как середину гипотенузы или как пересечение горизонтальной и вертикальной серединных перпендикуляров, выполняя вычисления и РАДИУС: Радиус равен половине диаметра. Диаметр — это отрезок, соединяющий (1,1) и (7,4), , и вы можете рассчитать его длину как Таким образом, радиус = примерно

Вписанные и описанные прямоугольные треугольники

Несколько учащихся в своих размышлениях о нашем блоке «Круги» отметили, что задания по оценке успеваемости помогли им «объединить все, чему мы научились, чтобы найти правильные ответы на сложные задачи».

Мы начали с диаграммы из урока формирующего оценивания проекта Mathematics Assessment Project. Вписывание и описание прямоугольных треугольников

и попросил студентов

1. Вычислите радиусы описанной окружности для прямоугольного треугольника со сторонами 5 единиц, 12 единиц и 13 единиц. Покажите и обоснуйте каждый шаг своих рассуждений.

2. С помощью математики подробно объясните, как вычислить радиусы описанной окружности прямоугольного треугольника со сторонами любой длины: a, b и c (где c — гипотенуза).

Второе задание было немного более структурированным. Круги в треугольниках – результат задания ученика в рамках проекта Mathematics Assessment Project.

Учащимся было дано следующее:

На этой диаграмме показана окружность, которая касается сторон прямоугольного треугольника, длина сторон которого равна 3 единицам, 4 единицам и 5 единицам.

1. Докажите, что треугольники AOX и AOY равны.

2. Что вы можете сказать о размерах отрезков CX и CZ?

3. Найти р, радиус окружности. Четко объясните свою работу и покажите все свои расчеты.

Интересно, что было бы, если бы мы попросили учащихся определить радиус вписанной окружности без такого количества вспомогательных линий, которые уже даны на рисунке? Вместо этого, что, если бы мы использовали ту же фигуру, что и в первом задании?

Другой учитель преподал этот урок моим ученикам. Она сохранила свою работу для меня, потому что даже с нарисованными вспомогательными линиями студенты по-разному понимали структуру (и особенно выражения, которые они написали для длин отрезков).

 

Затем их попросили определить радиус вписанной окружности для прямоугольного треугольника со сторонами 5, 12, 13, а затем их попросили обобщить полученные результаты.

На этой диаграмме показана окружность, которая касается сторон прямоугольного треугольника, длина сторон которого равна 5 единицам, 12 единицам и 13 единицам.

4. Нарисуйте вспомогательные линии, как в предыдущем задании, и найдите радиус окружности в этом прямоугольном треугольнике 5, 12, 13. Объясните свою работу и покажите свои расчеты.

5. С помощью математики подробно объясните, как вычислить радиусы вписанной окружности прямоугольного треугольника со сторонами любой длины: a, b и c (где c — гипотенуза).

 

Интересно, как технологии справляются с такими задачами?
У нас был подготовлен эскиз схемы для студентов, которые хотели ее использовать.

Учащиеся должны были измерить себя, чтобы конструкция помогла разобраться в математике. Я считаю, что эта технология может быть полезна тем, кто не знает, с чего начать. Что вы замечаете, когда треугольник правильный?

Может ли это помочь им  рассуждать абстрактно и количественно , начиная с количественного и доводя до обобщения? Может ли это помочь им разобраться в проблемах и упорно решать их , когда они не знают, что еще делать на бумаге?

У нас также был подготовлен скелет диаграммы для вписанного круга для тех, кто хотел его использовать.

Какие вспомогательные линии (или отрезки) вы бы построили и измерили для вписанной окружности?

Технология может помочь им сделать предположение о длине радиуса, а затем вернуться к математике, чтобы понять, почему.

Итак, путешествие продолжается… Может быть, когда-нибудь у меня хватит смелости начать наш блок «Круги» с этой задачи и позволить математике разворачиваться в контексте задачи по мере необходимости.