а)AO=CO(векторы); б)BO=OD(векторы); в)AB=AD(векторы)? Ответ обоснуйте. — Знания.site
Последние вопросы
Геометрия
1 минута назад
определите: a) наибольшую b) наименьшую сторону треугольника ABC, если AB>BC>AC. даю 93 баллаГеометрия
11 минут назад
помогитее пжжжжжжжж срочноГеометрия
16 минут назад
допоможіть будь ласка Геометрия
21 минут назад
У прямокутному трикутнику катети дорівнюють 3 см і 8 см. Знайдіть:1) тангенс гострого кута, який лежить проти меншого катета;2) синус гострого кута, який прилягає до більшого катета;3) косинус гострого кута, який лежить проти більшого катета.
Знайдіть:1) тангенс гострого кута, який лежить проти меншого катета;2) синус гострого кута, який прилягає до більшого катета;3) косинус гострого кута, який лежить проти більшого катета.Геометрия
36 минут назад
скільки сторін має окуплий многокутник, кожен кут якого дорівнює 108°допоможіть будь ласка Геометрия
36 минут назад
Знайдіть кути рівнобедреного трикутника якщо кут при вершині дорівнює 9041 минут назад
ПОЖАЛУЙСТА УМОЛЯЮ помогите у меня кр, а я ничего не понимаюДЕЛАТЬ 2 ВАРИАНТ РОБИТИ З ПОВНИМ ПОЯСНЕННЯМ (І З МАЛЮНКОМ)БУДЬ ЛАСКА ДОПОМОЖІТЬ, ВИ МОЯ ЄДИНА НАДІЯ Геометрия
56 минут назад
допоможіть пж пж пж Геометрия
1 час назад
2 Найдите площадь трапеции, основания которой равны 13 см и 7 см, а высота равна 8 см.
Геометрия
1 час назад
помогите пожалуйста, срочно очень Геометрия
2 часа назад
У якій точці графік функції у = 9 — х перетинає вісь абсцис? (-9; 0) (9;0) (0;9) (0; -9)2 часа назад
Серед наведених функцій укажіть пряму пропорційність у = 9 -х у=9/х у = 9 у = 9×2 y = 9xГеометрия
2 часа назад
№2. Стороны треугольника равны 39 см, 25 см, 56 см. Найдите площадь треугольника и радиус вписанной окружности.
2 часа назад
какая почва в влажных экваториальных лесах южной америки?Геометрия
2 часа назад
Контрольная по геометрии
Все предметы
Выберите язык и регион
English
United States
Polski
Polska
Português
Brasil
English
India
Türkçe
Türkiye
English
Philippines
Español
España
Bahasa Indonesia
Indonesia
Русский
Россия
How much to ban the user?
1 hour 1 day 100 years
1.Параллелограмм. 3.Ромб. 4.Теорема Фалеса. 5.Средняя линия треугольника. 6.Трапеция. 7.Теорема о пропорциональных отрезках. 8.Примеры.
|
|||||||||||||||||||||||||||||
| 1 2 3 4 5 6 7 8 9 10 11 12 | |||||||||||||||||||||||||||||
1.Параллелограмм |
|||||||||||||||||||||||||||||
|
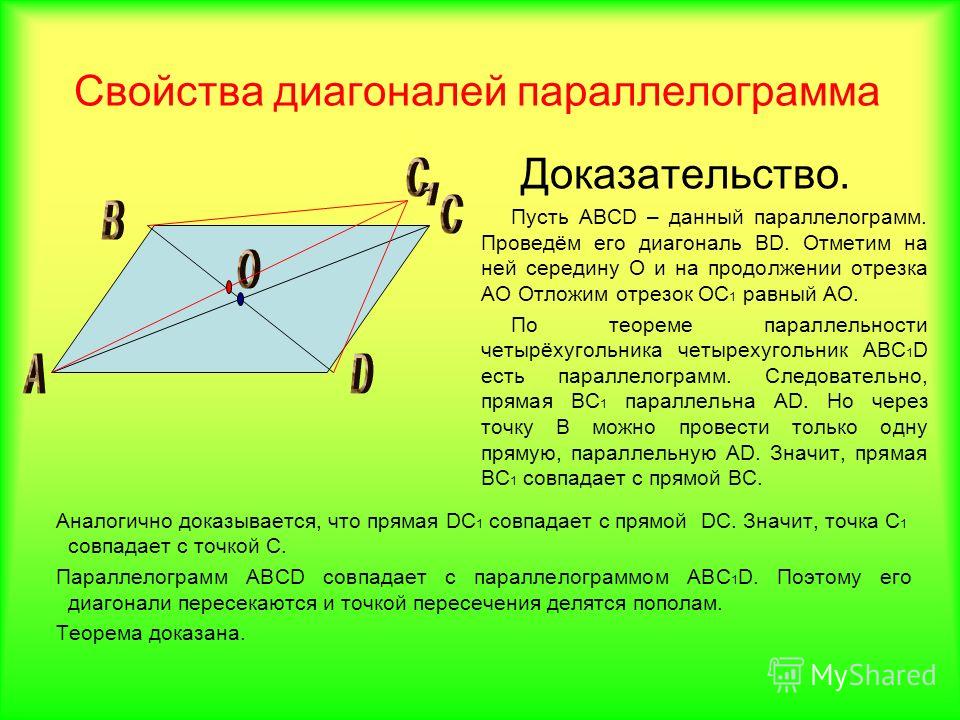
Параллелограмм — это геометрическая фигура, у которой диагонали пересекаются в точке, делящей их пополам, а противолежащие стороны параллельны. Теорема: если диагонали четырехугольника пересекаются и делятся этой точкой пересечения пополам, то такой четырехугольник называется параллелограммом. Доказательство. Пусть АВСD данный четырехугольник. Точка О — точка пересечения его диагоналей (рис.1). Тогда треугольники Δ АОD и Δ ВOC равны по двум сторонам и углу между ними. А следовательно, угол ODA равен углу CBO и угол OAD равен углу BCO. Таким образом, эти углы являются внутренними накрест лежащими для прямых AD и BC и секущей AC. А по признаку параллельности прямых, прямые AD и BC параллельны. Аналогично можно доказать, что прямая АВ параллельна ВС. Теорема доказана. |
Рис.1 Теорема. Параллелограмм. |
||||||||||||||||||||||||||||
2. Свойство диагоналей параллелограмма Свойство диагоналей параллелограмма |
|||||||||||||||||||||||||||||
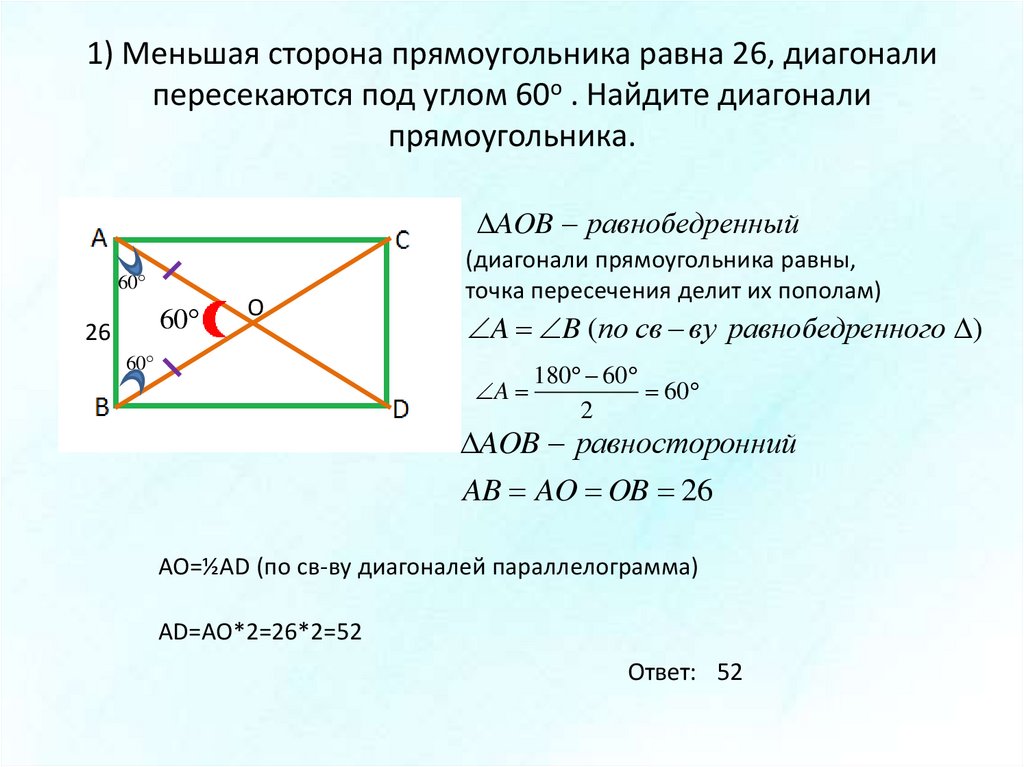
Теорема. если четырехугольник является параллелограммом, то его диагонали делятся точкой пересечения пополам. Доказательство. Пусть дан параллелограмм АВСD. (Рис. 2) Тогда его стороны AD и BC равны и лежат на параллельных прямых а и b. Если мы проведем секущие с и d так, чтобы прямая с проходила через точку А и С, а прямая d проходила через точку B и D, то угол ОАD будет равен углу ОСВ, а угол ОDА будет равен углу ОВС, как внутренние накрест лежащие. Следовательно, треугольники АОD и ВОС равны по стороне и прилегающим к ней углам. А отсюда следует и равенство сторон этих треугольников. Т.е. АО = ОС, а ВО = ОD. Сумма этих сторон и есть диагонали параллелограмма. |
Рис.2 Теорема. Свойство диагоналей параллелограмма. |
||||||||||||||||||||||||||||
3.Ромб |
|||||||||||||||||||||||||||||
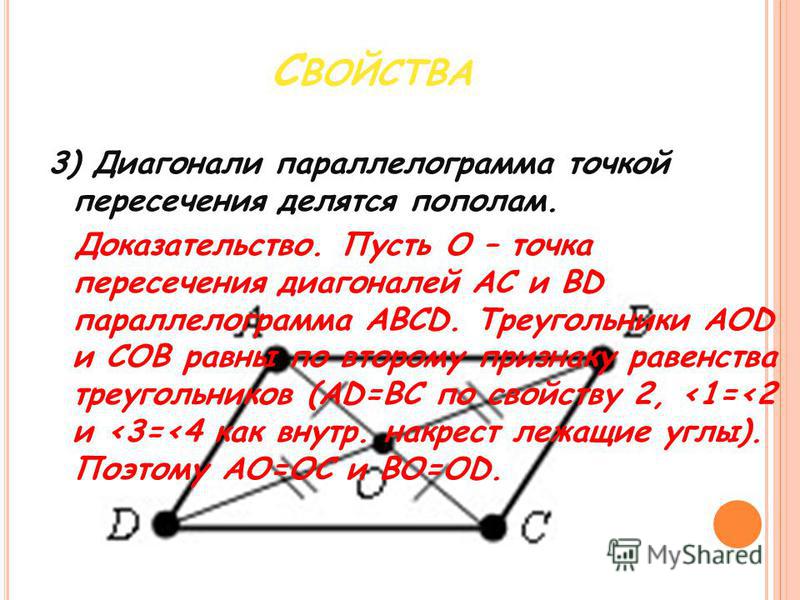
Ромб — это геометрическая фигура, у которой все стороны равны. Теорема. диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов. Доказательство. Пусть АВСD — ромб.(Рис. 3). Тогда треугольник АВС — равнобедренный. А это значит, что отрезок ВО, который является половиной диагонали, является биссектрисой медианой и высотой. |
Рис.3 Теорема. Свойство диагоналей ромба. |
||||||||||||||||||||||||||||
Задача |
|||||||||||||||||||||||||||||
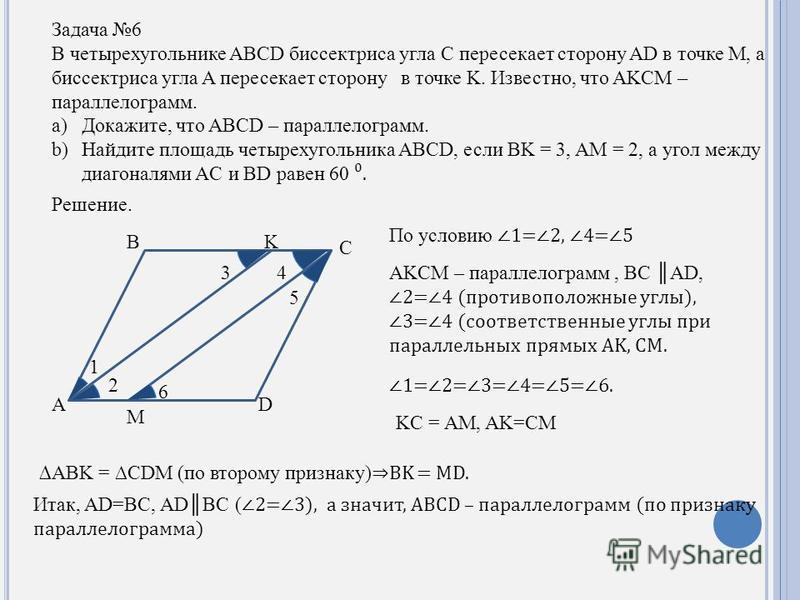
В параллелограмме АВСD проведена биссектриса угла А, которая пересекает сторону ВС в точке Е. Необходимо найти отрезки ВЕ и ЕС, если АВ = 9 см, АD = 14 см (рис.4) Решение. Так как прямая АЕ биссектриса, то это значит, что треугольники АВЕ и АЕР равны. Так как угол ВАЕ равен углу АЕР, а угол ЕАР равен углу ВЕА как внутренние накрест лежащие. |
Рис.4 Задача. |
||||||||||||||||||||||||||||
4.Теорема Фалеса |
|||||||||||||||||||||||||||||
|
Теорема: параллельные прямые, пересекающие стороны угла и отсекающие на одной его стороне равные отрезки, отсекают равные отрезки и на другой его стороне. Доказательство. |
Рис.5 Теорема Фалеса. |
||||||||||||||||||||||||||||
5.Средняя линия треугольника |
|||||||||||||||||||||||||||||
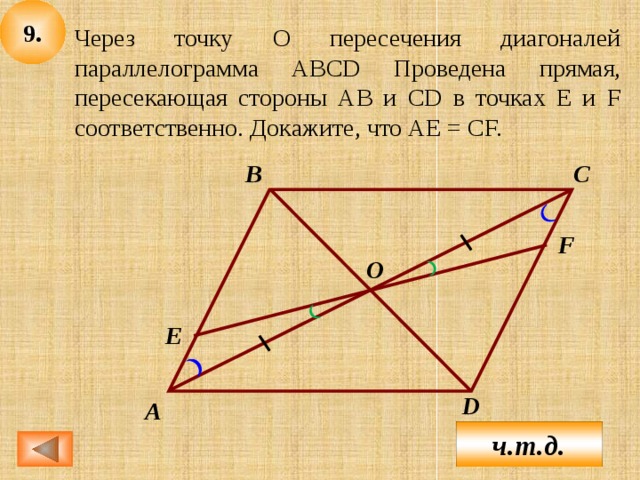
Теорема. средняя линия треугольника, которая соединяет середины двух данных сторон, параллельна третьей его стороне и равна ее половине. Доказательство. |
Рис.5 Теорема. Средняя линия треугольника. |
||||||||||||||||||||||||||||
6.Трапеция |
|||||||||||||||||||||||||||||
Трапеция — это геометрическая фигура, у которой только две противолежащие стороны параллельны. Теорема. средняя линия трапеции параллельна двум своим основаниям и равна их полусумме. Доказательство. Пусть АВСD — трапеция.(Рис. 6). Проведем прямую от вершины В через середину стороны СD точку Н к основанию, т.е. достроим треугольник АВО. Тогда треугольники ВСН и DHO равны по сторонам СН и НD и прилегающим к ним углам. Следовательно отрезок АО равен сумме оснований АD и ВС. Рассмотрим треугольник АВО. ЕН это средняя линия треугольника, которая равна половине основания АО, т.е. полусумме оснований трапеции АD и ВС. |
Рис.6 Теорема. Средняя линия трапеции. |
||||||||||||||||||||||||||||
7. Теорема о пропорциональных отрезках Теорема о пропорциональных отрезках |
|||||||||||||||||||||||||||||
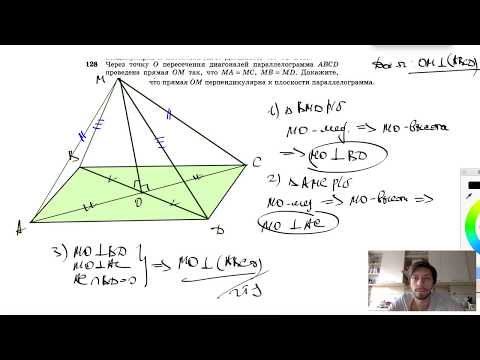
Теорема. параллельные прямые, которые пересекают стороны угла, отсекают от его сторон пропорциональные отрезки. Доказательство. Пусть дан угол и пересекающие его параллельные прямые. Разобьем угол ВAС параллельными прямыми на n частей. Тогда АВ = ns, a AB1 = ms. Где s — отрезок некоторой длины. По теореме Фалеса эти прямые разбивают сторону AС также на равные части. Тогда: |
Рис.7 Теорема о пропорциональных отрезках. |
||||||||||||||||||||||||||||
Допустим, что Отложим на луче АС отрезок АС2 Т.е. мы пришли к противоречию, так как изначально мы взяли отрезок АС2 = АС*АВ1/АВ. |
Рис.8 Теорема о пропорциональных отрезках. |
||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
Пример 1 |
|||||||||||||||||||||||||||||
Через точку пересечения диагоналей параллелограмма проведена прямая. Докажите, что ее отрезок, заключенный между параллельными сторонами, делится этой точкой пополам. |
|||||||||||||||||||||||||||||
Доказательство: Пусть ABCD данный параллелограмм. EF данный отрезок, проходящий через точку О пересечения диагоналей. Рассмотрим треугольники COF и AOE. Сторона АО треугольника АОЕ равна стороне ОС треугольника COF по свойству параллелограмма. Угол при вершине А треугольника АОЕ равен углу при вершине С треугольника COF, как внутренние накрест лежащие углы. Углы при вершине О у обоих треугольников равны как вертикальные. Отсюда можно сделать вывод, что треугольники АОЕ и COF равны по второму признаку равенства треугольников (по стороне и прилегающим к ней углам). Следовательно, отрезки OF и ОЕ равны. |
Рис. |
||||||||||||||||||||||||||||
Пример 2 |
|||||||||||||||||||||||||||||
Две стороны параллелограмма относятся как 3:4, а его периметр равен 2,8 м. Найдите стороны параллелограмма. (Рис.10) |
|||||||||||||||||||||||||||||
Решение: Пусть ABCD данный параллелограмм. Обозначим сторону АВ как 3х, а сторону ВС как 4х. Тогда составим следующее соотношение: 2*(3х + 4х) = 2,8 14х = 2,8 Отсюда: х = 0,2 м. Следовательно, АВ = 3х = 0,6 м. ВС = 4х = 0,8 м. |
Рис.10 Задача. Две стороны параллелограмма… |
||||||||||||||||||||||||||||
Пример 3 |
|||||||||||||||||||||||||||||
В параллелограмме ABCD перпендикуляр, опущенный из вершины В на сторону AD, делит ее пополам. Найдите диагональ BD и стороны параллелограмма, если периметр параллелограмма равен 4 м, а периметр треугольника ABD равен 3 м. (Рис.11) |
|||||||||||||||||||||||||||||
Решение: Так как перпендикуляр BE, опущенный на сторону AD, делит ее пополам, то треугольники ABE и BED равны по первому признаку равенства треугольников (по двум сторонам и углу между ними). Обозначим сторону АВ как х, а сторону AD — как 2y. Тогда можно составить следующие соотношения: PABCD = 2*(х + 2y) = 4, PABD = 2x +2y = 3 Следовательно, PABCD = 2х + 4y = 4, а 2х = 4 — 4y. Тогда подставим 4 — 4y во второе уравнение: 4 — 4y + 2y = 3 и,следовательно, y = 0,5, а х = 1 АВ = BD = 1 м. AD = 1 м. |
Рис.11 Задача. В параллелограмме ABCD перпендикуляр… |
||||||||||||||||||||||||||||
Пример 4 |
|||||||||||||||||||||||||||||
В прямоугольный треугольник, каждый катет которого равен 8 см, вписан прямоугольник, имеющий с треугольником общий угол. |
|||||||||||||||||||||||||||||
Решение: Пусть АВС данный треугольник. АВ = АС = 8 см. Тогда углы при вершинах В и С равны 45°. А следовательно, углы при вершине Е в треугольниках FEC и BDE также равны 45°. Если обозначить часть катета АF как х, то FC будет равно 8 — х. Отсюда следует, что FE = AD = 8-х, а BD = х. Теперь можно составить следующее соотношение: РADEF = 2*(х + 8 — х) = 16 см. Периметр прямоугольника ADEF равен 16 см. |
Рис.12 Задача. В прямоугольный треугольник… |
||||||||||||||||||||||||||||
Пример 5 |
|||||||||||||||||||||||||||||
Докажите, что если у параллелограмма диагонали перпендикулярны, то он является ромбом. |
|||||||||||||||||||||||||||||
Доказательство: Пусть АВСD данный параллелограмм. По свойству параллелограмма, у него противоположные стороны параллельны и равны. Следовательно, стороны АВ и CD можно рассматривать как параллельные прямые, а диагональ BD — как секущую. Тогда в треугольниках АВО и DOC углы при вершинах B и D равны как внутренние накрест лежащие. Так же как и углы при вершинах А и С. Отсюда следует, что эти треугольники равны по второму признаку равенства треугольников (по стороне и прилегающим к ней углам). Сторона АВ = DC и внутренние накрест лежащие углы при них равны. Следовательно, АО = ОС, а ВО = OD. Теперь рассмотрим треугольники AOD и DOC. Они также равны, но по первому признаку равенства треугольников. Сторона АО = ОС, а сторона OD у них общая. Следовательно, можно сделать вывод, что сторона AD = DC = AB = BC, т.е. данный параллелограмм является ромбом. |
Рис.13 Задача. Докажите, что если у параллелограмма… |
||||||||||||||||||||||||||||
| 1 2 3 4 5 6 7 8 9 10 11 12 | |||||||||||||||||||||||||||||
Содержание |
|||||||||||||||||||||||||||||
| Страница 1 | Страница 7 | ||||||||||||||||||||||||||||
1. Основные фигуры планиметрии. Основные фигуры планиметрии.
2.Аксиомы планиметрии. 3.Смежные углы. 4.Вертикальные углы. 5.Перпендикулярные прямые. 6.Признаки равенства треугольников. |
1.Движение и его свойства.
2.Симметрия относительно точки. 3.Симметрия относительно прямой. 4.Параллельный перенос и его свойства. |
||||||||||||||||||||||||||||
| Страница 2 | Страница 8 | ||||||||||||||||||||||||||||
|
1.Параллельность прямых.
2.Признаки параллельности прямых. 3.Свойство углов при пересечении параллельных прямых. 4.Сумма углов треугольника. 5.  Единственность перпендикуляра к прямой. Единственность перпендикуляра к прямой.
6.Высота, биссектриса и медиана треугольника. 7.Свойство медианы равнобедренного треугольника. |
1.Вектор и его абсолютная величина.
2.Сложение векторов. 3.Умножение вектора на число. 4.Разложение вектора по двум неколлинеарным векторам. 5.Скалярное произведение векторов. |
||||||||||||||||||||||||||||
| Страница 3 | Страница 9 | ||||||||||||||||||||||||||||
|
1.Окружность.
2.Окружность описанная около треугольника. 3.Окружность вписанная в треугольник. 4.Геометрическое место точек. |
1. Преобразование подобия и его свойства. Преобразование подобия и его свойства.
2.Подобие фигур. Подобие треугольников по двум углам. 3.Подобие треугольников по двум пропорциональным сторонам и углу между ними. 4.Подобие треугольников по трем пропорциональным сторонам. 5.Подобие прямоугольных треугольников. |
||||||||||||||||||||||||||||
| Страница 4 | Страница 10 | ||||||||||||||||||||||||||||
|
1.Параллелограмм.
2.Свойства диагоналей параллелограмма. 3.Ромб. 4.Теорема Фалеса. 5.Средняя линия треугольника. 6.Трапеция. 7.Теорема о пропорциональных отрезках. |
1.Углы, вписанные в окружность.
2.Пропорциональность хорд и секущих окружности. 3.Теорема косинусов. 4.Теорема синусов. 5.Соотношение между углами и сторонами в треугольнике. |
||||||||||||||||||||||||||||
| Страница 5 | Страница 11 | ||||||||||||||||||||||||||||
|
1.Теорема Пифагора.
2.Египетский треугольник. 3.Соотношение между углами и сторонами в прямоугольном треугольнике. 4.Основные тригонометрические тождества. |
1.Многоугольники. Правильные многоугольники.
2.Радиус вписанной и описанной окружностей правильных многоугольников. 3.Подобие многоугольников. 4.Длина окружности. |
||||||||||||||||||||||||||||
| Страница 6 | Страница 12 | ||||||||||||||||||||||||||||
1. Декартова система координат. Декартова система координат.
2.Расстояние между точками. 3.Уравнение окружности. 4.Уравнение прямой. 5.Координаты точки пересечения. |
1.Площадь прямоугольника.
2.Площадь параллелограмма. 3.Площадь треугольника. 4.Площадь круга. 5.Площадь подобных фигур. 6.Площадь трапеции. |
||||||||||||||||||||||||||||
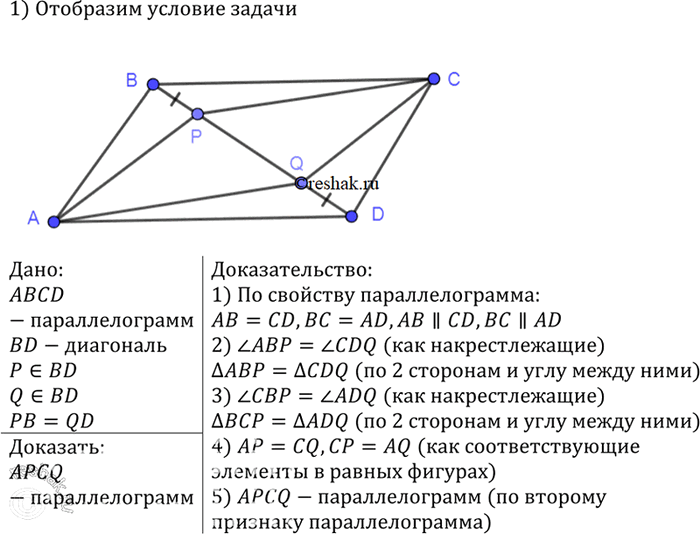
ABCD — параллелограмм, а O — точка пересечения его диагоналей. Если точки P, Q, R, S являются серединами OA, PB, QC, RD соответственно, то точки Q, O, S
Дата обновления: 27-06-2022
Text Solution
A
образуют треугольник
B
не лежат в одной плоскости
C
лежат на одной прямой
D
не лежат на одной прямой
0 Ответ4 00003 НИКИТА ПУБЛИКАЦИЯ-ВЕКТОР-ВОПРОСЫ С НЕСКОЛЬКИМ ВЫБОРОМ
20 видеоРЕКЛАМА
Аб Падхай каро бина адс ке
Хариэдо Д. Н. Про и дехо сари видео бина киси ад ки рукаават ке!
Н. Про и дехо сари видео бина киси ад ки рукаават ке!
Видео по теме
ABCD — ромб и P,Q,R,S являются серединами AB,BC,CD,DA соответственно. Докажите, что PQRS представляет собой прямоугольник.
P и Q — точки на противоположных сторонах AD и BC параллелограмма ABCD, такие, что PQ проходит через точку пересечения O его диагоналей AC и BD. Покажите, что PQ делится пополам в точке O.
26522190
समांत выполнительный O से एक रेखा खींची गई है जो ad तथा bc को क्रमशः p तथा q पर पшить क क क है।।।।। सिद्ध कीजिए कि रेखाखण्ड pq समांतर चतुर्भुज को दो बराबर क्षेत्रफल वाले भागों में विभ क क है।।।।
105884868
ABCD — четырехугольник, в котором P, Q, R и S — середины сторон AB, BC, CD и DA. АС — диагональ. Покажите, что :
PQRS — параллелограмм.
203476048
A : ABCD — параллелограмм. Если G — точка пересечения его диагоналей, а O — любая точка, то OA + OB + OC + OD = 4OG
R : В параллелограмме диагонали делят друг друга пополам.
217272321
Text Solution
P, Q, R и S — середины сторон AB, BC, CD и DA параллелограмма ABCD соответственно. Если площадь ABCD равна 88 кв.см, то площадь PQRS равна
233232278
ЕСЛИ P,Q,R и S являются соответственно серединами сторон параллелограмма ABCD, то покажите, что (PQRS) = 12 ар (ABCD)
379895733
ABCD — параллелограмм, P и Q — точки на диагонали AC такие, что AP=QC, тогда четырехугольник BPDQ — это :
449930063
В параллелограмме ABCD середины BC и AD Q и P соответственно. Докажите, что если диагонали параллелограмма ABCD пересекаются в точке O, то POQ будет прямой.
480152314
Текстовое решение
समान्ता यदि ∠ВОС=90∘ तथा ∠BDC=40∘ हो, तो ∠OAB= ?
603147113
P и Q — точки на противоположных сторонах AD и BC параллелограмма ABCD, такие, что PQ проходит через точку пересечения O его диагоналей AC и BD. Покажите, что PQ делится пополам в точке O.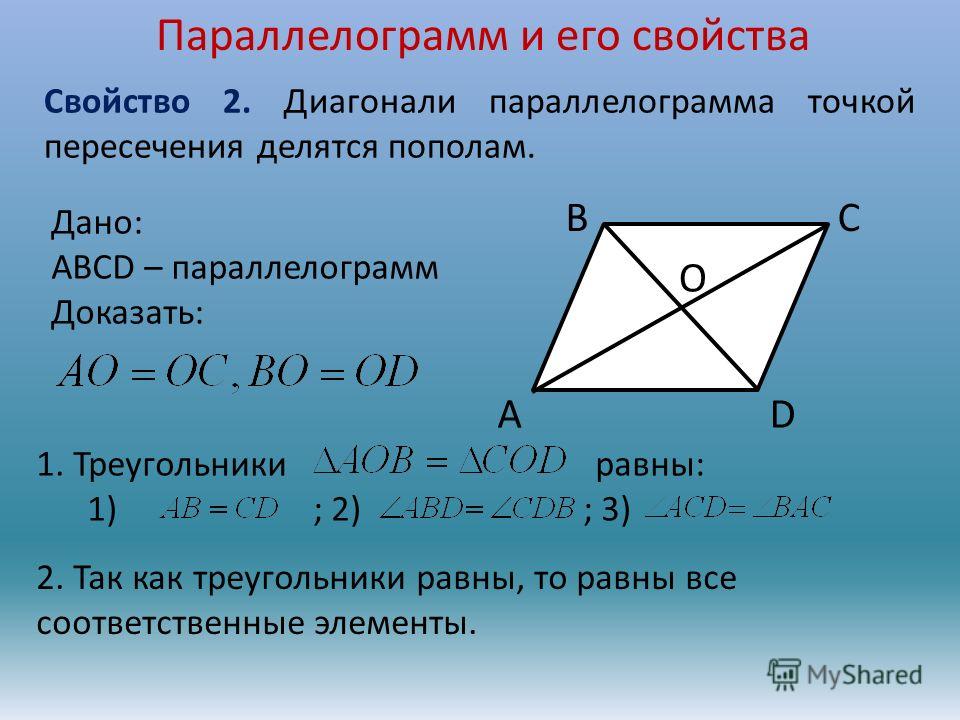
642505469
В параллелограмме ABCD точка P — середина стороны AD. Прямая BP пересекает диагональ AC в точке Q. Тогда отношение AQ:QC=
642817811
ABCD — параллелограмм, а P — середина стороны AD. Прямая BP пересекает диагональ AC в Q. Тогда отношение AQ : QC =
642818029
Пересекутся в точке пересечения диагонали O четырехугольника ABCD таким образом OA: OC= 3: 2 То есть Является ли ABCD параллелограммом? Почему и почему бы и нет?
642856899
Рассмотрим следующий четырехугольник ABCD, в котором P,Q,R,S — середины сторон.
Покажите, что PQRS является параллелограммом.
642941360
CA Диагонали параллелограмма
CA Диагонали параллелограммаЗанятия в классе и самооценка в классе
16 октября 2000 г.
Задача 1
была задана как групповое задание в классе. Время отведено 25 минут. Эта теорема является «если и только если», поэтому решение состоит из двух частей.
Задача 2 была быстро продемонстрирована на слайде и не выполнялась в групповом режиме.
Задача 1. Диагонали параллелограмма
Укажите определение параллелограмма (тот, что в B&B). Докажите, что четырехугольник является параллелограммом тогда и только тогда, когда его диагонали делят друг друга пополам. (Другими словами, диагонали пересекаются в точке M, которая является серединой каждой диагонали.)
Определение. Четырехугольник ABCD является параллелограммом, если AB параллелен CD, а BC параллелен DA.
Утверждение 1. Если ABCD — параллелограмм, то диагонали ABCD делят друг друга пополам.
Доказательство утверждения 1.
Пусть O — пересечение диагоналей AC и BD. Утверждение можно переформулировать так: О — середина АС, а также середина BD.
Поскольку O находится на отрезке AC, O является серединой AC, если AO = CO. Точно так же O является серединой BD, если BO = DO. Это то, что мы докажем, используя конгруэнтные треугольники.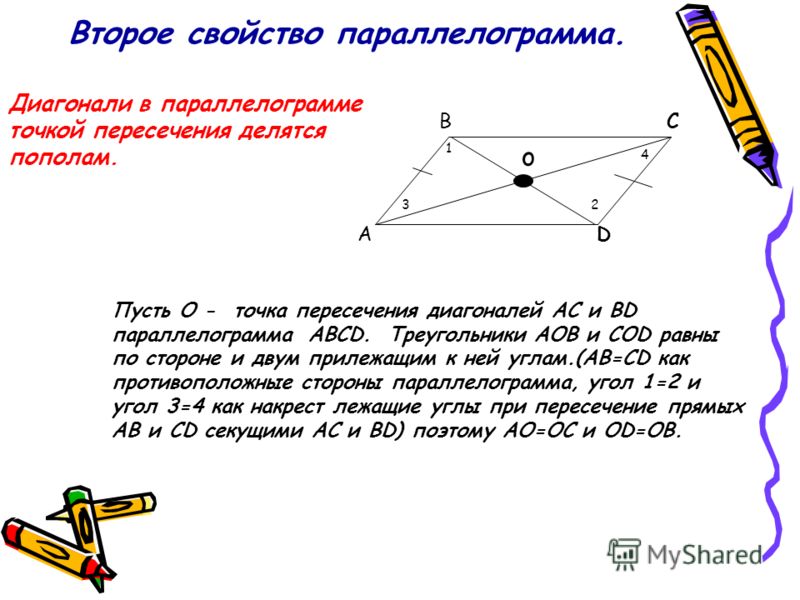
Сначала мы показываем, что треугольник ABO подобен треугольнику CDO, используя Угол-Угол. Так как прямая AC является секущей параллельных прямых AB и CD, то угол OAB = угол CAB = угол ACD = угол OCD. Кроме того, по вертикальным углам угол AOB = угол COD. Таким образом, треугольник ABO подобен треугольнику CDO.
Затем мы покажем, что эти два треугольника конгруэнтны, показав, что отношение подобия равно 1. Мы знаем из домашнего задания (*), что противоположные стороны ABCD, AB = CD. Это две соответствующие стороны подобных треугольников, поэтому треугольники ABO и CDO равны.
Из сравнения заключаем, что АО = СО и ВО = DO.
QED
Утверждение 2. Если ABCD — четырехугольник, у которого диагонали AC и BD делят друг друга пополам, то ABCD — параллелограмм.
Доказательство утверждения 2.
Пусть M — пересечение AC и BD. Нам дано, что M является серединой AC, а также BD, поэтому MA = MC и MB = MD.
Мы также знаем, что угол AMB = угол CMD по вертикальным углам. Таким образом, мы заключаем, что треугольник AMB конгруэнтен треугольнику CMD по SAS.
Таким образом, мы заключаем, что треугольник AMB конгруэнтен треугольнику CMD по SAS.
Соответственные углы равны. Таким образом, угол MAB (равный углу CAB) и угол MCD (равный углу ACD) равны. Поскольку AC является секущей прямых AB и CD, из этих равных внутренних углов следует, что прямые AB и CD параллельны.
Таким образом, мы видим, что две противоположные стороны ABCD параллельны. Поскольку в этих двух сторонах не было ничего особенного, используя тот же аргумент, мы также можем заключить, что BC и DA параллельны, поэтому по определению ABCD является параллелограммом.
Задача 2. Ромб
Доказательство: В домашнем задании было доказано, что если четырехугольник ABCD имеет равные противоположные стороны, то это параллелограмм. Это следует из этого результата.
(b) Докажите, что параллелограмм с перпендикулярными диагоналями является ромбом.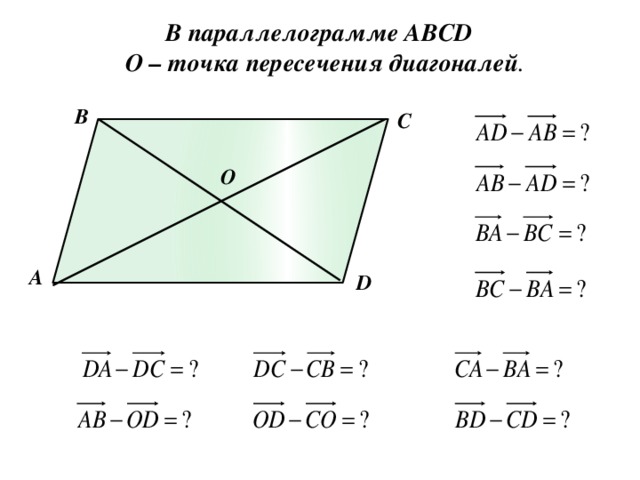
Доказательство: Из задачи 1 мы знаем, что диагонали параллелограмма ABCD делят друг друга пополам. Пусть М — пересечение диагоналей. Отсюда мы знаем, что MA = MC и MB = MD.
Если мы также предположим, что AC перпендикулярен BC, то каждый из углов AMB, AMD, CMB и CMD будет прямым. Таким образом, треугольники AMB, AMD, CMB и CMD конгруэнтны по SAS. Отсюда следует, что все гипотенузы конгруэнтны: AB = AD = CB = CD. Это говорит о том, что ABCD по определению является ромбом.
QED
(*) Доказательство домашней задачи. (Противоположные стороны параллелограмма равны.)
Утверждение: если ABCD — параллелограмм, то его противоположные стороны равны.
Доказательство. По определению прямая AB параллельна прямой CD, а прямая BC параллельна прямой DA. Мы должны доказать, что AB = CD и BC = DA.
Докажем, что треугольник ABC равен треугольнику CDA по ASA. Два треугольника имеют общую сторону АС = СА.
Чтобы доказать равенство углов, мы используем секущую.

 Знайдіть:1) тангенс гострого кута, який лежить проти меншого катета;2) синус гострого кута, який прилягає до більшого катета;3) косинус гострого кута, який лежить проти більшого катета.
Знайдіть:1) тангенс гострого кута, який лежить проти меншого катета;2) синус гострого кута, який прилягає до більшого катета;3) косинус гострого кута, який лежить проти більшого катета.

 Страница 4
Страница 4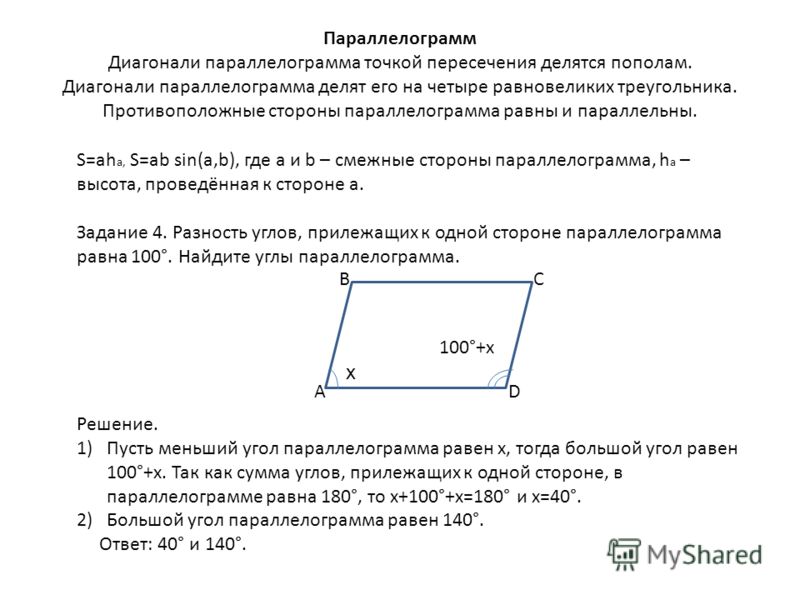
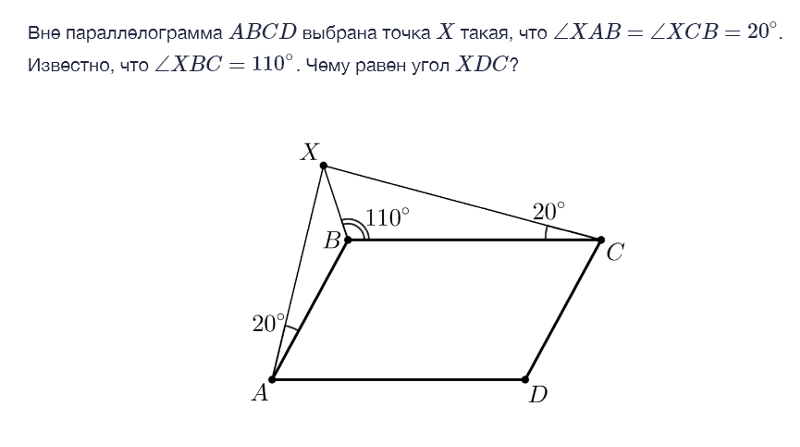
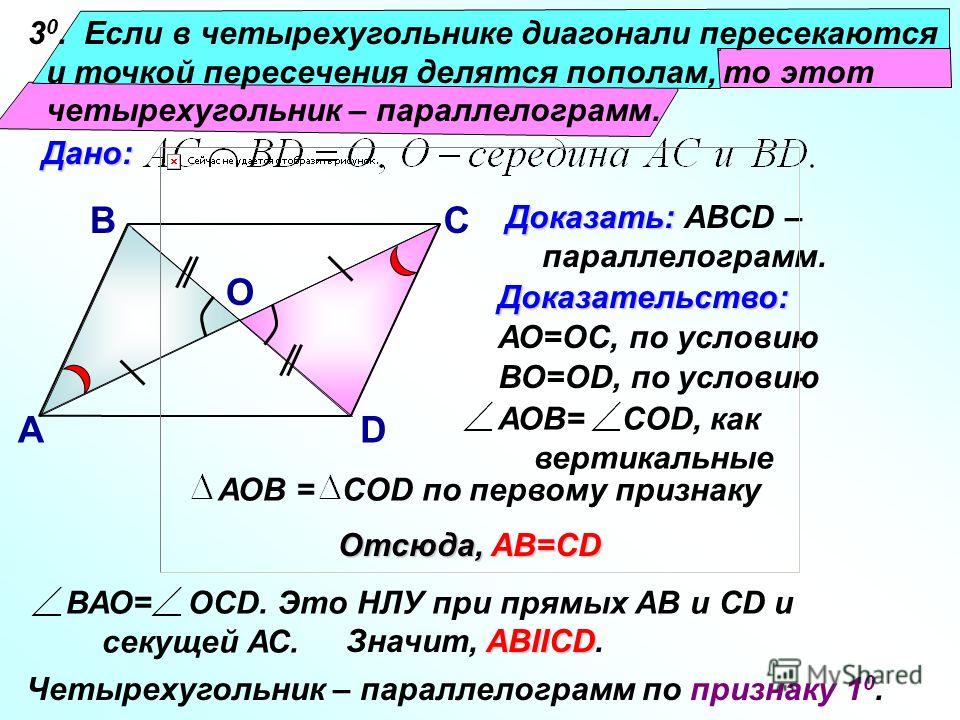 Следовательно диагонали ромба АС и ВD пересекаются под прямым углом.
Следовательно диагонали ромба АС и ВD пересекаются под прямым углом.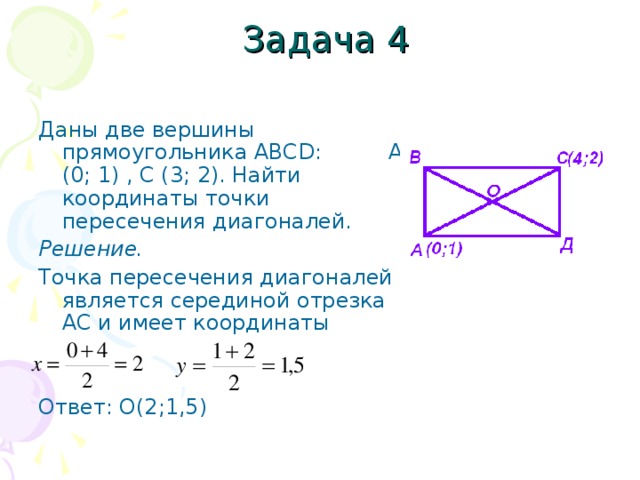 Следовательно АВЕР — ромб, так как угол ВАЕ равен углу ЕАР ( по условию). Отсюда следует, что АВ = ВЕ = 9 см, а ЕС = 5 см.
Следовательно АВЕР — ромб, так как угол ВАЕ равен углу ЕАР ( по условию). Отсюда следует, что АВ = ВЕ = 9 см, а ЕС = 5 см.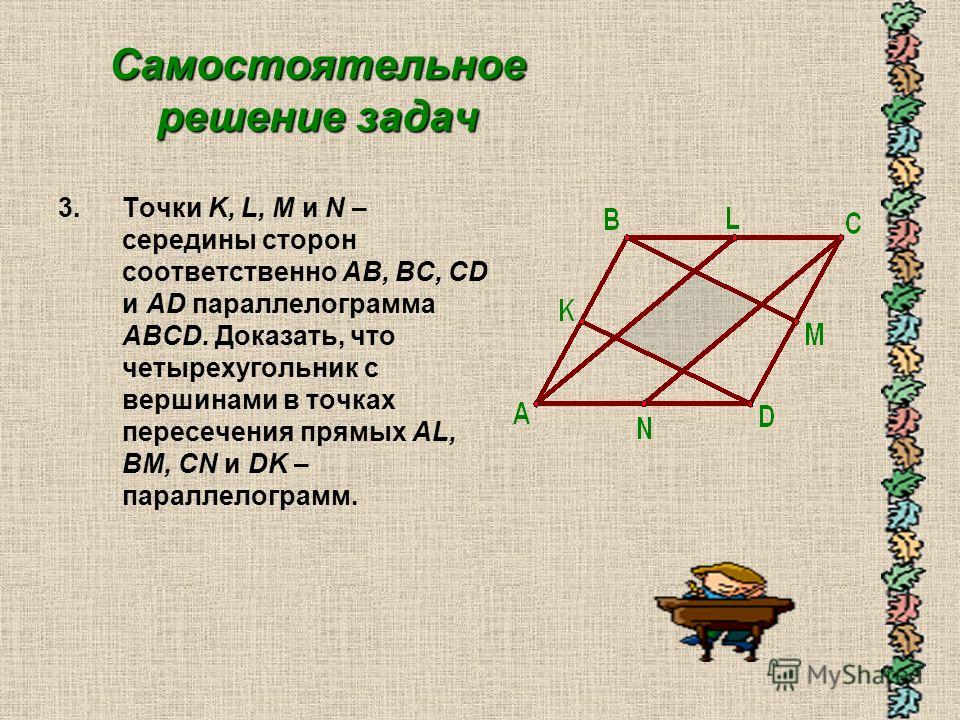 Пусть дан угол и пересекающие его параллельные прямые (рис.5). Точки А1А2А3А4 и В1В2В3В4 — точки пересечения. Проведем прямую ОЕ. Тогда А1ЕОА3 — параллелограмм. И ОЕ = А1А3 Треугольники В1В2Е и ОВ2В3 равны по стороне (ОВ2 = ЕВ2) и прилегающим к ней углам. Из равенства треугольников следует, что В1В2 = В2В3.
Пусть дан угол и пересекающие его параллельные прямые (рис.5). Точки А1А2А3А4 и В1В2В3В4 — точки пересечения. Проведем прямую ОЕ. Тогда А1ЕОА3 — параллелограмм. И ОЕ = А1А3 Треугольники В1В2Е и ОВ2В3 равны по стороне (ОВ2 = ЕВ2) и прилегающим к ней углам. Из равенства треугольников следует, что В1В2 = В2В3.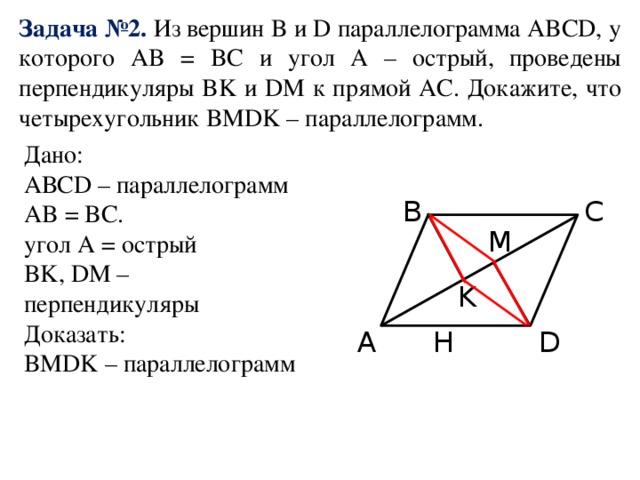 Пусть АВС — треугольник. Отрезок ЕР соединяет середины сторон АВ и ВС (Рис. 5). Тогда по теореме Фалеса отрезок ЕР параллелен основанию АС, так как он делит стороны АВ и ВС на равные части.
Пусть АВС — треугольник. Отрезок ЕР соединяет середины сторон АВ и ВС (Рис. 5). Тогда по теореме Фалеса отрезок ЕР параллелен основанию АС, так как он делит стороны АВ и ВС на равные части.
 (Рис.9)
(Рис.9) 9 Задача. Через точку пересечения диагоналей…
9 Задача. Через точку пересечения диагоналей…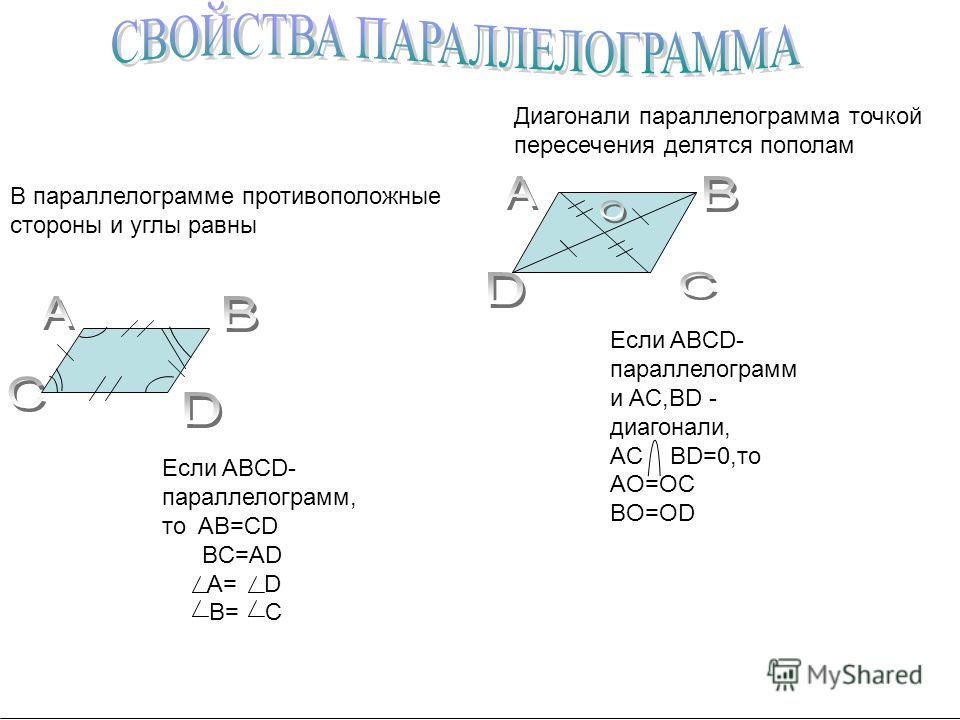
 У них сторона АЕ равна стороне ED, сторона BE — общая, а углы при вершине Е равны 90°.Отсюда следует, что диагональ BD равна стороне АВ.
У них сторона АЕ равна стороне ED, сторона BE — общая, а углы при вершине Е равны 90°.Отсюда следует, что диагональ BD равна стороне АВ.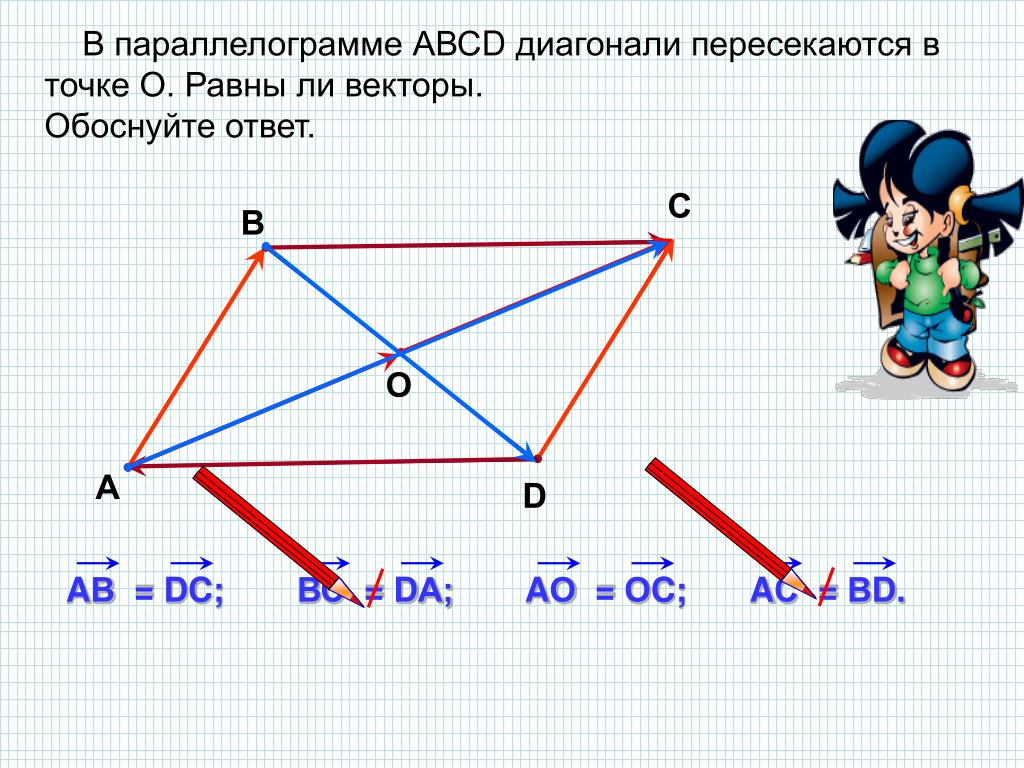 Найдите периметр прямоугольника.(Рис.12)
Найдите периметр прямоугольника.(Рис.12) (Рис.13)
(Рис.13)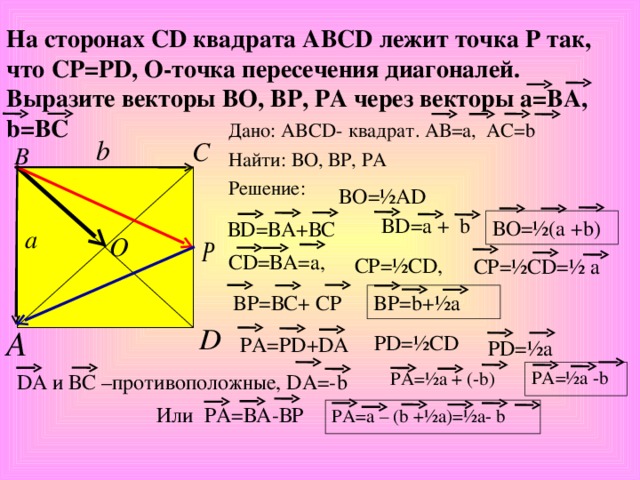 Углы при вершине О равны 90°. Т.е. по двум сторонам и углу между ними.
Углы при вершине О равны 90°. Т.е. по двум сторонам и углу между ними.
Leave A Comment