Электрон движется в магнитном поле с индукцией 2 мТл по винтовой линии радиусом
Условие задачи:
Электрон движется в магнитном поле с индукцией 2 мТл по винтовой линии радиусом 2 см и шагом 5 см. С какой скоростью влетел электрон в магнитное поле?
Задача №8.2.23 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(B=2\) мТл, \(R=2\) см, \(h=5\) см, \(\upsilon-?\)
Решение задачи:
Так как электрон движется в магнитном поле по винтовой линии, значит он влетел в него под некоторым углом \(\alpha\) к линиям индукции. Электрон в этом поле совершает сложное движение, состоящее из:
- равномерного прямолинейного движения со скоростью \(\upsilon \cdot \cos \alpha\) вдоль линий индукции магнитного поля;
- равномерного движения по окружности со скоростью \(\upsilon \cdot \sin \alpha\) в плоскостях, перпендикулярных линиям индукции магнитного поля.
Два этих движения дают в сумме движение электрона по так называемой винтовой линии.
Искомый шаг винта \(h\) – это расстояние, которое пройдет электрон вдоль линий индукции магнитного поля за время, равное периоду вращения электрона \(T\). Поэтому:
\[h = \upsilon \cos \alpha \cdot T\;\;\;\;(1)\]
Зная скорость движения электрона по окружности, можно найти период вращения электрона \(T\) по формуле:
\[T = \frac{{2\pi R}}{{\upsilon \sin \alpha }}\;\;\;\;(2)\]
Подставим (2) в (1), тогда:
\[h = \upsilon \cos \alpha \cdot \frac{{2\pi R}}{{\upsilon \sin \alpha }}\]
\[h = \frac{{2\pi R}}{{tg\alpha }}\]
\[tg\alpha = \frac{{2\pi R}}{h}\]
\[\alpha = arctg\left( {\frac{{2\pi R}}{h}} \right)\;\;\;\;(3)\]
На электрон, движущийся в магнитном поле, действует сила Лоренца \(F_Л\), которую определяет следующая формула:
\[{F_Л} = B\upsilon e\sin \alpha \;\;\;\;(4)\]
Здесь \(B\) – индукция магнитного поля, \(\upsilon\) – скорость электрона, \(e\) – модуль заряда электрона, \(\alpha\) – угол между вектором скорости и вектором магнитной индукции. 6}\;м/с = 7570\;км/с\]
6}\;м/с = 7570\;км/с\]
Ответ: 7570 км/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
8.2.22 Если конденсатор с расстоянием между пластинами 1 см определенным образом
8.2.24 Заряженная частица влетает в однородное магнитное поле перпендикулярно линиям
8.2.25 Протон и альфа-частица (4He2), ускоренные одинаковой разностью потенциалов, влетают
Задачи по теме Магнитное поле
Задача 1.
Два протона движутся параллельно друг другу с одинаковой скоростью υ = 300 км/с. Найти отношение сил электрического и магнитного взаимодействия данных протонов.
Ответ:
Задача 2.
Электрон движется
в однородном магнитном поле с индукцией В = 4 мТл
перпендикулярно линиям индукции. Найдите
частоту n обращения электрона.
Удельный заряд электрона равен .
Ответ:
Задача 3.
Протон движется со скоростью υ = 106 м/с перпендикулярно однородному магнитному полю с индукцией В = 1 Тл. Найти силу, действующую на протон, и радиус окружности, по которой он движется.
Задача 4.
Электрон движется в однородном магнитном поле с индукцией В = 0,1 Тл перпендикулярно линиям поля. Определить силу, действующую на электрон со стороны поля, если радиус кривизны траектории R = 0,5 см.
Ответ:
Задача 5.
Электрон в однородном магнитном поле с индукцией В = 0,1 Тл движется по окружности. Найти силу кругового тока I, создаваемого движущимся электроном.
Ответ:
Задача 6.
Электрон движется в однородном магнитном поле с индукцией В = 0,015 Тл по окружности радиусом R = 10 см. Определить импульс электрона.
Ответ:
Задача 7.
Электрон ускоряется однородным электрическим полем, напряженность которого Е = 1,6 кВ/м. Пройдя в электрическом поле некоторый путь, он влетает в однородное магнитное поле и начинает двигаться по окружности радиусом R = 2 мм. Какой путь прошел электрон в электрическом поле? Индукция магнитного поля В = 0,03 Тл. Начальная скорость электрона υ0 = 0.
Ответ:
Задача 8.
Ток I = 0,5 А течет по тонкому замкнутому проводнику (см. рис.). Радиус изогнутой части R = 120 мм, угол 2φ = 90º. Найти магнитную индукцию в точке О.
Ответ:
Задача 9.
Сила тока в кольце радиусом R равна I. Определите индукцию магнитного поля в произвольной точке, лежащей на перпендикуляре, восстановленном к плоскости кольца из его центра.
Ответ:
Задача 10.
По бесконечно длинному проводнику ABC, изогнутому под прямым углом (см. рис.), течет ток I. Во сколько раз изменится индукция магнитного поля в точке M, если в точке В присоединить бесконечно длинный прямой провод BD так, чтобы ток I разветвлялся в точке В на две равные части, а ток в проводнике АВ оставался прежним?
Ответ:
Задача 11.
Проволочный контур в виде квадрата со стороной a = 20 см расположен в магнитном поле так, что его плоскость перпендикулярна линиям индукции магнитного поля. Индукция магнитного поля
 Контур повернули на угол α = 60º. На
сколько и как изменился магнитный поток,
пронизывающий контур?
Контур повернули на угол α = 60º. На
сколько и как изменился магнитный поток,
пронизывающий контур?Ответ:
Задача 12.
По двум длинным параллельным проводникам, находящимся на расстоянии l = 5 см друг от друга, протекают токи в одном направлении. Сила тока I1 = I2 = 10 А. Определить индукцию магнитного поля в точке, находящейся на расстоянии r = 3 см от каждого проводника.
Ответ:
Задача 13.
В прямом проводе длиной l = 0,1 м сила тока I = 6 А. Определить напряженность магнитного поля в точке, лежащей на расстоянии r = 0,5 м от середины провода.
Ответ:
Задача 14.
Проволочное кольцо
с током находится в однородном магнитном
поле, индукция которого В = 0,01 Тл.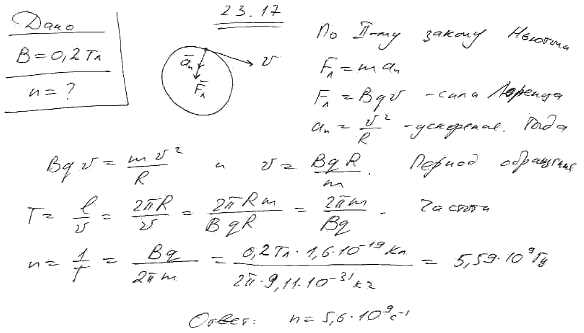 Сила тока в кольце I = 0,5 А.
Радиус кольца R = 2 см.
Какой максимальный момент сил может
действовать на кольцо со стороны
магнитного поля?
Сила тока в кольце I = 0,5 А.
Радиус кольца R = 2 см.
Какой максимальный момент сил может
действовать на кольцо со стороны
магнитного поля?
Ответ:
Задача 15.
Определите силу, с которой действует бесконечно длинный прямой провод на прямоугольный контур, расположенный в плоскости провода (см. рис.). Сила тока в проводе I, а в контуре I1. Стороны контура AD и BC имеют длину a и расположены параллельно проводу. Расстояние от AD до провода равно x. Длина сторон AB = DC = h. Направления токов указаны на рисунке стрелками.
Ответ: Контур притягивается к проводу с силой .
Задача 16.
На горизонтальных рельсах, находящихся в вертикальном однородном магнитном поле, лежит стальной брусок, перпендикулярный рельсам. Расстояние между рельсами
 Масса бруска m = 300 г,
коэффициент трения между бруском и
рельсами µ = 0,20.
Чтобы брусок сдвинулся с места, по нему
необходимо пропустить ток силой I = 40 А.
Какова индукция В магнитного поля?
Масса бруска m = 300 г,
коэффициент трения между бруском и
рельсами µ = 0,20.
Чтобы брусок сдвинулся с места, по нему
необходимо пропустить ток силой I = 40 А.
Какова индукция В магнитного поля?Ответ:
Задача 17.
Горизонтальный проводник массой m = 30 г подвешен за концы на двух проводах. Средняя часть проводника, имеющая длину l = 50 см, находится в вертикальном однородном магнитном поле с индукцией
Ответ:
Задача 18.
Горизонтальное
сверхпроводящее кольцо, по которому
течет ток силой I = 2,0 А,
«парит» в неоднородном магнитном поле
(см. рис.). Вектор магнитной индукции в
точках, где находится кольцо, образует
угол α = 30º с осью кольца и равен
по модулю В = 0,10 Тл. Найдите массу m кольца, если его радиус R = 5,0 см.
Найдите массу m кольца, если его радиус R = 5,0 см.
Задача 19.
К кольцу из медной проволоки, площадь сечения которого S = 1 мм2, приложено напряжение U = 0,15 В. При этом сила тока в кольце I = 10 А. Найти индукцию магнитного поля в его центре. Удельное сопротивление меди
Ответ:
Задача 20.
Вдоль клина с углом α при основании проложены рельсы, расстояние между которыми l. По рельсам с трением (коэффициент трения равен µ) скользит проводящий брусок массой m. Какой ток I следует пропустить через брусок, чтобы он не скользил вниз, если вся система находится в магнитном поле, индукция которого
Ответ:
Задача 21.
Под длинной
горизонтальной шиной на двух одинаковых
пружинах (жесткость каждой равна k)
подвешен провод длиной l. Когда в шине и проводе токи отсутствуют,
расстояние между ними равно h.
Найдите расстояние между шиной и
проводом, если по шине течет ток I,
а по проводу i.
Провод не может выйти из вертикальной
плоскости.
Когда в шине и проводе токи отсутствуют,
расстояние между ними равно h.
Найдите расстояние между шиной и
проводом, если по шине течет ток I,
а по проводу i.
Провод не может выйти из вертикальной
плоскости.
Ответ: а) Если токи I и i текут в одну сторону, то расстояние между шиной и проводом может быть: (устойчивое равновесие) или (неустойчивое равновесие). Если , т.е. ,
провод притянется к шине.
б) Если токи I и i текут в противоположных направлениях, то провод отталкивается от шины и будет в устойчивом равновесии на расстоянии .
Задача 22.
Постоянный магнит
имеет вид кольца с узким зазором между
полюсами. Средний диаметр кольца d = 20 см.
Ширина зазора b = 2,0 мм,
индукция магнитного поля в зазоре
В = 40 мТл.
Пренебрегая рассеянием магнитного поля
на краях зазора, найти модуль напряженности
магнитного поля внутри магнита.
Ответ:
Задача 23.
Прямоугольный контур ABCD, стороны которого имеют длину a и b, находится в однородном магнитном поле с индукцией B и может вращаться вокруг оси ОО´ (см. рис.). По контуру течет ток I. Определите работу, совершенную магнитным полем при повороте контура на 180º, если вначале плоскость контура была перпендикулярна вектору индукции магнитного поля.
Ответ:
Задача 24.
По проводу, согнутому в виде квадрата со стороной a = 10 см, проходит постоянный ток. Плоскость квадрата составляет угол α = 20º с линиями индукции магнитного поля В = 0,1 Тл. Сила тока в проводе I = 20 А. Вычислить работу, которую необходимо совершить для того, чтобы удалить провод за пределы поля.
Ответ:
Задача 25.
Вычислить магнитную индукцию внутри длинного соленоида с железным сердечником (µ = 183), если на l = 40 см его длины намотано N = 400 витков проволоки. Сила тока в соленоиде I = 8 А.
Ответ:
Задача 26.
Обмотка длинного соленоида сделана из провода диаметром d = 2·10-3 м. Витки плотно прилегают друг к другу. При какой силе тока напряженность магнитного поля в соленоиде H = 8000 А/м?
Ответ:
Задача 27.
Из какого материала изготовлена обмотка соленоида длиной l = 0,3 м, если диаметр соленоида D = 0,05 м, напряженность магнитного поля на его оcи H = 15 А/м, напряжение на концах обмотки U = 0,9 В? Диаметр провода d = 10-3 м.
Ответ:
Задача 28.
Катушка помещена в однородное магнитное поле индукцией В = 5 мТл так, что ось катушки составляет угол α = 60º с вектором магнитной индукции. Радиус катушки R = 20 см. На сколько нужно изменить число витков катушки, чтобы магнитный поток через нее увеличился на ΔФ = 0,1 Вб?
Ответ:
Задача 29.
Две пластины из магнетиков с проницаемостями µ1 и µ2 сложены вместе и помещены в перпендикулярное к ним однородное поле с индукцией В0 (см. рис.). Штриховой линией показана воображаемая цилиндрическая поверхность с образующими, параллельными В0, и основаниями площади S, перпендикулярными к В0. Чему равны поток ФВ вектора В и поток ФН вектора Н через эту поверхность?
Ответ: ,
.
Задача 30.
Индукция магнитного поля в вакууме вблизи плоской поверхности однородного изотропного магнетика равна В, причем вектор В составляет угол α с нормалью к поверхности. Магнитная проницаемость магнетика µ. Найти индукцию В´ магнитного поля в магнетике вблизи поверхности.
Ответ:
Фарадей
ФарадейЗакон Фарадея
Задача:
Небольшая круглая поисковая катушка используется для поиска рассеянных магнитных полей. вокруг трансформатора. Диаметр катушки 1,5 см, выходная мощность подключен к идеальному вольтметру. Для поля рассеяния 1 мТл на частоте 60 Гц как сколько витков потребуется, чтобы поисковая катушка дала показания 1 мВ?
Решение:
- Концепций:
Закон Фарадея - Рассуждение:
Напряжение в катушке индуцируется изменяющимся магнитным потоком. магнитный поток изменяется с частотой f = 60 Гц.
магнитный поток изменяется с частотой f = 60 Гц. - Детали расчета:
ε = -∂F/∂t = ЭДС индукции, F = ∫ A B ∙ n dA, F ≈ BA = B 0 e iωt πR 2 N, N = количество витков, когда лицевая сторона катушки перпендикулярна направление магнитного поля.
∂F/∂t = iωB 0 e iωt πR 2 N = -ε = V = V 0 e i(ωt+φ) .
V 0 = ωB 0 πR 2 N, N = V 0 /(ωB 0 πR 2 ) .
V rms = V 0 /(√2) = 1 мВ – показания вольтметра.
N = √2*10 -3 В/(2π*60 с -1 *10 -3 T*π(7,5 10 -3 м) 2 ) = 21,
Проблема:
(a) Катушка имеет индуктивность 2 мГн, а ток через
он изменяется от 0,2 А до 1,5 А за время 0,2 с. Найдите величину
средняя ЭДС индукции в катушке за это время.
(b) Круглая катушка из 25 витков проволоки имеет диаметр 1 м. Это
расположен осью вдоль направления магнитного поля Земли
(величина 50 мкТл), а затем за 0,2 с переворачивается на 180 o . Что
возникает средняя ЭДС?
Решение:
- Концепты:
Закон Фарадея, ЭДС индукции - Рассуждение:
Магнитный поток через катушку меняется, и нас просят найти ЭДС индукции. - Детали расчета:
(а) L = 2 мГн, dI/dt = (1,5–0,2) А/0,2 с = 6,5 А/с.
ε = -LdI/dt = -(0,002 Вс/А)(6,5 А/с) = -0,013 В.
Знак минус указывает на то, что ЭДС индукции противодействует изменениям потока, которые произвел его.
|ε| = 13 мВ.
(б) ε = -dΦ/dt. Φ = NAB = 25π(0,5 м) 2 50*10 -6 Т = 9,82*10 -4 Тм 2 .
dΦ/dt = 2(9,82*10 -4 Tm 2 )/(0,2 с) = 9,82*10 -3 В = 9,82 мВ.
(Поток не просто падает до нуля, он меняет знак. Это вводит
коэффициент 2.)
Это вводит
коэффициент 2.)
Проблема:
Известны умные фермеры, чьи земли пересекают большие линии электропередач.
украсть электроэнергию, протянув провод рядом с линией электропередач и используя
индуцированный ток.
Предположим, что фермер размещает прямоугольную петлю с двумя сторонами длиной a.
параллельно линии электропередач, ближайшая на расстоянии 5 м от нее. Петля
и силовая линия лежат в одной плоскости. Пусть длина сторон
перпендикулярно линии электропередач быть b = 0,5 м. По линии электропередач проходит 60 Гц.
переменного тока с пиковым током 10 кА.
(a) Если фермер хочет, чтобы пиковое напряжение составляло 170 В (пиковое
стандартная мощность 120 В переменного тока) какой должна быть длина a?
(b) Если оборудование, которое фермер подключает к контуру, имеет сопротивление R =
5 Ом, каково среднее энергопотребление фермера?
(c) Если энергетическая компания взимает 10 центов за кВтч, какова денежная
стоимость энергии, украденной каждый день?
(Дайте числовой ответ!)
Решение:
- Концепты:
Закон Фарадея - Рассуждение:
Магнитный поток через петлю меняется со временем. Этот поток
изменение индуцирует ЭДС. ЭДС вызывает протекание тока, который
рассеивает энергию.
Этот поток
изменение индуцирует ЭДС. ЭДС вызывает протекание тока, который
рассеивает энергию. - Детали расчета:
(a) Закон Ампера: B = μ 0 I/(2πr), B окружает линия электропередачи.
Поток B через прямоугольную петлю: F = a[μ 0 I/(2π)] ∫ 5 м 5,5 м др/об = а[μ 0 I/(2π)]ln(5,5/5).
ЭДС = -dF/dt = -a[μ 0 /(2π)](dI/dt)ln(5,5/5).
Пиковая ЭДС = a[μ 0 /(2π)](2π*60/с*10 4 A)ln(5,5/5) = a*0,072 В/м.
Для пиковой ЭДС 170 В нам нужно а = 2,37 км.
(b) P = В 2 среднеквадратичное значение /R = (120 В) 2 /(5 Ом) = 2,88 кВт.
(c) 2,88 кВт * 24 ч = 69,12 кВтч. Денежная стоимость составляет 6,91 доллара США за день.
Проблема:
Непроводящее кольцо массой M, радиусом R и полным зарядом
Равномерно распределенный по кольцу Q висит горизонтально, подвешенный на
непроводящие тонкие («безмассовые») струны, как показано.
Равномерно возрастающее магнитное поле B = B 0 т
направление вниз включается в момент времени t = 0,
(a) Найти крутящий момент на кольце через B 0 , M, R и Q.
(б)
Если струны, поддерживающие кольцо, создают крутящий момент -αφ,
где φ – угол, под которым
поворотов кольца, запишите уравнение движения через B 0 , M, R, Q и
а.
Решение:
- Концепты:
Закон Фарадея - Рассуждение:
Изменяющийся магнитный поток через кольцо индуцирует ЭДС. Результирующий электрическое поле действует на заряд Q на кольце. Эта сила создает крутящий момент относительно центра кольца. - Детали расчета:
а) ЭДС, индуцированная в кольце, равна
. ∮ Γ E ∙d r = -∂ / ∂t∫ A B ∙ n dA = -πR 2 ∂ B /∂t = -πR 2 B 0 .
Таким образом, величина индуцированного электрического поля равна предоставлено
2πRE = πR 2 В 0 , Э = РБ 0 /2.
Направление из E тангенциальная, против часовой стрелки для увеличения Б .
Крутящий момент на кольце τ = QRE = QR 2 B 0 /2 в вертикальном направлении.
(b) Общий крутящий момент τ всего = Id 2 φ/dt 2 = MR 2 d 2 φ/dt 2 = QR 2 B 0 /2 — αφ, где мы измеряем φ против часовой стрелки от положения равновесия.
Уравнение движения: d 2 φ/dt 2 = QB 0 /(2M) — αφ/(MR 2 ).
Результирующее движение:
Гармонические колебания относительно положения φ 0 = QR 2 B 0 /(2α) с угловой частотой ω = (α/(MR 2 )) ½ .
Проблема:
Ускоритель электронов использует изменяющийся во времени магнитный поток через плоскость
круговая петля радиусом R = 0,85 м, и электроны всегда движутся в этой
круговой путь с этим радиусом. Магнитная индукция в плоскости петли
Магнитная индукция в плоскости петли
B(r) = B 0 — Kr 2 , r < R; В = 0, г > Р,
всюду нормаль к плоскости петли с r расстоянием от
центр петли.
(а) Покажите, что в любой момент времени средняя магнитная индукция в
петля B av , должна быть связана с B R через B av = 2B R . Оценить К.
(b) B 0 линейно увеличивается от 0 до 1,2 Тл за 5,3 с.
Вычислите прирост энергии за оборот для электронов и максимальное электронное
энергия достигнута.
Решение:
- Концепты:
Закон Фарадея, ЭДС индукции, движение по круговой орбите при релятивистской скорости - Рассуждение:
Изменяющийся магнитный поток через круглую петлю индуцирует ЭДС. результирующее электрическое поле касается контура и ускоряет электрон. Легкий электрон вскоре достигает релятивистской скорости. - Детали расчета:
(а) Вы можете показать часть (а), используя релятивистские или нерелятивистские уравнения.
Для электрона на круговой орбите, лежащей в плоскости x-y перпендикулярно магнитному полю B = B k и с центром в происхождение у нас есть
F = -q e v × B (R) = -q e vB(R)( r /r) (единицы СИ).
Для частицы на круговой орбите центростремительная сила равна F = -(γmv 2 /R)( r /r).
[Предположим, что частица движется по круговой орбите радиусом r с постоянной скоростью v.
x = rsinωt, y = -rcosωt,
v x = ωrcosωt, v y = ωrsinωt,
p x = γmωrcosωt, p y = γmωrsinωt,
F x = dp x /dt = -γmω 2 rcosωt = -γmω 2 х, F y = dp y /dt = γmω 2 rcosωt = -γmω 2 лет.
F = -γmω 2 r = -(γmv 2 /r 2 )r.]
Таким образом, мы имеем q e vB(R) = γmv 2 /R = pv/R, B(R) = p/(q e R).
|ε| «=» |∂F/∂t| — величина ЭДС индукции. Предположим, что B увеличивается со временем.
2πRE = ∂(B ср πR 2 )/∂t, E = (R/2)дБ в среднем /dt.
Величина тангенциальной силы, ускоряющей электрон, равна
F t = q e E = (q e R/2)dB avg /dt.
Таким образом, мы имеем dp/dt = (q e R/2)дБ avg /dt, и dp/dt = (q e R)дБ(R)/dt.
½ дБ среднее /dt = дБ(R)/dt, ΔB в среднем /2 = ΔВ(R).
Если мы начнем с B = 0, мы получим B avg = 2B(R).
Б(р) = В 0 — Кр 2 , r < R, πR 2 B среднее = 2π∫(B 0 — Kr 2 )rdr с пределами интегрирования 0 и R.
B avg = B 0 — КР 2 /2, B(R) = B 0 — КР 2 , B 0 — КР 2 /2 = 2(Б 0 — КР 2 ),
Б 0 = (3/2)КР 2 , К = (2/3)В 0 /R 2 .
B(r) = B 0 (1 — (2/3)r 2 /R 2 ).
(б) |ε| = ∂(B среднее πR 2 )/∂t = (2πR 2 /3)дБ 0 /dt = энергия прирост на единицу заряда за оборот.
q e |ε| = прирост энергии электрона за оборот.
дБ 0 /dt = (1,2 Тл)/(5,3 с), q e |ε| «=» 5,48*10 -20 Дж.
Чтобы найти полную полученную энергию, заметим:
F = dp/dt = q e E = константа. p = q e Et. Энергия = (p 2 c 2 + m 2 c 4 ) ½ .
E = (R/2)дБ ср. /dt = (2/3)(R/2)дБ 0 /dt = (R/3)дБ 0 /dt.
p = q e (R/3)(1,2 T/5,3 с)t. Через 5,3 с p = q e (R/3)1,2 Тл = 5,44*10 -20 кгм/с.
Энергия = ((5,44*10 -20 кгм/с) 2 c 2 *(1 МэВ/1,6*10 -13 Дж) 2 + (0,511 МэВ) 2 ) ½ = 102 МэВ.
Полученная энергия: 102 МэВ — 0,511 МэВ.
Проблема:
А пространственно-однородная плотность тока j = й 0 cosωt течет через отверстие тора вдоль оси тора, как показано. внутренний радиус тора равен r, а поперечное сечение квадратное со сторонами a (a << р). Тор сделан из изоляционный материал с m = μ 0 . Проволока с сопротивлением R намотана вокруг тора всего за N витков. Определить силу тока в проводе.
Решение:
- Концепций:
Закон Ампера, закон Фарадея - Рассуждение:
Закон Ампера, ∮ Γ B ∙d с = μI через_Γ дает B внутри тора. Поскольку поток B через проволочные петли вокруг тора изменяется, в проволочных петлях индуцируется ЭДС и текущие потоки.
Предположим, что R велико, и пренебрегаем самоиндукцией контуров. - Детали расчета:
B внутри тора тангенциальный (по часовой стрелке для j указывает на бумага),
2πrB(r) = μ 0 j 0 cosωt № 2 ,
B(r) = μ 0 j 0 cosωt r/2.
Поскольку a << r, мы предполагаем, что B приблизительно постоянна внутри тор.
(Примечание: r здесь не переменная, но радиус тора.)
Поток B через один виток провода равен B(r)a 2 . Полный поток через N контуров равен NB(r)a 2 .
ЭДС, индуцируемая в проводе, равна
∮ Γ E ∙d r = -∂ / ∂t∫ A B ∙ n dA = -Na 2 ∂ B /∂t.
Имеем V = Na 2 μ 0 ωj 0 sinωt р/2.
I = V/R = Na 2 мк 0 ωj 0 sinωt р/(2р).
Задача:
Петля провода сопротивления R и катушка
собственной индуктивности L окружает площадь A. Пространственно однородное магнитное поле
прикладывается перпендикулярно плоскости петли со следующим моментом
зависимость:
При t < 0 поле равно нулю, при 0 < t < t 0 B(t)
= kt, при t > t 0 поле остается постоянным при B 0 = kt 0 .
(a) Рассчитайте ток I в контуре для всех моментов времени t > 0, учитывая, что I = 0.
для t = 0,
(b) Сделайте простые наброски зависимости тока от времени для t 0 < Л/П и т 0 > Л/П..
Решение:
- Концепты:
Закон Фарадея, правило Ленца - Рассуждение:
Магнитный поток через нитевидную петлю меняется со временем. Этот изменение потока индуцирует ЭДС. - Детали расчета:
(а) Поток Φ = BA = ktA для t < t 0 , Φ = BA = kt 0 A для t > t 0 .
ЭДС = -dΦ/dt = -kA при t < t 0 , Φ = BA = 0 при t > t 0 .
Результирующий ток течет по часовой стрелке.
Для t < t 0 : IR + LdI/dt = kA, dI/dt = kA/L — IR/L,
Попробуйте I = a — bexp(-ct), тогда a = kA/R, c = R/L, I = 0 при t = 0 дает b = кА/Р,
I(t) = (kA/R)(1 — exp(-Rt/L)).
Для t > t 0 : dI/dt = -IR/L, I(t) = I(t 0 )exp(-R(t — т 0 )/л)
(б)
Проблема:
Квадрат
петля со стороной b сделана из провода массой m и пренебрежимо малым электрическим сопротивлением. В петле есть зазор, который можно закрыть переключателем. Изначально переключатель
открыть. Петля поворачивается вдоль своей верхней горизонтальной стороны и помещается в слабое вертикальное однородное магнитное поле B, как показано на рисунке. Затем петля затягивается
горизонтальное положение, переключатель замкнут, а петля отпущена.
В конце концов, петля останавливается из-за сопротивления воздуха. Найдите угол θ
что плоскость петли составляет с вертикалью в конечном положении.
собственная индуктивность петли L.
В петле есть зазор, который можно закрыть переключателем. Изначально переключатель
открыть. Петля поворачивается вдоль своей верхней горизонтальной стороны и помещается в слабое вертикальное однородное магнитное поле B, как показано на рисунке. Затем петля затягивается
горизонтальное положение, переключатель замкнут, а петля отпущена.
В конце концов, петля останавливается из-за сопротивления воздуха. Найдите угол θ
что плоскость петли составляет с вертикалью в конечном положении.
собственная индуктивность петли L.
Решение:
- Концепты:
ЭДС индукции, квазистатические ситуации - Рассуждение:
Провод не имеет сопротивления. Поток B через контур равен постоянный. Любое изменение потока внешнего поля через контур равно немедленно отменяется изменением потока F = LI из-за индуцированного тока в петле.
Таким образом, мы имеем Bb 2 = Bb 2 sinθ + LI.
(начальный поток = конечный поток) - Детали расчета:
В равновесии гравитационный момент должен компенсировать момент на токовая петля в магнитном поле.
Величина гравитационного момента относительно оси вращения:
(m/4)g b sinθ + 2(m/4)g (b/2) sinθ = ½ б мг sinθ.
Величина магнитного момента относительно оси вращения:
Iб 2 Б cosθ.
Нам нужно:
½ b мг sinθ = Ib 2 B cosθ.
У нас есть два уравнения для двух неизвестных, I и θ,
I = (Bb 2 /L)(1 — sinθ) и tanθ = 2IbB/(мг).
Комбинируя эти уравнения, мы получаем
загар θ = C(1 — sinθ), с C = 2b 3 B 2 /(мгл).
Так как поле слабое, θ << 1, тангенс θ ~ sin θ ~ θ, θ = C (1 - θ), θ = С/(1 + С).
PHY1160C, Основы физики II
Гл. 20: 4, 12, 21, 24, 30, 64
20,4 Заряд 1,5 x 10 — 10 Кл движется со скоростью 1,0 км/с через магнитное поле в таком направлении, что магнитная сила на нем максимальна. Что такое магнитное поле прочность, если максимальное усилие на заряде 8 х 10 — 8 Н?
F max = q v B
B = F макс. /[q v]
/[q v]
В = 8 х 10 — 8 Н / [(1,5 х 10 — 10 С)(1000 м/с)]
Б = 0,533 Т
20.12 Электрон движется по окружности путь, перпендикулярный магнитному полю B = 1,25 Т, при скорости 1,2 x 10 4 РС. Каков радиус кругового пути электрона?
С = 90, грех = 1
Это тоже центростремительная сила,
q v B = m v 2 / r
r = м v / [q B]
r = (9,11×10 -31 кг) (1,2×10 4 м/с) / [(1,6×10 -19 С) (1,25 Т)]
г = 5,47 х 10 -8 м
20,21 Магнитное поле силой 100 Тл ограничивается областью 5,0 см, как показано на рис. Рисунок 20.47. Электрон проходит область со скоростью 5,16 x 10 6 м/с.
как показано. Определить угловое отклонение.
Рисунок 20.47. Электрон проходит область со скоростью 5,16 x 10 6 м/с.
как показано. Определить угловое отклонение.
[ Магнитное поле силой 100 Тл настолько сильное, что он не просто немного отклоняет электрон, как предполагает мой анализ. Скорее, электрон сделал бы круг — или половину круга. Так что цифры нереальные! Попробуйте два варианта этого:
20.21 а; Электрон попадает в область, где магнитное поле составляет 100 Тл, движущихся перпендикулярно магнитному полю со скоростью 5,16 х 10 6 м/с. Каков радиус круга, по которому он теперь движется это? Он совершит полукруг «орбиты», а затем выйдет из региона. с магнитным полем. Каков радиус этой полукруглой траектории.
20.21 б; Магнитное поле Земли примерно 5 х 10 .
— 5 Тл или 50 х 10 — 6 Тл. Несколько большее магнитное поле
100 x 10 — 6 T ограничивается
участок размером 5,0 см, как показано на рис. 20.47. Электрон проходит через область
со скоростью 5,16 x 10 6 м/с, как показано на рисунке. Определять
угловое отклонение.
20.47. Электрон проходит через область
со скоростью 5,16 x 10 6 м/с, как показано на рисунке. Определять
угловое отклонение.
Это второй вопрос, решение которого я изначально было.]
20.21 а; Электрон попадает в область, где магнитное поле составляет 100 Тл, движущихся перпендикулярно магнитному полю со скоростью 5,16 х 10 6 м/с. Каков радиус круга, по которому он теперь движется это? Он совершит полукруг «орбиты», а затем выйдет из региона. с магнитным полем. Каков радиус этой полукруглой траектории.
С магнитным полем это сильное , электрон не собирается отклоняться только немного. Он будет двигаться по кругу — фактически полукругом. Магнитная сила
F магазин = q v B
Ф м = (1,6 х 10 — 19 C)(5,16 x 10 6 м/с)(100 Т)
F магазин = 8,26 x 10 — 11 Н
Эта сила обеспечивает центростремительную силу,
F c = m v 2 /r
r = m v 2 /F c
r = (9,11 х 10 — 31 )(5,16 х 10 6 м/с) 2 / (8,26 х 10 — 11 Н)
г = 2,9х 10 — 7 м
Это очень маленький радиус, но масса электрона очень слишком маленький
20. 21 б; Магнитное поле Земли примерно 5 х 10 .
— 5 Тл или 50 х 10 — 6 Тл. Несколько большее магнитное поле
100 x 10 — 6 T ограничивается
участок размером 5,0 см, как показано на рис. 20.47. Электрон проходит через область
со скоростью 5,16 x 10 6 м/с, как показано. Определять
угловое отклонение.
21 б; Магнитное поле Земли примерно 5 х 10 .
— 5 Тл или 50 х 10 — 6 Тл. Несколько большее магнитное поле
100 x 10 — 6 T ограничивается
участок размером 5,0 см, как показано на рис. 20.47. Электрон проходит через область
со скоростью 5,16 x 10 6 м/с, как показано. Определять
угловое отклонение.
Это второй вопрос, решение которого я изначально было.]
Рисунок 20.47 Проблема 20.21
20.21b предполагает, что v x остается постоянным. Тогда мы можем использовать что для определения времени электрон проводит с этой магнитной силой в теме. Это позволит нам вычислить v и и, исходя из этого, угол отклонения.
Сначала найдите силу, действующую на электрон,
С = 90, грех = 1,0
F = 8,256 x 10 — 17 Н
Хотя это кажется очень малой силой, помните, что она действует на очень маленькая масса , масса электрона
а = Ф/м
a = 8,256 x 10 — 17 N / 9,11 x 10 — 31 кг
а = 9,16 х 10 13 м/с 2
Как долго действует это ускорение?
т = с/в
t = 0,05 м / ( 5,16 x 10 6 м/с )
т = 9,69 х 10 — 9 с
Если это ускорение все в направлении y, что будет конечная составляющая скорости в направлении y?
v y = 0 + (9,16 x 10 13 м/с 2 ) (9,69 x 10 -9 с)
v y = 8,88 x 10 5 м/с
Угол отклонения дано
Если мы используем приближение, что v x = v x = 5,16 х 10 6 м/с, затем
загар = 0,172
= 9,76 o
При таком малом угле отклонения наши два приближения таковы:
действительно, разумно. Ускорение почти полностью в
y-направление, а x-компонент скорости остается почти
постоянный.
Ускорение почти полностью в
y-направление, а x-компонент скорости остается почти
постоянный.
20,24 В районе, где магнитное поле Земли в 5,0 х 10 — 5 T и составляет угол 60° с Землей. поверхности, определить силу на прямом проводе длиной 2,0 м, по которому ток 8,0А прямо вверх.
F = I l B sin
F = (8,0 A) (2,0 м)( 5,0 x 10 — 5 T) (sin 30°)
F = (8,0 А) (2,0 м) (5,0 x 10 — 5 T) (0,50)
F = 4 x 10 — 4 Н
Сила перпендикулярна как магнитному полю, так и текущий. Сила направлена в бумагу (или экран). Да, это действительно в бумаги (или экрана)!
20.30 По линии электропередач проходит 2500 А течение с востока на запад. Какое магнитное поле на 10 м ниже линия?
Из уравнения 20. 10,
10,
В = 5 х 10 -5 Т
20,54 А Ток 4,5 А протекает через 20-витковый прямоугольный рулон 2,5 х 10 — 2 м 2 площадь. Катушка вращается в магнитном поле 0,20 Тл. Рассчитайте крутящий момент для каждой из ориентаций, показанных ниже.
Символ указывает на провод, по которому идет ток из с.; указывает текущий переход в страницу.
= (20)(4,5 А)(0,025 м 2 )(0,20 Тл) sin
Угол в этом уравнении — это угол между магнитным полем и нормальный (направление перпендикулярно ) плоскости катушка. То есть, угол между магнитным полем и линией, нарисованной перпендикулярно плоскости катушка. Это означает, что углы для этого уравнения являются , а не углы, отмеченные в эти цифры; скорее равно 90 o минус каждое из этих угла ! Будьте осторожны с этот!
Для части (а)
= (20) (4,5 А) (0,025 м 2 ) (0,20 Тл) (1,00)
= 0,45 м-N
Для части (б)
= (20) (4,5 А) (0,025 м 2 ) (0,20 Тл) (0,866)
= 0,39 м-N
Для части (с)
= (20) (4,5 А)(0,025 м 2 ) (0,20 Тл) (0,500)
= 0,225 м-N
Для части (d)
т = (20) (4,5 А) (0,025 м 2 ) (0,20 Т)(0,)
= 0
20,64 [ Пожалуйста, пропустите вопрос 20.

 магнитный поток изменяется с частотой f = 60 Гц.
магнитный поток изменяется с частотой f = 60 Гц. Это вводит
коэффициент 2.)
Это вводит
коэффициент 2.) Этот поток
изменение индуцирует ЭДС. ЭДС вызывает протекание тока, который
рассеивает энергию.
Этот поток
изменение индуцирует ЭДС. ЭДС вызывает протекание тока, который
рассеивает энергию.





Leave A Comment