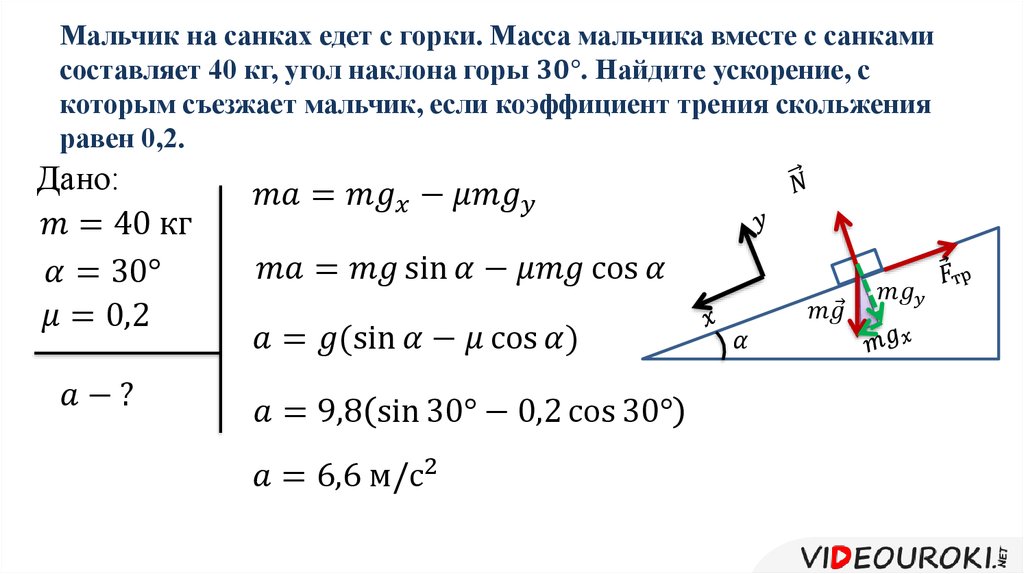
Физические основы механики
ЦЕЛЬ РАБОТЫ
Изучение равнопеременного и равномерного прямолинейных движений в поле земного тяготения. Определение ускорения свободного падения.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ
Основные законы динамики материальных точек — это законы Ньютона. В частности, второй закон Ньютона, математическая запись которого, как известно, имеет вид:
|
|
(1) |
называют основным уравнением динамики.
Эскиз машины Атвуда показан на рис. 1.
Рис. 1. Эскиз машины Атвуда
Два одинаковых груза с массами М соединены нитью, перекинутой через неподвижный блок. Если на один из грузов положить перегрузок массой m (в виде шайбы), то система приходит в ускоренное движение.
Основное уравнение динамики для груза с перегрузком имеет вид:
|
|
(2) |
а для другого груза (без перегрузка):
|
|
(3) |
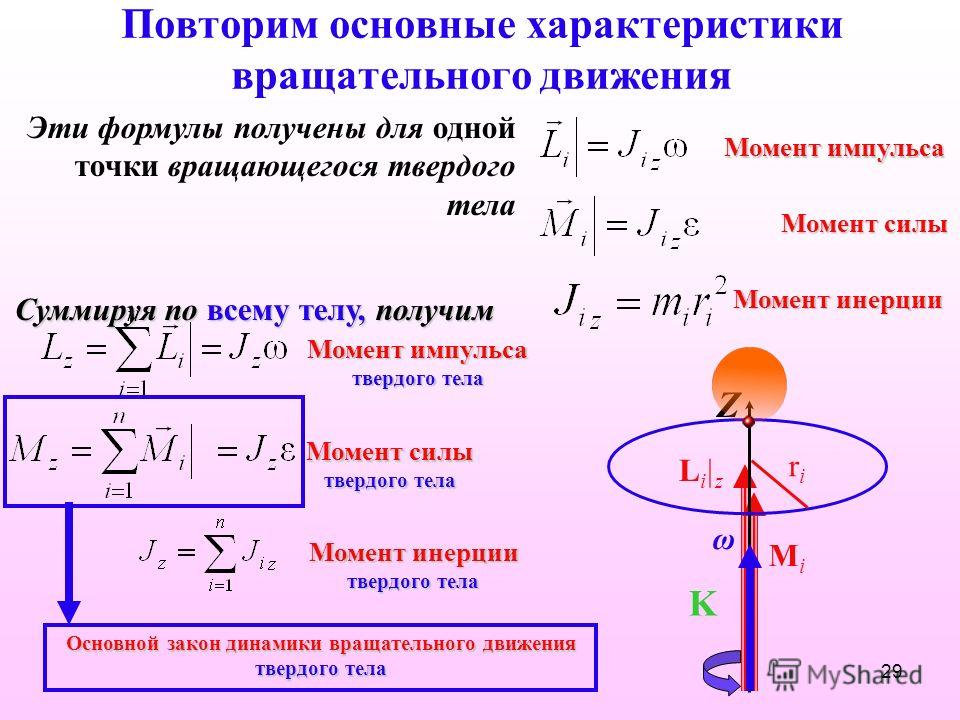
Основное уравнение динамики вращательного движения неподвижного блока имеет вид:
|
|
(4) |
где SMk — алгебраическая сумма моментов сил, действующих на блок, относительно оси вращения; I — момент инерции блока относительно оси вращения; e — его угловое ускорение.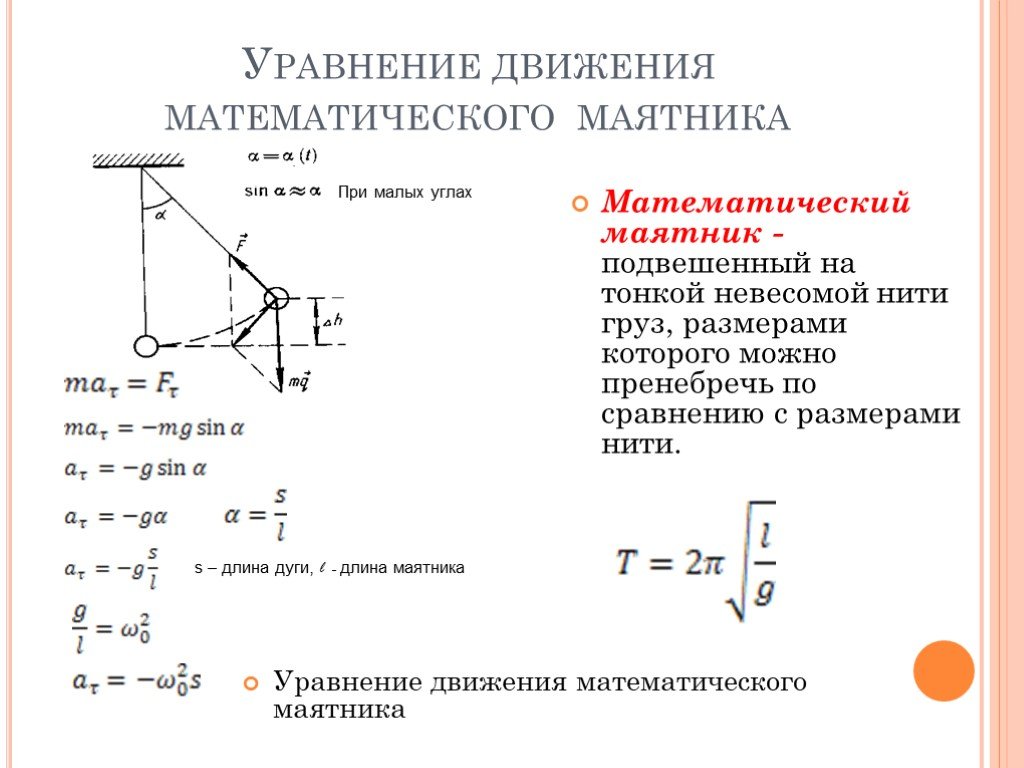
Если вращение по часовой стрелке считать положительным, то, согласно рис. 1, получим
|
|
(4а) |
где: R — радиус блока; Мтр — момент силы трения.
Будет считать, что нить невесомая, нерастяжимая и не скользит по блоку. Из условия невесомости нити следует:
|
|
(5) |
Из условия нерастяжимости нити следуют равенства модулей перемещений, скоростей и ускорений грузов и нити:
|
|
(6) |
Наконец, в отсутствие скольжения нити по блоку, ускорение грузов и нити а равно модулю тангенциального ускорения точек обода блока:
или
|
|
(7) |
Проецируя уравнения (2) и (3) на ось
|
|
(8) |
Умножая первое из уравнений (8) на (-1), и складывая все уравнения (8), получим
|
|
|
В данной лабораторной установке момент сил трения настолько мал, что выполняется неравенство
|
|
(10) |
Кроме того, в лабораторной установке величина момента инерции I блока такова, что справедливо другое неравенство:
|
|
(11) |
Пренебрегая малыми величинами, из уравнения (9) получим формулу для расчёта ускорения а системы грузов под действием перегрузка массой m:
|
|
(12) |
а модули сил натяжения нити Т1 и Т2 по обе стороны блока равны:
|
|
(13) |
Можно сказать, что равенство (13) выполняется при двух предположениях (10) и (11).
Равноускоренное движение системы грузов вдоль оси у описывается уравнениями движения произвольной точки системы:
где у1, v1 — начальные параметры.
Исключая из этих уравнений время t, при условии v1=0, получим
|
|
(14) |
Система грузов перемещается на величину sy=L1, двигаясь равноускоренно под действием перегрузка массой m с ускорением, которое определяется формулой (12).
В точке с координатой у2 и скоростью v2 перегрузок подхватывается столиком, и система грузов движется равномерно, перемещаясь на величину
 Подставляя в равенство (14) формулу
Подставляя в равенство (14) формулуполучим
|
|
(15) |
При изменении L2 меняется время t, измеряемое секундомером, но ускорение а должно оставаться неизменным.
С помощью формулы (15) найдём расчётную формулу для величины ускорения
|
|
(16) |
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
К основанию 1 экспериментальной установки (см. рис. 2), которая стоит на ножках 2, прикреплена вертикальная стойка 3. К стойке крепится кронштейн 4, который может перемещаться вдоль стойки. На кронштейне находится столик для снятия перегрузка.
рис. 2), которая стоит на ножках 2, прикреплена вертикальная стойка 3. К стойке крепится кронштейн 4, который может перемещаться вдоль стойки. На кронштейне находится столик для снятия перегрузка.
Рис. 2. Схема экспериментальной установки
На верхнем конце стойки находится неподвижный блок 5. Для наблюдения ускоренного движения грузов на правый груз 6 помещают перегрузок 7 и поднимают их в верхнее положение путем нажатия кнопок «+» или «-». Значение массы перегрузка показывается в окне «масса После нажатия кнопки «ПУСК» начинается ускоренное движение грузов и перегрузка до того момента, когда столик 4 подхватит перегрузок. Одновременно включается миллисекундомер, измеряющий время равномерного движения грузов до остановки. Итак, во время равноускоренного движения грузы проходят расстояние L1 (см. рис. 1) и приобретают скорость v2, с которой, двигаясь равномерно, проходят расстояние L2 за время t, измеренное миллисекундомером в секундах и показанное в окне «время».
Для подготовки прибора к следующему измерению нажимают кнопку «СБРОС».
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Упражнение 1. ИЗМЕРЕНИЕ УСКОРЕНИЯ ГРУЗОВ
1. Измерьте расстояние L с помощью линейки и занесите результат в таблицу измерений 1. Цена деления линейки 1 см.
Обратите внимание на необходимость записывать данные в системе СИ, то есть, в метрах.
Таблица 1
|
m=… кг |
L=… м |
L2=… м |
|
|
№ наблюдения |
Время ti, с |
||
|
1 |
|||
|
2 |
|||
|
3 |
|||
|
4 |
|||
|
5 |
|||
2. Выберите значение массы перегрузка m и занесите ее значение в таблицу 1. Выбор производится мышкой с помощью нажатия ей на кнопки со значками «+» или «-». Значение массы перегрузка показывается в окне «масса». Оптимальным для выбора является значение массы от 5 до 10 г. Учтите, что масса в данной работе определена при взвешивании тел на весах с точностью, равной половине цены деления весов. Приборная погрешность весов составляла 0.1 г.
Выберите значение массы перегрузка m и занесите ее значение в таблицу 1. Выбор производится мышкой с помощью нажатия ей на кнопки со значками «+» или «-». Значение массы перегрузка показывается в окне «масса». Оптимальным для выбора является значение массы от 5 до 10 г. Учтите, что масса в данной работе определена при взвешивании тел на весах с точностью, равной половине цены деления весов. Приборная погрешность весов составляла 0.1 г.
Обратите внимание на необходимость записывать данные в системе СИ, то есть, в килограммах.
3. Установите, взяв мышкой, кронштейн со столиком на некотором расстоянии L2 от нижнего фиксатора расстояний. Возможные пределы варьирования расстояния от 12 до 25 см. Измерьте установленное расстояние L2 по линейке, взяв отсчёт по красной черте. Результаты измерения запишите в таблицу 1 результатов измерений 1. Цена деления линейки 1 см.
Обратите внимание на необходимость записывать данные в системе СИ, то есть, в метрах.
4. Нажмите кнопку «ПУСК».
5. После остановки грузов запишите в таблицу 1 время t равномерного движения грузов, измеренное миллисекундомером и показанное на табло «время». Время необходимо записывать в системе СИ, то есть в секундах. Погрешность миллисекундомера составляет 0.001 с.
6. Нажмите кнопку «СБРОС».
7. Повторите пункты 3 — 5 ещё четыре раза, не меняя расстояние L2.
8. Вычислите среднее значение времени <t>. Результат занесите в таблицу расчетов 2.
Таблица 2
|
№ наблюдения |
ti |
ti-<t> |
(ti-<t>)2 |
|
1 |
|||
|
2 |
|||
|
3 |
|||
|
4 |
|||
|
5 |
|||
|
Суммы |
Sti=… |
S(ti-<t>)2 |
|
|
<t>=… |
s=… |
||
|
E= |
9. Найдите отклонения каждого из пяти измерений ti от среднего значения времени <t>.
Найдите отклонения каждого из пяти измерений ti от среднего значения времени <t>.
10. Возведите в квадрат каждое отклонение и просуммируйте квадраты отклонений.
11. Рассчитайте среднее квадратичное отклонение s, применив для его расчёта формулу для выборочной оценки S(<t>) стандартного отклонения результата измерения по формуле из теории погрешностей
12. Умножив это значение среднего квадратичного отклонения на коэффициент Стьюдента, найдём полуширину доверительного интервала в определении времени
где tP(n) — коэффициент Стьюдента, соответствующий вероятности Р и числу степеней свободы n=n-1.
Для n=5 измерений при рекомендуемой доверительной вероятности P=0.9 имеем из таблицы коэффициентов Стьюдента t0.9(5-1)=2.13.
13. Приборная погрешность в определении времени в нашем случае значительно меньше случайной, поэтому приборная погрешность в определении времени в данном случае не учитывается.
Тогда результат измерения времени t запишем в виде
14. Произведите расчет относительной погрешности в определении времени Et (в процентах) по формуле:
15. Приборная погрешность в определении расстояний уже не может быть отброшена, так как случайной погрешности здесь нет, Тогда для расстояний L и L2 имеем приборные погрешности, равные половине цены деления линейки
16. Ускорение грузов а рассчитывается по формуле (16), в которую подставляется среднее значение времени <t> и измеренные линейкой значения расстояний L и L2.
17. Относительная погрешность в определении ускорения найдётся по формуле:
18. Результат измерения ускорения а запишется в виде
Упражнение 2. ИЗМЕРЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ
19. Определите величину ускорения свободного падения g по формуле
Определите величину ускорения свободного падения g по формуле
При этом значение массы грузов принять равным M=90 г.
20. Полуширину доверительного интервала Dg найдите с помощью формулы
Значения погрешностей в определении масс в данной работе принять равными приборной погрешности при их взвешивании:
21. Оформите отчёт по работе.
ВЫПОЛНЕНИЕ ЛАБОРАТОРНОЙ РАБОТЫ
На рис.3 представлена реальная лабораторная установка, используемая для выполнения данной работы.
Рис.3. Лабораторная установка «Машина Атвуда»
После ознакомления с принципом работы установки необходимо проделать работу на виртуальной лабораторной установке, представленной в правом окне. В процессе выполнения измерений можно свернуть-развернуть окно с описанием лабораторной работы либо свернуть-развернуть окно с лабораторной установкой.
После окончания измерений следует сохранить результаты работы. Для этого необходимо нажать на клавишу или. После этого будет предложено сохранить результаты в файле, имя которого — название лабораторной работы (имя файла изменять не рекомендуется), месторасположение — рабочий стол (можно изменить место сохранения файла). Так как результаты сохраняются в формате html, в дальнейшем вы можете просмотреть результаты, открыв сохраненный файл, а также можете отправить файл на проверку правильности выполнения лабораторной работы преподавателю.
Для этого необходимо нажать на клавишу или. После этого будет предложено сохранить результаты в файле, имя которого — название лабораторной работы (имя файла изменять не рекомендуется), месторасположение — рабочий стол (можно изменить место сохранения файла). Так как результаты сохраняются в формате html, в дальнейшем вы можете просмотреть результаты, открыв сохраненный файл, а также можете отправить файл на проверку правильности выполнения лабораторной работы преподавателю.
РЕКОМЕНДАЦИИ
по оформлению отчета по лабораторным работам (физика)
1. Отчет оформляют в электронном виде в редакторе Word
2. Объем отчета составляет 2-3 страницы.
3. В отчете необходимо указать:
3.1 Фамилию, имя, отчество студента;
3.2 Номер группы;
3.3 Дисциплину;
3.4 Фамилию, имя, отчество преподавателя;
4. Рекомендуемая структура отчета:
4.1 Название работы;
4.2 Цель работы;
4.3 Таблицы измерений и таблицы расчетов, сохраненные в виде отдельного файла.
4.5 Формулы и законы, используемые для расчетов;
4.6 Результаты расчетов, не вошедшие в таблицу расчётов;
4.7 Выводы, которые можно сделать из работы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что называется системой отсчета?
2. Дайте определение материальной точки.
3. Сравните понятия пути и перемещения.
4. Дайте определения средней и мгновенной скоростей.
5. Дайте определения среднего и мгновенного ускорений.
6. Укажите формулы, связывающие кинематические величины при равноускоренном прямолинейном движении.
7. Дайте определение силы.
8. Что характеризует масса тела?
9. Сформулируйте основные законы динамики — законы Ньютона.
10. Какая система тел называется изолированной?
11. Сформулируйте законы сохранения импульса и полной механической энергии системы.
12. Какое движение тела называется свободным падением?
13. Как изменится ускорение свободного падения при подъеме с уровня моря на высоту h=10 км? Радиус Земли R3=6 370 км.
14. При каком условии ускорения тел, используемых в машине Атвуда, одинаковы по модулю?
Формула для ускорения грузов на машине атвуда — Dudom
Задание: Экспериментально проверить законы равномерного и равноускоренного движений. Определить ускорение свободного падения с предельной относительной погрешностью e, не превышающей 5 %.
Оборудование и принадлежности: установка для проведения измерений, набор грузов, весы.
| Рис. 1 |
Для проверки законов кинематики и определения ускорения свободного падения в работе используется машина Атвуда, схема устройства которой показана на рис. 1.
Через блок перекинута нить с двумя одинаковыми грузами 1 и 2 на концах, масса каждого груза М. В этом случае система находится в равновесии. Если на один из грузов положить перегрузок малой массы m, то грузы будут двигаться равноускоренно. На пути груза с перегрузком установлена кольцевая платформа “П”. На кольцевой платформе перегрузок снимается и дальше грузы движутся равномерно.
На кольцевой платформе перегрузок снимается и дальше грузы движутся равномерно.
Для изучения равноускоренного движения используются перегрузки меньшего диаметра, которые вместе с грузом проходят через кольцевую платформу. Расстояния h и H (рис. 1) можно изменять передвижением верхней и средней муфт.
На средней и нижней платформе установлены фотоэлектрические датчики. Перекрытие светового пучка верхнего датчика грузом служит для запуска, а нижнего — для остановки миллисекундомера.
Электромагнит установки при помощи фрикционной муфты при не включенной кнопке “пуск” удерживает систему ролика с грузами в состоянии покоя.
Общие сведения. Из определения скорости и ускорения материальной точки:
(1)
следуют выражения для радиус-вектора, пути и вектора скорости:
(2)
(3)
(4)
Из уравнений (3) и (4) следует, в частности, что при равномерном движении (а = 0) вектор скорости остаётся постоянным , а путь, пройденный материальной точкой за время t равен:
(5)
При равноускоренном (a = const) движении без начальной скорости(vo = 0) получаем:
(6)
(7)
Исключая время t из соотношений (6) и (7), найдём связь пути, скорости и ускорения материальной точки при равноускоренном движении без начальной скорости:
(8)
При изучении кинематики материальной точки полезно использовать графический метод. На графике зависимости s(t) при равномерном движении (уравнение (5)) скорость материальной точки равна тангенсу угла наклона прямой графика к оси абсцисс t. На графике зависимости v(t) при прямолинейном равноускоренном движении материальной точки ускорение равно тангенсу угла наклона графика (прямой линии) к оси абсцисс t. Это можно использовать для графического определения скорости и ускорения материальной точки из опыта.
На графике зависимости s(t) при равномерном движении (уравнение (5)) скорость материальной точки равна тангенсу угла наклона прямой графика к оси абсцисс t. На графике зависимости v(t) при прямолинейном равноускоренном движении материальной точки ускорение равно тангенсу угла наклона графика (прямой линии) к оси абсцисс t. Это можно использовать для графического определения скорости и ускорения материальной точки из опыта.
При небольших скоростях (v«c) движения материальной точки постоянной массы её ускорение, по второму закону Ньютона:
(9)
Угловое ускорение твердого тела определяется соотношением (основной закон динамики вращательного движения твёрдого тела):
(10)
Теория работы. Если на груз 1 положить перегрузок массой m, то он начнёт двигаться с ускорением a, которое можно найти с помощью законов динамики для грузов 1, 2 и для блока:
(11)
(12)
(13)
где I – момент инерции блока, e – его угловое ускорение. Уравнения (11) — (12) записаны в проекции на ось Y, уравнение (13) – в проекции на ось Z, совпадающую по направлению с вектором углового ускорения блока. При этом предполагалось, что масса нити и силы трения пренебрежимо малы, нить нерастяжимая и не скользит по блоку. Ускорение грузов численно равно тангенциальному ускорению точек на краю блока (нить не скользит по блоку). Поэтому угловое ускорение блока
Уравнения (11) — (12) записаны в проекции на ось Y, уравнение (13) – в проекции на ось Z, совпадающую по направлению с вектором углового ускорения блока. При этом предполагалось, что масса нити и силы трения пренебрежимо малы, нить нерастяжимая и не скользит по блоку. Ускорение грузов численно равно тангенциальному ускорению точек на краю блока (нить не скользит по блоку). Поэтому угловое ускорение блока
(14)
Из уравнений (11) — (14) находим:
(15)
Момент инерции блока
. Если масса блока mo много меньше массы грузов, то из (15) следует, что
(16)
Движение грузов на машине Атвуда описывается соотношениями (5)-(8), в которых ускорение a задаётся формулой (16), а путь s – это расстояние, пройденное грузом 1.
Если груз 1 на участке h движется равноускоренно, а на участке H – равномерно (рис.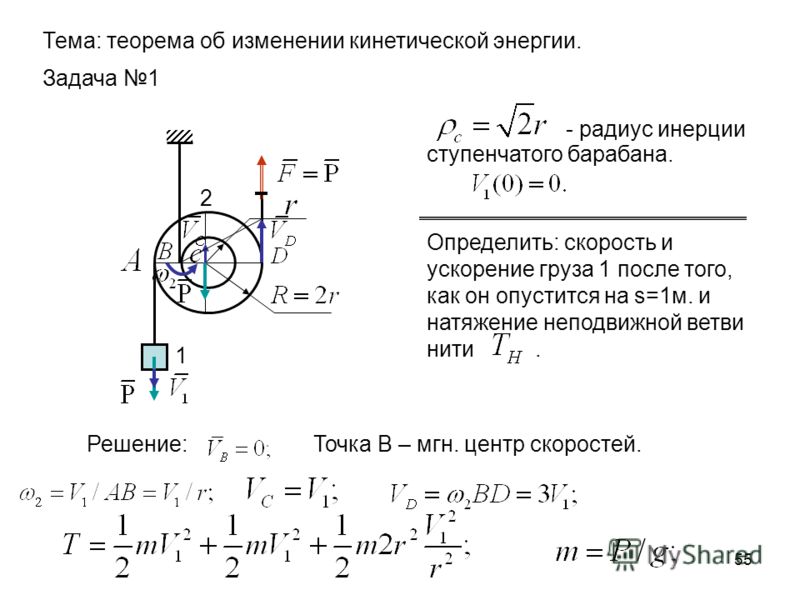 1), то его движение описывается уравнениями (5) и, (8) соответственно, которые в данном случае принимают вид:
1), то его движение описывается уравнениями (5) и, (8) соответственно, которые в данном случае принимают вид:
(17)
(18)
где ускорение a находится из (16). Из уравнений (16) — (18) находим ускорение свободного падения g:
(19)
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Студент — человек, постоянно откладывающий неизбежность. 10825 —
| 7386 — или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Использование простых механизмов в физике позволяет изучать различные природные процессы и законы. Одним из этих механизмов является машина Атвуда. Рассмотрим в статье, что она собой представляет, для чего используется, и какие формулы описывают принцип ее работы.
Одним из этих механизмов является машина Атвуда. Рассмотрим в статье, что она собой представляет, для чего используется, и какие формулы описывают принцип ее работы.
Что такое машина Атвуда?
Названная машина представляет собой простой механизм, состоящий из двух грузов, которые соединены переброшенной через неподвижный блок нитью (веревкой). В данном определении следует пояснить несколько нюансов. Во-первых, массы грузов в общем случае являются разными, что обеспечивает наличие у них ускорения под действием силы тяжести. Во-вторых, нить, связывающая грузы, считается невесомой и нерастяжимой. Эти предположения значительно облегчают последующие расчеты уравнений движения. Наконец, в-третьих, неподвижный блок, через который переброшена нить, также считается невесомым. Кроме того, во время его вращения пренебрегают силой трения. Ниже на схематическом рисунке показана эта машина.
Вам будет интересно: Пространственная экономика: описание специальностей и структура
Машина Атвуда была изобретена английским физиком Джорджем Атвудом в конце XVIII века. Служит она для изучения законов поступательного движения, точного определения ускорения свободного падения и экспериментальной проверки второго закона Ньютона.
Служит она для изучения законов поступательного движения, точного определения ускорения свободного падения и экспериментальной проверки второго закона Ньютона.
Уравнения динамики
Каждый школьник знает, что ускорение у тел появляется только в том случае, если на них оказывают действие внешние силы. Данный факт был установлен Исааком Ньютоном в XVII веке. Ученый изложил его в следующем математическом виде:
Где m – инерционная масса тела, a – ускорение.
Изучение законов поступательного движения на машине Атвуда предполагает знание соответствующих уравнений динамики для нее. Предположим, что массы двух грузов равны m1 и m2, причем m1>m2. В таком случае первый груз будет перемещаться вниз под действием силы тяжести, а второй груз будет двигаться вверх под действием силы натяжения нити.
Рассмотрим, какие силы действуют на первый груз. Их две: сила тяжести F1 и сила натяжения нити T. Силы направлены в разных направлениях. Учитывая знак ускорения a, с которым перемещается груз, получаем следующее уравнение движения для него:
Что касается второго груза, то на него действуют силы той же природы, что и на первый. Поскольку второй груз движется с ускорением a, направленным вверх, то уравнение динамики для него принимает вид:
Поскольку второй груз движется с ускорением a, направленным вверх, то уравнение динамики для него принимает вид:
Вам будет интересно: Что такое подполье? Подпольная организация «Молодая гвардия». Антифашистское движение
Таким образом, мы записали два уравнения, в которых содержатся две неизвестных величины (a и T). Это означает, что система имеет однозначное решение, которое будет получено далее в статье.
Расчет уравнений динамики для равноускоренного движения
Как мы видели из записанных выше уравнений, результирующая сила, действующая на каждый груз, остается неизменной в процессе всего движения. Масса каждого груза также не меняется. Это означает, что ускорение a будет постоянным. Такое движение называют равноускоренным.
Изучение равноускоренного движения на машине Атвуда заключается в определении этого ускорения. Запишем еще раз систему динамических уравнений:
Чтобы выразить значение ускорения a, сложим оба равенства, получаем:
F1 – F2 = a*(m1 + m2) =>
a = (F1 – F2)/(m1 + m2).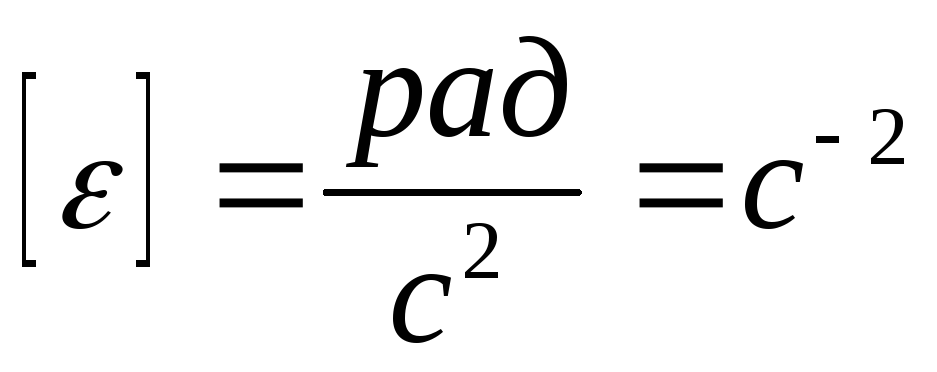
Подставляя явное значение сил тяжести для каждого груза, получаем конечную формулу для определения ускорения:
a = g*(m1 – m2)/(m1 + m2).
Отношение разницы масс к их сумме называют числом Атвуда. Обозначим его na, тогда получим:
Проверка решения уравнений динамики
Выше мы определили формулу для ускорения машины Атвуда. Она является справедливой только в том случае, если справедлив сам закон Ньютона. Проверить этот факт можно на практике, если провести лабораторную работу по измерению некоторых величин.
Лабораторная работа с машиной Атвуда является достаточно простой. Суть ее заключается в следующем: как только грузы, находящиеся на одном уровне от поверхности, отпустили, необходимо засечь время движения грузов секундомером, а затем, измерить расстояние, на которое переместился любой из грузов. Предположим, что соответствующие время и расстояние равны t и h. Тогда можно записать кинематическое уравнение равноускоренного движения:
Откуда ускорение определяется однозначно:
Отметим, что для увеличения точности определения величины a, следует проводить несколько экспериментов по измерению hi и ti, где i – номер измерения.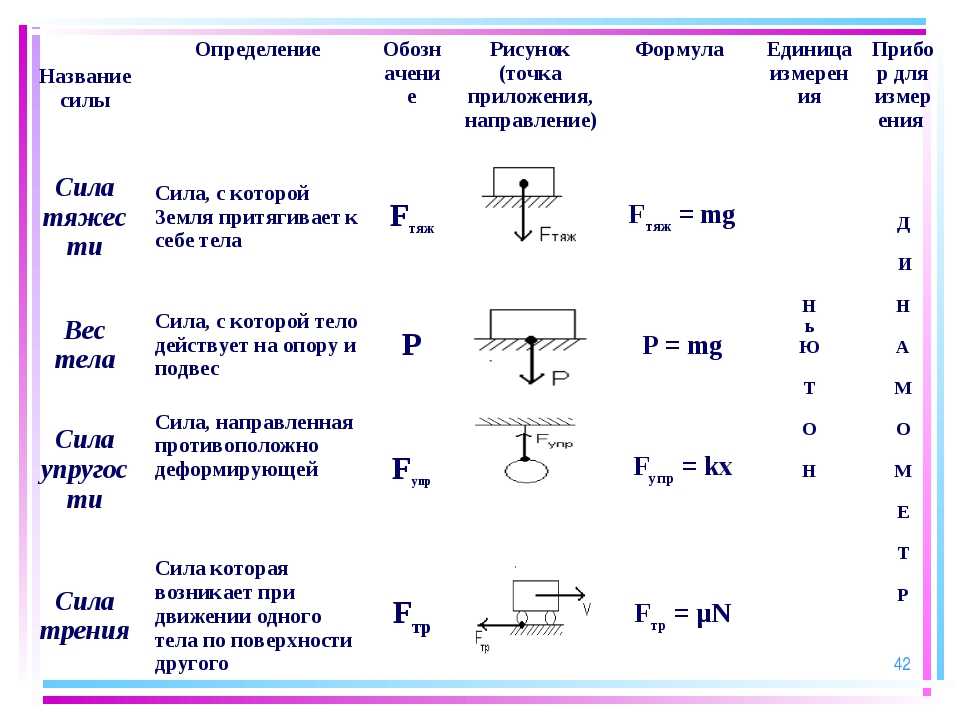 После вычисления значений ai, следует рассчитать среднюю величину acp из выражения:
После вычисления значений ai, следует рассчитать среднюю величину acp из выражения:
Где m – количество измерений.
Приравнивая это равенство и полученное ранее, приходим к следующему выражению:
Если данное выражение оказывается справедливым, то таковым также будет и второй закон Ньютона.
Расчет силы тяжести
Выше мы предположили, что значение ускорения свободного падения g нам известно. Однако при помощи машины Атвуда определение силы тяжести также оказывается возможным. Для этого вместо ускорения a из уравнений динамики следует выразить величину g, имеем:
Чтобы найти g, следует знать, чему равно ускорение поступательного перемещения. В пункте выше мы уже показали, как его находить экспериментальным путем из уравнения кинематики. Подставляя формулу для a в равенство для g, имеем:
Вычислив значение g, несложно определить силу тяжести. Например, для первого груза ее величина будет равна:
Определение силы натяжения нити
Сила T натяжения нити является одним из неизвестных параметров системы динамических уравнений. Выпишем еще раз эти уравнения:
Выпишем еще раз эти уравнения:
Если в каждом равенстве выразить a, и приравнять оба выражения, тогда получим:
(F1 – T)/m1 = (T – F2)/m2 =>
T = (m2*F1 + m1*F2)/(m1 + m2).
Подставляя явные значения сил тяжести грузов, приходим к конечной формуле для силы натяжения нити T:
T = 2*m1*m2*g/(m1 + m2).
Машина Атвуда имеет не только теоретическую пользу. Так, подъемник (лифт) использует при своей работе контргруз с целью подъема на высоту полезного груза. Такая конструкция значительно облегчает работу двигателя.
Измерение ускорения свободного падения на машине Атвуда
КИНЕМАТИКА И ДИНАМИКА ПОСТУПАТЕЛЬНОГО движения ТЕЛ
К основным понятиям кинематики, характеризующим механическое движение, относятся: траектория, длина пути, перемещение, а также мгновенная скорость и ускорение.
Траекторией материальной точки называется линия, описываемая этой точкой при ее движении относительно выбранной системы отсчета.
Длина участка траектории, пройденного точкой за промежуток времени
, называется длиной пути (путем) , пройденной за это время.
Положение точки в декартовой системе координат описывается тремя ее координатами x, y ,z или ее радиусом-вектором
– вектором, проведенным из начала координат к данной точке (рис.2.1).
Вектор
,
направленный от положения точки в момент времени
к ее положению в момент времени , называется перемещением точки за промежуток времени . Векторравен приращению радиуса-вектора точки за время.
Мгновенной скоростью
(т.е. скоростью в данный момент времени) называется предел, к которому стремится отношение при стремящемся к нулю:
. (2.1)
Таким образом, мгновенная скорость есть первая производная радиуса-вектора по времени. Вектор мгновенной скорости направлен по касательной к траектории движения точки.
Вектор мгновенной скорости направлен по касательной к траектории движения точки.
При
модуль вектора равен длине малого участка траектории (пути), следовательно,
, (2.2)
т.е. модуль скорости равен первой производной пути по времени.
Производная скорости по времени называется ускорением:
. (2.3)
Если известны зависимости ускорения и скорости от времени, а также значение скорости в начальный момент времени
, то зависимости скорости и пути от времени можно определить по формулам:
при равномерном прямолинейном движении
, (2.4)
при равноускоренном прямолинейном движении
, (2.5)
. (2.6)
Если при движении абсолютно твердого тела любая прямая, соединяющая две его точки, остается параллельной самой себе, то такое движение называют поступательным.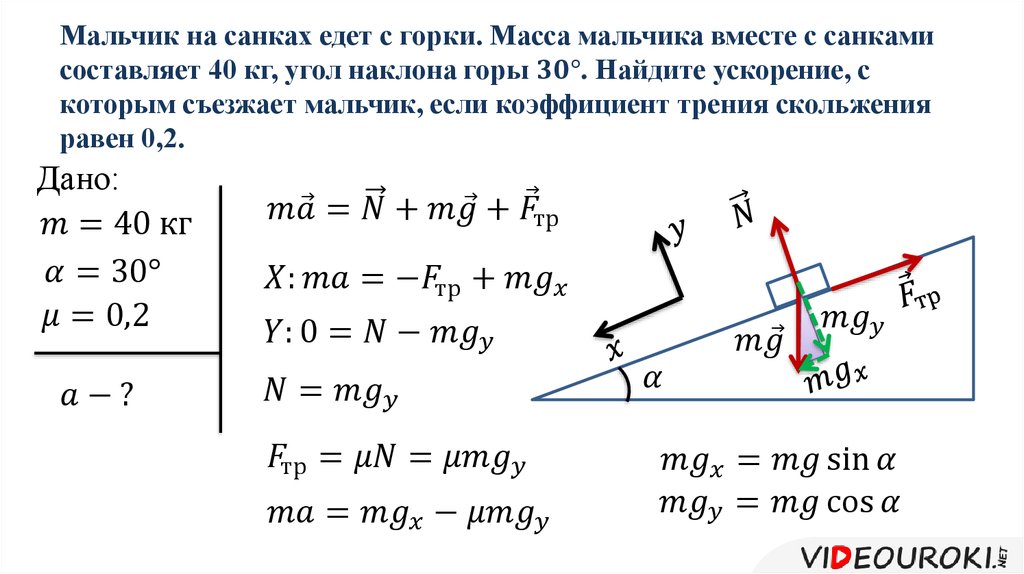 Для кинематического описания поступательного движения твердого тела достаточно рассмотреть движение какой-либо одной его точки.
Для кинематического описания поступательного движения твердого тела достаточно рассмотреть движение какой-либо одной его точки.
В динамике тело характеризуется массой. Масса тела – это физическая величина, являющаяся мерой его инерционных и гравитационных свойств.
Количественной мерой взаимодействия тел является сила. Она характеризуется значением, направлением и точкой приложения, т.е. является вектором. Тела могут взаимодействовать как при непосредственном соприкосновении, так и через силовые поля.
В основе классической динамики лежат три закона Ньютона.
1. Всякое тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока внешнее воздействие не заставит его изменить это состояние.
Первый закон Ньютона утверждает, что состояние покоя или равномерного прямолинейного движения не требует для своего поддержания каких-либо внешних воздействий. В этом проявляется особое динамическое свойство тел, называемое инертностью.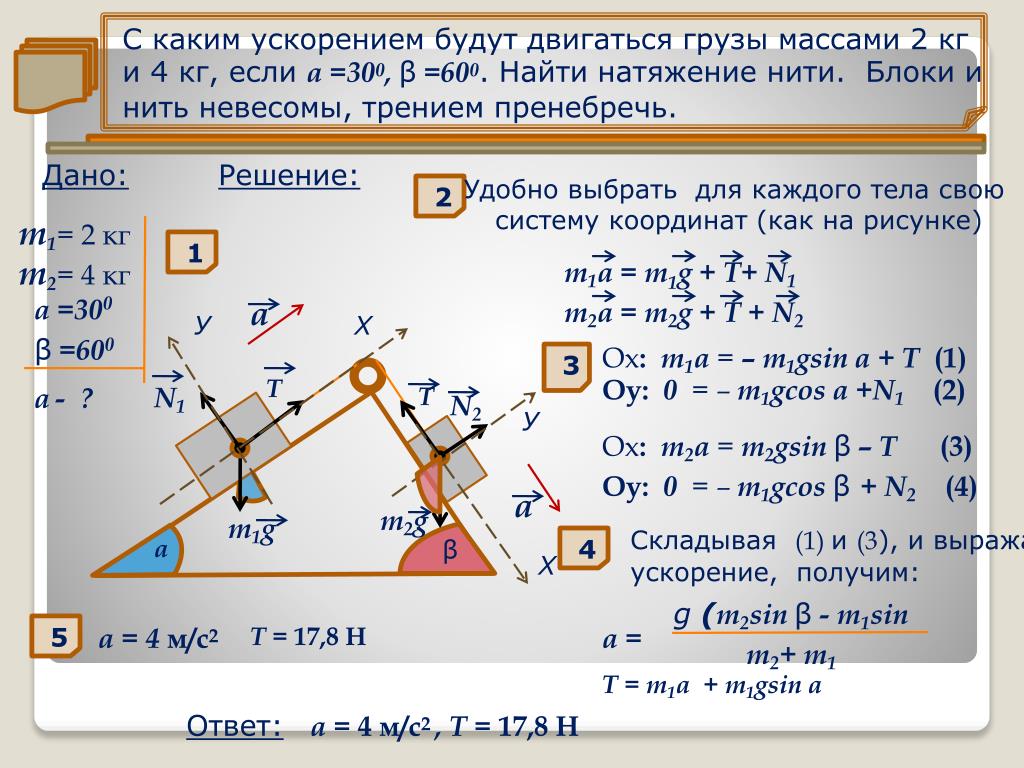 Соответственно первый закон Ньютона называют законом инерции, а движение тела, свободного от внешних воздействий, – движением по инерции.
Соответственно первый закон Ньютона называют законом инерции, а движение тела, свободного от внешних воздействий, – движением по инерции.
2. Ускорение тела пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе тела:
. (2.7)
При одновременном действии на тело нескольких сил
ускорение тела определяется их равнодействующей, т.е. в этом случае
(2.8)
Второй закон Ньютона является основным законом динамики. Если известны начальное состояние материальной точки (ее координаты и скорость в какой-либо начальный момент времени) и действующие на нее силы, то с помощью второго закона Ньютона можно рассчитать состояние материальной точки в любой последующий момент времени.
3. При взаимодействии двух тел силы, с которыми они действуют друг на друга, равны по величине и противоположны по направлению.
Приборы и принадлежности: машина Атвуда FPM-02 с набором грузов и перегрузков.
Теория метода и описание прибора
Машина Атвуда предназначена для исследования прямолинейного равномерного и равноускоренного движений. В данной работе она применяется для измерения ускорения силы тяжести g.
Через блок, установленный на подшипнике таким образом, чтобы он мог вращаться с возможно меньшим сопротивлением, перекинута нить с двумя одинаковыми грузиками массой M каждый (рис. 2.2).
При этом система находится в равновесии. Если по одну сторону блока добавить небольшой грузик (перегрузок) массой m, система получит ускорение a и, двигаясь с этим ускорением, пройдет путь S1.
На кольце Д перегрузок m будет снят (отцеплен), а грузики M, двигаясь равномерно, пройдут путь S2.
Если
– время равноускоренного движения, то
. (2.9)
(2.9)
Для равномерного движения, время которого
измеряется с помощью секундомера,
. (2.10)
Скорость равномерного движения является конечной скоростью равноускоренного движения на предыдущем участке пути, т.е.
Выразим из формулы (2.9) время
и подставим в последнее соотношение:
. (2.12)
Чтобы выяснить, от чего зависит ускорение системы, рассмотрим силы, действующие на правый и левый грузы системы. На каждый из них действует сила тяжести
В проекциях на направления движения грузов будем иметь:
Решая систему уравнений относительно ускорения a, получим:
. (2.13)
Из формулы (2.13) видим, что сила, сообщающая системе грузов с общей массой 2M+m ускорение, равна силе тяжести перегрузка, т.е. если выражение (2.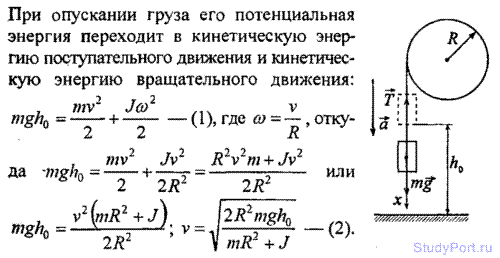 13) подставить в соотношение (2.12), то полученное выражение можно использовать для экспериментального определения ускорения свободного падения g. Действительно,
13) подставить в соотношение (2.12), то полученное выражение можно использовать для экспериментального определения ускорения свободного падения g. Действительно,
. (2.14)
Здесь все величины, кроме g, поддаются измерению. Тогда
, (2.15)
где М – масса правого или левого грузика; m – масса перегрузка; S1 – длина пути равноускоренного движения; S2 – длина пути равномерного движения; t2 – время равномерного движения.
Порядок выполнения работы и обработка результатов
Ускорение свободного падения измерим на машине Атвуда ФРМ. Подробное описание этого прибора можно получить у лаборанта.
Подготовка прибора к измерениям
1. Навесить на блок нить с грузиками массой
и проверить, находится ли система в состоянии равновесия.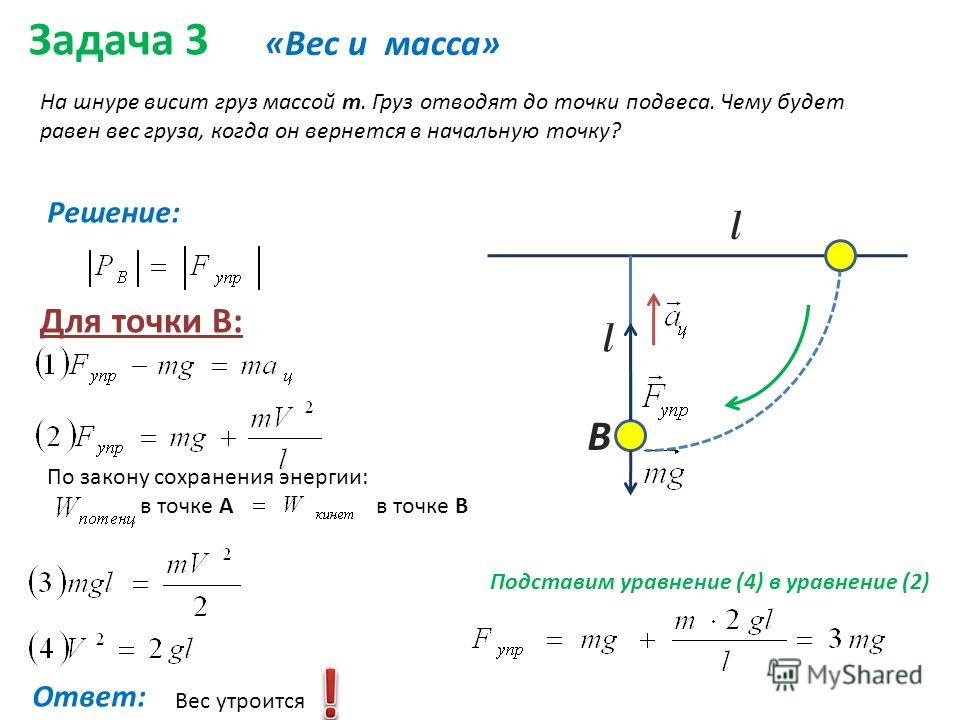
2. При помощи регулируемых ножек основания привести колонну прибора в вертикальное положение, ориентируясь по положению нити с грузиками (отвес).
3. Установить средний кронштейн на заданной высоте над нижним кронштейном так, чтобы правый грузик, опускаясь, проходил через середину рабочего окошка фотоэлектрических датчиков. Измерить по миллиметровой шкале колонны длину пути S2.
4. Установить верхний кронштейн на заданной высоте над средним кронштейном в одной плоскости с ним и с нижним кронштейном. Измерить длину пути S1.
5. Нажать клавишу “сеть”, проверяя, все ли индикаторы секундомера высвечивают нуль и светятся ли лампочки обоих фотоэлектрических датчиков.
6. Переместить правый грузик в верхнее положение, положить на него перегрузок и проверить, находится ли система в состоянии покоя.
7. Провести пробное измерение, нажимая клавишу “пуск”: проверить, возникло ли движение, был ли на дополнительном кронштейне отцеплен перегрузок m, измерил ли миллисекундомер время t2 прохождения пути S2 правым грузиком и была ли система после прохождения этого пути заторможена.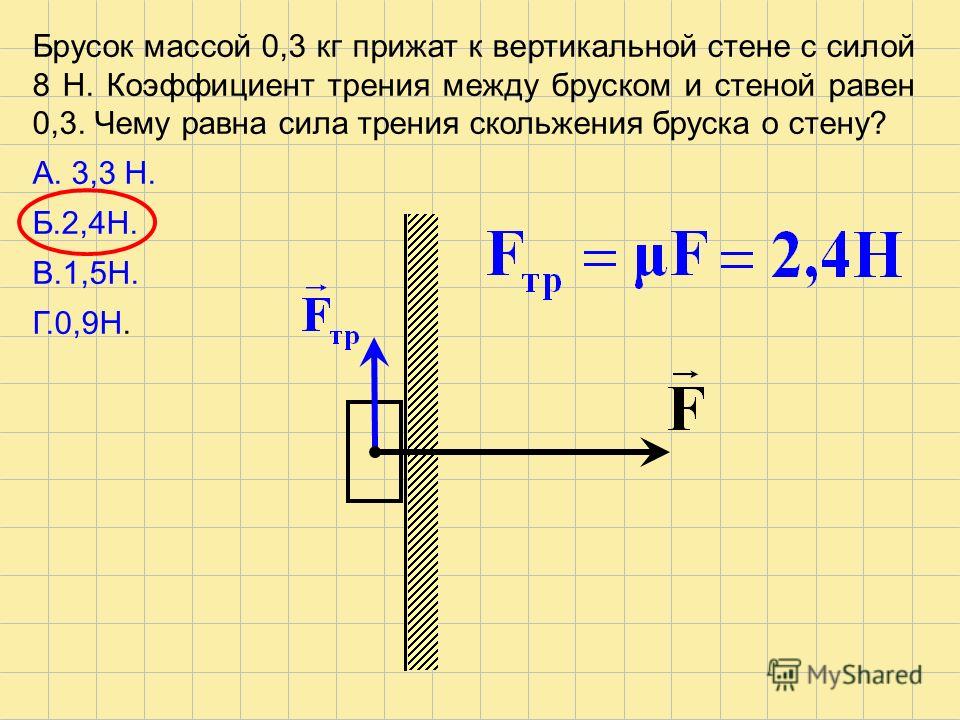
8. Отжать клавишу “сброс” и проверить, возникло ли обнуление показаний миллисекундомера и освобождение электромагнитом блокировки блока.
9. Переместить правый грузик в верхнее положение и отжать клавишу “пуск”, проверив, возникла ли блокировка блока.
1. Положить на правый грузик массой М заданный перегрузок массой m.
2. Согласовать нижнюю грань правого грузика с чертой на верхнем кронштейне.
3. Измерить при помощи шкалы на колонне прибора пути равноускоренного S1 и равномерного движений S2.
4. Нажать клавишу “пуск”.
5. После окончания движения системы снять показание времени t2, измеренного миллисекундомером.
6. Измерения повторить не менее 5 раз. Вычислить среднее значение времени. Данные измерений и вычислений записать в табл. 2.1.
«>

 .. Используйте данные задачи в рамке, чтобы найти общий PSI, необходимый для вертикально движущегося цилиндра не только для подъема данного груза, но и для его ускорения до конечной скорости за указанное время. Или ускорить его от более низкой до более высокой скорости.
.. Используйте данные задачи в рамке, чтобы найти общий PSI, необходимый для вертикально движущегося цилиндра не только для подъема данного груза, но и для его ускорения до конечной скорости за указанное время. Или ускорить его от более низкой до более высокой скорости. Здесь показаны примеры трех распространенных форм. Многие другие формы показаны в справочниках по машинам.
Здесь показаны примеры трех распространенных форм. Многие другие формы показаны в справочниках по машинам. ..
.. 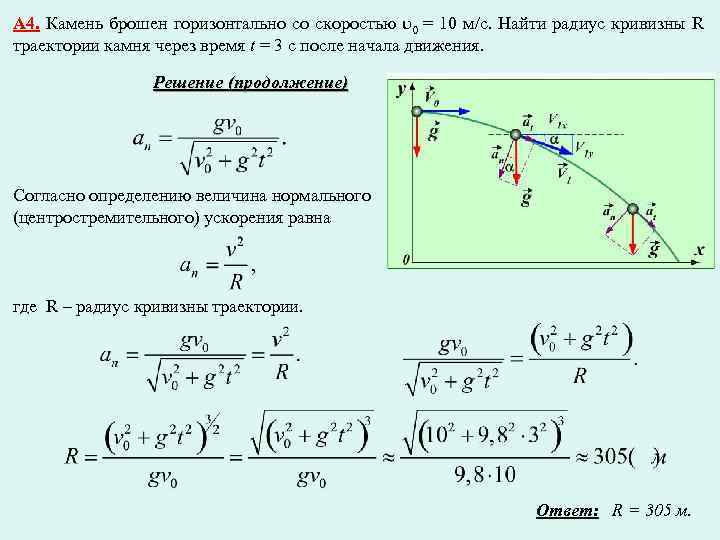 Дополнительный крутящий момент для ускорения можно рассчитать по этой базовой формуле:
Дополнительный крутящий момент для ускорения можно рассчитать по этой базовой формуле: Диаметр трубы 10 дюймов Н.Д. x 7 дюймов В.Д.
Диаметр трубы 10 дюймов Н.Д. x 7 дюймов В.Д. .
.



 Более крупный двигатель также означает более высокую стоимость и большую занимаемую площадь, что не является наиболее желательным для конструкции машин.
Более крупный двигатель также означает более высокую стоимость и большую занимаемую площадь, что не является наиболее желательным для конструкции машин.
 Мы не можем рассчитать инерцию нагрузки без учета инерции ротора двигателя.
Мы не можем рассчитать инерцию нагрузки без учета инерции ротора двигателя. 
 Если вы используете коэффициент безопасности 2, то нам понадобится шаговый двигатель, который может выдавать крутящий момент 1,7 Нм при частоте вращения около 1200 об/мин; в зависимости от скорости разгона/торможения. Коэффициенты безопасности определяются на основе точности переменных.
Если вы используете коэффициент безопасности 2, то нам понадобится шаговый двигатель, который может выдавать крутящий момент 1,7 Нм при частоте вращения около 1200 об/мин; в зависимости от скорости разгона/торможения. Коэффициенты безопасности определяются на основе точности переменных. Небольшое увеличение размеров, если все сделано правильно, может продлить срок службы или улучшить характеристики двигателя.
Небольшое увеличение размеров, если все сделано правильно, может продлить срок службы или улучшить характеристики двигателя.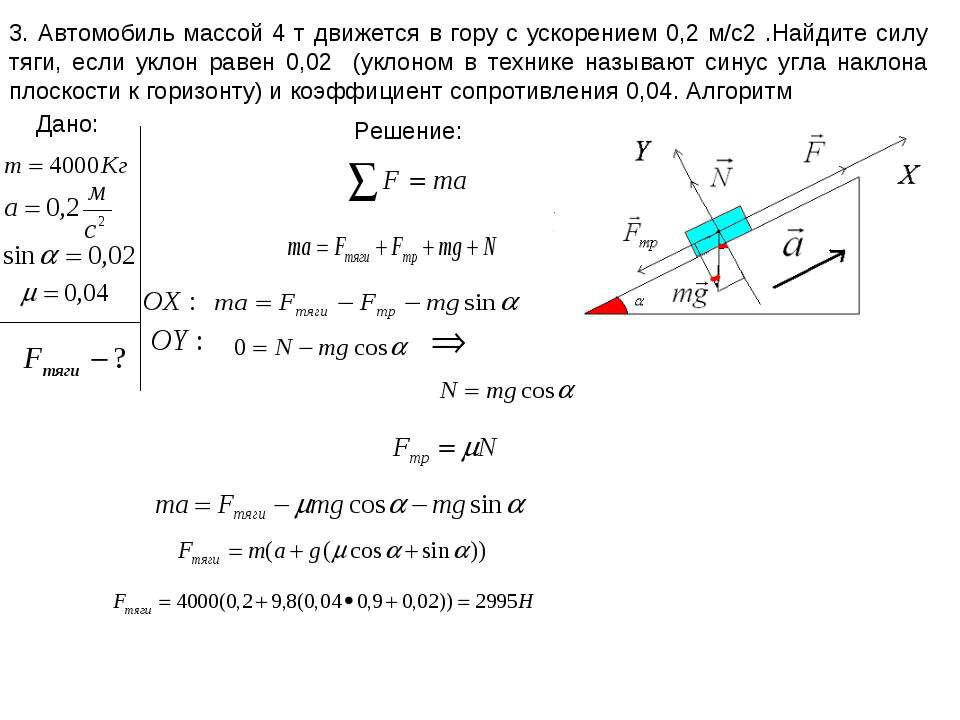 Поскольку пиковый крутящий момент требует высокого уровня тока двигателя, он не может поддерживаться постоянно без перегрева двигателя.
Поскольку пиковый крутящий момент требует высокого уровня тока двигателя, он не может поддерживаться постоянно без перегрева двигателя.
 1200[об/мин]
1200[об/мин] 
Leave A Comment