Импульс тела, закон сохранения импульса
ОпределениеИмпульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:
p = mv
Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).
Направление импульса всегда совпадает с направлением скорости (p↑↓v), так как масса — всегда положительная величина (m > 0).
Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.
Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:
10 г = 0,01 кг
Импульс равен:
p = mv = 0,01∙300 = 3 (кг∙м/с)
Относительный импульс
ОпределениеОтносительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:
p1отн2
p1отн2— импульс первого тела относительно второго, m1 — масса первого тела, v1отн2 — скорость первого тела относительно второго, v1и v2 — скорости первого и второго тела соответственно в одной и той же системе отсчета.
Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.
Сначала переведем единицы измерения в СИ:
15 т = 15000 кг
p1отн2 = m1(v1 – v2) = 15000(20 – 15) = 75000 (кг∙м/с) = 75∙103(кг∙м/с)
Изменение импульса тела
ОпределениеИзменение импульса тела — векторная разность между конечным и начальным импульсом тела:∆p = p – p0 = p + (– p0)
∆p — изменение импульса тела, p — конечный импульс тела, p0 — начальный импульс тела
Частные случаи определения изменения импульса тела
Абсолютно неупругий удар | |
| Конечная скорость после удара: v = 0. p = 0. Модуль изменения импульса тела равен модулю его начального импульса: ∆p = p0. | |
Абсолютно упругий удар | |
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p. | |
Пуля пробила стенку | |
Модуль изменения импульса тела равен разности модулей начального и конечного импульсов: ∆p = p0 – p = m(v0 – v) | |
Радиус-вектор тела повернул на 180 градусов | |
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p = 2mv0 | |
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали | |
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0 Угол падения равен углу отражения: α = α’ Модуль изменения импульса в этом случае определяется формулой: | |
Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.
В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.
Вычисляем:
Второй закон Ньютона в импульсном виде
Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:
Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:
Подставим это выражение во второй закон Ньютона и получим:
Или:
F∆t — импульс силы, ∆p — изменение импульса тела
Пример №4.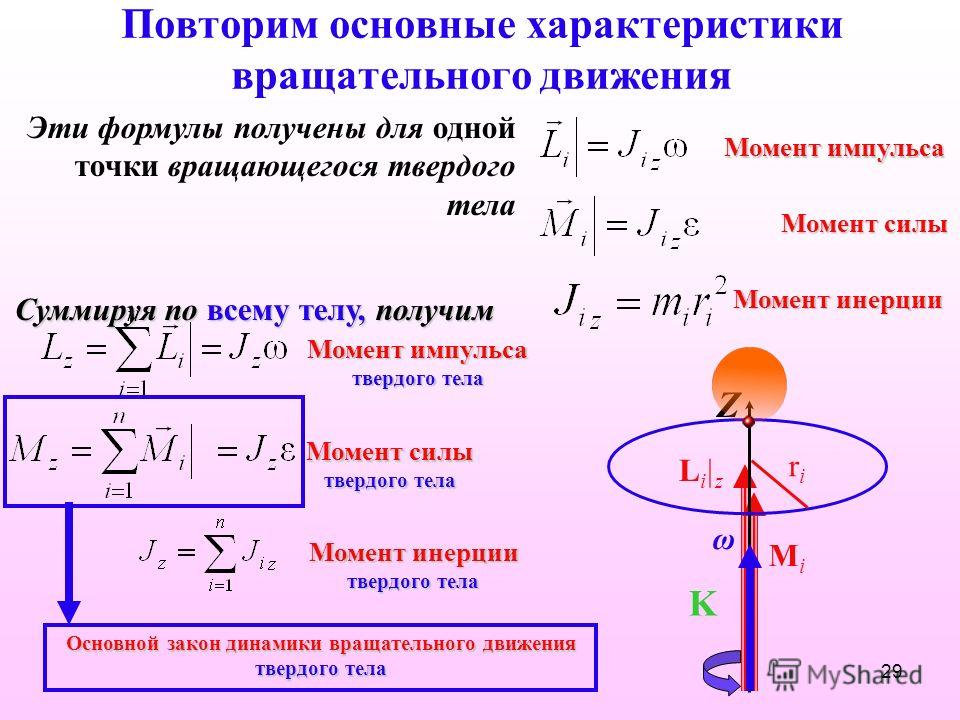 Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?
Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?
Из формулы импульса силы выразим модуль силы:
Реактивное движение
ОпределениеРакета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.
Второй закон Ньютона в импульсном виде:
Реактивная сила:
Второй закон Ньютона для ракеты:
Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с.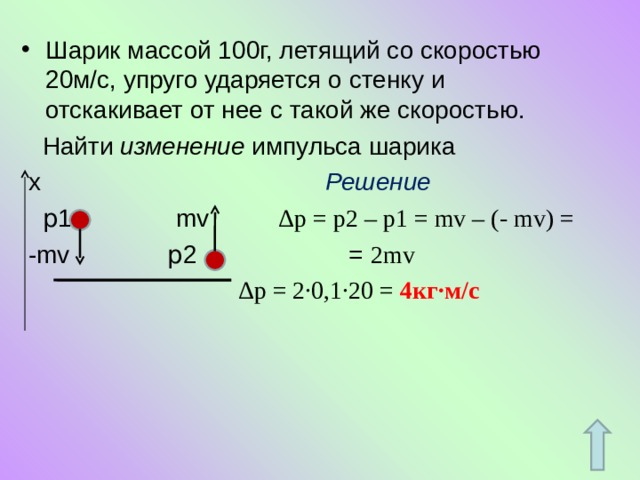
Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:
V = a∆t
Выразим ускорение из второго закона Ньютона для ракеты:
Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:
Отсюда ускорение равно:
Выразим формулу для скорости и сделаем вычисления:
Суммарный импульс системы тел
ОпределениеСуммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:
Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.
Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:
Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.
Закон сохранения импульса в проекции на горизонтальную ось
Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:
- положителен, если его направление совпадает с направлением оси ОХ;
- отрицателен, если он направлен противоположно направлению оси ОХ.
При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.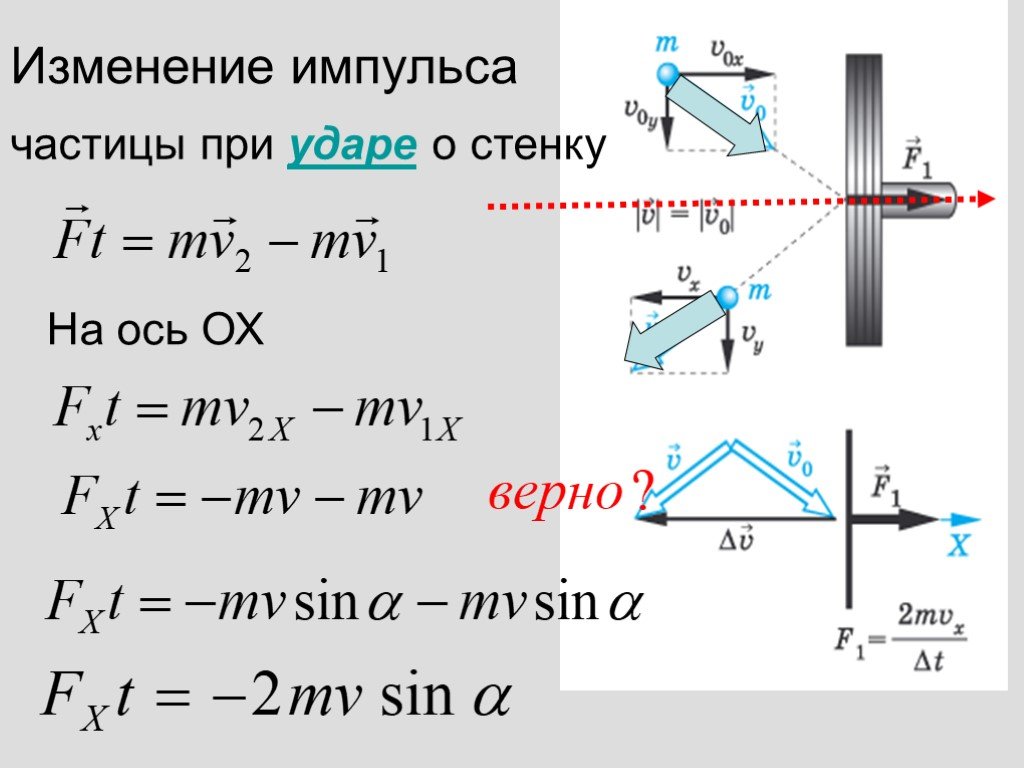
Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)
| Неупругое столкновение с неподвижным телом | m1v1 = (m1 + m2)v |
| Неупругое столкновение движущихся тел | ± m1v1 ± m2v2 = ±(m1 + m2)v |
| В начальный момент система тел неподвижна | 0 = m1v’1 – m2v’2 |
| До взаимодействия тела двигались с одинаковой скоростью | (m1 + m2)v = ± m1v’1 ± m2v’2 |
Сохранение проекции импульса
В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.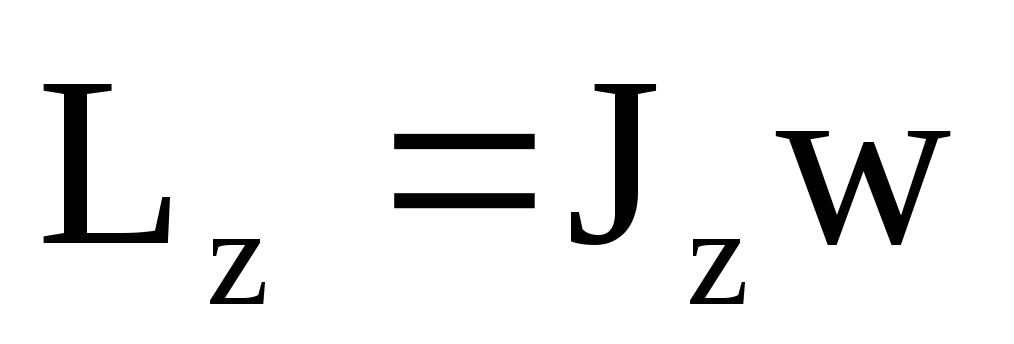
Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.
Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:
m2v2 = (m1 + m2)v
Отсюда скорость равна:
Задание EF17556Импульс частицы до столкновения равен −p1, а после столкновения равен −p2, причём p1 = p, p2 = 2p, −p1⊥−p2. Изменение импульса частицы при столкновении Δ−p равняется по модулю:
а) p
б) p√3
в) 3p
г) p√5
Алгоритм решения
1.Записать исходные данные.
2.Построить чертеж, обозначить векторы начального и конечного импульсов, а также вектор изменения импульса. Для отображения вектора изменения импульса использовать правило сложения векторов методом параллелограмма.
Для отображения вектора изменения импульса использовать правило сложения векторов методом параллелограмма.
3.Записать геометрическую формулу для вычисления длины вектора изменения импульса.
4.Подставить известные значения и вычислить.
Решение
Запишем исходные данные:
• Модуль импульса частицы до столкновения равен: p1 = p.
• Модуль импульса частицы после столкновения равен: p2 = 2p.
• Угол между вектором начального и вектором конечного импульса: α = 90о.
Построим чертеж:
Так как угол α = 90о, вектор изменения импульса представляет собой гипотенузу треугольника, катами которого являются вектора начального и конечного импульсов. Поэтому изменение импульса можно вычислить по теореме Пифагора:
Δp=√p21+p22
Подставим известные данные:
Δp=√p2+(2p)2=√5p2=p√5
.
Ответ: гpазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17695На рисунке приведён график зависимости проекции импульса на ось Ox тела, движущегося по прямой, от времени. Как двигалось тело в интервалах времени 0–1 и 1–2?
Как двигалось тело в интервалах времени 0–1 и 1–2?
а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно
б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено
в) в интервалах 0–1 и 1–2 двигалось равномерно
г) в интервалах 0–1 и 1–2 двигалось равноускорено
Алгоритм решения
1.Записать формулу, связывающую импульс тема с его кинематическими характеристиками движения.
2.Сделать вывод о том, как зависит характер движения от импульса.
3.На основании вывода и анализа графика установить характер движения тела на интервалах.
Решение
Импульс тела есть произведение массы тела на его скорость:
p = mv
Следовательно, импульс и скорость тела — прямо пропорциональные величины. Если импульс с течением времени не меняется, то скорость тоже. Значит, движение равномерное. Если импульс растет линейно, то и скорость увеличивается линейно. В таком случае движение будет равноускоренным.
В таком случае движение будет равноускоренным.
На участке 0–1 импульс тела не менялся. Следовательно, на этом участке тело двигалось равномерно. На участке 1–2 импульс тела увеличивался по линейной функции, следовательно, на этом участке тело двигалось равноускорено.
Верный ответ: б.
Ответ: бpазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF22730 Камень массой 3 кг падает под углом α = 60° к горизонту в тележку с песком общей массой 15 кг, покоящуюся на горизонтальных рельсах, и застревает в песке (см. рисунок). После падения кинетическая энергия тележки с камнем равна 2,25 Дж. Определите скорость камня перед падением в тележку.Алгоритм решения
1.Записать исходные данные.
2.Записать закон сохранения импульса применительно к задаче.
3.Записать формулу кинетической энергии тела.
4.Выполнить общее решение.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса камня: m1 = 3 кг.
• Масса тележки с песком: m2 = 15 кг.
• Кинетическая энергия тележки с камнем: Ek= 2,25 Дж.
Так как это абсолютно неупругий удар, закон сохранения импульса принимает вид:
m1v1+m2v2=(m1+m2)v
Учтем, что скорость тележки изначально была равна нулю, а к ее движению после столкновения привела только горизонтальная составляющая начальной скорости камня:
m1v1cos.α=(m1+m2)v
Выразить конечную скорость системы тел после столкновения мы можем через ее кинетическую энергию:
Ek=(m1+m2)v22..
Отсюда скорость равна:
v=√2Ekm1+m2..
Выразим скорость камня до столкновения через закон сохранения импульса и подставим в формулу найденную скорость:
v1=(m1+m2)vm1cos.α..=(m1+m2)m1cos.α..·√2Ekm1+m2..
Подставим известные данные и произведем вычисления:
v1=(3+15)3cos. 60o..·√2·2,253+15..=12·√0,25=12·0,5=6 (мс..)
60o..·√2·2,253+15..=12·√0,25=12·0,5=6 (мс..)
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF22520Снаряд, имеющий в точке О траектории импульсp0, разорвался на два осколка. Один из осколков имеет импульс −p1 . Импульс второго осколка изображается вектором:
а) −−→AB
б) −−→BC
в) −−→CO
г) −−→OD
Алгоритм решения
1.Сформулировать закон сохранения импульса и записать его в векторной форме.
2.Применить закон сохранения импульса к задаче.
3.Выразить из закона импульс второго осколка и найти на рисунке соответствующий ему вектор.
Решение
Согласно закону сохранения импульса, импульс замкнутой системы тел сохраняется. Записать его можно так:
−p1+−p2=−p′ 1+−p′2
Можем условно считать осколки замкнутой системой, так как они не взаимодействуют с другими телами.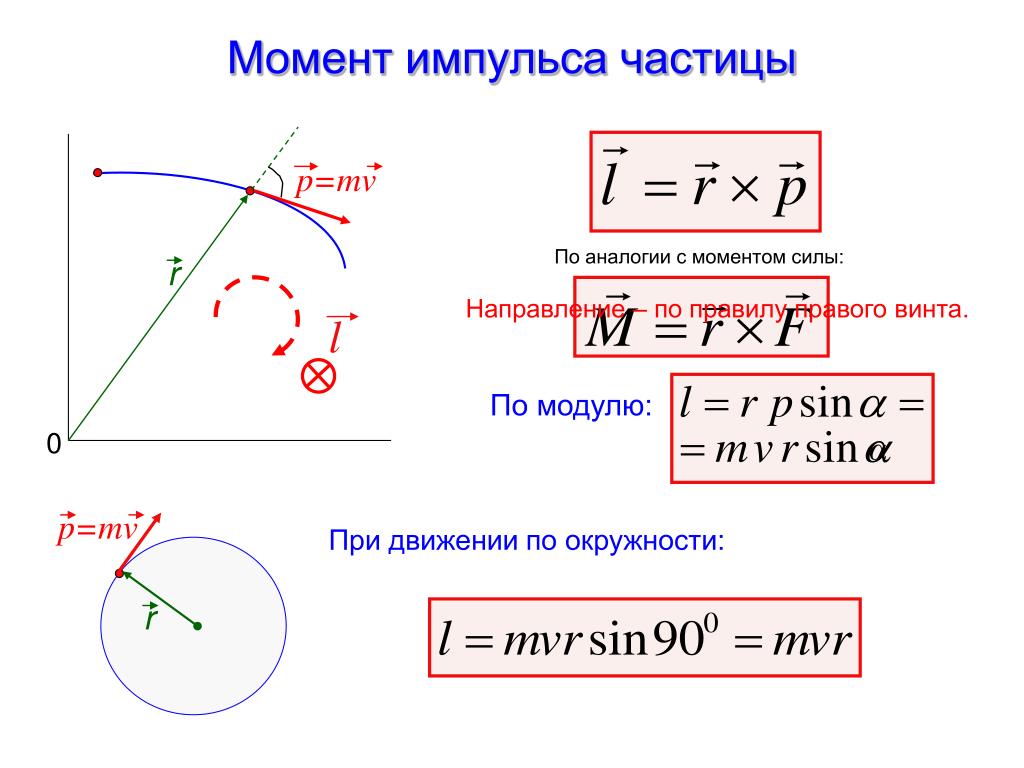 Применяя к ним закон сохранения импульса, получим:
Применяя к ним закон сохранения импульса, получим:
−p0=−p1+−p2
Отсюда импульс второго осколка равен векторной разности импульса снаряда и импульса первого осколка:
−p2=−p0−−p1
Известно, что разностью двух векторов является вектор, начало которого соответствует вычитаемому вектору, а конец — вектору уменьшаемому. В нашем случае вычитаемый вектор — вектор импульса первого осколка. Следовательно, начало вектора импульса второго осколка лежит в точке А. Уменьшаемый вектор — вектор импульса снаряда. Следовательно, конец вектора лежит в точке В. Следовательно, искомый вектор — −−→AB.
Ответ: аpазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18122Летящая горизонтально со скоростью 20 м/с пластилиновая пуля массой 9 г попадает в груз неподвижно висящий на нити длиной 40 см, в результате чего груз с прилипшей к нему пулей начинает совершать колебания. Максимальный угол отклонения нити от вертикали при этом равен α = 60°. Какова масса груза?
Какова масса груза?
Ответ:
а) 27 г
б) 64 г
в) 81 г
г) 100 г
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Сделать чертеж, отобразив начальное, промежуточное и конечное положение тел.
3.Записать закон сохранения импульса для момента столкновения и закон сохранения механической энергии для момента максимального отклонения нити от положения равновесия.
4.Выполнить решение задачи в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса пластилиновой пули: m = 9 г.
• Скорость пластилиновой пули: v = 20 м/с.
• Длина нити: l = 40 см.
• Максимальный угол отклонения нити: α = 60°.
Переведем единицы измерения величин в СИ:
Сделаем чертеж:
Нулевой уровень — точка А.
После неупругого столкновения пули с грузом они начинают двигаться вместе. Поэтому закон сохранения импульса для точки А выглядит так:
mv=(m+M)V
После столкновения система тел начинается двигаться по окружности. Точка В соответствует верхней точке траектории. В этот момент скорость системы на мгновение принимает нулевое значение, а потенциальная энергия — максимальное.
Закон сохранения энергии для точки В:
(m+M)V22..=(m+M)gh
V22..=gh
Высоту h можно определить как произведение длины нити на косинус угла максимального отклонения. Поэтому:
V=√2glcos.α
Подставим это выражение в закон сохранения импульса для точки А и получим:
Выразим массу груза:
Ответ: вpазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | Просмотров: 18.6k
Импульс. Закон сохранения импульса | Физика
1.
 Импульс
ИмпульсВ некоторых случаях удается исследовать взаимодействие тел, не используя выражения для сил, действующих между телами. Это возможно благодаря тому, что существуют физические величины, которые остаются неизменными (сохраняются) при взаимодействии тел. В этой главе мы рассмотрим две такие величины – импульс и механическую энергию.
Начнем с импульса.
Физическую величину , равную произведению массы тела m на его скорость , называют импульсом тела (или просто импульсом):
= m.
Импульс – векторная величина. Модуль импульса p = mv, а направление импульса совпадает с направлением скорости тела. Единицей импульса является 1 (кг * м)/с.
? 1. По шоссе в направлении на север со скоростью 40 км/ч едет грузовик массой 3 т. В каком направлении и с какой скоростью должен ехать легковой автомобиль массой 1 т, чтобы его импульс был равен импульсу грузовика?
? 2. Мяч массой 400 г свободно падает без начальной скорости с высоты 5 м, После удара мяч отскакивает вверх, причем модуль скорости мяча в результате удара не изменяется.
а) Чему равен и как направлен импульс мяча непосредственно перед ударом?
б) Чему равен и как направлен импульс мяча сразу после удара?
в) Чему равно и как направлено изменение импульса мяча в результате удара? Найдите изменение импульса графически.
Подсказка. Если импульс тела был равен 1, а стал равен 2, то изменение импульса ∆ = 2 – 1.
2. Закон сохранения импульса
Важнейшим свойством импульса является то, что при определенных условиях суммарный импульс взаимодействующих тел остается неизменным (сохраняется).
Поставим опыт
Две одинаковые тележки могут катиться по столу вдоль одной прямой практически без трения. (Этот опыт можно поставить при наличии современного оборудования.) Отсутствие трения – важное условие нашего опыта!
Установим на тележках защелки, благодаря которым тележки после столкновения движутся как одно тело. Пусть правая тележка вначале покоится, а левой толчком сообщим скорость 0 (рис. 25.1, а).
25.1, а).
После столкновения тележки движутся вместе. Измерения показывают, что их общая скорость в 2 раза меньше, чем начальная скорость левой тележки (25.1, б).
Обозначим массу каждой тележки m и сравним суммарные импульсы тележек до и после столкновения.
Мы видим, что суммарный импульс тележек остался неизменным (сохранился).
Может быть, это справедливо только тогда, когда тела после взаимодействия движутся как единое целое?
Поставим опыт
Заменим защелки на упругую пружину и повторим опыт (рис. 25.2).
На этот раз левая тележка остановилась, а правая приобрела скорость, равную начальной скорости левой тележки.
? 3. Докажите, что и в этом случае суммарный импульс тележек сохранился.
Может быть, это справедливо только тогда, когда массы взаимодействующих тел равны?
Поставим опыт
Закрепим на правой тележке еще одну такую же тележку и повторим опыт (рис. 25.3).
Теперь после столкновения левая тележка стала двигаться в противоположном направлении (то есть влево) со скоростью, равной –/3, а сдвоенная тележка стала двигаться вправо со скоростью 2/3.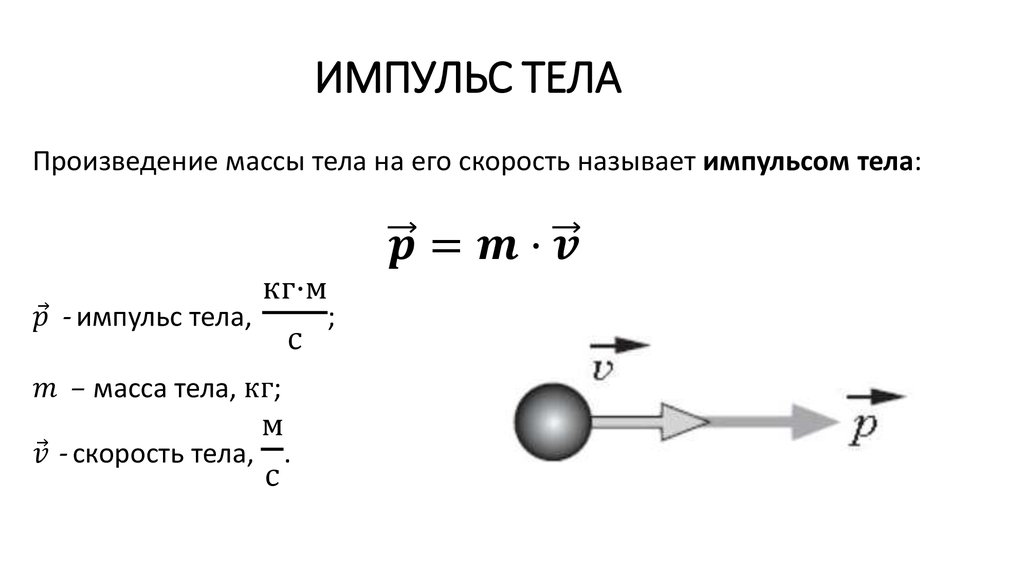
? 4. Докажите, что и в этом опыте суммарный импульс тележек сохранился.
Чтобы определить, при каких условиях суммарный импульс тел сохраняется, введем представление о замкнутой системе тел. Так называют систему тел, которые взаимодействуют только друг с другом (то есть не взаимодействуют с телами, не входящими в эту систему).
В точности замкнутых систем тел в природе не существует – хотя бы потому, что невозможно «отключить» силы всемирного тяготения.
Но во многих случаях систему тел с хорошей точностью можно считать замкнутой. Например, когда внешние силы (силы, действующие на тела системы со стороны других тел) уравновешивают друг друга или ими можно пренебречь.
Именно так и было в наших опытах с тележками: действующие на них внешние силы (сила тяжести и сила нормальной реакции) уравновешивали друг друга, а силой трения можно было пренебречь, Поэтому скорости тележек изменялись только вследствие их взаимодействия друг с другом.
Описанные опыты, как и многие другие, подобные им, свидетельствуют о том, что выполняется
закон сохранения импульса: векторная сумма импульсов тел, составляющих замкнутую систему, не изменяется при любых взаимодействиях между телами системы:
Закон сохранения импульса выполняется только в инерциальных системах отсчета.
Закон сохранения импульса как следствие законов Ньютона
Покажем на примере замкнутой системы двух взаимодействующих тел, что закон сохранения импульса – следствие второго и третьего законов Ньютона.
Обозначим массы тел m1 и m2, а их начальные скорости 1 и 2. Тогда векторная сумма импульсов тел
Пусть в течение промежутка времени ∆t взаимодействующие тела двигались с ускорениями 1 и 2.
? 5. Объясните, почему изменение суммарного импульса тел можно записать в виде
Подсказка. Воспользуйтесь тем, что для каждого тела ∆ = m∆, а также тем, что ∆ = ∆t.
? 6. Обозначим 1 и 2 силы, действующие соответственно на первое и второе тело. Докажите, что
Подсказка. Воспользуйтесь вторым законом Ньютона и тем, что система замкнута, вследствие чего ускорения тел обусловлены только силами, с которыми эти тела действуют друг на друга.
? 7. Докажите, что
Подсказка. Воспользуйтесь третьим законом Ньютона.
Воспользуйтесь третьим законом Ньютона.
Итак, изменение суммарного импульса взаимодействующих тел равно нулю. А если изменение некоторой величины равно нулю, то это означает, что эта величина сохраняется.
? 8. Почему из приведенного рассуждения следует, что закон сохранения импульса выполняется только в инерциальных системах отсчета?
3. Импульс силы
Есть такая поговорка: «Знать бы, где упадешь, – соломки постелил бы». А зачем нужна «соломка»? Почему спортсмены на тренировках и соревнованиях падают или прыгают на мягкие маты, а не на твердый пол? Почему после прыжка надо приземляться на согнутые ноги, а не на выпрямленные? Зачем в автомобилях нужны ремни и подушки безопасности?
Мы сможем ответить на все эти вопросы, познакомившись с понятием «импульс силы».
Импульсом силы называют произведение силы на промежуток времени ∆t, в течение которого действует эта сила.
Название «импульс силы» не случайно «перекликается» с понятием «импульс». Рассмотрим случай, когда на тело массой m в течение промежутка времени ∆t действует сила .
Рассмотрим случай, когда на тело массой m в течение промежутка времени ∆t действует сила .
? 9. Докажите, что изменение импульса тела ∆ равно импульсу действующей на это тело силы:
Подсказка. Воспользуйтесь тем, что ∆ = m∆, и вторым законом Ньютона.
Перепишем формулу (6) в виде
Эта формула представляет собой другую форму записи второго закона Ньютона. (Именно в таком виде сформулировал этот закон сам Ньютон.) Из нее следует, что на тело действует большая сила, если его импульс существенно изменяется за очень краткий промежуток времени ∆t.
Вот почему при ударах и столкновениях возникают большие силы: удары и столкновения характеризуются как раз малым интервалом времени взаимодействия.
Чтобы ослабить силу удара или уменьшить силы, возникающие при столкновении тел, надо удлинить промежуток времени, в течение которого происходит удар или столкновение.
? 10. Объясните смысл поговорки, приведенной в начале этого раздела, а также ответьте на другие вопросы, помещенные в том же абзаце.
? 11. Мяч массой 400 г ударился о стену и отскочил от нее с той же по модулю скоростью, равной 5 м/с. Перед самым ударом скорость мяча была направлена горизонтально. Чему равна средняя сила давления мяча на стену, если он соприкасался со стеной в течение 0,02 с?
? 12.Чугунная болванка массой 200 кг падает с высоты 1,25 м в песок и погружается в него на 5 см.
а) Чему равен импульс болванки непосредственно перед ударом?
б) Чему равно изменение импульса болванки за время удара?
в) Сколько времени длился удар?
г) Чему равна средняя сила удара?
Дополнительные вопросы и задания
13. Шарик массой 200 г движется со скоростью 2 м/с влево. Как должен двигаться другой шарик массой 100 г, чтобы суммарный импульс шариков был равен нулю?
14. Шарик массой 300 г равномерно движется по окружности радиусом 50 см со скоростью 2 м/с. Чему равен модуль изменения импульса шарика:
а) за один полный период обращения?
б) за половину периода обращения?
в) за 0,39 с?
15. Первая доска лежит на асфальте, а вторая такая же – на рыхлом песке. Объясните, почему в первую доску легче забить гвоздь, чем во вторую?
Первая доска лежит на асфальте, а вторая такая же – на рыхлом песке. Объясните, почему в первую доску легче забить гвоздь, чем во вторую?
16. Пуля массой 10 г, летевшая со скоростью 700 м/с, пробила доску, после чего скорость пули стала равной 300 м/с. Внутри доски пуля двигалась в течение 40 мкс.
а) Чему равно изменение импульса пули вследствие прохождения сквозь доску?
б) С какой средней силой пуля действовала на доску при прохождении сквозь нее?
Импульс: определение, формула, уравнение и единицы измерения
Мы часто слышим слово импульс, особенно в спорте. Когда команда, например, играет хорошо и стабильно выигрывает, мы говорим, что у команды есть импульс. Хотя мы можем не использовать это слово в количественном смысле в повседневной жизни, импульс на самом деле связан с математикой, когда речь идет о физике.
Что такое линейный импульс?
Любой движущийся объект с массой имеет импульс. В этом объяснении мы рассматриваем объекты, движущиеся линейно. Так что же такое линейный импульс?
Так что же такое линейный импульс?
Линейный импульс — это произведение массы и скорости объекта.
Расчет импульса
Импульс любого объекта зависит от двух вещей: массы и скорости. Мы можем выразить это математически как:
p=m·v
Здесь p — импульс, m — масса, измеренная в килограммах (кг), а v — скорость, измеренная в метрах в секунду (м/с). Импульс — это векторная величина с единицами измерения кг⋅м/с . Как видно из уравнения, импульс объекта будет увеличиваться, если увеличивается его скорость (прямо пропорциональная зависимость). Чем больше импульс у объекта, тем больше силы ему нужно, чтобы остановиться.
Что такое импульс?
Предположим, вы едете на машине с определенной скоростью. Этот импульс будет зависеть от массы автомобиля и скорости, с которой он движется. Теперь предположим, что вы хотите остановить машину. Как бы вы это сделали?
Во-первых, вы нажмете на тормоза, которые быстро остановят автомобиль за счет большой силы торможения . Сила торможения, необходимая для остановки автомобиля, зависит от импульса автомобиля.
Сила торможения, необходимая для остановки автомобиля, зависит от импульса автомобиля.
Еще один способ остановить машину — снять ногу с педали и позволить трению вступить в игру. В этом сценарии небольшое количество силы применяется в течение длительного периода времени.
В любом случае движущаяся машина остановится, но что это за сила, необходимая для остановки движущегося тела? Это называется импульсом i .
Импульс — это изменение импульса объекта при приложении силы в течение определенного периода времени.
Импульс=F∆t
Единицей измерения импульса являются ньютон-секунды (Н·с). В результате область под графиком сила-время даст импульс или изменение импульса.
Что такое теорема об импульсе-импульсе?
Теорема об импульсе-импульсе просто утверждает, что изменение импульса равно изменению импульса.
Выразим это математически следующим образом:
F∆t=∆p
Если мы далее разложим изменение импульса, мы получим:
F∆t=mvf-mvi
Здесь mv f — конечный импульс, а mv i — начальный импульс.
Скорость изменения импульса может быть выражена как:
F=m(v-u)∆t
Здесь v — конечная скорость, а u — начальная скорость.
Что такое закон сохранения количества движения?
Так же, как в химии у нас есть закон сохранения материи, а в физике у нас есть закон сохранения энергии. Мы можем расширить эти понятия, чтобы сформулировать другой закон, известный как закон сохранения импульса.
Сохранение линейного количества движения : Полный импульс в изолированной системе, в которой не действуют внешние силы, сохраняется. Суммарный импульс до столкновения двух тел будет равен суммарному импульсу после столкновения. Полная энергия также сохраняется для такой системы.
Предположим, у вас есть два объекта массами m 1 и m 2 , движущиеся навстречу друг другу со скоростями u 1 и u 2 .
Два объекта вот-вот столкнутся, Усама Адил – StudySmarter Originals
Оба объекта сталкиваются друг с другом через некоторое время и действуют друг на друга с силами F 1 и F 2 .
Когда объекты сталкиваются, они воздействуют друг на друга силой, заставляя их на мгновение останавливаться, Усама Адил – StudySmarter Originals
После столкновения два объекта будут двигаться в противоположном направлении со скоростями v 1 и v 2 соответственно.
После столкновения оба объекта движутся в противоположном направлении с разными скоростями, Усама Адил — StudySmarter Originals
Поскольку закон сохранения импульса гласит, что импульс сталкивающихся объектов сохраняется, мы можем вывести следующее уравнение:
F1=-F2
m1(v1-u1)t1=-m2(v2-u2)t2
Поскольку t 1 и t 2 одинаковы, поскольку оба объекта сталкивались в течение одинакового времени, мы можем сократить уравнение до
m1v1-m1u1=-m2v2+m2u2
Преобразование вышеприведенного дает
m1u1+m2u2=m1v1+m2v2
Это уравнение утверждает сохранение линейного количества движения (т.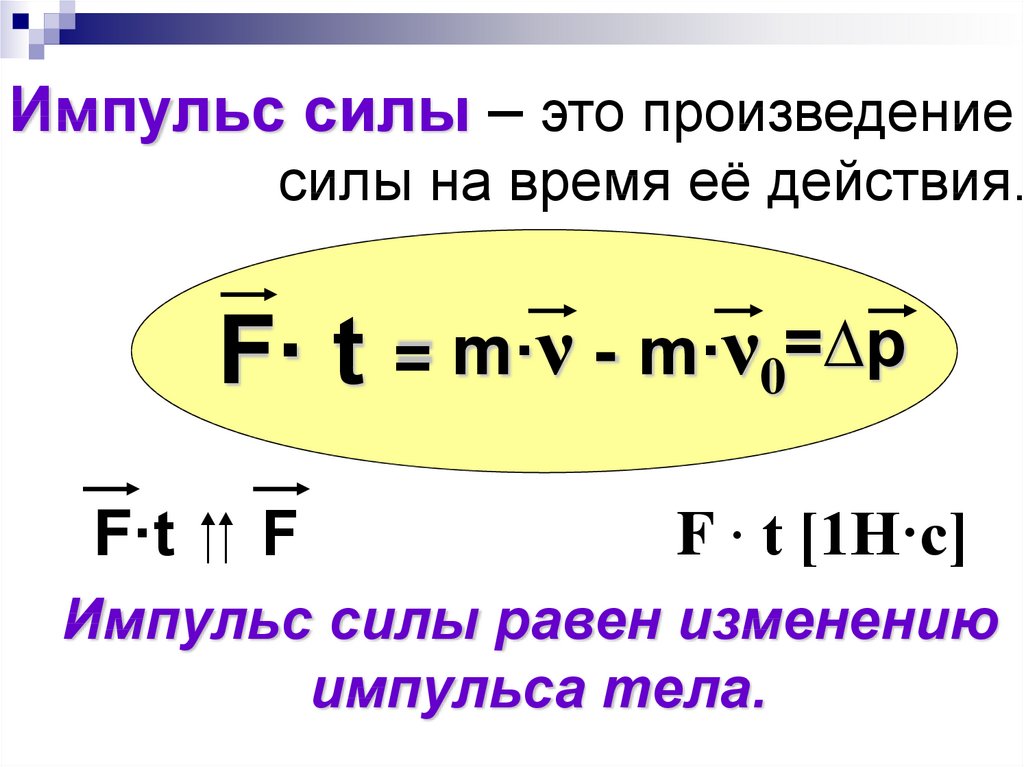 е. полный импульс до столкновения равен полному импульсу после столкновение). После удара скорости меняются, а массы остаются постоянными .
е. полный импульс до столкновения равен полному импульсу после столкновение). После удара скорости меняются, а массы остаются постоянными .
Импульс: существуют ли разные типы столкновений?
Не каждое столкновение приводит к раздельному раздвижению объектов. Например, есть сценарии, в которых объекты сталкиваются, а иногда и объединяются, образуя новые объекты. Имейте в виду, что линейный импульс сохраняется при любом типе столкновения .
Столкновения
Столкновение происходит всякий раз, когда движущийся объект входит в контакт с другим объектом, который находится в состоянии покоя или в движении.
Шары для бильярда на столе.
Упругие столкновения
При упругих столкновениях объекты, соприкасающиеся , остаются отдельными . Другими словами, объекты не объединяются, чтобы сформировать новый объект. Полная кинетическая энергия и импульс сохраняются в этом типе столкновения, поэтому объекты отскакивают друг от друга без потери энергии .
Теперь вам может быть интересно, всякий раз, когда кто-то пинает мяч, стопа человека не уходит в отдельном направлении (было бы ужасно, если бы это произошло!). Так что же это за столкновение?
Многие столкновения не являются абсолютно упругими , например, когда футболист пинает мяч. Но нога игрока и мяч остаются разделенными после того, как игрок ударит по мячу. Прежде чем игрок ударит по мячу, мяч находится в состоянии покоя, а стопа движется с высокой скоростью. После того, как игрок ударит по мячу, мяч летит в том направлении, в котором его ударили.
Мы называем все эти сценарии почти упругими столкновениями , потому что некоторая форма энергии преобразуется в звук или тепло и т. д.
Совершенно неупругие столкновения
двигаться вместе как одна масса . Когда мы исследуем совершенно неупругие столкновения, мы можем рассматривать два отдельных объекта как одиночный объект после столкновения . Следовательно, с точки зрения импульса:
Следовательно, с точки зрения импульса:
p1+p2=ptotal
m1v1+m2v2=(m1+m2)vf
Обратите внимание, что v f будет зависеть от величин и направлений двух начальных скоростей.
Иногда мы можем аппроксимировать автомобильные аварии абсолютно неупругими столкновениями, в которых суммарный импульс сохраняется . Однако полная энергия не сохраняется , потому что часть энергии преобразуется в звук, тепло и внутреннюю энергию. Разбившиеся автомобили никогда не вернутся в исходное положение после столкновения, поэтому такие виды столкновений называются неупругими.
- При упругих столкновениях полный импульс и полная энергия сохраняются.
- При неупругих столкновениях полный импульс сохраняется, но полная энергия не сохраняется.
Завершение столкновений
В реальной жизни никакое столкновение не является упругим или совершенно неупругим, но находится где-то посередине, что мы можем просто обозначить как неупругих столкновений , потому что они подразумевают, что в результате столкновений теряется некоторая энергия. Однако мы часто приближаем столкновение к любой из крайностей, чтобы упростить расчеты.
Однако мы часто приближаем столкновение к любой из крайностей, чтобы упростить расчеты.
Импульс — ключевые выводы
- Импульс — это произведение массы и скорости объекта.
- Чем выше импульс, тем больше силы потребуется, чтобы остановить объект.
- Импульс – это сила, приложенная в течение определенного интервала времени.
- Теорема об импульсе-импульсе утверждает, что импульс – это изменение импульса. Площадь под графиком сила-время дает импульс.
- Закон сохранения импульса гласит, что полный импульс до столкновения двух тел равен общему импульсу после столкновения.
- При упругих столкновениях полный импульс и полная энергия сохраняются.
- При неупругих столкновениях полный импульс сохраняется, но полная энергия не сохраняется.
Изображения
Упругое столкновение двух частиц одинаковой массы, одна из которых покоится. https://commons.wikimedia.org/wiki/File:Elastic_collision. svg
svg
29.4 Photon Momentum – College Physics
Глава 29 Введение в квантовую физику
Резюме
- Свяжите линейный импульс фотона с его энергией или длиной волны и примените сохранение линейного импульса к простым процессам, связанным с испусканием, поглощением или отражением фотонов.
- Качественно объясните наблюдаемое увеличение длины волны фотона и объясните значение длины волны Комптона.
Квант электромагнитного излучения, который мы называем фотоном , обладает свойствами, аналогичными свойствам частиц, которые мы можем видеть, таких как песчинки. Фотон взаимодействует как единое целое при столкновениях или при поглощении, а не как протяженная волна. Массивные кванты, такие как электроны, также ведут себя как макроскопические частицы — чего и следовало ожидать, поскольку они являются мельчайшими единицами материи. Частицы обладают не только энергией, но и импульсом. Несмотря на то, что фотоны не имеют массы, уже давно существуют доказательства того, что электромагнитное излучение переносит импульс. (Максвелл и другие, изучавшие электромагнитные волны, предсказывали, что они будут нести импульс.) В настоящее время хорошо установлен факт, что фотоны до имеют импульс. На самом деле импульс фотона определяется фотоэлектрическим эффектом, когда фотоны выбивают электроны из вещества. На рис. 1 показаны макроскопические признаки импульса фотона.
Несмотря на то, что фотоны не имеют массы, уже давно существуют доказательства того, что электромагнитное излучение переносит импульс. (Максвелл и другие, изучавшие электромагнитные волны, предсказывали, что они будут нести импульс.) В настоящее время хорошо установлен факт, что фотоны до имеют импульс. На самом деле импульс фотона определяется фотоэлектрическим эффектом, когда фотоны выбивают электроны из вещества. На рис. 1 показаны макроскопические признаки импульса фотона.
На рис. 1 показана комета с двумя выступающими хвостами. Чего большинство людей не знает о хвостах, так это того, что они всегда указывают в сторону от Солнца, а не следуют за кометой (как хвост овцы Бо Пипа). Хвосты комет состоят из газов и пыли, испаряющихся с тела кометы, и ионизированного газа. Частицы пыли отскакивают от Солнца, когда от них рассеиваются фотоны. Очевидно, фотоны переносят импульс в направлении своего движения (от Солнца), и часть этого импульса передается пылинкам при столкновениях. На атомы и молекулы газа в голубом хвосте больше всего влияют другие частицы излучения, такие как протоны и электроны, исходящие от Солнца, а не импульс фотонов.
Хвосты комет состоят из газов и пыли, испаряющихся с тела кометы, и ионизированного газа. Частицы пыли отскакивают от Солнца, когда от них рассеиваются фотоны. Очевидно, фотоны переносят импульс в направлении своего движения (от Солнца), и часть этого импульса передается пылинкам при столкновениях. На атомы и молекулы газа в голубом хвосте больше всего влияют другие частицы излучения, такие как протоны и электроны, исходящие от Солнца, а не импульс фотонов.
Связи: сохранение импульса
Импульс сохраняется не только во всех областях физики, но и у всех типов частиц. Мы ожидаем, что частицы с массой будут иметь импульс, но теперь мы видим, что безмассовые частицы, включая фотоны, также обладают импульсом.
Импульс сохраняется в квантовой механике так же, как в теории относительности и классической физике. Некоторые из самых ранних прямых экспериментальных свидетельств этого были получены при рассеянии рентгеновских фотонов электронами в веществах, названном комптоновским рассеянием в честь американского физика Артура Х. Комптона (189).2–1962). Примерно в 1923 году Комптон заметил, что рентгеновские лучи, рассеянные от материалов, имеют пониженную энергию, и правильно проанализировал это как результат рассеяния фотонов на электронах. Это явление можно рассматривать как столкновение двух частиц — фотона и электрона, покоящихся в материале. Энергия и импульс сохраняются при столкновении. (См. рис. 2). В 1929 году он получил Нобелевскую премию за открытие этого рассеяния, которое теперь называется эффектом Комптона , потому что оно помогло доказать, что импульс фотона равен
Комптона (189).2–1962). Примерно в 1923 году Комптон заметил, что рентгеновские лучи, рассеянные от материалов, имеют пониженную энергию, и правильно проанализировал это как результат рассеяния фотонов на электронах. Это явление можно рассматривать как столкновение двух частиц — фотона и электрона, покоящихся в материале. Энергия и импульс сохраняются при столкновении. (См. рис. 2). В 1929 году он получил Нобелевскую премию за открытие этого рассеяния, которое теперь называется эффектом Комптона , потому что оно помогло доказать, что импульс фотона равен
[латекс] {р =} [/ латекс] [латекс] {\ гидроразрыва {ч} {\ лямбда}} [/ латекс],
, где [латекс]{h}[/латекс] — постоянная Планка, а [латекс] {\ лямбда} [/латекс] — длина волны фотона. (Обратите внимание, что релятивистский импульс, заданный как [латекс]{р = \gamma mu}[/латекс], действителен только для частиц, имеющих массу.)
Рисунок 2. Эффект Комптона — это название, данное рассеянию фотона электроном. Энергия и импульс сохраняются, что приводит к уменьшению обоих для рассеянного фотона. Изучая этот эффект, Комптон подтвердил, что фотоны обладают импульсом.
Энергия и импульс сохраняются, что приводит к уменьшению обоих для рассеянного фотона. Изучая этот эффект, Комптон подтвердил, что фотоны обладают импульсом.Мы видим, что импульс фотона мал, так как [латекс]{р = h/ \lambda}[/латекс] и [латекс]{ч}[/латекс] очень малы. Именно по этой причине мы обычно не наблюдаем импульс фотона. Наши зеркала не отскакивают, когда от них отражается свет (разве что в мультфильмах). Комптон увидел эффекты импульса фотона, потому что он наблюдал рентгеновские лучи, которые имеют небольшую длину волны и относительно большой импульс, взаимодействующие с самой легкой из частиц, электроном.
Пример 1. Сравнение импульсов электрона и фотона
(a) Рассчитайте импульс видимого фотона с длиной волны 500 нм. б) Найдите скорость электрона с таким же импульсом. в) Чему равна энергия электрона и как она соотносится с энергией фотона?
Стратегия
Нахождение импульса фотона является прямым применением его определения: [латекс]{р = \фрак{ч}{\лямбда}}[/латекс]. Если мы обнаружим, что импульс фотона мал, то можно предположить, что электрон с таким же импульсом будет нерелятивистским, что позволит легко найти его скорость и кинетическую энергию из классических формул. 9{-6} \;\text{eV}}[/latex]
Если мы обнаружим, что импульс фотона мал, то можно предположить, что электрон с таким же импульсом будет нерелятивистским, что позволит легко найти его скорость и кинетическую энергию из классических формул. 9{-6} \;\text{eV}}[/latex]
Энергия фотона [латекс]{E}[/latex] равна
[латекс]{E =}[/латекс] [латекс]{\ frac{hc}{\lambda}}[/latex] [латекс]{=}[/latex] [латекс]{\frac{1240 \;\text{eV} \cdot \text{nm}}{500 \; \text{нм}}}[/латекс] [латекс]{= 2,48 \;\текст{эВ}}[/латекс]
, что примерно на пять порядков больше.
Обсуждение
Импульс фотона действительно мал. Даже если у нас их огромное количество, общий импульс, который они несут, невелик. Электрон с таким же импульсом имеет скорость 1460 м/с, что явно нерелятивистски. Более массивная частица с таким же импульсом будет иметь еще меньшую скорость. Это подтверждается тем фактом, что для придания электрону того же импульса, что и у фотона, требуется гораздо меньше энергии. Но в квантово-механическом масштабе, особенно для фотонов высокой энергии, взаимодействующих с малыми массами, импульс фотона имеет большое значение. Даже в больших масштабах импульс фотонов может оказывать влияние, если их достаточно и если ничто не препятствует медленному отдаче материи. Одним из примеров являются кометные хвосты, но есть также предложения построить космические паруса, в которых используются огромные легкие зеркала (сделанные из алюминированного майлара) для отражения солнечного света. В космическом вакууме зеркала постепенно отскакивали и могли фактически перемещать космический корабль с места на место в Солнечной системе. (См. рис. 3.)
Даже в больших масштабах импульс фотонов может оказывать влияние, если их достаточно и если ничто не препятствует медленному отдаче материи. Одним из примеров являются кометные хвосты, но есть также предложения построить космические паруса, в которых используются огромные легкие зеркала (сделанные из алюминированного майлара) для отражения солнечного света. В космическом вакууме зеркала постепенно отскакивали и могли фактически перемещать космический корабль с места на место в Солнечной системе. (См. рис. 3.)
 2}[/латекс] становится
2}[/латекс] становится[латекс]{E = ПК}[/латекс]
или
[латекс] {p =} [/ латекс] [латекс] {\ гидроразрыва {E} {c}} [/ латекс] [латекс] {\ текст {(фотоны)}} [/ латекс]
Чтобы проверить справедливость этого соотношения, обратите внимание, что [латекс]{Е = hc/ \lambda}[/латекс] для фотона. Подставив это в [latex]{p=E/c}[/latex], вы получите
[латекс] {р = (hc/ \lambda) /c =}[/латекс] [латекс]{\ гидроразрыва {ч} {\ lambda}}[/латекс]
, как определено экспериментально и обсуждалось выше. Таким образом, [латекс]{p=E/c}[/латекс] эквивалентен результату Комптона [латекс]{p=h/ \lambda}[/латекс]. Для дальнейшей проверки связи между энергией фотона и импульсом см. пример 29.0003
Детекторы фотонов
Почти все системы обнаружения, о которых говорилось до сих пор, — глаза, фотопластинки, фотоумножители в микроскопах и ПЗС-камеры — полагаются на свойства частиц фотонов, взаимодействующих с чувствительной областью. Вызывается изменение, и либо это изменение каскадируется, либо записывается огромное количество точек, чтобы сформировать изображение, которое мы обнаруживаем. {-19{-15} \;\text{eV} \cdot \text{s}}[/latex] и [latex]{hc= 1240 \;\text{eV} \cdot \text{nm}}[/latex] может быть особенно полезным для задач и упражнений этого раздела.
{-19{-15} \;\text{eV} \cdot \text{s}}[/latex] и [latex]{hc= 1240 \;\text{eV} \cdot \text{nm}}[/latex] может быть особенно полезным для задач и упражнений этого раздела.
- Фотоны имеют импульс, определяемый формулой [латекс]{р = \фрак{ч}{\лямбда}}[/латекс], где [латекс]{\лямбда}[/латекс] — длина волны фотона.
- Энергия и импульс фотона связаны соотношением
[latex]{p = \frac{E}{c}}[/latex], где [latex]{E = hf=hc/ \lambda}[/latex] для фотона .
Задачи и упражнения 9{-21} \;\text{kg} \cdot \text{м/с}}[/latex]. Какова его длина волны? (b) Рассчитайте его энергию в МэВ.
4: (a) Вычислите импульс фотона с длиной волны [латекс]{2,50 \;\мю \текст{м}}[/латекс]. б) Найдите скорость электрона с таким же импульсом. в) Чему равна кинетическая энергия электрона и чем она отличается от энергии фотона?
5: Повторите предыдущую задачу для фотона с длиной волны 10,0 нм.
6: (a) Рассчитайте длину волны фотона, имеющего тот же импульс, что и протон, движущийся со скоростью 1,00% скорости света.



Leave A Comment