Тесты, варианты ЕГЭ по Математике с решениями и ответами
Узнай свой уровень знаний по математике всего за 8 минут. Все, что нужно, — это честность!
Знакомься. Наш супер-тест для тех, кто перешел в 11-й класс: Анкета
А также для родителей, который собираются самостоятельно подготовить «ребенка» к ЕГЭ.
И даже для учителей.
Всего 8 минут и никакого решения задач.
Ты просто отвечаешь: «Да» или «Нет» Анкета
Читай вопросы внимательно.
Обрати внимание, что здесь нет вариантов «получается иногда» или «однажды видел, как это делать». Если решаешь «пятьдесят на пятьдесят», лучше честно указать: «не решаю». Зачем обманывать себя?
Заодно узнаешь, какие вообще темы есть на ЕГЭ по математике в каждой из 19 задач Профильного уровня.
В конце нажми кнопку «Посчитать».
Как ты догадался, результат – твои тестовые баллы на ЕГЭ.
Тест разработан Анной Малковой и командой ЕГЭ-Студии. Проверен и откалиброван. Его проходили десятки наших учеников, и результаты с высокой точностью совпадали с теми, которые они получали на Пробных ЕГЭ.
Мы также подготовили для тебя варианты Профильного ЕГЭ по математике с решениями и ответами.
- ЕГЭ, профильный уровень. Тренировочный вариант 1
- ЕГЭ, профильный уровень. Тренировочный вариант 2
- ЕГЭ, профильный уровень. Тренировочный вариант 3
- ЕГЭ, профильный уровень. Тренировочный вариант 4
- ЕГЭ, профильный уровень. Тренировочный вариант 5
- ЕГЭ-2018, профильный уровень. Разбор задач 13-19
- Нерешаемые задачи ЕГЭ по математике
- Стрим 20 августа 2020 года. Лучшие задачи ЕГЭ-2020
Рекомендации по решению вариантов:
1. Не надо сразу просматривать задачи (и решения) всех вариантов. Такое читерство вам только помешает. Берите по одному! Задачи решайте
2. Если почти ничего не получилось – начинать надо не с решения вариантов, а с изучения математики. Например, на нашем Онлайн-курс подготовки к ЕГЭ.
3. Как оценить свой уровень?
Вам поможет наша Таблица перевода первичных баллов ЕГЭ в тестовые
Задания 1 части (№1 – 12) оцениваются в 1 первичный балл каждое.
Задания 13, 14, 15 – в 2 первичных балла каждое.
Задания 16 и 17 – 3 балла.
Задания 18 и 19 – 4 балла!
Если вы набрали не менее 60 тестовых баллов за весь вариант – у вас высокие шансы сдать ЕГЭ на 90+. Если заниматься, конечно.
Если набрали около 40 баллов… что же, это типичная картина на старте 11-го класса. И даже для того, чтобы получить 70+, надо будет хорошо поработать. И тем более для 80+ и 90+. И не расстраивайтесь – у наших учеников это хорошо получается.
Если ниже 35 баллов – значит, увы, уже отстаете.
Потому что многие задания ЕГЭ – например, задачи 1, 2, 3, 4, 6, 8, 11 и даже 16… — легко может решить и учащийся 9-10 класса.
4. Обязательно разберите правильные решения. Удачи!
Спасибо за то, что пользуйтесь нашими статьями.
Публикация обновлена: 07.02.2023
Тесты ЕГЭ по математике профильного уровня 2023
| Тема | Результат | Задания | |||
|---|---|---|---|---|---|
| 1. | Простейшие текстовые задачи Вычисления Округление с недостатком Округление с избытком Проценты Проценты и округление |
Не изучена | Отработать | ||
2. |
Чтение графиков и диаграмм Определение величины по графику Определение величины по диаграмме Вычисление величин по графику или диаграмме |
Не изучена | Отработать | ||
| 3. | Планиметрия: вычисление длин и площадей Многоугольники: вычисление длин и углов Многоугольники: вычисление площадей Круг и его элементы Координатная плоскость |
Не изучена | Отработать | ||
| 4. | Начала теории вероятностей Теоремы о вероятностях событий |
Не изучена | Отработать | ||
| 5. | Простейшие уравнения Линейные, квадратные, кубические уравнения Рациональные уравнения Иррациональные уравнения Показательные уравнения Логарифмические уравнения Тригонометрические уравнения |
Не изучена | Отработать | ||
6. |
Прямоугольные треугольники Равнобедренные треугольники Треугольники общего вида Параллелограмм Трапеция Центральные и вписанные углы Касательная, хорда, секущая Вписанные окружности Описанные окружности |
Не изучена | Отработать | ||
| 7. | Производная и первообразная Физический смысл производной Производная и касательная Применение производной к исследованию функций Определение свойств производной по заданной функции Определение свойств функции по заданной производной Первообразная |
Не изучена | Отработать | ||
| 8. | Стереометрия Куб Прямоугольный параллелепипед Элементы составных многогранников Площадь поверхности составного многогранника Объем составного многогранника Призма Пирамида Комбинации тел Цилиндр Конус Сфера, шар |
Не изучена | Отработать | ||
9. |
Вычисления и преобразования Алгебраические выражения Рациональные выражения Иррациональные выражения Степенные выражения Логарифмические выражения Тригонометрические выражения |
Не изучена | Отработать | ||
| 10. | Задачи с прикладным содержанием Разные задачи Линейные уравнения и неравенства Квадратные и степенные уравнения и неравенства Иррациональные уравнения и неравенства Рациональные уравнения и неравенства Логарифмические уравнения и неравенства Тригонометрические уравнения и неравенства Показательные уравнения и неравенства |
Не изучена | Отработать | ||
| 11. | Текстовые задачи Задачи на сплавы и смеси Задачи на движение по прямой Задачи на движение по окружности Задачи на движение по воде Задачи на производительность Задачи на прогрессии Задачи на проценты |
Не изучена | Отработать | ||
12. |
Наибольшее и наименьшее значение функций Исследование частных Исследование произведений Исследование показательных и логарифмических функций Исследование тригонометрических функций Исследование функций без помощи производной |
Не изучена | Отработать | ||
| Часть 2 | |||||
| 13. | Уравнения Рациональные и иррациональные уравнения Логарифмические и показательные уравнения Тригонометрические уравнения Тригонометрические уравнения, исследование ОДЗ Уравнения смешанного типа |
Отработать | |||
| 14. | Углы и расстояния в пространстве Задача на доказательство и вычисление Угол между скрещивающимися прямыми Угол между прямой и плоскостью Угол между плоскостями Расстояние от точки до прямой и до плоскости Расстояние между прямыми и плоскостями Сечения многогранников Объёмы многогранников Тела вращения: цилиндр, конус, шар |
Отработать | |||
15. |
Неравенства Рациональные неравенства Иррациональные неравенства Показательные неравенства Логарифмические неравенства Неравенства с логарифмами по переменному основанию Неравенства с модулем Смешанные неравенства |
Отработать | |||
| 16. | Планиметрическая задача Многоугольники и их свойства Окружности и треугольники Окружности и четырёхугольники Окружности и системы окружностей Задача на доказательство и вычисление |
Отработать | |||
| 17. | Практические задачи Банки, вклады, акции Кредиты (с установленными размерами платежей) Кредиты (с установленной схемой уменьшения долга) Задачи на оптимальный выбор Разные задачи |
Отработать | |||
18. |
Уравнения, неравенства, системы с параметром Комбинация «кривых» Кусочное построение графика функции Комбинация прямых Координаты (x, a) Левая и правая части в качестве отдельных графиков Перебор случаев Подвижная галочка Расстояние между точками Симметрия в решениях Уравнение окружности Функции, зависящие от параметра Уравнения с параметром Расположение корней квадратного трехчлена Использование симметрий, оценок, монотонности |
Отработать | |||
| 19. | Числа и их свойства Числа и их свойства Числовые наборы на карточках и досках Последовательности и прогрессии Сюжетные задачи |
Отработать | |||
Вопросы 1Если Log x (1/8) = — 3/2, то x равноА. — 4 Б. 4 С. 1/4 Д. 10 Вопросы 220 % от 2 равноА. 20 Б. 4 С. 0,4 Д. 0,04 Вопросы 3Если Log 4 (x) = 12, то log 2 (x / 4) равноА. 11 Б. 48 С. -12 д. 22 Вопросы 4Население страны увеличивалось в среднем на 2% в год с 2000 по 2003 год. Если население этой страны на 31 декабря 2003 г. тысяча была быА. 1 846 000 Б. 1 852 000 К. 1 000 000 Д. 1 500 000 Вопросы 5f — квадратичная функция, график которой представляет собой параболу, открывающуюся вверх и имеющую вершину на оси x. График новой функции g, определяемой соотношением g(x) = 2 — f(x — 5), имеет диапазон, определяемый интерваломА.  [-5, + бесконечность) [-5, + бесконечность) Б. [ 2 , + бесконечность) С. (- бесконечность, 2] д. (- бесконечность, 0] Вопросы 6f — функция такая, что f(x) < 0. График новой функции g, определяемой формулой g(x) = | е (х) | является отражением графика fА. по оси Y Б. по оси х C. на линии y = x D. на линии y = — x Вопросы 7Если график y = f(x) преобразовать в график 2y — 6 = — 4 f(x — 3), точка (a, b) на графике y = f(x) станет точкой (A, B) на графике 2y — 6 = — 4 f(x — 3), где A и B задаются формулойА. А = а — 3, В = б Б. А = а — 3, В = б С. А = а + 3, В = -2 б Д. А = а + 3, В = -2 б +3 Вопросы 8Когда парабола, представленная уравнением y — 2x 2 = 8 x + 5 переносится на 3 единицы влево и на 2 единицы вверх, новая парабола имеет вершину вА. (-5 , -1) Б. (-5 , -5) С. (-1 , -3) Д. (-2 , -3) Вопросы 9Графики двух линейных уравнений a x + b y = c и b x — a y = c, где ни один из коэффициентов a, b, c не равен нулю,А.  параллельны параллельны Б. пересекаются в точке (0,0) С. пересекаются в двух точках Д. перпендикулярно Вопросы 10Графики двух уравнений y = a x 2 + b x + c и y = A x 2 + B x + C, такие, что a и A имеют разные знаки и что величины b 2 — 4 a c и B 2 — 4 A C равны отрицательный,А. пересекаются в двух точках Б. пересекаются в одной точке С. не пересекаются D. ничего из вышеперечисленного Вопросы 11Для x больше или равного нулю и меньше или равного 2 ?, sin x и cos x оба уменьшаются на интервалахА. (0 , ?/2) Б. (?/2, ?) С. (?, 3?/2) Д. (3 ? / 2 , 2 ?) Вопросы 12Три решения уравнения f (x) = 0 равны -2, 0 и 3. Следовательно, три решения уравнения f (x — 2) = 0 равныА. — 4, -2 и 1 Б.-2, 0 и 3 С. 4, 2 и 5 Д. 0, 2 и 5 Вопросы 13Три решения уравнения f (x) = 0 равны — 4, 8 и 11. Следовательно, три решения уравнения f (2 x) = 0 равныА.  — 2, 4 и 11/2 — 2, 4 и 11/2 Б. — 8, 16 и 22 С. — 4, 8 и 11 Д. 2, 19/2 и 7/2 Вопросы 14Школьный комитет состоит из 2 учителей и 4 учеников. Количество различных комитетов, которые могут быть сформированы из 5 преподавателей и 10 студентов, равноА. 10 Б. 15 С. 2100 д. 8 Вопросы 15Пять разных книг (A, B, C, D и E) должны быть расставлены на полке. Книги C и D должны располагаться первыми и вторыми, начиная справа от полки. Количество различных порядков, в которых могут быть расположены книги A, B и E, равноА. 5! Б. 3! С. 2! Д. 3! * 2! Вопросы 16Среднее значение набора данных равно 10, а его стандартное отклонение равно 1. Если мы добавим 5 к каждому значению данных, то среднее значение и стандартное отклонение станутA. среднее значение = 15, стандартное отклонение = 6 B. среднее = 10, стандартное отклонение = 6 C. среднее значение = 15, стандартное отклонение = 1 D.  среднее = 10, стандартное отклонение = 1 среднее = 10, стандартное отклонение = 1Вопросы 17Экзаменационные баллы всех 500 студентов были записаны, и было установлено, что эти баллы были распределены нормально. Если балл Джейн на 0,8 стандартного отклонения выше среднего, то сколько с точностью до единицы учащиеся набрали больше баллов, чем Джейн?А. 394 Б. 250 С. 400 Д. 106 Вопросы 18Если f(x) — нечетная функция, то | е (х) | являетсяА. нечетная функция B. четная функция C. ни нечетный, ни четный Д. четные и нечетные Вопросы 19Период | грех (3x) | являетсяА. 2 ? Б. 2 ? / 3 С. ? / 3 Д. 3 ? Вопросы 20Когда металлический шарикоподшипник помещается внутрь цилиндрического сосуда радиусом 2 см, высота воды внутри сосуда увеличивается на 0,6 см. Радиус шарикоподшипника с точностью до десятых долей сантиметраА. 1 см Б. 1,2 см С. 2 см Д. 0,6 см Вопросы 21Период 2 sin x cos x равенА.  4 ? 2 4 ? 2 Б. 2 ? С. 4 ? Д. ? Вопросы 22Вероятность того, что электронное устройство, произведенное компанией, не работает должным образом, равна 0,1. Если куплено 10 устройств, то вероятность с точностью до тысячной того, что 7 устройств будут исправно работать, равнаА. 0,057 Б. 0,478 С. 0,001 Д. 0 Ответы на вышеуказанные вопросы1б, 2в, 3г, 4а, 5в, 6б, 7г, 8а, 9г, 10в11б, 12г, 13а, 14в, 15б, 16в, 17д, 18б, 19в, 20б 21д, 22а. Дополнительные ссылки и ссылки на вопросы и задачи по математикематематические вопросы и задачи с подробными решениями. |
Объяснение ответов на тест ACT по математике 2021-22
перейти к содержанию Ниже приведены пояснения к полному тесту по математике ранее выпущенного ACT из бесплатного учебного пособия «Подготовка к тесту ACT» на 2021–2022 годы (форма 2176CPRE), доступного здесь для бесплатной загрузки в формате PDF.
Тест ACT Math, описанный ниже, начинается на странице 22 руководства (24 в PDF-файле). Другие объяснения ответов в этой серии статей:
- Объяснения ответов на английском языке из 2021-2022 ACT Practice Test
- Объяснения ответов по математике из практического теста ACT 2021–2022 гг. (эта статья)
- Чтение пояснений к ответам на практический тест ACT 2021-2022
- Объяснения научных ответов из практического теста ACT 2021–2022 гг.
- Письменные объяснения ответов из 2021-2022 ACT Practice Test
Когда вы закончите изучение этого официального тренировочного теста ACT, начните тренироваться с нашими собственными 10 полноценными тренировочными тестами ACT.
ACT Практический тест Математика Ответ Объяснение 2021-2022Вопрос 1 «бумага в банке» ответ E
Этот вопрос проверяет ваше понимание вероятности.
- В банке 15 листов бумаги.
 Восемь из этих частей меньше 9.
Восемь из этих частей меньше 9. - Вероятность вытягивания нужных фигур равна .
- Таким образом, вероятность равна .
Вопрос 2 «» ответ J
Этот вопрос проверяет ваше понимание работы с алгебраическими выражениями.
- Сначала мы добавляем подобные термины () и ()
- Тогда мы получим . Это правильный ответ.
Вопрос 3 «10 + 3(12 ÷ (3x)) » ответ 16
Этот вопрос проверяет ваше понимание упрощения выражения с помощью PEMDAS.
- Первый шаг — подставить x = 2.
- Это упростит уравнение до 10 + 3(12 ÷(3⋅2))
- Упрощая изнутри скобок, мы получили бы 10 + 3 (12 ÷(6))
- Что будет равно 10+3(2) = 10+6 = 16.
Вопрос 4 «⎪6 − 4⎪ − ⎪3 − 8⎪» ответ G
Этот вопрос проверяет ваше понимание упрощения выражений абсолютного значения.
- Прямые скобы | используются для указания абсолютного значения выражения между двумя скобками.

- Первым шагом будет упрощение двух выражений внутри прямых скобок. Это упростило бы уравнение до |2| – |-5|.
- Следующим шагом является вычисление абсолютного значения каждого члена. Это упростило бы выражение до 2 – 5.
- Наконец, выполнение окончательного вычитания даст ответ -3.
Вопрос 5 «(4c-3d)(3c+d)» ответ C
Этот вопрос проверяет наше понимание распределительного свойства.
- Для расчета мы начнем с умножения всех членов во второй скобке на член 4c. Это даст 4c(3c) + 4c(d). Это упростит до +4cd.
- Следующим шагом будет умножение всех слагаемых во второй скобке на слагаемое (-3d). Это даст -3d(3c) – 3d(d). Это упростит до .
- Объединяем члены из первого и второго шагов, получаем . Затем, комбинируя подобные термины, мы получаем выражение . Это окончательный ответ.
Вопрос 6 «Оценки учащихся» ответ F
Этот вопрос проверяет ваше понимание применения пропорций в постановке текстовых задач.
- Мы знаем, что есть 180 студентов, поэтому, если студенты получили пятерку, это будет означать, что 45 студентов получили пятерку.
- Мы также знаем, что учащиеся получили оценку B, так что это означает, что из 180 учащихся 60 получили оценку B.
- Следовательно, мы можем подсчитать количество студентов, получивших оценку C, вычитая из общего числа учащихся, получивших оценку A или B. Это можно рассчитать следующим образом: 180-45-60 = 75, .
- Таким образом, количество студентов, получивших оценку C за курс, равно 75.
Вопрос 7 «Skipper’s Pond» ответ B
Этот вопрос проверяет ваше понимание применения пропорций в постановке текстовых задач.
- Нам сказали, что уравнение для представления количества рыбы в пруду имеет вид .
- Следовательно, в 2006 году значение x равно 2006 – 2000 = 6.
- Подстановка этого значения x в уравнение оставит уравнение . Это означает, что на начало 2006 года в пруду было 192 рыбы.

Вопрос 8 «Скорость» ответ H
Этот вопрос проверяет ваше понимание скорости и расстояния.
- Поскольку мы знаем, что Маниш находился в 510 км от Батон-Руж в 8:00 и в 105 км от Батон-Руж в 13:00, мы можем сделать вывод, что Маниш преодолел за это время 510–105 км. Это 405 км.
- Время, необходимое для преодоления 405 км, составляет 5 часов, что является разницей между 13:00 и 8:00 утра.
- Основываясь на этом, мы могли бы рассчитать скорость, разделив 405 км на 5 часов, что дало бы скорость 81 км в час.
Вопрос 9 «треугольник с параллельными прямыми» ответ D
Этот вопрос проверяет ваше понимание подобных треугольников и параллельных прямых.
- Поскольку мы знаем, что это константа, а что параллельно, мы можем сказать, что ADE похож на ABC.
- Отсюда можно сделать вывод, что отношения сторон подобны.
- В частности, отношение равно отношению .
- Значение, которое упрощает .

- Мы знаем, что = = . Решая для получаем, что = 42.
Вопрос 10 «Катерина» ответ G
Этот вопрос проверяет ваше понимание скорости и того, как она рассчитывается.
- Катерина Среднее количество минут пробега одной мили можно рассчитать, разделив общее количество минут на общее количество пройденных миль.
- Общее количество минут требует от нас перевести часы в минуты, умножив их на 60. Выполнив этот шаг, мы получим, что количество пройденных минут равно 150 минутам.
- Общее количество миль равно 15.
- Среднее количество минут на милю можно рассчитать, разделив 150 на 15. Это даст 10 минут на милю.
Вопрос 11 «шарики» ответ B
Этот вопрос проверяет ваше понимание вероятности и алгебраических манипуляций.
- В настоящее время есть 8 красных шариков из 24 шариков. Если мы добавим x новых красных шариков, новое количество красных шариков будет 8 + x, а общее количество шариков будет 24 + x.

- Вероятность вытащить красный шарик равна . Мы знаем, что это равно .
- Приравняв два уравнения друг к другу, мы можем упростить их до уравнения 3 (24+x) = 5 (8 + x).
- Решая x, мы получаем 16, то есть количество дополнительных красных шариков, которые нужно добавить в мешок.
Вопрос 12 «средняя точка» ответ G
Этот вопрос проверяет ваше понимание вероятности и алгебраических манипуляций.
- Мы знаем, что середина равна (2,1).
- Из точки C (6,8) проходим 4 единицы влево и 7 единиц вниз, чтобы попасть в среднюю точку.
- Следовательно, чтобы попасть в точку D, нам нужно пройти такое же расстояние от средней точки.
- Таким образом, точка D будет представлена точкой (2-4, 1-7). Это равно (-2,-6).
Вопрос 13 «сверхурочные» ответ D
Этот вопрос проверяет ваше понимание текстовых задач и алгебраических манипуляций.
- Мы знаем, что за первые 40 часов Томас получает 15 долларов.

- После первых 40 часов Томас получает 15 долларов x 1,5 = 22,5 доллара.
- Поскольку Томас проработал 46 часов, его общая заработная плата до вычетов составляет 40 x 15 $ + 6 x 22,5 $ = 600 $ + 135 $ = 735 $.
- Поскольку 117 долларов вычитаются из суммы вычетов, сумма денег, которая остается у Томаса, составляет 735-117 долларов = 618 долларов.
Вопрос 14 «Свежие сладости» ответ J
Этот вопрос проверяет ваше понимание денежных выражений.
- За 2 поездки Жанель купила 3 сумки по 3 доллара за сумку и 4 сумки по 2,80 доллара за сумку.
- Сумма, которую она потратила, составила 9 долларов в понедельник и 11,20 доллара в среду, всего 20,20 доллара.
- Если бы она купила сразу 7 мешков, то заплатила бы 2,60 доллара за мешок, что в сумме составило бы 18,20 доллара.
- Она бы сэкономила 2 доллара.
Вопрос 15 «3% от 4,14 x » ответ A
Этот вопрос проверяет ваше понимание упрощения выражений с процентами.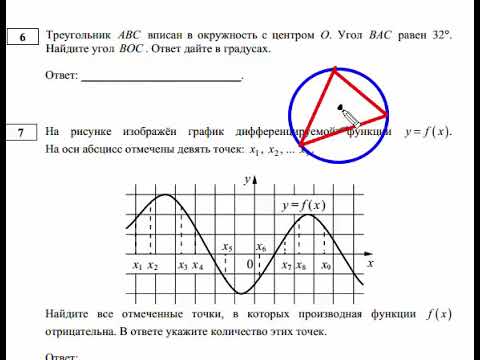
- 3% от 4,14 х = 0,03 х 4,14 х = 3 х 4,14 х 100 = 12,42 х 100 = 1242.
Вопрос 16 «значение x» ответ K
Этот вопрос проверяет ваше понимание решения алгебраических уравнений.
- Чтобы найти значение x, удовлетворяющее уравнению -3 (4x – 5) = 2 (1 – 5x), мы начнем с распределения значений в обеих скобках.
- В итоге мы получаем уравнение -12x + 15 = 2 – 10x. Комбинируя подобные члены, мы получаем 13 = 2x.
- х = .
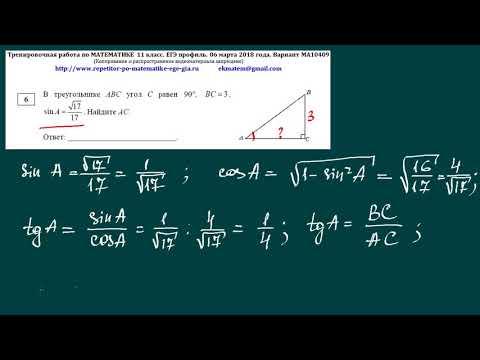
Вопрос 17 «прямоугольный треугольник» ответ D
Этот вопрос проверяет ваше понимание синуса угла в треугольнике.
- Sin A = .
- Грех А =
Вопрос 18 « » ответ J
Этот вопрос проверяет ваше понимание упрощающих показателей.
- Начнем с извлечения кубического корня из дроби, чтобы исключить 3 из показателя степени. Делая это, мы получаем термин: .
- Чтобы устранить отрицательный знак в показателе степени, возьмем обратную дробь.
 Мы заканчиваем с термином .
Мы заканчиваем с термином . - Возведя в квадрат числитель и знаменатель, мы получим значение: .
Вопрос 19 «Прогулка Лото» ответ A
Этот вопрос проверяет ваше понимание теоремы Пифагора.
- Суммируя количество ярдов, которые Лото прошел на восток и север отдельно, мы получаем 20 ярдов на восток и 11 ярдов на север.
- Чтобы найти расстояние, которое прошел бы Лото, если бы он мог идти прямо, мы применяем теорему Пифагора, чтобы получить уравнение:
- Находя x, мы получаем x = 22,83.
- Общая разница в расстоянии, которое Лото сэкономил бы, составляет 20 + 11 – 22,83 = 8,17 ярда, что составляет примерно 8 ярдов.
Вопрос 20 «стандартная оценка» ответ F
Этот вопрос проверяет ваше понимание решения алгебраических уравнений.
- Мы знаем, что z = 2 = .
- Решая x, мы получаем x = 90.
Вопрос 21 «круг» ответ E
Этот вопрос проверяет ваше понимание треугольников в окружении круга.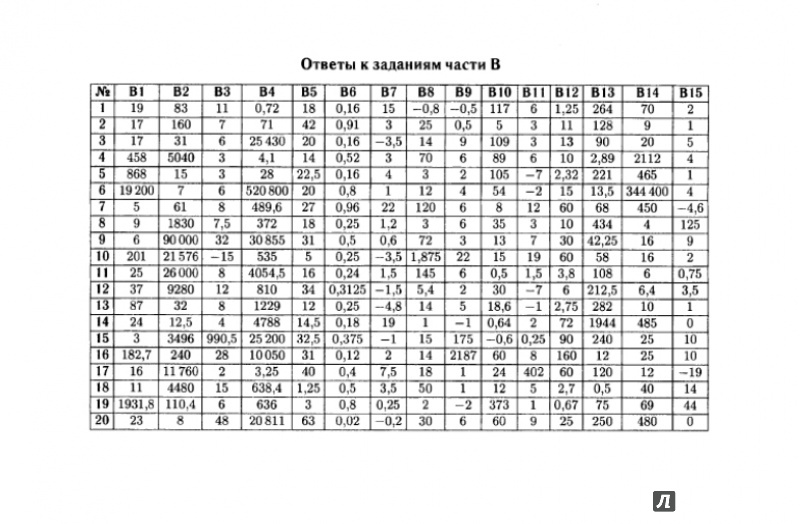
- Подходя к этому, мы можем начать с рассмотрения вариантов ответа и проверки их наличия в круге с центром в точке O.
- Треугольник АВО остроугольный. Поскольку это радиус, а также радиус, мы знаем, что A = B. Поскольку мы знаем, что AOB равен 60 градусам, мы можем сделать вывод, что A и B оба равны 60 градусам.
- Следовательно, АОВ также является равносторонним треугольником.
- Поскольку мы знаем, что и оба радиуса окружности, мы можем заключить, что DOC является равнобедренным треугольником. DOC также является прямоугольным треугольником, поскольку угол DOC равен 90 градусам.
- Следовательно, единственный треугольник, который не показан на рисунке, — это разносторонний треугольник.
Вопрос 22 «наклон» ответ G.
Этот вопрос проверяет ваше понимание параллельных линий и наклонов.
- Если линия параллельна x + 5y = 9, мы можем заключить, что они имеют одинаковый наклон.
- Решая уравнение относительно y, получаем, y = .
 Итак, наклон есть.
Итак, наклон есть.
Вопрос 23 «y = » ответ E
Этот вопрос проверяет ваше понимание решения уравнений.
- Поскольку мы знаем, что x > 1, мы знаем, что y не может быть отрицательным или равным 0. Следовательно, единственным возможным вариантом ответа является 0,9.и 1.9
- Заглушка 0,9 для y; мы получаем x = – 9. Поскольку x должен быть больше 1, мы можем сделать вывод, что для y работает только 1,9.
- Подставляя 1.9 вместо y, мы получаем x = 2,111. Поскольку x больше 1, мы можем сделать вывод, что это правильный ответ.
Вопрос 24 «все положительные целые числа» ответ H.
Этот вопрос проверяет ваше понимание простых делителей.
- Чтобы число делилось на 15 и 35, оно должно быть кратно обоим делителям числа.
- 15 имеет простые делители 5 и 3. 35 имеет простые делители 5 и 7.
- Наименьшее общее кратное 5 x 3 x 7. Это 105.
Вопрос 25 «треугольник ABC» ответ D
Этот вопрос проверяет ваше понимание углов.
- Если = , то B = C. Поскольку угол A равен 58 градусам, мы можем вычислить сумму B и C, вычитая 58 из 180.
- 180 – 58 = 122 градуса. Поскольку B равно C, оба угла равны 61 градусу.
Вопрос 26 «Поверхность Земли» ответ G
Этот вопрос проверяет ваше понимание вероятности.
- Чтобы найти вероятность приземления на воду, мы должны найти площадь, покрытую водой, и разделить это значение на общую площадь на поверхности Земли.
- Искомое уравнение должно быть P = . Вынесение на множители и деление числителя и знаменателя на дает уравнение .
- Р =
Вопрос 27 «статистические тесты» ответ E
Этот вопрос проверяет ваше понимание среднего значения, медианы и формы ряда чисел.
- До 8-го теста среднее, медиана и мода Джамала были 79, 80 и 80 соответственно.
- После того, как он набрал 90 баллов в 8-м тесте, среднее значение Джамала составило 80,13. Его медиана по-прежнему была 80, а его мода по-прежнему была 80.
 Следовательно, единственное значение, которое изменилось, было его средним значением, которое было больше.
Следовательно, единственное значение, которое изменилось, было его средним значением, которое было больше.
Вопрос 28 «сплошная прямоугольная призма» ответ H
Этот вопрос проверяет ваше понимание трехмерных фигур.
- Сплошная прямоугольная призма имеет стороны длиной 5, 6 и 7 единиц. Следовательно, всего 210 кубов.
- Так как черные кубики и белые кубики чередуются одинаково, мы можем сделать вывод, что половина кубиков черные, а половина белые.
- Половина от 210 равна 105.
Вопрос 29 «Квадрат ABCD» ответ C
Этот вопрос проверяет вашу способность вычислять площади квадратов и прямоугольников.
- Если одна сторона квадрата ABCD имеет длину 12 метров, то площадь квадрата равна 144 .
- Поскольку мы знаем, что ширина прямоугольника составляет 8 метров, разделив 144 на 8 метров, мы получим длину 18 метров.
Вопрос 30 «среднее», ответ H
Этот вопрос проверяет ваше понимание средних значений ряда чисел.
- Мы знаем, что среднее чисел w, x, y и z равно 92,0. Следовательно, сумма w, x, y и z может быть представлена уравнением. ш + х + у + г = 4 х 92 = 368,
- Мы знаем, что z равно 40, поэтому сумма w, x и y равна 368 – 40 = 328.
- Мы также знаем, что 4-е число нового списка равно 48, поэтому сумма чисел нового списка равна выражению w + x + y + 48. Подставим 328 вместо суммы w, x и y дает выражение 328 + 48 = 376,
- Разделив 376 на 4, мы получим среднее значение 94,0.
Вопрос 31 «вектор» ответ B
Этот вопрос проверяет ваше понимание скорости и векторов.
- Поскольку вектор j представляет 1 милю в час на север, -j будет представлять 1 милю в час на юг.
- Скорость Марии составляет 12 миль в час к югу, что соответствует -12j.
Вопрос 32 « стаканы» ответ К.
Этот вопрос проверяет ваше понимание сложения дробей.
- Для начала добавим объем воды в каждый из стаканов.

- Чтобы равномерно распределить эту воду по 4 стаканам, мы разделим ее на 4. В результате каждый стакан будет полным.
Вопрос 33 «ковровая плитка» ответ D
Этот вопрос проверяет ваше понимание площади поверхности.
- Для начала мы конвертируем длину и ширину пола его гостиной в дюймы. футы = 100 дюймов. Аналогично, 10 футов = 120 дюймов.
- Следовательно, площадь пола гостиной в квадратных дюймах составляет 100 дюймов x 120 дюймов = 12 000 .
- Каждая ковровая плитка имеет площадь 20 дюймов x 20 дюймов = 400 . Разделив площадь пола гостиной на 400 каждой ковровой плитки, мы получим 30 ковровых плиток, необходимых для покрытия этой площади.
Вопрос 34 «Координатная плоскость» ответ F
Этот вопрос проверяет ваше понимание уравнения окружности.
- Окружность с центром () и радиусом r должна быть нанесена на карту уравнением .
- Подставив соответствующие () = (8,5) и r = 9 в уравнение, мы получим ответ .

Вопрос 35 «Общая стоимость» ответ E
Этот вопрос проверяет ваше понимание применения алгебры к текстовым задачам.
- Поскольку каждый тест Yq стоит 2500 долларов, а было проведено 1000 тестов, стоимость теста Yq составила 2 500 000 долларов.
- Аналогичным образом, каждый тест Sam77 стоит 50 груш, и было проведено 1000 тестов, общая стоимость теста Sam77 составила 50 000 долларов.
- Сложение этих двух чисел дает общую стоимость 2 550 000 долларов США.
Вопрос 36 «процент добровольцев» ответ J
Этот вопрос проверяет ваше понимание процентов.
- Количество людей, являющихся носителями гена Yq77, можно рассчитать, сложив всех людей, у которых был положительный тест на Yq. Это равно 590 + 25 = 615.
- Так как всего было протестировано 1000 человек, или 61,5% носителей гена Yq77.
Вопрос 37 «сколько добровольцев» ответ C
Этот вопрос проверяет ваше понимание таблиц.
- Чтобы подсчитать, сколько добровольцев получили неверный результат теста Sam77, мы должны сложить людей, у которых был отрицательный результат теста Sam77, но положительный тест Yq, и людей, у которых был положительный тест Sam77, но отрицательный тест Yq. .
- Эти два числа равны 25 и 10 соответственно, поэтому общее количество добровольцев, получивших неправильный результат теста Sam77, равно 25 + 10 = 35.
Вопрос 38 «НЕ обладает Yq77» ответ F
Этот вопрос проверяет ваше понимание вероятности.
- Количество добровольцев с положительным результатом теста Sam77 составило 590 + 10 = 600.
- Из этих добровольцев только у 10 не было гена Yq77.
- Следовательно, вероятность равна .
Вопрос 39 «Матрицы» ответ B
Этот вопрос проверяет ваше понимание матричных манипуляций.
- Чтобы вычислить произведение X и Y, мы должны перемножить матрицы.
- Это можно сделать следующим образом.

Вопрос 40 «симметрия» ответ F
Этот вопрос проверяет ваше понимание линий симметрии.
- Разносторонний треугольник — это треугольник, у которого все три стороны имеют разную длину. Это не будет иметь вертикальной линии симметрии.
- Линия будет иметь вертикальную линию симметрии. Квадрат будет иметь вертикальную линию симметрии. Пятиугольник будет иметь вертикальную линию симметрии. Параллелограмм будет иметь вертикальную линию симметрии.
Вопрос 41 «» ответ A.
Этот вопрос проверяет ваше понимание решения квадратного уравнения.
- Чтобы решить это уравнение, мы можем начать с вычитания 15 из обеих частей. Получаем уравнение.
- Мы можем факторизовать это, чтобы получить (6x+5)(4x-3) = 0. Полагая 6x+5 = 0 и 4x -3 = 0, мы получаем два решения для этого уравнения как и .
- Большее из этих двух решений равно .
Вопрос 42 «» ответ J
Этот вопрос проверяет ваше понимание синуса и косинуса обычных углов./15df8669cdd3689.s.siteapi.org/img/969066a8e31101484960ddf7ce3e8084e1219d1b.jpg)
- Чтобы решить эту проблему, мы должны знать, что . Следовательно, мы можем использовать это, чтобы заменить на .
- Точно так же мы можем заменить из второго члена на .
- Следовательно, исходное уравнение упрощается до = 1.
- Из вариантов ответа единственным, значение которого = 1, является .
Вопрос 43 «площадь круга» ответ D
Этот вопрос проверяет ваше понимание окружности и площади круга.
- Мы знаем, что длина окружности = . Решая относительно r, получаем r = 6, .
- Площадь круга . Подставляя r = 6, мы получаем площадь как .
Вопрос 44 «Смесь растворителей», ответ G.
Этот вопрос проверяет ваше понимание процентных соотношений и смесей.
- Мы знаем, что из 25 литров 40% растворителя и 60% воды. Отсюда можно сделать вывод, что 0,40 х 25 литров растворителя = 10 литров.
- Таким образом, если добавить x литров растворителя, количество растворителя будет равно 10 + x.
 Кроме того, новая смесь будет иметь объем 25 + х.
Кроме того, новая смесь будет иметь объем 25 + х. - Таким образом, процент растворителя в новой смеси будет равен .
- Поскольку мы знаем, что это 50% или 0,50, мы можем приравнять эти два значения друг к другу и найти x.
- Упрощая, получаем 10 + x = (25 + x )(0,5). Дальнейшее упрощение показывает нам, что 0,5x = 2,5, поэтому x = 5, .
Вопрос 45 «» ответ E
Этот вопрос проверяет ваше понимание упрощения выражений с дробями.
- Чтобы упростить это уравнение, мы находим общее кратное двух знаменателей, которое будет .
- Следовательно, нам пришлось бы умножать числитель первого члена на (x-y), а числитель второго члена на (x+y).
- Новое выражение после объединения двух терминов будет .
- Разлагая на множители числитель и знаменатель, получаем .
Вопрос 46 «Реклама на странице» ответ F.
Этот вопрос проверяет ваше понимание решения текстовых задач с помощью алгебры.
- Если Карлос продал c рекламных объявлений, Мэри продала 2c рекламных объявлений, а Джеймс продал 6c рекламных объявлений.
- Всего было продано c + 2c + 6c = 9c рекламных объявлений.
- Следовательно, Карлос продал все рекламные объявления.
Вопрос 47 «цветочный магазин» ответ D
Этот вопрос проверяет ваше понимание перестановок.
- Для первого места у Эмили есть 6 растений на выбор.
- После посадки первого растения у Эмили остается только 5 растений на выбор для второго места.
- Наконец, после посадки первых двух растений у Эмили остается только 4 растения на выбор для третьего места.
- Умножая эти варианты, мы получаем 6 х 5 х 4 = 120 различных вариантов расположения растений.
Вопрос 48 «Квадратичная функция f » ответ G
Этот вопрос проверяет ваше понимание площади треугольника.
- Чтобы вычислить площадь мы начнем с использования формулы площади треугольника = .

- Исходя из этого, основанием треугольника является расстояние между точкой М и точкой Р, равное 6а-2а = 4а.
- Высота треугольника — это расстояние от точки Q до отрезка MP, равное 5b.
- Следовательно, площадь равна .
Вопрос 49 «Точка M», ответ D
Этот вопрос проверяет ваше понимание наклона линии на координатной плоскости.
- Наклон может быть представлен уравнением .
- Мы знаем, что числитель отрицательный, потому что точка Q имеет меньшее значение y, чем точка M.
- По мере перемещения точки Q вправо разница увеличивается.
- Следовательно, наклон будет отрицательным, но будет увеличиваться по мере увеличения значения Q.
Вопрос 50 «f(5a)» ответ K
Этот вопрос проверяет ваше понимание функции, построенной на координатной плоскости.
- Чтобы найти значение f(5a) , мы смотрим на квадратичную функцию и находим, где она пересекает линию x = 5 a.

- Глядя на кривую, мы видим, что это происходит на 8b, что является правильным ответом.
Вопрос 51 «Присяжные заседатели», ответ D
Этот вопрос проверяет ваше понимание дробей и десятичных знаков.
- Мы знаем, что если мы пригласим x человек, то на самом деле появится только 0,4x людей.
- Из них одна треть освобождена, так что две трети остаются. В частности, из первоначально приглашенных x человек остаются.
- Мы знаем, что это выражение должно равняться 60 человекам для состава жюри. Отсюда получаем уравнение.
- Находя x, получаем x = 225 человек, которых необходимо вызвать.
Вопрос 52 «275-я цифра», ответ K
Этот вопрос проверяет ваше понимание повторяющихся цифр в десятичных дробях.
- Поскольку мы знаем, что десятичная дробь 0,6295 повторяется через каждые 4 цифры, мы должны разделить 275 на 4.
- Разделив 275 на 4, мы получим 68 с остатком 3.

- Это будет означать, что 272-я цифра будет 5. Тогда следующие три цифры будут 6, 2 и 9 в этом порядке.
- Исходя из этого, 275-я цифра будет 9..
Вопрос 53 « » ответ A
Этот вопрос проверяет ваше понимание факторизации квадратичной функции.
- Поскольку мы знаем, что , мы знаем, что решение f(x) можно найти, разложив f(x). f (х) = (х + 2) (х-2).
- Следовательно, два решения для f(x) равны x = 2 и x = -2.
- Поскольку мы знаем, что эти два решения x делают f(x) равным 0, мы можем положить г(х) равны этим значениям.
- Таким образом, мы получаем два уравнения для g(x). х +3 = 2 и х + 3 = -2.
- Решив оба уравнения относительно x, мы получим x = -1 и -5.
Вопрос 54 «p и n» ответ G
Этот вопрос проверяет ваше понимание целых чисел и абсолютных величин.
- Поскольку мы знаем, что p — положительное число, n — отрицательное число и |p| > |n|, мы можем присвоить значения как p, так и n, которые удовлетворяют этим условиям.

- В частности, мы можем назначить p = 5 и n = -3. Тогда мы сможем решить все уравнения;
- ;
- ;
- Из этих вариантов ответа наибольшее выражение
Вопрос 55 « » ответ B
Этот вопрос проверяет ваше понимание мнимых чисел и вычислений с использованием i .
- Начиная с , , затем , , и .
- Подставляя эти значения в уравнение, мы получаем
- . Упрощая это уравнение, мы имеем, что равно -1.
Вопрос 56 «координатная плоскость» ответ K
Этот вопрос проверяет ваше понимание наклонов и линий на координатной плоскости.
- Первое уравнение имеет вид x + 2y ≤ 6. Преобразовав это уравнение для решения для y, мы получим y ≤ -0,5x + 3. Это будет означать, что наклон линии отрицательный, и заштрихованная область должна быть ниже этой линии.
- Из всех вариантов ответа только F и K имеют линию с отрицательным наклоном и заштрихованную область под линией.

- Второе уравнение . Преобразовав это уравнение и разделив на 3, мы получим уравнение .
- Чтобы сделать выбор между F и K, мы можем найти две точки пересечения y окружности, и если они лежат под прямой y ≤ -0,5x + 3, мы знаем, что ответ равен K.
- Две точки пересечения y окружности можно вычислить, установив x = 0 в уравнении окружности.
- В итоге мы получаем уравнение , поэтому y = 2 или y = -2 .
- Подставляя положительную точку пересечения оси y (x,y) = (0,2) в уравнение прямой, мы получаем 2 ≤ -0,5(0) + 3. Упрощая, получаем 2 ≤ 3, что равно верно, поэтому правильный ответ К.
Вопрос 57 «действительные числа» ответ D
Этот вопрос проверяет ваше понимание вашего понимания умножения и деления на 0.
- Поскольку , мы можем заключить, что d = 0,
- Поскольку abc = d, мы знаем, что abc = 0.
- Поскольку ac = 1, мы знаем, что b(1) = 0. Итак, b = 0.
Вопрос 58 « функция косинуса» ответ K
Этот вопрос проверяет ваше понимание функции косинуса и функций.
- Мы знаем, что точка пересечения по оси y равна 3, значит, если x = 0, y должно быть равно 3. Поскольку cos(0) = 1, мы знаем, что константа, умножающая косинус, должна быть равна 3.
- Мы также знаем, что , по графику. Подставляя все значения x, мы получаем y = 3 cos(2x) как решение, которое дает y равное -3.
Вопрос 59 «летающий змей» ответ B
Этот вопрос проверяет ваше понимание треугольников, их сторон и углов.
- В показанном треугольнике недостающий угол равен 60 градусам.
- Тогда мы могли бы составить такое уравнение, что . Решив это для длины строки, мы получим = длина строки. Подставляя значения и , мы можем упростить до .
Вопрос 60 «издатель» ответ F
Этот вопрос проверяет ваше понимание использования алгебры для решения текстовых задач.
- Мы знаем, что издатель берет 15 долларов за первую книгу и 12 долларов за каждую дополнительную копию.


 Ответы предоставлены и расположены в нижней части страницы. Вопросы были разработаны, чтобы проверить глубокое понимание математических концепций. Также даны подробные пояснения и решения этих вопросов.
Ответы предоставлены и расположены в нижней части страницы. Вопросы были разработаны, чтобы проверить глубокое понимание математических концепций. Также даны подробные пояснения и решения этих вопросов. Восемь из этих частей меньше 9.
Восемь из этих частей меньше 9.
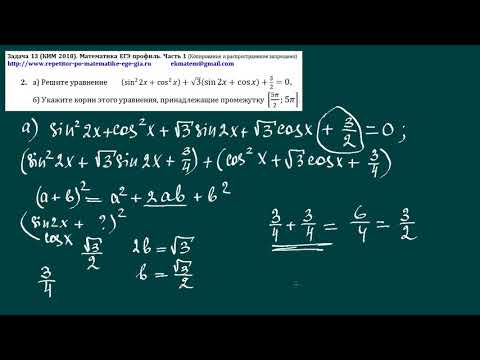

 Мы заканчиваем с термином .
Мы заканчиваем с термином . Итак, наклон есть.
Итак, наклон есть. Следовательно, единственное значение, которое изменилось, было его средним значением, которое было больше.
Следовательно, единственное значение, которое изменилось, было его средним значением, которое было больше.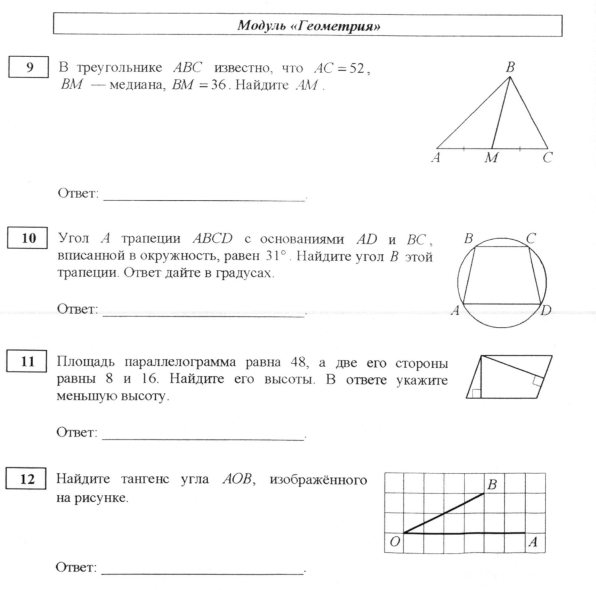


 Кроме того, новая смесь будет иметь объем 25 + х.
Кроме того, новая смесь будет иметь объем 25 + х.




Leave A Comment