Задачи средняя линия трапеции 9 класс: Решение задач по теме «Средняя линия трапеции»

Решение задач по теме «Средняя линия трапеции»

Задачи по теме: средняя линия трапеции

9 класс Вариант 1

1) В равнобедренной трапеции средняя линия равна 10, а периметр 36 см. Найдите боковые стороны этой трапеции

2) В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 4.

3) В равнобедренной трапеции острые углы , боковая сторона 10 см, а большее основание 15 см. Найдите меньшее основание и среднюю линию трапеции.

Задачи по теме: средняя линия трапеции

9 класс Вариант 2

1) Средняя линия трапеции равна 30 см, а одно из оснований в два раза меньше другого. Найдите основания трапеции.

2) В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 6.

3) В равнобедренной трапеции острые углы 45, расстояние между основаниями 4 см, а меньшее основание 5см. Найдите большее основание и среднюю линию трапеции.

Задачи по теме: средняя линия трапеции

9 класс Вариант 3

1) Разность оснований трапеции равна 8 см, а средняя линия равна 20 см. Найдите основания этой трапеции.

2) В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 10, а меньшее основание BC равно 4.

3) В трапеции ABCD AD, Найдите среднюю линию трапеции, если известно, что ее диагональ перпендикулярна боковой стороне.

Задачи по теме: средняя линия трапеции

9 класс Вариант 4

1) Боковые стороны равнобедренной трапеции равны по 15 см, а средняя линия этой трапеции 25 см. Найдите периметр этой трапеции.

2) В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 12, а меньшее основание BC равно 4.

3) В трапеции MHKP MP, Найдите среднюю линию трапеции, если известно, что ее диагональ перпендикулярна боковой стороне.

Задачи по теме: средняя линия трапеции

9 класс Вариант 1

1) В равнобедренной трапеции средняя линия равна 10, а периметр 36 см. Найдите боковые стороны этой трапеции

Задачи по теме: средняя линия трапеции

9 класс Вариант 2

Задачи по теме: средняя линия трапеции

9 класс

Вариант 3

1) Разность оснований трапеции равна 8 см, а средняя линия равна 20 см. Найдите основания этой трапеции.

Задачи по теме: средняя линия трапеции

9 класс

Вариант 4

Средняя линия трапеции

Урок 10. Геометрия 9 класс ФГОС

Данный урок познакомит учащихся с определением средней линии трапеции, а так же будут проведены доказательства её свойств. На протяжении урока рассматриваются примеры решения разнообразных задач, что позволит учащимся успешно усвоить новый материал.

Конспект урока «Средняя линия трапеции»

Вспомним, какую фигуру называют трапецией.

Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Параллельные стороны трапеции называют её основаниями, а две другие — боковыми сторонами.

Известны два частных случая трапеции. Равнобокая трапеция, у которой боковые стороны равны. И прямоугольная трапеция, у которой один из углов прямой.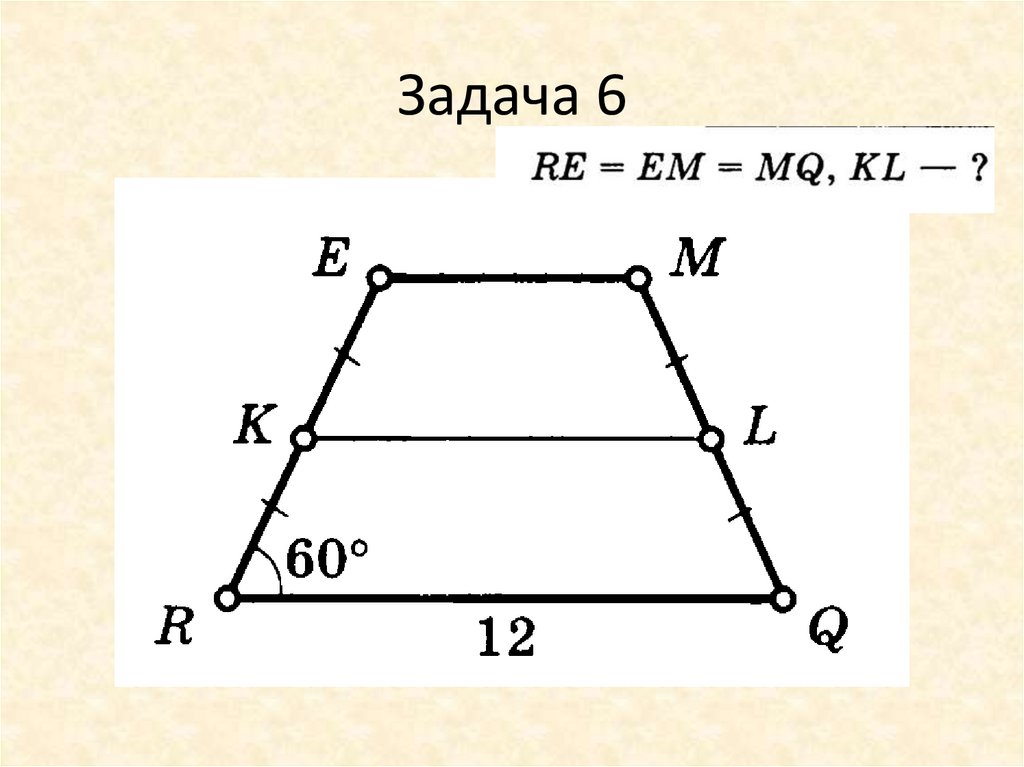

К слову, у такой трапеции будет два прямых угла.

Повторив определение трапеции, введём понятие средней линии трапеции.

Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон.

Изобразим средние линии трапеций изображённых на рисунке.

Для этого сначала найдём их боковые стороны. Далее отметим точками их середины. Ну, а потом проведем средние линии.

Выполним задание. Пользуясь данными рисунков, указать пункты, в которых является средней линией трапеции .

На первом рисунке точка М не является серединой боковой стороны AB, поэтому МN не является средней линией трапеции.

На втором рисунке точки М и N — середины сторон BC и AD, но они являются основаниями трапеции. А по определению средняя линия трапеции соединяет середины боковых сторон. Значит, в данном случае МN не является средней линией.

На третьем рисунке видим, что точки М и N — середины боковых сторон. Причём по рисунку понятно, что эта трапеция — равнобокая.

Так получаем, что МN в данном случае — средняя линия трапеции ABCD.

Посмотрев на следующий рисунок, не трудно заметить, что МN соединяет середину одного из оснований и середину одной из боковых сторон, а не середины боковых сторон. Поэтому МN не является средней линией.

На рисунке под номером 5 точки М и N середины боковых сторон АB и CD трапеции ABCD. Значит, МN — её средняя линия.

В последнем случае точки М и N не поровну делят боковые стороны трапеции, поэтому МN не является её средней линией.

Мы получили, что только на рисунках под номерами 3 и 5 изображены средние линии трапеции.

Как и средняя линия треугольника, средняя линия трапеции обладает определёнными свойствами.

Теорема. Средняя линия трапеции параллельна основаниям и равна их полусумме.

Доказательство.

Что и требовалось доказать.

Выполним задание, где, пользуясь этой теоремой и данными рисунков, найдём длины средних линий трапеций.

Длина средней линии трапеции равна полусумме оснований.

На рисунке а известны длины оснований. Поэтому не составит никакого труда найти, что .

Перейдём к рисунку б.

Известен периметр трапеции, тогда можем записать,

В последнем случае также дан периметр трапеции и известны боковые стороны.

Записав периметр через стороны, и, подставив известные значения, можем выразить сумму оснований.

Задача. В трапеции найти длины оснований и , если в два раза больше и длина средней линии равна .

Решение.

Ответ: мм, мм.

Задача. В прямоугольной трапеции . Найти длину средней линии , если , а угол .

Решение.

Ответ: .

Подведём итоги нашего урока.

Сегодня мы познакомились с понятием средней линии трапеции. Это отрезок, соединяющий середины её боковых сторон.

При этом мы выяснили, что средняя линия трапеции обладает следующими свойствами: она параллельна основаниям трапеции и равна их полусумме.

Так же мы рассмотрели примеры применения этих знаний при решении задач.

Предыдущий урок 9 Применение векторов к решению задач

Следующий урок 11 Разложение вектора по двум неколлинеарным векторам

Получите полный комплект видеоуроков, тестов и презентаций Геометрия 9 класс ФГОС

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Рабочий лист для урока: Теорема о среднем сегменте трапеции | Нагва

Начать практику

В этом задании мы потренируемся находить неизвестные длины трапеций, используя теорему о середине трапеции.

Q1:

Предположим, что 𝐴𝐵=128 и 𝑋𝑌=95. Что такое 𝐶𝐷?

Q2:

Если 𝐵𝐴=24 см и 𝐷𝐶=26 см, найдите длину 𝐾𝐹.

A𝐾𝐹=50см
B𝐾𝐹=100см
C𝐾𝐹=312см
D𝐾𝐹=24,98см
E𝐾𝐹=25см

Q3:

В трапеции 𝐴𝐵𝐶𝐷 где 𝐴𝐷⫽𝐵𝐶, точка 𝑋 — середина 𝐴𝐵, 𝑌 — середина 𝐷𝐶, и 𝑋𝑌=27см. Площадь трапеции 513 см

2 и 𝐵𝐶=29см.

Найдите длину 𝐴𝐷 и перпендикулярное расстояние между 𝐴𝐷 и 𝐵𝐶.

A𝐴𝐷=25 см, расстояние 19 см
B𝐴𝐷=83 см, расстояние 17,7 см
C𝐴𝐷=25 см, расстояние 20,5 см
D𝐴𝐷=83см, расстояние 19см
E𝐴𝐷=83 см, расстояние 6,2 см

Q4:

Если площадь трапеции 1377 см ² , а его высота 51 см, найдите длину его среднего основания.

Q5:

Верно или неверно: Средняя линия трапеции — это линия, пересекающая любую точку одна нога до середины другой ноги; его длина равна половине суммы длин двух оснований трапеции.

AИстинно
BЛожь

Q6:

𝐴𝐵𝐶𝐷 — трапеция, где 𝐴𝐵∥𝐶𝐷. 𝑋𝑌 соединяет середины ног 𝐴𝐷 и 𝐵𝐶. Если 𝐴𝐵=7𝑥+15, 𝐶𝐷=2𝑥+4, и 𝑋𝑌=23, найдите значение 𝑥.

А3
В13
С49
Д94
Е18

Q7:

Какая из следующих формул является правильной для измерения длины 𝑋𝑌 в показанной трапеции, используя теорему о середине трапеции?

А𝐶𝐷=𝑋𝑌+𝐴𝐵2
B𝑋𝑌=𝐶𝐷+𝐴𝐵2
C𝑋𝑌=𝐶𝐷+𝐴𝐵
Д𝐴𝐵=𝑋𝑌+𝐶𝐷
E𝐴𝐵=𝑋𝑌+𝐶𝐷2

Q8:

На рисунке 𝐿𝐻 — середина трапеции 𝐹𝐺𝐽𝐾. Какова ценность 𝑥?

Q9:

Найдите длину среднего основания трапеции, параллельные основания которой равны 107 см и 246 см.

Nagwa использует файлы cookie, чтобы обеспечить вам максимальное удобство на нашем веб-сайте. Узнайте больше о нашей Политике конфиденциальности.

DLL3 МАТЕМАТИКА 9 НЕДЕЛЯ-.docx

1 из 3

Верхний обрезанный слайд

Скачать для чтения в автономном режиме

Образование 9000 4

математика

DLL3 MATH 9 WEEK-.docx

ЕЖЕДНЕВНО ЖУРНАЛ УРОКА Школа SAN AGUSTIN INTEGRATED SCHOOL 9 класс Учитель ANGELA CAMILLE P. CARIAGA Предмет Математика Дата и время 25-29 ноября 2019 г. (10:00-11:00) ЧЕТВЕРТЬ ТРЕТЬЯ I. ЦЕЛИ понедельник вторник среда Четверг Пятница A. Стандарты содержания Учащийся демонстрирует понимание ключевых понятий параллелограммов и подобия треугольников. B. Цель выполнения Учащийся способен исследовать, анализировать и решать задачи, связанные с параллелограммами и подобием треугольников, посредством соответствующего и точного представления. C. Учебные компетенции/цели (Напишите код LC для каждого) Учащийся доказывает теоремы о трапециях и воздушных змеях. (М9ГЭ-IIId-2) Напомним определение трапеции и ее части. Докажите и примените теоремы о трапециях и воздушных змеях. Оцените теоремы о воздушных змеях в реальной жизни. II.СОДЕРЖАНИЕ (предмет) Теоремы о трапеции Теоремы о трапеции Теоремы о трапеции Теоремы о трапеции ВИКТОРИНА НА НЕДЕЛЮ III. ОБРАЗОВАТЕЛЬНЫЕ РЕСУРСЫ А. Ссылки 1. Страницы руководства для учителя TG МАТЕМАТИКА 9, стр. 217-218 TG МАТЕМАТИКА 9, стр. 218-219 TG МАТЕМАТИКА 9, стр. 219-220 TG МАТЕМАТИКА 9, стр. 216 – 217 TG МАТЕМАТИКА 9, стр. 211-217 2. Страницы материалов для учащихся LM MATH 9, стр. 330-331 LM MATH 9, стр. 331-334 LM MATH 9, стр. 335-336 LM MATH 9, стр. 329-331 LM MATH 9, стр. 311-329 3. Страницы учебника 4. Дополнительные материалы от LRDMS B. Другие учебные ресурсы Интернет/наглядные пособия Интернет/наглядные пособия Интернет/наглядные пособия Интернет/наглядные пособия IV. ПРОЦЕДУРЫ Подготовительные мероприятия 1. Молитва 2. Посещаемость/задание 3. Управление классом Подготовительные мероприятия 1. Молитва 2. Посещаемость/задание 3. Управление классом Подготовительные мероприятия 1. Молитва 2. Посещаемость/задание 3. Управление классом Подготовительные мероприятия 4. Молитва 5. Посещаемость/задание 6. Управление классом Подготовительные мероприятия 1.Молитва 2.Посещаемость/задание 3.Управление классом A. Обзор прошлого урока или презентация новый урок Предварительная деятельность: «4 ФОТО 1 СЛОВО» Предварительная деятельность Предварительная деятельность: АНАГРАММА ВЫПОЛНЯЕМЫЕ ЗАДАЧИ B. Установление цели нового урок Задание 1. Что за ловушка! Материалы для учащихся, с. 330 1. Какова форма свободного бросить переулок выше? 2. Опишите углы внутри 4- двусторонняя фигура 3.Какие стороны фигуры появляются быть параллельным? Конгруэнтны? Вы уже были в Пикниковая роща? Вы знали что простой воздушный змей прилетел на Picnic Grove поделился свойства геометрического фигура называется воздушный змей? C. Представление примеров/примеров новый урок Занятие 2. ДАВАЙТЕ ДОКАЗАТЬ! Материал для учащихся, п. 330 – 331 Обсуждение урока через показательные примеры. (доказательство) Обсуждение урока на наглядном примере с объяснением,
Обсуждение новых концепций и практика новые навыки №1. Мероприятие 3. Определите меры, указанные переменными а, б и в. Иллюстративные примеры Используйте коррекцию в два столбца, чтобы ответить на активность. Дано: Кайт ВЕРЕВКА Докажите: площадь кайта ROPE = ½ (ОЕ)(ПР) D. Обсуждение новых концепций и отработка новых навыков №2 Анализ Анализ Анализ E. Развитие мастерства (приводит к Формирующее оценивание 3.) Деятельность 4. Нарисуйте трапецию с данным меры. База 1 = 11 м База 2 = х Медиана = 15 м Базовые углы = 95° и 88° Найдите меры отрезка x и углы y и z. ТРАП представляет собой равнобедренную трапецию с средний . Определить отношение существует между каждым из следующий: Дано: MARI — воздушный змей с диагонали и выполните следующее: F. Поиск практического применения концепции и навыки в повседневной жизни Деятельность 5. ТРИАДА Пусть учащиеся выходят за пределы классе и искать по крайней мере три объекта или структуры с трапециевидной формы. Пусть докажут это с помощью измерения его стороны и углы. Много разных видов декоративные/лекарственные растения найден в Тагайтае из-за его хороший климат. Рестораны, как Сад Сони популярен благодаря свежие и органические блюда, учитывая этот горшок со свежими цветами. Найдите ХР. Дано: JKLM — воздушный змей с и Докажите: ∠К ∠М Это то, что и . Посредством ________ Имущество ≌ . Это означает, что ΔJKL ≌ ΔJML на ________ Итак, ∠K ≌∠M на ________. . G. Обобщение и реферат об уроке Теорема о среднем отрезке Медиана трапеции равна параллельно каждому основанию и его То, что нужно запомнить: 1. Углы при основании равнобедренного трапеции равны. То, что нужно запомнить 1. Диагонали воздушного змея являются ⊥.
длина равна половине суммы длины оснований. 2. Диагонали равнобедренного трапеции 3. Медиана трапеции равна параллельно основанию и его длина равна половине суммы длины оснований. 4. Медиана трапеции делит пополам каждую из диагоналей. 2. Ровно одна пара напротив ∠s есть ≌. 3. Ровно одна диагональ воздушный змей делит пару пополам напротив ∠s. H. Оценка обучения Викторина Викторина Викторина I. Дополнительные действия для подачи заявки и восстановление Исследование, доказывающее трапеции. Изучите доказательство в два столбца. Принесите все материалы для задачи на завтра. V. ЗАМЕЧАНИЯ VI.ОТРАЖЕНИЕ A. Количество учащихся, заработавших 80% Б. Нет. учащихся, набравших менее 80% ( требует ремонта) C. Количество учащихся, которые догнали урок D. Количество учащихся, которые продолжают требовать исправление E. Какая из моих стратегий обучения работает хорошо? Почему? F. С какими трудностями я столкнулся, какие мой директор/руководитель может мне помочь решать? G.

Решение задач по теме «Средняя линия трапеции»