Импульс. Закон сохранения импульса — Электронный учебник по законам сохранения

Задача 1

Вдоль оси Ох движется тело массой m=1 кг со скоростью V0= 2 м/с. Вдоль направления движения действует сила F = 4 Н в течение некоторого времени t = 2 с. Определите скорость тела после окончания действия этой силы.

Для решения этой задачи в первую очередь важно вспомнить о том, что такое импульс, импульс тела .

 

 

Рис. 1. Выбор системы отсчета

 

 

 

 

Вспоминая, что импульс силы – это изменение импульса тела, запишем следующее выражение: .

Теперь уравнение согласуем с выбранной системой отсчета. Сила F при проекции на ось Х будет с положительным знаком, а значит:

.

Затем, преобразовав это уравнение, выделив из него ту скорость, которую нужно определить, запишем следующее выражение: .

Ответ: 10 м/с.

Задача 2

Тележка с человеком на ней движется вдоль прямой со скоростью 2 м/с. Человек спрыгивает с тележки в горизонтальном направлении, противоположном направлению движения тележки, со скоростью 1 м/с. Определите скорость тележки после того, как с нее спрыгнул человек. Масса человека в 1,5 раза больше, чем масса тележки.

 

 

 

Рис. 2. Проекции импульса тел на ось Х

 

 

 

 

 

В первом случае, обратите внимание, и тележка, и человек едут вместе, значит, скорость у них одинакова, мы можем записать для данной системы отсчета, связанной с осью Ох, следующее выражение: .

Затем, когда человек спрыгивает с тележки, импульс этих двух тел можно записать следующим образом: .

Знак минус показывает, что скорость человека направлена в противоположную сторону, а скорость тележки со знаком плюс будет направлена в ту же сторону, что и первоначальная скорость, т.е. вдоль оси Ох.

Записав эти выражения для начального состояния и состояния после взаимодействия, воспользуемся законом сохранения импульса.

 

По закону сохранения импульса импульс в первом случае будет равен импульсу во втором случае: Р0х = Рх..

Записав это соотношение, переписываем, раскрываем скобки выражений: (m1+m2).

V1=-m2.V2+m1.V¢1.

Скорость V¢1 и нужно определить. Выразим массу человека через массу тележки, но так, чтобы масса была выражена в одних единицах: (m1+1,5 m1).V1=-1,5m1.V2+m1.V¢1.

Массу m1 мы можем вынести за скобку и сократить:

2,5 m1.V1=-1,5 m1.V2+m1.V¢1. Когда подставляем значения для скоростей, получаем ответ: .

м Эта задача хорошо иллюстрирует реактивное движение. Человек, который спрыгнул с тележки в противоположную сторону, увеличил скорость самой тележки. Не правда ли, это хорошо сочетается с тем, как из ракеты вырываются с некоторой скоростью газы и придают дополнительную скорость оболочке, т.е. самой ракете.

Задача 3

Шарик массой m1=1 кг.

скользит по идеально гладкой поверхности со скоростью v1=4 м/с и абсолютно упруго сталкивается с таким же по размеру шариком массой m2=3 кг. Определите скорость шариков после удара?
Решение:
По закону сохранения импульса при абсолютно неупругом ударе . 

ОХ: 

Ответ: 1 м/с

 Задача 4

Мячик массой 70 г. падает на пол под углом 600 к нормали и под таким же углом отскакивает без потери скорости. Определите импульс суммарной силы, действовавшей на мячик во время удара, если его скорость равна 30

м/с.
Решение:
Покажем на рисунке изменения скорости мячика в процессе удара: 
Запишем 2-й закон Ньютона 
По построению определяем, что . Величина импульса суммарной силы, действовавшей на мячик во время удара, равна 
Ответ: 

 

Задача 5

Мальчик массой 40 кг, стоя на коньках кидает камень массой 1 кг со скоростью 8 м/с. под углом 600 к горизонту. Определите скорость, с которой мальчик начнет двигаться по льду в результате броска?


Решение:
На систему мальчик — камень не действуют ни  какие горизонтальный силы. В инерциальной системе отчета, связанной с землей, проекция суммарного импульса системы на горизонтальную ось должны оставаться неизменной:

Скорость мальчика после броска 
Ответ: 0.1 м/с

 

Задача 6

Два мальчика массами 40 кг. и 50 кг. неподвижно стоят на горизонтальной поверхности на роликовых коньках и держатся за концы невесомой веревки. Затем первый из них начинает тянуть веревку со скоростью 0.09 м/с. С какой скоростью относительно земли будет двигаться второй мальчик?


Решение:
Обозначим скорости, с которыми мальчики будут относительно земли, через и  , тогда их в проекции на ось ОХ:

Внешние силы, действующие в системе мальчик — веревка, уравновешивают друг друга, поэтому выполняется закон сохранения импульса:
В проекции на ось ОХ:
Скорость второго мальчика относительно земли 
Ответ: 0. 04 м/с

 

Задача 7

Снаряд в верхней точке своей траектории разорвался на два осколка с массами m1=3 кг  и m2=5 кг. Скорость снаряда непосредственно перед разрывом равнялась v0=600 м/с, скорость большего осколка сразу после разрыва равнялась

v2=800 м/с, а направление ее совпало с направлением движения снаряда перед разрывом. Определите скорость малого осколка сразу после разрыва.


Решение:
Выберем за положительное направление скорости снаряда v0 и запишем закон сохранения импульса.




Значит, и меньший осколок летел в том же направлении.
Ответ: 

Решение задач по теме «Закон сохранения импульса» (разработка урока)

Библиографическое описание:

Бахтина, И. В. Решение задач по теме «Закон сохранения импульса» (разработка урока) / И. В. Бахтина. — Текст : непосредственный // Молодой ученый. — 2019. — № 48 (286). — С. 125-128. — URL: https://moluch.ru/archive/286/64672/ (дата обращения: 27.04.2023).



Тема урока: Решение задач по теме «Закон сохранения импульса»

Цели: в ходе урока обучить ребят поэтапному решению задач по теме «Закон сохранения импульса» с использованием плана и отработать умение пользоваться им при решении задач различного уровня сложности, в том числе и нестандартных.

Развивать умение мыслить логически, выражать неизвестную физическую величину из полученной формулы, совершенствовать счетные навыки ребят.

Оборудование:авторская презентация «Решение задач по теме «Закон сохранения импульса», сборник задач (автор Л. А. Кирик)

Ход урока:

  1. Оргмомент.
  2. Фронтальный опрос, проверка усвоения основных понятий предыдущего урока:

— Дайте определение импульса тела, укажите, как он обозначается;

— Назовите единицу импульса в СИ;

— Из двух шаров различной массы, имеющих одинаковые скорости, больший импульс будет у шара ……

— Из двух шаров равной массы, движущихся с различными скоростями, больший импульс имеет…

— Укажите, проекция какого из шаров будет положительной, отрицательной и равной нулю. Поясните свой ответ;

— Дайте определение замкнутой системы тел;

— Сформулируйте закон сохранения импульса, запишите формулу;

— Рыбак сидит в лодке, покоящейся на поверхности воды. Что произойдёт с лодкой, если он начнёт переходить с носа лодки на корму?

— Две тележки равной массы движутся навстречу друг другу с равными по модулю скоростями. Чему равен импульс системы тел?

3. Сообщение темы урока. Изложение нового материала.

Ребята, сегодня на уроке мы познакомимся с особенностями решения расчетных задач по теме «Закон сохранения импульса», но, самое главное, научимся преодолевать сложности, которые могут возникнуть у вас в процессе работы над задачей. Как показывает многолетняя практика, основная проблема возникает из-за того, что отсутствует универсальная формула, которая будто «по мановению волшебной палочки» сразу могла бы вас привести к правильному решению задачи! В каждом конкретном случае формулы будут различными, и именно для того, чтобы вам было проще, я хочу предложить воспользоваться планом.

Поверьте, с его использованием решение задач превращается в настоящее удовольствие! Это совсем не сложно, ведь его НЕ нужно заучивать, им просто нужно руководствоваться (учащиеся записывают план в тетрадь).

План решения задач на закон сохранения импульса

1) Сделать рисунок, на котором обозначить направления: оси координат, векторов скорости тел до и после взаимодействия;

2) Глядя на рисунок, записать в векторном виде закон сохранения импульса;

3) Записать закон сохранения импульса в проекции на ось координат;

4) Из полученного уравнения выразить неизвестную величину и найти её значение.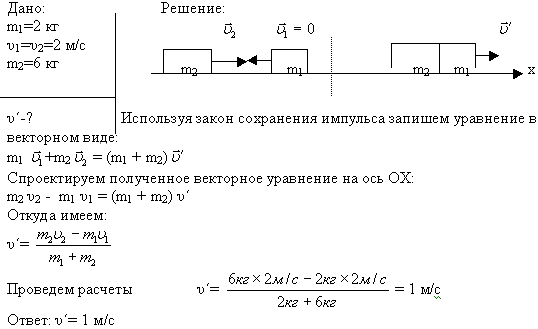

Особенно хочу обратить ваше внимание на важность рисунка!

Именно рисунок— ваш основной помощник для того, чтобы правильно записать формулу закона сохранения импульса для конкретной задачи, которую вы решаете в данный момент, он же поможет вам правильно расставить знаки проекций импульсов тел на ось координат, допустив минимум ошибок!

4.Знакомство с решением задачи по плану (работа с презентацией):

5. Решение обучающимися задач у доски с подробными комментариями.

Дети выходят по очереди к доске и с опорой на предложенный план, записанный у каждого в тетради, решают предложенные учителем задачи.

−Вагон массой 20 т, движущийся со скоростью 0,3 м/с, нагоняет вагон массой 30 т, движущийся со скоростью 0,2 м/с. Какова скорость вагонов после того, как сработает сцепка?

−Какую скорость приобретёт лежащее на льду чугунное ядро, если пуля, летящая горизонтально со скоростью 500 м/с, отскочит от него и будет двигаться в противоположном направлении со скоростью 400 м/с? Масса пули 10 г, масса ядра 25 кг.

−Человек, массой 80 кг переходит с носа на корму в покоящейся лодке длиной s = 5 м. Какова масса лодки, если она за время этого перехода переместилась в стоячей воде на L = 2 м? Сопротивление воды не учитывать.

(В случае возникновения каких-либо сложностей при решении задачи, можно в любой момент обратиться к нужному слайду презентации, и, без сомнения, настроенная анимация позволит акцентировать внимание обучающихся именно на тех местах, которые чаще всего вызывают затруднения у учеников).

6. Самостоятельное решение задачи в тетради с последующей проверкой.

−Два человека массой 60 кг и 90 кг стоят на носу и на корме в лодке, покоящейся на поверхности озера. Они решают поменяться местами. На какое расстояние сместится при этом лодка, если ее длина 5м, а масса 150 кг?

7. Домашнее задание.

1. Начинающий ковбой, накинув лассо на бегущего быка, от рывка полетел вперёд со скоростью 5 м/с, а скорость быка уменьшилась с 9 м/с до 8 м/с. Какова масса быка, если масса ковбоя 70 кг?

8. Подведение итогов урока.

Литература:

  1. Л. А. Кирик Самостоятельные и контрольные работы по физике 9 класс. Москва, Илекса, 2005.
  2. Презентация «Решение задач по теме «Закон сохранения импульса»» [Электронный ресурс]: Персональный сайт учителя физики Бахтиной Ирины Владимировны. URL:https://bakhtinairina.ucoz.ru/load/prezentacii_9_klass/reshenie_zadach_po_teme_quot_zakon_sokhranenija_impulsa_quot/13–1–0–12 (дата обращения: 29. 11.2019).

Основные термины (генерируются автоматически): сохранение импульса, решение задач, ось координат, больший импульс, вагон массой, равная масса, решение задачи, скорость.

Сохранение импульса

На каждое действие есть противодействие, равное по величине и противоположное по направлению (третий закон Ньютона). Предположим, у нас есть два объекта O1 (масса m1) и O2 (масса m2), которые движутся навстречу друг другу по прямой на гладкой поверхности без трения, затем они сталкиваются. Если F12 (действие) — это сила, действующая со стороны О1 на О2, а F21 (реакция) — это сила, действующая со стороны О2 на О1, то согласно третьему закону Ньютона запишем
         F12 = — F21 (действие и противодействие равны по модулю и в противоположном направлении, F12 и F21 — векторы)
         F12 = m1 a1 ; a1 ускорение объекта O1 и определяется как (Δv / Δt)
         F21 = m2 a2 ; a2 ускорение объекта O2 и определяется как (Δv / Δt)
Подставить для получения
        m1 (Δv / Δt) O1 = — m2 (Δv / Δt) O2
м1 (Δv) O1 = м2 ( Δv) O1
Пусть v1i (начальная) и v1f (конечная) — скорости O1 до и после столкновения соответственно, а v2i (начальная) и v2f (конечная) — скорости O2 до и после столкновения соответственно.
        m1 (v1f — v1i) = — m2 (v2f — v2i)
, что также может быть записано как

m1 v1i + m2 v2i = m1 v1f + m2 v2f

Импульс ДО взаимодействия = импульс ПОСЛЕ взаимодействия

Вышеизложенное показывает, что, когда на систему не действуют никакие внешние силы, импульсы до и после взаимодействия равны, и, следовательно, имеет место сохранение импульса.

Пример 1


Мальчик массой 35 кг прыгает (из состояния покоя) в движущуюся тележку массой 70 кг, уже движущуюся со скоростью 5 м/с вправо. Какова скорость тележки после того, как в нее запрыгнул мальчик?

Решение примера 1
У нас есть два предмета: мальчик и тележка. Взаимодействие
— это когда мальчик запрыгивает на тележку.
Пусть v1i и v2i — скорости мальчика и тележки перед прыжком мальчика (начальные скорости)
     v1i = 0 и v2i = 5 м/с
Момент Pi системы мальчик-тележка перед прыжком
     pi = момент мальчика + момент тележки = 35 0 + 70 5 = 350 кг м/с
Пусть v скорость тележки (с мальчиком в ней) , импульс тележки равен
     p = (35 + 70) v
Сохранение импульса
     350 = (35 + 70) v
     v = 350 / 105 = 3,3 м/с вправо.

Пример 2

Мальчик массой 35 кг, бегущий вправо со скоростью 2 м/с, запрыгивает в состоянии покоя на тележку массой 70 кг. Какова скорость тележки и мальчика после того, как мальчик запрыгнул в нее?

Решение примера 2
Система из двух предметов: мальчик и тележка, взаимодействие происходит, когда мальчик запрыгивает на тележку.
Пусть v1i и v2i — скорости мальчика и тележки перед прыжком мальчика в
     v1i = 2 и v2i = 0
Момент Pi системы мальчик-тележка перед прыжком
     pi = момент мальчика + момент тележки = 35 2 + 70 0 = 70 кг м/с
Пусть v скорость тележки (с мальчиком в ней), импульс тележки равен
     p = (35 + 70) v
Импульсы равны до и после взаимодействия: сохранение импульсов
     70 = (35 + 70) v
     v = 70 / 105 = 0,7 м/с вправо.

Пример 3


Пистолет массой 5 ​​кг стреляет пулей массой 15 грамм со скоростью 1000 м/с вправо. Какова скорость отдачи орудия?

Решение примера 3
Будем считать движение вправо положительным.
Система из двух объектов: пули и пистолета
Взаимодействие происходит при выстреле пули.
Начальные скорости: Пусть v1i и v2i будут скоростями ружья и пули перед выстрелом.
     v1i = 0 и v2i = 0
Момент Pi системы (ружья и пули) перед выстрелом из ружья равен
     pi = момент ружья + момент пули = 5 0 + 0,015 0 = 0
Конечные скорости: Пусть v1f будет скорость пушки и v2f скорость пули (конечные скорости), импульс после выстрела равен
     p = 5 v1f + 0,015 1000
Импульсы равны до и после взаимодействия: сохранение импульсов
     0 = 5 v1f + 15
     v1f = — 15 / 5 = — 3 м/с влево (знак минус).

Дополнительные ссылки
1 — Физика высшего уровня — Диплом IB — Крис Хэмпер — Пирсон
2 — Физика — Рэймонд А. Серуэй и Джерри С. Фон
Холт, Рейнхарт и Уинстон — Harcourt Education Company

сообщить об этом объявление

Сохранение импульса — физика для старших классов

Все ресурсы по физике для старших классов

6 Диагностические тесты 233 практических теста Вопрос дня Карточки Учитесь по концепции

Справка по физике для старших классов » Движение и механика » Импульс » Сохранение импульса

Мяч брошен на запад и сталкивается с мячом в воздухе. Если шары слиплись при столкновении и упали прямо на землю, какова была скорость второго шара?

 

Возможные ответы:

восток

восток

запад

восток

вниз 900 25

Правильный ответ:

восточный

Пояснение:

Мы знаем, что если шары после столкновения упали прямо вниз, то суммарный импульс в горизонтальном направлении равен нулю. Единственное движение происходит из-за гравитации, а не из-за любого оставшегося горизонтального импульса. Исходя из закона сохранения импульса, начальное и конечное значения импульса должны быть равны. Если конечный горизонтальный импульс равен нулю, то начальный горизонтальный импульс также должен быть равен нулю.

 

В нашей ситуации конечный импульс будет равен нулю.

 

Используйте заданные значения массы каждого шара и начальной скорости первого шара, чтобы найти начальную скорость второго.

 

Знак минус говорит нам, что второй мяч движется в направлении, противоположном первому, то есть он должен двигаться на восток.

Сообщить об ошибке

Два мяча одинаковой массы (зеленый и желтый) падают с одинаковой высоты и отскакивают от пола. Желтый мяч отскакивает на более высокую позицию. Какой шар испытывает больший по величине импульс при ударе о пол?

Возможные ответы:

Желтый шар

Оба шара подверглись импульсу одинаковой величины

Зеленый шар

Невозможно сказать, так как в задаче не указан временной интервал и сила

Правильный ответ:

Желтый шар

Пояснение:

Импульс равен изменению импульса. Изменение импульса равно произведению массы на изменение скорости.

 

Желтый мяч отскакивает выше и, следовательно, имеет более высокую скорость после отскока. Поскольку он имеет более высокую скорость после столкновения, общее изменение импульса больше. Следовательно, поскольку изменение импульса больше, импульс выше.

 

Сообщить об ошибке

 Мяч, движущийся со скоростью, ударяет по неподвижному мячу. После столкновения мяч движется со скоростью . Какова скорость второго шара?

Возможные ответы:

Правильный ответ:

Пояснение:

Это пример упругого столкновения. Мы начинаем с двух масс и заканчиваем двумя массами без потери энергии.

 

Мы можем использовать закон сохранения импульса, чтобы приравнять начальный и конечный члены.

 

 

Подставьте данные значения и найдите .

900 25

 

 

Сообщить об ошибке

Объект перемещается вправо на . Он сталкивается лоб в лоб с объектом, движущимся влево на скорости . Какое утверждение является верным?

Возможные ответы:

Суммарный импульс до столкновения и после столкновения

Суммарный импульс до и после столкновения равен нулю.

Суммарный импульс до и после столкновения равен 

Ничего из вышеперечисленного неверно

Правильный ответ:

Суммарный импульс до и после столкновения равен нулю.

Пояснение:

Общий импульс до столкновения равен импульсу каждого объекта, сложенному вместе.

 

 

 

Помните, что движение влево означает, что объект имеет отрицательную скорость

 

9002 5

 

Полный импульс =

Согласно закону сохранения импульса, общий импульс в конце должен быть равен общему импульсу в начале.