Задача про рукопожатия: Математика. Рукопожатия. Логические задачи, головоломки, тесты на интеллект, логические игры

Дискретная математика, комбинаторика, теория чисел

Сообщения без ответов | Активные темы | Избранное

Правила форума

В этом разделе нельзя создавать новые темы.

Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».

Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.

Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.

Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.

boriska	Задача про рукопожатия. 29.06.2015, 01:37
11/08/13 128	Есть задача: Каждый из людей ,когда-либо живших на Земле, сделал определенное число рукопожатий. Докажите, что число людей, сделавших нечетное количество рукопожатий, четно! Скажите, сойдет ли такое ее решение? Если число людей, сделавших нечетное количество рукопожатий, нечетно, тогда общее для всех этих людей количество рукопожатий нечетно — а это невозможно, потому что в рукопожатии всегда принимают участие 2 человека. Пришли к противоречию, соответственно число людей, сделавших нечетное количество рукопожатий, четно!

ИСН	Re: Задача про рукопожатия. 29.06.2015, 01:48
Заслуженный участник 18/05/06 13406 с Территории	Ну в общем, Вы всё правильно понимаете, но когда излагаете, то слова выходят не те. Что такое «общее для всех этих людей количество рукопожатий»? Предположим, «все эти люди» — это один я, и я сделал 1315 рукопожатий. Может такое быть? Да отчего же нет?

boriska	Re: Задача про рукопожатия. 29.06.2015, 02:32
11/08/13 128	Спасибо! Не может быть, потому как количество рукопожатий не более , где — это количество людей. — 29.06.2015, 02:44 — А так, будет правильно? Назовем всех тех, кто делает нечетное количество рукопожатий утками. Тех, что делает четное количество рукопожатий — чайками. А всех людей назовем птицами. Если уток нечетное количество, то все утки сделали нечетное количество рукопожатий, что невозможно, потому как число рукопожатий, сделанных птицами четно (потому как каждому засчитывается дважды), число рукопожатий, сделанных всеми чайками четно, потому как каждая делала четное количество рукопожатий. Получаем противоречие.

ИСН	Re: Задача про рукопожатия. 29.06. 2015, 02:47
Заслуженный участник 18/05/06 13406 с Территории	boriska в сообщении #1031991 писал(а): Не может быть, потому как количество рукопожатий не более , где — это количество людей. Да почему же нет? Вот я родился. Сделал одно рукопожатие. Сделал другое. Сделал третье. Сделал четвёртое. Сделал пятое… И так постепенно сделал 1315. Почему нет? Это не больше, чем , где — это количество людей. Количество людей — семь миллиардов. Дальше не читал.

boriska	Re: Задача про рукопожатия. 29.06.2015, 02:58
11/08/13 128	в рукопожатии ровно 2 человека участвуют и каждому оно засчитывается. Потому 1 человека быть не может, не с кем пожимать руки

ИСН	Re: Задача про рукопожатия. 29.06.2015, 09:06
Заслуженный участник 18/05/06 13406 с Территории	Так я не один. Нас семь миллиардов, говорю же. Я ведь не сам себе пожимал руки.

TOTAL	Re: Задача про рукопожатия. 29.06.2015, 12:47
Заслуженный участник 23/08/07 5176 Нов-ск	(Оффтоп) boriska в сообщении #1031987 писал(а): Есть задача: Каждый из людей ,когда-либо живших на Земле, сделал определенное число рукопожатий. Докажите, что число людей, сделавших нечетное количество рукопожатий, четно! Засчитываются ли рукопожантия с домашними животными? За сколько рукопожатий засчитывается рукопожание с человеком без сознания?

Евгений Машеров	Re: Задача про рукопожатия. 29.06.2015, 23:36
Заслуженный участник 11/03/08 8654 Москва	(Оффтоп) Засчитываются ли рукопожатия с нерукопожатными?

boriska	Re: Задача про рукопожатия. 30.06.2015, 13:38
11/08/13 128	Все эти люди — это все-таки 1 Вы или 7 миллиардов? (Оффтоп) Поглумиться тут любят, как я заметил

ИСН	Re: Задача про рукопожатия. 30.06.2015, 13:46
Заслуженный участник 18/05/06 13406 с Территории	Я читаю Ваши сообщения и использую упоминавшиеся в них понятия; если от длительного повторения понятия куда-то убежали, то можно и повторить. Вы там выделяли общность людей, сделавших нечетное количество рукопожатий. Вот они и есть «все эти люди». Но совершают ли они эти рукопожатия исключительно внутри своего подмножества? Да нет же.

Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию

Страница 1 из 1

[ Сообщений: 10 ]

Модераторы: Модераторы Математики, Супермодераторы

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей

Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения

Найти:

Основы комбинаторики — что это, определение и ответ

Решение комбинаторных задач заключаются в нахождении различных комбинаций элементов какого-либо множества. Отсюда и название раздела математики – комбинаторика.

От количества задействованных элементов множества и способов их комбинирования зависит подход к решению задачи. Каждый из типов задач имеет свои специальные формулы для расчета комбинаций, но пока для понимания сути расположения элементов множества проще всего использовать различные визуализации.

ЗАДАЧИ ПЕРВОГО ТИПА:

Пример №1:

Турист собирается посетить за лето три города – Москву, Санкт-Петербург и Казань. Сколько существует вариантов поездок, если каждый город турист посетит один раз?

1. У нас есть множество, состоящее из трёх городов. Обозначим их как М, С и К. Задачи такого типа отличаются тем, что мы должны комбинировать все элементы множества между собой без повторений.

2. Подумаем, какие варианты поездок существуют. Обозначим три ситуации, где первым город является один из городов:

3. Если города не могут повторяться, тогда после М возможно поехать только в С или К, после С только в М или К, а после К только в М или С. Дополним схему:

4. Если турист уже посетил города в порядке \(M \Rightarrow C\), то ему остается посетить только К. Если он проехал путь \(M \Rightarrow K,\) ему остается посетить только С. Аналогично проанализируем каждый маршрут и заполним схему до конца:

5. В итоге у нас получились следующие комбинации посещения городов: МСК, МКС, СМК, СКМ, КМС, КСМ. Итого 6 различных маршрутов.

Ответ: 6.

ЗАДАЧИ ВТОРОГО ТИПА:

Пример №2:

При встрече 7 приятелей пожали друг другу руки. При этом каждый пожал руку с каждым. Сколько всего было рукопожатий?

1. Обычно друг другу жмут руки именно два человека, поэтому будет рассматривать всевозможные пары друзей. Этот тип задач отличается от первого тем, что в наших комбинациях будут участвовать не все 7 элементов множества друзей сразу, а только по два из них. То есть обозначим каждого друга цифрой от 1 до 7 и будем комбинировать из этих чисел пары, они будут являться подмножеством множества друзей.

2. При этом пары, содержащие одинаковые элементы, неважно в каком порядке, считаются одинаковыми. Это значит, что рукопожатия друзей, например, 2 и 7 равно рукопожатию друзей 7 и 2. Будем брать именно ту пару, которая начинается на меньшую цифру. В данном случае рукопожатие именно этих людей запишем как 27.

3. Аналогично примеру №1 будем анализировать друзей по одному. Выпишем, какому количеству человек может пожать руку первый приятель:

12, 13, 14, 15, 16, 17 – 6 раз пожмёт кому-либо руку первый друг.

Сам себе он пожать руку не может, поэтому получилось 7 – 1 = 6 рукопожатий

4. Второй друг пожмёт руку друзьям такими комбинациями:

23, 24, 25, 26, 27 – 5 раз.

Он не пожмет руку сам себе и первому другу, т.к. их рукопожатие мы уже посчитали. Аналогично рукопожатия каждого следующего приятеля будет уменьшаться на 1:

34, 35, 36, 37 – 4 раза пожал руку третий приятель;

45, 46, 47 – 3 раза четвёртый;

56, 57 – 2 раза пятый;

67 – и 1 раз шестой.

5. Посчитаем, сколько раз происходило рукопожатие каких-либо друзей. Получим

\(6 + 5 + 4 + 3 + 2 + 1 = 21\)

Ответ: 21.

ЗАДАЧИ ТРЕТЬЕГО ТИПА:

Есть лампочки четырех цветов – синего (с), красного (к), зеленого (з) и жёлтого (ж). Сколько существует комбинаций их включения? Вариант, когда все выключены тоже является одной из комбинаций.

1. Здесь нам снова неважен порядок включения лампочек, важно сколько и какие именно могут гореть одновременно. Будем рассматривать варианты включения разного количества лампочек.

2. Существует только один вариант, что лампочки выключены. Если лампочки включены по одной, то это может быть 4 варианта: с, к, ж или з:

3. Если горят две лампочки, то существует 6 таких комбинаций. Подобрать их можно так же, как мы находили пары в примере №2. Аналогично найдем уже тройки горящих лампочек, таких вариантов будет 4. И существует один вариант, когда горят все лампочки.

Горят ноль лампочек:	—	1 вариант
Горит одна лампочка:	с к з ж	4 варианта
Горят две лампочки:	ск сз сж кз кж зж	6 вариантов
Горят три лампочки:	скз скж кзж зжс	4 варианта
Горят четыре лампочки:	скзж	1 вариант

4. Таким образом существует 16 различных вариантов одновременного включения лампочек, включая вариант, когда горят все лампочки и не горит не одной.

То есть мы нашли все возможные варианты подмножеств множества лампочек, включая пустое множество и само множество лампочек.

Рукопожатий

Возраст от 11 до 14 лет

Уровень сложности

Студент из замка Мирнс сделал полезная связь с другой проблемой, опубликованной в этом месяц:

Это похоже на определение количества строк в Mystic Rose.

Допустим, есть n человек. Первый человек пожимает руку другие n-1 человек.
Затем второй человек пожимает руку другому n-2 люди.
И так далее, пока (n-1)-й человек не пожмет руку n-му человек.

Таким образом, количество рукопожатий равно (n-1) + (n-2)… + 3 + 2 + 1, что равно (n-1)(n)/2.

Другой способ рассмотрения состоит в том, что каждый человек имеет в общей сложности n-1 рукопожатий, и есть n человек, поэтому будет (n-1)(n) рукопожатия, но это включает каждое рукопожатие дважды (1 и 2, 2 и 1) поэтому деление на 2 дает правильный ответ.

Асваат из Garden International Школа в Куала-Лумпуре, Малайзия, упомянула, что метод решение этой проблемы, связанной с метод, которым пользовался Гаусс, когда он был еще молодой студент.

Джо из начальной школы Хоув Парк тоже заметил связи с другой работой:

Если встретились, например, 10 математиков, то первый сделает 9 рукопожатий, второй делает 8, третий делает 7 и так далее, пока десятый находит, что он уже со всеми поздоровался и так больше не делает.

Это дает 9+8+7+6+5+4+3+2+1+0 рукопожатий, а это 45.

Но посмотрите на последовательность… это 9-й треугольник число.
(см. рисунок Треугольные числа и/или Умный Карл)

Формула для T-го треугольного числа: T(T+1)/2
В задаче о рукопожатии, если есть n человек, то число рукопожатий эквивалентно (n-1)-му треугольному числу.

Подставляя T = n-1 в формулу для треугольных чисел, мы можем вывести формулу для количества рукопожатий между n человек:

Количество рукопожатий = (n-1)(n)/2

Джейми из Garden International Школа согласилась и использовала это понимание, чтобы исправить ошибку Сэма.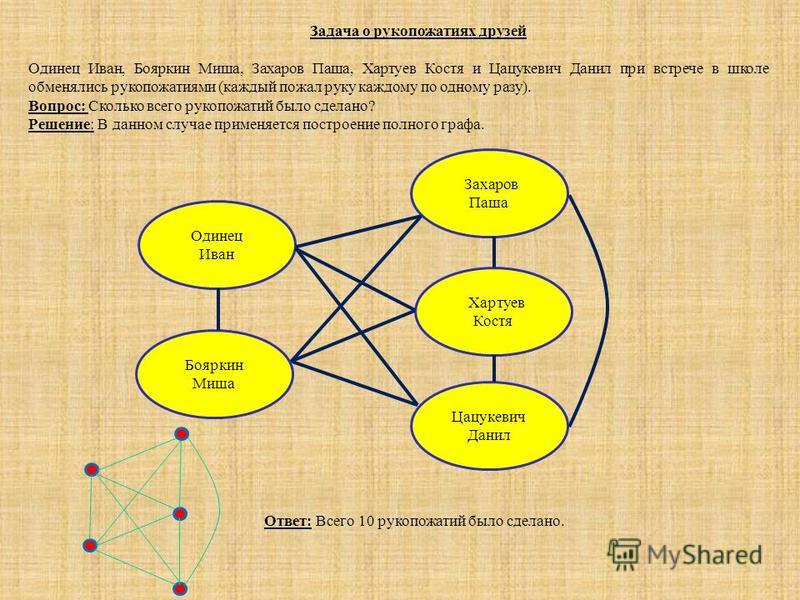 рассуждение:

Метод Сэма неверен, потому что он не разделил ответ на 2. Если вы не разделите его на 2, вы будете считать количество рукопожатия между парами математиков дважды.

Если встречаются 20 математиков:
20 x 19 = 380
380 / 2 = 190 (общее количество рукопожатий)

Если встречается 161 математик:
161 x 160 = 25760

всего 257602 / 8 рукопожатий

Может ли быть ровно 4851 рукопожатие на собрании, где все пожимают друг другу руки?

Мы знаем, что 4851 рукопожатие — это между 20 математиками и 160 математики. Итак, начнем с проверки 100 математики.
Общее количество рукопожатий = 100 x 99 / 2 = 4950

Это слишком много, так что теперь я попробую 99 математиков.
Общее количество рукопожатий = 99 x 98 / 2 = 4851
Следовательно, может быть ровно 4851 рукопожатие, когда 99 встречаются математики.

Может ли быть ровно 6214 рукопожатий на собрании, где все пожимают друг другу руки?

Начнем с проверки 112 математиков.
Общее количество рукопожатий = 112 x 111/ 2 = 6216

Это слишком много, так что теперь я попробую 111 математиков.
Общее количество рукопожатий = 111 x 110 / 2 = 6105
Это слишком мало, поэтому не может быть ровно 6214 рукопожатий.

Джозеф из Bradon Forest School и Табита из школы Норвуд использовала аналогичные рассуждения:

. Рассуждения Сэма неверны, потому что вы должны учитывать только уникальные состоявшиеся рукопожатия. Он должен изменить свой метод, деление на 2. В каждом рукопожатии участвуют 2 математика, поэтому только половина рукопожатий Сэма уникальны. 92 -99 = 97024$

Так что да, если 99$ математиков встретятся, то будет 4851$ рукопожатия

$6214$ рукопожатия?
Нет, ближайшее треугольное число $6216$, а $6214$ не является треугольное число

$3655$ рукопожатия?
Да, $86$ Математики

$7626$ рукопожатий?
Да, $124$ Математики

$8656$ рукопожатия?
Нет, ближайшее треугольное число $8646$, а $8656$ не является номер треугольника.

Мы получили еще много правильных решений, в том числе очень четкие от Сиддхартхи и Тасуку из Международной школы сада в Куала Лумпур, Бен из школы Бедминстер Даун, Абхинав из Бангкокской школы Патана и Люк из Maidstone Grammar Школа. Молодцы и спасибо вам всем.

Количество рукопожатий на вечеринке — Задача 1

Формула для количества рукопожатий, возможных на вечеринке с n людьми:

# рукопожатий = n*(n — 1)/2.

Это связано с тем, что каждый из n человек может пожать руку n — 1 человеку (они не пожали бы себе руку), а рукопожатие между двумя людьми не считается дважды.

Эту формулу можно использовать для любого количества людей. Например, в группе из 10 человек найдите возможное количество рукопожатий.

# рукопожатий = 10*(10 — 1)/2. # рукопожатий = 10*(9)/2. # рукопожатий = 90/2. # рукопожатий = 45

Итак, 10 человек могут совершить 45 рукопожатий.

математическое моделирование нелинейные функции диагонали

Допустим, вы пригласили 10 человек на вечеринку, сколько возможных рукопожатий будет? И снова я буду считать рукопожатие, как если бы два человека встречались друг с другом, это было бы одно рукопожатие. Что мы собираемся сделать, так это использовать математическое моделирование, что означает, что вы как бы используете изображение для описания проблемы.

Итак, допустим, у вас есть два человека, математическая модель которых будет просто отрезком линии, и вы скажете, что возможное количество рукопожатий здесь равно одному.

Итак, наша цель — вычислить количество рукопожатий для n человек, так что давайте рассмотрим еще пару примеров. Допустим, у вас есть три человека, математическая модель будет 1, 2, 3 человека и будет три рукопожатия, поэтому три человека три рукопожатия. У вас есть четыре человека, у вас будет четыре точки, которые представляют людей на этой вечеринке, и у вас будет четыре рукопожатия, но у вас также будет еще два.

Итак, у нас есть один, три, всего шесть. Итак, я заметил, что у нас здесь нет линейной функции, мы сделаем последнюю. Если у вас на вечеринке пять человек, у вас будет пять человек, а затем у вас будет еще пять рукопожатий, всего 10. да ладно, это треугольные числа, поэтому я знаю формулу, или вы могли бы сказать, хорошо, глядя на мою модель, как я могу придумать количество рукопожатий. Ну, количество людей, которое мы собираемся сказать, равно n, и если у меня есть один человек. сколько раз я мог пожать друг другу руки. Здесь я мог пожать руку один раз, что на один меньше, чем два. Здесь я мог встряхнуть два раза, что на один меньше, чем три. Здесь я мог встряхнуть один, два, три раза. Итак, я вижу, что количество рукопожатий на единицу меньше, чем общее количество людей, потому что я могу пожать руку всем присутствующим, кроме себя.

Как и в случае с диагональной задачей, мы будем считать каждое из этих рукопожатий. Так что мне придется разделить весь этот термин на 2.