X y 0 x 2y 2: Mathway | Популярные задачи

2

Экстремум функции нескольких переменных онлайн

Примеры решенийНайти производную Определитель матрицы Ранг матрицы Умножение матрицМетод Гаусса Точки разрыва функции Найти интегралДиф уравнения онлайнМетод множителей Лагранжа

Назначение сервиса. Онлайн-калькулятор используется для нахождения в онлайн режиме наибольшего и наименьшего значения функции двух переменных (см. пример). Решение оформляется в формате Word.

• Решение онлайн
• Видеоинструкция
• Оформление Word

Правила ввода функций:

Для функции трех переменных можно использовать матрицу Гессе. Функция z = f(x,y) имеет максимум в точке M₀ (x₀;y₀), если f(x₀;y₀) > f(x;y) для всех точек (x;y), достаточно близких к точке (x₀;y₀) и отличных от неё. Функция z = f(x,y) имеет минимум в точке M₀(x₀;y₀), если f(x₀;y₀) 0;y₀) и отличных от неё. Максимум и минимум функции называются экстремумами функции.
Исследование функции двух переменных на экстремум проводят по следующей схеме.
1. Находят частные производные dz/dx и dz/dy.
2. Решают систему уравнений:
и таким образом находят критические точки функции.

3. Находят частные производные второго порядка:
4. Вычисляют значения этих частных производных второго порядка в каждой из найденных в п.2 критических точках M(x₀;y₀).
5. Делаю вывод о наличии экстремумов:
а) если AC – B² > 0 и A < 0 , то в точке M имеется максимум;
б) если AC – B² > 0 и A > 0 , то в точке M имеется минимум;
в) если AC – B² < 0, то экстремума нет;
г) если AC – B² = 0, то вопрос о наличии экстремума остается открытым;

Пример №1.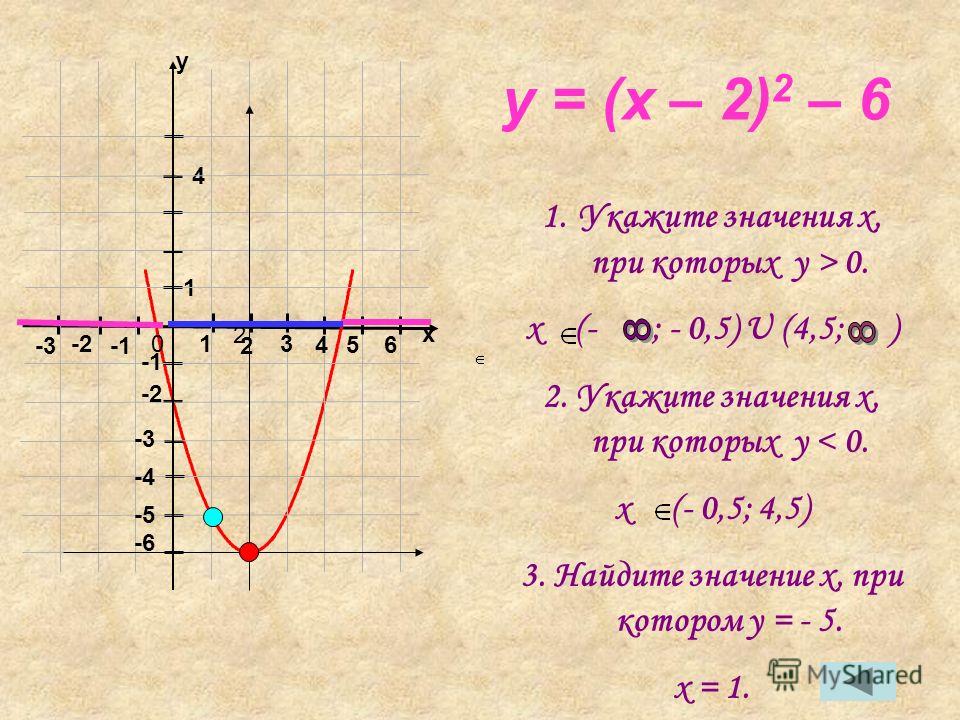

Найти экстремумы функции f(x,y)=x³+xy²+x²+y² и определить по критерию Сильвестра их тип.
Решение.
1. Найдем первые частные производные.


2. Решим систему уравнений.
3x²+2x+y²=0
2xy+2y=0
Получим:
а) Из первого уравнения выражаем x и подставляем во второе уравнение:
x = -1
y²+1=0
Данная система уравнений не имеет решения.
б) Из первого уравнения выражаем y и подставляем во второе уравнение:


или


или
Откуда x₁ = -2/3; x₂ = 0; x₃ = -2/3; x₄ = 0
Данные значения x подставляем в выражение для y. Получаем: y₁ = 0; y₂ = 0; y₃ = 0; y₄ = 0
Количество критических точек равно 2: M₁(-2/3;0), M₂(0;0)
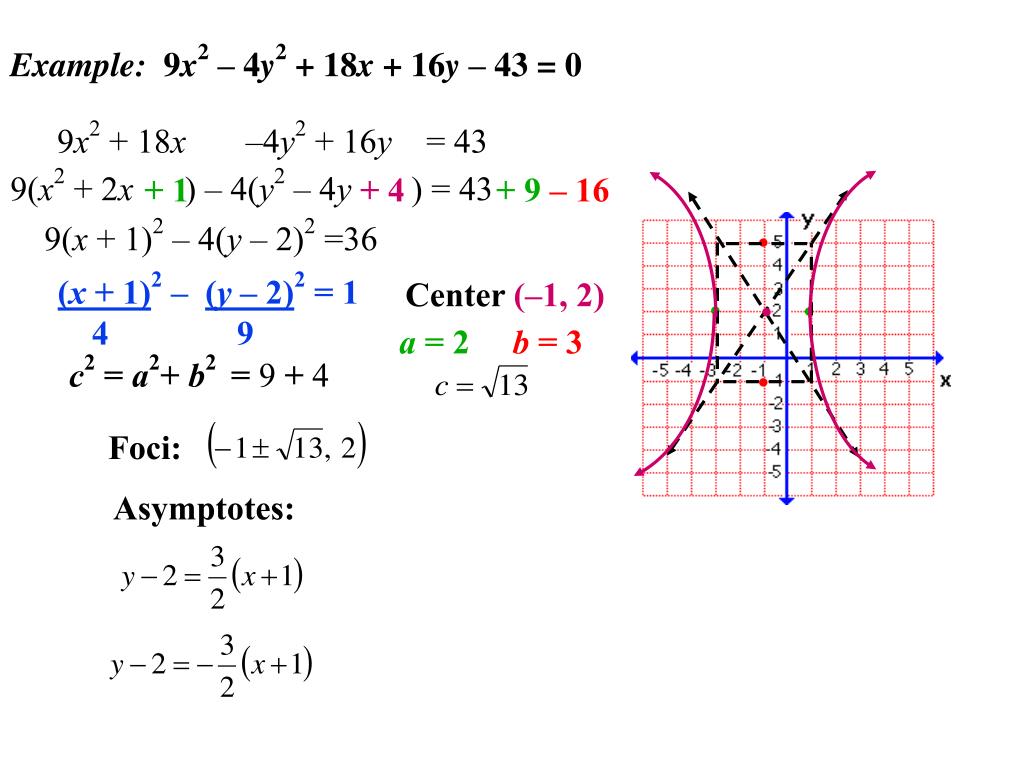
3.