Найдите расстояние от оси цилиндра до секущей плоскости. ГДЗ, задача 530, Геометрия, 10-11 класс, Атанасян Л.С. – Рамблер/класс
Найдите расстояние от оси цилиндра до секущей плоскости. ГДЗ, задача 530, Геометрия, 10-11 класс, Атанасян Л.С. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Высота цилиндра равна 12 см, а радиус основания равен 10 см.
Лучший ответ
приветик
еще ответы
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Юмор
Олимпиады
ЕГЭ
Компьютерные игры
похожие вопросы 5
Докажите, что треугольники подобны. Вопросы и задачи 64, Геометрия, 10-11 класс, Атанасян Л.С.
Привет. Запуталась при решении, нужна помощь знатоков!!!
Три прямые, проходящие через одну точку и не лежащие в одной (Подробнее…)
ГДЗГеометрия11 класс10 классАтанасян Л.С.
Самостоятельная работа 19. Вариант 2. № 2 ГДЗ Геометрия 9 класс Зив Б.Г. Помогите доказать, используя параллельный перенос
№ 2 ГДЗ Геометрия 9 класс Зив Б.Г. Помогите доказать, используя параллельный перенос
Используя параллельный перенос, докажите, что углы при основании равнобедренной трапеции равны между собой.
ГДЗЭкзаменыГеометрия9 классЗив Б. Г.
Почему сейчас школьники такие агрессивные ?
Новости10 классБезопасность
Какой был проходной балл в вузы в 2017 году?
Какой был средний балл ЕГЭ поступивших в российские вузы на бюджет в этом году? (Подробнее…)
Поступление11 классЕГЭНовости
11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.
11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос., шь (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
«Делай добро, бросай его в воду.
 ..»: 26. Цилиндр
..»: 26. Цилиндр 26. Цилиндр
и вписать ответы в таблицу ниже
26.1. Задание. В цилиндрический сосуд налили 2000
воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в см. куб.
26.2. Задание. В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 2 раза больше первого? Ответ выразите в см.
26.3. Задание Объем первого цилиндра равен 12 м3. У второго цилиндра высота в три раза больше, а радиус основания — в два раза меньше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах.
26.4. Задание Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на пи.
26.5. Задание В цилиндрический сосуд налили 6 куб. см воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в 1,5 раза. Найдите объём детали. Ответ выразите в куб. см.
26.6. Задание Одна цилиндрическая кружка в полтора раза выше второй, зато вторая вдвое шире. Найдите отношение объема первой кружки к объему второй.
26.7. Задание. Высота цилиндра равна 12 см, а радиус основания равен 10 см. Цилиндр пересечен плоскостью, параллельной его оси, так, что в сечении получился квадрат. Найдите расстояние от оси цилиндра до секущей плоскости.
26.8. Задание. Сколько понадобится краски, чтобы покрасить снаружи бак цилиндрической формы с диаметром основания 1, 5 м и высотой 3 м, если на один кв.
***********************
Вписать ответы
******************************************************
Конус. Выполнить задания
1.
Задание . Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
2. Задание . Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 3 раза?
3. Задание
4. Задание. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 3 раза?
5. Задание. Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшится в 1,5 раза, а образующая останется прежней?
Главная страница
Подписаться на: Сообщения (Atom)
Математическая задача: Поверхность цилиндра, объем
Площадь основания и площадь оболочки относятся как 3:5. Его высота на 5 см меньше радиуса основания. Вычислите площадь поверхности и объем.
Его высота на 5 см меньше радиуса основания. Вычислите площадь поверхности и объем.
Правильный ответ:
S = 10367,26 см 2V = 70685,83 см 3
= 5S3π2 S22
5 rhπr2=53 2ч =53 5r=6h h=r−5 h=25 см r=30 см S=2πr2+2πrh=2π⋅30⋅(30+25)=10367,26 см2
V=πr2h=π302⋅25=70685,83 см3
Нашли ошибку или неточность? Не стесняйтесь
пишите нам. Спасибо!
Советы по использованию связанных онлайн-калькуляторов
Воспользуйтесь нашим калькулятором коэффициентов.
Совет: конвертер единиц объема поможет вам преобразовать единицы объема.
Для решения этой математической задачи вам необходимо знать следующие знания:
- объемная геометрия
- цилиндр
- площадь поверхности
- планиметрия
- окружность
- основные функции
- отношение
Единицы физических величин:
Класс задачи:
- средняя школа
Мы рекомендуем вам посмотреть этот обучающий видеоролик по этой математической задаче: video1
- Расчет 81405
Нарисуйте сетку цилиндра, у которого отношение радиуса основания к высоте равно 2 : 3. Вычислите объем и поверхность цилиндра, если его высота 9см (эскиз, расчет, ответ).
Вычислите объем и поверхность цилиндра, если его высота 9см (эскиз, расчет, ответ). - Осевой разрез
Осевой разрез цилиндра имеет диагональ 40 см. Размер раковины и поверхность основания находятся в соотношении 3:2. Вычислите объем и площадь поверхности этого цилиндра. - Ролик
Корпус цилиндра имеет ту же площадь, что и одно из его оснований. Высота цилиндра 23 дм. Чему равен радиус основания цилиндра? - Оболочка цилиндра
Рассчитайте площадь оболочки цилиндра высотой 1,6 м с радиусом основания 0,4 м. - Площадь поверхности цилиндра
Объем цилиндра, высота которого равна радиусу основания, составляет 678,5 дм³. Вычислите площадь его поверхности. - Вращающийся 28501
Какие пакеты в форме оболочки вращающегося конуса могут вместить больше всего попкорна? Первый мешок имеет высоту 20 см, а длина его стороны 24 см. Второй мешок имеет радиус основания 10 см и высоту 25 см. - Рассчитать 24011
Имеется цилиндр с радиусом основания 3 см и высотой 12 см. Рассчитать а) поверхность цилиндра б) объем цилиндра
Рассчитать а) поверхность цилиндра б) объем цилиндра - Вычислить 24941
Вычислить поверхность и объем цилиндра с радиусом основания 5 см и высотой 8 см. - Цилиндр
Во вращающемся цилиндре дано: поверхность оболочки (без оснований) S = 96 см² и объем V = 192 см куб. Вычислите радиус и высоту этого цилиндра. - Треугольный 6610
Оболочка вращающегося цилиндра в четыре раза больше содержимого его основания. Определить объем правильной треугольной призмы, вписанной в цилиндр. Радиус дна цилиндра равен 10 см. - Объем конуса
Рассчитайте объем конуса, если площадь его основания равна 78,5 см², а площадь оболочки 219,8 см². - Круглый 4690
Коническая оболочка с радиусом основания 20 см и высотой 50 см разворачивается в круглый вырез. Насколько велик центральный угол этого выреза? - Площадь боковой поверхности
Отношение площади основания вращающегося конуса к площади его боковой поверхности равно 3:5. Вычислите поверхность и объем конуса, если его высота v = 4 см.
- Поверхность
Поверхность цилиндра 1570 см²; его высота 15 см. Найдите объем и радиус основания. - Параметры 28521
Основные параметры вращающегося конуса: радиус основания 5 см, высота конуса 12 см и сторона конуса 13 см. Рассчитайте: a/объем конуса b/поверхность конуса - Рассчитайте 20893
Объем цилиндра 193 см³, а радиус его основания 6,4 см. Вычислите высоту и поверхность цилиндра с точностью до 1 знака после запятой. - Треугольная призма
Рассчитайте площадь поверхности и объем трехсторонней призмы с основанием в виде прямоугольного треугольника, если его стороны равны а=3см, b=4см, с=5см и высота призмы v =12см.
- все задачи по математике17100
- алгебра 4945
- арифметика 3560
- базовые функции 5290
- комбинаторика 900 6 073939 геометрия гониометрия и тригонометрия 505
Площадь поверхности a Цилиндр
Площадь поверхности цилиндра можно определить как общее пространство, занимаемое плоскими поверхностями оснований цилиндра и его криволинейной поверхностью.
Площадь поверхности цилиндра имеет различные практические применения, такие как расчет количества материала, необходимого для изготовления цилиндрического контейнера, определение площади поверхности труб, используемых в сантехнике, и т. д. Давайте узнаем больше о том, что такое площадь поверхности цилиндра и как рассчитать общую площадь поверхности и площадь боковой поверхности цилиндра.
| 1. | Что такое площадь поверхности цилиндра? |
| 2. | Площадь поверхности цилиндра Формула |
| 3. | Общая площадь поверхности цилиндра (TSA) |
| 4. | Изогнутая поверхность цилиндра (CSA) |
| 5. | Различия между TSA и CSA цилиндра |
| 6. | Как рассчитать SA цилиндра? |
7. | Часто задаваемые вопросы о площади поверхности цилиндра |
Что такое площадь поверхности цилиндра?
Площадь поверхности цилиндра относится к общей площади, которую покрывают криволинейная поверхность цилиндра и круглые основания. Общая площадь поверхности цилиндра включает площадь двух оснований цилиндра (каждое из которых имеет форму круга) и площадь криволинейной поверхности. Площадь поверхности выражается в квадратных единицах, таких как квадратные сантиметры, квадратные дюймы, квадратные футы и так далее. Цилиндр — это трехмерный твердый объект, состоящий из двух круглых оснований, соединенных изогнутой гранью. Обратите внимание на приведенный ниже рисунок, на котором показаны различные части цилиндра, используемые для определения площади поверхности цилиндра.
Площадь поверхности цилиндра Формула
Формула площади поверхности цилиндра используется для нахождения площади, занимаемой основаниями цилиндра и криволинейной поверхностью цилиндра.
- TSA цилиндра = 2πr 2 + 2πrh (или) 2πr (r + h)
- CSA цилиндра = 2πrh
Вы заметили что-то общее в обеих формулах? Да, это 2πrh. Поскольку TSA = CSA + 2 (площадь двух кругов), мы имеем TSA = 2πrh + 2 (πr
Общая площадь поверхности цилиндра (TSA)
Общая площадь поверхности цилиндра (TSA цилиндра) получается путем сложения площади двух оснований и площади криволинейной поверхности. Рассмотрим цилиндр, основание которого имеет радиус «r» и высоту цилиндра «h». Таким образом, формула для полной площади поверхности цилиндра имеет следующий вид:
Общая площадь поверхности цилиндра = площадь двух оснований + площадь криволинейной поверхности.
- Мы знаем, что площадь каждого основания (круга) равна πr 2 .
- Но как найти площадь криволинейной поверхности? Для этого проведем небольшой эксперимент. Возьмите жестяную банку из-под кока-колы и вырежьте ее верхнюю и нижнюю (мы вырезаем, так как просто находим «изогнутую» поверхность) грани. Затем разрежьте оставшуюся цилиндрическую часть по вертикали (по высоте) и откройте ее. Мы видим, что цилиндрическая форма превратилась в прямоугольник. Нам нужно найти его длину и ширину. Его ширина — это не что иное, как высота цилиндра «h», а его длина — это длина окружности основания, равная 2πr (чтобы заметить это, просто закройте прямоугольник обратно к цилиндру). Тогда площадь прямоугольника есть не что иное, как площадь криволинейной поверхности, которая равна длине × ширине = 2πr × h = 2πrh. Таким образом, площадь криволинейной поверхности цилиндра = 2πrh.
Таким образом, общая площадь поверхности цилиндра (TSA) = πr 2 + πr 2 + 2πrh = 2πr 2 + 2πrh = 2πr (r + h).
Пример: Найдите общую площадь поверхности (TSA) цилиндра радиусом 5 см и высотой 8 см.
Решение: Полную площадь поверхности (TSA) цилиндра можно рассчитать по формуле TSA = 2πr(r + h).
Подставляя значения r = 5, h = 8, получаем:
TSA = 2πr(r + h) = 2πr(r + h) = 2 × 3,14 × 5(5 + 8) = 408,41 см 2
Более подробный и геометрический вывод TSA цилиндра приведен ниже.
TSA of Cylinder Formula
Площадь любой формы – это занимаемое ею пространство. Цилиндр имеет 2 плоские поверхности, которые представляют собой круги, и изогнутую поверхность, которая открывается в виде прямоугольника. Рассмотрим приведенный ниже цилиндр, высота которого равна «h», а радиус — «r». Давайте откроем цилиндр в 2-мерной форме и поймем это.
Обратите внимание на приведенный выше рисунок, на котором площадь изогнутой поверхности раскрывается в виде прямоугольника, а два основания представляют собой круги.
- Теперь площадь двух кругов равна (πr 2 + πr 2 ), радиус основания которых равен r.
- В прямоугольнике одна сторона равна высоте цилиндра h , а длина этого прямоугольника равна длине окружности, то есть 2πr.
- Таким образом, площадь этого прямоугольника (l × b) равна 2πr × h = 2πrh, что также является площадью криволинейной поверхности цилиндра.
- Следовательно, общая площадь поверхности цилиндра = 2πr 2 + 2πrh = 2πr(r + h)
Изогнутая поверхность цилиндра (CSA)
Площадь криволинейной поверхности (CSA) цилиндра — это площадь поверхности, покрытая только его криволинейной поверхностью. Если радиус основания цилиндра равен «r», а высота цилиндра равна «h», площадь криволинейной поверхности цилиндра рассчитывается по следующей формуле:
CSA of Cylinder Formula
Криволинейная поверхность цилиндра (или) CSA цилиндра = 2πrh
где,
- r = радиус цилиндра
- h = высота цилиндра
- π = 22/7 или 3,14
Формула поперечного сечения цилиндра уже была получена в предыдущем разделе.
Пример: Найдите площадь криволинейной поверхности цилиндра радиусом 7 см и высотой 14 см.
Решение: Площадь криволинейной поверхности цилиндра можно рассчитать по формуле CSA = 2πrh.
Подставляя значения r = 7, h = 14, получаем: CSA = 2πrh = 2 × 3,14 × 7 × 14 = 615,8 см 2 .
Различия между TSA и CSA цилиндра
Основное различие между общей площадью поверхности (TSA) и площадью криволинейной поверхности (CSA) цилиндра заключается в том, что TSA представляет собой сумму площадей всех поверхностей цилиндра, включая два круглых основания и криволинейную поверхность. , а CSA — это только площадь криволинейной поверхности. В следующей таблице лучше всего представлены различия между TSA и CSA цилиндра.
| Недвижимость | АСП цилиндра | CSA цилиндра |
|---|---|---|
| Определение | Сумма площадей всех поверхностей цилиндра, включая два круглых основания и изогнутую поверхность.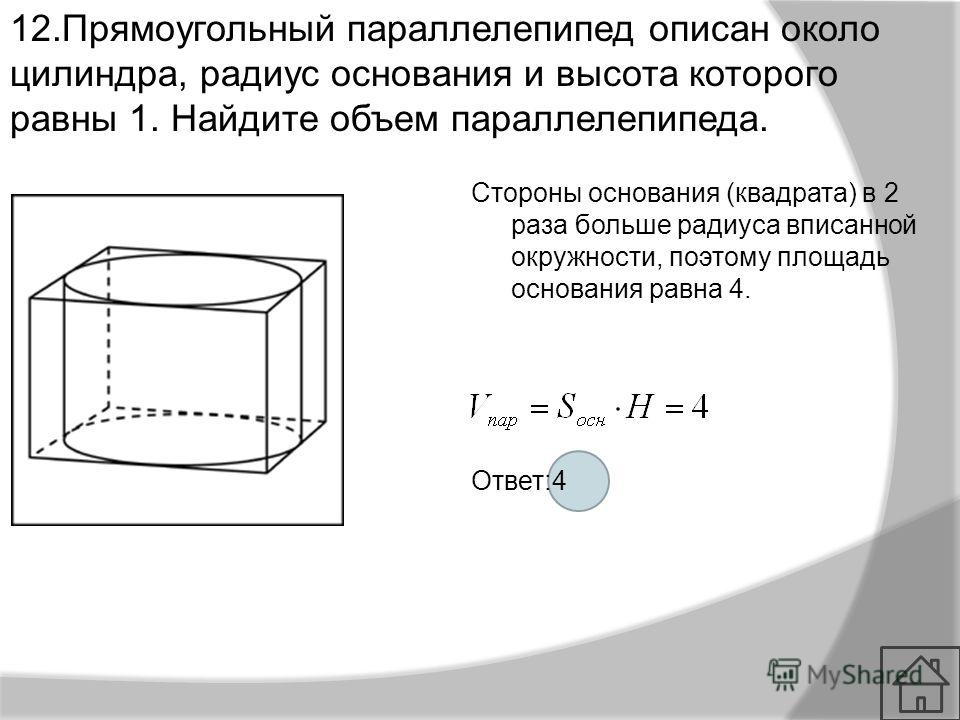 | Площадь криволинейной поверхности цилиндра, исключая площади двух круглых оснований. |
| Формула | 2πr (г + ч) | 2πrh |
| Применение | TSA используется для определения количества материала, необходимого для изготовления цилиндрического контейнера. | CSA используется для определения количества упаковочной бумаги, необходимой для упаковки цилиндрического подарка. |
| Отношения | TSA включает CSA (и два круглых основания). | CSA является частью TSA. Следовательно, CSA меньше, чем TSA. |
| Пример | Если r = 6 и h = 11, то общая площадь поверхности равна 2π(6)(6+11) = 640,88 квадратных единиц. | Если r = 6 и h = 11, то площадь криволинейной поверхности составляет 2π(6)(11) = 414,69 квадратных единиц. |
Как рассчитать SA цилиндра?
Площадь поверхности цилиндра равна площади, занимаемой основаниями цилиндра и криволинейной поверхностью цилиндра. Используя приведенные ниже шаги, давайте найдем общую площадь поверхности цилиндра, имеющего радиус 7 единиц и высоту 9единицы измерения.
Используя приведенные ниже шаги, давайте найдем общую площадь поверхности цилиндра, имеющего радиус 7 единиц и высоту 9единицы измерения.
- Шаг 1: Обратите внимание на радиус ‘r’ и высоту ‘h’ цилиндра. Убедитесь, что оба имеют одинаковые единицы измерения. Здесь r = 7, h = 9
- Шаг 2: В данном вопросе нам нужно найти общую площадь поверхности цилиндра, поэтому мы будем использовать формулу для полной площади поверхности цилиндра, общая площадь поверхности = 2πr(r + h)
- Шаг 3: Подставьте данные значения и дайте ответ в квадратных единицах. Подставляя значения в формулу, получаем общую площадь поверхности = 2πr(r + h) = 2π × 7(7 + 9) = 2π × 112 = 2 × 3,14 × 112 = 703,6 квадратных единиц.
☛ Связанные статьи
- Объем цилиндра
- Правый круговой цилиндр
- Разница между площадью и площадью поверхности
- Калькулятор площади цилиндра
Cuemath — одна из ведущих мировых обучающих платформ по математике, предлагающая онлайн-уроки по математике в прямом эфире один на один для классов K-12. Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах. Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.
Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах. Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.
Примеры площади поверхности цилиндра
Пример 1: Радиус цилиндра 5 дюймов, а высота цилиндра 15 дюймов. Найдите площадь цилиндра. (Возьмите значение пи как 3.14)
Решение:
Радиус, r = 5 в
Высота цилиндра, h = 15 в
Площадь поверхности цилиндра: A = 2πr(r+h )
= 2π × 5 × (5 + 15)
= 2π × 5 × 20
= 2 × 3,14 × 5 × 20
= 628
Ответ: Площадь поверхности цилиндра составляет 628 квадратных дюймов.
Пример 2: Самуэль имеет цилиндр со стороной TSA 1728π квадратных единиц. Найдите высоту цилиндра, если радиус основания окружности равен 24 единицам.

Решение:
Общая площадь поверхности цилиндра, A = 1728π; радиус (r) = 24; ч = ?
Подставим данные значения в формулу, чтобы найти высоту цилиндра.
A = 2πr(r + h)
1728π = 2π × 24 × (24 + h)
⇒ 1728/48 = (24 + h)
⇒ 36 = (24 + h)
⇒ h 12
Ответ: Высота цилиндра 12 единиц.
Пример 3: Укажите истинное или ложное значение.
а) Общая площадь поверхности цилиндра получается путем сложения площади двух оснований и площади криволинейной поверхности.
b.) Общая площадь поверхности цилиндра рассчитывается по формуле Общая площадь поверхности = 2πrh
Решение:
а.) Верно, TSA цилиндра получается путем сложения площади двух оснований и площади CSA.
b.) Неверно, общая площадь поверхности цилиндра рассчитывается по формуле Общая площадь поверхности = 2πr(r + h).
Ответ: (a) Верно (b) Ложно
перейти к слайдуперейти к слайдуперейти к слайду
Как ваш ребенок может освоить математические понятия?
Мастерство в математике приходит с практикой и пониманием «почему» за «что». Испытайте разницу Cuemath.
Испытайте разницу Cuemath.
Записаться на бесплатный пробный урок
Практические вопросы по площади поверхности цилиндра
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о площади поверхности цилиндра
Что такое площадь поверхности цилиндра?
Площадь поверхности цилиндра определяется как общая площадь или область, покрытая поверхностью формы. Поскольку цилиндр имеет 2 плоские поверхности и 1 изогнутую поверхность, общая площадь поверхности включает площадь плоских поверхностей и площадь криволинейной поверхности. Площадь поверхности цилиндра выражается в квадратных единицах, например, м 2 , дюймы 2 , см 2 , ярды 2 и т. д.
Как найти площадь поверхности цилиндра?
Площадь поверхности цилиндра можно найти, используя следующие шаги:
- Шаг 1: Запишите радиус основания ‘r’ и высоту ‘h’ цилиндра.
 Убедитесь, что единицы измерения совпадают.
Убедитесь, что единицы измерения совпадают. - Шаг 2: Примените соответствующую формулу, чтобы найти площадь поверхности цилиндра, заданную как
- Площадь изогнутой поверхности цилиндра = 2πrh
- Общая площадь поверхности цилиндра = 2πr(h + r)
- Шаг 3: Подставьте данные значения и выразите ответ в квадратных единицах.
Как найти площадь поверхности цилиндра с открытым верхом?
Площадь поверхности цилиндра с открытым верхом можно рассчитать, найдя площадь одного основания и криволинейной поверхности. Таким образом, площадь цилиндра без верха можно выразить как площадь поверхности цилиндра с открытым верхом = πr 2 + 2πrh = πr(r + 2h), где r — радиус, а h — высота цилиндра. Следует отметить, что мы взяли площадь одного основания, потому что у цилиндра нет вершины.
Какова общая площадь поверхности цилиндра Формула?
Формула для расчета общей площади поверхности цилиндра выражается следующим образом: общая площадь поверхности цилиндра = 2πr(r + h). Эта общая площадь поверхности включает площадь двух оснований (2πr 2 ) и площадь изогнутой поверхности (2πrh). Здесь «r» — радиус, а «h» — высота цилиндра.
Эта общая площадь поверхности включает площадь двух оснований (2πr 2 ) и площадь изогнутой поверхности (2πrh). Здесь «r» — радиус, а «h» — высота цилиндра.
☛Также проверьте:
- Формулы площади поверхности
- Формулы измерения
По какой формуле найти площадь основания цилиндра?
Основание цилиндра имеет форму круга. Следовательно, формула для нахождения площади основания цилиндра выражается как πr 2 , где r — радиус основания цилиндра. Если требуется площадь обоих оснований, то она будет, πr 2 + πr 2 = 2πr 2 .
Как найти площадь поверхности цилиндра с диаметром и высотой?
Если диаметр и высота цилиндра известны, мы можем найти площадь поверхности цилиндра, используя ту же формулу. Мы можем получить радиус цилиндра, используя диаметр, поскольку диаметр = 2 × радиус. После нахождения радиуса мы можем использовать формулу Общая площадь поверхности цилиндра = 2πr(r + h)
Как рассчитать площадь поверхности цилиндра с помощью калькулятора?
Площадь поверхности цилиндра можно легко определить с помощью «калькулятора площади поверхности цилиндра».

 Вычислите объем и поверхность цилиндра, если его высота 9см (эскиз, расчет, ответ).
Вычислите объем и поверхность цилиндра, если его высота 9см (эскиз, расчет, ответ). Рассчитать а) поверхность цилиндра б) объем цилиндра
Рассчитать а) поверхность цилиндра б) объем цилиндра

 Убедитесь, что единицы измерения совпадают.
Убедитесь, что единицы измерения совпадают.
Leave A Comment