Высота равностороннего треугольника – формула

4.7

Средняя оценка: 4.7

Всего получено оценок: 168.

4.7

Средняя оценка: 4.7

Всего получено оценок: 168.

Равносторонний треугольник определяется всего одной величиной – значением стороны. Все стороны в таком треугольнике равны между собой, а углы известны заранее и равны 60 градусам каждый, поэтому чтобы посчитать любую характеристику или величину равностороннего треугольника достаточно знать его сторону. Убедимся в этом и выведем формулу высоты равностороннего треугольника.

Что такое равносторонний треугольник?

Для начала нужно вспомнить, что такое равносторонний треугольник, определить некоторые его свойства и только тогда выводить формулу высоты.

Равносторонний треугольник – это треугольник, все стороны которого равны между собой. Все углы в таком треугольнике равны между собой (60 градусов).

Рис. 1. Правильный треугольник.

Равносторонний треугольник является равнобедренным, но основанием можно считать любую часть треугольника.

2\over4}}$$

Если в том же малом прямоугольном треугольнике обратить внимание на известный острый угол, то можно вывести значение высоты через синус угла в 60 градусов.

Синус – это отношение противолежащего катета к гипотенузе.

Воспользуемся этим отношением и выразим высоту.

$$sin(60)={h\over {a}}$$

$h=a*sin(60)={a*\sqrt{3}\over{2}}$ – как видно, получился тот же результат, что и в первом способе. Это говорит о том, что в равностороннем треугольнике только две формулы высоты, а все остальные способы доказательства можно свести к получившимся выводам.

Что мы узнали?

Мы узнали, что такое равносторонний треугольник, вывели несколько формул для нахождения высоты равностороннего треугольника. Показали несколько путей вывода формул, которые могут помочь быстро вспомнить, как находится высота или использовать те же приемы для нахождения других величин в равностороннем треугольнике.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

  • Никита Червоненко

    4/5

  • Nikita Repey

    5/5

  • Лиля Келгёкмен

    4/5

Оценка статьи

4.7

Средняя оценка: 4.7

Всего получено оценок: 168.

А какая ваша оценка?

Высота равностороннего треугольника | Треугольники

Какими свойствами обладает высота равностороннего треугольника? Как найти высоту равностороннего треугольника через его сторону, радиусы вписанной или описанной окружностей?

Теорема 1

(свойство высоты равностороннего треугольника)

В равностороннем треугольнике высота, проведённая к любой стороне, является также его медианой и биссектрисой.

Доказательство:

Пусть в треугольнике ABC AB=BC=AC.

Так как AB=BC, треугольник ABC равнобедренный с основанием AC.

Проведём высоту BF.

По свойству равнобедренного треугольника, BF является также его медианой и биссектрисой

(то есть, AF=FC, ∠ABF=∠CBF).

 

Аналогично, рассмотрев треугольник ABC как равнобедренный с основанием BC и треугольник ABC — равнобедренный с основанием AB, доказываем, что высоты AK и CD являются также его медианами и биссектрисами

(то есть, BK=KC, ∠BAK=∠CAK; AD=BD, ∠ACD=∠BCD).

Что и требовалось доказать.

Теорема 2

(свойство высот равностороннего треугольника)
Все три высоты равностороннего треугольника равны между собой.

Доказательство:

Пусть в треугольнике ABC AB=BC=AC.

AK, BF и CD — его высоты.

В прямоугольных треугольниках ABF, BCD и CAK:

гипотенузы AB, BC и CA равны по условию,

∠BAF=∠CBD=∠ACK (как углы равностороннего треугольника).

Следовательно, треугольники ABF, BCD и CAK равны (по гипотенузе и острому углу).

Из равенства треугольников следует равенство соответствующих сторон: BF=CD=AK.

Что и требовалось доказать.

Из теорем 1 и 2 следует, что в равностороннем треугольнике все высоты, медианы и биссектрисы равны между собой.

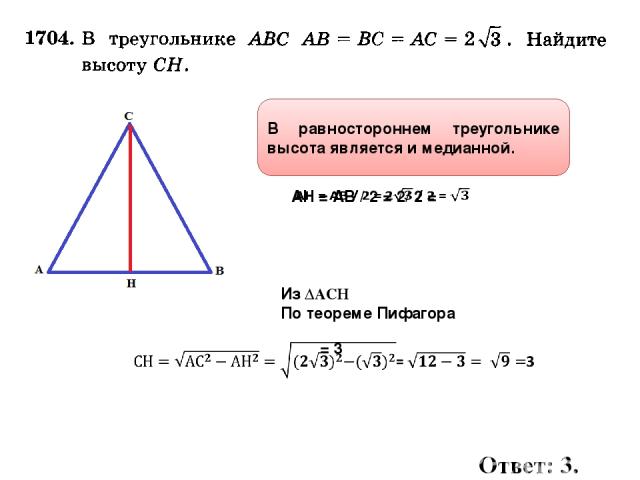
1) Найдём высоту равностороннего треугольника через его сторону.

В треугольнике ABC AB=BC=AC=a.

BF — высота, BF=h.

Рассмотрим прямоугольный треугольник ABF.

По определению синуса,

   

   

Отсюда формула высоты равностороннего треугольника через его сторону:

   

(2-й способ: из прямоугольного треугольника ABF по теореме Пифагора

   

2) Выразим высоту равностороннего треугольника через радиусы вписанной и описанной окружностей.

Точка O — центр правильного треугольника — является также центром его вписанной и описанной окружностей. Как центр вписанной окружности O — точка пересечения биссектрис треугольника. В правильном треугольнике биссектрисы и медианы совпадают. Следовательно, также является O точкой пересечения медиан.

А так как медианы треугольника в точке пересечения делятся в отношении 2 к 1, считая от вершины, то BO:OF=2:1, то есть

   

   

BO — радиус описанной окружности, OF — вписанной: BO=R, OF=r.

Следовательно, высота равностороннего треугольника равна трём радиусам вписанной окружности:

   

и в полтора раза больше радиуса описанной окружности:

   

   

   

Высота равностороннего треугольника – формула, метод, часто задаваемые вопросы

Высота равностороннего треугольника – это прямая линия, проведенная из вершины к противоположной стороне треугольника таким образом, что она делит треугольник на две равные прямоугольные части. угловые треугольники. Это также известно как высота треугольника, который начинается с вершины и является серединным перпендикуляром к противоположной стороне. Равносторонний треугольник – это треугольник, у которого все стороны имеют одинаковую длину и все углы имеют одинаковую величину. Давайте узнаем больше о высоте равностороннего треугольника в этой статье.

1. Какова высота равностороннего треугольника?
2. Формула высоты равностороннего треугольника
3. Часто задаваемые вопросы о высоте равностороннего треугольника

Какова высота равностороннего треугольника?

Высота равностороннего треугольника — это линия, проведенная из любой вершины треугольника на противоположной стороне. Эта линия является биссектрисой противоположной стороны. Это означает, что он делит противоположную сторону пополам на две равные части и образует угол 90° на нем. Высота равностороннего треугольника также известна как высота, которая делит треугольник на два конгруэнтных прямоугольных треугольника, как показано на следующем рисунке.

Определение равностороннего треугольника

Равносторонний треугольник определяется как треугольник, у которого все три стороны и углы равны. Значение каждого угла составляет 60 градусов, поэтому он также известен как равноугольный треугольник. Равносторонний треугольник считается правильным многоугольником или правильным треугольником, так как углы и стороны равны.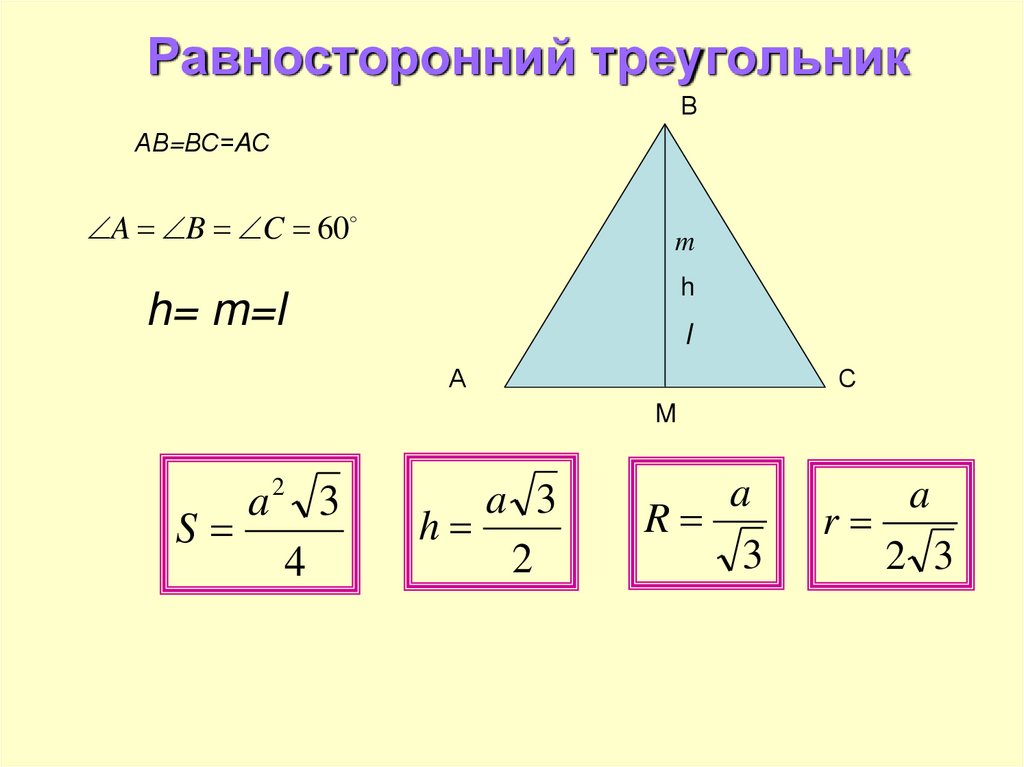

Формула высоты равностороннего треугольника

Высоту равностороннего треугольника можно вычислить по теореме Пифагора. Формула, используемая для нахождения высоты равностороннего треугольника, выглядит следующим образом:

Высота равностороннего треугольника (h) = ½(√3a) или (a√3)/2

, где «a» — сторона равностороннего треугольника. равносторонний треугольник. Это означает, что если известна длина стороны равностороннего треугольника, мы можем легко найти высоту треугольника.

Пример: Если одна сторона равностороннего треугольника равна 12 единицам, какова его высота?

Решение: Дано, длина стороны а = 12 единиц.

Воспользуемся формулой высоты равностороннего треугольника, h = (a√3)/2. Подставляя значение «а», получаем h = (12√3)/2 = 6√3 = 10,39 единиц. Следовательно, высота равностороннего треугольника равна 10,39 ед.

Формула высоты равностороннего треугольника Доказательство

Мы знаем, что высота делит равносторонний треугольник на два прямоугольных треугольника. Поэтому применим теорему Пифагора, которая гласит: Гипотенуза 2 = Основание 2 + Высота 2

Если мы посмотрим на приведенную выше цифру, каждая сторона равностороннего треугольника будет представлена ​​буквой «а», поскольку все стороны равны, поэтому основание равно также обозначается буквой «а», а высота = h. Также известно, что высота делит треугольник на два равных прямоугольных треугольника, а основание делится на две равные части. Это означает, что если мы воспользуемся теоремой Пифагора для одного из прямоугольных треугольников, это можно выразить как

а 2 = ч 2 + (а/2) 2

⇒ ч 2 = а 2 – (а 2 62) / ⇒ ч 2 = ( 3a 2 )/4

Или, h = ½(√3a)

Таким образом, формула для высоты равностороннего треугольника: h = ½(√3a), которая также может быть записана как, h = ( a√3)/2

Высота равностороннего треугольника, если известна сторона

Высоту равностороннего треугольника можно легко вычислить, если известна сторона. Поскольку все стороны равностороннего треугольника равны, и мы знаем, что высота делит треугольник на конгруэнтные прямоугольные треугольники, мы можем применить теорему Пифагора и найти высоту, как описано в разделе, данном выше. Следовательно, если дана одна сторона равностороннего треугольника, формула для нахождения высоты равностороннего треугольника будет следующей: h = ½ (√3a), где «a» представляет собой длину стороны равностороннего треугольника.

Высота равностороннего треугольника при заданной площади

Высоту равностороннего треугольника можно вычислить, зная площадь треугольника. Мы знаем, что площадь равностороннего треугольника можно рассчитать по формуле Площадь равностороннего треугольника = √3/4 × (сторона) 2 . Итак, если мы знаем площадь, мы можем подставить ее значение в эту формулу, чтобы получить длину стороны. Зная длину стороны, мы можем использовать следующую формулу, чтобы найти высоту. Высота равностороннего треугольника, h = ½(√3a).

Пример: Найдите высоту равностороннего треугольника, если его площадь равна 24 кв.

Решение: Дано, площадь равностороннего треугольника = 24 ед.

24 = √3/4 × (сторона) 2

(сторона) 2 = (24 × 4)/√3

сторона = 7,4 единицы

Теперь, когда мы знаем длину стороны, мы можно вычислить высоту равностороннего треугольника по формуле h = ½(√3a), где h — высота, а a — длина стороны. Здесь «а» = 7,4 единицы

ч = ½(√3a)

ч = ½(√3 × 7,4) = 6,4 единицы.

Высота равностороннего треугольника при заданном периметре

Высоту равностороннего треугольника можно вычислить, если известен периметр треугольника. Мы знаем, что периметр равностороннего треугольника вычисляется по формуле, периметр равностороннего треугольника = 3а. Также известно, что все стороны равностороннего треугольника равны по длине, поэтому, если известен периметр, мы можем вычислить длину стороны по этой формуле. После вычисления длины стороны можно найти высоту по формуле высота равностороннего треугольника = ½(√3a).

Пример: Найдите высоту равностороннего треугольника, если его периметр равен 21 единице.

Решение:

Дан периметр равностороннего треугольника = 21 единица

Сначала найдем длину стороны по формуле Периметр равностороннего треугольника = 3a

21 = 3a

a = 7 единиц

Теперь мы можем рассчитать высоту равностороннего треугольника по формуле h = ½(√3a), где h — высота, а a — длина стороны. Мы рассчитали длину стороны как «а» = 7 единиц

ч = ½(√3a)

ч = ½(√3 × 7) = 6,06 единиц.

Похожие темы

  • Гипотенуза
  • Площадь равностороннего треугольника

Часто задаваемые вопросы о высоте равностороннего треугольника

Какова высота равностороннего треугольника в математике?

Высота равностороннего треугольника — это прямая линия, проведенная из вершины к противоположной стороне треугольника таким образом, что она делит треугольник на два равных прямоугольных треугольника. Это также известно как высота треугольника, который начинается с вершины и является серединным перпендикуляром к противоположной стороне.

Какая формула высоты равностороннего треугольника?

Высоту равностороннего треугольника можно вычислить по теореме Пифагора. Формула, которая используется для нахождения высоты равностороннего треугольника: Высота равностороннего треугольника (h) = (a√3)/2; где «а» — сторона равностороннего треугольника. Это означает, что если известна длина стороны равностороннего треугольника, мы можем легко найти высоту треугольника.

Как найти высоту равностороннего треугольника, если дана сторона?

Высоту равностороннего треугольника можно легко вычислить, если известна его сторона. Мы знаем, что все стороны равностороннего треугольника равны, а высота делит треугольник на два конгруэнтных прямоугольных треугольника. Следовательно, мы можем применить теорему Пифагора и найти высоту. Формула для нахождения высоты равностороннего треугольника: h = (a√3)/2, где «a» представляет собой длину стороны равностороннего треугольника.

Как найти высоту равностороннего треугольника, зная площадь?

Высоту равностороннего треугольника можно вычислить, если известна площадь треугольника. Мы знаем, что площадь равностороннего треугольника можно рассчитать по формуле Площадь равностороннего треугольника = √3/4 × (сторона) 2 . Итак, если мы знаем площадь, мы можем подставить ее значение в эту формулу, чтобы получить длину стороны. Зная длину стороны, мы можем использовать следующую формулу, чтобы найти высоту. Высота равностороннего треугольника, h = ½(√3a).

Как найти высоту равностороннего треугольника, зная периметр?

Зная периметр равностороннего треугольника, мы можем легко найти его высоту. Формула, которая используется для нахождения периметра равностороннего треугольника: периметр = 3а, где «а» представляет длину стороны. Используя эту формулу, мы можем найти длину стороны после подстановки значения периметра. После того, как длина стороны вычислена, мы можем использовать формулу Высота равностороннего треугольника, h = ½ (√3a), чтобы найти высоту равностороннего треугольника.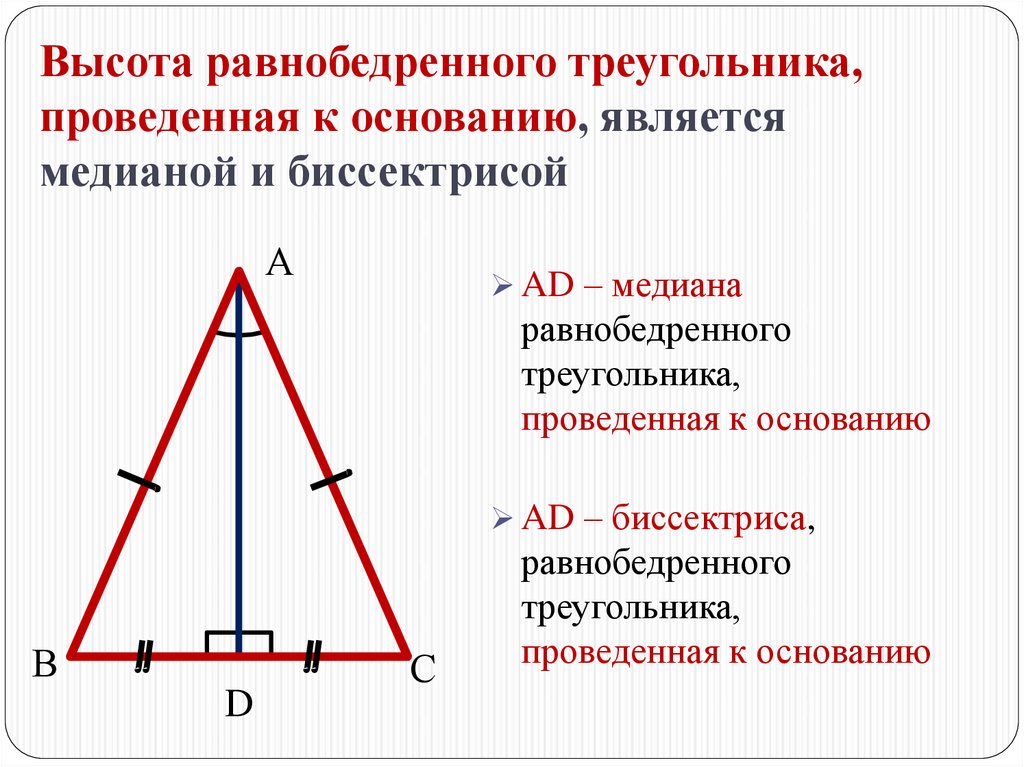

Как найти высоту равностороннего треугольника по теореме Пифагора?

Мы знаем, что высота делит равносторонний треугольник на два прямоугольных треугольника. Следовательно, мы можем использовать теорему Пифагора, чтобы найти высоту равностороннего треугольника. Теорема Пифагора гласит: Гипотенуза 2 = Основание 2 + Высота 2

Поэтому возьмем один из прямоугольных треугольников, у которого длина стороны (в данном случае гипотенуза) = a, h = высота треугольника, а а/2 — третья сторона. Используя теорему Пифагора, можно вывести формулу высоты равностороннего треугольника и выразить ее следующим образом:

а 2 = ч 2 + (а/2) 2

⇒ ч 2 = а 2 – (а 2 62) / ⇒ ч 2 = ( 3a 2 )/4

Или h = ½(√3a)

Какова высота равностороннего треугольника со стороной, равной 6 единицам?

Если длина стороны равностороннего треугольника равна 6 единицам, его высоту можно рассчитать по формуле Высота равностороннего треугольника, h = ½(√3a), где «a» представляет длину стороны. Подставляя значение «а» в формулу,

Высота равностороннего треугольника, h = ½(√3a) = ½(√3 × 6) = 3√3 = 5,19 единиц.

Как найти высоту равностороннего треугольника

Все ресурсы по геометрии среднего уровня

8 Диагностические тесты 250 практических тестов Вопрос дня Карточки Learn by Concept

Intermediate Geometry Help » Плоская геометрия » Треугольники » Равнобедренные треугольники » Как найти высоту равностороннего треугольника

ΔABC — равносторонний треугольник со стороной 12.

Найдите высоту ΔABC (с точностью до десятых) .

Возможные ответы:

10.6

9.8

10.0

10.4

10.2

2 90 Правильный ответ: 3

10,4

Пояснение:

Равнобедренные треугольники имеют стороны одинаковой длины и углы равны 60°.

Чтобы найти высоту, мы можем провести высоту к одной из сторон, чтобы разделить треугольник на два равных 30-60-90 треугольников.

Теперь сторона исходного равностороннего треугольника  (назовем его «а»)   является гипотенузой треугольника 30-60-90. Поскольку треугольник 30-60-90 — это особый треугольник, мы знаем, что его стороны равны х, х и 2х соответственно.

Таким образом, а = 2х и х = а/2.
Высота равностороннего треугольника =

Сообщить об ошибке

ΔABC — равносторонний треугольник со стороной 8.

Найти высоту (с точностью до десятых) .

Возможные ответы:

7.5

7.1

6.9

7.3

6.7

90 Правильный ответ 002 6,9

Пояснение:

Равнобедренные треугольники имеют стороны одинаковой длины, а углы равны 60°. Чтобы найти высоту, мы можем провести высоту к одной из сторон, чтобы разбить треугольник на два равных треугольника 30-60-90.

Теперь сторона исходного равностороннего треугольника (давайте назовем это «а»)  является гипотенузой треугольника 30-60-90. Поскольку треугольник 30-60-90 — это особый треугольник, мы знаем, что его стороны равны х, х и 2х соответственно.

Таким образом, а = 2х и х = а/2.
Высота равностороннего треугольника = 

Сообщить об ошибке

Какова высота равностороннего треугольника со стороной 8 дюймов?

Возможные ответы:

Правильный ответ:

Объяснение:

Равносторонний треугольник имеет три конгруэнтные стороны, а также равносторонний треугольник с тремя конгруэнтными углами, каждый из которых равен 60 градусов.

Чтобы найти высоту, мы разделим треугольник на два специальных 30 — 60 — 90 прямоугольных треугольников, проведя линию из одного угла в центр противоположной стороны.

Этот отрезок будет высотой и будет противоположен одному из углов в 60 градусов и примыкает к углу в 30 градусов. Специальный прямоугольный треугольник дает отношение сторон , и . Гипотенеза, сторона, противоположная 9Угол 0 градусов, представляет собой полную длину одной стороны треугольника и равен . Используя эту информацию, мы можем найти длины каждой стороны специального треугольника.

Сторона с длиной будет высотой (напротив угла 60 градусов). Высота в дюймах.

Сообщить об ошибке

Какова высота треугольника со сторонами 4, 4, 4?

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы решить, проще всего сначала визуализировать отношение высоты к остальным сторонам треугольника:

Высота является одной из сторон прямоугольного треугольника. Гипотенуза равна 4, а другой катет равен 2, или половина стороны основания равна 4. Чтобы определить высоту, используйте теорему Пифагора:

вычтите 4 из обеих сторон

возьмите квадратный корень из обеих сторон

Сообщить об ошибке

 

Если длина всех сторон равностороннего треугольника равна , то какой будет высота треугольника? Округлите до десятых.

 

Возможные ответы:

Правильный ответ:

Объяснение:

Следующая формула может быть использована для определения высоты равностороннего треугольника, когда нам известны длины сторон:

Сообщить об ошибке

Равносторонний треугольник, показанный ниже, имеет длину стороны . Зная эту информацию, найдите высоту треугольника.

Возможные ответы:

Правильный ответ:

Пояснение:

Чтобы найти высоту равностороннего треугольника, мы можем разделить треугольник на два прямоугольных треугольника. На изображении ниже биссектриса представляет собой высоту, и мы можем найти высоту, применив теорему Пифагора:

Сообщить об ошибке

Найдите высоту равностороннего треугольника со стороной . Округлите ответ до десятых.

Возможные ответы:

Правильный ответ:

Пояснение:

Равносторонний треугольник имеет три равные стороны, как следует из его названия. Это также означает, что в результате треугольник также является равноугольным. То есть все его внутренние углы одинаковы. Поскольку сумма внутренних углов треугольника равна , это означает, что каждый внутренний угол равен .

Высота (пунктирная линия на диаграмме) — это длина, которая делит пополам вершинный угол и основание треугольника. Проведение пунктирной линии делит равносторонний треугольник на два конгруэнтных прямоугольных треугольника.

Related Posts

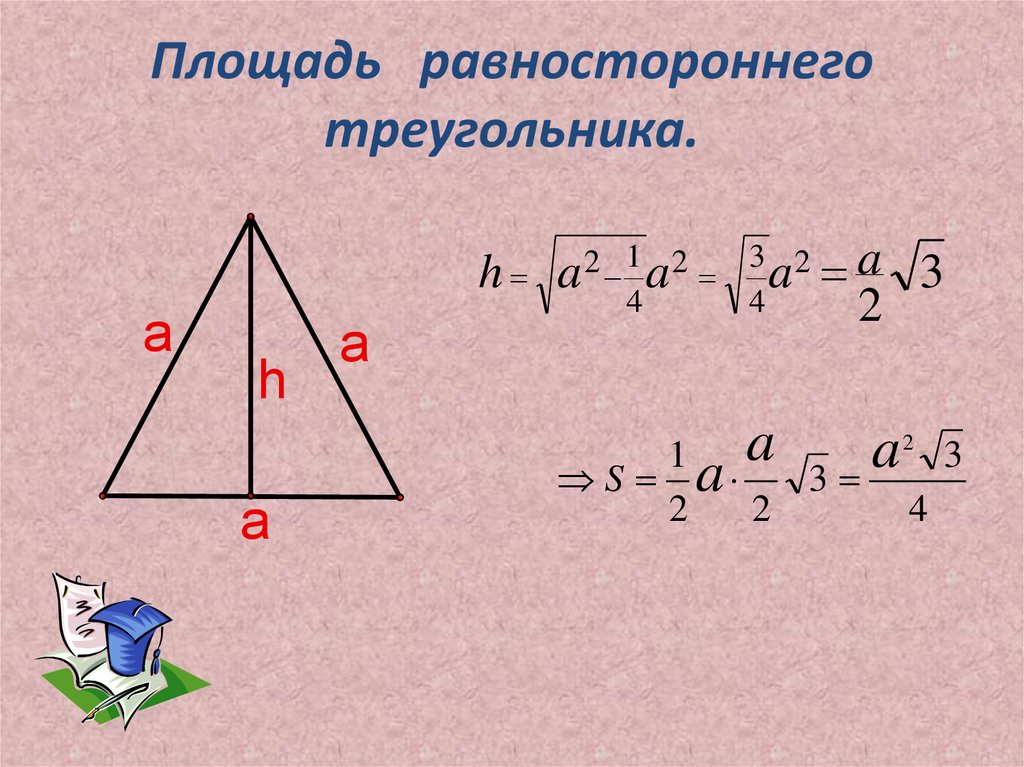
Leave A Comment